An effective neural network and fuzzy time series-based hybridized model to handle forecasting problems of two factors

Abstract

Fuzzy time series forecasting method has been applied in several domains, such as stock market price, temperature, sales, crop production and academic enrollments. In this paper, we introduce a model to deal with forecasting problems of two factors. The proposed model is designed using fuzzy time series and artificial neural network. In a fuzzy time series forecasting model, the length of intervals in the universe of discourse always affects the results of forecasting. Therefore, an artificial neural network- based technique is employed for determining the intervals of the historical time series data sets by clustering them into different groups. The historical time series data sets are then fuzzified, and the high-order fuzzy logical relationships are established among fuzzified values based on fuzzy time series method. The paper also introduces some rules for interval weighing to defuzzify the fuzzified time series data sets. From experimental results, it is observed that the proposed model exhibits higher accuracy than those of existing two-factors fuzzy time series models.

1 Introduction

Fuzzy time series forecasting method has been applied in several domains, such as stock market price, temperature, sales, crop production and academic enrollments. Application of fuzzy time series theory in forecasting problems was first introduced by Song and Chissom [28–30]. They presented the fuzzy time series model by means of fuzzy relational equations involving max–min composition operation, and applied the model to forecast the enrollments in University of Alabama. In 1996, Chen [4] used simplified arithmetic operations avoiding the complicated max–min operations, and their method produced better results. Later, many studies provided some improvements to the existing methods in terms of effective lengths of intervals, fuzzy logical relation and defuzzification techniques.

Hwang et al. in [12] used the differences of the available historical data as fuzzy time series instead of direct usage of raw numeric values. Unlike Song–Chissom and Chen approaches, Sah and Degtiarev’s proposed model [24] utilizes variations of the available historical data as fuzzy time series. Huarng tried to improve the forecasting accuracy based on the determination of effective length of intervals [10] and heuristic approaches [11]. Lee and Chou [17] forecasted the university enrollments by defining the supports of the fuzzy numbers that represent the linguistic values of the linguistic variables more appropriately.

Cheng et al. in [6] used entropy minimization to create the intervals. They also used trapezoidal membership functions in the fuzzification process. Chang [2] presented cardinality-based fuzzy time series forecasting model which builds weighted fuzzy rules according to calculating the cardinality of fuzzy relations. To obtain less number of intervals, Cheng [7] proposed a model using fuzzy clustering technique to partition the data effectively. Kai et al. [13] applied the K-means clustering algorithm to partition the universe of discourse into different groups. Singh and Borah [26] forecasted the university enrollments with the help of new proposed algorithm by dividing the universe of discourse of the historical time series data into different length of intervals.

Chen and Hwang [5] forecasted the daily average temperature of Taipei based on two-factors fuzzy time series. In this model, first factor is daily temperature, whereas the second factor is daily cloud density. They proposed two algorithms—Algorithm-B and Algorithm-B$^*$. Their experimental results show that the accuracy rate of Algorithm-B$^*$ is better than Algorithm-B. Lee et al. [20] proposed a new method to forecast the daily average temperature of Taipei and the Taiwan Futures Exchange (TAIFEX). In this model, high-order fuzzy logical relationship is constructed to increase the forecasting accuracy. Chang and Chen [3] forecasted the daily temperature using fuzzy C-means and fuzzy rules interpolation techniques. In this model, rules are constructed based on fuzzy C-means clustering algorithm. Then, this model performs fuzzy inference based on the multiple fuzzy rules interpolation scheme. Based on two-factors high-order fuzzy time series and automatic clustering techniques, Wang and Chen [32] proposed a new method to predict the daily average temperature and TAIFEX. Lee et al. [18, 19] presented a new method for temperature prediction and the TAIFEX forecasting based on two-factors high-order fuzzy logical relationships by hybridizing genetic algorithms with fuzzy time series method.

In this paper, we present a new model to deal with the forecasting problems of two factors. The proposed model is designed using fuzzy time series and artificial neural network (ANN). In this study, high-order fuzzy logical relationships are also employed to design the model. Hence, we have entitled this model as “Two-factors high-order neuro-fuzzy hybridized model.” The main purpose of designing such a hybridized model is explained next.

For fuzzification of time series data sets, the determination of length of intervals is very important. In case of most of the above discussed models [4, 11, 12, 28, 30], the lengths of the intervals were kept same. No any specific reason is mentioned for using the fixed lengths of intervals. Huarng [10] shows that effective lengths of intervals always affect the results of forecasting. Therefore, for the creation of effective length of intervals of the historical time series data sets, an ANN-based technique is adopted in this model.

Song and Chissom [28] adopted the following method to forecast enrollments of the University of Alabama:

$$\begin{aligned} Y(t)=Y(t-1)\circ R \end{aligned}$$

(1)

where $Y(t-1)$ is the fuzzified enrollment of year $(t-1),\,Y(t)$ is the forecasted enrollment of year “$t$” represented by fuzzy set, “$\circ$” is the max–min composition operator and “$R$” is the union of fuzzy relations. This method takes a lot of time to compute the union of fuzzy relations [5]. Therefore, to improve the efficiency of the proposed model, some rules for intervals weighing are proposed to defuzzify the fuzzified time series data sets. The proposed model exhibits higher accuracy than those of existing models [3, 5, 18–20, 32].

The rest of the paper is organized as follows: In Sect. 2, the basic concepts of fuzzy time series are briefly explained. Section 3 presents the application of ANN for creating intervals of historical time series data sets. In Sect. 4, new forecasting model based on hybridization of ANN with fuzzy time series is proposed. The performance of the model is assessed and presented in Sect. 5. Conclusions and directions for future work are discussed in Sect. 6.

2 Fuzzy sets and fuzzy time series-A brief overview

In $1965$, Zadeh [35] introduced the theory of fuzzy sets. According to Zadeh, “A fuzzy set is a class of objects with continuum of grades of membership. Such a set is characterized by a membership function which assigns to each object a grade of membership ranging between zero and one.” He also presented fuzzy arithmetic theory and its application [36–38]. Based on fuzzy sets theory, Song and Chissom [28–30] introduced the fuzzy time series concept. Here, we briefly reviewed some concepts of fuzzy time series from [28–30].

Definition 1

(Fuzzy Set) A fuzzy set is a class with varying degrees of membership in the set. Let $U$ be the universe of discourse, which is discrete and finite, then fuzzy set $A$ can be defined as follows:

$$\begin{aligned} A=\left\{ \mu _A(x_1)/x_1+\mu _A(x_2)/x_2+ \cdots \right\} =\Sigma _{i}\mu _A(x_i)/x_i \end{aligned}$$

(2)

where $\mu _A$ is the membership function of $A,\,\mu _A: U\, \rightarrow \left[0,1\right]$, and $\mu _A(x_i)$ is the degree of membership of the element $x_i$ in the fuzzy set $A$. Here, the symbol “+” indicates the operation of union and the symbol “/” indicates the separator rather than the commonly used summation and division in algebra, respectively.

When $U$ is continuous and infinite, then the fuzzy set $A$ of $U$ can be defined as:

$$\begin{aligned} A=\left\{ \int \mu _A(x_i)/x_i\right\} ,\forall x_i \in U \end{aligned}$$

(3)

where the integral sign stands for the union of the fuzzy singletons, $\mu _A(x_i)/x_i$.

Fuzzy time series concept was proposed in [29], and the main difference between the traditional time series and the fuzzy time series is that the values of the former are crisp numerical values while the values of the latter are fuzzy sets. The crisp numerical values can be represented by real numbers, whereas in fuzzy sets, the values of observations are represented by linguistic values. The definitions of fuzzy time series are briefly reviewed as follows:

Definition 2

(Fuzzy time series) Let $Y(t)(t=0, 1, 2, \ldots )$ be a subset of real numbers “$R$”L and the universe of discourse on which fuzzy sets $\mu _i(t)(i=1, 2, \ldots )$ are defined, and let $F(t)$ be a collection of $\mu _i(t)(i=1, 2, \ldots )$. Then, $F(t)$ is called a fuzzy time series on $Y(t)(t=0, 1, 2, \ldots )$.

From Definition 2, we can see that $F(t)$ is a function of time $t$ and $\mu _i(t)$ are the linguistic values of $F(t)$, where $\mu _i(t) (i=1, 2, \ldots )$ are represented by fuzzy sets and the values of $F(t)$ can be different at different times because the universe of discourse can be different at different times. Fuzzy time series can be divided into two categories which are the time-invariant fuzzy time series and the time-variant fuzzy time series.

If $F(t)$ is caused by $F(t-1)$, that is, $F(t-1)\rightarrow F(t)$, then this relationship can be represented as follows:

$$\begin{aligned} F(t)=F(t-1)\circ R(t,t-1) \end{aligned}$$

(4)

where $R(t, t-1)$ is the fuzzy relationship between $F(t)$ and $F(t-1)$. Here, “$R$” is the union of fuzzy relations and “$\circ$” is max–min composition operator. It is also called the first-order model of $F(t)$.

Definition 3

(Fuzzy time-variant and time-invariant series) Let $F(t)$ be a fuzzy time series, and $R(t, t-1)$ be a first–order model of $F(t)$. If $R(t, t-1)=R(t-1, t-2)$ for any time $t$, and $F(t)$ only has finite elements, then $F(t)$ is referred as a time-invariant fuzzy time series. Otherwise, it is referred as a time-variant fuzzy time series.

3 ANN and its application for creation of intervals

ANN is a computational model that is inspired by the human brain [1, 27]. ANN is composed of large number of interconnected nodes or neurons, which usually operate in parallel, and are configured in regular architectures. Researchers employ ANN in various forecasting problems (like electric load forecasting [31], short-term precipitation forecasting [16], long-rage summer monsoon rainfall forecasting [25], etc.), due to its capability to extract relationships between the input and output data.

Data clustering is a popular approach for automatically finding classes, concepts, or groups of patterns [9]. Time series data are pervasive across all human endeavors, and their clustering is one of the most fundamental applications of data mining [14, 23]. In literature, many data clustering algorithms [8, 22, 33] have been proposed, but their applications are limited to the extraction of patterns that represent points in multi-dimensional spaces of fixed dimensionality [34]. In our proposed model, a distance-based clustering algorithm, that is, the self-organizing feature maps (SOFM) are employed for determining the intervals of the historical time series data sets by clustering them into different groups. SOFM is developed by Kohonen [15], which is a class of neural networks with neurons arranged in a low-dimensional (often two-dimensional) structure, and trained by an iterative unsupervised or self-organizing procedure [21]. SOFM converts the patterns of arbitrary dimensionality into response of one-dimensional or two-dimensional arrays of neurons, that is, it converts a wide pattern space into a feature space. The neural network performing such a mapping is called feature map. The training process of SOFM consists of the following steps [27]:

step 1

Initialize the weights ($W_{uv}$) and learning rate ($\alpha$).

step 2

When stopping condition is false, then perform Steps 2–8.

step 3

For each input vector (X), perform Steps 3–5.

step 4

For each $v=1$ to m, compute the square of the Euclidean distance as:

$$\begin{aligned} D(v)=\sum _{u=1}^{n}(X_u-W_{uv})^2 \end{aligned}$$

(5)

step 5

Obtain winning unit index (J), so that $D(J)=$minimum.

step 6

Calculate weights of winning unit as:

$$\begin{aligned} W_{uv}(new)=W_{uv}(old)+\alpha [X_u-W_{uv}(old)] \end{aligned}$$

(6)

step 7

Reduce the learning rate ($\alpha$) by using the following formula:

$$\begin{aligned} \alpha (t+1)=0.5\alpha (t) \end{aligned}$$

(7)

step 8

Reduce radius of topological neighborhood network.

step 9

Test for stopping condition of the network.

Based on the above-mentioned algorithm, the historical time series data sets are partitioned into different length of intervals. These intervals are presented in Sect. 4.

4 Proposed ANN and fuzzy time series hybridized model

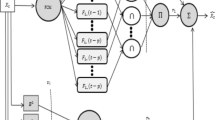
In this section, we introduce a new forecasting model based on hybridization of ANN with fuzzy time series. The architecture of the proposed model consists of six phases as shown in Fig. 1. For verification of model, the historical data sets of the daily average temperature and the daily cloud density from June 1996 to September 1996 in Taipei, Taiwan [5] are used, which are shown in Tables 1 and 2, respectively. In these data sets, the daily average temperature is called the main factor, and the daily average cloud density is called the second factor.

Fig. 1

Two-factors high-order neuro-fuzzy hybridized model

Table 1 Historical data of the daily average temperature from June 1996 to September 1996 in Taipei (Unit: $^\circ \text{ C}$)

Table 2 Historical data of the daily average cloud density from June 1996 to September 1996 in Taipei (Unit: $\%$)

In the following, we apply the proposed model to predict the daily temperature of Taipei from June 1996 to September 1996. To explain the functionality of each phase of the model, the daily average temperature and the daily cloud density data sets from June 1, 1996 to June 30, 1996, are considered as an example. Each phase of the model is explained as follows:

Phase 1

Divide the universe of discourse into different length of intervals.

Define the universe of discourse “$A$” of the main factor and the universe of discourse “$B$” of the second factor of the historical time series data sets. Let $A=[M_{min},M_{max}]$, where $M_{min}$ and $M_{max}$ are the minimum and maximum values of the main factor, respectively. Let $B=[N_{min},N_{max}]$, where $N_{min}$ and $N_{max}$ are the minimum and maximum values of the second factor, respectively.

Based on Tables 1 and 2, we have the universe of discourse of the daily average temperature $A=[26.1,30.9]$, and the universe of discourse of the cloud density $B=[10,96]$. By applying the SOFM algorithm, divide the universe of discourse “$A$” into different lengths of intervals as $a_1, a_2,\ldots ,$ and $a_n$. Similarly, divide the universe of discourse “$B$” into different lengths of intervals as $b_1, b_2,\ldots ,$ and $b_n$. For each interval, the centroid is calculated by taking the mean of the upper bound and lower bound of the interval. Each interval bears a weight equal to the frequency of the interval. The resulting intervals, centroids and weights for the considered data sets are shown in Tables 3 and 4.

Table 3 Intervals, elements of intervals, centroids and weights for the daily temperature for June 1996

Table 4 Intervals, elements of intervals, centroids and weights for the daily cloud density for June 1996

Phase 2

Define linguistic terms for each of the interval.

The universe of discourse “$A$” of the main factor is divided into $n$ intervals (i.e., $a_1, a_2,\ldots ,$ and $a_n$). Assume that there are $n$ linguistic variables (i.e., $U_1, U_2, \ldots , U_n$) represented by fuzzy sets, where $1\le i \le n$, shown as follows:

$$\begin{aligned} U_{1}&= 1/a_1 + 0.5/a_2 + 0/a_3 + 0/a_4 + 0/a_5 \\&+ \cdots + 0/a_{n-2} + 0/a_{n-1} + 0/a_n,\\ U_{2}&= 0.5/a_1 + 1/a_2 + 0.5/a_3 + 0/a_4 + 0/a_5\\&+ \cdots + 0/a_{n-2} + 0/a_{n-1} + 0/a_n,\\ U_{3}&= 0/a_1 + 0.5/a_2 + 1/a_3 + 0.5/a_4 + 0/a_5 \\&+ \cdots + 0/a_{n-2} + 0/a_{n-1} + 0/a_n,\\&\vdots \\ U_{n}&= 0/a_1 + 0/a_2 + 0/a_3 + 0/a_4 + 0/a_5 \\&+ \cdots + 0/a_{n-2} + 0.5/a_{n-1} + 1/a_n. \end{aligned}$$

Similarly, the universe of discourse “$B$” of the second factor is divided into $m$ intervals (i.e., $b_1, b_2,\ldots ,$ and $b_m$). Assume that there are $m$ linguistic variables (i.e., $V_1, V_2, \ldots , V_m$) represented by fuzzy sets, where $1\le i \le m$, shown as follows:

$$\begin{aligned} V_{1}&= 1/b_1 + 0.5/b_2 + 0/b_3 + 0/b_4 + 0/b_5 \\&+ \cdots + 0/b_{m-2} + 0/b_{m-1} + 0/b_m,\\ V_{2}&= 0.5/b_1 + 1/b_2 + 0.5/b_3 + 0/b_4 + 0/b_5 \\&+ \cdots +0/b_{m-2} + 0/b_{m-1} + 0/b_m,\\ V_{3}&= 0/b_1 + 0.5/b_2 + 1/b_3 + 0.5/b_4 + 0/b_5\\&+ \cdots + 0/b_{m-2} + 0/b_{m-1} + 0/b_m,\\&\vdots \\ V_{m}&= 0/b_1 + 0/b_2 + 0/b_3 + 0/b_4 + 0/b_5\\&+ \cdots + 0/b_{m-2} + 0.5/b_{m-1} + 1/b_m. \end{aligned}$$

The maximum membership values of both $U_i$ and $V_i$ occur at intervals $a_i$ and $b_i$, respectively.

Phase 3

Fuzzify the historical time series data sets of the main factor and the second factor.

If the time series data of the main factor belong to the interval $a_i$, where $1\le i \le n$, then fuzzify the time series data of the main factor into fuzzy set $U_i$. Similarly, if the time series data of the second factor belong to the interval $b_i$, where $1 \le i \le m$, then fuzzify the time series data of the second factor into fuzzy set $V_i$.

The fuzzified values of the main factor and second factor for June 1996 time series data sets are shown in Table 5. The fourth and fifth columns of Table 5 represent the centroids and weights of the corresponding intervals for the main factor, respectively. In Table 5, only fuzzified values of the second factor are shown (last column), because for forecasting the main factor, only fuzzified values of the second factor are required.

Table 5 Fuzzified daily temperature (with their corresponding centroids and weights) and cloud density for June 1996

Phase 4

Establish the fuzzy logical relationships between the fuzzified main factor and the fuzzified second factor.

We can establish the $n$th-order fuzzy logical relationship based on the fuzzified main factor and the fuzzified second factor. If there exists a fuzzy logical relationship between $U_i$ and $V_i$, where $U_i$ and $V_i$ denote the fuzzified main factor and second factor of day “$i$,” respectively, then the two-factors $n$th-order fuzzy logical relationship can be represented as follows:

$$\begin{aligned} ((U_{ni}, V_{ni}), \ldots , (U_{n2}, V_{n2}), (U_{n1}, V_{n1}))\rightarrow U_i \end{aligned}$$

(8)

Here, $(U_{ni}, V_{ni}),\,\ldots ,\,(U_{n2}, V_{n2}),\,(U_{n1}, V_{n1})$ represent fuzzified values of day $n-i,\,\ldots$, day $n-2$, day $n-1$ and day $i$, respectively, where $2 \le i \le n$. The left-hand side and right-hand side of fuzzy logical relationship (8) are called the previous state and the current state, respectively. Here, $U_{ni},\,\ldots ,\,U_{n2}$ and $U_{n1}$ represent the fuzzified values of the main factor of days $n-i,\,\ldots ,\,n-2$, and $n-1$, respectively. Similarly, $V_{ni},\,\ldots ,\,V_{n2}$, and $V_{n1}$ represent the fuzzified values of the second factor of days $n-i,\,\ldots ,\,n-2$, and $n-1$, respectively.

Based on fuzzy logical relationship (8) and Table 5, the first-order and the second-order fuzzy logical relationships of two factors are formed, which are shown in Tables 6 and 7, respectively. In Tables 6 and 7, the symbol “?” represents an unknown value.

Table 6 Two-factors first-order fuzzy logical relationships between the fuzzified temperature and cloud density data of June 1996

Table 7 Two-factors second-order fuzzy logical relationships between the fuzzified temperature and cloud density data of June $1996$

Phase 5

Form the fuzzy logical relationship groups.

If the $n$th-order fuzzy logical relationships have the same previous state, then, the $n$th-order fuzzy logical relationships can be divided into a $n$th-order fuzzy logical relationship group. Consider the following $n$th-order fuzzy logical relationships given as follows:

$$\begin{aligned} \begin{array}{c} ((U_{ni}, V_{ni}), \ldots , (U_{n2}, V_{n2}), (U_{n1}, V_{n1}))\rightarrow U_k\\ ((U_{ni}, V_{ni}), \ldots , (U_{n2}, V_{n2}), (U_{n1}, V_{n1}))\rightarrow U_s\\ \vdots \\ ((U_{ni}, V_{ni}), \ldots , (U_{n2}, V_{n2}), (U_{n1}, V_{n1}))\rightarrow U_n \end{array} \end{aligned}$$

Then, the $n$th-order fuzzy logical relationship group can be formed as follows:

$$\begin{aligned} ((U_{ni}, V_{ni}), \ldots , (U_{n2}, V_{n2}), (U_{n1}, V_{n1}))\rightarrow U_k, U_s, \ldots , U_n \end{aligned}$$

(9)

The first-order fuzzy logical relationship groups are formed based on Table 6, which are shown in Table 8; and the second-order fuzzy logical relationship groups are formed based on Table 7, which are shown in Table 9. If the same fuzzy logical relationship appears more than once, it is included only once in the group

Table 8 Two-factors first-order fuzzy logical relationship groups of the fuzzified temperature and cloud density data of June $1996$

Table 9 Two-factors second-order fuzzy logical relationship groups of the fuzzified temperature and cloud density data of June $1996$

Phase 6

Compute the forecasted values.

To compute the forecasted values, the rules for interval weighing are proposed. These rules are presented as follows:

• Rule 1. For forecasting day, $D(t)$, the previous state’s fuzzified values of the main factor and the second factor are considered from days, $D(t-n), \ldots , D(t-2)$ to $D(t-1)$; where “$t$” is the current day which we want to forecast and “$n$” is the order of fuzzy logical relationships. The Rule 1 is applicable only if there is only one fuzzified value in the current state. The steps under Rule 1 are given as follows:

• Step 1. For forecasting day, $D(t)$, obtain the previous state’s fuzzified values of the main factor and the second factor from days $D(t-n)$ to $D(t-1)$ as $(U_{ni}, V_{ni}), \ldots , (U_{n2},$ $V_{n2})$ and $(U_{n1}, V_{n1})$.

• Step 2. Find the fuzzy logical relationship group whose previous state is $((U_{ni}, V_{ni}), \ldots ,$ $(U_{n2}, V_{n2}),\,(U_{n1}, V_{n1}))$, and the current state is $U_k$, that is, the fuzzy logical relationship group is in the form of $((U_{ni}, V_{ni}), \ldots , (U_{n2}, V_{n2}), (U_{n1}, V_{n1})) \rightarrow U_k$, then, the forecasted value is calculated based on the following step.

• Step 3. Find the interval where the maximum membership value of $U_k$ occurs. Let this interval be $a_k$. This interval $a_k$ has the corresponding centroid $C_k$. This centroid $C_k$ is the forecasted value for day, $D(t)$.

• Rule 2. This rule is applicable if there are more than one fuzzified values in the current state. The steps under Rule 2 are given as follows:

• Step 1. For forecasting day, $D(t)$, obtain the previous state’s fuzzified values of the main factor and the second factor from days $D(t-n)$ to $D(t-1)$ as $(U_{ni},\,V_{ni}), \ldots , (U_{n2}, V_{n2})$ and $(U_{n1}, V_{n1})$.

• Step 2. Find the fuzzy logical relationship group whose previous state is $((U_{ni}, V_{ni}), \ldots ,$ $(U_{n2}, V_{n2}),\,(U_{n1}, V_{n1}))$, and the current state is $U_k, U_s, \ldots , U_n$, that is, the fuzzy logical relationship group is in the form of $((U_{ni}, V_{ni}), \ldots , (U_{n2}, V_{n2}), (U_{n1}, V_{n1})) \rightarrow U_k, U_s, \ldots , U_n$, then, the forecasted value is calculated based on the following step.

• Step 3. Find the intervals where the maximum membership values of $U_k, U_s, \ldots , U_n$ occur, and let these intervals be $a_k, a_s, \ldots , a_n$, respectively. These intervals have the corresponding centroids $C_k, C_s, \ldots , C_n$ and weights $W_k, W_s, \ldots , W_n$, respectively.

• Step 4. The forecasted value for day, $D(t)$ is calculated as follows:

  $$\begin{aligned} Forecast\left( t \right)=\frac{\sum ^{n}_{i=1}C_kW_k + C_sW_s + \cdots + C_nW_n}{\sum ^{n}_{i=1}W_k + W_s + \cdots + W_n } \end{aligned}$$

  (10)

• Rule 3. This rule is applicable only if there is an unknown value in the current state. The steps under Rule 3 are given as follows:

• Step 1. For forecasting day, $D(t)$, obtain the previous state’s fuzzified values of the main factor and the second factor from days $D(t-n)$ to $D(t-1)$ as $(U_{ni},\,V_{ni}), \ldots , (U_{n2},$ $V_{n2})$ and $(U_{n1}, V_{n1})$.

• Step 2. Find the fuzzy logical relationship group whose previous state is $((U_{ni}, V_{ni}), \ldots ,$ $(U_{n2}, V_{n2}),\,(U_{n1}, V_{n1}))$, and the current state is “?” (the symbol “?” represents an unknown value), that is, the fuzzy logical relationship group is in the form of $((U_{ni}, V_{ni}), \ldots , (U_{n2}, V_{n2}), (U_{n1}, V_{n1})) \rightarrow ?$, then, the forecasted value is calculated based on the following step.

• Step 3. Find the intervals where the maximum membership values of $U_{ni}, \ldots , U_{n2}, U_{n1}$ occur, and let these intervals be $a_{n-i}, \ldots , a_{n-2}, a_{n-1}$, respectively. These intervals have the corresponding centroids $C_{n-i},\ldots ,C_{n-2},C_{n-1}$ and weights $W_{n-i},\ldots ,$ $W_{n-2}, W_{n-1}$, respectively.

• Step 4. The forecasted value for day, $D(t)$ is calculated as follows:

  $$\begin{aligned} Forecast\left( t \right)=\frac{\sum \nolimits ^{n}_{i=1}C_{n-i}W_{n-i} + \cdots + C_{n-2}W_{n-2} + C_{n-1}W_{n-1} }{\sum \nolimits ^{n}_{i=1}W_{n-i} + \cdots + W_{n-2} + W_{n-1}} \end{aligned}$$

  (11)

Based on the proposed method, we have presented here two examples to compute forecasted values of daily average temperature as follows:

• Ex 1. Based on two-factors first-order fuzzy logical time series, an example is presented here to forecast the temperature on day, $D(t)$. Suppose, we want to forecast the temperature on June 7, 1996, in Taipei. To compute this value, the fuzzified temperature and cloud density values of the previous state are required. For forecasting day, $D$(June 7), the fuzzified temperature and cloud density values for day, $D$(June 6) are obtained from Table 5, which are $U_{11}$ and $V_9$, respectively. Then, obtain the fuzzy logical relationship group whose previous state is $(U_{11}, V_9)$ from Table 8. In this case, the fuzzy logical relationship group is $(U_{11}, V_9) \rightarrow U_{11}, U_8$ (i.e., Group 6). Therefore, Rule 2 is applicable here, because the current state has two fuzzified values. Now, find the intervals where the maximum membership values of $U_{11}$ and $U_8$ occur from Table 3, which are $a_{11}$ and $a_8$, respectively. The corresponding centroid and weight for the interval $a_{11}$ are 29.57 and 3, respectively. The corresponding centroid and weight for the interval $a_{8}$ are 28.75 and 4, respectively. Now, based on Eq. 10, the forecasted temperature for day, $D$(June 7) can be computed as:

  $$\begin{aligned} \frac{(29.57 \times 3 + 28.75 \times 4)}{3 + 4} = 29.10 \end{aligned}$$

• Ex 2. Based on two-factors second-order fuzzy logical time series, an example is presented here to forecast the temperature on day, $D(t)$. Suppose, we want to forecast the temperature on June 4, 1996, in Taipei. To compute this value, the fuzzified temperature and cloud density values of the previous state are required. For forecasting day, $D$(June 4), the fuzzified temperature and cloud density values for days, $D$(June 2) and $D$(June 3) are obtained from Table 5, which are $(U_4, V_6)$ and $(U_9, V_6)$, respectively. Then, obtain the fuzzy logical relationship group whose previous state is $((U_4, V_6),(U_9, V_6))$ from Table 9. In this case, the fuzzy logical relationship group is $((U_4, V_6),(U_9, V_6)) \rightarrow U_{13}$ (i.e., Group 2). Therefore, Rule 1 is applicable here, because in the current state, only one fuzzified value is available. Now, find the interval where the maximum membership value for fuzzy set $U_{13}$ occurs from Table 3, which is $a_{13}$. The interval $a_{13}$ has the centroid 30.73, which is the forecasted temperature for day, $D$(June 4).

The daily average temperature of June 1996 is forecasted based on the two-factors second-order fuzzy logical time series, which is shown in Table 10.

Table 10 Forecasted daily average temperature of June 1996 based on the two-factors second-order fuzzy logical time series (Unit: $^\circ \text{ C}$)

5 Experimental results

The proposed model computes the forecasted values with the help of hybridization of ANN (SOFM neural network) with the fuzzy time series. For training process, the daily temperature and the daily cloud density data sets from June 1, 1996 to June 30, 1996, are employed. In the testing process, the data sets of the daily temperature and the daily cloud density from July 1996 to September 1996 are used. During the learning process of neural network, different experiments were made to set additional parameters like learning rate, epochs, initial weight, learning radius, etc. to obtain optimal results, and we have chosen the ones that exhibit the best behavior in terms of accuracy. The determined optimal values of all these parameters are listed in Table 11.

Table 11 Additional parameters and their values during the learning process of SOFM neural network

The main downside of fuzzy time series forecasting model is that increase in the number of intervals increases accuracy rate of forecasting, and decreases the fuzziness of time series data sets. Therefore, in this study, the parameter called “optimum number of intervals” for the main-factor and second-factor time series data sets are decided using a heuristic approach. We have tried different values for this parameter, and calculate the average forecasting error rate (AFER) for different orders for the months – June, July, August and September. The equation for AFER is presented next.

$$\begin{aligned} AFER = \frac{|F_i-A_i|/A_i}{N}\times 100\% \end{aligned}$$

(12)

Here, $A_i$ and $F_i$ denote the actual and forecasted temperature for day $i$, and $N$ denotes the total number of days to be forecasted.

All these experimental results are plotted in graphs for different orders and intervals as shown in Fig. 2, and we have chosen the “optimum number of intervals” (shown in Table 11) for the main factor and second factor that exhibit the best behavior in terms of AFER. The experimental results of our proposed model are presented in Table 12 in terms of AFER. The forecasting results of the proposed model are then compared with existing models proposed by Chen and Hwang [5], Lee et al. [20], Lee et al. [18], Lee et al. [19], Chang and Chen [3], and Wang and Chen [32]. The comparative analyses in Tables 12, 13, 14, 15, 16, 17 and 18 signify that our proposed model exhibits higher accuracy than those of considered competing models [3, 5, 18–20, 32].

Fig. 2

AFER curves for June, July, August and September (top to bottom) with different orders and intervals

Table 12 The average forecasting error rates to forecast the temperature from June 1996 to September 1996 in Taipei for different orders based on proposed model

Table 13 The average forecasting error rates to forecast the temperature from June 1996 to September 1996 in Taipei with different window bases based on Chen and Hwang [5] model

Table 14 The average forecasting error rates to forecast the temperature from June 1996 to September 1996 in Taipei for different orders based on Lee et al. [20] model

Table 15 The average forecasting error rates to forecast the temperature from June 1996 to September 1996 in Taipei for different orders based on Lee et al. [18] model

Table 16 The average forecasting error rates to forecast the temperature from June 1996 to September 1996 in Taipei for different orders based on Lee et al. [19] model

Table 17 The average forecasting error rates to forecast the temperature from June 1996 to September 1996 in Taipei with different window bases (fifteen generated fuzzy rules) based on Chang and Chen [3] model

Table 18 The average forecasting error rates to forecast the temperature from June 1996 to September 1996 in Taipei for different orders based on Wang and Chen [32] model

6 Conclusions and directions for future work

In this paper, a new model is proposed for handling two-factors forecasting problems based on the hybridization of ANN with fuzzy time series. For generation of intervals of time series data sets, SOFM neural network is used. Then, some proposed rules of interval weighing are used to compute the forecasted values. From empirical analyses of experimental results, it is evident that our model is superior compared to the considered competing models in terms of accuracy.

Still, there are scopes to apply the model in some other domains in a flexible way as follows:

• 1. To check the accuracy and performance of the model by forecasting the temperature for different regions,

• 2. To test the performance of the model for different types of financial, stocks and marketing data sets, and

• 3. To enhance this model so that it can deal with multi-dimensional time series data set.