A systematic investigation of cross-validation in GWR model estimation: empirical analysis and Monte Carlo simulations

Abstract

In geographically weighted regression, one must determine a window size which will be used to subset the data locally. Typically, a cross-validation procedure is used to determine a globally optimal window size. Preliminary investigations indicate that the global cross-validation score is heavily influenced by a small number of observations in the dataset. At present, the ramifications of this behaviour in cross-validation are unknown. The research reported here explores the extent to which individual and groups of observations impact optimal window size determination, and whether one can explain why some points are more influential than others. In addition, we strive to examine the impact neighbourhood specification has on model quality in terms of predictive capabilities and the ability of the method to retrieve spatially varying processes. The analysis is based on several datasets and using simulated data in order to compare and validate results. The results provide some practical guidelines for the use of cross-validation.

1 Introduction

In geographically weighted regression (GWR), cross-validation (CV) is a frequently used method for determining the optimal neighbourhood size required for model estimation. According to a simple bibliometric analysis of the GWR literature indexed on The Web of Knowledge and Google Scholar, 35 of 64 papers identified used cross-validation, 13 used the Akaike Information Criterion, 9 used predefined, maximum likelihood or other bandwidths, and 7 did not mention the method used. Despite the popularity of the cross-validation approach for calibrating the kernel bandwidth and estimating spatially varying coefficients in GWR, there have not been any investigations in the geographical literature that we are aware of regarding the behaviour and properties of this commonly used procedure.

The use of cross-validation in GWR can be traced back to an early suggestion by Brunsdon et al. (1996) to minimize the following ‘leave-one-out’ score:

$${\mathbf{CV}} = \sum\limits_{i = 1}^n {\left[y_{i} - {\hat{y}}_{\ne i} \left(b \right)\right]}^{2}. $$

(1)

This CV score is a function of bandwidth b (a parameter that determines a neighbourhood size), where ${\hat{y}}_{\ne i} {\left(b \right)}$ is the estimated value of y _i after the observation at location i is removed. Generally, the CV can be thought of as a continuous function of the bandwidth. However, when neighbourhood size is discretized over the number of nearest neighbours (rather than some continuous measure such as distance), it is possible to forgo the use of a function minimization algorithm by simply computing the CV statistic for each feasible neighbourhood size. Of course, when n is large, a sample of bandwidths can be used to approximate the shape of the CV versus bandwidth curve and a near optimal neighbourhood size can be found.

The motivation for using cross-validation is based on the existence of an optimum neighbourhood size. CV minimization should retrieve an optimal bandwidth, one that is operating on the spatial process being modelled.. However, since the CV score is a function value dependent on the sum of the squared errors associated with estimating $\hat{{y}}_{\ne i} {\left(b \right)}$ at each point in the data set, and each point contributes a scalar value toward the CV score, it is possible to assess the merits of this assumption. Examination of the CV score in this paper reveals that it is possible for some points to have much larger errors relative to others which therefore impact the CV score disproportionately. As a result, the bandwidth optimization process can be driven by a small selection of highly influential points. This raises questions about the properties of cross-validation and the global optimum thus obtained for GWR estimation.

In this paper, we describe a method for exploring the cross-validation score with respect to the contributions of individual observations. Using three spatial datasets we then discuss the impact individual observations can have on bandwidth selection and show that model estimation is sensitive to bandwidth selection both in terms of goodness-of-fit and coefficient estimation. Furthermore, the method used to investigate the contributions of observations to the CV score suggests a number of modifications to the cross-validation score. We explore these alternative formulations of the cross-validation statistic using empirical examples and Monte Carlo simulations. Finally, we describe some guidelines for the use of this cross-validation in GWR, and suggest some directions for future research.

2 Data and model descriptions

2.1 Data

This analysis draws on three datasets to ensure that the results are reproducible and not merely artefacts of any particular set of data. The first dataset was used by Páez et al. (2001) in a study of land price estimation in Sendai, Japan. The dataset consists of 479 observations of 1996 land values obtained from Sendai City’s Information Office, and land use data taken from The Basic Planning Survey for Sendai Metropolitan Area (1995). The independent variables entered into the model under various transformations include: distances to the CBD and two sub-centres, percentage of residential and commercial land use, and population density. The second dataset obtained from the Municipal Property Assessment Corporation (MPAC) consists of 33,494 freehold residential sales prices for the City of Toronto (2001–2003). The structural attribute data (also obtained from MPAC) was augmented with neighbourhood level data from the Statistics Canada 2001 Census of Population. For a full treatment of this dataset please see Long (2006). The variables used in our analysis are: parcel area and frontage, the dwelling age and squared dwelling age, the sale date, and distance to nearest public transit station. The third dataset consists of 429 land-price observations in Sapporo, Japan. The explanatory variables include the property frontage, the distance to the nearest arterial road, an index of development and the distance to the CBD.

2.2 Geographically weighted regression

Geographically weighted regression is used to estimate locally linear coefficients and estimates of the dependent variable. The GWR model is formally defined as:

$$P_{i} = \beta_{0i} + {\mathop \sum \limits_k}\beta_{ki} X_{ki} + \varepsilon_{i}$$

(2)

where P _i is the ith observation of the dependent variable, X _ki is the ith observation of the kth independent variable, ɛ _i is the ith value of a normally distributed error vector with mean equal to zero, β_0i is the constant estimated for local regression i, and β _ki is the regression coefficient estimated for regression i and variable k. This differs from ordinary least squares regression by utilizing distinct constants and regression parameters for each point, rather than a single set of global parameters.

The estimation algorithm essentially iterates through n weighted least square regressions, each one modified by a unique distance–decay weight matrix. Estimation for point i thus takes the form:

$${\mathbf{B}}_{\mathbf{i}} = {\mathbf{(X}}^{\mathbf{T}} {\mathbf{W}}_{\mathbf{i}} {\mathbf{X)}}^{- {\mathbf{1}}} {\mathbf{X}}^{\mathbf{T}} {\mathbf{W}}_{\mathbf{i}} {\mathbf{P}}, $$

(3)

where B _i is the vector of estimated coefficients for observation i, P is the vector of observed dependent variables, X is the n ×  k matrix of explanatory variables, and W _i is a diagonal distance–decay weight matrix specific to i’s location relative to the surrounding observations (Fotheringham et al. 2002).

To produce distance-weighted neighbourhoods with each containing q nearest neighbours, Fotheringham et al. (2002) suggests using the following bi-square function:

$$W_{{ij}} = [1 - (d_{{ij}} /b)^{2} ]^{2} \quad \hbox{if}\,d_{{ij}} < b\,\hbox{and}\, 0\,\hbox{otherwise}. $$

(4)

This function produces numbers that are near-normal in their distribution for d _ij < b, and 0 for distances greater than or equal to b. The key to remember for this function is that b adapts from observation to observation since it is defined as the maximum of the distances between observation i and its q nearest neighbours.

3 CV Decomposition

The cross-validation score is examined by means of decomposition. The CV matrix is a two dimensional structure with rows corresponding to observations in the dataset and columns corresponding to a subset of feasible neighbourhood sizes. Each cell, CV _ir , contains the squared error term, ${\left[y_{i} - {\hat{y}}_{\ne i} \left(b_{r} \right)\right]}^{2}$ of the ith location using the rth feasible number of neighbours. In large datasets we take a proper subset of feasible neighbourhoods since the number of possible bandwidths is large and generally, the CV versus bandwidth curve is smooth. Note that each column sum in this matrix corresponds to a CV score as defined in Eq. (1). And the bandwidth corresponding to the column with the smallest sum can be used to approximate the globally optimal bandwidth. The CV procedure minimized at 70 nearest neighbours for Sendai, 200 for Toronto, and 50 for Sapporo.

The contribution of each point to the CV score is assessed through the exploration of the CV matrix. We can think of each row sum as corresponding to the aggregate influence of each point. In the Sendai land price example, we tested 46 different neighbourhood sizes on 479 locations. The row sums ranged from 0.026 to 115.44. There is a substantial difference in influence between the endpoints of this range. If we were to assume that the errors for the two extreme locations were constant across all bandwidths, we would find that one point on average has more than 4,000 times the influence than the other. This is an indication that the CV score is linked to model performance at the more influential locations. This polarization is present in all of the datasets tested. For instance, in the Toronto dataset, minimum and maximum row sums ranged between 988 and virtually 0. It is important to note that we found that influential points affected CV scores across all bandwidths, even at the global optimums. For example, in Toronto, at 200 neighbours, CV errors ranged from 20 to negligible, demonstrating the existence of points that highly impact the total of the CV score. In addition to identification, our goal is to measure the contribution of a point to the CV procedure and the influence of this value on selection of the global optimum. To separate the points that most contribute to the CV from the rest, each record is given an influence score. The influence score is an arbitrary measure and several ranking schemes were tested including the squared error at the smallest bandwidth or optimal bandwidth. Unlike these alternatives, using the row sum is bandwidth independent and as such is a more holistic measure of influence.

Figure 1 is a graph of the separated and cumulative sum of squared errors of the most influential points (top 10%) and the remaining locations in the Sendai dataset. Quite clearly, each curve in the graph has a unique minimum; the top 10% at 60 neighbours; the remaining 90% at 140 neighbours; and the combined minimum at 70 neighbours. One interpretation of the unique minima is that the effect of the 50 most influential observations is to move the optimum bandwidth from 140 to 70 nearest neighbours. In this case, 70 neighbours may not be the optimal bandwidth if we care to obtain the best estimates for 90% of the observations. The same effect is prevalent in the other datasets. For instance, in the Toronto dataset, the cumulative CV curve mimics the sharp decline in error over the smaller bandwidths of the highly influential points, while the curve pertaining to the rest of the points is much flatter, exhibiting a minimum at 180 neighbours.

Fig. 1

Cumulative and separated contributions of influential and non-influential observations in Sendai

Independent of where the curves reach their minima, the bandwidths where they intersect are also of interest as they can be used to visualize the share of influence each group carries. For Sendai, the 10 and 90% curves intersect twice at roughly 100 and 460 nearest neighbours—so at these bandwidths, each group’s squared errors are contributing equally to the CV score. It follows that for bandwidths between 100 and 460 neighbours, the 50 (or 10%) most influential points account for more than 50% of the total CV score. In Toronto, this split was polarized further, where the top 10% of observations account for 70% of the total CV sum for most of the bandwidths. This is quite remarkable in light of the differently shaped CV-Bandwidth curves exhibited by the influential points and indicates that the global optimum may not be representative for the majority of points in the dataset.

The visualization technique above can be generalized by arranging the same data into cumulative percentiles, rather than splitting the points into two groups. Such a graph allows one to see the marginal impact of adding the next set of more influential points. Each dot represents a cumulative partial column sum in the CV matrix. For example, in the Sendai graph (Fig. 2a) the bottom-left point is the sum of the least influential 1% of squared errors in the 30 neighbour bandwidth. The point above that is the sum of the smallest 2% of squared errors. The point to the right is the sum of the smallest 1% at the 40 neighbour bandwidth, and so on. The line connects the minimum values of each cumulative curve. For ease of interpretation, quintiles are represented by a larger marker. The Sendai graph shows a clear progressive pattern of influential points drawing the global optimum toward smaller bandwidths. In fact, it shows that the highest 1% of cases is responsible for bringing the optimum down from 100 to 70 neighbours; the highest 10% from 140 to 70 neighbours; and the highest 20% from 180 to 70 neighbours. Clearly, these influential points are substantially shifting the optimum away from a bandwidth that is more suitable for the majority of locations. The difference in the general shape of influential and non-influential curves is also quite striking. The less influential curves are quite flat whereas the curves belonging to the more influential points exhibit a steep decrease in error across the smaller bandwidths and then a steep increase away from their minimums toward larger bandwidths. This indicates that the majority of points are less sensitive to changes in bandwidth while the errors of the influential points are more leveraged. Interestingly, in Toronto we see the same general pattern of the influential points requiring smaller and smaller bandwidths, except the pattern is broken by the top percentile which accounts for a shift in the optimum from 160 to 200 neighbours (Fig. 2b). For Sapporo (Fig. 2c), we see a the top 20% of influential points drawing the optimum bandwidth from 70 down to 40 neighbours before the most influential draw the optimum back up to 50.

Fig. 2

Cross-validation partial sums in percentiles

The visualization of the above phenomena raises the question of how well the global optimum represents local neighbourhood conditions. Specifically, for each point, i, there is a single bandwidth b* _i such that ${\left[y_{i} -{\hat{y}}_{\ne i}\left(b^{*}_{i}\right)\right]}^{2}$ is less than the sum of squared errors for any other bandwidth. We call this b* _i the location specific optimum. This value can be easily found by searching the CV matrix for columns containing row-wise minima. Figure 3 contains histograms of local optima for the three datasets. The most salient feature of the histogram is its bimodal nature; nearly half of all optima lie in either the most local or the most global of bandwidths. In Sendai, about 110 observations favour an extremely localized window of regression, perhaps even smaller than the 30 nearest neighbours tested here. Alternatively, for approximately 55 observations, GWR behaves optimally when every point is included in the local regression. One should not equate this scenario to a global regression since the model used here utilizes a distance decay weight matrix as defined above. The presence of such a bipolar distribution is of interest since it implies that a global optimum will largely consist of a compromise between locations at the two extremes, and will probably misrepresent the majority of local minima. Interestingly, the distributions of local optima in the Sapporo and Toronto datasets exhibited similar bimodal patterns, indicating the prevalence of this problem across multiple empirical datasets.¹

Fig. 3

Histograms of local optima

The characterization of local minima of influential points can be used as a clue in determining the cause of influence. The histogram in Fig. 4 contains frequency counts of local minima amongst the most influential 5% of points in Sendai. The most apparent pattern in the histogram is that 48% of the influential observations have local optima in the 30 neighbour bandwidth and 84% have their minima at 100 neighbours or less. In contrast, for the entire population, only 23% are optimal at 30 neighbours, and 47% at 100 neighbours or less. Furthermore, only 8% of the influential observations are optimal in neighbourhoods consisting of 400 or more neighbours, in contrast to 20% for the entire sample. Clearly, influential points exhibit quite a distinct distribution, highly skewed towards smaller bandwidths. This skew may account for the global optimum being pulled towards lower and lower bandwidths as increasing numbers of influential points are added to the CV score.

Fig. 4

Histogram of influential optima in Sendai

Since cross-validation for influential points optimizes at smaller bandwidths, perhaps there is a geographic pattern of where influential points are located on the ground. Figure 5 shows the location of the most influential and non-influential points in the Sendai dataset. Clearly there is a strong tendency for influential points to cluster near the centre of the city. Páez found that central areas of this dataset exhibit higher levels of heterogeneity (Páez et al. 2001). This heterogeneity could be responsible for large local errors and hence more influence in the CV procedure. Furthermore, heterogeneous areas are likely to perform better under more localized regimes (Páez et al. 2001).

Fig. 5

Locations of least- and most-influential points in Sendai

Conversely, points of low influence are clustered in several areas within a central annulus surrounding the city. Typically, suburban areas are more homogeneous in nature than their downtown cores. Empirical evidence suggests this to be fact in Sendai (Páez et al. 2001). This homogeneity could allow for more accurate estimates at larger bandwidths as long as extraneous variance in the form of local outliers is not introduced.

In Toronto, over and above the clear pattern of geographical clustering of high and low influence points, it was observed that the most influential 10% of points had a mean sale price of $441,000 while the remaining points sold on average for $335,000. This prompted us to check for such patterns in the other datasets and we found that influential points routinely exhibit higher values of the dependent variable as compared to their less influential counterparts. Other tests revealed significant correlation between the aggregate influence score (measured as the row-sum of the CV matrix) and the dependent variable. This relationship may represent a bias inherent to the cross-validation procedure. Later, we examine a modification to the CV procedure in an attempt to attend to this finding.

4 GWR sensitivity to bandwidth selection

In this section, we compare GWR results for a variety of bandwidths in order to determine the impacts of bandwidth specification. Four bandwidths are tested for each dataset: the global optimum, the bandwidths corresponding to the bimodal histograms of local optima, and the optimum bandwidth after removing the top 10% of influential points from the cross-validation sum (deemed the 90% Optimum). In addition to these, we analyse a varying bandwidth model specification using the local optimum for each point. The comparison of measures is in terms of goodness-of-fit and coefficient stability.

4.1 Goodness-of-fit

The pseudo-R ² and sum of squared errors (SSE) are two measures used to describe the aggregate explanatory power of a GWR regression model (Farber and Yeates 2006; Páez et al. 2002b; Zhang and Gove 2005; Zhang et al. 2005). These measures relate to the distribution of errors which depend on the bandwidth selected via the cross-validation score. One assumes a high goodness-of-fit exists at the globally optimal bandwidth since overall cross-validation errors are minimized. Thus, goodness-of-fit should peak near the global optimum and decrease as bandwidths change in either direction. Interestingly, the results do not show this to be the case. Rather goodness-of-fit peaks when bandwidths are small, and decreases as bandwidths increase (see Table 1). When dealing with small sub-samples, the leave-one-out estimation may be poor due to the missing data at the target location. However, regression on the same neighbourhood in the presence of the target location’s data improves the estimate substantially, thus some small bandwidths produce better fitting estimates than the cross-validated optimum. Certainly, the benefit of the leave-one-out procedure is understood in terms of producing robust estimates for out-of-sample observations.

Table 1 Goodness of fit measures for various bandwidths

4.2 Extreme coefficients

Even though estimation accuracy is maximized at smaller bandwidths, when the focus of analysis is exploratory, not predictive, one is primarily concerned with the spatial and aspatial distributions of estimated parameters. Past research shows that GWR analyses are prone to estimating extreme coefficients including sign reversals (Farber 2004), which may contradict a priori expectations of strength and direction of relationships. Since the exploration of coefficient variability is one of the main strengths of GWR analysis, the presence of wildly fluctuating coefficients is problematic since it may be a sign of over-fitting in the local models or the presence of local multicollinearity or some other local violation of weighted-least-squares regression (Wheeler and Tiefelsdorf 2005). Relating this back to cross-validation and bandwidth size, there is a relationship between coefficient heterogeneity and bandwidth size, explained by Fotheringham et al. as the variance-bias trade off (Fotheringham et al. 2002). Using a simple measure of standard deviation, a monotonic inverse relation between bandwidth size and coefficient variability is observed (see Table 2). Coefficient variability increases as bandwidth decreases. The problem is that smaller bandwidths, which typically produce tighter fitting predictions, exhibit higher levels of coefficient variability and are plagued with extreme coefficients perhaps as a result of over-fitting. If this is the case, the cross-validation procedure is thus driven by error minimization and ignores the hazards of extreme coefficient estimation. An optimization procedure which balances the dual objective of maximizing goodness-of-fit and producing a set of non-extreme estimates would benefit future GWR analysis.

Table 2 Coefficient standard deviations for various bandwidths

5 Modified cross-validation

In this section we test several modifications of the cross-validation procedure in light of our findings concerning its characteristics and behaviour. There are two issues we consider. The first is the significant relationship between the cross-validation statistic and the dependent variable, and the second is the impact on bandwidth selection of points with disproportionate contributions to the CV score. There are admittedly other concerns, primarily regarding extreme coefficient estimation, but more research is required to develop robust multi-criteria or iterative procedures to cope with this. Instead, the modifications tested here are attempts at standardizing the traditional cross-validation statistic in order to deal with the aforementioned issues.

5.1 Modification 1: Y-standardization

Each of the three datasets tested in this paper exhibited statistically significant correlation between the dependent variable and the aggregate cross-validation influence measure. This bias can be mitigated by down-weighting individual points’ contributions according to the size of the dependent variable. In particular, each point’s CV contribution was divided by the observed dependent value, explicitly reducing the influence of higher valued observations. Throughout the rest of the paper, this modification is referred to as Y-standardization.

Reducing the influence of the dependent has little effect on the calibration procedure in spite of the observed relationship between influence and the dependent. For the Sendai, Toronto and Sapporo datasets, the Y-standardized cross-validation procedure behaved nearly exactly the same as the ordinary CV. Optimization occurs at the same bandwidth and the top 10% of influential points still account for more than 50% of the total CV score at the optimal bandwidth (see Fig. 6). For Sendai, correlation between sales price and influence does however drop from 0.24 to 0.06. For Toronto and Sapporo, correlation is reduced only marginally, from 0.06 to 0.05 and from 0.21 to 0.19, respectively. Interestingly, while Sendai and Sapporo exhibit a similar scale of correlation before Y-standardization, Y-standardization produces a strong reduction of correlation only in Sendai.

Fig. 6

Cumulative and separated contributions of influential and non-influential observations in sendai comparing traditional and Y-standardized CV

In all of the datasets, there is observed correlation between aggregate influence and the dependent variable, but the relative impact of most-influential observations compared to least-influential observations is far greater than the relative values of their dependent variables. This is perhaps why the above standardization technique fails to properly mitigate the impact of influential observations; the procedure is simply not powerful enough. If the dependent variable had a greater range, and if influence was more tightly correlated with it, then the Y-standardization technique would perhaps have a greater chance of equalizing the influence of individual observations. These conditions however are not expected to apply to the majority of experiments. A more democratic cross-validation method where each point has an equal influence on bandwidth selection is required. We put forward two alternatives next.

5.2 Modification 2: row-standardization

The first such modification is one which standardizes individual contributions by the aggregate measure of influence, defined as the row-sum of the CV matrix. Under this regime, deemed row-standardization, each observation’s contribution is divided by its row sum and thereby converted into a value between 0 and 1. This procedure is reminiscent of the row-standardization of spatial lag matrices in autoregressive models (Griffith 1988; Anselin 1988). If the CV error for a particular point and bandwidth is small in relation to errors for the same point using other bandwidths, then the row-standardized statistic for that point and bandwidth would be small and close to zero. Conversely, if the error is large in comparison to errors using other bandwidths, the statistic would have a value closer to unity. Similar to the traditional cross-validation procedure, the optimal bandwidth minimizes the sum of the standardized scores across all observations. Since each contribution is contained in (0,1), the effect is to have an optimization procedure which produces a bandwidth that is not tied to a handful of observations which typically have very large errors. We accept that some points are inherently poorly estimated, and search for the bandwidth at which GWR behaves well for the majority of observations.

Recall that each dataset exhibited a bimodal distribution of optimal local bandwidth. It is not surprising that each dataset also exhibits a bimodal distribution of worst local bandwidth (see Fig. 7). Even though many observations behave well under either of the bandwidth extrema, the converse is also true; many observations are poorly estimated under the extreme bandwidths. Moreover, those that behave well at local scales behave quite poorly at the global scale and vice versa. Upon removing scale as a factor in bandwidth selection by row-standardizing the CV matrix, the row-standardized optimum bandwidth is the one which never performs exceptionally poorly; by the same token, however, this bandwidth also rarely performs exceptionally well. Thus, the optimal bandwidths occur in the middle of the feasible range of all bandwidths. For Sendai, the optimal bandwidth is 210 neighbours; for Toronto it is 230; and for Sapporo it is 100. In all three cases, these bandwidths are situated near the middle of the set of bandwidths tested, favouring neither the more local nor global options. It is still unclear whether treating one extremum preferentially is more suitable than selecting the middle ground. Since, under the row-standardized cross-validation regime, each observation’s aggregate CV contribution is equal to one, there is no meaningful measure of overall influence through which we can visualize the cumulative and incremental contributions of points as above.

Fig. 7

Histogram of least optimal local bandwidths, Toronto

5.3 Modification 3: row-normalization

A third modification is put forward called Row-Normalization. In this method, the CV statistic is standardized by subtracting the mean and dividing by the standard deviation of the distribution of squared errors corresponding to each observation across all bandwidths. The scores are then right-shifted by subtracting the minimum standardized error of each row from the matrix in order to produce distributions starting with zero.

This modification is similar to the row standardized method above in that each error term is represented as a measure relative to the distribution of all error terms belonging to the same observation. One difference is that values start at zero and increase with respect to the distribution of errors for each point. In practice, Row-Normalized CV error terms ranged from zero to seven. This results in a broader distribution than the row standardized modification, but a much more compact distribution than the original cross-validation procedure. The normalized cross-validation procedure returns optimum bandwidths of 140, 170 and 40 nearest neighbours for Sendai, Toronto and Sapporo respectively. These bandwidths are very similar to the optimums obtained by the original cross-validation procedure after discarding the most influential observations. Clearly, this method is levelling the playing field without flattening the distribution as much as the percentage based row standardization modification.

5.4 Modified CV, goodness-of-fit and extreme coefficients

Above, the evidence establishes that both goodness-of-fit and the variability of coefficient estimates in GWR are related to the bandwidth used during estimation (Tables 1, 2). Then not surprisingly, the results of GWR estimations calibrated with the modified cross-validation procedures are also related to the respective optimum bandwidths. For the three datasets, Y-standardization produces the same bandwidths as the standard cross-validation procedure (Tables 3, 4). Due to the extreme bimodal distributions of optimal and worst bandwidths, the Row-Standardization procedure optimizes at mid-range bandwidths which are larger than the ones produced by the other calibration procedures. As a result, goodness-of-fit results are weaker while coefficients show less variability. Row-normalization optimizes at or near the 90% optimum (Table 1, 2). This results in high R-squares and moderate coefficient variability.

Table 3 Goodness of fit measures for modified CV procedures

Table 4 Coefficient standard deviations for modified CV procedures

5.5 Polarization index

In the end, we need to determine each modification’s ability to mitigate the polarization of influence amongst observations. We are most interested in the polarization taking place near the optimal bandwidth so the comparison of methods will be focused at each one’s respective optimum. The degree of polarization is measured as the share of the total CV sum belonging to the largest 10% of contributors. In a scenario without any polarization of influence, the top 10% should account for 10% of the total CV sum, thus we divide each term by 10% to convert the score into an index. In our tests (see Table 5), the standard CV procedure consistently returns a high polarization index, ranging between 5.4 and 6.9. The Y-standardization modification improves the index negligibly. Not surprisingly, the percent based row-standardization procedure produces the lowest levels of polarization, undoubtedly due to the compact nature of the distribution. Finally, the row-normalization procedure has scores slightly higher than the row-standardization, but vastly superior to the standard CV procedure.

Table 5 CV modifications, revealed optimum bandwidths, and polarization indices

6 A simulation experiment

Simulation can be used to explore the behaviour of the various cross-validation procedures in a controlled environment. The experimental design draws from a recent paper by Wang et al. where it was used to compare the performance of traditional GWR to a modified GWR using local spatially expanded coefficients (Wang et al. 2007). The objective of the experiment in our case is to test the goodness of fit and the ability of GWR to retrieve the coefficients of a spatially varying process under an array of cross-validation calibration methods (q.v. Wheeler and Calder 2007). The data generating process is defined as follows:

$$y_{i} = \beta_{0} \left(u_{i}, v_{i} \right) + \beta_{1} \left({u_{i}, v_{i}} \right) x_{i} + \varepsilon_{i} \quad \hbox{for}\;i = 1,2, \ldots, 625,$$

where the x _i are randomly drawn from a uniform distribution over the interval (0,1), and the ɛ _i are randomly drawn from a standard normal distribution. For a synthetic sample of 625 observations, spatial coordinate pairs (u _i , v _i ) are assigned as follows:

$$\left(u_{i}, v_{i} \right) = \left(0.5\bmod \left({i - 1,25} \right),0.5\hbox{fl}\left({i- 1}/{25}\right) \right)\quad \hbox{for}\;i = 1,2, \ldots, 625,$$

where mod(a, b) is the remainder of a divided by b, and fl(a) is the floor of a. Finally, the coefficients β₀ (u _i , v _i ) and β₁ (u _i , v _i ) are defined as functions of coordinate pairs (u,v) as:

• Case 1: $\beta_{0} \left({u,v} \right) = 1 + \frac{1}{6}\left({u + v} \right),\; \beta_{1} \left({u,v} \right) = 1 + \frac{1}{3}u;$

• Case 2: $\beta_{0} \left({u,v} \right) = 1 + 4\sin \left(\frac{1}{12}\pi u \right),\; \beta_{1} \left({u,v} \right) = 1 + \frac{1}{324}\left[36 -{\left({6 - u} \right)}^{2} \right]\left[36 - {\left({6 - v} \right)}^{2}\right].$

As seen in the accompanying illustrations (Fig. 8), in the first case, the coefficient surfaces are derived from simple planar functions of Cartesian coordinates, while in the second, they are derived from more complex sinusoidal and biquadratic expressions.

Fig. 8

True coefficient surfaces for Case 1 (top) and Case 2 (bottom)

Following the generation of y _i , the regular and modified cross-validation criteria are used to retrieve a bandwidth for which GWR produces coefficient estimates and predictions of the observed dependent variable. The estimates are stored and the process is repeated 100 times with new sets of randomly drawn variates.

Table 6 contains descriptive statistics of the parameter distributions generated via the Monte Carlo simulations. In general, the optimal bandwidths for Case 1 are much smaller than those returned for Case 2. Currently, the experiment does not tell if this is due to the level of complexity—linear surfaces versus biquadratic and sinusoidal ones—or the rate of change of the parameter surfaces. In the linear case, the partial derivatives are constant at 1/6 and 1/3 for β₀ (u _i , v _i ) and β₁ (u _i , v _i ) respectively, but in the more complex case, the rates of change have much higher peaks at approximately ±12 for β₀ (u _i , v _i ) and at ±10/9 for β₁ (u _i , v _i ). From a theoretical point of view, it seems reasonable that larger bandwidths achieve better performance on flatter surfaces since the local process at points further away from the target location may be quite similar to the process at the target location. Likewise, for faster changing processes, smaller bandwidths perform better since the process at points further away are likely to be quite dissimilar to the process at the target location. For both cases, traditional cross-validation routinely returns the smallest window sizes with the most compact distributions as illustrated by the means and standard deviations. The distribution of bandwidths returned by the row-standardized (CVRS) and row-normalized (CVRN) procedures are nearly identical and both produce large mean bandwidths compared to CV. Finally, the Y-standardized (CVYS) procedure produces highly variable bandwidth distributions, and in the worst case, returns much poorer fitting estimates of both the coefficients and the dependent variable.

Table 6 Descriptive statistics of simulation results

The pseudo-R ² in Table 6 is simply the squared correlation coefficient for the observed and predicted values of the dependent variable (the best estimates for each case and parameter are printed in bold.) For both cases, there is not much variation in the pseudo- R ² distributions across methods except that CVYS produces some very poor fitting models as evidenced by the minimum pseudo-R ² values and the standard deviations. Other than this, we see that CV consistently attains the highest predictive accuracy with the most consistency between replications.

Contrastingly, whereas CV attains the highest prediction accuracy in terms of estimating the dependent variable, we see that CVRN and CVRS are superior coefficient retrievers. This indicates that the modeling purpose may dictate the cross-validation methodology to use in that CV can be used to achieve higher prediction accuracy, while CVRN and CVRS can be used for inference and exploration. Furthermore, the CVYS procedure behaves quite poorly, neither attaining superior predictive nor inferential power.

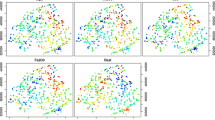
In addition to numeric descriptions of the simulation results, Figs. 9, 10, 11 and 12 provide graphical illustrations of two spatial aspects of the simulations. These figures show, for each coefficient-method pair, the mean retrieved surface and the mean bias surface. For brevity, we exclude the CVYS surfaces, since this method has been deemed inferior, and the CVRN surfaces, since CVRN returns results very similar to CVRS while CVRS has a more parsimonious implementation. The mean retrieved surface and mean bias are defined as:

$$\begin{aligned} \,& \hbox{Mean}\left({\hat{\beta}}_{k} \left(u_{i}, v_{i}\right)\right) = \frac{1}{R} \sum\limits_r^R{\hat{\beta}}_{kr}\left(u_{i}, v_{i}\right),\quad \hbox{for}\,k = 0,1\,\hbox{and i} = 1,2, \ldots 625; \\ \,& \hbox{MBIAS} \left({\hat{\beta}}_{k} \left(u_{i}, v_{i}\right)\right) = \frac{1}{R}\sum\limits_r^R {\left({\hat{\beta}}_{kr} \left(u_{i}, v_{i} \right) - \beta_{k} \left(u_{i}, v_{i}\right)\right)}^{2}, \quad \hbox{for} \,k = 0,1 \,\hbox{and i} =1,2, \ldots 625, \\ \end{aligned} $$

where ${\hat{\beta}}_{k} {\left(u_{i}, v_{i}\right)}$ is the GWR estimate of β _k (u _i , v _i ), and R is the number of Monte Carlo repetitions.

Fig. 9

Mean coefficient and bias surfaces, CV—Case 1

Fig. 10

Mean coefficient and bias surfaces, CVRS—Case 1

Fig. 11

Mean coefficient and bias surfaces CV—Case 2

Fig. 12

Mean coefficient and bias surfaces: CVRS—Case 2

In agreement with the numerical evidence, the surfaces of mean coefficient estimates mirror the true coefficient surfaces in Fig. 8 (also see Wang et al. 2007). Even though the mean surfaces capture the general trend of the true surfaces, anomalies are visible along the edges of the study area, probably due to more heterogeneous local neighbourhoods resulting from larger neighbourhoods in terms of distance (i.e. to find the same number of nearest neighbours, a location near the edge needs to cover a longer distance than one in the centre).

The mean bias surfaces more directly illustrate the spatial extent and magnitude of these edge-effects. Comparing the two cross-validation procedures for each case, at first glance it appears that the bias is far greater for the CVRS estimates thereby contradicting the numerical findings in Table 6 which indicate the opposite. However, on closer inspection it becomes evident that whereas the edge-effects are far more severe for the CVRS estimates, bias for the inner points is much greater for traditional CV than CVRS. Thus, CVRS, while producing better fitting surfaces overall, is more prone to deleterious edge-effects in comparison to traditional CV.

7 Conclusions

In this paper, we systematically studied GWR cross-validation using three distinct empirical datasets and Monte Carlo simulations. We describe a method used to decompose the cross-validation score in terms of individual observations. Afterward, using this method we illustrate that for three empirical spatial datasets, a selection of observations exert quite large influence on cross-validation scores. In the course of study, we discovered that global optimality may not be possible given the bimodal distribution of locally optimum bandwidths. Furthermore, we found that goodness-of-fit maximizes at small bandwidths, even if they are smaller than the optimum defined by the cross-validation procedure. In an attempt to attenuate the possibility of bandwidth selection being driven by a small number of influential observations, three simple modifications to the CV statistic were tested: Y-standardization, row-standardization; and row-normalization. Following the applications of the modified CV procedures to the empirical datasets, Monte Carlo simulations were used to study them in a controlled environment. From the empirical analysis, we discovered that both row-standardization and row-normalization significantly reduced the amount of influence any single point could have on bandwidth selection, while Y-standardization did not produce any noticeable effect. In the simulation studies we found that the traditional cross-validation method systematically returns smaller bandwidths as compared to the more democratic row-standardization and row-normalization techniques. Furthermore, traditional CV led to better estimates of the dependent variable. CVRS and CVRN, on the other hand, produce more accurate estimates of the local regression coefficients, but with a tendency, most likely due to the larger window sizes, to return high levels of bias around the edges of the study area.

This paper, while technical in nature, provides practical guidance to users of the GWR method. It serves as a cautionary note, that traditional cross-validation minimization is prone to the deleterious impacts of influential observations and may return bandwidths that are not optimized for coefficient retrieval. Furthermore, the cross-validation decomposition analysis supports earlier commentary on GWR that a single globally optimum bandwidth probably does not adequately represent observable spatial processes (Páez et al. 2002a). Finally, the findings from the simulation studies can help practitioners customize their cross-validation procedure according to their particular research goals, be they predictive or inferential in nature. Clearly, if the objective of the analysis is to explore spatially varying relationships, a row-normalization or standardization approach would be desirable, mindful of the potential for edge effects. In fact, one could combine two cross-validation approaches to assess the possible extent of edge effects. More generally, the empirical and simulation studies show that the cross-validation procedure has a strong impact on GWR coefficient estimates and predictions of the dependent variable, and practitioners should proceed cautiously in order to ensure the highest level of predictive or explanatory integrity.

Concerning further research, at the onset of this investigation, much attention was drawn to the existence and identification of influential CV observations. In this paper, the term “influential point” was borrowed to signify a point having disproportionate impact on bandwidth selection. At this time, it is unclear if these points are also influential in the more traditional sense of high leverage points or outliers (Fox 1997). At the very least, it should be clear that global outliers and influential points are not necessarily so with respect to local neighbourhood regressions. In local statistics, the global notion of outliers is conditioned by the neighbourhood size, thus allowing for discrepancy, the degree of outlying, to vary with neighbourhood scale. As such, it is possible for an observation to be an outlier at one spatial scale but not another. This observation partially motivated our approach for identifying influential points with respect to cross-validation: since points can be influential at any neighbourhood scale this requires the investigation of the influence of all points at all scales. Regarding the source of influence, the most intuitive explanation concerns spatial-outliers, observations whose attributes are different from those of other observations in the surrounding neighbourhood. These points can influence the estimation of local regressions for neighbourhoods which they are members of. During cross-validation they can either force the window size smaller to eliminate themselves from the membership. Alternatively, by contributing to larger window sizes, they can drown-out their effect on estimation. In either case, spatial-outliers are potentially disruptive of the cross-validation procedure. In addition, since spatial outliers are likely not well represented by any local regression process, their locally cross-validated error terms are likely quite high. These disproportionately high CV errors might influence the CV minimization procedure.

Similar to spatial-outliers, another possible source of cross-validation influence is a sudden shift in regression regimes. One of the various reasons for using GWR is to identify regime shifts; however, cross-validation can be influenced by a regime shift in a similar way to a spatial outlier. Indeed, an observation in one regime could be considered an outlier in a neighbourhood that consists of points primarily belonging to a second regime.

While spatial-outliers and regime changes quite possibly pose serious challenges to the reliability of cross-validation, understanding the reasons for their existence and the extent of their effect requires thorough experimental analysis. This paper provides a point of departure for such investigations by developing a method for exploring and measuring the impacts of individual observations. In addition, the paper also shows how different specifications of the cross-validation objective function can lead to more democratic and possibly more robust GWR estimation. A systematic investigation of the source and cause of cross-validation influence requires further study. Practitioners would greatly benefit from such analysis since the current data-cleaning methods pertain to global statistical methods and thus may not be entirely appropriate for local, moving windows approaches.

On a final note, in this paper we concentrated on bandwidth selection using cross validation instead of more recent alternatives, such as the use of the Akaike Information Criterion (Fotheringham et al. 2002). It is worth noting that in a recent paper, Nakaya et al. recognize the current void in research concerning the properties of GWR calibration methods, including AIC (Nakaya et al. 2005). Unfortunately for us, the AIC cannot be easily decomposed into contributions from individual points, and so our examination of influential points does not have a straightforward counterpart within the AIC framework. The lack of reported results, moreover, does not help to resolve the question of whether CV and AIC minimization tend to return similar or even identical bandwidths (e.g. Yu 2006). Clearly, this is one additional topic in need of further research.