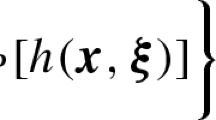Distributionally robust optimization with polynomial densities: theory, models and algorithms

Abstract

In distributionally robust optimization the probability distribution of the uncertain problem parameters is itself uncertain, and a fictitious adversary, e.g., nature, chooses the worst distribution from within a known ambiguity set. A common shortcoming of most existing distributionally robust optimization models is that their ambiguity sets contain pathological discrete distributions that give nature too much freedom to inflict damage. We thus introduce a new class of ambiguity sets that contain only distributions with sum-of-squares (SOS) polynomial density functions of known degrees. We show that these ambiguity sets are highly expressive as they conveniently accommodate distributional information about higher-order moments, conditional probabilities, conditional moments or marginal distributions. Exploiting the theoretical properties of a measure-based hierarchy for polynomial optimization due to Lasserre (SIAM J Optim 21(3):864–885, 2011), we prove that certain worst-case expectation constraints are polynomial-time solvable under these new ambiguity sets. We also show how SOS densities can be used to approximately solve the general problem of moments. We showcase the applicability of the proposed approach in the context of a stylized portfolio optimization problem and a risk aggregation problem of an insurance company.

1 Introduction

Since George Dantzig’s 1955 paper on linear programming under uncertainty [11], the field of stochastic programming has developed numerous methods for solving optimization problems that depend on uncertain parameters governed by a known probability distribution, see, e.g., [5, 41, 47]. Stochastic programming usually aims to minimize a probability functional such as the expected value, a percentile or the conditional value-at-risk of a given cost function. In practice, however, the distribution needed to evaluate this probability functional is at best indirectly observable through independent training samples. Thus, the stochastic programming approach is primarily useful when there is abundant training data. If data is scarce or absent, on the other hand, it may be more adequate to use a robust optimization approach, which models the uncertainty through the set of all possible (or sufficiently likely) uncertainty realizations and minimizes the worst-case costs. Robust optimization is the appropriate modeling paradigm for safety-critical applications with little tolerance for failure and has been popularized in the late 1990’s, when it was discovered that robust optimization models often display better tractability properties than stochastic programming models [1]. Distributionally robust optimization is a hybrid approach that attempts to salvage the tractability of robust optimization while maintaining the benefits of (limited) distributional information. In this context, uncertainty is modeled through an ambiguity set, that is, a family of typically infinitely many different distributions that are consistent with the available training data or any prior distributional information, and the objective is to minimize the worst-case expected costs across all distributions in the ambiguity set. A distributionally robust newsvendor model that admits an analytical solution has been investigated as early as in 1958 [44], and the theoretical properties of distributionally robust linear programs were first studied in 1966 [52]. Interest in distributionally robust optimization has also been fuelled by important applications in finance [38, 39]. However, only recently it was recognized that many distributionally robust optimization problems of practical relevance can actually be solved in polynomial time. Tractability results are available both for moment ambiguity sets, which contain all distributions that satisfy a finite number of moment conditions [12, 17, 51], as well as for metric-based ambiguity sets, which contain all distributions within a prescribed distance from a nominal distribution with respect to some probability metric [7, 36]. In all these cases, the extremal distributions that determine the worst-case expectation are discrete, and the number of their discretization points is often surprisingly small, e.g., proportional to the number of moment constraints. As these unnatural discrete distributions are almost always inconsistent with the available training samples, distributionally robust optimization models with moment and metric-based ambiguity sets are often perceived as overly pessimistic.

In an attempt to mitigate the over-conservatism of traditional distributionally robust optimization, several authors have studied moment ambiguity sets that require their member distributions to satisfy additional structural properties such as symmetry, unimodality, monotonicity or smoothness etc. By leveraging ideas from Choquet theory and polynomial optimization, it has been shown that the resulting distributionally robust optimization problems admit hierarchies of increasingly accurate semidefinite programming (SDP) bounds [40]. An exact SDP reformulation for the worst-case probability of a polytope with respect to all unimodal distributions with known first and second moments is derived in [50], while second-order conic reformulations of distributionally robust individual chance constraints with moment and unimodality information are reported in [31]. For a survey of recent results on distributionally robust uncertainty quantification and chance constrained programming problems with moment and structural information we refer to [22]. Even though unimodality or monotonicity conditions eliminate all discrete distributions from a moment ambiguity set, the extremal distributions that critically determine all worst-case expectations remain pathological. For example, all extremal unimodal distributions are supported on line segments emanating from a single point in space (the mode) and thus fail to be absolutely continuous with respect to the Lebesgue measure. Thus, the existing distributionally robust optimization models with structural information remain overly conservative. This observation motivates us to investigate a new class of ambiguity sets that contain only distributions with non-degenerate polynomial density functions.

This paper aims to study worst-case expectation constraints of the form

$$\begin{aligned} \inf \limits _{{\mathbb {P}} \in {\mathcal {P}}} {\mathbb {E}}_{\mathbb {P}} f(x,z) \ge 0, \end{aligned}$$

(1)

where $x\in {\mathbb {R}}^n$ is a decision vector, $z\in {\mathbb {R}}^m$ is an uncertain parameter governed by an ambiguous probability distribution ${\mathbb {P}} \in {\mathcal {P}}$, and f(x, z) is an uncertainty-affected constraint function that can be interpreted as a cost. In words, the constraint (1) requires that the expected value of the function f(x, z) given the decision x be nonnegative for every distribution in the ambiguity set $\mathcal P$. Throughout the paper we will assume that f(x, z) depends polynomially on z and that each distribution ${\mathbb {P}}\in \mathcal P$ admits a sum-of-squares (hence nonnegative) polynomial density function h(z) with respect to some prescribed reference measure $\mu$ on ${\mathbb {R}}^m$ (e.g., the Lebesgue measure). Imposing an upper bound on the polynomial degree of h(z) thus yields a finite-dimensional parameterization of the ambiguity set $\mathcal P$. Moreover, many popular distributional properties can be expressed through linear constraints on the coefficients of h(z) and are thus conveniently accounted for in the definition of ${\mathcal {P}}$. Examples include moment bounds, probability bounds for certain subsets of ${\mathbb {R}}^m$, bounds on conditional tail probabilities and marginal distribution conditions. Note that by fixing the marginal distributions of all components of z, the worst-case expectation problem on the left-hand side of (1) reduces to a Fréchet problem that seeks the worst-case copula of the uncertain parameters.

By leveraging a measure-based hierarchy for polynomial optimization due to Lasserre [28], we will demonstrate that the subordinate worst-case probability problem in (1) admits an exact SDP reformulation. Under mild additional conditions on f(x, z), we will further prove that the feasible set of the constraint (1) admits a polynomial-time separation oracle. Moreover, we will analyze the convergence of the worst-case expectation in (1) as the polynomial degree of h(z) tends to infinity, and we will illustrate the practical use of the proposed approach through numerical examples.

More succinctly, the main contributions of this paper can be summarized as follows:

• (i) Modeling power: We introduce a new class of ambiguity sets containing distributions that admit sum-of-squares polynomial density functions of degree at most 2r, $r\in \mathbb N$, with respect to a given reference measure. Ambiguity sets of this type are highly expressive as they conveniently accommodate distributional information about higher-order moments, conditional probabilities or conditional moments. They also allow the modeler to prescribe (not necessarily discrete) marginal distributions that must be matched exactly by all distributions in the ambiguity set.

• (ii) Computational tractability: A key advantage of working with sum-of-squares polynomial density functions is computational tractability in the sense that one may often formulate the emerging problems as SDPs. Specifically, we identify general conditions under which the worst-case expectations over the new ambiguity sets can be reformulated exactly as tractable SDPs with ${\mathcal {O}}{n+r \atopwithdelims ()r}$ variables. Finally, we delineate conditions under which the feasible sets of the worst-case expectation constraints admit a polynomial-time separation oracle and thus lend themselves to efficient optimization via the ellipsoid method.

• (iii) Convergence analysis: We demonstrate that, as r tends to infinity, the worst-case expectations over the new ambiguity sets converge monotonically to classical worst-case expectations over larger ambiguity sets that relax the polynomial density requirement. At the same time, we show that the extremal density functions converge to pathological discrete worst-case distributions characteristic for classical moment ambiguity sets without restrictions on the density functions. This convergence analysis showcases that our approach naturally embeds classical stochastic programming (for $r=0$) and the traditional approach to (distributionally) robust optimization (for $r\rightarrow \infty$) into a unifying framework.

• (iv) Numerical results: We showcase the practical applicability of the proposed approach in the context of a stylyzed portfolio optimization problem and a simple Fréchet problem inspired by [49] that models the risk aggregation problem of an insurance company.

The intimate relation between polynomial optimization and the problem of moments has already been exploited in several papers on distributionally robust optimization. For example, ideas from polynomial optimization give rise to SDP bounds on the probability of a semi-algebraic set [3] or the expected value of a piecewise polynomial [53] across all probability distributions satisfying a given set of moment constraints. These SDP bounds are tight in the univariate case or if only marginal moments are specified. Otherwise, one may obtain hierarchies of asymptotically tight SDP bounds. As an application, these techniques can be used to derive bounds on the prices of options with piecewise polynomial payoff functions, based solely on the knowledge of a few moments of the underlying asset prices [2]. Moreover, asymptotically tight SDP bounds that account for both moment and structural information are proposed in [40]. All these approaches differ from our work in that the ambiguity sets have discrete or otherwise degenerate extremal distributions.

Distributionally robust polynomial optimization problems over non-degenerate polynomial density functions that are close to a nominal density estimate (obtained, e.g., via a Legendre series density estimator) in terms of the $L_2$-distance are considered in [35]. In this work the non-negativity of the candidate density functions is not enforced explicitly, which considerably simplifies the problem and may be justified if the distance to the nominal density is sufficiently small. It is shown that the emerging distributionally robust optimization problems are equivalent to deterministic polynomial optimization problems that are not significantly harder than the underlying nominal problem and can be addressed by solving a sequence of tractable SDP relaxations.

Distributionally robust chance constraints with ambiguity sets containing all possible mixtures of a given parametric distribution family are studied in [30]. The mixtures are encoded through a probability density function on a compact parameter space. The authors propose an asymptotically tight SDP hierarchy of inner approximations for the feasible set of the distributionally robust chance constraint. In contrast, we explicitly represent all probability distributions in the ambiguity set through polynomial density functions that can capture a wide range of distributional features.

The paper is structured as follows. Section 2 reviews the measure-based approach to polynomial optimization due to Lasserre [28], which is central to this paper. Section 3 develops SDP hierarchies for worst-case expectations over ambiguity sets that contain probability measures with polynomial densities and investigates the convergence as the polynomial degree tends to infinity. Section 4 extends this analysis to ambiguity sets imposing moment conditions. Section 5 highlights the modeling power of the proposed approach, while Sect. 6 reports on numerical results for a portfolio design and a risk aggregation problem of an insurance company. Conclusions are drawn in Sect. 7.

2 Lasserre’s measure-based hierarchy for polynomial optimization

In what follows, we denote by $x^\alpha :=\prod _{i=1}^nx_i^{\alpha _i}$ the monomial of the variables $x = (x_1,\ldots ,x_n)$ with respective exponents $\alpha = (\alpha _1,\ldots ,\alpha _n) \in {{\mathbb {N}}}_0^n$, and we define $N(n,r):=\{\alpha \in {{\mathbb {N}}}_0^n: \sum _{i=1}^n\alpha _i\le r\}$ as the set of all exponents that give rise to monomials with degrees of at most r. We let $\varSigma [x]$ denote the set of all sum-of-squares (SOS) polynomials in the variables x, and we define $\varSigma [x]_r$ as the subset of all SOS polynomials with degrees of at most 2r.

Now consider the polynomial global optimization problem

$$\begin{aligned} p_{\min ,{{\mathbf {K}}}} := \min _{x \in {{\mathbf {K}}}} p(x) = \min _{x \in {{\mathbf {K}}}} \sum _{\alpha \in N(n,d)} p_\alpha x^\alpha , \end{aligned}$$

(2)

where $p(x) = \sum _{\alpha \in N(n,d)} p_\alpha x^\alpha$ is an n-variate polynomial of degree d, and ${{\mathbf {K}}}\subset {\mathbb {R}}^n$ a closed set with nonempty interior. In the subsequent discussion we always assume that a global minimizer exists. We also assume that the moments of a finite Borel measure $\mu$ supported on ${{\mathbf {K}}}$ are known in the sense that they are either available in closed form or efficiently computable. Recall that a finite Borel measure $\mu$ on ${\mathbb {R}}^n$ as a nonnegative set function defined on the Borel $\sigma$-algebra of ${\mathbb {R}}^n$, that is, the $\sigma$-algebra generated by all open sets in ${\mathbb {R}}^n$. By definition, $\mu$ must satisfy $\mu (\emptyset ) = 0$ and $\mu (\cup _{i=1}^\infty S_i) = \sum _{i=1}^\infty \mu (S_i)$ for any countable collection of disjoint, measurable sets $S_i \subset {\mathbb {R}}^n$, $i\in \mathbb N$, and $\mu ({\mathbb {R}}^n) < \infty$. The support of $\mu$, denoted by $\text{ supp }(\mu )$, is defined as the smallest closed set ${{\mathbf {K}}}$ with $\mu \left( {\mathbb {R}}^n{\setminus } {{\mathbf {K}}}\right) = 0$.

In the following we denote the (known) moments of $\mu$ by

$$\begin{aligned} m_{\alpha }({\mathbf {K}}):=\int _{{\mathbf {K}}}x^{\alpha }d\mu (x)\ \ \ \text { for } \alpha \in {{\mathbb {N}}}_0^n. \end{aligned}$$

(3)

Lasserre [28] introduced the following upper bound on $p_{\min ,{{\mathbf {K}}}}$,

$$\begin{aligned} \underline{p}_{{\mathbf {K}}}^{(r)}:= & {} \min _{h \in \varSigma [x]_r} \left\{ \int _{{\mathbf {K}}}p(x)h(x) d\mu (x) \; : \; \int _{{\mathbf {K}}}h(x) d\mu (x)=1 \right\} \nonumber \\= & {} \min _{h \in \varSigma [x]_r} {{\mathbb {E}}}_{x \sim ({\mathbf {K}},h)} [p(x)], \end{aligned}$$

(4)

where r is a fixed integer, and $x \sim ({\mathbf {K}},h)$ indicates that x is a random vector supported on ${\mathbf {K}}$ that is governed by the probability measure $h\cdot d\mu$. It is known that $\underline{p}_{{\mathbf {K}}}^{(r)}$ is equal to the smallest generalized eigenvalue of the system

$$\begin{aligned} Av = \lambda Bv, \end{aligned}$$

(5)

where $v \ne 0$ is the generalized eigenvector corresponding to $\lambda$, while the symmetric matrices A and B are of size ${n + r \atopwithdelims ()r}$ with rows and columns indexed by N(n, r), and

$$\begin{aligned} A_{\alpha , \beta } = \sum _{\delta \in N(n,d)} p_\delta m_{\alpha +\beta +\delta }({\mathbf {K}}), \quad B_{\alpha , \beta } = m_{\alpha +\beta }({\mathbf {K}}) \quad \text { for } \alpha , \beta \in {N}(n,r). \end{aligned}$$

(6)

A review of solution techniques for the generalized eigenvalue problem may be found in [18, §8.7.2]. Lasserre [28] established conditions on $\mu$ and ${{\mathbf {K}}}$ ensuring that $\lim _{r\rightarrow \infty } \underline{p}_{{\mathbf {K}}}^{(r)} = p_{\min ,{{\mathbf {K}}}}$, and the rate of convergence was subsequently studied in [8,9,10] for special choices of $\mu$ and ${{\mathbf {K}}}$. The most general condition under which convergence is known to hold, as shown in [29, Theorem 2.2], is when $\mu$ is supported on a closed, basic semi-algebraic set ${{\mathbf {K}}}$ with nonempty interior, all moments of $\mu$ are finite, and there is $M>0$ such that

$$\begin{aligned} \int _{{\mathbf {K}}}x_i^{2k}d\mu (x) \le (2k)!M \;\;\; \forall i\in \{1,\ldots ,n\},k \in {\mathbb {N}}. \end{aligned}$$

(7)

For example, if one defines $\mu$ in terms of a finite Borel measure $\varphi$ with supp$(\varphi ) = {{\mathbf {K}}}$ via

$$\begin{aligned} d\mu (x) = \exp \left( -c|x_1|-\cdots -c|x_n|\right) d\varphi (x) \end{aligned}$$

(8)

for some fixed $c>0$, then $\mu$ satisfies the conditions (7); see [28, §3.2].

We summarize the known convergence results in Table 1.

Table 1 Known rates of convergence for the Lasserre hierarchy

2.1 Examples of known moments

The moments (3) are available in closed form, for example, if $\mu$ is the Lebesgue measure and ${{\mathbf {K}}}$ is an ellipsoid or triangulated polytope; see, e.g., [10, 28]. For the canonical simplex, $\varDelta _n=\{x\in {{\mathbb {R}}}^n_+:\sum _{i=1}^n x_i \le 1\}$, we have

$$\begin{aligned} m_{\alpha }(\varDelta _n)={\prod _{i=1}^n\alpha _i!\over (\sum _{i=1}^n \alpha _i +n)!}, \end{aligned}$$

(9)

see, e.g., [26, Equation (2.4)] or [21, Equation (2.2)]. One may trivially verify that the moments for the hypercube ${{\mathbf {Q}}}_n=[0,1]^n$ are given by

$$\begin{aligned} m_{\alpha }({{\mathbf {Q}}}_n)=\int _{{{\mathbf {Q}}}_n}x^{\alpha }dx=\prod _{i=1}^n \int _0^1x_i^{\alpha _i}dx_i=\prod _{i=1}^n \frac{1}{\alpha _i+1}. \end{aligned}$$

The moments for the unit Euclidean ball are given by

$$\begin{aligned} m_{\alpha }(B_1(0)) = \left\{ \begin{array}{ll} {\pi ^{(n-1)/2}2^{(n+1)/ 2} \prod _{i=1}^n\left( \alpha _i-1\right) !! \over (n+\sum _{i=1}^n \alpha _i)!!} &{} \quad \text {if } \alpha _i \text { is even for all } i,\\ 0 &{} \quad \text { otherwise,} \end{array} \right. \end{aligned}$$

(10)

where the double factorial of any integer k is defined through

$$\begin{aligned} k!! = \left\{ \begin{array}{l@{\quad }l} k\cdot (k-2)\cdots 3\cdot 1 &{} \text {if } k>0 \text { is odd,}\\ k\cdot (k-2)\cdots 4\cdot 2 &{} \text {if } k>0 \text { is even,}\\ 1 &{} \text {if } k=0 \text { or } k=-1. \end{array} \right. \end{aligned}$$

When ${{\mathbf {K}}}$ is an ellipsoid, one may obtain the moments from (10) via an affine variable transformation. Another tractable support set that will become relevant in Sect. 6.1 of this paper is the knapsack polytope, that is, the intersection of a hypercube and a half-space; the moments for this and other related polytopes are derived in [34]. Finally, in Sect. 6.3 we will work with the nonnegative orthant ${{\mathbf {K}}}= {\mathbb {R}}^n_+$. Since ${{\mathbf {K}}}$ is unbounded in this case, we need to introduce a measure of the form (8). A suitable choice that corresponds to $c = 1/2$ and $d\varphi (x) = \exp \left( -\frac{1}{2}\sum _{i=1}^n x_i\right) dx$ in (8) is

$$\begin{aligned} d\mu (x) = \exp \left( -\sum _{i=1}^n x_i\right) dx. \end{aligned}$$

This is the exponential measure associated with the orthogonal Laguerre polynomials.

We will also use another choice of measure for ${{\mathbf {K}}}= {\mathbb {R}}^n_+$ in Sect. 6.3, namely the lognormal measure,

$$\begin{aligned} d\mu (x) = \prod _{i=1}^n \frac{1}{x_i v_i \sqrt{2\pi }} \exp \left( - \frac{(\ln (x_i) - {\bar{z}}_i)^2}{2 v_i^2} \right) dx_i, \end{aligned}$$

(11)

where ${\bar{z}}_i$ and $v_i$ represent prescribed location and scale parameters for all $i = 1,\ldots ,n$. In this case the moments of $\mu$ are given by

$$\begin{aligned} m_{\alpha }({\mathbf {K}}) = \prod _{i=1}^n \exp (\alpha _i {\bar{z}}_i + (\alpha _i v_i)^2 / 2). \end{aligned}$$

(12)

One may verify that these moments do not obey the bounds in (7). When using the lognormal measure we are therefore not guaranteed convergence of the Lasserre hierarchy.

We stress that, even though these examples of known moments are limited, they include typical sets that are routinely used in (distributionally) robust optimization to represent uncertainty sets or supports, most notably budget uncertainty sets and ellipsoids.

3 Distributionally robust constraints with ambiguous polynomial density functions

Consider now a worst-case feasibility expectation of the form (1), where $z \in {\mathbb {R}}^m$ represents a random vector with support ${{\mathbf {K}}}\subset {\mathbb {R}}^m$, assumed to be closed and with nonempty interior. Suppose that the constraint function f(x, z) displays a polynomial dependence on z. In particular, assume that $f(x,z)=\sum _{\beta \in N(m,d)}f_{\beta }(x)z^\beta$ has degree d in z, where the $f_\beta :{\mathbb {R}}^n \rightarrow {\mathbb {R}}$ are functions of x only.

If the ambiguity set ${\mathcal {P}}$ contains all distributions that have an SOS polynomial density of degree at most 2r, $r>1$, with respect to a fixed, finite Borel measure $\mu$ supported on ${\mathbf {K}}$, then the worst-case expectation constraint (1) reduces to

$$\begin{aligned} f_{{{\mathbf {K}}}}^{(r)}(x) := \inf _{h\in \varSigma [z]_r}\left\{ \int _{{\mathbf {K}}}f(x,z)h(z)d\mu (z) \ \ : \; \int _{{\mathbf {K}}}h(z)d\mu (z)=1\right\} \ge 0. \end{aligned}$$

(13)

Formally speaking, we consider an ambiguity set of the form

$$\begin{aligned} {\mathcal {P}} = \left\{ h\cdot d\mu \;:\; h\in \varSigma [z]_r, \; \int _{{\mathbf {K}}} h(z)d\mu (z)=1 \right\} . \end{aligned}$$

(14)

We assume that the moments of the measure $\mu$ on ${{\mathbf {K}}}$ are available, and we again use the notation

$$\begin{aligned} m_{\alpha }({\mathbf {K}}):=\int _{{\mathbf {K}}}z^{\alpha }d\mu (z)\ \ \ \text { for } \alpha \in {{\mathbb {N}}}^m_0. \end{aligned}$$

Expressing $h\in \varSigma [z]_r$ as $h(z)=\sum _{\alpha \in N(m,2r)}h_{\alpha }z^{\alpha }$, the left-hand-side of (13) may be re-written as

$$\begin{aligned} \begin{array}{cl} \displaystyle \inf _{h_\alpha : \alpha \in N(m,2r)} &{} \displaystyle \sum _{\beta \in N(m,d)}f_{\beta }(x)\sum _{\alpha \in N(m,2r)}h_{\alpha }m_{\alpha +\beta }({\mathbf {K}})\\ \text { s.t. } &{} \displaystyle \sum _{\alpha \in N(m,2r)}h_{\alpha }m_{\alpha }({\mathbf {K}})=1,\\ &{} \displaystyle \sum _{\alpha \in N(m,2r)}h_{\alpha }z^{\alpha }\in \varSigma [z]_r. \end{array} \end{aligned}$$

(15)

Since the condition that h be a sum-of-squares polynomial is equivalent to a linear matrix inequality in the coefficients of h, problem (15) constitutes a tractable SDP in $h_\alpha$, $\alpha \in N(m,2r)$, if x is fixed. The next theorem establishes that we can also efficiently optimize over the feasible set of the constraint (13) whenever the coefficient functions $f_\beta$ are concave and ${{\mathbf {K}}}\subset {\mathbb {R}}^m_+$.

Theorem 1

Assume that all $f_{\beta }$ are concave functions of x whose supergradients are efficiently computable. Moreover, assume that ${{\mathbf {K}}}\subset {\mathbb {R}}^m_+$. Then, the set of $x \in {\mathbb {R}}^n$ that satisfy the worst-case expectation constraint (13) is convex and admits a polynomial-time separating hyperplane oracle.

Proof

We have to show that the function $f_{{{\mathbf {K}}}}^{(r)}(x)$ defined in (13) is concave in x. To this end, we may rewrite this function as

$$\begin{aligned} f_{{{\mathbf {K}}}}^{(r)}(x) = \inf _{h \in \varSigma [z]_r} \sum _{\beta \in N(m,d)} {\mathbb {E}}_{z \sim ({{\mathbf {K}}},h)}\left[ z^\beta \right] f_{\beta }(x). \end{aligned}$$

For each $h \in \varSigma [z]_r$, the function ${\mathbb {E}}_{z \sim ({{\mathbf {K}}},h)}\left[ z^\beta \right] f_{\beta }(x)$ is concave in x because ${{\mathbf {K}}}\subset {\mathbb {R}}^m_+$ implies that ${\mathbb {E}}_{z \sim ({{\mathbf {K}}},h)}\left[ z^\beta \right] \ge 0$. Thus, $f_{{{\mathbf {K}}}}^{(r)}(x)$ is the point-wise infimum of an infinite collection of concave functions and is therefore itself concave (see, e.g., [42, Theorem 5.5]). This allows us to conclude that the set ${\mathcal {C}} := \{x \in {\mathbb {R}}^n \; | \; f_{{{\mathbf {K}}}}^{(r)}(x) \ge 0\}$ is convex.

If ${\bar{x}} \notin {\mathcal {C}}$, i.e., $f_{{{\mathbf {K}}}}^{(r)}({\bar{x}}) < 0$, then we may construct a hyperplane that separates ${\bar{x}}$ from ${\mathcal {C}}$ as follows. Let ${\bar{h}} \in \varSigma [z]_r$ be such that

$$\begin{aligned} f_{{\bar{h}}}({\bar{x}}) := \sum _{\beta \in N(m,d)} {\mathbb {E}}_{z \sim ({{\mathbf {K}}},{\bar{h}})}\left[ z^\beta \right] f_{\beta }({\bar{x}}) < 0. \end{aligned}$$

In particular, we may choose ${\bar{h}}$ to be the worst-case density obtained by solving the SDP (15) with fixed $x= {\bar{x}}$. Now let $\partial f_{{\bar{h}}}({\bar{x}})$ denote a supergradient of $f_{{\bar{h}}}$ at ${\bar{x}}$. Note that, by assumption, such a supergradient is available in polynomial time. By the definition of a supergradient, we now have

$$\begin{aligned} \partial f_{{\bar{h}}}({\bar{x}})^T (x - {\bar{x}}) \ge f_{{\bar{h}}}(x) - f_{{\bar{h}}}({\bar{x}}) \ge -f_{{\bar{h}}}({\bar{x}})>0 \quad \forall x \in {\mathcal {C}}. \end{aligned}$$

Thus, the hyperplane $\{x \in {\mathbb {R}}^n \; | \; \partial f_{\bar{h}}({\bar{x}})^T (x - {\bar{x}}) =0\}$ separates ${\bar{x}}$ from ${\mathcal {C}}$. $\square$

Theorem 1 implies that if all coefficient functions $f_{\beta }$ are concave, one may minimize a convex function of x over a feasible set given by constraints of the type (13) in polynomial time, e.g., by using the ellipsoid method, provided that an initial ellipsoid is known that contains an optimal solution [20].

Finally, we point out that, due to the convergence properties of the Lasserre hierarchy, one recovers the usual robust counterpart (robust against the single worst-case realization of z as in [1]) in the limit as r tends to infinity.

Theorem 2

Assume that ${{\mathbf {K}}}\subset {\mathbb {R}}^n$ is closed with nonempty interior. Then, in the limit as $r \rightarrow \infty$, the constraint (13) reduces to the usual robust counterpart constraint

$$\begin{aligned} \min _{z \in {{\mathbf {K}}}} f(x,z) \ge 0. \end{aligned}$$

More precisely, if $x \in {{\mathbf {K}}}$ is fixed, and $({{\mathbf {K}}},\mu )$ satisfies one of the assumptions in Table 1, one has

$$\begin{aligned} \lim _{r \rightarrow \infty } f_{{{\mathbf {K}}}}^{(r)}(x) = \min _{z \in {{\mathbf {K}}}} f(x,z). \end{aligned}$$

Moreover, the rate of convergence is as given in Table 1, depending on the choice of $({{\mathbf {K}}},\mu )$.

Proof

For fixed x, the computation of $f_{{{\mathbf {K}}}}^{(r)}(x)$ is an SDP problem of the form (4), and the required convergence result therefore follows from the convergence of the Lasserre hierarchy (4), as summarized in Table 1. $\square$

4 Approximate solution of the general problem of moments

In applications it is often possible to reduce the ambiguity set ${\mathcal {P}}$ by including information about the moments of the unknown probability distribution at play. For example, if there is prior information about the location or the dispersion of the random vector z, one can include constraints on its mean vector or its covariance matrix into the definition of the ambiguity set. Specifically, if it is known that ${{\mathbb {E}}}_{z \sim ({\mathbf {K}},h)} [z^{\beta _i}]=\gamma _i$ for some $\beta _i\in \mathbb N_0^n$ and $\gamma _i\in {\mathbb {R}}$ for $i=1,\ldots ,p$, one can restrict the ambiguity set (14) by including the moment constraints

$$\begin{aligned} \int _{{\mathbf {K}}} z^{\beta _i} h(z) d\mu (z)=\sum _{\alpha \in N(m,2r)}h_{\alpha }m_{\alpha +\beta _i}({\mathbf {K}})=\gamma _i \quad \forall i = 1,\ldots ,p, \end{aligned}$$

which reduce to simple linear equations for the coefficients $h_{\alpha }$, $\alpha \in N(m,2r)$, of the density function h. In this setup, the maximization over the ambiguity set corresponds to a general problem of moments (see, e.g., [46]), where one optimizes the expectation of a function of a random variable over a set of probability measures with known generalized moments. To formalize this problem and to showcase how our approach relates to it, we assume throughout this section that ${{\mathbf {K}}}\subset {\mathbb {R}}^n$ is a nonempty closed set, while $f_0, f_1, \ldots , f_p$ are real-valued Borel-measurable functions on ${{\mathbf {K}}}$. Moreover, we assume that $\mu$ is a finite Borel measure on ${{\mathbf {K}}}$ such that $f_0,\ldots ,f_p$ are $\mu$-integrable.

Definition 1

The general problem of moments is defined as the optimization problem

$$\begin{aligned} b_0:=\inf _{\nu \in {\mathcal {P}}_0} \left\{ \int _{{{\mathbf {K}}}_0} f_0(z)d\nu (z) \; : \; \int _{{{\mathbf {K}}}_i} f_i(z)d\nu (z) = b_i \;\forall i = 1,\ldots ,p\right\} , \end{aligned}$$

(16)

where ${\mathcal {P}}_0$ is the set of all Borel probability measures supported on ${{\mathbf {K}}}$, and ${{\mathbf {K}}}_i$ is a Borel-measurable subset of ${{\mathbf {K}}}$ for each $i=0,\ldots ,p$.

We now showcase that in the presence of moment information our polynomial-based approach may be used to approximately solve problem (16), and we will illustrate this through concrete examples in Sect. 6. We begin by recalling the following result due to Rogosinsky [43].

Theorem 3

Let ${\mathbf {K}}_i$, $i=0,\ldots ,p$, be Borel-measureable subsets of ${{\mathbf {K}}}$. Then there exists an atomic Borel measure $\mu '$ on ${{\mathbf {K}}}$ with a finite support of at most $p+2$ points so that

$$\begin{aligned} \int _{{{\mathbf {K}}}_i} f_i(z)d\mu (z) = \int _{{{\mathbf {K}}}_i} f_i(z)d\mu '(z) \quad \forall i = 0,\ldots ,p. \end{aligned}$$

Proof

An elementary proof is given by Shapiro [46, Lemma 3.1]; see also Lasserre [27]. $\square$

The following corollary is an immediate consequence of Theorem 3.

Corollary 1

If the problem (16) has a solution, it has a solution that is an atomic measure supported on at most $p+2$ points in ${{\mathbf {K}}}$, i.e., a convex combination of at most $p+2$ Dirac delta measures supported on ${{\mathbf {K}}}$.

In what follows we show how the atomic measure solution, whose existence is guaranteed by Corollary 1, may be approximated arbitrarily well by SOS polynomial density functions.

Theorem 4

Assume that problem (16) has an optimal solution, ${{\mathbf {K}}}\subset {\mathbb {R}}^n$ has nonempty interior, the functions $f_0$, $f_1$, $\ldots$, $f_p$ are polynomials, and that the sets ${{\mathbf {K}}}_i$ are closed ($i=0,\ldots ,p$). Also assume that ${{\mathbf {K}}}$ and $\mu$ satisfy one of the assumptions in Table 1. Then, as r tends to infinity,

$$\begin{aligned} \varepsilon (r) := \inf _{h \in \varSigma _r} \max _{i \in \{0,\ldots ,p\}} \left| \int _{{{\mathbf {K}}}_i} f_i(z)h(z)d\mu (z) - b_i\right| \end{aligned}$$

converges to zero at the rate (see also Table 1):

• 1. $\varepsilon (r) = o(1)$ if ${{\mathbf {K}}}$ is basic semi-algebraic, all moments of $\mu$ are finite, and (7) holds;

• 2. $\varepsilon (r) = o(1)$ if ${{\mathbf {K}}}$ is compact and $\mu$ a finite Borel measure;

• 3. $\varepsilon (r) = O(r^{-1/4})$ if ${{\mathbf {K}}}$ is compact and satisfies an interior cone condition, and $\mu$ is the Lebesgue measure;

• 4. $\varepsilon (r) = O(r^{-1/2})$ if ${{\mathbf {K}}}$ is a convex body, and $\mu$ is the Lebesgue measure;

• 5. $\varepsilon (r) = O(r^{-1})$ if ${{\mathbf {K}}}= [-1,1]^n$, and $d\mu (x) = \prod _{i=1}^n (1-x_i^2)^{-1/2}dx_i$.

Proof

We first outline the proof strategy. The high-level idea is to approximate the discrete solution of the moment problem (16) by a convex combination of probability distributions with SOS density functions. Each density is obtained from the Lasserre hierarchy (4), applied to a suitable polynomial (denoted by ${\hat{p}}$ below).

Define the functions

$$\begin{aligned} {\widehat{f}}_i(z) = \left\{ \begin{array}{cl} f_i(z) &{}\quad \text{ if } z \in {{\mathbf {K}}}_i, \\ 0 &{}\quad \text {else,} \end{array} \right. \end{aligned}$$

for $i =0,\ldots ,p$. Thus, each ${\widehat{f}}_i$ is Borel-measurable. Moreover, fix $a \in {{\mathbf {K}}}$, and let ${{\widehat{p}}}$ be a polynomial with global minimizer a such that ${{\widehat{p}}}(a) = 0$ and

$$\begin{aligned} {{\widehat{p}}}(z) \ge [\widehat{f_i}(z)- \widehat{f_i}(a)]^2 \quad \forall z \in {{\mathbf {K}}},\; i \in \{0,\ldots ,p\}. \end{aligned}$$

(17)

For example, ${\widehat{p}}$ may be defined through

$$\begin{aligned} {{\widehat{p}}}(z)&= \sum _{i=0}^p [f_i(z)- f_i(a)]^2 + \sum _{i: a \notin {{\mathbf {K}}}_i} \frac{f_i(z)^2 \Vert z-a\Vert ^2}{(\text{ dist }(a,{{\mathbf {K}}}_i))^2} \\&\quad + \sum _{i: a \in {{\mathbf {K}}}_i} \frac{f_i(a)^2 \Vert z-a\Vert ^2}{(\min _{j:a \notin {{\mathbf {K}}}_j} \text{ dist }(a,{{\mathbf {K}}}_j))^2}, \end{aligned}$$

where $\text{ dist }(a,{{\mathbf {K}}}_i) = \inf _{z \in {{\mathbf {K}}}_i} \Vert z-a\Vert$ is the Euclidean distance of a to the closed set ${{\mathbf {K}}}_i$. Indeed, the polynomial ${{\widehat{p}}}$ is nonnegative and has the global minimizer $z=a$ with ${{\widehat{p}}}(a) = 0$. Moreover, one may verify that (17) holds by distinguishing the four cases (for fixed $i \in \{0,1,\ldots ,p\}$):

• (i) $a \in {{\mathbf {K}}}_i$ and $z \in {{\mathbf {K}}}_i$,

• (ii) $a \in {{\mathbf {K}}}_i$ and $z \notin {{\mathbf {K}}}_i$,

• (iii) $a \notin {{\mathbf {K}}}_i$ and $z \in {{\mathbf {K}}}_i$,

• (iv) $a \notin {{\mathbf {K}}}_i$ and $z \notin {{\mathbf {K}}}_i$.

It is immediate to verify that (17) holds for cases (i) and (iv). For case (ii), note that

$$\begin{aligned} {\hat{p}}(z)\ge & {} [f_i(z)- f_i(a)]^2 + \frac{f_i(a)^2 \Vert z-a\Vert ^2}{(\min _{j:a \notin {{\mathbf {K}}}_j} \text{ dist }(a,{{\mathbf {K}}}_j))^2}\\\ge & {} f_i(a)^2 -2f_i(z)f_i(a) +f_i(z)^2 + f_i(a)^2 \\= & {} [\widehat{f_i}(z)- \widehat{f_i}(a)]^2 + (f_i(z)-f_i(a))^2 \\\ge & {} [\widehat{f_i}(z)- \widehat{f_i}(a)]^2. \end{aligned}$$

Case (iii) may be verified similarly.

The idea is now to apply the Lasserre hierarchy to minimize ${{\widehat{p}}}$. For a given probability density $h \in \varSigma [z]_r$ with $\int _{{{\mathbf {K}}}} h(z)d\mu (z) =1$, we write as before

$$\begin{aligned} {\mathbb {E}}_{z \sim ({{\mathbf {K}}},h)} [{{\widehat{p}}}(z)] = \int _{{{\mathbf {K}}}} {\widehat{p}}(z) h(z)d\mu (z). \end{aligned}$$

Recalling the notation of the Lasserre hierarchy from (4), we set $\underline{{\widehat{p}}}_{{\mathbf {K}}}^{(r)} =\min _{h \in \varSigma [z]_r} {{\mathbb {E}}}_{z \sim ({\mathbf {K}},h)} [{\widehat{p}}(z)]$. If $\mu$ and ${{\mathbf {K}}}$ satisfy any of the conditions in Table 1, we have $\lim _{r \rightarrow \infty } \underline{{\widehat{p}}}_{{\mathbf {K}}}^{(r)} = 0$, with the rate of convergence as indicated in the table. Thus, for any $\varepsilon > 0$ there is a sufficiently large $r_a \in {\mathbb {N}}$ and a density $h_a \in \varSigma [z]_{r_a}$ such that

$$\begin{aligned} {\mathbb {E}}_{z \sim ({{\mathbf {K}}},h_a)} \left[ (\widehat{f_i}(z) - \widehat{f_i}(a))^2\right] \le \underline{\widehat{p}}_{{\mathbf {K}}}^{(d)} \le {\varepsilon ^2} \quad \forall i \in \{0,\ldots ,p\}. \end{aligned}$$

(18)

The asymptotics of the polynomial degree $r_a$ needed to drive the error below $\varepsilon$ follows from the convergence rates reported in Table 1. For example, if ${{\mathbf {K}}}$ is a convex body and $\mu$ is the Lebesgue measure, we may assume that $r_a = O\left( \frac{1}{\epsilon ^2} \right)$, or equivalently that $\varepsilon = \varepsilon (r_a) = O(r_a^{-1/2})$.

Using Jensen’s inequality, we have, for each $i \in \{0,\ldots ,p\}$,

$$\begin{aligned} {\mathbb {E}}_{z \sim ({{\mathbf {K}}},h_a)} \left[ (\widehat{f_i}(z) - \widehat{f_i}(a))^2\right]\ge & {} \left( {\mathbb {E}}_{z \sim ({{\mathbf {K}}},h_a)} [(\widehat{f_i}(z) - \widehat{f_i}(a))]\right) ^2 \\= & {} \left\{ \begin{array}{ll} \left[ \int _{{{\mathbf {K}}}_i} f_i(z) h_a(z)d\mu (z) - f_i(a)\right] ^2 &{} \text{ if } a \in {{\mathbf {K}}}_i, \\ \left[ \int _{{{\mathbf {K}}}_i} f_i(z)h_a(z)d\mu (z)\right] ^2 &{} \text{ if } a \notin {{\mathbf {K}}}_i. \end{array}\right. \end{aligned}$$

We conclude that, for $i \in \{0,\ldots ,p\}$,

$$\begin{aligned} \left| \int _{{{\mathbf {K}}}_i} f_i(z)h_a(z)d\mu (z) - f_i(a) \right| \le \varepsilon \text{ if } a \in {{\mathbf {K}}}_i, \;\; \left| \int _{{{\mathbf {K}}}_i} f_i(z)h_a(z)d\mu (z) \right| \le \varepsilon \text{ if } a \notin {{\mathbf {K}}}_i. \end{aligned}$$

(19)

In this sense, the measure $h_a(z) d\mu (z)$ can be viewed as an approximation of the Dirac point measure $\delta _a$ that concentrates unit mass at a.

In the following we denote by $\nu = \sum _{j=0}^{p+1} \lambda _j\delta _{a_j}$ an atomic measure that is optimal in (16) with atoms $a_j \in {{\mathbf {K}}}$ and corresponding probabilities $\lambda _j\ge 0$, $j=0,\ldots , p+1$, where $\sum _{j=0}^{p+1} \lambda _j = 1$. The atomic measure $\nu$ exists due to Corollary 1 and because the generalized moment problem (16) is solvable by assumption.

By the optimality and feasibility of $\nu$ in (16) we have

$$\begin{aligned} \int _{{{\mathbf {K}}}_i} f_i d\nu = \sum _{j:a_j \in {{\mathbf {K}}}_i} \lambda _j f_i(a_j) = b_i \quad \forall i \in \{0,\ldots ,p\}. \end{aligned}$$

We now approximate the atomic measure $\nu$ by a measure of the form $\sum _j \lambda _j h_{a_j}(z) d\mu (z)$, where $h_{a_j}$ is an SOS density of degree $r_{a_j}$, say, as in (18) with $a = a_j$. Setting $r = \max _j r_{a_j}$ and $h = \sum _j \lambda _j h_{a_j} \in \varSigma [z]_r$, we may use (19) to conclude that

$$\begin{aligned}&\left| \int _{{{\mathbf {K}}}_i} f_i(z)h(z)d\mu (z) - b_i\right| \\&\quad \le \sum _{j:a_j \in {{\mathbf {K}}}_i} \lambda _j \left| \int _{{{\mathbf {K}}}_i} f_i(z)h_{a_j}(z)d\mu (z) - f_i(a_j)\right| \\&\qquad + \sum _{j:a_j \notin {{\mathbf {K}}}_i} \lambda _j \left| \int _{{{\mathbf {K}}}_i} f_i(z)h_{a_j}(z)d\mu (z) \right| \le \sum _j \lambda _j \varepsilon = \varepsilon , \end{aligned}$$

for each $i \in \{0,\ldots ,p\}$.

Note again that the relation between $\varepsilon$ and r follows from Table 1. For example, if ${{\mathbf {K}}}$ is a convex body and $\mu$ is the Lebesgue measure, we may assume that $\varepsilon = \varepsilon (r) = O(r^{-1/2})$. The other cases listed in the theorem statement can be proved analogously. $\square$

As a consequence of Theorem 4, we may obtain approximate solutions to the generalized problem of moments (16) by solving SDPs of the form:

$$\begin{aligned}&\min _{h \in \varSigma [z]_r} \left\{ \int _{{{\mathbf {K}}}_0} f_0(z)h(z)d\mu (z) \; : \; \int _{{{\mathbf {K}}}_i} f_i(z)h(z)d\mu (z) \in [b_i-\varepsilon (r),b_i+\varepsilon (r)] \;\right. \nonumber \\&\left. \quad \forall i = 1,\ldots ,p\right\} \end{aligned}$$

(20)

for $r \in {\mathbb {N}}$, and where we may assume $\varepsilon (r) >0$ depends on r as indicated in the theorem statement.

In analogy to Theorem 2, Theorem 4 has interesting implications for distributionally robust optimization. Indeed, if we replace the set ${\mathcal {P}}_0$ of all probability measures used in (16) by the ambiguity set (14) of all probability measures with SOS densities of degree at most 2r, then we essentially obtain the SDP problem (20) (modulo the tolerance $\varepsilon (r)$ that is needed to ensure feasibility). By Theorem 4, the solution of the SDP (20) converges to the solution of (16) as $r \rightarrow \infty$. Thus we may again view r as the degree of conservatism (or risk-aversion), to be chosen by a user for the problem at hand. We will see detailed examples of such modeling in Sect. 6.

Finally, we emphasize that the tolerance $\varepsilon (r)$ is unavoidable. For example, the constraint

$$\begin{aligned} \int _0^1 z^2 d\mu (z) = 0 \end{aligned}$$

for $\mu$ is solved by the Dirac delta centered at zero, but it admits no solution of the form $d\mu (z) = h(z)dz$ with $h \in \varSigma _r$ for any r.

We remark that the SDP hierarchy (20) is different from the one studied by Lasserre [27], where an outer approximation of the cone of finite Borel measures supported on ${{\mathbf {K}}}$ is used, whereas we use an inner approximation. The advantage of the inner approximation is that it allows us to derive the convergence result of Theorem 4, which quantifies the error in terms of the SOS density degrees.

5 Modeling power

The ambiguity set ${\mathcal {P}}$ defined in (14) contains all distributions supported on a convex body ${\mathbf {K}}$ that have an SOS polynomial density $h\in \varSigma [z]_r$ with respect to a prescribed reference measure $\mu$.

In stochastic programming, it is common to model $\mu$ as a probability measure that best reflects one’s information about the stochastics of the uncertain problem parameter z. Thus, $\mu$ is typically constructed by fitting a parametric model to a given dataset by using some methods of statistics. Classical stochastic programming takes this estimated model at face value and ignores the possibility that the true data-generating distribution might deviate from $\mu$. In this paper, we suggest to construct $\mu$ as one would do in stochastic programming, which implies that stochastic programming actually emerges as a special case of our distributionally robust optimization approach if we set $r=0$. Setting $r>0$, on the other hand, implies that we do not place full trust in $\mu$ but take into consideration other probability measures that have a polynomial density function $h \in \varSigma [z]_r$ with respect to $\mu$. Intuitively, the less we trust in $\mu$, the higher we should set r. Thus, r can be interpreted as a regularization parameter to be tuned via cross-validation, for instance.

Another possible motivation for the choice of r comes from approximation theory. If one wants to safeguard against a class of distributions, e.g., truncated multivariate normal distributions on some convex body ${\mathbf {K}}$ with norm of the covariance matrix in some range and mean in some interval, then there are theorems from approximation theory that tell one what the degree of the polynomial SOS density should be to get an approximation of the truncated normal density within $\epsilon$ on K.

For example, the following result is implicit in [8].

Theorem 5

Consider a convex body ${\mathbf {K}}$ and a truncated exponential-type distribution on ${\mathbf {K}}$ with probability density given by

$$\begin{aligned} P_f(x) = \frac{\exp (-f(x))}{\int _{{\mathbf {K}}} \exp (-f(x)) dx}, \end{aligned}$$

where f is a polynomial of degree d that is nonnegative on ${\mathbf {K}}$. Then, there exists a probability density $h \in \varSigma _{rd}$ such that

$$\begin{aligned} P_{f}(x) \le h(x) \le P_{f}(x) + \frac{ {(f(x))^{2r+1} }}{(2r+1)!\int _{{{\mathbf {K}}}} \exp (-f(x))dx}. \end{aligned}$$

One may therefore choose r such that h is a sufficiently good approximation of $P_f$, for some class of f where the maximal value of f on ${{\mathbf {K}}}$ may be bounded.

We have seen that for any fixed r, the worst-case expectation $f_{{{\mathbf {K}}}}^{(r)}(x)$ on the left-hand-side of the worst-case feasibility constraint (13) can be computed efficiently for any fixed x by solving the SDP (15). As decision-makers may have access to prior information that restricts the set of admissible density functions $h\in \varSigma [z]_r$, we demonstrate now that the ambiguity set ${\mathcal {P}}$ admits several generalizations that preserve the SDP-representability of the worst-case expectation.

Moment information As discussed at length in Sect. 4, conditions on (mixed) moment values of different random variables give rise to simple linear conditions on the polynomial coefficients of h.

Confidence information If the random vector z is known to materialize inside a given Borel set ${\mathbf {C}}\subset {\mathbb {R}}^m$ with probability $\gamma \in [0,1]$, we can add the condition ${{\mathbb {P}}}_{z \sim ({\mathbf {K}},h)} [z\in \mathbf C]=\gamma$ to the definition of the ambiguity set ${\mathcal {P}}$. Moreover, if the moments $m_\alpha ({\mathbf {K}}\cap {\mathbf {C}})$ of the reference measure $\mu$ over ${\mathbf {K}}\cap {\mathbf {C}}$ are either available analytically or efficiently computable for all $\alpha \in N(m,2r)$, then this condition can be re-expressed as the following simple linear equation in the polynomial coefficients of h.

$$\begin{aligned} \int _{{\mathbf {K}}} {\mathbf {1}}_{{\mathbf {C}}}\, h(z) d\mu (z)= \sum _{\alpha \in N(m,2r)} h_{\alpha }m_{\alpha }({\mathbf {K}} \cap {\mathbf {C}}) = \gamma \end{aligned}$$

Upper and lower bounds on ${{\mathbb {P}}}_{z \sim ({\mathbf {K}},h)} [z\in {\mathbf {C}}]$ can be handled similarly in the obvious manner. In the context of purely moment-based ambiguity sets, such probability bounds have been studied in [51].

Conditional probabilities Given any two Borel sets ${\mathbf {C}}_1,{\mathbf {C}}_2\subset {\mathbb {R}}^m$ and a probability $\gamma \in [0,1]$, we can also enforce the condition ${{\mathbb {P}}}_{z \sim ({\mathbf {K}},h)} [z\in {\mathbf {C}}_2|z\in {\mathbf {C}}_1]=\gamma$ in the definition of ${\mathcal {P}}$. If the moments $m_\alpha (\mathbf K\cap {\mathbf {C}}_1)$ and $m_\alpha ({\mathbf {K}}\cap {\mathbf {C}}_1\cap {\mathbf {C}}_2)$ of the reference measure $\mu$ are either available analytically or efficiently computable for all $\alpha \in N(m,2r)$, then this condition can be re-expressed as

$$\begin{aligned}&\int _{{\mathbf {K}}} {\mathbf {1}}_{{\mathbf {C}}_1\cap {\mathbf {C}}_2}\, h(z) d\mu (z)= \gamma \int _{{\mathbf {K}}} {\mathbf {1}}_{{\mathbf {C}}_1}\, h(z) d\mu (z) \\&\quad \iff \quad \sum _{\alpha \in N(m,2r)} h_{\alpha }\left( m_{\alpha }({\mathbf {K}} \cap {\mathbf {C}}_1\cap {\mathbf {C}}_2 ) - \gamma \, m_{\alpha }({\mathbf {K}} \cap {\mathbf {C}}_1 )\right) =0, \end{aligned}$$

which is again linear in the coefficients of h. Upper and lower bounds on conditional probabilities can be handled similarly.

Conditional moment information If it is known that ${{\mathbb {E}}}_{z \sim ({\mathbf {K}},h)} [z^{\beta }|\mathbf C]=\gamma$ for some $\beta \in {\mathbb {N}}_0^n$, Borel set $\mathbf C\subset {\mathbb {R}}^m$ and $\gamma \in {\mathbb {R}}$, while the moments $m_{\alpha + \beta }({\mathbf {K}}\cap {\mathbf {C}})$ of the reference measure $\mu$ over set ${\mathbf {K}}\cap {\mathbf {C}}$ are either available analytically or efficiently computable for all $\alpha \in N(m,2r)$, then one can add the following condition to the ambiguity set ${\mathcal {P}}$, which is linear in the coefficients of h.

$$\begin{aligned}&\int _{{\mathbf {K}}} z^{\beta } {\mathbf {1}}_{{\mathbf {C}}}\, h(z) d\mu (z)= \gamma \int _{{\mathbf {K}}} {\mathbf {1}}_{{\mathbf {C}}}\, h(z) d\mu (z) \\&\quad \iff \quad \sum _{\alpha \in N(m,2r)} h_{\alpha }\left( m_{\alpha +\beta }({\mathbf {K}}\cap {\mathbf {C}}) - \gamma \, m_{\alpha }({\mathbf {K}} \cap {\mathbf {C}} )\right) =0, \end{aligned}$$

Multiple reference measures The distributions in the ambiguity set ${\mathcal {P}}$ defined in (14) depend both on the reference measure $\mu$ as well as the density function h. A richer ambiguity set can be constructed by specifying multiple reference measures $\mu _i$ with corresponding density functions $h^i\in \varSigma [z]_r$, $i=1,\ldots ,p$. The distributions in the resulting ambiguity set are of the form $\sum _{i=1}^ph^i\cdot d\mu _i$. If the moments $m^i_\alpha (\mathbf K)$ of the reference measure $\mu _i$ over ${\mathbf {K}}$ are either available analytically or efficiently computable for all $\alpha \in N(m,2r)$ and $i=1,\ldots ,p$, then the normalization constraint can be recast as

$$\begin{aligned} \sum _{\alpha \in N(m,2r)} h^i_{\alpha }m^i_{\alpha }({\mathbf {K}})=\gamma _i~\forall i=1,\ldots ,p\quad \text {and} \quad \sum _{i=1}^p\gamma _i=1, \end{aligned}$$

where $\gamma =(\gamma _1,\ldots ,\gamma _p)\ge 0$ constitutes an auxiliary decision vector. The resulting ambiguity set can be interpreted as a convex combination of p ambiguity sets of the form (14) and thus lends itself for modeling multimodality information; see, e.g., [24]. In this case, $\gamma _i$ captures the probability of the i-th mode, which may itself be uncertain. Thus, $\gamma$ should range over a subset of the probability simplex, e.g., a $\phi$-divergence uncertainty set of the type studied in [7].

Marginal distributions It is often easier to estimate the marginal distributions of all m components of a random vector z instead of the full joint distribution. Marginal distribution information can also be conveniently encoded in ambiguity sets of the type (14). To see this, assume that the marginal distribution of $z_i$ is given by $\mu _i$ and is supported on a compact interval ${\mathbf {K}}_i\subset \mathbb R$, $i=1,\ldots ,m$. In this case it makes sense to set and to define the reference measure $\mu$ through $d\mu =\prod _{i=1}^m d\mu _i$. Thus, $\mu$ coincides with the product of the known marginals. The requirement

then ensures that the marginal distribution of $z_i$ under $h\cdot d\mu$ exactly matches $\mu _i$. If the moments $m_{\alpha _i}(\mathbf K_i)$ of the marginal distribution $\mu _i$ over ${\mathbf {K}}_i$ are either available analytically or efficiently computable for all $\alpha _i =1,\ldots , 2r$, then the above condition simplifies to the linear equations

$$\begin{aligned}&\sum _{\begin{array}{c} \alpha \in N(m,2r) \\ \alpha _i=0 \end{array}} h_{\alpha } \prod _{j\ne i} m_{\alpha _j}({\mathbf {K}}_j)=1\quad \text {and}\nonumber \\&\sum _{\begin{array}{c} \alpha \in N(m,2r) \\ \alpha _i=\ell \end{array}} h_{\alpha } \prod _{j\ne i} m_{\alpha _j}({\mathbf {K}}_j)=0 ~\forall \ell =1,\ldots , 2r, \ \forall i = 1,\ldots ,m. \end{aligned}$$

(21)

Situations where the marginals of groups of random variables are known can be handled analogously. Note that when all marginals are known, there is only ambiguity about the dependence structure or copula of the components of z [45]. Quantifying the worst-case copula amounts to solving a so-called Fréchet problem. In distributionally robust optimization, Fréchet problems with discrete marginals or approximate marginal matching conditions have been studied in [13, 14, 49].

We emphasize that, in contrast to the existing approaches in the literature, our method allows us to match any (continuous or discrete) marginal distributions exactly instead of matching only some of their moments.

We illustrate the proposed construction in the following example, where, for ease of exposition, $\mu _1$ and $\mu _2$ are chosen to be uniform measures.

Example 1

Consider a bivariate random vector $z = (z_1, z_2)$ supported on ${{\mathbf {K}}}= [0, 1]^2$, and assume that the marginal distributions of $z_1$ and $z_2$ are known to be governed by the uniform probability measures $\mu _1$ and $\mu _2$ supported on [0, 1], respectively. In this case it makes sense to define the reference measure $\mu$ through $d\mu =d\mu _1 \cdot d\mu _2$. For ease of exposition, we model the probability density function of z with respect to $\mu$ as a polynomial h of degree 2, that is, we set

$$\begin{aligned} h(z) = h_{00} + h_{10}z_1 + h_{01} z_2 + h_{11} z_1 z_2 + h_{20} z_1^2 + h_{02} z_2^2. \end{aligned}$$

Integrating h with respect to $\mu _2$ and $\mu _1$ along $z_2$ and $z_1$ yields the marginal densities

$$\begin{aligned} h_{z_1}(z_1)&= h_{00} + h_{10} z_1 + \frac{1}{2} h_{01} + \frac{1}{2} h_{11} z_1 + h_{20} z_1^2 + \frac{1}{3} h_{02}, \\ h_{z_2}(z_2)&= h_{00} + \frac{1}{2} h_{10} + h_{01} z_2 + \frac{1}{2} h_{11} z_2 + \frac{1}{3} h_{20} + h_{02} z_2^2, \end{aligned}$$

respectively. Here we used the assumption that $\mu _1$ and $\mu _2$ are uniform measures on [0, 1], which implies that their (non-central) first and second moments are given by $\frac{1}{2}$ and $\frac{1}{3}$, respectively. For $z_1$ to be distributed according to $\mu _1$, its marginal density must satisfy $h_{z_1}(z_1)=1$ for all $z_1\in [0,1]$, which is equivalent to the conditions $h_{20}=0$, $h_{10} + h_{11} / 2 = 0$ and $h_{00}+h_{01}/2+h_{02}/3=1$. Similarly, $z_2$ is distributed according to $\mu _2$ if and only if $h_{02}=0$, $h_{01} + h_{11} / 2 = 0$ and $h_{00}+h_{10}/2+h_{20}/3=1$. If we set $h_{11}=\epsilon$, these conditions imply that $h_{20}=h_{02}=0$, $h_{10}=h_{01}=-\epsilon /2$ and $h_{00}=1+\epsilon /4$. In summary, any admissible quadratic density function of z can be represented as

$$\begin{aligned} h(z) = 1+\frac{\epsilon }{4} -\frac{\epsilon }{2} (z_1 + z_2) + \epsilon z_1 z_2 \end{aligned}$$

and is thus determined by the single parameter $\epsilon$. Note that h is nonnegative on ${{\mathbf {K}}}$ if $\epsilon \in [-4,4]$.

Besides the ambiguity set ${\mathcal {P}}$, the constraint function f also admits some generalizations that preserve the SDP-representability of the worst-case expectation in (13).

Uncertainty quantification problems If the constraint function f in (13) is given by $f(x,z)={\mathbf {1}}_{{\mathbf {C}}}$ for some Borel set ${\mathbf {C}}\subset {\mathbb {R}}^m$, then the worst-case expectation reduces to the worst-case probability of the set ${\mathbf {C}}$. Moreover, if the moments $m_\alpha ({\mathbf {K}}\cap {\mathbf {C}})$ of the reference measure $\mu$ over ${\mathbf {K}}\cap {\mathbf {C}}$ are either available analytically or efficiently computable for all $\alpha \in N(m,2r)$, then the worst-case probability can be computed by solving a variant of the SDP (15) with the alternative objective function

$$\begin{aligned} \sum _{\alpha \in N(m,2r)}h_{\alpha }m_{\alpha }({\mathbf {K}}\cap \mathbf C). \end{aligned}$$

6 Numerical experiments

In the following we will exemplify the proposed approach to distributionally robust optimization in the context of financial portfolio analysis (Sect. 6.1), portfolio selection (Sect. 6.2) and risk aggregation (Sect. 6.3).

6.1 Portfolio analysis

Consider a portfolio optimization problem, where the decision vector $x \in {\mathbb {R}}^n$ captures the percentage weights of the initial capital allocated to n different assets. By definition, one thus has $x_i \in [0,1]$ for all $i= 1,\ldots ,n$ and $\sum _{i} x_i = 1$. We assume that the asset returns $r_i = (u_i + l_i) / 2 + z_i (u_i - l_i) / 2$ depend linearly on some uncertain risk factors $z_i \in [-1,1]$ for all $i=1,\ldots , n$, where $u_i$ and $l_i$ represent known upper and lower bounds on the i-th return, respectively. In this framework, we denote by $z\in {\mathbb {R}}^n$ the vector of all risk factors and by ${\mathbf {K}}=[-1,1]^n$ its support. Moreover, the portfolio return can be expressed as

$$\begin{aligned} f(x,z) = \sum \limits _{i=1}^n x_i \cdot ((u_i + l_i) / 2 + z_i (u_i - l_i) / 2). \end{aligned}$$

Unless otherwise stated, we set $\mu$ to the Lebesgue measure on ${\mathbb {R}}^n$. Modeling the probability density functions as SOS polynomials allows us to account for various statistical properties and stylized facts of real asset returns as described in [6]. For example, the proposed approach can conveniently capture gain loss asymmetry, i.e., the observation that large drawdowns in stock prices and stock index values are more common than equally large upward movements. This feature can be modeled by assigning a higher probability to an individual asset’s large upward returns than to its low downward returns. Specifically, the ambiguity set may include the conditions ${\mathbb {P}}_{z \sim ({\mathbf {K}},h)}(z_i \le a_i ) = \gamma _1$ and ${\mathbb {P}}_{z \sim ({\mathbf {K}},h)}(z_i \ge b_i ) = \gamma _2$ for some thresholds $a_i<b_i$ and confidence levels $\gamma _1 > \gamma _2$.

Similarly, our approach can handle correlations of extreme returns. As pointed out in [6], in spite of the widespread use of the covariance matrix, ‘in circumstances when stock prices undergo large fluctuations [...], a more relevant quantity is the conditional probability of a large (negative) return in one stock given a large negative movement in another stock.’ An example constraint on the conditional probability of one asset’s low performance given another assets’ lower performance is ${\mathbb {P}}_{z \sim ({\mathbf {K}},h)}(z_i \le \underline{r}_i| z_j \le \underline{r}_j ) \le \gamma$, where ${\underline{r}}_i$ and ${\underline{r}}_j$ are given thresholds, while $\gamma$ is a confidence level.

In this numerical experiment we evaluate the probability that the return of a fixed portfolio x materializes below a prescribed threshold ${\underline{r}}$, that is, we evaluate the worst case of the probability

$$\begin{aligned} {\mathbb {P}}_{z \sim ({\mathbf {K}},h)} \left( r(x,z) \le \underline{r} \right) \end{aligned}$$

over an ambiguity set ${\mathcal {P}}$ of the form (14) with the additional moment constraints ${{\mathbb {E}}}_{z \sim ({\mathbf {K}},h)} [z^{\beta _i}]=\gamma _i$ for some given exponents $\beta _i\in {\mathbb {N}}_0^n$ and targets $\gamma _i\in {\mathbb {R}}$ for $i=1,\ldots ,p$. This corresponds to computing the integral of the density function over the knapsack polytope ${\mathbf {K}} \cap {\mathbf {A}}(x,u,l, \underline{r} )$, where

$$\begin{aligned} {\mathbf {A}}(x,u,l, \underline{r} ) = \left\{ z\in {\mathbb {R}}^n: \ \sum _{i=1}^n x_i (u_i - l_i) z_i /2 \le \underline{r} - \sum _{i=1}^n x_i (u_i + l_i) / 2 \right\} \end{aligned}$$

represents a halfspace in ${\mathbb {R}}^n$ that depends on the fixed portfolio x, the return bounds $l=(l_1,\ldots l_n)$ and $u=(u_1,\ldots ,u_n)$, and the threshold ${\underline{r}}$. To formulate this problem as an SDP, we first need to compute the moments of the monomials with respect to the Lebesgue measure over the given knapsack polytope by using the results of [34]. The worst-case probability problem can then be reformulated as the SDP

$$\begin{aligned} \begin{array}{cl} \displaystyle \sup \limits _{h(z)} \ &{} \displaystyle \sum _{\alpha \in N(n,2r)} h_{\alpha }m_{\alpha }({\mathbf {K}} \cap {\mathbf {A}}(x,u,l, \underline{r} )) \\ \text {s.t.} \ &{} \displaystyle \sum _{\alpha \in N(n,2r)}h_{\alpha }m_{\alpha }({\mathbf {K}})=1, \\ &{} \displaystyle \sum _{\alpha \in N(n,2r)}h_{\alpha }m_{\alpha +\beta _i}({\mathbf {K}})=\gamma _i \quad \forall i = 1,\ldots ,p, \\ &{} \displaystyle \sum _{\alpha \in N(n,2r)}h_{\alpha }z^{\alpha }\in \varSigma [z]_r. \end{array} \end{aligned}$$

(22)

In the numerical experiment we assume that there are $n = 2$ assets with lower and upper return bounds $l = (0.8, 0.7)^\top$ and $u = (1.2, 1.3)^\top$, respectively. We evaluate the probability that the return of the fixed portfolio $x = (0.75, 0.25)^\top$ falls below the threshold $\underline{r} = 0.9$ (the minimum possible return of the portfolio is 0.775). We assume that the only known moment information about the asset returns is that their means both vanish, that is, we set $p=2$, $\beta _1=(1,0)$, $\beta _2=(0.1)$ and $\gamma _1=\gamma _2=0$. Table 2 reports the exact optimal values of the SDP (22) for $r = 1,\ldots ,12$. The last value in the table (labeled $r=\infty$) provides the worst-case probability across all distributions satisfying the prescribed moment conditions (not only those with a polynomial density) and was computed using the methods described in [23]. In this case, one can also show that there exists a worst-case distribution with only two atoms. It assigns probability 0.31 to the scenario $z=(1,1)^\top$ and probability 0.69 to the scenario $z=(-0.44,-0.44)^\top$. All SDPs are solved using SeDuMi [48] via the CVX interface [19].

Table 2 Worst-case probability of the portfolio return falling below ${\underline{r}}$ computed by solving the SDP (22)

6.2 Mean-variance portfolio selection

We now study a portfolio optimization problem that minimizes the worst-case variance subject to a lower bound on the worst-case mean of the portfolio return. This amounts to solving a distributionally robust optimization problem where an investor selects the portfolio allocation vector x, while a fictitious adversary chooses the density function h(z) of the asset return distribution with the goal to inflict maximum damage to the investor. Specifically, we solve the optimization problem

$$\begin{aligned} \begin{array}{ll} \displaystyle \min \limits _x \ &{} \displaystyle \sup _{{\mathbb {P}} \in {\mathcal {P}}} \textstyle {\mathbb {E}}_{{\mathbb {P}}} \left[ \bigg ( \sum \limits _{i=1}^n x_i \cdot ((u_i + l_i) / 2 + z_i (u_i - l_i) / 2) \right. \\ &{} \qquad \qquad \left. \textstyle - {\mathbb {E}}_{{\mathbb {P}}}\bigg [ \sum \limits _{i=1}^n x_i \cdot ((u_i + l_i) / 2 + z_i (u_i - l_i) / 2)\bigg ] \bigg )^2 \right] \\ \text {s.t.} \ &{}\displaystyle \inf _{{\mathbb {P}} \in {\mathcal {P}}} \textstyle {\mathbb {E}}_{{\mathbb {P}}} \bigg [ \sum \limits _{i=1}^n x_i \cdot ((u_i + l_i) / 2 + z_i (u_i - l_i) / 2) \bigg ] \ge \underline{r} \\ &{} 1^\top x = 1 \\ &{} x \ge 0, \end{array} \end{aligned}$$

(23)

where the asset returns are explained by a vector of risk factors $z\in {{\mathbf {K}}}=[-1,1]^n$ as in Sect. 6.1, while the ambiguity set containing all possible distributions of z is defined as

$$\begin{aligned} {\mathcal {P}}=\left\{ h \cdot dz\; :\; h\in \varSigma [z]_r,~ \int _{{\mathbf {K}}}h(z)\, dz=1,~ \int _{{\mathbf {K}}}z\,h(z)\,dz=0 \right\} . \end{aligned}$$

In the numerical experiments we will assume that there are $n=3$ assets whose returns have known upper and lower bounds $u = (1,1.2, 1.3)^\top$ and $l = (1,0.85, 0.8)^\top$, respectively, and known mean values $(u + l) / 2$. This choice implies that asset 1 is risk-free. For ease of exposition, we henceforth set $v^\pm _i=(u_i \pm l_i) / 2$ for $i=1\ldots ,n$. As z has zero mean under every ${\mathbb {P}}\in {\mathcal {P}}$, the return target constraint reduces to the linear inequality $\sum _{i=1}^n x_i v^+_i \ge {\underline{r}}$, while the objective function simplifies to

$$\begin{aligned}&\sup \limits _{h\in \varSigma [z]_r} \left\{ \int _{{\mathbf {K}}}\left( \sum \limits _{i=1}^n x_i z_i v_i^- \right) ^2 h(z) dz\;:\; \int _{{\mathbf {K}}}h(z)\, dz=1,~ \int _{{\mathbf {K}}}z\,h(z)\,dz=0\right\} . \end{aligned}$$

(24)

Next, we define $m_r(z)$ as the vector of all monomials of degree at most r in the variables z. Then, any SOS density function $h\in \varSigma [z]_r$ can be represented as $h(z) = m_r(z)^\top H m_r(z)$ for some positive semidefinite coefficient matrix H. Moreover, it is useful to introduce the matrices

$$\begin{aligned} M^0= \int _{{\mathbf {K}}}m_r(z)m_r(z)^\top dz,\qquad M^i= \int _{{\mathbf {K}}}z_i m_r(z)m_r(z)^\top dz\quad \forall i=1,\ldots , n, \end{aligned}$$

and

$$\begin{aligned} A^{ij} = \int _{{\mathbf {K}}}z_iv_i^- z_jv_j^- m_r(z)m_r(z)^\top dz\quad \forall i,j=1,\ldots , n. \end{aligned}$$

Using this notation, the worst-case variance problem (24) can be reformulated as the SDP

$$\begin{aligned} \begin{array}{cl} \sup \limits _{H \succeq 0} &{} \mathop {\sum }\limits _{i,j=1}^n x_i x_j \langle H, A^{ij} \rangle \\ \text {s.t.} &{} \langle H, M^0 \rangle = 1,\quad \langle H, M^i \rangle = 0 \quad \forall i = 1, \ldots , n, \end{array} \end{aligned}$$

where $\langle \cdot , \cdot \rangle$ stands for the trace inner product. The SDP dual to the above problem is given by

$$\begin{aligned} \begin{array}{cl} \displaystyle \inf _{\gamma } &{} \gamma _0 \\ \text {s.t.} &{} \mathop {\sum }\limits _{i=0}^n \gamma _i M^i \succeq \mathop {\sum }\limits _{i,j=1}^n x_ix_j A^{ij}. \end{array} \end{aligned}$$

(25)

Strong duality holds because $M^0\succ 0$ as an outer product of the vector $m_r(z)$ of all monomials of degree at most r in the variables z, integrated over a convex body with non-empty interior. Therefore, the dual SDP is strictly feasible. Substituting (25) into (23) converts the distributionally robust portfolio selection problem to the nonlinear SDP

$$\begin{aligned} \begin{array}{cl} \displaystyle \inf _{x,\gamma } &{} \gamma _0 \\ \text {s.t.} &{} \mathop {\sum }\limits _{i=0}^n \gamma _i M^i \succeq \sum \limits _{i,j=1}^n x_ix_j A^{ij}\\ &{} \sum \limits _{i=1}^n x_i v_i \ge {\underline{r}}\\ &{} 1^\top x = 1 \\ &{} x \ge 0. \end{array} \end{aligned}$$

(26)

In the following we will demonstrate that (26) is a convex optimization problem. Indeed, by recalling the definition of the matrices $A^{ij}$, introducing a Borel-measurable matrix-valued function Y(z) and using Schur complements, the nonlinear matrix inequality in (26) can be reformulated as

$$\begin{aligned}&\textstyle \mathop {\sum }\limits _{i=0}^n \gamma _i H^i \succeq \int _{{\mathbf {K}}}\left( \mathop {\sum }\limits _{i=1}^n x_i z_i v_i\right) ^2 m_r(z)m_r(z)^\top dz \\&\quad \iff \left\{ \begin{array}{l} \exists Y(\cdot )\text { Borel-measurable}:~ \mathop {\sum }\limits _{i=0}^n \gamma _i H^i \succeq \int _{{\mathbf {K}}}Y(z)\, dz,\\ Y(z)\succeq \left( \sum \limits _{i=1}^n x_i z_i v_i\right) ^2 m_r(z)m_r(z)^\top \quad \forall z\in {{\mathbf {K}}}\end{array}\right. \\&\quad \iff \left\{ \begin{array}{l} \exists Y(\cdot )\text { Borel-measurable}:~\mathop {\sum }\limits _{i=0}^n \gamma _i H^i \succeq \int _{{\mathbf {K}}}Y(z)\, dz,\\ \textstyle \begin{pmatrix} 1 &{}\quad \left( \sum \limits _{i=1}^n x_i z_i v_i\right) m_r(z)^\top \\ \left( \sum \limits _{i=1}^n x_i z_i v_i\right) m_r(z) &{}\quad Y(z)\end{pmatrix} \succeq 0 \quad \forall z\in {{\mathbf {K}}}. \end{array}\right. \end{aligned}$$

This reasoning shows that the feasible set of the first constraint in (26) can be expressed through uncountably many linear matrix inequalities. Thus, the feasible set of (26) can be viewed as a finite-dimensional projection of an infinite-dimensional convex set. As convexity is preserved under projections, we conclude that (26) is indeed a convex optimization problem. We can thus solve (26) to global optimality using the PENLAB solver [15] via the YALMIP modeling language [32].

Figures 1 and 2 visualize the worst-case standard deviation of the portfolio return and the corresponding optimal portfolio weights as the return threshold ${\underline{r}}$ is swept. The following observations are in order. First, if ${\underline{r}}$ is smaller or equal to the risk-free return, it is optimal to allocate all the capital to the risk-free asset, in which case the standard deviation of the portfolio return vanishes. As ${\underline{r}}$ increases, the investor is forced to shift capital to the risky assets, which leads to an increase of the worst-case standard deviation. Moreover, increasing the degree 2r of the polynomial density functions amounts to giving the adversary more flexibility to inflict damage. Thus, the worst-case standard deviation increases with r for any fixed return target $\underline{r}$. We further observe that the portfolio weights as well as the worst-case standard deviation display a distinct kink when the structure of the optimal portfolio changes, that is, when the weight of the risk-free asset drops to 0, in which case the corresponding no-short-sales constraint becomes active.

Fig. 1

Mean-standard deviation efficient frontiers for $r\in \{0,2,4,6\}$

Fig. 2

Optimal portfolio compositions for $r\in \{0,4\}$

6.3 Risk aggregation

In the third experiment we study the risk aggregation problem of an insurer holding a portfolio of different random losses $z_i$, $i=1,\ldots , n$, corresponding to different types of insurance claims, e.g., life, vehicle, health or home insurance policies, etc. Inspired by [49, § 6], we aim to estimate the worst-case probability that the sum of the n losses exceeds a critical threshold $b=10$ beyond which the insurance company would be driven into illiquidity. Formally, we aim to maximize

$$\begin{aligned} {\mathbb {P}}_{z \sim ({\mathbf {K}},h)} \left( z_1 + \ldots + z_n \ge b \right) \end{aligned}$$

(27)

across all distributions in an ambiguity set ${\mathcal {P}}$, which reflects the prior distributional information available to the insurer. We will consider different models for the domain ${{\mathbf {K}}}$ of $z=(z_1,\ldots , z_n)$, the reference measure $\mu$ on ${{\mathbf {K}}}$ and the ambiguity set ${\mathcal {P}}$. Throughout the experiments we will always assume that the reference measure is separable with respect to the losses, that is, we assume that

$$\begin{aligned} d\mu (z) = \varrho _1(z_1) \cdots \varrho _n(z_n) dz, \end{aligned}$$

where $\varrho _i$ denotes a given density function (with respect to the Lebesgue measure) of the random variables $z_i$ for each $i=1,\ldots , n$. We will consider the following complementary settings:

• 1. Lognormal densities: We set ${{\mathbf {K}}}= {\mathbb {R}}^n_+$ and let $\varrho _i$ be a lognormal density function defined earlier in (11), but repeated here for convenience:

  $$\begin{aligned} \varrho _i(z_i) = \frac{1}{z_i v_i \sqrt{2\pi }} \exp \left( - \frac{(\log (z_i) - {\bar{z}}_i)^2}{2 v_i^2} \right) , \end{aligned}$$

  (28)

  where ${\bar{z}}_i$ and $v_i$ represent prescribed location and scale parameters, $i = 1,\ldots ,n$.

• 2. Exponential densities: We set ${{\mathbf {K}}}= {\mathbb {R}}^n_+$ and let $\varrho _i$ be the exponential density function with unit rate parameter defined through $\varrho _i(z_i)=\exp (-z_i)$, $i=1,\ldots , n$. The resulting reference measure is intimately related to the orthogonal Laguerre polynomials.

• 3. Uniform densities: We set ${{\mathbf {K}}}= [0,M]^n$ for some constant $M>0$ and let $\varrho _i$ be the uniform density function defined through $\varrho _i(z_i)=1/M$, $i=1,\ldots , n$. Note that under this choice the reference measure is proportional to the Lebesgue measure.

In order to reformulate the risk aggregation problem as a tractable SDP, we need the moments of the reference measure $\mu$ over the hypercube ${\mathbf {K}}$ and over the knapsack polytope $\mathbf K\cap {\mathbf {C}}$, where

$$\begin{aligned} {\mathbf {C}} = \{z \in {\mathbb {R}}^n: \ \ z_1 + \ldots + z_n \ge b \}. \end{aligned}$$

For all classes of density functions described above, the moments of $\mu$ are indeed accessible. Specifically, under the lognormal densities, the moments of $\mu$ over ${\mathbf {K}}$ are given by (12) and are repeated here for convenience:

$$\begin{aligned} m_{\alpha }({\mathbf {K}})= & {} \int _{{\mathbf {K}}} \left( \prod _{i=1}^n z_i^{\alpha _i} \right) \prod _{i=1}^n \frac{1}{z_i v_i \sqrt{2\pi }} \exp \left( - \frac{(\log (z_i) - {\bar{z}}_i)^2}{2 v_i^2} \right) dz \\= & {} \prod _{i=1}^n \exp (\alpha _i {\bar{z}}_i + (\alpha _i v_i)^2 / 2). \end{aligned}$$

Moreover, the moments of $\mu$ over ${\mathbf {K}}\cap {\mathbf {C}}$ can be expressed as

$$\begin{aligned} m_{\alpha }({\mathbf {K}}\cap {\mathbf {C}})&=m_{\alpha }({\mathbf {K}}) -m_{\alpha }({\mathbf {K}}\backslash {\mathbf {C}})\\&=m_{\alpha }({\mathbf {K}}) - \int _{{\mathbf {K}}\backslash {\mathbf {C}}} \left( \prod _{i=1}^n z_i^{\alpha _i} \right) \prod _{i=1}^n \frac{1}{z_i v_i \sqrt{2\pi }} \exp \left( - \frac{(\log (z_i) - \bar{z}_i)^2}{2 v_i^2} \right) dz. \end{aligned}$$

To evaluate the integral in the last line, we use the cubature routine adsimp($\cdot$) in MATLAB, which greedily refines a simplicial partition of the integration domain by iteratively subdividing the simplices with the largest estimated integration errors [16]. For the polynomial degrees considered in our experiments, the moments computed with this routine are sufficiently precise to result in numerically stable optimization problems. For higher degrees, however, computing sufficiently precise moments takes too much time or is not achievable. Note that for the exponential and the uniform densities, the moments of the reference measure $\mu$ over ${\mathbf {K}}$ and ${\mathbf {K}}\cap {\mathbf {C}}$ are available in closed form.

We assume that the insurance company is able to estimate the marginal distributions of the individual losses either exactly or approximately by using a combination of statistical analysis and probabilistic modeling. However, the insurer has no information about the underlying copula. This type of distributional information is often justified in practice because obtaining reliable marginal information requires significantly less data than obtaining exact dependence structures; see, e.g., [33]. Throughout the experiment we assume that there are $n=2$ random losses governed by lognormal probability density functions of the form (28) with parameters ${\bar{z}}_1 = -0.3$, $\bar{z}_2 = 0.4$, $v_1 = 0.8$ and $v_2 = 0.5$. The ambiguity set $\mathcal P$ then contains all distributions of the form $h\cdot d\mu$, $h\in \varSigma [z]_r$, under which the marginals of the losses follow the prescribed lognormal distributions either exactly or approximately. More precisely, we model the marginal distributional information as follows:

Fig. 3

Histograms of the lognormal marginal distributions of $z_1$ (left) and $z_2$ (right)

• 1. Marginal distribution matching: The lognormal distributions of the individual losses are matched exactly by any distribution $h\cdot d\mu$ in the ambiguity set. This can be achieved by defining the reference measure $\mu$ as the product of the marginal lognormal distributions and by requiring that h satisfies (21). Note that under the alternative reference measures corresponding to the uniform or exponential density functions, lognormal marginals cannot be matched exactly with polynomial densities of any degrees. This is because the lognormal density function can neither be expressed as a polynomial nor as the product of a polynomial with the exponential density. Note also that an exact matching of (non-discrete) marginal distributions cannot be enforced with the existing numerical techniques for solving Fréchet problems proposed in [13, 14, 49].

• 2. Marginal moment matching: The marginals of the individual losses have the same moments of order 0, 1 or 2 as the prescribed lognormal distributions. Note that this kind of moment matching can be enforced under any of the reference measures corresponding to lognormal, exponential or uniform density functions. Moreover, moment matching is also catered for in [49] bar the extra requirement that the joint distribution of the losses must have an SOS polynomial density.

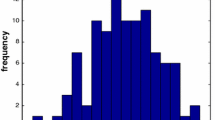
• 3. Marginal histogram matching: We may associate a histogram with each marginal lognormal distribution as illustrated in Fig. 3 and require that the marginals of the losses under the joint distribution $h\cdot d\mu$ have the same histograms. This condition can be enforced under any of the reference measures corresponding to lognormal, exponential or uniform density functions. In the numerical experiments, we use histograms with 20 bins of width 0.25 starting at the origin. Histogram matching is also envisaged in [49]. Formally, we thus define the ambiguity set as

  $$\begin{aligned} {\mathcal {P}}= & {} \left\{ h\cdot d\mu \;:\; h\in \varSigma [z]_r, \; \int _{{\mathbf {K}}} h(z)d\mu (z)=1,\right. \\&\left. \int _{{{\mathbf {K}}}} {\mathbf {1}}_{B_l}(z) h(z)\, d\mu (z) =p_l ~\forall l =1,\ldots ,L \right\} , \end{aligned}$$

  where $B_l\subset {{\mathbf {K}}}$ is the l-th bin, $p_l=\int _{{{\mathbf {K}}}} {\mathbf {1}}_{B_l}(z) \, d\mu (z)$ is its probability under the reference measure and $L\in {\mathbb {N}}$ is the total number of bins. As indicated above, in the numerical experiments we set $L=40$. Moreover, we define the bins as $B_l=\{ z\in {{\mathbf {K}}}: (l-1)/4\le z_1\le l/4 \}$ for $l=1,\ldots ,20$ and $B_l=\{ z\in {{\mathbf {K}}}: (l-1)/4\le z_2\le l/4 \}$ for $l=21,\ldots ,40$. Note that since lognormal distributions are supported on ${\mathbb {R}}_+$, we have $\sum _{l=1}^{20} p_l = \sum _{l=21}^{40} p_l<1$, and thus $\mathcal P$ is empty unless the square $[0,5]^2$ is a strict subset of ${{\mathbf {K}}}$. In the experiments this condition is enforced both for the lognormal and the exponential reference measures, in which case we set ${{\mathbf {K}}}={\mathbb {R}}_+^2$, as well as for the uniform reference measure, in which case we set ${{\mathbf {K}}}=[0,10]^2$.

Table 3 Worst-case probabilities for the lognormal reference measure

For ${{\mathbf {K}}}={\mathbb {R}}_+^2$ and the reference measure corresponding to the lognormal density functions, the worst-case values of the probability (27) are reported in Table 3. Results are shown for $r\le 5$, which corresponds to polynomial densities of degrees at most 10. The last row of the table ($r=\infty$) provides the worst-case probabilities across all distributions satisfying the prescribed moment or histogram conditions (not only those with a polynomial density) and was computed using the methods described in [49]. Note that under moment matching up to order 2, the worst-case probability for $r=5$ amounts to 0.0021, as opposed to the much higher probability of 0.0615 obtained with the approach from [49]. A similar observation holds for histogram matching. The requirement that the distributions in the ambiguity set be sufficiently regular in the sense that they admit a polynomial density function with respect to the reference measure is therefore restrictive and effectively rules out pathological discrete worst-case distributions. Moreover, the worst-case probabilities under exact distribution matching and under histogram matching are of the same order of magnitude for all $r\le 5$ but significantly smaller than the worst-case pobability under histogram matching for $r=\infty$. A key question to be asked in practice is thus whether one deems the class of distributions $h\cdot d\mu$ with $h \in \varSigma [z]_r$ to be rich enough to contain all ‘reasonable’ distributions.

Table 4 Worst-case probabilities for the exponential reference measure

Table 5 Worst-case probabilities for the uniform reference measure

Table 4 reports the worst-case probabilities corresponding to the reference measure on ${{\mathbf {K}}}={\mathbb {R}}_+^2$ induced by the exponential density functions. For low values of r, the polynomial densities lack the necessary degrees of freedom to match all imposed moment constraints. In these situations, the worst-case probability problem becomes infeasible (indicated by ‘−’). When feasible, however, we managed to solve the problem for r up to 12. The density functions corresponding to large values of r are highly flexible and thus result in worst-case probabilities that are closer to those obtained by the benchmark method from [49], which relaxes the restriction to a subspace of polynomial densities. Similar phenomena are also observed in the context of histogram matching. It was impossible to match the prescribed histogram probabilities exactly for all $r\le 12$. We thus relaxed the histogram matching conditions in the definition of the ambiguity set to allow for densities whose implied marginal histograms are within a prescribed $\ell _1$-distance from the target histograms.

This approximate histogram matching condition is easily captured in our framework and gives rise to a few extra linear constraints on the coefficients of the polynomial density function. Table 4 reports the worst-case probabilities for three different tolerances on the histogram mismatch in terms of the $\ell _1$-distance. We observe that the resulting worst-case probabilities are significantly larger than those obtained under the lognormal reference measure and increase with the $\ell _1$-tolerance.

Finally, Table 5 reports the worst-case probabilities corresponding to the uniform reference measure on ${{\mathbf {K}}}= [0,10]^2$. The results are qualitatively similar to those of Table 4, but they also show that the choice of the reference measure plays an important role when r is small.

7 Conclusions

In this paper, we present first steps towards using SOS polynomial densities in distributionally robust optimization for problems that display a polynomial dependence on the uncertain parameters. The main advantages of this approach may be summarized as follows:

• 1. The proposed framework is tractable (in the sense of polynomial-time solvability) for SOS density functions of any fixed degree.

• 2. The approach offers considerable modeling flexibility. Specifically, one may conveniently encode various salient features of the unknown distribution of the uncertain parameters trough linear constraints and/or linear matrix inequalities.

• 3. In the limit as the degree of the SOS density functions tends to infinity, one recovers the usual robust counterpart or generalized moment problem. One may therefore view the degree of the density as a tuning parameter that captures the model’s ‘level of conservativeness.’

The approach also suffers from shortcomings that necessitate further work and insights:

• 1. The approach is not applicable to objective or constraint functions that display a general (decision-dependent) piecewise polynomial dependence on the uncertain parameters as is the case for the recourse functions of linear two-stage stochastic programs.

• 2. The proposed distributionally robust optimization problems can be reduced to generalized eigenvalue problems or even semidefinite programs of large sizes that are often poorly conditioned.