Abstract
Beck and Teboulle’s FISTA method for finding a minimizer of the sum of two convex functions, one of which has a Lipschitz continuous gradient whereas the other may be nonsmooth, is arguably the most important optimization algorithm of the past decade. While research activity on FISTA has exploded ever since, the mathematically challenging case when the original optimization problem has no minimizer has found only limited attention. In this work, we systematically study FISTA and its variants. We present general results that are applicable, regardless of the existence of minimizers.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We assume that

with inner product \(\langle \cdot | \cdot \rangle \) and associated norm \(||\, \cdot \, ||\). We also presuppose throughout the paper that

satisfy the following:
Assumption 1.1
- (A1):
-
f is convex and Fréchet differentiable on \(\mathcal {H}\), and \({\nabla {f} } \) is \(\beta \)-Lipschitz continuous with \(\beta \in ]0, {+}\infty [\);
- (A2):
-
g is convex, lower semicontinuous, and proper;
- (A3):
-
\(\gamma \in ]0,1/\beta ]\) is a parameter.
One fundamental problem in optimization is to
For convenience, we set

and where we follow standard notation in convex analysis (as employed, e.g., in [8]). Then many algorithms designed for solving (3) employ the forward-backward or proximal gradient operator T in some fashion. Since the advent of Nesterov’s acceleration [22] (when \(g\equiv 0\)) and Beck and Teboulle’s fast proximal gradient method FISTA [11] (see also [9, Chapter 10]), the literature on algorithms for solving (3) has literally exploded; see, e.g., [1,2,3, 5, 7, 11, 18, 22] for a selection of key contributions. Indeed, out of nearly one million mathematical publications that appeared since 2009 and are indexed by Mathematical Reviews, the 2009-FISTA paper [11] by Beck and Teboulle takes the number two spot! (In passing, we note that it has been cited more than 6,000 times on Google Scholar where it now receives about 3 new citations every day!) The overwhelming majority of these papers assume that the problem (3) has a solution to start with. Complementing and contributing to these analyses, we follow a path less trodden:
The aim of this paper is to study the behaviour of the fast proximal gradient methods (and monotone variants), in the case when the original problem (3) does not necessarily have a solution.
Before we turn to our main results, let us state the FISTA or fast proximal gradient method:
Algorithm 1.2
(FISTA) Let \(x_{0} \in \mathcal {H}\), set \(y_{1}:=x_{0}\), and update

where T is defined in (4), \(\mathbb {N}^{*}:=\{1,2,\ldots \}\), and \((\tau _n)_{n\in \mathbb {N}^{*}}\) is a sequence of real numbers in \([1,+\infty [\).
Note that when \(\tau _n\equiv 1\), one obtains the classical (unaccelerated) proximal gradient method. There are two very popular choices for the sequence \((\tau _n)_{n\in \mathbb {N}^{*}}\) to achieve acceleration. Firstly, given \(\tau _1 :=1\), the classical FISTA [10, 11, 16, 22] update is

The second update has the explicit formula

where \(\rho \in [2, {+}\infty [\); see, e.g., [3, 5, 15, 27].
Convergence results of the sequence generated by FISTA under a suitable tuning of  can be found in [1, 5, 15]. The relaxed case was considered in [7] and error-tolerant versions were considered in [2, 3]. In addition, for results concerning the rate of convergence of function values, see [10, 11, 26, 27]. The authors of [16] established a variant of FISTA that covers the strongly convex case. An alternative of the classical proximal gradient algorithm with relaxation and error is presented in [19] (see also [8, 13, 26]). Finally, a new forward-backward splitting scheme (for finding a zero of a sum of two maximally monotone operators) that includes FISTA as a special case was proposed in [18].
can be found in [1, 5, 15]. The relaxed case was considered in [7] and error-tolerant versions were considered in [2, 3]. In addition, for results concerning the rate of convergence of function values, see [10, 11, 26, 27]. The authors of [16] established a variant of FISTA that covers the strongly convex case. An alternative of the classical proximal gradient algorithm with relaxation and error is presented in [19] (see also [8, 13, 26]). Finally, a new forward-backward splitting scheme (for finding a zero of a sum of two maximally monotone operators) that includes FISTA as a special case was proposed in [18].
The main difference between our work and existing work is that we focus on the minimizing property of the sequences generated by FISTA and MFISTA in the general framework, i.e., when the set  is possibly empty. Let us now list our main results:
is possibly empty. Let us now list our main results:
-
Theorem 5.3 establishes the behaviour of FISTA in the possibly inconsistent case; moreover, our assumption on
 (see (39)) is very mild.
(see (39)) is very mild. -
Theorem 5.5 concerns FISTA when
 behaves similarly to the Beck–Teboulle choice.
behaves similarly to the Beck–Teboulle choice. -
Theorem 5.10 deals with the case when
 is bounded; see, in particular, (ii)(a) and (v)(b).
is bounded; see, in particular, (ii)(a) and (v)(b). -
Theorem 6.1 considers MFISTA [10], the monotone version of FISTA, when Assumption 4.1 is in force and
 is unbounded.
is unbounded.
To the best of our knowledge, Theorem 5.3 is new. The proof of Theorem 5.5, which can be viewed as a “discrete version” of [3, Theorem 2.3], relies on techniques seen in [3, Theorem 2.3] and [1, Proposition 3]; items (ii)–(vi) are new. A result similar to Theorem 5.5(ii) was mentioned in [6, Theorem 4.1]. However, no proof was given, and the parameter sequence there is a special case of the one considered in Theorem 5.5. Items (vii)(a) and (vii)(a) is a slight modification of [4, Proposition 4.3]. Concerning Theorem 5.10, items (i)–(iv) and (v)(b) are new while (v)(a) was proven in [1, Corollary 20(iii)]. Item (i) in the classical case (\(\tau _{n} \equiv 1\)) relates to [12, Theorem 4.2] where linesearches were employed. In Theorem 6.1, items (i)–(v) are new. Compared to [10, Theorem 5.1], we allow many possible choices for the parameter sequence in Theorem 6.1(vi); see, e.g., Examples 4.4–4.6. In addition, by adapting the technique of [1, Theorem 9], we improve the convergence rate of MFISTA under the condition (110) in Theorem 6.1.
There are also several minor results worth emphasizing: Lemma 2.4 is new. The notion of quasi-Fejér monotonicity is revisited in Lemma 2.7; however, our error sequence need not be positive. The assumptions in Lemma 3.2 and Lemma 3.3 are somewhat minimal, which allow us to establish the minimizing property of FISTA and MFISTA in the case where there are possibly no minimizers in Sects. 5 and 6. Example 4.5 is new. Proposition 5.12 describes the behaviour of  in the classical proximal gradient (ISTA) case while Corollary 5.15 provides a sufficient condition for strong convergence of \((x_n)_{n\in \mathbb {N}^{*}}\) in this case. The new Proposition 5.14 presents some progress towards the still open question regarding the convergence of
in the classical proximal gradient (ISTA) case while Corollary 5.15 provides a sufficient condition for strong convergence of \((x_n)_{n\in \mathbb {N}^{*}}\) in this case. The new Proposition 5.14 presents some progress towards the still open question regarding the convergence of  generated by classical FISTA. The weak convergence part in Corollary 5.15 was considered in [4]; however, our new Fejérian approach allows us to obtain strong convergence when
generated by classical FISTA. The weak convergence part in Corollary 5.15 was considered in [4]; however, our new Fejérian approach allows us to obtain strong convergence when  .
.
Let us now turn to the organization of this paper. Classical results on real sequences and new results on the Fejér monotonicity are recorded in Sect. 2. The “one step” behaviour of both FISTA and MFISTA is carefully examined in Sect. 3. In Sect. 4, we investigate properties of the parameter sequence \((\tau _n)_{n\in \mathbb {N}^{*}}\). Our main results on FISTA and MFISTA are presented in Sects. 5 and 6 respectively. The concluding Sect. 7 contains a discussion of open problems.
A final note on notation is in order. For a sequence  and an extended real number \(\xi \in \left[ {-}\infty , {+}\infty \right] \), the notation \(\xi _{n}\uparrow \xi \) means that
and an extended real number \(\xi \in \left[ {-}\infty , {+}\infty \right] \), the notation \(\xi _{n}\uparrow \xi \) means that  is increasing (i.e., \(\xi _n\leqslant \xi _{n+1}\)) and \(\xi _{n} \rightarrow \xi \) as \(n\rightarrow {+}\infty \). Likewise, \(\xi _{n}\downarrow \xi \) means that
is increasing (i.e., \(\xi _n\leqslant \xi _{n+1}\)) and \(\xi _{n} \rightarrow \xi \) as \(n\rightarrow {+}\infty \). Likewise, \(\xi _{n}\downarrow \xi \) means that  is decreasing (i.e., \(\xi _{n}\geqslant \xi _{n+1}\)) and \(\xi _{n}\rightarrow \xi \) as \(n\rightarrow {+}\infty \). For any other notation not defined, we refer the reader to [8].
is decreasing (i.e., \(\xi _{n}\geqslant \xi _{n+1}\)) and \(\xi _{n}\rightarrow \xi \) as \(n\rightarrow {+}\infty \). For any other notation not defined, we refer the reader to [8].
2 Auxiliary results
In this section, we collect results on sequences which will make the proofs in later sections more structured.
Lemma 2.1
Let  be an increasing sequence in \([1, {+}\infty [\) such that \(\lim \tau _{n} = {+}\infty \). Then
be an increasing sequence in \([1, {+}\infty [\) such that \(\lim \tau _{n} = {+}\infty \). Then

Proof
See Appendix A. \(\square \)
Lemma 2.2
Let  and
and  be sequences in \(\mathbb {R}_{+}\). Suppose that \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n} = {+}\infty \) and that \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n}\beta _{n} < {+}\infty \). Then \(\varliminf \beta _{n} =0 \).
be sequences in \(\mathbb {R}_{+}\). Suppose that \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n} = {+}\infty \) and that \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n}\beta _{n} < {+}\infty \). Then \(\varliminf \beta _{n} =0 \).
Proof
See Appendix B. \(\square \)
The novelty of the following result lies in the fact that the error sequence  need not lie in \(\mathbb {R}_{+}\).
need not lie in \(\mathbb {R}_{+}\).
Lemma 2.3
Let  be a sequence in \(\mathbb {R}\), let
be a sequence in \(\mathbb {R}\), let  be a sequence in \(\mathbb {R}_{+}\), and let
be a sequence in \(\mathbb {R}_{+}\), and let  be a sequence in \(\mathbb {R}\). Suppose that
be a sequence in \(\mathbb {R}\). Suppose that  is bounded below, that
is bounded below, that

and that the series \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\) converges in \(\mathbb {R}\). Then the following hold:
-
(i)
 is convergent in \(\mathbb {R}\).
is convergent in \(\mathbb {R}\). -
(ii)
\(\sum _{n \in \mathbb {N}^{*}}\beta _{n} < {+}\infty \).
Proof
See Appendix C. \(\square \)
Lemma 2.4
Let  be a sequence of real numbers. Consider the following statements:
be a sequence of real numbers. Consider the following statements:
-
(i)
 converges in \(\mathbb {R}\).
converges in \(\mathbb {R}\). -
(ii)
\(\sum _{n \in \mathbb {N}^{*}}\alpha _{n}\) converges in \(\mathbb {R}\).
-
(iii)
 converges in \(\mathbb {R}\).
converges in \(\mathbb {R}\).
Suppose that two of the statements (i)–(iii) hold. Then the remaining one also holds.
Proof
See Appendix D. \(\square \)
The following result is stated in [25, Problem 2.6.19]; we provide a proof in Appendix E for completeness.
Lemma 2.5
Let  be a decreasing sequence in \(\mathbb {R}_{+}\). Then
be a decreasing sequence in \(\mathbb {R}_{+}\). Then

The following variant of Opial’s lemma [23] will be required in the sequel.
Lemma 2.6
Let C be a nonempty subset of \(\mathcal {H}\), and let  and
and  be sequences in \(\mathcal {H}\). Suppose that \(u_{n} - v_{n} \rightarrow 0\), that every weak sequential cluster point of
be sequences in \(\mathcal {H}\). Suppose that \(u_{n} - v_{n} \rightarrow 0\), that every weak sequential cluster point of  lies in C, and that, for every \(c \in C\),
lies in C, and that, for every \(c \in C\),  converges. Then there exists \(w \in C\) such that \(u_{n} \rightharpoonup w\) and \(v_{n}\rightharpoonup w\).
converges. Then there exists \(w \in C\) such that \(u_{n} \rightharpoonup w\) and \(v_{n}\rightharpoonup w\).
Proof
For every \(c \in C\), since \(u_{n}-v_{n}\rightarrow 0\) and  converges, we deduce that
converges, we deduce that  converges. In turn, because every weak sequential cluster point of
converges. In turn, because every weak sequential cluster point of  belongs to C, [8, Lemma 2.47] yields the existence of \(w \in C\) satisfying \(v_{n} \rightharpoonup w\). Therefore, because \(u_{n}-v_{n}\rightarrow 0\), we conclude that
belongs to C, [8, Lemma 2.47] yields the existence of \(w \in C\) satisfying \(v_{n} \rightharpoonup w\). Therefore, because \(u_{n}-v_{n}\rightarrow 0\), we conclude that  and
and  converge weakly to w. \(\square \)
converge weakly to w. \(\square \)
We next revisit the notion of quasi-Fejér monotonicity in the Hilbert spaces setting studied in [17]. This plays a crucial role in our analysis of Proposition 5.14. Nevertheless, to fit our framework of Proposition 5.14, the error sequence  is not required to be positive in Lemma 2.7. The proof is based on [17, Proposition 3.3(iii) and Proposition 3.10].
is not required to be positive in Lemma 2.7. The proof is based on [17, Proposition 3.3(iii) and Proposition 3.10].
Lemma 2.7
Let C be a nonempty subset of \(\mathcal {H}\), let  be a sequence in \(\mathcal {H}\), and let
be a sequence in \(\mathcal {H}\), and let  be a sequence in \(\mathbb {R}\). Suppose that
be a sequence in \(\mathbb {R}\). Suppose that

and that \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\) converges in \(\mathbb {R}\). Then the following hold:
-
(i)
For every \(c \in C\), the sequence
 converges in \(\mathbb {R}\).
converges in \(\mathbb {R}\). -
(ii)
Suppose that \({\text {int}}C \ne \varnothing \). Then
 converges strongly in \(\mathcal {H}\).
converges strongly in \(\mathcal {H}\).
Proof
-
(i):
This is a direct consequence of Lemma 2.3(i).
-
(ii):
We follow along the lines of [17, Proposition 3.10]. Let \(v \in {\text {int}}C\) and \(\rho \in ]0, {+}\infty [\) be such that
 . Define a sequence
. Define a sequence  in C via
in C via  (12)
(12)
We now verify that

Fix \(n \in \mathbb {N}^{*}\). If \(u_{n+1}=u_{n}\), then (11) implies that \(\varepsilon _{n} \geqslant 0\), and therefore (13) holds. Otherwise, because \(v_{n} \in C\), (11) yields \(||u_{n+1}-v_{n} ||^{2} \leqslant ||u_{n}-v_{n} ||^{2} +\varepsilon _{n}\). In turn, using (12), we obtain

and after expanding both sides and simplifying terms, we get (13). Consequently, owing to (13) and the convergence of \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\), we derive from Lemma 2.3(ii) that \(\sum _{n \in \mathbb {N}^{*}}2\rho ||u_{n+1}-u_{n} || < {+}\infty \). Hence, by completeness of \(\mathcal {H}\),  converges strongly to a point in \(\mathcal {H}\). \(\square \)
converges strongly to a point in \(\mathcal {H}\). \(\square \)
We conclude this section with a simple identity. If x, y, and z are in \(\mathcal {H}\), then

3 One-step results
The aim of this section is to present several results on performing just one step of FISTA or MFISTA. This allows us to present subsequent convergence results more clearly. Recall that Assumption 1.1 is in force and (see (4)) that

Clearly,

Lemma 3.1
(Beck–Teboulle) The following holds:

Proof
See Appendix F. \(\square \)
Lemma 3.2
(one FISTA step) Let  , let \(\tau \) and \(\tau _{+}\) be in \([1, {+}\infty [ \), and set
, let \(\tau \) and \(\tau _{+}\) be in \([1, {+}\infty [ \), and set

In addition, let \(z \in {\text {dom}}{h}\), and set

Then the following hold:
-
(i)
 .
. -
(ii)
 .
. -
(iii)
Suppose that \(\tau \leqslant \tau _{+}\), that
 , and that \( \inf h > {-}\infty \). Then
, and that \( \inf h > {-}\infty \). Then  (21)
(21)
Proof
First, since \(z \in {\text {dom}}{h}\), we get from (17), (19), and (20) that \(\mu \in \mathbb {R}\) and \(\mu _{+} \in \mathbb {R}\). Next, because \(x_{+} = Ty_{+}\), we derive from (18) (applied to  ) that
) that

-
(i):
We derive from (22), (15), and (19) that
 (23a)
(23a) (23b)
(23b)and thus, since
 , the conclusion follows.
, the conclusion follows. -
(ii):
Since \(x_{+} = Ty_{+}\), applying (18) to
 gives
gives  (24)
(24)Therefore, because \(\tau _{+} -1 \geqslant 0\) by assumption, it follows from (22) and (24) that
 (25a)
(25a)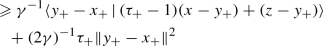 (25b)
(25b) (25c)
(25c)In turn, on the one hand, multiplying both sides of (25) by \(\tau _{+} >0\), we infer from (15) (applied to
 ) and the very definition of \(u_{+}\) that
) and the very definition of \(u_{+}\) that  (26a)
(26a) (26b)
(26b) (26c)
(26c)On the other hand, since
 due to (19), the definition of u yields
due to (19), the definition of u yields  (27)
(27)Altogether,
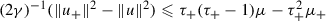 , which implies the desired conclusion.
, which implies the desired conclusion. -
(iii):
Since
 and, by assumption, \(\tau _{+}^{2} -\tau _{+} -\tau ^{2} \leqslant 0\), we deduce that
and, by assumption, \(\tau _{+}^{2} -\tau _{+} -\tau ^{2} \leqslant 0\), we deduce that  . Hence, because \(0 < \tau \leqslant \tau _{+}\) and
. Hence, because \(0 < \tau \leqslant \tau _{+}\) and  , it follows that
, it follows that 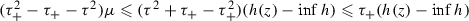 . Consequently, (ii) implies that
. Consequently, (ii) implies that  (28a)
(28a) (28b)
(28b) (28c)
(28c)as required.\(\square \)
The analysis of the following lemma follows the lines of [10, Theorem 5.1].
Lemma 3.3
(one MFISTA step). Let  , let \(\tau \) and \(\tau _{+}\) be in \([1, {+}\infty [\), and set
, let \(\tau \) and \(\tau _{+}\) be in \([1, {+}\infty [\), and set

Furthermore, let \(w \in {\text {dom}}h\), and define

Then the following hold:
-
(i)
 .
. -
(ii)
 .
.
Proof
First, since \(z_{+} = Ty_{+}\), using (18) with  and (15) with
and (15) with  yields
yields


-
(i):
On the one hand, by the very definition of \(x_{+}\) and (31),
 , and thus,
, and thus,  (32)
(32)On the other hand, due to (29),
 (33a)
(33a)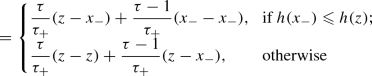 (33b)
(33b) (33c)
(33c)and since \(\tau \geqslant 1\), it follows that
$$\begin{aligned} ||y_{+}-x || \leqslant \frac{\tau }{\tau _{+}}||z-x_{-} ||. \end{aligned}$$(34) -
(ii):
Applying (18) to the pair
 and noticing that \(z_{+} = Ty_{+}\), we get
and noticing that \(z_{+} = Ty_{+}\), we get  (35)
(35)
In turn, since \(\tau _{+}\geqslant 1\), the very definition of \(x_{+}\), (31), and (35) imply that






Thus, since \(\tau _{+} >0\), it follows from (15) (applied to  ) that
) that


Furthermore, by the definition of \(y_{+}\), we have  , which asserts that
, which asserts that  . Combining this and (37) entails that
. Combining this and (37) entails that

which completes the proof. \(\square \)
4 The parameter sequence
A central ingredient of FISTA and MFISTA is the parameter sequence  . In this section, we present various properties of the parameter sequence as well as examples. From this point onwards, we will assume the following:
. In this section, we present various properties of the parameter sequence as well as examples. From this point onwards, we will assume the following:
Assumption 4.1
We assume that  is a sequence of real numbers such that
is a sequence of real numbers such that

Remark 4.2
A few observations regarding Assumption 4.1 are in order.
-
(i)
It is clear from (39) that
 (40)
(40) -
(ii)
Because
 is increasing, $$\begin{aligned} \tau _{n} \uparrow \tau _{\infty } \overset{(40)}{\in } \left[ 1, {+}\infty \right] . \end{aligned}$$(41)
is increasing, $$\begin{aligned} \tau _{n} \uparrow \tau _{\infty } \overset{(40)}{\in } \left[ 1, {+}\infty \right] . \end{aligned}$$(41) -
(iii)
Due to (40) and the assumption that
 , it is straightforward to verify that
, it is straightforward to verify that  (42)
(42) -
(iv)
For every \( n \in \mathbb {N}^{*}\), since
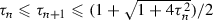 by (39), it follows from (42) and (40) that
by (39), it follows from (42) and (40) that 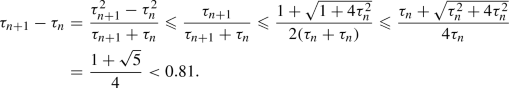 (43)
(43)
Lemma 4.3
The following hold:
-
(i)
\(\varlimsup (\tau _n/n)\leqslant \tau _1/2\).
-
(ii)
Using the convention that \(\tfrac{1}{ {+}\infty }= 0\), we have
 (44)
(44) -
(iii)
Suppose that \(\lim \tau _{n} = {+}\infty \). Then
$$\begin{aligned} \lim \frac{\tau _{n}-1}{\tau _{n+1}} = 1. \end{aligned}$$(45)
Proof
-
(i):
We claim that
 \(\tau _n\leqslant \tau _1(n+\sqrt{n})/2\). The inequality is clear when \(n=1\). Assume that, for some integer \(n\geqslant 1\), we have \(\tau _n\leqslant \tau _1(n+\sqrt{n})/2\). Then, on the one hand, we derive from (39) that $$\begin{aligned} \tau _{n+1} \leqslant \frac{1+\sqrt{1+4\tau _n^2}}{2} \leqslant \frac{\tau _1+\sqrt{\tau _1^2+\tau _1^2(n+\sqrt{n})^2}}{2} =\frac{\tau _1\big (1+\sqrt{1+(n+\sqrt{n})^2}\big )}{2}. \end{aligned}$$(46)
\(\tau _n\leqslant \tau _1(n+\sqrt{n})/2\). The inequality is clear when \(n=1\). Assume that, for some integer \(n\geqslant 1\), we have \(\tau _n\leqslant \tau _1(n+\sqrt{n})/2\). Then, on the one hand, we derive from (39) that $$\begin{aligned} \tau _{n+1} \leqslant \frac{1+\sqrt{1+4\tau _n^2}}{2} \leqslant \frac{\tau _1+\sqrt{\tau _1^2+\tau _1^2(n+\sqrt{n})^2}}{2} =\frac{\tau _1\big (1+\sqrt{1+(n+\sqrt{n})^2}\big )}{2}. \end{aligned}$$(46)On the other hand, since \((n+\sqrt{n+1})^2-(1+(n+\sqrt{n})^2) =2n(\sqrt{n+1}-\sqrt{n})>0\), we obtain \(\sqrt{1+(n+\sqrt{n})^2}<n+\sqrt{n+1}\). Altogether, \(\tau _{n+1}<\tau _1(n+1+\sqrt{n+1})/2\), which concludes the induction argument. Consequently, \(\varlimsup (\tau _n/n) \leqslant \lim \tau _1(n+\sqrt{n})/(2n)=\tau _1/2\).
-
(ii):
First, since
 by (39), we infer from (41) that
by (39), we infer from (41) that  . Next, by (42) and (39), we have
. Next, by (42) and (39), we have  (47a)
(47a) (47b)
(47b)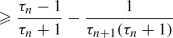 (47c)
(47c) (47d)
(47d)and hence, we get from (41) that
 , as desired.
, as desired. -
(iii):
Follows from (ii) and (41).
\(\square \)
Example 4.4
The condition
and the quotient
play significant roles in subsequent convergence results. Here are the two popular examples of sequences that satisfy Assumption 4.1 as well as (48) already seen in Sect. 1:
-
(i)
[10, 11, 16, 22] Set \(\tau _{1} :=1\), and set
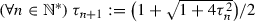 . Then, it is straightforward to verify that
. Then, it is straightforward to verify that  and that
and that  is an increasing sequence in \([1, {+}\infty [\). Moreover, an inductive argument shows that
is an increasing sequence in \([1, {+}\infty [\). Moreover, an inductive argument shows that  , from which we obtain \(\tau _\infty =+\infty \) and
, from which we obtain \(\tau _\infty =+\infty \) and  . This and Lemma 4.3(i) guarantee that \(\lim (\tau _n/n)=1/2\). Furthermore, it is part of the folklore that
. This and Lemma 4.3(i) guarantee that \(\lim (\tau _n/n)=1/2\). Furthermore, it is part of the folklore that  (50)
(50)for completeness, a proof is provided in Appendix G.
-
(ii)
[3, 5, 15, 27] Let \(\rho \in [2, {+}\infty [\), and define
 . Then, clearly
. Then, clearly  is an increasing sequence in \([1, {+}\infty [\) with \(\tau _\infty =+\infty \) and, for every \(n \in \mathbb {N}^{*}\), we have
is an increasing sequence in \([1, {+}\infty [\) with \(\tau _\infty =+\infty \) and, for every \(n \in \mathbb {N}^{*}\), we have  ,
,  (51)
(51)and
$$\begin{aligned} \frac{\tau _n-1}{\tau _{n+1}} =\frac{n-1}{n+\rho } =1-\frac{1+\rho }{n}+ {\mathrm {O}}{\bigg (\frac{1}{n^2}\bigg ) }. \end{aligned}$$(52)
We now turn to examples of the condition

which is of some interest in Sect. 5 (see (107)) and Sect. 6. Further examples of sequences that satisfy (53) can be found in [1, Section 5].
Example 4.5
Let \(\rho \in \bigl ]1, {+}\infty \bigr [ \) and set

Then

If  , then the sequence
, then the sequence  satisfies (53) with
satisfies (53) with  .
.
Proof
Indeed, since  , we derive from (42), (43), and (54) that
, we derive from (42), (43), and (54) that


as claimed. The remaining implication follows readily. \(\square \)
Example 4.6
[7] Let  , set
, set

and suppose that one of the following holds:
-
(i)
\(d=0\).
-
(ii)
\(d \in ]0,1]\) and
 .
.
Aujol and Dossal’s [7, Lemma 3.2] yields

Let us add to their analysis by pointing out that if (ii) holds, then (53) holds with  . Indeed, (57) and (58) assert that
. Indeed, (57) and (58) assert that

Also, note that if \(d\in ]0,1[\), then  (by L’Hôpital’s rule) in contrast to Example 4.4.
(by L’Hôpital’s rule) in contrast to Example 4.4.
5 FISTA
In this section, we present three main results on FISTA. We again recall that Assumption 1.1 is in force and (see (4)) that

Algorithm 5.1
(FISTA). Let \(x_{0} \in \mathcal {H}\), set \(y_{1}:=x_{0}\), and update

where T is as in (60) and  satisfies (39).
satisfies (39).
We assume for the remainder of this section that

We also set


The first two items of the following result are due to Attouch and Cabot; see [1, Proposition 3].
Lemma 5.2
The following holds:
-
(i)
 .
. -
(ii)
The sequence
 is decreasing and convergent to a point in \([ {-}\infty , {+}\infty [\).
is decreasing and convergent to a point in \([ {-}\infty , {+}\infty [\). -
(iii)
Suppose that \(\inf _{n \in \mathbb {N}^{*}} \sigma _{n} > {-}\infty \). Then the following hold:
-
(a)
 .
. -
(b)
Suppose that \(\sup _{n \in \mathbb {N}^{*}}\tau _{n} < {+}\infty \). Then
 and \(\sum _{n \in \mathbb {N}^{*}} ||x_{n}-x_{n-1} ||^{2} < {+}\infty \).
and \(\sum _{n \in \mathbb {N}^{*}} ||x_{n}-x_{n-1} ||^{2} < {+}\infty \).
-
(a)
Proof
-
(i):
For every \(n \in \mathbb {N}^{*}\), Lemma 3.2(i) (applied to
 ) asserts that
) asserts that  , from which the desired inequality follows. (ii): A consequence of (i) and (64).
, from which the desired inequality follows. (ii): A consequence of (i) and (64). -
(iii)(a):
By (i) and (63),
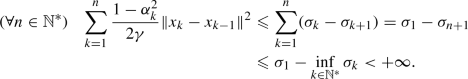 (65)
(65)Thus,
 , as claimed.
, as claimed. -
(iii)(b):
Because the function
 is increasing and
is increasing and  , we see that
, we see that  ; therefore,
; therefore,  (66)
(66)Combining (66) and (a) yields the conclusion. \(\square \)
We are ready for our first main result which establishes a minimizing property of the sequence  generated by Algorithm 5.1 in the general setting.
generated by Algorithm 5.1 in the general setting.
Theorem 5.3
The following holds:

Proof
Let us first establish that

To do so, we proceed by contradiction: assume that there exists \(N\in \mathbb {N}^{*}\) such that  . Then, there exists \(z \in {\text {dom}}h\) satisfying
. Then, there exists \(z \in {\text {dom}}h\) satisfying

In turn, set  . For every \(n \geqslant N\), in the light of Lemma 3.2(ii) (applied to
. For every \(n \geqslant N\), in the light of Lemma 3.2(ii) (applied to  ), we get
), we get


Furthermore, due to (69),

Let us consider the following two possible cases.
-
(a)
\(\tau _{\infty } = {+}\infty \): By (41), \(\tau _{n}\rightarrow {+}\infty \). Next, we derive from (42), (70) and (71) that
 or, equivalently, by the very definition of
or, equivalently, by the very definition of  ,
,  (72)
(72)Consequently, since \(\tau _{n} \uparrow {+}\infty \), taking the limit superior in (72) gives
 , which contradicts (69).
, which contradicts (69). -
(b)
\(\tau _{\infty } < {+}\infty \): Set
 . Then, by (71),
. Then, by (71),  and, by (42) and (69),
and, by (42) and (69),  . In turn, on the one hand, combining (70) and Lemma 2.3(ii), we infer that
. In turn, on the one hand, combining (70) and Lemma 2.3(ii), we infer that  . On the other hand, because
. On the other hand, because  and
and 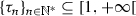 by our assumption and (40),
by our assumption and (40),  (73)
(73)
from which we deduce that  . Altogether, Lemma 2.2 and (71) guarantee that
. Altogether, Lemma 2.2 and (71) guarantee that  , i.e.,
, i.e.,  . Consequently, due to the inequality
. Consequently, due to the inequality  , it follows from (69) that
, it follows from (69) that  , which is absurd.
, which is absurd.
To summarize, we have reached a contradiction in each case, and therefore (68) holds. Thus, because  as \(n\rightarrow {+}\infty \), we infer from (68) that
as \(n\rightarrow {+}\infty \), we infer from (68) that  as \(n\rightarrow {+}\infty \). Finally, (68) guarantees that
as \(n\rightarrow {+}\infty \). Finally, (68) guarantees that  , which completes the proof. \(\square \)
, which completes the proof. \(\square \)
Remark 5.4
In Theorem 5.3, we do not know whether or not  converges to \(\inf h\). However, Theorem 5.5, Theorem 5.10, and Proposition 5.8 suggest a positive answer.
converges to \(\inf h\). However, Theorem 5.5, Theorem 5.10, and Proposition 5.8 suggest a positive answer.
We are now ready for our second main result (Theorem 5.5), which is a discrete version of Attouch et al.’s [3, Theorem 2.3]. When  is as in Example 4.4(ii) with \(\rho =2\), items (ii) and (iv) were mentioned (without a detailed proof) in [6, Theorem 4.1]. The analysis of Theorem 5.5(iii) was motivated by Attouch and Cabot’s [1, Proposition 3]. Furthermore, the boundedness of the sequences
is as in Example 4.4(ii) with \(\rho =2\), items (ii) and (iv) were mentioned (without a detailed proof) in [6, Theorem 4.1]. The analysis of Theorem 5.5(iii) was motivated by Attouch and Cabot’s [1, Proposition 3]. Furthermore, the boundedness of the sequences  and
and  in the consistent case was first obtained in Attouch et al.’s [4, Proposition 4.3]; here, we slightly modified the proof of this result to obtain the boundedness of
in the consistent case was first obtained in Attouch et al.’s [4, Proposition 4.3]; here, we slightly modified the proof of this result to obtain the boundedness of  in a more general setting.
in a more general setting.
Theorem 5.5
Suppose that

For every \(z \in {\text {dom}}h\), set  . Then the following hold:
. Then the following hold:
-
(i)
For every \(z \in {\text {dom}}{h}\), we have
 (75)
(75)and
 (76)
(76) -
(ii)
 .
. -
(iii)
 is asymptotically regular, i.e., \(x_{n} - x_{n-1} \rightarrow 0\).
is asymptotically regular, i.e., \(x_{n} - x_{n-1} \rightarrow 0\). -
(iv)
Every weak sequential cluster point of
 belongs to \({{\,\mathrm{Argmin}\,}}{h}\).
belongs to \({{\,\mathrm{Argmin}\,}}{h}\). -
(v)
Suppose that
 has a bounded subsequence. Then \({{\,\mathrm{Argmin}\,}}{h} \ne \varnothing \).
has a bounded subsequence. Then \({{\,\mathrm{Argmin}\,}}{h} \ne \varnothing \). -
(vi)
Suppose that \({{\,\mathrm{Argmin}\,}}{h} = \varnothing \). Then \(||x_{n} || \rightarrow +\infty \).
-
(vii)
Suppose that \({{\,\mathrm{Argmin}\,}}{h} \ne \varnothing \). Then the following hold:
-
(a)
(Beck–Teboulle [11])
 as \(n\rightarrow {+}\infty \); more precisely, for every \(z \in {{\,\mathrm{Argmin}\,}}h\),
as \(n\rightarrow {+}\infty \); more precisely, for every \(z \in {{\,\mathrm{Argmin}\,}}h\), 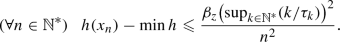 (77)
(77) -
(b)
The sequences
 and
and  are bounded.
are bounded.
-
(a)
Proof
Set  . Since
. Since  , we see that
, we see that
-
(i):
Take \(z \in {\text {dom}}{h}\), and set
 (79)
(79)Now, for every \(n \in \mathbb {N}^{*}\), since \(\inf {h} > -\infty \), \(\tau _{n} \leqslant \tau _{n+1},\) and
 , applying Lemma 3.2(iii) to
, applying Lemma 3.2(iii) to  yields
yields  . Hence, because
. Hence, because  is increasing and
is increasing and  , an inductive argument gives
, an inductive argument gives  (80a)
(80a) (80b)
(80b) (80c)
(80c)Therefore, since (75) trivially holds when \(n=1\), we obtain the conclusion. Consequently, (76) readily follows from (75).
-
(ii):
For every \(z \in {\text {dom}}{h}\), taking the limit superior over n in (76) and using (78) yields
 . Consequently, letting
. Consequently, letting  , we conclude that
, we conclude that  , as desired.
, as desired. -
(iii):
First, due to (63),
 , and thus, $$\begin{aligned} \inf _{n \in \mathbb {N}^{*}}\sigma _{n} > {-}\infty . \end{aligned}$$(81)
, and thus, $$\begin{aligned} \inf _{n \in \mathbb {N}^{*}}\sigma _{n} > {-}\infty . \end{aligned}$$(81)Hence, we conclude via Lemma 5.2(ii) that
 is convergent in \(\mathbb {R}\). In turn, on the one hand, (ii) and (63) imply that
is convergent in \(\mathbb {R}\). In turn, on the one hand, (ii) and (63) imply that  (82)
(82)On the other hand, (81) and Lemma 5.2(a) yield
 , and since
, and since  due to Lemma 2.1 and (78), we get from Lemma 2.2 that $$\begin{aligned} \varliminf ||x_{n}-x_{n-1} ||^{2} = 0. \end{aligned}$$(83)
due to Lemma 2.1 and (78), we get from Lemma 2.2 that $$\begin{aligned} \varliminf ||x_{n}-x_{n-1} ||^{2} = 0. \end{aligned}$$(83)Altogether, combining (82) and (83) yields \(x_{n}-x_{n-1}\rightarrow 0\), as announced.
-
(iv):
Let x be a weak sequential cluster point of
 , say \(x_{k_{n}}\rightharpoonup x\). Then, since h is convex and lower semicontinuous, it is weakly sequentially lower semicontinuous by [8, Theorem 9.1]. Hence, (ii) entails that
, say \(x_{k_{n}}\rightharpoonup x\). Then, since h is convex and lower semicontinuous, it is weakly sequentially lower semicontinuous by [8, Theorem 9.1]. Hence, (ii) entails that  , which ensures that \(x \in {{\,\mathrm{Argmin}\,}}{h}\).
, which ensures that \(x \in {{\,\mathrm{Argmin}\,}}{h}\). -
(v):
Combine (iv) and [8, Lemma 2.45].
-
(vi):
This is the contrapositive of (v).
-
(vii)(a):
Clear from (i) and (74).
-
(vii)(b):
Fix \(z \in {{\,\mathrm{Argmin}\,}}h\). For every \(n \geqslant 2\), because
 , we derive from (75) that
, we derive from (75) that  (84)
(84)
and now a simple expansion gives







In turn,

Hence, since  and
and  , we get
, we get

from which the boundedness of  follows. Consequently, because
follows. Consequently, because  and both sequences on the right-hand side are bounded due to (84) and (87), we conclude that
and both sequences on the right-hand side are bounded due to (84) and (87), we conclude that  is bounded, as announced. \(\square \)
is bounded, as announced. \(\square \)
Remark 5.6
By choosing the sequence  as in Example 4.4(i), we shall see in Proposition 5.8 that Theorem 5.5(ii) is still valid even when the assumption that \(\inf {h}> - \infty \) is omitted. Therefore, it is appealing to conjecture that this assumption can be left out in Theorem 5.5(ii). In stark contrast, it is crucial to assume that h is bounded from below in Theorem 5.5(iii), as illustrated in Example 5.7.
as in Example 4.4(i), we shall see in Proposition 5.8 that Theorem 5.5(ii) is still valid even when the assumption that \(\inf {h}> - \infty \) is omitted. Therefore, it is appealing to conjecture that this assumption can be left out in Theorem 5.5(ii). In stark contrast, it is crucial to assume that h is bounded from below in Theorem 5.5(iii), as illustrated in Example 5.7.
Example 5.7
Suppose that \(\mathcal {H}= \mathbb {R}\), that \(f :\mathcal {H}\rightarrow \mathbb {R}: x \mapsto -x\), that \(g = 0\), that \(\gamma =1\), and that \(\tau _{n}\uparrow \tau _\infty = {+}\infty \). Then, since \({{\text {Prox}}_{g}} = {\text {Id}}\) and  , we see that (61) turns into
, we see that (61) turns into

Hence,  , and upon setting
, and upon setting  , we obtain
, we obtain

Let us establish that \( z_{n} \rightarrow {+}\infty . \) First, since \(y_{1}=x_{0}\) by Algorithm 5.1, we get from (88) that \(z_{1} =x_{1}-x_{0} = x_{1}-y_{1} = 1 \). In turn, by induction and (89),  . We now suppose to the contrary that \(\xi :=\varliminf z_{n} \in \mathbb {R}_{+}\). Then, taking the limit inferior over n in (89) and using Lemma 4.3 yield \(\xi = 1 + 1\cdot \xi = 1 + \xi \), which is absurd. Therefore, \(\xi = {+}\infty \), and it follows that \(x_{n} - x_{n-1} = z_{n}\rightarrow {+}\infty \).
. We now suppose to the contrary that \(\xi :=\varliminf z_{n} \in \mathbb {R}_{+}\). Then, taking the limit inferior over n in (89) and using Lemma 4.3 yield \(\xi = 1 + 1\cdot \xi = 1 + \xi \), which is absurd. Therefore, \(\xi = {+}\infty \), and it follows that \(x_{n} - x_{n-1} = z_{n}\rightarrow {+}\infty \).
Proposition 5.8
Suppose that the sequence  is as in Example 4.4(i). Then
is as in Example 4.4(i). Then  .
.
Proof
First, as seen in Example 4.4(i),

Now it is sufficient to show that  . To do so, fix \(z \in {\text {dom}}{h}\), and set
. To do so, fix \(z \in {\text {dom}}{h}\), and set  . Then, according to Lemma 3.2(ii) and (90),
. Then, according to Lemma 3.2(ii) and (90),

Thus,

Hence, because \( \lim \tau _{n} = +\infty \), taking the limit superior over n yields  . Consequently, since z is an arbitrary element of \({\text {dom}}{h}\), we conclude that
. Consequently, since z is an arbitrary element of \({\text {dom}}{h}\), we conclude that  , as required. \(\square \)
, as required. \(\square \)
Remark 5.9
Proposition 5.8 is a special case of the accelerated inexact forward-backward splitting developed in [28]; see [28, Theorem 4.3 and Remark 3].
We now turn to our third main result, which concerns the case where the parameter sequence  in Assumption 4.1 is bounded.
in Assumption 4.1 is bounded.
Theorem 5.10
Suppose that \(\tau _{\infty } < {+}\infty \). Then the following hold:
-
(i)
 .
. -
(ii)
Assume that \(\inf h > {-}\infty \). Then the following hold:
-
(a)
\(\sum _{n \in \mathbb {N}^{*}}||x_{n}-x_{n-1} ||^{2} < {+}\infty \).
-
(b)
Every weak sequential cluster point of
 lies in \({{\,\mathrm{Argmin}\,}}h\).
lies in \({{\,\mathrm{Argmin}\,}}h\).
-
(a)
-
(iii)
Assume that
 has a bounded subsequence. Then \({{\,\mathrm{Argmin}\,}}h \ne \varnothing \).
has a bounded subsequence. Then \({{\,\mathrm{Argmin}\,}}h \ne \varnothing \). -
(iv)
Assume that \({{\,\mathrm{Argmin}\,}}h = \varnothing \). Then \(||x_{n} || \rightarrow {+}\infty \).
-
(v)
Assume that \({{\,\mathrm{Argmin}\,}}h \ne \varnothing \). Then the following hold:
-
(a)
(Attouch–Cabot [1])
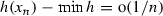 as \(n\rightarrow {+}\infty \).
as \(n\rightarrow {+}\infty \). -
(b)
\( \sum _{n \in \mathbb {N}^{*}}n ||x_{n}-x_{n-1} ||^{2} < {+}\infty . \) As a consequence,
 .
.
-
(a)
Proof
-
(i):
Since, by (63),
 and, by Lemma 5.2(ii),
and, by Lemma 5.2(ii),  converges to a point \(\sigma \in [ {-}\infty , {+}\infty [\), it is enough to verify that \(\sigma = \lim \sigma _{n} = \inf h\). Assume to the contrary that $$\begin{aligned} {-}\infty \leqslant \inf h< \sigma . \end{aligned}$$(93)
converges to a point \(\sigma \in [ {-}\infty , {+}\infty [\), it is enough to verify that \(\sigma = \lim \sigma _{n} = \inf h\). Assume to the contrary that $$\begin{aligned} {-}\infty \leqslant \inf h< \sigma . \end{aligned}$$(93)It then follows that \(\inf _{n \in \mathbb {N}^{*}}\sigma _{n} > {-}\infty \), and Lemma 5.2(b) thus yields \(||x_{n}-x_{n-1} ||^{2} \rightarrow 0\), from which and (63) we deduce that
 . This and Theorem 5.3 imply that \(\sigma = \inf h\). This and (93) yield a contradiction.
. This and Theorem 5.3 imply that \(\sigma = \inf h\). This and (93) yield a contradiction. -
(ii)(a):
Our assumption ensures that \(\inf _{n \in \mathbb {N}^{*}}\sigma _{n} > {-}\infty \), and therefore, thanks to the boundedness of
 , Lemma 5.2(b) yields \(\sum _{n \in \mathbb {N}^{*}}||x_{n}-x_{n-1} ||^{2} < {+}\infty \).
, Lemma 5.2(b) yields \(\sum _{n \in \mathbb {N}^{*}}||x_{n}-x_{n-1} ||^{2} < {+}\infty \). -
(ii)(b),
(iii), and (iv): Similar to Theorem 5.5(iv), (v), and (vi), respectively.
-
(v):
Fix \(z \in {{\,\mathrm{Argmin}\,}}h\), and set
 . By (41), we have $$\begin{aligned} \tau _{n} \uparrow \tau _{\infty }, \end{aligned}$$(94)
. By (41), we have $$\begin{aligned} \tau _{n} \uparrow \tau _{\infty }, \end{aligned}$$(94)which implies that \(\tau _{n}^{2} - \tau _{n+1}^{2}+\tau _{n+1} \rightarrow \tau _{\infty }\). Therefore, because \(\tau _{\infty }\in ]0, {+}\infty [\), there exists \(N \in \mathbb {N}^{*}\) such that
 (95)
(95)Next, for every \(n \geqslant N\), using Lemma 3.2(ii) with
 , we get
, we get  . Hence, because
. Hence, because  and, by (42),
and, by (42),  , Lemma 2.3(ii) and (95) give
, Lemma 2.3(ii) and (95) give  . This, (ii)(a), and (63) ensure that
. This, (ii)(a), and (63) ensure that  (96)
(96)Furthermore, Lemma 5.2(ii) and (i) yield
$$\begin{aligned} \sigma _{n}-\min h \downarrow 0. \end{aligned}$$(97) -
(v)(a):
Appealing to (96) and (97), Lemma 2.5 guarantees that
 . Consequently, since
. Consequently, since  , the conclusion follows.
, the conclusion follows. -
(v)(b):
Thanks to (96) and (97), we derive from Lemma 2.5 that
 (98)
(98)and hence, by Lemma 5.2(i),
 . Thus, because
. Thus, because  due to the boundedness of
due to the boundedness of  and Lemma 5.2(b), we conclude that \(\sum _{n \in \mathbb {N}^{*}}n ||x_{n}-x_{n-1} ||^{2} < {+}\infty \). This gives \(n||x_{n}-x_{n-1} ||^{2} \rightarrow 0\), i.e.,
and Lemma 5.2(b), we conclude that \(\sum _{n \in \mathbb {N}^{*}}n ||x_{n}-x_{n-1} ||^{2} < {+}\infty \). This gives \(n||x_{n}-x_{n-1} ||^{2} \rightarrow 0\), i.e.,  as \(n\rightarrow {+}\infty \), as desired.
as \(n\rightarrow {+}\infty \), as desired.
\(\square \)
Remark 5.11
-
(i)
In the case of the classical forward-backward algorithm (without the extrapolation step) with linesearches, results similar to Theorem 5.10(i) and (iv) were established in [12, Theorem 4.2] by Bello Cruz and Nghia. To the best of our knowledge, Theorem 5.10(i) is new in the setting of Algorithm 5.1.
-
(ii)
Theorem 5.10(v)(a) was obtained by Attouch and Cabot [1, Corollary 20(iii)]. Here we provide a proof based on the technique developed in [1] to be self-contained.
-
(iii)
The summabilities established in Theorem 5.10(ii)(a) and (v)(b) are new. Nevertheless, in the case of the forward-backward algorithm, i.e., when \(\tau _{n} \equiv 1\), Theorem 5.10(v)(b) appears implicitly in the Beck and Teboulle’s proof of [11, Theorem 3.1].
In the case of the classical forward-backward algorithm, by applying [14, Corollary 1.5] to the forward-backward operator  , we obtain further information on the sequence
, we obtain further information on the sequence  as follows.
as follows.
Proposition 5.12
Suppose that  , and setFootnote 1\(^{,}\)Footnote 2
, and setFootnote 1\(^{,}\)Footnote 2 . Then \(x_{n}- x_{n-1}\rightarrow v\).
. Then \(x_{n}- x_{n-1}\rightarrow v\).
Proof
By assumption, Algorithm 5.1 becomes  . Next, we learn from [21, Proposition 3.2 and Corollary 4.2] that T is averaged, i.e., there exists \(\alpha \in ]0,1 [\) and a nonexpansive operator \(R :\mathcal {H}\rightarrow \mathcal {H}\) such that
. Next, we learn from [21, Proposition 3.2 and Corollary 4.2] that T is averaged, i.e., there exists \(\alpha \in ]0,1 [\) and a nonexpansive operator \(R :\mathcal {H}\rightarrow \mathcal {H}\) such that  . Hence, we conclude via [14, Proposition 1.3 and Corollary 1.5] that \(x_{n} - x_{n-1} = T^{n}x_{0} - T^{n-1}x_{0} \rightarrow v\). For an alternative proof of [14, Corollary 1.2] in the Hilbert space setting, see [21, Proposition 2.1]. \(\square \)
. Hence, we conclude via [14, Proposition 1.3 and Corollary 1.5] that \(x_{n} - x_{n-1} = T^{n}x_{0} - T^{n-1}x_{0} \rightarrow v\). For an alternative proof of [14, Corollary 1.2] in the Hilbert space setting, see [21, Proposition 2.1]. \(\square \)
Remark 5.13
Some comments are in order.
-
(i)
In stark contrast to Proposition 5.12 and Theorem 5.10, if \(\tau _{\infty }= {+}\infty \), then it may happen that \(||x_{n}-x_{n-1} || \rightarrow {+}\infty \) (see Example 5.7).
-
(ii)
For a recent study on the forward-backward operator T, we refer the reader to [21].
Proposition 5.14
Suppose that \({{\,\mathrm{Argmin}\,}}h\ne \varnothing \), that  converges in \(\mathbb {R}\), and that \(\tau _{n}||x_{n}-x_{n-1} || \rightarrow 0\). Then the following hold:
converges in \(\mathbb {R}\), and that \(\tau _{n}||x_{n}-x_{n-1} || \rightarrow 0\). Then the following hold:
-
(i)
 .
. -
(ii)
The sequence
 converges weakly to a point in \({{\,\mathrm{Argmin}\,}}h\).
converges weakly to a point in \({{\,\mathrm{Argmin}\,}}h\). -
(iii)
Suppose that
 . Then
. Then  converges strongly to a point in \({{\,\mathrm{Argmin}\,}}h\).
converges strongly to a point in \({{\,\mathrm{Argmin}\,}}h\).
Proof
Set

Since, by (40) and (99),  and since, by our assumption, \(\tau _{n}||x_{n}-x_{n-1} || \rightarrow 0\), we see that
and since, by our assumption, \(\tau _{n}||x_{n}-x_{n-1} || \rightarrow 0\), we see that
Next, due to our assumption and


we see that
Let us now establish that

Fix \(z \in {{\,\mathrm{Argmin}\,}}h\) and \(n \in \mathbb {N}^{*}\). Applying Lemma 3.2(ii) to  and invoking (42) yields
and invoking (42) yields


from which and (99) we obtain (103).
-
(i):
Since, by assumption,
 converges and since, by (41),
converges and since, by (41),  converges in \(\mathbb {R}\), it follows that
converges in \(\mathbb {R}\), it follows that  is convergent in \(\mathbb {R}\). Therefore, due to Theorem 5.3,
is convergent in \(\mathbb {R}\). Therefore, due to Theorem 5.3,  .
. -
(ii):
In the light of (i), arguing similarly to the proof of Theorem 5.5(iv), we conclude that
 (105)
(105)In turn, appealing to (102) and (103), Lemma 2.7(i) implies that
 (106)
(106)Thus, combining (100), (105), and (106), we get via Lemma 2.6 that
 converges weakly to a point in \({{\,\mathrm{Argmin}\,}}h\).
converges weakly to a point in \({{\,\mathrm{Argmin}\,}}h\). -
(iii):
Since
 , owing to Lemma 2.7(ii), we derive from (102) and (103) that there exists \(z \in \mathcal {H}\) such that \(z_{n } \rightarrow z\). Hence, by (100), \(x_{n}\rightarrow z\), and (ii) implies that \(z \in {{\,\mathrm{Argmin}\,}}h\). To sum up,
, owing to Lemma 2.7(ii), we derive from (102) and (103) that there exists \(z \in \mathcal {H}\) such that \(z_{n } \rightarrow z\). Hence, by (100), \(x_{n}\rightarrow z\), and (ii) implies that \(z \in {{\,\mathrm{Argmin}\,}}h\). To sum up,  converges strongly to a minimizer of h.
converges strongly to a minimizer of h.
\(\square \)
Corollary 5.15
Suppose that \({{\,\mathrm{Argmin}\,}}h \ne \varnothing \) and that \(\sup _{n \in \mathbb {N}^{*}}\tau _{n} < {+}\infty \). Then  converges weakly to a point in \({{\,\mathrm{Argmin}\,}}h\). Moreover, if
converges weakly to a point in \({{\,\mathrm{Argmin}\,}}h\). Moreover, if  , then the convergence is strong.
, then the convergence is strong.
Proof
By Theorem 5.10(v), we see that  and \(||x_{n}-x_{n-1} || \rightarrow 0\), and since \(\sup _{n \in \mathbb {N}^{*}}\tau _{n} < {+}\infty \), it follows that
and \(||x_{n}-x_{n-1} || \rightarrow 0\), and since \(\sup _{n \in \mathbb {N}^{*}}\tau _{n} < {+}\infty \), it follows that  and \(\tau _{n}||x_{n}-x_{n-1} || \rightarrow 0\). The conclusion thus follows from Proposition 5.14. \(\square \)
and \(\tau _{n}||x_{n}-x_{n-1} || \rightarrow 0\). The conclusion thus follows from Proposition 5.14. \(\square \)
Remark 5.16
Consider the setting of Corollary 5.15. Although the weak convergence of the sequence  has been shown in [1, Corollary 20(iv)], our Fejér-based proof here is new and may suggest other approaches to tackle the convergence of
has been shown in [1, Corollary 20(iv)], our Fejér-based proof here is new and may suggest other approaches to tackle the convergence of  in the setting Theorem 5.5(vii).
in the setting Theorem 5.5(vii).
We conclude this section with an instance where the assumption of Proposition 5.14 holds.
Example 5.17
Suppose, in addition to Assumption 4.1, that there exists \(\delta \in ]0,1 [\) such that

(see Examples 4.5 and 4.6). Then Attouch and Cabot’s [1, Theorem 9] yields  and \(\tau _{n}||x_{n}-x_{n-1} || \rightarrow 0 \).
and \(\tau _{n}||x_{n}-x_{n-1} || \rightarrow 0 \).
6 MFISTA
In this section, we discuss the minimizing property of the sequence generated by MFISTA. The monotonicity of function values allows us to overcome the issue stated in Remark 5.4. Compared to Beck and Teboulle’s [10, Theorem 5.1] (see also [9, Theorem 10.40]), we allow other possibilities for the choice of  in Theorem 6.1(vi). Furthermore, we provide in item (vii), which was motivated by [1, Theorem 9], a better rate of convergence.
in Theorem 6.1(vi). Furthermore, we provide in item (vii), which was motivated by [1, Theorem 9], a better rate of convergence.
Theorem 6.1
In addition to Assumption 4.1, suppose that \(\tau _{\infty }= {+}\infty \). Let \(x_{0} \in \mathcal {H}\), set \(y_{1}:=x_{0}\), and update

where T is as in (16). Furthermore, set

Then the following hold:
-
(i)
 is decreasing and
is decreasing and  .
. -
(ii)
 is decreasing and \( \sigma _{n} \downarrow \inf h\).
is decreasing and \( \sigma _{n} \downarrow \inf h\). -
(iii)
Suppose that \(\inf h > {-}\infty \). Then \(z_{n} - x_{n-1}\rightarrow 0\) and \(x_{n}-x_{n-1}\rightarrow 0\).
-
(iv)
Suppose that
 has a bounded subsequence. Then \({{\,\mathrm{Argmin}\,}}h \ne \varnothing \).
has a bounded subsequence. Then \({{\,\mathrm{Argmin}\,}}h \ne \varnothing \). -
(v)
Suppose that \({{\,\mathrm{Argmin}\,}}h = \varnothing .\) Then \(||x_{n} || \rightarrow {+}\infty \).
-
(vi)
Suppose that \({{\,\mathrm{Argmin}\,}}h \ne \varnothing .\) Then
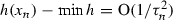 as \(n\rightarrow {+}\infty \).
as \(n\rightarrow {+}\infty \). -
(vii)
Suppose that \({{\,\mathrm{Argmin}\,}}h\ne \varnothing \) and that there exists \(\delta \in ]0,1[\) such that
$$\begin{aligned} (\forall n\in \mathbb {N}^{*})\quad \tau _{n+1}^{2}-\tau _n^2\leqslant \delta \tau _{n+1}. \end{aligned}$$(110)Then
 (111)
(111)and
 (112)
(112)
Proof
-
(i):
By (108), the sequence
 is decreasing, from which we have
is decreasing, from which we have 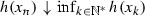 . Therefore, it suffices to prove that
. Therefore, it suffices to prove that 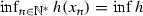 . To this end, assume to the contrary that
. To this end, assume to the contrary that  . This yields the existence of a point \(w \in {\text {dom}}h\) such that
. This yields the existence of a point \(w \in {\text {dom}}h\) such that  (113)
(113)Set
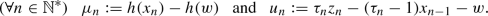 (114)
(114)In turn, for every \(n \in \mathbb {N}^{*}\), because, by (42),
 and, by (113), \(\mu _{n}> 0\), it follows from Lemma 3.3(ii) (applied to
and, by (113), \(\mu _{n}> 0\), it follows from Lemma 3.3(ii) (applied to  ) that
) that  (115)
(115)Hence,
 (116)
(116)Consequently, since
 and \(\tau _{n}\rightarrow {+}\infty \), we derive from (116) that
and \(\tau _{n}\rightarrow {+}\infty \), we derive from (116) that  , which contradicts (113).
, which contradicts (113). -
(ii):
Let us first show that
 is decreasing. Towards this end, for every \( n\in \mathbb {N}^{*}\), we deduce from Lemma 3.3(i) that
is decreasing. Towards this end, for every \( n\in \mathbb {N}^{*}\), we deduce from Lemma 3.3(i) that  . Therefore,
. Therefore,  (117)
(117)and because
 , we conclude that
, we conclude that  (118)
(118)It remains to show that \(\sigma _{n}\rightarrow \inf h\). Set \(\sigma :=\inf _{n \in \mathbb {N}^{*}}\sigma _{n}\). Due to (118),
$$\begin{aligned} \sigma _{n}\downarrow \sigma \end{aligned}$$(119)and it therefore suffices to prove that \(\sigma = \inf h\). Let us argue by contradiction: assume that \(\sigma > \inf h \geqslant {-}\infty \). By (117),
 (120)
(120)which implies that
 . Thus, since
. Thus, since  by Lemma 2.1, Lemma 2.2 guarantees that \(\varliminf ||z_{n}-x_{n-1} ||^{2} =0\), i.e., \(\varliminf ||z_{n}-x_{n-1} || = 0\). In turn, let
by Lemma 2.1, Lemma 2.2 guarantees that \(\varliminf ||z_{n}-x_{n-1} ||^{2} =0\), i.e., \(\varliminf ||z_{n}-x_{n-1} || = 0\). In turn, let  be a strictly increasing sequence in \(\mathbb {N}^{*}\) such that \(||z_{k_{n}} - x_{k_{n}-1} || \rightarrow \varliminf ||z_{n}-x_{n-1} ||= 0\). It follows from (i) and (119) that
be a strictly increasing sequence in \(\mathbb {N}^{*}\) such that \(||z_{k_{n}} - x_{k_{n}-1} || \rightarrow \varliminf ||z_{n}-x_{n-1} ||= 0\). It follows from (i) and (119) that  . Consequently, \(\sigma =\inf h\), which violates the assumption that \(\sigma > \inf h\). To summarize, we have shown that \(\sigma _{n}\downarrow \inf h\).
. Consequently, \(\sigma =\inf h\), which violates the assumption that \(\sigma > \inf h\). To summarize, we have shown that \(\sigma _{n}\downarrow \inf h\). -
(iii):
Since \(\inf h > {-}\infty \), combining (i), (ii), and (109) gives \(z_{n} -x_{n-1} \rightarrow 0\). To show that \(x_{n}-x_{n-1}\rightarrow 0\), we infer from (108) that, for every \(n \in \mathbb {N}^{*}\), \(x_{n}-x_{n-1}=x_{n-1}-x_{n-1} = 0\) if
 , and \(x_{n}-x_{n-1} = z_{n}-x_{n-1}\) otherwise; therefore,
, and \(x_{n}-x_{n-1} = z_{n}-x_{n-1}\) otherwise; therefore,  . Consequently, because \(z_{n}-x_{n-1}\rightarrow 0\), it follows that \(x_{n}-x_{n-1}\rightarrow 0\), as required.
. Consequently, because \(z_{n}-x_{n-1}\rightarrow 0\), it follows that \(x_{n}-x_{n-1}\rightarrow 0\), as required. -
(iv)
and (v): Straightforward.
-
(vi):
Fix \(w \in {{\,\mathrm{Argmin}\,}}h\) and define
 . Due to (42) and the fact that
. Due to (42) and the fact that  , Lemma 3.3(ii) entails that
, Lemma 3.3(ii) entails that  . Hence,
. Hence,  (121)
(121)which verifies the claim.
-
(vii):
Let us adapt the notation of (vi). Since \(\{\mu _{n}\}_{n\in \mathbb {N}^{*}}\subseteq \mathbb {R}_{+}\), we derive from Lemma 3.3(ii) and (110) that
$$\begin{aligned}&(\forall n\in \mathbb {N}^{*})\quad \tau _{n+1}^2\mu _{n+1}+(2\gamma )^{-1}||u_{n+1} ||^{2}\nonumber \\&\quad \leqslant \tau _{n+1}(\tau _{n+1}-1)\mu _{n}+(2\gamma )^{-1}||u_{n} ||^{2} \end{aligned}$$(122a)$$\begin{aligned}&\quad =\tau _{n}^{2}\mu _{n}+(2\gamma )^{-1}||u_{n} ||^{2} -\big (\tau _{n}^{2}-\tau _{n+1}^{2}+\tau _{n+1}\big )\mu _{n} \end{aligned}$$(122b)$$\begin{aligned}&\quad \leqslant \tau _{n}^{2}\mu _n+(2\gamma )^{-1}||u_{n} ||^{2} -(1-\delta )\tau _{n+1}\mu _n. \end{aligned}$$(122c)
On the other hand, since \(\delta \in ]0,1[\) and \(\{\mu _n\}_{n\in \mathbb {N}^{*}}\subseteq \mathbb {R}_{+}\), it follows that \(\{(1-\delta )\tau _{n+1}\mu _n\}_{n\in \mathbb {N}^{*}}\subseteq \mathbb {R}_{+}\). Combining this, (122), and Lemma 2.3(ii), we infer that \((1-\delta )\sum _{n\in \mathbb {N}^{*}}\tau _{n+1}\mu _n< {+}\infty \). In turn, since \((\tau _n)_{n\in \mathbb {N}^{*}}\) is increasing and \(1-\delta >0\), it follows that \(\sum _{n\in \mathbb {N}^{*}}\tau _{n}\mu _n< {+}\infty \). Consequently, since \((\mu _n)_{n\in \mathbb {N}^{*}}\) is decreasing due to (i) and since clearly \(\sum _{n\in \mathbb {N}^{*}}\tau _{n}= {+}\infty \), [1, Lemma 22] ensures that

which establishes (111). In turn, we deduce from (110), (123), and (i) that
which verifies (112). \(\square \)
Remark 6.2
In Theorem 6.1, the assumption that \(\tau _{\infty }= {+}\infty \) is actually not needed in items (i) and (iv)–(vii). For clarity, let us sketch the proof of (i) under the assumption that \(\tau _\infty < {+}\infty \). Assume that \(\tau _\infty < {+}\infty \). We infer from the first inequality in (115) that
and it follows from Lemma 2.3(ii) that \(\sum _{n\in \mathbb {N}^{*}}(\tau _n^2-\tau _{n+1}^2+\tau _{n+1}) \mu _n< {+}\infty \). One may argue similarly to the case (b) in the proof of Theorem 5.3 to obtain \(\varliminf \mu _n=0\) or, equivalently, \(\varliminf h(x_n) =h(w)\), which contradicts (113). Therefore \(\inf _{n\in \mathbb {N}^{*}}h(x_n)=\inf h\) and we get \(h(x_n)\downarrow \inf _{n\in \mathbb {N}^{*}}h(x_n)=\inf h\). Items (iv) and (v) follow from this. In addition, note that we did not use the assumption that \(\tau _\infty = {+}\infty \) in the proof of (vi) and (vii). It is, however, worth pointing out that the conclusion of Theorem 6.1(vi) is not so interesting when \(\tau _{\infty }< {+}\infty \).
7 Open problems
We conclude this paper with a few open problems.
- P1:
-
In Theorem 5.3, is it true that
 ?
? - P2:
-
What can be said about the conclusions of Theorem 5.5(iii) and (vii)(b) if
 ?
? - P2:
-
Suppose that \({{\,\mathrm{Argmin}\,}}h \ne \varnothing \). Do the sequences generated by Algorithm 5.1 and (108) always converge weakly to a point in \({{\,\mathrm{Argmin}\,}}h\)?
References
Attouch, H., Cabot, A.: Convergence rates of inertial forward-backward algorithms. SIAM J. Optim. 28, 849–874 (2018)
Attouch, H., Cabot, A., Chbani, Z., Riahi, H.: Inertial forward-backward algorithms with perturbations: application to Tikhonov regularization. J. Optim. Theory Appl. 179, 1–36 (2018)
Attouch, H., Chbani, Z., Peypouquet, J., Redont, P.: Fast convergence of inertial dynamics and algorithms with asymptotic vanishing viscosity. Math. Program. Ser. B 168, 123–175 (2018)
Attouch, H., Chbani, Z., Riahi, H.: Rate of convergence of the Nesterov accelerated gradient method in the subcritical case \(\alpha \le 3\). ESAIM Control Optim. Calc. Var. (2019). https://doi.org/10.1051/cocv/2017083
Attouch, H., Peypouquet, J.: The rate of convergence of Nesterov’s accelerated forward-backward method is actually faster than \(1/k^2\). SIAM J. Optim. 26, 1824–1834 (2016)
Attouch, H., Peypouquet, J., Redont, P.: Fast convergence of an inertial gradient-like system with vanishing viscosity. (2015) arXiv:1507.04782
Aujol, J.-F., Dossal, C.: Stability of over-relaxations for the forward-backward algorithm, application to FISTA. SIAM J. Optim. 25, 2408–2433 (2015)
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces, second edn. Springer, New York (2017)
Beck, A.: First-Order Methods in Optimization. SIAM, Philadelphia (2017)
Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18, 2419–2434 (2009)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problem. SIAM J. Imaging Sci. 2, 183–202 (2009)
Bello Cruz, J.Y., Nghia, T.T.A.: On the convergence of the forward-backward splitting method with linesearches. Optim. Methods Softw. 31, 1209–1238 (2016)
Bredies, K.: A forward-backward splitting algorithm for the minimization of non-smooth convex functionals in Banach space. Inverse Probl. 25, 015005 (2009)
Bruck, R.E., Reich, S.: Nonexpansive projections and resolvents of accretive operators in Banach spaces. Houst. J. Math. 3, 459–470 (1977)
Chambolle, A., Dossal, C.: On the convergence of the iterates of the “fast iterative shrinkage/thresholding algorithm”. J. Optim. Theory Appl. 166, 968–982 (2015)
Chambolle, A., Pock, T.: An introduction to continuous optimization for imaging. Acta Numer. 25, 161–319 (2016)
Combettes, P.L.: Quasi-Fejérian analysis of some optimization algorithms. In: Butnariu, D., Censor, Y., Reich, S. (eds.) Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications, vol. 8, pp. 115–152. North-Holland, Amsterdam (2001)
Combettes, P.L., Glaudin, L.E.: Quasinonexpansive iterations on the affine hull of orbits: from Mann’s mean value algorithm to inertial methods. SIAM J. Optim. 27, 2356–2380 (2017)
Combettes, P.L., Salzo, S., Villa, S.: Consistent learning by composite proximal thresholding. Math. Program. Ser. B 167, 99–127 (2018)
Kaczor, W.J., Nowak, M.T.: Problems in Mathematical Analysis. I. Real Numbers, Sequences and Series. American Mathematical Society, Providence, RI (2000)
Moursi, W.M.: The forward-backward algorithm and the normal problem. J. Optim. Theory Appl. 176, 605–624 (2018)
Nesterov, Y.E.: A method for solving the convex programming problem with convergence rate \(O(1/k^{2})\). Dokl. Akad. Nauk 269, 543–547 (1983)
Opial, Z.: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 73, 591–597 (1967)
Pazy, A.: Asymptotic behavior of contractions in Hilbert space. Israel J. Math. 9, 235–240 (1971)
Rǎdulescu, T.-L., Rǎdulescu, V.D., Andreescu, T.: Problems in Real Analysis: Advanced Calculus on the Real Axis. Springer, New York (2009)
Schmidt, M., Roux, N.L., Bach, F.: Convergence rates of inexact proximal-gradient methods for convex optimization. In: Shawe-Taylor, J., Zemel, R.S., Bartlett, P.L., Pereira, F., Weinberger, K.Q. (eds.) Advances in Neural Information Processing Systems 24, pp. 1458–1466. Curran Associates Inc., Red Hook (2011)
Su, W., Boyd, S., Candès, E.J.: A differential equation for modeling Nesterov’s accelerated gradient method: theory and insights. J. Mach. Learn. Res. 17, 1–43 (2016)
Villa, S., Salzo, S., Baldassarre, L., Verri, A.: Accelerated and inexact forward-backward algorithms. SIAM J. Optim. 23, 1607–1633 (2013)
Acknowledgements
We thank two referees for their very careful reading and constructive comments. HHB and XW were partially supported by NSERC Discovery Grants while MNB was partially supported by a Mitacs Globalink Graduate Fellowship Award.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
1.1 Appendix A
For the sake of completeness, we provide the following proof of Lemma 2.1 based on [20, Problem 3.2.43].
Proof of Lemma 2.1
Because  due to the assumption that
due to the assumption that  , it is sufficient to establish that
, it is sufficient to establish that

Indeed, since \(\tau _{n}\rightarrow {+}\infty \), there exists \(N \in \mathbb {N}^{*}\) such that

Now, set  , and
, and  . Then, on the one hand, since
. Then, on the one hand, since  is increasing and positive, we have
is increasing and positive, we have  , and
, and  is therefore an increasing sequence in \(\mathbb {R}_{+}\); moreover, due to (127),
is therefore an increasing sequence in \(\mathbb {R}_{+}\); moreover, due to (127),  . On the other hand, because \(\tau _{n}\rightarrow {+}\infty \), we have \(\sigma _{n} =\tau _{n+1}^{2}-\tau _{1}^{2} \rightarrow {+}\infty \). Altogether, since
. On the other hand, because \(\tau _{n}\rightarrow {+}\infty \), we have \(\sigma _{n} =\tau _{n+1}^{2}-\tau _{1}^{2} \rightarrow {+}\infty \). Altogether, since

by the fact that  is increasing, we see that
is increasing, we see that  . It follows that the partial sums of
. It follows that the partial sums of  do not satisfy the Cauchy property. Hence, since
do not satisfy the Cauchy property. Hence, since  , we obtain
, we obtain
Consequently, in the light of (127),

and (126) follows. \(\square \)
1.2 Appendix B
Proof of Lemma 2.2
Let us argue by contradiction. Towards this goal, assume that \(\varliminf \beta _{n} \in ] 0, {+}\infty ]\) and fix \( \beta \in ] 0 , \varliminf \beta _{n} [\). Then, there exists \(N \in \mathbb {N}^{*}\) such that  , and hence, because
, and hence, because  , we have
, we have  , it follows that \(\sum _{n \geqslant N}\alpha _{n}\beta _{n} \geqslant \sum _{n \geqslant N} \beta \alpha _{n} = {+}\infty \), which violates our assumption. To sum up, \(\varliminf \beta _{n} = 0\). \(\square \)
, it follows that \(\sum _{n \geqslant N}\alpha _{n}\beta _{n} \geqslant \sum _{n \geqslant N} \beta \alpha _{n} = {+}\infty \), which violates our assumption. To sum up, \(\varliminf \beta _{n} = 0\). \(\square \)
1.3 Appendix C
The following self-contained proof of Lemma 2.3 follows [17, Lemma 3.1] in the case \(\chi =1\); however, we do not require the error sequence  to be positive.
to be positive.
Proof of Lemma 2.3
-
(i):
Set \(\alpha :=\varliminf _{n}\alpha _{n} \in \left[ \inf _{n \in \mathbb {N}^{*}}\alpha _{n}, {+}\infty \right] \) and let
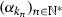 be a subsequence of
be a subsequence of  that converges to \(\alpha \). We first show that \(\alpha < {+}\infty \). Since
that converges to \(\alpha \). We first show that \(\alpha < {+}\infty \). Since 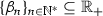 , it follows from (9) that
, it follows from (9) that  . Thus,
. Thus, 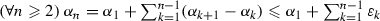 ; in particular,
; in particular, 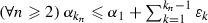 . Hence, since \(\alpha _{k_{n}}\rightarrow \alpha \) and \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\) converges, it follows that \(\alpha \leqslant \alpha _{1} + \sum _{k \in \mathbb {N}}\varepsilon _{k } < {+}\infty \), as claimed. In turn, to establish the convergence of
. Hence, since \(\alpha _{k_{n}}\rightarrow \alpha \) and \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\) converges, it follows that \(\alpha \leqslant \alpha _{1} + \sum _{k \in \mathbb {N}}\varepsilon _{k } < {+}\infty \), as claimed. In turn, to establish the convergence of  , it suffices to verify that \(\varlimsup _{n}\alpha _{n} \leqslant \varliminf _{n} \alpha _{n}\). Towards this goal, let \(\delta \) be in \(]0, {+}\infty [\). Then, on the one hand, Cauchy’s criterion ensures the existence of \(k_{n_{0}} \in \mathbb {N}^{*}\) such that \(\alpha _{k_{n_{0} } } - \alpha \leqslant \delta /2 \) and that
, it suffices to verify that \(\varlimsup _{n}\alpha _{n} \leqslant \varliminf _{n} \alpha _{n}\). Towards this goal, let \(\delta \) be in \(]0, {+}\infty [\). Then, on the one hand, Cauchy’s criterion ensures the existence of \(k_{n_{0}} \in \mathbb {N}^{*}\) such that \(\alpha _{k_{n_{0} } } - \alpha \leqslant \delta /2 \) and that 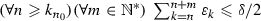 . On the other hand, because
. On the other hand, because 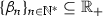 , (9) implies that
, (9) implies that 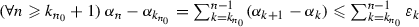 . Altogether,
. Altogether, 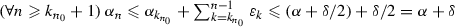 , from which we deduce that \(\varlimsup _{n} \alpha _{n} \leqslant \alpha + \delta \). Consequently, since \(\delta \) is arbitrarily chosen in \(]0, {+}\infty [\), it follows that \(\varlimsup _{n}\alpha _{n} \leqslant \alpha = \varliminf _{n}\alpha _{n}\), and therefore,
, from which we deduce that \(\varlimsup _{n} \alpha _{n} \leqslant \alpha + \delta \). Consequently, since \(\delta \) is arbitrarily chosen in \(]0, {+}\infty [\), it follows that \(\varlimsup _{n}\alpha _{n} \leqslant \alpha = \varliminf _{n}\alpha _{n}\), and therefore,  converges to \(\alpha \).
converges to \(\alpha \). -
(ii):
We derive from (9) that
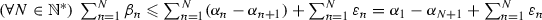 . Hence, since \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\) is convergent and, by (i), \(\lim _{n}\alpha _{n} =\alpha \), letting \(N \rightarrow {+}\infty \) yields \(\sum _{n \in \mathbb {N}} \beta _{n} \leqslant \alpha _{1} - \alpha + \sum _{n \in \mathbb {N}}\varepsilon _{n } < {+}\infty \), and so \(\sum _{n \in \mathbb {N}^{*}}\beta _{n} < {+}\infty \), as required.
. Hence, since \(\sum _{n \in \mathbb {N}^{*}}\varepsilon _{n}\) is convergent and, by (i), \(\lim _{n}\alpha _{n} =\alpha \), letting \(N \rightarrow {+}\infty \) yields \(\sum _{n \in \mathbb {N}} \beta _{n} \leqslant \alpha _{1} - \alpha + \sum _{n \in \mathbb {N}}\varepsilon _{n } < {+}\infty \), and so \(\sum _{n \in \mathbb {N}^{*}}\beta _{n} < {+}\infty \), as required.
\(\square \)
1.4 Appendix D
Proof of Lemma 2.4
Indeed, since 


we readily obtain the conclusion. \(\square \)
1.5 Appendix E
Proof of Lemma 2.5
“\(\Rightarrow \)”: Since  is a decreasing sequence in \(\mathbb {R}_{+}\) and \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n} < {+}\infty \), it follows that \(n\alpha _{n}\rightarrow 0\) (see, e.g., [20, Problem 3.2.35]). Invoking the assumption that \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n} < {+}\infty \) once more, we infer from Lemma 2.4 that
is a decreasing sequence in \(\mathbb {R}_{+}\) and \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n} < {+}\infty \), it follows that \(n\alpha _{n}\rightarrow 0\) (see, e.g., [20, Problem 3.2.35]). Invoking the assumption that \(\sum _{n \in \mathbb {N}^{*}}\alpha _{n} < {+}\infty \) once more, we infer from Lemma 2.4 that  , as desired.
, as desired.
“\(\Leftarrow \)”: A consequence of Lemma 2.4. \(\square \)
1.6 Appendix F
Proof of Lemma 3.1
This is similar to the one found in [11, Lemma 2.3] and included for completeness; see also [15, Lemma 3.1]. Fix  . On the one hand, by (A1) and (A3) in Assumption 1.1, \({\nabla {f} } \) is Lipschitz continuous with constant \(\gamma ^{-1}\), from which, the Descent Lemma (see, e.g., [8, Lemma 2.64]), and the convexity of f we infer that
. On the one hand, by (A1) and (A3) in Assumption 1.1, \({\nabla {f} } \) is Lipschitz continuous with constant \(\gamma ^{-1}\), from which, the Descent Lemma (see, e.g., [8, Lemma 2.64]), and the convexity of f we infer that



On the other hand, because  , [8, Proposition 12.26] asserts that
, [8, Proposition 12.26] asserts that


Altogether, upon adding (132) and (133), it follows that



which yields (18). \(\square \)
1.7 Appendix G
Proof of (50)
Recall that \(\lim (\tau _n/n)=1/2\). In turn, because \((\forall n\in \mathbb {N}^{*})\) \(\tau _n^2=\tau _{n+1}^2-\tau _{n+1}\), it follows that
and therefore that
Hence, (50) holds. \(\square \)
Rights and permissions
About this article
Cite this article
Bauschke, H.H., Bui, M.N. & Wang, X. Applying FISTA to optimization problems (with or) without minimizers. Math. Program. 184, 349–381 (2020). https://doi.org/10.1007/s10107-019-01415-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-019-01415-x




 (see (
(see ( behaves similarly to the Beck–Teboulle choice.
behaves similarly to the Beck–Teboulle choice. is bounded; see, in particular, (ii)(a) and (v)(b).
is bounded; see, in particular, (ii)(a) and (v)(b). is unbounded.
is unbounded. is convergent in
is convergent in  converges in
converges in  converges in
converges in  converges in
converges in  converges strongly in
converges strongly in  . Define a sequence
. Define a sequence  in C via
in C via 
 .
. .
. , and that
, and that 


 , the conclusion follows.
, the conclusion follows. gives
gives 

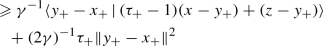

 ) and the very definition of
) and the very definition of 


 due to (
due to (
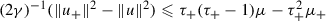 , which implies the desired conclusion.
, which implies the desired conclusion. and, by assumption,
and, by assumption,  . Hence, because
. Hence, because  , it follows that
, it follows that 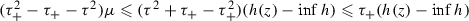 . Consequently, (ii) implies that
. Consequently, (ii) implies that 


 .
. .
. , and thus,
, and thus, 

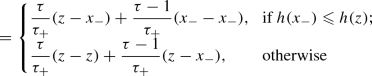

 and noticing that
and noticing that 

 is increasing,
is increasing,  , it is straightforward to verify that
, it is straightforward to verify that 
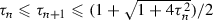 by (
by (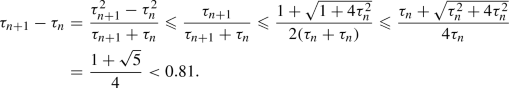


 by (
by ( . Next, by (
. Next, by (

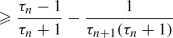

 , as desired.
, as desired.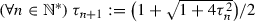 . Then, it is straightforward to verify that
. Then, it is straightforward to verify that  and that
and that  is an increasing sequence in
is an increasing sequence in  , from which we obtain
, from which we obtain  . This and Lemma
. This and Lemma 
 . Then, clearly
. Then, clearly  is an increasing sequence in
is an increasing sequence in  ,
, 
 .
. .
. is decreasing and convergent to a point in
is decreasing and convergent to a point in  .
. and
and  ) asserts that
) asserts that  , from which the desired inequality follows. (ii): A consequence of (i) and (
, from which the desired inequality follows. (ii): A consequence of (i) and (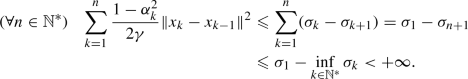
 , as claimed.
, as claimed. is increasing and
is increasing and  , we see that
, we see that  ; therefore,
; therefore, 
 or, equivalently, by the very definition of
or, equivalently, by the very definition of  ,
, 
 , which contradicts (
, which contradicts ( . Then, by (
. Then, by ( and, by (
and, by ( . In turn, on the one hand, combining (70) and Lemma
. In turn, on the one hand, combining (70) and Lemma  . On the other hand, because
. On the other hand, because  and
and 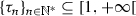 by our assumption and (
by our assumption and (


 .
. is asymptotically regular, i.e.,
is asymptotically regular, i.e.,  belongs to
belongs to  has a bounded subsequence. Then
has a bounded subsequence. Then  as
as 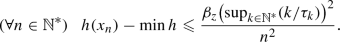
 and
and  are bounded.
are bounded.
 , applying Lemma
, applying Lemma  yields
yields  . Hence, because
. Hence, because  is increasing and
is increasing and  , an inductive argument gives
, an inductive argument gives 


 . Consequently, letting
. Consequently, letting  , we conclude that
, we conclude that  , as desired.
, as desired. , and thus,
, and thus,  is convergent in
is convergent in 
 , and since
, and since  due to Lemma
due to Lemma  , say
, say  , which ensures that
, which ensures that  , we derive from (
, we derive from (
 .
. lies in
lies in  has a bounded subsequence. Then
has a bounded subsequence. Then 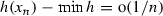 as
as  .
. and, by Lemma
and, by Lemma  converges to a point
converges to a point  . This and Theorem
. This and Theorem  , Lemma
, Lemma  . By (
. By (
 , we get
, we get  . Hence, because
. Hence, because  and, by (
and, by ( , Lemma
, Lemma  . This, (ii)(a), and (63) ensure that
. This, (ii)(a), and (63) ensure that 
 . Consequently, since
. Consequently, since  , the conclusion follows.
, the conclusion follows.
 . Thus, because
. Thus, because  due to the boundedness of
due to the boundedness of  and Lemma
and Lemma  as
as  .
. converges weakly to a point in
converges weakly to a point in  . Then
. Then  converges strongly to a point in
converges strongly to a point in  converges and since, by (
converges and since, by ( converges in
converges in  is convergent in
is convergent in  .
.

 converges weakly to a point in
converges weakly to a point in  , owing to Lemma
, owing to Lemma  converges strongly to a minimizer of h.
converges strongly to a minimizer of h. is decreasing and
is decreasing and  .
. is decreasing and
is decreasing and  has a bounded subsequence. Then
has a bounded subsequence. Then 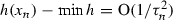 as
as 

 is decreasing, from which we have
is decreasing, from which we have 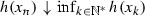 . Therefore, it suffices to prove that
. Therefore, it suffices to prove that 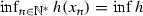 . To this end, assume to the contrary that
. To this end, assume to the contrary that  . This yields the existence of a point
. This yields the existence of a point 
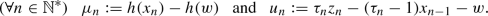
 and, by (
and, by ( ) that
) that 

 and
and  , which contradicts (
, which contradicts ( is decreasing. Towards this end, for every
is decreasing. Towards this end, for every  . Therefore,
. Therefore, 
 , we conclude that
, we conclude that 

 . Thus, since
. Thus, since  by Lemma
by Lemma  be a strictly increasing sequence in
be a strictly increasing sequence in  . Consequently,
. Consequently,  , and
, and  . Consequently, because
. Consequently, because  . Due to (
. Due to ( , Lemma
, Lemma  . Hence,
. Hence, 
 ?
? ?
? is closed and convex by [
is closed and convex by [ be a subsequence of
be a subsequence of  that converges to
that converges to  , it follows from (
, it follows from ( . Thus,
. Thus, 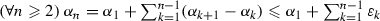 ; in particular,
; in particular, 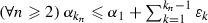 . Hence, since
. Hence, since  , it suffices to verify that
, it suffices to verify that 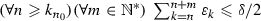 . On the other hand, because
. On the other hand, because  , (
, (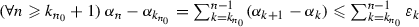 . Altogether,
. Altogether, 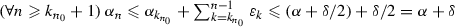 , from which we deduce that
, from which we deduce that  converges to
converges to 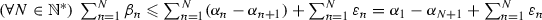 . Hence, since
. Hence, since