Abstract
We consider the fully dynamic bin packing problem, where items arrive and depart in an online fashion and repacking of previously packed items is allowed. The goal is, of course, to minimize both the number of bins used as well as the amount of repacking. A recently introduced way of measuring the repacking costs at each timestep is the migration factor, defined as the total size of repacked items divided by the size of an arriving or departing item. Concerning the trade-off between number of bins and migration factor, if we wish to achieve an asymptotic competitive ratio of \(1 + \epsilon \) for the number of bins, a relatively simple argument proves a lower bound of \(\Omega ({1}/{\epsilon })\) for the migration factor. We establish a nearly matching upper bound of \(O({1}/{\epsilon }^4 \log {1}/{\epsilon })\) using a new dynamic rounding technique and new ideas to handle small items in a dynamic setting such that no amortization is needed. The running time of our algorithm is polynomial in the number of items nand in \({1}/{\epsilon }\). The previous best trade-off was for an asymptotic competitive ratio of \({5}/{4}\) for the bins (rather than \(1+\epsilon \)) and needed an amortized number of \(O(\log n)\) repackings (while in our scheme the number of repackings is independent of n and non-amortized).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For the classical bin packing problem, we are given a set I of items with a size function \(s:I\rightarrow (0,1]\) and need to pack them into as few unit sized bins as possible. In practice, the complete instance is often not known in advance, which has lead to the definition of a variety of online versions of the bin packing problem. First, in the classical online bin packing [43], items arrive over time and have to be packed on arrival. Second, in dynamic bin packing [13], items may also depart over time. This dynamic bin packing model is often used for instance in
the placement and movement of virtual machines onto different servers for cloud computing [6, 8, 30, 31, 40, 45],
the development of guaranteed quality of service channels over certain multi-frequency time division multiple access systems [36],
the placement of processes, which require different resources, onto physical host machines [41, 42],
the resource allocation in a cloud network where the cost depends upon different parameters [14, 34].
Third and fourth, we may allow already packed items to be slightly rearranged, leading to online bin packing with repacking (known as relaxed online bin packing) [19] and dynamic bin packing with repacking (known as fully dynamic bin packing) [23]. See Table 1 for a short overview on the different models.
The amount of repacking can be measured in different ways. We can either count the total number of moved items at each timestep or the sum of the sizes of the moved items at each timestep. If one wants to count the number of moved items, one typically counts a group of tiny items as a single move. A shifting move [19] thus involves either a single large item or a bundle of small items in the same bin of total size s with \({1}/{10}\le s\le {1}/{5}\). Such a bundle may consists of up to \(\Omega (n)\) (very small) items. If an algorithm measures the repacking by shifting moves, a new tiny item may lead to a large amount of repacking. In order to guarantee that a tiny item i with size s(i) only leads to a small amount of repacking, one may allow to repack items whose size adds up to at most \(\beta \cdot s(i)\). The term \(\beta \) is called the migration factor [37] or shortly migration. Note that shifting moves and migration factor are incomparable in the sense that a small migration factor does not imply a small number of shifting moves and vice versa.
In order to measure the quality of an online algorithm, we compare the costs incurred by an online algorithm with the costs incurred by an optimal offline algorithm. An online algorithm receives as input a sequence of items \(I=(i_{1},i_{2},i_{3},\ldots )\) and decides at each timestep t, where to place the item \(i_t\) without knowing future items \(i_{t+1},i_{t+2},\ldots \). We denote by \(I(t)=(i_{1},i_{2},\ldots ,i_{t})\) the instance containing the first t items of the instance I and by \({{\textsc {opt}}}(I(t))\) the minimal number of bins needed to pack all items in I(t). Note that the packings corresponding to \({{\textsc {opt}}}(I(t))\) and \({{\textsc {opt}}}(I(t+1))\) may differ significantly, as those packings do not need to be consistent. For an online algorithm A, we denote by A(I(t)) the number of bins generated by the algorithm on the input sequence I(t). Note that A must make its decision online, while \({{\textsc {opt}}}(I(t))\) is the optimal value of the offline instance. The quality of an algorithm for the online bin packing problem is typically measured by its asymptotic competitive ratio. An online algorithm A is called an asymptotic\(\alpha \)-competitive algorithm, if there is a function \(f\in o({{\textsc {opt}}})\) such that \(A(I(t))\le \alpha {{\textsc {opt}}}(I(t))+f(I(t))\) for all instances I and all \(t\le |I|\). The infimum \(\alpha \) such that A is an asymptotic \(\alpha \)-competitive algorithm is called the asymptotic competitive ratio of A, denoted by \(r_{\infty }^{{{\mathrm{on}}}}(A)\), i.e., the ratio is defined as \(r_{\infty }^{{{\mathrm{on}}}}(A)=\inf \{\alpha \mid A\) is an asymptotic \(\alpha \)-competitive algorithm\(\}\).
The online algorithm A thus has a double disadvantage: It does not know future items and we compare its quality to the optimal offline algorithm which may produce arbitrary different packings at time t and time \(t+1\). In order to remedy this situation, one may also compare the solution generated by A to a non-repacking optimal offline algorithm. This non-repacking optimal offline algorithm knows the complete instance, but is not allowed to repack. We make use of the stronger notion, where we compare our generated solution against an optimal repacking algorithm. The absolute competitive ratio is defined similar as above, but requires the function f in the above definition to be 0, i.e., \(A(I(t))\le \alpha {{\textsc {opt}}}(I(t))\).
In this work, we present new results in fully dynamic bin packing where we measure the quality of an algorithm against a repacking optimal offline algorithm and achieve an asymptotic competitive ratio of \(1 + \epsilon \). The amount of repacking is bounded by  . While we measure the amount of repacking in terms of the migration factor, we also prove that our algorithm uses at most
. While we measure the amount of repacking in terms of the migration factor, we also prove that our algorithm uses at most  shifting moves. Our algorithm runs in time polynomial in the instance size and in \({1}/{\epsilon }\).
shifting moves. Our algorithm runs in time polynomial in the instance size and in \({1}/{\epsilon }\).
1.1 Previous results on online variants of bin packing
The survey of Christensen et al. [12] contains many results on multidimensional bin packing problems. For the onedimensional case, we give a short overview in the following.
1.1.1 Online bin packing
The classical version of online bin packing problem was introduced by Ullman [43]. In this classical model, items arrive over time and have to be packed at their arrival, while one is not allowed to repack already packed items. Ullman gave the very first online algorithm FirstFit for the problem and proved that its absolute competitive ratio is at most 2. The next algorithm NextFit was given by Johnson [28], who proved that its absolute competitive is also at most 2. The analysis of the FirstFit algorithm was refined by Johnson et al. [29], who proved that its asymptotic competitive ratio is at most \({17}/{10}\). A revised version of FirstFit, called Revised FirstFit was shown to have asymptotic competitive ratio of at most \({5}/{3}\) by Yao [47]. A series of developments of so called harmonic algorithms for this problem was started by Lee and Lee [33] and the best known algorithm of this class which has asymptotic competitive ratio at most 1.58889 was given by Seiden [38]. These bounds were further improved by Heydrich and van Stee to 1.5815 in [21]. Currently, the best algorithm achieves an asymptotic competitive ratio of 1.57829 and is due to Balogh et al. [1]. The lower bound on the absolute approximation ratio of \({3}/{2}\) also holds for the asymptotic competitive ratio as shown by Yao [47]. This lower bound was first improved independently by Brown [9] and Liang [35] to 1.53635 and subsequently to 1.54014 by van Vliet [46] and finally to 1.54037 by Balogh, Békési and Galambos [3].
The question on the absolute approximation ratio was settled by Balogh et al. [2], who showed an algorithm with absolute approximation ratio of \({5}/{3}\) matching a long-known lower bound.
1.1.2 Relaxed online bin packing model
In contrast to the classical online bin packing problem, Gambosi et al. [19] considered the online case where one is allowed to repack items. They called this model the relaxed online bin packing model and proved that the lower bound on the competitive ratio in the classical online bin packing model can be beaten. They presented an algorithm that uses 3 shifting moves and has an asymptotic competitive ratio of at most \({3}/{2}\), and an algorithm that uses at most 7 shifting moves and has an asymptotic competitive ratio of \({4}/{3}\). In another work, Ivković and Lloyd [22] gave an algorithm that uses  amortized shifting moves and achieves an asymptotic competitive ratio of \(1+\epsilon \). In this amortized setting, shifting moves can be saved up for later use and the algorithm may repack the whole instance sometimes. Epstein and Levin [16] used the measure of the migration factor to give an algorithm that has an asymptotic competitive ratio of \(1+\epsilon \) and a migration factor of
amortized shifting moves and achieves an asymptotic competitive ratio of \(1+\epsilon \). In this amortized setting, shifting moves can be saved up for later use and the algorithm may repack the whole instance sometimes. Epstein and Levin [16] used the measure of the migration factor to give an algorithm that has an asymptotic competitive ratio of \(1+\epsilon \) and a migration factor of  . This result was improved by Jansen and Klein [25] who achieved polynomial migration. Their algorithm uses a migration factor of
. This result was improved by Jansen and Klein [25] who achieved polynomial migration. Their algorithm uses a migration factor of  to achieve an asymptotic competitive ratio of \(1+\epsilon \).
to achieve an asymptotic competitive ratio of \(1+\epsilon \).
Concerning lower bounds on the migration factor, Epstein and Levin [16] showed that no optimal solution can be maintained while having a constant migration factor (independent of \({1}/{\epsilon }\)). Furthermore, Balogh et al. [4] proved that a lower bound on the asymptotic competitive ratio of 1.3877 holds, if the amount of repacking is measured by the number of items and one is only allowed to repack a constant number of items.
1.1.3 Dynamic bin packing
An extension to the classical online bin packing model was given by Coffman et al. [13], called the dynamic bin packing model. In addition to the insertion of items, items also depart over time. No repacking is allowed in this model. It is easily seen that no algorithm can achieve a constant asymptotic competitive ratio in this setting. In order to measure the performance of an online algorithm A in this case, one compares the maximum number of bins used byA with the maximum number of bins used by an optimal offline algorithm, i.e., an algorithm A in this dynamic model is called an asymptotic\(\alpha \)-max-competitive algorithm, if there is a function \(f\in o(\text {max-}\textsc {opt})\), where \(\text {max-}\textsc {opt}(I)=\max _{t} {{\textsc {opt}}}(I(t))\) such that \(\max _{t} A(I(t))\le \alpha \cdot \max _{t}{{\textsc {opt}}}(I(t))+f(I)\) for all instances I. The infimum of all such \(\alpha \) is called the asymptotic max-competitive ratio ofA. Coffman et al. modified the FirstFit algorithm and proved that its asymptotic max-competitive ratio is at most 2.897. Furthermore, they showed a lower bound of 2.5 on the asymptotic max-competitive ratio when the performance of the algorithm is compared to a repacking optimal offline algorithm, i.e., \(\max _{t} {{\textsc {opt}}}(I(t))\).
In the case that the performance of the algorithm is compared to an optimal non-repacking offline algorithm, Coffman et al. showed a lower bound of 2.388. This lower bound on the non-repacking optimum was later improved by Chan et al. [10] to 2.428 and even further in a later work by Chan et al. [11] to 2.5.
1.1.4 Fully dynamic bin packing
We consider the dynamic bin packing when repacking of already packed items is allowed. This model was first investigated by Ivković and Lloyd [23] and is called fully dynamic bin packing. In this model, items arrive and depart in an online fashion and limited repacking is allowed. The quality of an algorithm is measured by the asymptotic competitive ratio as defined in the classical online model (no maximum is taken as in the dynamic bin packing model). Ivković and Lloyd developed an algorithm that uses amortized  many shifting moves (see definition above) to achieve an asymptotic competitive ratio of \({5}/{4}\). Based upon our work, Gupta et al. [20] developed an algorithm for fully dynamic bin packing w ith an amortized migration factor of
many shifting moves (see definition above) to achieve an asymptotic competitive ratio of \({5}/{4}\). Based upon our work, Gupta et al. [20] developed an algorithm for fully dynamic bin packing w ith an amortized migration factor of  that achieves an asymptotic competitive ratio of \(1+\epsilon \). Note that their algorithm repacks the complete instance every once in a while and thus only has a bounded amortized migration factor. In contrast, we guarantee a worst-case migration factor and are thus not allowed to repack the complete instance. Furthermore, Gupta et al. [20] and Feldkord et al. [18] studied the case of uniform movement costs (where the repacking of an item incurs a cost of 1 independent of its size). It was shown that an asymptotic competitive ratio of \(\alpha +\epsilon \) can be achieved with worst-case migration of
that achieves an asymptotic competitive ratio of \(1+\epsilon \). Note that their algorithm repacks the complete instance every once in a while and thus only has a bounded amortized migration factor. In contrast, we guarantee a worst-case migration factor and are thus not allowed to repack the complete instance. Furthermore, Gupta et al. [20] and Feldkord et al. [18] studied the case of uniform movement costs (where the repacking of an item incurs a cost of 1 independent of its size). It was shown that an asymptotic competitive ratio of \(\alpha +\epsilon \) can be achieved with worst-case migration of  [18] and that every algorithm achieving asymptotic competitive ratio of \(\alpha -\epsilon \) needs amortized migration depending on the number of items [20].
[18] and that every algorithm achieving asymptotic competitive ratio of \(\alpha -\epsilon \) needs amortized migration depending on the number of items [20].
1.1.5 Related results on the migration factor
Since the introduction of the migration factor, several problems were considered in this model and different robust algorithms for these problems have been developed. Following the terminology of Sanders et al. [37] we sometimes use the term (online) approximation ratio instead of competitive ratio. Hence, we also use the term asymptotic polynomial time approximation scheme (APTAS) and asymptotic fully polynomial time approximation scheme (AFPTAS) in the context of online algorithms. If the migration factor of an algorithm A only depends upon the approximation ratio \(\epsilon \) and not on the size of the instance, we say that Ais a robust algorithm.
In the case of online bin packing, Epstein and Levin [16] developed the first robust APTAS for the problem using a migration factor of  . They also proved that there is no online algorithm for this problem that has a constant migration factor and maintains an optimal solution. The APTAS by Epstein and Levin was later improved by Jansen and Klein [25], who developed a robust AFPTAS for the problem with migration factor
. They also proved that there is no online algorithm for this problem that has a constant migration factor and maintains an optimal solution. The APTAS by Epstein and Levin was later improved by Jansen and Klein [25], who developed a robust AFPTAS for the problem with migration factor  . In their paper, they developed new linear program (LP)/ integer linear program (ILP) techniques, which we also make use of to obtain polynomial migration. It was shown by Epstein and Levin [17] that their APTAS for bin packing can be generalized to packing d-dimensional cubes into unit cubes. Sanders et al. [37] developed a robust polynomial time approximation scheme (PTAS) for the makespan scheduling problem on identical machines where the objective is to minimize the so called makespan i.e. the maximum load over all machines. Their algorithm has a migration factor of
. In their paper, they developed new linear program (LP)/ integer linear program (ILP) techniques, which we also make use of to obtain polynomial migration. It was shown by Epstein and Levin [17] that their APTAS for bin packing can be generalized to packing d-dimensional cubes into unit cubes. Sanders et al. [37] developed a robust polynomial time approximation scheme (PTAS) for the makespan scheduling problem on identical machines where the objective is to minimize the so called makespan i.e. the maximum load over all machines. Their algorithm has a migration factor of  . Skutella and Verschae [39] studied the makespan scheduling problem as well as the problem of maximizing the minimum load over all machines. They considered those problems in the fully dynamic setting, where jobs may also depart and showed that there is no robust (PTAS) for those problems with constant migration. The main reason for the nonexistence is due to very small jobs. By using an amortized migration factor, they developed a (PTAS) for both of the problems with an amortized migration factor of
. Skutella and Verschae [39] studied the makespan scheduling problem as well as the problem of maximizing the minimum load over all machines. They considered those problems in the fully dynamic setting, where jobs may also depart and showed that there is no robust (PTAS) for those problems with constant migration. The main reason for the nonexistence is due to very small jobs. By using an amortized migration factor, they developed a (PTAS) for both of the problems with an amortized migration factor of  . Robust algorithms for the online strip packing problem were studied by Jansen et al. [26]. They developed an algorithm with asymptotic competitive ratio of \(1+\epsilon \) and amortized migration factor of \({{\mathrm{poly}}}(1/\epsilon )\). Furthermore, they show an amortized migration factor is needed to obtain an asymptotic competitive ratio of \(1+\epsilon \).
. Robust algorithms for the online strip packing problem were studied by Jansen et al. [26]. They developed an algorithm with asymptotic competitive ratio of \(1+\epsilon \) and amortized migration factor of \({{\mathrm{poly}}}(1/\epsilon )\). Furthermore, they show an amortized migration factor is needed to obtain an asymptotic competitive ratio of \(1+\epsilon \).
1.2 Our contributions
1.2.1 Main result
In this work, we investigate the fully dynamic bin packing model. We measure the amount of repacking by the migration factor; but our algorithm uses a bounded number of shifting moves as well. Since the work of Ivković and Lloyd from 1998 [23], no progress was made on the fully dynamic bin packing problem concerning the asymptotic competitive ratio of \({5}/{4}\). It was also unclear whether the number of shifting moves (respectively migration factor) must depend on the number of packed items n. In this paper we give positive answers for both of these concerns. We develop an algorithm that provides at each time step t a packing using at most  bins. The algorithm uses a migration factor of
bins. The algorithm uses a migration factor of  by repacking at most
by repacking at most  bins. Hence, the generated solution can be arbitrarily close to the optimum solution, and for every fixed \(\epsilon \) the provided migration factor is constant (it does not depend on the number of packed items). The running time is polynomial in n and \({1}/{\epsilon }\). In case that no deletions are used, the algorithm has a migration factor of
bins. Hence, the generated solution can be arbitrarily close to the optimum solution, and for every fixed \(\epsilon \) the provided migration factor is constant (it does not depend on the number of packed items). The running time is polynomial in n and \({1}/{\epsilon }\). In case that no deletions are used, the algorithm has a migration factor of  , which beats the best known migration factor of
, which beats the best known migration factor of  by Jansen and Klein [25]. Since the number of repacked bins is bounded, so is the number of shifting moves as it requires at most \(O({1}/{\epsilon })\) shifting moves to repack a single bin. Furthermore, we prove that there is no asymptotic approximation scheme for the online bin packing problem with a migration factor of \(o({1}/{\epsilon })\) even in the case that no items depart (and even if
by Jansen and Klein [25]. Since the number of repacked bins is bounded, so is the number of shifting moves as it requires at most \(O({1}/{\epsilon })\) shifting moves to repack a single bin. Furthermore, we prove that there is no asymptotic approximation scheme for the online bin packing problem with a migration factor of \(o({1}/{\epsilon })\) even in the case that no items depart (and even if  ). Our algorithm for the case that no items depart is also significantly easier than the algorithm presented in [25].
). Our algorithm for the case that no items depart is also significantly easier than the algorithm presented in [25].
1.2.2 Outline of the paper
-
In order to obtain a lower bound on the migration factor in Sect. 2, we construct a series of instances that provably need a migration factor of \(\Omega ({1}/{\epsilon })\) in order to have an asymptotic approximation ratio of \(1+\epsilon \).
-
In Sect. 3, we show how to handle large items in a fully dynamic setting. The fully dynamic setting involves more difficulties in the rounding procedure, in contrast to the setting where large items may not depart, treated in [25]. A simple adaption of the dynamic techniques developed in [25] does not work here (see the introduction of Sect. 3). We modify the offline rounding technique by Karmarkar and Karp [32] such that a feasible rounding structure can be maintained when items are inserted or removed. This way, we can make use of the LP-techniques developed in Jansen and Klein [25].
-
In Sect. 4, we explain how to deal with small items in a dynamic setting. In contrast to the setting where departure of items is not allowed, the fully dynamic setting provides major challenges in the treatment of small items. An approach is thus developed where small items of similar size are packed near each other. We describe how this structure can be maintained as new items arrive or depart. Note that the algorithm of Ivković and Lloyd [23] relies on the ability to manipulate up to \(\Omega (n)\) very small items in constant time. See also their updated work for a thorough discussion of this issue [24].
-
In order to unify the different approaches for small and large items, in Sect. 5, we develop an advanced structure for the packing. We give novel techniques and ideas to manage this mixed setting of small and large items. The advanced structure makes use of a potential function, which bounds the number of bins that need to be reserved for incoming items.
2 Lower bound
We start by showing that there is no robust (asymptotic) approximation scheme for bin packing with migration factor of \(o({1}/{\epsilon })\), even if  . This improves the lower bound given by Epstein and Levin [16], which states that no algorithm for bin packing, that maintains an optimal solution can have a constant migration factor. Previously it was not clear whether there exists a robust approximation algorithm for bin packing with sublinear migration factor or even a constant migration factor.
. This improves the lower bound given by Epstein and Levin [16], which states that no algorithm for bin packing, that maintains an optimal solution can have a constant migration factor. Previously it was not clear whether there exists a robust approximation algorithm for bin packing with sublinear migration factor or even a constant migration factor.
Theorem 1
For a fixed migration factor \(\gamma > 0\), there is no robust approximation algorithm for bin packing with asymptotic approximation ratio better than \(1 + (6\lceil \gamma \rceil +5)^{-1}\).
Proof
Let  be an approximation algorithm with migration factor \(\gamma > 0\) and \(c=\lceil \gamma \rceil \). We will now construct an instance such that the asymptotic approximation ratio of
be an approximation algorithm with migration factor \(\gamma > 0\) and \(c=\lceil \gamma \rceil \). We will now construct an instance such that the asymptotic approximation ratio of  with migration factor c is at least \(1+ \frac{1}{6c+5}\). The instance contains only two types of items: An A-item has size \(a=\frac{{3}/{2}}{3c+2}\) and a B-item has size \(b={1}/{2}-{a}/{3}\). For \(M\in {\mathbb {N}}\), let
with migration factor c is at least \(1+ \frac{1}{6c+5}\). The instance contains only two types of items: An A-item has size \(a=\frac{{3}/{2}}{3c+2}\) and a B-item has size \(b={1}/{2}-{a}/{3}\). For \(M\in {\mathbb {N}}\), let
be the instance consisting of 2M insertions of B-items, followed by \(2M(c+1)\) insertions of A-items. Denote by r(t) the approximation ratio of the algorithm  at time \(t\in {\mathbb {N}}\). The approximation ratio of the algorithm is thus \(r=\max _{t}\{r(t)\}\).
at time \(t\in {\mathbb {N}}\). The approximation ratio of the algorithm is thus \(r=\max _{t}\{r(t)\}\).
The insertion of the B-items produces a packing with \(\beta _1\) bins containing a single B-item and \(\beta _2\) bins containing two B-items. These are the only possible packings and hence \(\beta _1+2 \beta _2=2M\). The optimal solution is reached if \(\beta _1=0,\beta _2=M\). We thus have an approximation ratio of
which is strictly monotonically decreasing in \(\beta _2\).
The A-items, which are inserted afterwards, may either be put into bins which only contain A-items or into bins which contain only one B-item. The choice of a, b implies \(2\cdot b+a>1\) which shows that no A-item can be put into a bin containing two B-items. Denote by \(\alpha \) the number of bins containing only A-items. The existing B-items may not be moved as the choice of a, b implies \(b>c\cdot a>\gamma \cdot a\). At most \(\frac{{1}/{2}+{a}/{3}}{a}=c+1\) items of type A may be put into the bins containing only one B-item. Note that this also implies that a bin containing one B-item and \(c+1\) items of type A is filled completely. The optimal packing thus consists of 2M of those bins and the approximation ratio of the solution is given by
There are at most \(\beta _1\cdot (c+1)\) items of type A which can be put into bins containing only one B-item. The remaining \((2M-\beta _1)(c+1)\) items of type A therefore need to be put into bins containing only A-items. We can thus conclude \(\alpha \ge (2M-\beta _1)(c+1) a=(2M-2M+2\beta _2)(c+1)a=2\beta _2(c+1)a\). As noted above, \(\frac{{1}/{2}+{a}/{3}}{a}=c+1\) and thus \((c+1)a={1}/{2}+{a}/{3}\). Hence the approximation ratio is at least
which is strictly monotonically increasing in \(\beta _2\).
As \(r\ge \max \{r_1,r_2\}\), a lower bound on the approximation ratio is thus given if \(r_1=r_2\) by \(\frac{2M-\beta }{M}=\frac{2M+\beta \cdot {2a}/{3}}{2M}\) for a certain \(\beta \). Solving this equation leads to \(\beta =\frac{M}{{a}/{3}+1}\). The lower bound is thus given as
by the choice of a. Note that this lower bound is independent from M. Hence, r is also a lower bound on the asymptotic approximation ratio of any algorithm as the optimal value of the instance grows with M. \(\square \)
We obtain the following corollary:
Corollary 1
There is no robust/dynamic (asymptotic) approximation scheme for bin packing with a migration factor \(\gamma \le {1}/{6}({1}/{\epsilon }-11) = \Theta ({1}/{\epsilon })\).
3 Dynamic rounding
The goal of this section is to give a robust AFPTAS for the case that only large items arrive and depart. In the first subsection, we present a general rounding structure. In the second subsection we give operations on how the rounding can be modified such that the general structure is preserved. We give the final algorithm in Sect. 3.4, which is performed when large items arrive or depart. Finally, the correctness is proved by using the (LP/ILP) techniques developed in [25].
In [25], the last two authors developed a dynamic rounding technique based on an offline rounding technique from Fernandez de la Vega and Lueker [44]. However, a simple adaption of these techniques does not work in the dynamic case where items may also depart. In the case of the offline rounding by Fernandez de la Vega and Lueker, items are sorted and then collected in groups of the same cardinality. When a new item arrives in an online fashion, this structure can be maintained by inserting the new item to its corresponding group. By shifting the largest item of each group to the left, the cardinality of each group (except for the first one) can be maintained. However, shifting items to the right whenever an item departs leads to difficulties in the (LP/ILP) techniques. As the rounding for a group may increase, patterns of the existing (LP/ILP) solution might become infeasible. We overcome these difficulties by developing a new dynamic rounding structure and operations based on the offline rounding technique by Karmarkar and Karp [32]. We believe that the dynamic rounding technique based on Karmarkar and Karp is easier to analyze since the structure can essentially be maintained by shifting items.
Formally, a bin packing instance consists of a set of items\(I=\{i_{1},i_{2},\ldots ,i_{n}\}\) with size function\(s:I\rightarrow [0,1]\cap {\mathbb {Q}}\). A feasible solution is a mapping \(B:I\rightarrow {\mathbb {N}}\) such that \(\sum _{i\in B^{-1}(j)}s(i)\le 1\) for all \(j\in {\mathbb {N}}\). A single set \(B^{-1}(j)\) is called a bin. The goal is to find a solution with a minimal number of bins, i.e. we want to minimize \(|\{j\in {\mathbb {N}}\mid B^{-1}(j)\ne \emptyset \}|\). The smallest value of \(k\in {\mathbb {N}}\) such that a packing with k bins exists is denoted by \({{\textsc {opt}}}(I,s)\) or if the size function is clear by \({{\textsc {opt}}}(I)\). A trivial lower bound is given by the value \({{\textsc {size}}}(I,s)=\sum _{i\in I}s(i)\).
3.1 LP-formulation
Let I be an instance of bin packing with m different item sizes \(s_1, \ldots , s_m\). Suppose that for each item \(i_k \in I\) there is a size \(s_j\) with \(s(i_k) = s_j\). A configuration \(C_i\) is a multiset of sizes \(\{ a(C_i,1):s_1, a(C_i,2):s_2, \ldots a(C_i,m):s_m \}\) with \(\sum _{1\le j\le m} a(C_i,j)s_j \le 1\), where \(a(C_i,j)\) denotes how often size \(s_j\) appears in configuration \(C_i\). We denote by  the set of all configurations. We consider the following LP relaxation of the bin packing problem:
the set of all configurations. We consider the following LP relaxation of the bin packing problem:

Component \(b_j\) states the number of items \(i_k\) in I with \(s(i_k) = s_j\) for \(j = 1, \ldots , m\). This LP-formulation, known as the configuration LP, is first described by Eisemann [15]. Suppose that each size \(s_j\) is larger or equal to \(\epsilon /14\) for some \(\epsilon \in (0,1/2]\). Since the number of different item sizes is m, the number of feasible packings for a bin is bounded by  . Obviously an optimal integral solution of the LP gives a solution to our bin packing problem. We denote by \({{\textsc {opt}}}(I)\) the value of an optimal integral solution. An optimal fractional solution is a lower bound for the optimal value. We denote the optimal fractional solution by \({{\textsc {lin}}}(I)\).
. Obviously an optimal integral solution of the LP gives a solution to our bin packing problem. We denote by \({{\textsc {opt}}}(I)\) the value of an optimal integral solution. An optimal fractional solution is a lower bound for the optimal value. We denote the optimal fractional solution by \({{\textsc {lin}}}(I)\).
3.2 Rounding
To obtain an LP formulation of fixed (independent of |I|) dimension, we use a rounding technique based on the offline AFPTAS by Karmarkar and Karp [32]. In order to use the technique for our dynamic setting, we give a more general rounding. This generalized rounding has a certain structure that is maintained throughout the algorithm and guarantees an approximate solution for the original instance. First, we divide the set of items into small ones and large ones. An item i is called small if \(s(i) <{\epsilon }/{14}\), otherwise it is called large. Instance I is partitioned accordingly into a set of large items \(I_{L}\) and a set of small items \(I_{S}\). We treat small items and large items differently. Small items can be packed using an algorithm presented in Sect. 4.1 while large items will be assigned using an ILP. In this section we discuss how to handle large items.
First, we characterize the set of large items more precisely by their sizes. We say that two large items \(i,i'\) are in the same size category if there is an \(\ell \in {\mathbb {N}}\) such that \(s(i)\in (2^{-(\ell +1)},2^{-\ell }]\) and \(s(i')\in (2^{-(\ell +1)},2^{-\ell }]\). Denote the set of all size categories by W. As every large item has size at least \({\epsilon }/{14}\), the number of size categories is bounded by \(\log ({1}/{\epsilon })+5\). Next, items of the same size category are characterized by their block, which is either  or
or  . The rounding technique of Karmarkar and Karp [32] depends on some parameter k. This parameter is a fixed value in the offline setting, but might increase or decrease in a fully dynamic online setting over time. In order to avoid a large number of repackings when this parameter changes, we will round some of the items for parameter \(k+1\) (the ones in the
. The rounding technique of Karmarkar and Karp [32] depends on some parameter k. This parameter is a fixed value in the offline setting, but might increase or decrease in a fully dynamic online setting over time. In order to avoid a large number of repackings when this parameter changes, we will round some of the items for parameter \(k+1\) (the ones in the  -blocks) and some of them for parameter k (the one in the
-blocks) and some of them for parameter k (the one in the  -blocks). Whenever k increases, we will make sure that the
-blocks). Whenever k increases, we will make sure that the  -blocks are empty and whenever k decreases, the
-blocks are empty and whenever k decreases, the  -blocks will be empty. Finally, we order to items with the same size category decreasingly by their size. We thus assign them a position\(r\in {\mathbb {N}}\) in their corresponding block.
-blocks will be empty. Finally, we order to items with the same size category decreasingly by their size. We thus assign them a position\(r\in {\mathbb {N}}\) in their corresponding block.
Summarizing, we partition the set of large items into a set of groups  . A group \(g \in G\) consists of a triple \((\ell ,X,r)\) with size category \(\ell \in W\), block
. A group \(g \in G\) consists of a triple \((\ell ,X,r)\) with size category \(\ell \in W\), block  and position \(r \in {\mathbb {N}}\). The rounding function is defined as a function \(R: I_L \mapsto G\) that maps each large item \(i\in I_L\) to a group\(g\in G\). By g[R] we denote the set of items being mapped to the group g, i.e., \(g[R]=\left\{ i\in I_L \mid R(i)=g\right\} \).
and position \(r \in {\mathbb {N}}\). The rounding function is defined as a function \(R: I_L \mapsto G\) that maps each large item \(i\in I_L\) to a group\(g\in G\). By g[R] we denote the set of items being mapped to the group g, i.e., \(g[R]=\left\{ i\in I_L \mid R(i)=g\right\} \).
Let \(q(\ell ,X)\) be the maximal \(r\in {\mathbb {N}}\) such that \(|(\ell ,X,r)[R]|> 0\). If \((\ell ,X_1,r_1)\) and \((\ell ,X_2,r_2)\) are two different groups, we say that \((\ell ,X_1,r_1)\) is left of \((\ell ,X_2,r_1)\), if  and
and  or \(X_1=X_2\) and \(r_1<r_2\). We say that \((\ell ,X_1,r_1)\) is right of \((\ell ,X_2,r_2)\), if it is not left of it and if the two groups are not the same.
or \(X_1=X_2\) and \(r_1<r_2\). We say that \((\ell ,X_1,r_1)\) is right of \((\ell ,X_2,r_2)\), if it is not left of it and if the two groups are not the same.
Given an instance (I, s) and a rounding function R, we define the rounded size function \(s^R\) by rounding the size of every large item \(i \in g[R]\) up to the size of the largest item in its group, hence \(s^R(i)=\max \left\{ s(i') \mid R(i')=R(i)\right\} \). We denote by \({{\textsc {opt}}}(I,s^R)\) the value of an optimal solution of the rounded instance \((I,s^R)\).
Depending on a parameter k, we define the following properties for a rounding function R.
- (a)
For each \(i\in (\ell ,X,r)[R]\) we have \(2^{-(\ell +1)}<s(i)\le 2^{-\ell }\).
- (b)
For each \(i\in (\ell ,X,r)[R]\) and each \(i'\in (\ell ,X,r')[R]\) and \(r<r'\), we have \(s(i)\ge s(i')\).
- (c)
For each \(\ell \in W\) and
 we have
we have  and
and  .
. - (d)
For each \(\ell \in W\) and each
 we have
we have  and furthermore
and furthermore  .
.
Property (a) guarantees that the items are categorized correctly according to their sizes. Property (b) guarantees that items of the same size category are sorted by their size and properties (c) and (d) define the number of items in each group (Fig. 1).
Lemma 1
For \(k = \left\lfloor \frac{{{\textsc {size}}}(I_{L},s)\cdot \epsilon }{2(\lfloor \log ({1}/{\epsilon })\rfloor +5)}\right\rfloor \), the number of non-empty groups in G is bounded from above by \(({8}/{\epsilon }+2)(\log ({1}/{\epsilon })+5)\) assuming that \({{\textsc {size}}}(I_L,s) > {8}/{\epsilon }\cdot (\lceil \log ({1}/{\epsilon })\rceil +5)\).
Proof
Using the definition of k and the assumption, we show \(\frac{2{{\textsc {size}}}(I_{L},s)}{k-1}\le {8}/{\epsilon }(\lfloor \log ({1}/{\epsilon })\rfloor +5)\). To simplify the presentation, let \(\Lambda =(\lfloor \log ({1}/{\epsilon })\rfloor +5)\). We have
As \({{\textsc {size}}}(I_L,s)> {8}/{\epsilon }\cdot (\lceil \log ({1}/{\epsilon })\rceil +5)\), we have \({\epsilon }/{2}{{\textsc {size}}}(I_L,s) \ge 4\Lambda \). We can thus bound:
For a size category \(\ell \in W\), let \(I(\ell ,s)=\{i\in I\mid 2^{-(\ell +1)} < s(i)\le 2^{-\ell }\). Note that property (c) and property (d) imply  . Hence property (a) implies that
. Hence property (a) implies that  and therefore
and therefore  . We can now bound the total number of used groups by
. We can now bound the total number of used groups by

The total number of used groups is therefore bounded by  . \(\square \)
. \(\square \)
The following lemma shows that the rounding function does in fact yield a \((1+\epsilon )\)-approximation.
Lemma 2
Given an instance (I, s) with items greater than \(\epsilon /14\) and a rounding function R fulfilling properties (a) to (d), then \({{\textsc {opt}}}(I,s^R) \le (1+\epsilon ) OPT (I,s)\).
Proof
As (I, s) only contains large items, \(I_L=I\). Define for every \(\ell \in W\) the instances  , \(J=\bigcup _{\ell \in W}J_{\ell }\) and
, \(J=\bigcup _{\ell \in W}J_{\ell }\) and  . We will now prove, that the error generated by this rounding is bounded by \(\epsilon \). As each solution to \(J\cup K\) yields a solution to J and a solution to K, we get \({{\textsc {opt}}}(J\cup K,s^R)\le {{\textsc {opt}}}(J,s^{R})+{{\textsc {opt}}}(K,s^{R})\). For
. We will now prove, that the error generated by this rounding is bounded by \(\epsilon \). As each solution to \(J\cup K\) yields a solution to J and a solution to K, we get \({{\textsc {opt}}}(J\cup K,s^R)\le {{\textsc {opt}}}(J,s^{R})+{{\textsc {opt}}}(K,s^{R})\). For  , we have
, we have  because of property (a). We can therefore pack at least \(2^{\ell }\) items from
because of property (a). We can therefore pack at least \(2^{\ell }\) items from  into a single bin. Hence, we get with property (c) that
into a single bin. Hence, we get with property (c) that

We can therefore bound \({{\textsc {opt}}}(K,s^{R})\) as

Using property (b), for each item in \(((\ell ,X,r+1)[R]),s^R)\) we find a unique larger item in \((\ell ,X,r)[R]\). Therefore we have for every item in the rounded instance \((J,s^R)\) an item with larger size in instance (I, s) and hence
The optimal value of the rounded solution can be bounded by
\(\square \)
We therefore have a rounding function, which generates only  different item sizes and the generated error is bounded by \(\epsilon \).
different item sizes and the generated error is bounded by \(\epsilon \).
3.3 Rounding operations
Let us consider the case where large items arrive and depart in an online fashion. Formally this is described by a sequence of pairs \(S=(i_{1},A_{1}),\ldots ,(i_{n},A_{n})\) where \(A_{i}\in \{\textsf {Insert},\textsf {Delete}\}\). Let \(S(t',t)\) be the subsequence starting with \(t'\) and ending in t, i.e. \(S(t',t)=(i_{t'},A_{t'}),\ldots ,(i_{t},A_{t})\). At each time \(t\in \{1,\ldots ,n\}\), we need to pack the item \(i_{t}\) into the corresponding packing of \(i_{1},\ldots ,i_{t-1}\) if \(A_{i}=\textsf {Insert}\) or remove the item \(i_{t}\) from the corresponding packing of \(i_{1},\ldots ,i_{t-1}\) if \(A_{i}=\textsf {Delete}\). We will denote the instance at time t by \(I(t)=\{i_{t'} \mid (i_{t'},\textsf {Insert})\in S(t',t) \wedge (i_{t'},\textsf {Delete})\not \in S(t',t)\}\) and the corresponding packing by \(B_t\). We will also round our items and denote the rounding function at time t by \(R_t\). The large items of I(t) are denoted by \(I_{L}(t)\subseteq I(t)\). At time t, we are allowed to repack several items with a total size of \(\beta \cdot s(i_{t})\) but we intend to keep the migration factor \(\beta \) as small as possible. The term \({{\textsc {repack}}}(t)=\sum _{i, B_{t-1}(i)\ne B_t(i)}s(i)\) denotes the sum of the items which are moved at time t. The migration factor\(\beta \) of an algorithm is then defined as \(\max _t\left\{ {{{\textsc {repack}}}(t)}/{s(i_t)}\right\} \). As the value of \({{\textsc {size}}}\) will also change over the time, we define the value \(\kappa (t)\) as
As shown in Lemma 1, we will make use of the value \(k(t):= \lfloor \kappa (t)\rfloor \).
We present operations that modify the current rounding \(R_t\). Associated with this rounding is the rounded size function \(s^{R_t}\) and the configuration LP \(LP(I(t),s^{R_t})\). A packing \(B_t\) of the instance is described by an ILP solution \(y_t\), based upon a fractional LP solution \(x_t\). We will now modify \(R_t\), \(B_t\), \(y_t\) and \(x_t\) to obtain values \(R_{t+1}\), \(B_{t+1}\), \(y_{t+1}\), and \(x_{t+1}\) for the new instance \(I(t+1)\). At every time t the rounding \(R_t\) maintains properties (a) to (d). Therefore the rounding provides an asymptotic approximation ratio of \(1+\epsilon \) (Lemma 2) while maintaining only  many groups (Lemma 1). We will now show how to adapt this rounding to a dynamic setting, where items arrive or depart online.
many groups (Lemma 1). We will now show how to adapt this rounding to a dynamic setting, where items arrive or depart online.
In the following, fix some rounding \(R=R_t\), some packing \(B=B_t\), a corresponding ILP solution \(y=y_t\), and a corresponding fractional LP solution \(x=x_t\). Our rounding R is manipulated by different operations, called the insert, delete, shiftA and shiftB operation. Some ideas behind the operations are inspired by Epstein and Levin [16]. The insert operation is performed whenever a large item arrives and the delete operation is performed whenever a large item departs. The shiftA/shiftB operations are used to modify the number of groups that are contained in the  and
and  block. As we often need to filter the largest items of a group g belonging to a rounding R, we denote this item by \(\lambda (g,R)\).
block. As we often need to filter the largest items of a group g belonging to a rounding R, we denote this item by \(\lambda (g,R)\).
shift: A shift operation takes two groups \((\ell ,X_1,r_1)\) and \((\ell ,X_2,r_2)\), where \((\ell ,X_1,r_1)\) is left of \((\ell ,X_2,r_2)\), and a rounding function R and produces a new rounding function \(R'\) and packing \(B'\) by shifting the largest item from \((\ell ,X_2,r_2)\) to \((\ell ,X_2,r_2-1)\) and so on until \((\ell ,X_1,r_1)\) is reached (Fig. 2).
If \(X_1=X_2\), we thus construct the new rounding \(R'\) with
- 1.
\((\ell ,X_2,r_2-j-1)[R']=((\ell ,X_2,r_2-j-1)[R]\cup \{\lambda ((\ell ,X_2,r_{2}-j),R))\} \setminus \{\lambda ((\ell ,X_2,r_2-j-1),R)\} \) for \(j=0,\ldots ,r_{2}-r_{1}-2\),
- 2.
\((\ell ,X_2,r_2)[R']=(\ell ,X_2,r_2)[R] \setminus \{\lambda ((\ell ,X_2,r_2),R)\}\), and
- 3.
\((\ell ,X_2,r_1)[R']=(\ell ,X_2,r_1)[R]\cup \{\lambda ((\ell ,X_2,r_{1}+1),R)\}\).
If
 and
and  , we construct the new rounding \(R'\) with
, we construct the new rounding \(R'\) with- 1.
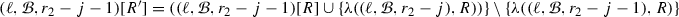 for \(j=0,\ldots ,r_2-1\),
for \(j=0,\ldots ,r_2-1\), - 2.
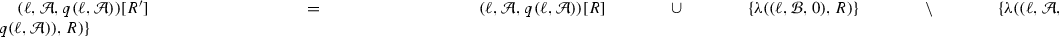 ,
, - 3.
 for
for  , and
, and - 4.
 .
.
For all groups g left of \((\ell ,X_1,r_1)\) or right of \((\ell ,X_2,r_2)\) set \(g[R']=g[R]\). Whenever a shift-operation on \((\ell ,X_{1},r_{1})\) and \((\ell ,X_{2},r_{2})\) is performed, the LP solution x and the corresponding ILP solution y are updated to \(x'\) and \(y'\). Let \(C_i\) be a configuration containing \(\lambda ((\ell ,X_2,r_2),R)\) with \(x_i\ge 1\). Let \(C_j = C_i \setminus s(\lambda ((\ell ,X_2,r_2),R))\) be the configuration without \(\lambda ((\ell ,X_2,r_2),R)\). Set \(x'_j = x_j +1\), \(y'_j = y_j +1\) and \(x'_i = x_i -1\), \(y'_i = y_i -1\). In order to add the new item in \((\ell ,X_1,r_1)\), set \(x_h' = x_h +1\) and \(y'_h = y_h +1\) for the index h with \(C_h = \{1:s(\lambda ((\ell ,X_1,r_1),R)) \}\). The remaining configurations do not change.
- 1.
insert: To insert item \(i_t\), find the corresponding group \((\ell ,X,r)\) with
\(s(i_t)\in (2^{-(\ell +1)},2^{-\ell }]\),
\(\min \left\{ s(i) \mid i\in (\ell ,X,r-1)\right\} > s(i_t)\) and
\(s(\lambda ((\ell ,X,r+1),R))\le s(i_t)\).
We will then insert \(i_t\) into \((\ell ,X,r)\) and get the rounding \(R'\) by shifting the largest element of \((\ell ,X,r)\) to \((\ell ,X,r-1)\) and the largest item of \((\ell ,X,r-1)\) to \((\ell ,X,r-2)\) and so on until
 is reached. Formally, set \(R^*(i_{t})=(\ell ,X,r)\) and \(R^*(i_j)=R(i_j)\) for \(j\ne t\). The rounding function \(R'\) is then obtained by applying the shift operation on \(R^*\) i.e. the new rounding is
is reached. Formally, set \(R^*(i_{t})=(\ell ,X,r)\) and \(R^*(i_j)=R(i_j)\) for \(j\ne t\). The rounding function \(R'\) is then obtained by applying the shift operation on \(R^*\) i.e. the new rounding is  . See Fig. 3 for a sketch.
. See Fig. 3 for a sketch.If
 is too large now, we have to create a new rounding group
is too large now, we have to create a new rounding group  . Additionally, we shift the largest item in
. Additionally, we shift the largest item in  to this new group
to this new group  . The final rounding \(R''\) is then obtained by setting
. The final rounding \(R''\) is then obtained by setting  , i.e. we increment the number of each rounding group by 1. Note that the largest item in
, i.e. we increment the number of each rounding group by 1. Note that the largest item in  is already packed into a bin of its own due to the shift operation. Hence, no change in the packing or the (LP/ILP) solution is needed. The insert operation thus yields a new packing \(B'\) (or \(B''\)) which uses two more bins than the packing B.
is already packed into a bin of its own due to the shift operation. Hence, no change in the packing or the (LP/ILP) solution is needed. The insert operation thus yields a new packing \(B'\) (or \(B''\)) which uses two more bins than the packing B.In order to pack the new item, let i be the index with \(C_i=\{1:s(\lambda ((\ell ,X,r),R'))\}\), as \(i_t\) is rounded to the largest size in \((\ell ,X,r)[R]\) after the shift. Place item \(i_t\) into a new bin by setting \(B'(i_t)=\max _j B(i_j)+1\) and \(x_i' = x_i +1\) and \(y_i'=y_i +1\).
delete: To delete item \(i_t\) from the group \((\ell ,X,r)\) with \(R(i_t)=(\ell ,X,r)\), we remove \(i_t\) from this group and move the largest item from \((\ell ,X,r+1)\) into \((\ell ,X,r)\) and the largest item from \((\ell ,X,r+2)\) into \((\ell ,X,r+1)\) and so on until \((\ell ,B,q(\ell ,B))\). Formally, the rounding \(R'\) is described by the expression \(\textsf {shift} ((\ell ,X,r),(\ell ,B,q(\ell ,B)),R^*)\), where
$$\begin{aligned} g[R^*]= {\left\{ \begin{array}{ll} (\ell ,X,r)[R]\setminus \{i_t\} &{} g=(\ell ,X,r)\\ g[R] &{} \text {else} \end{array}\right. }. \end{aligned}$$As a single shift operation is used, the delete operation yields a new packing \(B'\) which uses one more bin than the packing B. See Fig. 4 for a sketch.
For the LP/ILP solution, let \(C_i\) be a configuration containing \(\lambda ((\ell ,B,q(\ell ,B)),R)\) with \(x_i\ge 1\). Let \(C_j = C_i \setminus s(\lambda ((\ell ,B,q(\ell ,B)),R))\) be the configuration without the item \(\lambda ((\ell ,B,q(\ell ,B)),R)\). Set \(x'_j = x_j +1\), \(y'_j = y_j +1\) and \(x'_i = x_i -1\), \(y'_i = y_i -1\). Set \(B'(i_j) = B(i_j)\) for all \(j \ne t\) in order to remove the item \(i_t\) from the packing.
To control the number of groups in  and
and  we introduce operations shiftA and shiftB that increase or decrease the number of groups in
we introduce operations shiftA and shiftB that increase or decrease the number of groups in  respectively
respectively  . An operation shiftA increases the number of groups in
. An operation shiftA increases the number of groups in  by 1 and decreases the number of groups in
by 1 and decreases the number of groups in  by 1. Operation shiftB is roughly the inverse of shiftA.
by 1. Operation shiftB is roughly the inverse of shiftA.
shiftA: In order to move a group from
 to
to  , we will call \(2^\ell \) times
, we will call \(2^\ell \) times  to receive the rounding \(R^*\). Instead of opening a new bin for each of those \(2^\ell \) items in every shift operation, we rather open one bin containing all items. Since every item in the corresponding size category has size \(\le 2^{-\ell }\), the items fit into a single bin. The group
to receive the rounding \(R^*\). Instead of opening a new bin for each of those \(2^\ell \) items in every shift operation, we rather open one bin containing all items. Since every item in the corresponding size category has size \(\le 2^{-\ell }\), the items fit into a single bin. The group  has now the same size as the groups in
has now the same size as the groups in  . We transfer
. We transfer  to block
to block  . Hence, we define the final rounding \(R'\) as
. Hence, we define the final rounding \(R'\) as  for
for  and
and  as well as
as well as  for
for  . The resulting packing \(B'\) hence uses one more bin than the packing B. See Fig. 5 for a sketch.
. The resulting packing \(B'\) hence uses one more bin than the packing B. See Fig. 5 for a sketch.shiftB: In order to move a group from
 to
to  , we will call \(2^\ell \) times
, we will call \(2^\ell \) times  to receive the rounding \(R^*\). As before in shiftA, we open a single bin containing all of the \(2^\ell \) items. The group
to receive the rounding \(R^*\). As before in shiftA, we open a single bin containing all of the \(2^\ell \) items. The group  has now the same size as the groups in
has now the same size as the groups in 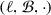 . We transfer
. We transfer  to block
to block  . Similar to shiftA we define the final rounding \(R'\) as
. Similar to shiftA we define the final rounding \(R'\) as  for
for  and
and  as well as
as well as  . The resulting packing \(B'\) hence uses one more bin than the packing B.
. The resulting packing \(B'\) hence uses one more bin than the packing B.
Lemma 3
Let R be a rounding function fulfilling properties (a) to (d). Applying one of the operations insert, delete, shiftA or shiftB on R results in a rounding function \(R'\) fulfilling properties (a) to (d).
Proof
Property (a) is always fulfilled as no item is moved between different size categories and the insert operation inserts an item into its appropriate size category.
As the order of items never changes and the insert operation inserts an item into the appropriate place, property (b) also holds.
For properties (c) and (d), we first note that the operation \(\textsf {shift}(g,g',R)\) increases the number of items in g by 1 and decreases the number of items in \(g'\) by 1. The insert operation consists of adding a new item to a group g followed by a  operation. Hence the number of items in every group except for
operation. Hence the number of items in every group except for  (which is increased by 1) remains the same. The delete operation consists of removing an item from a group g followed by a
(which is increased by 1) remains the same. The delete operation consists of removing an item from a group g followed by a  operation. Therefore, the number of items in all groups except for
operation. Therefore, the number of items in all groups except for  (which is decreased by 1) remains the same. As the number of items in
(which is decreased by 1) remains the same. As the number of items in  and
and  are treated separately and may be smaller than \(2^{\ell }\cdot k\) respectively \(2^{\ell }\cdot (k-1)\), properties (c) and (d) are always fulfilled for the insert and the delete operation. Concerning the shiftA operation, we increase the number of items in a group
are treated separately and may be smaller than \(2^{\ell }\cdot k\) respectively \(2^{\ell }\cdot (k-1)\), properties (c) and (d) are always fulfilled for the insert and the delete operation. Concerning the shiftA operation, we increase the number of items in a group  by \(2^\ell \). Therefore, it now contains \(2^{\ell }(k-1)+2^\ell = 2^{\ell }\cdot k\) items, which equals the number of items in groups of block
by \(2^\ell \). Therefore, it now contains \(2^{\ell }(k-1)+2^\ell = 2^{\ell }\cdot k\) items, which equals the number of items in groups of block  . As this group is now moved to block
. As this group is now moved to block  , the properties (c) and (d) are fulfilled. Symmetrically the shiftB operation decreases the number of items in a group \((\ell ,A,q(\ell ,A))\) by \(2^{\ell }\). Therefore the number of items in the group is now \(2^{\ell }\cdot k - 2^\ell =2^{\ell }\cdot (k-1)\), which equals the number of items in the groups of block B. As this group is now moved to block
, the properties (c) and (d) are fulfilled. Symmetrically the shiftB operation decreases the number of items in a group \((\ell ,A,q(\ell ,A))\) by \(2^{\ell }\). Therefore the number of items in the group is now \(2^{\ell }\cdot k - 2^\ell =2^{\ell }\cdot (k-1)\), which equals the number of items in the groups of block B. As this group is now moved to block  , the properties (c) and (d) are fulfilled. \(\square \)
, the properties (c) and (d) are fulfilled. \(\square \)
According to Lemma 1 the rounded instance \((I,s^R)\) has  different item sizes (given a suitable k). Using the LP formulation of Eisemann [15] from Sect. 3.1, the resulting LP called \(LP(I,s^R)\) has
different item sizes (given a suitable k). Using the LP formulation of Eisemann [15] from Sect. 3.1, the resulting LP called \(LP(I,s^R)\) has  constraints. We say a packing Bcorresponds to a rounding R and an integral solution y of the ILP if all items in \((I,s^R)\) are packed by B according to y.
constraints. We say a packing Bcorresponds to a rounding R and an integral solution y of the ILP if all items in \((I,s^R)\) are packed by B according to y.
Lemma 4
Applying any of the operations insert, delete, shiftA or shiftB on a rounding function R and ILP solution y with corresponding packing B defines a new rounding function \(R'\) and a new feasible integral solution \(y'\) of \(LP(I,s^{R'})\).
Proof
We have to analyze how the LP for instance \((I,s^{R'})\) changes in comparison to the LP for instance \((I,s^R)\).
shiftOperation A single \(\textsf {shift}(g_1,g_2,R)\) operation moves one item from each group g between \(g_1\) and \(g_2\) into g and one item out of g. As no item is moved out of \(g_1\) and no item is moved into \(g_2\), the number of items in \(g_1\) is increased by 1 and the number of items in \(g_2\) is decreased by 1. The right hand side of the \(LP(I,s^R)\) is defined by the cardinalities |g[R]| of the rounding groups g in R. As only the cardinalities of \(g_1\) and \(g_2\) change by \(\pm 1\) the right hand side changes accordingly to \(\pm 1\) in the corresponding components of y. The moved item from \(g_2\) is removed from the configuration and a new configuration containing the new item of \(g_1\) is added. The LP and ILP solutions x and y are being modified such that \(\lambda (g_2,R)\) is removed from its configuration and a new configuration is added such that the enhanced right hand side of \(g_1\) is covered. Since the largest item \(\lambda (g,R)\) of every group g between \(g_1\) and \(g_2\) is shifted to its left group, the size \(s^{R'}(i)\) of item \(i\in g[R]\) is defined by \(s^{R'}(i)=s(\iota (g,R))\), where \(\iota (g,R)\) is the second largest item of g[R]. Therefore each item in \((I,s^{R'})\) is rounded to a smaller or equal value as \(s(\iota (g,R))\le s(\lambda (g,R))\). All configurations of \((I,s^R)\) can thus be transformed into feasible configurations of \((I,s^{R'})\).
insertOperation The insert operation consists of inserting the new item into its corresponding group g followed by a shift operation. Inserting the new item into g increases the right hand side of the LP by 1. To cover the increased right hand side, we add a new configuration \(\{1:s^{R'}(i)\}\) containing only the new item. In order to reflect the change in the LP solution, the new item is added into an additional bin. The remaining changes are due to the shift operation already treated above.
deleteOperation The delete operation consists of removing an item i from its corresponding group g followed by a shift operation. Removing the new item from g decreases the right hand side of the LP by 1. The current LP and ILP solutions x and y do not need to be changed to cover the new right hand side. The remaining changes are due to the shift operation already treated above.
shiftA/shiftBOperation As the shiftA and shiftB operations consist only of repeated use of the shift operation, the correspondence between the packing and the (LP/ILP) solution follows simply by induction. \(\square \)
3.4 Algorithm for dynamic bin packing
We will use the operations from the previous section to obtain a dynamic algorithm for bin packing with respect to large items. The operations insert and delete are designed to process the input depending of whether an item is to be inserted or removed. Keep in mind that the parameter \(k(t) = \lfloor \kappa (t)\rfloor = \left\lfloor \frac{{{\textsc {size}}}(I_{L}(t))\cdot \epsilon }{2(\lfloor \log ({1}/{\epsilon })\rfloor +5)} \right\rfloor \) changes over time as \({{\textsc {size}}}(I_{L}(t))\) may increase or decrease. In order to fulfill the properties (c) and (d), we need to adapt the number of items per group whenever k(t) changes. The shiftA and shiftB operations are thus designed to manage the dynamic number of items in the groups as k(t) changes. Note that a group in the  -block with parameter k(t) has by definition the same number of items as a group in the
-block with parameter k(t) has by definition the same number of items as a group in the  -block with parameter \(k(t)-1\) assuming they are in the same size category. If k(t) increases, the former
-block with parameter \(k(t)-1\) assuming they are in the same size category. If k(t) increases, the former  -block is treated as the new
-block is treated as the new  -block in order to fulfill the properties (c) and (d) while a new empty
-block in order to fulfill the properties (c) and (d) while a new empty  -block is introduced. To be able to rename the blocks, the
-block is introduced. To be able to rename the blocks, the  -block needs to be empty. Accordingly the
-block needs to be empty. Accordingly the  -block needs to be empty if k(t) decreases in order to treat the old
-block needs to be empty if k(t) decreases in order to treat the old  -block as new
-block as new  -block. Hence we need to make sure that there are no groups in the
-block. Hence we need to make sure that there are no groups in the  -block if k(t) increases and vice versa, that there are no groups in the
-block if k(t) increases and vice versa, that there are no groups in the  -block if k(t) decreases.
-block if k(t) decreases.
3.5 Two auxiliary algorithms
We will make use of two very useful algorithms throughout this work. The algorithm improve was developed in [25] to improve the objective value of an LP with integral solution y and corresponding fractional solution x. For a vector \(z \in {\mathbb {R}}^n\) let V(z) be the set of all integral vectors \(v = (v_1, \ldots v_n)^T\) such that \(0 \le v_i \le z_i\).
Let x be an approximate solution of the LP \(\min \left\{ \left\| x\right\| _1 \mid Ax \ge b, x \ge 0 \right\} \), call it \((*)\), with m inequalities (excluding the non-negativity constraints) and let \(\left\| x\right\| _1 \le (1+ \delta ) {{\textsc {lin}}}\) and \(\left\| x\right\| _1 \ge 2 \alpha (1/ \delta +1)\), where \({{\textsc {lin}}}\) denotes the fractional optimum of the LP, \(\alpha \in {\mathbb {N}}\) is part of the input of the algorithm (see Jansen and Klein [25]), and \(0< \delta < 1\) is some precision. Let y be an approximate integral solution of the LP with \(\left\| y\right\| _1 \le {{\textsc {lin}}}+2C\) for some value \(C \ge \delta {{\textsc {lin}}}\) and with \(\left\| y\right\| _1 \ge (m+2)(1/\delta +2)\). Suppose that both x and y have only \(\le C\) non-zero components. For every component i we suppose that \(y_i \ge x_i\). Furthermore we are given indices \(a_1, \ldots ,a_K\), such that the non-zero components \(y_{a_j}\) are sorted in non-decreasing order, i.e., \(y_{a_1} \le \cdots \le y_{a_K}\).
Algorithm 1
(improve)
- 1.
Set \(x^{var} := 2 \frac{ \alpha (1 / \delta +1)}{\left\| x\right\| }x\), \(x^{fix} := x - x^{var}\) and \(b^{var} = b - A(x^{fix})\)
- 2.
Compute an approximate solution \(\hat{x}\) of the LP \(\min \left\{ \left\| x\right\| _1 \mid Ax \ge b^{var}, x\ge 0 \right\} \) with approximation ratio \((1+ \delta /2)\)
- 3.
If \(\left\| x^{fix} + {\hat{x}}\right\| _1 \ge \left\| x\right\| _1\) then set \(x' = x\), \({\hat{y}} = y\) and goto step 9
- 4.
Choose the largest \(\ell \) such that the sum of the smallest components \(y_1, \ldots , y_{\ell }\) is bounded by \(\sum _{1\le i \le \ell } y_{a_i} \le (m+2)(1/ \delta +2)\)
- 5.
For all i set \({\bar{x}}^{fix}_{i} = {\left\{ \begin{array}{ll} 0 &{} \text {if }\quad i= a_j, j \le \ell \\ x^{fix}_i &{} \text {else} \end{array}\right. }\) and \({\bar{y}}_i = {\left\{ \begin{array}{ll} 0 &{} \text {if }\quad i= a_j, j \le \ell \\ y_i &{} \text {else} \end{array}\right. }\)
- 6.
Set \({\bar{x}} = {\hat{x}} + x_{\ell }\) where \(x_{\ell }\) is a vector consisting of the components \(x_{a_1}, \ldots ,x_{a_{\ell }}\). Reduce the number of non-zero components to at most \(m+1\) by solving a linear equation system
- 7.
Set \(x' = {\bar{x}}^{fix} + {\bar{x}}\)
- 8.
For all non-zero components i set \({\hat{y}}_i = \max \{\lceil x'_i \rceil , {\bar{y}}_i \}\)
- 9.
If possible choose \(d \in V({\hat{y}}-x')\) such that \(\left\| d\right\| _1 = \alpha (1/ \delta +1)\) otherwise choose \(d \in V({\hat{y}}-x')\) such that \(\left\| d\right\| _1 < \alpha (1/ \delta +1)\) is maximal
- 10.
Return \(y' = {\hat{y}} -d\)
In the following, we prove that the algorithm improve applied to the bin packing ILP actually generates a new improved packing \(B'\) from the packing B with corresponding LP and ILP solutions \(x'\) and \(y'\). We therefore use Theorem 2 and Corollary 2 that were proven in [25].
Theorem 2
(Theorem 8 in [25]) Let x be a solution of the LP \((*)\) with \(\left\| x\right\| _1 \le (1+\delta ) {{\textsc {lin}}}\) and furthermore \(\left\| x\right\| _1 \ge 2 \alpha (1/ \delta +1)\). Let y be an integral solution of the LP with \(\left\| y\right\| _1 \le {{\textsc {lin}}}+2C\) for some value \(C \ge \delta {{\textsc {lin}}}\) and with \(\left\| y\right\| _1 \ge (m+2)(1/\delta +2)\). Solutions x and y have the same number of non-zero components and for each component we have \(x_i \le y_i\). The algorithm \(\textsc {improve}(x,y,\alpha )\) then returns a fractional solution \(x'\) with \(\left\| x'\right\| _1 \le (1+ \delta ){{\textsc {lin}}}-\alpha \) and an integral solution \(y'\) where one of the two properties hold: \(\left\| y'\right\| _1 = \left\| y\right\| _1 - \alpha \) or \(\left\| y'\right\| _1 = \left\| x'\right\| _1 + C\). Both \(x'\) and \(y'\) have at most C non-zero components and the distance between \(y'\) and y is bounded by  .
.
Corollary 2
(Corollary 9 in [25]) Let \(\left\| x\right\| _1 = (1+ \delta '){{\textsc {lin}}}\) for some \(\delta ' \ge \delta \) and \(\left\| x\right\| _1 \ge 2 \alpha (1/ \delta +1)\) and let \(\left\| y\right\| _1 \le {{\textsc {lin}}}+ 2C\) for some \(C \ge \delta '{{\textsc {lin}}}\) and \(\left\| y\right\| _1 \ge (m+2)(1/\delta +2)\). Solutions x and y have the same number of non-zero components and for each component we have \(x_i \le y_i\). Then algorithm \(\textsc {improve}(x,y,\alpha )\) returns a fractional solution \(x'\) with \(\left\| x'\right\| _1 \le \left\| x\right\| _1 - \alpha = (1+ \delta '){{\textsc {lin}}}- \alpha \) and integral solution \(y'\) where one of the two properties hold: \(\left\| y'\right\| _1 = \left\| y\right\| _1 - \alpha \) or \(\left\| y'\right\| _1 = \left\| x\right\| _1 - \alpha + C\). Both, \(x'\) and \(y'\) have at most C non-zero components and the distance between \(y'\) and y is bounded by  .
.
In the following, let \(\Delta = \epsilon + \delta + \epsilon \delta \) and \(C = \Delta {{\textsc {opt}}}(I,s) + m\).
Theorem 3
Given a rounding function R and the LP defined for \((I,s^{R})\), let x be a fractional solution of the LP with \(\left\| x\right\| _1 \le (1+ \Delta ) {{\textsc {opt}}}(I,s)\), \(\left\| x\right\| _1 \ge 2\alpha (1/\delta +1)\) and \(\left\| x\right\| _1 = (1+\delta '){{\textsc {lin}}}(I,s^{R})\) for some \(\delta '>0\). Let y be an integral solution of the LP with \(\left\| y\right\| _1 \ge (m+2)(1/\delta +2)\) and corresponding packing B such that \(\max _i B (i) = \left\| y\right\| _1 \le (1+ 2\Delta ) {{\textsc {opt}}}(I,s)+m\). Suppose x and y have the same number \(\le C\) of non-zero components and for all components i we have \(y_i \ge x_i\). Then algorithm \(\textsc {improve}(x,y,\alpha )\) returns a new fractional solution \(x'\) with \(\left\| x'\right\| _1 \le (1+ \Delta ) {{\textsc {opt}}}(I,s) - \alpha \) and also a new integral solution \(y'\) with corresponding packing \(B'\) such that
Further, both solutions \(x'\) and \(y'\) have the same number \(\le C\) of non-zero components and for each component we have \(x'_i \le y'_i\). The number of changed bins from the packing B to the packing \(B'\) is bounded by  .
.
Proof
To use Theorem 2 and Corollary 2 we have to prove that certain conditions follow from the prequisites of Theorem 3. We have \(\max _i B (i) = \left\| y\right\| _1 \le (1+ 2\Delta ) {{\textsc {opt}}}(I,s)+m\) by condition. Since \( {{\textsc {opt}}}(I,s) \le {{\textsc {opt}}}(I,s^{R})\) we obtain for the integral solution y that \(\left\| y\right\| _1 \le 2\Delta {{\textsc {opt}}}(I,s)+m + {{\textsc {opt}}}(I,s^{R}) \le 2 \Delta {{\textsc {opt}}}(I,s)+ m + {{\textsc {lin}}}(I,s^{R}) +m\). Hence by definition of C we get \(\left\| y\right\| _1 \le {{\textsc {lin}}}(I,s^{R}) + 2C\). This is one requirement to use Theorem 2 or Corollary 2. We distinguish the cases where \(\delta ' \le \delta \) and \(\delta ' > \delta \) and look at them separately.
Case 1\(\delta ' \le \delta \). For the parameter C we give a lower bound by the inequality \(C > \Delta {{\textsc {opt}}}(I,s) = (\delta + \epsilon + \delta \epsilon ){{\textsc {opt}}}(I,s)\). Lemma 2 shows that \({{\textsc {opt}}}(I,s^R) \le (1+\epsilon ){{\textsc {opt}}}(I,s)\) and therefore yields
and hence \(C > \delta {{\textsc {lin}}}(I,s^R)\). We can therefore use Theorem 2.
Algorithm improve returns by Theorem 2 an \(x'\) with \(\left\| x'\right\| _1 \le (1+\delta ){{\textsc {lin}}}(I,s^{R})-\alpha \le (1+\delta ){{\textsc {opt}}}(I,s^{R})-\alpha \) and an integral solution \(y'\) with \(\left\| y'\right\| _1 \le \left\| x'\right\| _1 + C\) or \(\left\| y'\right\| _1 \le \left\| y\right\| _1 - \alpha \). Using that \({{\textsc {opt}}}(I,s^R) \le (1+\epsilon ){{\textsc {opt}}}(I,s)\) we can conclude \(\left\| x'\right\| _1 \le (1+ \delta )(1+ \epsilon ){{\textsc {opt}}}(I,s) - \alpha = (1+\Delta ){{\textsc {opt}}}(I,s) - \alpha \). In the case where \(\left\| y'\right\| _1 \le \left\| x'\right\| _1 + C\) we can bound the number of bins of the new packing \(B'\) by \(\max _i B' (i) = \left\| y'\right\| _1 \le \left\| x'\right\| _1 + C \le (1 + 2 \Delta ) {{\textsc {opt}}}(I,s)+ m - \alpha \). In the case that \(\left\| y'\right\| _1 \le \left\| y\right\| _1 - \alpha \) we obtain \(\max _i B' (i) = \left\| y'\right\| _1 \le \left\| y\right\| _1 - \alpha \le (1+ 2\Delta ) {{\textsc {opt}}}(I,s) +m- \alpha \). Furthermore we know by Theorem 2 that \(x'\) and \(y'\) have at most C non-zero components.
Case 2\(\delta ' > \delta \). First we prove that C is bounded from below. Since \(\left\| x\right\| _1 = (1+\delta ') {{\textsc {lin}}}(I,s^R) \le (1+ \Delta ) {{\textsc {opt}}}(I,s) = {{\textsc {opt}}}(I,s) + \Delta {{\textsc {opt}}}(I,s) \le {{\textsc {opt}}}(I,s^R) + \Delta {{\textsc {opt}}}(I,s) \le {{\textsc {lin}}}(I,s^R) + m + \Delta {{\textsc {opt}}}(I,s) = {{\textsc {lin}}}(I,s^R) +C\) we obtain that \(C\ge \delta ' {{\textsc {lin}}}(I,s^R)\), which is a requirement to use Corollary 2. By using Algorithm improve on solutions x with \(\left\| x\right\| _1 = (1+\delta '){{\textsc {lin}}}(I,s^{R})\) and y with \(\left\| y\right\| _1 \le {{\textsc {lin}}}(I,s^{R}) + 2C\) we obtain by Corollary 2 a fractional solution \(x'\) with \(\left\| x'\right\| _1 \le \left\| x\right\| _1 - \alpha \le (1+\Delta ){{\textsc {opt}}}(I,s) - \alpha \) and an integral solution \(y'\) with either \(\left\| y'\right\| _1 \le \left\| y\right\| _1 - \alpha \) or \(\left\| y'\right\| _1 \le \left\| x\right\| _1 + C - \alpha \). So for the new packing \(B'\) we can guarantee that \(\max _i B' (i) = \left\| y'\right\| _1 \le \left\| y\right\| _1 - \alpha = \max _i B (i) - \alpha \le (1+ 2\Delta ) {{\textsc {opt}}}(I,s) +m - \alpha \) if \(\left\| y'\right\| _1 \le \left\| y\right\| _1 - \alpha \). In the case that \(\left\| y'\right\| _1 \le \left\| x\right\| _1 + C - \alpha \), we can guarantee that \(\max _i B' (i) = \left\| y'\right\| _1 \le \left\| x\right\| _1 + C - \alpha \le (1+ \Delta ) {{\textsc {opt}}}(I,s)+ C - \alpha \le (1+ 2\Delta ) {{\textsc {opt}}}(I,s) +m - \alpha \). Furthermore we know by Corollary 2 that \(x'\) and \(y'\) have at most C non-zero components.
Theorem 2 as well as Corollary 2 state that the distance \(\left\| y'-y\right\| _1\) is bounded by  . Since y corresponds directly to the packing B and the new integral solution \(y'\) corresponds to the new packing \(B'\), we know that only
. Since y corresponds directly to the packing B and the new integral solution \(y'\) corresponds to the new packing \(B'\), we know that only  bins of B need to be changed to obtain packing \(B'\). \(\square \)
bins of B need to be changed to obtain packing \(B'\). \(\square \)
We will also make use of the auxiliary Algorithm 2 (ReduceComponents). Due to a delete-operation, the value of the optimal solution \({{\textsc {opt}}}(I,s)\) might decrease. Since the number of non-zero components has to be bounded by \(C = \Delta {{\textsc {opt}}}(I,s) + m\), the number of non-zero components might have to be adjusted down. The following algorithm describes how a fractional solution \(x'\) and an integral solution \(y'\) with reduced number of non-zero components can be computed such that \(\left\| y-y'\right\| _1\) is bounded. The idea behind the algorithm is also used in the Improve algorithm. The smallest \(m+2\) components are reduced to \(m+1\) components using a standard technique presented for example in [5]. Arbitrary many components of \(x'\) can thus be reduced to \(m+1\) components without making the approximation guarantee worse.
Algorithm 2
(ReduceComponents)
- 1.
Choose the smallest non-zero components \(y_{a_1}, \ldots , y_{a_{m+2}}\)
- 2.
If \(\sum _{1\le i \le m+2} y_{a_i} \ge (1/ \Delta +2)(m+2)\) then return \(x=x'\) and \(y=y'\)
- 3.
Reduce the components \(x_{a_1}, \ldots , x_{a_{m+2}}\) to \(m+1\) components \({\hat{x}}_{b_1}, \ldots , {\hat{x}}_{b_{m+1}}\) with \(\sum _{j=1}^{m+2}x_{a_{j}}=\sum _{j=1}^{m+1}{\hat{x}}_{b_{j}}\)
- 4.
For all i set \(x'_i = {\left\{ \begin{array}{ll} {\hat{x}}_i +x_i &{} \text {if } \quad i= b_j \text { for some } j \le m \\ 0 &{} \text {if } \quad i= a_j \text { for some } j \le m+1 \\ x_i &{} \text {else} \end{array}\right. }\)
and \({\hat{y}}_i = {\left\{ \begin{array}{ll} \lceil {\hat{x}}_i + x'_i \rceil &{} \text {if }\quad i= b_j\text { for some } j \le m \\ 0 &{} \text {if }\quad i= a_j\text { for some } j \le m+1 \\ y_i &{} \text {else} \end{array}\right. }\)
- 5.
If possible choose \(d \in V({\hat{y}}-x')\) such that \(\left\| d\right\| _1 = m+1\) otherwise choose \(d \in V({\hat{y}}-x')\) such that \(\left\| d\right\| _1 < m+1\) is maximal
- 6.
Return \(y' = {\hat{y}} -d\)
The following theorem shows that the algorithm above yields a new fractional solution \(x'\) and a new integral solution \(y'\) with a reduced number of non-zero components.
Theorem 4
Let x be a fractional solution of the LP with \(\left\| x\right\| _1 \le (1+ \Delta ) {{\textsc {opt}}}(I,s)\). Let y be an integral solution of the LP with \(\left\| y\right\| _1 \le (1+ 2\Delta ) {{\textsc {opt}}}(I,s)+m\). Suppose x and y have the same number \(\le C+1\) of non-zero components and for all components i we have \(y_i \ge x_i\). Using the Algorithm \(\textsc {ReduceComponents}\) on x and y returns a new fractional solution \(x'\) with \(\left\| x'\right\| _1 \le (1+ \Delta ) {{\textsc {opt}}}(I,s)\) and a new integral solution \(y'\) with \(\left\| y'\right\| _1 \le (1+ 2 \Delta ) {{\textsc {opt}}}(I,s) +m\). Further, both solutions \(x'\) and \(y'\) have the same number of non-zero components and for each component we have \(x'_i \le y'_i\). The number of non-zero components is now at most C. Furthermore, we have that \(\left\| y-y'\right\| _1 \le 2\cdot (1/\Delta +3) (m+2)\).
Proof
Case 1\(\sum _{1\le i \le m+2} y_{a_i} \ge (1/ \Delta +2)(m+2)\). We will show that in this case, x and y already have \(\le C\) non-zero components and returns \(x' = x\) and \(y' =y\). Since \(\sum _{1\le i \le m+2} y_{a_i} \ge (1/ \Delta +2)(m+2)\) the components \(y_{a_1}, \ldots , y_{a_{m+2}}\) have an average size of at least \((1/ \Delta +2)\) and since \(y_{a_1}, \ldots , y_{a_{m+2}}\) are the smallest components, all components of y have average size at least \((1/ \Delta +2)\). The size \(\left\| y\right\| _1\) is bounded by \((1+ 2\Delta ) {{\textsc {opt}}}(I,s)+m\). Hence the number of non-zero components can be bounded by \(\frac{(1+ 2\Delta ) {{\textsc {opt}}}(I,s)+m}{{1}/{\Delta }+2} \le \Delta {{\textsc {opt}}}(I,s)+ \Delta m \le C\).
Case 2\(\sum _{1\le i \le m+1} y_{a_i} < (1/ \Delta +2)(m+2)\). We have to prove different properties for the new fractional solution \(x'\) and the new integral solution \(y'\).
Number of non-zero components: The only change in the number of non-zero components is in step 3 of the algorithm, where the number of non-zero components is reduced by 1. As x, y have at most \(C+1\) non-zero components, \(x',y'\) have at most C non-zero components. In step 4 of the algorithm, \({\hat{y}}\) is defined such that \({\hat{y}}_i \ge x'_i\). In step 5 of the algorithm d is chosen such that \({\hat{y}}_i -d \ge x'_i\). Hence we obtain that \(y'_i = {\hat{y}}_i -d \ge x'_i\).
Distance betweenyand\(y'\): The only steps where components of y changes are in step 4 and 5. The distance between y and \({\hat{y}}\) is bounded by the sum of the components that are set to 0, i.e., \(\sum _{j=1}^{m+2}y_{a_{j}}\) and the sum of the increase of the increased components \(\sum _{j=1}^{m+1}\lceil {\hat{x}}_{b_{j}}\rceil \le \sum _{j=1}^{m+1}{\hat{x}}_{b_{j}} +m+1 = \sum _{j=1}^{m+2}x_{a_{j}} +m+1\). As \(\sum _{j=1}^{m+2}x_{a_{j}}\le \sum _{j=1}^{m+2}y_{a_{j}} < (1/ \Delta +2)(m+2)\), we obtain that the distance between y and \({\hat{y}}\) is bounded by \(2\cdot (1/\Delta +2)(m+2)+m+1\). Using that \(\left\| d\right\| _1 \le m+1\), the distance between y and \(y'\) is bounded by \(\left\| y'-y\right\| _1 < 2\cdot (1/\Delta +3) (m+2)\).
Approximation guarantee: The fractional solution x is modified by condition of step 3 such that the sum of the components does not change. Hence \(\left\| x'\right\| _1=\left\| x\right\| _1\le (1+\Delta ){{\textsc {opt}}}(I,s)\).
Case 2a\(\left\| d\right\| _1 < m+1\). Since d is chosen maximally we have for every non-zero component that \(y'_i-x'_i <1\). Since there are at most \(C=\Delta {{\textsc {opt}}}(I,s)+m\) non-zero components we obtain that \(\left\| y'\right\| _1 \le \left\| x'\right\| _1 + C \le (1+ 2\Delta ){{\textsc {opt}}}(I,s)+m\). Case 2b\(\left\| d\right\| _1 = m+1\). By definition of \({\hat{y}}\) we have \(\left\| {\hat{y}}\right\| _1 \le \left\| y\right\| _1 + \sum _{j=1}^{m+1} \lceil \hat{x_{b_j}}+x_{b_j}\rceil - \sum _{j=1}^{m+2}x_{a_j} \le \left\| y\right\| _1 + m+1\). We obtain for \(y'\) that \(\left\| y'\right\| _1 = \left\| {\hat{y}}\right\| _1 - \left\| d\right\| _1 \le \left\| y\right\| _1 + m+1 - (m+1) =\left\| y\right\| _1 \le (1+ 2\Delta ) {{\textsc {opt}}}(I,s)+m\). \(\square \)
3.6 Large items
In the following, we describe the algorithm to handle the large items. The treatment of small items is described in Sect. 4 and the general case is described in Sect. 5. We denote the number of all groups in all  -blocks at time t by
-blocks at time t by  and the number of groups in all
and the number of groups in all  -blocks at time t by
-blocks at time t by  . To make sure that the
. To make sure that the  -block (respectively the
-block (respectively the  -block) is empty when k(t) increases (decreases) the ratio
-block) is empty when k(t) increases (decreases) the ratio  needs to correlate to the fractional digits of \(\kappa (t)\) at time t denoted by \(\Delta (t)\). Hence we partition the interval [0, 1) into exactly
needs to correlate to the fractional digits of \(\kappa (t)\) at time t denoted by \(\Delta (t)\). Hence we partition the interval [0, 1) into exactly  smaller intervals
smaller intervals  . We will make sure that \(\Delta (t)\in J_i\) iff
. We will make sure that \(\Delta (t)\in J_i\) iff  . Note that the term
. Note that the term  is 0 if the
is 0 if the  -blocks are empty and the term is 1 if the
-blocks are empty and the term is 1 if the  -blocks are empty. This way, we can make sure that as soon as k(t) increases, the number of
-blocks are empty. This way, we can make sure that as soon as k(t) increases, the number of  -blocks is close to 0 and as soon as k(t) decreases, the number of
-blocks is close to 0 and as soon as k(t) decreases, the number of  -blocks is close to 0. Therefore, the
-blocks is close to 0. Therefore, the  -block can be renamed whenever k(t) changes. The algorithm uses shiftA and shiftB operations to adjust the number of groups in the
-block can be renamed whenever k(t) changes. The algorithm uses shiftA and shiftB operations to adjust the number of groups in the  - and
- and  -blocks. Recall that a shiftA operation reduces the number of groups in the
-blocks. Recall that a shiftA operation reduces the number of groups in the  -block by 1 and increases the number of groups in the
-block by 1 and increases the number of groups in the  -block by 1 (shiftB works vice versa). Let d be the number of shiftA/shiftB operations that need to be performed to adjust
-block by 1 (shiftB works vice versa). Let d be the number of shiftA/shiftB operations that need to be performed to adjust  .
.
In the following algorithm we make use of the algorithm improve, which was developed in [25] to reduce the number of used bins. Using improve(x) on a packing B using \(\max _i B(i) \le (1+{\bar{\epsilon }}){{\textsc {opt}}}+ C\) bins for some  and some additive term C yields a new packing \(B'\) using \(\max _i B(i) \le (1+{\bar{\epsilon }}){{\textsc {opt}}}+ C-x\) bins. We use the operations in combination with the improve algorithm to obtain a fixed approximation guarantee.
and some additive term C yields a new packing \(B'\) using \(\max _i B(i) \le (1+{\bar{\epsilon }}){{\textsc {opt}}}+ C-x\) bins. We use the operations in combination with the improve algorithm to obtain a fixed approximation guarantee.
Algorithm 3
(AFPTAS for large items)


The following lemma shows that the number of shifted groups d can be bounded by 11. See Fig. 6 for an example.
Lemma 5
At most 11 groups are shifted from A to B (or B to A) in Algorithm 3.
Proof
Since the value \(|{{\textsc {size}}}(I(t-1))-{{\textsc {size}}}(I(t))|\) changes at most by 1 we can bound \(D = |\kappa (t-1) - \kappa (t)|\) by \(\frac{\epsilon }{2(\lfloor \log (1/\epsilon )\rfloor +5)}\le \frac{\epsilon }{\log ({1}/{\epsilon })+5}\) to obtain the change in the fractional part. By Lemma 1 the number of intervals (equaling the number of groups) is bounded by \((\frac{8}{\epsilon }+2)(\log ({1}/{\epsilon })+5)\). Using  and the fact that the number of groups
and the fact that the number of groups  increases or decreases at most by 1, we can give a bound for the parameter d in both cases by
increases or decreases at most by 1, we can give a bound for the parameter d in both cases by
Hence, the number of shiftA/shiftB operations is bounded by 11. \(\square \)
Lemma 6
Every rounding function \(R_t\) produced by Algorithm 3 fulfills properties (a) to (d) with parameter \(k(t)= \left\lfloor \frac{{{\textsc {size}}}(I_{L})\cdot \epsilon }{2(\lfloor \log (1/\epsilon )\rfloor +5)}\right\rfloor \), as long as all conditions to use algorithm improve are fulfilled.
We will later show in the proof of Theorem 5, that the preconditions for improve are fulfilled.
Proof
Since Algorithm 3 uses only the operations insert, delete, shiftA and shiftB, the properties (a) to (d) are always fulfilled by Lemma 3 and the (LP/ILP) solutions x, y correspond to the rounding function by Lemma 4.
Note that as exactly d groups are shifted from  to
to  (or
(or  to
to  ) the algorithm maintains the property that
) the algorithm maintains the property that  . Whenever k(t) increases by 1, the value \(\Delta (t)\) flips from 1 (implying that the
. Whenever k(t) increases by 1, the value \(\Delta (t)\) flips from 1 (implying that the  -block is empty), to 0 (implying that the
-block is empty), to 0 (implying that the  -block is empty). Hence the
-block is empty). Hence the  -block is renamed to be the new
-block is renamed to be the new  -block. Vice versa, wenever k(t) decreases the
-block. Vice versa, wenever k(t) decreases the  -block is empty and the
-block is empty and the  -block is renamed to be the new
-block is renamed to be the new  -block. Therefore the number of items in the groups is dynamically adapted to match with the parameter k(t). \(\square \)
-block. Therefore the number of items in the groups is dynamically adapted to match with the parameter k(t). \(\square \)
We will prove that the migration between packings \(B_t\) and \(B_{t+1}\) is bounded by  and that we can guarantee an asymptotic approximation ratio such that \(\max _{i} \{B_{t}(i)\} \le (1+2\Delta ) {{\textsc {opt}}}(I(t),s) + \text {poly}({1}/{\Delta })\) for a parameter
and that we can guarantee an asymptotic approximation ratio such that \(\max _{i} \{B_{t}(i)\} \le (1+2\Delta ) {{\textsc {opt}}}(I(t),s) + \text {poly}({1}/{\Delta })\) for a parameter  and for every \(t \in {\mathbb {N}}\).
and for every \(t \in {\mathbb {N}}\).
Theorem 5
Algorithm 3 is an AFPTAS with running time  and migration factor at most
and migration factor at most  for the fully dynamic bin packing problem with respect to large items.
for the fully dynamic bin packing problem with respect to large items.
Proof
Set \(\delta = \epsilon \). Then  . We assume in the following that \(\Delta \le 1\) (which holds for \(\epsilon \le \sqrt{2}-1\)).
. We assume in the following that \(\Delta \le 1\) (which holds for \(\epsilon \le \sqrt{2}-1\)).
We prove by induction that four properties hold for any packing \(B_t\), rounding \(R_t\), and the corresponding LP solutions. Let x be a fractional solution of the LP defined by the instance \((I(t),s^{R_{t}})\) and y be an integral solution of this LP. The properties (2) to (4) are necessary to apply Theorem 3 and property (1) provides the wished upper bound on the cost of the approximated solution for the bin packing problem.
- (1)
\(\max _i \{B_t(i)\} = \left\| y\right\| _1 \le (1+ 2\Delta ){{\textsc {opt}}}(I(t),s) +m\) (the number of bins is bounded)
- (2)
\(\left\| x\right\| _1 \le (1+ \Delta ) {{\textsc {opt}}}(I(t),s)\)
- (3)
for every configuration i we have \(x_i \le y_i\)
- (4)
x and y have the same number of non-zero components and that number is bounded by \(\Delta {{\textsc {opt}}}(I(t),s) +m\)
To apply Theorem 3, we furthermore need a guaranteed minimal size for \(\left\| x\right\| _1\) and \(\left\| y\right\| _1\). According to Theorem 3 the integral solution y needs \(\left\| y\right\| _1 \ge (m+2)({1}/{\delta } +2)\) and \(\left\| x\right\| _1 \ge 8 ({1}/{\delta } +1)\) as we set \(\alpha \le 4\). By condition of the while-loop, the call of improve is made iff \({{\textsc {size}}}(I(t),s) \ge 8 ({1}/{\delta } +1)\) and \({{\textsc {size}}}(I(t),s) \ge (m+2)({1}/{\delta } +2)\). Since \(\left\| y\right\| _1 \ge \left\| x\right\| _1 \ge {{\textsc {size}}}(I(t),s)\) the requirements for the minimum size are fulfilled. As long as the instance is smaller than \(8 ({1}/{\delta } +1)\) or \((m+2)({1}/{\delta } +2)\) an offline algorithm for bin packing is used. Note that there is an offline algorithm which fulfills properties (1) to (4) as shown by Jansen and Klein [25].
Now let \(B_t\) be a packing with \({{\textsc {size}}}(I(t),s) \ge 8 ({1}/{\delta } +1)\) and \({{\textsc {size}}}(I(t),s) \ge (m+2)({1}/{\delta } +2)\) for instance I(t) with solutions x and y of the LP defined by \((I(t),s^{R_t})\). Suppose by induction that the properties (1) to (4) hold for the instance I(t). We have to prove that these properties also hold for the instance \(I(t+1)\) and the corresponding solutions \(x''\) and \(y''\). The packing \(B_{t+1}\) is created by the repeated use of an call of improve for x and y followed by an operation (insert, delete, shiftA or shiftB). We will prove that the properties (1) to (4) hold after a call of improve followed by an operation.
Improve: Let \(x'\) be the resulting fractional solution of Theorem 3, let \(y'\) be the resulting integral solution of Theorem 3 and let \(B'_t\) be the corresponding packing. Properties (1) to (4) are fulfilled for x, y and \(B_t\) by induction hypothesis. Hence, all conditions are fulfilled to use Theorem 3. By Theorem 3, the properties (1) to (4) are still fulfilled for \(x'\), \(y'\) and \(B'_t\) and moreover we get \(\left\| x'\right\| _1 \le (1+ \Delta ) {{\textsc {opt}}}(I(t),s)- \alpha \) and \(\left\| y'\right\| _1 = \max _i B'_t (i) \le (1+ 2 \Delta ) {{\textsc {opt}}}(I(t),s) + m - \alpha \) for chosen parameter \(\alpha \). Let \(x''\) and \(y''\) be the fractional and integral solution after an operation is applied to \(x'\) and \(y'\). We have to prove that the properties (1) to (4) are also fulfilled for \(x''\) and \(y''\).
Operations: First we take a look at how the operations modify \(\left\| x'\right\| _1\) and \(\left\| y'\right\| _1 =\max _i B'_t (i)\). By construction of the insert operation, \(\left\| x'\right\| _1\) and \(\left\| y'\right\| \) are increased at most by 2. By construction of the delete operation, \(\left\| x'\right\| _1\) and \(\left\| y'\right\| _1\) are increased by 1. By construction of the shiftA and shiftB operation, \(\left\| x'\right\| _1\) and \(\left\| y'\right\| _1\) are increased by 1. An improve(2) call followed by an insert operation therefore yields \(\left\| y''\right\| = \left\| y'\right\| _1 +2 = (1+ 2\Delta ){{\textsc {opt}}}(I(t),s) +m -2 +2 = (1+ 2\Delta ){{\textsc {opt}}}(I(t+1),s) +m\) since \({{\textsc {opt}}}(I(t),s) \le {{\textsc {opt}}}(I(t+1),s)\). An improve(4) call followed by a delete operation yields \(\left\| y''\right\| = \left\| y'\right\| _1 + 1 = (1+ 2\Delta ){{\textsc {opt}}}(I(t),s) + m -3 \le (1+ 2\Delta ){{\textsc {opt}}}(I(t+1),s) + (1+2\Delta ) +m - 3 \le (1+ 2\Delta ){{\textsc {opt}}}(I(t+1),s) + m\) since \({{\textsc {opt}}}(I(t),s) \le {{\textsc {opt}}}(I(t+1),s) +1\) (an item is removed) and \(\Delta \le 1\). For an improve(1) call followed by a shiftA or shiftB operation, we have that \(\left\| y''\right\| = \left\| y'\right\| _1 -1 + 1 = (1+ 2\Delta ){{\textsc {opt}}}(I(t),s) + m\), as the items (and thus the optimum) does not change.
This concludes the proof that property (1) is fulfilled for \(I(t+1)\). The proof that property (2) holds is analog since \(\left\| x'\right\| _1\) increases in the same way as \(\left\| y'\right\| _1\) and \(\left\| x'\right\| _1 \le (1+ \Delta ) {{\textsc {opt}}}(I(t),s) - \alpha \). For property (3) note that in the operations a configuration \(C_i\) of the fractional solution x is increased by 1 if and only if the configuration \(C_i\) in y is increased by 1. Therefore the property that for all configurations \(x''_i \le y''_i\) retains from \(x'\) and \(y'\). By Theorem 3, the number of non-zero components of \(x'\) and \(y'\) is bounded by \(\Delta {{\textsc {opt}}}(I(t),s) +m \le \Delta {{\textsc {opt}}}(I(t+1),s) +m\) in case of an insert operation. If an item is removed, the number of non-zero components of \(x'\) and \(y'\) is bounded by \(\Delta {{\textsc {opt}}}(I(t),s) +m \le \Delta {{\textsc {opt}}}(I(t+1),s) +m +1 = C+1\). By Theorem 4, the algorithm ReduceComponents guarantees that there are at most \(C=\Delta {{\textsc {opt}}}(I(t+1),s) +m\) non-zero components. By construction of the shift-operation, \(x''\) and \(y''\) might have two additional non-zero components. But since these are being reduced by Algorithm 3 (note that we increased the number of components being reduced in step 6 by 2 to- see [25] for details), the LP solutions \(x''\) and \(y''\) have at most \(\Delta {{\textsc {opt}}}(I(t+1),s) +m\) non-zero components which proves property (4). Algorithm 3 therefore has an asymptotic approximation ratio of \(1+\epsilon \).
We still need to examine the migration factor of Algorithm 3. In the case that the offline algorithm is used, the size of the instance is smaller than  or smaller than
or smaller than  . Hence the migration factor in that case is bounded by
. Hence the migration factor in that case is bounded by  . If the instance is bigger the call of improve repacks at most
. If the instance is bigger the call of improve repacks at most  bins by Theorem 3. Since every large arriving item has size \(> {\epsilon }/{14}\) and
bins by Theorem 3. Since every large arriving item has size \(> {\epsilon }/{14}\) and  we obtain a migration factor of
we obtain a migration factor of  for the Algorithm improve. Since the migration factor of each operation is also bounded by
for the Algorithm improve. Since the migration factor of each operation is also bounded by  , we obtain an overall migration factor of
, we obtain an overall migration factor of  .
.
The main complexity of Algorithm 3 lies in the use of Algorithm improve for bin packing. Combining the analysis by Jansen and Klein [25] with the AFPTAS due to Jansen and Kraft [27], the running time of improve is bounded by  . By using heap structures to store the items, each operation can be performed in time
. By using heap structures to store the items, each operation can be performed in time  at time t, where n(t) denotes the number of items in the instance at time t. As the number of non-zero components is bounded by
at time t, where n(t) denotes the number of items in the instance at time t. As the number of non-zero components is bounded by  , the total running time of the algorithm is bounded by
, the total running time of the algorithm is bounded by  . As this is polynomial in n(t) and in \({1}/{\epsilon }\) we can conclude that Algorithm 3 is an AFPTAS. \(\square \)
. As this is polynomial in n(t) and in \({1}/{\epsilon }\) we can conclude that Algorithm 3 is an AFPTAS. \(\square \)
If no deletions are present, we can use a simple FirstFit algorithm (as described by Jansen and Klein [25]) to pack the small items into the bins. This does not change the migration factor or the running time of the algorithm and we obtain a robust AFPTAS with  migration for the case that no items is removed. This improves the best known migration factor of
migration for the case that no items is removed. This improves the best known migration factor of  [25].
[25].
4 Handling small items
In this section we present methods for dealing with arbitrary small items in a dynamic online setting. First, we present a robust AFPTAS with migration factor of  for the case that only small items arrive and depart. In Sect. 6 we generalize these techniques to a setting where small items arrive into a packing where large items are already packed and can not be rearranged. In a robust setting without departing items, small items can easily be treated by packing them greedily via the classical FirstFit algorithm of Johnson et al. [29] (see Epstein and Levin [16] or Jansen and Klein [25]). However, in a setting where items may also depart, small items need to be treated much more carefully. We show that the FirstFit algorithm does not work in this dynamic setting.
for the case that only small items arrive and depart. In Sect. 6 we generalize these techniques to a setting where small items arrive into a packing where large items are already packed and can not be rearranged. In a robust setting without departing items, small items can easily be treated by packing them greedily via the classical FirstFit algorithm of Johnson et al. [29] (see Epstein and Levin [16] or Jansen and Klein [25]). However, in a setting where items may also depart, small items need to be treated much more carefully. We show that the FirstFit algorithm does not work in this dynamic setting.
Lemma 7
Using the FirstFit algorithm to pack small items may lead to an arbitrarily bad approximation.
Proof
Suppose, that there is an algorithm  with migration factor c which uses FirstFit on items with size \(< {\epsilon }/{14}\). We will now construct an instance where
with migration factor c which uses FirstFit on items with size \(< {\epsilon }/{14}\). We will now construct an instance where  yields an arbitrary bad approximation ratio. Let \(b={\epsilon }/{14}-\delta \) and \(a={\epsilon }/{(14c)}-({(\delta +c\delta )}/{c})\) for a small \(\delta \) such that \({(1-b)}/{a}\) is integral. Note that \(ac<b\) by definition. Furthermore, let \(M\in {\mathbb {N}}\) be an arbitrary integer and consider the instance
yields an arbitrary bad approximation ratio. Let \(b={\epsilon }/{14}-\delta \) and \(a={\epsilon }/{(14c)}-({(\delta +c\delta )}/{c})\) for a small \(\delta \) such that \({(1-b)}/{a}\) is integral. Note that \(ac<b\) by definition. Furthermore, let \(M\in {\mathbb {N}}\) be an arbitrary integer and consider the instance
with
After the insertion of all items, there are M bins containing an item of size b and \({1-b}/{a}\) items of size a (see Fig. 7a). As \(ac<b\), the deletion of the items of size a can not move the items of size b. The remaining M bins thus only contain a single item of size b (see Fig. 7b), while \(\lceil M\cdot b\rceil \) bins would be sufficient to pack all of the remaining items. The approximation ratio is thus at least \({M}/{M\cdot b}={1}/{b}\approx \frac{1}{\epsilon }\) and thus grows as \(\epsilon \) shrinks.
Construction in the proof of Lemma 7. a A single bin after the insertion. b A single bin after the deletion
\(\square \)
In order to avoid this problem, we design an algorithm which groups items of similar size together. Using such a mechanism would therefore put the second item of size b into the first bin by shifting out an appropriate number of items of size a and so on. Our algorithms achieves this grouping of small items by enumerating the bins and maintaining the property, that larger small items are always left of smaller small items.
4.1 Only small items
We consider a setting where only small items exist, i.e., items with a size less than \( {\epsilon }/{14}\). First, we divide the set of small items into different size intervals \(S_\ell \) where \(S_\ell =\left[ \frac{\epsilon }{2^{\ell +1}},\frac{\epsilon }{2^\ell }\right) \) for \(\ell \ge 3\). Let \(b_1,\ldots , b_m\) be the used bins of our packing. We say a size category \(S_{\ell }\) is bigger than a size category \(S_{\ell '}\) if \(\ell <\ell '\), i.e., the item sizes contained in \(S_\ell \) are larger (note that a size category \(S_\ell \) with large index is called small). We say a bin \(b_i\) is filled completely if it has less than \(\frac{\epsilon }{2^\ell }\) remaining space, where \(S_{\ell }\) is the biggest size category appearing in \(b_i\). Furthermore we label bins \(b_i\) as normal or as buffer bins and partition all bins \(b_1,\ldots , b_m\) into queues\(Q_1, \ldots , Q_{d}\) for \(|Q| \le m\). A queue is a subsequence of bins \(b_i, b_{i+1} \ldots , b_{i+c}\) where the first bins \(b_i, \ldots , b_{i+c-1}\) are normal bins and the last bin \(b_{i+c}\) is a buffer bin. We denote the i-th queue by \(Q_i\) and the number of bins in \(Q_i\) by \(|Q_i|\). The unique buffer bin of queue \(Q_i\) is denoted by \(bb_i\). See Fig. 8 for a sketch.
We will maintain a special form for the packing of small items such that the following properties are always fulfilled. For the sake of simplicity, we assume that \({1}/{\epsilon }\) is integral.
- (1)
For every item \(i\in b_j\) with size \(s(i)\in S_{\ell } \) for some \(\ell ,j \in {\mathbb {N}}\), there is no item \(i' \in b_{j'}\) with size \(s(i') \in S_{\ell '}\) such that \(j'>j\) and \(\ell ' > \ell \). This means: Items are ordered from left to right by their size intervals.
- (2)
Every normal bin is filled completely.
- (3)
The length of each queue is at least \({1}/{\epsilon }\) and at most \({2}/{\epsilon }\) except for the last queue \(Q_d\).
Note that property (1) implies that all items in the same size interval \(S_j\) are packed into consecutive bins \(b_x, b_{x+1}, \ldots , b_{x+c}\). Items in the next smaller size category \(S_{j+1}\) are then packed into bins \(b_{x+c}, b_{x+c+1}, \ldots \) and so on. We denote by \(b_{S(\ell )}\) the last bin in which an item of size interval \(S_\ell \) appears. We denote by \(S_{>\ell }\) the set of smaller size categories \(S_{\ell '}\) with \(\ell ' > \ell \), i.e. \(S_{>\ell }=\bigcup _{\ell '>\ell }S_{\ell '}\). Note that items in size category \(S_{>\ell }\) are smaller than items in size category \(S_\ell \).
The following lemma guarantees that a packing that fulfills properties (1) to (3) is close to the optimum solution.
Lemma 8
If properties (1) to (3) hold, then at most  bins are used in the packing for every \(\epsilon \le {1}/{3}\).
bins are used in the packing for every \(\epsilon \le {1}/{3}\).
Proof
Let C be the number of used bins in our packing. By property (2) we know that all normal bins have less than \({\epsilon }/{14}\) free space. Property (3) implies that there are at most \(\epsilon \cdot C +1\) buffer bins and hence possibly empty. The number of normal bins is thus at least \((1-\epsilon )\cdot C-1\). Therefore we can bound the total size of all items by \(\ge (1-{\epsilon }/{14})\cdot ((1-\epsilon )\cdot C-1)\). As \({{\textsc {opt}}}(I,s)\ge {{\textsc {size}}}(I,s) \ge (1-{\epsilon }/{14})\cdot ((1-\epsilon )\cdot C-1)\) and \(\frac{1}{(1-{\epsilon }/{14})(1-\epsilon )} \le 1+ 2\epsilon \) for \(\epsilon \le {1}/{3}\) we get \(C \le (1+2\epsilon ) {{\textsc {opt}}}(I,s) +2.\)\(\square \)
We will now describe the operations that are applied whenever a small item has to be inserted or removed from the packing. The operations are designed such that properties (1) to (3) are never violated and hence a good approximation ratio can be guaranteed by Lemma 8 at every step of the algorithm. The operations are applied recursively such that some items from each size interval are shifted from left to right (insert) or right to left (delete). The recursion halts if the first buffer bin is reached. Therefore, the free space in the buffer bins will change over time. Since the recursion always halts at the buffer bin, the algorithm is applied on a single queue \(Q_k\).
The following insert/delete operation is defined for a whole set \(J = \{i_1, \ldots , i_n \}\) of items. If an item i of size interval \(S_{\ell }\) has to be inserted or deleted, the algorithm is called with insert\((\{ i \},b_{S(\ell )}, Q_k)\) respectively delete\((\{i\},b_x, Q_k)\), where \(b_x\) is the bin containing item i and \(Q_k\) is the queue containing bin \(b_{S(\ell )}\) or \(b_x\). Recall that \(S_{\ell }=\left[ \frac{\epsilon }{2^{\ell +1}},\frac{\epsilon }{2^{\ell }}\right) \) is a fixed interval for every \(\ell \ge 3\) and \(S_{\le \ell }=\bigcup _{i=1}^{\ell }S_{i}\) and \(S_{>\ell }=\bigcup _{\ell '>\ell }S_{\ell '}\).
Algorithm 4
(insert or delete for only small items)
insert\((J,b_x,Q_k)\):
Insert the set of small items \(J = \{i_1, \ldots , i_n \}\) with size \(s(i_j) \in S_{\le \ell }\) into bin \(b_x\). (By Lemma 9 the total size of J is bounded by
 times the size of the item which triggered the first insert operation.)
times the size of the item which triggered the first insert operation.)Remove just as many items \(J' = \{ i'_1, \ldots , i'_m \}\) of the smaller size interval \(S_{>\ell }\) appearing in bin \(b_x\) (starting by the smallest) such that the items \(i_1, \ldots , i_n\) fit into the bin \(b_x\). If there are not enough items of smaller size categories to insert all items from I, insert the remaining items from I into bin \(b_{x+1}\).
Let \(J'_{\ell '}\subseteq J'\) be the items in the respective size interval \(S_{\ell '}\) with \(\ell '>\ell \). Put the items \(J'_{\ell '}\) recursively into bin \(b_{S(\ell ')}\) (i.e., call insert\((J'_{\ell '},b_{S(\ell ')},Q_k)\) for each \(\ell '>\ell \)). If the buffer bin \(bb_k\) is left of \(b_{S(\ell ')}\) call insert\((J'_{\ell '},bb_k,Q_k)\) instead.
delete\((J,b_x,Q_k)\):
Remove the set of items \(J= \{ i_1, \ldots , i_n \}\) with size \(s(i_j) \in S_{\le \ell }\) from bin \(b_x\) (By Lemma 9 the total size of J is bounded by
 times the size of the item which triggered the first delete operation.)
times the size of the item which triggered the first delete operation.)Insert as many small items \(J'=\{i'_1, \ldots , i'_m\}\) from \(b_{S(\ell ')}\), where \(S_{\ell '}\) is the smallest size interval appearing in \(b_x\) such that \(b_x\) is filled completely. If there are not enough items from the size category \(S_{\ell '}\), choose items from size category \(S_{\ge \ell '+1}\) in bin \(b_{x+1}\).
Let \(J'_{\ell '}\subseteq J'\) be the items in the respective size interval \(S_{\ell '}\) with \(\ell '>\ell \). Remove items \(J'_{\ell '}\) from bin \(b_{S(\ell ')}\) recursively (i.e., call delete\((J'_{\ell '},b_{S(\ell ')},Q_k)\) for each \(\ell '>\ell \)). If the buffer bin \(bb_k\) is left of \(b_{S(\ell ')}\), call delete\((J'_{\ell '},bb_k,Q_k)\) instead.
Using the above operations maintains the property of normal bins to be filled completely. However, the size of items in buffer bins changes. In the following we describe how to handle buffer bins that are being emptied or filled completely.
Algorithm 5
(Handle filled or emptied buffer bins)
Case 1: The buffer bin of \(Q_i\) is filled completely by an insert operation.
Label the filled bin as a normal bin and add a new empty buffer bin to the end of \(Q_i\).
If \(|Q_i|>{2}/{\epsilon }\), split \(Q_i\) into two new queues \(Q'_i,Q''_i\) with \(|Q''_i|=|Q'_i|+1\). The buffer bin of \(Q''_i\) is the newly added buffer bin. Add an empty bin labeled as the buffer bin to \(Q'_i\) such that \(|Q'_i|=|Q''_i|\).
Case 2: The buffer bin of \(Q_i\) is being emptied due to a delete operation.
Remove the now empty bin.
If \(|Q_{i}| \ge |Q_{i+1}|\) and \(|Q_{i}|> {1}/{\epsilon }\), choose the last bin of \(Q_{i}\) and label it as new buffer bin of \(Q_i\).
If \(|Q_{i+1}| > |Q_i|\) and \(|Q_{i+1}|> {1}/{\epsilon }\), choose the first bin of \(Q_{i+1}\) and move the bin to \(Q_i\) and label it as buffer bin.
If \(|Q_{i+1}| = |Q_i| = {1}/{\epsilon }\), merge the two queues \(Q_i\) and \(Q_{i+1}\). As \(Q_{i+1}\) already contains a buffer bin, there is no need to label another bin as buffer bin for the merged queue.
Creating and deleting buffer bins this way guarantees that property (3) is never violated since queues never exceed the length of \({2}/{\epsilon }\) and never fall below \({1}/{\epsilon }\).
Figure 9a shows an example call of insert(\(\{ i \}\),\(b_x\),\(Q_k\)). Item i with \(s(i)\in S_1\) is put into the corresponding bin \(b_x\) into the size interval \(S_1\). As \(b_x\) now contains too many items, some items from the smallest size interval \(S_2\) are put into the last bin \(b_{x+2}\) containing items from \(S_2\). Those items in turn push items from the smallest size interval \(S_3\) into the last bin containing items of this size and so on. This process terminates if either no items need to be shifted to the next bin or the buffer bin \(bb_k\) is reached.
It remains to prove that the migration of the operations is bounded and that the properties are invariant under those operations.
Lemma 9
-
(i)
Let I be an instance that fulfills properties (1) to (3). Applying operations insert/delete on I yields an instance \(I'\) that also fulfills properties (1) to (3).
-
(ii)
The migration factor of a single insert/delete operation is bounded by
 for all \(\epsilon \le {2}/{7}\).
for all \(\epsilon \le {2}/{7}\).
Proof
Proof for (i): Suppose the insert/delete operation is applied to a packing which fulfills properties (1) to (3). By construction of the insert operation, items from a size category \(S_\ell \) in bin \(b_x\) are shifted to a bin \(b_y\). The bin \(b_y\) is either \(b_{S(\ell )}\) or the buffer bin left of \(b_{S(\ell )}\). By definition \(b_y\) contains items of size category \(S_{\ell }\). Therefore property (1) is fulfilled. Symmetrically, by construction of the delete operation, items from a size category \(S_\ell \) in bin \(b_{S(\ell )}\) are shifted to a bin \(b_x\). By definition \(b_x\) contains items of size category \(S_{\ell }\) and property (1) is therefore fulfilled. For property (2): Let \(b_x\) be a normal bin, where items \(i_1, \ldots , i_n\) of size category \(S_{\le \ell }\) are inserted. We have to prove that the free space in \(b_x\) remains smaller than \({\epsilon }/{2^\ell }\), where \(S_\ell \) is the smallest size category appearing in bin \(b_x\). By construction of the insert operation, just as many items of size categories \(S_{>\ell }\) are shifted out of bin \(b_x\) such that \(i_1,\ldots ,i_n\) fit into \(b_x\). Hence the remaining free space is less than \(\frac{\epsilon }{2^{\ell }}\) and bin \(b_x\) is filled completely. The same argumentation holds for the delete operation. Property (3) is always fulfilled by definition of Algorithm 5.
Proof for (ii): According to the insert operation, in every recursion step of the algorithm, it tries to insert a set of items into a bin \(b_{x'}\), starting with an insert\((\{ i \},b_{x'},Q_k)\) operation. Let \({{\textsc {insert}}}(S_{\le \ell +y}, b_x)\) (\(x\ge x'\)) be the size of all items in size categories \(S_{\ell '}\) with \(\ell ' \le \ell +y\) that the algorithm tries to insert into \(b_x\) as a result of an insert\((\{ i \},b_{x'},Q_k)\) call. Let \({{\textsc {pack}}}(b_x)\) be the size of items that are actually packed into bin \(b_x\). We have to distinguish between two cases. In the case that \({{\textsc {insert}}}(S_{\le \ell +y}, b_x) = {{\textsc {pack}}}(b_x)\) there are enough items of smaller size categories \(S_{>\ell +y}\) that can be shifted out, such that items I fit into bin \(b_x\). In the case that \({{\textsc {insert}}}(S_{\le \ell +y}, b_x) > {{\textsc {pack}}}(b_x)\) there are not enough items of smaller size category that can be shifted out and the remaining size of \({{\textsc {insert}}}(S_{\le \ell +y}, b_x) - {{\textsc {pack}}}(b_x)\) has to be shifted to the following bin \(b_{x+1}\). Under the assumption that \({{\textsc {insert}}}(S_{\le \ell }, b_x)\le 1\) for all x and \(\ell \) (which is shown in the following) all items fit into \(b_{x+1}\). Note that no items from bins left of \(b_{x}\) can be shifted into \(b_{x+1}\) since \(b_x = b_{S(\ell +y)}\) is the last bin where items of size category \(S_{\le \ell +y}\) appear. Hence all items shifted out from bins left of \(b_{x}\) are of size categories \(S_{\le \ell +y}\) (property (1)) and they are inserted into bins left of \(b_{x+1}\). We prove by induction that for each \({{\textsc {insert}}}(S_{\le \ell +y}, b_x)\) the total size of moved items is at most
The claim holds obviously for \({{\textsc {insert}}}(S_{\le \ell }, b_{x'})\) since \(b_{x'}=b_{S(\ell )}\) is the bin where only item i is inserted. Fig. 10 shows all cases to consider.
All cases to consider in Lemma 9. a Case 1. b Case 2a. c Case 2b
Case 1 \({{\textsc {insert}}}(S_{\le \ell + y}, b_x) > {{\textsc {pack}}}(b_x)\)
In this case, the size of all items that have to be inserted into \(b_{x+1}\) can be bounded by the size of items that did not fit into bin \(b_x\) plus the size of items that were removed from bin \(b_x\). We can bound \({{\textsc {insert}}}(S_{\le \ell +{\bar{y}}}, b_{x+1})\) where \({\bar{y}} > y\) is the largest index \(S_{\ell +{\bar{y}}}\) appearing in bin \(b_{x}\) by
Case 2\({{\textsc {insert}}}(S_{\le \ell +y}, b_x) = {{\textsc {pack}}}(b_x)\)
Suppose that the algorithm tries to insert a set of items I of size categories \(S_{\le \ell +{\bar{y}}}\) into the bin \(b_{x+1} = b_{S(\ell +{\bar{y}})}\). The items I can only be shifted from previous bins where items of size category \(S_{\le \ell +{\bar{y}}}\) appear. There are only two possibilities remaining. Either all items I are shifted from a single bin \(b_{{\hat{x}}}\) (\({\hat{x}} \le x\)) or from two consecutive bins \(b_{{\hat{x}}},b_{{\hat{x}}+1}\) with \({{\textsc {insert}}}(S_{\le \ell +y}, b_{{\hat{x}}}) > {{\textsc {pack}}}(b_{{\hat{x}}})\).
Note that \(b_{x+1}\) can only receive items from more than one bin if there are bins \(b_{{\hat{x}}},b_{{\hat{x}}+1}\) with \({{\textsc {insert}}}(S_{\le \ell +y}, b_{{\hat{x}}}) > {{\textsc {pack}}}(b_{{\hat{x}}})\) such that \(b_{x+1}=b_{S(\ell +{\bar{y}})}\) and all items shifted out of \(b_{{\hat{x}}},b_{{\hat{x}}+1}\) and into \(b_{x+1}\) are of size category \(S_{\ell +{\bar{y}}}\). Hence bins left of \(b_{{\hat{x}}}\) or right of \(b_{{\hat{x}}+1}\) can not shift items into \(b_{x+1}\).
Case 2a All items I are shifted from a single bin \(b_{{\hat{x}}}\) with \({\hat{x}} \le x\) (note that \({\hat{x}}<x\) is possible since \({{\textsc {pack}}}(b_x) = {{\textsc {insert}}}(S_{\le \ell +y}, b_x)\) can be zero). The total size of items that are shifted out of \(b_{{\hat{x}}}\) can be bounded by \({{\textsc {insert}}}(S_{\le \ell +y},b_{{\hat{x}}})+\frac{\epsilon }{2^{\ell +y}}\). By induction hypothesis \({{\textsc {insert}}}(S_{\le \ell +y}, b_{{\hat{x}}})\) is bounded by \(s(i)+3\sum _{j=1}^{y}\frac{\epsilon }{2^{\ell +j}}\). Since all items that are inserted into \(b_{x+1}\) come from \(b_{{\hat{x}}}\), the value \({{\textsc {insert}}}(S_{\le \ell +{\bar{y}}},b_{x+1})\) (\({\bar{y}}>y\)) can be bounded by \({{\textsc {insert}}}(S_{\le \ell +y}, b_{{\hat{x}}}) + \frac{\epsilon }{2^{\ell +y}} \le s(i)+3\sum _{j=1}^{y}\frac{\epsilon }{2^{\ell +j}}+\frac{\epsilon }{2^{\ell +y}}< s(i) + 3 \sum _{j=1}^{{\bar{y}}} \frac{\epsilon }{2^{\ell +j}}\) where \(S_{\ell +{\bar{y}}}\) is the smallest size category inserted into \(b_{x+1}\). Note that the items I belong to only one size category \(S_{\ell +{\bar{y}}}\) if \({\hat{x}}<x\) since all items that are in size intervals \(S_{<\ell +{\bar{y}}}\) are inserted into bin \(b_{{\hat{x}}+1}\).
Case 2b Items I are shifted from bins \(b_{{\hat{x}}}\) and \(b_{{\hat{x}}+1}\) (\({\hat{x}}+1 \le x\)) with \({{\textsc {insert}}}(S_{\le \ell +y}, b_{{\hat{x}}}) > {{\textsc {pack}}}(b_{{\hat{x}}})\). In this case, all items I belong to the size category \(S_{\ell +{\bar{y}}}\) since \(b_{{\hat{x}}}\) is left of \(b_x\). Hence all items which are inserted into \(b_{{\hat{x}}+1}\) are from I, i.e., \({{\textsc {insert}}}(S_{\le \ell +y},b_{{\hat{x}}}) = {{\textsc {pack}}}(b_{{\hat{x}}}) + {{\textsc {pack}}}(b_{{\hat{x}}+1})\) as all items in I belong to the same size category \(S_{\ell +{\bar{y}}}\). We can bound \({{\textsc {insert}}}(S_{\ell +{\bar{y}}},b_{x+1})\) by the size of items that are shifted out of \(b_{{\hat{x}}}\) plus the size of items that are shifted out of \(b_{{\hat{x}}+1}\). We obtain
This yields that \({{\textsc {insert}}}(S_{\le \ell +y},b_x)\) is bounded by \(s(i) + 3 \sum _{j=1}^{{\bar{y}}} \frac{\epsilon }{2^{\ell +j}}\) for all bins \(b_x\) in \(Q_k\). Now, we can bound the migration factor for every bin \(b_x\) of \(Q_k\) for any \(y\in {\mathbb {N}}\) by \({{\textsc {pack}}}(b_x) + \frac{\epsilon }{2^{\ell +y}} \le {{\textsc {insert}}}(S_{\le \ell +y},b_x) + \frac{\epsilon }{2^{\ell +y}}\). Using the above claim, we get:
Since there are at most \({2}/{\epsilon }\) bins per queue, we can bound the total migration of insert\((\{ i \},b_{S(\ell )}, Q_k)\) by  . Note also that \(s(i) \le {\epsilon }/{14}\) for every i implies that \({{\textsc {insert}}}(S_{\le \ell }, b_x)\) is bounded by \({\epsilon }/{2}\) for all x and \(\ell \) .
. Note also that \(s(i) \le {\epsilon }/{14}\) for every i implies that \({{\textsc {insert}}}(S_{\le \ell }, b_x)\) is bounded by \({\epsilon }/{2}\) for all x and \(\ell \) .
Suppose that items \(i_1, \ldots , i_n\) of size interval \(S_{\ell +y}\) have to be removed from bin \(b_x\). In order to fill the emerging free space, items from the same size category are moved out of \(b_{S(\ell )}\) into the free space. As the bin \(b_x\) may already have additional free space, we need to move at most a size of \({{\textsc {size}}}(i_1,\ldots ,i_n)+{\epsilon }/{2^{\ell +y}}\). Using a symmetric proof as above yields a migration factor of  . \(\square \)
. \(\square \)
5 Handling small items in the general setting
In the scenario that there are both item types (small and large items), we need to be more careful in the creation and the deletion of buffer bins. To maintain the approximation guarantee, we have to make sure that as long as there are bins containing only small items, the remaining free space of all bins can be bounded. Packing small items into empty bins and leaving bins with large items untouched does not lead to a good approximation guarantee as the free space of the bins containing only large items is not used. In this section we consider the case where a sequence of small items is inserted or deleted. We assume that the packing B of large items does not change and thus fix such a packing. Therefore the number of bins containing large items equals a fixed value \(\Lambda (B)\). In the previous section, all bins \(b_{i}\) had a capacity of 1. In order to handle a mixed setting, we will treat a bin \(b_i\) containing large items as having capacity of \(c(b_i) = 1-S\), where S is the total size of the large items in \(b_i\). The bins containing small items are enumerated by \(b_1, \ldots ,b_{L(B)}, b_{L(B)+1}, \ldots , b_{m(B)}\) for some \(L(B)\le m(B)\) where \(c(b_1),\ldots ,c(b_{L(B)})< 1\) and \(c(b_{L(B)+1})=\cdots = c(b_{m(B)})=1\). Additionally we have a separate set of bins, called the heap bins, which contain only large items. This set of bins is enumerated by \(h_1, \ldots h_{h(B)}\). Note that \(L(B)+h(B)=\Lambda (B)\). In general we may consider only bins \(b_i\) and \(h_i\) with capacity \(c(b_i) \ge {\epsilon }/{14}\) and \(c(h_i) \ge {\epsilon }/{14}\) since bins with less capacity are already packed well enough for our approximation guarantee as shown by Lemma 9. Therefore, full bins are not considered in the following.
As before, we partition the bins \(b_1,\ldots ,b_{L(B)}, b_{L(B)+1}, \ldots ,b_{m(B)}\) into queues \(Q_1, \ldots , Q_{\ell (B)} , Q_{\ell (B) +1}, \ldots ,Q_{d(B)}\) such that \(b_1, \ldots b_{L(B)}\) are put into the queues \(Q_1, \ldots Q_{\ell (B)}\) and \(b_{L(B)+1}, \ldots b_{m(B)}\) are put into \(Q_{\ell (B)+1}, \ldots , Q_{d(B)}\). If the corresponding packing B is clear from the context, we will simply write \(h,L,\ell ,d,m,\Lambda \) instead of h(B), L(B) etc. We denote the last bin of queue \(Q_i\)—which is a buffer bin—by \(bb_i\). The buffer bin \(bb_{\ell }\) is special and will be treated differently in the insert and delete operation. Note that the bins containing large items \(b_1,\ldots ,b_{L(B)}\) are enumerated first. This guarantees that the free space in the bins containing large items is used before new empty bins are opened to pack the small items. However, enumerating bins containing large items first leads to a problem if a buffer bin is being filled and a new bin has to be inserted right to the filled bin according to Algorithm 5. Instead of inserting a new empty bin, we insert a heap bin at this position. Since the heap bin contains only large items, we do not violate the order of the small items (see Fig. 11). As the inserted heap bin has remaining free space (is not filled completely) for small items, it can be used as a buffer bin. In order to get an idea of how many heap bins we have to reserve for Algorithm 5 where new bins are inserted or deleted, we define a potential function. As a buffer bin is being filled or emptied completely, Algorithm 5 is executed and inserts or deletes buffer bins. The potential function \(\Phi (B)\) thus bounds the number of buffer bins in \(Q_1, \ldots , Q_{\ell (B)}\) that are about to get filled or emptied. The potential \(\Phi (B)\) is defined by
where the fill ratio\(r_i\) is defined by \(r_i=\frac{s(bb_i)}{c(bb_i)}\) and \(s(bb_i)\) is the total size of all small items in \(bb_i\). Note that the potential only depends on the queues \(Q_1, \ldots , Q_{\ell (B)}\) and the bins which contain small and large items. The term \(r_i\) intends to measure the number of buffer bins that become full. According to Case 1 of the previous section, a new buffer bin is opened whenever \(bb_i\) is filled, i.e., \(r_i \approx 1\). Hence the number of buffer bins getting filled is bounded by the sum \(\sum _{i=1}^{\ell -1} r_i\). The term \(\epsilon \Lambda \) in the potential measures the number of bins that need to be inserted due to the length of a queue exceeding \({2}/{\epsilon }\), as we need to split this queue \(Q_i\) into two queues of length \({1}/{\epsilon }\) according to Case 1. Each of those queues needs a buffer bin, hence we need to insert a new buffer bin out of the heap bins. Therefore the potential \(\Phi (B)\) bounds the number of bins which will be inserted as new buffer bins according to Case 1.
Just like in the previous section we propose the following properties to bound the approximation ratio and the migration factor. The first three properties remain the same as in Sect. 4.1 and the last property gives the desired connection between the potential function and the heap bins.
- (1)
For every item \(i\in b_j\) with size \(s(i)\in S_\ell \) for some \(j,\ell \in {\mathbb {N}}\), there is no item \(i' \in b_{j'}\) with size \(s(i') \in S_{\ell '}\) such that \(j'>j\) and \(\ell ' > \ell \). This means: Items are ordered from left to right by their size intervals.
- (2)
Every normal bin of \(b_1,\ldots ,b_m\) is filled completely
- (3)
The length of each queue is at least \({1}/{\epsilon }\) and at most \({2}/{\epsilon }\) except for \(Q_{\ell }\) and \(Q_{d}\). The length of \(Q_{\ell }\) and \(Q_{d}\) is only limited by \(1\le |Q_{\ell }|,|Q_d|\le {1}/{\epsilon }\). Furthermore, \(|Q_{\ell +1}| = 1\) and \(1 \le |Q_{\ell +2}| \le {2}/{\epsilon }\).
- (4)
The number of heap bins \(H_1, \ldots , H_{h}\) is exactly \(h = \lfloor \Phi (B) \rfloor \)
Since bins containing large items are enumerated first, property (1) implies in this setting that bins with large items are filled before bins that contain no large items. Note also that property (3) implies that \(\Phi (B) \ge 0\) for arbitrary packings B since \(\epsilon \Lambda \ge \ell -1+\epsilon \) and thus \(\lceil \epsilon \Lambda \rceil \ge \ell \). The following lemma proves that a packing which fulfills properties (1) to (4) provides a solution that is close to the optimum.
Lemma 10
Let \(M = m + h\) be the number of used bins and \(\epsilon \le {1}/{4}\). If properties (1) to (4) hold, then at most \(\max \{ \Lambda , (1+5\cdot \epsilon ){{\textsc {opt}}}(I,s)+4 \}\) bins are used in the packing.
Proof
Case 1 There is no bin containing only small items, i.e., \(L=m\). Hence all items are packed into \(M=L+h = \Lambda \) bins.
Case 2 There are bins containing only small items, i.e., \(L<m\). Property (3) implies that the number of queues d is bounded by \(d\le \epsilon m+4\). Hence the number of buffer bins is bounded by \(\epsilon m+4\) and the number of heap bins \(\Phi (B)\) (property (4)) is bounded by \(\Phi (B) = \sum _{i=1}^{\ell -1} r_i + \lceil \epsilon \Lambda \rceil - \ell \le \ell -1 + \epsilon \Lambda +1 - \ell = \epsilon \Lambda \) as \(r_i\le 1\). Since \(\Lambda < M\), we can bound \(\Phi (B)\) by \(\Phi (B) < \epsilon M\). The number of normal bins is thus at least \(M - (\epsilon m + 5) - (\epsilon M - 1) \ge M - 2 \epsilon M - 4 = (1-2\epsilon )M- 4\). By property (2), every normal bin has less than \({\epsilon }/{14}\) free space and the total size S of all items is thus at least \(S \ge (1-{\epsilon }/{14})(1-2\epsilon )M-4\). Since \({{\textsc {opt}}}(I,s)\ge S\), we have \({{\textsc {opt}}}(I,s)\ge (1-{\epsilon }/{14})(1-2\epsilon )M-4\). A simple calculation shows that \(\frac{1}{(1-{\epsilon }/{14})(1-2\epsilon )}\le (1+5\epsilon )\) for \(\epsilon \le {1}/{4}\). Therefore we can bound the number of used bins by \((1+5\epsilon ){{\textsc {opt}}}(I,s)+4\). \(\square \)
According to property (4) we have to guarantee, that if the rounded potential \(\lfloor \Phi (B) \rfloor \) changes, the number of heap bins has to be adjusted accordingly. The potential \(\lfloor \Phi (B) \rfloor \) might increases by 1 due to an insert operation. Therefore the number of heap bins has to be incremented. If the potential \(\lfloor \Phi (B) \rfloor \) decreases due to a delete operation, the number of heap bins has to be decremented. In order to maintain property (4), we have to make sure that the number of heap bins can be adjusted whenever \(\lfloor \Phi (B) \rfloor \) changes. Therefore we define the fractional part \(\{ \Phi (B) \}=\Phi (B)-\lfloor \Phi (B)\rfloor \) of \(\Phi (B)\) and put it in relation to the fill ratio \(r_{\ell }\) of \(bb_{\ell }\) (the last bin containing large items) through the following invariant:
where \(s^{(\ell )}\) is the biggest size of a small item appearing in \(bb_{\ell }\). The Heap Equation ensures that the potential \(\Phi (B)\) is correlated to \(1-r_{\ell }\). The values may only differ by the small term \(\frac{s^{(\ell )}}{c(bb_{\ell })}\). Note that the Heap Equation can always be fulfilled by shifting items from \(bb_{\ell }\) to queue \(Q_{\ell +1}\) or vice versa.
Assuming the Heap Equation holds and the potential \(\lfloor \Phi (B)\rfloor \) increases by 1, we can guarantee that buffer bin \(bb_{\ell }\) is nearly empty. Hence, the remaining items can be shifted to \(Q_{\ell +1}\) and \(bb_\ell \) can be moved to the heap bins. The bin left of \(bb_\ell \) becomes the new buffer bin of \(Q_\ell \). Vice versa, if \(\lfloor \Phi (B)\rfloor \) decreases, we know by the Heap Equation that \(bb_{\ell }\) is nearly full. Hence, we can label \(bb_{\ell }\) as a normal bin and open a new buffer bin from the heap at the end of queue \(Q_{\ell }\). Our goal is to ensure that the Heap Equation is fulfilled at every step of the algorithm along with properties (1) to (4). Therefore we enhance the delete and insert operations from the previous section. Whenever a small item i is inserted or removed, we will perform the operations described in Algorithm 4 (which can be applied to bins of different capacities) in the previous section. This will maintain properties (1) to (3). If items are inserted or deleted from queue \(Q_{\ell }\) (the last queue containing large and small items) the recursion does not halt at \(bb_{\ell }\). Instead the recursion goes further and halts at \(bb_{\ell +1}\). Thus, when items are inserted into bin \(bb_\ell \) according to Algorithm 4, the bin \(bb_\ell \) is treated as a normal bin. Items are shifted from \(bb_{\ell }\) to queue \(Q_{\ell +1}\) until the Heap Equation is fulfilled. This way we can make sure that the Heap Equation maintains fulfilled whenever an item is inserted or removed from \(Q_{\ell }\).
Algorithm 6
(insert or delete small items for the mixed setting)
insert\((i,b_x,Q_j)\):
Use Algorithm 4 to insert item i into \(Q_j\) with \(j < \ell \).
Let \(i_1, \ldots , i_m\) be the items that are inserted at the last step of Algorithm 4 into \(bb_j\).
For \(k = 1, \ldots , m\) do
- 1.
Insert item \(i_k\) into bin \(bb_j\).
- 2.
If \(bb_j\) is completely filled use Algorithm 5.
- 3.
If the potential \(\lfloor \Phi (B) \rfloor \) increases use Algorithm 7 (see below) to adjust the number of heap bins (property (4)).
- 4.
Decrease the fill ratio \(r_\ell \) of \(bb_\ell \) by shifting the smallest items in \(bb_\ell \) to \(Q_{\ell +1}\) until \((1 - r_{\ell }) \le \{ \Phi (B) \}\) to fulfill the Heap Equation.
- 1.
delete\((i,b_x,Q_j)\):
Use Algorithm 4 to remove item i from bin \(b_x\) in queue \(Q_j\) with \(j < \ell \).
Let \(i_1, \ldots , i_m\) be the items that are removed at the last step of Algorithm 4 from \(bb_j\).
For \(k = 1, \ldots , m\) do
- 1.
If \(bb_j\) is empty use Algorithm 5.
- 2.
Remove item \(i_k\) from bin \(bb_j\).
- 3.
If the potential \(\lfloor \Phi (B) \rfloor \) decreases use Algorithm 7.
- 4.
Increase the fill ratio \(r_\ell \) of \(bb_\ell \) by shifting the smallest items in \(bb_\ell \) to \(Q_{\ell +1}\) until \((1 - r_{\ell }) \ge \{ \Phi (B) \}\) to fulfill the Heap Equation.
- 1.
For the correctness of step 4 (the adjustment to \(r_{\ell }\)) note the following: In case of the insert operation, the potential \(\Phi (B)\) increases and we have \(\Phi (B) \ge 1-r_\ell \). As items are being shifted from \(bb_\ell \) to \(Q_{\ell +1}\), the first time that \((1 - r_{\ell }) \le \{ \Phi (B) \}\) is fulfilled, the Heap Equation is also fulfilled. Since the fill ratio of \(bb_\ell \) changes at most by \(\frac{s^{(\ell )}}{c(bb_\ell )}\) as an item (which has size at most \(s^{(\ell )}\)) is shifted to \(Q_{\ell +1}\) we know that \(| (1 - r_{\ell }) - \{ \Phi (B) \} | \le \frac{s^{(\ell )}}{c(bb_\ell )}\). Correctness of step 4 in the delete operation follows symmetrically.
The potential \(\Phi (B)\) changes if items are inserted or deleted into queues \(Q_1, \ldots , Q_{\ell -1}\). Due to these insert or delete operations it might happen that the potential \(\lfloor \Phi (B) \rfloor \) increases or that a buffer bin is being filled or emptied. The following operation is applied as soon as an item is inserted or deleted into a buffer bin and the potential \(\lfloor \Phi (B) \rfloor \) increases or decreases.
Algorithm 7
(Change in the potential)
Case 1: The potential \(\lfloor \Phi (B) \rfloor \) increases by 1.
According to the Heap Equation, the remaining size of small items in \(bb_{\ell }\) can be bounded. Shift all small items from \(bb_{\ell }\) to \(Q_{\ell +1}\).
If \(|Q_{\ell }| >1\) then label the now empty buffer bin \(bb_{\ell }\) as a heap bin and the last bin in \(Q_{\ell }\) is as a buffer bin.
If \(Q_{\ell }\) only consists of the buffer bin (i.e., \(|Q_{\ell }| = 1\)), shift items from \(bb_{\ell -1}\) to \(Q_{\ell +1}\) until the heap equation is fulfilled. If \(bb_{\ell -1}\) becomes empty, remove \(bb_{\ell -1}\) and \(bb_{\ell }\). The bin left to \(bb_{\ell -1}\) becomes the new buffer bin of \(Q_{\ell -1}\). The queue \(Q_{\ell }\) is deleted and \(Q_{\ell -1}\) becomes the new last queue containing large items.
Case 2: The potential \(\lfloor \Phi (B) \rfloor \) decreases by 1.
According to the Heap Equation, the remaining free space in \(bb_{\ell }\) can be bounded. Shift items from \(bb_{\ell +1}\) to \(bb_{\ell }\) such that the buffer bin \(bb_{\ell }\) is filled completely.
Add the new buffer bin from the heap to \(Q_{\ell }\).
If \(|Q_{\ell }| = {1}/{\epsilon }\) label an additional heap bin as a buffer bin to create a new queue \(Q_{\ell +1}\) with \(|Q_{\ell +1}| = 1\).
Like in the last section we also have to describe how to handle buffer bins that are being emptied or filled completely. We apply the same algorithm when a buffer bin is being emptied or filled but have to distinguish now between buffer bins of \(Q_1, \ldots , Q_{\ell }\) and buffer bins of \(Q_{\ell +1}, \ldots , Q_{d}\). Since the buffer bins in \(Q_{\ell +1},\ldots ,Q_{d}\) all have capacity 1, we will use the same technique as in the last section. If a buffer bin in \(Q_{1},\ldots ,Q_{\ell }\) is emptied or filled, we will also use a similar technique. But instead of inserting a new empty bin as a new buffer bin, we take an existing bin out of the heap. And if a buffer bin from \(Q_1, \ldots Q_{\ell }\) is being emptied (it still contains large items), it is put into the heap. This way we make sure that there are always sufficiently many bins containing large items which are filled completely.
Lemma 11
Let B be an packing which fulfills the properties (1) to (4) and the Heap Equation. Applying Algorithm 7 or Algorithm 5 on B during an insert/delete operation yields an packing \(B'\) which also fulfills properties (1) to (4). The migration to fulfill the Heap Equation is bounded by  .
.
Proof
Analysis of Algorithm7 Properties (1) and (2) are never violated by the algorithm because the items are only moved by shift operations. Property (3) is never violated because no queue (except for \(Q_{\ell }\)) exceeds \({2}/{\epsilon }\) or falls below \({1}/{\epsilon }\) by construction. Algorithm 7 is called during an insert or delete operation. The Algorithm is executed as items are shifted into or out of buffer \(bb_j\) such that \(\lfloor \Phi (B)\rfloor \) changes.
In the following, we prove property (4) for the packing \(B'\) assuming that \(\lfloor \Phi (B) \rfloor = h(B)\) holds by induction. Furthermore we give a bound for the migration to fulfill the heap equation:
Case 1 The potential \(\lfloor \Phi (B) \rfloor \) increases during an insert operation, i.e., it holds \(\lfloor \Phi (B') \rfloor = \lfloor \Phi (B) \rfloor +1\). Let item \(i^*\) be the first item that is shifted into a bin \(bb_j\) such that \(\lfloor \Phi (B) + r^* \rfloor = \lfloor \Phi (B') \rfloor \), where \(r^*\) is the fill ratio being added to \(bb_j\) by item \(i^*\). In this situation, the fractional part changes from \(\{\Phi (B)\} \approx 1\) to \(\{\Phi (B')\} \approx 0\).
In the case that \(|Q_{\ell }|> 1\), the buffer bin \(bb_{\ell }\) is being emptied and moved to the heap bins. The bin left of \(bb_{\ell }\) becomes the new buffer bin \(bb'_\ell \) of \(Q_{\ell }\). Hence the number of heap bins increases and we have \(h(B') = h(B) +1 = \lfloor \Phi (B) \rfloor +1 = \lfloor \Phi (B') \rfloor \), which implies property (4). To give a bound on the total size of items needed to be shifted out of (or into) bin \(bb_\ell \) to fulfill the heap equation, we bound the term \(|(1 - r'_{\ell }) - \{ \Phi (B') \}|\) by some term
 , where \(r'_\ell \) is the fill ratio of \(bb'_\ell \) and s(i) is the size of the arriving or departing item. If the term \(|(1 - r'_{\ell }) - \{ \Phi (B') \}|\) can be bounded by C, the fill ratio of \(bb'_\ell \) has to be adjusted to fulfill the heap equation according to the insert and delete operations. This can be done by shifting a total size of at most C items out of (or into) \(bb'_\ell \). The bin \(bb'_\ell \) is completely filled by property (3) and therefore has a fill ratio of \(r'_\ell \ge \frac{c(bb_\ell ) - s^{(\ell )}}{c(bb_\ell )} \ge 1- 2 \frac{s^{(\ell )}}{\epsilon }\), where \(s^{(\ell )} \le \frac{\epsilon }{2^k}\) is the largest size of a small item appearing in \(bb_\ell \) and \(S_k\) is the largest size category appearing in \(bb'_\ell \). Let \(k'\) be the largest size category appearing in bin \(bb_j\). As the bin \(bb'_\ell \) is right of \(bb_j\) we know \(k \le k'\) (property (1)) and hence \(s^{(\ell )} \le 2 s(i^*)\). We get \(r'_{\ell } \ge 1 - 4 \frac{s(i^*)}{\epsilon }\). Using that \(\{ \Phi (B') \} \le r^* \le 2 {s(i^*)}/{\epsilon }\), we can bound \(|(1 - r'_{\ell }) - \{ \Phi (B') \}|\) by
, where \(r'_\ell \) is the fill ratio of \(bb'_\ell \) and s(i) is the size of the arriving or departing item. If the term \(|(1 - r'_{\ell }) - \{ \Phi (B') \}|\) can be bounded by C, the fill ratio of \(bb'_\ell \) has to be adjusted to fulfill the heap equation according to the insert and delete operations. This can be done by shifting a total size of at most C items out of (or into) \(bb'_\ell \). The bin \(bb'_\ell \) is completely filled by property (3) and therefore has a fill ratio of \(r'_\ell \ge \frac{c(bb_\ell ) - s^{(\ell )}}{c(bb_\ell )} \ge 1- 2 \frac{s^{(\ell )}}{\epsilon }\), where \(s^{(\ell )} \le \frac{\epsilon }{2^k}\) is the largest size of a small item appearing in \(bb_\ell \) and \(S_k\) is the largest size category appearing in \(bb'_\ell \). Let \(k'\) be the largest size category appearing in bin \(bb_j\). As the bin \(bb'_\ell \) is right of \(bb_j\) we know \(k \le k'\) (property (1)) and hence \(s^{(\ell )} \le 2 s(i^*)\). We get \(r'_{\ell } \ge 1 - 4 \frac{s(i^*)}{\epsilon }\). Using that \(\{ \Phi (B') \} \le r^* \le 2 {s(i^*)}/{\epsilon }\), we can bound \(|(1 - r'_{\ell }) - \{ \Phi (B') \}|\) by  . Hence the Heap Equation can be fulfilled by shifting items of total size
. Hence the Heap Equation can be fulfilled by shifting items of total size  at the end of the insert operation.
at the end of the insert operation.If \(|Q_{\ell }| = 1\), a set of items in the buffer bin \(bb_{\ell -1}\) is shifted to \(Q_{\ell +1}\) to fulfill the Heap Equation. Since items are being removed from \(bb_{\ell -1}\), the potential decreases. If \(r_{\ell -1} > \{ \Phi (B') \}\), there are enough items which can be shifted out of \(bb_{\ell -1}\) such that we obtain a new potential \(\Phi (B'') < \Phi (B') - \{\Phi (B')\}\). Hence \(\lfloor \Phi (B'')\rfloor = \lfloor \Phi (B)\rfloor \) and the Heap Equation is fulfilled. Note that the size of items that are shifted out of \(bb_{\ell -1}\) is bounded by
 , where s is the biggest size of an item appearing in \(bb_{\ell -1}\). If \(r_{\ell -1}\le \{ \Phi (B') \}\), all items are shifted out of \(bb_{\ell -1}\). As the number of queues decreases, we obtain the new potential \(\Phi (B'') = \Phi (B') - r_{\ell -1} + 1= \lfloor \Phi (B') \rfloor +\{\Phi (B')\}-r_{\ell -1} + 1 \ge \lfloor \Phi (B')\rfloor +1 \). Hence \(\lfloor \Phi (B'')\rfloor = \lfloor \Phi (B)\rfloor +2\). The buffer bins \(bb_{\ell -1}\) and \(bb_{\ell }\) are moved to the heap and thus \(h(B'')=h(B)+2=\lfloor \Phi (B)\rfloor + 2=\lfloor \Phi (B'')\rfloor \) (property (4)). Note that if \(r_{\ell -1} \le \{ \Phi (B') \}\), item \(i^*\) is not inserted into bin \(bb_{\ell -1}\) as \(r_{\ell -1} \ge r^* > \{ \Phi (B') \}\). Therefore, bin \(bb_j\) is left of \(bb_{\ell -1}\) and we can bound the fill ratio of the bin left of \(bb_{\ell -1}\) called \(r''_{\ell }\) by \(1 - 2 \frac{s(i^*)}{\epsilon }\). Using
, where s is the biggest size of an item appearing in \(bb_{\ell -1}\). If \(r_{\ell -1}\le \{ \Phi (B') \}\), all items are shifted out of \(bb_{\ell -1}\). As the number of queues decreases, we obtain the new potential \(\Phi (B'') = \Phi (B') - r_{\ell -1} + 1= \lfloor \Phi (B') \rfloor +\{\Phi (B')\}-r_{\ell -1} + 1 \ge \lfloor \Phi (B')\rfloor +1 \). Hence \(\lfloor \Phi (B'')\rfloor = \lfloor \Phi (B)\rfloor +2\). The buffer bins \(bb_{\ell -1}\) and \(bb_{\ell }\) are moved to the heap and thus \(h(B'')=h(B)+2=\lfloor \Phi (B)\rfloor + 2=\lfloor \Phi (B'')\rfloor \) (property (4)). Note that if \(r_{\ell -1} \le \{ \Phi (B') \}\), item \(i^*\) is not inserted into bin \(bb_{\ell -1}\) as \(r_{\ell -1} \ge r^* > \{ \Phi (B') \}\). Therefore, bin \(bb_j\) is left of \(bb_{\ell -1}\) and we can bound the fill ratio of the bin left of \(bb_{\ell -1}\) called \(r''_{\ell }\) by \(1 - 2 \frac{s(i^*)}{\epsilon }\). Using  , the heap equation can be fulfilled by shifting items of total size
, the heap equation can be fulfilled by shifting items of total size  at the end of the insert operation.
at the end of the insert operation.
Case 2 The potential \(\lfloor \Phi (B) \rfloor \) decreases during a delete operation, i.e., it holds \(\lfloor \Phi (B') \rfloor = \lfloor \Phi (B) \rfloor -1\) = \(\lfloor \Phi (B) - r^* \rfloor \), where \(r^*\) is the fill ratio being removed from a buffer bin \(bb_j\) due to the first shift of an item \(i^*\) that decreases the potential. According to Algorithm 7, buffer bin \(bb_{\ell }\) is being filled completely and a new buffer bin for \(Q_{\ell }\) is inserted from the heap. Hence the number of heap bins decreases and we have \(\lfloor \Phi (B') \rfloor = h(B) - 1 = h(B')\). As \(\lfloor \Phi (B)\rfloor -1=\Phi (B)-\{\Phi (B)\}-1=\lfloor \Phi (B)-r^*\rfloor \), it holds that \(\{\Phi (B)\}\le r^*\) and by the heap equation, the fill ratio of \(bb_\ell \) is \(r_\ell \ge r^*+s^{(\ell )}\), where \(s^{(\ell )}\) is the largest size of a small item in \(bb_{\ell }\). As above, \(r^*\) and \(s^{(\ell )}\) can be bounded by
 . The total size shifted from \(Q_{\ell +1}\) into bin \(bb_\ell \) can thus be bounded by
. The total size shifted from \(Q_{\ell +1}\) into bin \(bb_\ell \) can thus be bounded by 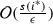 . Furthermore \(\{ \Phi (B') \} \ge 1 - r^*\) (as \(\Phi (B')=\Phi (B)-r^*\)) and \(r'_\ell = 0\), therefore we can bound \(|(1 - r'_{\ell }) - \{ \Phi (B') \}|\) by
. Furthermore \(\{ \Phi (B') \} \ge 1 - r^*\) (as \(\Phi (B')=\Phi (B)-r^*\)) and \(r'_\ell = 0\), therefore we can bound \(|(1 - r'_{\ell }) - \{ \Phi (B') \}|\) by  and the Heap Equation can be fulfilled by shifting a total size of at most
and the Heap Equation can be fulfilled by shifting a total size of at most  items. In the case that \(|Q_{\ell }|={1}/{\epsilon }\), a new queue \(Q_{\ell +1}\) is created which consists of a single buffer bin (inserted from the heap), which does not contain small items, i.e., \(h(B'') = h(B') -1 = h(B) -2\), where \(B''\) is the packing after the insertion of item \(i^*\). Let \(\Phi (B'')\) be the potential after the queue \(Q_{\ell +1}\) is created. Then \(\Phi (B'')= \sum _{i=1}^{\ell (B'')-1}r_i +\epsilon \Lambda -\ell (B'') = \sum _{i=1}^{\ell (B')-2}r_i+\epsilon \Lambda -\ell (B')-1=\Phi (B')-1\), as the buffer bin \(bb_{\ell }\) is now counted in the potential, but does not contain any small items and thus \(r''_\ell =0\). Hence \(\Phi (B'') = \Phi (B') -1 = h(B') -1 = h(B'')\).
items. In the case that \(|Q_{\ell }|={1}/{\epsilon }\), a new queue \(Q_{\ell +1}\) is created which consists of a single buffer bin (inserted from the heap), which does not contain small items, i.e., \(h(B'') = h(B') -1 = h(B) -2\), where \(B''\) is the packing after the insertion of item \(i^*\). Let \(\Phi (B'')\) be the potential after the queue \(Q_{\ell +1}\) is created. Then \(\Phi (B'')= \sum _{i=1}^{\ell (B'')-1}r_i +\epsilon \Lambda -\ell (B'') = \sum _{i=1}^{\ell (B')-2}r_i+\epsilon \Lambda -\ell (B')-1=\Phi (B')-1\), as the buffer bin \(bb_{\ell }\) is now counted in the potential, but does not contain any small items and thus \(r''_\ell =0\). Hence \(\Phi (B'') = \Phi (B') -1 = h(B') -1 = h(B'')\).
Analysis of Algorithm5
Algorithm 5 is executed as an item \(i^*\) is moved into a buffer bin \(bb_{j}\) such that \(bb_j\) is completely filled or it is executed if the buffer bin \(bb_j\) is emptied by moving the last item \(i^*\) out of the bin. As in the analysis of Algorithm 7, properties (1) and (2) are never violated by the algorithm as the items are only moved by shift operations. Property (3) is never violated because no queue (except for \(Q_{\ell }\)) exceeds \({2}/{\epsilon }\) or falls below \({1}/{\epsilon }\) by construction.
It remains to prove property (4) and a bound for the migration to fulfill the heap equation:
Case 1 An item \(i^*\) is moved into the buffer bin \(bb_j\) such that \(bb_j\) is filled completely for some \(j<\ell \). According to Algorithm 5, a bin is taken out of the heap and labeled as the new buffer bin \(bb'_j\) with fill ratio \(r'_j= 0\) of queue \(Q_j\), i.e., the number of heap bins decreases by 1. Let \(\Phi (B)\) be the potential before Algorithm 5 is executed and let \(\Phi (B')\) be the potential after Algorithm 5 is executed. The potential changes as follows:
$$\begin{aligned} \Phi (B)-\Phi (B')= (r_j - r'_j) - (\ell (B) - \ell (B')). \end{aligned}$$Since \(r'_j = 0\), the new potential is \(\Phi (B') = \Phi (B) - r_j \approx \Phi (B) -1\) (assuming \(\ell (B) = \ell (B')\), as the splitting of queues is handled later on).
If \(\lfloor \Phi (B') \rfloor = \lfloor \Phi (B) \rfloor - 1\), property (4) is fulfilled since the number of heap bins decreases by \(h(B') = h(B) - 1 = \lfloor \Phi (B) \rfloor -1 = \lfloor \Phi (B') \rfloor \). As \(r_j \ge \frac{c(bb_j)-s}{c(bb_j)}\), where s is the biggest size category appearing in \(bb_j\) and \(s^{(\ell )} \le 2 s(i^*)\), we obtain for the fractional part of the potential that \(\{ \Phi (B) \} - \{ \Phi (B') \} \le 2 \frac{s^{(\ell )}}{\epsilon } \le 4 \frac{s(i^*)}{\epsilon }\). Hence the Heap Equation can be fulfilled by shifting items of total size
 at the end of the insert operation as in the above proof.
at the end of the insert operation as in the above proof.In the case that \(\lfloor \Phi (B') \rfloor = \lfloor \Phi (B) \rfloor = \lfloor \Phi (B) - r_j \rfloor \), we know that the fractional part changes by \(\{ \Phi (B') \} = \{ \Phi (B) \} - r_j\). Since the bin \(bb_j\) is filled completely, we know that \(r_j \ge \frac{c(bb_j)-s^{(\ell )}}{c(bb_j)} \approx 1\) and hence \(\{ \Phi (B) \} \ge r_j \approx 1\) and \(\{ \Phi (B') \} \le 1-r_j \approx 0\). According to the Heap Equation, items have to be shifted out of \(r_{\ell }\) such that the fill ratio \(r_{\ell }\) changes from \(r_{\ell } \le 1-r_j\) to \(r_{\ell } \approx 1\). Therefore we know that as items are shifted out of \(bb_{\ell }\) to fulfill the Heap Equation, the buffer bin \(bb_{\ell }\) is being emptied and moved to the heap (see Algorithm 7). We obtain for the number of heap bins that \(h(B') = h(B) +1 -1 = h(B)\) and hence \(h(B') = \lfloor \Phi (B') \rfloor \) (property (4)). As \(\{ \Phi (B) \} \ge r_j \ge 1- 4 \frac{s(i^*)}{\epsilon }\), the Heap Equation implies that
 . The buffer bin \(bb_\ell \) is thus emptied by moving a total size of
. The buffer bin \(bb_\ell \) is thus emptied by moving a total size of  items out of the bin. Let \(bb'_\ell \) be the new buffer bin of \(Q_\ell \) that was left of \(bb_\ell \). The Heap Equation can be fulfilled by shifting at most
items out of the bin. Let \(bb'_\ell \) be the new buffer bin of \(Q_\ell \) that was left of \(bb_\ell \). The Heap Equation can be fulfilled by shifting at most  out of \(bb'_\ell \) since
out of \(bb'_\ell \) since  .
.In the case that \(|Q_j| > {2}/{\epsilon }\), the queue is split into two queues and an additional heap bin is inserted, i.e., \(h(B'') = h(B') -1\). As the potential changes by \(\Phi (B'') = \Phi (B') + (\ell (B') - \ell (B'')) = \Phi (B') - 1\), we obtain again that \(h(B'') = \lfloor \Phi (B'')\rfloor \).
Case 2 Algorithm 5 is executed if bin \(bb_j\) is emptied due to the removal of an item \(i^*\) as a result of a delete\((i,b_x,Q_j)\) call. According to Algorithm 5, the emptied bin is moved to the heap, i.e., the number of heap bins increases by 1. Depending on the length of \(Q_j\) and \(Q_{j+1}\), the bin right of \(bb_j\) or the bin left of \(bb_{j}\) is chosen as the new buffer bin \(bb'_j\). The potential changes by \(\Phi (B') = \Phi (B) + r'_j\), where \(r'_j\) is the fill ratio of \(bb'_j\) as in case 1.
If \(\lfloor \Phi (B') \rfloor = \lfloor \Phi (B) \rfloor + 1\) property (4) is fulfilled since the number of heap bins increases by \(h(B') = h(B) + 1\). As bin \(bb'_j\) is completely filled, the fill ratio is bounded by \(r'_j \ge 1-2 \frac{s^{(\ell )}}{\epsilon }\), where s is the largest size appearing in \(bb'_j\). Since the bin \(b_x\) has to be left of, we know that \(s^{(\ell )} \le 2s(i)\). We obtain for the fractional part of the potential that \(\{ \Phi (B) \} \ge \{ \Phi (B') \} - 2 \frac{s^{(\ell )}}{\epsilon } \le 4 \frac{s(i)}{\epsilon }\). Hence the Heap Equation can be fulfilled by shifting items of total size
 at the end of the delete operation.
at the end of the delete operation.In the case that \(\lfloor \Phi (B') \rfloor = \lfloor \Phi (B) \rfloor = \lfloor \Phi (B) + r'_j \rfloor \), we know that the fractional part changes similar to case 1 by \(\{ \Phi (B') \} = \{ \Phi (B) \} + r'_j\). Since the bin \(bb_j\) is filled completely, we know that \(r_j \ge \frac{c(bb_j)-s^{(\ell )}}{c(bb_j)} \approx 1\) and hence \(\{ \Phi (B') \} \ge r_j \approx 1\) and \(\{ \Phi (B) \} \le 1-r_j \approx 0\). According to the Heap Equation, items have to be shifted to \(bb_{\ell }\) such that the fill ratio \(r_{\ell }\) changes from \(r_{\ell } \approx 0\) to \(r_{\ell } \approx 1\). Therefore we know that as items are shifted into \(bb_{\ell }\) to fulfill the Heap Equation, \(bb_{\ell }\) is filled completely and a bin from the heap is labeled as the new buffer bin of \(Q_{\ell }\) (see Algorithm 7). We obtain for the number of heap bins that \(h(B') = h(B) -1 +1 = h(B)\) and hence \(h(B') = \Phi (B')\) (property (4)). The Heap Equation can be fulfilled similarly to case 1 by shifting items of total size
 .
.
\(\square \)
Using the above lemma, we can finally prove the following central theorem, which states that the migration of an insert/delete operation is bounded and that properties (1) to (4) are maintained.
Theorem 6
-
(i)
Let B be a packing which fulfills properties (1) to (4) and the Heap Equation. Applying insert\((i,b_x,Q_j)\) or delete\((i,b_x,Q_j)\) on a packing B yields an instance \(B'\) which also fulfills properties (1) to (4) and the Heap Equation.
-
(ii)
The migration factor of an insert/delete operation is bounded by
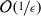 .
.
Proof
Suppose a small item i with size s(i) is inserted or deleted from queue \(Q_j\). The insert and delete operation basically consists of an application of Algorithm 4 and iterated use of steps (1) to (3) where Algorithms 5 and 7 are used and items in \(bb_\ell \) are moved to \(Q_{\ell +1}\) and vice versa. Let B be the packing before the insert/delete operation and let \(B'\) be the packing after the operation.
Proof for (i): Now suppose by induction that property (1) to (4) and the Heap Equation are fulfilled for packing B. We prove that property (4) and the Heap Equation maintain fulfilled after applying an insert or delete operation on B resulting in the new packing \(B'\). Properties (1) to (3) hold by conclusion of Lemma 9 and Lemma 11. Since the potential and the number of heap bins only change as a result of Algorithm 5 or Algorithm 7, property (4) maintains fulfilled also. By definition of step 4 in the insert operation, items are shifted from \(bb_\ell \) to \(Q_{\ell +1}\) until the Heap Equation is fulfilled. By definition of step 4 of the delete operation, the size of small items in \(bb_{\ell }\) is adjusted such that the Heap Equation is fulfilled. Hence the Heap Equation is always fulfilled after application of insert\((i,b_x,Q_j)\) or delete\((i,b_x,Q_j)\).
Proof for (ii): According to Lemma 9, the migration factor of the usual insert operation is bounded by  . By Lemma 11, the migration in Algorithm 5 and Algorithm 7 is also bounded by
. By Lemma 11, the migration in Algorithm 5 and Algorithm 7 is also bounded by  . It remains to bound the migration for step 4 in the insert/delete operation. Therefore we have to analyze the total size of items to be shifted out or into \(bb_\ell \) in order to fulfill the Heap Equation.
. It remains to bound the migration for step 4 in the insert/delete operation. Therefore we have to analyze the total size of items to be shifted out or into \(bb_\ell \) in order to fulfill the Heap Equation.
Since the size of all items \(i_1, \ldots , i_k\) that are inserted into \(bb_j\) is bounded by 7s(i) (see Lemma 9) and the capacity of \(bb_j\) is at least \({\epsilon }/{14}\), the potential \(\Phi (B)\) changes by at most  . By Lemma 11 the size of items that needs to be shifted out or into \(bb_\ell \) as a result of Algorithm 5 or 7 is also bounded by
. By Lemma 11 the size of items that needs to be shifted out or into \(bb_\ell \) as a result of Algorithm 5 or 7 is also bounded by  . Therefore the size of all items that need to be shifted out or into \(bb_\ell \) in step (4) of the insert/delete operation is bounded by
. Therefore the size of all items that need to be shifted out or into \(bb_\ell \) in step (4) of the insert/delete operation is bounded by  .
.
Shifting a total size of  to \(Q_{\ell +1}\) or vice versa leads to a migration factor of
to \(Q_{\ell +1}\) or vice versa leads to a migration factor of  (Lemma 9). Fortunately, we can modify the structure of queues \(Q_{\ell +1}\) and \(Q_{\ell +2}\) such that we obtain a smaller migration factor. Assuming that \(Q_{\ell +1}\) consists of a single buffer bin, i.e., \(|Q_{\ell +1}| = 1\), items can directly be shifted from \(bb_\ell \) to \(bb_{\ell +1}\) and therefore we obtain a migration factor of
(Lemma 9). Fortunately, we can modify the structure of queues \(Q_{\ell +1}\) and \(Q_{\ell +2}\) such that we obtain a smaller migration factor. Assuming that \(Q_{\ell +1}\) consists of a single buffer bin, i.e., \(|Q_{\ell +1}| = 1\), items can directly be shifted from \(bb_\ell \) to \(bb_{\ell +1}\) and therefore we obtain a migration factor of  . A structure with \(|Q_{\ell +1}| = 1\) and \(1 \le |Q_{\ell +2}| \le {2}/{\epsilon }\) [see property (3)] can be maintained by changing Algorithm 5 in the following way:
. A structure with \(|Q_{\ell +1}| = 1\) and \(1 \le |Q_{\ell +2}| \le {2}/{\epsilon }\) [see property (3)] can be maintained by changing Algorithm 5 in the following way:
If \(bb_{\ell +1}\) is filled completely, move the filled bin to \(Q_{\ell +2}\).
If \(|Q_{\ell +2}| > {2}/{\epsilon }\), split \(Q_{\ell +2}\) into two queues.
If \(bb_{\ell +1}\) is being emptied, remove the bin and label the first bin of \(Q_{\ell +2}\) as \(bb_{\ell +1}\).
If \(|Q_{\ell +2}| = 0\), remove \(Q_{\ell +2}\).
\(\square \)
6 Handling the general setting
In the previous section, we described how to handle small items in a mixed setting. It remains to describe how large items are handled in this mixed setting. Algorithm 3 describes how to handle large items only. However, in a mixed setting, there are also small items and we have to make sure that properties (1) to (4) and the Heap Equation maintain fulfilled as a large item is inserted or deleted. Algorithm 3 changes the configuration of at most  bins (Theorem 5). Therefore, the size of large items in a bin b (\(= 1-c(b)\)) changes, as Algorithm 3 may increase or decrease the capacity of a bin. Changing the capacity of a bin may violate properties (2) to (4) and the Heap Equation. We describe an algorithm to change the packing of small items such that all properties and the Heap Equation are fulfilled again after Algorithm 3 was applied.
bins (Theorem 5). Therefore, the size of large items in a bin b (\(= 1-c(b)\)) changes, as Algorithm 3 may increase or decrease the capacity of a bin. Changing the capacity of a bin may violate properties (2) to (4) and the Heap Equation. We describe an algorithm to change the packing of small items such that all properties and the Heap Equation are fulfilled again after Algorithm 3 was applied.
The following algorithm describes how the length of a queue \(Q_{j}\) is adjusted if the length \(|Q_{j}|\) falls below \({1}/{\epsilon }\):
Algorithm 8
(Adjust the queue length)
Remove all small item \(I_S\) from \(bb_{j}\) and add \(bb_j\) to the heap.
Merge \(Q_j\) with \(Q_{j+1}\). The merged queue is called \(Q_j\).
If \(|Q_{j}|> {2}/{\epsilon }\) split queue \(Q_j\) by adding a heap bin in the middle.
Insert items \(I_S\) using Algorithm 6.
The following algorithm describes how the number of heap bins can be adjusted.
Algorithm 9
(Adjust number of heap bins)
Decreasing the number of heap bins by 1.
Shift small items from \(Q_{\ell +1}\) to \(bb_{\ell }\) until \(bb_{\ell }\) is filled completely
Label a heap bin as the new buffer bin of \(Q_{\ell }\)
Increasing the number of heap bins by 1.
Shift all small items from \(bb_{\ell }\) to \(Q_{\ell +1}\)
Label \(bb_{\ell }\) as a heap bin
Label the bin left of \(bb_{\ell }\) as new buffer bin of \(Q_{\ell }\)
Note that the Heap Equation can be fulfilled in the same way, by shifting items from \(bb_{\ell }\) to \(Q_{\ell +1}\) or vice versa.
Using these algorithms, we obtain our final algorithm for the fully dynamic \(bin packing \) problem.
Algorithm 10
(AFPTAS for the mixed setting)
If i is large do
If i is small use Algorithm 6
Combining all the results from the current and the previous section, we finally prove the central result that there is fully dynamic AFPTAS for the \(bin packing \) problem with polynomial migration.
Theorem 7
Algorithm 10 is a fully dynamic AFPTAS for the \(bin packing \) problem, that achieves a migration factor of at most  by repacking items from at most
by repacking items from at most  bins. It has running time
bins. It has running time  .
.
Proof
Approximation guarantee: By definition of the algorithm, it generates at every timestep t a packing \(B_t\) of instance I(t) such that properties (1) to (4) are fulfilled. According to Lemma 10, at most  bins are used where \(\Lambda \) is the number of bins containing large items. Since we use Algorithm 3 to pack the large items, Theorem 5 implies that
bins are used where \(\Lambda \) is the number of bins containing large items. Since we use Algorithm 3 to pack the large items, Theorem 5 implies that  . Hence the number of used bins can be bounded in any case by
. Hence the number of used bins can be bounded in any case by  .
.
Migration factor: Note that the Algorithm uses Algorithm 6 or Algorithm 3 to insert and delete small or large items. The migration factor for Algorithm 6 is bounded by  due to Theorem 6 while the migration factor for Algorithm 3 is bounded by
due to Theorem 6 while the migration factor for Algorithm 3 is bounded by  due to Theorem 5.
due to Theorem 5.
It remains to bound the migration needed to adjust the heap bins, the length of a queue falling below \({1}/{\epsilon }\) and the Heap Equation if a large item arrives and Algorithm 3 is applied.
Suppose the number of heap bins has to be adjusted by 1. In this case Algorithm 9 shifts items from \(Q_{\ell +1}\) to \(bb_{\ell }\) or vice versa until \(bb_{\ell }\) is either filled or emptied. Hence, the size of moved items is bounded by 1. Since the size of the arriving or departing item is \(\ge {\epsilon }/{14}\) the migration factor is bounded by  . In the same way, a migration of at most
. In the same way, a migration of at most  is used to fulfill the Heap Equation which implies that the migration in step 5 is bounded by
is used to fulfill the Heap Equation which implies that the migration in step 5 is bounded by  .
.
If \(|Q_j|\) falls below \({1}/{\epsilon }\), the two queues \(Q_j\) and \(Q_{j+1}\) are merged by emptying \(bb_j\). The removed items are inserted by Algorithm 6. As their total size is bounded by 1 and the algorithm has a migration factor of  , the size of the moved items is bounded by
, the size of the moved items is bounded by  . The migration needed to merge two queues can thus be bounded by
. The migration needed to merge two queues can thus be bounded by  .
.
Note that the proof of Theorem 5 implies that at most  bins are changed by Algorithm 3. The total size of the items \(I_S\) which are removed in step 2 is thus bounded by \(\gamma \). Similarly, the length of at most \(\gamma \) queues can fall below \({1}/{\epsilon }\). The migration of step 3 is thus bounded by \(\gamma \cdot {1}/{\epsilon ^2}\). As at most \(\gamma \) buffer bins are changed, the change of the potential (and thus the number of heap bins) is also bounded by \(\gamma \) and the migration in step 4 can be bounded by \(\gamma \cdot {1}/{\epsilon }\). The migration in step 6 is bounded by \(s(I_S) \cdot {1}/{\epsilon }\le \gamma \cdot {1}/{\epsilon }\) as Algorithm 6 has migration factor \({1}/{\epsilon }\). The total migration of the adjustments is thus bounded by
bins are changed by Algorithm 3. The total size of the items \(I_S\) which are removed in step 2 is thus bounded by \(\gamma \). Similarly, the length of at most \(\gamma \) queues can fall below \({1}/{\epsilon }\). The migration of step 3 is thus bounded by \(\gamma \cdot {1}/{\epsilon ^2}\). As at most \(\gamma \) buffer bins are changed, the change of the potential (and thus the number of heap bins) is also bounded by \(\gamma \) and the migration in step 4 can be bounded by \(\gamma \cdot {1}/{\epsilon }\). The migration in step 6 is bounded by \(s(I_S) \cdot {1}/{\epsilon }\le \gamma \cdot {1}/{\epsilon }\) as Algorithm 6 has migration factor \({1}/{\epsilon }\). The total migration of the adjustments is thus bounded by  .
.
Running time: The handling of small items can be performed in linear time while the handling of large items requires  (see Theorem 5). The total running time of the algorithm is thus
(see Theorem 5). The total running time of the algorithm is thus  . \(\square \)
. \(\square \)
References
Balogh, J., Békési, J., Dósa, G., Epstein, L., Levin, A.: A new and improved algorithm for online bin packing. CoRR arXiv:1707.01728 (2017)
Balogh, J., Békési, J., Dósa, G., Sgall, J., van Stee, R.: The optimal absolute ratio for online bin packing. In: SODA, pp. 1425–1438. SIAM (2015)
Balogh, J., Békési, J., Galambos, G.: New lower bounds for certain classes of bin packing algorithms. In: Workshop on Approximation and Online Algorithms (WAOA), LNCS, vol. 6534, pp. 25–36 (2010)
Balogh, J., Békési, J., Galambos, G., Reinelt, G.: Lower bound for the online bin packing problem with restricted repacking. SIAM J. Comput. 38(1), 398–410 (2008)
Beling, P., Megiddo, N.: Using fast matrix multiplication to find basic solutions. Theor. Comput. Sci. 205(1–2), 307–316 (1998)
Beloglazov, A., Buyya, R.: Energy efficient allocation of virtual machines in cloud data centers. In: 10th IEEE/ACM International Conference on Cluster, Cloud and Grid Computing, CCGrid 2010, pp. 577–578 (2010)
Berndt, S., Jansen, K., Klein, K.: Fully dynamic bin packing revisited. In: APPROX-RANDOM, LIPIcs, vol. 40, pp. 135–151. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2015)
Bobroff, N., Kochut, A., Beaty, K.: Dynamic placement of virtual machines for managing SLA violations. In: 10th IFIP/IEEE International Symposium on Integrated Network Management, IM 2007, pp. 119–128 (2007)
Brown, D.: A lower bound for on-line one-dimensional bin packing algorithms. Technical Report R-864, Coordinated Science Laboratory University of Illinois Urbana (1979)
Chan, J., Lam, T., Wong, P.: Dynamic bin packing of unit fractions items. Theor. Comput. Sci. 409(3), 521–529 (2008)
Chan, J., Wong, P., Yung, F.: On dynamic bin packing: an improved lower bound and resource augmentation analysis. Algorithmica 53(2), 172–206 (2009)
Christensen, H.I., Khan, A., Pokutta, S., Tetali, P.: Approximation and online algorithms for multidimensional bin packing: a survey. Comput. Sci. Rev. 24, 63–79 (2017)
Coffman, E., Garey, M., Johnson, D.: Dynamic bin packing. SIAM J. Comput. 12(2), 227–258 (1983)
Daudjee, K., Kamali, S., López-Ortiz, A.: On the online fault-tolerant server consolidation problem. In: 26th ACM Symposium on Parallelism in Algorithms and Architectures, SPAA ’14, pp. 12–21 (2014)
Eisemann, K.: The trim problem. Manag. Sci. 3(3), 279–284 (1957)
Epstein, L., Levin, A.: A robust APTAS for the classical bin packing problem. Math. Program. 119(1), 33–49 (2009)
Epstein, L., Levin, A.: Robust approximation schemes for cube packing. SIAM J. Optim. 23(2), 1310–1343 (2013)
Feldkord, B., Feldotto, M., Riechers, S.: A tight approximation for fully dynamic bin packing without bundling. In: ICALP (2018)
Gambosi, G., Postiglione, A., Talamo, M.: Algorithms for the relaxed online bin-packing model. J. Comput. 30(5), 1532–1551 (2000)
Gupta, A., Guruganesh, G., Kumar, A., Wajc, D.: Fully-dynamic bin packing with limited repacking. In: ICALP (2018)
Heydrich, S., van Stee, R.: Beating the harmonic lower bound for online bin packing. In: ICALP, LIPIcs, vol. 55, pp. 41:1–41:14. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2016)
Ivković, Z., Lloyd, E.: Partially dynamic bin packing can be solved within \(1 + \epsilon \) in (amortized) polylogarithmic time. Inf. Process. Lett. 63(1), 45–50 (1997)
Ivković, Z., Lloyd, E.: Fully dynamic algorithms for bin packing: being (mostly) myopic helps. SIAM J. Comput. 28(2), 574–611 (1998)
Ivković, Z., Lloyd, E.: Fully dynamic bin packing. In: Fundamental Problems in Computing, pp. 407–434. Springer (2009)
Jansen, K., Klein, K.: A robust AFPTAS for online bin packing with polynomial migration. In: International Colloquium on Automata, Languages, and Programming (ICALP), pp. 589–600 (2013)
Jansen, K., Klein, K., Kosche, M., Ladewig, L.: Online strip packing with polynomial migration. In: APPROX-RANDOM, LIPIcs, vol. 81, pp. 13:1–13:18. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2017)
Jansen, K., Kraft, S.E.J.: A faster FPTAS for the unbounded knapsack problem. In: IWOCA, Lecture Notes in Computer Science, vol. 9538, pp. 274–286. Springer (2015)
Johnson, D.: Fast algorithms for bin packing. J. Comput. Syst. Sci. 8(3), 272–314 (1974)
Johnson, D., Demers, A., Ullman, J., Garey, M., Graham, R.: Worst-case performance bounds for simple one-dimensional packing algorithms. SIAM J. Comput. 3(4), 299–325 (1974)
Jung, G., Joshi, K., Hiltunen, M., Schlichting, R., Pu, C.: Generating adaptation policies for multi-tier applications in consolidated server environments. In: 2008 International Conference on Autonomic Computing, ICAC 2008, 2–6 June 2008, Chicago, Illinois, USA, pp. 23–32 (2008)
Jung, G., Joshi, K., Hiltunen, M., Schlichting, R., Pu, C.: A cost-sensitive adaptation engine for server consolidation of multitier applications. In: Proceedings of 10th International Middleware Conference on Middleware 2009, ACM/IFIP/USENIX, pp. 163–183 (2009)
Karmarkar, N., Karp, R.: An efficient approximation scheme for the one-dimensional bin-packing problem. In: 23rd Annual Symposium on Foundations of Computer Science (FOCS), pp. 312–320. IEEE Computer Society (1982)
Lee, C., Lee, D.: A simple on-line bin-packing algorithm. J. ACM (JACM) 32(3), 562–572 (1985)
Li, Y., Tang, X., Cai, W.: On dynamic bin packing for resource allocation in the cloud. In: 26th ACM Symposium on Parallelism in Algorithms and Architectures, SPAA ’14, pp. 2–11 (2014)
Liang, F.: A lower bound for on-line bin packing. Inf. Process. Lett. 10(2), 76–79 (1980)
Park, J., Savagaonkar, U.R., Chong, E., Siegel, H., Jones, S.: Efficient resource allocation for QoS channels in MF-TDMA satellite systems. In: Proceedings of Conference on 21st Century Military Communications, MILCOM 2000, vol. 2, pp. 645–649. IEEE (2000)
Sanders, P., Sivadasan, N., Skutella, M.: Online scheduling with bounded migration. Math. Oper. Res. 34(2), 481–498 (2009)
Seiden, S.: On the online bin packing problem. J. ACM 49(5), 640–671 (2002)
Skutella, M., Verschae, J.: Robust polynomial-time approximation schemes for parallel machine scheduling with job arrivals and departures. Math. Oper. Res. 41(3), 991–1021 (2016)
Srikantaiah, S., Kansal, A., Zhao, F.: Energy aware consolidation for cloud computing. In: Proceedings of the 2008 Conference on Power Aware Computing and Systems, HotPower’08, p. 10 (2008)
Stolyar, A.: An infinite server system with general packing constraints. Oper. Res. 61(5), 1200–1217 (2013)
Stolyar, A., Zhong, Y.: A large-scale service system with packing constraints: minimizing the number of occupied servers. In: Proceedings of the ACM SIGMETRICS/International Conference on Measurement and Modeling of Computer Systems, pp. 41–52. ACM (2013)
Ullman, J.: The Performance of a Memory Allocation Algorithm. Technical Report. Princeton University (1971)
de la Fernandez Vega, W., Lueker, G.: Bin packing can be solved within \(1+ \epsilon \) in linear time. Combinatorica 1(4), 349–355 (1981)
Verma, A., Ahuja, P., Neogi, A.: pMapper: power and migration cost aware application placement in virtualized systems. In: Proceedings of the 9th International Middleware Conference on Middleware 2008, ACM/IFIP/USENIX, pp. 243–264 (2008)
Vliet, A.: An improved lower bound for on-line bin packing algorithms. Inf. Process. Lett. 43(5), 277–284 (1992)
Yao, A.: New algorithms for bin packing. J. ACM (JACM) 27(2), 207–227 (1980)
Acknowledgements
We would like to thank Till Tantau for his valuable comments and suggestions to improve the presentation of the paper. We also thank the anonymous reviewers for their detailed and valuable feedback.
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported by DFG Project, Entwicklung und Analyse von effizienten polynomiellen Approximationsschemata für Scheduling- und verwandte Optimierungsprobleme, Ja 612/14-1 and Ja 612/14-2.
A preliminary version of this work has appeared at APPROX/RANDOM 2015 as [7].
Rights and permissions
About this article
Cite this article
Berndt, S., Jansen, K. & Klein, KM. Fully dynamic bin packing revisited. Math. Program. 179, 109–155 (2020). https://doi.org/10.1007/s10107-018-1325-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-018-1325-x






 and
and 
 we have
we have  and
and  .
. we have
we have  and furthermore
and furthermore  .
.
 and
and  , we construct the new rounding
, we construct the new rounding 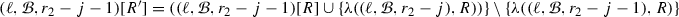 for
for 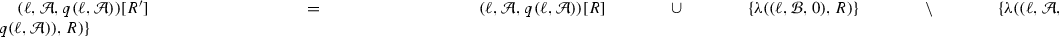 ,
, for
for  , and
, and .
.
 is reached. Formally, set
is reached. Formally, set  . See Fig.
. See Fig.  is too large now, we have to create a new rounding group
is too large now, we have to create a new rounding group  . Additionally, we shift the largest item in
. Additionally, we shift the largest item in  to this new group
to this new group  . The final rounding
. The final rounding  , i.e. we increment the number of each rounding group by 1. Note that the largest item in
, i.e. we increment the number of each rounding group by 1. Note that the largest item in  is already packed into a bin of its own due to the
is already packed into a bin of its own due to the 
 to
to  , we will call
, we will call  to receive the rounding
to receive the rounding  has now the same size as the groups in
has now the same size as the groups in  . We transfer
. We transfer  to block
to block  . Hence, we define the final rounding
. Hence, we define the final rounding  for
for  and
and  as well as
as well as  for
for  . The resulting packing
. The resulting packing  to
to  , we will call
, we will call  to receive the rounding
to receive the rounding  has now the same size as the groups in
has now the same size as the groups in  . We transfer
. We transfer  to block
to block  . Similar to
. Similar to  for
for  and
and  as well as
as well as  . The resulting packing
. The resulting packing 



 times the size of the item which triggered the first
times the size of the item which triggered the first  times the size of the item which triggered the first
times the size of the item which triggered the first 
 for all
for all 

 , where
, where  . Hence the Heap Equation can be fulfilled by shifting items of total size
. Hence the Heap Equation can be fulfilled by shifting items of total size  at the end of the
at the end of the  , where s is the biggest size of an item appearing in
, where s is the biggest size of an item appearing in  , the heap equation can be fulfilled by shifting items of total size
, the heap equation can be fulfilled by shifting items of total size  at the end of the
at the end of the  . The total size shifted from
. The total size shifted from 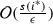 . Furthermore
. Furthermore  and the Heap Equation can be fulfilled by shifting a total size of at most
and the Heap Equation can be fulfilled by shifting a total size of at most  items. In the case that
items. In the case that  at the end of the
at the end of the  . The buffer bin
. The buffer bin  items out of the bin. Let
items out of the bin. Let  out of
out of  .
. at the end of the
at the end of the  .
.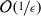 .
.