Friendly bin packing instances without Integer Round-up Property

Abstract

It is well known that the gap between the optimal values of bin packing and fractional bin packing, if the latter is rounded up to the closest integer, is almost always null. Known counterexamples to this for integer input values involve fairly large numbers. Specifically, the first one was derived in 1986 and involved a bin capacity of the order of a billion. Later in 1998 a counterexample with a bin capacity of the order of a million was found. In this paper we show a large number of counterexamples with bin capacity of the order of a hundred, showing that the gap may be positive even for numbers which arise in customary applications. The associated instances are constructed starting from the Petersen graph and using the fact that it is fractionally, but not integrally, 3-edge colorable.

1 Introduction

Given $n$ items each having a non-negative integer weight $w_j$ ($j=1, \dots , n$) and sufficiently many bins of identical integer capacity $C$, the Bin Packing Problem (BPP) asks for the minimum number of bins that can accommodate all the items. The BPP is strongly $\mathcal {NP}$-hard and computationally challenging even for moderate-size instances.

It is one of the most important problems in combinatorial optimization, because models a large variety of real-world applications. The associated literature is enormous. We refer the interested reader to the following surveys: [1] (approximation algorithms), [2] (linear programming models) and [3] (lower bounds).

1.1 Set partitioning formulation

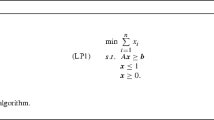
Effective exact algorithms for the BPP are usually based on the classical formulation by [4, 5]. This method characterizes the BPP by using the set of all feasible combinations of items inside a bin. Since this set is of exponential size, column generation techniques are generally needed to solve the associated linear programming relaxation, which is known as the Fractional BPP (FBPP). Then, branch-and-price is generally used to achieve an integer solution.

We define a pattern $P$ as a subset of items that fits into a bin. We describe the pattern by a column $(a_{1P}, \dots , a_{jP}$, $\dots , a_{n P})^T\in \{0,1\}^n$, where $a_{jP}$ takes value 1 if item $j$ is in pattern $P$, 0 otherwise. Let $\mathcal{{P}}$ be the family of all valid patterns, i.e., the set of patterns $P$ for which

$$\begin{aligned} \sum _{j=1}^n w_j a_{jP} \le C. \end{aligned}$$

(1)

Let also $z_P$ be a binary variable taking the value 1 if pattern $P$ is used, 0 otherwise ($P \in \mathcal{{P}}$). The BPP can be modeled as the following Set Partitioning Problem:

$$\begin{aligned}&\min \sum _{P\in \mathcal{{P}}} z_P \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{P \in \mathcal{{P}}} a_{jP} z_{P} = 1, \quad j = 1, \dots , n, \end{aligned}$$

(3)

$$\begin{aligned}&z_{P} \in \{0,1\}, \quad P \in \mathcal{{P}}, \quad \end{aligned}$$

(4)

where constraints (3) impose that each item $j$ is packed in one bin. The FBPP is then obtained by replacing (4) with $0\le z_{P} \le 1,\ P \in \mathcal{{P}}$.

It is well known that the FBPP can be solved by generating columns by solving a Knapsack Problem. Indeed, the FBPP is the customary example of column generation given in textbooks. Since the FBPP can be handled effectively despite the potentially huge number of variables, model (2)–(4) is the mathematical programming formulation of the BPP that is used in practice. It has two huge advantages over the descriptive formulation with binary variables indicating if a bin is used and if an item is packed in a bin. First of all, the descriptive formulation is widely symmetric, whereas in the formulation (2)–(4) there is no symmetry at all. Second, while the optimal value of the linear relaxation of the descriptive formulation is the trivial lower bound $\sum _{j=1}^n w_j / C$, the optimal FBPP value is a very strong lower bound, as discussed in the next section.

A variant of the FBPP studied in the literature, see, e.g., [6, 7], is the one in which patterns satisfy the capacity constraint but may contain an arbitrarily large number of copies of each item. According to [8], we call this variant the Unbounded FBPP. The optimal value of the Unbounded FBPP is a worse lower bound than the one of the FBPP, see [8], and the only slight practical advantage for using this variant is that generating columns, by the solution of Unbounded Knapsack Problems, is a bit simpler.

1.2 The Integer Round-up Property and counterexamples

Anybody doing computational experiments with the formulation (2)–(4) would notice that, basically in all cases, the optimal FBPP value, rounded up to the closest integer, yields the optimal BPP value. The latter property is called the Integer Round-up Property.

The fact that the Integer Round-up Property cannot hold in general follows if one assumes $\mathcal {P}\not =\mathcal {NP}$, given that the BPP is strongly $\mathcal {NP}$-hard and the FBPP solvable in pseudo-polynomial time by the ellipsoid algorithm (this fact is mentioned explicitly, e.g., in [8]).

Nevertheless, the first explicit BPP instance without the Integer Round-up Property was presented by Marcotte [9], and had $C=$ 3,397,386,255 (see Table 1). Such a large number was derived by making use of a strong $\mathcal {NP}$-completeness reduction of $4$-Partition, in which the numbers are defined in a complicated way. In [9], it is stated that “in any counterexample to the Integer Round-up Property, the numbers are likely to be of the same order of magnitude”. This is in fact not the case, as shown already by Chan et al. [10], where a counterexample with $C =$ 1,111,139 is given. Moreover, while for the instance given in [9] the optimal BPP solution value is 6 and the optimal FBPP solution value is 5 (even before rounding), the instance given in Chan et al. [10] is best possible in terms of relative integrality gap as these values are respectively 4 and 3 (and it is easy to see that, in case the optimal FBPP value is at most 2 the same holds for the optimal BPP value, see, e.g., [8]). Specifically, the instance in Chan et al. [10] is used within the proof of the main result in that paper, namely that the worst-case absolute ratio between the optimal BPP and FBPP value is 4/3.

Table 1 BPP instances for which the Integer Round-up Property does not hold

Note that for the Unbounded FBPP it is much easier to construct examples without the Integer Round-up Property, e.g., for the instance with $C=132$, $n=11$ and $(w_j)=(44, 44, 33, 33, 33, 12, 12, 12, 12, 12, 12)$, mentioned in [11], the optimal BPP solution value is 3 and the optimal Unbounded FBPP solution value (after rounding) is 2.

We conclude this short review by mentioning the main open problem related with the Integer Round-up Property, namely the so-called Modified Integer Round-up Conjecture, stating that the maximum difference between the optimal BPP and the optimal rounded-up FBPP solution values is 1. This is open also if the FBPP is replaced by its Unbounded version. For the state-of the-art on this conjecture see [12] and the references therein.

1.3 Edge coloring: a well-understood counterpart

A natural counterpart of the BPP is the Edge Coloring Problem (ECP). Consider an undirected graph $G=(V,E)$, and for each vertex $i\in V$ let $\delta (i)$ denote the set of edges incident to $i$. $G$ is called $k$ -regular if $|\delta (i)|=k$ for all $i\in V$. Recall that $M\subseteq E$ is called a matching if $|M\cap \delta (j)|\le 1$ for all $j\in V$. Given a weight $w_j$ associated with each edge $j\in E$ and a subset of edges $M\subseteq E$, we let $w(M):=\sum _{j\in M} w_j$.

The ECP calls for a partition of the edge set $E$ into the minimum number of matchings. Its Fractional ECP (FECP) counterpart can be formulated as the LP relaxation of the Set Partitioning Problem (2)–(4), where now $\mathcal{{P}}$ denotes the collection of all the matchings of $G$ and, for $P\in \mathcal{{P}}$ and $j\in E$, $a_{jP}=1$ if edge $j$ is in matching $P$.

For simple graphs, without parallel edges, a lot is known about the relation between ECP and FECP. It is elementary to see that the optimal FECP value is at least the maximum degree $\max _{i\in V} |\delta (i)|$. Then, Vizing’s theorem, which states that the optimal ECP value is at most the maximum degree plus 1, implies that the difference between the ECP and FECP optimal values is at most one. The smallest example (in all respects: ECP optimal value, number of vertices, number of edges) for which this happens is the famous Petersen Graph, which is 3-regular. In other words, the Petersen Graph is the smallest counterexample to the Integer Round-up Property for the ECP.

2 Much simpler counterexamples from edge coloring

Instances with the numbers as in the counterexamples in Marcotte [9] and Chan et al. [10] appear to be unlikely to arise in practice. In this paper we show that the Integer Round-up Property does not hold for instances involving much smaller numbers. Indeed, the smallest instance that we could find, in terms of capacity, has $C=100$, 24 items and weights ranging form 22 to 61. The smallest instance in terms of number of items has 13 items, $C=146$ and weights ranging form 5 to 65. In addition, we found several thousands such instances, associated with the solution of suitable Integer Linear Programs. We call these instances friendly because of their very small size.

Table 1 gives a brief overview of the state of the art before and after our work. For most of our instances, the optimal BPP and FBPP solution values are, respectively, 4 and 3. The key idea to construct these instances is to start from ECP counterexamples. Their structure allows one to easily check that the Integer Round-up Property does not hold.

2.1 The key idea

Proposition 1

Consider a $k$-regular graph $G=(V,E)$ for which the optimal ECP and FECP solution values are respectively $k+1$ and $k$. Suppose there exist a positive integer $C$ and a positive integer weight $w_j$ for each edge $j\in E$ such that, for each $M\subseteq E$, $w(M)=C$ if and only if $M$ is a perfect matching. Then, the BPP instance with capacity $C$ and one item of weight $w_j$ for each edge $j\in E$ does not have the Integer Round-up Property.

Proof

All the positive variables in the optimal FECP solution $z^*$ must correspond to perfect matchings, i.e., each must correspond to a subset of $|V|/2$ edges, since: (i) $\sum _{j=1}^n a_{jP}\le |V|/2$ holds for all ${P \in \mathcal{{P}}}$; (ii) the FECP constraints imply $\sum _{j=1}^n \sum _{P \in \mathcal{{P}}} a_{jP} z^*_{P}=\sum _{P \in \mathcal{{P}}} (\sum _{j=1}^n a_{jP}) z^*_{P}= |E| = k|V|/2$; and (iii) the objective function is such that $\sum _{P \in \mathcal{{P}}} z^*_{P} = k$, which is possible only if $\sum _{j=1}^n a_{jP} = |V|/2$ for all $z^*_{P}>0$. (Observe that this also implies that $|V|$ is even for the graphs we consider.) The FECP solution also defines an optimal FBPP solution for the instance defined in the statement, since the sum of the item weights is exactly $kC$, implying a lower bound of $k$ on the FBPP solution.

If there was an optimal BPP solution of value $k$, all associated bins would be exactly filled to their capacity. By the property in the statement, the set of items in each bin would then correspond to a perfect matching $M$ of $G$, i.e., $E$ could be partitioned into perfect matchings, i.e., the optimal ECP solution would have value $k$, which is not the case by the choice of $G$. This implies that the optimal BPP solution has value at least $k+1$, i.e., the instance defined does not have the Integer Round-up Property.

The simplest example of weights that meet the requirement in Proposition 1 is probably the following.

Proposition 2

Consider a $k$-regular graph $G=(V,E)$ and number its vertices from 0 to $|V|-1$ in an arbitrary way. Let $C:=\sum _{i=0}^{|V|-1} k^i$, and, for each edge $(i,h)\in E$, let $w_{(i,h)}:=k^i+k^h$. Then, for each $M\subseteq E$, $w(M)=C$ if and only if $M$ is a perfect matching.

Proof

The if part is implied by the definition of $C$. In order to show the only if one, note that $C$ is equal to $1, \ldots , 1$ (with $|V|$ digits) in base $k$. Given $M\subseteq E$ with $w(M)=C$, we prove by induction on $i$ that $M$ contains exactly one edge incident with each vertex $i\in V$. The basis of the induction, $i=0$, follows from the fact that the least significant digit of $w(M)$ (in base $k$) is equal to $|M\cap \delta (0)|$ modulo $k$, and can be 1 only if $|M\cap \delta (0)|=1$, since $|\delta (0)|=k$. The main induction step is proved similarly, considering that, at iteration $i$, $M$ contains exactly one edge incident on vertices $0, \ldots , i-1$, and the $i-$th digit of $w(M)$ can be 1 only if $|M\cap \delta (i)|=1$.

The idea in Proposition 1 guides our computational search of counterexamples with small $C$, so eventually it is the one leading to our best result in terms of minimum number of items. However, if the aim is to construct on the paper such counterexamples, we can relax the fairly tight requirement that $w(M)=C$ only if $M$ is a perfect matching, and assign weights as in Proposition 2 with the powers of $k$ replaced by powers of $2$.

Proposition 3

Consider a $k$-regular graph $G=(V,E)$ for which the optimal ECP and FECP solution values are respectively $k+1$ and $k$, and number its vertices from $0$ to $|V|-1$ in an arbitrary way. Let $C:=\sum _{i=0}^{|V|-1} 2^i$, and, for each edge $(i,h)\in E$, let $w_{(i,h)}:=2^i+2^h$. Then, the BPP instance with capacity $C$ and one item $j$ of weight $w_j=w_{(i,h)}$ for each edge ${(i,h)}\in E$ does not have the Integer Round-up Property.

Proof

With respect to the proof of Proposition 1, we have to exclude the existence of a BPP solution of value $k$ by a different argument. If such a solution existed, there would be a partition of $E$ into $k$ edge subsets $M_1, \ldots , M_k$ such that $w(M_i)=C$ for $i=1, \ldots , k$. Reasoning as in the proof of Proposition 2, each of these subsets would contain at least one edge incident with $0$, which implies that each of them would contain exactly one such edge, since $|\delta (0)|=k$. Again, induction on $i$ shows that each of $M_1, \ldots , M_k$ would be a perfect matching, and the optimal ECP solution would have value $k$, a contradiction.

Since our aim is to find instances with small values of $C$, we can improve upon Proposition 3 as follows.

Proposition 4

Consider a $k$-regular graph $G=(V,E)$ for which the optimal ECP and FECP solution values are respectively $k+1$ and $k$, and number its vertices from $0$ to $|V|-1$ in an arbitrary way. Assign weight $\rho (i):=2^{i-1}$ to each vertex $i$ in $1, \dots , |V|-1$, and set $\rho (0)=0$. Let $C:=\sum _{i=1}^{|V|-1} 2^{i-1}$, and, for each edge $(i,h)\in E$, let $w_{(i,h)}:=\rho (i)+\rho (h)$. Then, the BPP instance with capacity $C$ and one item $j$ of weight $w_j=w_{(i,h)}$ for each edge ${(i,h)}\in E$ does not have the Integer Round-up Property.

Proof

Reasoning as in the proof of Proposition 3, we exclude, by contradiction, the existence of a BPP solution $M_1, \ldots , M_k$. Using an induction on vertices $1, \dots , |V|-1$, we can show that each edge subset $M_i$ contains exactly one edge incident with these vertices. From the proof of Proposition 1 we know that $|V|$ is even in the graph we are considering, and hence each edge subset must contain at least one edge incident with $0$. Since $|\delta (0)|=k$, each subset $M_i$ is a perfect matching, and hence the optimal ECP solution would have value $k$, a contradiction.

We conclude this part by observing that the edge weights in the statement of Proposition 4 are in some sense as small as possible.

Observation 1

If $\mathcal {P}\not =\mathcal {NP}$, for every fixed $k\ge 3$, there does not exist an alternative version of Proposition 4 in which the edge weights are polynomial in $|V|$ and $|E|$.

Proof

Note first of all that, by assigning weights to the edges of a generic $k$-regular graph $G$ as in Proposition 4, we can test if the optimal ECP value for $G$ is $k$ by testing if the associated optimal BPP value is $k$. More precisely, if the BPP value is $k$, then all bins in an optimal solution correspond to perfect matchings of $G$ and the associated ECP solution has value $k$. Otherwise, the BPP value is larger than $k$ and the edges of $G$ cannot be partitioned into perfect matchings, so the ECP solution value is larger than $k$.

Now, testing if the optimal ECP value for a generic $k$-regular graph is $k$ is strongly $\mathcal {NP}$-complete for every fixed $k\ge 3$. On the other hand, testing if the optimal BPP value is $k$, for $k$ fixed and not part of the input, can be done in pseudopolynomial time (i.e., in time polynomial in $n$ and $C$), by dynamic programming, where a generic state indicates the total weight in each bin after having packed the items up to $j$ (there are $O(nC^k)$ states in total). Therefore, if there existed the alternative version in the statement, we could check in polynomial time if the optimal ECP value is $k$.

2.2 Counterexamples derived from the Petersen graph

The smallest graph fulfilling the requirements in Propositions 1 and 3 is the Petersen Graph, a very famous $3$-regular graph that is depicted in Fig. 1. By applying Proposition 3 we get $C=1,023$ and $n=15$. By applying Proposition 4 we get the edge weights in Fig. 1c, which is the smallest counterexample that we could construct by hand, with $C=511$ and $n=15$. In fact, we get a few counterexamples by considering non-isomorphic vertex numberings.

Fig. 1

The Petersen graph and a counterexample derived from Proposition 4. a Vertex indices, b vertex weights, c edge weights

The instance of Fig. 1c can be improved by removing the item of size $1$, thus leading to a counterexample with $14$ items.

Observation 2

Given a BPP instance without the Integer Round-up Property and with optimal value $z^*$, it is possible to remove up to $z^*-1$ items of size $1$ without affecting the property.

Proof

We use a simple argument by contradiction. If the reduced BPP instance has the Integer Round-up Property, it must have an optimal solution consisting of $z^*-1$ bins. Moreover it must be impossible to accommodate all the removed items in the $z^*-1$ bins (otherwise the original problem would have a smaller optimal solution). Since the removed items have size $1$, the empty space in the bins used by the optimal solution to the reduced problem is strictly smaller than the number of removed items. It follows that the total item size of the original instance is strictly greater than $C(z^*-1)$ and the trivial continuous bound gives the lower bound value $z^*$ for BPP, a contradiction.

We can obtain more counterexamples by using other $3$-regular graphs for which the FECP and ECP solution values are respectively $3$ and $4$, e.g., using the Snark Graphs. In Table 2 we show the values of $n$ and $C$ for the BPP instances without Integer Round-up Property derived from some of these graphs by using Proposition 4 and Observation 2.

Table 2 Size of the BPP instances derived from Snark graphs using Proposition 4 and Observation 2

2.3 Defining item weights by integer linear programming

In order to try to find counterexamples with $C$ smaller than those provided in the previous section, we formulated the problem of assigning weights to the edges in the Petersen Graph so as to meet the requirements in Proposition 1 as an optimization problem. Let $\mathcal{{M}}$ denote the family of all perfect matchings of the graph and $\mathcal{{N}}$ the family of all other edge subsets. Let $w_j$ be a variable indicating the weight to be assigned to edge $j\in E$. An Integer Linear Programming (ILP) formulation of the problem of finding an instance with smallest $C$ is the following:

$$\begin{aligned}&\min C \end{aligned}$$

(5)

$$\begin{aligned}&\sum _{j \in M} w_j = C, \quad M\in \mathcal{{M}}, \end{aligned}$$

(6)

$$\begin{aligned}&\sum _{j \in N} w_j \ge C + 1 - \varDelta (1-t_N), \quad N\in \mathcal{{N}}, \end{aligned}$$

(7)

$$\begin{aligned}&\sum _{j \in N} w_j \le C - 1 + \varDelta t_N, \quad N\in \mathcal{{N}}, \end{aligned}$$

(8)

$$\begin{aligned}&w_j \in \mathbb {Z}_+, \quad j\in E, \end{aligned}$$

(9)

$$\begin{aligned}&t_N \in \{0,1\}, \quad N\in \mathcal{{N}}. \end{aligned}$$

(10)

Here, the binary variables $t_N$ and the “big M” constant $\varDelta$ are introduced to express by linear constraints the disjunction $\sum _{j\in N}w_j \le C-1 \vee \sum _{j\in N}w_j \ge C+1$ for $N\in \mathcal{{N}}$. As one may expect, this is a tough problem for a general-purpose solver. We run CPLEX 12.1 for about one CPU month on a Pentium Intel 3 GHz, using depth-first strategy and a callback to keep track of all the integer solutions found. We could obtain just three integer solutions, the smallest one having $C=863$.

In order to try to obtain smaller instances, we relaxed the requirement of Proposition 1, which imposes that $w(M)=C$ only if $M$ is a perfect matching. The problem can be modeled with the following Mixed ILP, in which the integer variables $w_j$ have been replaced by real variables $x_j$, for $j\in E$, and the bin size is normalized to one.

$$\begin{aligned}&\max \gamma \end{aligned}$$

(11)

$$\begin{aligned}&\sum _{j \in M} x_j = 1, \quad M\in \mathcal{{M}}, \end{aligned}$$

(12)

$$\begin{aligned}&\sum _{j \in N} x_j \ge 1 + \gamma - \varDelta (1-t_N), \quad N\in \mathcal{{N}}, \end{aligned}$$

(13)

$$\begin{aligned}&\sum _{j \in N} x_j \le 1 - \gamma + \varDelta t_N, \quad N\in \mathcal{{N}}, \end{aligned}$$

(14)

$$\begin{aligned}&x_j \ge 0, \quad j\in E, \end{aligned}$$

(15)

$$\begin{aligned}&\gamma \ge 0, \quad \end{aligned}$$

(16)

$$\begin{aligned}&t_N \in \{0,1\}, \quad N\in \mathcal{{N}}. \end{aligned}$$

(17)

The model maximizes the minimum distance $\gamma$ that separates the sum of the $x_j$ from 1 for all $N\in \mathcal{{N}}$. Whenever a feasible solution is found, we can easily convert it into a solution of model (5)–(10), by finding the smallest integer $C$ such that $C x_j$ is integer for all $j\in E$. If $\gamma$ is strictly positive no set $N\in \mathcal{{N}}$ can have weight 1 and all the requirements of Proposition 1 are satisfied, but if $\gamma =0$ there may be one or more sets $N\in \mathcal{{N}}$ with the same weight of the matchings. In this case the solution can still give a counterexample to the Integer Round-up Property if one can prove that all sets $N\in \mathcal{{N}}$ with weight 1 are not used in any optimal ECP solution.

From a computational point of view we preferred to run CPLEX 12.1 on model (11)–(17), store each feasible solution found during the search with a callback, and check if the corresponding BPP solution has or not the property by solving directly the BPP instance to the optimum. After about one CPU month, we obtained several thousand instances and got $C$ down to $146$. The best solutions we found are illustrated in Table 3, noting that we are also storing different solutions with the same value of $C$.

Table 3 Some counterexamples with $C \le 300$ found by solving the Mixed ILP (11)–(17)

All the instances in the table have 13 items, that is our best result in terms of number of items. Originally these instances had two items of weight 1, that were then removed by using Observation 2 (this was not the case for the majority of larger-size instances, where all items typically have weights larger than 1). The complete list of instances is available from the authors upon request.

As a final remark, note that we also checked that each of these instances is no longer a counterexample if any further item is deleted, or if any two items are merged into a single one whose weight is their sum.

3 Finding counterexamples by contraction

Given a BPP instance and two items $i$ and $j$ such that $w_i+w_j\le C$, the item-contraction of $i$ and $j$ (contraction for short in the following) amounts to replacing these two items by a new item of size $w_i+w_j$. A special class of BPP instances is the following.

Definition 1

A BPP instance is Integer Round-up Perfect if the instance itself and all the instances obtained from it by any sequence of contractions have the Integer Round-up Property.

The following result is fairly simple but we could not find it mentioned in the literature.

Observation 3

BPP on Integer Round-Up Perfect instances can be solved in pseudopolynomial time.

Proof

The optimal solution of the problem can be obtained by solving the following sequence of $O(n^3)$ FBPPs.

First of all, solve the FBPP associated with the initial instance, and let $k$ be the rounded-up value, which is also the optimal BPP value.

Then repeat the following as long as a contraction is possible (i.e., as long as there are at least two items that would fit together in a bin): by trying all possible contractions, find one such that the rounded-up value of the resulting FBPP instance is not larger than $k$. At least one such contraction exists since at least two items are packed in the same bin in the optimal BPP solution.

When no contraction is possible, we have $k$ items each obtained by contracting (in some sequence) the set of items in the same bin in an optimal solution of the original BPP instance, i.e., we have such a solution. The number of contractions is $O(n)$, since each of them decreases the number of items by $1$, and the number of candidates for each contraction is $O(n^2)$. The statement follows from the well-known fact that the FBPP can be solved in pseudopolynomial time (see, e.g., [8]).

The above proof gives us a method to construct new counterexamples to the Integer Round-up Property by contraction. Indeed, if the starting instance is not integer Round-up Perfect, at some iteration all the contractions we can perform on the current instance, lead to a FBPP solution of value $k+1$. So the current instance is a counterexample to the property.

We have applied this technique to the most well-known benchmark sets of instances for the BPP (namely, set_1, set_2, set_3, t_60, t_120, t_249, t_501, u_120, u_250, u_500, and u_1000) finding a few tens of small instances without the Integer Round-up Property. The smallest of such instances has $n=24$ and $C=100$, that is our best result in terms of bin size. In Table 4 we report the counterexamples with $C \le 150$. The columns report, respectively, the bin capacity, the number of items, the minimum and maximum item weight, the rounded up value of the optimal solution value for FBPP, $\lceil z(F\!B\!P\!P)\rceil$, and the optimal solution value for BPP, $z(BPP)$. This last value has been computed using the branch-and-price algorithm for the BPP described in Section 5 of [13].

Table 4 Some counterexamples with $C \le 150$ found by contraction

4 Conclusions and future research directions

The main result of this paper is a method for finding thousands of small-size Bin Packing instances that do not have the Integer Round-up Property. The instance with smallest capacity we found has 24 items and $C=100$, the instance with the smallest number of items has 13 items and $C=146$. These instances disprove a long-termed conjecture indicating that only artificial and very complicated instances do not have this property. We have based our search on the fact that some graphs are fractionally, but not integrally, 3-edge colorable, and on the fact that the BPP on Integer Round-Up Perfect instances can be solved in pseudopolynomial time.

From this work several ideas for future research arise. First of all note that there is no evidence that the optimal BPP value for an instance defined as in Section 2.1 will coincide with the optimal ECP solution value, i.e., in principle this instance may be a counterexample to the Modified Integer Round-up Conjecture mentioned in the introduction. However, for all the cases we considered, the optimal BPP value was of course $k+1$ as well, which is absolutely not surprising as the Conjecture appears to be very hard to disprove. And even only finding BPP instances without the Integer Round-up Property for which the optimal FBPP value is not integer (i.e., the additive gap without rounding up is larger than one) is an interesting research direction, see, e.g., [11, 14].

Even less surprising is the fact that we completely failed when trying to prove that conjecture from the Modified Integer Round-up Property for ECP by using some sort of inverse of our construction, which would define an ECP instance starting from a BPP one. Equally unsuccessful were the attempts to try to prove the equivalence of the Modified Integer Round-up Conjecture for BPP and for ECP on multigraphs, that remain two separate key open questions in Mathematical Programming.