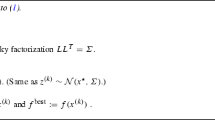SpeeDP: an algorithm to compute SDP bounds for very large Max-Cut instances

Abstract

We consider low-rank semidefinite programming (LRSDP) relaxations of unconstrained $\{-1,1\}$ quadratic problems (or, equivalently, of Max-Cut problems) that can be formulated as the non-convex nonlinear programming problem of minimizing a quadratic function subject to separable quadratic equality constraints. We prove the equivalence of the LRSDP problem with the unconstrained minimization of a new merit function and we define an efficient and globally convergent algorithm, called SpeeDP, for finding critical points of the LRSDP problem. We provide evidence of the effectiveness of SpeeDP by comparing it with other existing codes on an extended set of instances of the Max-Cut problem. We further include SpeeDP within a simply modified version of the Goemans–Williamson algorithm and we show that the corresponding heuristic SpeeDP-MC can generate high-quality cuts for very large, sparse graphs of size up to a million nodes in a few hours.

1 Introduction

We consider a semidefinite programming (SDP) problem in the form

$$\begin{aligned} \min _X \left\{ Q \bullet X : \mathrm{diag}(X)=e, X \succeq 0 \right\} \!, \end{aligned}$$

(1)

where $Q\in \fancyscript{S}^n$ is given, $X\in \fancyscript{S}^n$ ($\fancyscript{S}^n$ being the space of the $n \times n$ real symmetric matrices), the symbol ‘$\bullet$’ denotes the trace-inner product, $e\in \mathbb R ^n$ is the vector of all ones, $\mathrm{diag}(X)$ stands for the $n$-vector corresponding to the main diagonal of $X$, and, finally, the constraint $X\succeq 0$ requires $X$ to be positive semidefinite.

Semidefinite programming problems of this form arise as relaxations of unconstrained $\{-1,1\}$ quadratic problems (see, e.g., [8, 12, 23, 28]):

$$\begin{aligned} \min _x \left\{ x^TQx : x \in \{-1,1\}^n\right\} , \end{aligned}$$

(2)

which are equivalent to the Max-Cut problem.

Given the weighted adjacency matrix $A$ of a weighted graph $G=(N,E)$, the Max-Cut problem calls for a bipartition $(S,N{\setminus }S)$ of its nodes so that the weight of the corresponding cut, i.e., of the edges that go across the two sets of the bipartition, is maximized. Denote by $L$ the Laplacian matrix associated with $A$ and defined by $L:=\mathrm{diag}(Ae)-A$. Represent each bipartition $(S,N{\setminus }S)$ by an $n$-vector defined by $x_{i}=1$ for $i \in S$ and $x_{i}=-1$ for $i \notin S$. Then the Max-Cut problem can be formulated as

$$\begin{aligned} \max _x \left\{ \frac{1}{4} x^T L x : x \in \{-1,1\}^n\right\} . \end{aligned}$$

(3)

Since $x^T Lx= L\bullet xx^T$ and $xx^T \succeq 0$ with $\mathrm{diag}(xx^T)=e$, it is known that problem (1) with $Q=-\frac{1}{4}L$ provides a relaxation of Max-Cut. Producing a solution to problem (1) efficiently is then of great interest for solving the corresponding integer problem (2) exactly or for designing good heuristics (see, e.g., [30, 32]).

The aim of this paper is twofold: on one side we define an efficient algorithm for solving large scale instances of problem (1); on the other, by exploiting this useful tool, we make it possible to apply a Goemans–Williamson type heuristic to find good feasible solutions to very large instances of Max-Cut.

It is well known that problem (1) can be solved by semidefinite interior point methods. However, these approaches typically become less attractive for instances $n>20000$ because those methods that make use of an explicit representation of the basis matrix $X$ have excessive memory requirements, while those that are based on iterative methods (and usually solve the dual of problem (1)) are, to the best of our knowledge, still too slow in practice. These limitations have motivated searching for methods that are less demanding in terms of memory allocation and of computational cost. In this perspective, the constraint structure of problem (1) has been exploited in the literature to define special purpose algorithms.

One possibility is to reformulate the dual to (1) as an eigenvalue optimization problem that can be solved, e.g., by spectral bundle methods [19].

The other option is to use nonlinear programming reformulations that eliminate the semidefiniteness constraint from the primal problem (1) (see, e.g., [2, 5–7, 11, 16, 20, 21]). This is the line of research this paper falls into. Indeed, using the Gramian representation, any given matrix $X\succeq 0$ with rank $r$ can be written as $X=VV^T$, where $V$ is an $n\times r$ real matrix. Therefore, the positive semidefiniteness constraint can be eliminated and problem (1) reduces to the low rank SDP (LRSDP) formulation

$$\begin{aligned} \min _{V\in \mathbb R ^{n\times r}}\left\{ Q \bullet VV^T : \mathrm{diag}(VV^T)=e\right\} . \end{aligned}$$

(4)

Problem (4) can be written as the nonlinear programming (NLP) problem

$$\begin{aligned} \min _{v\in \mathbb R ^{nr}} \left\{ q_r(v)=\sum _{i=1}^n\sum _{j=1}^n q_{ij}v_i^Tv_j : \Vert v_i\Vert ^2=1, \quad i=1,\ldots ,n\right\} , \end{aligned}$$

(5)

where $v_i$, $i=1,\ldots ,n$, with $r\le n$, are the columns of the matrix $V^T$ and $v\in \mathfrak R ^{nr}$ is the vector obtained by stacking the column vectors $v_i$ for $i=1, \ldots , n$. Indeed this relaxation was first derived by Goemans and Williamson in [12] by replacing each variable $x_i$ of problem (2) with a vector $v_i\in \mathbb R ^r$. It is possible to state conditions that ensure correspondence among global solutions of problem (5) and solutions of problem (1). Moreover, although problem (5) is non-convex, it is also possible to state necessary and sufficient optimality conditions that can be used to check global optimality [15, 16, 21].

In most of the papers based on solving problem (5), the solution is achieved by means of an unconstrained reformulation. Indeed, the first idea of an unconstrained model for problem (1) goes back to Homer and Peinado [20], but the dimension of the resulting problem makes the method prohibitive for large scale problems. Burer and Monteiro in [7] introduced an augmented Lagrangian for solving the low rank reformulation of general linearly constrained SDP problems. In the numerical results section of [7], for the special case (4) arising from Max-Cut, they combine the Homer and Peinado approach with the “low rank idea”. By introducing the change of variables $X_{ij}=v_i^Tv_j/\Vert v_i\Vert \Vert v_j\Vert$, where $v_i\in \mathbb R ^r$, $i=1,\ldots , n$, with $r\ll n$, they get the unconstrained program

$$\begin{aligned} \min _{ v\in \mathbb R ^{nr}} \left\{ \phi (v) = \sum _{i=1}^n \sum _{j=1}^n q_{ij} \frac{ v_i^Tv_j}{\Vert v_i\Vert \Vert v_j\Vert },\quad v_i\in \mathbb R ^r\right\} . \end{aligned}$$

(6)

In [16], the constraints structure in problem (5) is exploited to get an expression of the Lagrange multipliers $\lambda _i$, for $i=1,\ldots ,n$, in closed form as a function of the variables $v$ (see (10)). Using such an expression in the augmented Lagrangian function for problem (5) and choosing a sufficiently large value $\eta >0$ for the penalty parameter, the authors obtain an exact penalty function of the form

$$\begin{aligned} P(v) = \sum _{i=1}^n\sum _{j=1}^n q_{ij}v_i^Tv_j + \sum _{i=1}^n \lambda _i(v) \left(\Vert v_i\Vert ^2-1\right) + \frac{1}{2 \eta } \sum _{i=1}^n \left(\Vert v_i\Vert ^2-1\right)^2. \end{aligned}$$

(7)

A single unconstrained minimization of the twice continuously differentiable function $P$ is enough to find a stationary point of problem (5). Computational experiments in [16] with the resulting algorithmic scheme, called EXPA, showed significant computational advantages with respect to the best codes available in literature.

In this paper, we start from (6) to get a new unconstrained problem, for which we retain a complete equivalence with problem (1). The specific feature of this formulation is that we add a regularization term to the function $\phi$ in (6), which ensures compactness of the level sets of the new merit function. This allows us to use standard optimization algorithms to solve problem (5). As we discuss in Sect. 4, this new unconstrained approach has some advantages also over (7), which are confirmed by the numerical results reported in Sect. 6. Indeed, the new algorithmic scheme, called SpeeDP, outperforms the best existing methods for solving problem (1). Furthermore, SpeeDP (like other similar low rank approaches) has some nice features that can be exploited to design a Max-Cut heuristic to find good cuts for very large graphs. Indeed, if the value of $r$ is fixed to a value independent of $n$ (and if, as it is reasonable to assume for large sparse instances, the graph has $\fancyscript{O}(n)$ edges), SpeeDP is able to derive a valid lower bound for problem (1), requiring $\fancyscript{O}(n)$ memory. In addition, it outputs the Gramian matrix of a solution $X$ to problem (1). This implies that, once SpeeDP has produced a solution, the famous Goemans–Williamson algorithm proposed in [12] can be applied to find a good cut, essentially without any additional computational effort. Therefore, it is possible to produce also an upper bound (close to the SDP bound) for very large instances of problem (2). These features altogether make it possible to find cuts in sparse graphs with millions of nodes and edges, with observed gap lower than 5 % (when the edge weights are all positive) in quite practical computation times.

Papers describing heuristics for Max-Cut abound in the literature. However, only in a few cases these algorithms provide a bound on the optimality error for the generated solutions that is close enough to the optimum to be of practical use.¹ Excluding the heuristics with a certified a priori bound (like the one of Goemans and Williamson) the only cases when this bound is computed are those of the exact algorithms that compute an upper bound on the value of an optimal solution, by solving a relaxation of problem (3). If these algorithms are interrupted at an early stage, they provide a heuristic cut, as a side product, along with an upper bound on the optimal value. However, the computational studies based on this type of exact algorithms consider graphs much smaller than those used for the test bed of this paper (see, e.g., [24] for the polyhedral relaxations and [32] for a combination of SDP and polyhedral relaxation). Despite the fact that we proposed a slight modification of the Goemans and Williamson algorithm, our primary intent is not to contribute to the algorithms for Max-Cut with a new heuristic but rather to make it feasible to compute an SDP based upper bound for very large instances.

Before concluding this section, we note that other relaxations for problem (2) have been proposed in literature. Among these, besides the above mentioned polyhedral relaxations, we mention the second order cone (SOC) approximation (see, e.g.,[22, 26]). Computational experiments based on SOC relaxation consider much smaller instances than the ones considered in this paper (see also the computational results in [32]). However, to the best of our knowledge, a comparison between SOCP and low rank SDP approaches, when embedded in a branch and bound procedure, has not been performed yet and would require further research work.

The paper is structured as follows: in Sect. 2 we report on some known results about the LRSDP problem (4). In Sect. 3 we define the new unconstrained reformulation, while in Sect. 4 we formally define the algorithm SpeeDP. In Sect. 5 we define our heuristic, SpeeDP-MC, for finding good feasible solutions to large sparse instances of Max-Cut. In Sect. 6 we compare the performance of SpeeDP against other existing approaches for the SDP problem (1) on an extended set of instances of the Max-Cut problem. Furthermore, we use SpeeDP-MC to find good solutions to large and huge Max-Cut instances from random graphs.

2 Key results on the low rank SDP formulation and notation

In this section we define our basic notation and we report some useful results on the LRSDP formulation (4).

Throughout the paper, for an $r\times n$ matrix $M$, by $\mathrm{vec}(M)\in \mathbb R ^{rn}$ we denote the operator that creates a column vector by stacking the column vectors of $M$. Given a vector $v\in \mathbb R ^m$, we define $B_\rho (v)=\{y\in \mathbb R ^m:~\Vert y-v\Vert < \rho \}$, for some $\rho >0$. For a given scalar $x$, by $(x)_+$ we denote the maximum between $x$ and zero, namely $(x)_+=\max (x,0)$.

A global minimum point of (4) is a solution to problem (1) provided that

$$\begin{aligned} r\ge r_{\min }=\min _{X\in \fancyscript{X}^*_\mathrm{SDP}}\text{ rank}(X), \end{aligned}$$

where $\fancyscript{X}^*_\mathrm{SDP}$ denotes the optimal solution set of problem (1). Although the value of $r_{\min }$ is not known, an upper bound can easily be computed by exploiting the result proved in [1, 18, 29], that gives

$$\begin{aligned} r_{\min }\le \widehat{r} = \frac{\sqrt{8n+1}-1}{2}. \end{aligned}$$

(8)

Let $v\in \mathbb R ^{nr}$ be the vector obtained by stacking the column vectors $v_i$ for $i=1,\dots , n$. We say that a point $v^*\in \mathbb R ^{nr}$ solves problem (1) if $X^*=V^*V^{*T}$ is an optimal solution to problem (1) (where $\mathrm{vec}(V^{*T})=v^*$). This implies, by definition, that $r\ge r_{\min }$.

The Karush–Kuhn–Tucker (KKT) conditions for problem (5) are written as follows: for some $\lambda \in \mathbb R ^n$

$$\begin{aligned} \begin{array}{ll} \displaystyle \sum \limits _{j=1}^n q_{ij}{v}_j + {\lambda }_i {v}_i=0,&\quad i=1,\ldots ,n\\ \Vert {v_i}\Vert ^2=1,\quad&\quad i=1,\ldots ,n. \end{array} \end{aligned}$$

(9)

We define a stationary point of problem (5) to be a $\hat{v}\in \mathbb{R }^{nr}$ satisfying (9) with a suitable multiplier $\hat{\lambda }\in \mathbb R ^n$. Given a local minimizer $\hat{v}\in \mathbb{R }^{nr}$ of problem (5), the KKT conditions are necessary for optimality and there exists a unique $\hat{\lambda }\in \mathbb R ^n$ such that $(\hat{v},\hat{\lambda })$ satisfies (9). Indeed, given a pair $({v},{\lambda })$ satisfying the conditions (9), the multiplier ${\lambda }$ can be expressed uniquely as a function of $v$, namely

$$\begin{aligned} \lambda _i(v)=-{{v}_i}^T\sum _{j=1}^n q_{ij}{v}_j,\quad i=1,\ldots ,n. \end{aligned}$$

(10)

By substituting the expression of ${\lambda }$ in the first condition of (9), we get

$$\begin{aligned} \sum _{j=1}^n q_{ij}\left(I_r- v_i v_i^T\right) v_j=0 \quad i=1,\ldots ,n. \end{aligned}$$

(11)

Although problem (5) is non-convex, the primal-dual optimality conditions for (1), combined with the necessary optimality conditions for (5), lead to the global optimality condition proved in [15, 16] and stated in the next proposition.

Proposition 1

A point $v^*\in \mathbb R ^{nr}$ is a global minimizer of problem (5) that solves problem (1) if and only if it is a stationary point of problem (5) and satisfies

$$\begin{aligned} Q+{\mathrm{Diag}} (\lambda (v^*)) \succeq 0, \end{aligned}$$

where $\lambda (v^*)$ is computed according to (10).

Thanks to the above proposition, given a stationary point of problem (5), we can prove its optimality by just checking that a certain matrix is positive semidefinite.

Another global condition has been proved in [21] for a slightly more general convex SDP problem which includes problem (1) as a special case. It is proved that a local minimizer $\widehat{V}\in \mathbb R ^{n \times r}$ of the LRSDP problem provides a global solution $\widehat{X}=\widehat{V}{\widehat{V}}^T$ of the original SDP problem if $\widehat{V}$ is rank deficient, namely if $\mathrm{rank}(\widehat{V})<r$. Actually, looking at the proof, it turns out that the assumption that $\widehat{V}$ is a local minimizer can be relaxed. Instead, it is enough to require that $\widehat{V}$ satisfies the second order necessary conditions for the LRSDP problem (see [14] for the restatement and the proof of this condition).

3 A new unconstrained formulation of the SDP problem

We start with the unconstrained formulation (6) proposed in [7], where it was shown to be quite effective in computations. It is easy to show that problems (4) and (6) are equivalent (see [13]). However, function $\phi$ in (6) is not defined at those points where $\Vert v_i\Vert =0$ for at least one index $i$, and it has non compact level sets, so that standard convergence results for unconstrained minimization methods are not immediately applicable.

We modify the objective function $\phi$ given in (6) in order to obtain an unconstrained problem that can be solved by standard methods. In particular, we add the regularization term

$$\begin{aligned} \sum _{i=1}^n\frac{(\Vert v_i\Vert ^2-1)^2}{d(v_i)}, \end{aligned}$$

(12)

where the term

$$\begin{aligned} d(v_i) = \delta ^2-\Big (1-\Vert v_i\Vert ^2\Big )_+^2,\quad 0<\delta <1 \end{aligned}$$

(13)

acts as a shifted barrier on the open set

$$\begin{aligned} S_{\delta }=\{v\in \mathbb R ^{nr}\,:\,\Vert v_i\Vert ^2 > 1-\delta ,\quad i=1,\ldots ,n\}. \end{aligned}$$

For a fixed $\varepsilon >0$ and for a fixed $r\ge 1$, we consider the unconstrained minimization problem

$$\begin{aligned} \min _{v\in \mathbb R ^{nr}}\left\{ ~f_\varepsilon (v)= \phi (v)+\frac{1}{\varepsilon }\sum _{i=1}^n\frac{(\Vert v_i\Vert ^2-1)^2}{d(v_i)},\;v\in S_\delta \right\} . \end{aligned}$$

(14)

Both $\phi$ and $S_{\delta }$ depend on $r$; however, we omit the explicit indication of this dependency to simplify notation.

We start by investigating the theoretical properties of $f_\varepsilon$. This function is continuously differentiable on the open set $S_\delta$ with gradient components

$$\begin{aligned} \nabla _{v_i}f_\varepsilon (v)= \nabla _{v_i}\phi (v) + \frac{4}{\varepsilon }\frac{(\Vert v_i\Vert ^2-1)}{d(v_i)} \left[1 - \frac{(\Vert v_i\Vert ^2-1)(1-\Vert v_i\Vert ^2)_+}{d(v_i)}\right] v_i, \end{aligned}$$

where

$$\begin{aligned} \nabla _{v_i}\phi (v)=\frac{2}{\Vert v_i\Vert }\left[\sum _{j=1}^n q_{ij} \left(I_r -\frac{v_i}{\Vert v_i\Vert }\frac{{v_i}^T}{\Vert v_i\Vert } \right)\frac{v_j}{\Vert v_j\Vert }\right]. \end{aligned}$$

The first important property is the compactness of the level sets of function $f_\varepsilon$, which guarantees the existence of a solution to problem (14). In the following, $\fancyscript{F}$ stands for the feasible set of problem (5), i.e.,

$$\begin{aligned} \fancyscript{F}= \{v\in \mathbb R ^{nr}\,:\,\Vert v_i\Vert ^2 = 1,\quad i=1,\ldots ,n\}. \end{aligned}$$

Proposition 2

For every given $\varepsilon >0$ and for every given $v^0\in \fancyscript{F}$, the level set $\fancyscript{L}_{\varepsilon }(v^0)=\{v\in S_\delta :~f_{\varepsilon }(v)\le f_{\varepsilon }(v^0)\}$ is compact and

$$\begin{aligned} \fancyscript{L}_{\varepsilon }(v^0)\subseteq \left\{ v\in \mathbb R ^{nr}: \Vert v_i\Vert ^2\le (2\overline{C}\varepsilon \delta ^2)^\frac{1}{2}+1,\quad i=1,\ldots ,n\right\} , \end{aligned}$$

(15)

with $\overline{C}=\sum _{i=1}^n\sum _{j=1}^n |q_{ij}|>0$.

Proof

First, for every $v\in \mathbb R ^{nr}$, with $v_i\ne 0$ for $i=1,\dots , n$, we have that

$$\begin{aligned} \phi (v)&= \sum _{i=1}^n\sum _{j=1}^n q_{ij} \frac{v_i^Tv_j}{\Vert v_i\Vert \Vert v_j\Vert } \ge -\sum _{i=1}^n\sum _{j=1}^n |q_{ij}|\frac{|v_i^Tv_j|}{\Vert v_i\Vert \Vert v_j\Vert } \ge -\overline{C}.\nonumber \end{aligned}$$

Hence, we get

$$\begin{aligned} f_{\varepsilon }(v) \ge -\overline{C}+\frac{1}{\varepsilon }\frac{(\Vert v_i\Vert ^2-1)^2}{\delta ^2},\quad \text{ for} \text{ all} i=1,\ldots ,n. \end{aligned}$$

(16)

For every given $v\in \fancyscript{L}_{\varepsilon }(v^0)$, as $v^0\in \fancyscript{F}$, we can write $f_\varepsilon (v)\le f_\varepsilon (v^0)=\phi (v^0)\le \overline{C}$, so that, using (16), we get $\Vert v_i\Vert ^2\le (2\overline{C}\varepsilon \delta ^2)^\frac{1}{2}+1$, $i=1,\ldots ,n$. This implies that (15) holds and hence that $\fancyscript{L}_{\varepsilon }(v^0)$ is bounded.

On the other hand, any limit point $\hat{v}$ of a sequence of points $\{v^k\}$ in $\fancyscript{L}_{\varepsilon }(v^0)$ cannot belong to the boundary of $S_\delta$. Indeed, if $\Vert \hat{v}_i\Vert ^2=1-\delta$ for some $i$, then (13) implies $d(\hat{v}_i)=0$, and hence $\lim _{k\rightarrow \infty }f_\varepsilon (v^k)=\infty$; but this contradicts $v^k \in \fancyscript{L}_{\varepsilon }(v^0)$ for $k$ sufficiently large. Therefore, the level set $\fancyscript{L}_{\varepsilon }(v^0)$ is also closed and the claim follows.

$\square$

The following theorem states the correspondence between stationary points, local/global minimizers of (14), and stationary points, local/global minimizers of (5), respectively.

This result exploits an interesting property of the objective function $\phi$ of problem (6). For every $v\in S_\delta$, its gradient with respect to $v_i$ is orthogonal to the vector $v_i$, namely the following holds, for $i=1,\ldots ,n$:

$$\begin{aligned} v_i^T\nabla _{v_i} \phi (v)=2\left[\sum _{j=1}^n q_{ij} \left(\frac{v_i^T}{\Vert v_i\Vert } -\frac{v_i^Tv_i}{\Vert v_i\Vert ^2}\frac{{v_i}^T}{\Vert v_i\Vert } \right)\frac{v_j}{\Vert v_j\Vert }\right]=0. \end{aligned}$$

(17)

Theorem 1

For every $\varepsilon >0$ and $r\ge 1$, $\hat{v}$ is a stationary point, a local/global minimizer of (14) in $S_\delta$ if and only if it is a stationary point, a local/global minimizer of (5), respectively.

Proof

First, we recall that, for every $v\in S_\delta$, $v_i\ne 0$ for all $i=1,\ldots ,n$. Furthermore, by definition of $\nabla _{v_i}f_\varepsilon (v)$ and by (17), we get, for every $v_i$ with $i=1,\ldots ,n$,

$$\begin{aligned} v_i^T \nabla _{v_i}f_\varepsilon (v)=\frac{4}{\varepsilon } \frac{(\Vert v_i\Vert ^2-1)v_i^Tv_i}{d(v_i)}\left(1 - \frac{(\Vert v_i\Vert ^2-1)(1-\Vert v_i\Vert ^2)_+}{d(v_i)}\right). \end{aligned}$$

Therefore, if $\Vert v_i\Vert ^2\ge 1$, we get

$$\begin{aligned} v_i^T \nabla _{v_i}f_\varepsilon (v)=\frac{4}{\varepsilon }\frac{(\Vert v_i\Vert ^2-1)\Vert v_i\Vert ^2}{\delta ^2}, \end{aligned}$$

(18)

otherwise

$$\begin{aligned} v_i^T \nabla _{v_i}f_\varepsilon (v)=\frac{4}{\varepsilon }\frac{(\Vert v_i\Vert ^2-1)\Vert v_i\Vert ^2}{d(v_i)} \left(1+\frac{(\Vert v_i\Vert ^2-1)^2}{d(v_i)}\right). \end{aligned}$$

(19)

Furthermore, if $v\in \fancyscript{F}$,

$$\begin{aligned} f_\varepsilon (v)&= q_r(v)\end{aligned}$$

(20)

$$\begin{aligned} \nabla _{v_i}f_\varepsilon (v)&= 2\sum _{j=1}^n q_{ij}(I_r -v_i{v_i}^T)v_j,\quad i=1,\ldots ,n. \end{aligned}$$

(21)

Now we prove the correspondences stated in our claims.

Case 1. (Correspondence of stationary points).

Necessity. By (18) and (19), with $\hat{v}\in S_\delta$ a stationary point of $f_{\varepsilon }$, we have $\hat{v}\in \fancyscript{F}$. Hence, as a result of (21) and (11), $\hat{v}$ is a stationary point also for problem (5).

Sufficiency. Let $\hat{v}$ be a stationary point for problem (5). Then, $\hat{v}\in \fancyscript{F}$ and (11) holds, so that from (21) we get $\nabla _{v_i}f_\varepsilon (\hat{v})=0$ for $i=1,\ldots ,n$.

Case 2. (Correspondence of global minimizers).

Necessity. By Proposition 2, the function $f_{\varepsilon }$ admits a global minimizer $\hat{v}$, which is obviously a stationary point of $f_{\varepsilon }$ and hence we have that $\hat{v}\in \fancyscript{F}$, so that $f_{\varepsilon }(\hat{v})=q_r(\hat{v})$. We proceed by contradiction. Assume that a global minimizer $\hat{v}$ of $f_{\varepsilon }$ is not a global minimizer of problem (5). Then there exists a point $v^*$, global minimizer of problem (5), such that $f_\varepsilon (\hat{v})=q_r(\hat{v}) > q_r(v^*)= f_{\varepsilon }(v^*)$, but this contradicts the assumption that $\hat{v}$ is a global minimizer of $f_{\varepsilon }$.

Sufficiency. The claim is true by similar arguments.

Case 3. (Correspondence of local minimizers).

Necessity. Since $\hat{v}$ is a local minimizer of $f_{\varepsilon }$, it is a stationary point of $f_{\varepsilon }$, so that $\hat{v}\in \fancyscript{F}$. Thus, $f_{\varepsilon }(\hat{v}) =q_r(\hat{v})$. Furthermore, there exists a $\rho >0$ such that $q_r(\hat{v})=f_{\varepsilon }(\hat{v})\le f_{\varepsilon }(v)$, for all $v\in S_\delta \cap B_\rho (\hat{v})$. Therefore, by using (20), for all $v\in \fancyscript{F}\cap B_\rho (\hat{v})$, we have $q_r(\hat{v})\le f_{\varepsilon }(v)=q_r(v)$ and hence $\hat{v}$ is a local minimizer for problem (5).

Sufficiency. Since $\hat{v}$ is a local minimizer of (5), there exists a $\rho >0$ such that, for all $v\in \fancyscript{F}\cap B_\rho (\hat{v})$, $q_r(\hat{v})=f_\varepsilon (\hat{v})\le q_r(v)=f_\varepsilon (v)$. We want to show that there exists $\gamma$ such that, for all $v\in S_\delta \cap B_\gamma (\hat{v})$, we get $f_\varepsilon (\hat{v})\le f_\varepsilon (v)$. It is sufficient to show that there is a $\gamma >0$ such that, for all $v\in S_\delta \cap B_\gamma (\hat{v})$, we have that $p(v)\in \fancyscript{F}\cap B_\rho (\hat{v})$, where $p(v)$ has components $p_i(v)={v_i}/{\Vert {v}_i\Vert }$ for $i=1,\dots , n$.Indeed, in this case we have $q_r(\hat{v}) = f_\varepsilon (\hat{v})\le q_r(p(v))= f_\varepsilon (p(v))\le f_\varepsilon (v)$. Given $v_i\ne 0\in \mathbb R ^r$, its projection over the unit norm set is simply ${v_i}/{\Vert v_i\Vert }$, so that for $\hat{v}\in \fancyscript{F}$ we have $\left\Vert\,v_{i}-\hat{v}_{i}\right\Vert\ge \left\Vert\,v_{i}-v_{i}/\left\Vert\,v_{i}\right\Vert\right\Vert$. Hence, for a chosen $\gamma <{\rho }/{2}$, we can write

$$\begin{aligned} \Vert p(v)-\hat{v}\Vert ^2&= \sum _{i=1}^n \left\Vert\hat{v}{_i} - \frac{v_i}{\Vert v_i\Vert } \right\Vert^2= \sum _{i=1}^n \left\Vert\hat{v}{_i}-\frac{v_i}{\Vert v_i\Vert } + v_i- v_i\right\Vert^2 \\&\le \sum _{i=1}^n \left(\Vert \hat{v}{_i}-v_i\Vert ^2+\left\Vert v{_i} - \frac{v_i}{\Vert v_i\Vert }\right\Vert^2+2\Vert \hat{v}{_i}-v_i\Vert \left\Vert v{_i} - \frac{v_i}{\Vert v_i\Vert } \right\Vert\right)\\&\le \sum _{i=1}^n 4\Vert \hat{v}{_i}-v_i\Vert ^2= 4\Vert \hat{v}-v\Vert ^2< 4\gamma ^2<\rho ^2. \end{aligned}$$

Therefore, we have $f_\varepsilon (\hat{v})\le f_\varepsilon (v)$ for all $v\in S_\delta \cap B_\gamma (\hat{v})$, so that $\hat{v}$ is a local minimizer also for (14).$\square$

4 SpeeDP: an efficient algorithm for solving the SDP problem

In this section, we define an algorithm for solving problem (1) that exploits the results stated in the previous sections.

In Sect. 2 we have seen that for $r\ge r_{\min }$ a global solution of problem (5) provides a solution to problem (1). Moreover, Theorem 1 states a complete correspondence between problems (5) and (14). Since $f_\varepsilon$ is continuously differentiable over the set $S_\delta$ and, by Proposition 2, it has compact level sets, we can find a stationary point of problem (14) by applying any globally convergent unconstrained minimization method (see, e.g., [4]).

The value of $r_{\min }$ is not known a priori and, in principle, the only computable value of $r$ that guarantees the correspondence between solutions of (1) and global solutions of (5), is given by the number $\widehat{r}$ defined in (8). However, computational tests show that this value is usually larger than the actual value needed to obtain a solution to problem (1). Following the idea presented in [16] and [7], we use an incremental rank scheme starting with $r\ll \widehat{r}$, and we employ the global optimality condition of Proposition 1 to prove optimality of the current solution.

Concerning the method for finding a stationary point of problem (14), we select a gradient type method defined by an iteration of the form

$$\begin{aligned} v^{k+1}_i=v^{k}_i-\alpha ^k\nabla _{v_i}f_\varepsilon (v^k)\quad i=1,\ldots ,n, \end{aligned}$$

(22)

where $\alpha ^k\in (0,\alpha _M]$, for some $\alpha _M>0$, is obtained by a suitable line-search procedure satisfying

$$\begin{aligned} f_\varepsilon (v^{k+1})\le f_\varepsilon (v^0), \end{aligned}$$

(23)

with $v^0\in \fancyscript{F}$.

The choice of a gradient type method for the minimization of $f_{\epsilon }$ guarantees (see Proposition 3 below) that, for $\varepsilon$ sufficiently large, the whole sequence of iterations stays in the set $\{v\in \mathbb R ^{nr}\,:\, \Vert v_i\Vert ^2\ge 1,\, i=1,\ldots ,n\}$. Hence, for $\varepsilon$ sufficiently large, the barrier term (13) reduces to a constant, thus avoiding the annoying effect of getting close to the boundary of $S_\delta$, which might negatively affect the behavior of the algorithm.

Proposition 3

Let $\{v^k\}$ be the sequence generated with the iterative scheme (22) for a given $v^0\in \fancyscript{F}$, where each $\alpha ^k$ satisfies (23) and $\alpha ^k\le \alpha _M$. Then, there exists $\bar{\varepsilon }>0$ such that, for every $\varepsilon \ge \bar{\varepsilon }$, we have, for all $k$,

$$\begin{aligned} \Vert v^k_i\Vert \ge 1,\quad i=1,\ldots ,n. \end{aligned}$$

Proof

By (23), for a fixed value $\varepsilon >0$ the sequence $\{v^k\}$ stays in the compact level set $\fancyscript{L}_{\varepsilon }(v^0)$. The proof is by induction. Assume that there exists $\bar{\varepsilon }>0$ such that, for any $\varepsilon \ge \bar{\varepsilon }$, it is true that $\Vert v^k_i\Vert ^2\ge 1$. We show that the same is true also for $k$ replaced $k+1$. We can write

$$\begin{aligned} \Vert v^{k+1}_i\Vert ^2&= \Vert v^k_i\Vert ^2+(\alpha ^k)^2\Vert \nabla _{v_i}f_\varepsilon (v^k)\Vert ^2-2\alpha ^k(v^k_i)^T \nabla _{v_i}f_\varepsilon (v^k)\nonumber \\&\ge \Vert v^k_i\Vert ^2 -\frac{8\alpha _M}{\varepsilon \delta ^2}(\Vert v^k_i\Vert ^2-1)\Vert v^k_i\Vert ^2\nonumber , \end{aligned}$$

where we use (18). If $\Vert v^k_i\Vert =1$, then $\Vert v^{k+1}_i\Vert ^2\ge 1$. Otherwise, if $\Vert v^k_i\Vert >1$, we need to verify that a value of $\bar{\varepsilon }$ exists such that, for all $\varepsilon \ge \bar{\varepsilon }$,

$$\begin{aligned} (\Vert v^k_i\Vert ^2-1)-\frac{8\alpha _M}{\varepsilon \delta ^2}(\Vert v^k_i\Vert ^2-1)\Vert v^k_i\Vert ^2 \ge 0, \end{aligned}$$

namely

$$\begin{aligned} 1 -\frac{8\alpha _M}{\varepsilon \delta ^2}\Vert v^k_i\Vert ^2\ge 0. \end{aligned}$$

(24)

By Proposition 2, we have that $\Vert v^k_i\Vert ^2\le (2\overline{C}\varepsilon \delta ^2)^\frac{1}{2}+1$ for all $k$, which combined with (24) implies that $\varepsilon$ has to satisfy

$$\begin{aligned} \varepsilon -8\frac{\alpha _M}{\delta ^2}\left((2\overline{C}\delta ^2\varepsilon )^\frac{1}{2}+1 \right)\ge 0, \end{aligned}$$

which is possible for a sufficiently large value of $\varepsilon$.$\square$

At this point we are ready to define the algorithm SpeeDP.

• ALGORITHM SpeeDP

• Initialization. Set integers $2\le r^1<r^2<\cdots <r^p$ with $r^p\in [ \widehat{r}, n]$, where $\widehat{r}$ is

•    given by (8). Choose $\varepsilon >0$, $\delta \in (0,1)$, and $tol_\varepsilon > 0$.

• For $j=1,\ldots ,p$ do:

•    S.0 Set $r=r^j$.

•    S.1 Starting from $v^0\in \fancyscript{F}$, find a stationary point $\overline{v}\in \mathbb{R }^{nr}$ of problem (14)

•          by a gradient type method satisfying (22) and (23).

•    S.2 Compute the multiplier $\overline{\lambda }$ with (10).

•    S.3 Determine the minimum eigenvalue $\mu _{\min }(\overline{\lambda })$ of $Q+\mathrm{Diag}(\overline{\lambda })$.

•    S.4 If $\mu _{\min }(\overline{\lambda })\ge -tol_\varepsilon$, then exit.

• Return $\overline{v}$, $\overline{r}=r^j$, $\overline{\lambda }$, and $\mu _{\min }(\overline{\lambda })$.

SpeeDP returns $\overline{v}$ and $\mu _{\min }(\overline{\lambda })$. If $\mu _{\min }(\overline{\lambda })\ge -tol_\varepsilon$, then the matrix $Q+{\mathrm{Diag}}(\overline{\lambda })$ is positive semidefinite within a tolerance $tol_\varepsilon$ so that a solution (or a good approximation) to problem (1) is obtained as $X^*=\overline{V}\,\overline{V}^T$, where $\overline{V}\in \mathbb{R }^{n\times \overline{r}}$ is such that $\mathrm{vec}(\overline{V}^T) = \overline{v}$. Recall that the value

$$\begin{aligned} z_{LB}=-e^T\overline{\lambda }+n\mu _{\min }(\overline{\lambda }), \end{aligned}$$

provides a lower bound to the solution of problem (1) (see, e.g, [16, 31]). Incidentally, note that the bound is valid for every $\overline{\lambda }$; moreover for every $\overline{v}\in \mathbb{R }^{n \overline{r}}$, if $\overline{\lambda }$ is computed by means of (10), it is easy to check that $-e^T\overline{\lambda }=Q\bullet \overline{V}\,\overline{V}^T$.

Finally, we want to stress the advantages of the SpeeDP algorithm based on the merit function $f_\varepsilon$ over the scheme EXPA based on the penalty function (7) introduced in [16].

• The theoretical properties of the exact penalty function (7) depend on the penalty parameter $\eta$ that is required to be smaller than a certain threshold value. However, choosing a small value of $\eta$ may negatively affect both the efficiency and the accuracy of the algorithm EXPA. On the contrary, the equivalence properties of the merit function introduced in this paper hold for any value of the parameter $\epsilon >0$.

• Each computation of the penalty function  (7) requires the evaluation of the multiplier function $\lambda (v)$ as in (10) which is not needed in the function $f_{\epsilon }$. This implies that the computation of $f_{\epsilon }$ requires less matrix-vector products than the evaluation of the function (7), with a significant reduction of computational time.

All these advantages are supported by the numerical results reported in Sect. 6.

5 SpeeDP-MC: a heuristic for large scale Max-Cut instances

In this section we combine the algorithm SpeeDP for computing the SDP bound with a heuristic for the Max-Cut problem (3). Note that, differently from the previous sections, here we address a maximization problem. Therefore, the meanings of the terms “lower” and “upper” bound have now to be referred to problem (3).

Our heuristic is essentially the one due to Goemans and Williamson and described in [12], integrated with SpeeDP and a few simple additional details.

Let $X$ be the optimal solution to (1) and let $v_i\in \mathbb R ^r$, $i=1,\ldots ,n$, be vectors whose Gramian matrix coincides with $X$. Recall that the Goemans–Williamson (GW) algorithm outputs the node bipartition $(S,N{\setminus }S)$ with $S=\{i : h^Tv_i \ge 0\}$, where $h\in \mathbb R ^r$ is generated from a uniform random distribution on the unit sphere $\{x\in \mathbb R ^r : \Vert x\Vert =1\}$.

We choose the GW heuristic for two main reasons. First, because it has a good theoretical approximation ratio. Indeed, the expected weight of $(S,N{\setminus }S)$ is shown in [12] to be at most 12.1 % below the optimal value of (1) for instances with a nonnegative weighted adjacency matrix (a more general case is treated in [27, 28]). Second, because the only ingredient necessary to run the algorithm is the set of vectors $v_i\in \mathbb R ^r$, $i=1,\ldots ,n$, which are precisely the SpeeDP output. Hence SpeeDP makes it possible to apply the GW approximation algorithm to very large graphs since, on the one hand, it is able to solve problem (1) in a reasonable amount of time also for very large graphs and, on the other hand, it provides the vectors $v_i$, $i=1,\ldots ,n$, “for free”.

To the contrary, once the SDP bound has been computed with interior point methods, additional computational effort is necessary to produce the vectors $v_i$, with $i=1,\ldots ,n$.

In our procedure the cut provided by the Goemans–Williamson algorithm is then improved by means of a 1-opt local search, where all possible moves of a single vertex to the opposite set of the partition are checked and moves are made until no further improvement is possible.

In [10], where a similar heuristic is described but problem (1) is solved by an interior point algorithm, a particularly successful step is proposed to further improve on the solution. The whole procedure is repeated a few times where the solution matrix $X$ of problem (1) is replaced by the convex combination $X^{\prime }=\alpha X+(1-\alpha )\hat{x}\hat{x}^T$, $0<\alpha <1$, where $\hat{x}$ is the representative vector of the current best cut. The idea behind this step is to bias the Goemans–Williams rounding with the current best cut or, put it differently, to force the rounding procedure to generate a cut in a neighborhood of the current best solution.

This step does not require to solve problem (1) again, but needs the Cholesky factorization of the matrix $X^{\prime }$.

We use a similar technique in our procedure. However, to avoid the Cholesky factorization, which is not suitable for very large instances, we solve a new problem (1) after perturbing the objective function. Matrix $Q$ is replaced by the perturbed matrix $Q^\prime$ given by $Q^\prime = Q+\beta \hat{x}\hat{x}^T$ with $\beta >0$.

Such a perturbation has again the effect of moving the solution of problem (1) and hence of the Goemans–Williamson rounding, towards a neighborhood of the current best integral solution. With the new objective function $Q^\prime$ we solve problem (1) with SpeeDP and repeat the rounding and the 1-opt improvement as well. The whole procedure is repeated a few times with different values of $\beta$.

Summarizing, the scheme of our heuristic algorithm is as follows:

• ALGORITHM SpeeDP-MC

• Data A graph $G=(N,E)$, its Laplacian matrix $L$, $\;\alpha >0$, $\;k_{\max }$.

• Initialization Set $Q=-\frac{1}{4} L$, $\;\hat{x}=e$ and $\;\overline{\beta }= \alpha \sum _{i,j}|q_{ij}|/|E|$.

• For $k=k_{max},\ldots ,0$ do:

•    S.0 Set $\beta = k\overline{\beta }$ and $Q^\prime =Q+\beta (\hat{x}\hat{x}^T)$.

•    S.1 Apply SpeeDP to problem (1) with $Q=Q^\prime$ and let $v_i$, $i=1,\ldots ,n$ be the

•          returned solution and $z_{LB}$ the corresponding computed lower bound.

•    S.2 Apply the Goemans–Williamson hyperplane rounding technique to the

•          vectors $v_i$, $i=1,\ldots ,n$. This gives a bipartition representative vector $\bar{x}$.

•    S.3 Apply the 1-opt improvement to $\bar{x}$. This gives a new bipartition

•          representative vector $\tilde{x}$. If $Q^\prime \bullet \tilde{x}\tilde{x}^T < Q^\prime \bullet \hat{x}\hat{x}^T$, set $\hat{x} = \tilde{x}$.

• Return Best cut $\hat{x}$, lower bound $-Q^\prime \bullet \hat{x}\hat{x}^T$, upper bound $-z_{LB}$.

Note that the amount of perturbation decreases after each iteration until it gets to zero. We stress that repeating step 1 several times is not as expensive as it may appear, because we make use of a warm start technique: beginning from the second iteration, we start SpeeDP from the solution found at the previous step, so that each computation of the minimum is sensibly cheaper than the first one.

Besides the ability of treating graphs of very large sizes, another advantage of SpeeDP-MC is that it also provides a solution with a guaranteed optimality error bound, since it outputs an upper and lower bound on the value of the optimal cut.

6 Numerical results

In this section, we describe our computational experience both with algorithm SpeeDP for solving problem (1), and with the heuristic SpeeDP-MC for finding good Max-Cut solutions for large graphs.

SpeeDP is implemented in Fortran 90 and all the experiments have been run on a PC with 2 GB of RAM.

The parameters $\delta$ and $\varepsilon$ in (14) have been set to $0.25$ and $10^{3}\cdot \delta ^{-1}$, respectively. The tolerance $tol_\varepsilon$ has been set to $10^{-3}$.

For the unconstrained optimization procedure we use a Fortran 90 implementation of the non-monotone version of the Barzilai–Borwein method proposed in [17] which satisfies (22) and (23).

As for the choice of the starting value $r^1$ of the rank, we use the same rule based on $n$ as in [16] using values $8\le r^1\le 30$ for $n$ from 100 up to more than $20000$. The updating rule for the rank $r^{j}$ is simple $r^{j+1}=\min \left\{ \lfloor r^{j}\cdot 1.5 \rfloor ,\widehat{r} \right\}$ where $\widehat{r}$ is given in (8).

Positive semidefiniteness of $Q + {\mathrm{Diag}}(\overline{\lambda })$ is checked by means of the subroutines dsaupd and dseupd of the ARPACK library.

As a first step, we consider SpeeDP for solving problem (1). We compare the performance of SpeeDP with the best codes in literature in the main classes of methods for solving problem (1): interior point methods, Spectral Bundle methods, and low rank NLP methods.

As an interior point method we select the dual-scaling algorithm defined in [3] and implemented in the software DSDP (version 5.8) downloaded from the web page.² The code DSDP is considered particularly efficient for solving problems with low-rank structure and sparsity in the data (as it is the case for Max-Cut instances). In addition, DSDP has relatively low memory requirements for an interior point method, and is indeed able to solve instances up to around 10000 nodes. As a Spectral Bundle method, we use SB, which can be found in [19] and is downloadable from the web page.³

To make a comparison with other NLP based methods, we choose the code SDPLR-MC, proposed by Burer and Monteiro in [7], downloadable from the web page,⁴ and the code EXPA proposed in [16].

Both EXPA and SDPLR-MC have a structure similar to SpeeDP. Indeed, the main scheme differs in the way of finding a stationary point for problem (5). We remark that SDPLR-MC does not check the global optimality condition $Q + \mathrm{Diag}(\overline{\lambda }) \succeq 0$, while both EXPA and SpeeDP do.

Our benchmark set consists of standard instances of the Max-Cut problem with number of nodes ranging from 100 to 20000 and different degrees of sparsity. The first set of problems belongs to the SDPLIB collection of semidefinite programming test problems (hosted by B. Borchers) that can be downloaded from the web page.⁵ The second set of problems belongs to the group Gset of randomly generated problems by means of the machine-independent graph generator rudy [33]. These problems can also be downloaded from Burer’s web page (see footnote 4).

SpeeDP, EXPA, SDPLR-MC, and SB solve all the test problems, whereas DSDP runs out of memory on the two largest problems (G77 and G81 of the Gset collection). Hence we eliminate these two test problems in the comparisons with DSDP.

We compare the different codes on the basis of the level of accuracy and of the computational time. Besides reporting detailed results in tables, we use a graphical view of the results by using the performance profile, proposed in [9]. Given a set of solvers $S$ and a set of problems $P$, we compare the performance of a solver $s\in S$ on problem $p\in P$ against the best performance obtained by any solver in $S$ on the same problem. To this end we define the performance ratio

$$\begin{aligned} r_{p,s}=\frac{ t_{p,s} }{ \min \{ t_{p,s^\prime }:s^\prime \in S \}}, \end{aligned}$$

where $t_{p,s}$ is the performance criterion used, and we consider a cumulative distribution function $\rho _s(\tau ) = \frac{1}{|P|}~ |\{ p\in P: r_{p,s}\le \tau \}|$. Then we draw $\rho _s(\tau )$ with respect to the parameter $\tau$ that is represented on the $x$-axis with a logarithmic scale. The ‘higher’ the resulting curve the better is the corresponding method with respect to the criterion chosen; efficiency is measured by how fast the curve reaches the value of 1 (since all the methods solve all the problems, all the methods eventually reach the performance value $1$ if a sufficiently large $\tau$ is allowed).

As for the accuracy, following [25], we report the primal and/or the dual objective function values obtained by the five methods in Table 1. DSDP gives both primal and dual values in output, SpeeDP, EXPA, and SDPLR-MC return the primal objective value only, while SB produces a value of the dual objective function that is a bound on the optimal value of problem (1). Furthermore, we plot the performance profile in Fig. 1, choosing the relative duality gap as a performance criterion. In particular, we consider the relative difference between the primal value $f^*_{p,s}$ of any solver $s$ on problem $p$ and dual value $f_{p,\mathtt{DSDP}}^*$ given by DSDP, namely we set

$$\begin{aligned} t_{p,s} = \frac{f^*_{p,s}-f_{p,\mathtt{DSDP}}^*}{1+|f^*_{p,s}|+|f_{p,\mathtt{DSDP}}^*|}. \end{aligned}$$

By analyzing them, it emerges that, as for the accuracy, SpeeDP can be considered comparable with DSDP, whereas EXPA, SDPLR-MC, and SB are usually worse.

Table 1 Optimal values

Fig. 1

Performance profile with performance criterion equal to primal–dual gap

As for the computational efficiency, we do not report the CPU times of our computational experiments explicitly; instead in Fig. 2 we give an overall view of the results by showing the performance profile of the five methods where the performance criterion $t_{p,s}$ is the CPU time in seconds needed by solver $s$ to solve problem $p$. The results related to the two problems G77 and G81 are reported separately in Table 2. It emerges from these profiles and from the table that SpeeDP outperforms all the other methods.

Fig. 2

CPU time performance profiles

Table 2 Optimal values and computation time for G77 and G81

Finally, we report on the numerical results obtained by the heuristic algorithm SpeeDP-MC described in Sect. 5 applied to some large random graphs. SpeeDP-MC is implemented in C and uses the Fortran 90 version of SpeeDP as a routine. As for the parameters, in the experiments we set $k_{\max } = 2$ and $\alpha = 10^{-2}$. We generated 500 random vectors $h$ in the Goemans–Williamson heuristic and we selected the one that provides the best cut. We used the graph generator rudy [33] to produce instances with several sizes and densities and different weights. We first considered graphs with node sizes $n$ equal to $500+i\cdot 250$, for $i=0,\ldots ,8$ and with edge densities equal to $10\,\%+i \cdot 10\,\%$, for $i=0,\ldots , 9$. For each pair (n,density) we generated three different graphs with positive weights ranging between 1 and 100. Details on the results can be found in [14]. We draw in Fig. 3 the average CPU time and in Fig. 4 the gap obtained, as a function of the graph density.

Fig. 3

Average SpeeDP-MC CPU time for random graphs

Fig. 4

Average SpeeDP-MC gap for random graphs

As it emerges from the figures, the heuristic is able to produce a good cut in a small amount of time. As expected, the performance of the heuristic is better on sparse graphs in term of time, but the gap decreases when the graph density increases. The average gap on all instances is 1.5 % and the average CPU time is 340.6 s, while the average gap obtained by a plain Goemans–Williamson algorithm (no 1-opt improvement and $k_{\max }=0$) is $2.04\,\%$ with an average CPU time of 95.7 s.

Furthermore, we consider huge graphs, in order to explore how far we can go with the number of nodes. For this set of instances, we run SpeeDP-MC on a machine with 6 GB of RAM and we set $k_{\max } = 5$ and $\alpha = 10^{-2}$.

We generate three random graphs with $100001$ nodes, $7050827$ edges and different edge weights. For this set of graphs, given the huge size, we choose not to increment $r$ in SpeeDP and we set $r=60$. The results are shown in Table 3, where we report the weight ranges, the upper bound value, the weight of the best cut obtained by SpeeDP-MC, and finally the total CPU time and the % gap for both SpeeDP-MC and the plain GW heuristic.

We also generated some 6-regular graphs (3D toroidal grid graphs) with 1030301 nodes, 3090903 edges, and different edge weights. Also in this case $r$ was not allowed to change and was set to a value of 90. The results are reported in Table 4. To the best of our knowledge, no other methods can achieve this accuracy for graphs of comparable size.

Table 3 Random sparse graphs with 100001 nodes and 7050827 edges

Table 4 6-regular graphs with 1030301 nodes and 3090903 edges

7 Concluding remarks and future work

In this paper we define SpeeDP, a fast globally convergent algorithm for solving problem (1), which belongs to the family of low rank nonlinear programming approaches. SpeeDP outperforms existing methods for solving the special structured semidefinite programming problem (1) and provides both a primal and an approximate dual bound. We also define a heuristic algorithm for Max-Cut, which is a straightforward enhancement of the Goemans–Williamson method, and is able to handle graphs with up to millions of nodes and edges. The heuristic produces both a feasible cut and a valid bound, hence it can certify the maximal deviation of the weight of this cut from the optimum. As a future step, we plan to include SpeeDP in a branch-and-bound scheme similarly to what has been done for an interior point method in the BiqMac code of [32]. This way, we aim at increasing the size of the Max-Cut instances that can be solved exactly by semidefinite programming.