Type-2 zigzag uncertain multi-objective fixed-charge solid transportation problem: time window vs. preservation technology

Abstract

Urgency of fresh items is increasing day by day everywhere. During transportation over a long distance, the rate of deterioration is also increasing for perishable items, and if the items are not reaching at destination within a specified time, then they are no longer fresh. Based on the fact, the customers loose the quality and quantity of items; as a result, suppliers are penalized for the occurrence of any such a situation. This problem is resolved by introducing two criteria such as time window restrictions and preservation technology in the proposed study. To prevent the deterioration rate, we find a strategy by formulating a model for multi-objective fixed-charge solid transportation problem with two criteria and then finalize one of them. To ensure that the necessary fresh items are to reached at the destination just in time, we introduce several objectives such as transportation cost, transportation time, preservation cost, penalty charge for time window, carbon emission with cap policy, deterioration, etc., such that these are optimized simultaneously. Again source, demand and conveyance capacity are not precisely estimated for different real-life situations. Here, we address such situation by choosing type-2 zigzag uncertain variable. Expected value operator is initiated to convert such uncertainty into crisp form, and then three approaches, namely, fuzzy programming, Pythagorean hesitant fuzzy programming and global criterion method are utilized to find Pareto-optimal solution. Finally two numerical examples are put to check the appropriateness of the formulated study. The results along with discussions and conclusions are described at last. The main contribution is that the deterioration of transported perishable items is reduced by imposing one of the proposed criteria according to the economical or other conditions of systems.

1 Introduction

This section introduces several generations of transportation problem (TP), application of time-window (TW) restriction and preservation technology (PT), carbon emission, and appearance of uncertainty.

Motivation: Generally, different types of perishable items or volatile liquids are reached at destinations by covering long distance, lengthy time. Some of them are losing their quality and quantity due to deterioration (e.g., damage, spoilage, dryness, evaporation, etc.). Most important and sensitive perishable items as fruits, fish, blood, medicine, dairy products, vegetables, flowers, alcohol, petroleum fuel, etc., which have a high deterioration rate and cannot be produced easily. In view of this, suppliers loose the production cost on these items and customers cannot avail the required fresh items. As a result, the total charge of the remaining items is increasing. For disposing such items, several effects can occur as, economic losses, environmental affects, consumed of natural resources, decreasing of food safety and fluctuating of orders, etc. So customers face some hesitations for demanding such items from a particular company and they prefer to order such items from other companies. Hence, company or industry takes care the challenging situation for distributing such items. Therefore, the quality of items will be maintained without any economical loss, and customers will get satisfaction. This type of problem is solved by inserting two types of technologies such as TW restriction and PT.

In operational research, uncertainty becomes an unavoidable factor to deal with complexity in real-world applications (in Science, Technology, Engineering and Management or, in short: in STEM). Uncertainty theory with its uncertainty distributions is now a useful branch of axiomatic mathematics to include all uncertainties in designing models under real-life situation. Most of the real-world uncertainty are tackled by fuzzy set theory, random set theory, rough set theory and uncertain set theory. (i) Fuzzy set theory is based on possibility theory which tackles systematic type of uncertainty. (ii) Random set theory handles the uncertainty for random phenomena and random variable, defined on probability space that maps from sample space to real numbers. (iii) Uncertain set theory deals the uncertain information by uncertain variable that describes from uncertainty space to the set of real numbers. If a situation arises under indefinite circumstances whose nature is neither random nor fuzzy, then the situation cannot be tackled by probability theory or fuzzy set theory. Uncertain variables are significant option to overcome such uncertainty, when historical information is not enough for random variables, and possibility theory is not working for a fuzzy variable which is reliable only through membership values. Liu (2007) proposed uncertainty theory and redefined it by Liu (2010). Liu and Ha (2010) proposed the expected value operator for an independent uncertain variable. Each step of a TP faces different unwanted critical situations (e.g., production rate fluctuation, unpleasant road condition, traffic jam, poor weather condition, temperature change, demand rate hesitation, etc.) which cause the required data to be inexact. One type of uncertainty is always connected in a real-life scenario which is challenged by domain experts for evaluating the belief degree with an evaluation grade. Mathematically, four types of uncertain variable (linear, zigzag, normal, log-normal) exist in the literature. The membership function of a zigzag uncertain variable is very much similar to triangular fuzzy membership function. If it is very tough to present the triangular fuzzy membership function, then zigzag uncertain variable is an alternative option. The time when uncertainty occurs more, then type-2 zigzag uncertain variable is initiated that extended from type-1 zigzag uncertain variable. In such a situation, we recommend to study both TW and PT by including type-2 zigzag uncertain variable, and we analyze both restrictions to select a better application such that fresh items are delivered within required time.

For delivering perishable items, the TW restriction is a significant issue. Generally, a TW is applied for fuel delivery to gas station, reaching of military equipment to several fields during wars, urban or industrial waste collection, cash distribution, carrying most important perishable items, etc. Fügenschuh (2006) applied TWs in vehicle routing problem. For strictness, the TW concept is subdivided into a hard TW and a soft TW. For a soft TW that was utilized by Wang and Yin (2018), there exists a penalty charge, but in case of a hard TW, it does not exist. In scientific fields, TW restriction needs a great attention. Inclusion of this restriction for transshipment meets the customers’ demand, as customers always have a demand regarding the delivery time. Here, the TW refers to each vehicle of the transportation system to keep the total elapsed time in an interval, provided by customer or demand centre. If the elapsed time is under a lower bound for providing a hard time interval, then vehicles are to wait for such early service and to incur a penalty charge called as an early service penalty. For reaching the items before the lower bound of provided time interval, destinations are unable to unload the items in excess of the demands capacity. Some industries are not capable to receive these items due to lack of service man or receiver, at that time they may have taken their interval or break time. As a result some parts of the items will start to deteriorate due to refrigeration systems do not work at this waiting moment for stopping the engine of the vehicle. Hence, the profit of total system will be decreased. To balance the profit of demand centres of such situations, they impose a penalty of early service. If the elapsed time crosses the upper bound of time interval, then the transportation system is penalized due to late service, and called as late service penalty. Many items automatically deteriorate after a certain time and, therefore, a huge amount of losses occurs in quantity, quality and being economic, and the demand rate of such items decreases for late service. These penalty charges are the economic loss of transportation which increase the transportation cost. To avoid such penalty charges for violating TW constraints, the transportation system tries to keep the elapsed time in the provided interval and therefore the perishable items will be reached at destination within the required time. Such TW constraint was incorporated by Yan and Zhang (2015), Tirkolaee et al. (2017), Shen et al. (2018), Tirkolaee et al. (2019) in several research works.

Furthermore, PT is another payable extensive criterion to prevent loss and to decrease the chemical reaction of perishable items. If PT (e.g., refrigeration, airtight process, deep-freezing, ice packeting, drying machine, etc.) is attached to perishable items, then the deterioration rate decreases and quality of most part of such items remains same, and the profit will be increased. Such PT was adopted by Giri et al. (2017), He and Huang (2013), Hsu et al. (2010), Pervin et al. (2020) for preventing deterioration in different applications.

TP was proposed by Hitchcock (1941). The important factor of TP is to shift the items from different sources to several destinations. Several types of vehicles are used to distribute the items from sources to destinations. The case when the vehicle capacity is included with source and demand; then TP is considered as a solid transportation problem (STP). Shell (1955) introduced STP, and Haley (1962) defined the solution procedure for solving STP. Das et al. (2020b) represented an STP which was evaluated by heuristic approaches. During the transfer of the items, there exists a certain type of an extra charge (e.g., renting charge, toll tax, permit fees, etc.) which is called as fixed-charge. Hence, TP/STP extends to fixed-charge transportation problem (FCTP)/fixed-charge solid transportation (FCSTP). Hirsch and Dantzig (1968) first initiated FCTP. Ghosh and Roy (2020) proposed an FCTP with multiple objective functions including a product blending constraint in fuzzy-rough situation. They analyzed a fixed-charge by considering truck load constraints in the presence of transfer station. An FCTP was displayed by Midya and Roy (2020) for which the problem was evaluated by rough programming.

If any type of business, industry or supply chain process includes a TP in an enlarge way, then there exist several criteria (e.g., transportation cost, carbon emission cost, preservation cost, penalty charge for time window, transportation time, deterioration rate, etc.). The criteria are contradictory in nature. These criteria must be optimized at the same time, but a conventional TP is not capable to tackle such a problem. This situation is controlled by incorporating multi-objective decision making problem, and we establish an integrated model of multi-objective transportation problem (MOTP). Classical MOTP can be extended as multi-objective fixed-charge transportation problem (MOFCTP) or multi-objective fixed-charge solid transportation problem (MOFCSTP) by including fixed-charge or by including vehicle capacity.

Adhami and Ahmad (2020) proposed an MOTP that was evaluated through Pythagorean hesitant fuzzy programming (PHFP). Ghosh et al. (2020) instigated a simple model of MOFCSTP in fully intuitionistic fuzzy situations. A two-stage MOTP was proposed by Roy et al. (2017) and the problem was evaluated by the selection of goal values, where the parameters are grey numbers. Roy et al. (2019) designed a model for MOFCSTP with multiple items in two-fold uncertain situation.

Carbon emission is now a great challenge in global ecosystem, as most parts of greenhouse gas (GHG) are $CO_2$ whose major part is coming from industry, transport sector, disposal area, human activity, and burning of fossil fuel, etc. Deterioration of items is caused by chemical reaction, temperature change, which also emits a certain amount of $CO_2$. Investment of PT in transportation causes $CO_2$ gas emissions, and therefore a tax for this emission is included with transportation cost. Khanna and Yadav (2020) thought about such situation where carbon emission was occurred by deterioration, investment of PT, and they analyzed the problem by introducing different carbon policies. Public health is effected for such emission, and global climate becomes warmer and warmer. It is noted that transportation system releases a major part of carbon. To mitigate this emission, the government of each country introduced a rule named as Kyoto protocol (Oberthür and Ott 1999). The rule states that a maximum allowable range of $CO_2$ is permitted for each vehicle with its nature, but if the vehicle emits more carbon than the maximum range, then a certain amount of cost will be penalized as a penalty charge to the owner of the vehicle.

Industry and organization put their attention on the negative effect of GHG emission and try to find an innovative method to minimize such emission. Many researchers have concentrated in their study to highlight the environmental issues that relates with carbon emission reduction. Ali et al. (2020) applied the carbon measure performance in a green supply chain for sustainable development and presented a scenario of developing country. Das et al. (2020a) analyzed several carbon regulations as tax, cap, offset policy on a green MOSTP.

Ghosh et al. (2022) initiated several combined policies of carbon mechanism on an MOSTP to reduce carbon emission. Wu et al. (2020) constructed a model for carbon emission reduction of transportation during collection of wet waste through a vehicle routing problem.

Now we place several research contributions in Table 1 which are connected to this work.

Table 1 Contributions of authors’ work and ongoing study

The remainder part of this paper is designed as follows: Section 2 depicts the basic definitions based on type-2 zigzag uncertain environment. Notations with assumptions and model formulation under uncertain environment, and extended model are displayed in Sect. 3. Section 4 briefly describes three methods, namely, fuzzy programming (FP), PHFP and global criterion method (GCM). Two numerical examples are studied in Sect. 5. Section 6 provides optimal results with discussions, contribution with limitations, managerial insights and sensitivity analysis.

Section 7 summarizes the concluding remarks with the outlooks of future researches.

2 Preliminaries

In this section, uncertain space, uncertain measure based on reference Liu (2007), are defined to establish the proposed model.

Definition 1

(Liu 2007): Assume that $\Gamma$ is a non-empty set and L be a $\sigma$-algebra over $\Gamma$. Each element $\Lambda \in L$ is called an event, i.e., measurable set. A number $M(\Lambda )$ finds the belief degree of the uncertain event $\Lambda$. The triplet $(\Gamma , L, M)$ is said to be an uncertain space if the uncertain measure M satisfies the following axioms:

Axiom 1: (Normality axiom) $M(\Gamma )=1$.

Axiom 2: (Duality axiom) $M(\Lambda )+M(\Lambda ^c)=1$, for any event $\Lambda \in L$. $\Lambda ^c$ is the complement of $\Lambda$.

Axiom 3: (Subadditivity axiom) For every countable sequence of events $\Lambda _1, \Lambda _2, \ldots$, we have $M \bigg \{\bigcup _{i=1}^{\infty } \Lambda _i \bigg \} \le \Sigma _{i=1}^{\infty } M \bigg \{\Lambda _i \bigg \}$.

Axiom 4: (Product axiom) Let $(\Gamma _i, L_i, M_i)$ be the uncertain space for $i=1, 2, \ldots$, then product of uncertain measures is also an uncertain measure that satisfies $M \bigg \{\Pi _{i=1}^{\infty } \Lambda _i \bigg \} = {\bigwedge }_{i=1}^{\infty } M \bigg \{\Lambda _i \bigg \}$.

Definition 2

(Liu 2007): A measurable function $\xi$ from an uncertain space $(\Gamma , L, M)$ to the set of real numbers is called as an uncertain variable if $\xi \in B$, for any Borel set B of real numbers.

Definition 3

(Liu 2010): Uncertain distribution $\Phi$ of an uncertain variable $\xi$ is defined by $\Phi (x)= M \{ \xi \le x \}, \forall ~ x \in \mathbb {R}$. An uncertain distribution $\Phi (x)$ is said to be regular if it is a continuous and strictly increasing function with respect to x at which $0<\Phi (x)<1$ and $\lim _{x \rightarrow -\infty } \Phi (x)=0$, $\lim _{x \rightarrow +\infty } \Phi (x)=1$.

Definition 4

(Liu 2010): An uncertain variable $\xi \sim Z(a,b,c)$, $a, b, c \in \mathbb {R}$ and $a<b<c$ is said to be zigzag if it has the uncertain distribution function $\Phi (x)$ as:

$$\begin{aligned} \Phi (x)=\left\{ \begin{array}{ll} 0,&{}\text{ if } x \le a,\\ \frac{x-a}{2(b-a)},&{}\text{ if } a< x \le b,\\ \frac{x-2b+c}{2(c-b)},&{}\text{ if } b < x \le c,\\ 1 ,&{}\text{ if } x > c. \end{array} \right. \end{aligned}$$

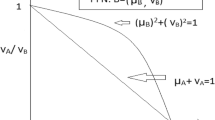
Fig. 1 presents the distribution function of zigzag uncertain variable Z(a, b, c).

Fig. 1

Graphical presentation of zigzag uncertain distribution function

Definition 5

(Liu 2010): The inverse uncertain distribution function of Z(a, b, c) is denoted as $\phi ^{-1}$ and defined as:

$$\begin{aligned} \Phi ^{-1}(\alpha )=\left\{ \begin{array}{ll} (1-2\alpha )a+2\alpha b,&{}\text{ if } \alpha \le 0.5,\\ (2-2\alpha )b+(2\alpha -1)c,&{}\text{ if } \alpha > 0.5. \end{array} \right. \end{aligned}$$

Definition 6

(Liu 2007, 2010): For an uncertain variable $\xi$, the expected value is defined by

$$\begin{aligned} E[\xi ]=\int _0^\infty M \{\xi \ge r\} dr- \int _{-\infty }^0 M \{\xi \le r\}dr. \end{aligned}$$

The useful presentation of the expected value is as:

$$\begin{aligned} E[\xi ]=\int _0^1 \Phi ^{-1}(\alpha ) d\alpha . \end{aligned}$$

Here $\Phi ^{-1}(\alpha )$ is the inverse uncertain distribution of regular uncertain variable $\xi$. For zigzag uncertain variable Z(a, b, c), the expected value is $E[\xi ]=(a+2b+c)/4$.

Definition 7

(Sengupta et al. 2020): Let $Z(a,b,c; \theta _l, \theta _r)$ is a type-2 zigzag uncertain variable, with a and c as the lower and upper possible achievement values and b is the most prospective value lies in [a, c]. Here, $\theta _l, \theta _r \in [0,1]$ (parameters) denote the characterizing degree of this uncertainty.

Definition 8

(Zadeh 1965): Fuzzy set is an analytical part in a universal set. The closed form of uncertainty of fuzzy set is presented by membership grade. For universal set X, a fuzzy set $\tilde{A}$ can be expressed as $\tilde{A}$ = $\{ x,\mu _{\tilde{A}}(x) : x \in X\}$, where $\mu _{\tilde{A}}(x):~X\rightarrow [0,1]$, is the membership of x in $\tilde{A}$.

Definition 9

(Yager and Abbasov 2013): Let X be a universal set, then a Pythagorean fuzzy set (PFS) $\tilde{A}^p$ in X is explained as: $\tilde{A}^p=\{ \langle x,\mu _{\tilde{A}^p}(x),\gamma _{\tilde{A}^p}(x) \rangle : 0\le \mu _{\tilde{A}^p}^2(x)+ \gamma _{\tilde{A}^p}^2(x)\le 1, \mu _{\tilde{A}^p}(x),\gamma _{\tilde{A}^p}(x) \in [0,1], x\in X\}$, where $\mu _{\tilde{A}^p}(x)$ and $\gamma _{\tilde{A}^p}(x)$ are the membership and non-membership functions. The degree of indeterminacy of an element x in the set $\tilde{A}^p$ is defined as the function $\pi _{\tilde{A}^p}(x)=\sqrt{1-\mu _{\tilde{A}^p}^2(x)-\gamma _{\tilde{A}^p}^2(x)}$. Hence, $\mu _{\tilde{A}^p}(x)+\gamma _{\tilde{A}^p}(x)\ge 1$ or $\mu _{\tilde{A}^p}(x)+\gamma _{\tilde{A}^p}(x)\le 1$.

Definition 10

(Liang and Xu 2017): Pythagorean hesitant fuzzy set (PHFS) is introduced by the hesitant situation of PFS. For universal set X, PHFS $\tilde{\check{A}}$ is defined as: $\tilde{\check{A}}=\{\langle x,\mu _{\tilde{\check{A}}}(x),\gamma _{\tilde{\check{A}}}(x)\rangle :x\in X\}$, where $\mu _{\tilde{\check{A}}}(x)$ and $\gamma _{\tilde{\check{A}}}(x)$ are the sets of some values in [0, 1] denoting the possible Pythagorean hesitant membership and Pythagorean hesitant non-membership degree of the element $x \in X$ to the set $\tilde{\check{A}}$, respectively with the conditions $0\le \theta , \eta \le 1$ and $0\le {\theta }^2+{\eta }^2 \le 1$, where $\theta \in \mu _{\tilde{\check{A}}}(x)$, $\eta \in \gamma _{\tilde{\check{A}}}(x),~\forall ~ x ~\in X$. Here, the membership and non-membership degrees are chosen as hesitant fuzzy elements.

Reduction method of type-2 zigzag uncertain variable: Uncertain measure is used to calculate the degree of belief to an event whereas the uncertain variable considers the imprecise information by quality. For critical structure of type-2 zigzag uncertain variable, defuzzification cannot be easily obtained. We select expected value operator from the literature to convert type-2 zigzag uncertain variable into type-1 zigzag uncertain variable. Again inserting expected value operator, we obtain the crisp value. Using the expected value operator on a type-2 zigzag uncertain variable $Z(a,b,c;\theta _l,\theta _r)$, we determine the generated type-1 uncertain distribution as:

$$\begin{aligned} \phi ^{exp}_{\xi }(x)=\left\{ \begin{array}{ll} \frac{x-a}{2(b-a)}-\frac{1}{4}(\theta _l-\theta _r) \frac{x-a}{2(b-a)},&{}\text{ if } x \in (a, \frac{a+b}{2}] ,\\ \frac{x-a}{2(b-a)}-\frac{1}{4}(\theta _l-\theta _r) \frac{b-x}{2(b-a)},&{}\text{ if } x \in (\frac{a+b}{2}, b] ,\\ \frac{x+c-2b}{2(c-b)}-\frac{1}{4}(\theta _l-\theta _r) \frac{x-b}{2(c-b)},&{}\text{ if } x \in (b, \frac{b+c}{2}] ,\\ \frac{x+c-2b}{2(c-b)}-\frac{1}{4}(\theta _l-\theta _r) \frac{c-x}{2(c-b)},&{}\text{ if } x \in (\frac{b+c}{2}, c], \end{array} \right. \end{aligned}$$

for any $x \in (a,b) \cup (b,c)$. The inverse uncertain distribution is defined as:

$$\begin{aligned} \Phi ^{-1}(\alpha )=\left\{ \begin{array}{ll} \frac{4a-a(\theta _l-\theta _r)+8(b-a)\alpha }{4-(\theta _l-\theta _r)},&{}\text{ if } \alpha \in (0, 0.25] ,\\ \frac{4a+b(\theta _l-\theta _r)+8(b-a)\alpha }{4+(\theta _l-\theta _r)} ,&{}\text{ if } \alpha \in (0.25, 0.5] ,\\ \frac{8b-4c-b(\theta _l-\theta _r)+8(c-b)\alpha }{4-(\theta _l-\theta _r)} ,&{}\text{ if } \alpha \in (0.5, 0.75] ,\\ \frac{8b-4c+c(\theta _l-\theta _r)+8(c-b)\alpha }{4+(\theta _l-\theta _r)} ,&{}\text{ if } \alpha \in (0.75, 1]. \end{array} \right. \end{aligned}$$

Utilizing the expected value operator, the final crisp value is defined as:

$E[\xi ]= \frac{1}{4-(\theta _l-\theta _r)} \bigg [\frac{3a+4b+c-(\theta _l-\theta _r)(a+b)}{4}\bigg ]+ \frac{1}{4+(\theta _l-\theta _r)} \bigg [\frac{a+4b+3c+(\theta _l-\theta _r)(c+b)}{4}\bigg ]$.

3 Problem illustration

This section formulates the proposed model by adding usable notations and assumptions.

3.1 Problem grounding

Generally TW and PT are applied in distinct areas. PT is used to prevent the deterioration rate of transported perishable items or volatile liquid such that these will be reached at destination by keeping the quality and the quantity as same as of loading or packeting time. TW concept is applied in time-bound transportation where time variation is an important matter. TW restriction always stresses on time, therefore it is most relevant in scientific area. General TP includes some constraints. If TW restriction is added as a constraint, then customer’s demand increases. For this case the transportation cost is reduced by imposing time interval and minimizing the time duration within it. The deterioration is a general phenomenon for perishable items, and the increasing rate of deterioration is proportional to the decreasing rate of profit. Some of enterprises concentrate on PT as a most significant option to reduce deterioration by investing PT. We investigate both PT and TW in this study to analyze that will be more suitable between them to transport perishable items such that total loss will be minimized. Selecting more suitable criteria, we highlight the advantages of this application. Keeping in mind, environment management is a pivotal factor and to present a green transportation, it is needful to find a strategy which reduces total carbon emission. There exist different regulations to reduce this GHG emission. Our problem includes only carbon cap policy under tax such that it can reduce the emission in an effective way. If the historical information is available, then indeterminacy is handled by probability theory, but when information is not previously accessible then uncertain theory is applicable to estimate the degree of belief. Zigzag uncertain variable is capable to denote linguistic term which can replace triangular fuzzy membership function. To overcome more complex uncertainty, type-2 zigzag uncertain variable is augmented from zigzag uncertain variable. Our focus is to establish the model of MOFCSTP with parameters of the constraints like source, demand, and conveyance as type-2 zigzag uncertain variables. The main goal is to derive a Pareto optimal solution of the proposed study that minimizes total cost in terms of transportation cost, fixed-charge, penalty cost for allowable TW, carbon emission cost (from transportation and from PT), preservation cost. In addition to the above, transportation time and deterioration rate are optimized with presence of PT and TW restriction independently.

3.2 Notations and assumptions of the proposed study

A list of required notations explained in Table 2 and necessary assumptions are considered here to formulate the model of MOFCSTP with PT and TW restriction.

Table 2 Useful notations with their nature and descriptions

Assumptions:

• $\tilde{\hat{a}}_i>0$, $\tilde{\hat{b}}_j>0$, ${\tilde{\hat{e}}_{k}}>0$, $\forall ~i,~j,~k.$

• Elapsed time is the total time of loading, unloading and transportation of shifted items.

• Total elapsed time $T_j$ of $j^{th}$ distribution centre is expressed mathematically as: $\sum _{i=1}^I \sum _{k=1}^K {t}_{ijk} {\eta }_{ijk}, ~\forall ~j$.

• PT works from loading time to receiving time.

• When only TW restriction is included on transportation, then a minimum refrigeration cost is added with fixed-charge which is not a preservation cost and this refrigeration works only on vehicle’s running time.

• Penalty charge for TW is described as:

  $$\begin{aligned} P_j=\left\{ \begin{array}{ll} P^e_{j},&{}\text{ if } T_j < ET_j,\\ 0,&{}\text{ if } ET_j\le T_j\le LT_j,\\ P^l_{j},&{}\text{ if } T_j>LT_j. \end{array} \right. \end{aligned}$$

• Total carbon emission from transportation and from PT: $E=E_1+E_2 = e^1 D_{ijk} x_{ijk}+\alpha e^2 t_{ijk} x_{ijk}$.

3.3 Integrated multi-objective optimization model

Here, we design the mathematical model (Model 1) of MOFCSTP with uncertain variables. This model includes all the criteria of both PT and TW restriction.

Model 1

$$\begin{aligned} \text{ minimize }&{Z}_1=\sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K \bigg [{x}_{ijk}{c}_{ijk}+ {y}_{ijk}{f}_{ijk}\bigg ]+\theta [E-C]^+ + \alpha \sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K\nonumber \\&\qquad \qquad {p}_{r} t_{ijk}{x}_{ijk} +\sum _{j=1}^J P_j\bigg [{[ET_j-T_j]^+}+{[T_j-LT_j]^+}\bigg ]\end{aligned}$$

(1)

$$\begin{aligned} \text{ minimize }&{Z}_2=\sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K {t}_{ijk}{\eta }_{ijk}\end{aligned}$$

(2)

$$\begin{aligned} \text{ minimize }&{Z}_3=\sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K d_{ijk} t_{ijk}x_{ijk}\bigg / {\alpha } \sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K d_{ijk}t_{ijk}x_{ijk}\end{aligned}$$

(3)

$$\begin{aligned} \text{ subject } \text{ to }&\sum _{j=1}^J \sum _{k=1}^K {x}_{ijk} \le {\tilde{\hat{a}}_i} ~~(i=1,2,\ldots ,I),\end{aligned}$$

(4)

$$\begin{aligned}&\sum _{i=1}^I \sum _{k=1}^K(1-d_{ijk}t_{ijk}){x}_{ijk} \ge {\tilde{\hat{b}}_j} ~~(j=1,2,\ldots ,J),\end{aligned}$$

(5)

$$\begin{aligned}&\sum _{i=1}^I \sum _{k=1}^K(1-\alpha d_{ijk}t_{ijk}){x}_{ijk} \ge {\tilde{\hat{b}}_j} ~~(j=1,2,\ldots ,J),\end{aligned}$$

(6)

$$\begin{aligned}&\sum _{i=1}^I \sum _{j=1}^J {x}_{ijk} \le {\tilde{\hat{e}}_k} ~~(k=1,2,\ldots ,K),\end{aligned}$$

(7)

$$\begin{aligned}&T_j\in [ET_j, LT_j] ~~\forall ~j,\end{aligned}$$

(8)

$$\begin{aligned}&{x}_{ijk}\ge 0, \forall ~i,~j,~k.~~ \end{aligned}$$

(9)

Here, $[ET_j-T_j]^+ = {\max } \big \{ET_j-T_j, 0 \big \}$ and $[T_j-LT_j]^+ = {\max } \big \{T_j-LT_j, 0 \big \}$ are the soft TW restrictions. Also $[E-C]^+ = {\max } \big \{E-C, 0 \big \}$ appears in the constraint for the carbon cap policy. The feasibility condition of this TP is labelled as follows: $\sum _{i=1}^m {\tilde{\hat{a}}_i}\ge \sum _{j=1}^J {\tilde{\hat{b}}_j}$; $\sum _{k=1}^K {\tilde{\hat{e}}_k}\ge \sum _{j=1}^J {\tilde{\hat{b}}_j}.$

Model 1 incorporates three objective functions. The first objective is the total cost, where $1^{st}$ sum represents the transportation cost and the fixed-charge from $i^{th}$ source to $j^{th}$ destination through $k^{th}$ conveyance. The $2^{nd}$ portion describes carbon emission cost which considers when total emission E (defined in assumptions) is greater than cap value C, otherwise its value is zero. $3^{rd}$ part includes preservation cost for perishable items, and it is considered whenever PT is added from $i^{th}$ source to $j^{th}$ destination and the transportation is completed by $k^{th}$ type of vehicles. Last sum calculates the penalty cost for violation of TW restriction, where the $j^{th}$ destination declares the time interval as $[ET_j, LT_j]$. If total elapsed time is below from $ET_j$, then the penalty charge $P_e$ is considered for waiting time of early service, and if total elapsed time crosses $LT_j$, then the penalty charge $P_l$ includes for late service. It holds $P_j = 0$, if total elapsed time belongs to the defined time interval. The second objective says about the total elapsed time from $i^{th}$ source to $j^{th}$ destination by $k^{th}$ class of conveyance. Third objective is the total deterioration from $i^{th}$ source to $j^{th}$ destination through $k^{th}$ mode of vehicles, and it is considered with or without presence of PT. Constraints (4) explain the source condition, and constraints (5), (6) describe the demand condition for two separate criteria. Constraints (7) expresses as the state of conveyance capacity. Constraints (8) illustrate the hard TW constraint for each demand, and constraints (9) outline for non-negativity restriction.

3.3.1 Identical deterministic model

Since Model 1 is connected with uncertain variable, so this model cannot be evaluated easily.

Using expected value operator, we convert Model 1 into deterministic form as Model 2.

Model 2

$$\begin{aligned} \text{ Equations }&(1)-(3)\nonumber \\ \text{ subject } \text{ to }&\sum _{j=1}^J \sum _{k=1}^K {x}_{ijk} \le E[{\tilde{\hat{a}}_i}] ~~(i=1,2,\ldots ,I),\end{aligned}$$

(10)

$$\begin{aligned}&\sum _{i=1}^I \sum _{k=1}^K(1-d_{ijk}t_{ijk}){x}_{ijk} \ge E[{\tilde{\hat{b}}_j}] ~~(j=1,2,\ldots ,J),\end{aligned}$$

(11)

$$\begin{aligned}&\sum _{i=1}^I \sum _{k=1}^K(1-\alpha d_{ijk}t_{ijk}){x}_{ijk} \ge E[{\tilde{\hat{b}}_j}] ~~(j=1,2,\ldots ,J), \end{aligned}$$

(12)

$$\begin{aligned}&\sum _{i=1}^I \sum _{j=1}^J {x}_{ijk} \le E[{\tilde{\hat{e}}_k}] ~~(k=1,2,\ldots ,K), \\&{\text{ constraints }}~(8)-(9). \nonumber \end{aligned}$$

(13)

The feasibility conditions of this TP are also deterministic form as: $\sum _{i=1}^m E[\tilde{\hat{a}}_{i}]\ge \sum _{j=1}^J E[\tilde{\hat{b}}_{j}]$,  $\sum _{k=1}^K E[\tilde{\hat{e}}_{k}]\ge \sum _{j=1}^J E[\tilde{\hat{b}}_{j}].$

3.3.2 Extension of model

To shrink the deterioration, we impose two restrictions. To analyze and select best restriction, we generate our proposed model by splitting into two separate models; one is under TW restriction in Model 3A and another is under inclusion of PT, defined in Model 3B as follows:

Model 3A (with TW):

$$\begin{aligned} \text{ minimize }&{Z}_1=\sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K \bigg [{x}_{ijk}{c}_{ijk}+ {y}_{ijk}{f}_{ijk}\bigg ]+\theta [E_1-C]^+ \nonumber \\&\qquad \quad + \sum _{j=1}^J P_j\bigg [{[ET_j-T_j]^+}+ {[T_j-LT_j]^+}\bigg ]\\ \text{ minimize }&{Z}_2=\sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K {t}_{ijk}{\eta }_{ijk}\\ \text{ minimize }&{Z}_3=\sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K d_{ijk}t_{ijk}x_{ijk}\\ \text{ subject } \text{ to }&{\text{ constraints }}~(8)-(11),~(13). \end{aligned}$$

Model 3B (MOFCSTP with PT):

$$\begin{aligned} \text{ minimize }&{Z}_1=\sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K \bigg [{x}_{ijk}{c}_{ijk}+ {y}_{ijk}{f}_{ijk}\bigg ]+\theta [E-C]^+ + {\alpha }\sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K \nonumber \\&{p}_{r} t_{ijk}{x}_{ijk} \\ \text{ minimize }&{Z}_2=\sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K {t}_{ijk}{\eta }_{ijk} \\ \text{ minimize }&{Z}_3={\alpha }\sum _{i=1}^I \sum _{j=1}^J \sum _{k=1}^K t_{ijk}d_{ijk}x_{ijk} \\ \text{ subject } \text{ to }&{\text{ constraints }}~(9)-(10),~(12)-(13). \nonumber \end{aligned}$$

The feasibility conditions of Model 3A and Model 3B are same as Model 2.

Definition 11

A solution $x^*=({x}^*_{ijk}:i=1,2,\ldots ,I;j=1,2,\ldots ,J;k=1,2,\ldots ,K) \in F$ (where F is the feasible region) is said to be a Pareto-optimal solution (an efficient solution) of Model 3A/Model 3B if there exists no other $x=({x}_{ijk}:i=1,2,\ldots ,I;j=1,2,\ldots ,J;k=1,2,\ldots ,K) \in F$ such that ${Z_u}(x)\le {Z_u}(x^*),~ u=1,2,3$ and ${Z_u}(x)< {Z_u}(x^*)$ for at least one u.

4 Solution mode

The proposed study subsists three objective functions and each of them opposes to other objectives. There does not exist a single solution which will optimize all these objectives concurrently, i.e., it will be best for one objective and may be worst for the others. To get a compromise solution of the multi-objective decision making, we include three techniques which provide a Pareto-optimal solution that optimizes all the objective functions at a time. There exist several fuzzy techniques and non-fuzzy techniques from which we select two fuzzy techniques as FP and PHFP, and a non-fuzzy technique as GCM. FP was proposed by Zimmermann (1978) and the stepwise procedure are followed from reference Ghosh et al. (2020). GCM was initiated by Miettinen (1999) and this method is outlined from reference Ghosh and Roy (2020).

4.1 Pythagorean hesitant fuzzy programming

PHFP is a modified and improved fuzzy method based on PHFS, that finds the Pareto-optimal solution of the proposed model of MOFCSTP. This programming strives to maximize the Pythagorean hesitant membership grade and minimize the Pythagorean hesitant non-membership grade, and decision maker (DM) chooses the appropriate hesitant values corresponding to each membership and non-membership function in an efficient way. A novelty of PHFP is that its solution reports the spectrum of uncertainty in a unique way that different from FP. Using the PHFP solution criteria we follow the stepwise procedure is

• Step 4.2.1: Transform the type-2 zigzag uncertain multi-objective model into deterministic form and solve each objective problem independently with subject to all constraints.

• Step 4.2.2: Substitute the obtained solution in each objective function and select the positive ideal solution (PIS) and negative ideal solution (NIS) corresponding to every objective function as follows: PIS = $L_u$ = $\min \{Z_{u1},Z_{u2},Z_{u3}\}$ and NIS = $U_u$ = $\max \{Z_{u1},Z_{u2},Z_{u3}\}$ $(u=1,2,3)$, where $Z_{ur}$ = $Z_u(X^r)~(r=1,2,3)$.

• Step 4.2.3: Utilize PIS and NIS, construct the membership and the non-membership function corresponding to each objective function in Pythagorean hesitant fuzzy environment as:

  $$\begin{aligned} \mu _h^P(Z_u(x))=\left\{ \begin{array}{ll} 1,&{}\text{ if } {Z_u(x)}< L_{u},\nonumber \\ \alpha _u \big (\frac{U_u-Z_u(x)}{U_{u}-{L_{u}}}\big ),&{}\text{ if } L_{u}\le {Z_u(x)}\le U_{u},\nonumber \\ 0 ,&{}\text{ if } {Z_u(x)}> U_{u}, \end{array} \right. \\ \nu _h^P(Z_u(x))=\left\{ \begin{array}{ll} 0,&{}\text{ if } {Z_u(x)} < L_{u},\nonumber \\ \beta _u\big (\frac{{Z_u(x)}-L_{u}}{U_{u}-L_{u}}\big ),&{}\text{ if } L_{u}\le {Z_u(x)}\le U_{u},\nonumber \\ 1 ,&{}\text{ if } {Z_u(x)} > U_{u}. \end{array} \right. \end{aligned}$$

  Here, $\alpha _u, \beta _u \in [0,1]$ are the sets of hesitant values correspond to membership and non-membership functions, respectively.

• Step 4.2.4: To detect the maximum degree for satisfaction and minimum degree for rejection, the PHFP model for solving multi-objective decision making problem is reported as follows:

  Model 4

  $$\begin{aligned} \text{ maximize }&\frac{\eta _1^2+\eta _2^2+\eta _3^2}{3}-{\frac{\zeta _1^2+\zeta _2^2+\zeta _3^2}{3}}\\ \text{ subject } \text{ to }&[\mu _h^P(Z_u(x))]^2\ge {\eta _u^2}~(u=1,2,3),\\&[\nu _h^P(Z_u(x))]^2\le {\zeta _u^2}~(u=1,2,3),\\&{\eta _u^2}\ge {\zeta _u^2},\\&{\eta _u^2}+{\zeta _u^2} \in [0,1], {\eta _u^2} \in [0,1], {\zeta _u^2} \in [0,1],\\&{\text{ constraints }}~(9),(10),(13),\nonumber \\&{\text{ constraints }}~(8),(11)~{\text{ or } \text{ constraint }}~(12). \end{aligned}$$

  Here $\eta _u$ and $\zeta _u$ are the membership grades and the non-membership grades corresponding to each objective function.

• Step 4.2.5: Solve Model 4 by the LINGO iterative scheme with parameters $\eta _u$ and $\zeta _u$ to achieve Pareto-optimal solution(s) of the proposed model(s).

Theorem 1

If $(x^*,\eta _u^*, \zeta _u^*)$ is an optimal solution of Model 4 then it is also a Pareto-optimal (an efficient) solution of Model 3A/Model 3B or both.

Proof

The proof of this theorem is apparent from reference Ghosh et al. (2022). $\square$

5 Case study

To check the applicability of our proposed model, two real-life case studies are performed in this research. Example 1 is experiment for perishable items and Example 2 is illustrated for volatile liquid.

Example 1: We select a fruit supply transportation system that shifts grapes from three states (Madhyapradesh, Uttarpradesh, Maharashtra) to four states (West Bengal, Odisha, Jharkhand, Bihar) of India. Grapes have begun to deteriorate after 48 hours (approximate) from collection time without preservation. During long time transportation, the rate of deterioration is also increased. To reach the fruits at destination in such a way that the quantity and the quality remain same, we consider two types of investment (PT and TW) independently. Both cases try to optimize cost, time and deterioration in intelligent process by imposing different conditions. We define the input data by inserting three source points $(I=3)$, four demand centres $(J=4)$ and two types of conveyances $(K=2)$. Source, demand and conveyance data are as type-2 zigzag uncertain variable with their deterministic values, transportation cost with fixed-charge (in Rupees), distance (in kilometers), rate of deterioration (in %), elapsed time with time interval for hard TW (in hours) are presented in Tables 3, 4, 5, 6, 7, 8. Rate of preservation (in %), preservation cost (per unit item per unit time), tax for extra carbon emission of cap policy, penalty charge for TW, rate of carbon emission (for transportation and for PT), and carbon cap value are presented in Table 9.

Table 3 Supply, demand and conveyance capacity

Table 4 Transportation cost

Table 5 Fixed-charge

Table 6 Distance for transportation

Table 7 Elapsed time and hard TW interval

Table 8 Deterioration rate for perishable items

Table 9 Carbon emission rate, tax, carbon cap, preservation rate, preservation cost, penalty charge for TW

Example 2: An industrial application of alcohol transportation from production plant to petroleum refinery is chosen in this example. Methanol is a volatile liquid that is produced in industry by the hydrogenation of carbon monoxide, and transported as a raw material. Methanol is blended into gasoline to produce high-octane efficient fuel that has lower emission rate than ordinary gasoline. We survey two source centres (Bihar and Uttarpradesh) and two petroleum refineries (West Bengal and Odisha). Methanol transportation is of high risk, therefore, special hazard and incident responses of training are needed. Vehicles must put a placard with necessary permission from the government to authorize transport. We select drum (55 gallons) as container to transport methanol, whereas two types $(K=2)$ of vehicle capacity, two supply centres $(I=2)$ and two demand points $(J=2)$ are defined with input data. All the other data, whose units are same as of Example 1 (except source, demand and vehicle capacity in gallons), are displayed in Tables 10, 11, 12, 13.

Table 10 Supply, demand and conveyance capacity

Table 11 Transportation cost, fixed-charge, distance

Table 12 Elapsed time with hard TW interval and deterioration rate

Table 13 Carbon emission rate, tax, carbon cap, preservation rate, preservation cost, penalty charge for TW

6 Results and discussions

We solve both examples by three approaches and derive the Pareto-optimal solutions. The values of the objective functions are presented in Table 14. From Table 14, we observe that the PHFP provides better Pareto-optimal values (shown in bold face) than the other two approaches, namely FP and GCM.

Table 14 Objective function values for Example 1 and Example 2

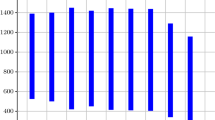
To show the effect of PT and TW restriction on this MOTP of perishable items, The Pareto-optimal solutions obtained in PHFP are displayed graphically in Figs. 2, 3, 4, 5

Fig. 2

Pareto-optimal solution for Z1 (EX1)

Fig. 3

Pareto-optimal solution for Z2 and Z3 (EX1)

Fig. 4

Pareto-optimal solution for Z1 (EX2)

Fig. 5

Pareto-optimal solution for Z2 and Z3 (EX2)

Figures 2 and 4 show that transportation cost (TC), fixed-charge (FC), emission charge (EC) and penalty charge (PeC) or preservation cost (PrC) are fluctuating in both examples, but total cost in PT is greater than in the TW case. Figures 3 and 5 display that time and deterioration are better when PT is included for both examples. Both TW and PT cases include transportation cost and fixed-charge, but TW considers the GHG emission for the transportation case only. In contrast, PT includes GHG emission from transportation and from PT. Therefore, in the TW case, the total emission may be held under cap value. Then the penalty charge for cap policy is not included. But a penalty charge is considered for a TW restriction, if the required time does not belong to the provided interval of the hard TW. This penalty charge is nil, if the elapsed time fulfils the TW restriction. PT imposes a preservation cost in the whole duration of transportation which is never neglected. Again, carbon emission is increased for extra emission from PT. Therefore, the total emission may be overtaken the cap value and penalty charge may be imposed for the cap policy. For these causes, the total investment cost of PT exceeds the total investment cost of TW case. Some situations arise when the quantity and the quality of items are more important than money, then PT must be selected rather than the TW case. TW restriction has some extra advantages. For example, (i) it is important for transporting military equipments, (ii) the total carbon emission for TW case is lower when using PT, (iii) penalty charge for violation of TW restriction may or may not appear. To improve the states of the environment and to prevent from global warming, TW restriction is also a suitable criterion.

6.1 Contributions and limitations of the proposed study

The present study provides some research contributions and defines some limitations which are presented as follows:

• Equating to the references (Shen et al. 2018; Tirkolaee et al. 2017, 2019; Wang and Yin 2018; Wu et al. 2020) for single objective problem, we modify the research gap by establishing a mathematical model of MOFCSTP.

• To reduce GHG emission, the authors of the references (Maity et al. 2019; Tirkolaee et al. 2019, 2017; Wang and Yin 2018; Yan and Zhang 2015) inaugurated their proposed model without carbon emission, whereas the authors Wu et al. (2020) included carbon emission without any carbon policy. We design this study by adding carbon emission from transportation and from PT, and introduce a carbon cap policy.

• To prevent the deterioration of perishable items, the authors of references (He and Huang 2013; Maity et al. 2019; Shen et al. 2018; Tirkolaee et al. 2019, 2017; Wu et al. 2020; Yan and Zhang 2015) did not choose any technology in their study. We impose PT in the present model that minimizes the deterioration rate of transported perishable items.

• To minimize elapsed time or to minimize deterioration rate of some sensitive perishable items, the authors of references (Adhami and Ahmad 2020; Giri et al. 2017; He and Huang 2013; Hsu et al. 2010; Khanna and Yadav 2020; Maity et al. 2019; Wu et al. 2020) did not restrict any extra condition, but we extend this research by inserting TW restriction that provides several advantages to prevent deterioration and to optimize elapsed time.

• To control real-life scenario, the authors of the existing literature (Giri et al. 2017; He and Huang 2013; Hsu et al. 2010; Khanna and Yadav 2020; Shen et al. 2018; Tirkolaee et al. 2017; Wang and Yin 2018; Wu et al. 2020; Yan and Zhang 2015) did not incorporate any type of uncertainty. But the proposed study is executed by initiating a new environment, namely type-2 zigzag uncertain.

• To evaluate the Pareto-optimal solution of proposed model and to check the validity of model, we employ two fuzzy techniques, namely, FP and PHFP, and a non-fuzzy technique, GCM. Two scenarios with PT and TW restriction are analyzed to select the best technology.

• The limitation of this pioneering is that the problem is based on a TW restriction but it is not chosen with a vehicle routing problem. The deterioration is incorporated for perishable items whereas waste management is not. We take three objective functions from a real a point of view, but sustainability is not yet analyzed here. Those extensions are planned in our future research.

6.2 Managerial implications

An effective model of transportation problem is studied in this paper.

The following managerial implications are summarized from the numerical study.

• The formulated model of MOTP becomes more realistic on the ground of type-2 zigzag uncertain environment that helps DM to select the right option easily for controlling any uncertainty. This study provides an opportunity to solve a problem for transporting perishable or volatile items, and helps to select a choice between PT and TW restriction. This study balances cost, time and deterioration, which are most challenging tasks for DM.

• The supplier company finds any trade-off between PT and TW restriction for minimum carbon emission cost by the adjusted cap value of carbon cap policy. The present study addresses an improved result of less emission cost, and the enterprise pays more attention to an environment friendly transportation channel. Therefore, the coordinated model is beneficial from an environmental viewpoint.

• The discussion shows that demand depends on deterioration rate, so it is practical for real-life scenario that a supplier must provide actual quality of items. Otherwise the total profit will be decreased by paying a preservation cost or a penalty charge. Again, total deterioration values depend on the elapsed time, so that the organization can easily determine the impact of PT and TW restriction. Based on this and from this experiment, the DM will certainly select the appropriate potential type.

• Introduction of a TW restriction as constraints in this formulated model plays a positive role for customers’ satisfaction. The organization can improve the way for obtaining less elapsed time within a time interval. Both the supply and demand centers are facilitated by the variant values of a hard TW interval and penalty charge for the violation of a soft TW restriction.

• From Table 14, it is analyzed that investment cost leads to a contradictory situation. Financially strong company selects PT whenever the quality of items is more important, and a financially weak company chooses a TW strategy with less emission cost. Our proposed approach provides two insights such that the supplied company invests the suitable strategy in an actual situation.

6.3 Sensitivity analysis

This subsection analyzes the impact of source, demand and conveyance parameters through the sensitivity analysis of PHFP. Both examples with PT are analyzed to interpret the range of these parameters in the objective function, as we obtain a better result when PT is used. We examine the range of parameters and find the effect of slide change by keeping the same optimal solution. This analysis is applicable only whenever one parameter is changed at a time and the other parameters will be kept at their initial values. In this analysis, the basic variables need not to be changed, but its values may vary. The ranges of these parameters are determined by a convenient method.

First, the DM selects the allocation of the basic variables to the optimal solution of MOFCSTP. Now, fluctuating the value of each parameter by setting the other parameters at the place of the actual values, we solve the problem by PHFP with LINGO 19 iterative scheme. The fluctuation process is continued until no feasible solution comes out or the basic variable changes in an optimal solution. Examining the range of each parameter, we trace the changing values which are highlighted in Table 15 for a clearer perspective.

Table 15 Ranges of supply, demand and conveyance of Example 1 and Example 2

7 Conclusion and future research scopes

Nowadays, governments and researchers have put their attention on public health and food safety which have been affected by TP. Keeping this on mind, we have established an MOFCSTP model which have been analyzed by two separate criteria such as PT and TW. Main focus has to prevent the deterioration, as the quality must be keep good with any financial condition. Since the TW criterion has been imposed a penalty charge by putting a restriction for the violation of time interval, therefore, this helps to reach the items at a destination within the provided time interval with the least deterioration of items by time minimization. Again PT preserves the items by incurring a preservation cost and extends the non-deterioration period of items by managing the quality and the quantity loss. Since the environmental condition is a vital issue, therefore to reduce carbon emission from transportation and from PT, a carbon cap policy has been included. We have incorporated a type-2 zigzag uncertain variable to accommodate more information of tackling real-life situations. Analyzing two case studies, we concluded that the quality and the quantity of the items are better when we have considered PT during transporting for perishable items or volatile liquid. We have included a TW restriction for the financial side and from the environmental viewpoint.

Future research will be continued by taking normal or log-normal variables or Gaussian type-2 fuzzy variables in the proposed model based on sustainability (Yan et al. 2020; Rosario et al. 2020). Intervals can be multiplied, defining cubes which can be generalized to ellipsoids (Kropat et al. 2011). A waste management process with perishable items may be chosen in the proposed model.