1 Introduction

Shipping is the major international transportation mode and liner shipping service has increased significantly during recent years (Yao et al. 2012). World Shipping Council states that “there are almost 6000 ships, mostly container ships operating in liner services and container ships come in a variety of sizes.” In the liner shipping service, container ships operate on closed routes and follow a published schedule to transport containers between origin and destination ports. In this paper, for a heterogeneous fleet liner shipping service we propose a new approach to design a robust schedule against unexpected delays at ports.

According to Ronen (2011), bunker fuel cost constitutes three quarters of the operating cost of a larger container ship when fuel price is around 500 USD per ton. Therefore, shipping companies prefer slow steaming to reduce the fuel consumption cost during the journey. Hence, speed decisions are critical for the cost performance of a liner shipping service.

Liner shipping companies announce fixed schedules in advance and it is important for these companies to provide a reliable schedule to its customers. In a recent study based on interviews and surveys with practitioners, Yuen and Thai (2015) state that time-related factors, such as on-time pick-up and delivery, has the greatest impact on customer satisfaction. Therefore, punctual arrival and departure of container ships is also of utmost importance to the liner shipping companies. In this paper, we define a service level measure based on published departure times at ports and develop a model that trades off fuel burn and on-time departure objectives. In particular, we define service level at a given port for a certain ship type as the probability that the ship will depart from the port on-time, i.e. at the fixed departure time preannounced by the liner shipping company. Furthermore, we define overall service level for a liner shipping service as the weighted sum of service levels for every port-ship type pair.

Many factors such as congestion, fluctuation of container handling times and weather conditions affect actual arrival and departure times of ships. For absorbing possible delays, shipping companies insert some buffer times in their schedules. However, buffer times have to be allocated with care through the schedule. Therefore, a careful schedule design with departure times at ports and speed levels between ports is essential to allocate buffer times appropriately along the schedule.

Given published departure times of a ship at two successive ports in the schedule, increased speed (decreased sailing time) between the two ports implies higher fuel burn but longer buffer time between two departures. Longer buffer times help to tolerate longer delays due to handling operations and waiting times at ports. In the expense of fuel cost, the company can have a more robust schedule. The planner has to make a trade-off between fuel burn cost and service level (on-time departure performance). Since we consider a heterogeneous fleet with different ships having different fuel efficiencies, the trade-off has to be made for each ship-port pair. In this paper, we develop a liner ship scheduling model that makes departure time, speed and service level decisions simultaneously.

We consider a single heterogeneous fleet deployed on a single closed-loop route. The problem is to find a cyclic schedule, i.e. periodic departure times at each port for the shipping service. We develop a model that finds departure times at ports, sailing speed on each leg for each ship type and service levels at the ports. We define chance constraints for the probability of on-time departure at each port. Our model determines service level (on-time departure probability) at each port and guarantees that an overall service level is achieved. Since, it’s a heterogeneous fleet, each ship can sail at a different speed on the same leg but has to follow the same departure times at ports.

Different sources of uncertainties in liner shipping service have been considered in the literature. In a recent study, Wang and Meng (2012b) deal with designing a robust schedule for a homogeneous fleet liner ship service. They consider uncertainty in waiting times of ships and handling times of cargoes in their study. They formulate the problem as a mixed-integer nonlinear stochastic programming model. For solving the model, they apply sample average approximation method and linearize the nonlinear terms in the model.Differently, in this paper, we consider a heterogeneous fleet where each ship type has different engine characteristics and hence a different fuel burn function. We also propose a new service level measure for the entire schedule. We define a service level for each port-ship type pair so that different ship types can have different speeds on the same leg. We then combine all port-ship type pairs’ service levels in a single single service level measure. In the overall service level measure, each port has a weight to represent the different importance levels of ports for a liner shipping company. This allows our model to find speed for each ship type on each leg and service level for each port-ship type pair. We formulate the scheduling problem as a chance constrained mixed integer program and reformulate chance constraints and fuel burn functions via second order conic inequalities.

Christiansen and Fagerholt (2002) consider uncertainties in liner shipping operations and propose a method to find robust schedules. Assuming fixed speeds, they first generate all feasible schedules and then evaluate the schedules using a penalty cost term to find a robust schedule. Wang and Meng (2012a) consider uncertainty of port time and sailing speed control in designing a schedule for a liner shipping service. Their objective is to minimize the total expected fuel consumption and operating cost. They develop a mixed integer nonlinear convex stochastic problem and approximate the objective function by applying piecewise linearization. Qi and Song (2012) consider designing a schedule for a liner shipping service to minimize the total fuel consumption under port time uncertainty. They consider stochastic port times and delays in arrival times of ships and use a simulation based stochastic approximation method to solve the problem. These studies consider homogeneous fleet on a single route. However, in practice, different ship types can be employed on the same route, which is the case studied here. As mentioned before, we propose a different service level measure which takes into account the differences between ports and ships.

There is a comprehensive survey and taxonomy around speed models in maritime in the study of Psaraftis and Kontovas (2013). They have reviewed the related papers in this area and classified them according to various criteria. There is usually a nonlinear relation between speed and fuel consumption. Small changes in speed may cause large changes in fuel consumption rate. Fuel consumption of a ship depends on a number of factors related to its size, speed, power plant and deadweight of a ship according to European Commission European Commission (2000). Water depth and weather condition also affect fuel consumption rate. According to fuel consumption data of ships, different fuel consumption functions with different coefficients are derived. We summarize the functions that are used in the maritime literature in Appendix 1. In most of the studies, fuel consumption is considered to be a function of speed only. However, some articles have derived functions that are dependent on speed and displacement of a ship. In general, power functions and exponential functions are used in the literature. Most of the studies approximate fuel consumption per day as a cubic function of speed. However, Psaraftis and Kontovas (2013) indicate that this approximation is good for tankers and bulk carries, but it may not be good for container ships and for these ships, exponent 4, 5 or even higher could be considered. In our problem, we use the fuel burn function given by Yao et al. (2012).

1.1 Contribution of the study

This study contributes to the literature in different aspects. The first one is considering the heterogeneous fleet case in robust scheduling of liner ship services. We show that if fuel burn is minimized for the whole fleet, different ship types have different speeds and different buffer times on the same leg. Our model schedules departure times, speeds and buffer times for a heterogeneous fleet.

The second one is considering the fact that the ports are different in capacity, demand, congestion, and many other factors. So, handling and waiting times might also be different at the ports. Each port has a different importance and priority for a liner shipping company. Therefore, company may prefer to provide different levels of service at different ports. In this paper, we provide a model that can control service levels at different ports.

The third new aspect of this study is proposing a new service level measure for the liner shipping service schedule. We first define service level at a port as the probability of on-time departure of a ship from that port. Furthermore, we define an overall service level measure for the entire route. The overall service level measure represents the priority choices of the company among ports.

The rest of the paper is organized as follows. In Sect. 2, we give a comprehensive statement of the problem, assumptions and mathematical model. We then, reformulate the model and give MISOCP representation of the model in Sect. 3. Finally, in Sect. 4, we present computational results.

2 Problem definition

We consider a liner shipping service provided by a fleet of ships for a set of ports. Each ship sails on the same fixed tour, visiting all the ports in the service and ending at the starting port. Departure time at a port is the same for each period, i.e. if the period is one week, a departure time at a port is a certain time of a certain day of the week and it is fixed. We assume a weekly schedule as liner shipping companies mostly provide weekly regular services. If the entire tour takes k weeks, then the service requires k ships so that weekly service frequency can be provided to the ports. We assume that a set of ports, a fixed tour with known duration (N weeks) and a fleet of N ships is given. As we assume a heterogeneous fleet, we assume that fuel burn functions, speed limits are different and known for all ships.

Handling time refers to the time that is needed for loading and unloading cargoes at a port. Waiting time for a ship is the duration that a ship has to wait after arriving at a port but before loading-unloading operations begin. For the major ports, waiting time might be higher due to higher congestion at those ports. We assume that handling times may be different for different ship types due to ship size, but waiting time at a port is the same for all ship types. We model the uncertainty in handling and waiting times using probability distributions. Handling operations and waiting times are composed of detailed processes. However, similar to studies in the literature, such as Bellsolà et al. (2017), we assume that handling and waiting times at the ports of the sailing route follow normal distribution. Nevertheless, our modeling approach can still be used for any distribution for waiting and handling time given that the distribution has a quantile function that can be evaluated at different probability levels.

In order to absorb unexpected delays, buffer time is inserted in a schedule. As an example, in Fig. 1, there are three ports on a closed service route. Each ship visits the first port after finishing the round-trip journey. The difference between departure times at two sequential ports is given by the sum of the sailing time, buffer time and the mean of handling and waiting times.

Fig. 1
figure 1

Illustration of the problem

Full size image

In this study, we measure service level of a ship-port pair as the probability of on-time departure of a ship from a port. In other words, service level for a ship-port pair is the probability that total waiting and handling time does not exceed mean waiting and handling time plus the buffer time. A similar service level measure is defined in a robust airline scheduling problem by Serasu Duran et al. (2015). In practice, propagation of a delay can be avoided by speeding up the ship to catch up its original schedule. The service level for a ship-port pair is determined by the amount of buffer time allocated to the leg that arrives at the port. We assume different service levels for different ship types, because fuel efficiencies of ships may differ. Longer buffer times can be inserted for the ships which are more fuel efficient. In this study, we define an overall service level measure as a weighted combination of ship-port pair service levels.

Mean and variance of handling and waiting times can be significantly different at different ports. In addition, each port might have different degree of importance for the liner shipping company. At major ports or the ports with higher demand, deviation from published schedule may pose higher losses to the shipping company. To take into account this fact, we assign a weight for each port in the problem. Since service levels could be different for the port-ship type pairs, sailing times and buffer times could also be different between ship types on the sailing legs. However, overall service level of the service route should be satisfied and common departure time for the different ship types should be determined at each port.

In this paper, the problem considered is to schedule a liner shipping service, i.e. determining weekly departure times from ports so that the total fuel burn of fleet is minimized while an overall service level is achieved. We next give the mathematical model for the problem.

2.1 Mathematical model for the problem

We start with the notation used in our model:

Sets :

  • R : set of ship types; \(r \in R\) represents a ship type

  • \(\varGamma \) : set of port-of-calls; \(i \in \varGamma \) represents a port number

  • L : set of possible values for delay probabilities; \(l \in L\) represents a delay probability

Indices and parameters :

  • I : number of port-of-calls on the route

  • N : number of ships deployed

  • \(n_{r}\) : number of deployed ships of type r on the route

  • \(v^{r}_{min}\) : minimum speed for a ship of type r (in knots)

  • \(v^{r}_{max}\) : maximum speed for a ship of type r (in knots)

  • \(l_{ij}\) : ocean distance (nautical miles) between port i and port j

  • \(\tilde{w}_{i}\) : random variable for waiting time at port i with mean \(\mu ^{w}_{i}\) and std. dev. \(\sigma ^{w}_{i}\)

  • \(\tilde{h}_{i}^r\) : random variable for handling time for ship type r at port i with mean \(\mu ^{h}_{ir}\) and std. dev. \(\sigma _{i}^{hr}\)

  • \(p_{fuel}\) :the bunker price (USD/ton)

  • \(\MakeUppercase {w}_{i}\) : weight of the ith port-of-call

  • \({\alpha _{i}^{lr}}\) : probability level l for a ship of type r to have a delay at the ith port-of-call

  • \(1-\beta \) : overall service level

Decision variables :

  • \(d_{i} = \)published departure time at port i\(\forall {i} \in \varGamma \)

  • \(s^{r}_{ij} = \)sailing time of a ship of type r between port i and port j       \(\forall {i,j}\in \varGamma \)

$$\begin{aligned} y_{i}^{lr}=\left\{ \begin{array}{ll} 1 &{} \text {if service level}\, (1-\alpha _{i}^{lr}) \hbox { is selected for a ship of type } r \hbox { at the }\, i\mathrm{th}\, \hbox {port-of-call} \\ 0 &{} \text {otherwise} \end{array}\right. \end{aligned}$$

2.2 Service level

In this study, we measure the overall service level of a liner shipping service schedule by the weighted sum of port service levels for all ship types. Overall service level can be expressed as

$$\begin{aligned} (1-\beta ) = \sum _{i \in I} \sum _{r \in R} W_i \frac{n_r}{N} (1-A_i^r) \end{aligned}$$

\(W_i\) gives the relative importance of port i and it is determined by the decision maker. In our model, \(W_i \ge 0\) for all i and \(\sum _{i \in I} W_i = 1\), so \(W_i\) is a normalized value between zero and one. \(\frac{n_r}{N}\) is the ratio of the number of type r ships in the fleet to the fleet size. We include \(n_r/N\) as a multiplier in the overall service measure so that it is weighted in accordance with the fleet mix. \((1-A_i^r)\) is the service level at port i for ship type r, which is equal to the probability that a type r ship departs from port i on scheduled departure time. Since \(\sum _{i \in I} W_i = 1\) and \(\sum _{r \in R} \frac{n_r}{N} = 1\), \((1-\beta )\) is always between zero and one. \((1-\beta )\) can be interpreted as a weighted probability of having no delayed departures. For each port-ship type pair (i, r), \((1-A_i^r)\) is the probability of on-time departure and \(W_i \frac{n_r}{N}\) is the corresponding weight. \((1-\beta )\) is the weighted sum of all on-time probabilities. In the next section, we present a mathematical formulation in which the overall service level is formulated as a constraint.

2.3 Mathematical formulation

Next, we give the mathematical formulation for the problem. In our formulation port i is the ith port of call in the route.

$$\begin{aligned} \min&\sum _{i\in \varGamma }\sum _{{r \in R}}f_{i,i+1}^{r}{(s^{r}_{i,i+1})}\;l_{i,i+1}p_{fuel}\;n_{r} \end{aligned}$$
(1)
$$\begin{aligned} \text {s.t. }&\text {Pr}\left( d_{i+1}\le d_{i}+s^{r}_{i,i+1}+\tilde{w}_{i+1}+\tilde{h}_{i+1}^r\right) \le \sum _{l\in L} \alpha _{i+1}^{lr}y_{i+1}^{lr}&\forall {i}\in \varGamma \;\text {,}\;\forall {r} \in R \end{aligned}$$
(2)
$$\begin{aligned}&{l_{i,i+1}}/{v^{r}_{max}}\le s^{r}_{i,i+1}\le {l_{i,i+1}}/{v^{r}_{min}}&\forall {i}\in \varGamma \;\text {,}\;\forall {r}\in R \end{aligned}$$
(3)
$$\begin{aligned}&d_{I+1}-d_{1}=168\,\sum _{r \in R}n_{r} \end{aligned}$$
(4)
$$\begin{aligned}&\sum _{i\in \varGamma }\sum _{l \in L} \sum _{r \in R}\MakeUppercase w_{i} \left( n_{r}/N \right) \alpha _{i}^{lr}y_{i}^{lr} \le \beta \end{aligned}$$
(5)
$$\begin{aligned}&\sum _{l \in L}{y_{i}^{lr}}=1&\forall {i}\in \varGamma \; ,\;\forall {r}\in R \end{aligned}$$
(6)
$$\begin{aligned}&d_{1}=0 \end{aligned}$$
(7)
$$\begin{aligned}&s^{r}_{i,i+1}\ge 0, d_{i}\ge 0 \;,\; y_{i}^{lr}\in \left\{ 0,1\right\}&\forall {i}\in \varGamma \; {,}\;\forall {r}\in R \end{aligned}$$
(8)

In the objective function, \(f_{i,i+1}^{r}{\left( s^{r}_{i,i+1}\right) }\) is the fuel burn rate(tons/mile) of a ship of type r on leg \(\left( i,i+1\right) \). The objective function gives the total fuel cost of all ships in the fleet for all legs on the route. We use a cubic fuel burn function which will be discussed in Sect. 3.

Constraint (2) ensures that probability of delay at port \((i+1)\) for a ship of type r is less than or equal to the selected probability level \(\left( \alpha _{i+1} ^{lr} \right) \). This probability can be controlled by the amount of buffer time between ports i and \(i+1\). As discussed before, buffer time is determined by the departure times at port i and \(i+1\) and the sailing time from port i to port \(i+1\). The selected \(\alpha _{i+1}^{lr}\) on the right hand side of constraint (2) is the probability of delayed departure for ship type r from port \(i+1\).

Constraint (3) guarantees that the chosen sailing times on legs are within the bounds determined by the speed upper and lower bounds of ships. A speed upper bound exists for each ship. Similarly, a speed lower bound may exist due to some technical disadvantages of slow steaming.

Constraint (4) ensures that the schedule is able to satisfy the weekly frequency. Port with index \(\left( I+1\right) \) refers the port 1 after finishing a round-trip journey. For a ship, the difference between two successive departures from the same port must be equal to one week (168 hours).

Constraint (5) is necessary for satisfying the overall service level required for the route. This constraint ensures that the weighted sum of allowable delayed departure probabilities chosen for ship-port pairs is less than or equal to \(\beta \), which is the overall service level target set by the schedule planner.

Constraint (6) guarantees that exactly one service level is selected for each port-ship type pair and constraint (7) assumes that departure time from port 1 is zero.

2.4 Chance constraints

The given model consists of chance constraints (2). Next, assuming that handling and waiting times follow normal distributions we transform chance constraints into linear constraints. We define a set for delay probability values which includes discrete points. The decision variable \(y_{i}^{lr}\) is a binary variable that is equal to one if service level \((1-\alpha _{i}^{lr})\) is selected for a ship of type r at the port i. Constraint (2) can be written as follows:

$$\begin{aligned}&d_{i}+s^{r}_{i,i+1}+\sum _{l\in L} \phi ^{-1}\left( 1-\alpha _{i+1}^{lr}\right) y_{i+1}^{lr}\sqrt{{\sigma _{i+1}^{w}}^2+{\sigma _{i+1}^{hr}}^2 }\nonumber \\&\quad +\mu _{i+1}^{w}+\mu _{i+1}^{hr}\le d_{i+1}, \forall {i}\in \varGamma ,\forall {r}\in R \end{aligned}$$
(9)

where \(\phi ^{-1}\) is the quantile function for the normal distribution that represents waiting and handling time.

In this formulation, we assume that handling and waiting times follow normal distributions. However, for any probability distribution for port times (waiting plus handling time) chance constraint (2) can be approximated as a linear inequality if it has a quantile function which can be evaluated at \((1-\alpha _{i}^{lr})\) values.

The model given above does not take into account the situations where an excessive delay at one port causes delays in the subsequent ports on the route. In our model, we distribute total tour time among the legs by considering port time distributions at ports and fuel efficiencies of ships. In practice if a ship experiences a departure delay at a port, then the container ship captain can speed up the ship to catch the scheduled arrival time to the next port. Alternatively, the ship can arrive late to the next port, consuming the buffer time designated for that port. This would mean an increased probability of departure delay. Delays at ports and propagation effects can be considered as a future research.

Next, we give the SOCP representation of the model.

3 SOCP representation of the model

In SOCP, a linear function is minimized over the intersection of an affine set and the product of second-order cones ( Aharon and Arkadi 2013 and Alizadeh and Goldfarb 2003). The fuel consumption function that we use in our study is given by Yao et al. (2012). The function is defined to give fuel burn per day for given speed level.

$$\begin{aligned} f(v_{ij}^{r})=p_{r} {v_{ij}^{r}}^3+q_{r} \end{aligned}$$

Fuel consumption in tons per nautical mile could be represented as

$$\begin{aligned} f\left( v_{ij}^{r}\right) =\frac{p_{r} }{24}{v_{ij}^{r}}^2+\frac{q_{r}}{24v_{ij}^{r}} \end{aligned}$$

Since \(l_{ij}=v_{ij}^{r}s_{ij}^{r}\), fuel consumption as a function of sailing time can be reformulated as

$$\begin{aligned} f\left( s_{ij}^{r}\right) =\frac{p_{r}l_{ij}^2 }{24} \frac{1}{{s_{ij}^{r}}^2}+\frac{q_{r}}{24l_{ij}} s_{ij}^{r} \end{aligned}$$

After applying these changes, the objective function of the model becomes

$$\begin{aligned}&\mathbf {\min } \sum _{i\in \varGamma }\sum _{r \in R} \left( {p_{r} }{l_{i,i+1}}^{3} \frac{1}{{s_{ij}^{r}}^2} + {q_{r}} s_{i,i+1}^{r} \right) p_{fuel} n_{r} \end{aligned}$$
(10)

For reformulating the objective function we first replace the term \( \frac{1}{{s_{ij}^{r}}^2}\) with auxiliary variable \(t_{i,i+1}^{r} \ge 0\).

$$\begin{aligned}&\mathbf {\min } \sum _{i\in \varGamma }\sum _{r \in R} \left( {p_{r} }{\left( l_{i,i+1}\right) }^{3}t_{i,i+1}^{r}+{q_{r}}s_{i,i+1}^{r}\right) p_{fuel}n_{r} \end{aligned}$$
(11)

and add the following constraint set to the model (dropped \(i, i+1\) and r indices for simplicity)

$$\begin{aligned}&\frac{1}{{s}^2}\le t \end{aligned}$$
(12)

Constraint (12) can be represented using SOCP inequalities, so first we have to transform this constraint as hyperbolic constraints. By defining a new variable \(\tau \) , Inequality (12) can be equivalently written as

$$\begin{aligned} {\tau }^2&\le t \end{aligned}$$
(13)
$$\begin{aligned} 1&\le {s} \tau \end{aligned}$$
(14)

Inequalities (13) and (14) are hyperbolic inequalities and can be represented via SOCP inequalities below:

$$\begin{aligned}&\left\| \begin{array}{cc}2\tau \\ t-1\end{array} \right\| \le t+1 \end{aligned}$$
(15)
$$\begin{aligned}&\left\| \begin{array}{cc}2\\ s-\tau \end{array} \right\| \le s+\tau \end{aligned}$$
(16)

After adding constraints (15) and (16), the model will be reformulated as follows

$$\begin{aligned} \min&\sum _{i \in \varGamma } \sum _{r \in R} \left( {p_{r}} {l_{i,i+1}}^{3} t_{i,i+1}^{r} + {q_{r}} s_{i,i+1}^{r} \right) p_{fuel} n_{r} \nonumber \\ \text{ s.t. }&4 {\tau _{i,i+1}^{r}}^{2}+{\omega _{i,i+1}^{r}}^{2} \le {\rho _{i,i+1}^{r}}^{2} \quad \forall {i}\in \varGamma ,\forall {r}\in R \end{aligned}$$
(17)
$$\begin{aligned}&4+{\eta _{i,i+1}^{r}}^{2} \le {\nu _{i,i+1}^{r}}^{2}\quad \forall {i}\in \varGamma ,\forall {r}\in R \end{aligned}$$
(18)
$$\begin{aligned}&t_{i,i+1}^{r} - 1 = \omega _{i,i+1}^{r} \quad \forall {i}\in \varGamma ,\forall {r}\in R \end{aligned}$$
(19)
$$\begin{aligned}&t_{i,i+1}^{r}+1 = \rho _{i,i+1}^{r} \quad \forall {i}\in \varGamma ,\forall {r}\in R \end{aligned}$$
(20)
$$\begin{aligned}&s_{i,i+1}^{r} - \tau ^{r}_{i,i+1} = \eta _{i,i+1}^{r} \quad \forall {i}\in \varGamma ,\forall {r}\in R \end{aligned}$$
(21)
$$\begin{aligned}&s_{i,i+1}^{r}+\tau ^{r}_{i,i+1} = \nu _{i,i+1}^{r} \quad \forall {i}\in \varGamma ,\forall {r}\in R \end{aligned}$$
(22)
$$\begin{aligned}&\rho _{i,i+1}^{r},\nu _{i,i+1}^{r} \ge 0,\omega _{i,i+1}^{r},\eta _{i,i+1}^{r} \text{ free } \quad \forall {i}\in \varGamma ,\forall {r}\in R \nonumber \\&\text{ and } \text{ constraints }{(3)-{(8)}, {(9)}} \end{aligned}$$
(23)

Du et al. (2011) proposes using SOCP representations of fuel burn functions in a berth allocation problem. They provide SOCP representation of power functions in the form of \(f(s)=c s^{(a/b)-1}\) where s is the sailing time, c is a positive constant and a, b are integers such that \(a \ge 2b\) so that the function is convex.

Exponential fuel burn functions are also used in the literature. As shown by Nemirovski (2000), exponential function could be approximated as following:

For every \(p\ge 1,\)

$$\begin{aligned} exp(x)=\lim _{r\rightarrow \infty } {\left( 1+\dfrac{x}{2^{r}}+ \dfrac{1}{2}{\left( \dfrac{x}{2^r} \right) }^{2}+...+ \dfrac{1}{p!}{\left( \dfrac{x}{2^r} \right) }^{p} \right) }^{2^r} \end{aligned}$$
(24)

We can simplify expression (24) as

$$\begin{aligned} exp(x)= \lim _{r\rightarrow \infty } {\left( 1+c_{1}{x}+ c_{2}x^{2}+...+ c_{p}x^{p} \right) }^{2^r} \end{aligned}$$
(25)

It is observed from expression (25) that all the terms are in the form of power function. So each term could be represented as a SOCP in a way that we explained before. Therefore, exponential functions could also be represented as SOCP by using this approximation. In the next section, we present the results of computational experiments.

4 Numerical results

In this section, we present computational results on proposed model. In our experiments we use three service routes: Europe East Asia trade (AE) route (Notteboom and Vernimmen 2008), Asia Europe Express (AEX) route (Yao et al. 2012) and Atlantic Pacific Express (APX) route (Yao et al. 2012). Table 1 gives number of ports, frequency and fleet composition for these service routes. Fleet compositions are determined based on preliminary run results.

Table 1 Service routes
Full size table

We consider two types of ships: Type A and Type B. We give the speed ranges and fuel consumption functions in Table 2. As mentioned before, fuel consumption function that we consider in our study is in the form \(f(v_{ij}^{r})=p_{r} (v_{ij}^{r})^3+q_{r}\) and calculates fuel burn in tons per day. Corresponding fuel burn function of sailing time and tons per nautical mile is \(f(s_{ij}^{r})=\frac{p_{r} \cdot l_{ij}^2 }{24} {s_{ij}^{r}}^{-2}+\frac{q_{r}}{24 \cdot l_{ij}}s_{ij}^r\). We take the values of the coefficients \(p_{r}\) and \(q_{r}\) for different container ships from Yao et al. (2012). They are given in Table 2. We express speeds (v) in knots (nautical miles/hour) and give speed limits for each ship type in Table 2. Optimal speed for a Type A ship is 14.8 knots, while optimal speed for a Type B ship is 16.06 knots. Obviously, both consumption functions are convex. A Type B ship can sail faster, but when speed is higher than 18.0 knots, it is more expensive to speed up a Type B ship than a Type A ship.

Table 2 Properties of the container ships
Full size table

While defining the proposed service measure for a liner ship service, we use a weight value for each port. Different factors could be considered by the scheduler in defining the weights for the ports. Those factors may differ from company to company. In our experiments, we assign proxy weights according to traffic data of the ports. We use numbers of arrivals and the expected arrivals of ships at the ports at a specific time interval according to data provided on www.marinetraffic.com. In order to find \(W_i\) for port i on a service route, we divide sum of arrivals and expected arrivals of ships to port i to the total number of arrivals and expected arrivals to all ports on the route. We give the weights of ports and sailing distances between the ports in Appendix 2.

In our mathematical model we choose service levels at ports from a discrete set (L) of values. We use the set of delay probabilities \(L=\{0,005, 0.01,0.02,0.03, \ldots ,0.39,0.40 \}\) in all runs.

We choose three experimental factors to explore. The first one is the overall service level (\(1-\beta \)) imposed to the model. If the service level is increased the model will insert more idle time, i.e. increase speeds of ships and change the schedule. The second one is the waiting and handling times at the ports. As mentioned before, uncertainties that we consider in this study are due to fluctuations of handling and waiting times. We assume that these random parameters follow normal distribution. For simplicity, we combined handling and waiting time random variables into a single random variable. We give the experimental factors and levels of each factor in Table 3. For each parameter, we define two levels. We also assume the fuel price of \(\$550\) per ton in all the experiments. \(\mu \) and \(\sigma \) variables are uniformly generated over given intervals in Table 3.

Table 3 Experimental factors
Full size table

We performed all experiments on a 64-bit Windows 10 computer with 8 GB memory and Intel Core i7-3770 3.40 GHz CPU using IBM ILOG CPLEX 12.5. The average CPU time required to solve instances of AE route was 0.054 CPU seconds. For AEX and APX routes the average CPU times required were 0.078 and 0.79 CPU seconds, respectively. The CPU times were small as the number of ships and the number of ports were limited, which is also the case in practice.

We first study effects of these factors on fuel cost, sailing times, departure times, service levels and buffer times. We analyze effects of time windows on optimal solutions. Furthermore, we study the relation between weights of the port-of-calls and service levels. Finally, we do comparisons between fuel consumption costs of our model and other feasible methods.

4.1 Effects on fuel cost

We first consider the effect of experimental factors on fuel consumption. We did the experiments for route AE and took ten replications for each setting. We give average total fuel cost for each setting in Table 4. We see that when the overall service level decreases, fuel consumption decreases since ships can sail at lower speeds. However, as overall service level decreases, reliability of a schedules decreases. Also, we observe that decreasing mean waiting and handling time (\(\mu \)) leads to significant saving in fuel cost while the same service level could be achieved at lower sailing speeds. As the variability of handling and waiting times (\(\sigma \)) increases, we observe that fuel consumption increases. Since round-trip journey time is fixed, as \(\sigma \) is increased, more buffer time must be inserted in the schedule, so the ships are forced to sail at higher speeds. For the case with zero variability, total fuel consumption cost will be \(18.56\; (\$10^6) \). Even though the changes in service level caused around one percent change in fuel consumption cost in our results, as three quarters of operating cost of a ship may come from fuel costs (Ronen 2011), a careful service level decision can produce significant gains for a liner shipping company.

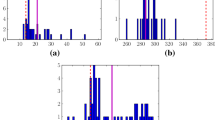
Table 4 Effects of experimental factors on fuel consumption cost
Full size table

In addition, in order to see effects of overall service level on fuel consumption cost more clearly, we plotted the fuel costs for the different values of overall service level in Fig. 2. From the figure it is obvious that as the overall service level of the route increases, total fuel consumption also increases. Moreover, as the service level increases, it becomes more expensive to improve it further.

Fig. 2
figure 2

Effect of overall service level on total fuel consumption cost

Full size image

4.2 Effects of experimental factors on schedules

We next explore how the experimental factors affect service levels, buffer times and speed levels for different ship types. For each ship type, Table 5 gives average speed, average buffer time per leg and weighted average service level at ports. The results are given for route AE, for ten replications. In all cases, we observe that average speed for ship type A is slightly higher than average speed for ship type B. This is due to the fact that ship type A is more fuel efficient than B, which can be observed in Fig. 3. Since, it is cheaper to speed up ship type A, we also observe that in all cases ship type A has longer average buffer time on the legs. As a result, service level provided by ship type A is higher than the service level provided by ship type B.

As the overall service level \((1-\beta )\) required by the decision maker increases, average speeds increase so that we create more buffer time on the legs and achieve higher service levels for both ship types. If mean waiting and handling time (\(\mu \)) increases, we speed up ships to absorb increased port times due to uncertainty. We observe that average buffer time slightly decreases for ship type A and slightly increases for ship type B. Weighted average service levels change accordingly. When the variability in waiting and handling time (\(\sigma \)) increases, we again observe a speed increase for both ship types. This creates additional buffer times on legs so that the required service level is achieved. Weighted average service levels change slightly.

Table 5 Effects on schedule (route AE)
Full size table

4.3 Fixed versus variable service levels on a route

In this section, we focus on the benefits of having variable service levels for different ship-port pairs compared to having equal service level at all ports. In the literature, it is assumed that all ships provide the same service level at all ports. Our model determines optimal speed values and service levels that minimize total fuel consumption while ensuring an overall service level. We carry out a numerical study to see how our model (variable service level approach) performs compared to fixed service level approach. Fixed service level approach can be easily implemented in our model by fixing all service levels at all ports to \(1-\beta \).

Also, we want to observe the benefits of variable service level approach in two different cases. In each case we consider different fuel cost function pairs for two ship types. In the first case, we use Type A, Type B ships described in Table 2. The fuel consumption functions are shown in Fig. 3. In the second case, we change the coefficients of our fuel consumption functions so that Ship Type A has smaller fuel cost and is cheaper to speed up compared to the first case. In the second case, fuel consumption for Ship Type B is higher and it is more expensive to speed up compared to the first case. For ship type A fuel consumption function is \(0.000158 v^2 + 0.875/v\) and for ship type B it is \(0.000354 v^2 + 2.33/v\). The altered fuel consumption functions are shown in Fig. 4. We refer to the case in Fig. 3 as “F1” and the case in Fig. 4 as “F2”.

Fig. 3
figure 3

Fuel consumption functions (F1)

Full size image
Fig. 4
figure 4

Fuel consumption functions (F2)

Full size image

We solve problem for route AEX. We generate eight settings and took ten replications for F1 and F2 scenarios. We give the results in Table 6. The table shows fuel consumption costs for variable and fixed service level approaches for different experimental settings and the cost improvement achieved by variable service level approach over the fixed service level approach.

Table 6 Effect of Variable Service Level (Route AEX)
Full size table

From Table 6, we can observe that controlling service level at each port for each ship type provides savings on fuel cost while the same overall service level target is obtained. We also observe that as \(\mu \) and \(\sigma \) values increase, the variable service level approach achieves higher cost improvement over the fixed service level approach. This is due to the fact that when \(\mu \) and \(\sigma \) values increase, ships have to sail at higher speeds. When ships sail at higher speeds, variable service level approach can achieve a better trade-off between service levels and fuel consumption, usually by operating fuel efficient ships at higher speeds with higher service levels. Also, cost improvement achieved when \((1-\beta )=0.9\) is higher than the improvement when \((1-\beta )=0.8\). This indicates that when service level is higher, our approach performs better.

When we compare fuel cost improvements for F1 and F2 scenarios, we see that fuel cost improvement achieved by proposed model is higher for F2. This shows that when the difference between the fuel efficiencies of ships is higher, our approach achieves higher savings in fuel compared to fixed service level approach. In conclusion, while having flexibility to provide different service levels at different ports, our model achieves a better cost performance than the fixed service level approach.

4.4 Effects of weights on service levels

In this section, we demonstrate the service levels achieved by our model. We performed experiments on a single instance for APX route. We set \(\beta = 0.9\), \(\mu _i\text { (in days)} = 0.61\) and \(\sigma _i \text { (in days)} = 0.19\) for all i. Table 7 shows the service levels at all ports. The first column shows the name of the port-of-call. Second column refers to the order of the port-of-call in the route. Third and fourth columns refer to the service levels of ship types A and B. The last column shows the weight (\(w_i\)) of each port. All columns are sorted from largest to smallest according to the importance weights of the ports. It is observed from Table 7 that as the weight of a port decreases, the model assigns lower service levels to that port.

Table 7 Effects of weights on service levels
Full size table

4.5 Effects of time windows

In this section, we consider time window restrictions on departure times so that the the departure time at a port must be chosen from a given time interval. For including time windows in the problem, the Constraint (26) is added to the model. In this constraint, \(d_{l}^i\) and \(d_{u}^i\) are lower and upper bounds of time windows, respectively.

$$\begin{aligned} d_{l}^i\le d_{i}\le d_{u}^i i=1,2,\ldots ,I\ \end{aligned}$$
(26)

For studying effects of time windows, we considered route AEX. We generated time windows by considering the order of calls at ports. We did the experiment for the setting (\(\beta \): 0.9, \(\mu \) level: H, \(\sigma \) level: L). Effect of time windows on total fuel consumption cost is seen in Table 8. From the table, we see that including time time windows, fuel consumption cost increases by 0.42%. By including time window restrictions in scheduling decisions, ships have to depart from the ports at specific time intervals and this forces ships to sail at different speeds than the speeds in the case without time windows.

Table 8 Effect of time winodws on fuel consumption cost
Full size table

As can be seen in Table 9, including time windows in the model has changed the service levels of ship types at some ports. This happens since time window restrictions limit the amount of buffer time on some legs while allowing more buffer time in others. Hence, both the speed and service level decisions are affected and led to a solution with higher fuel consumption. In the next section, we give concluding remarks.

Table 9 Effect of time windows on service levels
Full size table

5 Conclusion

In this paper, we studied a heterogeneous fleet liner ship scheduling problem. We focused on handling and waiting time uncertainties in a schedule and proposed a new service level measure which considers different ship types and takes into account the fact that some ports may be more critical for the service. We considered a heterogeneous fleet of container ships on a single route. The objective was minimizing total fuel consumption cost of fleet during the round-trip journey time. We developed a mixed integer nonlinear model which minimizes total fuel cost while ensuring that a certain overall service level is achieved. Different than the studies in the literature our model assigns service levels to the ship type - port pairs. We reformulated the proposed model as a MISOCP problem.

Our numerical experiments have demonstrated that assigning different service levels for port-ship type pairs might be more beneficial to the shipping company than assigning equal service levels to all pairs. We observed that, in terms of fuel consumption, proposed model performs better when required service level (\((1-\beta )\) is higher, when waiting and handling times (\(\mu \)) are longer and when variability of waiting and handling time (\(\sigma \)) is higher. Furthermore, we showed that if the fleet is more diverse in terms of fuel efficiency, then proposed model performs better.

This research can be extended by considering time dependent waiting and handling times, i.e. at different times of the day different waiting and handling time levels are experienced at the ports. This would require determining arrival times at ports carefully so that, if possible, a ship arrives at a port at the times when the port is not so busy. Also, the study can be extended to more realistic distributions of waiting and handling time.