Introduction

Wind climate in Tainan (the fourth biggest city at southwest of Taiwan) has been acting potential for inducing high winds in many areas due to the Asia monsoon and tropical cyclones during the summer season and the northeast trade winds during the winter season (Hsu and Chen 2002). Therefore, wind power is considered to be a significant alternative for electricity in this city.

The approaches of wind energy potential for specific areas using various probability distribution functions have been carried out in previous studies. Weibull wind speed distribution is one of the famous approaches for estimating wind energy. Rosen et al. (1999) analyzed wind energy potential of two windy sites located in the coastal region of Eritrea using the Weibull distributions proposed by Mulugetta and Drake (1996). The results indicated that the generated electricity from the wind with the 10-m wind speed of 9.5 m/s would be cheaper than the energy supplied by diesel. Jamil et al. (1995) estimated wind energy density in Iran based on the two-parameter Weibull wind speed distribution. Similarly in Taiwan, Chang et al. (2003) evaluated the wind energy potential by investigating the yearly wind speed distribution and wind power density for the entire country. The two-parameter Weibull wind speed distribution was used to estimate the wind energy generated by an ideal turbine. The results demonstrated the wind energy potential in Taiwan. However, for the local or residential area of Taiwan, due to the different wind energy potential, the wind turbine located should be re-designed or modified.

The optimization of turbine blades plays a crucial role in designing wind turbine systems and improving their performance. Based on the outward appearance of the turbine blade, wind turbine systems can be classified as horizontal-axis wind turbine (HAWT) or vertical-axis wind turbine (VAWT). Researchers in the field of wind energy generally prefer HAWT to VAWT because of its superior ability to capture wind energy. The geometry of HAWT blades is meant to create an airfoil in each section of the blade in order to improve aerodynamic performance. Considering the aerodynamic load on the turbine blades, five to seven airfoils may be required along the spanwise direction (Kima et al. 2013). Two approaches are commonly employed to numerically analyze the aerodynamic performance of HAWT blades. One approach is based on blade element momentum theory (BEMT), whereas the other involves computational fluid dynamics (CFD). One-dimensional (1D) BEMT has been widely used to calculate the optimal chord length and pitch angle in each blade section during the design process, and then to determine aerodynamic load through integration (Guo et al. 2015; Sedaghat et al. 2014; Sedaghat and Mirhosseini 2012; Vaz et al. 2011). BEMT was originally used to present the curves for lift and drag coefficients. Lanzafame and Messina (2007, 2009, 2010a, b, 2012) built a mathematical model with which to calculate the lift and drag values of S809 airfoil at Reynolds number of 1 × 106 based on experimental data and then combined this model with BEMT equations for the prediction of aerodynamic performance in NREL series turbines. The VC stall model developed by Viterna and Corrigan (1981) for the purpose of predicting lift and drag coefficients at the stall region has been successfully applied to BEMT to simulate the aerodynamic behavior of constant-speed turbines under higher wind speed conditions and variable-speed turbines with low tip speed ratio (TSR) regions (Bai and Hsiao 2010; Bai et al. 2014; Hsiao et al. 2013; Martínez et al. 2005; Vaz et al. 2011). Three-dimensional (3D) correction factors, such as the tip loss factor, the hub loss factor, and the stall delay model, have also been included in the BEMT equations to further enhance accuracy (Bai et al. 2014; Martínez et al. 2005). At present, the flow structure associated with rotating turbine blades can be simulated using the CFD approach in conjunction with Reynolds-averaged Navier–Stokes (RANS) equations and appropriate turbulence models, such as the k-ω SST turbulence model (Hsiao et al. 2013; Pape and Lecanu 2004). Pape and Lecanu (2004) investigated the aerodynamic performance of an NREL wind turbine using the k-ω SST turbulence model, the results of which are in good agreement with the experiment results at low wind speeds. Tachos et al. (2010) predicted the aerodynamic performance of NREL PHASE II wind turbines by solving steady-state RANS equations. A combination of four turbulence models (Spalart–Allmaras, k-ε, k-ε renormalization group, and k-ω SST) with the RANS equations and the k-ω SST turbulence model has proven the best model for simulation. Bechmann et al. 2011 simulated a MEXICO rotor using RANS equations using the k-ω SST turbulence model and managed to obtain an accurate wake simulation of approximately 2.5 rotor diameters downstream. At high TSRs, the BEMT method sometimes over-predicts the power coefficient of wind turbines, as verified using a fully 3D CFD simulation model in conjunction with the k-ω SST turbulence model (Krogstad and Lund 2012). In addition, Lanzafame et al. (2013) developed 3D CFD model for predicting the performance of a micro HAWT and evaluating the capabilities of the 1D BEM model. Two turbulence models, two-equation SST k-ω fully turbulent and four-equation transitional SST models, were used, compared, and validated using NREL PHASE VI experimental data. Less than 6 % of error was obtained between simulated and experimental results. In our previous studies, we developed in-house simulation code that included all correction factors required by BEMT for the aerodynamic design and prediction of HAWT blades (Bai and Hsiao 2010; Bai et al. 2014). However, the code that is used to lay out the shape of the turbine blades is based on the characteristics of an axial-flux permanent magnet (AFPM) generator with a power output of 400 W. The radius of the blade used in the HAWT system in this study is 0.65 m, which is capable of producing 530 W of mechanical power at a rated wind speed of 12 m/s, as measured using a 5 N m torque transducer through Architecture and Building Research Institute (ABRI) wind tunnel (Bai et al. 2014). Despite the fact that the performance can be measured by conducting experiments in a wind tunnel, this approach tends to be limited with regard to the diameter of the turbine blades. For example, our aim was to develop a 10 kW HAWT system; however, the resulting device exceeds the specifications of the ABRI wind tunnel, the largest wind tunnel in Taiwan. Thus, we adopted a numerical approach to the analysis of aerodynamic performance of the turbine blades. Unfortunately, our in-house code remains limited with regard to predicting aerodynamic performance, due to restrictions on the prediction of lift and drag coefficients before the stall angle of attack, which only can be obtained using the lookup table method. Furthermore, writing code of this kind can take a great deal of time. Finally, we identified a number of problems with regard to the geometry of the turbine blade designed using BEMT, such as an unrealistically high distribution of chord length in the inboard region, which could encumber manufacturing processes and drive up costs. The problem of excessive twist angle distribution in the blade root region could lead to difficulties in assembly between the hub and generator. The fact is that most of the mechanical torque is generated in the spanwise areas within a 60–90 % range in the near-root region.

In order to design a wind turbine suitable for a specific location in Taiwan (Guiren Dist., Tainan, Taiwan, shown in Fig. 1), the objective was to design a 6-m-diameter turbine blade for a 10 kW variable-speed HAWT. The designed regional HAWT blade was based on the wind energy potential in Tainan estimated using Weibull wind speed distribution. We employed BEMT and CFD numerical approaches for the analysis of aerodynamic characteristics and performance. The main contributions of this paper are as follows: (1) estimation of wind power density in Tainan, Taiwan; (2) formulation of a design procedure for HAWT blades; (3) development of mathematical models adapted to BEMT for the prediction of aerodynamic performance; and (4) application of CFD to simulate pressure distribution and the flow characteristics across the surface of the designed turbine blade. The analysis of wind power density in Tainan, Taiwan, is addressed in “Analysis of the wind data of Tainan, Taiwan” section. The procedures used in the design of the turbine blade using BEMT are presented in “Turbine blade design” section. In Performance analysis” section, we describe BEMT and CFD. In Results and discussion” section, we discuss the shape of the blade based on BEMT, and present a comparison of aerodynamic performance using the two numerical approaches as well as the aerodynamic characteristics observed using CFD.

Fig. 1
figure 1

Location of Tainan in Taiwan

Full size image

Analysis of the wind data of Tainan, Taiwan

The wind speed data were obtained from Taiwan Central Weather Bureau (Central Weather Bureau 2015). Figure 2 shows the monthly average wind speeds for the height of 8.1 m in the years of 2003–2008 in Tainan, Taiwan, indicating that the average wind speed is 4.5 m/s. The maximum and minimum wind speeds occurred in January and June, respectively. Weibull distribution can be characterized by its probability density function (f(V)). This function is useful to quickly point out the average of annual production for a given wind turbine. The Weibull probability density function is written as

$$ f\left( V \right) { = }\left( {\frac{k}{c}} \right)\left( {\frac{V}{c}} \right)^{k - 1} e^{{\left[ { - \left( {\frac{V}{c}} \right)^{k} } \right]}}, $$
(1)

where c is the scale parameter, k is the shape parameter, and V is the wind speed. According to analytical and empirical methods such as the maximum likelihood method (Seguro and Lambert 2000), the c and k can be estimated in the following equations:

$$ k = \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{n} V_{i}^{k} ln\left( {V_{i} } \right)}}{{\mathop \sum \nolimits_{i = 1}^{n} V_{i}^{k} }} - \frac{{\mathop \sum \nolimits_{i = 1}^{n} ln\left( {V_{i} } \right)}}{n}} \right)^{ - 1} $$
(2)
$$ c = \left( {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} V_{i}^{k} } \right)^{{\frac{1}{k}}}, $$
(3)

where V i is the wind speed in time stage i and n is the number of non-zero wind speed data points. Two mean wind speeds for estimating wind energy including most probable wind speed (V MP), the most frequent wind speed for a given wind probability, and wind speed carrying maximum energy (V MaxE), the wind speed carrying the maximum amount of wind energy, were obtained after the scale and shape parameters have been calculated. These two parameters are expressed as follows:

$$ V_{\text{MP}} = c\left( {\frac{k - 1}{k}} \right)^{{\frac{1}{k}}} $$
(4)
$$ V_{\text{MaxE}} = c\left( {\frac{k + 2}{k}} \right)^{{\frac{1}{k}}}. $$
(5)
Fig. 2
figure 2

Monthly mean wind speed for 10 m height of Tainan

Full size image

It is noted that the V MaxE is one of the significant characters for determining rated wind speed HAWT blade design (Mathew et al. 2002; Oyedepo et al. 2012). The power of wind when the wind flows thorough the blade sweep area with efficiency effect is given by

$$ P\left( V \right) = \frac{1}{2}\rho AV^{3} C_{\text{p}} \eta, $$
(6)

where ρ is the air density, C p is the power coefficient, and η is the electrical–mechanical efficiency. The power coefficient has a theoretical maximum value marked by Betz limit, C p,max = 16/27 = 0.593. Modern HAWTs have C p between 0.4 and 0.5 (Schubel and Crossley 2012). The wind power density indicates the amount of available energy on-site converted to electricity by a wind turbine, represented as the wind power per unit area (P/A) expressed as follows:

$$ \frac{P}{A} = \mathop \int \limits_{0}^{\infty } {\text{f}}\left( V \right)P\left( V \right){\text{d}}V = \frac{1}{2}\rho c^{3} \varGamma \left( {\frac{k + 3}{k}} \right), $$
(7)

where Γ is the Gamma function. Table 1 shows the 6-year monthly wind characteristics for Tainan, Taiwan. Apparently, Tainan has relatively good condition in this aspect.

Table 1 Monthly wind characteristics in Tainan, Taiwan
Full size table

Turbine blade design

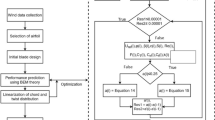
The HAWT turbine blade was designed based on the wind data and wind power density from the previous section. Figure 3 presents a flowchart of the procedure implemented in this study: (1) design of the blade, (2) prediction of aerodynamic performance, and (3) calculation of forces acting on the blade. We selected the S822 airfoil for BEMT calculation in laying out the shape of the turbine blade. This required the definition of initial design parameters, such as (1) rated power, P r , (2) rated wind speed, V r , (3) design tip speed ratio, λ d, (4) the number of blades, N b, (5) blade radius, R, (6) blade radius at root, R root, and (7) designed angle of attack, α d, as shown in Table 2. Here, we selected α d of 6° for the S822 airfoil to maximize the lift–drag ratio with a Reynolds number of 3 × 105 (Selig et al. 1995). We adopt the rated wind speed of 11 m/s and the radius of blade of 3.0 m to the blade design according to the statistical analysis of wind data in Tainan, Taiwan. It is noted that the radius of blade can be calculated as

$$ R = \sqrt {\frac{{2P_{r} }}{{\rho \pi V_{r}^{3} C_{\text{pa}} \eta_{\text{g}} }}}, $$
(8)

where C pa (=0.48) and η g (=0.90) are the assumptions of power coefficient and generator efficiency, respectively.

Fig. 3
figure 3

Flowchart used in aerodynamic design and analysis of HAWT blade

Full size image
Table 2 Initial design parameters
Full size table

Equations (9) and (10) are used to calculate the distribution of the chord length of the airfoil as well as the pitch angles for each section of the blades as follows:

$$ cr = \frac{8\pi r}{{N_{\text{b}} C_{\text{l,max}} }} \left\{ 1 - {\cos} \left[ \frac{2}{3}{ \tan }^{ - 1} \left( \frac{1}{{\lambda_{r}}}\right)\right]\right\} $$
(9)
$$ \theta_{\text{p}} = \frac{2}{3}{ \tan }^{ - 1} \left( \frac{1}{{\lambda_{r} }} \right) - \alpha_{\text{d}}, $$
(10)

where r is the local radius of the blade, C l,max is the lift coefficient associated with the maximum lift–drag ratio, and λ r is the local tip speed ratio. The chord length calculation for each section was derived from the overall rotor power coefficient equation, which is obtained by Wilson and Lissaman (Wilson and Lissaman 1974). It is noted that Eq. (9) includes the effects of wake rotation, but ignores the effects of drag coefficient and tip loss correction.

Performance analysis

Blade element momentum theory (BEMT)

BEMT is used to characterize aerodynamic performance, such as torque (T m ), mechanical power (P m ), thrust (F T ), and power coefficient (C P), using the values of chord length and pitch angle. The prediction results depend on the accuracy of axial (a) and angular (a′) induction factors and are obtained using an iterative process. The initial values of a and a′ are 0 in calculating the angle of relative wind (φ) and angle of attack (α), which can be written as follows:

$$ \varphi = { \tan }^{ - 1}\left[ \frac{1 - a}{{ ( 1 + a^{'} )\lambda_{r} }} \right]$$
(11)
$$ \alpha = \varphi - \theta_{\text{p}}. $$
(12)

When α is less than the stall angle of attack (α s), the lift (C l) and drag (C d) coefficients are calculated as follows:

$$ C_{l} = C_{{{\text{l,}}2}} \alpha^{2} + C_{{{\text{l,}}1}} \alpha + C_{{{\text{l,}}0}} $$
(13)
$$ C_{d} = C_{{{\text{d,}}3}} \alpha^{3} + C_{{{\text{d,}}2}} \alpha^{2} + C_{{{\text{d,}}1}} \alpha + C_{{{\text{d,}}0}}, $$
(14)

where the coefficients of C l,0, C l,1, C l,2, C d,0, C d,1, C d,2, and C d,3 are as listed in Table 3. When α > α s, the VC stall model can be used to calculate C l and C d.

$$ C_{\text{l}} = \frac{1}{2}C_{\text{d,max}} {\text{sin2}}\left( \alpha \right) + \frac{{K_{\text{L}} { \cos }^{2} (\alpha )}}{{{\text{sin(}}\alpha )}} $$
(15)
$$ C_{\text{d}} = C_{\text{d,max}} { \sin }^{2} (\alpha ) + K_{\text{D}} {\text{cos(}}\alpha ), $$
(16)

where K L and K D are written as

$$ K_{\text{L}} = \left[ {C_{\text{l,s}} - C_{\text{d,max}} {\text{sin(}}\alpha_{\text{s}} ) {\text{cos(}}\alpha_{\text{s}} )} \right]\frac{{{\text{sin(}}\alpha_{\text{s}} )}}{{{ \cos }^{2} (\alpha_{\text{s}} )}} $$
(17)
$$ K_{\text{D}} = \frac{{C_{\text{d,s}} - C_{\text{d,max}} { \sin }^{2} (\alpha_{\text{s}} )}}{{{\text{cos(}}\alpha_{\text{s}} )}}, $$
(18)

where C l,s and C d,s are the lift and drag coefficients at α s, respectively, and C d,max depends on the aspect ratio (AR) as follows:

$$ C_{{{\text{d,max}} }} = \left\{ {\begin{array}{ll} {1.11 + 0.018AR,} & {AR \le 50} \\ {3.01,} & {AR > 50} \\ \end{array} } \right. . $$
(19)
Table 3 Parameters used in the calculation of lift and drag coefficients
Full size table

It should be noted that Eqs. (15) and (16) are empirical equations (Selig et al. 1995).

Due to the effects of centrifugal pumping, stalling of the rotating turbine blade first occurs at an angle of attack higher than that obtained in the experiment based on the 2D airfoil (Lee and Wu 2013; Yu et al. 2011), which is also referred to as the stall delay model, represented as

$$ C_{\text{l,3D}} = C_{\text{l}} + 3\left( {\frac{c(r)}{r}} \right)^{2} \Delta C_{\text{l}} $$
(20)
$$ C_{\text{d,3D}} = C_{\text{d}} + 3\left( {\frac{c(r)}{r}} \right)^{2} \Delta C_{\text{d}}, $$
(21)

where ∆C l and ∆C d are, respectively, the differences between the lift and drag coefficients obtained when the flow did not separate, and c(r)/r is the local chord normalized by the radial direction. Based on the basic airfoil theory and the stall delay characteristics, the ΔC l and ΔC d are written as

$$ \Delta C_{\text{l}} = f_{\text{l}} \left( {C_{\text{l,p}} - C_{\text{d}} } \right) $$
(22)
$$ \Delta C_{\text{d}} = f_{\text{d}} \left( {C_{\text{d}} - C_{{{\text{d}},0}} } \right), $$
(23)

where C l,p = 2π(α − α 0), C d,0 = C d for α = 0.

The functions of f l and f d are expressed as

$$ f_{\text{l}} = \frac{1}{2\pi }\left[ {\frac{{1.6\left( {\frac{c}{r}} \right)}}{0.1267}\frac{{x - \left( {\frac{c}{r}} \right)^{{\frac{z}{\tau }\frac{R}{r}}} }}{{y + \left( {\frac{c}{r}} \right)^{{\frac{z}{\tau }\frac{R}{r}}} }} - 1} \right] $$
(24)
$$ f_{\text{d}} = \frac{1}{2\pi }\left[ {\frac{{1.6\left( {\frac{c}{r}} \right)}}{0.1267}\frac{{x - \left( {\frac{c}{r}} \right)^{{\frac{z}{2\tau }\frac{R}{r}}} }}{{y + \left( {\frac{c}{r}} \right)^{{\frac{z}{2\tau }\frac{R}{r}}} }} - 1} \right] $$
(25)
$$ \tau = \frac{\omega R}{{\sqrt {V^{2} - \left( {\omega R} \right)^{2} } }}, $$
(26)

where x, y, z are determined by empirical correction factors.

The tip loss factor described by Prandtl can be written as follows:

$$ F = \frac{2}{\pi }\cos^{ - 1} \left\{ { \exp - \frac{{N_{\text{b}} (1 - r/R)}}{2(r/R)\sin \varphi }} \right\}. $$
(27)

a and a′ are obtained using momentum theory and blade element theory following algebraic manipulation. They can be rewritten as

$$ a = \frac{{C_{\text{x}} \sigma }}{{4F{ \sin }^{2} \varphi + C_{\text{x}} \sigma }} $$
(28)
$$ a^{'} { = }\frac{{C_{y} ( 1 - a )\sigma }}{{4F\lambda { \sin }^{2} \varphi }}, $$
(29)

where C x and C y are functions of the lift and drag coefficients and σ is the local solidity, written as

$$ C_{x} = C_{\text{l}} \cos \varphi + C_{\text{d}} \sin \varphi $$
(30)
$$ C_{y} = C_{l} \sin \varphi - C_{\text{d}} \cos \varphi $$
(31)
$$ \sigma = \frac{{N_{\text{b}} cr}}{2\pi r}. $$
(32)

A correction from Spera (Manwell et al. 2002) is applied to large values of the axial induction factor for use in the calculation of the thrust coefficient (C T) as follows:

$$ C_{\text{T}} = \frac{{\sigma ( 1- a)^{2} C_{x} }}{{{ \sin }^{2} \varphi }}. $$
(33)

If C T > 0.96, then the axial induction factor can be rewritten as

$$ a = \frac{1}{F}\left\{ 0. 1 4 3+ \left[ 0 . 0 2 0 3- 0. 6 4 2 7 \left( 0. 8 8 9 - C_{\text{T}}\right)\right]^{ 0. 5} \right\}. $$
(34)

Likewise, if C T < 0.96, then the axial induction factor is solved using Eq. (28).

Finally, the mechanical torque, thrust, and power coefficient of the turbine blade can be calculated as follows:

$$ {\text{d}}T_{\text{m}} = \rho {\text{FV}}4a^{'} ( 1 - a )\pi r^{3} \omega {\text{d}}r $$
(35)
$$ {\text{d}}F_{\text{T}} = \rho {\text{F}}V^{2} 4a ( 1 - a)\pi {\text{rd}}r $$
(36)
$$ C_{\text{p}} = \frac{{P_{\text{m}} }}{{\frac{1}{2}\rho \pi R^{2} V^{3} }}, $$

where P m is the product of T m and ω.

Computational fluid dynamics (CFD)

An incompressible Navier–Stokes solver was applied to predict the aerodynamic characteristics of the turbine blade. Simulations were performed using the commercial CFD software FLUENT™ with second-order upwind spatial discretization. The resulting system of equations was solved using a simple coupled solution. Despite the availability of various turbulence models in FLUENT ™, including one-equation and two-equation models, we limited our investigation to Menter’s two-equation shear stress transport (SST) k-ω model, which is widely used for helicopter rotors (Menter 1994).

The Cartesian coordinate system was selected as the computational domain, in which the positive x-axis is in the streamwise direction, the positive y-axis is in the vertically upwind direction, and the z-axis is aligned toward the right-hand side. The original coordinate system was set to be the hub center; therefore, the rotational axis is clockwise.

In terms of boundary conditions, only one of the turbine blades was explicitly modeled during computation, which accounts for 120° of the three-bladed turbine. The other turbine blades were dealt with using periodic boundary conditions. We used the moving reference frame (MRF) function for the area of simulation around the turbine blade in order to simplify the assumptions of incompressible and steady-state flow conditions. Tests were conducted at the rotational speeds of between 153 and 382 rpm (TSRs of 5–10, as shown in Table 4). We specified the values of wind speed between 4 and 16 m/s for the inlet boundary and pressure of 0 Pa was selected for the outlet boundary. Symmetric condition was applied to the top boundary and no-slip conditions were applied to the hub and surface of the turbine blade.

Table 4 Parametric information for all the cases
Full size table

Because the MRF function is used to simulate the rotational flow field, the computational domain is selected as a cylinder shape and has been set equal to 8R and 25R (R is the radius of turbine blade) in the upstream and downstream directions, respectively, and the 5R is selected for the radial direction.

A grid system was implemented using POINTWISE™, which is divided into three steps. First, we developed the boundary layer flow region around the turbine blade using 416,160 structured cells in order to resolve the turbulent boundary layer. The wall distance (y+) of the first point from the wall surface was approximately 1. Figure 4 presents the y+ distribution on V = 12 m/s with λ = 7. It can be seen that the y+ values are around 1. The MRF associated with the inner flow region was composed of unstructured triangular grids with 630,174 cells. Finally, the outer flow region extending to the three sides of the inner flow region was constructed using 262,027 unstructured tetrahedron cells. The geometry and mesh domain of the turbine blade in CFD simulation is presented in Fig. 5. Table 5 presents grid-sensitivity analysis at a wind speed of 12 m/s and λ = 7. The mechanical torque in Case 4, Case 5, and Case 6 varies less than 0.12 % and the power coefficient is around 0.40 for Case 4, Case 5, and Case 6. Based on these tests, we choose the grid with 1,308,361 cells for all computations reported next.

Fig. 4
figure 4

Typical y+ values for 3D computational results at a wind speed of 12 m/s with λ = 7

Full size image
Fig. 5
figure 5

Mesh domain used in CFD simulation

Full size image
Table 5 Grid-sensitivity analysis for a wind speed of 12 m/s and λ = 7
Full size table

It is noted that the testing wind speeds were selected from 4 to 16 m/s, and the tip speed ratios were chosen between 5 and 10 for each testing wind speed. In other words, there are 96 cases being simulated in this study (Table 4). Because the unstructured grids were meshed in the MRF zone, the total cells for each case are not the same as the example of V = 12 m/s with λ = 7 (1,308,361 cells). At any rate, all cases were performed with grid-sensitivity analysis, as seen in Table 5. After grid-sensitivity analysis, the grid numbers for each case were chosen between 1,300,000 and 1,450,000 cells.

Results and discussion

Table 6 presents the chord lengths and pitch angles for each section of the blade, which were obtained using Eqs. (8) and (9). It can be clearly seen that the maximum chord is 0.566 m at r = 0.467 (m) and the maximum pitch angle is 41.1° at r = 0.150 m. This configuration, which is obtained when BEMT is applied directly to the design of the turbine blade shape, can cause considerable difficulties in the manufacture and assembly of the rotor and generator. Thus, we modified the chord lengths from r = 1.100 m to r = 0.150 m, as shown in Table 6. This necessitated a slight adjustment to the sectional pitch angles from r = 0.783 m to r = 0.150 m. The criterion used in the modification of chord length and pitch angle was maintenance of continuity. To facilitate the connection of a pitch control system, we modified the turbine blade root as a cylindrical shape for connection to the hub. At r = 0.467 m and r = 0.783 m, we used S823 and S823-like airfoils instead of the S822 airfoil to allow a continuous connection with the cylinder. The values of the chord and pitch angle before and after modification are presented in Table 6. Figure 6 illustrates the layout of the airfoils in each section of the blade. Figure 7a presents the 10 kW turbine blade with the radius of 3 m, made using composite material. Figure 7b presents the 10 kW HAWT system currently installed on the Guiren campus of National Cheng Kung University, Tainan, Taiwan.

Table 6 Layout of turbine blade in each section before and after modification
Full size table
Fig. 6
figure 6

Layout of turbine blade designed in this study

Full size image
Fig. 7
figure 7

a 10 kW turbine blade and b operational system located in Tainan, Taiwan

Full size image

Figure 8 plots the mechanical torque values of the HAWT, as determined using the two numerical approaches. These results are in perfect agreement with the BEMT at rotational speeds between 191 and 382 rpm. The maximum deviation between the BEMT and CFD results is 17 % at a rotational speed of 382 rpm. It should be noted that CFD simulation was conducted only within the steady-state flow region, in which the angle of attack along the turbine blade is within 15°. At rotational speeds below 191 rpm, flow may separate and become unpredictable.

Fig. 8
figure 8

Comparison of mechanical torque, as determined using the two numerical approaches

Full size image

Distribution in the angle of attack can be examined using Eqs. (11)–(34). The maximum mechanical torques, as calculated using BEMT and CFD, were observed at rotational speeds of 229 rpm, with values of 535.1 and 513.3 n m, respectively. This region is also associated with the maximum lift-to-drag ratio.

Figure 9 illustrates the results of thrust force obtained by the two numerical approaches. The results obtained from BEMT and CFD are in perfect agreement (within 2 % error) at wind speeds between 4 and 16 m/s. The thrust force was also shown to grow rapidly with an increase in wind speed, reaching 4000 n at a wind speed of 16 m/s.

Fig. 9
figure 9

Comparison of thrust force, as determined using the two numerical approaches

Full size image

As shown in Fig. 10, we compared the mechanical power of the CFD results with those of BEMT at a tip speed ratio (TSR) of 7. Compared to the study performed by Lanzafame et al. (2013), the CFD results are in good agreement with the BEMT results (within 3 % error) at wind speeds between 4 and 16 m/s. Both numerical approaches indicate that the HAWT produces 12,000 W at a wind speed of 12 m/s.

Fig. 10
figure 10

Comparison of mechanical power at designed tip speed ratio, as calculated using the two numerical approaches

Full size image

As shown in Fig. 11, at a TSR of 6, the highest power coefficient values calculated by BEMT and CFD are 0.430 and 0.411, respectively. Modifications to the blade geometry in the root region shifted the TSR associated with the maximum power coefficient from 7 to 6. This represents a reduction in the power coefficient of approximately 7 %, which remains in an acceptable range. The power coefficient begins decreasing with TSR values higher or lower than 6, due to a decrease in the lift-to-drag ratio. A separation of flow may occur at a TSR of less than 5.

Fig. 11
figure 11

Comparison of the power coefficient at a wind speed of 12 m/s, as calculated using the two numerical approaches

Full size image

Figure 12 presents surface pressure contours on the upper and lower surfaces of the turbine blade at the designed TSR with a wind speed of 12 m/s. The highest pressure distribution was observed along the leading edge of the lower surface from r = 1.3 m to r = 3.0 m. Meanwhile on the upper surface, the lowest pressure distribution on the upper surface was observed in the area of the leading edge between r = 1.8 m and r = 3.0 m. Torque is generated in the wind turbine via the pressure difference between upper and lower surfaces. Clearly, most of the power is produced near the blade tip region (r = 1.8 m and r = 3.0 m), due to the large pressure difference, whereas no power is generated in the region of the blade root (r = 0.15 m to r = 1.0 m).

Fig. 12
figure 12

Pressure contours across the upper and lower surfaces at the designed tip speed ratio

Full size image

Figure 13 illustrates a sectional pressure field at a wind speed of 12 m/s. Between λ = 5 and λ = 7, the pressure difference at the tip of the turbine blade is higher than that at the root. No pressure difference was observed at the blade root (r = 0.467 m). Additionally, the pressure differences at r = 2.683 m, r = 2.05 m, and r = 1.417 m are higher in the case of λ = 7 than in the case of λ = 5. This means that the former produces more power than does the latter.

Fig. 13
figure 13

Sectional pressure field at V = 12 m/s: a λ = 5 and b λ = 7

Full size image

Figure 14 presents the velocity contours and streamlines for r = 2.683 m, r = 2.05 m, r = 1.417 m, and r = 0.467 m at a wind speed of 12 m/s. The flow is fully attached at a TSR of 7 at r = 2.683 m, r = 2.05 m, and r = 1.417 m. In this case, the angle of attack is close to 6°, which is the angle of attack designed to maximize the lift-to-drag ratio of the S822 airfoil at a Reynolds number of 3 × 105. In the case of λ = 7 at r = 0.467 m (S823-like airfoil), a separation in flow can be clearly observed along the trailing edge, where the angle of attack is close to 14°. At a TSR of 5, we also observed the separation of flow. Note that the separation bubble grows by 16 % between the tip of the blade (r = 2.683 m) and the root (r = 0.467 m).

Fig. 14
figure 14

Comparison of power coefficient at a wind speed of 12 m/s, as determined using the two numerical approaches

Full size image

Figure 15 presents the limiting streamlines on the upper surface of the turbine blade at a wind speed of 12 m/s. At the designed TSR of 7, most of the flow field remains attached to the surface of the blade with only a slight separation occurring at the root of the blade (r = 0.15 m to r = 1.35 m). When the TSR was decreased from 7 to 5, the separation of flow near the root of the turbine blade appears to spread across most of the blade span except the tip region, which is affected by blade tip loss. The area affected by flow separation was shown to increase with a decrease in TSR.

Fig. 15
figure 15

Limiting streamlines on the upper surface of the turbine blade at a wind speed of 12 m/s

Full size image

Conclusions

In this study, the BEMT approach was used to design the regional turbine blade for a 10 kW HAWT suitable for the area of Tainan, Taiwan. The wind energy potential in this area was first analyzed through the Weibull wind speed distribution. The resulting monthly mean wind power density was then adapted to the BEMT design of the blade. The geometry of the turbine blades, including the sectional chord and pitch angle, were laid out in accordance with the initial design parameters (P r , V r , λ d, N b, R, R root, α d). In the region of the turbine blade root, three geometries (S823, S823-like, and a cylinder) were adopted to facilitate the connection of a pitch control system to the turbine blade. Mathematical models were developed to enable the calculation of lift and drag coefficients for S822 and S823 airfoils. These models were then combined with BEMT equations to predict the aerodynamic performance of the resulting turbine blade. The CFD approach was additionally applied for the simulation of aerodynamic performance and compared the results with those obtained using BEMT. The results of the two methods, including mechanical torque, thrust force, mechanical power, and power coefficient, are in perfect agreement at wind speeds of 4 to 16 m/s with a TSR between 5 and 10. At rated wind speeds and the designed TSR, the average values obtained for mechanical power and the power coefficient are approximately 12 kW and 0.42, respectively. The pressure distribution and flow fields observed through CFD simulation indicate that flow separation would occur at a TSR of 5 and that the separation bubble increases by 16 % between the tip of the turbine blade (r = 2.683 m) and the root (r = 0.467 m). To improve the power coefficient outside the designed TSR, future studies might focus on adjusting the pitch angle of the turbine blade.