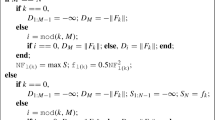A new class of nonmonotone adaptive trust-region methods for nonlinear equations with box constraints

Abstract

A nonmonotone trust-region method for the solution of nonlinear systems of equations with box constraints is considered. The method differs from existing trust-region methods both in using a new nonmonotonicity strategy in order to accept the current step and a new updating technique for the trust-region-radius. The overall method is shown to be globally convergent. Moreover, when combined with suitable Newton-type search directions, the method preserves the local fast convergence. Numerical results indicate that the new approach is more effective than existing trust-region algorithms.

1 Introduction

We consider the constrained system of nonlinear equations

$$\begin{aligned} F(x)=0,\quad x \in \varOmega , \end{aligned}$$

(1)

where $\varOmega \subseteq \mathbb R^n$ is defined by

$$\begin{aligned} \varOmega :=\{ x \in \mathbb R^n \mid l_i\le x_i \le u_i \, \ \ \forall i=1, \ldots , n \}, \end{aligned}$$

(2)

for some given lower and upper bounds satisfying $-\infty \le l_i < u_i\le +\infty$ for all $i=1,\ldots ,n$, and $F: \mathcal O \rightarrow \mathbb R^n$ is assumed to be continuously differentiable on an open set $\mathcal O \subseteq \mathbb R^n$ such that $\varOmega \subseteq \mathcal O$. Hence, we are looking for a solution of the nonlinear equation $F(x)=0$ belonging to a region that is defined by some box constraints.

In many instances, the bound constraints occur quite naturally and have a monetary or physical meaning. They are also helpful to locate a solution if some a priori information is available regarding the area in which the solution belongs to, and they can be used to avoid regions in which F or some of its components are not defined. Note also that more general inequality constraints can be reformulated as a box-constrained system simply by adding suitable slack variables.

The nonlinear system of Eq. (1) with box constraints (2) therefore represents an important class of problems for which a number of different methods have been devised especially during the last 15 years. Among those which have the desirable properties of being both globally and locally fast convergent, we refer the reader to the papers [5–10, 27, 29, 35, 37, 41, 46] and references therein. The majority of these papers deal with trust-region-type methods to get global convergence, though some line search techniques are also available. Local convergence is guaranteed in different ways using projected Newton steps, active-set strategies, affine-scaling interior-point techniques, or QP-based methods.

The main focus in this paper is a trust-region strategy for the solution of the system (1) which uses a new nonmonotonicity strategy combined with a corresponding strategy for the updating of the trust-region radius. Both ingredients play a significant role for the practical behaviour of trust-region methods [23, 38]. In principle, the nonmonotonicity is often very helpful for highly nonlinear functions with narrow curved valleys, and might also improve the likelihood to find a global minimum. On the other hand, the choice of the trust-region radius is crucial and too big/small trust-region radius may imply a number of unsuccessful iterations where essentially the iterates are unchanged, and there is a high computational cost of the overall procedure.

The nonmonotonicity idea was first used in the watchdog strategy by Chamberlain et al. [11] to avoid the Maratos effect in SQP-type methods. The seminal paper by Grippo et al. [24] introduces a general nonmonotonicity technique for unconstrained optimization that subsequently turned out to be extremely useful in different areas to improve the efficiency of several methods. Their technique has been further generalized in the paper [25]. On the other hand, it has also been noted by several authors [1, 2, 4, 12, 39, 44] that the original nonmonotonicity strategy by Grippo et al. [24] has some disadvantages so that there are a couple of recent contributions which try to avoid these disadvantages by using a more careful nonmonotonicity strategy. We postpone a more detailed discussion of this subject to Sect. 2 where we also introduce our new technique.

From a theoretical point of view, we would like to point out that there are some differences regarding nonmonotonicities used within line search and trust-region methods. To this end, let us define the natural merit function

$$\begin{aligned} f(x):=\frac{1}{2}\,\Vert F(x)\Vert _2^{2}, \end{aligned}$$

(3)

associated to the given nonlinear system of equations, and note that the constrained system of equations can be restated as the optimization problem

$$\begin{aligned} \min \ f(x)\quad \text {s.t.} \quad x\in \varOmega . \end{aligned}$$

(4)

The global convergence theory of any method for the solution of (1) tries to find at least a stationary point of (4), i.e. a vector $x^*\in \varOmega$ satisfying

$$\begin{aligned} \nabla f(x^*)^T(x-x^*)\ge 0, \quad \ \forall ~x\in \varOmega . \end{aligned}$$

(5)

The paper is organized in the following way: Sect. 2 introduces our new nonmonotonicity strategy together with a corresponding updating rule for the trust-region radius and finally states the complete trust-region framework together with some preliminary results. The global convergence analysis is carried out in Sect. 3 and shows that every accumulation point of a sequence generated by our nonmonotone trust-region method is a stationary point of (4). Locally fast convergent modifications of our nonmonotone trust-region method are presented in Sect. 4, where three different strategies are discussed in detail. Numerical results are then presented in Sect. 5, and we close with some final remarks in Sect. 6.

Notation: The symbol $\Vert \cdot \Vert$ denotes the Euclidean vector norm or the associated matrix norm, while $\Vert \cdot \Vert _\infty$ is the maximum norm of a vector. For a vector $x \in \mathbb R^n$ with components $x_i$ and an index set $I \subseteq \{ 1, \ldots , n \}$, the subvector $x_I \in \mathbb R^{| I |}$ consists of all components $x_i \ (i \in I)$. Similarly, for a matrix $A = (a_{ij}) \in \mathbb R^{n \times n}$ and index sets $I, J \subseteq \{ 1, \ldots , n \}$, we write $A_{IJ}$ for the submatrix with the elements $a_{ij} \ (i \in I, j \in J)$. Given a nonempty, closed, and convex set $X \subseteq \mathbb R^n$, we write $P_X(x)$ for the (Euclidean) projection of a vector $x \in \mathbb R^n$ onto X. Recall that these projections are very easy to compute when X is described by box constraints. In particular, the natural residual

$$\begin{aligned} p(x) := P_{\varOmega } (x - \nabla f(x)) - x, \end{aligned}$$

(6)

is simple to evaluate for the $\varOmega$ from (2), and it is well-known that $x^*$ is a solution of $p(x) = 0$ if and only if $x^*$ satisfies the stationary point condition from (5).

2 Trust-region algorithm

This section gives the details of our trust-region algorithm. Compared to existing methods, it uses both a different nonmonotonicity strategy for accepting a new iterate and a new updating technique for the trust-region radius. The corresponding details are given in Sects. 2.1 and 2.2, respectively. The resulting trust-region method is then presented in Sect. 2.3 together with some preliminary results.

2.1 Nonmonotonicity technique

We first recall the quadratic model that is used in the context of trust-region methods. Given an iterate $x^k \in \varOmega$, we define

$$\begin{aligned} q_k(d)&:=\frac{1}{2}\Vert F(x^k)+F'(x^k)d\Vert ^2\\&= f(x^k)+\nabla f(x^k)^Td+\frac{1}{2}d^TF'(x^k)^TF'(x^k)d\\&= f^k+(g^k)^Td+\frac{1}{2}\, d^T J_k^T J_k d, \end{aligned}$$

where, for simplicity of notation, we set

$$\begin{aligned} f^k:=f(x^k),\quad \ F^k := F(x^k), \; \ g^k:=\nabla f(x^k), \,\ J_k:=F'(x^k), \end{aligned}$$

throughout this paper; note that we will sometimes also write $g_k$ instead of $g^k$ whenever this is more convenient. Using the $\ell _{\infty }$-norm for the trust-region, our trust-region subproblem then reads as follows:

$$\begin{aligned} \min _{d}\ q_k(d)\quad \text {s.t.}\quad x^k+d\in \varOmega , \quad \ \ \Vert d\Vert _\infty \le \varDelta _k, \end{aligned}$$

where $\varDelta _k > 0$ denotes a given trust-region radius. Defining $l^k, u^k \in \mathbb R^{n}$ component-wise by

$$\begin{aligned} l^{k}_{j}:=\max \,\{l_j-x^{k}_{j},\ -\varDelta _{k}\},\ u^{k}_{j}:=\min \,\{u_j-x^{k}_{j},\,\varDelta _{k}\},\ \quad \forall ~j=1,\ldots ,n, \end{aligned}$$

(7)

the trust-region subproblem is equivalent to

$$\begin{aligned} \min _{d}\ q_k(d)\quad \text {s.t.}\quad l^k\le d \le u^k, \end{aligned}$$

(8)

where the inequalities are taken component-wise. Since $l^k_j \le 0$ and $u_j^k \ge 0$ for all $j = 1, \ldots , n$, the zero vector is always feasible for (8).

In traditional trust-region approaches, the ratio

$$\begin{aligned} \frac{f^k-f(x^k+d^k)}{q_k(0)-q_k(d^k)}, \end{aligned}$$

(9)

between the actual and predicted reduction around the current iterate $x^k$ is used as a measure for the agreement between the quadratic model $q_k$ and the nonlinear objective function f. The first use of a nonmonotone technique in a trust-region framework is, to the best of our knowledge, attributed to Deng et al. [13]. They presented the following ratio

$$\begin{aligned} r_k:=\frac{f^{l(k)}-f(x^k+d^k)}{q_k(0)-q_k(d^k)}, \end{aligned}$$

(10)

where

$$\begin{aligned} f^{l(k)} := f(x^{l(k)}) := \max _{0\le j\le m(k)}\{f^{k-j}\},\ \ k \in \mathbb N_0:=\mathbb N\cup \{0\}, \end{aligned}$$

(11)

with $m(0)=0$ and $0\le m(k)\le \min \{m(k-1)+1,M\}$ with $M\ge 1$. Note that the index l(k) is, usually, not uniquely defined in (11) since the maximum may be attained at different iterates, but as this non-uniqueness is irrelevant for our convergence theory, l(k) just denotes one of the iteration counters where the maximum is attained. As already noted in the introduction, however, this classical nonmonotonicity rule has some drawbacks. In particular, this strategy is based on a decrease with respect to the maximum function value within the last few iterations and, therefore, completely discards small intermediate function values. This motivated some authors to take a convex combination or a weighted average of former successive iterates [41, 44]. The strategy used by Zhang and Hager [44] for a line search method in unconstrained optimization has been applied to a nonmonotone trust-region framework by Ahookhosh and Amini [41], where the ratio (10) is changed to

$$\begin{aligned} \widehat{r}_k:=\frac{C^k-f(x^k+d^k)}{q_k(0)-q_k(d^k)}, \end{aligned}$$

(12)

with

$$\begin{aligned} C^{k}:= \left\{ \begin{array}{ll} f^{k},\ \ &{} \quad \hbox {if } \quad k=0, \\ \big (\eta ^{k-1}Q^{k-1}C^{k-1}+f^k\big )/Q^k\ \ &{} \quad \hbox {if } \quad k\ge 1,\\ \end{array} \right. \end{aligned}$$

(13)

and

$$\begin{aligned} Q^{k}:= \left\{ \begin{array}{ll} 1,\ \ &{} \quad \hbox {if } \quad k=0, \\ \eta ^{k-1}Q^{k-1}+1,\ \ &{} \quad \hbox {if } \quad k\ge 1,\\ \end{array} \right. \end{aligned}$$

(14)

where $\eta ^{k-1} \in [\eta ^{\min },\eta ^{\max }]$ for certain parameters $0 \le \eta ^{\min } \le \eta ^{\max } \le 1$.

To develop the global convergence results that are available for the monotone case, Ulbrich [41] presented a variant of the nonmonotone technique (11), which is as follows

$$\begin{aligned} f^{l(k)}_{\lambda }:= \left\{ \begin{array}{ll} f^k,\ \ &{} \hbox {if } \quad k=0, \\ \max \Big \{f^k,\sum _{j=0}^{m(k)-1}\lambda _{k,j}f^{k-j}\Big \},\ \ &{} \hbox {if } \quad k\ge 1,\\ \end{array} \right. \end{aligned}$$

(15)

where $\lambda \in (0,1/M]$, and $\lambda _{k,j}\ge \lambda$ satisfying $\sum _{j=0}^{m(k)-1}\lambda _{k,j}=1$. This formula can be a good approximation for (11) if we choose $\lambda$ sufficiently small and set

$$\begin{aligned} \lambda _{k,j}=\lambda \ \ \text {if} \ \ j \ne l(k), \lambda _{k,j}=1-(m(k)-1)\lambda . \end{aligned}$$

(16)

Of course, in [41], it is proposed that iterations $k, k-1, \ldots , k-m(k)+1$ used in (15) are successful, but, we use (15) with this difference that the mentioned iterations may be successful or unsuccessful.

Lemma 1

The inequality $f^k \le f^{l(k)}_{\lambda } \le f^{l(k)}$ holds for all $k \in \mathbb N_0$ such that the iterates $x^0, x^1, \ldots , x^k$ exist.

Proof

The statement is obviously true for $k = 0$ since $m(0) = 0$ by definition. Hence, consider an arbitrary $k \ge 1$. Since we always have $f^{l(k)} \ge f^k$, it follows that

$$\begin{aligned} f^{l(k)}_{\lambda }= & {} \max \left\{ f^k,\sum _{j=0}^{m(k)-1} \lambda _{k,j}f^{k-j}\right\} \le \max \left\{ f^k,f^{l(k)}\sum _{j=0}^{m(k)-1}\lambda _{k,j}\right\} \\= & {} \max \left\{ f^k,f^{l(k)}\right\} =f^{l(k)}, \end{aligned}$$

Moreover

$$\begin{aligned} f^{l(k)}_{\lambda }=\max \left\{ f^k,\sum _{j=0}^{m(k)-1} \lambda _{k,j}f^{k-j}\right\} \ge f^k, \end{aligned}$$

and this completes the proof. $\square$

In order to introduce a potentially more efficient nonmonotonicity technique and to establish the global convergence results, we replace $C^{k-1}$ by $f^{l(k)}_{\lambda }$ in (13). The main idea is to set up a weaker sequence relation to the generated sequence (15) whenever iterates are near the optimizer. In other words, we produce the new nonmonotone formula

$$\begin{aligned} \widetilde{C}^k_{\lambda }:= \left\{ \begin{array}{ll} f^k,\ \ &{} \quad \hbox {if } \; k=0, \\ \big (\eta ^{k-1}Q^{k-1}f^{l(k)}_{\lambda }+f^k\big )/Q^k\ \ &{} \quad \hbox {if } \; k\ge 1,\\ \end{array} \right. \end{aligned}$$

(17)

with $\eta ^{k-1} \in [\eta ^{\min },\eta ^{\max }]$ and $\eta ^{\min }, \eta ^{\max }$ as before, and with $Q^k$ satisfying (14). Finally, we introduce the new ratio as

$$\begin{aligned} \widetilde{r}_k:=\frac{\widetilde{C}^k_{\lambda }-f(x^k+d^k)}{q_k(0)-q_k(d^k)}. \end{aligned}$$

(18)

The definition of $\widetilde{C}^k_{\lambda }$ implies the following result which, to some extent, motivates the updating rule for the sequence $Q^k$.

Lemma 2

The inequality $f^k \le \widetilde{C}^k_{\lambda } \le f^{l(k)}_{\lambda } \le f^{l(k)}$ holds for all $k \in \mathbb N_0$ such that the iterates $x^0, x^1, \ldots , x^k$ exist.

Proof

The statement is obviously true for $k = 0$ since $m(0) = 0$ by definition. Hence consider an arbitrary $k \ge 1$. Since we always have $f^{l(k)} \ge f^{l(k)}_{\lambda }\ge f^k$, it follows that

$$\begin{aligned} \widetilde{C}^k_{\lambda } = \big ( \eta ^{k-1} Q^{k-1} f^{l(k)}_{\lambda } + f^k \big ) / Q^k \le \big ( \eta ^{k-1} Q^{k-1} f^{l(k)}_{\lambda } + f^{l(k)}_{\lambda } \big ) / Q^k = f^{l(k)}_{\lambda }\le f^{l(k)}, \end{aligned}$$

where the last equality comes from the definition of $Q^k$. Similarly, we obtain

$$\begin{aligned} \widetilde{C}^k_{\lambda } = \big ( \eta ^{k-1} Q^{k-1} f^{l(k)}_{\lambda } + f^k \big ) / Q^k \ge \big ( \eta ^{k-1} Q^{k-1} f^k + f^k \big ) / Q^k = f^k, \end{aligned}$$

and this completes the proof. $\square$

The previous result makes clear that our ratio (18) is more restrictive than the classical nonmonotone criterion (10) derived from the original paper by Grippo et al. [24]. On the other hand, it leaves more freedom than the monotone variant (9).

2.2 Adaptive radius strategy

The overall behavior of the trust-region method is very sensitive to the updating rule for the trust-region radius $\varDelta _k$. Classical updating schemes depend on the size of the ratio from (9) between the actual and predicted reduction. This often works quite satisfactory. On the other hand, it measures the agreement between the actual and predicted reduction essentially only in the direction of the vector $d^k$. Hence this ratio might be close to one though f might be a highly nonlinear function for which $q_k$ is not a good approximation. In general, the traditional updating rule may therefore lead to unnecessarily large or small values of $\varDelta _k$, resulting in a number of subsequent iterations where only this radius gets changed, and this increases the total iteration count and the total cost of the underlying algorithm.

In other words, the previous value $\varDelta _{k-1}$ might not be a good starting point to compute the new radius $\varDelta _k$. An alternative choice within a monotone trust-region framework was suggested in [3, 21, 45] where the authors take the current value $\Vert F^k \Vert = \Vert F(x^k) \Vert$ as the basis. This avoids large values of $\varDelta _k$ close to a solution, and tries to overcome small values of $\varDelta _k$ far away from a solution. Furthermore, the size of unconstrained Newton-type steps are, under a nonsingularity condition, within a constant times $\Vert F(x^k) \Vert$ which motivates, to some extent, the strategy applied in [3, 21, 45].

Since we use a nonmonotone trust-region method, it is natural to replace $\Vert F^k \Vert$ by its counterpart from the nonmonotonicity strategy. Similar updating has also been suggested recently in [17, 18]. Specifically, let us define

$$\begin{aligned} F^{l(k)}:=\max _{0\le j\le m(k)}\{\Vert F^{k-j}\Vert \}, \quad \ \ k \in \mathbb N_0. \end{aligned}$$

(19)

Based on the new technique (15), we propose a new adaptive radius procedure to control the radius size by

$$\begin{aligned} \varDelta _{k}:= \left\{ \begin{array}{ll} \sigma _1\varDelta _{k-1},\ \ &{} \quad \hbox {if } \; \widetilde{r}_{k-1} < \rho _1, \\ P_{[\varDelta _{\min }, \varDelta _{\max }]} ( \widehat{C}^{k} ), \ \ &{} \quad \hbox {if } \; \widetilde{r}_{k-1}\in [\rho _1,\rho _2), \\ P_{[\varDelta _{\min }, \varDelta _{\max }]} ( \sigma _2 \widehat{C}^{k}),\ \ &{} \quad \hbox {if } \; \widetilde{r}_{k-1} \ge \rho _2. \\ \end{array} \right. \end{aligned}$$

(20)

where $0<\rho _1<\rho _2<1$ (step acceptance parameter), $0< \sigma _1< 1 < \sigma _2$ (trust-region scaling parameter) and $\varDelta _{\max }> \varDelta _{\min } > 0$ are suitable constants, $P_{[\varDelta _{\min }, \varDelta _{\max }]} ( \cdot )$ denotes the projection onto the interval $[\varDelta _{\min }, \varDelta _{\max }]$, and

$$\begin{aligned} \widehat{C}^k:= \left\{ \begin{array}{ll} \Vert F^k\Vert ,\ \ &{} \quad \hbox {if } \; k=0, \\ \big (\eta ^{k-1}Q^{k-1}F^{l(k)}+\Vert F^k\Vert \big )/Q^k\ \ &{} \quad \hbox {if } \; k\ge 1,\\ \end{array} \right. \end{aligned}$$

(21)

in which $Q^k$ satisfies (14). Note that the updating of $\varDelta _k$ follows traditional rules for $\widetilde{r}_{k-1} < \rho _1$ (this case corresponds to the unsuccessful iterations), but that the updating is different in the other cases.

Note also that, after each successful iteration, the new trust-region radius is at least as large as a given positive number $\varDelta _{\min }$. This avoids the trust-region radius to be very small after a successful iteration, and this fact plays an important role both in our global and in the local convergence analysis. To the best of our knowledge, such a strategy occurred, for the first time, in the paper [26] by Jiang et al. and has subsequently been applied also by some other authors, see, e.g., [31, 41]. The introduction of the upper bound $\varDelta _{\max }$ is not needed from a theoretical point of view, but avoids unnecessarily large trust-regions.

Similar to Lemma 2, we can also prove the following result.

Lemma 3

The inequality $\Vert F^k \Vert \le \widehat{C}^k \le F^{l(k)}$ holds for all $k \in \mathbb N_0$ such that the iterates $x^0, x^1, \ldots , x^k$ exist.

Hence the new sequence $\widehat{C}^k$ is always larger than $\Vert F^k\Vert$, and this helps to prevent a shrinking of the radius whenever the iterates are far away from a solution. On the other hand, the upper bound $F^{l(k)}$ of $\widehat{C}^k$ together with the updating rule (20) implies that the radius becomes not too large when we are close to a solution. These features are supposed to yield a better or more reasonable control of the radius size than the classical updating scheme. The numerical results given in Sect. 5 indicate that this is indeed the case.

2.3 Algorithm

In this section, we describe in detail our nonmonotone trust-region-type method for the solution of box-constrained nonlinear equations, prove some of its elementary properties and, in particular, show that the algorithm is well-defined. We begin with a formal statement of our nonmonotone trust-region method which is fully motivated by the corresponding discussion in the previous sections.

Algorithm 1

(Nonmonotone trust-region method—global version)

• (S.0) Choose $x^0 \in \varOmega$, $\varDelta _0 > 0$, $0< \rho _1< \rho _2 < 1$, $0< \sigma _1< 1 < \sigma _2$, $\varDelta _{\max }> \varDelta _{\min } > 0$, $\varepsilon \ge 0$, and set $k := 0$, $\widetilde{C}^0_{\lambda } := f(x^0)$, $\widehat{C}^0:= \Vert F(x^0) \Vert$.

• (S.1) If $\Vert p(x^k) \Vert _{\infty } \le \varepsilon$: STOP.

• (S.2) Define $l^k, u^k$ by (7), and compute $d^k$ as an approximate solution of the trust-region subproblem (8).

• (S.3) Compute the ratio

  $$\begin{aligned} \widetilde{r}_{k} := \frac{\widetilde{C}^{k}_{\lambda } - f(x^k+d^k)}{q_k(0) - q_k(d^k)}. \end{aligned}$$

  If $\widetilde{r}_{k} \ge \rho _1$, we set $x^{k+1} := x^k + d^k$ and call iteration k successful; otherwise, we set $x^{k+1} := x^k$ and call iteration k unsuccessful.

• (S.4) Compute $\widetilde{C}^{k+1}_{\lambda }$ and $\widehat{C}^{k+1}$ using (17) and (21), respectively.

• (S.5) Update the trust-region-radius according to

  $$\begin{aligned} \varDelta _{k+1} := \left\{ \begin{array}{ll} \sigma _1 \varDelta _k, &{} \quad \text {if } \quad \widetilde{r}_{k} < \rho _1, \\ P_{[\varDelta _{\min }, \varDelta _{\max }]} ( \widehat{C}^{k+1} ), &{} \quad \text {if } \quad \widetilde{r}_{k} \in [\rho _1, \rho _2), \\ P_{[\varDelta _{\min }, \varDelta _{\max }]} (\sigma _2 \widehat{C}^{k+1}), &{} \quad \text {if } \quad \widetilde{r}_{k} \ge \rho _2 . \end{array} \right. \end{aligned}$$

• (S.6) Set $k \leftarrow k+1$, and go to (S.1).

In our subsequent convergence analysis, we assume implicitly that $\varepsilon = 0$ and that Algorithm 1 generates an infinite sequence, i.e., it does not terminate after finitely many iterations in a stationary point of the optimization problem (4). Note also that, by construction, all vectors $x^k$ generated by Algorithm 1 belong to the feasible set $\varOmega$.

Note that we only require an approximate solution of the trust-region subproblem in (S.2). While this is a very vague formulation, the subsequent convergence theory clarifies what is really needed to get global and superlinear convergence. The minimizer of $q_k$ along the projected steepest descent direction $\widetilde{d}^k:=\mu p_k$, in which $\mu \in [0,1]$, is Cauchy point, i.e.,

$$\begin{aligned} d_k=t_k\widetilde{d}^k, \end{aligned}$$

which the scalar $t_k>0$ is a solution of the one-dimensional problem

$$\begin{aligned} t_k:=\arg \min _{t\ge 0} q_k(t\widetilde{d}^k)\ \ \text {s.t} \ \ l^k\le t\widetilde{d}^k\le u^k. \end{aligned}$$

The following result is our counterpart of a standard inequality known from [36] for the unconstrained trust-region subproblem based on the $l_2$-norm. Here we deal with the $l_\infty$-norm which, in addition, is restricted to the feasible set described by box constraints. A very similar result has been shown previously in [43] in the context of box constrained optimization problems under the additional assumption (translated to our context) that $J_k$ is nonsingular. Here we modify the technique of proof to allow also singular matrices $J_k$. Note that similar results are known for box-constrained equations in the context of affine-scaling interior-point methods, cf. [28, 28, 29, 42].

Lemma 4

Given an iterate $x^k$ and a solution $d^k$ of the trust-region subproblem (8), it holds that

$$\begin{aligned} q_k(0)-q_k(d^k)\ge \frac{1}{2}\,\Vert p(x^k)\Vert _{\infty } \, \min \left\{ \frac{\Vert p(x^k)\Vert _{\infty }}{\Vert J_k^T J_k \Vert }, \Vert p(x^k) \Vert _\infty , \varDelta _k\right\} , \end{aligned}$$

(22)

(with the usual interpretation that the minimum is attained at the second or third term if the denominator $\Vert J_k^T J_k \Vert$ in the first term is zero).

Proof

Recall that $p_k := p(x^k) = P_{\varOmega } ( x^k - g^k) - x^k$, and let us define

$$\begin{aligned} d := \mu p_k \quad \text {with} \quad \mu := \min \left\{ 1, \frac{\varDelta _k}{\Vert p_k \Vert _{\infty }} \right\} , \end{aligned}$$

(23)

where, without loss of generality, we can assume that $p_k \ne 0$ (otherwise, the statement obviously holds since zero is always feasible for the subproblem (8), apart from the fact that the algorithm would have stopped at iteration k). Note also that we skipped the dependence of d and $\mu$ on the index k for notational convenience.

The definition of d from (23) implies

$$\begin{aligned} x^k + d = x^k + \mu p_k = (1- \mu ) x^k + \mu P_{\varOmega } (x^k - g^k) \in \varOmega , \end{aligned}$$

since $\mu \in [0,1]$ and $\varOmega$ is convex. Furthermore, we have $\Vert d \Vert _{\infty } \le \varDelta _k$ by construction. Hence d is feasible for (8). Consequently, the scaled vector

$$\begin{aligned} \widetilde{d} := t d = t d + (1-t) 0 \quad \text {for } \quad 0 \le t \le 1, \end{aligned}$$

is feasible for (8) since both d and the zero vector belong to the convex feasible set of (8). Let us consider

$$\begin{aligned} \varphi (t) := q_k (\widetilde{d}) - q_k(0) = q_k ( t d ) - q_k(0) = t g_k^T d + \frac{1}{2} t^2 d^T J_k^T J_k d . \end{aligned}$$

In order to compute the minimizer of this one-dimensional function over all $t \in [0,1]$, we distinguish two cases.

Case 1: $d^T J_k^T J_k d > 0$. Then $\varphi$ is a strictly convex quadratic function with a unique minimizer in [0, 1] given by

$$\begin{aligned} \bar{t} := \text {argmin}_{t \in [0,1]} \varphi (t) = \min \left\{ - \frac{g_k^T d}{d^T J_k^T J_k d}, 1 \right\} , \end{aligned}$$

(note that $g_k^T d < 0$, cf. the following analysis). Since $d^k$ is the minimum of the subproblem (8), it follows that

$$\begin{aligned} q_k ( d^k ) - q_k (0) \le \varphi ( \bar{t} ) = \left\{ \begin{array}{ll} - \frac{1}{2} (g_k^T d)^2 / ( d^T J_k^T J_k d ), &{} \quad \text {if } \quad -g_k^T d \le d^T J_k^T J_k d, \\ g_k^T d + \frac{1}{2} d^T J_k^T J_k d, &{} \quad \text {else}. \end{array} \right. \end{aligned}$$

Taking into account that $d^T J_k^T J_k d < - g_k^T d$ in the second case, we obtain

$$\begin{aligned} q_k ( d^k ) - q_k (0) \le \varphi ( \bar{t} ) \le \left\{ \begin{array}{ll} - \frac{1}{2} (g_k^T d)^2 / ( d^T J_k^T J_k d ), &{} \quad \text {if } \quad -g_k^T d \le d^T J_k^T J_k d, \\ \frac{1}{2} g_k^T d, &{} \quad \text {else}. \end{array} \right. \end{aligned}$$

Now, we have

$$\begin{aligned} - g_k^T d= & {} - \mu g_k^T p_k \\= & {} \mu ( -g^k )^T \big ( P_{\varOmega } (x^k - g^k) - x^k \big ) \\= & {} \mu \big ( (x^k - g^k) - P_{\varOmega } (x^k - g^k) \big )^T \big ( P_{\varOmega } (x^k - g^k) - x^k \big ) \\&+ \, \mu \big ( P_{\varOmega } (x^k - g^k) - x^k \big )^T \big ( P_{\varOmega } (x^k - g^k) - x^k \big ) \\\ge & {} \mu \big \Vert P_{\varOmega } (x^k - g^k) - x^k \big \Vert ^2 =\mu \Vert p_k \Vert ^2\ge \mu \Vert p_k \Vert _{\infty }^2, \end{aligned}$$

where the first inequality comes from the projection theorem, and the second inequality follows immediately from that fact that $\Vert \cdot \Vert$ represents the Euclidean norm. Putting the last two estimates together, we obtain

$$\begin{aligned} q_k (0) - q_k (d^k)&\ge - \varphi (\bar{t}) \\&\ge \min \left\{ \frac{1}{2} \frac{(g_k^T d)^2}{d^T J_k^T J_k d}, - \frac{1}{2} g_k^T d \right\} \\&\ge \frac{1}{2} \min \left\{ \frac{\mu ^2 \Vert p_k \Vert ^4}{d^T J_k^T J_k d}, \mu \Vert p_k \Vert ^2 \right\} \\&\ge \frac{1}{2} \min \left\{ \frac{\mu ^2 \Vert p_k \Vert ^4}{\Vert J_k^T J_k \Vert \Vert d \Vert ^2}, \mu \Vert p_k \Vert ^2 \right\} \\&\mathop {=}\limits ^{(23)} \frac{1}{2} \min \left\{ \frac{\mu ^2 \Vert p_k \Vert ^4}{\mu ^2 \Vert J_k^T J_k \Vert \, \Vert p_k \Vert ^2}, \mu \Vert p_k \Vert ^2 \right\} \\&= \frac{1}{2} \Vert p_k \Vert \min \left\{ \frac{\Vert p_k \Vert }{\Vert J_k^T J_k \Vert }, \mu \Vert p_k \Vert \right\} \\&\ge \frac{1}{2} \Vert p_k \Vert _{\infty } \min \left\{ \frac{\Vert p_k \Vert _{\infty }}{\Vert J_k^T J_k \Vert }, \mu \Vert p_k \Vert _{\infty } \right\} \\&\mathop {=}\limits ^{(23)} \frac{1}{2} \Vert p_k \Vert _{\infty } \min \left\{ \frac{\Vert p_k \Vert _{\infty }}{\Vert J_k^T J_k \Vert }, \Vert p_k \Vert _\infty , \varDelta _k \right\} . \end{aligned}$$

This is the desired inequality in Case 1.

Case 2: $d^T J_k^T J_k d = 0$. Then $\varphi (t) = t g_k^T d$ is a linear function. Using (23), the feasibility of $x^k$, and the monotonicity of the projection operator, we have

$$\begin{aligned} g_k^T d= & {} \mu g_k^T p_k \\= & {} - \mu ( - g^k )^T \big ( P_{\varOmega } (x^k - g^k) - x^k \big ) \\= & {} - \mu ( - g^k )^T \big ( P_{\varOmega } (x^k - g^k) - P_{\varOmega } (x^k) \big ) \\\le & {} 0. \end{aligned}$$

Furthermore, since $P_{\varOmega } (x^k - g^k ) \ne P_{\varOmega } (x^k)$ (otherwise, we would have $p_k = 0$ and the algorithm would have stopped), standard properties of the projection operator guarantee that the inequality $g_k^T d \le 0$ is strict. Hence d is a descent direction, and it follows that, again, there is a unique minimizer of $\varphi (t)$ on [0, 1] given by

$$\begin{aligned} \bar{t} := \text {argmin}_{t \in [0,1]} \varphi (t) = 1. \end{aligned}$$

Note that we also have $- g_k^T d > 0 = d^T J_k^T J_k d$. Hence we obtain as in Case 1, where the minimum is attained at $\bar{t} = 1$, that

$$\begin{aligned} q_k (0) - q_k ( d^k ) \ge \frac{1}{2} \Vert p_k \Vert _{\infty } \min \big \{ \Vert p_k \Vert _\infty , \varDelta _k \big \}. \end{aligned}$$

Together with Case 1, this completes the proof. $\square$

Note that the previous result implies that the denominator in the definition of the ratio $\widetilde{r}_{k}$ in (S.3) is always positive if $d^k$ is the solution of (8). In particular, it therefore follows that Algorithm 1 is well-defined.

Lemma 4 assumes that $d^k$ is an exact solution of the convex quadratic trust-region subproblem from (8). However, the proof of this result explicitly computes, in a very simple way, Cauchy point (though the notion of a Cauchy point is nonunique in the constrained case) which satisfies the central inequality (22), so that, in particular, each global minimum also satisfies this inequality. To have the constructive procedure from the proof of Lemma 4 explicitly available, we recall the corresponding technique in the following algorithm.

Algorithm 2

(Procedure to compute an inexact solution $d^k$ of (8))

• (a) Define $\mu _k := \min \big \{ 1, \frac{\varDelta _k}{\Vert p(x^k) \Vert _\infty } \big \}$.

• (b) Set $\widetilde{d}^k := \mu _k p(x^k)$.

• (c) Set $t_k := \min \big \{ - \frac{g_k^T \widetilde{d}^k}{( \widetilde{d}^k)^T J_k^T J_k \widetilde{d}^k}, 1 \big \}$ (where the minimum is attained at 1 if the denominator is zero).

• (d) Compute $d^k := t_k \widetilde{d}^k$.

The two main properties of the vector $d^k$ computed in Algorithm 2 are summarized in the following result which follows immediately from Lemma 4 and the construction of $d^k$.

Lemma 5

The vector $d^k$ computed by Algorithm 2 satisfies inequality (22) and $\Vert d^k \Vert _\infty \le \Vert p(x^k) \Vert _\infty$.

In principle, it is possible to find approximate solutions $d^k$ of the trust-region subproblem (8) whose size is not related to $\Vert p (x^k) \Vert _\infty$. On the other hand, both properties mentioned in Lemma 5 turn out to be important for our global convergence analysis. We therefore make the following assumption.

Assumption 1

There exist constants $c, c_1, c_2 > 0$ such that the approximate solutions $d^k$ computed in (S.2) of Algorithm 1 satisfy

• (a) $\Vert d^k \Vert _{\infty } \le c \Vert p(x^k) \Vert _{\infty }$ for all $k \in \mathbb N_0$;

• (b) $q_k(0) - q_k(d^k) \ge c_1 \Vert p(x^k) \Vert _\infty \min \big \{ \frac{\Vert p(x^k) \Vert _\infty }{\Vert J_k^T J_k \Vert }, c_2 \Vert p(x^k) \Vert _\infty , \varDelta _k \big \}$ for all $k \in \mathbb N_0$.

Recall that this assumption is satisfied with $c := 1, c_1 := 0.5, c_2 := 1$ by the approximate solution $d^k$ computed in Algorithm 2. Conditions like those summarized in Assumption 1 arise quite frequently in the context of trust-region methods. Assumption 1 (a), for example, also occurs, at least implicitly, within the class of affine-scaling interior-point methods when a certain scaling matrix is assumed to be bounded, cf. [29, 41, 42]. On the other hand, Assumption 1 (b) guarantees a decrease which is at least as good as a fraction of the Cauchy step computed in Algorithm 2; in particular, it implies that the vectors $d^k$ gives a better value of the quadratic model $q_k$ than the zero vector.

In our subsequent global convergence analysis, only Assumption 1 (b) is required in the first preliminary results, but in order to get a final convergence result, Assumption 1 (a) is also needed.

3 Global convergence

We present the global convergence properties of Algorithm 1. To this end, we begin with some technical results in Sect. 3.1 and then discuss the global convergence itself in Sect. 3.2.

3.1 Some technical results

In order to prove global convergence of Algorithm 1, we first need to establish a number of preliminary results. We begin by showing that, the sequence $f^{l(k)}$ is monotonically decreasing.

Lemma 6

Let the sequence $\{x^k\}$ be generated by Algorithm 1 such that the approximate solutions $d^k$ satisfy Assumption 1 (b). Then the sequences $\{f^{l(k)}\}$ and $\{F^{l(k)}\}$ are monotonically decreasing, hence convergent.

Proof

See [24]. $\square$

An immediate consequence of the previous result is the fact that the entire sequence $\{ x^k \}$ generated by Algorithm 1 remains in the (feasible) level set $L(x^0) := \{ x \in \varOmega \mid f(x) \le f(x^0) \}$ of the starting point $x^0$.

Corollary 1

Assume that the sequence $\{ d^k \}$ satisfies Assumption 1 (b). Then all iterates $x^k$ generated by Algorithm 1 belong to the level set $L(x^0)$.

Proof

In view of Lemma 6, we get $f^k \le f^{l(k)} \le f^{l(0)} = f^0 = f(x^0)$, and this implies that any iterate $x^k$ generated by Algorithm 1 belongs to the level set $L(x^0)$. $\square$

To establish suitable convergence properties of Algorithm 1, we also state the following standard assumption.

Assumption 2

The sequence of Jacobian matrices $\{ J_k \}$ is bounded, i.e. there exists some number $\varkappa > 0$ such that $\Vert J_k \Vert \le \varkappa$ for all $k \in \mathbb N_0$.

Using Assumption 2, we also obtain the following consequence.

Corollary 2

Suppose that Assumption 2 holds, and the sequence $\{ d^k \}$ satisfies Assumption 1 (b). Then there are constants $\gamma _1, \gamma _2 > 0$ such that

$$\begin{aligned} q_k(0) - q_k(d^k) \ge \gamma _1 \Vert p(x^k) \Vert _{\infty }^2 \min \big \{ \gamma _2, \varDelta _k \big \}, \end{aligned}$$

for all $k \in \mathbb N_0$.

Proof

In view of Assumptions 1 (b) and 2, we have

$$\begin{aligned} q_k(0) - q_k (d^k) \ge c_1 \Vert p(x^k) \Vert _{\infty } \min \bigg \{ \frac{\Vert p(x^k) \Vert _{\infty }}{\varkappa ^2}, c_2 \Vert p(x^k) \Vert _\infty , \varDelta _k \bigg \}. \end{aligned}$$

Since $\Vert F(x^k) \Vert \le \Vert F(x^0) \Vert$ for all $k \in \mathbb N_0$ by Corollary 1, and since $\Vert g^k \Vert = \Vert J_k^T F(x^k) \Vert \le \Vert J_k \Vert \Vert F(x^k) \Vert \le \varkappa \Vert F(x^0) \Vert$ by Assumption 2, the nonexpansiveness of the projection operator immediately yields

$$\begin{aligned} \Vert p(x^k) \Vert = \Vert P_{\varOmega } (x^k - g^k) - P_{\varOmega } (x^k) \Vert \le \Vert g^k \Vert \le \varkappa \Vert F(x^0) \Vert , \end{aligned}$$

and a similar bound then holds for the expression $\Vert p(x^k) \Vert _{\infty }$ due to the equivalence of all norms in finite-dimensional spaces. For some constant $\varkappa _\infty > 0$, we therefore get

$$\begin{aligned} q_k(0) - q_k (d^k)\ge & {} c_1 \Vert p(x^k) \Vert _{\infty } \min \bigg \{ \frac{\Vert p(x^k) \Vert _{\infty }}{\varkappa ^2}, c_2 \Vert p(x^k) \Vert _\infty , \frac{\Vert p(x^k) \Vert _{\infty } \varDelta _k}{\Vert p(x^k) \Vert _{\infty }} \bigg \} \\\ge & {} c_1 \Vert p(x^k) \Vert _{\infty }^2 \min \bigg \{ \frac{1}{\varkappa ^2}, c_2, \frac{\varDelta _k}{\Vert p(x^k) \Vert _{\infty }} \bigg \} \\\ge & {} c_1 \Vert p(x^k) \Vert _{\infty }^2 \min \bigg \{ \frac{1}{\varkappa ^2}, c_2, \frac{\varDelta _k}{\varkappa _\infty \Vert F(x^0) \Vert _\infty } \bigg \}\\\ge & {} \frac{c_1 \Vert p(x^k) \Vert _{\infty }^2}{\varkappa _\infty \Vert F(x^0) \Vert _{\infty }^2 } \min \bigg \{\min \bigg \{ \frac{\varkappa _\infty \Vert F(x^0) \Vert _{\infty }^2}{\varkappa ^2}, c_2\varkappa _\infty \Vert F(x^0) \Vert _\infty \bigg \}, \varDelta _k\bigg \}\\= & {} \gamma _1 \Vert p(x^k) \Vert _{\infty }^2 \min \big \{ \gamma _2, \varDelta _k \big \}, \end{aligned}$$

which $\gamma _1:=\frac{c_1}{\varkappa _\infty \Vert F(x^0) \Vert _{\infty }^2 }$ and $\gamma _2:=\min \{ \frac{\varkappa _\infty \Vert F(x^0) \Vert _{\infty }^2}{\varkappa ^2}, c_2\varkappa _\infty \Vert F(x^0) \Vert _\infty \}$. This yields the desired result. $\square$

The following lemma shows that there are infinitely many successful iterations in Algorithm 1.

Lemma 7

Let Assumption 2 be satisfied and suppose that Assumption 1 (b) holds for the sequence $\{ d^k \}$. Then there exist infinitely many successful iterations in Algorithm 1.

Proof

To prove, we first suppose that there are only finitely many successful iterations. Similarly to Lemma 3.3 in [17], we then can obtain, for all $k \in \mathbb N_0$ sufficiently large, that

$$\begin{aligned} \frac{f(x^k) - f(x^k + d^k)}{ q_k (0) - q_k (d^k)} \ge \rho _1 . \end{aligned}$$

Taking into account that $\widetilde{C}^{k}_{\lambda } \ge f(x^k)$ in view of Lemma 2 (since we assume there are only finitely many successful iterations, this is actually an equality for all k sufficiently large), we eventually have another successful iteration, a contradiction to our assumption. $\square$

3.2 Main global convergence results

In order to obtain a suitable global convergence result, we need the following additional smoothness assumption regarding the objective function f.

Assumption 3

The function f is uniformly continuous on the level set $L(x^0)$.

Note that this assumption is satisfied, in particular, if f is Lipschitz-continuous on $L(x^0)$. This situation occurs, e.g., if $L(x^0)$ is bounded, which certainly holds if the feasible set $\varOmega$ itself is bounded.

The following result plays a fundamental role in our global convergence analysis and shows, in particular, that the entire sequence $\{ f(x^k) \}$, though nonmonotone, converges.

Proposition 4

Let $\{ x^k \}$ be a sequence generated by Algorithm 1 such that the approximate solutions $d^k$ in (S.2) satisfy Assumption 1. Suppose further that Assumptions 2 and 3 hold. Then

$$\begin{aligned} \lim _{k \rightarrow \infty } f^{l(k)} = \lim _{k \rightarrow \infty } f^{l(k)}_{\lambda }=\lim _{k \rightarrow \infty } \widetilde{C}^{k}_{\lambda } = \lim _{k \rightarrow \infty } f(x^k), \end{aligned}$$

in particular, these limits exist.

Proof

In view of Lemma 2, it suffices to show that $\lim _{k \rightarrow \infty } f^{l(k)} = \lim _{k \rightarrow \infty } f(x^k)$ holds. We further note that the limit $\lim _{k \rightarrow \infty } f^{l(k)}$ exists by Lemma 6.

Define $\widehat{1} (k) := l (k+M+2)$ for all $k \in \mathbb N_0$. Then $\widehat{1}(k) \ge k+2$, and we can write

$$\begin{aligned} x^{k+1} = x^{\widehat{1}(k)} - \sum _{j=1}^{\widehat{1}(k) - k - 1} \big ( x^{\widehat{1}(k) - j +1} - x^{\widehat{1}(k) - j} \big ). \end{aligned}$$

(24)

We want to show that

$$\begin{aligned} \lim _{k \rightarrow \infty } \Vert x^{k+1} - x^{\widehat{1}(k)} \Vert _\infty = 0, \end{aligned}$$

(25)

then it follows that

$$\begin{aligned} \lim _{k \rightarrow \infty } f(x^{l(k)}) = \lim _{k \rightarrow \infty } f(x^{\widehat{1}(k)}) = \lim _{k \rightarrow \infty } f(x^{k+1}) = \lim _{k \rightarrow \infty } f(x^k), \end{aligned}$$

where the first equality follows from the fact that $\{ \widehat{1}(k) \}$ is a subsequence of $\{ l(k) \}$, the second equality uses (25) and the assumed uniform continuity of f (recall that all iterates $x^k$ belong to the level set $L(x^0)$ in view of Corollary 1), and the third equality is obvious.

Hence it suffices to verify (25). To this end, we exploit (24) and show simultaneously, by induction, that

$$\begin{aligned} \lim _{k \rightarrow \infty } \big \Vert x^{\widehat{1}(k) - j + 1} - x^{\widehat{1}(k) - j} \big \Vert _\infty = 0 \quad \forall j = 1, 2, \ldots \end{aligned}$$

(26)

and

$$\begin{aligned} \lim _{k \rightarrow \infty } f(x^{\widehat{1}(k) - j}) = \lim _{k \rightarrow \infty } f(x^{\widehat{1}(k)}) \quad \forall j = 1, 2, \ldots . \end{aligned}$$

(27)

Note that we have assumed that k is large enough to make the indices $\widehat{1}(k) -j+1$ (or $\widehat{1}(k) -j$) nonnegative. Since

$$\begin{aligned} \widehat{1}(k) - k - 1 = l(k+M+2) - k - 1 \le (k+M+2) - k - 1 = M+1 \quad \forall k \in \mathbb N_0, \end{aligned}$$

the number of terms in the sum (24) is uniformly bounded by the constant $M+1$, hence (26) implies (25).

Let us begin our induction with $j = 1$, and let $K \subseteq \mathbb N_0$ be the (infinite) subset of successful iterations. For any $k \in K$, we obtain from Lemma 2 that

$$\begin{aligned} f^{l(k)} - f(x^{k+1}) = f^{l(k)} - f(x^k+d^k) \ge \widetilde{C}^{k}_{\lambda } - f(x^k+d^k) \ge \rho _1 \big ( q_k(0) - q_k(d^k) \big ), \end{aligned}$$

hence

$$\begin{aligned} f^{l(k)} - f(x^{k+1}) \ge \rho _1 \text {pred}_{k}, \end{aligned}$$

(28)

where $\text {pred}_k := q_k(0) - q_k (d^k)$ denotes the predicted reduction which, in view of Assumption 1 (b), is always nonnegative. Replacing k by $l(k)-1$ and assuming $l(k)-1 \in K$, we therefore get

$$\begin{aligned} f^{l(l(k)-1)} - f(x^{l(k)}) \ge \rho _1 \text {pred}_{l(k)-1} \ge 0. \end{aligned}$$

Since the left-hand side converges to zero by Lemma 6, it follows that

$$\begin{aligned} \lim _{k \rightarrow \infty } \text {pred}_{l(k)-1} = 0, \end{aligned}$$

(29)

provided that $l(k) - 1 \in K$ for all $k \in \mathbb N_0$. Using Assumptions 1 and 2, we further obtain

$$\begin{aligned} \text {pred}_{l(k)-1}\ge & {} c_1 \big \Vert p(x^{l(k)-1}) \Vert _\infty \min \bigg \{ \frac{\Vert p(x^{l(k)-1}) \Vert _\infty }{\varkappa ^2}, c_2 \Vert p(x^{l(k)-1}) \Vert _\infty , \varDelta _{l(k)-1} \bigg \} \\\ge & {} c_1 \big \Vert p(x^{l(k)-1}) \Vert _\infty \min \bigg \{ \frac{\Vert p(x^{l(k)-1}) \Vert _\infty }{\varkappa ^2}, c_2 \Vert p(x^{l(k)-1}) \Vert _\infty , \Vert d^{l(k)-1} \Vert _\infty \bigg \} \\\ge & {} \frac{c_1}{c^2} \big \Vert d^{l(k)-1} \Vert _\infty \min \bigg \{ \frac{\Vert d^{l(k)-1} \Vert _\infty }{\varkappa ^2}, c_2 \big \Vert d^{l(k)-1} \big \Vert _\infty , c \big \Vert d^{l(k)-1} \Vert _\infty \bigg \} \\= & {} \widetilde{\gamma } \big \Vert d^{l(k)-1} \big \Vert _\infty ^2\ge \widetilde{\gamma } \big \Vert x^{l(k)} - x^{l(k)-1} \big \Vert _\infty ^2, \end{aligned}$$

with $\widetilde{\gamma } := \frac{c_1}{c^2} \min \big \{ \frac{1}{\varkappa ^2}, c_2, c \big \}$ being constant. Hence (29) implies

$$\begin{aligned} \lim _{k \rightarrow \infty } \big \Vert x^{l(k)} - x^{l(k)-1}\big \Vert _\infty = 0; \end{aligned}$$

(30)

in view of its derivation, this limit holds only under the assumption that all iterations $l(k)-1$ are successful, however, it trivially holds if some of even all of these iterations are unsuccessful since then we have $x^{l(k)} = x^{l(k)-1}$. Since $\{ \widehat{1}(k) \}$ is a subsequence of $\{ l(k) \}$, we therefore obtain (26) for $j = 1$. Using (26) together with the uniform continuity of f, we also obtain (27) from Lemma 6 and (26) with $j = 1$.

Suppose that (26) and (27) hold for some $j \in \mathbb N$, and consider the index $j+1$. Using (28) and substituting k by $\widehat{1}(k) -j-1$ and assuming, for the moment, that $\widehat{1}(k)-j-1 \in K$, we get

$$\begin{aligned} f( x^{l(\widehat{1}(k) - j - 1)} ) - f(x^{\widehat{1} (k) - j}) \ge \rho _1 \text {pred}_{\widehat{1}(k) - j - 1}. \end{aligned}$$

(31)

Note that we have

$$\begin{aligned} \lim _{k \rightarrow \infty } f(x^{l(k)}) = \lim _{k \rightarrow \infty } f(x^{\widehat{1}(k)}) = \lim _{k \rightarrow \infty } f(x^{\widehat{1}(k) - j}), \end{aligned}$$

where the first equality comes from the fact that $\{ \widehat{1}(k) \}$ is a subsequence of $\{ l(k) \}$, and the second equality uses the induction hypothesis from (27). We therefore obtain from Lemma 6 that the left-hand side of (31) converges to zero, hence it follows that $\text {pred}_{\widehat{1}(k) - j - 1} \rightarrow 0$ for $k \rightarrow \infty$ provided that all iterations $\widehat{1}(k) - j - 1$ are successful. Similar to the derivation of (30), this implies

$$\begin{aligned} \lim _{k \rightarrow \infty } \big \Vert x^{\widehat{1}(k) - j} - x^{\widehat{1}(k) - j - 1} \big \Vert _\infty = 0, \end{aligned}$$

(32)

and this limit holds independent of whether or not the iterations $\widehat{1}(k) - j - 1$ are successful. Finally, using (32) together with Assumption 3, and exploiting the induction hypothesis (27), we also obtain

$$\begin{aligned} \lim _{k \rightarrow \infty } f(x^{\widehat{1}(k)-j-1}) = \lim _{k \rightarrow \infty } f(x^{\widehat{1}(k) - j}) = \lim _{k \rightarrow \infty } f(x^{\widehat{1}(k)}), \end{aligned}$$

and this completes our induction. $\square$

The previous result may be viewed as our main step in proving global convergence of Algorithm 1. We only need one more lemma before coming to the main result of this section.

Lemma 8

Let Assumption 2 hold, and suppose that the sequence $\{ d^k \}$ satisfies Assumption 1 (b). Let $\{ x^k \}_\mathcal {K}$ be a subsequence converging to a point $x^*$. If $x^*$ is not a stationary point of (4), then

$$\begin{aligned} \liminf _{k \rightarrow \infty , k \in \mathcal {K}} \varDelta _k > 0. \end{aligned}$$

Proof

Define the index set

$$\begin{aligned} \overline{\mathcal {K}} := \{ k - 1 \mid k \in \mathcal {K} \}. \end{aligned}$$

Then the subsequence $\{ x^{k+1} \}_{k \in \overline{\mathcal {K}}}$ converges to $x^*$. We have to show that

$$\begin{aligned} \liminf _{k \rightarrow \infty , k \in \overline{\mathcal {K}}} \varDelta _{k+1} > 0. \end{aligned}$$

Suppose this does not hold. Subsequencing if necessary, we can therefore assume that

$$\begin{aligned} \lim _{k \rightarrow \infty , k \in \overline{\mathcal {K}}} \varDelta _{k+1} = 0. \end{aligned}$$

(33)

In view of the updating rule for the trust-region radius (note that the lower bound $\varDelta _{\min } > 0$ used for all successful iterations plays a central role here), this implies that all iterates $k \in \overline{\mathcal {K}}$ with k sufficiently large are unsuccessful. Hence we have

$$\begin{aligned} \widetilde{r}_{k} < \rho _1, \end{aligned}$$

(34)

and $x^{k+1} = x^k$ for all $k \in \overline{\mathcal {K}}$ large enough. Since $\{ x^{k+1} \}_{k \in \overline{\mathcal {K}}}$ converges to $x^*$ by assumption, this also implies that the subsequence $\{ x^k \}_{k \in \overline{\mathcal {K}}}$ converges to $x^*$. Taking into account the updating $\varDelta _{k+1} = \sigma _1 \varDelta _k$ for all unsuccessful iterations k, we therefore obtain

$$\begin{aligned} \lim _{k \rightarrow \infty , k \in \overline{\mathcal {K}}} \varDelta _k = 0, \end{aligned}$$

(35)

from (33).

Since the limit point $x^*$ is non-stationary by assumption, there exists a constant $\delta > 0$ such that $\Vert p(x^k) \Vert _{\infty } \ge \delta$ for all $k \in \overline{\mathcal {K}}$. Exploiting Corollary 2 and using (35), we therefore obtain

$$\begin{aligned} q_k(0) - q_k (d^k) \ge \gamma _1 \Vert p(x^k) \Vert _\infty ^2 \min \{ \gamma _2, \varDelta _k \} \ge \gamma _1 \delta ^2 \varDelta _k \ge \gamma _1 \delta ^2 \Vert d^k \Vert _{\infty }, \end{aligned}$$

(36)

for all $k \in \overline{\mathcal {K}}$ sufficiently large, and for suitable constants $\gamma _1, \gamma _2 > 0$. Using the continuous differentiability of f, we can find, for each $k \in \mathbb N_0$, a vector $\xi ^k = x^k + \theta _k d^k, \theta _k \in (0,1),$ such that

$$\begin{aligned} f(x^k + d^k) = f(x^k) + \nabla f(\xi ^k)^T d^k. \end{aligned}$$

(37)

Since $\{ d^k \}_{k \in \overline{K}} \rightarrow 0$ in view of (35) and $\{ x^k \}_{k \in \overline{\mathcal {K}}} \rightarrow x^*$, we also have $\{ \xi ^k \}_{k \in \overline{\mathcal {K}}} \rightarrow x^*$. Using (36), (37), and Assumption 2, we therefore get

$$\begin{aligned} \left| \frac{f(x^k) - f(x^k + d^k)}{q_k(0) - q_k(d^k)} - 1 \right|= & {} \frac{\big | q_k(d^k) - f(x^k+d^k) \big |}{q_k(0) - q_k(d^k)} \\= & {} \frac{\big | \nabla f(x^k)^T d^k + \frac{1}{2} (d^k)^T J_k^T J_k d^k - \nabla f(\xi ^k)^T d^k \big |}{q_k(0) - q_k(d^k)} \\\le & {} \frac{\Vert \nabla f(x^k) - \nabla f(\xi ^k) \Vert \Vert d^k \Vert + \frac{1}{2} \varkappa ^2 \Vert d^k \Vert ^2}{\gamma _1 \delta ^2 \Vert d^k \Vert _\infty } \\\le & {} \widetilde{\gamma } \bigg ( \big \Vert \nabla f(x^k) - \nabla f(\xi ^k) \big \Vert + \frac{1}{2} \varkappa ^2 \Vert d^k \Vert \bigg ) \\\rightarrow & {} 0 \quad \text {for } k \rightarrow \infty , \ k \in \overline{\mathcal {K}}, \end{aligned}$$

where $\widetilde{\gamma } > 0$ denotes a suitable constant. Hence

$$\begin{aligned} \frac{f(x^k) - f(x^k+d^k)}{q_k(0) - q_k(d^k)} \ge \rho _1 \quad \forall k \in \overline{\mathcal {K}} \text { sufficiently large}. \end{aligned}$$

In view of Lemma 2, this implies

$$\begin{aligned} \widetilde{r}_{k} = \frac{\widetilde{C}^{k}_{\lambda } - f(x^k+d^k)}{q_k(0) - q_k(d^k)} \ge \rho _1 \quad \forall k \in \overline{\mathcal {K}} \text { sufficiently large}, \end{aligned}$$

a contradiction to (34). $\square$

The following is our main global convergence result and shows that every accumulation point of a sequence $\{ x^k \}$ generated by Algorithm 1 is a stationary point of problem (4).

Theorem 1

Let Assumptions 2 and 3 hold, and let $\{ x^k \}$ be a sequence generated by Algorithm 1 such that the approximate solutions of the trust-region subproblem satisfy Assumption 1. If there exists an accumulation point of the sequence $\{ x^k \}$, then every accumulation point $x^*$ is a stationary point of (4).

Proof

Let $\{ x^k \}_{k \in \mathbf {K}}$ be a subsequence converging to $x^*$. Since $x^{k+1} = x^k$ for all unsuccessful iterations k, and since there are infinitely many successful iterations in view of Lemma 7, we can assume without loss of generality that all iterations $k \in \mathbf {K}$ are successful.

Suppose that $x^*$ is not a stationary point of (4). Then there exists a constant $\delta > 0$ such that $\Vert p(x^k) \Vert _\infty \ge \delta$ for all $k \in \mathbf {K}$ sufficiently large. Since the iterates $k \in \mathbf {K}$ are successful by construction, we obtain from Lemma 2 and Corollary 2 that

$$\begin{aligned} f^{l(k)} - f(x^k+d^k)\ge & {} \widetilde{C}^{k}_{\lambda } - f(x^k+d^k)\\\ge & {} \rho _1 \big ( q_k(0) - q_k(d^k) \big )\\\ge & {} \rho _1 \gamma _1 \Vert p(x^k) \Vert _\infty ^2 \min \{ \gamma _2, \varDelta _k \}\\\ge & {} \rho _1 \gamma _1 \delta ^2 \min \big \{ \gamma _2, \varDelta _k \big \}, \end{aligned}$$

for all $k \in \mathbf {K}$ sufficiently large. Since $f^{l(k)} - f(x^k+d^k) \rightarrow _\mathbf {K} 0$ due to Proposition 4, we obtain $\varDelta _k \le \gamma _2$ for all $k \in \mathbf {K}$ large enough and $\lim _{k \rightarrow \infty , k \in \mathbf {K}} \varDelta _k = 0$, but this contradicts Lemma 8. $\square$

Lemma 7 showed that there exist infinitely many successful iterations in Algorithm 1. We now denote the set of successful iterations in Algorithm 1 as follows

$$\begin{aligned} \widetilde{K}:=\left\{ k\in \mathbb {N}_0\mid \widetilde{r}_k\ge \rho _1\right\} . \end{aligned}$$

Let us define $\{k_i\}_{i\in \mathbb {N}_0}$ as the members of $\widetilde{K}$ such that $k_0<k_1<k_2<\cdots$. In the following remark, we show that the formula (15) can be rewritten, for $k_i\in \widetilde{K}$, as follows

$$\begin{aligned} f^{l(k_i)}:=\sum _{p=0}^{s'}\widetilde{\lambda }_{k_i,p}f^{k_{i-p}}, \end{aligned}$$

where $s'\le s:=m(k)-1$ and $\sum _{p=0}^{s'}\widetilde{\lambda }_{k_i,p}=1$. In other words, we can rewrite $f^{l(k_i)}$ as a convex combination of some function values of successful iterations.

Remark 1

In order to prove the next theorem, we first need to define the set of unsuccessful iterations by $\mathcal {J}:=\bigcup _{i=0}^{\infty }\mathcal {J}_{i}$, in which $\mathcal {J}_{0}:=\{k\mid k<k_0\}$ and $\mathcal {J}_{i}:=\{k\mid k_{i-1}<k<k_i\}$ for $i\ge 1$, and then we explain the above representation of $f^{l(k_i)}$. To do so, we have, for $i\ge s$, the following three cases:

• (a) If all iterations $k_i-1, k_i-2, \ldots , k_i-s'$ are successful ($s'=s$), then the definition $\widetilde{K}$, for $p=0,\ldots ,s'$, leads to

  $$\begin{aligned} f^{k_{i}-p}=f^{k_{i-p}}, \end{aligned}$$

  and therefore $f^{l(k_i)}$ can be represented as

  $$\begin{aligned} f^{l(k_i)}:=\sum _{p=0}^{s}\widetilde{\lambda }_{k_i,p}f^{k_{i-p}}, \end{aligned}$$

  (38)

  where $\widetilde{\lambda }_{k_i,p}=\lambda _{k_i,p}$ for $p=0,\ldots ,s$.

• (b) If all iterations $k_i-1, k_i-2, \ldots , k_i-s$ are unsuccessful ($s'\le s$), then these unsuccessful iterations belong to $\mathcal {J}$. According to Algorithm 1, it is possible that $x^{k_i-p}:=x^{k_{i-1}}$ for some $p\in \{1,\ldots ,s\}$ provided that $k_i-p\in \mathcal {J}_{i}$, $x^{k_i-p}:=x^{k_{i-2}}$ for some $p\in \{1,\ldots ,s\}$ and that $k_i-p\in \mathcal {J}_{i-1}$, and so on, hence

  $$\begin{aligned} f^{l(k_i)}:=\sum _{p=0}^{s'}\widetilde{\lambda }_{k_i,p}f^{k_{i-p}}, \end{aligned}$$

  (39)

  where $\widetilde{\lambda }_{k_i,0}=\lambda _{k_i,0}$ and the remainder of the coefficients $\widetilde{\lambda }_{k_i,p}$, for $p\in \{1,\ldots ,s'\}$, are as the sum of some coefficients $\lambda _{k_i,p}$ such that $\sum _{p=0}^{s'}\widetilde{\lambda }_{k_i,p}=1$.

• (c) If some iterations $k_i-1, k_i-2, \ldots , k_i-s$ are successful and some other are unsuccessful, then the representation of $f^{l(k_i)}$ is a combination of (38) and (39).

For $i<s$, we have the following cases:

• (i) In the special case of $i=0$, since $k_0-1, k_0-2, \ldots , k_0-s<k_0$, they belong to $\mathcal {J}_{0}$, then Algorithm 1 implies $f^{k_0-p}=f^{k_0}$ for $p\in \{1,\ldots ,s'\}$ and hence $f^{l(k_i)}=f^{k_0}$.

• (ii) For $i=1$, since $k_1-1, k_1-2, \ldots , k_1-s<k_1$, we have the following items:

  • (a) If one of the mentioned iterations is $k_0$ and the remainder of iterations belong to $\mathcal {J}_{0}$, then $f^{l(k_i)}=f^{k_0}$.

  • (b) If one of the mentioned iterations is $k_0$ and the remainder of iterations belong to $\mathcal {J}_{1}$, then $f^{l(k_i)}$ is a convex combination of $f^{k_0}$ and $f^{k_1}$.

  • (c) If all iterations of $k_1-1, k_1-2, \ldots , k_1-s$ belong to $\mathcal {J}_{1}$, then $f^{l(k_i)}=f^{k_1}$.

• (iii) For $i=2,\ldots ,s-1$, we can write, similar to two previous cases, $f^{l(k_i)}$ in terms of one of $f^{k_p}$ for $p=0,\ldots ,s-1$ or the convex combination of $f^{k_0}, f^{k_1}, \ldots , f^{k_{s-1}}$ or the convex combination of some $f^{k_0}, f^{k_1}, \ldots , f^{k_{s-1}}$.

Next, we only need to restrict our attention to the case where there are infinitely many successful iterations.

Theorem 2

Let Assumption 2 hold, and suppose that the sequence $\{ d^k \}$ satisfies Assumption 1. Then

$$\begin{aligned} \liminf _{k\rightarrow \infty } \Vert p(x^k)\Vert _{\infty }=0. \end{aligned}$$

Proof

By contradiction, suppose that $\liminf _{k\rightarrow \infty } \Vert p(x^k)\Vert _{\infty }=0$ is not satisfied. Hence, let us assume that there is a constant $\delta >0$ and an infinite subset $\underline{\mathcal {K}}\subseteq \mathbb {N}_0$ such that

$$\begin{aligned} \Vert p(x^k)\Vert _\infty \ge \delta , \quad \ \ \forall k\in \underline{\mathcal {K}}. \end{aligned}$$

By induction, we first show for $k_i\in \widetilde{K}$ (for $i\ge 1$)

$$\begin{aligned} f^{k_i}<f^0-\rho _1\lambda \sum _{j=0}^{i-2}\text {pred}_{k_j}-\rho _1\text {pred}_{k_{i-1}} \le f^0-\rho _1\lambda \sum _{j<i}\text {pred}_{k_j}, \end{aligned}$$

(40)

where $\text {pred}_j := q_j(0) - q_j (d^j)$ and i is the index of successful iterations.

For the case $i=1$, we first show that $f^{k_1}=f^{k_0+1}$ since the members of set $\{k_0+1,k_0+2,\ldots ,k_1-1\}$ are the index of unsuccessful iterations between $k_0$ and $k_1$, according to Algorithm 1 ($\widetilde{r}_{k_0+j}<\rho _1$), we have $x^{k_0+j}:=x^{k_0}$ for $j=1,\ldots ,k_1-k_0-1$. From this fact and since

$$\begin{aligned} \frac{f^{l(k_0)}_{\lambda }-f^{k_0+1}}{\text {pred}_{k_0}}\ge \widetilde{r}_{k_0}\ge \rho _1, \end{aligned}$$

we have

$$\begin{aligned} f^{k_1}=f^{k_0+1}=f^{l(k_0)}_{\lambda }-(f^{l(k_0)}_{\lambda }-f^{k_0+1}) <f^{l(k_0)}_{\lambda }-\rho _1\text {pred}_{k_0}\le f^0-\rho _1\text {pred}_{k_0}. \end{aligned}$$

Let us now make the induction hypothesis, namely, that (40) holds for $1,2,\ldots ,i$. Note that, similar case $i=1$, we have $f^{k_{i+1}}=f^{k_{i}+1}$ since the members of set $\{k_i+1,k_i+2,\ldots ,k_{i+1}-1\}$ are the index of unsuccessful iterations between $k_i$ and $k_{i+1}$, according to Algorithm 1, we have $x^{k_i+j}:=x^{k_i}$ for $j=1,\ldots ,k_{i+1}-k_{i}-1$. We have the following two cases:

1) If $\widetilde{C}^{k_i}_{\lambda }=f^{l(k_i)}_{\lambda }=f^{k_i}$, then the induction hypothesis implies

$$\begin{aligned} f^{k_{i+1}}&=f^{k_{i}+1}=f^{k_{i}}-(f^{k_{i}}-f^{k_{i}+1})= f^{k_{i}}-(f^{l(k_i)}_{\lambda }-f^{k_{i}+1})\\&<f^0-\rho _1\lambda \sum _{j=0}^{i-2}\text {pred}_{k_j}-\rho _1 \text {pred}_{k_{i-1}}-\rho _1\text {pred}_{k_{i}}\\&\mathop {\le }\limits ^{\lambda \le 1}f^0-\rho _1\lambda \sum _{j=0}^{i-1} \text {pred}_{k_j}-\rho _1\text {pred}_{k_{i}} \end{aligned}$$

2) If $\widetilde{C}^{k_i}_{\lambda } \ne f^{k_i}$, then $f^{l(k_i)}_{\lambda }\ge \widetilde{C}^{k_i}_{\lambda } > f^{k_i}$ and Remark 1 leads to $f^{l(k_i)}_{\lambda }=\sum _{p=0}^{s'}\widetilde{\lambda }_{k_i,p}f^{k_{i-p}}$. This fact along with

$$\begin{aligned} \frac{f^{l(k_i)}_{\lambda }-f^{k_{i+1}}}{\text {pred}_{k_i}}\ge \widetilde{r}_{k_i}\ge \rho _1, \end{aligned}$$

implies

$$\begin{aligned} f^{k_{i+1}}= & {} f^{k_{i}+1}=f^{l(k_i)}_{\lambda } -(f^{l(k_i)}_{\lambda }-f^{k_i+1})=\sum _{p=0}^{s'} \widetilde{\lambda }_{k_i,p}f^{k_{i-p}}-(f^{l(k_i)}_{\lambda }-f^{k_i+1})\\< & {} \sum _{p=0}^{s'}\widetilde{\lambda }_{k_i,p} \left( f^0-\rho _1\lambda \sum _{j=0}^{i-p-2}\text {pred}_{k_j}- \rho _1\text {pred}_{k_{i-p-1}}\right) -\rho _1\text {pred}_{k_{i}} \end{aligned}$$

Now, by using these facts that $\{0,\ldots ,s'\}\times \{0,\ldots ,i-s'-2\}\subset \{(p,r)\mid 0\le p\le s', 0\le j\le i-p-2\}$, $\widetilde{\lambda }_{k_i,0}+\widetilde{\lambda }_{k_i,1}+ \cdots +\widetilde{\lambda }_{k_i,s'}=1$ and $\widetilde{\lambda }_{k_i,p}\ge \lambda$, we can obtain the above inequality as follows

$$\begin{aligned} f^{k_{i+1}}<&f^{0}-\rho _1\lambda \sum _{j=0}^{i-s'-2}\left( \sum _{p=0}^{s'} \widetilde{\lambda }_{k_i,p}\right) \text {pred}_{k_j} -\rho _1\lambda \sum _{p=0}^{s'}\text {pred}_{k_{j-p-1}}-\rho _1\text {pred}_{k_i}\\\le & {} f^{0}-\rho _1\lambda \sum _{j=0}^{i-s'-2}\text {pred}_{k_j} -\rho _1\lambda \sum _{j=i-s'-1}^{i-1}\text {pred}_{k_j}-\rho _1\text {pred}_{k_i}\\= & {} f^{0}-\rho _1\lambda \sum _{j=0}^{i-1}\text {pred}_{k_j}-\rho _1\text {pred}_{k_i}\\\le & {} f^{0}-\rho _1\lambda \sum _{j<i+1}\text {pred}_{k_j}. \end{aligned}$$

By Corollary 2, for $k_i\in \widetilde{K}\cap \underline{\mathcal {K}}$, we have

$$\begin{aligned} f^{l(k_i)}_{\lambda }-f^{k_i+1}&\ge \widetilde{C}^{k_i}_{\lambda }-f^{k_i+1}\ge \rho _1\text {pred}_{k_i}\ge \rho _1 \gamma _1\Vert p(x^{k_i})\Vert ^2_\infty \\ \min \{\gamma _2,\varDelta _{k_i}\}&\ge \rho _1\gamma _1\delta ^2\min \{\gamma _2,\varDelta _{k_i}\}. \end{aligned}$$

Proposition 4, as $i\rightarrow \infty$, implies that

$$\begin{aligned} \varDelta _{k_i}\le \gamma _2, \end{aligned}$$

(41)

leading

$$\begin{aligned} \text {pred}_{k_i}\ge \gamma _1\delta ^2\varDelta _{k_i}. \end{aligned}$$

Hence, if there exists $K'\subset K'':=\widetilde{K}\cap \underline{\mathcal {K}}$ such that $\sum _{k\in K'}\varDelta _{k}=\infty$, we have

which this is a contradiction. Therefore,

This fact leads to

$$\begin{aligned} \sum _{k_i\in K''}\varDelta _{k_i}<\infty , \end{aligned}$$

and then

This fact implies that the sequence $\{x^{k_i}\}_{k_i\in K''}$ is cauchy, hence convergent. But by Theorem 1, every accumulation point is a stationary point and this would yield the desired contradiction. $\square$

Now we give a stronger result on the global convergence which is for all limit points.

Theorem 3

Let Assumption 2 hold, and suppose that the sequence $\{ d^k \}$ satisfies Assumption 1. Then

$$\begin{aligned} \lim _{k\rightarrow \infty } p(x^k)=0. \end{aligned}$$

Proof

Assume, by contradiction, that the conclusion does not hold, then there is a subsequence of successful iterations such that

$$\begin{aligned} \Vert p(x^{t_i})\Vert _\infty \ge 2\delta >0, \end{aligned}$$

for some $\delta >0$ and for all i. Theorem 2 guarantees that, for each i, there exists a first successful iteration $l(t_i)> t_i$ such that $\Vert p(x^{l(t_i)})\Vert _\infty <\delta$. Let us denote $l_i:=l(t_i)$ and define the index set $\varLambda ^i:=\{k\mid t_i\le k<l_i\}$. Thus, there exists another subsequence ${l_i}$ such that

$$\begin{aligned} \Vert p(x^{k})\Vert _\infty \ge \delta , \quad \ \ \forall k\in \varLambda ^i\ \ \text {and}\ \ \Vert p(x^{l_i})\Vert _\infty <\delta . \end{aligned}$$

(42)

Let us define $\varLambda :=\cup _{i=0}^{\infty }\varLambda ^i$. Then, we have

$$\begin{aligned} \liminf _{k\rightarrow \infty ,k\in \varLambda } \Vert p(x^k)\Vert _\infty \ge \delta , \end{aligned}$$

which the proof of Theorem 2 implies

$$\begin{aligned} \sum _{k\in \varLambda }\varDelta _{k}<\infty , \end{aligned}$$

and consequently

$$\begin{aligned} \lim _{i\rightarrow \infty }\sum _{k\in \varLambda ^i}\varDelta _{k}= 0. \end{aligned}$$

Hence

$$\begin{aligned} \Vert x^{t_i}-x^{l_i}\Vert _\infty\le & {} \sum _{j\in \varLambda ^i}\Vert x^{j}-x^{j+1}\Vert _ \infty \le \sum _{j\in \varLambda ^i}\varDelta _{j}\rightarrow 0,\ \ \text {as} \ \ i\rightarrow \infty , \end{aligned}$$

which deduces from continuity of p(x) on $L(x^0)$

$$\begin{aligned} \lim _{i\rightarrow \infty }\Vert p(x^{t_i})-p(x^{l_i})\Vert _\infty =0. \end{aligned}$$

This is a contradiction since (42) implies $\Vert p(x^{t_i})-p(x^{l_i})\Vert _\infty \ge \delta$. $\square$

4 Local convergence

Algorithm 1, as it stands, is globally convergent, but not necessary locally fast convergent since, thus far, we only assume that the approximate solution $d^k$ computed in (S.2) satisfies the (gradient-like) conditions from Assumption 1. However, the method can be combined with suitable Newton-like steps in order to obtain a trust-region method with both global and local fast convergence properties. Three possibilities are presented in the following sections.

4.1 The projected Newton step

Here we follow an idea by Ulbrich [41]. The analysis is therefore similar to the one from that paper, but carried out (more or less) in detail since several steps will also be used in the two subsequent sections where other Newton-type steps are considered.

Recall that $\varOmega$ denotes the feasible set, defined by some lower bounds $l_i$ and upper bounds $u_i$. Let us define

$$\begin{aligned} \varOmega _k := \big \{ d \in \mathbb R^n \mid l_i - x_i^k \le d_i \le u_i - x_i^k \quad \text {and} \quad - \varDelta _k \le d_i \le \varDelta _k \ \forall i = 1, \ldots , n \big \}, \end{aligned}$$

which is the feasible set of the trust-region subproblem (8) at iteration k. Assuming that $J_k = F'(x^k)$ is nonsingular, we further set

$$\begin{aligned} d^k_N := - J(x^k)^{-1} F(x^k), \quad d^k_{PN} := P_\varOmega (x^k + d^k_N) - x^k, \quad d^k_{P} := P_{\varOmega _k} (d^k_N), \end{aligned}$$

(43)

i.e., $d^k_N$ is the unconstrained Newton-direction which, in general, is not feasible in our constrained setting, whereas $d^k_{PN}$ denotes the projected Newton direction, hence $x^k + d^k_{PN} = P_{\varOmega }(x^k + d^k_N) \in \varOmega$ is always feasible. On the other hand, $d^k_{PN}$ might not be a feasible candidate for the current trust-region subproblem, hence we also define $d^k_P$ as the projection of the unconstrained Newton-direction onto the set $\varOmega _k$.

All these search directions are superlinearly convergent directions in the following sense: Suppose that $x^*$ denotes a solution of the given problem (1) such that the Jacobian $J(x^*)$ is nonsingular, and assume further that we have an arbitrary sequence $\{ x^k \}$ converging to $x^*$, then it holds that

$$\begin{aligned} \Vert x^k + d^k_N - x^* \Vert = o ( \Vert x^k - x^* \Vert ) \quad \text {and} \quad \Vert x^k + d^k_{PN} - x^* \Vert = o ( \Vert x^k - x^* \Vert ); \end{aligned}$$

the former is simply the standard property of the unconstrained Newton method, and the latter is a direct consequence of this fact using the nonexpansiveness of the projection operator. Since, as noted in [41], it holds that $d^k_P = d^k_{PN}$ locally (cf. our analysis below), it follows that also $d^k_P$ is a superlinearly convergent direction in the above sense. As soon as one can take $x^{k+1} := x^k + d^k$ for a superlinearly convergent direction $d^k$, one therefore has a locally superlinearly convergent method.

After these preliminary comments, we now present a locally fast convergent modification of Algorithm 1.

Algorithm 3

(Nonmonotone Projected Newton-type Trust-Region Method)

Identical to Algorithm 1, except that (S.2) should be replaced by:

• (S.2) Define $l^k, u^k$ by (7). Compute $d^k_P$ from (43) and

  $$\begin{aligned} \widetilde{r}_{k}^{P} := \frac{\widetilde{C}^{k}_{\lambda } - f(x^k+d^k_P)}{q_k(0) - q_k(d^k_P)}. \end{aligned}$$

  If $\widetilde{r}_{k}^{P} \ge \rho _1$, we set $d^k := d^k_P, x^{k+1} := x^k + d^k$, and call iteration k successful; otherwise, or if $d^k_P$ cannot be calculated, we compute a vector $d^k$ satisfying Assumption 1 (e.g., by using Algorithm 2) and define the ratio

  $$\begin{aligned} \widetilde{r}_{k} := \frac{\widetilde{C}^{k}_{\lambda } - f(x^k+d^k)}{q_k(0) - q_k(d^k)}. \end{aligned}$$

  If $\widetilde{r}_{k} \ge \rho _1$, we set $x^{k+1} := x^k + d^k$ and still call iteration k successful. In all other cases, we define $x^{k+1} := x^k$ and call iteration k unsuccessful.

Our primary aim will be to show that, locally around a solution $x^*$ of (1) such that $J(x^*)$ is nonsingular, the ratio test $\widetilde{r}_{k}^{P} \ge \rho _1$ is satisfied. In view of our previous comments, this then implies the local superlinear convergence of Algorithm 3. The global convergence properties known for Algorithm 1 are, more or less, inherited by Algorithm 3; we will comment on this later in this section.

We begin our local analysis with the following technical result.

Lemma 9

Let $x^*$ be an accumulation point of a sequence $\{ x^k \}$ generated by Algorithm 3 such that $x^*$ is a solution of (1) with $J(x^*)$ being nonsingular, and suppose that Assumption 2 holds. Then, for every given $\theta \in (0,1)$, there exists a neighbourhood of $x^*$ such that for any $x^k$ from this neighbourhood where $k-1$ is a successful iteration, the following statements hold:

• (a) $\Vert d^k_P - d^k_N \Vert \le \Vert x^k + d^k_N - x^* \Vert$;

• (b) $\big | q_k(d^k_P) \big | \le \gamma \Vert F(x^k) \Vert \Vert x^k + d^k_N - x^* \Vert$ for some constant $\gamma > 0$;

• (c) $( 1 - \theta ) f(x^k) \le q_k(0) - q_k(d^k_P) \le (1 + \theta ) f(x^k)$.

Proof

(a) Since $J(x^*)$ is nonsingular, there exist constants $\alpha > 0$ and $\xi > 0$ such that

$$\begin{aligned} \Vert J(x)^{-1} \Vert \le \alpha \quad \text {(uniform boundedness of inverse Jacobians)} \end{aligned}$$

(44)

and

$$\begin{aligned} \xi \Vert x - x^* \Vert \le \Vert F(x) \Vert \quad \text {(local error bound condition)} \end{aligned}$$

(45)

for all x in a sufficiently small neighbourhood of $x^*$. Moreover, since F is continuously differentiable, there exists a constant $L > 0$ with

$$\begin{aligned} \Vert F(x) - F(x^*) \Vert \le L \Vert x - x^* \Vert \quad \text {(local Lipschitz condition)} \end{aligned}$$

(46)

for all x sufficiently close to $x^*$.

Now, let $x^k$ be given such that $k-1$ is a successful iteration and such that $x^k$ is sufficiently close to $x^*$. In particular, let conditions (44), (45), and (46) hold with $x = x^k$, and assume that $\alpha \Vert F(x^k) \Vert < \varDelta _{\min }$ is satisfied. Then we obtain from (44) and the definition of the Newton direction that

$$\begin{aligned} \Vert d^k_N \Vert = \Vert J_k^{-1} F(x^k) \Vert \le \alpha \Vert F(x^k) \Vert < \varDelta _{\min } \le \varDelta _k, \end{aligned}$$

where the last inequality follows from the updating rule of the trust-region radius together with the fact that $k-1$ is assumed to be a successful iteration. Hence the trust-region bound is locally inactive, and we therefore obtain

$$\begin{aligned} d^k_P = P_{\varOmega _k} (d^k_N) = P_{\varOmega - x^k} (d^k_N) = P_{\varOmega } (x^k + d^k_N) -x^k = d^k_{PN}. \end{aligned}$$

(47)

This implies

$$\begin{aligned} \Vert d^k_P \Vert = \Vert d^k_{PN} \Vert = \Vert P_{\varOmega } (x^k+d^k_N) - P_{\varOmega } (x^k) \Vert \le \Vert d^k_N \Vert . \end{aligned}$$

(48)

Since $x^* \in \varOmega$, it follows from the definition of the projection that

$$\begin{aligned} \Vert d^k_P - d^k_N \Vert = \Vert d^k_{PN} - d^k_N \Vert = \Vert P_{\varOmega } (x^k+d^k_N) - (x^k+d^k_N) \Vert \le \Vert x^* - ( x^k + d^k_N ) \Vert ,\nonumber \\ \end{aligned}$$

(49)

hence assertion (a) follows.

(b) We still assume that $x^k$ is sufficiently close to $x^*$ such that the inequalities from the proof of part (a) hold. Then

$$\begin{aligned} \Vert d^k_N \Vert \le \alpha \Vert F(x^k) \Vert = \alpha \Vert F(x^k) - F(x^*) \Vert \le \alpha L \Vert x^k - x^* \Vert , \end{aligned}$$

in view of (44) and (46), hence we obtain from (48), (49), Assumption 2, and $q_k(d^k_N)=0$ (by definition) that

$$\begin{aligned} \big | q_k(d^k_P) \big |= & {} \big | q_k(d^k_P) - q_k(d^k_N) \big | \\= & {} \bigg | g_k^T (d^k_P - d^k_N) + \frac{1}{2} (d^k_P + d^k_N)^T J_k^T J_k (d^k_P - d^k_N) \bigg | \\\le & {} \big \Vert J_k^T F(x^k) + \frac{1}{2} J_k^T J_k (d^k_P + d^k_N) \big \Vert \cdot \Vert d^k_P - d^k_N \Vert \\\le & {} \big ( \varkappa \Vert F(x^k) \Vert + \varkappa ^2 \Vert d^k_N \Vert \big ) \Vert d^k_P - d^k_N \Vert \\\le & {} \big ( \varkappa + \alpha \varkappa ^2 \big ) \Vert F(x^k) \Vert \Vert x^k + d^k_N - x^* \Vert \\= & {} \gamma \Vert F(x^k) \Vert \Vert x^k + d^k_N - x^* \Vert , \end{aligned}$$

for some constant $\gamma > 0$, hence statement (b) holds.

(c) Given the parameter $\theta \in (0,1)$ and using (45), we can assume without loss of generality (exploiting the local superlinear convergence property of the Newton direction) that $x^k$ is sufficiently close to $x^*$ such that, in addition to the previous inequalities, we also have

$$\begin{aligned} 2 \gamma \frac{\Vert x^k + d^k_N - x^* \Vert }{\Vert F(x^k) \Vert } \le \frac{2 \gamma }{\xi } \frac{\Vert x^k + d^k_N - x^* \Vert }{\Vert x^k - x^* \Vert } \le \theta . \end{aligned}$$

Dividing the inequality from statement (b) by $f(x^k) = \frac{1}{2} \Vert F(x^k) \Vert ^2$, we therefore obtain, on the one hand, that

$$\begin{aligned} \frac{q_k(0) - q_k(d^k_P)}{f(x^k)}&= \frac{f(x^k) - q_k(d^k_P)}{f(x^k)} =1 - \frac{q_k(d^k_P)}{f(x^k)}\ge 1 - \frac{\big | q_k(d^k_P) \big |}{f(x^k)} \ge 1 \\&\quad - 2 \gamma \frac{\Vert x^k + d^k_N - x^* \Vert }{\Vert F(x^k) \Vert } \ge 1 - \theta , \end{aligned}$$

and, on the other hand, that

$$\begin{aligned} \frac{q_k(0) - q_k(d^k_P)}{f(x^k)} = 1 - \frac{q_k(d^k_P)}{f(x^k)} \le 1 + \frac{\big | q_k(d^k_P) \big |}{f(x^k)} \le 1 + \theta . \end{aligned}$$

Hence, we have

$$\begin{aligned} 1 - \theta \le \frac{q_k(0) - q_k (d^k_P)}{f(x^k)} \le 1 + \theta . \end{aligned}$$

Multiplication with $f(x^k)$ yields assertion (c). $\square$

Note that statements (a) and (b) of the previous result hold for any $x^k$ sufficiently close to $x^*$, independent of the given parameter $\theta$. This parameter, whose precise value has an influence of the size of the neighbourhood, appears in statement (c) only.

We next show that the search direction $d^k_P$, locally, satisfies the two conditions from Assumption 1.

Lemma 10

Let the assumptions from Lemma 9 hold. Then, for any $x^k$ sufficiently close to $x^*$ where $k - 1$ is a successful iteration, the direction $d^k_P$ satisfies Assumption 1.

Proof

(a) We first note that the assumed nonsingularity of $J(x^*)$ implies that the function $\Vert p( \cdot ) \Vert$ provides a local error bound, i.e., there exists a constant $\beta > 0$ such that $\beta \Vert x - x^* \Vert \le \Vert p(x) \Vert$ for all x sufficiently close to $x^*$, see, e.g., [20, Proposition 5.3.7]. Together with the previous observations and constants from the proof of Lemma 9, we therefore obtain

$$\begin{aligned} \Vert d^k_P \Vert= & {} \Vert d^k_{PN} \Vert \ = \ \Vert P_{\varOmega } (x^k + d^k_N) - P_{\varOmega } (x^k) \Vert \ \le \ \Vert d^k_N \Vert \ \le \ \alpha \Vert F(x^k) \Vert \\= & {} \alpha \Vert F(x^k) - F(x^*) \Vert \ \le \ \alpha L \Vert x^k - x^* \Vert \ \le \ \frac{\alpha L}{\beta } \Vert p(x^k) \Vert , \end{aligned}$$

for all $x^k$ sufficiently close to $x^*$. This implies that Assumption 1 (a) holds for $d^k = d^k_P$ and all $x^k$ sufficiently close to $x^*$.

(b) Using Assumption 2, we obtain

$$\begin{aligned} \Vert p(x^k) \Vert = \Vert P_{\varOmega } ( x^k - g^k ) - P_{\varOmega } (x^k) \Vert \le \Vert g^k \Vert \le \varkappa \Vert F(x^k) \Vert , \end{aligned}$$

for all $x^k$ sufficiently close to $x^*$, hence it follows that there is a constant $\gamma > 0$ such that

$$\begin{aligned} \Vert p(x^k) \Vert ^2_\infty \le \gamma f(x^k). \end{aligned}$$

Given an arbitrary parameter $\theta \in (0,1)$ and using Lemma 9 (c), we therefore obtain

$$\begin{aligned} q_k(0) - q_k(d^k_P) \ge (1-\theta ) f(x^k) \ge \frac{1 - \theta }{\gamma } \Vert p(x^k) \Vert _\infty ^2, \end{aligned}$$

for $x^k$ close enough to $x^*$. Since iteration $k-1$ is assumed to be successful and $x^k$ is sufficiently close to $x^*$, we have $\varDelta _k \ge \varDelta _{\min } \ge \Vert p(x^k) \Vert _\infty$, hence it follows that

$$\begin{aligned} q_k(0) - q_k(d^k_P) \ge \frac{1 - \theta }{\gamma } \Vert p(x^k) \Vert _\infty \min \big \{ \Vert p(x^k) \Vert _\infty , \varDelta _k \big \}. \end{aligned}$$

This implies that Assumption 1 (b) also holds for $d^k = d^k_P$ and all $x^k$ sufficiently close to $x^*$. $\square$

We now state the main local convergence result of Algorithm 3.

Theorem 4

Let $x^*$ be an accumulation point of a sequence $\{ x^k \}$ generated by Algorithm 3 such that $x^*$ is a solution of (1) with $J(x^*)$ being nonsingular, and suppose that Assumption  2 holds. Then the following statements hold:

• (a) The entire sequence $\{ x^k \}$ converges to $x^*$.

• (b) Eventually, only projected Newton steps $d^k = d^k_P$ are taken.

• (c) The sequence $\{ x^k \}$ converges superlinearly to $x^*$.

Proof

By assumption, there is a subsequence converging to $x^*$. In particular, this means that there must be infinitely many successful iterations. But this is also clear since otherwise Algorithm  3 would eventually reduce to Algorithm 1, hence the statement would follow from Lemma 7. Hence, we can assume without loss of generality that we have an iterate $x^k$ sufficiently close to $x^*$ such that iteration $k-1$ was successful. In particular, this implies that we can apply Lemma 9.

We first note, using $d^k_P = d^k_{PN}$ once again (cf. (47)), that

$$\begin{aligned} \frac{f(x^k) - f(x^k + d^k_{P})}{q_k(0) - q_k(d^k_{P})}= & {} \frac{f(x^k) - f(x^k + d^k_{PN})}{q_k(0) - q_k(d^k_{PN})} \\= & {} \frac{f(x^k) - f(x^k+ d^k_{PN})}{f(x^k)} \cdot \frac{f(x^k)}{q_k(0) - q_k(d^k_{PN})} \\= & {} \bigg ( 1 - \frac{f(x^k + d^k_{PN})}{f(x^k)} \bigg ) \frac{f(x^k)}{q_k(0) - q_k(d^k_P)}. \end{aligned}$$

The first factor on the right-hand side is arbitrarily close to one for $x^k$ sufficiently close to $x^*$ due to the superlinear convergence property of the (projected) Newton direction, cf. [30, Proposition 8], and the second factor can also be assumed to be arbitrarily close to one due to Lemma 9 (c) where $\theta$ was an arbitrary number from (0, 1) . Using Lemma 2, it therefore follows that $\widetilde{r}_{k}^{P} \ge \rho _1$, hence iteration k is also successful, and $x^{k+1} = x^k + d^k_P = x^k + d^k_{PN}$. In particular, it follows from standard properties of the local convergence of the (projected) Newton direction that the new iterate $x^{k+1}$ is even closer to $x^*$ than $x^k$, hence we can repeat the previous arguments and obtain by induction that the entire sequence $\{ x^k \}$ converges to $x^*$ and that eventually only projected Newton steps $d^k = d^k_P$ are taken, which implies the local superlinear convergence of the method. This means that statements (a), (b), and (c) hold. $\square$

Theorem 4 describes the local convergence of Algorithm 3. It provides a local superlinear rate of convergence, but, in a similar way, one can also verify a local quadratic convergence rate provided that $J(\cdot )$ is locally Lipschitz continuous around the solution $x^*$.

On the other hand, Algorithm 3 might not have the same global convergence properties as Algorithm 1 since, globally, the two conditions from Assumption 1 may not hold for the projected Newton direction, especially when the corresponding sequence of inverse Jacobians $J_k^{-1}$ becomes very ill-conditioned. However, in practice, one can test whether these two conditions hold with suitable constants, and then we inherit the global convergence theory from Algorithm 1. Lemma 10 then says that, locally, we still take the fast convergent projected Newton direction provided that the corresponding constants are chosen appropriately, i.e., in this sense Algorithm 3 is both globally and locally fast convergent.

4.2 The active-set Newton step

This section presents an active-set Newton step that goes back to [27]. It is based on a suitable identification of the correct active set at a solution $x^*$ and comes from a more general framework presented in [19]. Some authors use this active-set strategy also from a global point of view which has the advantage that the dimension of the corresponding subproblems are smaller than for the full-dimensional problem. On the other hand, such an active-set strategy yields some undesirable discontinuity. Taking into account that global convergence can be obtained by some very simple and cheap calculations (like the Cauchy-type step from Algorithm 2), our feeling is that the active-set strategy should be used only to get local fast convergence where the computation of a Newton-type step might really reduce the overall costs and the discontinuity might not occur in case the correct active set has already been identified.

For a precise definition of the active-set trust-region method, we choose a constant $\delta > 0$ such that

$$\begin{aligned} \delta < \frac{1}{2} \min _{i=1, \ldots , n} \big | u_i - l_i \big |, \end{aligned}$$

(50)

and then define

$$\begin{aligned} \delta _k := \min \big \{ \delta , \gamma \sqrt{\Vert F(x^k) \Vert } \big \}, \end{aligned}$$

(51)

where $\gamma > 0$ denotes another constant. Given an iterate $x^k$, we then set

$$\begin{aligned} \mathcal A_k:= & {} \big \{ i \mid x_i^k - l_i \le \delta _k \text { or } u_i - x_i^k \le \delta _k \big \}, \\ \mathcal I_k:= & {} \big \{ 1, \ldots , n \big \} {\setminus } \mathcal A_k, \end{aligned}$$

which are approximations of the active and inactive sets at a given solution $x^*$, defined by

$$\begin{aligned} \mathcal A_* := \big \{ i \mid x_i^* \in \{ l_i, u_i \} \big \} \quad \text {and} \quad \mathcal I_* := \big \{ i \mid x_i^* \in (l_i, u_i) \big \}, \end{aligned}$$

respectively. In fact, it is easy to see that one always has the inclusion $\mathcal A_k \subseteq \mathcal A_*$ for all $x^k$ sufficiently close to $x^*$. Moreover, and more interestingly, if $J(x^*)$ is nonsingular (or $\Vert F( \cdot ) \Vert$ provides a local error bound), then one can show that

$$\begin{aligned} \mathcal A_k = \mathcal A_* \quad \text {and} \quad \mathcal I_k = \mathcal I_*, \end{aligned}$$

(52)

for all $x^k$ from a sufficiently small neighbourhood of $x^*$, see [27, Lemma 9.7] for details. Hence the active set can, locally, be identified correctly, even without a strict complementarity or related nondegeneracy condition.

Based on these index sets, we construct a direction vector $d^k = d^k_{AS}$ (AS stands for active set) in the following way: For each $i \in \mathcal A_k$, we define

$$\begin{aligned} d_i^k := \left\{ \begin{array}{ll} l_i - x_i^k, &{} \quad \text {if } x_i^k - l_i \le \delta _k, \\ u_i - x_i^k, &{} \quad \text {if } u_i - x_i^k \le \delta _k, \end{array} \right. \end{aligned}$$

(53)

(note that there is no ambiguity in this definition due to the choice of $\delta , \delta _k$ in (50), (51)), whereas for the inactive indices, we then compute $d^k_{\mathcal I_k}$ as a solution of the linear system of equations

$$\begin{aligned} J(x^k)_{\mathcal I_k \mathcal I_k} d^k_{\mathcal I_k} = - F(x^k)_{\mathcal I_k} - J(x^k)_{\mathcal I_k \mathcal A_k} d^k_{\mathcal A_k}. \end{aligned}$$

(54)

Note that this linear system arises from the first block row of the usual Newton equation

$$\begin{aligned} \left( \begin{array}{cc} J(x^k)_{\mathcal I_k \mathcal I_k} &{} J(x^k)_{\mathcal I_k \mathcal A_k} \\ J(x^k)_{\mathcal A_k \mathcal I_k} &{} J(x^k)_{\mathcal A_k \mathcal A_k} \end{array} \right) \left( \begin{array}{c} d^k_{\mathcal I_k} \\ d^k_{\mathcal A_k} \end{array} \right) = - \left( \begin{array}{c} F(x^k)_{\mathcal I_k} \\ F(x^k)_{\mathcal A_k} \end{array} \right) , \end{aligned}$$

(55)

when replacing $d^k_{\mathcal A_k}$ by the expression from (53). Putting these pieces together, we then define (possibly after a suitable permutation of the components)

$$\begin{aligned} d^k_{AS} := \left( \begin{array}{cc} d^k_{\mathcal I_k} \\ d^k_{\mathcal A_k} \end{array} \right) . \end{aligned}$$

(56)

Assuming also that the submatrix $J(x^*)_{\mathcal I_* \mathcal I_*}$ is nonsingular, it follows that this vector is a superlinearly convergent direction in the sense that $\big \Vert x^k + d^k_{AS} - x^* \big \Vert = o ( \Vert x^k - x^* \Vert )$ for any sequence $\{ x^k \}$ converging to $x^*$, cf. [27, Lemma 9.13] for a proof. However, $d^k_{AS}$ might not be feasible for the trust-region subproblem (8), hence we also define its projection by

$$\begin{aligned} d^k_{PAS} := P_{\varOmega _k} (d^k_{AS}). \end{aligned}$$

(57)

The following is the variant of Algorithm 1 which includes the active-set Newton method as a local search direction. It is identical to Algorithm 3 except that $d^k_P$ gets replaced by $d^k_{PAS}$ everywhere.

Algorithm 4

(Nonmonotone Active-Set Newton-type Trust-Region Method)

Identical to Algorithm 1, except that (S.2) should be replaced by:

• (S.2) Define $l^k, u^k$ by (7). Compute $d^k_{PAS}$ from (57) and define

  $$\begin{aligned} \widetilde{r}_{k}^{AS} := \frac{\widetilde{C}^{k}_{\lambda } - f(x^k+d^k_{PAS})}{q_k(0) - q_k(d^k_{PAS})}. \end{aligned}$$

  If $\widetilde{r}_{k}^{AS} \ge \rho _1$, we set $d^k := d^k_{PAS}, x^{k+1} := x^k + d^k$, and call iteration k successful; otherwise, or if $d^k_{PAS}$ cannot be calculated, we compute a vector $d^k$ satisfying Assumption 1 (e.g., by using Algorithm 2) and define the ratio

  $$\begin{aligned} \widetilde{r}_{k} := \frac{\widetilde{C}^{k}_{\lambda } - f(x^k+d^k)}{q_k(0) - q_k(d^k)}. \end{aligned}$$

  If $\widetilde{r}_{k} \ge \rho _1$, we set $x^{k+1} := x^k + d^k$ and still call iteration k successful. In all other cases, we define $x^{k+1} := x^k$ and call iteration k unsuccessful.

To prove a local convergence theorem of Algorithm 4, we follow the technique of proof from the previous section and first state the following result which is the counterpart of Lemmas 9 and 10.

Lemma 11

Let $x^*$ be an accumulation point of a sequence $\{ x^k \}$ generated by Algorithm 4 such that $x^*$ is a solution of (1) with $J(x^*)$ and $J(x^*)_{\mathcal I_* \mathcal I_*}$ being nonsingular, and suppose that Assumption 2 holds. Then, for every given $\theta \in (0,1)$, there exists a neighbourhood of $x^*$ such that for any $x^k$ from this neighbourhood where $k-1$ is a successful iteration, the following statements hold:

• (a) $\Vert d^k_{PAS} - d^k_N \Vert \le \eta \Vert x^k + d^k_N - x^* \Vert$ for some constant $\eta > 0$;

• (b) $\big | q_k(d^k_{PAS}) \big | \le \gamma \Vert F(x^k) \Vert \Vert x^k + d^k_N - x^* \Vert$ for some constant $\gamma > 0$;

• (c) $( 1 - \theta ) f(x^k) \le q_k(0) - q_k(d^k_{PAS}) \le (1 + \theta ) f(x^k)$.

• (d) The direction $d^k_{PAS}$ satisfies Assumption  1.

Proof

By the proofs given for Lemmas 9 and 10 and Lemma 9.8 in [27], we skip the details. $\square$

Using Lemma 11, we can also obtain the central local convergence theorem for Algorithm 4. Its proof is similar to the one of Theorem 4, so we do not provide the details.

Theorem 5

Let $x^*$ be an accumulation point of a sequence $\{ x^k \}$ generated by Algorithm 4 such that $x^*$ is a solution of (1) with $J(x^*)$ and $J(x^*)_{\mathcal I_* \mathcal I_*}$ being nonsingular, and suppose that Assumption 2 holds. Then the following statements hold:

• (a) The entire sequence $\{ x^k \}$ converges to $x^*$.

• (b) Eventually, only active-set Newton steps $d^k = d^k_{PAS}$ are taken.

• (c) The sequence $\{ x^k \}$ converges superlinearly to $x^*$.

Note that the assumptions of Theorem 5 are stronger than those of Theorem 4 since, in addition to the nonsingularity of $J(x^*)$, also the nonsingularity of the submatrix $J(x^*)_{\mathcal I_* \mathcal I_*}$ is required.

4.3 The exact Newton step

The most natural choice is to compute the exact solution $d^k_E$ of the trust-region subproblem (8). Numerically, this is more expensive than the projected or active-set Newton direction since one has to compute a solution of a (convex) quadratic program as opposed to a solution of a (possibly reduced) linear system of equations. On the other hand, this approach might yield better numerical results, at least it is not clear a priori why the exact solution might not be a good choice from a numerical point of view. Moreover, it follows immediately from Lemma 4 that the exact solution $d^k_E$ satisfies Assumption 1 (b) for all $k \in \mathbb N_0$ without any further (nonsingularity) assumption on the problem. Of course, Assumption 1 (a) may not hold, but can be checked numerically and will also be shown to be satisfied locally under suitable conditions.

For our local convergence analysis, we consider the following modification of Algorithm 1 which simply replaces $d^k$ by $d^k_E$. Recall that global convergence can also be guaranteed if some care is taken regarding Assumption 1 (a), e.g., by switching to a Cauchy-type step whenever necessary. Since our focus is on the local convergence property, we do not consider such a modification here.

Algorithm 5

(Nonmonotone Exact Newton-type Trust-Region Method)

Identical to Algorithm 1, except that (S.2) should be replaced by:

• (S.2) Define $l^k, u^k$ by (7). Compute $d^k_E$ as the solution of the trust-region subproblem (8). Let

  $$\begin{aligned} \widetilde{r}_{k}^{E} := \frac{\widetilde{C}^{k}_{\lambda } - f(x^k+d^k_E)}{q_k(0) - q_k(d^k_E)}. \end{aligned}$$

  If $\widetilde{r}_{k}^{E} \ge \rho _1$, we set $d^k := d^k_E, x^{k+1} := x^k + d^k$, and call iteration k successful; otherwise, we set $x^{k+1} := x^k$ and call iteration k unsuccessful.

The convergence analysis is again along the lines of the previous two sections. First we have the following result.

Lemma 12

Let $x^*$ be an accumulation point of a sequence $\{ x^k \}$ generated by Algorithm 5 such that $x^*$ is a solution of (1) with $J(x^*)$ being nonsingular, and suppose that Assumption 2 holds. Then, for every given $\theta \in (0,1)$, there exists a neighbourhood of $x^*$ such that for any $x^k$ from this neighbourhood where $k-1$ is a successful iteration, the following statements hold:

• (a) $\Vert d^k_E - d^k_N \Vert \le \eta \Vert x^k + d^k_N - x^* \Vert$ for some constant $\eta > 0$;

• (b) $\big | q_k(d^k_E) \big | \le \gamma \Vert F(x^k) \Vert \Vert x^k + d^k_N - x^* \Vert$ for some constant $\gamma > 0$;

• (c) $( 1 - \theta ) f(x^k) \le q_k(0) - q_k(d^k_E) \le (1 + \theta ) f(x^k)$.

• (d) The direction $d^k_E$ satisfies Assumption 1.

Proof

Since $J(x^*)$ is nonsingular by assumption, there exists a constant $\alpha > 0$ such that $\Vert J_k^{-1} \Vert \le \alpha$ for all $x^k$ sufficiently close to $x^*$. Together with Assumption 2, this implies

$$\begin{aligned} \big \Vert d^k_E - d^k_N \big \Vert= & {} \big \Vert J_k^{-1} \big ( J_k d^k_E - J_k d^k_N \big ) \big \Vert \\\le & {} \alpha \big \Vert J_k d^k_E - J_k d^k_N \big \Vert \\= & {} \alpha \big \Vert J_k d^k_E + F(x^k) \big \Vert \quad (\text {Definition of} \quad d^k_N ) \\\le & {} \alpha \big \Vert J_k d^k_P + F(x^k) \big \Vert \quad (\text {with} \quad d^k_P \quad \text {from} \quad (43)) \\\le & {} \alpha \big \Vert \underbrace{F(x^k) + J_k d^k_N}_{= F(x^k) - F(x^k) = 0} \big \Vert + \alpha \big \Vert J_k d^k_P - J_k d^k_N \big \Vert \\= & {} \alpha \big \Vert J_k d^k_P - J_k d^k_N \big \Vert \\\le & {} \alpha \varkappa \big \Vert d^k_P - d^k_N \big \Vert \\\le & {} \alpha \varkappa \big \Vert x^k + d^k_N - x^* \big \Vert , \end{aligned}$$

where the second inequality uses the definition of $d^k_E$ together with the fact that $d^k_P$ is feasible for the trust-region subproblem (8), and the last inequality follows from Lemma 9 (a). This shows that statement (a) holds.

Furthermore, since $J(x^*)$ is nonsingular, it follows that, locally, $J_k^T J_k$ is uniformly positive definite, i.e., for all $x^k$ close enough to $x^*$, it holds that $d^T J_k^T J_k d \ge \mu \Vert d \Vert ^2$ for all $d \in \mathbb R^n$ with some constant $\mu > 0$. Since the zero vector is always feasible for the trust-region subproblem, we have $q_k(d^k_E) \le q_k(0)$ by definition of $d^k_E$. This can be rewritten as

$$\begin{aligned} g_k^T d^k_E + \frac{1}{2} (d^k_E)^T J_k^T J_k d^k_E \le 0. \end{aligned}$$

Using the Cauchy–Schwarz inequality, we therefore get

$$\begin{aligned} \frac{1}{2} \mu \Vert d^k_E \Vert ^2 \le \frac{1}{2} (d^k_E)^T J_k^T J_k d^k_E \le - g_k^T d^k_E \le \Vert g^k \Vert \Vert d^k_E \Vert . \end{aligned}$$

Together with Assumption 2, we then obtain

$$\begin{aligned} \frac{1}{2} \mu \Vert d^k_E \Vert \le \Vert g^k \Vert = \Vert J_k^T F(x^k) \Vert \le \varkappa \Vert F(x^k) \Vert . \end{aligned}$$

(58)

Exploiting once again the assumed nonsingularity of $J(x^*)$, it follows from (58) that there is a constant $\eta _1 > 0$ such that $\Vert d^k_E \Vert \le \eta _1 \Vert d^k_N \Vert$. Combining this with statement (a), one can verify assertions (b) and (c) in essentially the same way as the corresponding statements in Lemma 9. To this end, the only additional piece of information needed is that $d^k_E$ is also a superlinearly convergent direction, but this is an immediate consequence of part (a) since

$$\begin{aligned} \Vert x^k + d^k_E - x^* \Vert\le & {} \Vert x^k + d^k_N - x^* \Vert + \Vert d^k_E - d^k_N \Vert \\\le & {} ( 1 + \eta _1 ) \Vert x^k + d^k_N - x^* \Vert , \end{aligned}$$

and the Newton direction is known to be superlinearly convergent.

It remains to prove assertion (d). This statement can be derived from (58) similar to the proof of Lemma 10 (a), i.e., there exists a constant $c > 0$ such that $\Vert d^k_E \Vert \le c \Vert p(x^k) \Vert$. $\square$

Lemma 12 allows us to prove the following main local convergence result in a way similar to the proof of Theorem 6, hence we skip the details.

Theorem 6

Let $x^*$ be an accumulation point of a sequence $\{ x^k \}$ generated by Algorithm  5 such that $x^*$ is a solution of (1) with $J(x^*)$ being nonsingular, and suppose that Assumption 2 holds. Then the following statements hold:

• (a) The entire sequence $\{ x^k \}$ converges to $x^*$.

• (b) Eventually, the exact Newton step $d^k = d^k_E$ is always successful.

• (c) The sequence $\{ x^k \}$ converges superlinearly to $x^*$.

5 Numerical results

We first describe our test examples in Sect. 5.1, then give some details of the implemented algorithms in Sect. 5.2, and finally present the numerical results in Sect. 5.3.

5.1 Test problems

All test problems are taken from the literature, Table 1 provides the corresponding details, namely the name of each test problem, at least one reference from which the example is taken (this is not necessarily the original source of the corresponding example), the dimension, and the box constraints. The dimension ranges from $n = 2$ to $n = 1024$; we decided not to take larger problems since some of our algorithms have to solve a quadratic program at each iteration. The starting points, four for each test example, are in the interior of the box $\varOmega = [l,u]$ because this is required by some of the interior-point-type solvers that will be used in our comparative study. For example, we take $x^0 := l + \frac{\nu }{5} (u-l) \ (\nu = 1, 2, 3, 4)$ for all test problems which have both finite lower and finite upper bounds. Altogether, we have 46 test problems.

Table 1 List of test problems: Name of the example, reference(s), dimension, starting points (recall that $e^T = (1, \ldots , 1)$), and box constraints

5.2 Algorithms

In our next section, we compare eleven different solvers on the set of examples described before. The first three solvers are our methods from Algorithms 3–5, respectively:

• NMPNTRN: The nonmonotone projected Newton-type trust-region method from Algorithm 3.

• NMASTRN: The nonmonotone active-set Newton-type trust-region method from Algorithm 4.

• NMENTRN: The nonmonotone exact Newton-type trust-region method from Algorithm 5.

We use the test $\Vert F(x^k) \Vert _{\infty } < 10^{-6}$ as the main termination criterion. In all following cases, we count the corresponding test run as a failure

• Failure (1): the number of (successful) iterations reaches the upper bound 200.

• Failure (2): the trust-region size reduces below $\sqrt{\epsilon _m}$ where $\epsilon _m$ denotes the machine epsilon provided by the Matlab function eps.

• Failure (3): the scaling matrix $D_k$, generated by (1.5) in [6], cannot be computed because an overflow would be generated (only for STRSCNE and CODOSOL).

All methods use the parameters

$$\begin{aligned} \varDelta _0:= & {} 1, \ \varDelta _{\min } := 10^{-5}, \ \varDelta _{\max } := 10^5, \ \rho _1 := 0.1, \ \rho _2 := 0.9, \ \sigma _1 := 0.5, \\ \sigma _2:= & {} 2, \ \ \lambda =0.1, \end{aligned}$$

as well as the nonmonotonicity number $N := 10$ and $\lambda _{kj}$ is updated by (16); furthermore, the sequence $\{ \eta _k \}$ is generated by setting $\eta _0 := 0.85$ and using the updating

$$\begin{aligned} \eta _{k+1} := \left\{ \begin{array}{ll} \eta _0 / 2, &{} \quad \text {if } k = 0, \\ (\eta _k + \eta _{k-1})/2, &{} \quad \text {if } k \ge 1. \end{array} \right. \end{aligned}$$

The (convex) quadratic programs arising within the NMENTRN algorithm are solved using quadprog from the MATLAB optimization toolbox. All Jacobian matrices $J(x^k)$ are approximated by using finite differences.

In order to get an idea of the effectiveness of our nonmonotonicity strategy, we also implemented the following (monotone and nonmonotone) methods:

• PNTTR: This is the traditional (monotone) projected Newton-type trust-region method based on the ratio $r_k$ defined in (9) and the standard updating of the trust-region-radius

  $$\begin{aligned} \varDelta _{k+1} := \left\{ \begin{array}{ll} \sigma _1 \varDelta _k, &{} \quad \text {if } r_k < \rho _1, \\ \varDelta _k, &{} \quad \text {if } r_k \in [\rho _1, \rho _2), \\ \sigma _2 \varDelta _k, &{} \quad \text {if } r_k \ge \rho _2 . \end{array} \right. \end{aligned}$$

  The parameter settings and the termination criteria are the same as for the other methods.

• NMPNTRG: This is the nonmonotone projected Newton-type trust-region method motivated by the line search approach in Grippo et al. [24]. It is identical to the PNTTR except that the nonmonotone ratio test with $r_k$ from (10) is used.

• NMPNTRZ: This is the nonmonotone projected Newton-type trust-region method motivated by the line search approach by Zhang and Hager [44], using the ratio test based on (12) and the same updating rule for the sequence $\{ \eta _k \}$ as in our methods. The remaining parts are identical to methods PNTTR and NMPNTRG.

• NMPNTRA: This is the nonmonotone projected Newton-type trust-region method motivated by the nonmonotone approach in Ahookhosh et al. [1], using the same updating rule for the sequence $\{ \eta _k \}$ as in our methods. The remaining parts are identical to methods PNTTR, NMPNTRG and NMPNTRZ.

• NMPNTRU: This is the nonmonotone projected Newton-type trust-region method motivated by the nonmonotone trust-region approach in Ulbrich [41], using the ratio test $\overline{r}_k$ obtained by steps 4.1–4.3 of Algorithm 3.4 in [41] and the updating of the trust-region-radius

  $$\begin{aligned} \varDelta _{k+1} := \left\{ \begin{array}{ll} \sigma _1 \varDelta _k, &{} \quad \text {if } \quad \overline{r}_k < \rho _1, \\ \min \{\varDelta _k,\varDelta _{\min }\}, &{} \quad \text {if } \quad \overline{r}_k \in [\rho _1, \rho _2), \\ \min \{\sigma _2 \varDelta _k,\varDelta _{\min }\}, &{} \quad \text {if } \quad \overline{r}_k \ge \rho _2. \end{array} \right. \end{aligned}$$

• APNTRE: This is the adaptive projected Newton-type trust-region method motivated by the adaptive radius proposed in Esmaeili and Kimiaei [17], using the same updating rule for $\varDelta _k$ as in our methods.

Finally, we also use the two existing software packages STRSCNE and CoDoSol developped by Bellavia et al. in [6, 9], respectively. The corresponding source codes are available on the following web pages: http://strscne.de.unifi.it and http://codosol.de.unifi.it.

These methods are affine-scaling interior-point methods, and, similar to our algorithms NMPNTRN and NMASTRN, they only have to solve a linear system of equations per iteration. Our implementation uses all the default values of these two solvers except that our termination criterion is applied in order to get a fair comparative study.

5.3 Numerical results

Here we present a summary of the numerical results obtained for the eleven algorithms applied to the set of 46 test problems with four different starting points each, so altogether we have 184 test runs for each method.

Table 2 contains the number of failures for each algorithm using three different choices of the initial trust-region radius $\varDelta _0$. The standard choice $\varDelta _0 = 1$ will be the basis for the subsequent performance profiles, nevertheless, it is also interesting to see the behaviour of the methods for varying $\varDelta _0$. This table clearly indicates that our NMPNTRN solver is by far the most robust method, followed by NMENTRN. The performance of NMASTRN is the worst among our methods, but still comparable with PNTTR, STRSCNE and CoDoSol. Table 2 also shows that all nonmonotone solvers are superior to their monotone version PNTTR.

We next take a closer look at the numerical behaviour using different performance profiles [16]. To this end, we first present a comparative study of our three different methods NMPNTRN, NMASTRN, and NMENTRN, the corresponding performance profiles with respect to the number of (successful) iterations ($N_i$), number of function evaluations (which is equal to the number of total iterations plus one) ($N_f$) and CPU-times ($C_t$) are shown in Subfigures (a)–(c) of Fig. 1. This figure indicates that both the number of iterations and function evaluations for NMPNTRN and NMENTRN are, more or less, comparable. Hence the exact solution of the trust-region subproblems does not seem to help reducing the total number of iterations. Since NMPNTRN has to solve only one linear system of equations, the CPU-time is much better than for the QP-based solver NMENTRN. Since NMASTRN is worse than NMPNTRN with respect to all three performance measures, and since NMPNTRN is also the most robust solver, we view NMPNTRN as the best of our three algorithms and therefore take this method for the subsequent comparative studies with the other methods.

Table 2 Number of failures for different choices of $\varDelta _0$

Fig. 1

a–c A comparison among NMPNTRN, NMENTRN, and NMASTRN with the performance measures $N_i$, $N_f$ and $C_t$ for $\varDelta _0=1$, respectively. d–f A comparison among NMPNTRN, NMPNTRU, NMPNTRA, NMPNTRZ and NMPNTRG with the performance measures $N_i$, $N_f$ and $C_t$ for $\varDelta _0=1$, respectively. g–i A comparison among PGTTR, APGTRE, and NMASTRN with the performance measures $N_i$, $N_f$ and $C_t$ for $\varDelta _0=1$, respectively. j–l A comparison among NMPNTRN, STRSCNE, and CODOSOL with the performance measures $N_i$, $N_f$ and $C_t$ for $\varDelta _0=1$, respectively

We next compare our solver NMPNTRN with the other nonmonotone versions NMPNTRG, NMPNTRZ, NMPNTRA and NMPNTRU. The corresponding performance profiles, again using the number of (successful) iterations ($N_i$), the number of function evaluations ($N_f$) and the CPU-times ($C_t$) as a measure, are shown in Subfigures (d)–(f) of Fig. 1. Regarding the four measures, NMPNTRG, NMPNTRZ, NMPNTRA and NMPNTRU have a very similar behaviour and NMPNTRN is superior to all the other solvers. In addition, we compare our solver NMPNTRN with PNTTR and APNTRE. Subfigures (g)–(i) of Fig. 1 show that NMPNTRN is superior to both the other solvers.

Finally, we present a comparison of our NMPNTRN method with the two software packages STRSCNE and CoDoSol in Subfigures (j)–(l) of Fig. 1. Our method is definitely superior in terms of robustness, number of (successful) iterations, number of function evaluations and summation of triple of the number of (successful) iterations and the number of function evaluations. Regarding CPU-times, the situation is somewhat indefinite between NMPNTRN and CoDoSol. Here we should also say that we did not push our implementation to be as efficient as possible, for example, we produce some more output at each iteration than CoDoSol.

As a summary of the previous discussion, we can certainly say that NMPNTRN is the best solver among those tested in this section. Since also the corresponding QP-based solver NMENTRN behaves very well, this indicates that the new adaptive and nonmonotone trust-region strategy introduced in this paper works very successfully and seems to outperform existing strategies. Further improvements might be possible by replacing the globalization scheme from Algorithm 2 by other (existing) Cauchy-type steps. Corresponding tests have not been performed so far, also taking into account that the current version is already quite successful.

6 Final remarks

This paper suggests a new nonmonotonicity strategy for nonlinear equations with box constraints. Both the criterion for the acceptance of the current step and the updating rules for the trust-region radius are different from existing approaches. The numerical results indicate that these new techniques outperform existing and more traditional ones, while the theoretical results guarantee that we still have global and local fast convergence under suitable assumptions and for a variety of realizations of our approach. The global convergence result is proved.

The current approach can be translated to optimization problems with box constraints. The idea is, in principle, straightforward, and the details will be carried out as part of our future research.