Multi-step Chebyshev spectral collocation method for Volterra integro-differential equations

Abstract

We investigate multi-step Chebyshev spectral collocation method for Volterra integro-differential equations. We obtain numerical solution Y(t) and $Y'(t)$ to approximate unknown function y(t) and its derivative $y'(t)$ while Y(t) and $Y'(t)$ keep the relation that $Y'(t)$ is the derivative of Y(t). We discuss existence and uniqueness of the solution to corresponding discrete system. We provide convergence analysis for proposed method. Numerical experiments are carried out to confirm theoretical results.

1 Introduction

Volterra integro-differential equations (VIDEs) arise in many problems such as modelling of heredity effects and population dynamics. Due to this, many numerical methods are developed to solve these equations. Linz [13] generalized standard multistep methods to solved VIDEs. Brunner [2] studied implicit Runge–Kutta methods for VIDEs. Makroglou [14] proposed a block-by-block method for nonlinear VIDEs. Lin et al. [12] investigated Petrov–Galerkin Methods for Linear VIDEs. Zhang and Vandewalle [20] developed a numerical method based on the combination of general linear methods with compound quadrature rules for VIDEs with memory. Yi [19] investigated an h–p version of the continuous Petrov–Galerkin finite element method for nonlinear VIDEs. In his monograph, Brunner [3] provided basic principles and the analysis of collocation methods for Volterra integral and integro-differential equations.

Spectral methods are well known for their high precision in differential equations. The monograph [8] by Guo presents the basic algorithms, the main theoretical results, and some applications of spectral methods. In [9], Guo and Wang investigated Jacobi approximations in non-uniformly Jacobi-weighted Sobolev spaces. Some results serve as an important tool in the analysis of numerous quadratures and numerical methods for differential and integral equations. Canuto et al. [4] provided fundamentals of spectral methods on simple domains. In [15], Shen et al. provided a detailed presentation of basic spectral algorithms, a systematical presentation of basic convergence theory and error analysis for spectral methods. Global spectral methods were developed to solve Volterra type integral equations. Tang and his coworkers [16] proposed Legendre spectral collocation method to solve VIEs (Volterra integral equations). Subsequently, Chen and Tang [5–7] proposed Jacobi spectral collocation method to solve weakly singular VIEs. In [11], Li et al. proposed a parallel spectral method to solve VIEs. In [1, 10, 17, 18], global spectral methods were developed to solve VIDEs.

In this paper, we investigate multi-step Chebyshev spectral collocation method for the following VIDEs

$$\begin{aligned} \begin{aligned} y'(t)&=g(t)+a(t)y(t)+\int _{0}^{t}K(t,s)y(s)ds,\quad t\in (0,T],\\ y(0)&=y_{0}. \end{aligned} \end{aligned}$$

(1)

We assume that functions describing the above equation all possess continuous derivatives of at least order $m\ge 1$ on their respective domains, i.e.,

$$\begin{aligned} g(t),a(t)\in C^{m}([0,T]), K(t,s)\in C^{m}(\varOmega ),\varOmega :=\{(t,s):0\le s\le t\le T\}, \end{aligned}$$

(2)

where $C^{m}([a,b])$ is the space of functions possessing continuous derivatives of at least order $m\ge 1$ on their domain [a, b].

We divide the interval [0, T] into several subintervals $[\eta _{\mu },\eta _{\mu +1}],\mu =0,1,\ldots ,M$, $\eta _{0}=0$, $\eta _{M+1}=T$. In each subinterval $[\eta _{\mu },\eta _{\mu +1}]$, we set $N+1$ Chebyshev Gauss–Lobatta points as collocation points. We approximate $y'(t)$ at these collocations points by a continuous piecewise polynomial $Y'(t)$ of degree N. Then we define $Y(t):=y_0+\int _{0}^{t}Y'(s)ds$ to approximate y(t). Our method is to find $Y'(t)$ and Y(t). It is worth noting that $\frac{d}{dt}Y(t)=Y'(t)$. We discuss existence and uniqueness of the solution to the discrete systems. We provide convergence analysis to show that numerical errors decay at the rate $h^{m}N^{(1/2)-m}$ in space $L^{\infty }(0,T)$, where $h:=\max \{(\eta _{\mu +1}-\eta _{\mu })/2:\mu =0,1,\ldots ,M\}$. This result implies that employing more collocation points (N is larger), and dividing the interval [0, T] into more subintervals (h is smaller), the numerical solution will be more accurate. If given functions possess more regularity (m is larger), numerical errors decay faster. We carry our numerical experiments to confirm these theoretical results.

For the long interval [0, T] (T becomes larger), in order to obtain high precision numerical solution to (1), people using the global spectral collocation method (see [10]) will encounter the difficulty that finding the inverse of a large dimension matrix costs many time on computation. We avoid this problem by dividing the global interval [0, T] into several subintervals. The provided convergence analysis show that dividing the interval [0, T] does not make errors accumulate but even decay faster at the rate $h^{m}$. We carry out numerical experiment to confirm this result (see Example 3). Numerical experiment shows that multi-step method is more efficient than global method. We also investigate the availability of the proposed method for nonlinear VIDEs.

We choose Chebyshev Gauss–Lobatto points as collocation points because we note that the discrete Chebyshev transforms and the inverse discrete Chebyshev transforms are based on these points (see [4, page 495]). This two transforms enable one to transform freely between physical space and transform space. Fast Fourier transforms can be applied in computing this two transforms to significantly reduce computation. Legendre points are involved in the quadrature formulas in this paper because Gauss quadrature formulas with Legendre points are the best way to approximate the integral terms with smooth kernel.

This paper is organized as follows. In Sect. 2, we introduce the multi-step Chebyshev spectral-collocation method for VIDE (1). The existence and uniqueness of the solution to the discrete system is discussed in Sect. 3. Some useful lemmas for the convergence analysis will be provided in Sect. 4, and the convergence analysis in space $L^{\infty }$ will be given in Sect. 5. Numerical experiments are carried out in Sect. 6. Finally, in Sect. 7, we end with the conclusion and the future work.

2 Multi-step Chebyshev spectral-collocation method

In this section, we introduce the multi-step Chebyshev spectral collocation method for (1).

Divide the interval [0, T] into $M+1$ sub intervals $\delta _{\mu }:=[\eta _{\mu },\eta _{\mu +1}],\mu =0,1,\ldots ,M$, where $\eta _{0}=0,\eta _{\mu }<\eta _{\mu +1},\eta _{M+1}=T$. In each subinterval $\delta _{\mu }$, we set $N+1$ collocation points

$$\begin{aligned} t_{i}^{\mu }:=h_{\mu }x+\frac{\eta _{\mu +1}+\eta _{\mu }}{2},\quad i=0,1,\ldots ,N, \end{aligned}$$

where $h_{\mu }:=\frac{\eta _{\mu +1}-\eta _{\mu }}{2}$, $\{x_{i}\}_{i=0}^{N}$ is the set of Chebyshev Gauss–Lobatto points in the standard interval $[-1,1]$.

Use $y'^{\mu }_{i}$ to approximate $y'(t_{i}^{\mu })$, and

$$\begin{aligned} Y'_{\mu }(t):=\sum _{j=0}^{N}y'^{\mu }_{i}L_{j}^{\mu }(t),\quad t\in [\eta _{\mu },\eta _{\mu +1}] \end{aligned}$$

to approximate $y'|_{\delta _{\mu }}(t)$, i.e., the restriction of $y'(t)$ to $[\eta _{\mu },\eta _{\mu +1}]$. $L_{j}^{\mu }(t)$ is the jth Lagrange interpolation basic function, i.e.,

$$\begin{aligned} L_{j}^{\mu }(t):=\left( \prod \limits _{i=0,i\ne j}^{N}(t-t_{i}^{\mu })\right) \Bigg /\left( \prod \limits _{i=0,i\ne j}^{N}(t_{j}^{\mu }-t_{i}^{\mu })\right) . \end{aligned}$$

Then $y'(t)$ can be approximated by a function $Y'(t)$ defined on $[-1,1]$, i.e.,

$$\begin{aligned} Y'(t):=Y'_{\mu }(t), \quad \text { if } t\in [\eta _{\mu },\eta _{\mu +1}], \end{aligned}$$

which is a continuous functions whose restriction to $[\eta _{\mu },\eta _{\mu +1}]$ is polynomial of degree N. Define

$$\begin{aligned} Y(t):=y_{0}+\int _{0}^{t}Y'(s)ds, \quad t\in [0,T], \end{aligned}$$

(3)

which implies that

$$\begin{aligned} \frac{d}{dt}Y(t)=Y'(t). \end{aligned}$$

(4)

We use Y(t) to approximate y(t).

Discrete (1) as

$$\begin{aligned} y'(t_{i}^{\mu })= & {} g(t_{i}^{\mu })+a (t_{i}^{\mu })y(t_{i}^{\mu })+ \int _{0}^{t_{i}^{\mu }}K(t_{i}^{\mu },s)y(s)ds,\nonumber \\ y(0)= & {} y_{0}, \nonumber \\ i= & {} 0,1,\ldots ,N;\quad \mu =0,1,\ldots ,M. \end{aligned}$$

(5)

Replace y(t) and $y'(t)$ with Y(t) and $Y'(t)$ respectively,

$$\begin{aligned} \begin{aligned} y'^{\mu }_{i}\approx g(t_{i}^{\mu })+a(t_{i}^{\mu })Y(t_{i}^{\mu })+\int _{0}^{t_{i}^{\mu }} K(t_{i}^{\mu },s)Y(s)ds, \end{aligned} \end{aligned}$$

(6)

which can be rewritten as

$$\begin{aligned} \begin{aligned} y'^{\mu }_{i}&\approx g(t_{i}^{\mu })+a(t_{i}^{\mu })Y(t_{i}^{\mu })+\sum _{r=0}^{\mu -1} \int _{\eta _{r}}^{\eta _{r+1}}K(t_{i}^{\mu },s)Y(s)ds\\&\quad +\int _{\eta _{\mu }}^{t_{i}^{\mu }}K(t_{i}^{\mu },s)Y(s)ds. \end{aligned} \end{aligned}$$

(7)

Approximate integral terms by Gauss quadrature formula,

$$\begin{aligned} \begin{aligned} y'^{\mu }_{i}&= g(t_{i}^{\mu })+a(t_{i}^{\mu })Y(t_{i}^{\mu })+\sum _{r=0}^{\mu -1}h_{r} \sum _{k=0}^{N}K(t_{i}^{\mu },s_{r}(v_{k}))Y(s_{r}(v_{k}))w_{k} \\&\quad +\frac{x_{i}+1}{2}h_{\mu }\sum _{k=0}^{N} K(t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))Y(s_{\mu }(s(x_{i},v_{k})))w_{k}, \end{aligned} \end{aligned}$$

(8)

where $\{v_{k},w_{k}\}_{k=0}^{N}$ is the set of Legendre Gauss–Lobatto points and weights in standard interval $[-1,1]$, and

$$\begin{aligned} s_{r}(v):=h_{r}v+\frac{\eta _{r+1}+\eta _{r}}{2},\quad s(x_{i},v):=\frac{x_{i}+1}{2}v+\frac{x_{i}-1}{2}. \end{aligned}$$

(9)

On the other hand, from (3),

$$\begin{aligned} Y(t)=y(0)+\sum _{r=0}^{\mu -1}\int _{\eta _{r}}^{\eta _{r+1}}Y_{r}'(s)ds+\int _{\eta _{\mu }}^{t}Y_{\mu }'(s)ds. \end{aligned}$$

(10)

Note that $Y'_{r}(s),r=0,1,\ldots ,M$ are polynomials of degree N. Then integral terms in (10) can be exactly approximated by Gauss quadrature formula,

$$\begin{aligned} Y(t)=y(0)+\sum _{r=0}^{\mu -1}h_{r}\sum _{k=0}^{N}Y_{r}'(s_{r}(v_{k}))w_{k}+\frac{s^{-1}_{\mu }(t)+1}{2}h_{\mu }\sum _{k=0}^{N}Y_{\mu }'(s_{\mu }(s(s^{-1}_{\mu }(t),v_{k})))w_{k}, \end{aligned}$$

which can be written as

$$\begin{aligned} Y(t)= & {} y(0)+\sum _{r=0}^{\mu -1}h_{r}\sum _{j=0}^{N}y'^{r}_{j}\sum _{k=0}^{N}L_{j}^{r}(s_{r}(v_{k}))w_{k}\nonumber \\&+\frac{s^{-1}_{\mu }(t)+1}{2}h_{\mu }\sum _{j=0}^{N}y'^{\mu }_{j} \sum _{k=0}^{N}L_{j}^{\mu }(s_{\mu }(s(s^{-1}_{\mu }(t),v_{k}))w_{k}. \end{aligned}$$

(11)

where

$$\begin{aligned} s^{-1}_{\mu }(t):=\frac{2}{\eta _{\mu +1}-\eta _{\mu }} \left( t-\frac{\eta _{\mu +1}+\eta _{\mu }}{2}\right) ,\quad t\in [\eta _{\mu },\eta _{\mu +1}]. \end{aligned}$$

(12)

Note that $L_{j}^{r}(s_{r}(v))=F_{j}(v)$, where $F_{j}(v)$ is the jth Lagrange interpolation basic functions associated with Chebyshev Gauss–Lobatto points $\{x_{i}\}_{i=0}^{N}$ in standard interval $[-1,1]$. Then (11) can be written as

$$\begin{aligned} Y(t)= & {} y(0)+\sum _{r=0}^{\mu -1}h_{r}\sum _{j=0}^{N}y'^{r}_{j}\sum _{k=0}^{N}F_{j}(v_{k})w_{k}\nonumber \\&+\frac{s^{-1}_{\mu }(t)+1}{2}h_{\mu }\sum _{j=0}^{N}y'^{\mu }_{j} \sum _{k=0}^{N}F_{j}(s(s^{-1}_{\mu }(t),v_{k}))w_{k}. \end{aligned}$$

(13)

Combining (8) and (13) we obtain the numerical scheme for the proposed method in this paper,

$$\begin{aligned} y'^{\mu }_{i}= & {} g(t_{i}^{\mu })+a(t_{i}^{\mu })Y (t_{i}^{\mu })+\sum _{r=0}^{\mu -1}h_{r} \sum _{k=0}^{N}K(t_{i}^{\mu },s_{r}(v_{k}))Y(s_{r}(v_{k}))w_{k}\nonumber \\&+\frac{x_{i}+1}{2}h_{\mu }\sum _{k=0}^{N}K (t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k}))) Y(s_{\mu }(s(x_{i},v_{k})))w_{k}, \end{aligned}$$

(14)

$$\begin{aligned} Y(t)= & {} y(0)+\sum _{r=0}^{\mu -1}h_{r}\sum _{j=0}^{N}y'^{r}_{j} \sum _{k=0}^{N}F_{j}(v_{k})w_{k}\nonumber \\&+\frac{s^{-1}_{\mu }(t)+1}{2}h_{\mu }\sum _{j=0}^{N}y'^{\mu }_{j} \sum _{k=0}^{N}F_{j}(s(s^{-1}_{\mu }(t),v_{k}))w_{k},\nonumber \\ i= & {} 0,1,\ldots ,N;\mu =0,1,\ldots ,M. \end{aligned}$$

(15)

where $y'^{\mu }_{i},i=0,1,\ldots ,N;\mu =0,1,\ldots ,M$ are unknown elements which are used to construct $Y'(t)$ and Y(t) approximated to $y'(t)$ and y(t) respectively.

3 The existence and uniqueness of the solution to discrete system

In this section, we investigate the existence and uniqueness of discrete system (14) and (15). In order to implement the numerical scheme (14) and (15) by computer, we write it in matrix form. From (15),

$$\begin{aligned} Y(t)=y(0)+{\mathbb {F}}_{0}\sum _{j=0}^{\mu -1}h_{j}{\mathbb {U}}^{j}+h_{\mu }{\mathbb {F}}(s^{-1}_{\mu }(t)){\mathbb {U}}^{\mu },\quad t\in [\eta _{\mu },\eta _{\mu +1}], \end{aligned}$$

(16)

where

$$\begin{aligned} {\mathbb {U}}^{\mu }:= & {} [y'^{\mu }_{0},y'^{\mu }_{1},\ldots ,y'^{\mu }_{N}]',\quad \mu =0,1,\ldots ,M, \nonumber \\ {\mathbb {F}}_{0}:= & {} \left[ \sum _{k=0}^{N}F_{0}(v_{k})w_{k},\ \sum _{k=0}^{N} F_{1}(v_{k})w_{k},\ldots ,\ \sum _{k=0}^{N}F_{N}(v_{k})w_{k}\right] , \nonumber \\ \widehat{G}^{\mu }:= & {} y(0)+{\mathbb {F}}_{0}\sum _{j=0}^{\mu -1} h_{j}{\mathbb {U}}^{j}, \nonumber \\ {\mathbb {F}}(x):= & {} \frac{x+1}{2}\Big [\sum _{k=0}^{N}F_{0}\left( s(x,v_{k})\right) w_{k}, \ \sum _{k=0}^{N}F_{1}(s(x,v_{k}))w_{k},\ldots ,\nonumber \\&\sum _{k=0}^{N}F_{N}\left( s(x,v_{k})\right) w_{k}\Big ]. \end{aligned}$$

(17)

Then

$$\begin{aligned} \begin{aligned} a(t_{i}^{\mu })Y(t_{i}^{\mu })=a(t_{i}^{\mu })\widehat{G}^{\mu }+h_{\mu } a(t_{i}^{\mu }){\mathbb {F}}(x_{i}){\mathbb {U}}^{\mu }. \end{aligned} \end{aligned}$$

(18)

Note that

$$\begin{aligned} \begin{aligned} Y(s_{r}(v_{k}))&=\widehat{G}^{r}+h_{r}{\mathbb {F}} (s^{-1}_{r}(s_{r}(v_{k}))){\mathbb {U}}^{r} \\&=\widehat{G}^{r}+h_{r}{\mathbb {F}}(v_{k}){\mathbb {U}}^{r}. \end{aligned} \end{aligned}$$

(19)

Then

$$\begin{aligned} \begin{aligned}&\sum _{r=0}^{\mu -1}h_{r}\sum _{k=0}^{N}K(t_{i}^{\mu },s_{r}(v_{k}))Y(s_{r}(v_{k}))w_{k} \\&\quad =\sum _{r=0}^{\mu -1}h_{r}\sum _{k=0}^{N}K (t_{i}^{\mu },s_{r}(v_{k}))w_{k} [\widehat{G}^{r}+h_{r}{\mathbb {F}}(v_{k}){\mathbb {U}}^{r}]. \end{aligned} \end{aligned}$$

(20)

Note that

$$\begin{aligned} \begin{aligned} Y(s_{\mu }(s(x_{i},v_{k})))&=\widehat{G}^{\mu }+ h_{\mu }{\mathbb {F}}(s^{-1}_{\mu }(s_{\mu } (s(x_{i},v_{k})))){\mathbb {U}}^{\mu } \\&=\widehat{G}^{\mu }+h_{\mu }{\mathbb {F}}(s(x_{i},v_{k})){\mathbb {U}}^{\mu }. \end{aligned} \end{aligned}$$

(21)

Then

$$\begin{aligned} \begin{aligned}&\frac{x_{i}+1}{2}h_{\mu }\sum _{k=0}^{N}K (t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))Y(s_{\mu }(s(x_{i},v_{k})))w_{k} \\&\quad =\frac{x_{i}+1}{2}h_{\mu }\sum _{k=0}^{N}K (t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))w_{k} [\widehat{G}^{\mu } +h_{\mu }{\mathbb {F}}(s(x_{i},v_{k}){\mathbb {U}}^{\mu }] \\&\quad =h_{\mu }\widehat{G}^{\mu }\frac{x_{i}+1}{2}\sum _{k=0}^{N}K(t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))w_{k} \\&\qquad +h_{\mu }\left[ h_{\mu }\frac{x_{i}+1}{2}\sum _{k=0}^{N}K(t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))w_{k}{\mathbb {F}}(s(x_{i},v_{k}))\right] {\mathbb {U}}^{\mu }. \end{aligned} \end{aligned}$$

(22)

From (14) we have

$$\begin{aligned}&g(t_{i}^{\mu })+a(t_{i}^{\mu })Y(t_{i}^{\mu })+\sum _{r=0}^{\mu -1}h_{r}\sum _{k=0}^{N}K(t_{i}^{\mu },s_{r}(v_{k}))Y(s_{r}(v_{k}))w_{k} \nonumber \\&\qquad +\frac{x_{i}+1}{2}h_{\mu }\sum _{k=0}^{N}K(t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))Y(s_{\mu }(s(x_{i},v_{k})))w_{k} \nonumber \\&\quad =g(t_{i}^{\mu })+a(t_{i}^{\mu })\widehat{G}^{\mu }+\sum _{r=0}^{\mu -1}h_{r}\sum _{k=0}^{N}K(t_{i}^{\mu },s_{r}(v_{k}))w_{k}[\widehat{G}^{r} +h_{r}{\mathbb {F}}(v_{k}){\mathbb {U}}^{r}] \nonumber \\&\qquad +h_{\mu }\widehat{G}^{\mu }\frac{x_{i}+1}{2}\sum _{k=0}^{N}K(t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))w_{k} \nonumber \\&\qquad +h_{\mu }\left[ a(t_{i}^{\mu }){\mathbb {F}} (x_{i})+h_{\mu }\frac{x_{i}+1}{2}\sum _{k=0}^{N} K(t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))w_{k}{\mathbb {F}}(s(x_{i},v_{k})) \right] {\mathbb {U}}^{\mu }.\nonumber \\ \end{aligned}$$

(23)

Let

$$\begin{aligned} G_{i}^{\mu }:= & {} g(t_{i}^{\mu })+a(t_{i}^{\mu }) \widehat{G}^{\mu }+\sum _{r=0}^{\mu -1}h_{r}\sum _{k=0}^{N}K(t_{i}^{\mu }, s_{r}(v_{k}))w_{k}[\widehat{G}^{r} +h_{r}{\mathbb {F}}(v_{k}){\mathbb {U}}^{r}]\nonumber \\&\quad +h_{\mu }\widehat{G}^{\mu }\frac{x_{i}+1}{2}\sum _{k=0}^{N}K (t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))w_{k},\nonumber \\ {\mathbb {G}}^{\mu }:= & {} [G_{0}^{\mu },G_{1}^{\mu },\ldots ,G_{N}^{\mu }]',\nonumber \\ {\mathbb {A}}^{\mu }(i,:):= & {} a(t_{i}^{\mu }){\mathbb {F}}(x_{i})+ h_{\mu }\frac{x_{i}+1}{2}\sum _{k=0}^{N} K(t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))w_{k}{\mathbb {F}}(s(x_{i},v_{k})).\nonumber \\ \end{aligned}$$

(24)

Then the matrix form corresponding to (14) is

$$\begin{aligned} \begin{aligned} {\mathbb {U}}^{\mu }={\mathbb {G}}^{\mu }+h_{\mu }{\mathbb {A}}^{\mu }{\mathbb {U}}^{\mu },\quad \mu =0,1,\ldots ,M, \end{aligned} \end{aligned}$$

(25)

which is equal to

$$\begin{aligned} \begin{aligned} ({\mathbb {I}}-h_{\mu }{\mathbb {A}}^{\mu }){\mathbb {U}}^{\mu }={\mathbb {G}}^{\mu },\quad \mu =0,1,\ldots ,M. \end{aligned} \end{aligned}$$

(26)

Since $a(t),K(t,s),F_{j}(s)$ are continuous on their definition domain, then elements of matrix ${\mathbb {A}}^{\mu }$ are all uniformly bounded no matter what $\mu$ is. The Neumann Lemma ([3, page 87]) then shows that the inverse of the matrix

$$\begin{aligned} {\mathbb {B}}^{(\mu )}:={\mathbb {I}}-h_{\mu }{\mathbb {A}}^{\mu } \end{aligned}$$

exists whenever

$$\begin{aligned} \Vert h_{\mu }{\mathbb {A}}^{\mu }\Vert <1 \end{aligned}$$

for some matrix norm. This clearly holds whenever $h_{\mu },\mu =0,1,\ldots ,M$ are uniformly sufficient small. Then the matrix equation (26) possesses a unique solution which implies that so does for discrete system (14) and (15). We conclude this result as the following theorem.

Theorem 1

If $h_{\mu }(\mu =0,1,\ldots ,M)$ are uniformly sufficient small, then the discrete system (14) and (15) possess unique solution.

4 Useful lemmas

In this section, we give some lemmas which will be used in Sect. 5. For simplicity, let $\partial _{x}^{k}u(x):=\frac{\text {d}^{k}u}{\text {d}x^{k}}(x)$. Before giving lemmas, we introduce some spaces.

Let (a, b) be a bounded interval in real line, $\omega (x)$ is the Chebyshev weight function on (a, b). Set $L^{2}_{\omega }(a,b)$ be the measurable functions space equipped with the norm

$$\begin{aligned} \Vert u\Vert _{L^{2}_{\omega }(a,b)}:=\left( \int _{a}^{b}|u(x)|^{2}\omega (x)dx\right) ^{1/2}. \end{aligned}$$

Assume that $m\ge 1$ is an integer. $H^{m}_{\omega }(a,b)$ is a Sobolev space defined by

$$\begin{aligned} H^{m}_{\omega }(a,b):=\{u\in L^{2}_{\omega }(a,b):\text { for }0\le k\le m,\partial _{x}^{k}u(x)\in L^{2}_{\omega }(a,b)\}, \end{aligned}$$

Denote by $L^{\infty }(a,b)$ the measurable functions space with the norm

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(a,b)}:=\mathop {\text {ess sup}}\limits _{x\in (a,b)}|u(x)|. \end{aligned}$$

$L^{2}(a,b)$ is a space satisfying

$$\begin{aligned} \Vert u\Vert _{L^{2}(a,b)}:=\int _{a}^{b}u^{2}(x)dx<\infty . \end{aligned}$$

$H^{m}(a,b)$ is a Sobolev space defined by

$$\begin{aligned} H^{m}(a,b):=\{u\in L^{2}(a,b):\text { for }0\le k\le m,\partial _{x}^{k}u(x)\in L^{2}(a,b)\}. \end{aligned}$$

Let C([a, b]) be the continuous functions space on [a, b].

For $y\in C([0,T])$, define an interpolation operator $I_{N}$ as

$$\begin{aligned} I_{N}y(t):=I_{N}^{\mu }(y|_{\delta _{\mu }})(t),\text { if }t\in [\eta _{\mu },\eta _{\mu +1}],\quad 0\le \mu \le M, \end{aligned}$$

(27)

where $y|_{\delta _{\mu }}(t)$ is the restriction of y(t) to $\delta _{\mu }:=[\eta _{\mu },\eta _{\mu +1}]$, $I_{N}^{\mu }$ is the interpolation operator associated the collocation points $t_{i}^{\mu },i=0,1,\ldots ,N$ in $[\eta _{\mu },\eta _{\mu +1}]$, i.e.,

$$\begin{aligned} I_{N}^{\mu }(y|_{\delta _{\mu }})(t):=\sum \limits _{j=0}^{N}y|_{\delta _{\mu }} (t^{\mu }_{j})L_{j}^{\mu }(t),\quad t\in [\eta _{\mu },\eta _{\mu +1}]. \end{aligned}$$

Hereafter, C denotes a constant which is independent of N.

Lemma 1

[4] Assume that $u\in H_{\omega }^{m}(-1,1)(m$ is a positive integer), then

$$\begin{aligned} \Vert u-J_{N}u\Vert _{L^{\infty }(-1,1)}\le & {} CN^{(1/2)-m}\Vert \partial _{x}^{m}u\Vert _{L_{\omega }^{2}(-1,1)}, \end{aligned}$$

(28)

$$\begin{aligned} \Vert J_{N}u\Vert _{L^{\infty }(-1,1)}\le & {} C(\log N)\Vert u\Vert _{L^{\infty }(-1,1)}, \end{aligned}$$

(29)

where $J_{N}$ is the interpolation operator associated with Chebyshev Gauss–Lobatto points $\{x_{i}\}_{i=0}^{N}$ in standard interval $[-1,1]$.

Lemma 2

Assume that $y(s)\in C^{m}([0,T])(m$ is a positive integer), then

$$\begin{aligned} \Vert y-I_{N}y\Vert _{L^{\infty }(0,T)}\le & {} Ch^{m}N^{(1/2)-m}\Vert \partial _{s}^{m}y\Vert _{L^{\infty }(0,T)}, \end{aligned}$$

(30)

$$\begin{aligned} \Vert I_{N}y\Vert _{L^{\infty }(0,T)}\le & {} C(\log N)\Vert y\Vert _{L^{\infty }(0,T)}, \end{aligned}$$

(31)

where $h:=\max \{h_{\mu }:\mu =0,1,\ldots ,M\}$.

Proof

By the definition of $I_{N}^{\mu }$, $(I_{N}^{\mu }(y|_{\delta _{\mu }}))(t)$ is a function defined on $[\eta _{\mu },\eta _{\mu +1}]$. The variable transformation $s_{\mu }(x)$ defined by (9) changes it to be a new function defined on $[-1,1]$,

$$\begin{aligned} \begin{aligned} (I_{N}^{\mu }(y|_{\delta _{\mu }}))(s_{\mu }(x))&=\sum \limits _{j=0}^{N}y|_{\delta _{\mu }}(t^{\mu }_{j})L_{j}^{\mu }(s_{\mu }(x)) =\sum \limits _{j=0}^{N}y|_{\delta _{\mu }}(t^{\mu }_{j})F_{j}(x),\quad x\in [-1,1]. \end{aligned} \end{aligned}$$

(32)

In the other hand, $y|_{\delta _{\mu }}(s_{\mu }(x))$ is a function defined on $[-1,1]$. Its Lagrange interpolation polynomial associated with the Chebyshev Gauss–Lobatto points $x_{j},j=0,1,\ldots ,N$ in $[-1,1]$ is

$$\begin{aligned} \begin{aligned}J_{N}(y|_{\delta _{\mu }}(s_{\mu }(x)))&=\sum \limits _{j=0}^{N}y|_{\delta _{\mu }}(s_{\mu }(x_{j}))F_{j}(x),\quad x\in [-1,1]. \end{aligned} \end{aligned}$$

(33)

Note that

$$\begin{aligned} s_{\mu }(x_{j})=t^{\mu }_{j},\quad j=0,1,\ldots ,N. \end{aligned}$$

Inserting this into (33) yields

$$\begin{aligned} \begin{aligned}J_{N}(y|_{\delta _{\mu }}(s_{\mu }(x)))&=\sum \limits _{j=0}^{N}y|_{\delta _{\mu }}(t^{\mu }_{j})F_{j}(x),\quad x\in [-1,1]. \end{aligned} \end{aligned}$$

(34)

Combing (32) with (34) yields

$$\begin{aligned} (I_{N}^{\mu }(y|_{\delta _{\mu }}))(s_{\mu }(x))=J_{N}(y|_{\delta _{\mu }}(s_{\mu }(x))),\quad x\in [-1,1]. \end{aligned}$$

(35)

By (28)

$$\begin{aligned} \begin{aligned} \Vert y-I_{N}y\Vert _{L^{\infty }(0,T)}&=\max \limits _{0\le \mu \le M}\{\Vert y|_{\delta _{\mu }}(s_{\mu }(\cdot ))-J_{N}(y|_{\delta _{\mu }}(s_{\mu }(\cdot )))\Vert _{L^{\infty }(-1,1)}\} \\&\le CN^{\frac{1}{2}-m}\max \limits _{0\le \mu \le M}\{\Vert \partial ^{m}_{v}(y|_{\delta _{\mu }}(s_{\mu }(\cdot )))\Vert _{L^{2}_{\omega }(-1,1)}\} \\&=CN^{\frac{1}{2}-m}\max \limits _{0\le \mu \le M}\{h_{\mu }^{m}\Vert \partial _{s}^{m}(y|_{\delta _{\mu }})(s_{\mu }(\cdot ))\Vert _{ L^{2}_{\omega }(-1,1)}\} \\&\le CN^{\frac{1}{2}-m}\max \limits _{0\le \mu \le M}\{h_{\mu }^{m}\Vert \partial _{s}^{m}(y|_{\delta _{\mu }})(s_{\mu }(\cdot ))\Vert _{ L^{\infty }(-1,1)}\} \\&= CN^{\frac{1}{2}-m}\max \limits _{0\le \mu \le M}\{h_{\mu }^{m}\Vert \partial _{s}^{m}(y|_{\delta _{\mu }})(\cdot )\Vert _{ L^{\infty }(\delta _{\mu })}\} \\&\le Ch^{m}N^{\frac{1}{2}-m}\Vert \partial _{s}^{m}y\Vert _{ L^{\infty }(0,T)}. \end{aligned} \end{aligned}$$

(36)

This is (30).

Now we prove (31). It is obviously that

$$\begin{aligned} \begin{aligned} \Vert I_{N}y\Vert _{L^{\infty }(0,T)}=\max \limits _{0\le \mu \le M}\Vert I_{N}^{\mu }(y|_{\delta _{\mu }})\Vert _{L^{\infty }(\delta _{\mu })}. \end{aligned}\end{aligned}$$

(37)

By (29),

$$\begin{aligned} \begin{aligned} \Vert I_{N}^{\mu }(y|_{\delta _{\mu }})\Vert _{L^{\infty }(\delta _{\mu })}&=\Vert (I_{N}^{\mu }(y|_{\delta _{\mu }}))(s_{\mu }(\cdot ))\Vert _{L^{\infty }(-1,1)} =\Vert J_{N}(y|_{\delta _{\mu }}(s_{\mu }(\cdot )))\Vert _{L^{\infty }(-1,1)} \\&\le C(\log N)\Vert y|_{\delta _{\mu }}(s_{\mu }(\cdot ))\Vert _{L^{\infty }(-1,1)} =C(\log N)\Vert y|_{\delta _{\mu }}\Vert _{L^{\infty }(\delta _{\mu })} \\&\le C(\log N)\Vert y\Vert _{L^{\infty }(0,T)}, \end{aligned}\end{aligned}$$

(38)

which together with (37) yields

$$\begin{aligned} \Vert I_{N}y\Vert _{L^{\infty }(0,T)}\le C(\log N)\Vert y\Vert _{L^{\infty }(0,T)}. \end{aligned}$$

This leads to (31). $\square$

Lemma 3

[4] Assume that $u(x)\in H^{m}(-1,1)(m$ is a positive integer), $P_{N}(x)$ is a polynomial of degree not exceeding N. Then

$$\begin{aligned} \left| \int _{-1}^{1}u(x)P_{N}(x)dx-\sum _{k=0}^{N}u(v_{k})P_{N}(v_{k})w_{k}\right| \le CN^{-m} \Vert \partial _{x}^{m}u\Vert _{L^{2}(-1,1)}\Vert P_{N}\Vert _{L^{2}(-1,1)}. \end{aligned}$$

Lemma 4

Assume that $y(t)\in H^{m}(0,T)(m$ is a positive integer), $Q_{N}(t)$ is function whose restriction to $\delta _{\mu }:=[\eta _{\mu },\eta _{\mu +1}]$, $Q_{N}|_{\delta _{\mu }}(t)$, is a polynomial of degree not exceeding N. Then for $t\in [\eta _{\mu },\eta _{\mu +1}]$,

$$\begin{aligned}&\left| \int _{0}^{t}y(s)Q_{N}(s)ds-\sum _{r=0}^{\mu -1}h_{r}\sum _{k=0}^{N}y(s_{r}(v_{k}))Q_{N}|_{\delta _{r}}(s_{r}(v_{k}))w_{k}\right. \nonumber \\&\left. \qquad -h_{\mu }\frac{s^{-1}_{\mu }(t)+1}{2}\sum _{k=0}^{N}y(s_{\mu }(s(x(t),v_{k}))Q_{N}|_{\delta _{\mu }}(s_{\mu }(s(x(t),v_{k}))w_{k}\right| \nonumber \\&\quad \le C h^{m}N^{-m}\Vert \partial _{s}^{m}y\Vert _{L^{2}(0,t)}\Vert Q_{N}\Vert _{L^{2}(0,t)}, \end{aligned}$$

(39)

where $s^{-1}_{\mu }(t)$ is defined by (12).

Proof

Note that

$$\begin{aligned} \int _{0}^{t}y(s)Q_{N}(s)ds=\sum _{r=0}^{\mu -1}\int _{\eta _{r}}^{\eta _{r+1}}y(s)Q_{N}|_{\delta _{r}}(s)ds+\int _{\eta _{\mu }}^{t}y(s)Q_{N}|_{\delta _{\mu }}(s)ds. \end{aligned}$$

Use the variable transformation $s_{r}(v)$ to change the integration interval $[\eta _{r},\eta _{r+1}]$ to standard interval $[-1,1]$,

$$\begin{aligned} \int _{\eta _{r}}^{\eta _{r+1}}y(s)Q_{N}|_{\delta _{r}}(s)ds=h_{r}\int _{-1}^{1}y(s_{r}(v))Q_{N}|_{\delta _{r}}(s_{r}(v))dv. \end{aligned}$$

By Lemma 3,

$$\begin{aligned} \begin{aligned}&\left| h_{r}\int _{-1}^{1}y(s_{r}(v))Q_{N}|_{\delta _{r}}(s_{r}(v))dv-h_{r}\sum _{k=0}^{N}y(s_{r}(v_{k}))Q_{N}|_{\delta _{r}}(s_{r}(v_{k}))w_{k}\right| \\&\quad \le Ch_{r}N^{-m}\Vert \partial _{v}^{m}y(s_{r}(\cdot ))\Vert _{L^{2}(-1,1)}\Vert Q_{N}|_{\delta _{r}}(s_{r}(\cdot ))\Vert _{L^{2}(-1,1)} \\&\quad = Ch_{r}^{m+1}N^{-m}\Vert \partial _{s}^{m}y(s_{r}(\cdot ))\Vert _{L^{2}(-1,1)}\Vert Q_{N}|_{\delta _{r}}(s_{r}(\cdot ))\Vert _{L^{2}(-1,1)} \\&\quad =Ch^{m}N^{-m}\Vert \partial _{s}^{m}y(\cdot )\Vert _{L^{2}(\eta _{r},\eta _{r+1})}\Vert Q_{N}|_{\delta _{r}}(\cdot )\Vert _{L^{2}(\eta _{r},\eta _{r+1})}. \end{aligned} \end{aligned}$$

(40)

Therefore

$$\begin{aligned} \begin{aligned}&\left| \int _{\eta _{r}}^{\eta _{r+1}}y(s)Q_{N}|_{\delta _{r}}(s)ds-h_{r}\sum _{k=0}^{N}y(s_{r}(v_{k}))Q_{N}|_{\delta _{r}}(s_{r}(v_{k}))w_{k}\right| \\&\quad \le Ch^{m}N^{-m}\Vert \partial _{s}^{m}y(\cdot )\Vert _{L^{2}(\eta _{r},\eta _{r+1})}\Vert Q_{N}|_{\delta _{r}}(\cdot )\Vert _{L^{2}(\eta _{r},\eta _{r+1})}. \end{aligned} \end{aligned}$$

(41)

Similarly,

$$\begin{aligned}&\left| \int _{\eta _{\mu }}^{t}y(s)Q_{N}|_{\delta _{r}}(s)ds-h_{\mu }\frac{s^{-1}_{\mu }(t)+1}{2}\right. \nonumber \\&\left. \sum _{k=0}^{N} y(s_{\mu }(s(s^{-1}_{\mu }(t),v_{k}))Q_{N}|_{\delta _{\mu }}(s_{\mu }(s(s^{-1}_{\mu }(t),v_{k}))w_{k}\right| \nonumber \\&\quad \le Ch^{m}N^{-m}\Vert \partial _{s}^{m}y(\cdot )\Vert _{L^{2}(\eta _{\mu },t)}\Vert Q_{N}|_{\delta _{\mu }}(\cdot )\Vert _{L^{2}(\eta _{\mu },t)}. \end{aligned}$$

(42)

Then

$$\begin{aligned} \begin{aligned}&\left| \int _{0}^{t}y(s)Q_{N}(s)ds-\sum _{r=0}^{\mu -1}h_{r}\sum _{k=0}^{N}y(s_{r}(v_{k}))Q_{N}|_{\delta _{r}}(s_{r}(v_{k}))w_{k} \right. \\&\left. \qquad -h_{\mu }\frac{s^{-1}_{\mu }(t)+1}{2}\sum _{k=0}^{N}y(s_{\mu }(s(x(t),v_{k}))Q_{N}|_{\delta _{\mu }}(s_{\mu }(s(x(t),v_{k}))w_{k}\right| \\&\quad \le Ch^{m}N^{-m}\Bigg [\sum _{r=0}^{\mu -1}\Vert \partial _{s}^{m}y (\cdot )\Vert _{L^{2}(\eta _{r},\eta _{r+1})}\Vert Q_{N}|_{\delta _{r}} (\cdot )\Vert _{L^{2}(\eta _{r},\eta _{r+1})} \\&\qquad +\Vert \partial _{s}^{m}y(\cdot )\Vert _{L^{2}(\eta _{\mu },t)} \Vert Q_{N}|_{\delta _{\mu }}(\cdot )\Vert _{L^{2}(\eta _{\mu },t)}\Bigg ]. \end{aligned} \end{aligned}$$

(43)

By Cauch’s inequality which is stated as

$$\begin{aligned} \sum _{r=0}^{\mu }a_{r}b_{r}\le \left( \sum _{r=0}^{\mu }a_{r}^{2} \right) ^{\frac{1}{2}}\left( \sum _{r=0}^{\mu }b_{r}^{2}\right) ^{\frac{1}{2}}, \end{aligned}$$

we have

$$\begin{aligned} \begin{aligned}&\sum _{r=0}^{\mu -1}\Vert \partial _{s}^{m}y(\cdot )\Vert _{L^{2}(\eta _{r},\eta _{r+1})}\Vert Q_{N}|_{\delta _{r}}(\cdot )\Vert _{L^{2}(\eta _{r},\eta _{r+1})} \\&\qquad +\Vert \partial _{s}^{m}y(\cdot )\Vert _{L^{2}(\eta _{\mu },t)}\Vert Q_{N}|_{\delta _{\mu }}(\cdot )\Vert _{L^{2}(\eta _{\mu },t)} \\&\quad \le \left[ \sum _{r=0}^{\mu -1}\Vert \partial _{s}^{m}y(\cdot )\Vert ^{2}_{L^{2}(\eta _{r},\eta _{r+1})}+\Vert \partial _{s}^{m}y(\cdot )\Vert ^{2}_{L^{2}(\eta _{\mu },t)}\right] ^{\frac{1}{2}} \\&\qquad *\left[ \sum _{r=0}^{\mu -1}\Vert Q_{N}|_{\delta _{r}}(\cdot )\Vert ^{2}_{L^{2}(\eta _{r},\eta _{r+1})}+\Vert Q_{N}|_{\delta _{\mu }}(\cdot )\Vert ^{2}_{L^{2}(\eta _{\mu },t)}\right] ^{\frac{1}{2}} \\&\quad =\Vert \partial _{s}^{m}y(\cdot )\Vert _{L^{2}(0,t)}\Vert Q_{N}(\cdot )\Vert _{L^{2}(0,t)}, \end{aligned} \end{aligned}$$

(44)

which together with (43) yields (39). $\square$

Lemma 5

[16] Assume that $e(t)\in C([0,T])$ satisfying

$$\begin{aligned} e(t)\le u(t)+c\int _{0}^{t}e(s)ds,\quad t\in [0,T], \end{aligned}$$

(45)

where $u\in L^{\infty }(0,T),0<c<+\infty$. Then there exist a constant C independent of e(t) and u(t) such that

$$\begin{aligned} \Vert e\Vert _{L^{\infty }(0,T)}\le C\Vert u\Vert _{L^{\infty }(0,T)}. \end{aligned}$$

(46)

5 Convergence analysis

Theorem 2

Assume that Y(t) and $Y'(t)$ obtained by scheme (14) and (15) are approximations to y(t) and $y'(t)$ which lie in (1) with given functions possessing continuous derivatives of at least m order. Then

$$\begin{aligned} \begin{aligned} \Vert e_{i}\Vert _{L^{\infty }(0,T)}\le Ch^{m}N^{(1/2)-m}[\widehat{K}\Vert y\Vert _{L^{\infty }(0,T)}+ \Vert \partial ^{m+1}_{t}y\Vert _{L^{\infty }(0,T)}], \end{aligned} \end{aligned}$$

(47)

where $e_{0}(t):=y(t)-Y(t),\ e_{1}(t):=y'(t)-Y'(t),\widehat{K}:=\max \{\Vert \partial _{s}^{m}K(t,\cdot )\Vert _{L^{2}(0,t)}:t\in [0,T]\}$.

The error estimation result (47) implies that the delay of errors dependent of N, h, m. Employing more collocation points (N is larger), and dividing the interval [0, T] into more subintervals (h is smaller), the numerical solution will be more accurate. If given functions possess more regularity (m is larger), numerical errors decay faster. It is worth noting that N, h, m are independent of each other. We carry numerical experiments in Sect. 6 to confirm these theoretical results. Note that $\widehat{K}$, $\Vert y\Vert _{L^{\infty }(0,T)}$ and $\Vert \partial ^{m+1}_{t}y\Vert _{L^{\infty }(0,T)}$ will become larger if T becomes larger. This implies that for fixed N and h, a large T is not good for us to obtain high precision numerical solution. We carry out numerical experiment to investigate the effect of T on the decay of errors. For a large T, we investigate the difference between the global spectral collocation method and multi-step spectral collocation method. Numerical result show that multi-step spectral collocation method perform better. All of these numerical experiments will be carried out in Sect. 6.

Proof

Subtract (14) from (5),

$$\begin{aligned} \begin{aligned} y'(t_{i}^{\mu })-y'^{\mu }_{i}=a(t_{i}^{\mu })(y(t_{i}^{\mu })- Y(t^{\mu }_{i}))+\int _{0}^{t_{i}^{\mu }}K(t_{i}^{\mu },s)y(s)ds-S(t_{i}^{\mu }), \end{aligned} \end{aligned}$$

(48)

where

$$\begin{aligned} \begin{aligned} S(t_{i}^{\mu })&:=\sum _{r=0}^{\mu -1}h_{r}\sum _{k=0}^{N} K(t_{i}^{\mu },s_{r}(v_{k}))Y(s_{r}(v_{k}))w_{k} \\&\quad +\frac{x_{i}+1}{2}h_{\mu }\sum _{k=0}^{N}K (t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})))Y(s_{\mu }(s(x_{i},v_{k}))) w_{k}. \end{aligned} \end{aligned}$$

Multiply $L_{j}^{\mu }(t)$ to both side of (5) and sum up from $i=0$ to N,

$$\begin{aligned} \begin{aligned} I_{N}^{\mu }y'(t)-Y'_{\mu }(t)&=I_{N}^{\mu }[a(t)(y(t)-Y(t))]\\&\quad +I_{N}^{\mu }\left[ \int _{0}^{t}K(t,s)y(s)ds-S(t)\right] ,\quad t \in [\eta _{\mu },\eta _{\mu +1}]. \end{aligned} \end{aligned}$$

(49)

By the definition of $I_{N}$,

$$\begin{aligned} \begin{aligned} I_{N}y'(t)-Y'(t)=I_{N}[a(t)(y(t)-Y(t))]+I_{N} [\int _{0}^{t}K(t,s)y(s)ds-S(t)], \end{aligned} \end{aligned}$$

(50)

which can be rewritten as

$$\begin{aligned} \begin{aligned} e_{1}(t)=\sum _{i=1}^{4}E_{i}(t)+a(t)e_{0}(t)+\int _{0}^{t}K(t,s)e_{0}(s)ds, \end{aligned} \end{aligned}$$

(51)

where

$$\begin{aligned} \begin{aligned}&E_{1}(t):=y'(t)-I_{N}y'(t), \\&E_{2}(t):=I_{N}[a(t)e_{0}(t)]-a(t)e_{0}(t), \\&E_{3}(t):=I_{N}\left[ \int _{0}^{t}K(t,s)e_{0}(s)ds\right] -\int _{0}^{t}K(t,s)e_{0}(s)ds, \\&E_{4}(t):=I_{N}\left[ \int _{0}^{t}K(t,s)Y(s)ds-S(t)\right] . \end{aligned} \end{aligned}$$

(52)

By Lemma 2,

$$\begin{aligned} \Vert E_{1}\Vert _{L^{\infty }(0,T)}= \Vert y'-I_{N}y'\Vert _{L^{\infty }(0,T)}\le Ch^{m}N^{(1/2)-m}\Vert \partial ^{m+1}_{t}y\Vert _{L^{\infty }(0,T)}. \end{aligned}$$

(53)

From (4) we know that $\frac{d}{dt}e_{0}(t)=e_{1}(t)$ or $e_{0}(t)=\int _{0}^{t} e_{1}(s)ds$ which implies that $\Vert e_{0}\Vert _{L^{\infty }(0,T)}\le T\Vert e_{1}\Vert _{L^{\infty }(0,T)}$. Then by Lemma 2 with $m=1$,

$$\begin{aligned} \begin{aligned} \Vert E_{2}\Vert _{L^{\infty }(0,T)}&=\Vert I_{N}[a(t)e_{0}(t)]-a(t)e_{0}(t)\Vert _{L^{\infty }(0,T)}\\&\le ChN^{-1/2}\Vert \partial ^{1}_{t}[a(t)e_{0}(t)]\Vert _{L^{\infty }(0,T)} \\&=ChN^{-1/2}\Vert a'(t)e_{0}(t)+a(t)e_{1}(t)\Vert _{L^{\infty }(0,T)} \\&\le ChN^{-1/2}(T\Vert a'\Vert _{L^{\infty }(0,T)}+\Vert a\Vert _{L^{\infty }(0,T)})\Vert e_{1}\Vert _{L^{\infty }(0,T)}. \end{aligned} \end{aligned}$$

(54)

Similarly,

$$\begin{aligned} \begin{aligned} \Vert E_{3}\Vert _{L^{\infty }(0,T)}&\le Ch^{}N^{-1/2}\Vert \partial ^{1}_{t}\left[ \int _{0}^{t}K(t,s)e_{0}(s)ds\right] \Vert _{L^{\infty }(0,T)} \\&\le ChN^{-1/2}\Vert K(t,t)e_{0}(t)+\int _{0}^{t}\partial ^{1}_{t}K(t,s)e_{0}(s)ds\Vert _{L^{\infty }(0,T)} \\&\le ChN^{-1/2}[T\Vert K\Vert _{L^{\infty }(\varOmega )}+T^{2}\Vert \partial ^{1}_{t}K\Vert _{L^{\infty }(\varOmega )}]\Vert e_{1}\Vert _{L^{\infty }(0,T)}. \end{aligned} \end{aligned}$$

(55)

By Lemma 4,

$$\begin{aligned} \begin{aligned} \Vert E_{4}\Vert _{L^{\infty }(0,T)}&\le Ch^{m}N^{-m}\max \limits _{t\in [0,T]}\Vert \partial _{s}^{m}K (t,\cdot )\Vert _{L^{2}(0,t)}\Vert Y\Vert _{L^{\infty }(0,T)} \\&\le Ch^{m}N^{-m}\widehat{K} [\Vert y\Vert _{L^{\infty }(0,T)}+\Vert e_{0}\Vert _{L^{\infty }(0,T)}] \\&\le Ch^{m}N^{-m}\widehat{K} [\Vert y\Vert _{L^{\infty }(0,T)}+T\Vert e_{1}\Vert _{L^{\infty }(0,T)}]. \end{aligned} \end{aligned}$$

(56)

Combine (54), (55) and (56),

$$\begin{aligned}&\sum _{i=2}^{4}\Vert E_{i}\Vert _{L^{\infty }(0,T)} \le C[hN^{-1/2}(T\Vert a'\Vert _{L^{\infty }(0,T)}+\Vert a\Vert _{L^{\infty }(0,T)}+ T\Vert K\Vert _{L^{\infty }(\varOmega )} \nonumber \\&\quad +\, T^{2}\Vert \partial ^{1}_{t}K\Vert _{L^{\infty }(\varOmega )}) +h^{m}N^{-m}T\widehat{K}]\Vert e_{1}\Vert _{L^{\infty }(0,T)}+ Ch^{m}N^{-m}\widehat{K}\Vert y\Vert _{L^{\infty }(0,T)}.\qquad \quad \end{aligned}$$

(57)

Let

$$\begin{aligned} \begin{aligned} \widehat{C}(h,N)&:= CT[hN^{-1/2}(\Vert a'\Vert _{L^{\infty }(0,T)}+\Vert a\Vert _{L^{\infty }(0,T)}\\&\qquad +\Vert K\Vert _{L^{\infty }(\varOmega )}+T\Vert \partial ^{1}_{t}K\Vert _{L^{\infty }(\varOmega )}) +h^{m}N^{-m}\widehat{K}], \end{aligned} \end{aligned}$$

(58)

which implies that

$$\begin{aligned} \mathop {\lim _{h\rightarrow 0}}_{ \text { or }N\rightarrow +\infty }\widehat{C}(h,N)=0. \end{aligned}$$

We have

$$\begin{aligned} \begin{aligned} \sum _{i=2}^{4}\Vert E_{i}\Vert _{L^{\infty }(0,T)} \le&\widehat{C}(h,N)\Vert e_{1}\Vert _{L^{\infty }(0,T)} +Ch^{m}N^{-m}\widehat{K}\Vert y\Vert _{L^{\infty }(0,T)}, \end{aligned} \end{aligned}$$

(59)

which together with (51) and (53) yields

$$\begin{aligned} \begin{aligned} |e_{1}(t)|&\le \widehat{C}(h,N)\Vert e_{1}\Vert _{L^{\infty }(0,T)} +Ch^{m}N^{-m}\widehat{K}\Vert y\Vert _{L^{\infty }(0,T)}\\&\quad + Ch^{m}N^{(1/2)-m}\Vert \partial ^{m+1}_{t}y\Vert _{L^{\infty }(0,T)}+|a(t)e_{0}(t)|+\int _{0}^{t}|K(t,s)e_{0}(s)|ds. \end{aligned} \end{aligned}$$

(60)

Let

$$\begin{aligned} \begin{aligned} u(h,N,\Vert e_{1}\Vert _{L^{\infty }(0,T)})&:=\widehat{C}(h,N)\Vert e_{1}\Vert _{L^{\infty }(0,T)} +Ch^{m}N^{-m}\widehat{K}\Vert y\Vert _{L^{\infty }(0,T)}\\&\quad + Ch^{m}N^{(1/2)-m}\Vert \partial ^{m+1}_{t}y\Vert _{L^{\infty }(0,T)}. \end{aligned} \end{aligned}$$

(61)

Then (60) becomes

$$\begin{aligned} \begin{aligned} |e_{1}(t)|\le u(h,N,\Vert e_{1}\Vert _{L^{\infty }(0,T)})+|a(t)e_{0}(t)|+\int _{0}^{t}|K(t,s)e_{0}(s)|ds, \end{aligned} \end{aligned}$$

(62)

which can be rewritten as

$$\begin{aligned} |e_{1}(t)|\!\le u(h,N,\Vert e_{1}\Vert _{L^{\infty }(0,T)})\!+\!|a(t)|\!\int _{0}^{t}\!|e_{1}(s)|ds\!+\!\!\int _{0}^{t}\!|K(t,s)|\int _{0}^{s}\!|e_{1}(v)|dvds.\nonumber \\ \end{aligned}$$

(63)

By Dirichlet formula,

$$\begin{aligned} |e_{1}(t)|\le u(h,N,\Vert e_{1}\Vert _{L^{\infty }(0,T)})+|a(t)| \int _{0}^{t}|e_{1}(s)|ds+\int _{0}^{t}\left[ \int _{v}^{t}|K(t,s)|ds\right] |e_{1}(v)|dv.\nonumber \\ \end{aligned}$$

(64)

Then there exist constants c independent of $e_{1}(t)$, N and h such that

$$\begin{aligned} \begin{aligned} |e_{1}(t)|\le u(h,N,\Vert e_{1}\Vert _{L^{\infty }(0,T)})+c\int _{0}^{t}|e_{1}(s)|ds. \end{aligned} \end{aligned}$$

(65)

Note that $e_{1}(t)$ is a function dependent of h, N. At this points, $\Vert e_{1}\Vert _{L^{\infty }(0,T)}$ is a constant dependent of h and N. Fix h and N. Then (65) is a fixed inequality which implies that the relation between $e_{1}$ and $u(h,N,\Vert e_{1}\Vert _{L^{\infty }(0,T)})$ is fixed. By Lemma 5, there exist constant $C_{0}$ independent of $e_{1}(t)$, $u(h,N,\Vert e_{1}\Vert _{L^{\infty }(0,T)})$, N and h such that

$$\begin{aligned} \begin{aligned} \Vert e_{1}\Vert _{L^{\infty }(0,T)}\le C_{0}u(h,N,\Vert e_{1}\Vert _{L^{\infty }(0,T)}). \end{aligned} \end{aligned}$$

(66)

We can choose sufficiently small h and sufficiently large N such that

$$\begin{aligned} C_{0}\widehat{C}(h,N)<\frac{1}{2}. \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} \Vert e_{1}\Vert _{L^{\infty }(0,T)}&\le C_{0}u(h,N,\Vert e_{1}\Vert _{L^{\infty }(0,T)}) \\&<\frac{1}{2}\Vert e_{1}\Vert _{L^{\infty }(0,T)} +C_{0}h^{m}N^{-m}\widehat{K}\Vert y\Vert _{L^{\infty }(0,T)}\\&\quad + C_{0}h^{m}N^{(1/2)-m}\Vert \partial ^{m+1}_{t}y\Vert _{L^{\infty }(0,T)}, \end{aligned} \end{aligned}$$

(67)

which leads to that

$$\begin{aligned} \begin{aligned} \Vert e_{1}\Vert _{L^{\infty }(0,T)}\le Ch^{m}N^{(1/2)-m}[\widehat{K}\Vert y\Vert _{L^{\infty }(0,T)}+ \Vert \partial ^{m+1}_{t}y\Vert _{L^{\infty }(0,T)}]. \end{aligned} \end{aligned}$$

(68)

This is (47) for $e_{1}$. By the relation $\Vert e_{0}\Vert _{L^{\infty }(0,T)}\le T\Vert e_{1}\Vert _{L^{\infty }(0,T)}$ we obtain (47) for $e_{0}$. $\square$

6 Numerical experiments

In this section we carry out numerical experiments to confirm theoretical results obtained in Sect. 5.

Example 1

Consider VIDEs

$$\begin{aligned} \begin{aligned}&y'(t)=e^{t}(1-\sin t-t)+(\sin t) y(t)+\int _{0}^{t}e^{t-s}y(s)ds,\quad t\in [0,2], \\&y(0)=1. \end{aligned} \end{aligned}$$

(69)

The corresponding solution is $y(t)=e^{t},t\in [0,2]$.

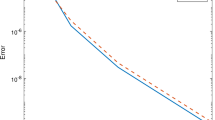
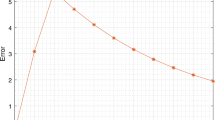
This example is provided to investigate effect of N and 1 / h on the delay of errors. Tables 1 and 2 list errors versus N and h. Figures 1 and 2 plot the behavior of decaying errors. We can see from Figs. 1 and 2 that refining mesh and employing more collocation points will enhance the precision of the numerical solution. This confirms theoretical results.

Table 1 Example 1: errors versus N with $h=1$

Table 2 Example 1: errors versus 1 / h with $N=3$

Fig. 1

Example 1: error versus N with $h=1$

Fig. 2

Example 1: errors versus 1 / h with $N=3$

The following numerical example is provided to underline the role of m in the performance of decaying errors.

Example 2

Consider VIDEs

$$\begin{aligned} \begin{aligned} y'(t)&=\left( m+\frac{1}{2}\right) t^{m-\frac{1}{2}}-t^{m+\frac{1}{2}}\sin t-\frac{1}{2m+2}t^{2m+2}+\sin t y(t)\\&\quad +\int _{0}^{t}s^{m+\frac{1}{2}}y(s)ds,\quad t\in [0,2],\\ y(0)&=0. \end{aligned} \end{aligned}$$

(70)

The corresponding solution is $y(t)=t^{m+\frac{1}{2}},t\in [0,2]$

It is worth noting that the kernel function is $K(t,s)=s^{m+\frac{1}{2}}$ whose derivative of $m+1$ order is singular at $s=0$. Tables 3 and 4 display errors versus N and 1 / h for $m=1,3$. The corresponding performance of errors are plotted in Figs. 3 and 4 from which we can see that errors decay faster if m is larger. This result is consistent with theoretical results.

Table 3 Example 2: errors versus N with $h=1$

Table 4 Example 2: errors versus 1 / h with $N=3$

Fig. 3

Example 2: errors versus N with $h=1$

Fig. 4

Example 2: errors versus 1 / h with $N=3$

Example 3

Consider VIDEs

$$\begin{aligned} \begin{aligned} y'(t)&=\cos t-\frac{1}{2}\sin 2t+\frac{\sin t}{4}(\cos 2t-1)-\frac{\cos t}{2}\left( t-\frac{1}{2}\sin 2t\right) \\&\quad +\cos ty(t)+\int _{0}^{t}\sin (t+s)y(s)ds,\quad t\in [0,T],\\ y(0)&=0. \end{aligned} \end{aligned}$$

(71)

The corresponding solution is $y(t)=\sin t,t\in [0,T]$

From (47) we know that $\widehat{K}$, $\Vert y\Vert _{L^{\infty }(0,T)}$ and $\Vert \partial ^{m+1}_{t}y\Vert _{L^{\infty }(0,T)}$ will become larger if T becomes larger. This implies that a large T goes against the decay of errors. Example 3 is provide to investigate the effect of T on the decay of errors. By the way, we compare the multi-step spectral collocation method with global spectral collocation method provided that T changes from 1 to 20. For the global method (h $=$ T/2), we let the number of collocation points in interval [0, T] be 11T. For the multi-step method (h $=$ 1/2), we let the number of collocation points in subinterval $[\mu ,\mu +1]$ be 11, which implies that the number of collocation points on interval [0, T] is 11T. Our goal in doing so is to maintain the same number (11T) of collocation points in interval [0, T] for both methods. The errors and time cost versus T are listed in Table 5. The performance of errors along with the change of T is plotted in Fig. 5 which shows that for both methods errors increase as T increases. This agrees with the theoretical result (47) in which $\widehat{K}$ and $\Vert \partial ^{m+1}_{t}y\Vert _{L^{\infty }(0,T)}$ increase as T increases. The behavior of time costs versus T for both method is plotted in Fig. 6 from which we can see that the multi-step method performs better than global method including global Legendre spectral collocation method.

Fig. 5

Example 3: errors versus T

Fig. 6

Example 3: time cost versus T

Table 5 Example 3: errors and time cost (seconds) versus T

For nonlinear VIDEs of the following form

$$\begin{aligned} \begin{aligned} y'(t)&=G(t,y(t))+\int _{0}^{t}K(t,s,y(s))ds, \\ y(0)&=y_{0}. \end{aligned} \end{aligned}$$

(72)

we can also design a numerical scheme similar to the linear case

$$\begin{aligned} y'^{\mu }_{i}= & {} G(t_{i}^{\mu },Y(t_{i}^{\mu }))+\sum _{r=0}^{\mu -1}h_{r}\sum _{k=0}^{N}K(t_{i}^{\mu },s_{r}(v_{k}),Y(s_{r}(v_{k})))w_{k}\\&+\frac{x_{i}+1}{2}h_{\mu }\sum _{k=0}^{N}K (t_{i}^{\mu },s_{\mu }(s(x_{i},v_{k})),Y(s_{\mu }(s(x_{i},v_{k}))))w_{k},\\ Y(t)= & {} y(0)+\sum _{r=0}^{\mu -1}h_{r}\sum _{j=0}^{N}y'^{r}_{j}\sum _{k=0}^{N} F_{j}(v_{k})w_{k}\\&+\frac{x(t)+1}{2}h_{\mu }\sum _{j=0}^{N}y'^{\mu }_{j}\sum _{k=0}^{N}F_{j} (s(x(t),v_{k}))w_{k},\\ i= & {} 0,1,\ldots ,N;\mu =0,1,\ldots ,M. \end{aligned}$$

Example 4

Consider nonlinear VIDEs

$$\begin{aligned} \begin{aligned} y'(t)&=-\frac{2}{3}\cos t+\cos ^{2} t+\cos ^{3} t-\frac{1}{3}(\cos ^{4}t+\sin ^{4}t)\\&\quad +\cos t y^{2}(t)+\int _{0}^{t}\sin (t+s)y^{2}(s)ds,\quad t\in [0,2],\\ y(0)&=0. \end{aligned} \end{aligned}$$

(73)

The corresponding solution is $y(t)=\sin t,t\in [0,2]$

Table 6 Example 4: errors versus N with $h=1$

Table 7 Example 4: errors versus 1 / h with $N=3$

Fig. 7

Example 4: errors versus N with $h=1$

Fig. 8

Example 4: errors versus 1 / h with $N=3$

Errors versus N and 1 / h are listed in Tables 6 and 7. The behavior of decay errors is plotted in Figs. 7 and 8 from which we can see that errors decay at power type. This shows that our method can handle the nonlinear VIDEs.

7 Conclusion and future work

We investigate multi-step Chebyshev spectral collocation method for Volterra integro-differential equations. We discuss existence and uniqueness of corresponding discrete system. We provide convergence analysis for proposed method. Numerical experiments are carried out to confirm theoretical results.

Our future work will focus on multi-step Chebyshev spectral collocation method for Volterra type integral equations with non-vanishing delay and partial Volterra integro-differential equations.