Introduction

Whenever we randomly sample sexually reproducing populations, we find correlations between the phenotypic values of traits: individuals that are similar in one respect (e.g. size) are also similar in others (e.g. speed). Phenotypic correlations can result from (1) simultaneous selection on multiple traits; (2) genetic interactions (e.g. pleiotropy, linkage disequilibrium), whereby selection on one trait results in concurrent changes in a linked trait (Lande 1984); and (3) environmental effects, whereby local environments influence the expression of phenotypically plastic traits (Via and Lande 1985). By determining the relative contributions of genetic versus environmental factors responsible for phenotypic correlations, we can clarify which traits are the potential targets of selection (Lande 1984; Via and Lande 1985).

For many traits, variation within a population seems likely to convey a fitness advantage to some individuals. One trait that has attracted considerable attention in studies of birds and mammals is learning ability. The ability to quickly and effectively adapt individual behaviour to meet ecological challenges may provide a selective advantage (Shettleworth 2001). For example, blue tits learn to synchronize their nesting period to coincide with peak caterpillar biomass based on previous foraging experience, and this matching enhances the condition and survival probability of their offspring and increases maternal fitness (Grieco et al. 2002). In contrast, the limited studies of Darwinian fitness in reptiles have focused primarily on the effects of variation in body size and athletic performance (Janzen 1993; Le Galliard et al. 2004). No studies have assessed whether variation in cognitive traits, such as learning ability, might also influence fitness in reptiles. In laboratory and semi-natural field experiments, reptiles use a diverse range of learning mechanisms to accomplish fitness-critical tasks, such as food location, predator avoidance and courtship behaviour (Burghardt 1977; Noble et al. 2012; Leal and Powell 2012; Wilkinson and Huber 2012). Therefore, individuals with greater learning ability might well have greater Darwinian fitness.

Positive correlations between phenotypic traits make it difficult to determine which trait(s) actually affects fitness. This may be especially relevant in reptiles, where a substantial literature demonstrates that incubation temperature influences the phenotypic expression of several morphological, physiological and behavioural traits (Deeming 2004). Recent research suggests that incubation temperature may also influence learning ability in reptiles. In a preliminary study, Amiel and Shine (2012) found that B. duperreyi incubated under different temperature regimes varied in their ability to learn the location of a safe refuge during a simulated predator attack. Incubation temperature is also known to influence the size and speed of hatchling B. duperreyi, although Amiel and Shine (2012) did not record significant correlations between learning ability and any morphological or performance traits in their lizard cohort. If incubation temperature does in fact influence learning ability in reptiles, then it may also produce positive correlations between learning ability and other traits. Such correlations would make it difficult to determine how learning ability contributes to Darwinian fitness in reptiles.

In the present study, we document high correlations between learning ability, body size and running speed within a cohort of young scincid lizards and suggest that environmental effects (incubation conditions) are responsible for these correlations.

Materials and methods

Egg collection and incubation

Three-lined skinks (Bassiana duperreyi) are oviparous montane lizards that are widely distributed in south-eastern Australia (Dubey and Shine 2010). Nests of this species are found over a large range of elevations, and eggs are naturally exposed to a wide range of incubation regimes. We collected B. duperreyi eggs from field sites at five different elevations (1060, 1080, 1240, 1615 and 1700 MASL) in the Brindabella Range, 40 km west of Canberra in the Australian Capital Territory. B. duperreyi lay their eggs in soft soil under loose rocks that serve as communal nesting sites. Oviposition usually occurs in early December and is highly synchronous (Elphick and Shine 1998), allowing us to time our fieldwork to coincide with egg-laying. We sampled nests every 2 weeks, beginning in late November when there were no eggs present. As a result, we know that the eggs we collected were laid no more than 14 days prior to collection.

Eggs were removed from natural nests and placed into 70-mL plastic jars filled with moist vermiculite (water potential = −200 kPa) for transport to the University of Sydney. Prior to incubation, we weighed each egg and transferred it to its own 64-mL glass jar filled with moist vermiculite (−200 kPa). Jars were covered with plastic wrap to prevent moisture loss. We randomly divided eggs from each nest among four 10-step Clayson incubators (Brisbane, Queensland, AUS). Two incubators were programmed to mimic ‘hot’ natural nest conditions (diel cycle of 24 ± 5 °C) and two were programmed to mimic ‘cold’ conditions (diel cycle of 18 ± 5 °C). We based these thermal regimes on temperature data collected from over 300 natural B. duperreyi nests as part of a long-term study of phenotypic plasticity in this species (Shine et al. 1997). We monitored incubator temperatures using iButton thermochrons (Dallas, Texas, USA).

Overall, we incubated 609 eggs from 34 nests containing 4–77 eggs (X + SE = 18.64 + 2.83 eggs), with roughly equal numbers of eggs collected from all 5 sites. A subset of 18 ‘hot’ (n = 10 males and n = 8 females) and 21 ‘cold’ (n = 9 males and n = 12 females) eggs was used for the present study. In an attempt to reduce the number of full and half-siblings in this experiment, we selected roughly equal numbers of eggs from each of the five elevations (9 eggs from 1700 MASL; 9 eggs from 1650 MASL; 7 eggs from 1240 MASL; 8 eggs from 1080 MASL; and 6 eggs from 1060 MASL). However, some of these eggs came from the same communal nests and we cannot rule out the possibility that some of our lizards may have had common parents.

Upon hatching, we recorded each lizard’s snout-vent length (SVL) and total length (including tail) using a transparent plastic ruler. We recorded each lizard’s mass using a Sartorius top-loading balance (Goettingen, GER), accurate to ±0.01 g. To determine individual sex, we manually applied pressure to the tailbase and recorded the presence or absence of hemipenes (Harlow 1996). To record individual running speed, we used a one metre wooden racetrack fitted with infrared photocells every 25 cm (Elphick and Shine 1998). We placed lizards in a holding area before they were released. They were then allowed to run down the racetrack. A researcher ‘chased’ the hatchling down the racetrack with an artist’s paintbrush to simulate a predatory attack, encouraging the hatchling to run at top speed and only making gentle physical contact to stimulate running if the lizard stopped during a trial. We recorded speed (m/s) as 1 m divided by the cumulative time it took a lizard to cross the final infrared beam. We ran each lizard three times at 27 °C and took the average of the three runs as the lizard’s final speed. A single researcher conducted all running trials in order to prevent researcher bias.

Lizard husbandry and maintenance

When lizards were not being tested, they were housed in communal plastic bins (64 × 41 × 21 cm) with sand substrate (maximum 10 hatchlings per bin). We used communal housing because studies in other vertebrate taxa show that social isolation negatively impacts learning ability (Wongwitdecha and Alexander Marsden 1996). Plastic flowerpot trays and PVC tubing provided environmental enrichment, as well as refuges. We provided the lizards with a 10:14-h light : dark cycle, 27 °C:22 °C day:night thermal regime, ad libitum access to water, and daily food.

Learning task

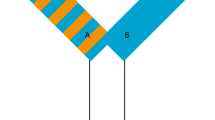
It was our aim to use an experimental paradigm that would produce results comparable to previous cognition studies, and simple Y- and T-mazes are among the most established methods of assessing learning ability in reptiles (Burghardt 1977; Macphail 1982; Wilkinson and Huber 2012). Therefore, to assess learning ability in B. duperreyi, we used Y-mazes with three 33 × 10 × 5 cm arms and a central decision point (Fig. 1). We constructed the mazes from opaque U-shaped electrical conduit (Tripac Distribution Pty Ltd, Sydney, New South Wales, AUS) fitted with clear plastic lids. In each maze, one arm was empty, while the other two arms contained identical wooden platforms, each with a single plastic feeding well. To provide the lizards with local cues during testing, we painted the arms containing the wooden platforms with contrasting colours (blue and orange) and patterns (striped or solid). Replication and reversal of all colour–pattern combinations allowed us to control for colour biases in our lizards.

Fig. 1
figure 1

Graphic representation of one of the Y-mazes we used to determine learning ability in hatchling B. duperreyi. Each maze had three arms of equal length. Two maze arms were painted with contrasting colours (orange and blue) and patterns (stripes and solids) to provide visual cues. All colour–pattern combinations were replicated and reversed in our study (four mazes total). Two arms contained feeding wells (A and B), whereas the third arm was empty and designated as the starting position for each trial (C). There was also a central decision point (D) we used to determine turning errors

Full size image

Previous studies have demonstrated that lizards can use different learning mechanisms (e.g. associative or spatial learning) to complete goal-oriented behavioural tasks (Wilkinson and Huber 2012). In the present study, we were not interested in which learning mechanism the lizards were using to locate their food reward. Rather, we were interested in the ability of the lizards to consistently improve their ability to solve a behavioural task (i.e. to learn the location of the food reward). This is because, for hatchling lizards, the ability to efficiently learn a novel behavioural task is likely to be biologically significant, regardless of the mechanism they use to achieve the goal. For example, hatchlings that learn the most direct route to a shelter increase their chances of surviving a predatory attack. It does not matter whether the hatchlings learn to locate the shelter using spatial location or visual cues, as long as they can reliably locate the shelter during an attack. Thus, we provided lizards with several different cues to help them navigate the maze (Day et al. 1999), including local colour cues (orange and blue, which are highly contrasting), local pattern cues (striped and solid) and external visual cues (the location of the mazes in the room remained constant and the lizards could navigate using objects outside of the maze). The lizards could have been using any combination of these cues to locate their reward. Lizards are also able to locate prey by flicking their tongues to sample chemical cues in the air (Cooper 1994). We attempted to control for such cues by coating each of the feeding wells with cricket scent prior to each trial and cleaning the maze floors with diluted (70 %) ethanol between trials.

Learning trials began 10 days after hatching, as soon as lizards were consistently eating crickets (Acheta domesticus). Learning trials ran for 15 consecutive days with each lizard completing one trial per day. For each lizard, the maze colour–pattern combination and the feeding well (left or right) were assigned prior to the first trial and remained consistent throughout all 15 trials. To start a learning trial, we inserted a food reward (one cricket) into the designated feeding well and then placed the lizard in the empty arm of the maze. We recorded how long it took the lizard to locate and consume the food reward and how many turning errors it made in each trial, using overhead surveillance cameras (Aucom Security, Bundoora, VIC, Australia). An error was recorded every time the lizard entered the decision point and turned away from the reward arm (Fig. 1). After 20 min, any lizard that had not located its reward was then placed on the correct feeding well and offered a cricket with forceps. To standardize hunger levels, we withheld food for 24 h prior to the first trial and provided one cricket per day thereafter. We restricted the hatchlings’ diets to crickets only so that they could not develop preferences for different food items, and thus, crickets should have equally motivated them all to complete the task. We tested all lizards at 27 °C ambient temperature. The same researcher scored all of the learning trials in order to avoid researcher bias.

Upon completion of the learning task, we released the lizards at their egg collection sites. All lizards were in good health and free of visible parasites upon release. All research was carried out under University of Sydney animal care protocol L04/12-2010/3/5449.

Learning metrics

Using a simple Y-maze design, animals demonstrate learning by (1) reducing the amount of time it takes to locate a reward and (2) progressively taking a more direct route to the reward over successive trials. Therefore, we used two learning metrics to assess differences in the rate of learning between lizards from our ‘hot’ and ‘cold’ incubation treatments. First, we assigned each hatchling a learning score based on the rate its probability of success within a trial increased over the 15 trials (henceforth referred to as ‘learning as success’). Here, we defined a successful trial as one where the hatchling located the food reward while making no turning errors (i.e. took the most direct route to the reward). We recorded all other scenarios (i.e. making at least one turning error and/or failing to locate the food) as failures, regardless of whether the hatchling eventually located the food reward. Thus, an increase in an individual’s probability of success over the 15 trials suggests that the hatchling progressively took a more direct route to the food reward. Second, we assigned each hatchling a learning score based on the rate it decreased its time to locate the food reward over the 15 trials (henceforth referred to as ‘learning as time’). The learning score is based on the rate at which time to locate food decreases with number of trials and is estimated in a hierarchical Bayesian framework as described below.

Two issues to consider when using metrics such as these are variability between individuals and parameter uncertainty. Within each incubation treatment, we may expect to find both fast and slow learners; yet, for either learning metric, there will be some uncertainty in the rate that each individual learns due to the unpredictable nature of hatchling behaviour in each trial. For example, a slow learner may be successful in individual trials with some probability, whereas a fast learner might not successfully complete every trial. Hierarchical Bayesian modelling is an ideal framework for addressing these issues because we can estimate group-level parameters, while accounting for the uncertainty in learning ability at the individual level. That is, learning ability is an individual parameter modelled as coming from a group-level distribution, and we estimate joint posterior distributions for parameters at both individual and group levels.

Measuring ‘learning as success’ in hatchlings

For each individual, we assumed that the probability \(p_{t,i}\) of success in trial t for individual i is given by

$$p_{t,i} = K\frac{1}{{1 + e^{{ - [\alpha_{i} + (t - 1)\beta_{i} ]}} }}$$
(1)

where α i models initial probability of success and β i models the change in success probability with number of trials. Both α i and β i are defined on the range [−∞, ∞]. For K = 1, Eq. 1 is a standard logistic regression function and K, defined on the range [0, 1] and modelling the maximum success rate, is included in the model because we did not expect that the success rate necessarily approaches one with the number of trials. In order to obtain a single, easily interpretable measure of learning, we modelled parameter K as a common parameter for all individuals and learning is expressed through β i , interpreted as a measure of the rate that individual i approaches K, with β i  > 0 indicating learning.

We define s t,i  = 1 if trial t of individual i was a success (otherwise s t,i  = 0), the likelihood is specified as

$$f_{1} ({\boldsymbol{s}}_{i} |\alpha_{i} ,\beta_{i} ,k) = \prod\limits_{t = 1}^{T} {{\text{Bernoulli}}(s_{t,i} |p_{t,i}}) ,$$
(2)

where s i denotes all T trials of individual I and p t,i is given by Eq. 1.

Measuring ‘learning as time’ in hatchlings

Because time to locate food is inherently positive, we modelled log-time and denote the logarithm of the time for individual i to locate the food in trial t as τ t,i , with τ i  = τ t,1, τ t,2,…,τ t,T , and define the likelihood of all T trials for individual i as

$$f_{2} (\tau_{i} |\gamma_{i} ,\delta_{i} ,\sigma_{\tau }^{2} ) = \prod\limits_{t = 1}^{T} {{\text{Normal (}}\tau_{t,i} |y,\sigma_{\tau }^{2} )} ,$$
(3)

where \(y = \gamma_{i} - (t - 1)\delta_{i} ,\) i.e., y is a linear function with intercept γ i and negative slope δ i . Parameter δ i is interpreted as a measurement of learning for individual i with positive values indicating learning. Residuals around y are expressed through \(\sigma_{\tau }^{2}\), and in order to reduce the number of parameters in the analysis, we made this a common parameter for all individuals.

Speed and body size in hatchlings

There is also uncertainty in our measure of hatchling run speeds, as these are based on three separate trials, Q = 3. For each individual i, we denote \(v_{q,i}\) as the speed measured in trial q and v i as the result of all Q races. We define the likelihood of all trials of individual i as

$$g(v_{i} |u_{i} ,k) = \prod\limits_{q = 1}^{Q} {{\text{Gamma (}}v_{q,i} |\theta ,k ) ,}$$

where scale parameter \(\theta = e^{{u_{i} }} /k\), and shape parameter k is modelled as a shared parameter between all individuals in the analysis.

Body size was measured by a single estimate per individual and uncertainty is not of particular concern. We define z i as the total length of individual i, given in log (mm).

Group-level models

Learning at the individual level was modelled either by ‘learning as success’ or ‘learning as time’ for each hatchling using two different models; yet, at the group level, the corresponding models have the same structure. For notation, we define l i as the learning measure of individual i and μ l as the group mean learning ability, with l i  = β i , μ l  = μ β , when we refer to learning as increased probability of success, and l i  = δ i , μ l  = μ β , when we refer to learning as decreased time to locate the food. The intercepts, α i or γ i , also have similar interpretation between the models, and we use ω i when referring to either learning metric or μ ω when referring to the group mean intercept. At the group level, intercepts were modelled by a normal distribution with mean μ ω and variance \(\sigma_{\omega }^{2}\), i.e., \(\omega_{i} \sim {\text{Normal(}}\mu_{\omega } ,\sigma_{\omega }^{2} ).\)

Because we were interested in correlations between learning, body size and speed, we modelled the group-level distribution of l i , z i and u i by a multivariate normal distribution (denoted MVN) with mean \({\boldsymbol{M}} = [\mu_{l} ,\mu_{z} ,\mu_{u}]\) and covariance Σ. In order to obtain posterior distributions of correlations and facilitate prior elicitation, we follow the separation strategy suggested by Gelman et al. (2004), whereby the covariance is split into correlations and standard deviations by Σ = SRS, with

$${\boldsymbol{R}} = \left[{\begin{array}{*{20}c} 1 & {R_{l,z} } & {R_{l,u} } \\ {R_{l,z} } & 1 & {R_{z,u} } \\ {R_{l,u} } & {R_{z,u} } & 1 \\ \end{array} } \right],\quad {\boldsymbol{S}} = \left[ {\begin{array}{*{20}c} {\sigma_{l} } & 0 & 0 \\ 0 & {\sigma_{z} } & 0 \\ 0 & 0 & {\sigma_{u} } \\ \end{array} } \right].$$

Here, \(R_{l,z} ,R_{l,u}\) and \(R_{z,u}\) are the coefficients of correlation between learning and body size, learning and speed, and body size and speed, respectively, and \(\sigma_{l} ,\sigma_{z}\) and \(\sigma_{u}\) are the corresponding residual standard deviations.

We wanted to compare the overall predicted correlations among these three traits (all hatchlings combined) with the predicted correlations within each incubation treatment (separate means for each treatment). This requires specifying slightly different models.

Incubation treatments combined, models 1 and 2

Denoting all data by \({\boldsymbol{D}} = [s_{1} ,s_{2} , \ldots ,s_{N} ,v_{1} ,v_{2} , \ldots ,v_{N} ,z_{1} ,z_{2} , \ldots ,z_{N} ],\) where N is the number of individuals in the study, the full Bayesian model for learning measured by success rate with the incubation treatment groups combined is written as

$$\begin{gathered} {\text{Model 1:}}P ({\boldsymbol{\alpha}},{\boldsymbol{\beta}},{\boldsymbol{u}},K,k,{\boldsymbol{M}},{\boldsymbol{\Sigma}},\mu_{\alpha } ,\sigma_{\alpha }^{2} |{\boldsymbol{D}} )\\ \alpha \left[ {\prod\limits_{i}^{N} {\left\{ {f_{1} \left( {\boldsymbol{S}}_{i} |\alpha_{i} ,\beta_{i} ,K)g(v_{i} |u_{i} ,k) \right)} \right\}} {\text{MVN}}([\beta_{i} ,u_{i} ,z_{i}]|{\boldsymbol{M}},{\boldsymbol{\Sigma}}) {\text{Normal (}}\alpha_{i} |\mu_{\alpha } ,\sigma_{\alpha }^{2} )} \right] \\ P(\mu_{\alpha } )P(\sigma_{\alpha }^{2} )P(K)P(k)P({\boldsymbol{M}})P({\boldsymbol{\Sigma}})\\ \end{gathered}$$

where \({\boldsymbol{\alpha}}= [\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{N} ],{\boldsymbol{\beta}}= [\beta_{1} ,\beta_{2} , \ldots ,\beta_{N} ],{\boldsymbol{u}} = [u_{1} ,u_{2} , \ldots ,u_{N} ]\) and \(P(\mu_{\alpha } )P(\sigma_{\alpha }^{2} )P(K)P(k)P({\boldsymbol{M}})P({\boldsymbol{\Sigma}})\) indicate priors.

For the equivalent model for learning measured by time to locate food, all data are instead denoted by \({\boldsymbol{D}} = [\tau_{1} ,\tau_{2} , \ldots ,\tau_{N},v_{1} ,v_{2} , \ldots ,v_{N},z_{1} ,z_{2} , \ldots ,z_{N} ]\) and the model is similarly written as

$$\begin{gathered} {\text{Model 2:}}P ({\boldsymbol{\gamma}},{\boldsymbol{\delta}},{\boldsymbol{u}},\sigma_{\tau }^{2} ,k,{\boldsymbol{M}},{\boldsymbol{\Sigma}},\mu_{\gamma } ,\sigma_{\gamma }^{2} |{\boldsymbol{D}})\\ \alpha \left[ {\prod\limits_{i}^{N} {\left\{ {f_{2} \left( {\tau_{t,i} |\gamma_{i} ,\delta_{i} ,\sigma_{\tau }^{2} } \right)g(v_{i} |u_{i} ,k)} \right\}} {\text{ MVN([}}\delta_{i} ,u_{i} ,z_{i} ]|{\boldsymbol{M}},{\boldsymbol{\Sigma}}) {\text{Normal }}\left( {\gamma_{i} |\mu_{\gamma } ,\sigma_{\gamma }^{2} } \right)} \right]\\ P(\mu_{\gamma } )P(\sigma_{\gamma }^{2} )P(\sigma_{\tau }^{2} )P(k)P({\boldsymbol{M}})P({\boldsymbol{\Sigma}})\\ \end{gathered}$$

where \({\boldsymbol{\gamma}}= [\gamma_{1} ,\gamma_{2} , \ldots ,\gamma_{N} ]\) and \({\boldsymbol{\delta}}= [\delta_{1} ,\delta_{2} , \ldots ,\delta_{N} ]\).

Incubation treatments separated, models 3 and 4

When including the effect of incubation treatment, we modelled the group-specific mean of M and μ ω , and when required, we denote groups with index j (i.e. M j and μ ω,j , where j = 1 refers to ‘hot’ treatment, and j = 2 to ‘cold’ treatment). Our main interest is differences M j , specifically mean learning ability as defined by either μ l,j  = μ β,j or μ l,j  = μ δ,j , and we may say that hot incubation group are better learners if μ l,1 > μ l,2. Also of interest are potential differences in intercept μ ω,j , which may indicate differences in initial performance. In order to obtain more precise estimates of these parameters of interest and to facilitate straightforward interpretation of the results, other parameters were modelled as shared between the groups. We also use notation N j to refer to the number of individuals in each group (N 1 = 18 and N 2 = 21) and the total number of trials per individual as T = 15.

The model for learning measured by success rate is then written as

$$\begin{gathered} {\text{Model 3:}}P ({\boldsymbol{\alpha}},{\boldsymbol{\beta}},{\boldsymbol{u}},K,k,{\boldsymbol{M}}_{1} ,{\boldsymbol{M}}_{2} ,{\boldsymbol{\Sigma}},\mu_{\alpha ,1} ,\mu_{\alpha ,2} \sigma_{\alpha }^{2} |{\boldsymbol{D}})\\ \alpha \prod\limits_{j = 1}^{2} {\left\{ {\left[ {\prod\limits_{i}^{{N_{1} }} {\left\{ {f_{1} \left({{\boldsymbol{S}}_{i} |\alpha_{i} ,\beta_{i} ,K)g(v_{i} |u_{i} ,k)} \right)} \right\}} {\text{MVN([}}\beta_{i} ,u_{i} ,z_{i} ]|{\boldsymbol{M}}_{j} ,{\boldsymbol{\Sigma}}) {\text{Normal (}}\alpha_{i} |\mu_{\alpha ,j} ,\sigma_{\alpha }^{2} )} \right]P(\mu_{\alpha ,j} )P({\boldsymbol{M}}_{{\boldsymbol{j}}} )} \right\}}\\ P(\sigma_{\alpha }^{2} )P(K)P(k)({\boldsymbol{\Sigma}}),\\ \end{gathered}$$

and the corresponding model for learning defined by time to locate food is written as

$$\begin{gathered} {\text{Model 4:}}P ({\boldsymbol{\gamma}},{\boldsymbol{\delta}},{\boldsymbol{u}},\sigma_{\tau }^{2} ,k,{\boldsymbol{M}},{\boldsymbol{\Sigma}},\mu_{\gamma } ,\sigma_{\gamma }^{2} |{\boldsymbol{D}} )\\ \alpha \prod\limits_{j = 1}^{2} {\left\{ {\left[ {\prod\limits_{i}^{{N_{1} }} {\left\{ {f_{2} \left( {\tau_{t,i} |\gamma_{i} ,\delta_{i} ,\sigma_{\tau }^{2} )g(v_{i} |u_{i} ,k)} \right)} \right\}} {\text{MVN([}}\delta_{i} ,u_{i} ,z_{i} ]|{\boldsymbol{M}}_{j} ,{\boldsymbol{\Sigma}}){\text{Normal(}}\gamma_{i} |\mu_{\gamma ,j} ,\sigma_{\gamma }^{2} )} \right]P(\mu_{\gamma ,j} )P({\boldsymbol{M}}_{{\boldsymbol{j}}} )} \right\}}\\ P(\sigma_{\gamma }^{2} )P(\sigma_{\tau }^{2} )P(k)P({\boldsymbol{\Sigma}}),\\ \end{gathered}$$

Bayesian inference involves specifying prior beliefs of parameters. Here, we use vague priors, hence making inference based mainly on the data. Prior elicitation is described in detail in Appendix A.1.1 (ESM). All parameters were estimated using Markov Chain Monte Carlo (MCMC), which involves constructing a Markov chain whose limiting distribution represents the posterior distribution of interest (see e.g. Gamerman and Lopes 2006). The MCMC algorithm is described in Appendix A.2. (ESM).

Posterior predictive probabilities

In two instances, we were particularly interested in obtaining probability statements to support claims about differences in parameters. First, for models 3 and 4, we wanted to know the probability that ‘hot’ treatment hatchlings learned faster than ‘cold’ treatment hatchlings, i.e., μ l,1 > μ l,2. Second, we were interested in the probability that separating individuals by incubation treatment reduces the correlation coefficients \(R_{l,z} ,R_{l,u}\) and \(R_{z,u}\). We therefore computed the posterior predictive probability of these statements, technically as the proportion of iterations of the MCMC that satisfy the specified conditions. Because we are estimating these group-level parameters in an hierarchical Bayesian framework, uncertainty about individual measures is incorporated in our probability statements.

Results

Differences in size and speed—Marginal posterior estimates (presented by median and 95 % central credibility intervals in brackets) of mean body size, given in log mm, were estimated at 4.04 [4.02, 4.06] and 3.97 [3.95, 3.99] for the ‘hot’ and ‘cold’ treatments, respectively, indicating that individuals in the ‘hot’ treatment group were larger than those in the ‘cold’ treatment. The marginal posterior estimates of mean speed, given in logarithm of average speed in m/s, were estimated at −0.92 [−0.99, −0.85] and −1.29 [−1.35, −1.22] for the ‘hot’ and ‘cold’ treatments, respectively, indicating faster individuals in the ‘hot’ treatment group. Estimates of size and speed for each hatchling were identical in all models.

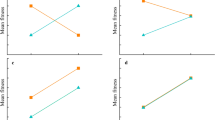
Differences in learning ability—Fig. 2 plots the mean success rate and mean log-time to locate the reward for each incubation group in every trial. Hatchlings from both the ‘hot’ and ‘cold’ incubation treatments increased their probability of successfully completing a trial and decreased their time to locate the food reward across the 15 trials. This change strongly suggests that hatchlings from both incubation treatments were capable of learning the maze task, but ‘hot’ individuals learned much more rapidly than ‘cold’ individuals. All hatchlings that did not successfully locate the food reward during the trial period readily ate when we offered them a cricket with forceps, suggesting that unsuccessful hatchlings were hungry and motivated to eat. Figure 3 plots the marginal distribution of mean learning ability (μ β,j or μ δ,j ) for each incubation treatment, using each learning metric (i.e. ‘learning as success’ and ‘learning as time’) from models 3 and 4. For the ‘hot’ treatment group, the distributions have most density above zero, providing strong evidence of learning. However, the distributions for the ‘cold’ treatment group are centred near zero, indicating little support for learning. We also computed the posterior predictive probability that the ‘hot’ treatment group learns faster than the ‘cold’ treatment group in models 3 and 4. This is estimated at ≫99 and 95 % for model 3 and 4, respectively, which indicates that no matter how we define learning; the ‘hot’ treatment group learned faster.

Fig. 2
figure 2

Left panel mean number of successful outcomes per trial for both the ‘hot’ (black dots) and ‘cold’ (grey dots) incubation treatments. The solid lines (corresponding to incubation treatment by colour) indicate the posterior predictive means, and the dashed lines indicate the corresponding 95 % central credibility interval. Right panel mean log-time to complete trials for both the ‘hot’ (black dots) and ‘cold’ (grey dots) treatments. The solid lines (corresponding to incubation treatment by colour) indicate the posterior predictive means, and the dashed lines indicate the corresponding 95 % central credibility interval

Full size image
Fig. 3
figure 3

Marginal posterior distributions of mean learning rate of B. duperreyi from ‘hot’ (solid) and ‘cold’ (dashed) incubation treatments, with learning defined either by time to locate food (left panel) or by increased probability of successfully locating the food reward (right panel). Positive values indicate support for learning (decreased time to locate food or increased success probability with the number of trials) and a value of zero indicates no learning

Full size image

A difference in intercept parameters would indicate differences in initial performance of the ‘hot’ and ‘cold’ incubation treatments. For example, ‘hot’ hatchlings may learn to locate their food faster because they are more active in the maze. The marginal posterior estimates of μ α,j (presented by median and 95 % central credibility intervals in brackets) were estimated at −2.7 [−4.2, −1.7] and −3.8 [−5.5, −2.5] for hot and cold treatment, respectively, and the corresponding estimate for μ γ,j at 7.0 [6.9, 7.1] and 7.1 [7.0, 7.2], respectively. The substantial overlap indicates no support for any initial differences in performance (Fig. 2).

Correlations between body size, running speed and learning ability—Figure 4 plots individual estimates of size, speed and learning against one another. Figure 5 plots the pairwise correlation coefficients between learning, body size and speed. When we combine data for all of the hatchlings (models 1 and 2, bottom row panels), the marginal posterior estimates are clearly above zero for both definitions of learning, indicating strong evidence for correlations. However, when we separate the hatchling into their incubation treatments (models 3 and 4, top panels), the distributions are consistently shifted downwards and generally show high posterior density below zero, indicating little or no support for correlations. We also computed the posterior predictive probability that the corresponding correlation coefficient is smaller in the model where groups are separated by incubation treatment. When learning is defined by time to locate food (comparing models 2 and 4), this probability was estimated at 95, 98 and 97 % for correlations between learning and size, learning and speed, and speed and size, respectively. The corresponding estimates when learning is defined by success probability (comparing models 1 and 3) are 87, 86 and 97 %, respectively.

Fig. 4
figure 4

Relationships between individual estimates of size, speed and learning ability, with grey and black indicating hatchlings from the cold and hot incubation treatments, respectively. For speed and learning, circles (cold treatment) or dots (hot treatment) indicate median of the marginal posterior estimates from Model 3 (‘learning as success’) and Model 4 (‘learning as time’), and error bars indicate the corresponding 95 % central credibility interval. Note that the speed and body size variables are consistent between models, and thus, the graphs of speed versus size produced by each model are identical (bottom two panels)

Full size image
Fig. 5
figure 5

Marginal posterior distributions of correlation coefficients between learning, size and speed for B. duperreyi. Left column shows results for models where learning is measured by time to locate food, and right column shows results for learning measured by success probability. The lower panels show results for analyses including all individuals as a single group, and the upper panels show results where the effect of treatment is removed by modelling group-specific means of lizards from ‘hot’ and ‘cold’ incubation

Full size image

Discussion

Overall, lizards that were larger were also faster and smarter (Fig. 4). However, the strong correlations estimated between body size, running speed and learning ability when we combined hatchlings from the ‘hot’ and ‘cold’ incubation treatments (models 1 and 2, Fig. 5, bottom row panels) largely disappeared when we removed the effect of incubation treatment (models 3 and 4, Fig. 5, top row panels). We found particularly strong evidence for this when we used ‘learning as time’ as the learning metric (probability estimated at 95, 98 and 97 % for correlation learning-size, learning-speed and speed-size, respectively). We found the same trend when we used ‘learning as success’ as the learning metric, though it had weaker support (probability estimated at 87, 86 and 97 %, respectively). However, because our models showed the same trends, regardless of the learning metric we used, we can confidently assert that the overall correlations were driven largely by the effect of incubation temperature on all three of these variables. This result means that ‘hot’ hatchlings were in general larger, faster and smarter than ‘cold’ hatchlings, resulting in a strong positive correlation between these traits when data from the two incubation treatments were combined. However, within either incubation treatment, there was no trend for larger individuals to be faster and/or smarter than smaller individuals. Our results suggest that incubation temperatures that optimized growth and locomotor speed also optimized cognitive function. In other words, larger lizards were faster and smarter because all three of these traits were consequences of their developmental history (i.e. they hatched from eggs that had been incubated at high temperatures), rather than because (for example) larger body size increases a lizard’s running speed or its intelligence, or because alleles for larger size are linked with alleles for faster learning or greater speed.

Note that the probability statements listed above refer to the probability that the correlation coefficients are lower in the separated models. Although we cannot conclude that there is no correlation in the separate models, we can say with some certainty that the correlation is lower than in the combined models. This approach is less sensitive to sample size than a frequentistic approach and avoids the erroneous conclusion that the lack of a significant correlation means that there is no correlation. Hence, the lower correlations found when separating the groups (models 3 and 4) are not merely the effect of lower sample size per group.

Our study further highlights the benefit of the hierarchical Bayesian framework when individual estimates are based on a limited number of trials. In our study, both speed and learning ability were assessed by repeated trials, and because of the somewhat unpredictable nature of animal behaviour, uncertainty at the individual level of these parameters becomes an issue. This can be seen in Fig. 4 where the error bars (indicating the 95 % central credibility interval of the marginal posterior of each individual parameter) are quite large. For example, within each group, there are some individuals that show strong support for learning (error bars do not overlap zero). This uncertainty about individual parameters is included in the estimates of group-level parameters and hence in the inference based on their posterior estimates. We thereby sidestep the random element that would follow from reliance upon a single point estimate at the individual level. With a larger number of trials per individual, this becomes less of an issue, but with, for instance, only three trials for speed, we cannot expect to have captured the average speed with sufficient accuracy.

In reptilian cognition studies, the problem of motivation is notoriously difficult to address (Burghardt 1977). When using food rewards, some individuals may perform better because they are hungrier or because they are more motivated by a particular reward. In the present study, we have attempted to control for motivation in four different ways. First, hatchlings were fed 3 crickets per day for 10 days prior to maze trials, enough time for all lizards to begin feeding consistently. We then withheld food for 24 h prior to the first maze trial and fed each lizard one cricket per day during trials to standardize hunger levels. This means that hatchlings should have been equally motivated to locate the food reward in the maze. Second, we offered hatchlings that failed to complete the maze task a single cricket after their trial time had expired. All hatchlings readily ate the crickets we offered them, suggesting that they were hungry but failed to locate the cricket in the maze. Third, we fed hatchlings crickets (and only crickets) for their entire lives in captivity, and we used the same prey type (crickets) as the only of food reward. This means that the hatchlings could not develop preferences for different food items and crickets should equally motivate them all (Balasko and Cabanac 1998). Fourth, all hatchlings were tested and maintained at the same temperatures during the experimental period so that baseline metabolic rates should have been similar (Angilletta 2001). Thus, we are confident that our results reveal actual differences in cognitive ability between B. duperreyi hatchlings from unique thermal regimes rather than differences in individual motivation.

Our results suggest a caveat to previous interpretations of the operation of natural selection. Several studies (including in lizards) have reported higher survival in individuals that are larger or faster than most of their cohort, thereby inferring selection on these traits (Janzen 1993; Irschick et al. 2005). Although we do not doubt that size and speed are sometimes important targets of selection, a high correlation between these two traits and learning ability (as shown in our study) raises the possibility that selection in such cases has worked on variation in learning ability rather than (or as well as) on size and speed. Faster learning could enhance fitness through its effects on resource acquisition or predator avoidance (Dukas 2004), and thus, selection may favour any number of underlying cognitive mechanisms associated with learning ability (e.g. attention, spatial memory, visual discrimination; Shettleworth 2009). Such effects might be important even if the effects of incubation temperature on learning ability are transitory. For precocial species with no parental care (including most reptiles), learning ability is likely to have the greatest impact on fitness during the hatchling stage, when juvenile animals are first learning to locate resources and escape predators (Burger 1998). However, incubation-induced effects also may persist for much of the animal’s life, as has been shown for size and locomotor ability in B. duperreyi (Elphick and Shine 1998). Unfortunately, almost no studies have assessed the adaptive significance of learning ability in the field (but see Thomas et al. 2001; Grieco et al. 2002).

Our study identifies oviparous ectotherms (such as most lizards) as ideal model systems for such research. Researchers may be able to separate cognitive traits from morphological and performance traits using established experimental manipulations during incubation (e.g. yolk removal (Warner and Shine 2007) or hormone applications (Radder et al. 2008)). They could then assess differences in cognitive abilities and use field studies to determine the relative importance of within-population variation in learning, body size and locomotor ability to individual survival and reproductive success (Warner and Shine 2007). Although such experiments are ethically impossible in humans, indirect evidence suggests an unexpected and intriguing parallel to our results in lizards. In humans, positive correlations between size, speed and learning may also be driven by phenotypically plastic responses to developmental conditions, rather than by underlying genetic variation (Samaras 2007; Tomporowski et al. 2008). More generally, analyses of phenotypic predictors of fitness within populations (a cornerstone of the Darwinian approach) might usefully be expanded to include cognitive traits. In many circumstances, an individual’s viability may depend more upon its behavioural flexibility than upon its size or speed.