Introduction

Landslide caused by slope failure has become one of the major geological disasters all over the world. The management of unfavorable geological slope has been one of the key scientific issues in the construction and operation of infrastructure in China. Slope safety evaluation is a significant prerequisite for geotechnical decision-making in landslide disaster prevention. The deterministic analysis with the factor of safety (FS) is still the most frequently employed method to evaluate the stability of the natural and engineered slopes (Chen et al. 2020a, b, c; Gao et al. 2019). At present, the most convenient method for calculating the slope safety of factor is the empirical chart method, and the numerical tools are widely employed to distinguish and visualize the failure modes of slopes under different conditions. Whatever method is adopted, it is necessary to consider the realistic properties and state of the slope soil comprehensively in order to obtain reliable results.

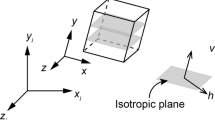
Due to the existence of lateral free surface and the unloading effect in slope, the stress redistribution is encountered of necessity. The stress state of soil body at different positions of slope is significantly discrepant, and the orientation of principal stress suffers various degrees of rotation (Fig. 1). The mechanical characteristic of soil which changed due to the varied stress states is termed the stress-induced anisotropy (Hu et al 2020; Li et al. 2021; Zhang et al. 2020; Li and Zhang 2020). Worldwide specialties have proposed many new constitutive models which are capable of featuring this soil anisotropic behavior for both granular and cohesive soil (Cudny and Staszewska 2021; Ghorbani and Alrey 2021; Ghorbani et al. 2021). Influenced by the stress-induced anisotropy, the dominant properties which have great impact on soil engineering behavior include the strength and stiffness (Hwang et al. 2002; Xu et al. 2021). Liu et al. (2021) investigated the qualitative relationships between principal stress directions and the anisotropic behavior, i.e., stress–strain development, after principal stress axis cycling. They concluded that the normalized strength of the remodeled loess nonlinearly decreases as the principal stress angle enlarges and reaches its lowest value when the principal stress angle is 90°. They further proposed the equations for calculating the anisotropic strength of loess under general stress condition. Zapata-Medina et al. (2020) evaluated the stiffness and strength anisotropy of some clay specimen from certain regions through a series of tests. They point out that for most overconsolidated clays, the stiffness anisotropy degree increases with the over consolidation ratio (OCR). And the failure friction angle under triaxial extension test is slightly larger than that under compression failure mode according to the effective stress failure envelopes.

Fig. 1
figure 1

Principal stress orientation variation in excavated slope

Full size image

With feasible description of soil stress-induced anisotropy, a train of research has introduced this feature into the analysis of slope stability (Conesa et al. 2019; Rao et al. 2019; Stockton et al 2019; Tang et al 2020; Ning et al 2021; Yeh et al. 2020). Liu et al. (2018) proposed the expressions of shear strength parameters by incorporating an anisotropic state scalar index, and applied it to slope stability analysis. According to their calculation, the factor of safety can be reduced by 22.0% when considering the anisotropy of strength. Rao et al. (2019) conducted a three-dimensional upper-bound limit analysis on reinforced slope stability problem and reached the conclusion that the factor of safety is negatively correlated with the anisotropic degree. Xia and Chen (2018) addressing at the seismic stability problem of an anchored slope analyzed the effect of anisotropic shear strength parameters. When the anisotropy is becoming notable, the yield acceleration factor showed obvious decreasing trend, indicating the slope seismic stability continuously reducing. The similar conclusions of the above studies indicate the importance of considering soil anisotropy in accurately evaluating the slope stability.

In this paper, a well-known empirical chart of assessing the slope factor of safety is firstly reviewed. Then, the quantification of clay strength and stiffness anisotropy is included through introducing the advanced constitutive model. The stability of unreinforced slope is investigated adopting the strength reduction method. A series of finite element models with different slope geometries and soil properties are established, and the numerical results are organized and analyzed to update the empirical chart.

Evolution of Taylor’s chart

Currently, empirical charts are used in practical cases as handy and efficient means for evaluating slope stability (Chen et al.2020a, b, c). Many stability charts with no requirement of tedious calculation are constructed and improved. The line-based stability charts for slopes raises great convenience in rapidly assessing FOS (Lim et al. 2016; Sahoo et al. 2019, 2020; Liu et al. 2022). Various forms of line-based stability charts are in use. Among existing slope stability charts, Taylor (1937) once used the friction circle method to propose simple design charts to assess the slope stability. The charts established determined relations to correlate the slope stability number with slope geometry, including slope angle and relative slope height. The charts were designed targeting at the homogeneous undrained clay slope stability problems, in which the ϕu=0. Three modes of failure circles were demarcated in Taylor (1937), namely shallow toe circle, deep toe circle, and mid-point circle, which will be introduced in the “Slip circle modes” section.

Based on Taylor’s achievements, Baker (2003) made an advancement of Taylor’s stability problem with quantization of two-dimensional coordinate system to capture the slip circle configurations within the slope plane. Steward et al. (2011) made further improvement in which compound slip circle modes were proposed considering the heterogeneous site soil condition. Five more specific failure modes were proposed taking the underlying hard soil layer into account, which is of more significance for practical engineering.

Stability number

In addition to the traditional safety factor index to represent the stability of slopes, a new dimensionless stability number Ns linked with soil physical and mechanical properties and slope geometry was proposed:

$${N}_{s}=\frac{\gamma H}{{s}_{u,\mathrm{mob}}}=\frac{\gamma HF}{{s}_{u}}$$
(1)

where γ is the unit weight of the undrained clayey soil, H represents the slope height, su,mob is the undrained shear strength mobilized along the slip circle within the clayey soil, while su stands for the undrained shear strength of the clayey soil, and F is the factor of safety calculated through strength reduction method. By normalizing the factor of safety, the stability number can be used to compare the slope stability conditions under different slope shapes and soil strengths.

Slip circle modes

For undrained homogeneous clay slope, three types of slope failure modes were identified according to a traditional cylindrical critical slip surface that is not astricted by deep buried hard stratum. The slip circle conditions are namely shallow toe circle, deep toe circle, and base circle as shown in Fig. 2. It was point out that for some steep slopes, the failure surface is generated above the slope toe elevation along a circular arc which is passing through the slope toe (as Fig. 2a shows the shallow toe circle mode). When the slope gradually becomes gentle, the sliding surface may break through the bottom of the slope and continue to develop downward, but still cut out from the toe, this failure mode is called deep toe circle. Furthermore, without the existence of deep stiff soil layer, the sliding surface in soft clay may continue to extend, the critical failure surface reaches the area beneath the slope toe, which leads to the base circle failure mode. The volume of the sliding body increases significantly as the slip circle mode changes.

Fig. 2
figure 2

Failure modes in Taylor (1937)

Full size image

The burial depth of stiff stratum plays dominant role in the stability and potential failure mode of multi-layered soil slope. The burial depth of stiff stratum is characterized with the index nd as shown in Fig. 3; it is the ratio of the distance from the top of the slope to the hard soil layer over the slope height. In view of the slope angle, buried depth of hard soil and soil strength, Steward et al. (2011) identified the slip surface of clay slope into five types as shown in Fig. 3.

Fig. 3
figure 3

Compound failure modes for multi-layered slope (Steward et al. 2011)

Full size image

Taylor’s chart for undrained clay slopes

A typical form of Taylor’s chart is shown in Fig. 4. The slope stability number can be obtained according to the general slope shape information with reference to the chart. Then the factor of safety can be calculated according to the NS equations (Eq. 1) with knowledge of soil properties.

Fig. 4
figure 4

Typical form of Taylor’s chart

Full size image

The improved charts proposed by Steward et al. (2011) use similar form and principles, only the division of slip circle modes is different. Therefore, the work of Steward et al. (2011) is not described in detail here.

Currently, the existed stability charts are generally designed for isotropic clay slope; the complex clay behavior is not taken into account. In this study, the difference in soil rotational principal stress is considered to capture the differential behavior of soil under various stress paths. The objective of this paper is to update the stability charts for clay slope with underlying hard soil with special focus on the clay stress-induced anisotropic behavior. To some extent, it can provide a useful reference to supplement and complete previous stability charts.

Soil anisotropic model

The importance and necessity of considering stress-induced anisotropy for the analysis of slope stability problems have been discussed in several studies (Stockton et al 2019; Tang and Wei 2019; Ning et al 2021). In this study, the NGI-ADP anisotropic constitutive model has been adopted. The core of this model is the ADP concept proposed by Bjerrum (1973). The model defines the behavior of clay under any stress state through three characteristic stress–strain relations under three different laboratory test paths: triaxial extension, direct simple shear, and triaxial compression. The three shear states are represented by the active (A), direct simple shear (DSS), and passive (P) loading stress paths, which form the kernel of the ADP concept. The model uses the undrained shear strengths under the three stress paths to define the anisotropic strength, which are suA, suDSS, and suP, respectively.

In order to model the stiffness anisotropy, the model employs three shear strains at failure, \({\gamma }_{f}^{C}\) for triaxial compression, \({\gamma }_{f}^{DSS}\) for direct simple shear, and \({\gamma }_{f}^{E}\) for triaxial extension. Combined with the undrained shear strength of the corresponding stress path, the anisotropic stiffness under the discrepant loading paths can be obtained. In addition to these three stress conditions, the model implements elliptical interpolation between failure strain and strength for arbitrary stress paths.

The shear modulus Gur for both loading and unloading is assumed to be isotropic and stress-independent when the soil is elastic. The development of shear stress and strain in the plastic state under the three paths is shown in Fig. 5. The yield criterion for the model is constructed based on a translated approximated Tresca criterion. In plane strain condition, it can be represented as

$$\begin{aligned}f=&\sqrt{{\left(\frac{{\sigma }_{yy}-{\sigma }_{xx}}{2}-\left(1-k\right){\tau }_{0}-k\frac{{s}_{u}^{A}-{s}_{u}^{P}}{2}\right)}^{2}+{({\tau }_{xy}\frac{{s}_{u}^{A}+{s}_{u}^{P}}{2{s}_{u}^{DSS}})}^{2}}\\&-k\frac{{s}_{u}^{A}+{s}_{u}^{P}}{2}=0\end{aligned}$$
(2)

where \(k=2\frac{\sqrt{{\gamma }^{p}/{\gamma }_{f}^{p}}}{1+{\gamma }^{p}/{\gamma }_{f}^{p}}\) when \({\gamma }^{p}<{\gamma }_{f}^{p}\), in which \({\gamma }^{p},{\gamma }_{f}^{p}\) are the plastic shear strain and the failure plastic shear strain; otherwise, k = 1.

Fig. 5
figure 5

Stress–strain curves for three stress paths adopted in NGI-ADP model

Full size image

Other than the six key input parameters described above, the other pre-defined input parameters required in the constitutive model are listed in Table 1. Note that the units for some indices are expressed under the plane strain state. The unloading/reloading shear modulus in the elastic stage is characterized by the dimensionless ratio Gur divided by the active undrained shear strength.

Table 1 Input parameters of NGI-ADP model
Full size table

In this model, the su shear strength ratio suP/suA is the critical parameter that directly characterizes the strength anisotropy. The ratio ranges from 0 to 1. The su ratio of 1 represents the ideal isotropic condition. The suDSS/suA is correlated with the suP/suA in this model and is defined to be

$$\frac{{s}_{u}^{DSS}}{{s}_{u}^{A}}=(1+\frac{{s}_{u}^{P}}{{s}_{u}^{A}})/2$$
(3)

This model NGI-ADP has been successfully employed in analyzing braced excavation displacement (Zhang et al. 2020) and embankment stability (Verreydt et al. 2019). It was further improved to describe the strain-softening behavior (Jostad 2014; Huynh et al. 2019), named NGI-ADPSoft. The model was implemented into a finite element procedure to perform simulations according to a full-scale failure test on soft clay deposit. It showed satisfactory capacity in predicting failure loads, confirming its feasibility in simulating clay post-peak softening behavior (D’Ignazio et al. 2017). However, the anisotropic characteristic in undrained strength and stiffness stands the key focus of this study; the perfect plasticity is employed as Fig. 5 indicates; no softening analysis is included in the following content.

Slope stability analysis

Finite element model

In this study, the anisotropic clay slopes were analyzed using the finite element software Plaxis (Panagoulias et al. 2018). A typical cross-section of the slope is shown in Fig. 6. The total thickness of the soft clay is 40 m. The slope height H is 10 m, and the depth from the toe of the slope to the underlying hard stratum/bedrock HD is 30 m. In subsequent parametric studies, HD is decreased to study the effects of the hard stratum on the stability analysis. Only the soft clay is modeled with the underlying bedrock represented by the bottom boundary of the FE model. The left and right boundaries of the finite element model are assumed to be fixed horizontally but free to move vertically, while the bottom boundary is assumed to be fixed both horizontally and vertically. The left and right vertical boundaries are located sufficiently away from the slope so as to have no influence on the slope response.

Fig. 6
figure 6

Slope geometry with parameters

Full size image

The properties of the soft clay are shown in Table 2. For the simulation of slope excavation, total five excavation stages are included in which 2 m of soil is excavated. Table 3 shows the range of values of the parametric study. The range of the shear strength ratio suP/suA considered in this study is based on previous laboratory and in situ test findings from various researchers including Grimstad et al. (2012) and Ukritchon and Boonyatee (2015). Note that some related parameters vary correspondingly, such as yref.

Table 2 Properties of anisotropic soft clay
Full size table
Table 3 Variations of parameters for systematic analysis
Full size table

A total of 180 cases are modeled and calculated in terms of different slope geometries and soil properties. The strength reduction method is adopted to determine the slope stability, as its feasibility is verified by abundant researches (Yuan et al. 2020; Tu et al. 2016). The method is designed to reduce the material properties, normally the strength indices. When the stress of an element exceeds the yield surface, the stress it cannot hold gradually transfers to surrounding soil element until a continuous sliding surface is formed. The reduction factor at the failure situation is the safety factor of the slope.

A total of 4164 triangular elements with 15 nodes were included. The default 15-node triangle element type provides fourth-order interpolation for displacement and is more accurate for strength reduction calculation in contrast with 6-node element. No structural members were included in the numerical model. The efforts of numerical model modification, repeated calculation, and result output can be completed by the interactive code of Plaxis and Python, which greatly improves the efficiency of modeling and post-processing. The modification, calculation, and extraction of a single FE model can be approximately completed in 2 min. The calculated results including development of slope stability number, soil displacement field, and sliding surface mode are extracted and analyzed.

Results analysis

Slope stability

In this study, the stability number Ns described in Eq. (1) is used to assess the stability of the slope. For anisotropic soils, the su term in Eq. (1) is replaced by suA. The factor of safety is determined from the finite element analysis using the strength reduction method. The stability number enables slopes with different geometries and soil properties to be compared with a higher Ns denoting a higher factor of safety.

Figure 7 shows the influence of the shear strength ratio su and the slope angle on the stability number. The general trend is for the stability number to decrease as the slope angle increases and the shear strength ratio decreases. When the shear strength ratio = 0.5, the stability number decreases by about 1/3 compared with the isotropic clay with shear strength ratio = 1.0 for very gentle slopes. As the slope angle increases, the stability number generally converges irrespective of the shear strength ratio. For steep slopes, the difference in the stability number is minimal. The results indicate that the clay anisotropy has a greater effect on the slope stability for a gentle slope compared with a steep slope. This is because for a steep slope, the failure mechanism is a shallow toe circle (Fig. 2a), and the stability is essentially governed by the active shear strength suA. This is discussed further in the “Slope failure mechanism” section.

Fig. 7
figure 7

Effects of slope angle and shear strength ratio on stability number

Full size image

The influence of the depth of the hard stratum on the stability number is shown in Fig. 8. The lines indicate the different thickness of soft soil layer below the bottom level of slope with the solid lines representing the isotropic cases and the dotted lines representing the anisotropic cases for shear strength ratio = 0.5. As in Fig. 7, the results indicate that apart from the case of the vertical slope, the stability number for the anisotropic cases are lower than for the isotropic case. In addition, the results indicate that as the depth index nd increases, the stability number reduces significantly for gentle slopes. When the slope angle β exceeds 60°, the differences become minimal. These phenomena are associated with the slope failure mechanisms, which will be discussed further in the “Slope failure mechanism” section.

Fig. 8
figure 8

Effects of depth to hard stratum on the stability number for suP/suA = 0.5 and 1.0

Full size image

Slope failure mechanism

As discussed in the “Slip circle modes” section, Steward et al. (2011) identified five different slip circle mechanisms: compound slope circle, compound toe circle, compound base circle, touch base circle, and shallow toe circle. As three of these circles are constrained by the hard stratum, the failure mechanism comprises of two separated arcs and a straight line along the soil-hard stratum interface as shown in Fig. 9b, d, e. The remaining two failure slip circles as Fig. 9a, c are not affected by the hard stratum. The development of the five failure mechanisms for anisotropic soils (suP/suA = 0.5) in terms of total displacement contours is summarized as follows:

  1. 1.

    For steep slopes in which the slope angle β> 60°, the shape of the failure circle is a shallow toe circle (Fig. 2a) and is independent of the hard stratum. The displacement contours and vectors for a typical vertical slope are shown in Fig. 9a. The slip circle does not develop below the elevation of toe of the slope. The displacement vectors show significant lateral soil displacements and minimal deformation of the soil beneath the toe of the slope. Therefore, the depth index nd which represents the relative depth to the hard stratum has minimal influence on the stability of steep slopes.

  2. 2.

    For a gentle slope with the hard stratum close to the bottom of the slope, the failure mechanism is a deep toe slip circle (as in Fig. 2b and Fig. 9b) that is cut off (i.e., intercepted) by the hard stratum and forms the compound toe circle.

  3. 3.

    For the base slip circle, the failure mechanism is either tangent to the hard stratum as or does not touch the hard stratum as shown in Fig. 9c. This generally occurs for gentle slopes where the hard stratum is quite deep.

  4. 4.

    For a gentle slope in which the depth to the hard stratum is small, the failure mechanism is a compound base circle (Fig. 9d).

  5. 5.

    The slope circle mechanism generally occurs in gentle slopes, with a deep slip surface as illustrated in Fig. 9c, d. However, when the depth to the hard stratum is very shallow, the compound slope circle mode is occasionally encountered as shown in Fig. 9e.

Fig. 9
figure 9

Deformation modes of slopes with various geometries

Full size image

The plots in Fig. 9 indicate that the failure slip surfaces for isotropic soils and anisotropic soils are similar. However, they differ in terms of the magnitude of the slope displacements, the mobilized shear stress, and the factor of safety.

Average undrained shear strength

Because of the complexities involved in using a numerical approach to analyze a slope with anisotropic shear strength properties, this section explores the feasibility of using an “average” undrained shear strength to perform an equivalent isotropic stability analysis of the slope.

The average shear strength su,ave here is defined to be the average value of the active shear strength suA and the passive shear strength suP. For example, for the case with suP/suA = 0.6, the average shear strength su,ave = 0.8suA. A total of 70 isotropic analyses were carried out using su,ave, and the computed factors of safety were compared with the corresponding anisotropic case. For all the cases, it was assumed that nd = 3. The effects of substituting anisotropic degree with average strength are plotted in Fig. 10. The longitudinal coordinate represents the safety factor calculated using isotropic average shear strength verses the safety factor computed with anisotropic constitutive model. Table 4 lists some of the computed results for comparison.

Fig. 10
figure 10

The safety factor computed using average undrained shear strength

Full size image
Table 4 Comparison of stability number using average strength and anisotropic cases
Full size table

The results indicate good agreement between the analyses using su,ave and the corresponding anisotropic cases for gentle slopes (i.e., slope angle is less than 60°), with relative errors of factor of safety of less than 5%. The performance of average isotropic constant undrained shear strength matches well with the anisotropic cases, indicating the approximate uniformity of the active and passive stress zones of soil mass. This phenomenon is consistent with the slope slip circle mode. For soft gentle slope with deep hard soil layer, the failure surface can be base circle, slope circle, or deep toe circle. The corresponding sliding angle is normally large, leading to extensive passive areas of soil.

While for steep slopes in which β exceeds 60°, the stability numbers of simplified average isotropic case are substantially smaller than the actual anisotropic results as marked in red in Table 4. The relative error reaches 18% for vertical slope. The lower stability number obtained using the average strength indicates that the average strength is obviously lower than the actual strength which is interpolated according to various stress state. Therefore, in the actual soil stress field, the soil under the active stress state accounts for the majority; the clay under passive stress covers less proportion as Fig. 9a shows. It was further discussed that for steep slopes, it is possible to use a larger “average” strength to substitute the complex anisotropic analysis. To this end, the “second-average” undrained shear strength su,ave’ = (suA + suDSS)/2 is proposed. The effect of the simplified isotropic average undrained analysis for steep slopes is shown in Table 5.

Table 5 Substitution effect of using “second-average” strength for steep slopes
Full size table

It can be concluded that for clay slopes in which slope angle is less than 60°, the simplicity of using the average isotropic constant strength instead of anisotropic interpolation strength is feasible. However, for steep slopes, it is suggested that a larger and more reasonable substitution value, i.e. su,ave’ = (suA + suDSS)/2, should be used to capture the practical slope response under stress-induced anisotropy.

Updated Taylor’s chart

Stability chart for anisotropic undrained clay slope

As the feasibility of using simplified “average” strength index is validated, hundreds of calculations have been run to efficiently locate the diversions of different critical slip circle modes for anisotropic undrained clay slopes with various geometries. Relevant stability chart is updated based on Taylor’s (1937) and Steward’s (2011) work. The updated Taylor’s chart is presented graphically in Fig. 11. The stability number is calculated using the undrained shear strength su,ave = (suA + suP)/2 for gentle slopes, in which the slope angle β <60° .For steep slopes, the “second-average” strength su,ave’ = (suA + suDSS)/2 is adopted. The y-axis represents the stability factor related to the safety factor, and the x-coordinate is the slope angle. The area enclosed by several groups of stiff stratum depth ratio (i.e., nd) is divided into five sub-areas according to different sliding surface modes. In this study, five different slip circle modes were identified as the legend shows.

Fig. 11
figure 11

Updated stability chart for anisotropic undrained clay slopes

Full size image

In Fig. 11, the blue area represents the failure mode of compound slope circle; it normally happens when the slope is gentle and the strata interface is very close to the bottom of the slope. The orange area covers the possibility of compound toe circle failure mode. When the depth of hard soil layer increases gradually, the green compound base circle mode becomes more possible. If the buried depth of hard soil is too deep to restrain the soft soil slope deformation, the touch base circle failure commonly occurs, which is marked in yellow. When the slope angle reaches 60°, it is very likely that the slope fails along the shallow toe circle. For very steep slopes, the sliding surface can hardly penetrate below the bottom elevation.

Case validations

Case 1

An undrained layered slope reported in Luo et al. (2019) was chosen. They employed the finite element tools to assess the slope failure pattern and safety factor of layered slope, which is available for validations of the presented anisotropic stability chart. For the two-layered slope in the referencing study, the average undrained shear strength of the upper clay is 25 kPa, unit weight γ = 20kN/m3, and slope height H = 5m. The stability number can be read as 4.9 from figure n with nd = 2 and β = 26.5°; the failure mode is identified to be compound base circle. From Eq. 1, the factor of safety can be calculated:

$$F=\frac{{N}_{s}\times {s}_{u,ave}}{\gamma H}=1.22$$

In Luo et al. (2019), the safety factor calculated via finite element method is 1.27, and they identified the slip circle mode as compound type, which is very close to the results obtained from the presented stability chart.

Case 2

An example from a study (Tang and Wei 2019) which also considers the anisotropy of soil strength is employed as another validation. The model also established a homogeneous soil slope and simulated the underlying hard soil layer by limiting the displacement of the base boundary. In the referencing study, the effective stress strength indices were adopted, and they were converted into undrained shear strength according to correlation principles proposed by Cheng (2001). The slope information includes as follows: su,ave = 146.9 kPa, β = 45°,nd= 2, γ = 20kN/m3, H = 20m.

The stability number in view of nd and β is Ns = 4.6, and the corresponding factor of safety is F = 1.69. The safety factor is quite similar to that of 1.78 calculated using the gravity increasing method in Tang and Wei (2019). However, there is no way to validate the correctness of slip circle mode because it is not mentioned in their study.

According to the identical results of the above two examples, it can be considered that the updated empirical chart performs well and can be used to estimate the stability and failure mode of anisotropic clay slopes with underlying stiff stratum.

Conclusions

The present study investigated the stability and possible sliding modes of the unreinforced slope with underlying stiff stratum and updated a well-known empirical chart by introducing the stress-induced anisotropy into slope stability analysis. A series of finite element models were established featuring with different slope geometries and soil properties, and the strength reduction method was employed to assess the slope stability. The main findings are as follows:

  1. 1.

    Through comparison of stability number between anisotropic and isotropic clay slopes, the slope stability may be overestimated ignoring the anisotropy characteristics of soil, especially for high and gentle slopes.

  2. 2.

    The burial depth of underlying stiff stratum plays a significant role in determining the slip circle mode. As the hard soil is buried deeper, the slope stability continuously decreases. While for steep slopes, stiff stratum has marginal effect on its stability number and failure mode.

  3. 3.

    The average isotropic constant undrained shear strength can be employed as the substitution for the stress-induced anisotropic strength and stiffness for gentle slopes. With the increase of slope angle, the effectiveness of substitution decreases gradually. Since the soil under passive stress state along the sliding surface is of minority for high and steep slopes, the actual overall strength is greater than the average shear strength. In this case, it is suggested to use a larger “second-average” strength to perform slope stability assessment.

  4. 4.

    A convenient empirical chart with consideration of clay strength and stiffness anisotropy is updated to evaluate the slope stability based on slope geometry and soil properties. Combined with existing research results, the effectiveness of the proposed chart for assessing the slope stability and possible failure mode is verified.