Introduction

Colluvial landslides that formed in ancient years are widely distributed in tropical and sub-tropical regions. Reactivations of this kind of geological masses are commonly triggered by intense rainfall (Wang and Sassa 2003; Crosta and Frattini 2003; Hong et al. 2005; Huang 2009). On the problems of rainfall-induced landslides, plenty of research has been conducted (Caine 1980; Iverson 2000; Cho and Lee 2001; Kim et al. 2004; Zhang et al. 2014) and indicates that the geological masses behave time dependent on the impacts of environmental factors. It is well known that the stability of landslide reduces gradually with rainfall infiltration. According to previous studies (Wang and Sassa 2003; Tu et al. 2009; Defersha and Melesse 2012), stress changing (e.g., the increases in pore water pressure, soil weight and seepage force) and the weakening of material strength are the two main factors that lead to the failure of landslides under rainfall condition. Therefore, simulating the rainfall infiltration on field and establishing the quantitative relations between hydrologic conditions and mechanical properties (e.g., stress and strength) are of great importance to evaluate the stability of landslides during rainfall.

Richards’ equation (1931) and Green and Ampt model (1911) are two mostly used theories in the analysis of rainfall infiltration problems. Richards’ equation, derived from Darcy’s law and mass conservation law, is regarded as the most accurate control model of water seepage in unsaturated soil (Zeballos et al. 2005; Chen and Young 2006). However, in its application to natural slopes with irregularly curved boundaries, it is hard to obtain the analytical solutions. Hitherto only simplified solutions of the infiltration problem of infinite slope were derived, respectively, by Hurley and Pantelis (1985), Iverson (2000), Zhan et al. (2013), Tsai and Chiang (2013). Even though numerical simulation techniques based on Richards’ equation are well developed for their accuracy of analyzing both steady and unsteady seepage (Cho and Lee 2001; Rahimi et al. 2010), these numerical models contain too many parameters and some of whose physical significance are not explicit and difficult to be determined (Montrasio and Valentino 2008).

Green–Ampt model, compared to Richards’ equation, is more succinct to simulate intense water infiltration into unsaturated soil regarding expression and solution. The model was originally developed to analyze infiltration process under horizontal ponding condition. In recent years, some expanded versions of the model have been developed and applied to sloping conditions, and further to evaluate the stability of landslide mass. (Chen and Young 2006; Gavin and Xue 2008; Muntohar and Liao 2009; Zhang et al. 2014). However, in these studies, slopes or landslides are assumed as infinite objects with straight surface and so water loss of the saturated layer above the wetting front are neglected. Therefore, the objective of this paper is to incorporate the influence of parallel water discharge into original Green–Ampt model under the condition of finite or naturally curved surface in order to develop an effective method to evaluate the time-dependent stability of colluvial landslides during intense rainfall.

For this purpose, the article is structured in the following sections: In Sect. 2, the theory background of Green–Ampt model and shear strength of layer-saturated soil are firstly introduced. Section 3 presents the implementing procedure of the improved approach in which the modification of Green–Ampt model and derivation of safety factor are described in detail. Section 4 provides a case study of the Shuping landslide to investigate its time-dependent stability during intense rainfall. Section 5 involves several discussions on the improved approach. Finally, conclusions are presented in Sect. 6.

Theory background

Green–Ampt model

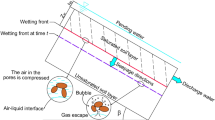
Green–Ampt model (1911) was originally developed to analyze the infiltration of ponded water into unsaturated soil. To describe the infiltration process, the concept of the wetting front was first proposed. Within the concept, the soil below the wetting front is unsaturated, while the soil above is fully saturated due to water infiltration (see Fig. 1). The wetting front moves down to the unsaturated layer under the action of gravity and matric suction. In summary, the soil is layer-saturated with water infiltrating into, and the interface between saturated and unsaturated layer constantly moves toward the unsaturated layer. By applying Darcy’s law, the infiltration rate of ponded water is expressed as

$$i = K_{\text{s}} \frac{{h_{\text{p}} + z_{{ * {\text{f}}}} + \psi_{\text{f}} }}{{z_{{ * {\text{f}}}} }}$$
(1)

in which K s is saturated permeability coefficient (m/s); h p is depth of ponded water (m); z *f is depth of the wetting front (m); and ψ f  is suction head at the wetting front (m).

Fig. 1
figure 1

Infiltration process of Green–Ampt model (Gavin and Xue 2008)

Full size image

Green–Ampt model is regarded as an approximation of Richards' equation, with the advantage of simplifying the process of solving infiltration equations. Therefore, the model was expanded to analyze both steady and unsteady rainfall infiltration problems in many literatures (Mein and Farrell 1974; Chu 1978; Diskin and Nazimov 1996; Van den Putte et al. 2013).

Shear strength of layer-saturated soil

The extended Mohr–Coulomb shear strength criterion, proposed by Fredlund and Rahardjo (1993), is widely applied to stability evaluation of unsaturated soil. The formula is expressed with two independent stress variables as

$$\tau = c^{\prime } + (\sigma - u_{\text{a}} )\tan \phi^{\prime } + (u_{\text{a}} - u_{\text{w}} )\tan \phi^{\text{b}}$$
(2)

where c ′ is effective cohesion (kPa); φ ′ is effective internal friction angle (°); u a is pore air pressure (kPa); u w is pore water pressure (kPa); (σ − u a) is net normal stress; (u a − u w) is matric suction; and φ b is friction angle reflecting the degree of matric suction increment. The terms on the right side of Eq. (2) represent the contributions of cohesion, net normal stress and matric suction to shear strength respectively.

Since matric suction is a state variable independent of net normal stress, it can be regarded as the contribution to cohesion. Apparent cohesion (c * ψ ) is hence defined as the sum of effective cohesion and matric suction; then,

$$\tau = c_{\psi }^{*} + (\sigma - u_{\text{a}} )\tan \phi^{\prime }$$
(3)
$$c_{\psi }^{*} = c^{\prime } + (u_{\text{a}} - u_{\text{w}} )\tan \phi^{\text{b}}$$
(4)

Because of the relatively complicated water distribution, Eq. (2) is inapplicable to mechanical analysis in limit equilibrium method. To assess the shear strength of layer-saturated soil, a simplified computing method was proposed by Montrasio (2008, 2009) based on model experiments (Silva 2000). It is assumed that the shear strength, provided by unsaturated and saturated layer, can be homogenized in a single layer that has an apparent cohesion as a function of the thickness of the saturated layer. It is concluded from a series of experimental results that the apparent cohesion of soil slice can be expressed as

$$c_{\psi } = c^{\prime } + (u_{\text{a}} - u_{\text{w}} )\tan \phi^{\text{b}} \cdot (1 - \eta )^{\text{m}}$$
(5)

where m is a constant parameter, generally taken as 3.4 according to tests (Montrasio and Valentino 2008), and η represents the thickness ratio of the saturated layer to the whole layer. In slice method of stability analysis, two vertical sides of soil slice are parallel; hence, η is taken as the area ratio of saturated layer to the whole layer.

Then, shear strength of the layer-saturated soil slice is written as Eq. (6):

$$\tau = c_{\psi } + (\sigma - u_{\text{a}} )\tan \phi^{\prime }$$
(6)

Equations (5) and (6) show that shear strength of layer-saturated soil is determined by two elements: mechanical parameters of the unsaturated soil and thickness of the saturated layer. For a certain landslide under rainfall condition, the mechanical parameters are taken as constant values, but the thickness of the saturated layer keeps increasing under prolonged infiltration. Therefore, Eqs. (1) and (6) formulate the basis of evaluation of landslide stability in Sect. 3.

Methodology

Infiltration model for a finite slope

Researches show that shallow soil of the slope is saturated in response to intense rainfall, and the saturated zone expands downward with prolonged rainfall (Crosta and Frattini 2003; Li et al. 2013). On the basis of the original Green–Ampt model, the infiltration rate of intense rainfall for the sloping surface can be expressed as follows (Chen and Young 2006):

$$i = K_{\text{s}} \frac{{h_{\text{f}} \cos^{2} \beta + \psi_{\text{f}} }}{{h_{\text{f}} \cos \beta }}$$
(7)

in which h f is depth of the wetting front in vertical direction (m) and β is dip angle of slope surface (°).

Various expanded versions of Green–Ampt model have been developed to analyze intense rainfall infiltration into infinite slope and further to evaluate of slope stability. However, these methods neglected the influence of water discharge parallel to slope surface.

The actual water exchange among slope surface, saturated and unsaturated layers is sketched in Fig. 2, which can be generalized in two aspects: On the one hand, the wetting front gradually moves downward perpendicular to slope surface with recharge from rainfall infiltration. On the other hand, water in saturated layer discharges downward parallel to slope surface under the effect of geometric conditions of the slope and hydraulic gradient. However, the parallel water discharge is neglected in previous expansions of the Green–Ampt (Pradel and Raad 1993; Chen and Young 2006; Muntohar and Liao 2009) that are not applicable to finite slopes or those with curved surfaces. Therefore, a modified Green–Ampt model is developed taking both water recharge and discharge into account (Fig. 3).

Fig. 2
figure 2

Contrast of the wetting front in actual situation to original Green–Ampt model

Full size image
Fig. 3
figure 3

Process of infiltration into a finite slope during intense rainfall

Full size image

To reveal the actual process of intense rainfall infiltration, the two stages before and after the formation of the wetting front are separately discussed (hereinafter referred as to Stage 1 and Stage 2). As suggested in most articles, soil moisture and suction head are regarded as constant values, irrespective of influences of groundwater and surface evaporation. In addition, rainfall is considered downward vertically with greater intensity than saturated permeability coefficient of soil.

  1. (1)

    Stage 1

    The shallow soil is unsaturated during the initial time of rainfall. With infiltration ability greater than rainfall intensity, rainfall completely infiltrates into the soil. Therefore,

    $$i = q\cos \beta$$
    (8)

    in which i is infiltration rate (m/s) and q is rainfall intensity (m/s). In consequence of prolonged infiltration, water content of the shallow soil transforms from naturally unsaturated state to saturated state so that the wetting front forms at a critical time. Therefore, infiltration rate at the critical time can be assessed by combining Eqs. (7) and (8):

    $$h_{\text{c}} = \frac{{\psi_{\text{f}} }}{{(q/K_{\text{s}} - 1)\cos^{2} \beta }}$$
    (9)

    in which h c is vertical depth of the wetting front at the critical time (m). Physically, cumulative rainfall infiltration I c (m) at the critical time is calculated as

    $$I_{\text{c}} = (\theta_{\text{s}} - \theta_{\text{i}} )h_{\text{c}} \cos \beta = \frac{{(\theta_{\text{s}} - \theta_{\text{i}} )\psi_{\text{f}} }}{{(q/K_{\text{s}} - 1)\cos \beta }}$$
    (10)

    in which θ s is volumetric water content of saturated soil and θ i is natural volume moisture content.

    Based on the conservation mass law, cumulative rainfall infiltration equals water increment in soil during the whole time. So the critical time t c is calculated as

    $$t_{\text{c}} = \frac{{I_{\text{c}} }}{q\cos \beta } = \frac{{(\theta_{\text{s}} - \theta_{\text{i}} )\psi_{\text{f}} }}{{q(q/K_{\text{s}} - 1)\cos^{2} \beta }}$$
    (11)
  2. (2)

    Stage 2

    When shallow soil gets saturated, the wetting front forms and runoff generates on the landslide surface. At this stage, water flow in the saturated layer contains two aspects as described above. Actual moving speed of the wetting front is determined by the apparent moving speed induced by perpendicular recharge and the reductive speed induced by parallel discharge.

    On the one hand, the perpendicular flow can be evaluated based on Green–Ampt model. The infiltration rate is obtained with combination of Eq. (7) and the derivative of cumulative rainfall infiltration that is defined as

    $$i = \frac{{{\text{d}}I}}{{{\text{d}}t}} = (\theta_{\text{s}} - \theta_{\text{i}} )\cos \beta \frac{{{\text{d}}h_{\text{f}} }}{{{\text{d}}t}}$$
    (12)

    in which I is the cumulative rainfall infiltration (m).

    Substituting Eq. (7) into Eq. (12), the apparent moving speed of wetting front can be written as

    $$\left( {\frac{{{\text{d}}h_{\text{f}} }}{{{\text{d}}t}}} \right)_{1} = K_{\text{s}} \frac{{h_{\text{f}} \cos^{2} \beta + \psi_{\text{f}} }}{{(\theta_{\text{s}} - \theta_{\text{i}} )h_{\text{f}} \cos^{2} \beta }}$$
    (13)

    On the other hand, water flow parallel to surface in saturated layer causes water discharge, thus reducing the speed of the wetting front relatively. It is known from Darcy’s law that

    $$K_{\text{s}} \sin \beta h_{\text{f}} {\text{d}}t = (\theta_{\text{s}} - \theta_{\text{i}} )L{\text{d}}h_{\text{f}}$$
    (14)

    in which L is slope length along surface direction (m). The relative reductive speed of the wetting front is expressed as

    $$\left( {\frac{{{\text{d}}h_{\text{f}} }}{{{\text{d}}t}}} \right)_{2} = K_{\text{s}} \frac{{h_{\text{f}} \sin \beta }}{{(\theta_{\text{s}} - \theta_{\text{i}} )L}}$$
    (15)

    The difference between Eqs. (13) and (15) is the actual moving speed of the wetting front, that is,

    $$\frac{{{\text{d}}h_{\text{f}} }}{{{\text{d}}t}} = \frac{{K_{\text{s}} }}{{(\theta_{\text{s}} - \theta_{\text{i}} )L}}\frac{{ - h_{\text{f}}^{2} \cos^{2} \beta \sin \beta + h_{\text{f}} L\cos^{2} \beta + L\psi_{\text{f}} }}{{h_{\text{f}}^{2} \cos^{2} \beta }}$$
    (16)

    Integrating Eq. (16) with respect to time under the initial condition that h f = h c when t = t c, yields

    $$\left. \begin{aligned} t - t_{\text{c}} = \frac{{(\theta_{\text{s}} - \theta_{\text{i}} )L}}{{K_{\text{s}} \sin \beta }}\left[ {\frac{B}{A - B}\ln \left( {\frac{{h_{\text{f}} \cos \beta + B}}{{h_{\text{c}} \cos \beta + B}}} \right) - \frac{A}{A - B}\ln \left( {\frac{{h_{\text{f}} \cos \beta + A}}{{h_{\text{c}} \cos \beta + A}}} \right)} \right] \hfill \\ \frac{A}{B} = - \frac{L\cos \beta }{2\sin \beta } \pm \frac{{\sqrt {L^{2} \cos^{2} \beta + 4L\psi_{\text{f}} \sin \beta } }}{2\sin \beta } \hfill \\ \end{aligned} \right\}$$
    (17)

    Equation (17) shows that actual movement of the wetting front is related to soil properties as well as geometric conditions of slope including length and inclination.

Infiltration simulation of natural landslides

For a natural landslide with irregularly curved surface, boundary conditions are complicated, limiting the application of analytical solution in spite of Richards’ equation or previous expanded Green–Ampt models. Therefore, physical simplification should be made for infiltration simulation of natural landslides.

Referring to the limit equilibrium method for stability evaluation, the landslide is divided into several slices with finite lengths and approximately straight sides as Fig. 4 shows. Then each single slice can be regarded as a finite slope and simulated by modified Green–Ampt model proposed above. The main procedure is summarized as follows:

Fig. 4
figure 4

Sketch of slices division for infiltration simulation of natural landslide

Full size image

Step 1 the whole landslide is divided into several slices according to its geometric conditions, making the sides of each slice to be as straight as possible. The slices are sequentially numbered from 1 to n.

Step 2 the geometric parameters of slices including slice length L j and angle β j along slice surface (j refers to No. j slice) are measured.

Step 3 based on the available geometric parameters and combination of physical and mechanical parameters of the soil, the required parameters in modified rainfall infiltration model are solved, including t cj , I cj , A j , B j , etc.

Step 4 for the whole landslide, variation of infiltration depth with rainfall duration was finally quantified by combining calculation result of each slice.

However, the solution calculated by the model is not precise due to the discontinuity of rainfall infiltration depths between adjacent slices. That is, different lengths and angles of the slices cause discrepancy in values of h fi calculated at the same time. However, just as slice method in the evaluation landslide stability, the accuracy of the calculation model is also improved with increased number of divided slices. Therefore, the number of slices should be determined corresponding to accuracy requirement in practical application.

Note that there are totally two categories of parameters including geometrical and physical parameters in modified infiltration model. These parameters can be measured or assessed by field investigations or laboratory tests shown as follows:

Field investigation, drilling and geophysical prospecting can be used to reveal the geological and hydrologic condition, further to obtain engineering geology plane and main sliding section. Division of soil slices and measurement of their geometric parameters are carried out on the basis of main sliding section.

Saturated hydraulic conductivity can be assessed by laboratory permeability test or in situ double-ring infiltrometer method. Natural volume moisture content is measured by moisture probes in-situ or oven-drying method in laboratory. Natural density is assessed by cutting ring method. To obtain saturated volume moisture content and saturated density, vacuum process should be carried out on the soil samples to make them totally saturated. The saturated volume moisture content and the saturated density are assessed by quality and volume measurement of the saturated samples. Suction head is a variable for depth, and it can be measured by tensiometers at different depths. The mean value of the measured results is adopted in modified Green–Ampt model.

Time-dependent stability of landslides during intense rainfall

The limit equilibrium method is used to evaluate the stability of colluvial landslide. The landslide mass is divided into n slices in terms of the geometrical boundary, and the factor of safety is obtained by solving the mechanical equilibrium equations of all the slices. Geometrical and mechanical profile of No. j slice are shown in Fig. 5a and b, respectively.

Fig. 5
figure 5

a Geometrical profile of a soil slice, b forces acting on the soil slice

Full size image

The forces acting on No. j soil slice include gravity (G j ), sliding resistance (T j ), seepage force (P j ), support (N j ) and thrust from two adjacent slices (E j − 1 and E j ), among which gravity is expressed as

$$G_{j} = \gamma (U_{j} - S_{j} ) + (\gamma_{\text{s}} - \gamma_{\text{w}} )S_{j}$$
(18)

where γ s and γ are saturated and natural unit weight of soil (N/m3), respectively. S j and U j  are area of saturated layer and whole slice (m2), respectively.

Seepage force parallel to the landslide surface is expressed as

$$P_{j} = \gamma_{\text{w}} h_{{{\text{f}}j}} L_{j} \sin \beta_{j} \cos \beta_{j}$$
(19)

where γ w is unit weight of water (N/m3).

Safety factor is generally taken as the determinant index in evaluation of landslide stability, which is defined as the ratio of sliding resistance to sliding force and calculated as

$$F_{\text{s}} = \frac{{\left[ {G_{j} \cos \alpha_{j} + E_{j - 1} \sin (\alpha_{j - 1} - \alpha_{j} )} \right]\tan \phi^{\prime } + c_{\psi j} l_{j} + E_{j} }}{{G_{j} \sin \alpha_{j} + P_{j} + E_{j - 1} \cos \left( {\alpha_{j - 1} - \alpha_{j} } \right)}}$$
(20)

where α j  is dip angle of sliding zone (°).

To obtain the value of F s, equilibrium iteration should be carried out under the condition that E 1 = 0 and E n  = 0. For the convenience of iteration, Eq. (20) is written as

$$E_{j} = F_{\text{s}} \left( {G_{j} \sin \alpha_{j} + P_{j} } \right) - \left( {G_{j} \cos \alpha_{j} \tan \phi^{\prime } + c_{\psi j} l_{j} } \right) + E_{j - 1} \lambda_{j}$$
(21)

where \(\lambda_{j} = F_{\text{s}} \cos (\alpha_{j - 1} - \alpha_{j} ) - \sin (\alpha_{j - 1} - \alpha_{j} )\tan \phi^{\prime }\).

The procedure of iteration is shown as follows: Firstly an arbitrary value of F s is given to compute E n using Eq. (21). Then repetitive computations are carried out by changing F s according to previous results until E n approach 0. The value of F s with a computation result that E n  = 0 is the true safety factor.

The mechanical parameters in Eqs. (18–21), including effective internal friction angle, effective cohesion and angle of suction, can be estimate by unsaturated shear test under different net normal stress and matric suction.

In conclusion, to evaluate the stability of a colluvial landslide during intense rainfall, we should firstly divide it into various soil slices (Sect. 3.2), then simulate infiltration process of each single slice (Sect. 3.1) and eventually calculate the time-dependent safety factor (Sect. 3.3).

Case study and results

Geology background

For the sake of evaluating the stability of landslide during intense rainfall, the Shuping landslide in Three Gorges Reservoir Region is selected as a case (as shown in Figs. 6 and 7). As a typical colluvial landslide, many studies have been documented regarding its engineering geological conditions, stability evaluation, monitoring of ground surface and deep displacement (Wang et al. 2008; Fu et al. 2010; Ren et al. 2015). The landslide area has simple monoclinic characteristics, where the bedrock, mantled by superficial deposits characterized by colluvium and elurium, has a general occurrence of 165°–120° and dips from 10° to 35°. Formation of the bedrock mainly includes upper (T2b3) heavy-layer purplish red mudstone and siltstone, middle member (T2b2) of moderately thick light gray limestone and marl, lower (T2b1) medium thick purplish red and gray–green siltstone with mudstone and shale of Triassic Badong formation.

Fig. 6
figure 6

a Location of the study area, b location of the Shuping landslide, c geomorphological delimitation of the Shuping landslide

Full size image
Fig. 7
figure 7

Engineering geology plane of the Shuping landslide (Lu et al. 2014). (1) Deluvium and eluvium sandstone or limestone gravel with silt clay; (2) debris gravel with silt clay of sliding mass; (3) Triassic mudstone and siltstone (T2b3); (4) Triassic limestone and marlstone (T2b2); (5) Triassic siltstone interbedded with mudstone and shale; (6) altitude; (7) landslide mass boundary; (8) active block boundary of landslide mass; (9) reservoir level; (10) roads; (11) longitude profile; (12) attitude

Full size image

Elevations of rear edge and leading edge of the landslide are 470 and 70 m, respectively. Terrain gradients range from 5° to 35°, with an average degree of approximately 22°. It stretches around 800 m from north to south, and extends 670 m from east to west, with the thickness of 10–70 m and total volume of 2070 × 104 m3. The landslide mass is partitioned into two blocks (active block and inactive block), the east of which is defined as the main slip zone considering its greater deformation. Table 1 provides the basic physical and mechanical parameters of soil in landslide mass.

Table 1 Physical and mechanical parameters of the soil in the Shuping landslide
Full size table

The rainfall in landslide area concentrates mostly between May and September, dominated by rainstorms. There are 120–140 rainy days per year, with maximum daily precipitation of 358 mm. Mean and maximum annual rainfall over years are around 1028.6 and 1430.6 mm, respectively. In this study, the rainfall intensity of 50 mm/h is chosen as the input value to assess its effect on the stability of Shuping landslide.

Infiltration analysis using modified Green–Ampt model

I1 − I2 profile of the landslide is selected, shown as Fig. 8, to analyze infiltration process and stability under a rainfall intensity of 50 mm/h. In view of its boundary and geometrical shape of slip surface, the landslide mass is divided into 8 slices, sequentially numbered 1#–8# from south to north. Analysis of the change in infiltration depth with rainfall duration was performed on the basis of modified Green–Ampt model proposed in Sect. 3.

Fig. 8
figure 8

Cross section along I1 − I2 profile of Shuping landslide

Full size image

Geometrical parameters of each slice including length and angle are firstly measured. Then with combination of physical parameters in Table 1, the critical time of shallow soil get saturated and its corresponding cumulative infiltration and depth of the wetting front are computed using Eqs. (3–5). Values of parameter A and B are determined by substituting geometrical parameters of each slice into Eq. (17).

Table 2 demonstrates parameters of each slice in the infiltration model gained from above. By substituting these parameters into Eq. (17), depths of the wetting front at various times are acquired.

Table 2 Infiltration parameters of soil slices of the Shuping landslide
Full size table

Variation of safety factor during rainfall

The safety factor of Shuping landslide during rainfall with intensity of 50 mm/h is obtained by iterative computations of Eq. (21) with the boundary conditions that E 1 = 0 and E 8 = 0, based on mechanical and geometrical parameters and infiltration analysis above. The correlation between safety factor and infiltration time is illustrated in Fig. 9. The safety factor decreases gradually due to rainfall infiltration with the value of 1.34 at initial time and 1.0 at 102 h, and it will be less than 1.0 after 102 h. Therefore, 102 h is the prewarning time of failure of Shuping landslide with the rainfall intensity of 50 mm/h.

Fig. 9
figure 9

Variation of safety factor of the Shuping landslide under rainfall intensity of 50 mm/h

Full size image

Discussions

The factors affecting the infiltration

Since several factors affect intense rainfall infiltration into landslides, in this section, an unsaturated landslide with straight surface is selected as an example for analyzing the infiltration process under different conditions using the modified Green–Ampt model. Parameters of the landslide are set as follows: θ i = 0.15, θ s = 0.45, K s = 1×10−6 m/s, S f = 50 cm and rainfall intensity is 3.6 cm/h.

The variation processes of depths of the wetting front for different slope lengths are presented in Fig. 10. Depth of the wetting front increases gradually under prolonged rainfall infiltration. Also shown is that longer infiltration path corresponds to slower moving speed of the wetting front. In addition, moving speed presents a positive correlation with slope length under the same slope angle, referred to as the apparent size effect. The apparent size effect becomes especially evident under short slope length and almost vanishes when slope length is longer than 60 m. As slope length approaches infinity, the modified model degrades into the original Green–Ampt model with the same computing result.

Fig. 10
figure 10

Impact of slope length on the movement of wetting front

Full size image

Figure 11 shows the infiltration processes for different slope angles using both the modified and original Green–Ampt models. The moving speed presents a negative correlation with slope angle in both models, referred as to the angle effect. The angle effect of infiltration reduces with the decrease in slope angle, and almost loses when slope angle is smaller than 15°. Compared with the result from original model, the moving speed computed by the modified model is lower, owing to the consideration of the seepage parallel to slope surface. Besides, the difference between moving speeds computed by both model becomes greater with the increase in slope angle, which is positively related to hydraulic gradient.

Fig. 11
figure 11

Impact of slope angle on the movement of wetting front

Full size image

Figure 12a shows the infiltration processes under different rainfall intensities using the modified Green–Ampt model and Fig. 12b shows the zoomed in window of the initial time. Moving speed of the wetting front accelerates with the increase in intensity when rainfall occurs. However, the differences are moderate and tend to be constant as rainfall continues. The depth-time lines are nearly parallel and even overlap when the infiltration lasts more than 150 h. As a matter of fact, according to Eq. (3), the infiltration rate mostly depends on the depth of the wetting front while is irrelevant to the rainfall intensity after the shallow soil gets saturated. The discrepancy of depth-time lines in Fig. 12 results from different critical depths and critical time when the wetting front forms.

Fig. 12
figure 12

Impact of rainfall intensity on the movement of wetting front

Full size image

Comparison of stabilities of the soil above different sliding surfaces

The related literatures (Pradel and Raad 1993; Ali et al. 2014; Suradi et al. 2014) have pointed out that planar sliding failure along the wetting front frequently occurs in mountainous areas due to rainfall infiltration. Also stabilities of the soil above the wetting front and the soil above the bedrock are inconsistent, and the former is generally less stable. For the sake of comparing the stability variations of the soils along these two potential sliding surfaces, a straight unsaturated landslide with bedrock underlying is taken as the study case. The landslide surface and the bedrock surface are parallel to each other with the same dip angle of 30°. The soil above bedrock has a thickness of 5 m and its parameters are set as: γ = 16.5 kN/m3, γ s = 19.5 kN/m3, θ i = 0.15, θ s = 0.45, c′ = 10 kPa, and φ′ = 28°, φ b = 15°.

The safety factor of soil above the bedrock is expressed as

$$F_{\text{s}} = \frac{{G\cos \beta \tan \phi^{\prime } + c_{\psi j} L}}{G\sin \beta + P}$$
(22)

in which G is the gravity of soil above the bedrock (N).

The safety factor of soil above the wetting front is expressed as

$$F_{\text{s}} = \frac{{G_{\text{s}} \cos \beta \tan \phi^{\prime } + c^{\prime } L}}{{G_{\text{s}} \sin \beta + P}}$$
(23)

in which G s is the submerged weight of soil above the wetting front (N).

The variation processes of safety factors with the depths of the wetting front under different matric suctions are shown in Fig. 13a, b. The safety factor of the soil above the wetting front is much larger than that of soil above bedrock surface at the occurrence of rainfall. However, the former drops rapidly with the moving of the wetting front and turns to be smaller than the latter at last.

Fig. 13
figure 13

Stability variation of soil above the bedrock surface and the wetting front a u a − u w = 10 kPa, b u a − u w = 100 kPa

Full size image

In Fig. 13a, b, z a and z b are the vertical depths of the wetting front, respectively, corresponding to sliding failure along the bedrock and along the wetting front, and z c is the vertical depth of the wetting front as the safety factors in two cases are the same. Comparing the values of z a, z b and z c, there are two probabilities discussed as follows:

  1. (1)

    When matric suction is small (u a − u w = 10 kPa in this study case), h a < h b < h c. It indicates that sliding failure is more likely to happen along the bedrock surface than along the wetting front.

  2. (2)

    When matric suction is large (u a − u w100 kPa in this study case), h c < h b < h a. It indicates that sliding failure is more likely to happen along the wetting front than along the bedrock surface. In this case, high attention should be paid to shallow failure.

Conclusions

To evaluate the time-dependent stability of colluvial landslides during intense rainfall, two critical processes are proposed: simulating rainfall infiltration and calculating safety factor.

In order to realistically simulate the rainfall infiltration into naturally irregular landslides, the original Green–Ampt model is modified so that seepages that are both perpendicular and parallel to slope surface can be taken into consideration. The landslide body is divided into several soil slices with approximately straight sides, which are regarded as finite slopes. To deduce the infiltration formula, seepages that are both perpendicular and parallel to slope surface are considered in calculation of each single slice based on Darcy’s law and mass conservation law.

The limit equilibrium method is used to calculate the safety factor of the soil above the bedrock surface. In this process, the shear strength criterion of layer-saturated soil is introduced to reveal the hydration weakening in the soil due to infiltration water. Besides, the safety factor formula reflects the influence of water on gravity and seepage force.

The case study of Shuping landslide indicates that rainfall infiltration resulted in the decline of the safety factor, while the declining rate was falling. Under the rainfall intensity of 50 mm/h, the Shuping landslide was likely to fail at the time of 102 h.

Moving speed of the wetting front presents a positive correlation with slope length under the same slope angle, referred as to the apparent size effect which becomes especially evident under short slope length. The angle effect that moving speed shows a negative correlation with slope angle in both models reduces with the decrease in slope angle. In addition, increase in rainfall intensity can induce greater moving speed of the wetting front when rainfall occurs, whereas the change is moderate and progressively removing as rainfall continues.

If matric suction is small, the landslide mass is likely to slide along the bedrock surface, but more likely to slide along the wetting front when matric suction becomes larger. Therefore, high attention should be paid to shallow failure.