Feature subset selection for classification of malignant and benign breast masses in digital mammography

Abstract

Computer-aided diagnosis of breast cancer is becoming increasingly a necessity given the exponential growth of performed mammograms. In particular, the breast mass diagnosis and classification arouse nowadays a great interest. Texture and shape are the most important criteria for the discrimination between benign and malignant masses. Various features have been proposed in the literature for the characterization of breast masses. The performance of each feature is related to its ability to discriminate masses from different classes. The feature space may include a large number of irrelevant ones which occupy a lot of storage space and decrease the classification accuracy. Therefore, a feature selection phase is usually needed to avoid these problems. The main objective of this paper is to select an optimal subset of features in order to improve masses classification performance. First, a study of various descriptors which are commonly used in the breast cancer field is conducted. Then, selection techniques are used in order to determine the most relevant features. A comparative study between selected features is performed in order to test their ability to discriminate between malignant and benign masses. The database used for experiments is composed of mammograms from the MiniMIAS database. Obtained results show that Gray-Level Run-Length Matrix features provide the best result.

1 Introduction

Breast cancer is the leading cause of cancer deaths among the female population [1]. The only way today to reduce it is its early detection using imaging techniques [2, 3]. Mammography is one of the most effective tools for prevention and early detection of breast cancer [4,5,6]. It is a screening tool used to localize suspicious tissues in the breast such as microcalcifications and masses. It allows also the detection of architectural distortion and bilateral asymmetry [7]. A mass is defined as a space-occupying lesion seen in, at least, two different projections [8]. Mass density can be high, isodense, low or fat containing. Moreover, mass margin can be circumscribed, microlobulated, indistinct or spiculated. Mass shape can be round, oval, lobular or irregular [9]. In recent years, screening campaigns are being organized in several countries. These campaigns generate a huge stream of mammograms, and it is still difficult for expert radiologists to provide accurate and consistent analysis. Therefore, computer-aided diagnosis (CAD) systems are developed to help the radiologists in detecting lesions and in taking diagnosis decisions [9,10,11,12,13,14].

A generic CAD system by image analysis includes two main stages: feature extraction stage followed by a classification stage. In the literature, various numbers of techniques are studied to describe breast abnormalities in digital mammograms. A lot of research has been done on the textural and shape analysis on mammographic images [1, 9, 14,15,16,17,18,19]. In this paper, the main objective is to determine which features optimize the classification performance.

In the process of pattern recognition, the goal is to achieve the best classification rate using required features. The extraction of these features from regions of the image is one of the important phases in this process. Features are defined as the input variables which are used for classification. The quality of a feature is related to its ability to discriminate observations from different classes. The characterization task often generates a large number of features, and the obtained features space may include a large number of irrelevant ones. This will induce greater computational cost, occupy a lot of storage space and decrease the classification performance. Thus, a feature selection phase is needed to avoid these problems. In this study, we propose an automated computer scheme in order to select an optimal subset of features for masses classification in digital mammography. The obtained results can be used in other applications such as segmentation and content-based image retrieval.

The remaining part of this paper is organized as follows. The next section gives an overview of the proposed methodology. Sections 3 to 5 describe the process of selecting features. Sections 6 and 7 present the combination of three classifiers and the different measures used to evaluate the classification performance. The experimental results are evaluated and discussed in Sect. 8. Finally, concluding remarks are given in the last section.

2 Methodology

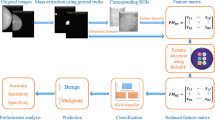
Our approach in this study is composed of two main stages: characterization and classification. Each of these stages is explained in detail by the flowchart given in Fig. 1.

Fig. 1

Flowchart of the proposed methodology performed in this study. a Characterization stage and b classification stage

2.1 Feature extraction

Various features have been proposed in the literature for the characterization of masses. These features are organized into families according to their nature [16]. The majority of studies focus on one family and analyze its performance. In this work, we propose to study the performance of a set of feature families. Then, we make a comparison between these families in order to select the best feature set. Finally, the most discriminant features are selected from the obtained feature set. The process is described in Fig. 2. {FS₁, FS₂, …, FS_i} denotes the set of feature families. For each feature family, we selected its most relevant features using a number of feature selection methods (FSM₁, FSM₂, …, FSM_j). After this step, we obtained for each FS the set {FSM₁(FS_i)}, {FSM₂(FS_i)}, …, {FSM_j(FS_i)} where FSM_j(FS_i) denotes FS_i selected features using FSM_j. Obtained results were used as input to the next step which is the selection of the best FSM that selects the most relevant features for each FS. Finally, we selected the optimal subset of features from the obtained results.

Fig. 2

Feature selection steps

Texture and shape are the major criteria for the discrimination between the benign and malignant masses. In this study, we have followed two main kinds of description techniques. The first employs texture features extracted from ROIs. The second is based on computer-extracted shape features of masses, since morphology is one of the most important factors in breast cancer diagnosis.

2.1.1 Texture analysis

Texture analysis is performed in each ROI selected in the previous phase. The texture feature space can be divided into two subspaces: statistical and frequential features.

a) Statistical features: The statistical textural features that we have used in this study can be grouped into five sets based on what they are derived from: First-Order Statistics (FOS), Gray-Level Co-occurrence Matrices (GLCM), Gray-Level Difference Matrices (GLDM), Gray-Level Run-Length Matrices (GLRLM) and Tamura features.

First-Order Statistics features: FOS provides different statistical properties of the intensity histogram of an image [20]. They depend only on individual pixel values and not on the interaction of neighboring pixels values. In this study, six first-order textural features were calculated: Mean value of gray levels, Mean square value of gray levels, Standard Deviation, Variance, Skewness and Kurtosis.

Fig. 3

Four directions of adjacency for calculating the GLCM features

Denoting by I(x,y) the image subregion pixel matrix, the formulae used for the metrics of the FOS features are as follows:

• Mean value of gray levels:

  $$M = \frac{1}{XY}\mathop \sum \limits_{x = 1}^{X} \mathop \sum \limits_{y = 1}^{Y} I\left( {x,y} \right)$$

  (1)

• Mean square value of gray levels:

  $${\text{MS}} = \frac{1}{XY}\mathop \sum \limits_{x = 1}^{X} \mathop \sum \limits_{y = 1}^{Y} \left[ {I\left( {x,y} \right)} \right]^{2}$$

  (2)

• Standard Deviation:

  $${\text{SD}} = \sqrt {\frac{1}{{\left( {XY - 1} \right)}}\mathop \sum \limits_{x = 1}^{X} \mathop \sum \limits_{y = 1}^{Y} \left[ {I\left( {x,y} \right) - M} \right]^{2} }$$

  (3)

• Variance:

  $$V = \frac{1}{{\left( {XY - 1} \right)}}\mathop \sum \limits_{x = 1}^{X} \mathop \sum \limits_{y = 1}^{Y} \left[ {I\left( {x,y} \right) - M} \right]^{2}$$

  (4)

• Skewness:

  $$S = \frac{1}{XY}\mathop \sum \limits_{x = 1}^{X} \mathop \sum \limits_{y = 1}^{Y} \left[ {\frac{{I\left( {x,y} \right) - M}}{SD}} \right]^{3}$$

  (5)

• Kurtosis:

  $$K = \left\{ {\frac{1}{XY}\mathop \sum \limits_{x = 1}^{X} \mathop \sum \limits_{y = 1}^{Y} \left[ {\frac{{I\left( {x,y} \right) - M}}{SD}} \right]^{4} } \right\} - 3$$

  (6)

Gray-Level Co-occurrence Matrix features: The second feature group is a robust statistical tool for extracting second-order texture information from images [15, 21]. The GLCM characterizes the spatial distribution of gray levels in the selected ROI. An element at location (i,j) of the GLCM represents the joint probability density of the occurrence of gray levels i and j in a specified orientation θ and specified distance d from each other (Fig. 3). Thus, for different θ and d values, different GLCMs are generated. Figure 4 shows how a GLCM with θ = 0° and d = 1 is generated. The number 4 in the co-occurrence matrix indicates that there are four occurrences of a pixel with gray level 3 immediately to the right of pixel with gray level 6.

Fig. 4

Construction principle of co-occurrence matrix. a Initial image, b co-occurrence matrix (θ = 0° and d = 1)

Nineteen features were derived from each GLCM. Specifically, the features studied are: Mean, Variance, Entropy, Contrast, Angular Second Moment (also called Energy), Dissimilarity, Correlation, Inverse Difference Moment (also called Homogeneity), Diagonal Moment, Sum Average, Sum Entropy, Sum Variance, Difference Entropy, Difference Mean, Difference Variance, Information Measure of Correlation 1, Information Measure of Correlation 2, Cluster Prominence and Cluster Shade.

Denoting by: Ng the number of gray levels in the image, p(i,j) the normalized co-occurrence matrix, p_x(i) and p_y(j) the row and column marginal probabilities, respectively, obtained by summing the columns or rows of p(i, j):

$$p_{x} \left( i \right) = \mathop \sum \limits_{j = 1}^{{N_{g} }} p\left( {i,j} \right)$$

(7)

$$p_{y} \left( j \right) = \mathop \sum \limits_{i = 1}^{{N_{g} }} p\left( {i,j} \right)$$

(8)

$$p_{x + y} \left( k \right) = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} p\left( {i,j} \right);\quad k = i + j = 2,3, \ldots ,2N_{g}$$

(9)

$$p_{x - y} \left( k \right) = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} p\left( {i,j} \right);\quad k = \left| {i - j} \right| = 0,1, \ldots ,N_{g}$$

(10)

The formulae used to calculate the GLCM features are as follows:

• Mean:

  $$M = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} i p\left( {i,j} \right)$$

  (11)

• Variance:

  $$V = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} \left[ {\left( {i - M} \right)^{2} p\left( {i,j} \right)} \right]$$

  (12)

• Entropy:

  $${\text{Ent}} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} \left[ {p\left( {i,j} \right) {\text{log}}\left( {p\left( {i,j} \right)} \right)} \right]$$

  (13)

• Contrast:

  $${\text{Cont}} = \mathop \sum \limits_{n = 0}^{{N_{g} - 1}} n^{2} \left\{ {\mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} p\left( {i,j} \right) ; \left| {i - j} \right| = n } \right\}$$

  (14)

• Angular Second Moment (also called Energy):

  $${\text{ASM}} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} \left\{ {p\left( {i,j} \right)} \right\}^{2 }$$

  (15)

• Dissimilarity:

  $${\text{Diss}} = \mathop \sum \limits_{i = 1}^{{N_{g} - 1}} \mathop \sum \limits_{j = 1}^{{N_{g} - 1}} \left( {\left| {i - j} \right| p\left( {i,j} \right)} \right)$$

  (16)

• Correlation:

  $${\text{Corr}} = \frac{{\left[ {\mathop \sum \nolimits_{i = 1}^{{N_{g} }} \mathop \sum \nolimits_{j = 1}^{{N_{g} }} \left( {ij} \right)p\left( {i,j} \right)} \right] - \mu_{x} \mu_{y} }}{{\sigma_{x} \sigma_{y} }}$$

  (17)

  where μ_x, μ_y, σ_x and σ_y are the Mean values and Standard Deviations of p_x and p_y, respectively.

  $$\mu_{x} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \left[ {i\mathop \sum \limits_{j = 1}^{{N_{g} }} p\left( {i,j} \right)} \right]$$

  (18)
  $$\mu_{y} = \mathop \sum \limits_{j = 1}^{{N_{g} }} \left[ {j\mathop \sum \limits_{i = 1}^{{N_{g} }} p\left( {i,j} \right)} \right]$$

  (19)
  $$\sigma_{x} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \left[ {\left( {i - \mu_{x} } \right)^{2} j\mathop \sum \limits_{j = 1}^{{N_{g} }} p\left( {i,j} \right)} \right]$$

  (20)
  $$\sigma_{y} = \mathop \sum \limits_{j = 1}^{{N_{g} }} \left[ {\left( {j - \mu_{y} } \right)^{2} \mathop \sum \limits_{i = 1}^{{N_{g} }} p\left( {i,j} \right)} \right]$$

  (21)

• Inverse Difference Moment (also called Homogeneity):

  $${\text{IDM}} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} \left[ {\frac{1}{{1 + \left( {i - j} \right)^{2} }}p\left( {i,j} \right)} \right]$$

  (22)

• Diagonal Moment:

  $${\text{DM}} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} (\frac{1}{2}\left( {\left| {i - j} \right|} \right) p\left( {i,j} \right))^{1/2}$$

  (23)

• Sum Average:

  $${\text{SA}} = \mathop \sum \limits_{i = 2}^{{2N_{g} }} \left[ {ip_{x + y} \left( i \right)} \right]$$

  (24)

• Sum Entropy:

  $${\text{SE}} = - \mathop \sum \limits_{i = 2}^{{2N_{g} }} \left[ {p_{x + y} \left( i \right) { \log }\left[ {p_{x + y} \left( i \right)} \right]} \right]$$

  (25)

• Sum Variance:

  $${\text{SV}} = \mathop \sum \limits_{i = 2}^{{2N_{g} }} \left[ {\left( {i - SA} \right)^{2} p_{x + y} \left( i \right)} \right]$$

  (26)

• Difference Entropy:

  $${\text{DE}} = - \mathop \sum \limits_{i = 1}^{{N_{g} }} \left[ {p_{x - y} \left( i \right) { \log }\left[ {p_{x - y} \left( i \right)} \right]} \right]$$

  (27)

• Difference Mean:

  $${\text{DMean}} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \left[ {i p_{x - y} \left( i \right)} \right]$$

  (28)

• Difference Variance:

  $${\text{DV}} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \left[ {\left( {i - {\text{DMean}}} \right)^{2} p_{x - y} \left( i \right)} \right]$$

  (29)

• Information Measure of Correlation 1:

  $${\text{IMC}}1 = \frac{HXY - HXY1}{{max\left\{ {HX,HY} \right\}}}$$

  (30)

  where HX and HY are the entropy of p_x and p_y, respectively.

  $$HX = - \mathop \sum \limits_{i = 1}^{{N_{g} }} p_{x} \left( i \right)\log \left( {p_{x} \left( i \right)} \right)$$

  (31)
  $$HY = - \mathop \sum \limits_{j = 1}^{{N_{g} }} p_{y} \left( j \right)\log \left( {p_{y} \left( j \right)} \right)$$

  (32)

  and

  $$HXY = - \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} \left[ {p\left( {i,j} \right) { \log }\left( {p\left( {i,j} \right)} \right)} \right]$$

  (33)
  $$HXY1 = - \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} \left[ {p_{x} \left( {i,j} \right) { \log }\left( {p_{x} \left( i \right)p_{y} \left( j \right)} \right)} \right]$$

  (34)

• Information Measure of Correlation 2:

  $${\text{IMC}}2 = \left[ {1 - { \exp }\left[ { - 2\left( {HXY2 - HXY} \right)} \right]} \right]^{1/2}$$

  (35)

  where

  $$HXY2 = - \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} \left[ {p_{x} \left( i \right) p_{y} \left( j \right) { \log }\left( {p_{x} \left( i \right)p_{y} \left( j \right)} \right)} \right]$$

  (36)

• Cluster Prominence:

  $${\text{CP}} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} \left( {i + j - 2M} \right)^{4} p\left( {i,j} \right)$$

  (37)

• Cluster Shade:

  $${\text{CS}} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{g} }} \left( {i + j - 2M} \right)^{3} p\left( {i,j} \right)$$

  (38)

Gray-Level Difference Matrix features: The GLDM features are extracted from the gray-level difference matrices vector of an image [22]. The GLDM vector is the histogram of the absolute difference of pixel pairs separated by a given displacement vector δ = (∆x,∆y), where I_δ(x,y)= |I(x + ∆x) − I(y + ∆y)| and ∆x and ∆y are integers. An element of GLDM vector p_δ(i) can be computed by counting the number of times that each value of I_δ(x,y) occurs. In practice, the displacement vector δ = (∆x,∆y) is usually selected to have a phase of value as 0°, 45°, 90° or 135° to obtain the oriented texture features. GLDM method is based on the generalization of a density function of gray-level difference. In this study, five GLDM features were calculated: Mean, Contrast, Angular Second Moment, Entropy and Inverse Difference Moment.

Denoting by f(i/δ) the probability density associated with possible values of I_δ, f(i/δ)= P(I_δ(x,y)= i) and M the number of gray-level differences, the formulae used for the metrics of the GLDM features are as follows:

• Mean:

  $${\text{Mean}} = \mathop \sum \limits_{i = 1}^{M} i\,f(i|\delta )$$

  (39)

• Contrast:

  $${\text{Cont}} = \mathop \sum \limits_{i = 1}^{M} i^{2}\,f\left( {i |\delta } \right)$$

  (40)

• Angular Second Moment:

  $${\text{ASM}} = \mathop \sum \limits_{i = 1}^{M} \left[ {f(i|\delta )} \right]^{2}$$

  (41)

• Entropy:

  $${\text{Ent}} = \mathop \sum \limits_{i = 1}^{M} - f\left( {i |\delta } \right)\ln \left( {f\left( {i |\delta } \right)} \right)$$

  (42)

• Inverse Difference Moment:

  $${\text{IDM}} = \mathop \sum \limits_{i = 1}^{M} \frac{f(i|\delta )}{{i^{2} + 1}}$$

  (43)

Gray-Level Run-Length Matrix features: GLRLM provides information related to the spatial distribution of gray-level runs (i.e., pixel structures of same pixel value) within the image [22]. Each gray-level run can be characterized by its gray level, length and direction. Textural features extracted from GLRLM evaluate the distribution of small (short runs) or large (long runs) organized structures within ROIs. For each of the four directions θ (0°, 45°, 90° and 135°), we can generate a GLRLM. Figure 5 shows an example of constructing a GLRLM with θ = 135°.

Fig. 5

Construction principle of GLRLM. a Initial image, b GLRLM (θ = 135°)

Denoting by Ng the number of gray levels, N_r the maximum run length and p(i,j) the (i,j)th element of the run-length matrix for a specific angle θ and a specific distance d (i.e., p_θ,_d(i,j)), each element of the run-length matrix represents the number of pixels of run length j and gray level i. Gray-Level Run-Number Vector and Run-Length Run-Number Vector are defined as follows:

• Gray-Level Run-Number Vector:

  $$p_{g} \left( i \right) = \mathop \sum \limits_{j = 1}^{{N_{r} }} p\left( {i,j} \right)$$

  (44)

  This vector represents the sum distribution of the number of runs with gray level i.

• Run-Length Run-Number Vector:

  $$p_{r} \left( j \right) = \mathop \sum \limits_{i = 1}^{{N_{g} }} p\left( {i,j} \right)$$

  (45)

  This vector represents the sum distribution of the number of runs with run length j.

• The total number of runs:

  $$N_{\text{runs}} = \mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{r} }} p\left( {i,j} \right)$$

  (46)

From each ROI, eleven GLRLM features are generated: Short Runs Emphasis (SRE), Long Runs Emphasis (LRE), Gray-Level Non-uniformity (GLN), Run-Length Non-uniformity (RLN), Run Percentage (RP), Low Gray-Level Run Emphasis (LGRE), High Gray-Level Run Emphasis (HGRE), Short Run Low Gray-Level Emphasis (SRLGE), Short Run High Gray-Level Emphasis (SRHGE), Long Run Low Gray-Level Emphasis (LRLGE) and Long Run High Gray-Level Emphasis (LRHGE).

The formulae used to calculate GLRLM features are as follows:

• Short Runs Emphasis:

  $${\text{SRE}} = \frac{1}{{N_{runs} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{r} }} \frac{{p\left( {i,j} \right)}}{{j^{2} }} = \frac{1}{{N_{runs} }}\mathop \sum \limits_{j = 1}^{{N_{r} }} \frac{{p_{r} \left( j \right)}}{{j^{2} }}$$

  (47)

• Long Runs Emphasis:

  $${\text{LRE}} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{r} }} p\left( {i,j} \right).j^{2} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{j = 1}^{{N_{r} }} p_{r} \left( j \right).j^{2}$$

  (48)

• Gray-Level Non-uniformity:

  $${\text{GLN}} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \left[ {\mathop \sum \limits_{j = 1}^{{N_{r} }} p\left( {i,j} \right)} \right]^{2} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \left[ {p_{g} \left( i \right)} \right]^{2}$$

  (49)

• Run-Length Non-uniformity:

  $${\text{RLN}} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{j = 1}^{{N_{r} }} \left[ {\mathop \sum \limits_{i = 1}^{{N_{g} }} p\left( {i,j} \right)} \right]^{2} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{j = 1}^{{N_{r} }} \left[ {p_{r} \left( j \right)} \right]^{2}$$

  (50)

• Run Percentage:

  $${\text{RP}} = \frac{{N_{\text{runs}} }}{{N_{\text{pixels}} }}$$

  (51)

  where N_pixels is the total number of pixels in the image.

• Low Gray-Level Run Emphasis:

  $${\text{LGRE}} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{r} }} \frac{{p\left( {i,j} \right)}}{{i^{2} }} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \frac{{p_{g} \left( i \right)}}{{i^{2} }}$$

  (52)

• High Gray-Level Run Emphasis:

  $${\text{HGRE}} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{r} }} p\left( {i,j} \right).i^{2} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} p_{r} \left( j \right).i^{2}$$

  (53)

• Short Run Low Gray-Level Emphasis:

  $${\text{SRLGE}} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{r} }} \frac{{p\left( {i,j} \right)}}{{i^{2} . j^{2} }}$$

  (54)

• Short Run High Gray-Level Emphasis:

  $${\text{SRHGE}} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{r} }} \frac{{p\left( {i,j} \right).i^{2} }}{{j^{2} }}$$

  (55)

• Long Run Low Gray-Level Emphasis:

  $${\text{LRLGE}} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{r} }} \frac{{p\left( {i,j} \right).j^{2} }}{{i^{2} }}$$

  (56)

• Long Run High Gray-Level Emphasis:

  $${\text{LRHGE}} = \frac{1}{{N_{\text{runs}} }}\mathop \sum \limits_{i = 1}^{{N_{g} }} \mathop \sum \limits_{j = 1}^{{N_{r} }} p\left( {i,j} \right).i^{2} . j^{2}$$

  (57)

Tamura features: Tamura et al. [23, 24] defined six texture features (coarseness, contrast, direction, linearity, regularity and roughness). The first three descriptors are based on concepts that correspond to human visual perception. They are effective and frequently used to characterize textures.

b) Frequential features: The second texture feature subspace is based on transformations. Texture is represented in a frequency domain other than the spatial domain of the image. Two different structural methods are considered: Gabor transform and two-dimensional wavelet transform.

Gabor filters: Gabor filter is widely adopted to extract texture features from the images [25, 26] and has been shown to be very efficient. Basically, Gabor filters are a group of wavelets, with each wavelet capturing energy at a specific frequency and a specific direction. After applying Gabor filters on the ROI with different orientations at different scales, we obtain an array of magnitudes:

$$E\left( {m,n} \right) = \mathop \sum \limits_{x} \mathop \sum \limits_{y} \left| {G_{mn} \left( {x,y} \right)} \right|$$

(58)

where m, n and G represent, respectively, the scale, orientation and filtered image.

These magnitudes represent the energy content at different scales and orientations of the image. Texture features are found by calculating the mean and variation of the Gabor filtered image. The following mean µ_mn and Standard Deviation σ_mn of the magnitude of the transformed coefficients are used to characterize the texture of the region.

$$\mu_{mn} = \frac{{E\left( {m,n} \right)}}{P \times Q}$$

(59)

$$\sigma_{mn} = \frac{{\sqrt {\mathop \sum \nolimits_{x} \mathop \sum \nolimits_{y} \left( {\left| {G_{mn} \left( {x,y} \right) - \mu_{mn} } \right|} \right)^{2} } }}{P \times Q}$$

(60)

Five scales and six orientations are used in common implementation, and the features vector f is created using μ_mn and σ_mn as the feature components.

$$f = \left( {\mu_{00} , \sigma_{00} , \mu_{01} , \sigma_{01} , \ldots , \mu_{30} , \sigma_{30} } \right)$$

(61)

Wavelets: Wavelets are very efficient for the characterization of texture in images (especially mammographic images) which may have different types of texture and require sufficient detail characterization. For this reason, it was chosen to be used in this study. The discrete wavelet transform (DWT) of an image is a transform based on the tree structure (successive low-pass and high-pass filters) as shown in Fig. 6. DWT decomposes a signal into scales with different frequency resolutions. The resulting decomposition is shown in Table 1. The image is divided into four bands: LL (left top), LH (right top), HL (left bottom) and HH (right bottom). High frequencies provide global information, while low frequencies provide detailed information hidden in the original image.

Fig. 6

Two-level wavelet decomposition tree (h: low-pass decomposition filter, g: high-pass decomposition filter, ↓2 down-sampling operation, A1, A2: approximated coefficient, D1, D2: detailed coefficient)

Table 1 Wavelet transform representation of an image (two levels)

Energy measures at different resolution levels are used to characterize the texture in the frequency domain.

To extract wavelet features, the type of wavelet mother function chosen is the Haar wavelet, and its mother function ψ(t) can be described as follows (Fig. 7):

Fig. 7

Haar wavelet

$$\psi \left( t \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill &\quad {0 \le t \le \frac{1}{2}} \hfill \\ { - 1} \hfill &\quad {\frac{1}{2} \le t \le 1} \hfill \\ 0 \hfill &\quad {\text{otherwise}} \hfill \\ \end{array} } \right.$$

(62)

2.1.2 Shape analysis

The shape features are also called the morphological or geometric features. These kinds of features are based on the shapes of ROIs. Seven Hu’s invariant moments were adopted for shape features extraction due to their reportedly excellent performance on shape analysis [16, 27]. These moments are computed based on the information provided by both the shape boundary and its interior region. Its values are invariant with respect to translation, scale and rotation of the shape. Given a function f(x,y), the (p,q)th moment is defined by:

$$M_{pq} = \mathop \int \limits_{ - \infty }^{ + \infty } \mathop \int \limits_{ - \infty }^{ + \infty } x^{p} y^{q} f\left( {x,y} \right)dxdy;\quad p, q = 0,1,2, \ldots$$

(63)

For implementation in digital form, Eq. 63 becomes:

$$M_{pq} = \mathop \sum \limits_{X} \mathop \sum \limits_{Y} x^{p} y^{q} f\left( {x,y} \right)$$

(64)

The central moments can then be defined in their discrete representation using the following formula:

$$\mu_{pq} = \mathop \sum \limits_{X} \mathop \sum \limits_{Y} \left( {x - \bar{x}} \right)^{p} \left( {y - \bar{y}} \right)^{q}$$

(65)

where

$$\bar{x} = \frac{{M_{10} }}{{M_{00} }}$$

(66)

$$\bar{y} = \frac{{M_{01} }}{{M_{00} }}$$

(67)

$\bar{x}$ and $\bar{y}$ are the coordinates of the image gravity center. The moments are further normalized for the effects of change of scale using the following formula:

$$\eta_{p,q} = \frac{{\mu_{p,q} }}{{\mu_{0,0}^{{\left( {1 + \frac{p + q}{2}} \right)}} }}$$

(68)

From the normalized central moments, a set of seven values Φ_i, 1 ≤ i ≤ 7, set out by Hu, may be computed by the following formulas:

$$\varPhi_{1} = \eta_{20} + \eta_{02}$$

(69)

$$\varPhi_{2} = \left( {\eta_{20} - \eta_{02} } \right)^{2} + 4\eta^{2}_{11}$$

(70)

$$\varPhi_{3} = \left( {\eta_{30} - 3\eta_{12} } \right)^{2} + \left( {\eta_{03} - 3\eta_{21} } \right)^{2}$$

(71)

$$\varPhi_{4} = \left( {\eta_{30} + \eta_{12} } \right)^{2} + \left( {\eta_{03} + \eta_{21} } \right)^{2}$$

(72)

$$\begin{aligned} \varPhi_{5} & = \left( {3\eta_{30} - 3\eta_{12} } \right)\left( {\eta_{30} + \eta_{12} } \right)\left[ {\left( {\eta_{30} + \eta_{12} } \right)^{2} - 3\left( {\eta_{21} + \eta_{03} } \right)^{2} } \right] \\ & \quad + \left( {3\eta_{21} - \eta_{03} } \right)(\eta_{21} + \eta_{03} ) \times \left[ {3\left( {\eta_{30} + \eta_{12} } \right)^{2} - \left( {\eta_{21} + \eta_{03} } \right)^{2} } \right] \\ \end{aligned}$$

(73)

$$\varPhi_{6} = \left( {\eta_{20} - \eta_{02} } \right)\left[ {\left( {\eta_{30} + \eta_{12} } \right)^{2} - \left( {\eta_{21} + \eta_{03} } \right)^{2} } \right] + 4\eta_{11} \left( {\eta_{30} + \eta_{12} } \right)\left( {\eta_{21} + \eta_{03} } \right)$$

(74)

$$\begin{aligned} \varPhi_{7} & = \left( {3\eta_{21} - \eta_{03} } \right)\left( {\eta_{30} + \eta_{12} } \right)\left[ {\left( {\eta_{30} + \eta_{12} } \right)^{2} - 3\left( {\eta_{21} + \eta_{03} } \right)^{2} } \right] \\ & \quad + \left( {3\eta_{12} - \eta_{30} } \right)(\eta_{21} + \eta_{03} ) \times \left[ {3\left( {\eta_{30} + \eta_{12} } \right)^{2} - \left( {\eta_{21} + \eta_{03} } \right)^{2} } \right] \\ \end{aligned}$$

(75)

Furthermore, fourteen significant descriptors are also developed in this section [28]:

• Area, defined as the number of pixels in the region.

• Perimeter, calculated as the distance around the boundary of the region.

• Compactness, calculated as:

  $$C = \frac{{P^{2} }}{4 \times \pi \times A}$$

  (76)

  where P and A represent the Perimeter and Area, respectively.

• Major Axis Length, defined as the length (in pixels) of the major axis of the ellipse that has the same normalized second central moments as the region.

• Minor Axis Length, defined as the length (in pixels) of the minor axis of the ellipse that has the same normalized second central moments as the region.

• Eccentricity, defined as the scalar that specifies the eccentricity of the ellipse that has the same second moments as the region. The eccentricity is the ratio of the distance between the foci of the ellipse and its Major Axis Length. The value is between 0 and 1. 0 and 1 are degenerate cases: An ellipse whose eccentricity is 0 is actually a circle, while an ellipse whose eccentricity is 1 is a line segment.

• Orientation is defined as the angle (in degrees ranging from − 90 to 90 degrees) between the x-axis and the major axis of the ellipse that has the same second moments as the region.

• Equivalent diameter specifies the diameter of a circle with the same area as the region. It is computed as:

  $${\text{Eq}}_{\text{diam}} = \sqrt {\frac{4 \times A}{\pi }}$$

  (77)

• Convex polygon area specifies the proportion of the pixels in the convex hull (the smallest convex polygon that can contain the region).

• Solidity specifies the proportion of the pixels in the convex hull that are also in the region. It is computed as the Area/ConvexArea where ConvexArea is a scalar that specifies the number of pixels in the convex hull.

• Euler Number specifies the number of objects in the region minus the number of holes in those objects.

• Extent specifies the ratio of pixels in the region to pixels in the total bounding box (the smallest rectangle containing the region). It is computed as the Area divided by the area of the bounding box.

• Mean Intensity, calculated as the mean of all the intensity values in the region.

• Aspect ratio, the aspect ratio of a region describes the proportional relationship between its width and its height. It is computed as:

  $${\text{Aspect}}_{\text{ratio}} = \frac{{x_{ {\max} } - x_{ {\min} } + 1}}{{y_{ {\max} } - y_{ {\min} } + 1}}$$

  (78)

  where (x_min, y_min) and (x_max, y_max) are the coordinates of the upper left corner and lower right corner of the bounding box.

3 Feature selection

At the stage of feature analysis, many features are generated for each ROI. The feature space is very large and complex due to the wide diversity of the normal tissues and the variety of the abnormalities. Only some of them are significant. With a large number of features, the computational cost will increase. Irrelevant and redundant features may affect the training process and consequently minimize the classification accuracy. The main goal of feature selection is to reduce the dimensionality by eliminating irrelevant features and selecting the best discriminative ones. Many search methods are proposed for feature selection. These methods could be categorized into sequential or randomized feature selection. Sequential methods are simple and fast but they could not backtrack, which means that they are candidate to fall into local minima. The problem of local minima is solved in randomized feature selection methods, but with randomized methods it is difficult to choose proper parameters.

To avoid problems of local minima and choosing proper parameters, we have opted to use five feature selection methods. Then, using an evaluation criterion, we retain the method that gives the best results among them. The feature selection methods that we have used are: tabu search (TS), genetic algorithm (GA), ReliefF algorithm (RA), sequential forward selection (SFS) and sequential backward selection (SBS). We used all extracted features as input for selection methods individually.

3.1 Tabu search

The tabu search is a meta-heuristic approach that can be used to solve combinatorial optimization problem. TS is conceptually simple and elegant. It has recently received widespread attention [25]. It is a form of local neighborhood search. It differs from the local search techniques in the sense that tabu search allows moving to a new solution which makes the objective function worse in the hope that it will not trap in local optimal solutions. Each solution S ∈ Ω has an associated neighborhood N(S) $\subseteq$ Ω where Ω is the set of feasible solutions. Each solution S’ ∈ N(S) is reached from S by an operation called a move to S’. Tabu search uses a short-term memory, called tabu list, to record and guide the process of the search. To avoid cycling, solutions that were recently explored are declared forbidden or tabu for a number of iterations. In this study, the size of the tabu list is set to be equal to 2. This size is reasonable to ensure diversity. Some additional precautions can be taken to avoid missing good solutions. These strategies are known as aspiration criteria. Aspiration level is a commonly used aspiration criterion. It is employed to override a solution’s tabu state. It allows a tabu move when it results in a solution with an objective value better than that of the current best-known solution. In addition to the tabu list, we can also use a long-term memories and other prior information about the solutions to improve the intensification and/or diversification of the search.

3.2 Genetic algorithm

Genetic algorithm is based on randomness in its search procedure to escape falling in local minima. First, a population of solutions based on the chromosomes is created. Then, the solutions are evolved by applying genetic operators such as mutation and crossover to find best solution based on the predefined fitness function (Fig. 8).

Fig. 8

Flowchart of the GA used in this study

The initial population of GA is created using the following formula:

$$P = round \left( {\left( {L - 1} \right) \times rand \left( {DF,200 \times DF} \right)} \right) + 1$$

(79)

where L and DF represent, respectively, the number of input features and the desired number of selected features. (In this work, DF = L/2.)

In GA, we use a fitness function based on the principle of max-relevance and min-redundancy (mRMR) [27]. The idea of mRMR is to select the set S with m features {x_i} that satisfies the maximization problem:

$$\hbox{max} \varPhi_{i} \left( {D,R} \right) ;\,\,\varPhi \left( {D,R} \right) = D - R$$

(80)

where D and R represent the max-relevance and min-redundancy, respectively, and are computed by the following formula:

$$D = \frac{1}{\left| S \right|}\mathop \sum \limits_{{x_{i} }} I(x_{i} ,y)$$

(81)

$$R = \frac{1}{{\left| S \right|^{2} }}\mathop \sum \limits_{{x_{i} ,x_{j} \in S}} I(x_{i} ,x_{j} )$$

(82)

where I(x_i,y) and I(x_i,x_j) represent the mutual information, which is the quantity that measures the mutual dependence of the two random variables and is computed using the following formula:

$$I\left( {x,y} \right) = H\left( x \right) + H\left( y \right) - H\left( {x,y} \right)$$

(83)

where H(.) is the entropy.

3.3 ReliefF algorithm

The key idea of the ReliefF algorithm is to estimate the quality of features according to how well their values distinguish between instances that are near to each other [29, 32]. ReliefF assigns a grade of relevance to each feature, and those features valued over a user given threshold are selected.

3.4 Sequential forward selection and sequential backward selection

SFS and SBS are classified as sequential search. The main idea of these algorithms is to add or remove features to the vector of selected features, and the iteration continues until all features are checked. Adding or removing a feature is based on one of many criteria functions that could be used. Misclassification, distance, correlation and entropy are examples of criteria functions. The main disadvantage of these algorithms is that they have a tendency to become trapped in local minima. In SFS, we start with empty list of selected feature, and successively, we add one useful feature to the list until no useful feature remains in the extracted input list. SBS instead begins with all features and repeatedly removes a feature whose removal yields the maximal performance improvement.

4 Feature dimension reduction

After selecting the most relevant features, the next step is to reduce the dimensionality of the feature set in order to minimize the computational complexity. The dimension reduction is carried out using the principal component analysis (PCA) method [30]. PCA is a powerful tool for analyzing the dependencies between the variables and compressing the data by reducing the number of dimensions, without losing too much information.

5 Feature performance

This stage has two main purposes: choosing the input parameters (distance, direction, scale, etc.), giving the best results and comparing types of features. Features are evaluated according to their discriminatory power. Five measures derived from Rodrigues approach [24] can be used as criteria for this purpose and described as follows:

5.1 The class classifier (CC) measure

The first measure is based on the detachment property. For a given class, the CC states whether or not a given class is detached from the other classes. To determine this measure, it is necessary to identify the regions occupied by elements of different classes. Every element of the class corresponds to a feature vector, and it is represented by a point in a multidimensional space. Therefore, the elements of a given class form a cloud of points included in a minimum bounding sphere (MBS). To determine the MBS of a class, we must identify its most central element (mce) and its radius. mce is the element closest to the center of the class’s MBS. It is the element s_i that minimizes Eq.  84.

$$\mathop \sum \limits_{{s_{j} \in s_{c} }} d(s_{i} ,s_{j} )$$

(84)

where S_C is the set of images of the class C in the test dataset S and d is a distance function for every element s_i ∈ S_C.

Then, the radius of the class C can be found as follows:

$$\mathop {\hbox{max} }\limits_{{s_{j} \in s_{c} }} (d(mce_{c} ,s_{j} ))$$

(85)

Once the mce_c and the radius of the given class C are identified, it is required to evaluate how much the other classes invade the MBS of each class C. This can be performed by measuring the distance from the mce_c to every element of the other classes. We consider that the elements whose distance from mce_c is smaller or equal to the radius of the class C invade the MBS of class C. For a given class, the CC measure assumes 1 (fully detached) if the class is not invaded by other classes’ elements, or 0 otherwise.

5.2 The class variance (CV) measure

The second measure is based on the condensation property. It states how condensed is each class. It corresponds to the distance variance of the elements to the center of the class. Knowing the mce_c and the radius of class C, we can calculate the CV measure. The average distance of the elements of the class C to the mce_c is calculated as:

$$\bar{d} = \frac{{\mathop \sum \nolimits_{{s_{j} \in s_{c} }} d\left( {s_{i} ,s_{j} } \right)}}{n - 1} ;\quad s_{j} \ne n$$

(86)

where n is the cardinality of class C and the variance of the class is given by:

$$S^{2} = \frac{{\mathop \sum \nolimits_{{s_{j} \in s_{c} }} (d\left( {mce_{c} ,s_{j} } \right) - \bar{d}}}{n - 1};\quad s_{j} \in mce_{c}$$

(87)

From these two measures, we proposed three other measures.

5.3 The total class classifier (TCC) measure

It corresponds to the sum of CCs.

$${\text{TCC}} = \mathop \sum \limits_{i = 1}^{t} {\text{CC}}_{{C_{i} }}$$

(88)

where t is the number of classes in ROIs database.

5.4 The weighted average of class classifiers (WACC) measure

It corresponds to the weighted average of CCs.

$${\text{WACC}} = \mathop \sum \limits_{i = 1}^{t} {\text{CC}}_{{C_{i} }} {\text{PC}}_{i}$$

(89)

where PC_i is the number of elements in each class.

5.5 The weighted average of class variances (WACV) measure

It corresponds to the weighted average of CVs.

$${\text{WACV}} = \mathop \sum \limits_{i = 1}^{t} {\text{CV}}_{{C_{i} }} {\text{PC}}_{i}$$

(90)

6 Classification

The main goal of this stage is to test the ability of most relevant features to discriminate between benign and malignant masses. Once the features relating to masses have been extracted and selected, they can then be used as inputs to the classifier to classify the regions of interest into benign and malignant. In the literature, various classifiers are described to distinguish between normal and abnormal masses. Each classifier has its advantages and disadvantages. In this work, we used three classifiers: multilayer perceptron (MLP), support vector machines (SVMs) and K-nearest neighbors (K-NNs) which have performed well in mass classification [16]. Then, we make a combination of these classifiers in order to exploit the advantages of each one of them and to improve the accuracy and efficiency of the classification system.

6.1 Multilayer perceptron (MLP)

MLP is regarded as one prominent tool for training a system as a classifier [16]. It uses simple connection of the artificial neurons to imitate the neurons in human. It also has a huge capacity of parallel computing and powerful remembrance ability. MLP is organized in successive layers: an input layer, one or more hidden layers and output layer.

6.2 Support vector machines (SVMs)

SVM is an example of supervised learning methods used for classification [28]. It is a binary classifier that for each given input data it predicts which of two possible classes comprise the input. It is based on the idea to look for the hyperplane that maximizes the margin between two classes.

6.3 K-nearest neighbors (K-NNs)

The K-NN classifier is well explored in the literature and has been proved to have good classification performance on a wide range of datasets [26]. The K-nearest neighbors of an unknown sample are selected from the training set in order to predict the class label as the most frequent one occurring in the K-neighbors. K is a parameter which can be adjusted, and it is usually an integer. It specifies the number of nearest neighbors. In this work, K is equal to 3 and Euclidean distance is used as a distance metric.

In order to accumulate the classifiers advantages and to exploit the complementarity between the three classifiers, we applied six fusion methods: Majority Vote (MV) which is based on voting algorithm and five other methods: Maximum (Max), Minimum (Min), Median (Med), Product (Prod) and Sum (S) which are based on posterior probability. Then, the best accuracy obtained after this combination is used as final result of classification.

MV technique is based on the principle of voting. The final decision is made by selecting the class with the greatest number of votes. MV is based on a majority rule expressed as follows:

$$E\left( x \right) = \left\{ {\begin{array}{*{20}l} {C_{i}\,\,if \mathop \sum \limits_{i} e\left( i \right) = \mathop {\hbox{max} }\limits_{{c_{i} \in \left\{ {1, \ldots ,M} \right\}}} \mathop \sum \limits_{j} e\left( j \right) \ge \alpha K} \hfill \\ {{\text{else}}\,\,{\text{reject}}} \hfill \\ \end{array} } \right.$$

(91)

where K is the number of classifiers (in our case K = 3); M is the number of classes (in our case M = 2); e_j(x)= C_i (i ∈ {1, …, M}) indicates that the classifier j assigned class C_i to x.

To calculate the five other methods (Max, Min, Med, Prod and Sum), we make the following assumptions:

• The decision of the kth classifier is defined as d_k,j∈{0,1}, k = 1, …, K; j = 1, …, M. If kth classifier chooses class ω_j, then d_k,j = 1, and 0, otherwise.

• X is the feature vector (derived from the input pattern) presented to the kth classifier.

• The outputs of the individual classifiers are P_k(ω_j|X), i.e., the posterior probability belonging to class j given the feature vector X.

The final ensemble decision is the class j that receives the largest support μ_j(x). Specifically

$$h_{\text{final}} \left( x \right) = \arg \mathop {\hbox{max} }\limits_{j} \mu_{j} \left( x \right)$$

(92)

where μ_j(x) are computed as follows:

• Maximum rule:

  $$\mu_{j} \left( x \right) = \mathop {\hbox{max} }\limits_{k = 1, \ldots ,K} \left\{ {d_{k,j} \left( x \right)} \right\}$$

  (93)

• Minimum rule:

  $$\mu_{j} \left( x \right) = \mathop {\hbox{min} }\limits_{k = 1, \ldots ,K} \left\{ {d_{k,j} \left( x \right)} \right\}$$

  (94)

• Median rule:

  $$\mu_{j} \left( x \right) = \mathop {med}\limits_{k = 1, \ldots ,K} \left\{ {d_{k,j} \left( x \right)} \right\}$$

  (95)

• Sum rule:

  $$\mu_{j} \left( x \right) = \mathop \sum \limits_{k = 1}^{K} d_{k,j} \left( x \right)$$

  (96)

• Product rule:

  $$\mu_{j} \left( x \right) = \mathop \prod \limits_{k = 1}^{K} d_{k,j} \left( x \right)$$

  (97)

7 Classification performance evaluation

A number of different measures are commonly used to evaluate the classification performance. These measures are derived from the confusion matrix which describes actual and predicted classes as shown in Table 2.

Table 2 Confusion matrix

• Rate of Positive Predictions:

  $${\text{RPP}} = \frac{{{\text{TP}} + {\text{FP}}}}{{{\text{TP}} + {\text{FN}} + {\text{FP}} + {\text{TN}}}}$$

  (98)

• Rate of Negative Predictions:

  $${\text{RNP}} = \frac{{{\text{TN}} + {\text{FN}}}}{{{\text{TP}} + {\text{FN}} + {\text{FP}} + {\text{TN}}}}$$

  (99)

• True Positive Rate (Sensitivity):

  $${\text{TPR}} = \frac{\text{TP}}{{{\text{TP}} + {\text{FN}}}}$$

  (100)

• False Negative Rate:

  $${\text{FNR}} = \frac{\text{FN}}{{{\text{TP}} + {\text{FN}}}}$$

  (101)

• False Positive Rate:

  $${\text{FPR}} = \frac{\text{FP}}{{{\text{TN}} + {\text{FP}}}}$$

  (102)

• True Negative Rate (Specificity):

  $${\text{TNR}} = \frac{\text{TN}}{{{\text{TN}} + {\text{FP}}}}$$

  (103)

• Positive Predictive Value:

  $${\text{PPV}} = \frac{\text{TP}}{{{\text{TP}} + {\text{FP}}}}$$

  (104)

• Negative Predictive Value:

  $${\text{NPV}} = \frac{\text{TN}}{{{\text{TN}} + {\text{FN}}}}$$

  (105)

• Accuracy:

  $${\text{AC}} = \frac{{{\text{TP}} + {\text{TN}}}}{{{\text{TP}} + {\text{FP}} + {\text{TN}} + {\text{FN}}}}$$

  (106)

• Mathews Correlation Coefficient:

  $${\text{MCC}} = \frac{{{\text{TP}} \times {\text{TN}} - {\text{FP}} \times {\text{FN}}}}{{\sqrt {\left( {{\text{TP}} + {\text{FP}}} \right) \times \left( {{\text{TP}} + {\text{FN}}} \right) \times \left( {{\text{TN}} + {\text{FP}}} \right) \times \left( {{\text{TN}} + {\text{FN}}} \right)} }}$$

  (107)

• F-measure:

  $$F = \frac{{2 \times {\text{PPV}} \times {\text{TPR}}}}{{{\text{PPV}} + {\text{TPR}}}}$$

  (108)

• G-measure:

  $$G = \sqrt {{\text{TNR}} \times {\text{TPR}}}$$

  (109)

A receiver operating characteristic (ROC) curve is also used for this stage. It is a plotting of true positive as a function of false positive. Higher ROC, approaching the perfection at the upper left hand corner, would indicate greater discrimination capacity (Fig. 9).

Fig. 9

ROC curve

8 Experimental results

All experiments were implemented in MATLAB. The source of the mammograms used in this experiment is the MiniMIAS database [31] which is publicly available for research. It contains left and right breast images for 161 patients. It is composed of 322 mammograms which includes 208 normal breasts, 63 ROIs with benign lesions and 51 ROIs with malignant (cancerous) lesions, and 80% set of abnormal images are used for training and 20% used for testing. Every X-ray film is 1024 × 1024 pixels in size, and each pixel is represented with an 8-bit word. The database includes a readme file, which details expert radiologist’s markings for each mammogram (MiniMIAS database reference number, character of background tissue, class of abnormality present, severity of abnormality, x,y image coordinates of center of abnormality and approximate radius (in pixels) of a circle enclosing the abnormality).

Figure 10 shows some cases representing three types of mammograms: normal (first line), benign (second line) and cancer (third line), downloaded from MiniMIAS database.

Fig. 10

Some samples from MiniMIAS database (normal (first line), benign (second line) and cancer (third line))

The first step in our experiments is to perform ROI selection. This involves separating the suspected areas they may contain abnormalities from the image. The ROIs are usually very small and limited to areas being determined as suspicious regions of masses. The suspicious area is an area that is brighter than its surroundings, has a regular shape with varying size and has fuzzy boundaries. Figure 11 shows two examples of masses (benign and malignant).

Fig. 11

Two examples of masses. a Benign and b malignant

The suspicious regions (benign or malignant) are marked by experienced radiologists who specified the center location and an approximate radius of a circle enclosing each abnormality. We used this information and a graphic editing tool to locate and cut the smallest square that contains the marked suspicious region. Each ROI contains only one mass. After running this step, we obtain manually for each mammogram an approximate binary mask (zero for black and one for white). Figure 12c shows one of the outputs acquired from this operation by using Fig. 12a as input. In Fig. 12c, the white region indicates the mass and the black region indicates the background. The resulting binary image will be useful in shape description.

Fig. 12

Resulting binary image. a Selection of ROI specified by an expert radiologist, b ROI containing only one mass, c mass shape in binary format

By multiplying the mask image with the origin image, we obtain the segmented mass as shown in Fig. 13.

Fig. 13

By multiplying the enhanced image (first raw) with the mask (second raw), we obtain the segmented mass shown in the third raw

Textural and shape features are calculated and extracted from the cropped ROIs. The features used in this study are listed in Table 3. For each selected ROI, the total number of computed features is 6 + 152 + 100 + 22 + 3+60 + 16 + 7+14 = 380.

Table 3 Features used in this study

Tables 4, 5, 6, 7, 8, 9, 10, 11 and 12 show the obtained texture and shape features of two examples of selected ROIs (ROI of “Mdb001.pgm” and ROI of  “Mdb028.pgm”).

Table 4 Examples of FOS features

Table 5 Examples of GLCM features (d = 1 and θ = 0°)

Table 6 Examples of GLDM features

Table 7 Examples of GLRLM features

Table 8 Examples of Tamura features

Table 9 Examples of Gabor features

Table 10 Examples of wavelet features

Table 11 Examples of Hu’s invariant moments

Table 12 Examples of other shape features

To extract Gabor transform features, five scales (1/2, 1/3, 1/4, 1/5 and 1/8) and six orientations (0, π/6, π/3, π/2, 2π/3 and 5π/6) are used. Figures 14 and 15 show, respectively, the obtained filter banc and two examples of filtered images.

Fig. 14

Filter banc used in this study

Fig. 15

Two examples of filtered images (ROI of “Mdb069.pgm”)

Applying levels of decomposition produced a large number of wavelet coefficients. So it was decided to use only two-level decomposition to reduce complexity. Figure 16 shows an example of a two-level decomposition through the Haar wavelet transform.

Fig. 16

Two-level decomposition of mammogram (ROI of “Mdb069.pgm”) through the Haar wavelet transform

With the aim of achieving optimum discrimination, a normalization procedure can be performed by assigning a weight to all features in order to measure their similarity on the same basis. The technique used was to project each feature onto a unit sphere. Features values are normalized between 0 and 1 according to the following formula:

$$Y = \left( {X - {\text{Min}}} \right)/\left( {{\text{Max}} - {\text{Min}}} \right)$$

(110)

where X is the initial feature value and Y is the feature value after normalization.

The next step is to select the most relevant features. To further explore our search space and to improve the optimal solution, we applied TS and GA ten times for feature selection, and each time the results are slightly changed from previous. Tables 13 and 14 show the selected features for each iteration. (Selected and rejected features are represented by 1 and 0, respectively.)

Table 13 Results of TS feature selection (FOS features)

Table 14 Results of GA feature selection (GLDM features)

Then, the obtained selected features (for both TS and GA) are ordered with respect to the number of occurrences of each feature in the 10 rounds and its score. The best solution corresponds to the highest score for both TS and GA. Tables 15 and 16 show the number of occurrences of each feature in the ten iterations.

Table 15 Selected features and the number of times it is selected by TS

Table 16 Selected features and the number of times it is selected by GA

The weight of each feature is calculated by applying ReliefF algorithm to the feature sets. Table 17 shows the obtained weights of HU’s invariant moments. Most relevant features correspond to the most high weights. In this case, {Mom_i, i = 1, …, 4} are the selected features from HU’s invariant moments.

Table 17 Weights of HU’s invariant moments using ReliefF algorithm

Table 18 shows the selected features using SFS and SBS for GLRLM features. (Selected and rejected features are represented by 1 and 0, respectively.)

Table 18 Selected features using SFS and SBS (GLRLM features)

Our experiment involved a binary classification, in which the classifier should recognize, whether a given ROI contains benign or malignant tissue. The goal of the experiments is to test which descriptor is best for describing mammographic images, i.e., to find out which combination of descriptors will give the best results. The effectiveness of the different feature sets is listed in Tables 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 and 33.

Table 19 Performance obtained for FOS features

Table 20 Performance obtained for GLCM features

Table 21 Performance obtained for GLDM features

Table 22 Performance obtained for GLRLM features

Table 23 Performance obtained for Tamura features

Table 24 Performance obtained for Gabor features

Table 25 Performance obtained for wavelet features

Table 26 Performance obtained for HU’s invariant moments features

Table 27 Performance obtained for other shape features

Table 28 Performance obtained for all statistical texture features

Table 29 Performance obtained for all frequential texture features

Table 30 Performance obtained for all texture features

Table 31 Performance obtained for all shape features

Table 32 Performance obtained for all features

Table 33 Best features performance

The best performances obtained for the texture and shape features correspond to GLRLM features using GA and Hu’s invariant moments using SFS, respectively. The GLRLM performance is more than performance obtained for GLRLM and Hu’s invariant moments features as shown in Table 34.

Table 34 Performance obtained for GLRLM and HU’s invariant moments features

Most relevant GLRLM and Hu’s invariant moments features are GLNU, RLNU, LGRE, SRLGLE, LRLGLE and Second Moment.

These features are then passed through three combined classifiers which determine which category the region of interest falls into to benign or malignant. Fivefold cross-validation is performed in the classification phase. We used this approach because the dataset has a relatively small number of samples. Finally, evaluation results are performed using measures presented in the previous section. The confusion matrix for selected features is presented in Tables 35, 36 and 37.

Table 35 Confusion matrix for selected GLRLM features using GA

Table 36 Confusion matrix for selected HU’s invariant moments using SFS

Table 37 Confusion matrix for selected GLRLM and HU’s invariant moments features

Table 38 shows the obtained performance measures of selected features.

Table 38 Performance measures

Table 39 depicts the classification precision and the area under ROC curve (AUC) of combined classifiers. The results show that the selected GLRLM features give best overall classification precision of 90.9%. Selected HU’s invariant moments provide the worst performance with 72.7%. Also, it is obvious that the classification of selected GLRLM features and HU’s invariant moments gives worse accuracy with an accuracy of 77.2%.

Table 39 Evaluation results

9 Conclusion

Digital mammography is the most common method for early breast cancer detection. Automated analysis of these images is very important, since manual analysis of these images is costly and inconsistent. In this paper, we made an analysis using nine different techniques for feature extraction. The proposed methodology is composed of two main stages that work in pipeline mode. The first stage consists of characterization and selection of the most relevant features. The second stage consists of classification of breast masses into benign and malignant. According to the provided examination, we can conclude that the best feature performance was achieved in the case of GLRLM descriptor. The obtained results can be used in other applications such as segmentation and content-based image retrieval.