1 Introduction

Plant classification based on the leaf images is very important and necessary with respect to agricultural information, ecological protection and plant automatic classification systems. It is well known that how to validly extract classification features is central to the plant recognition based on leaf images. Currently, the widely used features for plant recognition based on leaf image can be divided into color, shape, and texture features [1–13]. However, these techniques have not fully considered the following characteristics of plant leaf image data. (1) Diversity: plant leaf images differ from each other in a thousand ways. On the one hand, the same kind of plant leaves appear in many different colors, shapes and sizes (as shown in Fig. 1a); on the other hand, different plants sometimes have a similar shape (as shown in Fig. 1b). (2) Nonlinearity: plant leaves vary with period, location, and illumination conditions, and make them distributed under some nonlinear manifold. These properties lead to the existing plant classifying methods difficult to achieve satisfactory recognition results.

Fig. 1
figure 1

Sample images of plant leaves. a Large within-class difference, b large between-class similarity

Full size image

In plant leaf recognition and classification tasks, a key process is to reduce the dimensionality of these high-dimensionality unorganized leaf image data. Effective dimensional reduction algorithm can help to avoid the “curse of dimensionality” problem in making decisions and analyzing data efficiently. Over the past several decades, many dimensional reduction methods have been proposed. These methods could be divided into three categories according to whether utilizing the class information of the input samples: unsupervised, supervised and semi-supervised. Supervised methods have been proven to be more suitable for classification tasks than those unsupervised ones. In classification problems, the label information can be used to guide the procedure of dimensionality reduction. Among the existing methods, LDA [14] is one of the most commonly used linear supervised methods and has been widely applied to many high-dimensional classification problems. It encodes discriminant information by finding directions that maximize the ratio of between-class scatter to within-class scatter. However, there are two major drawbacks with LDA: the small-sample-size (SSS) problem and the Gaussian distribution assumption. Marginal fisher analysis (MFA) [15] is a supervised manifold learning-based method, which without the prior information on data distributions, the inter-class margin can better characterize the separability of different classes than the inter-class variance as in LDA. However, a disadvantage of MFA is that there are many parameters to be set empirically. In contrast to MFA, only one K-nearest-neighbor criterion is introduced to define the neighborhood graph in locality sensitive discriminant analysis (LSDA) [16]. Orthogonal discriminant projection (ODP) is another supervised manifold learning method [17]. ODP follows the supervised techniques and the label information is taken to model the manifold. In ODP, the weight between any two points is defined by using both local information and non-local information to explore the intrinsic structure of original data and to enhance the recognition ability.

It is well known that it is much easier to collect the unlabeled data than the labeled samples. Recently, semi-supervised learning has emerged as a hot topic in pattern recognition area. The semi-supervised learning algorithms effectively utilize a limited number of labeled samples and a large amount of unlabeled samples for real-world applications. Cai et al. [18] proposed a semi-supervised discriminant analysis (SDA), in which the labeled data points are used to maximize the discriminating ability, while the unlabeled data points are used to maximize the locality preserving power. Based on LSDA, Zhao et al. [19] proposed a locality sensitive semi-supervised (LSSS) feature selection method. Like LSDA, LSSS does not effectively consider the global information of the data. Zhang et al. [20] proposed a semi-supervised locally discriminant projection (SSLDP). SSLDP is sensitive to noise points. In our paper, like many manifold learning-based dimensionality reduction methods, the noise points are the leaves with poor quality, which may be caused by period, location, illumination, or other factors. Figure 2 illustrates some samples from the cherry blossoms leaves, where the first and second are normal, the others are noise points, which are very different from the normal samples.

Fig. 2
figure 2

Two normal and four noisy samples of cherry blossom leaves

Full size image

All the above-mentioned methods are summarized in the following Table 1.

Table 1 Summary of the dimensionality reduction methods
Full size table

Inspired by semi-supervised learning and ODP, we proposed a semi-supervised orthogonal discriminant projection (SSODP) method for plant leaf classification problem. In contrast to the original ODP algorithm, SSODP has the following desirable properties: (1) SSODP definitely utilizes the unlabeled sample information; (2) SSODP improves the weight construction by incorporating the reliability information.

The rest of the paper is organized as follows: ODP is briefly introduced in Sect. 2. SSODP is proposed in Sect. 3. Section 4 reports some experimental results based on two real plant leaf databases to demonstrate the effectiveness of the proposed method. Finally, conclusions and future work are drawn in the last section.

2 Orthogonal discriminant projection (ODP)

Assume there are n D-dimensional data points \( X_{1} ,X_{2} , \ldots X_{n} \), it is desirable to project these points into a linear subspace where the points with the same label are clustered closer and the points belonging to different classes are located farther. Let \( Y_{1} ,Y_{2} , \ldots ,Y_{n} \) denote the projections of \( X_{1} ,X_{2} , \ldots ,X_{n} \) in d-dimensional subspace, thus the projection can be expressed by \( Y_{i} = A^{T} X_{i} \), where A is a linear transformation matrix. ODP seeks to find the linear transformation through the following steps.

Firstly, an adjacency graph \( G = \left( {V,E,H} \right) \) is constructed using k nearest neighbor criterion, where G denotes the graph, V is the node set and E is the edge set. H is an adjacency matrix, whose elements are defined based on their both local information and class information:

$$ H_{ij} = \left\{ {\begin{array}{*{20}l} {E(X_{i} ,X_{j} ),} \hfill & {{\text{If }}X_{j} \in N (X_{i} ) {\text{ or }}X_{i} \in N (X_{j} )\quad {\text{and}}\quad C_{i} = C_{j} } \hfill \\ {E(X_{i} ,X_{j} ) \cdot \left( {1 - E(X_{i} ,X_{j} )} \right),} \hfill & {{\text{If }}X_{j} \in N (X_{i} ) {\text{ or }}X_{i} \in N (X_{j} )\quad {\text{and}}\quad C_{i} \ne C_{j} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. , $$
(1)

where \( E(X_{i} ,X_{j} ) = \exp \left[ { - d^{2} (X_{i} ,X_{j} )/\beta^{2} } \right] \), \( d(X_{i} ,X_{j} ) \) denotes the Euclidean distance between points \( X_{i} \) and \( X_{j} \), \( N (X_{i} ) \) is the k nearest neighborhoods of \( X_{i} \), \( C_{i} \) is the label of \( X_{i} \), and \( \beta \) is a parameter which is used as a regulator.

By introducing the weight matrix \( H = \{ H_{ij} \} \), the local scatter can be expressed to:

$$ \begin{aligned} J_{L} \left( A \right) & = \frac{1}{2}\frac{1}{n}\frac{1}{n}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {H_{ij} \left( {Y_{i} - Y_{j} } \right)^{2} } } \\ & = \frac{1}{2}\frac{1}{n}\frac{1}{n}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {H_{ij} \left( {A^{T} X_{i} - A^{T} X_{j} } \right)^{T} } } \\ & = \frac{1}{2}\frac{1}{n}\frac{1}{n}A^{T} \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {H_{ij} \left( {X_{i} - X_{j} } \right)\left( {X_{i} - X_{j} } \right)^{T} } } A \\ & = A^{T} S_{L} A \\ \end{aligned} $$
(2)

where \( S_{L} = \frac{1}{2}\frac{1}{n}\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {H_{ij} \left( {X_{i} - X_{j} } \right)\left( {X_{i} - X_{j} } \right)^{T} } } \).

After characterizing the local scatter, the non-local scatter can be characterized by the following expression,

$$ \begin{aligned} J_{N} \left( A \right) & = \frac{1}{2}\frac{1}{n}\frac{1}{n}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {(1 - H_{ij} )\left( {Y_{i} - Y_{j} } \right)^{2} } } \\ & = \frac{1}{2}\frac{1}{n}\frac{1}{n}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\left( {Y_{i} - Y_{j} } \right)^{2} } } - \frac{1}{2}\frac{1}{n}\frac{1}{n}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {H_{ij} \left( {Y_{i} - Y_{j} } \right)^{2} } } \\ & = A^{T} S_{T} A - A^{T} S_{L} A, \\ \end{aligned} $$
(3)

where \( S_{T} = \frac{1}{2}\frac{1}{n}\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {\left( {X_{i} - X_{j} } \right)\left( {X_{i} - X_{j} } \right)^{T} } } \).

After the local scatter and the non-local scatter have been constructed, an optimization objective function is devised to maximize the difference between them with the constraint of \( A^{T} A = I \). The objective function can be expressed as follows:

$$ \mathop {\arg \hbox{max} }\limits_{{A^{T} A = I}} A^{T} ((1 - \alpha )S_{T} - \alpha S_{{_{L} }}^{{}} )A , $$
(4)

where \( \alpha \) is an adjustable parameter.

The projecting matrix A is composed of the d eigenvectors associated with the d top eigenvalues of the following eigenvalue equation,

$$ ((1 - \alpha )S_{T} - \alpha S_{{_{L} }}^{{\prime }} )A = \lambda A . $$
(5)

Thus, the optimal linear features \( Y \) can be obtained by the following linear transformation:

$$ Y = A^{T} X . $$
(6)

3 Semi-supervised orthogonal discriminant projection (SSODP)

Motivated by Eq. (1), we present a new weight between any two points as follows:

$$ W_{ij} = \left\{ {\begin{array}{*{20}l} {\mathop {\text{Max}}\limits_{i} (D_{i} ) \cdot E(X_{i} ,X_{j} ) \cdot \left( {1 + E(X_{i} ,X_{j} )} \right),} \hfill & {{\text{If }}X_{j} \in N (X_{i} ) {\text{ or }}X_{i} \in N (X_{j} )\quad {\text{and}}\quad C_{i} = C_{j} ,i \ne j} \hfill \\ {\mathop {\text{Min}}\limits_{i} (D_{i} ) \cdot E(X_{i} ,X_{j} ) \cdot \left( {1 - E(X_{i} ,X_{j} )} \right),} \hfill & {{\text{If }}X_{j} \in N (X_{i} ) {\text{ or }}X_{i} \in N (X_{j} )\quad {\text{and}}\quad C_{i} \ne C_{j} } \hfill \\ {\mathop {\text{Mean}}\limits_{{X_{j} \in N(X_{i} )\;{\text{or}}\;X_{i} \in N(X_{j} )}} [E(X_{i} ,X_{j} )] \cdot E(X_{i} ,X_{j} ),} \hfill & {{\text{If }}X_{j} \in N (X_{i} ) {\text{ or }}X_{i} \in N (X_{j} )\quad {\text{and}}\quad X_{i} \;{\text{or}}\;X_{j} \;{\text{is unlabeled}}} \hfill \\ {0,} \hfill & {\text{otherwise}}, \hfill \\ \end{array} } \right. $$
(7)

where \( D_{i} = \frac{1}{k}\sum\nolimits_{{X_{j} \in N(X_{i} )}} {E(X_{i} ,X_{j} )} \) is the reliability of \( X_{i} \) (\( i = 1,2, \ldots ,n \)), \( {\text{Max}}_{i} (D_{i} ) \) and \( {\text{Min}}_{i} (D_{i} ) \) is the maximum and minimum of \( D_{i} \)(i = 1,2,…,n), respectively. \( {\text{Mean}}_{{X_{j} \in N(X_{i} )\;{\text{or}}\;X_{i} \in N(X_{j} )}} E(X_{i} ,X_{j} ) = \frac{1}{2k}\sum\nolimits_{{X_{j} \in N(X_{i} )\;{\text{or}}\;X_{i} \in N(X_{j} )}} {E(X_{i} ,X_{j} )} \) is the weight mean of \( X_{j} \) in \( N (X_{i} ) \) or \( X_{i} \) in \( N (X_{j} ) \), and make W ii  = 0 to avoid the self-similarity of data points.

Figure 3 shows the typical plot of W ij as a function of \( d^{2} (X_{i} ,X_{j} )/\beta^{2} \), where supposing \( D_{i} \) = 1(i = 1, 2,…,n), so \( {\text{Max}}_{i} (D_{i} ) = {\text{Min}}_{i} (D_{i} ) = {\text{Mean}}(D_{i} ) = 1 \).

Fig. 3
figure 3

Typical plot of W ij as a function of \( d^{2} (X_{i} ,X_{j} )/\beta^{2} \)

Full size image

In Fig. 3, the curve A1 denotes X j is among the k nearest neighborhoods of X i or X i is among the k nearest neighborhoods of X j and they belong to the same class. The curve A2 denotes X j is among the k nearest neighborhoods of X i or X i is among the k nearest neighborhoods of X j and they do not belong to the same class. The curve A3 denotes X j is among the k nearest neighborhoods of X i or X i is among the k nearest neighborhoods of X j and X i or X j is unlabeled. The curve A4 denotes the other cases, including W ij  = 0 to avoid self-loops.

According to the Eq. (7), W ij indicates that the neighboring points have more impact on the weight than the far-apart points. W ij reflects not only the class information and reliability information of the data, but also the basic neighborhood relation between two points. This property demonstrates the discriminant similarity of the data. Since the Euclidean distance \( d(X_{i} ,X_{j} ) \) is in the exponent, the parameter β is used to prevent \( d^{2} (X_{i} ,X_{j} ) \) from increasing too fast when \( d^{2} (X_{i} ,X_{j} ) \) is relatively large. The properties of W ij can be summarized as follows:

  1. 1.

    By using the same neighborhood size for all points in a data set the neighborhood is just large enough to include at least two neighbors in each neighborhood The justification for using local neighborhoods is based on the argument that the weights should depend on the local geometry rather than the global structure of the whole data set.

  2. 2.

    In Eq. (7), \( D_{i} \) expresses the reliability information; \( E(X_{i} ,X_{j} ) \) expresses local neighbor information; \( 1 + E(X_{i} ,X_{j} ) \) and \( 1 - E(X_{i} ,X_{j} ) \) express the discriminant information.

  3. 3.

    \( D_{i} \) of \( X_{i} \) is large if its k nearest neighbors are all closer to its vicinity, and small if they are far from its vicinity.

  4. 4.

    Since \( 1 < 1 + E(X_{i} ,X_{j} ) < 2 \) and \( 0 < 1 - E(X_{i} ,X_{j} ) < 1 \), when the Euclidean distance is equal, the within-class weight is larger than the between-class weight. This characteristic provides a certain chance to the points in the same class to have the larger weight than those in different classes, which is preferred for classification tasks.

  5. 5.

    With the decrease of the Euclidean distance, the between-class weight decreases toward 0. It means for the closer points from different classes that the larger \( E(X_{i} ,X_{j} ) \), the smaller \( 1 - E(X_{i} ,X_{j} ) \) and the smaller value of weight.

With the new definition of the weight W ij , the new semi-supervised dimensionality reduction algorithm is proposed as follows:

Due to the above properties of W ij , we apply W = [W ij ] to the original ODP for improving the discriminant ability of the dimensionality reduction methods. Given n D-dimensional data points \( X = (X_{1} ,X_{2} , \ldots ,X_{n} ) \), each column vector X i represents a sample, we can construct an undirected full connected graph \( G = \left( {V,E,W} \right) \), where each vertex represents a sample in X and the element W ij defined as Eq. (7) in matrix W is the weight of edge between node X i and X j . W ij can reflect the similarity between X i and X j . Considering a linear projection \( A \in R^{n \times d} \) that maps each point \( X_{i} \) in the original space to a lower dimensionality vector \( Y_{i} \in R^{d} ,Y_{i} = A^{T} X_{i} \), the local scatter \( J_{L}^{{\prime }} \) and non-local scatter \( J_{N}^{{\prime }} \) can be defined as follows:

$$ J_{L}^{{\prime }} \left( A \right) = \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {W_{ij} \left( {Y_{i} - Y_{j} } \right)^{2} } } $$
(8)
$$ J_{N}^{{\prime }} \left( A \right) = \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {(1 - W_{ij} )\left( {Y_{i} - Y_{j} } \right)^{2} } } $$
(9)

By simple algebraic formulation, Eq. (8) can be formulated as:

$$ \begin{aligned} \frac{1}{2}J_{L}^{{\prime }} (A) & = \frac{1}{2}\sum\limits_{i} {\sum\limits_{j} {W_{ij} \left( {A^{T} X_{i} - A^{T} X_{j} } \right)^{2} } } \\ & = \sum\limits_{i = 1}^{n} {\sum\limits_{i = 1}^{n} {A^{T} X_{i} D_{ii} X_{i}^{T} A} - \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {A^{T} X_{i} W_{ij} X_{j}^{T} A} } } \\ & = A^{T} XS_{L}^{{\prime }} X^{T} A \\ \end{aligned} $$
(10)

where \( S_{L}^{{\prime }} = D - W \) is the graph Laplacian of the within-class graph and \( W = \{ W_{ij} \} \), D is a diagonal matrix with entries \( D_{ii} = \sum\nolimits_{j} {W_{ij} } \).

Similarly, Eq. (9) can be formulated as:

$$ \begin{aligned} \frac{1}{2}J_{N}^{{\prime }} (A) & = \frac{1}{2}\sum\limits_{i} {\sum\limits_{j} {\left( {1 - W_{ij} } \right)\left( {A^{T} X_{i} - A^{T} X_{j} } \right)^{2} } } \\ & = A^{T} X(E_{ii} - F_{ij} )X^{T} A \\ & = A^{T} XS_{N}^{'} X^{T} A, \\ \end{aligned} $$
(11)

where \( S_{N}^{'} = E - F \) is the graph Laplacian of the between-class graph and, \( F = \{ 1 - W_{ij} \} \), E is a diagonal matrix with entries \( E = \sum\nolimits_{j} {(1 - W_{ij} )} \).

After the local scatter \( J_{L}^{{\prime }} \) and the non-local scatter \( J_{N}^{{\prime }} \) have been constructed, the objective function is written as:

$$ \begin{gathered} \arg \mathop {\hbox{max} }\limits_{A} \frac{{tr\left( {A^{T} XS_{N}^{{\prime }} X^{T} A} \right)}}{{tr\left( {A^{T} XS_{L}^{{\prime }} X^{T} A} \right)}} \hfill \\ s.t. \, A^{T} A = I. \hfill \\ \end{gathered} $$
(12)

The Lagrangian function of the problem Eq. (10) is

$$ \arg \mathop {\hbox{max} }\limits_{A} \frac{{tr\left( {A^{T} XS_{N}^{{\prime }} X^{T} A} \right)}}{{tr\left( {A^{T} XS_{L}^{{\prime }} X^{T} A} \right)}} - \lambda (A^{T} A - I) = 0 . $$
(13)

In order to get the \( d \)th orthogonal basis vector, we maximize the following objective function:

$$ \arg \mathop {\hbox{max} }\limits_{A} \frac{{tr\left( {A^{T} XS_{N}^{'} X^{T} A} \right)}}{{tr\left( {A^{T} XS_{L}^{'} X^{T} A} \right)}} $$
(14)

with the constraints \( a_{d}^{T} a_{1} = a_{d}^{T} a_{2} = \cdots = a_{d}^{T} a_{d - 1} = 0 \), where d is the output reduction dimensionality.

To solve the above optimization problem, we use the Lagrangian multiplier:

$$ f = a_{d}^{T} (XS_{N}^{{\prime }} X^{T} - \delta XS_{L}^{{\prime }} X^{T} )a_{d} - \lambda_{1} a_{d}^{T} a_{1} - \lambda_{2} a_{d}^{T} a_{2} - \cdots - \lambda_{d - 1} a_{d}^{T} a_{d - 1} $$
(15)

where \( \delta \) is a number to be determined.Set the partial derivative of \( f \) with respect to \( a_{d} \) to zero and obtain

$$ 2(XS_{N}^{{\prime }} X^{T} - \delta XS_{L}^{{\prime }} X^{T} )a_{d} - \lambda_{1} a_{1} - \lambda_{2} a_{2} - \cdots - \lambda_{d - 1} a_{d - 1} = 0 $$
(16)

Multiplying the left side of Eq. (14) by \( a_{d}^{T} \), we obtain

$$ a_{d}^{T} (XS_{N}^{{\prime }} X^{T} - \delta XS_{L}^{{\prime }} X^{T} )a_{d} = 0 \Rightarrow \delta = \frac{{tr\left( {A^{T} XS_{N}^{{\prime }} X^{T} A} \right)}}{{tr\left( {A^{T} XS_{L}^{{\prime }} X^{T} A} \right)}} . $$
(17)

According to the paper [21, 22], the orthogonal iterative algorithm of solving the orthogonal vectors of SSODP is summarized as follows:

  1. 1.

    Initialize A as an arbitrary column-orthogonal matrix.

  2. 2.

    Compute the trace ratio value \( \delta = \frac{{tr\left( {A^{T} XS_{N}^{{\prime }} X^{T} A} \right)}}{{tr\left( {A^{T} XS_{L}^{{\prime }} X^{T} A} \right)}} \).

  3. 3.

    Form the trace difference problem as \( A^{\prime } = \max_{{A^{T} A = I}} tr(A^{T} (XS_{N}^{\prime } X^{T} - \delta XS_{L}^{\prime } X^{T} )A) \).

  4. 4.

    Establish \( A^{{\prime }} \) by the d eigenvectors of \( XS_{N}^{{\prime }} X^{T} - \delta XS_{L}^{{\prime }} X^{T} \) corresponding to the d largest eigenvalues.

  5. 5.

    Update A by \( A^{{\prime }} \).

  6. 6.

    Iteratively perform steps (2)–(5) until convergence.

  7. 7.

    Output the final linear transformation matrix.

From the above iterative processes, we obtain the mapping matrix \( A = (a_{1} ,a_{2} , \ldots ,a_{d} ) \). The low-dimensional representation in the SSODP subspace is defined as follows:

$$ X \to Y = A^{T} X $$
(18)

4 Experiments

In this section, we apply the proposed method to plant leaf classification in two public leaf databases. One is ICL-Plant Leaf database (http://www.intelengine.cn/source.htm), which contains more than 30,000 leaf images of 362 plant species. All leaf images were captured in different seasons, and at different locations and natural illuminations. Another is Swedish leaf dataset. The Swedish leaf dataset [23] contains 1125 images of leaves uniformly distributed in 15 species. The Swedish leaf dataset is very challenging because of its high inter-species similarity.

In the two databases, the original leaf images contain footstalks or petioles, which are not suitable for robust leaf recognition, since the length and orientation of those footstalks may heavily depend on the collection process. So we crop and normalize (in scale and orientation) and resize them to 32 × 32 pixels by histogram equilibrium with 255 gray levels per pixel and with the white background. All leaf images are represented as points in vector space. A typical image of size 32 × 32 describes a point in 1024-dimensional vector space.

In the two databases, although all leaf images are provided with class labels, for each experiment, we randomly draw several samples from every database as a training set, among them, a random subset is used with labels as the labeled subset, and the remained are used as the unlabeled subset.

To verify the effectiveness of the proposed method, we compared it with RLDA [24], ODP [17], SDA [18], and SSLDP [20]. ODP only makes use of the labeled data points. However, SDA, SSDR and our proposed method make use of both labeled and unlabeled data points. The training set is used to learn the low-dimensional subspace with the projection matrix. The testing set is used to obtain the final recognition rate. In every experiment, firstly, we randomly select an amount of images from all selected images as training set and the rest as testing set; secondly, we execute the dimensionality reduction method on the training dataset and obtain the mapping matrix; then the testing set is projected into the low-dimensional feature subspace; finally, the plant leaf images of the testing set are recognized by a suitable classifier. The parameters k and β are determined empirically. In the following experiments, the 1-nearest-neighbor (1-NN) classifier with Euclidean distance is adopted to classify plant leaf images. In these methods, PCA is used for data preprocessing (dimension reduction) in order to avoid the singular matrix problem and improve the computational efficiency.

4.1 Experiments on ICL-plant leaf database

In experiments, we select 500 leaf images from 20 kinds of plants and each plant has 25 leaf images. Figure 4 shows 20 representative leaf images of 20 plant species.

Fig. 4
figure 4

The representative leaf images of 20 plant species

Full size image

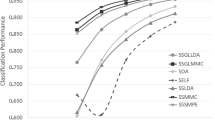
The classifying experiments are conducted to evaluate the effectiveness of the proposed method and to examine the effectiveness of the training number and the number of labeled points in training set on the performance. After all images preprocessed, from each kind of plant, we randomly select m leaf images as the training set, the rest (25 − m) is regarded as the test set, among them, l(l = 1, 2, 3, 4, 5, 6) labeled leaf images and m − l unlabeled leaf images. For each given m and l, a trial is independently performed 50 times. The maximal average result of every experiment is recorded. The average recognition rate means the performance of the classifier with the best set of fitted parameters. The final result is the average correct recognition rate and standard derivation over 50 random splits. We find that the proposed method is not sensitive to β when it is enough large, so we set β = 200. The other parameters k and d are decided by the maximal correct recognition results. Table 2 shows the performance of RLDA, ODP, SDA, SSLDP, and the proposed algorithm. As can be seen, our algorithm achieved 97.12 % recognition rate when six leaf labeled images per class were used for training, which is the best out of the six algorithms. We test the influence of selecting different dimensions in the reduced subspace on the recognition rate, as shown in Fig. 5, where m = 10 and l = 4. In general, the performance of all these methods varies with the number of dimensions. At the beginning, the recognition rates increase greatly as d increases. However, more dimensions do not lead to higher recognition rate after these methods attain the best results.

Table 2 Average correct recognition rates and standard derivation comparing with LPP, ODP, SDA, SSDR, SSLDP on the ICL-plant leaf database, where k = 15 and β = 200
Full size table
Fig. 5
figure 5

Plant leaf recognition rates versus the reduction dimensionality, where m = 10 and l = 4

Full size image

4.2 Experiments on Swedish leaf database

The Swedish leaf data set comes from a leaf classification project at Linköping University and the Swedish Museum of Natural History [23]. The data set contains the isolated leaves from 15 different Swedish tree species, with 75 leaves per species. Figure 6 shows the representative leaf images of 15 different Swedish trees.

Fig. 6
figure 6

The representative images of 15 different species in Swedish leaf database, one image per species. Note that some species are quite similar, e.g., the first, third, and ninth images

Full size image

The experimental design is the same as before. In every experiment, this procedure is also repeated 50 times and we obtain 50 maximal results for the proposed algorithm and each of the compared methods. The average recognition rates and standard derivations are recorded, as seen in Table 3. From Table 3, we can see three main points. First, OLDSE-ISSODP outperforms the other algorithms among all the cases. For example, when the ten leaf images per species are used for training, SSODP leads RLDA, ODP, SDA, and SSLDP up to 1.12, 4.05, 3.11, and 0.69 %, respectively. Second, SDA, SSLDP, and SSODP perform better than RLDA and ODP. The reason is that the semi-supervised methods make use of all the training images (including labeled and unlabeled images).

Table 3 Average recognition correct rates and standard derivation comparing with LPP, ODP, SDA, SSDR, SSLDP on the Swedish leaf database, where k = 10 and β = 200
Full size table

5 Discussion

From Tables 2, 3 and Fig. 5, we can see that the semi-supervised methods outperform ODP. The reason is that the semi-supervised methods make use of all the training images (including labeled and unlabeled images), while ODP only use the labeled data points. It is worth pointing out that the recognition rates in the optimizing procedure mainly depend on the ways of splitting the given training data set and the number of the labeled points. From Tables 2 and 3, as more leaf images and the labeled data points split from the given data set are used for training, the recognition rates increase for all the compared algorithms. This demonstrates that all the algorithms are capable of learning from these data points. Particularly, when l = 1, the recognition rates of SSLDP and SSODP are more than 70 %, so the intrinsic image manifold can still be estimated even with a single labeled leaf image per class.

From Tables 2, 3 and Fig. 5, we can see our method outperforms the other methods. A possible explanation is that our method is more robust. In fact, there are some irregular-shaped leaf images in the two plant leaf databases, which were taken from the same tree or from the same leaf in different sessions, so the similarity (or weight) of intra-leaf may be smaller than that of inter-leaf, as seen Fig. 1. As a result, nearest neighborhood points may belong to the different classes. Moreover, the leaf images were taken during two different sessions, so that the appearance of the same leaf image may look different, resulting in different distributions of the data points in the two sessions. The nearest neighbors of a point are more likely to belong to different classes. If points within the same nearest neighborhood are treated from the same class as ODP or SDA does, the recognition accuracy may be seriously affected. In our proposed method, we use \( {\text{Max}}_{i} (D_{i} ) \), \( {\text{Min}}_{i} (D_{i} ) \), and \( {\text{Mean}}_{{X_{j} \in N(X_{i} )\;{\text{or}}\;X_{i} \in N(X_{j} )}} \) to weaken the impact of the irregular-shaped or distorted leaves. In order to explain this conclusion, the experiments include several irregular-shaped leaf images in the training set and test set. To test whether our method is sensitive to such irregular-shaped leaf images, we remove them from the training set and conduct the experiments. The results indicate that the recognition rates are slightly affected by this kind of phenomenon. The reason might lie in the robust path-based similarity measurement [25]. In [25], the similarity expression \( \alpha_{i} = \sum\nolimits_{{X_{j} \in N(X_{i} )}} {E(X_{i} ,X_{j} )} \) is adopted to improve the robustness of the algorithm to noise points.

6 Conclusions and future works

Semi-supervised manifold learning-based methods have aroused a great deal of interest in dimensionality reduction. In this paper, a semi-supervised dimensionality reduction algorithm named semi-supervised orthogonal discriminant projection (SSODP) was proposed and applied successfully to leaf classification. SSODP utilizes all labeled and unlabeled samples to construct the weight between any pairwise points. The experiment results on leaf images demonstrated that SSODP is effective and feasible for leaf classification.

In SSODP, the common assumption is that we only have a limited number of labeled training samples. Developing an adaptive algorithm to automatically adjust the parameters k and β is our future work. In addition, in this paper, we focus on developing a semi-supervised manifold learning technique for leaf classification but do not systematically analyze the stability and robustness of the SSODP. This is a problem deserving further investigation.