Introduction

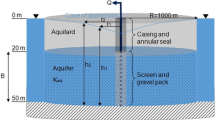
Worldwide, groundwater is one of the most important, safest and most reliable sources of freshwater. It is much less prone to evaporation and less vulnerable to contamination than surface water. Wells are the most common tools to extract and inject groundwater (and bank filtrate). Various applications of wells are summarized in Fig. 1. Here, the focus will be on the most common well type, the vertically screened well with an artificial filter pack, pumping groundwater from a porous, confined aquifer (Fig. 2). Influences of neighboring wells and ageing processes will not be discussed.

Fig. 1
figure 1

Types of water well use: a water supply, b dewatering for mining and construction, c injection, e.g. liquid waste disposal, d geothermal energy

Full size image
Fig. 2
figure 2

Main components of a vertical water well. 1 = screen, 2 = gravel pack, 3 = piezometer, 4 = sand filter, 5 = annular seal, 6 = annular fill, 7 = well head, 8 = protective cover, 9 = pipeline, 10 = air vent, 11 = water level of upper aquifer, 12 = water level of lower aquifer, 13 = electrical installations, 14 = foot cementation, 15 = upper aquifer, 16 = aquitard, 17 = lower aquifer (production aquifer), 18 = top soil, 19 = access door, 20 = soil backfill, 21 = pump, 22 = riser pipe, 23 = sump, 24 = borehole wall, 25 = drilling (or borehole) diameter, 26 = screen diameter, 27 = electric cable, 28 = backflow preventer valve, 29 = flow meter, 30 = protective cover of piezometer (modified after Houben and Treskatis 2007)

Full size image

Even today, most wells are dimensioned and designed purely based on the experience of the drilling company. Understanding the geological and technical constraints of the well geometry and its components can lead to a more efficient well design, which may lead a reduction of entrance losses and a deceleration of well ageing, thereby lowering costs and extending well life.

The number of wells differs markedly between countries (Table 1) and is a function of climate, agricultural practices and standard of living. In humid and densely populated countries with almost comprehensive water network coverage, like Denmark, the Netherlands and Germany, most of the groundwater is abstracted for public water supply by water utilities using relatively few wells, but at high pumping rates. In arid countries, where agriculture largely depends on irrigation from groundwater, well numbers are significantly higher. In India, the world’s largest user of groundwater, the estimated 20 million wells are mostly in use for irrigation but pump rather small volumes per well (Shah et al. 2004). In less densely populated countries, e.g. the USA and Canada, many households in the countryside are not connected to public water supply networks. In the USA, 13.25 million households therefore operate a private well, while 410,000 irrigation wells are in use—National Ground Water Association (NGWA) 2015. The sheer number of wells in use around the world merits studying their hydraulics.

Table 1 Groundwater abstraction (including bank filtrate and artificial recharge) and number of water wells in selected countries
Full size table

The energy demand of water supply also needs to be considered. In Germany, where more than three quarters of all drinking water comes from groundwater or bank filtrate, 0.5 % of the country’s primary energy demand are used for extraction, treatment and distribution of water (ATT et al. 2011). In India, around 100,000 GWh/year are used to run the irrigation wells, equivalent to 20 % of the electricity generated in the country (Shah et al. 2004). Since many pumps run on local diesel-fed electricity generators, their energy consumption would have to be added to this number.

The topic of well hydraulics is discussed in numerous review publications and textbooks, e.g. by Driscoll (1986), Roscoe Moss (1990), Vukovic and Soro (1992), Barker and Herbert (1992a, b), Parsons (1994) and Kasenow (2010). All of them, however, assess the topic from a different perspective and with different emphasis. In the meantime, new papers have been published and new methods, especially numerical simulations, have been introduced. The rationale for this study is to review the most important historical and new approaches describing well hydraulics, in order to show their possibilities and limitations. This review covers literature published over a period of more than 100 years. Some of the older literature is only available in German (e.g. Weisbach 1845; Smreker 1878, 1914; Forchheimer 1901a, b; Thiem 1906; Sichardt 1928; Kozeny 1933; Nahrgang 1954, 1965; Heinrich 1964; Klotz 1971) and is, thus, often ignored or sometimes even cited or interpreted incorrectly. In a paper related to this study (Houben 2015), the practical consequences of well hydraulics for well design are discussed in detail for all of the individual well components.

This paper mostly relies on analytical (closed form) and empirical equations that allow quantifying the contribution of well geometry and individual well components to total head loss. It will briefly touch upon more advanced, mostly numerical methods. Not included is a discussion of the field methods used to investigate well performance, especially step-discharge tests, which in the light of recent publications would merit their own review. This paper also refrains from an economic appraisal of well design, e.g. the capital and recurring costs resulting from the individual components discussed. The interested reader is referred to, e.g. Stoner et al. (1979) or Helweg (1982).

The term “hydraulics of water wells” includes all hydrodynamic processes occurring in the well interior, the screen, the gravel pack and the adjacent aquifer. Other terms used in literature are “near-field hydraulics of wells” (Houben and Hauschild 2011) and “well hydrodynamics” (von Hofe and Helweg 1998). One must not, however, confuse well hydraulics with pumping tests, which usually are done to gain information on aquifer properties (Batu 1998).

Background: radial flow of groundwater to wells

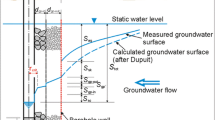
The most common assumption for the flow of groundwater towards a well is a radial symmetry of the flow field (Fig. 3a) although in reality the flow field may be distorted by the superposition of the natural background flow field (Fig. 3b). When a constant flux Q approaches a well, the radial cross-sectional area A which the water passes is continuously reduced when nearing the well. The velocity of flow v f therefore has to increase towards the well to account for the law of continuity (Fig. 4). For the idealized conditions of radially symmetric flow, the area can be expressed as the surface of a cylinder. The velocity may be expressed as

$$ {v}_{\mathrm{f}}=\frac{Q}{A}=\frac{Q}{2\cdot \pi \cdot r\cdot b} $$
(1)

where r is the radius (distance from well axis) and b the height of the cylinder here (= aquifer thickness); however, this does not take into account that water can only flow through the open area (note, all terms are defined in the Appendix). The open area A p available for flow can be the effective porosity of a porous granular medium or the open area fraction of a screen. Equation (2) is the one commonly used to calculate entrance velocities of wells at the screen.

Fig. 3
figure 3

Schematic illustration of flow towards a well in plan view: a radially symmetric cone of depression with no natural background gradient, b cone of depression with natural background gradient

Full size image
Fig. 4
figure 4

Flow velocity increase due to the decrease of throughflow area. Modified after Houben and Treskatis (2007)

Full size image
$$ {v}_{\mathrm{a}}=\frac{Q}{2\cdot \pi \cdot r\cdot b\cdot {A}_{\mathrm{p}}} $$
(2)

The regimes of flow in porous media

Delineation of flow regimes

Experimental investigations of the relationship between the hydraulic gradient and specific discharge show three regimes of flow (Fig. 5). At lower gradients, the relationship is fully linear and viscous effects dominate. This regime is described by the linear Darcy law (linear laminar flow) which hydrogeologists almost exclusively use to describe groundwater flow (Darcy 1856). At a certain threshold gradient, however, the corresponding specific discharge is lower than predicted by the linear Darcy law. Still, flow is mostly laminar here and thus called non-linear laminar flow or Forchheimer flow (Forchheimer 1901a, b). The relationship between hydraulic gradient and specific discharge for post-Darcian flow has been investigated by various authors—see, e.g. Basak (1977) for a review. The cause of non-Darcian effects is still a topic of discussion in literature. While Hassanizadeh and Gray (1987) concluded that microscopic viscous forces are the cause for the onset of nonlinearity, many other authors, including Barak (1987), Bear (1988) and Ma and Ruth (1993) ascribed the nonlinearity to microscopic inertial forces. At even higher gradients, flow becomes truly turbulent. This regime is sometimes called the post-Forchheimer regime (Kuwahara et al. 1998).

Fig. 5
figure 5

Relationship between hydraulic gradient and specific discharge and the regimes of linear-laminar (Darcy), non-linear laminar (Forchheimer) and turbulent (post-Forchheimer or Darcy-Weisbach) flow

Full size image

The dimensionless Reynolds number (Re) is commonly employed to separate the three regimes. As suggested by Chilton and Coburn (1931), Re for flow through porous media is defined as

$$ \mathrm{R}\mathrm{e}=\frac{\mathrm{inertial}\kern0.5em \mathrm{forces}}{\mathrm{viscous}\kern0.5em \mathrm{forces}}=\frac{0.5\cdot {\rho}_{\mathrm{w}}\cdot {q}^2}{\left(\frac{q}{2{d}_{\mathrm{c}}}\right)\cdot \mu }=\frac{\rho_{\mathrm{w}}\cdot q\cdot {d}_{\mathrm{c}}}{\mu }=\frac{q\cdot {d}_{\mathrm{c}}}{v} $$
(3)

In theory, the representative length for the porous matrix d c should be the diameter of a pore channel but in practice a representative grain size is often used instead, e.g. the mean grain diameter d 50 (Bear 2007). It should be noted that alternative definitions of the Reynolds number for flow through porous media exist, e.g. by Green and Duwez (1951), Ergun (1952) and Ma and Ruth (1993) but here Eq. (3) is used.

A good illustration of the different regimes can be found in the two-dimensional (2D) experiments by Chauveteau and Thirriot (1967). Where the Reynolds number is <2, streamlines remain fixed and flow obeys the Darcy law; however, with increasing Re, streamlines start to shift and static eddies occur in the divergent parts of the model. This non-linear laminar behavior becomes more pronounced with increasing Re. At Re = 75, streamlines begin to show effects of turbulence. Some authors (e.g. Williams 1981, 1985) only distinguish between linear laminar (Darcian) and turbulent flow discussing flow towards wells and omit the non-linear laminar regime.

The increase of flow velocity towards a well indicates that deviations from the Darcy law may occur, especially very close to the well.

There is considerable uncertainty on the upper limit of Darcy flow, or, in other words, which critical Reynolds number separates the linear laminar and the non-linear laminar regimes. Fancher and Lewis (1933) performed experiments with water, crude oil and gas flowing through unconsolidated sand, loosely compacted sandstone and lead shot. For unconsolidated porous media, they obtained critical Reynolds numbers of Re = 10–1,000, for the loosely consolidated rocks of Re = 0.4–3, whereas experiments by Ergun (1952) with gas flow through packed particles yielded Re = 3–10. The textbooks by Bear (1988) and Scheidegger (1974), both based on literature reviews, list values of Re = 1–10 and Re = 0.1–75, respectively. A good historical review of work on critical Reynolds numbers is found in Şen (1989) who deduced Recrit = 1–10 with a mean of 5. Bear (1988) pointed out that if the deviations from the Darcy law are indeed caused by inertial forces, no discrete critical Reynolds number value (Recrit) should exist. The Recrit should rather be defined as Reynolds numbers where deviations from Darcy’s law become measurable. As this may vary between experimental set-ups, it becomes clear why most authors give a range instead of one discrete value for Recrit. The lower boundary of the turbulent (post-Forchheimer) regime is also uncertain. Based on a literature review of experimental studies, Bear (1988) gives a range of Re = 60–150 for the onset of turbulence in porous media. At critical Reynolds numbers between Re = 100 (e.g. Bear 2007) and 800 (Trussell and Chang 1999), flow in porous media is considered to be fully turbulent.

An alternative criterion defining the transition between linear laminar and non-linear laminar flow is the Forchheimer number (Fo; Ma and Ruth 1993; Zeng and Grigg 2006).

$$ \mathrm{F}\mathrm{o}=\frac{k\cdot {\beta}^{\prime}\cdot {\rho}_{\mathrm{w}}\cdot q}{\mu } $$
(4)

Fo is the ratio of the pressure drop induced by liquid–solid interactions to the pressure drop induced by viscous resistance or, in other words, the ratio of non-linear to linear pressure losses. The critical Forchheimer number (Focrit), indicating transition from Darcy to Forchheimer flow is in the range of 0.005–0.02, corresponding to Re = 1–10 (Ma and Ruth 1993), while Zeng and Grigg (2006) give Focrit = 0.11 (at 10 % non-Darcy effect). Some authors prefer Fo over Re, due to the fact that Fo addresses macroscopic parameters (e.g. k) rather than the microscopic parameters (e.g. d c) contained in Re (Ruth and Ma 1992; Ma and Ruth 1993; Zeng and Grigg 2006; Cherubini et al. 2012). The problem with Fo is that it requires a value for the inertial factor or Forchheimer coefficient β’ which is often not readily available.

Flow laws for linear laminar (Darcy) flow

Throughout hydrogeology, flow processes in groundwater are almost exclusively described by the linear Darcy law (Darcy 1856), here for horizontal flow, with P = ρ∙g∙h

$$ Q=-\frac{k\cdot A}{\mu}\cdot \frac{\left({P}_{\mathrm{b}}-{P}_{\mathrm{a}}\right)}{L}=-k\cdot \frac{\rho \cdot g}{\mu}\cdot A\cdot \frac{\left({h}_{\mathrm{b}}-{h}_{\mathrm{a}}\right)}{L} $$
(5)

Dividing by the area A (q = Q/A), and setting the gradient I = (h b–h a)/L yields

$$ q=-k\cdot \frac{\uprho_{\mathrm{w}}\cdot g}{\mu}\cdot I=-K $$
(6)

Since flow can only take place in an open area, e.g. the pores, a correction for the effective porosity is needed to obtain the average flow velocity.

$$ {v}_{\mathrm{a}}=\frac{q}{\varPhi_{\mathrm{e}}} $$
(7)

Another way to express Darcy’s law, as a function of the Reynolds number (Eq. 8), was proposed by Williams (1985) for radial flow.

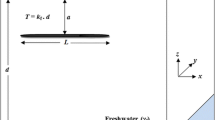
$$ \frac{dh}{dr}=\frac{a_1\cdot {v}^2\cdot \mathrm{R}\mathrm{e}}{g\cdot k\cdot {\mathrm{d}}_{\mathrm{c}}} $$
(8)

An application of the Darcy equation to radial-symmetric flow at steady state towards a fully penetrating well located in a confined, homogeneous and isotropic aquifer with even thickness in a circular island yields the Thiem equation (Thiem 1906). The derivation is found, for example, in Hendriks (2010).

$$ s={h}_2-{h}_1=\frac{Q}{2\cdot \uppi \cdot T}\cdot \ln \left(\frac{r_2}{r_1}\right) $$
(9)

with T = K · b

A similar analytical model for unconfined aquifers also exists, the so-called Dupuit-Forchheimer equation (Bear 2007; Hendriks 2010).

$$ {h_2}^2-{h_1}^2=\frac{Q}{\uppi \cdot K}\cdot \ln \left(\frac{r_2}{r_1}\right) $$
(10)

Flow laws for non-linear laminar (Forchheimer) flow

Even some of Darcy’s original data show a deviation from the linear relationship (Eq. 5) between gradient and specific discharge that he proposed (Darcy 1856; Firdaouss et al. 1997). At higher gradients and flow velocities, the specific discharge is less than predicted by Eq. (6) due to the occurrence of inertial effects. Such situations may occur close to wells and are therefore of particular interest here.

Flow equations for non-linear flow in porous media were proposed by various authors, the first probably being Smreker (1878, 1914). A good review is found in Bear (1988). Brinkman (1947) expanded the Darcy approach for flow through porous media by adding a second-order derivative of the velocity, thereby addressing the macroscopic shearing between fluid and pore walls. The pore diameters in most porous media, however, are small and the absolute variation of velocity across the pore throat is thus small (Zeng and Grigg 2006), making the Brinkman (1947) approach of little practical use for the scope of this study.

The most commonly used relationship for non-linear laminar flow is the Forchheimer (1901b) equation, which states that the hydraulic gradient (Eq. 11a) or the pressure loss (Eq. 11b) is a second-order polynomial function of the specific discharge. Forchheimer arrived at this equation empirically while trying to fit experimental data. Only later it was found that the first (linear) term in Eq. (11a) represents head losses caused by viscous forces and the second (quadratic) term those caused by inertial forces (e.g. Bear 1988, 2007). When the second term approaches zero, the Forchheimer equation equals Darcy’s law.

$$ \frac{dh}{dx}=\alpha \cdot q+\beta \cdot {q}^2=\frac{\mu }{k\cdot g\cdot \rho}\cdot q+\frac{\beta^{\prime }}{g}\cdot {q}^2=\frac{\mu }{k\cdot g\cdot \rho}\cdot q+\frac{C_2}{g\cdot \sqrt{k}}\cdot {q}^2 $$
(11a)

with α = 1/K and β = β′/g. Expressed for pressure, the Forchheimer law becomes

$$ \frac{dp}{dx}=\frac{\mu }{k}\cdot q+{\beta}^{\prime}\cdot \rho \cdot {q}^2 $$
(11b)

Forchheimer (1901b) originally proposed that introducing a third cubic term would improve the fit to the experimental data he used. While the first two terms have a physical meaning, the background of the third remains unclear.

$$ \frac{dh}{dx}=\alpha \cdot q+\beta \cdot {q}^2+\upgamma \cdot {q}^3 $$
(12a)

or, expressed for pressure (Firoozabadi and Katz 1979), as

$$ \frac{dp}{dx}=\frac{\mu }{k}\cdot q+{\beta}^{\prime}\cdot \rho \cdot {q}^2+{\upgamma}^{\prime}\cdot {\rho}^2\cdot {q}^3 $$
(12b)

It is important to be aware which form of the Forchheimer law is used, as it can be defined via the gradient (Eq. 11a), the pressure loss (Eq. 11b) or the head loss. There is considerable confusion in literature on the definition and nomenclature of the inertial factor or Forchheimer coefficient (Firoozabadi and Katz 1979). The best check is the unit.

The Forchheimer coefficient is determined through experiments and is usually assumed to be a property of the porous media (e.g. Firoozabadi and Katz 1979; Sriboonlue and Davies 1983; Venkataraman and Rao 1998; Sidiropoulou et al. 2007). Tiss and Evans (1989), however, showed that it is also influenced by the properties of the fluid. For β = 0 the Forchheimer equation becomes the Darcy equation. Several authors proposed empirical relationships to determine β, β′ or β*, from parameters of porous media such as permeability, porosity, characteristic lengths (of pores or grains) and tortuosity (e.g. Ergun 1952; Janicek and Katz 1955 (cited in Thauvin and Mohanty 1998); Geertsma 1974; Cox 1977 (cited in Barker and Herbert 1992b); Firoozabadi and Katz 1979; Sriboonlue and Davies 1983). Most follow the general form

$$ {\beta}^{\prime }=C\cdot {k}^{\mathrm{x}1}\cdot {\phi}^{\mathrm{y}}\cdot {\tau}^{\mathrm{z}} $$
(13)

One of the most popular was proposed by Geertsma (1974) who examined fully saturated consolidated and unconsolidated porous media (Eq. 14).

$$ {\beta}^{\prime }=0.005\cdot {k}^{-0.5}\cdot {\phi}^{-5.5} $$
(14)

This approach was later validated by Thauvin and Mohanty (1998) through a pore-network model and by further experimental data by Mathias and Todman (2010). According to Thauvin and Mohanty (1998), the Geertsma (1974) approach showed the best performance when compared to their network model.

Janicek and Katz (1955; cited in Thauvin and Mohanty 1998) proposed Eq. (15) for natural porous media

$$ {\beta}^{\prime }=1.82\cdot {10}^8\cdot {k}^{-0.75}\cdot {\phi}^{-1.25} $$
(15)

Liu et al. (1995) included permeability, porosity and tortuosity to obtain

$$ {\beta}^{\prime }=2.94\cdot {10}^7\cdot {k}^{-1}\cdot {\phi}^{-1}\cdot \tau $$
(16)

It should be noted that most relationships were derived from curve slopes in log-log plots and thus may contain a significant uncertainty. Firoozabadi and Katz (1979) noticed that the slope for unconsolidated sands is flatter than that for sandstones.

Ergun (1952) related β to porosity and the diameter of spherical grains (Eq. 17). This equation was evaluated in detail by Macdonald et al. (1979). Often B E = 1.75 is used. The grain diameter used here is that of a spherical grain.

$$ \upbeta ={B}_{\mathrm{E}}\cdot \left(\frac{1-\phi }{\phi^3}\cdot \frac{1}{g\cdot {d}_{\mathrm{g}}}\right) $$
(17)

Ward (1964) stated that the factor C 2 from Eq. (11a) equals 0.550 for all porous media. Alternatively, it can be obtained from the porosity for 0.336 < ф < 0.400 (Sriboonlue and Davies 1983) using:

$$ {C}_2=1.7\cdot {\left(76.63\cdot \frac{\phi^2}{\left(1-\phi \right)}-9.81\right)}^{-0.5} $$
(18)

The empirical Eq. (19) by Cox (1977; cited in Barker and Herbert 1992b) can be used for unconsolidated sediments. Here, the hydraulic conductivity K needs the unit cm/s. Despite the inconsistent unit, the obtained β * is dimensionless.

$$ {\beta}^{*}=0.5\cdot {K}^{-1.25} $$
(19)

Table 2 shows some coefficients of inertial flow for unconsolidated material from literature. Generally speaking, the inertial factor decreases with increasing grain size. Some values for consolidated sandstones are given for comparison. They are usually far higher than those for unconsolidated porous media.

Table 2 Range of inertial flow coefficients for unconsolidated material
Full size table

The Forchheimer equation has been validated theoretically (Irmay 1958; Hassanizadeh and Gray 1987; du Plessis and Masliyah 1988; Ma and Ruth 1993; Whitaker 1996; Giorgi 1997; Andrade et al. 1998; Chen et al. 2001; Fourar et al. 2004), confirmed by experimental and field observations (e.g. Macdonald et al. 1979; Kohl et al. 1997; Yamada et al. 2005; Zenner 2009; Moutsopoulos et al. 2009; Cherubini et al. 2012) and applied to a variety of situations of flow towards wells (e.g. Wen et al. 2011, 2014). Alternative expressions of the Forchheimer equation were developed by Ergun (1952) and by Trussell and Chang (1999). The Ergun (1952) approach includes the influence of porosity but is only valid for spherical grains and requires the experimental determination of a linear and a non-linear coefficient. The Trussell and Chang (1999) approach uses a characteristic grain diameter instead of a spherical diameter but requires information on tortuosity and a shape factor that describes the area-volume relationship.

Similar to the Thiem (1906) approach for Darcy flow, Engelund (1953) developed an analytical model for steady-state radial non-Darcian flow towards a well by combining the continuity equation and the Forchheimer Eq. (20), again assuming a horizontal isotropic confined aquifer of even thickness.

$$ s={h}_2-{h}_1=\frac{q_{\mathrm{d}}}{2\cdot \uppi \cdot K}\cdot \ln \frac{r_2}{r_1}+{\beta}^{*}\cdot {\left(\frac{q_d}{2\cdot \uppi \cdot K}\right)}^2\cdot \left(\frac{1}{r_1}-\frac{1}{r_2}\right) $$
(20)

If the specific discharge q is approximated by the discharge Q per unit of aquifer thickness b (or screen length L s), Eq. (17) takes the form (Barker and Herbert 1992b).

$$ s={h}_2-{h}_1=\frac{Q}{2\cdot \uppi \cdot K\cdot b}\cdot \ln \frac{r_2}{r_1}+{\beta}^{*}\cdot {\left(\frac{Q}{2\cdot \uppi \cdot K\cdot b}\right)}^2\cdot \left(\frac{1}{r_1}-\frac{1}{r_2}\right) $$
(21)

Another analytical model for radial Forchheimer flow to a well at steady state was developed by Ewing et al. (1999), and for a partially penetrating well by Upadhyay (1977). Some authors additionally distinguish between flow laws for different degrees of inertial flow (Mei and Auriault 1991; Firdaouss et al. 1997; Fourar et al. 2004; Panfilov and Fourar 2006; Nowamooz et al. 2009). They consider the Forchheimer Eq. (11a) to be valid for flow with a “mean” inertial contribution. The influence of weak and strong inertial flow is then represented by Eqs. (22) and (23), respectively (Mei and Auriault 1991; Firdaouss et al. 1997; Fourar et al. 2004; Panfilov and Fourar 2006; Nowamooz et al. 2009). It is noteworthy that Eq. (23) contains a third cubic term as already proposed by Forchheimer (1901b), with γ′ = γ*/μ.

$$ \frac{dp}{dx}=\frac{\mu }{k}\cdot q+{\gamma}^{*}\cdot \frac{\rho^2}{\mu}\cdot {q}^3 $$
(22)
$$ \frac{dp}{dx}=\frac{\mu }{k}\cdot q+{\beta}^{\prime}\cdot \rho \cdot {q}^2+{\gamma}^{*}\cdot \frac{\rho^2}{\mu}\cdot {q}^3 $$
(23)

Another empirical approach to describe non-Darcy flow in porous media is a power law function (Eq. 24). Although this is commonly attributed to and named after the Russian hydrologist Izbash (Izbash 1931, 1969; Soni et al. 1978; Watanabe 1982), it was already proposed by Forchheimer (1901b) in the same paper that contained the Forchheimer law.

$$ \frac{dh}{dx}={a}_{\mathrm{Iz}}\cdot {q}^{\mathrm{m}} $$
(24)

The coefficients a Iz and m have to be determined experimentally. The power constant m increases with increasing degree of turbulence and should range between 1 and 2 (Bordier and Zimmer 2000). At m = 1, the Izbash equation basically becomes the Darcy equation (Basak 1977). The Izbash equation has been applied frequently (e.g. Şen 1989; Wen et al. 2006, 2008a, b, 2009; Sedghi-Asl et al. 2014). For many applications, both the Forchheimer and Izbash equations are equally well suited to describe non-Darcian flow (Bordier and Zimmer 2000; Moutsopoulos et al. 2009; Qian et al. 2011; Tzelepis et al. 2015).

Flow laws for turbulent flow

For the commonly turbulent flow in tubes, the Darcy-Weisbach equation (Weisbach 1845) can be used.

$$ s={f}_{\mathrm{D}}\cdot \frac{L_{\mathrm{p}}}{d_{\mathrm{p}}}\cdot \frac{{v_{\mathrm{f}}}^2}{2g}={f}_{\mathrm{D}}\cdot \frac{L_{\mathrm{p}}}{d_{\mathrm{p}}}\cdot \frac{{\left(Q/A\right)}^2}{2g} $$
(25)

with A = π · d p 2/4.

The Darcy friction factor f D (often f D = λ) can be calculated using the approximation by Moody (1944) that is valid for values of Re that are common for most water wells of 4 · 103 < Re < 1 · 107 and for κ/d ≤ 0.01 (Eq. 26). The roughness of the material is addressed by the parameter κ.

$$ {f}_{\mathrm{D}}=0.0055\cdot \left[1+{\left(20000\cdot \frac{\kappa }{d_{\mathrm{p}}}+\frac{10^6}{\mathrm{Re}}\right)}^{\frac{1}{3}}\right] $$
(26)

More accurate values of f D may be obtained from the implicit Colebrook-White equation (Hamill 2001).

Several studies suggest that the Forchheimer equation, minus the viscous term, may also be used for post-Forchheimer flow, although with adapted coefficients β * (Burcharth and Andersen 1995; Trussell and Chang 1999). In this case, the viscous term in the Forchheimer equation becomes negligible. For radial flow this results in

$$ s={\beta}^{*}\cdot {\left(\frac{Q}{2\uppi \cdot K\cdot b}\right)}^2\cdot \left(\frac{1}{r_1}-\frac{1}{r_2}\right) $$
(27)

Williams (1985) adapted the Darcy-Weisbach Eq. (25) for turbulent flow in porous media, disregarding transitional non-linear laminar flow. Equation (28) describes the radial gradient as a function of the square of both the kinematic viscosity ν and the Reynolds number.

$$ \frac{dh}{dr}=\frac{a_2\cdot {\nu}^2\cdot \mathrm{R}\mathrm{e}{}^2}{g\cdot k\cdot {d}_{\mathrm{c}}} $$
(28)

Equations (25), (27) and (28) show a common characteristic of turbulent flow laws: the head gradient is proportional to the square of the flow rate.

Transient flow to wells

Most of the equations used so far assume steady-state flow conditions. Real wells, however, are commonly switched off and on. Usual pumping periods range between a few hours and a few days. Barker and Herbert (1992b) studied the time t 0 needed to reach quasi-steady state conditions in a partially penetrating well at a radial distance r 0 from the well. Based on Theis (1935), Barker and Herbert (1992b) studied the time t 0 needed to reach quasi-steady-state conditions (negligible small drawdown over time) in a partially penetrating well at a radial distance r 0 from the well. Compared to Thiem (1906), they found that the error in head loss between the well and the outer boundary for wells of small diameters (r w < r 0/10), is smaller than 10 % for times greater than t 0 when

$$ \frac{r_0{}^2\cdot S}{4\cdot {K}_{\mathrm{h}}\cdot b\cdot {t}_0}=0.48 $$
(29)

It should be noted that the Theis equation does not describe steady-state flow but here drawdown after some time is assumed to be low enough to justify quasi-steady-state conditions. After Hantush (1961a, b) the effects of partial penetration in a homogeneous anisotropic aquifer are only important up to a distance of

$$ {r}_0=1.5\cdot b\cdot \sqrt{\frac{K_{\mathrm{h}}}{K_{\mathrm{v}}}} $$
(30)

Combining Eqs. (29) and (30) yields to obtaining the time needed to reach quasi-steady-state

$$ {t}_0=1.2\cdot \frac{b{}^2\cdot S}{K_{\mathrm{h}}\cdot b}\cdot \frac{K_{\mathrm{h}}}{K_{\mathrm{v}}}=1.2\cdot \frac{b\cdot S}{K_{\mathrm{v}}} $$
(31)

If the time to reach quasi-steady state is significantly smaller than the pumping period, the quasi-steady-state assumption used in the equations in the preceding is justified (Barker and Herbert 1992b). Figure 6 shows that t 0 is less than 1 h for two K v values (10 % of typical aquifer K h values) and typical storage coefficients for confined aquifers ranging between 1 · 10−5 and 1 · 10−3. Considering the usual pumping periods which range between hours and days, the models, which are based on quasi-steady-state assumptions, are thus valid in most cases.

Fig. 6
figure 6

Time to reach quasi-steady-state conditions t 0 for a partially penetrating well as a function of storage coefficient S. Calculated using Eq. (31)

Full size image

Strictly speaking, the Theis (1935) formula which Eq. (28) is based upon already is only valid for confined aquifers. In fully penetrating wells, which will have a smaller r 0, the t 0 will also be much smaller (Barker and Herbert 1992b).

For linear-laminar flow, the well-known equations by Theis (1935) and Cooper and Jacob (1946) may be used to describe the transient development of drawdown around a well. For transient flow with an inertial component, the Forchheimer equation (Eq. 11a) can be extended by adding an acceleration term, as proposed by Polubarinova-Kochina (1962). Blick and Civan (1988) added another term that addresses momentum flux. Equation (32) thus contains four terms on the right side (in parentheses), describing the contributions of viscous flow, inertial flow, momentum flux and acceleration. A comparison of their capillary-orifice model to experimental data showed, however, that the last two terms become only important at very short times (<1 s) and can be safely ignored for standard well operations.

$$ \frac{dp}{dx}=-\left(\frac{\mu }{k}\cdot q\right)+\left({\beta}^{\prime}\cdot \rho \cdot q{}^2\right)+\left(\frac{\rho \cdot q}{\phi {}^2}\cdot \frac{\partial q}{\partial x}\right)+\left(\frac{\rho }{\phi}\cdot \frac{\partial q}{\partial t}\right) $$
(32)

An exact solution for transient Forchheimer flow to a well does not exist yet. Approximate solutions were proposed by Şen (1988, 1989), Kelkar (2000), Wu (2002), Moutsopoulos and Tsihrintzis (2005) and Wang et al. (2014). The approaches by Şen (1988), and the equivalent approaches by Kelkar (2000) and Wu (2002) were revised and expanded by Mathias et al. (2008). They showed that the transient drawdown, including Forchheimer losses, of a well pumped at a constant rate for large times, can be approximated by Eq. (33). Its form clearly shows its inheritance from the Theis (1935) and the Forchheimer equations (11a).

$$ s=\frac{Q}{4\cdot \uppi \cdot T}\cdot \left( \ln \frac{4\cdot T\cdot t}{S\cdot {r}_{\mathrm{w}}^2}-0.5772\right)+\left(\frac{\beta^{\prime}\cdot Q{}^2}{{\left(2\uppi \cdot b\right)}^2\cdot {r}_{\mathrm{w}}\cdot g}\right) $$
(33)

Flow laws for fractured media

For linear laminar flow in fractured media, the well known “Cubic law” (Snow 1968) may be used (Witherspoon et al. 1980; Zimmerman and Bodvarsson 1996; Klimczak et al. 2010). Flow in fractured media is, however, due to channeling, more likely to be affected by inertial or turbulent processes than in porous media. Nowamooz et al. (2009) pointed out that the Forchheimer equation (11a) and the ones for weak (Eq. 22) and strong (Eq. 23) inertial flow can be adapted for fractured media by setting k = b f 2/12 and A = b f  ⋅ w f (b f = aperture of fracture, w f = breadth of fracture). It should be noted that Eq. (34), which is the Forchheimer equation for fractured media, addresses one single fracture.

$$ \frac{dp}{dx}=\frac{12\cdot \mu }{{b_{\mathrm{f}}}^3\cdot {w}_{\mathrm{f}}}\cdot Q+\frac{\beta^{\prime}\cdot \rho }{{b_{\mathrm{f}}}^2\cdot {w_{\mathrm{f}}}^2}\cdot {Q}^2 $$
(34)

Mathematical modeling approaches for well hydraulics

Modeling of well hydraulics may rely on different mathematical approaches (see Yeh and Chang 2013 for a description of methods). The empirical and analytical models on which this manuscript is mainly based, allow the calculation of the hydraulics of water wells only for rather simple geometries, mostly one-dimensional (1D) or radially symmetric and usually at steady state. Numerical models allow for the inclusion of more complex geometries. Several authors developed purpose-specific numerical models (e.g. Cooley and Cunningham 1979; Kaleris et al. 1995; Von Hofe and Helweg 1998; Rushton 2006; Chenaf and Chapuis 2007), while others relied on commercially available groundwater modeling programs, such as MODFLOW (e.g. Barrash et al. 2006; Horn and Harter 2009; Houben and Hauschild 2011; McMillan et al. 2014), FEFLOW (Rubbert and Treskatis 2008) and HYDRUS-2D (Yakirevitch et al. 2010). There is at least one reactive transport model of flow to wells, based on PHAST (Larroque and Franceschi 2010).

When using numerical groundwater models that consider only Darcy flow for well studies, it should be good practice to calculate and present the Reynolds numbers obtained from the flow velocities for the model cells, at least for cells with high flow velocities (e.g. Houben and Hauschild 2011). This is a necessary check to see whether or to what degree the assumption of Darcian flow is appropriate. Many published models, however, fail to do so.

For the very popular groundwater modeling software MODFLOW, two extension packs for non-Darcian flow are available: CFP (conduit flow process) by Shoemaker et al. (2008) and NLFP (non-linear flow process) by Mayaud et al. (2014). The former addresses flow in discrete conduits or highly permeable layers, typical features for karstic or volcanic aquifers, embedded in a porous aquifer. It switches from laminar Darcy to turbulent Darcy-Weisbach flow at a chosen critical Reynolds number. NLFP considers a gradual transition between laminar and turbulent flow. It was checked against some simple but typical well hydraulics scenarios (Maynaud et al. 2014).

The Subsurface Flow Module provided in the finite element simulation software Comsol Multiphysics (COMSOL 2013) comes with pre-defined models for Darcy, Forchheimer, Darcy-Brinkman and Navier–Stokes flow which may be combined in one model. One of the examples provided is the 2D flow towards a well with a change in flow regime from Darcy to Darcy-Brinkman conditions with decreasing distance from the well and finally to Navier-Stokes flow in the well itself.

Hybrid analytical-numerical groundwater models have also been successfully applied to simulate transient groundwater flow to well screens (Székely 1992; Hemker 1999a, b). Hemker (1999a) split the flow into a radial (horizontal) flow component which was modeled analytically, and a vertical flow component which was modeled numerically using the finite difference technique.

Design criteria based on flow velocity

Critical screen entrance velocity

Probably the most commonly used design feature for water wells is the maximum permissible or critical entrance (or approach) velocity at the screen v crit (Driscoll 1986; Sterrett 2007). For radially symmetric cases, it is calculated after Eq. (2). Based on his practical experience, Sichardt (1928) proposed that the maximum approach velocity v crit is related to the hydraulic conductivity (Eq. 35). Huisman (1972) modified this approach by allowing a larger safety margin (Eq. 36). It should be noted that both equations are purely empirical and dimensionally inconsistent. Application of these equations yields the entrance velocities plotted in Fig. 7 which range below 0.01 m/s for common aquifer conductivities.

Fig. 7
figure 7

Critical entrance velocities as a function of aquifer hydraulic conductivity, calculated using Eq. 35 (black line) and 36 (red line)

Full size image
$$ {v}_{\mathrm{crit}}=\frac{\sqrt{K}}{15} $$
(35)
$$ {v}_{\mathrm{crit}}=\frac{\sqrt{K}}{30} $$
(36)

The most commonly cited maximum permissible entrance velocity v crit in literature is 0.03 m/s (0.1 ft/s) (Driscoll 1986; Sterrett 2007). Keeping the velocity below this level is said to limit head losses, maintain fully laminar flow conditions, prevent sand intake, minimize incrustations and even to control corrosion. This value probably goes back to a publication by Bennison (1947), who, however, did not support his proposition by any theoretical consideration, experimental or field observations. The best that can be said about this now almost mythical value is that it has not done any harm yet. Nevertheless, the value has found its way into many papers, e.g. Ahrens (1957a, b, 1970) who gives v crit = 0.1–0.25 ft/s (0.030–0.076 m/s), and textbooks, e.g. Campbell and Lehr (1973) or Driscoll (1986). Based on sandtank experiments, Wendling et al. (1997) defend velocities of 0.03–0.06 m/s as suitable, but rely on rather timid assumptions of permissible Reynolds numbers (Re < 10). Since v crit still appears in textbooks like the one by Sterrett (2007), it is widely used worldwide in well design. A second group of authors, e.g. Williams (1985), Roscoe Moss (1990), Parsons (1994), proposed far higher critical entrance velocities, ranging from 0.6 to 1.2 m/s (2–4 ft/s). The American Water Works Association (AWWA) published a standard (AWWA 1998) that “allowed” entrance velocities of up to 0.46 m/s (1.5 ft/s) but in its current standard (AWWA 2006), no single permissible velocity is specified any more.

By now, readers will probably ask themselves which school is (more) right on critical flow velocities and Reynolds numbers. Both invoke experimental studies as evidence (Roscoe Moss 1990; Wendling et al. 1997) but the upscaling from short experiments under idealized conditions to the long-term behavior of wells in a real aquifer is doubtful. Both quote practical experience but no statistically significant data set is presented. What would be needed is a test involving a set of identical wells, one group operated under conservative and the other under more liberal boundary conditions, both in the same homogeneous aquifer. The test would have to run for several years or even decades, as the processes in question are slow, and would need repeated monitoring of well yield, sand intake, incrustation and corrosion. Wells would need to be located sufficiently apart to avoid cross-well effects. However, aquifers are never homogeneous, neither from the hydraulic nor the hydrochemical point of view (Houben and Treskatis 2007), rendering the comparison of results from the two groups questionable. This, again, could only be overcome by a large number of wells to cancel out this background noise.

Elevated entrance velocities and especially turbulent conditions are often used to explain increased deposition of incrustations. Indeed it is true that turbulence can increase the build-up of incrustations (Zeppenfeld 2005; Houben 2006; Houben and Weihe 2010). There is, however, no obvious link between flow velocity and corrosion (Parsons 1994), something which is also quoted frequently in older literature.

Suffusion velocity

During normal operation, the flow velocity in the near field of a well should not induce suffusion, that is, the erosion and transport of particles from the gravel pack and the near-field of the aquifer. Washed-out particles reaching the well interior can damage both screen and pump by abrasion or form deposits in the well interior which may block parts of the screen. Only during well development, when particles need to be removed to improve the conductivity, may this criterion be deliberately violated. The minimum velocity v suf to mobilize particles of a diameter d suf from an unconsolidated porous aquifer with a steady granulometric curve is (modified after Busch et al. 1993)

$$ {v}_{\mathrm{suf}}=0.5\cdot K\cdot {\phi}_0\cdot \sqrt{\frac{\phi \cdot g\cdot {d}_{\mathrm{suf}}^2}{\upnu \cdot K}}=0.5\cdot K\cdot {\phi}_0\cdot \sqrt{\frac{\phi \cdot {d}_{\mathrm{suf}}^2}{k}} $$
(37)

with

$$ {\varphi}_0=0.6\cdot \left(\frac{\rho_{\mathrm{b}}}{\rho_{\mathrm{w}}}-1\right)\cdot {a}^{*}\cdot \sin \left(30{}^{\circ}+\vartheta /8\right) $$
(38)

and

$$ {a}^{*}=0.82-1.80\cdot \phi +0.0062\cdot \left(U-5\right) $$
(39)

The factor ϑ is the angle between the direction of flow investigated and the direction of the force of gravity, here for downward, horizontal and upward flow.

$$ \vartheta =\left\{\begin{array}{c}\hfill \downarrow 0{}^{\circ}\hfill \\ {}\hfill \to 90{}^{\circ}\hfill \\ {}\hfill \uparrow 180{}^{\circ}\hfill \end{array}\right. $$

Critical Reynolds number

Another way to assess the flow regime around a well, is to calculate the Reynolds numbers along a flow path towards a well and compare them to the critical values mentioned in the preceding. This has some advantages over the calculation of the entrance velocity alone. The Reynolds number does not only include the flow velocity, but also the properties of the fluid, which however, usually only vary within small limits. More importantly, it takes into account the grain size which can vary considerably between aquifer and gravel pack. When using Eq. (1), the flow velocity increases continuously towards the well and does not show any jumps at interfaces. Only when calculated after Eq. (2), can changes in porosity, e.g. between aquifer and gravel pack, be accounted for.

Again, there is considerable disagreement in the literature about the maximum “permissible” Reynolds number around water wells. The more conservative school prefers a critical Reynolds number of Re < 10 (e.g. Wendling et al. 1997). For the near-field of wells, Truelsen (1958), as well as Vukovic and Soro (1992), consider Reynolds numbers between 6 and 60 to be critical. Williams (1985) and Roscoe Moss (1990) cite a mean critical Reynolds number of 30 (range between Re = 15 and 50).

As with the entrance velocity, the highest Reynolds numbers are found in the immediate vicinity of the well (Fig. 8). Here, three scenarios, with two pumping rates each, were compared (Table 3; Fig. 8). The first scenario considers a well design commonly used in Germany (Fig. 8a). At the lower pumping rate, this well would even fulfill the restrictions of Re < 10 at the screen. The same well with a shorter screen length (Fig. 8b) would already come closer to the critical Re values proposed even by the less conservative authors. The third scenario, a slim well with a short screen (Fig. 8c), results in Reynolds numbers which have a noticeable non-laminar component but yet do not reach the limits for turbulent flow. The conspicuous jumps of the Reynolds number at the wellbore in Fig. 8 are caused by the sudden increase of the grain size between aquifer and gravel pack. The calculated entrance velocity at the screen (Tab. 3), would only fall below the conservative critical velocity of 0.03 m/s for the lower pumping rate for the first scenario. On the other hand, not even the highest entrance velocities obtained violate the less conservative critical entrance velocity of 0.45 m/s.

Fig. 8
figure 8

Reynolds Number (Re) as a function of distance from a pumping well for six set-ups (see Table 3) within three scenarios (a–c). Radial flow symmetry is assumed, calculated using Eq. (3)

Full size image
Table 3 Parameters used for example calculations and calculated entrance velocity (Eq. 2) at the screen (A p = 0.05)
Full size table

Critical radius

To avoid non-linear head losses in the gravel pack and the aquifer, thereby minimizing total losses the critical radius r crit (that is, the distance from the well center to where the transition from linear laminar to non-linear laminar flow occurs), should be inside the well screen (r crit < r s) where flow is turbulent anyway. Additionally, non-linear flow is often assumed to promote incrustation build-up and particle mobilization. Using any chosen critical Reynolds number, the critical radius r crit can be calculated with d c being the mean grain size (d 50; m) (Şen 1995):

$$ {r}_{\mathrm{c}\mathrm{rit}}=\frac{\left(\frac{Q}{B}\right)\cdot {d}_{\mathrm{c}}}{2\cdot \uppi \cdot v\cdot {\mathrm{Re}}_{\mathrm{c}\mathrm{rit}}} $$
(40)

Figure 9 shows that only with very conservative assumptions on the critical Reynolds number and high pumping rates will the critical radius reach values exceeding common screen diameters. Only in those cases would the transition zone between linear laminar and non-linear laminar flow fall into the gravel pack.

Fig. 9
figure 9

Critical radius as a function of pumping rate for four critical Reynolds numbers and two aquifer thicknesses (a–b), calculated using Eq. (40)

Full size image

To obtain r crit, Williams (1985) equated the hydraulic gradients from the Darcy and the Darcy-Weisbach Eqs. (8) and (28), giving:

$$ {\left[\frac{dh}{dr}\right]}_{\mathrm{c}\mathrm{rit}}={a}_1\cdot \frac{v{}^2}{g\cdot k\cdot {d}_{\mathrm{c}}}\cdot {\mathrm{Re}}_{\mathrm{c}}={a}_2\cdot \frac{v{}^2}{g\cdot k\cdot {d}_{\mathrm{c}}}\cdot {\mathrm{Re}}_{\mathrm{c}}{}^2 $$
(41)

The dimensionless constant a 2 mainly depends on the shape, packing, and size distribution of grains. Williams (1985) performed a series of physical model experiments evaluating hydraulic gradients at different flow rates for four gravel pack materials at varying distances from the well. The velocities at each of the radial distances and corresponding Reynolds numbers were then calculated. The critical Reynolds numbers were defined by a slope change in the Re vs. radial distance curves from 1 (laminar flow) to 2 (turbulent flow) and ranged between 15 and 50, with a mean of approximately 30. It should be noted that Williams (1985) only considered laminar Darcy and turbulent Darcy-Weisbach flow but no transitional regime.

Influence of well geometry on well hydraulics

Effect of screen and borehole diameter

In most cases, the diameter of the screen and casing is determined by the size of the submersible pump (Table 4). The casing needs to have a sufficient diameter to adequately accommodate the pump and leave enough clearance at both sides, allowing water to flow past and cool the motor, which is usually located below the intake.

Table 4 Typical dimensions of pumps, casing and borehole (modified after Tholen 2006)
Full size table

For wells with a single filter pack, the drilling diameter is commonly chosen to be 1.5–2 times larger than the casing diameter. For dual filter packs, the size of the inner pack, which is usually run in while being attached to the screen, has to be added.

Assuming linear laminar flow, the influence of the screen diameter on well yield can be investigated using the Thiem equation for both confined (Eq. 9) and unconfined aquifers (Eq. 10). With the parameters given in Fig. 10, it can easily be seen that even doubling the well diameter leads to a relatively weak increase in well yield (Q/s) of around 10 % for the confined and of 15 % for the unconfined case.The relationship between screen diameter and head loss in a well tapping a confined aquifer can also be quantified using an adapted form of the Thiem equation (Eq. 9) proposed by Parsons (1994), which addresses both aquifer and gravel pack.

$$ s=\frac{Q}{2\uppi \cdot {K}_{\mathrm{aq}}\cdot {K}_{\mathrm{gp}}\cdot B}\cdot \left[{K}_{\mathrm{gp}}\cdot \ln \left(\frac{r_0}{r_{\mathrm{b}}}\right)+{K}_{\mathrm{aq}}\cdot \ln \left(\frac{r_{\mathrm{b}}}{r_{\mathrm{s}}}\right)\right] $$
(42)
Fig. 10
figure 10

Effects of well radius on relative well yield—well yield of 6″ (150 mm) well = 100 %)—calculated using Eqs. (9) and (10)

Full size image

Figure 11 shows the results of the application of Eq. (42) to some standard well parameters. For the sake of simplicity, it was assumed that the borehole diameter is always 1.5 times that of the screen diameter. Similar to the observations from Fig. 10, even doubling the borehole diameter leads to a decrease of head loss by only around 8 %.

Fig. 11
figure 11

Effects of borehole radius on absolute and relative head loss (head loss of 4.5″ borehole = 100 %) in a confined aquifer, calculated using Eq. (42)

Full size image

Parsons (1994) states that the screen diameter only becomes significant when the gravel pack has the same hydraulic conductivity as the aquifer. This would be the case when the well is developed “naturally”; that is when no artificial gravel pack is inserted. Any increase of the screen diameter, however, would require an increase in the diameter of the borehole. In reality, the hydraulic conductivity of artificial gravel packs is designed to be at least one order of magnitude higher than that of the aquifer. In such cases, the effect of well screen radius on the hydraulic performance of the well is minimal. Roscoe Moss (1990) came to the same result.

If one agrees on a critical entrance velocity (v e = v crit), one can solve Eq. (2) for the diameter at which the flow to the well exceeds v crit. Again, this value for d crit should be smaller than the chosen screen diameter.

$$ {d}_{\mathrm{crit}}=\frac{Q}{\uppi \cdot {v}_{\mathrm{crit}}\cdot {A}_{\mathrm{p}}\cdot {L}_{\mathrm{s}}} $$
(43)

Figure 12 shows that the higher critical velocity can be maintained with even the smallest screen diameters. With the smaller critical entrance velocity, common screen diameters of 0.3 m (or 0.5 m) would curb the pumping rate at 50 (or 100) m3/h, at least at the screen length of 20 m used here.

Fig. 12
figure 12

Effects of well discharge on necessary minimum screen diameter to maintain two critical velocities. Calculated using Eq. (43)

Full size image

Effect of screen and borehole length

A design factor that strongly affects well performance is the length of the well screen. At steady state, the specific well capacity (or relative well yield) Q/s may be derived from the Thiem Eq. (9) with setting b = L s. Obviously, the relative well yield depends linearly on the screen length.

$$ \frac{Q}{s}=\frac{2\cdot \uppi \cdot K\cdot {L}_{\mathrm{s}}}{ \ln \left(\frac{r_{\mathrm{o}}}{r_{\mathrm{w}}}\right)} $$
(44)

Similar to the well diameter, the screen length can be manipulated so that the entrance velocity falls below the defined critical velocity, or, in other words, the critical radius (r crit) becomes smaller than the nominal screen radius (r s).

$$ {L}_{\mathrm{s}\ \mathrm{crit}}=\frac{Q}{\uppi \cdot {v}_{\mathrm{crit}}\cdot {A}_{\mathrm{p}}\cdot {d}_{\mathrm{s}}} $$
(45)

Figure 13 shows that the higher critical velocity can already be maintained with a few meters of screen. At the lower critical velocity and high pumping rates, several tens of meters of screen are needed. If the aquifer does not offer such a thickness, either the diameter has to be increased or the pumping rate decreased.

Fig. 13
figure 13

Effects of well discharge on necessary screen length to maintain two critical velocities at the screen entrance, calculated with Eq. (45)

Full size image

As can easily be seen from Eqs. (9), or (44), an increase in screen length will have a much more pronounced impact on yield and drawdown than an increase in screen diameter. The length appears in linear form in the Thiem equation Eq. (9), while the diameter does so in a logarithmic form. Screen lengths may vary from 1 to 100 or more meters (two orders of magnitude), depending on the aquifer thickness, while the drilling or screen diameter usually ranges between 0.1 and 1 m (one order of magnitude). A longer screen, however, does not mean that its diameter can be decreased as compensation, since small diameters and long screens create increasing head losses through upflow. Additionally, for technical reasons, deep wells need a certain (starting) drilling diameter. Petersen et al. (1955) proposed Eq. (46) to address the influence of both screen length and diameter at the same time. The value of 6 represents a combination of parameters that yields the smallest screen losses.

$$ \frac{11.31\cdot {C}_{\mathrm{c}}\cdot {A}_{\mathrm{p}}\cdot {L}_{\mathrm{s}}}{d_s}>6 $$
(46)

In practice, the length of the screen in thick aquifers is, however, often limited by economic and technical constraints, e.g. the drilling costs for deeper wells and the maximum drilling depth of the available rig, respectively. For unconfined aquifers of limited thickness (<50 m), often only the lower third or half is screened to keep drawdown above the screen and thus avoid screen pipe aeration (Driscoll 1986). In thicker aquifers, up to 80 % may be screened to obtain a higher efficiency. For confined aquifers, Driscoll (1986) recommends screening 80–90 % of the aquifer thickness, with the screen covering the centre of the aquifer, to avoid intake of fines from the under- and overlying aquitards into the well (Fig. 14). The maximum permissible drawdown, however, should be restricted to the top of the aquifer.

Fig. 14
figure 14

Recommendations for screen position and length for a confined and b unconfined aquifers (modified after Houben and Treskatis 2007)

Full size image

Apart from the drilling costs, long screens have some disadvantages. They can promote vertical flow in idle wells as they may connect (or short-circuit) zones of different heads and hydrochemical composition (Church and Granato 1996; Houben 2003), which may cause cross-contamination and enhance well ageing.

Effects of non-ideal well geometry

Effect of partial penetration

In an aquifer that is only partly screened over the aquifer thickness, flow to the well includes a vertical component. The water flowing vertically towards the well has to flow for a longer distance than for horizontal flow. It also has to overcome the vertical hydraulic conductivity of the aquifer, which is usually significantly smaller than the horizontal one. The resulting head loss is therefore greater than it would be for a fully screened aquifer (Driscoll 1986). The general hydraulics of partially penetrating wells was assessed by e.g. Hantush (1957, 1961a, b), Kirkham (1959), Dougherty and Babu (1984), Ruud and Kabala (1997); Cassiani and Kabala (1998); Cassiani et al. (1999), Chang and Chen (2002) and Yang and Yeh (2012).

Kozeny (1933) derived an equation that allows assessing the head loss effect of partial penetration s pp in a homogeneous aquifer at steady state (Kasenow 2010).

$$ {s}_{\mathrm{pp}}=\frac{Q}{\left[\frac{L_{\mathrm{s}}}{B}\left(1+\sqrt[7]{\left[\frac{r_{\mathrm{w}}}{\left(2B\left[\frac{L_{\mathrm{s}}}{B}\right]\right)}\right]\cdot \cos \left[\frac{\uppi \left(\frac{L_{\mathrm{s}}}{B}\right)}{2}\right]}\right)\right]\cdot \left[\raisebox{1ex}{$Q$}\!\left/ \!\raisebox{-1ex}{${s}_{100\%}$}\right.\right]} $$
(47)

The approach is, however, not valid for small aquifer thickness B, high percentages of penetration, and large well radius r w (Driscoll 1986). Some combinations of these conditions can lead to head losses smaller than those for fully penetrating wells, which is physically impossible.

Equation (48), based on Huisman (1972) and Todd (1980), allows calculating the additional drawdown due to partial penetration (p p > 0.20 ≙ > 20 % penetration) at steady state (Kasenow 2010).

$$ {s}_{\mathrm{p}\mathrm{p}}=\frac{Q}{2\uppi \cdot T}\cdot \frac{\left(1-{p}_{\mathrm{p}}\right)}{p_{\mathrm{p}}}\cdot \ln \left[\frac{\left(1-{p}_{\mathrm{p}}\right)\cdot {L}_{\mathrm{s}}}{r_{\mathrm{w}}}\right] $$
(48)

Barker and Herbert (1992b) present a modified form of this equation for an anisotropic aquifer, valid for partial penetrations 0.1 < p p < 0.9.

$$ {s}_{\mathrm{p}\mathrm{p}}=\frac{Q}{2\uppi \cdot {K}_{\mathrm{h}}\cdot B}\cdot \frac{\left(1-{p}_{\mathrm{p}}\right)}{p_{\mathrm{p}}}\cdot \ln \left[\frac{p_{\mathrm{p}}\cdot \left(1-{p}_{\mathrm{p}}\right)}{\left(2-{\upvarepsilon}^2\right)}\cdot \frac{B}{r_{\mathrm{b}}}\cdot \sqrt{\left(\frac{K_{\mathrm{h}}}{K_{\mathrm{v}}}\right)}\right] $$
(49)

with ε representing the eccentricity of the well

$$ \varepsilon =\frac{2{z}_{\mathrm{c}}}{B\cdot \left(1-{p}_{\mathrm{p}}\right)} $$
(50)

For standard situations, where 40–70 % of the aquifer thickness are screened and the anisotropy ratio of the hydraulic conductivity approximates 10, this relation can be simplified to a linear relationship which allows calculation of the ratio of the specific capacities SC (Q/s) of the actual, partially penetrating well (L s < B) and a comparative, theoretical fully penetrating (L s = B) well (Parsons 1994). This allows for quantification of how much of the capacity of a fully penetrating well is actually attained in the actual well.

$$ \frac{{\mathrm{SC}}_{\mathrm{L}}}{{\mathrm{SC}}_{\mathrm{B}}}=0.18+0.90\cdot \frac{L_{\mathrm{s}}}{B} $$
(51)

Figure 15 shows that the contribution of partial penetration to total drawdown can reach up to 1 m or more, but only for small partial penetration ratios and, thus, is probably not one of the bigger contributors.To reduce the effect of partial penetration for thick aquifers, Driscoll (1986) recommends using multiple short sections of well screen distributed over the aquifer thickness instead of one long, partially penetrating screen section.

Fig. 15
figure 15

Additional drawdown caused by partial penetration calculated after Huisman (1972, Eq. (48) and Barker and Herbert (1992b, Eq. 49). The red bar shows the area suitable for the linear approximation (Eq. 51) proposed by Parsons (1994)

Full size image

Non-uniform distribution of inflow over the screen

In reality, groundwater flow towards wells is not fully radially symmetric. Wells are integrated into a natural gradient field, which is superimposed onto the cone of depression that develops around the pumping well (Fig. 3b). The screen section facing the natural groundwater flow direction, therefore, receives more water than the opposite side (Houben 2006; Houben and Hauschild 2011). The ratio of upstream to downstream intake depends of course on the natural gradient. At a (rather high) background gradient of 0.01, the upgradient half of the screen takes in around 16 % more water than the downgradient side in the example by Houben and Hauschild (2011).

Many models assume that the inflow, or in other words, the flow rate or velocity, is uniformly distributed over the screen length. Nahrgang (1954) and Petersen et al. (1955) were amongst the first to show that this is actually not true (Fig. 16). Strictly speaking, uniform inflow would only occur in a well screened over the complete thickness of a homogeneous confined aquifer. In any other geometry, flow from above and below the screen has to converge onto the screen ends. Assuming uniform inflow may lead to erroneous calculations of drawdown, especially in wells with small screen length to aquifer thickness ratios and in layered aquifers (Ruud and Kabala 1997).

Fig. 16
figure 16

Effects of partial penetration on flow paths (dark blue) and screen inflow rate (red) in a confined aquifer: a fully screened, and b–d partial penetration

Full size image

Experiments, flow meter logs and numerical models verified that peaks of inflow velocity occur at the bottom and especially at the top of the screen in partially penetrating wells (Garg and Lal 1971; Cooley and Cunningham 1979; Kaleris 1989; Ruud and Kabala 1997; von Hofe and Helweg 1998; Korom et al. 2003; Houben 2006; Houben and Hauschild 2011; McMillan et al. 2014). In very long screens, only the upper sections, from the screen top down to a depth that satisfies Eq. (46), may contribute significantly to total inflow (Petersen et al. 1955). The deeper sections would be almost inactive. The position of the pump plays an important role, too. As it is commonly installed above the screen, the strongest inflow peak occurs at the top of the screen (Figs. 16 and 17).

Fig. 17
figure 17

Numerically modeled distribution of inflow over a well screen, with pump installed above the well screen (modified after Houben 2006). a cumulative screen inflow b relative contribution to total inflow

Full size image

In the light of the markedly non-uniform distribution of inflow, the debate on permissible entrance velocities should be reconsidered. Average entrance velocities calculated assuming uniform flow over a cylindrical area may be significantly lower than peak velocities occurring, e.g. close to the screen top. Flowmeter profiles are a good tool to identify the location and magnitude of such deviations.

Seepage face in unconfined aquifers

The seepage face is a phenomenon that occurs in all flow processes through porous media with a free surface which involve a sudden increase of hydraulic conductivity in the direction of flow. A seepage face is therefore a common feature in wells installed in unconfined aquifers. It does not occur in infiltration wells. Its occurrence is predicted by potential theory and is not caused by the resistance of the gravel pack itself (Busch et al. 1993).

The commonly employed Dupuit (1863) assumptions postulate that flow towards a well is horizontal, all water is supplied from the sides via constant head boundaries and that all water enters the well below the pumping water level (Fig. 18). All vertical flow components are ignored, including groundwater recharge and vertical flow in the cone of depression. Their occurrence, however, make the water table intercept the well face above the water level in the gravel pack. The vertical discontinuity between the water level within the well (or the gravel pack) and the height at which the water table intercepts the wellbore face is the seepage face (Fig. 18). The difference between the water table predicted using the Dupuit assumption and the one influenced by vertical flow usually becomes negligible at radial distances of r < 1.5 H (H = saturated initial thickness of aquifer).

Fig. 18
figure 18

Schematic sketch of a seepage face in a well screened in an unconfined aquifer (based on Gefell et al. 1994 and Rushton 2006)

Full size image

The seepage face can sometimes be identified visually during camera inspections of pumping wells by water entering the well above the pumping water level and running down the screen surface. Sometimes water cascading down the well from the seepage face can even be heard from aboveground. The percentage of inflow contributed by seepage flow can be significant.

The existence of a seepage face was first described by Sichardt (1928). Physical sandtank experiments that verified its existence were done, e.g. by Hall (1955), Gefell et al. (1994), Simpson et al. (2003) and Rubbert and Wohnlich (2006). The mathematical and physical background was studied by, e.g. Boulton (1951), Polubarinova-Kochina (1962), Kirkham (1967) and Kovács (1981). As no analytical solution is available (Bear 2007), and the procedure by Kirkham (1967) is rather tedious to apply, usually numerical models are applied to study seepage face problems (e.g. Sakthivadivel and Rushton 1989; Rushton 2006; Chenaf and Chapuis 2007; Yakirevitch et al. 2010; Behrooz-Koohenjani et al. 2011).

The existence of a seepage face often causes well yields which are less than expected from conventional Dupuit-based analysis (Rushton 2006). For the unconfined Yazor gravel at the River Wye (UK), with a small initial saturated thickness of 4.5 m, Rushton (2006) observed that increasing the pumping rate by 20 % (1,780–2,145 m3/day) caused an increase in drawdown of 65 % (1.7–2.8 m). In shallow aquifers with limited saturated thickness, this additional drawdown might easily cause problems. Figure 18 shows the vertical distribution of flow into a well affected by a seepage face.

Several empirical equations to estimate the height of the seepage face are available. The oldest approach is probably the graphical method by Kozeny (1953) which Gefell et al. (1994) transferred into an approximate equation. This approach was questioned by Kawecki (1995) and Wise and Clement (1995). The problem of the Kozeny approach is that it assumes a unit gradient for the maximum flow velocity at the well screen (Chenaf and Chapuis 2007).

The steady-state approximations by Boulton (1951), Kozeny (1953), Hall (1955), Boreli (1955), Schneebeli (1956), Heinrich (1964) and Brauns (1981, based on Sichardt (1928) and Dupuit (1863) were compared by Chenaf and Chapuis (2007) to a numerical model. They found that none of the models gave an appropriate prediction of the seepage face height. For common operating conditions, the non-dimensional graphical approach by Schneebeli (1956) came closest to the actual seepage face heights. Nahrgang (1965) approximated the length of the seepage faces as

$$ {L}_{\mathrm{sp}}=\frac{s^2}{2\cdot {H}_0} $$
(52)

A more elaborate approximation was proposed by Kresic (1997)

$$ {L}_{\mathrm{sp}}={H}_0-\frac{0.6}{H_0}\cdot \frac{H_0{}^2-{H}_{\mathrm{w}}{}^2}{ \ln \left(\frac{r_0}{r_{\mathrm{w}}}\right)}\cdot \ln \frac{r_0}{0.1{H}_0} $$
(53)

Another one was proposed by Schestakow (cited in Busch et al. 1993)

$$ {L}_{\mathrm{sp}}\approx \sqrt{\left(0.73\cdot \log \frac{\sqrt{Q/K}}{r_0}-0.51\right)\cdot \frac{Q}{K}+{H}_0^2-{H}_0} $$
(54)

Busch et al. (1993) point out that all equations used to calculate the height of the seepage face are of limited practical use. The transition zone between the Dupuit surface and the real, seepage face-affected surface is in reality often blurred by capillary effects. Furthermore, none of the equations addresses the common anisotropy in hydraulic conductivity of the aquifer. This is a serious flaw, since the vertical flow component, which strongly influences the seepage face, is of course strongest close to the well.

Influence of aquifer and borehole heterogeneity: do real wells look like textbook drawings?

Many models discussed in the preceding, especially the analytical ones, assume a homogeneous, isotropic distribution of hydraulic parameters and exact cylindrical geometries. In reality, however, exact shapes and homogeneous conditions cannot be expected, even in the anthropogenically engineered parts of a well (Fig. 19). Numerical models could easily be adapted to include such heterogeneities.

Fig. 19
figure 19

Schematic sketch of an ideal (left) and a real well (right). 1 = irregular wellbore surface (uneven borehole diameter), 2 = sand pockets (aquifer material) in gravel pack, 3 = inhomogeneous aquifer conductivity (layering)

Full size image

The influence of aquifer heterogeneity on the distribution of inflow over the screen length was studied by Houben and Hauschild (2011). They studied 50 variations of the heterogeneous conductivity field and found considerable distortions of the inflow distribution, but the general patterns (Houben and Hauschild 2011) persisted. In more extreme cases of heterogeneity, e.g. when highly permeable layers or conduits are present (e.g. fractures, karst caves, lava tubes), this might not be the case.

Unfortunately, there are few tools available that allow one to directly look at the exterior (borehole, annulus) of wells, especially after its completion. One of the few possibilities is to visit excavated dewatering wells in an open pit mine during operation (for pictures see Houben and Treskatis 2007). Quite frequently, the screen pipes were found to be rather eccentric, leaving a thin gravel pack at one side and a thick one on the other. The borehole showed significant variations in diameter, caused by partial collapse of the borehole wall during the drilling process. The gravel pack contained several pockets of aquifer material which had fallen into the annulus during installation of the filter. The gravel itself showed signs of grain-size gradation, which probably occurred during its backfilling. Initially, gravel packs often have a rather loose packing. Over time, its compactness might increase gradually by settling processes or abruptly, induced by mechanical rehabilitations or earthquakes. All models presented so far should be interpreted with these deviations from textbook sketches in mind.

Conclusions

When designing a water well, the whole aquifer—water well system and its individual components—and geometrical constraints have to be considered. Groundwater flow towards a well accelerates with decreasing distance to the screen. Therefore, the assumption of linear laminar (Darcy) flow is only valid, for common well set-ups, in the aquifer. In the gravel pack, non-linear laminar flow conditions become important (Fig. 8). Flow in the screen and in the well interior requires the application of turbulent flow laws. Table 5 lists the most important analytical approaches and their range of application. If two methods are listed as “usually applicable” for one set-up (e.g. Darcy or Forchheimer flow for the gravel pack), the decision on which to use, should be based on the Reynolds or Forchheimer number. It would, of course, be possible to always employ the Forchheimer approach and ignore the contribution of inertial flow, if it is too small.

Table 5 Analytical tools for hydraulic well component assessment and their application range (valid for common designs and operation parameters of screened vertical wells)
Full size table

A critical entrance velocity is commonly invoked for well design but an agreed permissible value remains elusive. Increasing the screen length is usually the easiest way to control the entrance velocity, as the influence of the screen or borehole diameter is less pronounced. The Reynolds number is probably more suitable to define the transition of flow regimes and, thus, the goodness of designs.

It is recommended that well owners investigate the aquifer thoroughly before commencing drilling. Exploration drillholes, pumping tests and geophysical surveys will provide a wealth of data that will be needed to do the calculations mentioned in the preceding, including, e.g. aquifer thickness, hydraulic conductivity, radius of the cone of depression, (natural) water level fluctuations and porosity. A paper related to this study (Houben 2015) shows the practical application of the analytical models discussed here for well design and investigates the relative contributions of individual well components to total head loss and how they may be improved.