Introduction

Water flow in low-permeability media (such as clay media) is an important process for a number of practical applications. For example, clay/shale formations have been considered as potential host rock for geological disposal of high-level radioactive waste because of their low permeability, low diffusion coefficient, high retention capacity for radionuclide, and ability to self-seal fractures (Tsang et al. 2012). Clay/shale formations also serve as the cap rock of geological formations where supercritical CO2 is stored for the purpose of CO2 sequestration. Water flow through the cap rock may be an important mechanism that needs to be considered for managing pressure buildup owing to injection of CO2 into the storage formation below the cap rock. Nowadays, exploration and recovery of unconventional energy resources, including shale oil and shale gas, become increasing important. The recovery of these resources requires improved understanding of and improved modeling approaches for water (and other fluid) flow within clay/shale formations under different conditions.

Water flow in porous media is traditionally described by Darcy’s law. In 1856, Henry Darcy investigated the flow of water in vertical homogeneous sand filters in connection with the fountains of the city of Dijon in France. From his experimental results, Darcy empirically discovered that water flux is directly proportional to the hydraulic gradient. However, it has been well documented that Darcy’s law is not adequate for clay media, as reviewed by Liu and Birkholzer (2012). For example, Hansbo (1960, 2001) reported that water flux in low-permeability clay is proportional to a power function of the hydraulic gradient when the gradient is less than a critical value, whereupon the relationship between water flux and gradient becomes linear for large gradient values. He explained this behavior by positing that a certain hydraulic gradient is required to overcome the maximum binding energy of mobile pore water. From their experimental results, Miller and Low (1963) also found the existence of a hydraulic gradient below which water is essentially immobile. Most recently, Xu et al. (2007) experimentally investigated the relationship between the flux of deionized water and hydraulic gradient in individual microtubes with diameters ranging from 2 to 30 μm. They demonstrated that water flow in microtubes with diameters of larger than 16 μm is consistent with Darcy’s law, but not for smaller diameters. In the latter cases, the relationship between water flux and hydraulic gradient becomes non-linear.

The aforementioned studies are all for saturated flow conditions. Laboratory test results seem to show that non-Darcian flow behavior becomes even more significant under unsaturated conditions. Cui et al. (2008) reported non-Darcian behavior for a range of observed hydraulic gradients under unsaturated conditions. Liu et al. (2013) developed a constitutive model for unsaturated flow when water can be considered as a power-law fluid; the model is consistent with the data set of Cui et al. (2008). (Power-law fluids are a special kind of non-Newtonian fluids.) Note that Liu et al. (2013) probably were the first to report relative-permeability formulations for power-law fluids. Power-law fluids are common in the processes of enhanced oil recovery (EOR) such as chemical flooding; thus, the work of Liu et al. (2013) could be applicable to modeling related EOR processes as well. As an effort to develop a general framework for modeling non-Darcian flow in low-permeability media, Liu and Birkholzer (2012) reported a new relationship between water flux and hydraulic gradient for both saturated and unsaturated water flow, and also developed an empirical formulation to relate permeability to a parameter characterizing non-Darcian flow behavior.

While considerable progress has been made for investigating non-Darcian flow in clay media, several key technical issues still need further research. This work is devoted to addressing the following issues related to geological disposal of high-level nuclear waste in clay/shale formations.

One of the most important technical questions for the performance of a shale/clay repository is the relative importance of advection versus diffusion in the damage zone near underground tunnels/drifts. Later, it is demonstrated that under normal conditions (under which there are no intersections between tunnels/drifts and conductive geological structures such as faults), the water flow velocity in the damage zone, as a result of non-Darcian flow behavior, is extremely small such that solute transport is dominated by diffusion, rather than advection. This is desirable because diffusion is a much slower transport mechanism for radionuclides.

As previously indicated, unsaturated flow is an important process for a shale/clay repository. To model the unsaturated flow process, one needs relative permeability as a function of water saturation. It will be shown that without incorporating non-Darcian flow behavior, significant errors can occur in the “measured” relative-permeability values, which is generally supported by an experimental data set.

A geological repository is subject to temperature evolution in the near field as a result of heat generated by nuclear waste. Thus, incorporating the impact of temperature on non-Darcian flow behavior is needed for assessing repository performance; however, studies on the subject are very limited in the literature. As a first step to resolve this issue, a hypothesis to consider the temperature impact based on limited test results from the petroleum literature is proposed.

Previous studies have only considered non-Darcian flow in one-dimensional (1D) and/or isotropic media (Liu and Birkholzer 2012); however, shale formations consist of bedding layers and are therefore generally anisotropic. To consider the bedding effects, an empirical relationship between water flux and hydraulic gradient for non-Darcian water flow in anisotropic cases is presented.

A review of relationships between water flux and hydraulic gradient

Non-Darcian flow behavior is characterized by non-linear relationships between water flux and hydraulic gradient. This section discusses several selected relationships available in the literature for completeness, while a more detailed review is given in Liu and Birkholzer (2012).

The well-known flux-gradient relationship is Darcy’s law given by

$$ q= Ki $$
(1)

where q (m/s) is water flux, K (m/s) is hydraulic conductivity and i (-) is hydraulic gradient. The preceding equation only includes magnitudes of variables for 1D flow and, therefore, q, K, and i are all positive. A similar treatment is used, for convenience, for all the other relationships to be discussed in this section.

To incorporate non-Darcian flow behavior in clay soils, Swartzendruber (1961) introduced a modified Darcy’s law based on a relation for dq/di:

$$ \frac{ dq}{ di}=K\left(1-{e}^{-i/I}\right) $$
(2)

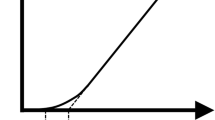
For a large value of hydraulic gradient i, dq/di approaches a constant K that is hydraulic conductivity. Parameter I is called the threshold gradient in this study and refers to the intersection between the i-axis and the linear part of the relationship (Fig. 1). Integrating, and using q = 0 at i = 0, leads to

$$ q=K\left[i-I\left(1-{e}^{-i/I}\right)\right] $$
(3)
Fig. 1
figure 1

Definition of threshold hydraulic gradient

Full size image

Equation (3) involves two parameters K and I. The equation of Swartzendruber (1961) has been evaluated with a number of data sets collected under saturated flow conditions and satisfactory agreements have been generally obtained (Swartzendruber 1961; Blecker 1970). However, it was found that Eq. (3) cannot capture the full range of non-Darcian flow behavior in clay media, especially under unsaturated conditions (Liu and Birkholzer 2012).

Another commonly used flux-gradient relationship for clay is given as (e.g., Bear 1979):

$$ \begin{array}{ll}q=0\hfill & \mathrm{for}\kern0.4em i\kern0.4em \le I\hfill \end{array} $$
(4)
$$ \begin{array}{ll}q=K\left(i-I\right)\hfill & \mathrm{for}\kern0.4em i\kern0.4em \ge I\hfill \end{array} $$
(5)

Similar to Eq. (3), the preceding equation involves only two parameters (K and I) and is mathematically simpler. It is obvious, however, from data available in the literature, that Eqs. (4) and (5) cannot adequately capture non-Darcian flow behavior (or non-linear flux-gradient relationship) at low i values (e.g., Swartzendruber 1961; Blecker 1970). Therefore, Eqs. (4) and (5) should be applied only when i is large. Also note that Eq. (5) is a limiting case of Eq. (3) for i/I → ∞.

In an effort to develop a general relationship between water flux and hydraulic gradient (that covers the full range of non-Darcian flow behavior under both saturated and unsaturated conditions), Liu and Birkholzer (2012) proposed to generalize Swartzendruber’s (1961) relationship using

$$ \frac{ dq}{ di}=K\left(1-{e}^{-{\left(\frac{i}{I\ast}\right)}^{\alpha }}\right) $$
(6)

where α is a positive constant, and I* is a parameter related to α and I. For α = 1, Eq. (6) is reduced to Eq. (2). For α → ∞, \( \frac{ dq}{ di}\to 0 \) when \( \frac{i}{I\ast }<1 \), and \( \frac{ dq}{ di}\to K \) when \( \frac{i}{I\ast }>1 \). In this case, Eq. (6) essentially represents the flux-gradient behavior given in Eqs. (4) and (5). Thus, with one more parameter (α), Eq. (6) can capture a relatively large range of non-Darcian flow behavior.

Integrating Eq. (6) with the condition of q = 0 at i = 0 yields

$$ q=K\left[i-\frac{I}{\gamma \left(\frac{1}{\alpha}\right)}\gamma \left(\frac{1}{\alpha },{\left(\frac{i}{I\ast}\right)}^{\alpha}\right)\right] $$
(7)

where

$$ I=\frac{I\ast }{\alpha}\gamma \left(\frac{1}{\alpha}\right) $$
(8)

and γ refers to the incomplete Gamma function and the Gamma function given by

$$ \gamma \left(a,x\right)={\displaystyle \underset{0}{\overset{x}{\int }}{t}^{a-1}{e}^{-t} dt} $$
(9)
$$ \gamma (a)={\displaystyle \underset{0}{\overset{\infty }{\int }}{t}^{a-1}{e}^{-t} dt} $$
(10)

Note that the physical meaning of parameter α is not fully understood yet; it may be associated with the pore-size distribution.

For a clay material, the degree of solid-water interaction and non-Darcian flow behavior can be characterized by permeability (k) (or pore size) and threshold gradient (I), respectively. Note that permeability is closely related to hydraulic conductivity and determined using data in the range showing a linear relationship between water flux and hydraulic gradient (Fig. 1). Thus, Liu and Birkholzer (2012), as shown in Fig. 2, present an empirical correlation between k and I based on data sets from a number of researchers (Lutz and Kemper 1959; Miller and Low 1963; Blecker 1970; Dubin and Moulin 1986; Zou 1996; Cui et al. 2008; Wang et al. 2011). These data sets can be reasonably fitted by a relationship between I and permeability k (m2)

$$ I=A{k}^B $$
(11)

with A = 4.0 × 10−12 and B = −0.78. This finding is very encouraging considering that the data sets were collected for different kinds of clay media and low-permeability materials and by different researchers. This may imply the existence of a universal relationship between I and permeability, although some degree of fluctuation exists in Fig. 2. Similar power-law relationships have also been reported in the literature of petroleum engineering (e.g., Zeng et al. 2010). Note that for unsaturated flow, k in Eq. (11) is replaced by relative permeability multiplied by permeability (Liu and Birkholzer 2012).

Fig. 2
figure 2

Correlation between permeability and threshold hydraulic gradient (I) (Liu and Birkholzer 2012)

Full size image

A demonstration of impact of non-Darcian flow on performance of a clay repository

As previously indicated, one major concern for a clay repository is that the hydromechanical perturbation caused by underground excavations during the construction stage could alter the properties of geological barriers compromising the safety performance of the repository system. The perturbation generally results in the excavation damaged zone (EDZ) around the repository tunnels and access shaft, because of a redistribution of in situ stresses and rearrangement of rock structures (Tsang et al. 2012). The higher concentration of macro- and microfractures in the EDZ increases the permeability by one or more orders of magnitude. Thus, the EDZ could act as a preferential flow path for advective transport. This is a very unfavorable condition because it can speed up radionuclide transport toward the biosphere. On the other hand, if water velocity in the EDZ would be small, diffusion could be the dominant mechanism for radionuclide transport. In this case, the impact of the EDZ on radionuclide transport is minimal. Therefore, the relative importance of advection versus diffusion in the EDZ is a key issue for assessing the performance of a clay repository.

Recently, Bianchi et al. (2014) conducted a comprehensive modeling study on the relative importance of advection versus diffusion within the EDZ. They developed a two-dimensional (2D) model of a generic repository including a single horizontal tunnel for waste emplacement, a vertical shaft, and a vertical cross section of the host-rock formation. The longitudinal axis of the horizontal tunnel, which has a total length L equal to 600 m, is located at z = −50 m (Fig. 3). The length of the model domain in the x direction is 2,000 m, such that boundary conditions imposed at the left and right boundaries are sufficiently distant from the tunnel and the shaft. The total thickness t HR of the host rock is 100 m, while the vertical extension of the shaft (h S) equals 50 m, from the end of the horizontal tunnel to the top boundary of the host formation. For their base case scenario, Bianchi et al. (2014) assumed a vertical hydraulic gradient, determined by the difference in hydraulic head between the values imposed at upper and lower boundaries of the flow model, equal to 1 m/m. This value is consistent with the hydraulic conditions of the Opalinus Clay at the Mont Terri site, Switzerland (Bianchi et al. 2014). The values of the hydrogeological parameters assigned to the host rock and the repository components were also chosen to be realistic with respect to values from several sources (Table 1).

Fig. 3
figure 3

Flow pattern for a 2D generic clay repository (Bianchi et al. 2014)

Full size image
Table 1 Parameter value for the generic clay repository (Bianchi et al. 2014)
Full size table

The base-case simulation results of Bianchi et al. (2014) are demonstrated in Fig. 3. The stream lines are generally in a vertical direction except within the EDZ surrounding the tunnel, and the water potential lines—each of which has constant water head (potential)—are generally in the horizontal direction. The simulations did not consider the non-Darcian flow behavior. Bianchi et al. (2014) found that for a given ambient hydraulic gradient, the upward water flow below the tunnel is intercepted by the high-permeability EDZ and advection indeed becomes important within the EDZ. They also found that the advection within the EDZ is limited by the amount of water flowing into it from the surrounding host rock. This is expected because when there is no water flowing into the EDZ, water velocity within the EDZ would be zero, even though the EDZ permeability is high.

In this study, the relative importance of advection versus diffusion within the EDZ was further investigated by incorporating the non-Darcian flow behavior. The model setup and parameter values in Bianchi et al. (2014) are employed herein. To simplify the analysis procedure, it was assumed that the EDZ permeability is infinite and the permeability of backfills in the tunnel is zero. Obviously, these assumptions generally lead to overestimation of the relative importance of advection within the EDZ. In this case, the EDZ has the same pressure head as the upper boundary in Fig. 3, because the EDZ is in equilibrium with the upper boundary. The simulation results from Bianchi et al. (2014) indicate that under steady-state conditions, the hydraulic gradient in the zone below the tunnel is very close to the uniform distribution. The same distribution is assumed here. With these assumptions and approximations, the hydraulic behavior of the EDZ can be easily determined without using numerical modeling. The hydraulic gradient below the tunnel will be twice as large as the ambient condition (or i = 2 m/m). The EDZ intercepts all the upward flow from the region below the tunnel. The water flow rate (and velocity) will be linear along the x-axis with zero value at the left end and the maximum value at the right end (Fig. 3).

The water flux into the EDZ from the lower portion of the clay formation in Fig. 3 is estimated with Eq. (3) (for simplicity) and for i = 2 m/m. Based on the mass balance, the maximum (horizontal) water flow rate within the EDZ is equal to the calculated water flux, multiplied by the length of the tunnel and by the upper diameter of the EDZ. Then, the maximum pore velocity within the EDZ is determined with the flow rate, its cross-sectional area, and fracture porosity. Figure 4 shows the normalized pore velocity as a function of threshold gradient I. The normalized velocity there refers to the ratio of the maximum pore velocity within the EDZ to that for Darcian flow (2.69E-16 m/s). The filled circle in Fig. 4 corresponds to the threshold hydraulic gradient I = 2,755 m/m calculated from Eq. (11) using permeability k = 5E-20 m2 (Table 1). Obviously, the non-Darcian flow has a significant impact on the water velocity. For the problem under consideration with I = 2,755 m/m, the water velocity corresponding to non-Darcian flow is more than three orders of magnitude smaller than that for the Darcian flow (Fig. 4).

Fig. 4
figure 4

The normalized pore velocity as a function of threshold gradient I. The normalized velocity refers to the ratio of the maximum pore velocity within the EDZ to that in the Darcian-flow case

Full size image

The relative importance of the advection within EDZ can be evaluated with the Peclet number, Pe (Bianchi et al. 2014):

$$ \mathrm{Pe}=\frac{ vL}{D} $$
(12)

where v (m/s) is the maximum pore velocity, L = 600 m is the length of the tunnel, and D (m2/s) is the effective diffusion coefficient within fractures (Table 1). Note that for D here, unlike in porous media, there is no need to consider the tortuosity factor because transport paths in fractures are close to straight lines. In general, Pe represents the ratio of the time for diffusion (L 2 /D) to the time for advection (L/v). For porous media, Pe < 1 is considered to correspond to the solute-transport regime with dominant diffusion. This criterion, however, is too strict for this study because the matrix diffusion process can significantly enhance the role of the diffusion process in fractured rock (Liu et al. 2007), but is not considered in the expression for Pe. Nevertheless, the calculated Pe values for the problem given in Fig. 3 are 0.6 in the non-Darcian flow case and 1666.7 in the Darcian flow case. It is obvious that solute transport within the EZD, as a result of non-Darcian flow behavior, is diffusion-dominated, even though the EDZ permeability is assumed to be infinite. In other words, advection is not the dominant transport mechanism within the EDZ because the water flow rate into the EDZ is essentially eliminated by the non-Darcian flow behavior in the shale formation. Note that the conclusion reached for this study holds only under conditions without intersections between the EDZ and the conductive geological structures that connect the high-permeability formations surrounding the host rock formation.

The non-Darcian flow behavior discussed here is consistent with the often-observed pressure-seal effects of shale formations. It is well known that a shale formation is capable of confining anomalous pressure over geologic time. Based on his analyses of pressure propagations, Deming (1994) concluded that the permeability needed for a geologic unit to act as a pressure seal over a time span of about one million years is in the range of 10−21–10−23 m2, a range generally lower than most measurements of shale permeability. Note that the use of lower permeability values than actual ones in Deming (1994) is essentially equivalent to the consideration of non-Darcian flow behavior when the hydraulic gradient is less than the threshold gradient (Fig. 1). The dominant mechanism for the anomalous pressure in shale formations has been an issue of debate in the literature. To the best of the author’s knowledge, this work is the first to propose the non-Darcian flow as the dominant mechanism. The osmotic pressure within shale formations has also been proposed as a major mechanism (e.g., Tremosa et al. 2012). It may contribute to the persistence of observed overpressures, but cannot explain the frequently observed pressures that are lower than hydrostatic ones in shale formations.

Influence of non-Darcian flow on observed relative permeability

In geologic repositories for radioactive waste disposal, compacted expansive clay soils (bentonites) are also often considered as buffer materials within an engineered barrier system, to be placed in the repository tunnels between the radioactive waste and the host rock. The bentonite is usually compacted at low water content, and then progressively wetted by water from the surrounding host formation. As a result, an unsaturated zone may develop within the near field of a clay repository while the other regions of host rock remain saturated. The unsaturated wetting process is accompanied by bentonite swelling, which ensures acceptable sealing of open spaces between waste packages and the corresponding host formation. Accurately modeling unsaturated flow in such clay materials is critical for assessing the performance of both clay rock and buffer materials for isolating radioactive wastes at a disposal site.

Unsaturated properties for clay, including relative permeability k r, are necessary inputs to modeling the unsaturated flow process. (Note that for simplicity, near-field unsaturated water flow is not considered in section “A demonstration of impact of non-Darcian flow on performance of a clay repository”.) In general, the relative permeability can be related to water saturation by (van Genuchten 1980):

$$ {k}_{\mathrm{r}}={S}_{\mathrm{e}}^{1/2}{\left\{\left[1-{\left(1-{S}_{\mathrm{e}}^{1/m}\right)}^m\right]\right\}}^2 $$
(13)

where m is a parameter related to pore size distribution and S e is the effective saturation defined by

$$ {S}_{\mathrm{e}}=\frac{S-{S}_{\mathrm{r}}}{1-{S}_{\mathrm{r}}} $$
(14)

where S and S r are water saturation and residual saturation, respectively.

Since parameter m can be determined from the relatively easily measured water retention curve, Eq. (13) provides an efficient way to estimate relative permeability. The measurements of relative permeability are difficult and take a long time. However, the validity of the van Genuchten (1980) relationship, as an empirical one, is an open question for the shale rock because there are very rare studies on the comparison between the relationship and measured relative-permeability data for the rock. Thus, laboratory measurements of clay/shale relative-permeability values are needed to verify constitutive models and/or serve as inputs to modeling studies. The major purpose of this section is to demonstrate that “measured” values for relative permeability are not true medium properties, but strongly depend on test conditions, as a result of non-Darcian flow behavior. By “true” relative permeability, the relative permeability associated with the linear regime for the curve in Fig. 1 is meant.

To measure the relative permeability, the hydraulic gradient (i) is generally fixed, and then water flux (q) is measured under steady-state condition. In this case, the “measured” relative permeability k rM can be calculated as

$$ {k}_{\mathrm{rM}}=\frac{q/i}{K} $$
(15)

For simplicity, Eq. (3) was used to describe the non-Darcian flow behavior. Note that under unsaturated conditions, conductivity (K) in Eq. (3) needs to be replaced by unsaturated conductivity (Kk r). In this case, Eq. (15) becomes

$$ {k}_{\mathrm{r}\mathrm{M}}=\left(1-\frac{1-{e}^{-\frac{i}{I_{\mathrm{unsat}}}}}{\frac{i}{I_{\mathrm{unsat}}}}\right){k}_{\mathrm{r}} $$
(16)

Herein, I and I unsat are denoted as the threshold hydraulic gradient under saturated and unsaturated conditions, respectively. To calculate I unsat with Eq. (11), the permeability (k) there needs to be replaced by unsaturated permeability (kk r) (Liu and Birkholzer 2012). As previously indicated, water flow under unsaturated conditions generally exhibits stronger non-Darcian flow behavior than that under saturated conditions, because the former corresponds to smaller sizes of pores occupied by water.

For demonstration purposes, and because of the lack of alternatives, it was assumed that k r in Eq. (16) can be represented by Eq. (13). When hydraulic gradient (i) in a test is given, k rM can be calculated from Eq. (16) with I unsat and k r obtained from Eqs. (11) and (13), respectively. The value for m is assigned to be 0.6 (Zheng et al. 2012). Figure 5 shows the calculated k rM curves as a function of the effective saturation. For each curve, the hydraulic gradient i is fixed. The threshold gradient I is determined from Eq. (11) with k = 5E-20 m2 (see section “A demonstration of impact of non-Darcian flow on performance of a clay repository”). Note that I = 0 corresponds to the “true” relative permeability curve calculated with Eq. (13).

Fig. 5
figure 5

“Measured” relative permeability (k r ) curves under different hydraulic gradients (i), as a function of the effective saturation (S e ). Note that I is the threshold gradient and I = 0 corresponds to the “true” relative permeability curve calculated with Eq. (13)

Full size image

Figure 5 shows that a measured relative permeability, for a given saturation, is significantly smaller than the “true” value, especially for the low saturations under which non-Darcian flow behavior becomes relatively strong. The measured curve is a function of the hydraulic gradient used in the test. A larger gradient gives results closer to the “true” values, which is expected from Fig. 1. If relatively small hydraulic gradients are used in tests, the measured relative permeability can be smaller than one under the saturated condition, because permeability (k) measurements are not made in the linear regime of the relationship between water flux and hydraulic gradient (Fig. 1). The differences between “measured” curves and the “true” curve would be even more dramatic if Eq. (7) with α values larger than one was used for describing the non-Darcian flow behavior, because it gives much smaller values for dq/di when the hydraulic gradient is smaller than the corresponding threshold gradient (Eq. 5). Nevertheless, Fig. 5 clearly indicates that without considering the non-Darcian flow behavior, the “measured” values for relative permeability involve large errors.

Our finding seems to be consistent with the relative permeability measurements of rock matrix from the unsaturated zone of Yucca Mountain (BSC 2004). Those measurements, for a given saturation, are dramatically smaller than what are predicted from the van Genuchten relationship (Eq. 13) for samples with (absolute) permeability values below 10−18 m2. The differences can be explained with the non-Darcian flow behavior in low-permeability media, as discussed in the previous.

There are several ways to recover the “true” relative permeability curve from raw measurements by incorporating the non-Darcian flow behavior. The ideal one would be to use large enough hydraulic gradients such that throughout the tests, the relationship between water flux and the gradient is in the linear regime (Fig. 1). However, this may not be feasible in practice because the threshold gradient can be huge for low saturations. When the relationship between permeability and the threshold gradient (e.g., Eq. 11) is known with confidence, the only unknown in Eq. (16) is k r for a given measurement k rm . In this case, k r can be estimated by solving Eqs. (11) (generalized for unsaturated conditions) and (16). If the required relationship between permeability and the threshold gradient is not known for a specific rock type, measurements for relative permeability with different hydraulic gradients, such as those shown in Fig. 5, need to be made. To recover the true curve, it is possible to simultaneously fit the measured curves using Eqs. (11), (13) and (16) with parameters A, B, and m being treated as fitting parameters. The advantage of this approach is that both the true relative permeability curve and the relationship between permeability and threshold gradient are simultaneously determined from measurements.

A hypothesis regarding the temperature dependence of the threshold hydraulic gradient

Performance assessment of a clay repository requires consideration of the impact of temperature on non-Darcian flow behavior, because such a repository is subject to temperature evolution in the near field as a result of heat generated by nuclear waste. This section presents a hypothesis regarding the temperature dependence of the threshold hydraulic gradient.

Studies of temperature impact on non-Darcian flow behavior are rare in the literature. To the best of the author’s knowledge, the only study related to temperature impact on non-Darcian water flow is Miller and Low (1963), who experimentally found that the critical hydraulic gradient (below which water is immobile) decreases with increasing temperature. They argued that this is because increased temperature may weaken the bounding between water molecules and the clay surface. Recently, Zeng et al. (2010) also reported an experimental investigation into temperature impact on oil flow processes in initially water-saturated low-permeability sandstone samples. They performed tests at two temperatures (70 and 90 °C) and found that observed threshold pressure gradient, in terms of oil mobility (or the ratio of permeability to temperature-dependent oil viscosity), does not depend on temperature. This is a potentially important result. Unfortunately, there are no data from a large range of temperatures to further verify their finding. However, their results are consistent with the argument of Miller and Low (1963) in that the weakened liquid–solid interaction should correspond to a low effective viscosity. Thus, as a first step, it is hypothesized that the finding of Zeng et al. (2010) can be applied to water flow in clay materials.

Based on this hypothesis, Eq. (11) becomes

$$ I=A{k}^B{\left(\frac{\mu_{\mathrm{ref}}}{\mu}\right)}^B $$
(17)

with A = 4.0 × 10−12 and B = −0.78, where μ and μ ref are water viscosities, respectively, at the current temperature and the reference temperature at which the data used to develop Eq. (11) were collected. Here the reference temperature is given as 25 °C.

Figure 6 shows the results calculated from Eq. (17) for several temperatures from 25 to 200 °C that cover the temperature range of interest to performance assessment of a clay repository. (The curve for 25 °C is identical to that in Fig. 2.) Viscosity values for different temperatures are taken from Weast et al. (1989) and Kestin et al. (1978). The threshold hydraulic gradient decreases with temperature, but the change is less than one order of magnitude for a given permeability (Fig. 6). Equation (17) allows for incorporating the temperature impact in modeling non-Darcian flow in clay or shale rocks, but it should be used with caution, especially when modeling results are sensitive to the temperature impact. More studies, both theoretical and experimental, are needed to develop more rigorous approaches for dealing with this temperature dependence.

Fig. 6
figure 6

The temperature dependence of the relationship between threshold hydraulic gradient (I) and permeability

Full size image

An approximate formulation of water flux in anisotropic media

In many studies, including modeling flow and transport in a clay repository, it is necessary to investigate multidimensional water-flow processes. However, most previous studies on the non-Darcian flow are for 1D cases. Recently, Liu and Birkholzer (2012) extended Eq. (7) to three-dimensional (3D), homogeneous and isotropic clay media:

$$ \mathbf{q}=-K\left[i-\frac{I}{\gamma \left(\frac{1}{\alpha}\right)}\gamma \left(\frac{1}{\alpha },{\left(\frac{i}{I\ast}\right)}^{\alpha}\right)\right]{\mathbf{n}}_i $$
(18)

where q (m/s) and n i (-) are water flux vector and unit vector for hydraulic gradient, respectively. The relationship between I and I* is given by Eq. (8). When the threshold gradient I approaches zero, Eq. (18) is reduced to the commonly used form of Darcy’s law. It should be emphasized that Eq. (18) is an empirical relationship developed from 1D test results. It is logical to directly extend Eq. (7) to Eq. (18) for homogeneous and isotropic cases because both equations are consistent with the 1D test condition, whereby flux and negative hydraulic gradient are along the same direction.

Shale formations are generally anisotropic, as a result of bedding structure. To model water flow in these formations, a formulation is needed for water flux in anisotropic media; however, because of the non-linear feature of the non-Darcian flow, it is not a trivial task to theoretically relate the flux-gradient relationship between different dimensions and/or between isotropic and anisotropic media. Thus, in this study, an approximate formulation of water flux in an anisotropic medium is presented. For simplicity, the spatial coordinate axes are chosen to be in the principal directions of the anisotropic medium (Bear 1979) such that one axis is perpendicular to the bedding plane. Then, the water-flux formulation for anisotropic media by extending Eq. (18) is proposed:

$$ \mathbf{q}=-\mathbf{K}\left[i-\frac{I}{\gamma \left(\frac{1}{\alpha}\right)}\gamma \left(\frac{1}{\alpha },{\left(\frac{i}{I*}\right)}^{\alpha}\right)\right]{\mathbf{n}}_i $$
(19)
$$ I=\frac{\sqrt{{\left({I}_{\mathrm{x}}{i}_{\mathrm{x}}\right)}^2+{\left({I}_{\mathrm{y}}{i}_{\mathrm{y}}\right)}^2+{\left({I}_{\mathrm{z}}{i}_{\mathrm{z}}\right)}^2}}{\sqrt{{\left({i}_{\mathrm{x}}\right)}^2+{\left({i}_{\mathrm{y}}\right)}^2+{\left({i}_{\mathrm{z}}\right)}^2}} $$
(20)

where K is the conductivity tensor, and subscripts x, y and z refer to components along three coordinate directions. Specifically, I j (j = x, y, z) is the measured threshold hydraulic gradient in the jth direction from 1D experiments. Because of the way the coordinate system was chosen, there are no cross terms in the conductivity tensor. It is also easy to show that the relation among the magnitude of conductivity, conductivity components, and hydraulic-gradient components has the same mathematical form as Eq. (20).

The reasonableness of the approximation (Eqs. 19 and 20) can be demonstrated by its consistency with known results. For 1D flow along the bedding direction (e.g., the x direction), Eq. (19) is reduced to Eq. (7) with I = I x. Similarly, if the z direction is perpendicular to the bedding plane, the expected result, I = I z, can also be gotten for 1D flow along the z direction. For isotropic cases (or I x = I y = I z), Eq. (18) can be recovered from Eqs. (19) and (20). Thus, Eqs. (19) and (20) give an approximate, yet practically reasonable way to model non-Darcian water flow in the bedding shale formations, while the exact formulation for water flux in anisotropic media is difficult to obtain.

Concluding remarks

This paper presents new results of a continuing effort to develop a general modeling framework for non-Darcian water flow in low-permeability media. Specifically, this communication is devoted to addressing several key issues related to geological disposal of high-level nuclear waste in shale formations.

One of the most important technical questions for the performance of a shale/clay repository is the relative importance of advection versus diffusion in the damage zone near underground tunnels/drifts. It is demonstrated that under normal conditions (under which there are no intersections between tunnels/drifts and conductive geological structures, such as faults), water flow velocity in the damaged zone, as a result of non-Darcian flow behavior, is extremely small such that solute transport is dominated by diffusion, rather than advection. The findings of this study are also consistent with the often-observed existence of persistent abnormal pressures in shale formations.

Unsaturated flow takes place in both the engineered barrier system and the host rock of a shale/clay repository. Relative permeability is the key parameter for modeling the unsaturated flow process. It is shown that without incorporating non-Darcian flow behavior, significant errors can occur in the determination of relative-permeability values from traditional measurement methods. How to recover the true relative permeability values from the measurements is also discussed.

A geological repository is subject to temperature evolution in the near field as a result of heat generated by nuclear waste. Thus, it is important to incorporate the impact of temperature on non-Darcian flow behavior in order to more accurately assess repository performance. As a first step toward resolving this issue, a hypothesis is proposed to consider the temperature impact based on limited test results from the petroleum literature. The hypothesis states that the threshold hydraulic gradient is a function of temperature-dependent mobility only.

Shale formations consist of bedding layers and are therefore generally anisotropic. To consider the bedding effects, an empirical relationship between water flux and hydraulic gradient for non-Darcian water flow in anisotropic media is also proposed. The relationship is consistent with the known relationships for 1D and 3D isotropic cases.