Parametric Sensitivity to Capillary Entry Pressure in Two-Phase Water–Gas Flow Models: Deep Geologic Disposal of Radioactive Waste

Abstract

In a deep geological repository for the long-term containment of radioactive waste, the engineered barriers and host clay rock inhibit the migration of gases, due to their low permeability and high gas entry pressure. Some experiments in the literature have focused on the measurement of gas entry pressure $(P_{\text {g,e}}$, but there is a lack of 2-phase flow (water–gas) modeling studies that include entry pressure effects in such porous media. In the present work, the modified Van Genuchten–Mualem model (Vogel et al. 2000) is extended to two-phase flow, incorporating the capillary entry pressure parameter $(P_{\text {c,e}})$, and a new data analysis approach is developed in order to characterize the water–gas constitutive relations (saturation curve, water permeability curve, gas permeability curve). This constitutive model is then implemented in the iTOUGH2 code (Wainwright and Finsterle 2016 in Global sensitivity and data-worth analyses in iTOUGH2: User’s guide) with a change of primary variables to be described below (capillary pressure is set as primary state variable instead of gas saturation). After regression tests for verifying the change of primary variables in iTOUGH2, two problems were modeled: first, numerical flow experiments were performed in a clay soil (code-to-code benchmark tests, and comparisons focused on entry pressure effects); secondly, water–gas migration was modeled based on an in situ gas injection experiment (PGZ1) performed in the French URL (Underground Research Laboratory) of Bure. Sensitivity analyses show that gas entry pressure is an important controlling factor which should not be neglected in simulations of gas migration in clayey materials.

1 Introduction

1.1 Mechanisms of Gas Transport in Low Permeability Porous Media

After closure of a deep geological repository (DGR), significant amounts of gases, mainly hydrogen ($H_2$), are expected to be produced through a number of processes including anaerobic corrosion of the metallic components used in the repository design, water radiolysis and degradation of organic materials. Consequently, the rise of gas pressure could affect the post-closure phase safety of the waste repository.

Fig. 1

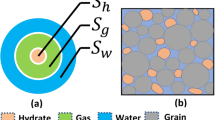
Schematic depiction of four main processes of gas transfer in clays (from Cuss et al. 2014)

A number of in situ and laboratory experiments were developed and investigated in order to understand the key mechanisms of gas migration in clayey materials (Marschall et al. 2005; Cuss et al. 2014; De La Vaissière et al. 2019). Four types of gas migration mechanisms are usually identified for gas transport in low permeability materials like the Callovo-Oxfordian (COx) at the Bure URL in France, and the Opalinus Clay at the Mont Terri URL in Switzerland (Fig. 1).

At low gas production rates, the gases are dissolved in the liquid water phase, and they migrate mainly by diffusion and advection as dissolved species: in that case, the main transport parameters are the permeability of the material, and the coefficient of solute diffusion in water.

As gas production rate increases, the inlet gas pressure and the dissolved gas concentration both rise. If gas pressure overcomes the value of the gas entry pressure $P_{\text {g,e}}$, a second type of gas transport process takes place, namely, two-phase water–gas flow. Gas entry pressure $P_{\text {g,e}}$ is the main variable for this second type of gas transport process (transition liquid flow $\leftrightarrow$ two-phase flow). In fact, the relevant porous medium parameter, in this case, is the capillary entry pressure $P_{\text {c,e}}$, while the gas entry pressure $P_{\text {g,e}}$ is a variable that depends also on liquid pressure $P_{\text {l}}$ according to the relation: $P_{\text {g,e}}=P_{\text {l}}+P_{\text {c,e}}$. In other words, for any given value of liquid pressure $P_{\text {l}}$, the gas entry pressure $P_{\text {g,e}}$ in the porous material is given by the capillary relation: $P_{\text {c,e}} = P_{\text {g,e}} - P_{\text {l}}$, where $P_{\text {c,e}}$ is a characteristic parameter of the porous medium.

If liquid pressure becomes high enough, then it may exceed a critical level of effective stress and may create dilation pathways through which gas will enter when the gas entry pressure is exceeded (that is, when $P_{\text {g}} > P_{\text {g,e}}=P_{\text {l}}+P_{\text {c,e}}$). This effect has been observed in a number of experiments on argillaceous materials (Angeli et al. 2009; Cuss et al. 2014; Wiseall et al. 2015).

Thus, given the fine porous structure and low permeability of host rock and engineered barriers, and given that they remain usually under conditions of near full water saturation in the presence of gas production, these materials constitute a capillary barrier for gas flow in a DGR. The gas phase must reach a pressure threshold before it can penetrate the porous medium (under some conditions, gas flow may also result in damages to the material due to high gas pressures).

Therefore, modeling gas migration requires an enhanced model that takes into account the gas entry pressure phenomenon, or more precisely, the capillary entry pressure $P_{\text {c,e}}$ as a two-phase parameter of the porous medium, in order to correctly quantify two-phase water–gas flow in such low permeability/fine grained porous materials at mesoscopic or larger scales.

It is the purpose of this paper to test and implement such modeling at various scales. In this and forthcoming studies, our general objective is to implement such enhanced two-phase model, taking into account $P_{\text {c,e}}$, in the context of radioactive waste disposal on various 3D spatial scales (e.g., Saâdi et al. 2020): scale of a waste cell (tens of meters); scale of a module comprising hundreds of cells (hundreds of meters); and possibly, scale of the entire repository site (kilometers horizontally). Material deformations or damages can also have an important effect, but they are not being considered in the present work.

1.2 Gas Entry Pressure, Capillary Entry Pressure

In this study the concept of capillary entry pressure at quasi-static equilibrium state will be used for the case of gas as the non-wetting phase and water as the wetting phase. Note however that a dynamic term (or kinetic term) has been added by several authors to extend the saturation curve ${P_{\text {c}}} ({S_w})$ to a relation of the form ${P_{\text {c}}} \left( {S_w} , \partial {S_w}/\partial t \right)$. Models accounting for such dynamic effects, based on pore scale modeling and/or upscaling methods, are especially interesting for studying hysteresis. These effects are beyond the scope of the present paper.

The capillary entry pressure $P_{\text {c,e}}$, is the threshold capillary pressure above which the gas phase can enter the porous material. It must be either positive or null (it is in fact set to zero by default in many porous media models). Recall that capillary pressure is a state variable defined as the difference between non-wetting phase (gas) pressure and wetting phase (water) pressure: $P_{\text {c}}=P_{\text {g}}-P_{\text {w}}$. Therefore, for any given liquid water pressure, the capillary entry pressure $P_{\text {c,e}}$ quantifies the threshold gas pressure (gas entry pressure) needed to displace water from the initially fully saturated medium.

It must be recognized that accurate measurement of gas entry pressure in low permeability materials may be a difficult task. This gas entry pressure represents the threshold at which water is displaced from the largest pores—but if there is only a small fraction of these largest pores, it is difficult to observe this displacement. Several authors presented overviews of available methods for measuring gas entry pressure. The main technique used for low permeability materials is the step-by-step approach (e.g., Boulin et al. 2013). Briefly, gas is injected, being initially placed in contact with the upstream surface of a fully saturated sample, at a pressure equal to pore water pressure. Gas pressure is then increased step by step, and when the capillary pressure becomes higher than entry pressure, water is displaced out of the sample.

The capillary entry pressure parameter $P_{\text {c,e}}$ depends on the micro-structure of the porous medium. At the scale of a single pore modeled as a cylindrical capillary tube of radius r, and the Young–Laplace equation defines the capillary pressure jump across the interface between the water and gas phases in the pore. This yields a simple relationship between the capillary threshold pressure $P_{\text {c,e}}$ and the radius r of the tube, as follows:

$$\begin{aligned} P_{\text {c,e}}= \frac{2 \sigma _{\text {g},\text {w}}\cos {\alpha }}{r}= P_{\text {g}}-P_{\text {w}} \end{aligned}$$

(1)

where $P_{\text {w}}$, $P_{\text {g}}$, $\sigma _{\text {g},\text {w}}$, and $\alpha$ are, respectively, the water pressure [Pa], the gas pressure [Pa], the surface tension of the gas/water interface [Pa.m] and the wetting angle. In general $\sigma _{\text {g},\text {w}}$ and $\alpha$ depend on the solid, the wetting fluid and the non-wetting fluid. In the case of perfect wetting, $\alpha = 0$ (more general $0< \alpha < \pi / 2$ for imperfect wetting).

We need now to consider $P_{\text {c,e}}$, as well as the other parameters (porosity, permeability) at the mesoscopic scale of many pores, i.e., at the scale of a Representative Elementary Volume (REV), as discussed for instance in Chap. 1 and Chap. 5 of Ababou (2018). The mesoscale parameter $P_{\text {c,e}}$ depends essentially on the distribution of pore sizes, on the connectivity between the pores, and also, on the possible existence of fissures. Therefore, an explicit determination of gas entry pressure is not a simple issue.

For example, the pore radius probability density function of the COx host rock presents a peak around 20 nm ($20 \times 10^{-9}$ m) (ANDRA 2005), corresponding to a capillary pressure of 14.55 MPa. However, this value of $P_{\text {c,e}}$ cannot be fully representative for the COx, because this value corresponds to the peak, not to the maximum pore radius in the distribution (which is difficult to quantify statistically). Furthermore, it does not account for the connectivity between the pores, and it does not account either for the presence of fissures. Experimental data on the COx, collected by Harrington et al. (2017), indicated a high uncertainty on the value of entry pressure, which can vary from 1 MPa (10 bars) for damaged samples, to values above 5 MPa (50 bars) for intact samples.

Note concerning pore size distribution measurements.Song et al. (2015) used Focused Ion Beam in combination with Scanning Electron Microscopy (FIB/SEM), for imaging the pore network of the COx claystone. They observed small porosity of 1.7–5.9% with a peak pore size around 50–90 nm. Then, 2D transmission electron microscopy (TEM) revealed a large amount of smaller pores (2–20 nm) with a local porosity of 14–25% and a peak size of 4–6 nm. However the measurement volume was on the order of 28–147 ${\upmu \text {m}}^3$ only, which cannot be representative of COx structure on larger macroscopic scales. Other studies by Song et al. (2016) indicate that fluid transport occurs through very limited parts of the pore network (fingering in the widest paths). Taking into account only the pores larger than 20 nm would lead to a gas entry pressure up to 14 MPa, but this value seems much higher than that measured in larger samples of the COx claystone. Several authors, e.g., ANDRA (2012), measured gas entry pressure in the COx at a bit less than 2 MPa, which is close to the value we use in this study.

Therefore, taking into account the gas entry pressure remains a challenging task in the physics of porous materials. Other challenges include the numerical aspects of switching between two flow regimes, from fully saturated liquid flow to liquid–gas flow and vice versa (a particularly delicate task).

The remainder of this paper is organized as follows. Section 2 presents the constitutive relationships to be used in the simulations, including a new model for entry pressure. Section 3 presents the modification of the iTOUGH2 simulation code and a verification test for iTOUGH2 using a semi-analytical solution. Section  4 presents benchmarks and sensitivity tests performed with three different numerical codes: iTOUGH2-EOS3, BIGFLOW 3D, and UNSAT 1D (the latter being a recent custom made code designed to accommodate entry pressure for testing purposes). The code-to-code benchmarks and sensitivity tests focus on the effect of gas entry, based on two types of numerical experiments: simulations of capillary rise in a clay soil with and without entry pressure, and simulation of a comprehensive field scale experiment PGZ1 performed at ANDRA’s Underground Research Laboratory (URL) in the COx clay rock formation (Callovo-Oxfordian), carried out with our upgraded version of the iTOUGH2-EOS3 code. Last conclusive Sect. 5 summarizes the results and briefly discusses perspectives.

2 Theory of Constitutive Relationships: Functional Models and Entry Pressure

In this paper, the hydrodynamic properties of the porous media for two-phase flow are based essentially on the Mualem–Van Genuchten model and its modification with entry pressure. Other models have been tested but are not retained in this study. For example, other simulations of the PGZ1 experiment have been carried out using Brooks and Corey’s model (1964) of hydraulic properties (not shown here). Note that this model contains already an entry pressure parameter. Its fitted $P_{\text {c,e}}$ value was much higher (3.85 MPa) than that obtained with Mualem–Van Genuchten (2 MPa). Furthermore, the Brooks and Corey’s model (1964) only fitted the experimental data for liquid saturations very close to 1.0.

2.1 Classical Van Genuchten/Mualem Model

Based on Poiseuille’s law for each interconnected pore, and on the representation of the tortuosity factor as a power of the actual saturation, Mualem (1976) proposed a model for the prediction of the relative permeability function from the water retention curve, defined as :

$$\begin{aligned} K_{\text {r,w}}(P_\text {c})= {S}_{\text {we}}^{\tau } \biggl [\frac{\int _{0}^{S_{\text {we}}} \frac{1}{{P}_{\text {c}}(S)}\, \mathrm {d}x }{\int _{0}^{1}\frac{1}{{P}_{\text {c}}(S)}\, \mathrm {d}x }\biggl ]^{2} \end{aligned}$$

(2)

where ${S}_{\text {we}}$ is the effective saturation, ${\tau }$ is a pore connectivity parameter (dimensionless exponent), and ${P}_{\text {c}}(S)$ is the capillary pressure–saturation relationship. When the Van Genuchten model Van Genuchten (1980) is used, the effective saturation can be expressed as:

$$\begin{aligned} S_{\text {we}}(P_{\text {c}})~=~ \frac{S(P_{\text {c}})-S_{{\text {wr}}}}{S_{{\text {ws}}}-S_{{\text {wr}}}} ~=~ \frac{\theta _{\text {w}}(P_{\text {c}})- \theta _{\text {r}}}{\theta _{\text {s}}-\theta _{\text {r}}} ~=~ [1+ (\alpha P_{\text {c}})^{n}]^{-m} \end{aligned}$$

(3)

where n, m, and $\alpha$ $[\text {Pa}^{-1}]$, are the physical parameters to be fitted. We note that in some works, $1 / \alpha$ is interpreted as an entry pressure, although it is, rather, a characteristic capillary pressure of the porous material. In fact, $\frac{\rho \times g}{\alpha }$ can be interpreted as a capillary length of the medium. Also, it can be shown that the pressure scale ${1 / \alpha }$ is near the inflection point of the $S_{\text {we}}(P_\text {c})$ curve. That inflection point is more readily seen graphically on Cartesian plots rather that semi-log plots. More precisely, let us denote $\lambda _{\text {Cap}}$ or $\lambda _{\text {C}}$ the capillary pressure at the inflection point of the effective saturation curve $S_{\text {we}}(P_\text {c})$. It can be shown that :

$$\begin{aligned} \lambda _{\text {C}} = \frac{1}{\alpha } \left( 1 - \frac{1}{n} \right) ^{1/n} \end{aligned}$$

(4)

This and other inflection point characteristics were analyzed and interpreted for instance in Ababou (1991). The latter noted that the inflection point of the saturation curve corresponds to a maximum moisture capacity $C_{\text {max}}$, calculated explicitly, and that it corresponds to the minimum energy required to extract or expel water from the porous medium.

Taking the value $n=1.656$ used here for the COx, we obtain $\lambda _{\text {C}}=15.705$ MPa. The corresponding effective saturation is $S_{\text {we,C}}=0.876$, which is quite far from full water saturation. In comparison, the entry pressure considered here for the COx is $P_{\text {c,e}} = 2~\text {MPa}$ which is much less than the inflection point $\lambda _{\text {C}}$. To sum up, these auxiliary calculations indicate that the inflection point pressure $\lambda _{\text {C}}$, which can be approximated roughly as $1/ \alpha$, is a “global” characteristic of the saturation curve, whereas the entry capillary pressure $p_{\text {c,e}}$ characterizes “locally” the curve near the state of full saturation. These two characteristic pressures are significantly different for most media and for the COx in particular.

By inserting [Eq. (3)] in [Eq. (8)], and taking $m=1-\frac{1}{n}$, Van Genuchten obtained the analytic formula for relative water permeability as shown below, which was later extended by Parker et al. for relative gas permeability:

$$\begin{aligned} K_{\text {r,w}}(P_\text {c})= & {} S_{\text {we}}^{\tau }[1-(1-(S_{\text {we}}(P_\text {c}))^\frac{1}{m})^m] \end{aligned}$$

(5)

$$\begin{aligned} K_{\text {r,g}}(P_\text {c})= & {} (1-S_{\text {we}})^{\tau ^{'}}[1-(S_{\text {we}}(P_\text {c}))^\frac{1}{m}]^{2m} \end{aligned}$$

(6)

where $\tau$ is the dimensionless tortuosity parameter related to pore water connectivity, taken here equal to $\tau =1/2$ (the value adopted by Mualem (1976)), and $\tau ^{'}$ is the gas tortuosity parameter related to gas connectivity. Parker et al. (1987) extended the van Genuchten–Mualem water permeability approach to determine the relative gas permeability with gas tortuosity $\tau ^{'}=1/2$; and Luckner et al. (1989) proposed the same formulation of $K_{\text {r,g}}$ with $\tau ^{'}=1/3$. In our study, the $\tau ^{'}$ will be fitted rather than imposed (see Table 3). Note: saturation-dependent tortuosity was introduced early, in the 1950s and 1960s, by several authors, as a power function of saturation (Burdine, Childs and Collis-George,$\ldots$); see also Chap. 5 in Ababou (2018).

Fig. 2

Parametric sensitivity of the VGM model with respect to parameter n. Other parameters are fixed: $S_{\text {ws}}=1$, $S_{\text {wr}}=0$, and $\alpha ^{-1}= 15$ MPa

Sensitivity analyses by Stephens and Rehfeldt (1985), Van Genuchten et al. (1991), and Vogel et al. (2000), as shown for instance in Fig. 2, indicate that relatively small changes in water retention curve near full water saturation can lead to a significant change in the unsaturated hydraulic conductivity function calculated from Mualem’s functional model. This sensitivity may affect the flow dynamics and could possibly induce numerical convergence problems as demonstrated by Vogel et al. (2000).

2.2 Modified Van Genuchten/Mualem Model (VGM/Pe)

To examine the sensitivity of the hydraulic conductivity (and of the flow) to the saturation curve near full liquid saturation, Vogel et al. (2000) and Ippisch et al. (2006) suggested the introduction of a gas-entry value in the van Genuchten model (or in a different model) particularly for $n \le 2$ or $\alpha \times P_{\text {c,e}} \ge 1$, especially for fine textured media with “large” (or more properly with non-negligible) capillary entry pressure $P_{\text {c,e}}$, according to Vogel et al. (2000). The new model is denoted “modified VGM model” or “VGM/Pe model” (Van Genuchten/Mualem model with entry pressure).

At this point, it is useful to examine briefly the meaning of the term “non-negligible” applied to entry pressure. The magnitude of entry pressure for a given porous medium can be evaluated by scaling the entry pressure by the inflection point pressure $\lambda _{\text {C}}$ discussed earlier, renamed here $P_{\text {c},0}$ for convenience. This scaling approach yields a dimensionless entry pressure $P_{\text {c,e}}/P_{\text {c},0}$ $\approx$ $\alpha . P_{\text {c,e}}$. This dimensionless number $(\alpha . P_{\text {c,e}})$ is 2% in the case of the Vogel clay experiment and 8% in numerical modeling of the PGZ1 experiment (presented later in this paper). These values are small, but they must be considered significantly different from zero—judging also by the effect $P_{\text {c,e}}$ has on gas flow in the numerical experiments.

The modification of the VGM model to take into account a nonzero gas entry pressure is based on the introduction of a fictitious parameter $S_{\text {ws}}^{*} \ge S_{\text {ws}}$ in the capillary model of VGM (Eq. (3)) which allows a modification of the saturation–pressure curve (normalized as an effective saturation curve), and then of the relative permeabilities $K_{\text {r,w}}(P_{\text {c}})$ and $K_{\text {r,g}}(P_{\text {c}})$ (deduced from the integration of $S((P_{\text {c}}))$). These two curves remain continuous after modification. Their expressions are shown just below:

$$\begin{aligned} S_{\text {w}}(P_{\text {c}})~=~ {\left\{ \begin{array}{ll} S_{\text {wr}} + \frac{S_{\text {ws}}^*-S_{\text {wr}}}{[1+ (\alpha P_{\text {c}})^{n}]^{m}} &{} \hbox { if}\ P_{\text {c}} \ge P_{\text {c,e}} \\ S_{\text {ws}} &{} \hbox { if}\ P_{\text {c}} \le P_{\text {c,e}} \end{array}\right. } \end{aligned}$$

(7)

where $S_{\text {ws}}^{*}$ is defined further below in (Eq. 13). Using the new capillary model, the resulting modified functional model of Mualem now becomes:

$$\begin{aligned} K_{\text {r,w}}(P_{\text {c}}) ~=~ \biggl [\frac{S_{\text {we}}}{S_{\text {we}}^{*}}\biggl ]^{\tau } \Biggl [\frac{\int _{0}^{S_{\text {we}}} \frac{1}{h(x)}\, \mathrm {d}x }{\int _{0}^{S_{\text {we}}^{*}}\frac{1}{h(x)}\, \mathrm {d}x }\Biggl ]^{2} ~=~ \biggl [\frac{S_{\text {we}}}{S_{\text {we}}^{*}}\biggl ]^{\tau } \Biggl [\frac{I_{S_{\text {we}}^\frac{1}{m}}(p,q) }{I_{{S_{\text {we}}^{*}}^\frac{1}{m}}(p,q)}\Biggl ]^{2} \end{aligned}$$

(8)

where $S_{\text {we}}~=~ \frac{S(P_{\text {c}})-S_{\text {wr}}}{S_{\text {ws}}^{*}-S_{\text {wr}}}$ the new effective saturation, $S_{\text {we}}^{*}~=~ \frac{S_{\text {ws}}-S_{\text {wr}}}{S_{\text {ws}}^{*}-S_{\text {wr}}}$ is the maximum of effective saturation, $p=m+\frac{1}{n}$, $q=1-\frac{1}{n}$, and I(p, q) is the incomplete beta function.

Similarly, we integrate the gas relative permeability to obtain the modified model (“VGM/Pe model”):

$$\begin{aligned} K_{\text {r,g}}(P_{\text {c}})= \left( 1-\frac{S_{\text {we}}}{S_{\text {we}}^{*}}\right) ^{\tau } \biggl [\frac{\int _{S_{\text {we}}}^{{S_{\text {we}}^{*}}} \frac{1}{h(x)}\, \mathrm {d}x }{\int _{0}^{S_{\text {we}}^{*}}\frac{1}{h(x)}\, \mathrm {d}x }\biggl ]^{2} = \left( 1-\frac{S_{\text {we}}}{S_{\text {we}}^{*}}\right) ^{\tau } \biggl [1-\frac{I_{S_{\text {we}}^\frac{1}{m}}(p,q) }{I_{{S_{\text {we}}^{*}}^\frac{1}{m}}(p,q)}\biggl ]^{2} \end{aligned}$$

(9)

If the “m” parameter is related to “n” by $m=1-\frac{1}{n}$, then the modified VGM model (VGM/Pe) is given by:

$$\begin{aligned} S_w(P_{\text {c}})= & {} {\left\{ \begin{array}{ll} S_{\text {wr}} + \frac{S_{\text {ws}}^*-S_{\text {wr}}}{[1+ (\alpha P_{\text {c}})^{n}]^{m}} &{} \hbox { if}\ P_{\text {c}} \ge P_{\text {c,e}} \\ S_{\text {ws}} &{} \hbox { if}\ P_{\text {c}} \le P_{\text {c,e}} \end{array}\right. } \end{aligned}$$

(10a)

$$\begin{aligned} K_{\text {r,w}}(P_{\text {c}})= & {} {\left\{ \begin{array}{ll} \biggl [\frac{S_{\text {we}}}{S_{\text {we}}^{*}}\biggl ]^{\tau } \Biggl [\frac{1-(1-(S_{\text {we}}\left( P_{\text {c}}))^\frac{1}{m}\right) ^m}{1-(1-(S_{\text {we}}^*)^\frac{1}{m})^m}\Biggl ]^2 &{} \hbox { if}\ P_{\text {c}} \ge P_{\text {c,e}} \\ 1 &{} \hbox { if}\ P_{\text {c}} \le P_{\text {c,e}} \end{array}\right. } \end{aligned}$$

(10b)

$$\begin{aligned} K_{\text {r,g}}(P_{\text {c}})= & {} {\left\{ \begin{array}{ll} \biggl [1-\frac{S_{\text {we}}}{S_{\text {we}}^{*}}\biggl ]^{\tau ^{'}}\Biggl [1-\frac{1-(1-(S_{\text {we}}(P_{\text {c}}))^\frac{1}{m})^m}{1-(1-(S_{\text {we}}^*)^\frac{1}{m})^m}\Biggl ]^2 &{} \hbox { if}\ P_{\text {c}} \ge P_{\text {c,e}} \\ 0 &{} \hbox { if}\ P_{\text {c}} \le P_{\text {c,e}} \end{array}\right. } \end{aligned}$$

(10c)

Note that, when $P_{\text {c,e}}=0$, this modified VGM model (“VGM/Pe”) reduces to the unmodified VGM model, as it should.

2.3 Parametrization of the Hydraulic Properties Models of Porous Media

The value of gas entry pressure $P_{\text {c,e}}$ should be the same for the nonlinear hydraulic constitutive relationships [Eq.  (10)].

Therefore, we performed a simultaneous fit of the hydraulic parameters to the experimental points of water retention, water permeability and gas permeability vs. capillary pressure. In this work, the RETC code Van Genuchten et al. (1991) for fitting and estimating simultaneously the water retention and the water permeability parameters was extended to include the gas permeability, and the new VGM/Pe model was implemented. As a result, the new objective function (single-objective function: SOF) is defined as the sum of three mean squared error functions (MSE) [Eq. (11)].

$$\begin{aligned} O_{\text {bj}}({\textbf {P}})= & {} O_{\text {bj}}({\textbf {P}})_{K_{\text {g}}} + O_{\text {bj}}({\textbf {P}})_{K_{\text {w}}} + O_{\text {bj}}({\textbf {P}})_{S_{\text {w}}} \end{aligned}$$

(11a)

where

$$\begin{aligned} O_{\text {bj}}({\textbf {P}})_{{S}_{\text {w}}}= & {} \frac{\text {MSE}([\hat{S}_{\text {w,i}}({\textbf {P}}),S_{\text {w,i}} ]_{i \in [1,N_{{\text{dataS}}}] })}{\overline{S_{{\text{w,data}}}}^2} \end{aligned}$$

(11b)

$$\begin{aligned} O_{\text {bj}}({\textbf {P}})_{K_{\text {w}}}= & {} \frac{{\text{MSE}}({\text{Log}}(\hat{K}_ {w,i}({\textbf {P}})),{\text{Log}}(K_{\text {w,i}})]_{i \in [1,N_{{\text{data}}_{K_{\text {w}}}}] })}{\overline{{\text{Log}}K_{{\text{w,data}}}}^2} \end{aligned}$$

(11c)

$$\begin{aligned} O_{\text {bj}}({\textbf {P}})_{K_{\text {g}}}= & {} \frac{\text {MSE}([\text {Log}(\hat{K}_{\text {g,i}}({\textbf {P}})),{\text{Log}}(K_{\text {g,i}}) ]_{i \in [1,N_{{\text{data}}_{K_{\text {g}}}}] })}{\overline{{\text{Log}}K_{{\text{g,data}}}}^2} \end{aligned}$$

(11d)

The choice of log-permeability rather than permeability in Eqs. 11c and 11d is motivated by the fact that the range of variation of permeability is much larger than the other variable (saturation).

The integers $N_{\text {data}_{S}}$, $N_{\text {data}_{K_{\text {g}}}}$, and $N_{\text {data}_{K_{\text {w}}}}$ are, respectively, the number of measured data of water saturation, gas permeability and water permeability.

The symbols ${S}_{\text {w,i}}$, ${K}_{\text {w,i}}$, and ${K}_{\text {g,i}}$ represent, respectively, the ith observed quantities of water saturation, water permeability and gas permeability. The “hat” quantities $\hat{S}_{\text {w,i}}({\textbf {P}})$, $\hat{K}_{\text {w,i}}({\textbf {P}})$,and $\hat{K}_{\text {g,i}}({\textbf {P}})$ are, respectively, the fitted water saturation, the fitted water permeability and the fitted gas permeability as a function of the parameter set P to be optimized:

$$\begin{aligned} {\textbf {P}}= (n,m,\alpha ,{S}_{\text {ws}},{S}_{\text {wr}},{k}_{0,\text {w}}, \tau ,{k}_{0,\text {g}},{\tau }^{'},{P_{\text {c,e}})} \end{aligned}$$

(12)

The new parameter $S_{\text {ws}}^{*}$ is not present in the set of optimized parameters, but it can be determined as a function of other parameters in the optimization procedure :

$$\begin{aligned} S_{\text {ws}}^* ~=~ S_{\text {wr}} + (S_{\text {ws}}-S_{\text {wr}})\times [1+ (\alpha P_{\text {c,e}})^{n}]^{m} \end{aligned}$$

(13)

The permeability curves also depend on parameters $k_{0,\text {w}}\,[\text {m}^2]$ and $k_{0,\text {g}} \,[\text {m}^2]$. These are, respectively, the “intrinsic” permeability to water (for a water saturated sample) and the “intrinsic” permeability to gas (for a gas-saturated sample). Theoretically, these two parameters are intrinsic to the porous medium and they should be identical: the intrinsic permeability $k_{0} \,[\text {m}^2]$ of the fluid-filled medium should not depend on the fluid (gas or water). However, in clayey materials, due to the slippage effect of gas flow (Boulin et al. 2008, Wang et al. 2016), and to chemical interactions between water and clay minerals, there is a difference between the measured permeability to gas and the measured permeability to water, which can be up to three orders of magnitude, as observed experimentally by Davy et al. (2007), MJahad (2012), and Yuan (2017). In this study, we choose to distinguish the water-saturated permeability and the gas-saturated permeability in our data modeling.

We also used a multi-objective optimization technique to characterize the hydraulic parameters of the COx based on the NSGA-II algorithm (Deb et al. 2002) Twarakavi et al. (2008), which is available in the Python Platypus library by Hadka (2012).

3 The iTOUGH2 Simulation Code

Because of the large spatial scales studied in a DGR, macroscopic flow and transport equations based on generalized Darcy and Fick laws are chosen in this work. Statistical methods like the lattice-Boltzmann method (Kutscher et al. 2019) can be a good alternative for studying two-phase flow in porous media. However, such methods are not suitable for large spatial scales (one reason among others is that they need more virtual storage to store both the distribution functions and the flow variables). Therefore, we have chosen an approach based on Darcy flow equations (PDE’s) describing macroscopic variables (pressure, areal flux density) defined at the scale of many grains/pores. The finite volume code iTOUGH2 (Finsterle (2016)), known for its robustness in solving compositional two-phase flow equations, has been chosen in our work.

In this study, therefore, we use the iTOUGH2 code, a multi-phase and multi-component computer code to model fluid flow and heat transport in porous media: Finsterle (2007, 2015, 2016). The iTOUGH2 code is closely related to the TOUGH2 code for water–gas flow (Pruess et al. 1999); it is more general than the TOUGH2 code in that it can handle numerical inversion problems and sensitivity analyses. The “i” prefix stands for “inversion.” The iTOUGH2 code was set up with a modular architecture.

There are two approaches for dealing with the implementation of capillary entry pressure in iTOUGH2.

The first approach ($S_{\text {g}}$-method) is based on Battistelli et al. (2017). In this approach, the phase transition from single-phase liquid to two-phase requires that the thermodynamic condition $P_{\text {l}} + P_{\text {c,e}} \ge P_{\text {partial}} + P_{\text {sat}}(P,T)$ be satisfied. This corresponds to a thermodynamic phase transition. The symbol $P_{\text {partial}}$ represents the partial pressure of air, and it is controlled by Henry’s law for dissolution or degassing.

The second approach (Pc-method) consists in changing the primary variables in the EOS3 module (Equation Of State 3): the capillary pressure is considered as a primary variable under two-phase conditions, instead of the gas phase saturation. In this approach, the transition from single liquid phase to

two-phase must satisfy the condition $P_{\text {g}} \ge P_{\text {l}}$ or equivalently $P_{\text {c}} \ge 0$. The capillary entry pressure $P_{\text {c}}$ is introduced only in the $P_{\text {c}}(S_{\text {l}})$, $K(P_{\text {c}})$ relationships.

Our numerical trials showed that severe numerical convergence problems (possibly within the Newton–Raphson iterations) are encountered when $S_{ls} < 1$ occurs with the SG-method, while these problems do not appear with the Pc-method. At any rate, this formulation (Pc-method) seems better adapted to deal with the modified Pe model with nonzero capillary entry pressure—which has a non-invertible $S_{\text {w}}(P_{\text {c}})$ curve.

Both methods have been implemented in iTOUGH2 code, but the emphasis here is on the Pc method which requires several changes in the code and needs more numerical verification and validation tests. In both approaches a nonzero gas entry pressure is introduced in the new modified VGM model (VGM/Pe).

3.1 Governing Equations for Two-Phase Flow

For all modules, TOUGH2 solves the same integral form of mass continuity and energy balance equations defined as:

$$\begin{aligned} \frac{{\text {d}}}{{\text {d}}t}\int _{V_{{i}}}M^\kappa \text {d}V_{{i}}=\int _{\varGamma _{{i}}}\overrightarrow{F^\kappa } \overrightarrow{n} \text {d}\varGamma _{{i}} + \int _{V_{{i}}}q^\kappa \text {d}V_{{i}} \end{aligned}$$

(14)

where $V_{n}$ is an arbitrary sub-domain of the flow system, bounded by a closed surface $\varGamma _{{i}}$; $\overrightarrow{n}$ is a normal vector on surface element $d\varGamma _{{i}}\,[\text {m}^2]$ pointing into $V_{{{i}}}\,[{\text {m}}^3]$; $\kappa$ $\in$ ${1,\ldots , N_{\text {k}}}$ labels the mass components (water, air, H2, solutes, ...); $\kappa =N_{{\text {K}}}+1$ refers to the heat component; and $q^\kappa \,[{\text {kg}}\,{\text {m}}^{-3} \times {\text {s}}^{-1}]$ denotes sinks and sources for the component $\kappa$. The other symbols represent physical quantities as explained below.

• $M^\kappa \,[{\text {kg}}\,{\text {m}}^{-3}]$ is the mass or energy per volume defined as:

  $$\begin{aligned} M^{\kappa }=\phi \sum _{\beta } S_\beta \rho _\beta X_{\beta }^{\kappa } \kappa \in 1,\ldots ,N_{k} \end{aligned}$$

  (15a)

  where $\phi$ [−] is the porosity, and the sum $\sum$ is over all existing phases $\beta \in \big \{ {\text {Liquid, Gas, NAPL}}\big \}$. The saturation of phase $\beta$ is denoted $S_\beta$, and the density of phase $\beta$ is denoted $\rho _\beta \,[{\text {kg}}\,{\text {m}}^{-3}]$. The symbol $X_{\beta }^{\kappa }$ [−] represents the mass fraction of component $\kappa$ present in phase $\beta$. In addition, $M^{N_{k}+1}$ represents the heat energy per unit volume (${\text {J}}\,{\text {m}}^{-3}$) :

  $$\begin{aligned} M^{N_{k}+1}=(1-\phi )\rho _{\text {R}} C_{\text {R}} T + \phi \sum _{\beta } S_\beta \rho _\beta u_{\beta }^{\kappa } \end{aligned}$$

  (15b)

  where $\rho _R\,[{\text {kg}}\,{\text {m}}^{-3}]$ and $C_{\text {R}}\,[{\text {J}}\,$°${\text {C}}^{-1}$] are, respectively, grain density and specific heat of the rock, T [°C] is temperature, and $u_{\beta }\,[{\text {J}}\times {\text {kg}}^{-1}]$ is specific internal energy in phase ${\beta }$.

• $F^\kappa \,[{\text {kg}}\,{\text {m}}^{-2}\times {\text {s}}^{-1}]$ is the total mass flux or heat flux. The mass flux term is the sum of advective transport flux ($F_{\text {adv}}$) through the porous medium (from Darcy’s law), plus molecular diffusive flux $F_{\text {diff}}$ expressed by Fick’s law, plus optionally hydrodynamic dispersion ($F_{\text {disp}}$) from an external module. They are expressed as:

  $$\begin{aligned} F_{\text {adv}}^{\kappa }= & {} -\sum _{\beta } X_{\beta }^{\kappa } K \frac{\rho _{\beta } k_{{\text {r}}\beta }}{u_{\beta }}( \nabla P_{\beta } -\rho _{\beta }g ) \kappa \in 1,\ldots ,N_{k} \end{aligned}$$

  (16a)
  $$\begin{aligned} F_{\text {disp}}^{\kappa }= & {} -\sum _{\beta } \rho _{\beta } \overline{D}_{\beta } \nabla X_{\beta }^{\kappa } \kappa \in 1,\ldots ,N_{k} \end{aligned}$$

  (16b)
  $$\begin{aligned} F_{\beta ,\text {diff}}^{\kappa }= & {} -\phi \tau _0 \tau _\beta \rho _{\beta } d_{\beta }^{\kappa }\nabla X_{\beta }^{\kappa } \kappa \in 1,\ldots ,N_{k} \end{aligned}$$

  (16c)

  where the product $\tau _0 \tau _\beta$ is the unsaturated tortuosity that includes a porous medium-dependent factor $\tau _0$ and a coefficient $\tau _\beta$ that depends on saturation of phase $\beta$; $\overline{D}_{\beta }\,[{\text {m}}^2/{\text {s}}]$ is the hydrodynamic dispersion coefficient; and $d_{\beta }^{\kappa }\,[{\text {m}}^2/{\text {s}}]$ is the molecular diffusion coefficient of component $\kappa$ in free fluid phase $\beta$. To be more precise, in our modeling study, diffusion is based on Fick’s law (see the molecular diffusion flux $F_{\beta ,{\text {diff}}}^{\kappa }$ just above), with diffusion coefficient of hydrogen gas in liquid water $D_{{\text {H2}}}^{{\text {H2O}}} = 2.0~10^{-9}$ ${{\text {m}}^{2}/s}$ (this reference value was then corrected by tortuosity). On the other hand, osmotic pressure and salinity of the COx brine (NaCl, KCl, ...)—see Vinsot et al. (2008)—could have effects on gas diffusion and dissolution, and could have an impact on liquid pressure (Croisé et al. 2005). However, these effects on gas diffusion and dissolution are neglected here, as they do not appear to be a dominant factor in the part of the COx where the in situ PGZ1 experiment was carried out. The general space-discretized form of the mass-conservation equations for each component $\kappa$ in a grid bloc i, using the integral finite difference method (IFDM), is given by Pruess et al. (1999):

  $$\begin{aligned} \frac{{\text {d}} M_i^\kappa }{{\text {d}}t}=\frac{1}{V_i}\sum _{j}A_{ij}{F}^\kappa _{ij} + q^\kappa _{i}=0 \end{aligned}$$

  (17)

  where j labels all the grid blocks that are connected to grid block i through the surface area $A_{{{ij}}}$. Then, Eq. (17) can be expressed in terms of a residual ${R}^{\kappa ,k+1}_{i}$:

  $$\begin{aligned} {R}^{\kappa ,k+1}_{{{i}}}={M}^{\kappa ,k+1}_{{{i}}}-{M}^{\kappa ,{\text {k}}}_{{{i}}}- \frac{\varDelta {\text {t}}}{V_{{i}}}\left\{ \sum _{j}A_{{{ij}}}{F}^{\kappa ,k+1}_{ij} + V_{i}q^{\kappa ,k+1}_{{\text {i}}}\right\} \end{aligned}$$

  (18)

  For each volume element (grid block) $V_{{i}}$, there are $\text {NEQ}=N_{{\text {k}}}+1$ equations, so that for a flow system with NEL grid blocks comprises a total of NEL$\times$ NEQ coupled nonlinear equations. The unknowns are the independent primary variables $({x_{{i}}})_{i \in \{{1,\ldots ,NEQ \times {\text {NEL}}}\}}$ and completely define the state of the flow system at time level $t_{k+1}$. This nonlinear system of equations is solved by a Newton–Raphson iteration scheme.

3.2 Modification of Primary Variables in the EOS3 Module of iTOUGH2

The primary variables depend on the equations of state (EOS). In the EOS3 module, the primary variables are ($P_\alpha$, $X_{\text {w}}^{air}$, T) for single-phase conditions and ($P_{\text {g}}$, $S_{\text {g}}$, T) for two-phase conditions.

Given the new model with nonzero entry pressure, modifications were necessary in iTOUGH2-EOS3 module in order to implement the new capillary model VGM/Pe. Thus, with our modification, the capillary pressure variable $P_{\text {c}}$ is used instead of gas saturation ($S_{\text {g}}$) in the two-phase flow regime: this is summarized in table Tab.1.

Table 1 Change of primary variables implemented in the EOS3 module of iTOUGH2

Note that, in the $P_{\text {c}}$-method, we are now solving with the (new) primary variables $(P_{\text {g}},P_{\text {c}},T)$ for the two-phase regime and primary variables $(P_{\alpha },{X_{\text {w}}}^{{\text {air}}},T)$ for the single-phase regime. There was no need to change the primary variables for the single-phase situation. The thermodynamic test (switching to two phase when ${X_{\text {w}}}^{{\text {air}}} \times H_{{\text {Henry}}} + P_{{\text {v,sat}}} \ge P_{\text {liquid}}$) is also left unchanged. In the two-phase flow regime we keep $S_{\text {l}}=1.0$ when $P_{\text {c}} \le P_{\text {c,e}}$.

In order to verify the new version of the EOS3 module in iTOUGH2, a numerical test is conducted using a semi-analytical solution: vertical infiltration in the Sand of Grenoble (Haverkamp et al. 1977).

3.3 Verification: Philip Infiltration Test in the Grenoble Sand

We consider an initially unsaturated homogeneous sand column, with an initial pressure head $h = - \frac{P_{\text {c}}}{\rho _{\text {w g}}} = -61.5$ cm, and we apply at the top of the column ($z=0$) a pressure head of $h=-23.73$ cm as a boundary condition. The corresponding top surface is wet, but not saturated $\theta _{\text {top}} \le \theta _{\text {s}}$. This verification test will use an analytical solution for unsaturated flow (Philip 1957), which assumes constant air pressure within the porous medium. To represent this unsaturated flow condition in the two-phase code iTOUGH2-EOS3 and to minimize the variations of gas pressure, we impose a “free” gas phase ($K_{\text {r,g}}=1.0$) and a constant gas pressure ($P_{\text {g}} = P_{\text {atm}}$) at the top and bottom of the column boundaries.

The nonlinear water saturation curve and water permeability curve vs. capillary pressure are given just below for the Grenoble Sand, along with the numerical values of their parameters:

$$\begin{aligned} S_{\text {we}}= & {} \frac{\theta - \theta _{\text {r}}}{\theta _{\text {s}} - \theta _{\text {r}}}= \frac{a_3}{a_3 +{h}^{a_4}} \end{aligned}$$

(19a)

$$\begin{aligned} k_{\text {r,w}}(P_{\text {c}})= & {} \frac{a_1}{a_1 +{h}^{a_2}} \end{aligned}$$

(19b)

where $\theta _{\text {s}}=0.287$, $\theta _{\text {r}}=0.075$, $a_1=1.175 \times 10^6$, $a_2=4.74$, $a_3=1.611\times 10^6$, $a_4=3.96$, and the intrinsic permeability is $k_0 = 9.6273\times 10^{-12}$ ${\text {m}}^2$.

This infiltration test consists in a comparison between the numerical solution obtained with (i) the original version of EOS3 in iTOUGH2, (ii) the modified (new) version of EOS3 in iTOUGH2, and (iii) the semi-analytical solution of Philip (1957). The result is shown in Fig. 3 in terms of water content profiles $\theta (z,t)$. The agreement between the three solutions is excellent (the three sets $\theta (z,t)$ profiles are nearly indistinguishable).

Fig. 3

Comparison of water content profiles $\theta$ vs. depth (z), at times $t=1,2,\ldots ,8$ hours, for the Grenoble Sand infiltration experiment, calculated numerically with the original and modified versions of iTOUGH2/EOS3 and analytically using the classical solution of Philip

4 Numerical Experiments and Applications

In this section two numerical simulations were carried out to study the effect of gas entry pressure on the flow dynamics. In a first stage, we implement benchmark tests of vertical flow based on the upward numerical experiment from Vogel et al. (2000), with or without gas entry pressure. The objective is to confirm the effect of gas entry pressure observed by Vogel et al. (2000) and to compare our numerical implementation in the iTOUGH2/EOS3 code with other codes available to us.

In a second stage, we focus on the in situ PGZ1 gas injection experiment performed with nitrogen gas De La Vaissière et al. (2019) in the COx rock. We model water flow and gas migration experiment in three dimensions (2D axi-symmetric), and we investigate again the effect of a nonzero gas entry pressure on the mechanism of gas transport in the host clay rock (COx).

4.1 Numerical Experiments of Vertical Unsaturated Flow

The numerical simulation investigated by Vogel et al. (2000) is reconsidered here; it consists of an upward flow in a homogeneous clay soil of 1 m length. The column was initially at equilibrium, with a capillary pressure head of 11 m at the bottom. The boundary condition of zero pressure head is imposed then in the bottom which leads to upward flow. The hydraulic properties of the clay soil are given in Table 2.

Table 2 Hydraulic parameters of the VGM model for the ‘Clay 12’ soil of Carsel and Parrish (1988) (from Vogel et al. 2000, Table 2)

The water relative permeability and the water retention curve of the soil are compared for zero and nonzero entry pressure in Fig. 4. Introducing a nonzero entry pressure in the capillary model does not affect much the saturation curve, due to the small decrease of saturation with the VGM model, but it has a significant effect on the water permeability function.

For a given capillary pressure, the water permeability with nonzero entry pressure is much higher than the water permeability predicted with zero entry pressure. This difference is due to the sensitivity of the unsaturated water permeability model near full water saturation, as shown earlier in Fig. 2, and also in Fig. 4 for the clay soil to be used for the next numerical experiments below.

Fig. 4

Soil hydraulic properties functions of capillary pressure, for the clay soil Vogel et al. (2000), with two different capillary entry pressures: $P_{\text {c,e}}=196$ Pa and $P_{\text {c,e}}=0$, respectively. Note that the two saturation curves at left are almost indistinguishable, while the two permeability curves at right are quite distinct

The set of test simulations (to be presented below) for the clay soil were performed using a nodal spacing of 0.10 cm, and a variable time step (maximum time step of 100 seconds). time step equal to 100 second. The results were obtained with three codes: the 3D Finite Volumes code iTOUGH2-EOS3 (two-phase flow); the 3D Finite Volumes code BIGFLOW 3D Ababou and Bagtzoglou (1993) (partially saturated/unsaturated flow); and a custom made UNSAT 1D Finite Difference code programmed in MATLAB based on the Richards equation. The latter code, UNSAT 1D, was developed in 2020 by M. Renou & R. Ababou, as part of the Master internship of Mourad Renou at the Institut de Mécanique des Fluides de Toulouse (France), essentially for benchmark purposes (as is the case here).

Figure 5 compares the upward flow rate Q(t) at the bottom of the column computed with the three codes in the case $P_{\text {c,e}}=0$. The resulting flux Q(t) is depicted in Log-Log scales (top of Fig. 5), and in Semi-Log scales (bottom of Fig. 5). The agreement between the three codes is quite good. All three codes exhibit flow rates Q(t) that follow the same decreasing power law, and that tend asymptotically towards a constant value as time increases.

Fig. 5

Comparison of upward water flux evolution Q(t) at the bottom of the column during capillary rise in the “Clay 12” soil. Three sets of simulations are compared (with different colors): BIGFLOW 3D code, UNSAT 1D MATLAB code, iTOUGH2-EOS3 code. The capillary entry pressure is taken zero in all three simulations ($P_{\text {c,e}}=0$). Above: Log-Log plot of Q(t). Below: Semi-Log plot of Q(t)

In addition, saturation profiles are presented in Fig. 6a, b, comparing UNSAT 1D vs. iTOUGH2-EOS3, and testing the sensitivity of the capillary rise to entry pressure: unmodified VGM model with $P_{\text {c,e}}=0$, vs. modified VGM model named “VGM/Pe” (here with $P_{\text {c,e}}=196$ Pa). In each case, with or without entry pressure, it can be seen that the saturation profiles from the two codes are quasi-identical, which confirms our previous validation of the new version of iTOUGH2-EOS3 (see earlier: “Modification of primary variables in the EOS3 module of iTOUGH2”). Concerning entry pressure, the effect of the (small) entry pressure $P_{\text {c,e}}=196$ Pa is clearly to enhance and accelerate capillary rise. For instance, at the early time $t=0.2$ day, the saturation “front” has risen by only 0.20 m without entry pressure, while it has risen up to 0.5 m above the bottom with entry pressure.

Fig. 6

Comparison of water saturation profiles $S_{\text {w}}(z,t)$ at times $t=0.2, 0.6, 1.0, 1.4, 2.0$ days, with and without capillary entry pressure, for upward flow in the “Clay 12” soil. Two sets of capillary rise simulations are compared: with the UNSAT 1D code (continuous curves) and with the iTOUGH2-EOS3 code (discontinuous curves). Above: $P_{\text {c,e}}=0$. Below: $P_{\text {c,e}}=196$ Pa

Similar comparison results are shown, this time in terms of capillary pressure profiles during capillary rise, with and without entry pressure, in Fig. 7. Again the comparison between iTOUGH2-EOS3 with UNSAT 1D is quite good, and again the effect of entry pressure is to accelerate the rise of the capillary pressure profiles.

Fig. 7

Comparison of capillary pressure profiles $P_{\text {c}}(z,t)$ at different times, with and without capillary entry pressure, for upward flow in the “Clay 12” soil. Two sets of capillary rise simulations are compared: with the custom made MATLAB UNSAT 1D code (continuous curves), and with the iTOUGH2-EOS3 code (discontinuous curves). Above: $P_{\text {c,e}}=0$. Below: $P_{\text {c,e}}=196$ Pa

Several other tests (not all shown here) were performed in order to confirm the benchmarking/cross-validation of iTOUGH2-EOS3 and to observe the (simulated) effect of entry pressure $P_{\text {c,e}}$. The next figure shows one detailed sensitivity test with respect to entry pressure for the capillary rise problem, comparing the water saturation profiles $S_{\text {w}}(z,t)$, as well as the water mass flux $Q(t)\,[kg/s]$ at the bottom boundary, with and without entry pressure ($P_{\text {c,e}}=0$ and $P_{\text {c,e}}=196$ Pa, respectively): see Fig. 8a–c. The saturation profiles shown on top (a, b) were calculated with both the iTOUGH2/EOS3 code and the custom made UNSAT 1D MATLAB code, and they were identical. The temporal plot of water mass flux Q(t) [kg/s] shown at the bottom (c) is computed with iTOUGH2-EOS3. The three sub-figures (a, b, c) clearly indicate again that the effect of entry pressure (even a small one) is to enhance capillary rise in terms of the rising saturation profiles and in terms of the upward water flux.

Fig. 8

Comparisons for upward flow in the “Clay 12” soil with and without capillary entry pressure ($P_{\text {c,e}}=196$ Pa, and $P_{\text {c,e}}=0$). Top (a, b): comparison of water saturation profiles $S_{\text {W}}(z,t)$ at times $t=0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0$ days without entry pressure (a) and with entry pressure (b). Bottom c: comparison of temporal mass flux Q(t) [kg/s] without entry pressure (blue curve below) vs. with entry pressure (red curve above)

To sum up, concerning entry pressure: a significant difference in the position of the wetting front profiles is observed, depending on zero or nonzero entry pressure. This is a consequence of the extreme sensitivity of the relative water permeability $K_{\text {r},\text {w}}(P_{\text {c}})$ to a small change in the water retention curve $S_{\text {w}}(P_{\text {c}})$ near full water saturation. This difference can lead to remarkably different simulation results for soils with fine structures and/or large entry pressures (the soil used in the present test is a fine textured clay). Due to this sensitivity, it appears necessary to use a modified VGM/Pe model, with nonzero entry pressure, for correctly predicting flow dynamics. This may be even more crucial when the water permeability curve parameters are estimated based solely on water retention data. In that case, it turns out that the permeability curves that are deduced from the water retention curve are much more influenced by $P_{\text {c,e}}$ than the water retention curve itself.

4.2 Modeling the PGZ1 Experiment

The experiment PGZ1-GAS De La Vaissière et al. (2014) is a field-scale experiment conducted by the French radioactive waste management agency (ANDRA) in the underground research laboratory (URL) located at Bure (France), in order to study the main mechanisms controlling gas migration in the Callovo-Oxfordian (COx) host clay rock. First, the hydraulic properties of the COx were fitted with the unmodified VGM model ($P_{\text {c,e}}=0$) and then with the modified VGM/Pe model ($P_{\text {c,e}}\ne 0$) in order to characterize the hydraulic properties of the COx based on data from Gérard (2011). Secondly, a numerical modeling of the gas injection experiment PGZ1-GAS1 over 423 days is presented, where the impact of a nonzero gas entry pressure is discussed.

For other references on PGZ1 data and simulations, see also De La Vaissière et al. (2014) and De La Vaissière et al. (2019). Concerning reference De La Vaissière et al. (2014): these authors present measurements of $P_{\text {g}}$(t) in the injection chamber, and measurements of $P_{\text {w}}$(t) in the other gallery, over a duration of 1.5 years. The initial state of the rock is not known precisely; a lithostatic pressure state is assumed, leading to a pressure value of roughly 4.5 MPa at the measurement site. Concerning De La Vaissière et al. (2019): these authors present PGZ1 measurements over a longer duration, roughly 10 years, including: gas pressure $P_{\text {g}}$(t) in the injection chamber, rock displacements and water pressure $P_{\text {w}}$(t) in the other borehole.

Other remarks concerning both the PGZ1 experiment and our present simulation tests: the experimental gas pressure named $P_{\text {g}}(t)$ is gas pressure measured vs. time in the injection chamber of borehole PGZ1202; we have neglected the possible effect of the second borehole PGZ1201 on flow in order to preserve an axi-symmetric geometry numerically; and we have adopted the hypothesis of a lithostatic pressure state, which leads to a pressure of approximately 4.5 MPa in the measurement region at the beginning of the gas injection test (initial pressure).

4.2.1 The PGZ1 Experimental System and Field Data

Fig. 9

Experiment layout of the PGZ1 experiment in the Meuse/Haute-Marne URL, with a zOome of the gas injection chamber De La Vaissière (2011); De La Vaissière et al. (2014)

The experimental layout consists in two parallel boreholes (PGZ1201, PGZ1202) with diameter of 76 mm and an inclination of $35^{\circ }$ from the DGR drift Fig. 9; each borehole is equipped with three intervals in order to monitor gas and water pressure. There is also a third borehole PGZ1031 with a diameter of 101 mm and an inclination of 48$^{\circ }$ from the GEX drift. This PGZ1031 borehole is equipped with extensometers to monitor axial deformation.

Fig. 10

Variable gas injection rate in the test chamber for the PGZ1201-GAS1 experiment over 423 days

We are interested here in the first phase (the “GAS1” phase), over a period of about 14 months (423 days), where six constant-rate pulses of nitrogen, at rates between 1 to 3 mLiter/min, were injected in the chamber of Interval 2 of the PGZ1201 borehole. Each constant rate pulse is followed by a pressure recovery phase (zero injection rate). The time sequence of the flow rate injection pulses is depicted in Fig. 10.

4.2.2 Numerical Model and Modeling Approach (PGZ1)

The model presented in Sect. 3 is used to simulate the migration of the two-phase flow and transport in porous media constituted of the EDZ (Excavation Damaged Zone), the COx host rock and the injection chamber, with a 2D-axisymmetric geometry (x, r) Fig. 11. The radius of the simulation domain is $R=5$ m, the length along the x-axis is 12 m. The EDZ is 4 cm thick, and it has a higher permeability as suggested in the report by De La Vaissière (2011). Interval 2 of the PGZ 1201 borehole denotes the injection chamber with a radius of 3.80 cm (Fig. 9).

Fig. 11

Geometry of the axi-symmetric simulation domain of the PGZ1-GAS1 experiment, with a zoom (at left) on the interval chamber and the EDZ. This figure also shows an example of the adaptive “rectilinear” mesh of the axi-symmetric domain used in the numerical model

4.2.3 Hydraulic Properties of the COx Host Rock (PGZ1 Experiment)

The two-phase hydraulic parameters for the COx are obtained by fitting simultaneously the experimental data of gas permeability, water permeability and water retention curve (from Gérard 2011) to the VGM and VGM/Pe models presented in Sect. 2. The simultaneous fit is performed using both optimization methods SOF and MOF (single- and multi-objective function, respectively). The single-objective function was described earlier in Eq. (11). The multi-objective method was implemented using the NSGA-II algorithm Twarakavi et al. (2008) coded in the Python Platypus library Hadka (2012).

In order to study the impact of a nonzero entry pressure, the COx hydraulic properties are first fitted with a zero entry pressure with the constraint $S_{\text {ws}}=1$ due to the lack of experimental data that are difficult to measure in the range of small capillary pressures. Secondly, the hydraulic properties are fitted for the VGM/Pe model with nonzero entry pressure “$P_{\text {c,e}}$,” where the following physical parameters are fixed: intrinsic permeability $k_{0,\textit{w}}\,[{\text {m}}^2]$, $k_{0,\text {g}}\,[{\text {m}}^2]$, full water saturation $S_{\text {ws}}$ and residual water saturation $S_{\text {wr}}$.

The resulting curves are shown in Fig. 12 for both optimization methods (including both cases $P_{\text {c,e}}=0$ and $P_{\text {c,e}} \ne 0$ on the same graphs).

Fig. 12

Optimal simultaneous fit of COx hydraulic properties (water retention curve $S_{\text {w}}(P_{\text {c}})$, absolute water permeability $K_{\text {w}}(P_{\text {c}})$ and absolute gas permeability $K_{\text {g}}(P_{\text {c}})$) using two distinct optimization methods: a single-objective function (RETC Code); and b multi-objective function. The data points are borrowed from Gérard (2011)

For both optimization methods, the constitutive relationships obtained with the optimized parameters indicate that the differences between the two models (VGM & VGM/Pe) are significant in terms of the relative permeability curves for water and gas, especially at low capillary pressures (that is, near full water saturation).

The optimized hydraulic parameters of the COx used in this part of the study, using the two different optimization methods explained above, are shown in Table 3.

Table 3 Parameters of hydraulic properties of the COx, determined by a simultaneous fit using the modified version of the RETC code Van Genuchten et al. (1991)

There are small differences between the parameters obtained by the two optimization methods (slight differences for parameters $P_{\text {c,e}}$ and $\tau$).

The EDZ hydraulic properties are assumed similar to those of the COx but with an intrinsic permeability of $6.52 \times 10^{-18}\,[{\text {m}}^2]$, three orders of magnitude greater than that of the COx, as suggested in a 2011 FORGE report De La Vaissière (2011). This EDZ permeability value is intermediate between those measured at small and large scale. It has been measured in situ at an intermediate scale (the borehole scale is less than 10 m in length and 10 cm in diameter). On larger scales, the EDZ permeability can be larger. In a theoretical model, Ababou et al. (2011) represented the EDZ around a drift at the Bure URL as a porous rock matrix with many small statistical fissures and larger fractures (chevron geometry). Their calculations indicated that equivalent macroscale permeability of the EDZ was about $2.8~10^{-16}\,{\text {m}}^2$. On the other hand, for small core samples, MJahad et al. (2017) (based on the PhD thesis of MJahad 2012) developed an approach to sort the damaged samples, the fissured samples and the intact samples. For the damaged core samples, the intrinsic permeability was in the range $1.0~10^{-20}$ to $1.0~10^{-18}\,\text {m}^2$.

4.2.4 Injection Chamber (PGZ1 Experiment)

The injection chamber is assumed to be a macroporous medium, with its specific hydraulic properties (Sentís 2014), and in particular, with an equivalent porosity $\phi =0.3491$ corresponding to an initial void volume of 1584 $\text {cm}^3$ within a total geometric volume of 4536 $\text {cm}^3$ for the annular space + filter + gas pipelines (De La Vaissière 2011). (Note: in numerical simulations, the chamber is discretized into an integer number of cells; for this reason the volume of the chamber can vary slightly depending on cell size: the porosity of the chamber is adjusted so that the chamber has the same volume of voids for all simulations; thus, the porosity of the chamber can vary slightly, e.g., 0.3279 vs. 0.3492 depending on mesh refinement).

4.2.5 Initial and Boundary Conditions (PGZ1 Experiment)

The intact rock and EDZ were initially saturated with a hydro-static condition of $P_{\text {w}}=4.5$ MPa. The water saturation in the injection chamber is assumed equal to 0.225 as suggested in De La Vaissière et al. (2014), with a gas pressure of 4 MPa a the start of the experiment. No flow is specified at the circular lateral boundaries, and a prescribed gas flow rate function of time is injected in the chamber (see Fig. 10).

4.3 Results and Discussion (PGZ1 Experiment)

In this section, the simulation results of the PGZ1-GAS experiment are presented. The measured and simulated gas pressure in the chamber vs. time is compared, and the effect of a nonzero gas entry pressure on the mechanism of two-phase flow is discussed.

Two points (or cells) were selected in order to follow gas pressure variation in time in the EDZ domain and in the intact rock (COx): point P1 corresponds to the first cell of the EDZ domain in contact with the chamber of injection, and point P2 is the first cell of the intact COx domain directly in contact with the EDZ. The adaptive mesh of the flow domain consists of 5229 rectilinear elements (Fig. 11), which are finer near the injection chamber and coarser further away from the chamber. In other words, the cells P1 and P2 are adjacent to each other; the first cell (P1) is in the EDZ, the second cell (P2) is in the COx host rock.

Simulations are run with an upstream weighting scheme for mobility and permeability, and the maximum time step allowed is 9600 s. Numerical trials showed that other weighting schemes for mobility and permeability (e.g., harmonic weighting) may affect the magnitude of the results, but the effect of gas entry pressure remained the same. At any rate, for any consistent weighting scheme (such as harmonic or arithmetic), the finer the mesh and the more the model approaches experimental data.

For the optimized COx hydraulic parameters obtained by the RETC code (single-objective function), the iTOUGH2-EOS3 code simulations were performed with two different choices of state variables in the code: the “PC-method” or $P_\text {c}$ method with primary state variables $({P_\text {g}},{P_\text {c}})$, and the “SG-method” or $S_\text {g}$ method with primary state variables $({P_\text {g}},{S_\text {g}})$ (note: these state variables choices hold only under 2-phase flow conditions, not single-phase flow). The results obtained by $P_{\text {c}}$ method are presented in Fig. 13a. The figure shows a good agreement between experimental and simulated gas pressure $P_{\text {g}}$(t) in the chamber during the “early” transient period of 73 days (first three peaks of gas pressure), whether $P_{\text {c,e}}=0$ or $P_{\text {c,e}}=1.997$ MPa. The main reason for this agreement over early times is that gas pressure in the chamber was initially less than rock water pressure, leading to gas transport only by diffusion (rather than gas flow). This early gas migration regime, therefore, cannot be used to test the difference between the two capillary flow models with or without entry pressure. Another related remark concerns the role of the gas injection chamber at early times: it behaves similarly to a void chamber, and its pressure increases linearly with injected volume following the law of ideal gases ($PV=nRT$), at least at early times.

After the third peak of the gas pressure signal, the VGM model simulates a faster penetration of gas in the COx, but with an underestimation of the measured gas pressure data. Unlike the VGM model, the VGM/Pe model simulates higher gas pressures and approaches remarkably the experimental data. This point can be explained by a delay of gas penetration in the COx formation with the VGM/Pe model. This delay is due to the fact that, with the nonzero entry pressure, larger quantities of gas need to be injected in order to overcome the gas entry threshold pressure $P_{\text {c,e}}=1.997$ MPa. This can be a major cause of increased gas pressure near the injection volume (i.e., the gas source).

Note also that the $P_{\text {c,e}}$ value obtained with the multi-objective method “MOF” (1.962 MPa) is slightly lower than that obtained by the single-objective method “SOF” (1.997 MPa). As a consequence, the simulated gas pressure in the chamber is slightly decreased with the MOF optimization method (Fig. 13b). However, this slight decrease does not greatly modify simulation of gas pressure in the chamber.

Similar results are obtained when using the $S_{\text {g}}$ method in iTOUGH2-EOS3 with $(P_{\text {g}},S_{\text {g}},T)$ as primary variables in the two-phase flow system, using the hydraulic parameters obtained by the “SOF” optimization method (Fig. 13c). However, this state variable method ($S_{\text {g}}$) requires more CPU time than the $P_{\text {c}}$ method.

The “barrier” phenomenon observed with the $P_{\text {g}}$(t) plots is also well demonstrated by the 2D axi-symmetric distributions of mass gas fraction and water saturation near the chamber at different times, as simulated with the VGM model (Fig. 15a, c) and with the VGM/Pe model (Fig. 15b, d), to be discussed further below. Let us point out that these figures show that a premature desaturation of the EDZ and COx host rock occurs with the VGM model, compared with the VGM/Pe model. This seems consistent with the behavior observed with the $P_{\text {g}}(t)$ plots.

For clarity, the organization of the subfigures in Fig. 15 is explained.

The first column of subfigures is for $Pe=0$:

• (a) Liquid water saturation “$S_{\text {w}}$” (for $P_{\text {c,e}}=0$);

• (c) Nitrogen gas mass fraction dissolved in the liquid (for $P_{\text {c,e}}=0$);

and the second column of subfigures is for $P_{\text {c,e}}=1.9977$ MPa:

• (b) Liquid water saturation “SL” (for $P_{\text {c,e}}=1.9977$ MPa);

• (d) Nitrogen gas mass fraction dissolved in the liquid (for $P_{\text {c,e}}=1.9977$ MPa).

The color codes in these subfigures are as follows:

• On the first row, (a) (b), the color bar for “$S_{\text {w}}$” goes from 0.985 to 1.0 (blue to red);

• On the second row, (c) (d), the color bar for the gas mass fraction ${X_{\alpha }}^{\beta }$ goes from $10^{-12}$ to 1.4 $\times$ $10^{-3}$ (blue–red). Note: the small gas mass fraction $1E-12$ is taken as the residual gas fraction for numerical reasons.

Fig. 13

Comparison between time-varying experimental and numerical gas pressure in the chamber simulated by VGM and VGM/Pe in PGZ1-GAS experiment: a PC method (state variable $p_{\text {c}}$ with hydraulic parameters optimized by SOF method. b PC method with hydraulic parameters optimized by MOF method. c SG method (state variable $S_{\text {g}}$ with hydraulic parameters optimized by SOF method

Fig. 14

Water saturation vs. time in the P1 and P2 cells, simulated with the VGM model ($P_{\text {c,e}}=0$) and with the VGM/Pe model ($P_{\text {c,e}}=2$ MPa). Points P1 and P2 are in two adjacent cells, respectively, in the EDZ (P1) and in the intact COx (P2)

Although the VGM/Pe model overestimates the measured gas pressure in the period from 60 to 135 days, where the gas phase started to penetrate in the EDZ domain (Fig. 14), this overestimation remains negligible by comparison with experimental uncertainties De La Vaissière et al. (2014). Another explanation of this overestimation is that $P_{\text {c,e}}$ of the EDZ is lower than that considered in our model (taken the same as that of the COx). Note: recall that cells (P1, P2) are adjacent; P1 is in the EDZ, P2 is in the COx.

Based on these experimental vs. simulated gas pressure signals $P_{\text {g}} (t)$, and based on the simulated spatial distributions of gas fraction and water saturation, the results can be interpreted as follows.

At the start of gas injection under prescribed flux rate, gas pressure $P_{\text {g}}(t)$ in the injection chamber was less than water pressure in the COx. The gas could be transported only as a solute, mostly by diffusion in water. Then, when gas pressure overcomes liquid water pressure, the COx clay rock de-saturates according to the two-phase flow simulation by the VGM model (e.g., saturation profiles at $T=101$ days shown in Fig. 15a). On the other hand, for the simulation performed with the VGM/Pe model, gas is transported only by diffusion in water during early times, at least until capillary pressure becomes higher than gas entry pressure, which then leads some time later to the desaturation of the COx (Fig. 15b, d).

Note that the magnitude of water desaturation in the EDZ and COx obtained with the VGM/Pe model is higher than that simulated by the VGM model without entry pressure (Figs. 14, 15). This could indicate that the convective gas flux in the rock abruptly increases when the capillary threshold is overcome; this phenomenon could also cause the observed higher pressure gradients occurring near fully water saturated zones with the VGM/Pe model (in contrast with the VGM model): see Figs. 14 and 15d. This implies that $P_{\text {c,e}}$ delays the water advance in the COx, which also reduces the advective transport of dissolved nitrogen gas in the COx. Note In fact, although water desaturation in the EDZ and COx is significant for the VGM/Pe model ($P_{\text {c,e}} = 1.997\,\text {MPa}$), its spatial extent within the COx is still smaller than that for the VGM model ($P_{\text {c,e}} = 0$). But the magnitude of water desaturation in the EDZ and COx obtained with the VGM/Pe model is higher than that simulated by the VGM model. When entry pressure is taken into account, the “nitrogen piston effect on water displacement” (Saâdi et al. 2020) becomes dominant within the COx as time increases.

To sum up, the effect of entry pressure $P_{\text {c,e}}$ is to block temporarily the advection of the dissolved nitrogen gas, as can be seen from gas mass fraction distributions in Fig. 15c, d. This “barrier effect” is also visible in the temporal plots shown earlier in Fig. 14.

Fig. 15

Simulated 2D spatial distributions of gas mass fraction and of water saturation for the PGZ1 experiment at different times T [days]. Left a, c: VGM model (without entry pressure). Right b, d: VGM/Pe model (with entry pressure)

5 Conclusions

In this paper, important two-phase flow phenomena in low permeability materials are investigated, in the context of radioactive waste disposal in deep geological formations. In particular, a detailed formulation and approach to characterize and quantify the gas entry pressure parameter in low permeability porous media is given. The important impact of gas entry pressure as a parameter influencing gas migration mechanisms is demonstrated via numerical experiments, including comparisons with in situ gas pressure measurements during a gas injection experiment in clay rock.

A detailed formulation of the modified van Genuchten/Mualem (VGM) model is provided, where a nonzero gas entry pressure is introduced (modified VGM model). The source code of iTOUGH2 is also modified accordingly, in order to accommodate this modified VGM model and to reproduce the vertical flow tests of Vogel et al. (2000)

The water and gas hydrodynamic parameters of the COx rock were investigated based on available data in the literature, for the (modified) VGM model of constitutive curves (water and gas permeability curves). The RETC fitting technique was extended to gas permeability. The experiment PGZ1-GAS was then modeled with the (modified) version of the iTOUGH2 code. The model was able to reproduce the key tendencies of the experimental results, and the introduction of the adequate value of gas entry pressure of the intact rock improves the modeling results . Introducing a nonzero gas entry pressure (or a capillary entry pressure parameter) clearly affects the transient dynamics of gas transport: in particular, there is a delay in gas intrusion in the host rock from the injection chamber, and a higher water flux when the gas pressure overcomes the capillary pressure threshold.

In light of these results, both from the benchmark tests of vertical flow and from the simulation of water–gas flow in the PGZ1-GAS experiment, it appears that the gas entry pressure is a key parameter and plays an important role in predicting the fate of gases in a DGR [e.g., gas piston effect in water displacement, Saâdi et al. (2020)]. Therefore, in such applications, a careful estimation of $P_{\text {c,e}}$ is necessary whenever low permeability and clayey materials are involved, as is the case for engineered barrier materials (bentonite, concrete, etc.) and for the host clay rock at several study sites (the Meuse/Haute-Marne URL at Bure in France, as well as other study sites like the Mont Terri URL in Switzerland).