Application of “panel-data” modeling to predict groundwater levels in the Neishaboor Plain, Iran

Abstract

The aim of this research was to predict groundwater levels in the Neishaboor plain, Iran, using a “panel-data” model. Panel-data analysis endows regression analysis with both spatial and temporal dimensions. The spatial dimension pertains to a set of cross-sectional units of observation. The temporal dimension pertains to periodic observations of a set of variables characterizing these cross-sectional units over a particular time span. Firstly, the available observation wells in the Neishaboor plain were clustered according to their fluctuation behavior using the “Ward” method, which resulted in six areal zones. Then, for each cluster, an observation well was selected as its representative, and for each zone, values of monthly precipitation and temperature, as independent variables, were estimated by the inverse-distance method. Finally, the performance of different panel-data regression models such as fixed-effects and random-effects models were investigated. The results showed that the two-way fixed-effects model was superior. The performance indicators for this model (R ² = 0.97, RMSE = 0.05 m and ME = 0.81 m) reveal the effectiveness of the method. In addition, the results were compared with the results of an artificial-neural-network (ANN) model, which demonstrated the superiority of the panel-data model over the ANN model.

Résumé

Le but de cette recherche était de prédire les niveaux de la nappe dans la plaine de Neishaboor, Iran, en utilisant un modèle avec “panneau de données”. L’analyse avec “panneau de données” fonde une analyse de régression comportant à la fois des dimensions spatiale et temporelle. La dimension spatiale se rapporte à un ensemble d’unités d’observation transversales. La dimension temporelle se rapporte aux observations périodiques d’un ensemble de variables caractérisant ces unités transversales sur un laps de temps donné. Dans un premier temps, les puits d’observation disponibles dans la Plaine de Neishaboor ont été regroupés en fonction de leur mode de fluctuation, en utilisant la méthode “Ward” qui a abouti à la définition de 6 zones. Ensuite, dans chaque groupe, un puits d’observation a été choisi pour sa représentativité et dans chaque zone, les valeurs de précipitations et de températures mensuelles, considérées comme variables indépendantes, ont été estimées par la méthode “inverse de la distance”. Enfin, la performance des différents modèles de régression par “panneau de données”, tels que les modèles à paramètres fixes et les modèles à paramètres aléatoires, a été examinée. Les résultats montrent que le modèle à paramètres fixes binaire est meilleur. Les indicateurs de performance de ce modèle (R ² = 0.97, RMSE = 0.05 m et ME = 0.81 m) révèlent l’efficacité de la méthode. De plus, les résultats ont été comparés à ceux d’un modèle de réseau de neurones artificiel (RNA), ce qui a démontré la supériorité du modèle avec “panneau de données” sur le modèle RNA.

Resumen

En esta investigación se predicen los niveles de agua subterránea en la planicie de Neishaboor, Irán, usando un modelo de “datos de panel”. El análisis de “datos de panel” está dotado de un análisis de regresión para las dimensiones espaciales y temporales. La dimensión espacial se refiere a un conjunto de unidades de secciones transversales de observación. La dimensión temporal se refiere a observaciones periódicas de un conjunto de variables que caracterizan estas unidades de secciones transversales en un lapso de tiempo determinado. En primer lugar, los pozos de observación disponibles en la planicie de Neishaboor se agruparon de acuerdo al comportamiento de las fluctuaciones usando el método “Ward”, lo cual se tradujo en seis zonas de áreas. Luego, para cada grupo se seleccionó un pozo de observación como representativo, y para cada zona se estimaron los valores de precipitación y temperatura mensual, como variables independientes, por el “método inverso de la distancia”. Finalmente, se investigaron las performances de diferentes modelos de regresión de “paneles de datos” tales como los modelos de efectos fijos y los modelos de efectos aleatorios. Los resultados mostraron que las dos formas del modelo de efectos fijos fueron superiores. Los indicadores de performance para este modelo (R ² = 0.97, RMSE = 0.05 m and ME = 0.81 m) revelan la efectividad del método. Además, .los resultados se compararon con los resultados de un modelo artificial de redes neuronales (ANN), lo cual demostró la superioridad del modelo de “datos de panel” sobre el modelo ANN.

摘要

本次研究旨在利用“面板数据”模型预测伊朗Neishaboor平原的地下水位. “面板数据”可进行分析时间和空间尺度上的回归分析. 空间尺度上适用于一系列代表性单元的观测, 时间尺度上适用于一系列以典型时间跨度上的代表性单元为特征的变量的周期性观测. 首先, 根据使用“监视”方法得到的水位波动情况对Neishaboor平原的可利用的观测井进行分组, 分为六个区域. 然后, 对于每一个群组, 以观测井作为代表, 对每一个区域的月降水量和温度值作为独立变量, 通过“反距离方法”进行估计. 最后对不同的面板数据回归模型, 如固定效应和随机效应模型的效果进行研究. 结果表明, 双向固定效应模型更好. 模型的成绩衡量指标 (R ² = 0.97, RMSE = 0.05 m and ME = 0.81 m) 显示了该法的有效性. 并将该结果与人工神经网络 (ANN) 模型的结果进行比较, 表明面板数据模型优于ANN模型.

Resumo

O objectivo desta investigação consistiu em prever os níveis de água subterrânea na planície de Neishaboor, Irão, usando um modelo de dados em painel (“panel-data”). A análise dados em painel contempla uma análise de regressão com dimensões espaciais e temporais. A dimensão espacial está relacionada com um conjunto de unidades de perfis de observação. A dimensão temporal está relacionada com observações periódicas de um conjunto de variáveis que caracterizam aquelas unidades de perfis durante um intervalo de tempo determinado. Primeiro, todos os furos de observação da planície de Neishaboor foram agrupados de acordo com o seu comportamento no que toca às oscilações, usando o método “Ward”, de que resultaram seis zonas superficiais. Depois, foi seleccionado um furo representativo de cada grupo e, para cada zona, foram estimados os valores de precipitação mensal e temperatura, como variáveis independentes, usando o método do inverso da distância. Por último, foi investigado o desempenho de diferentes modelos de regressão de dados em painel, tais como os modelos de efeitos-fixos (“fixed-effects”) e de efeitos-aleatórios (“random-effects”). Os resultados mostraram que o modelo de efeitos-fixos duplo sentido (“two-way”) foi superior. Os indicadores de desempenho deste modelo (R ² = 0.97, RMSE = 0.05 m and ME = 0.81 m) evidenciam a eficácia do método. Adicionalmente, os resultados foram comparados com os resultados de um modelo de rede neuronal artificial (RNA), tendo-se demonstrado a superioridade do modelo de dados em painel em relação ao modelo de RNA.

Introduction

Groundwater resources are considered to be significant and economical water resources. The comprehensive recognition and proper utilization of this valuable resource, especially in arid and semi-arid areas, has an important influence on the sustainable development of social and economic activities. Insufficient recognition and over-exploitation of aquifers leads to ever-growing depletion of the groundwater resources over time, manifested in declining groundwater levels. This results in decreasing discharge from qanats and springs, water-supply rationing, excessive reductions in agricultural yields, emergence of dry wells, groundwater quality deterioration and groundwater-flow pattern variations (Nayak et al. 2006). Therefore, it is necessary to predict groundwater-level fluctuations for a better understanding of the aquifer behavior in these areas. Prediction of water levels, if forecasted well in advance, may help the administrators to better plan and manage the groundwater utilization.

To date, a wide variety of models have been developed for and applied to groundwater-level forecasting. These include empirical time-series models, physically based or mechanistic models, and artificial-intelligence models (such as artificial neural networks and fuzzy logic). Empirical time-series models have been widely used for water-table depth modeling (e.g. Bierkens 1998; Knotters and Van Walsum 1997; Tankersley et al. 1993; Van Geer and Zuur 1997). The major disadvantage of an empirical approach is that these models are not adequate for forecasting when the dynamic behavior of the hydrological system changes with time (Bierkens 1998). On the other hand, the major disadvantage of physically based models is that they require enormous quantities of data that are generally difficult or expensive to collect, especially in developing countries. In an aquifer, the relationships between precipitation, aquifer abstractions, temperature, and groundwater levels are likely nonlinear rather than linear, and the models that approximate the processes in a linear form fail to represent the processes effectively (Bierkens 1998). Artificial neural network (ANN) and fuzzy-logic models (e.g. Allen et al. 2007; Maier and Dandy 2000; Sami et al. 2002) are greatly suited to dynamic nonlinear system modeling. However, these models tend to be used when understanding of the system is inadequate, and obtaining accurate predictions is more important than conceptualizing the actual physics of the system (Daliakopoulos et al. 2005).

Empirical time-series models can predict groundwater levels in observation wells separately. However, Izady et al. (2009) developed a new model based on time-series data that can predict groundwater levels in multiple observation wells at the same time. Although the results of the model were good, the physics of the system were not considered in the model. In comparison, the “Panel-data” model (Arellano 2003; Baltagi 2005; Hsiao 2003) is able to predict groundwater levels in different observation wells simultaneously. Moreover, its most important benefits are two-fold: (1) to improve the efficiency of estimates; and (2) to broaden the scope of inference (Baltagi 2005; Hsiao 2003). In other words, panel-data models are better able to study the dynamics of adjustment. Indeed, cross-sectional distributions (datasets that are spatially distributed but at a single moment in time) that look relatively stable hide a multitude of changes. Actually, many effects that are simply not detectable in pure cross-sectional or pure time-series data can be analyzed and explained using panel-data modeling.

The term “panel-data” refers to the pooling of observations on a cross-section of observation wells over several time periods. This can be achieved by surveying a number of observation wells and following them over time. On the other hand, panel-data analysis endows regression analysis with both a spatial and temporal dimension. The spatial dimension pertains to a set of cross-sectional units of observation. The terms spatial and cross-sectional are used here in the sense of data, and not in the sense of physical landforms. In other words, a cross-section is a set of records/data at specific locations at the same time. The temporal dimension pertains to periodic observations of a set of variables characterizing these cross-sectional units over a particular time-span (Yaffee 2003). The combination of time-series with cross-sections enhances the quality and quantity of data in ways that would be impossible if only one of these two dimensions were used (Gujarati 2003). Moreover, an important advantage of the panel-data model is that valuable information about relationships between different observation wells can be extracted (Hsiao 2003). Panel-data models can be placed into two categories: static and dynamic models. Each of these can be sub-categorized into complete or balanced, with the same temporal length for all individuals, and incomplete or imbalanced, with different temporal lengths.

Unfortunately, application of panel-data modeling in the field of water resources management has so far been limited, although it has been widely applied in economics research (e.g. Arbués et al. 2004; De Cian et al. 2007; Moeltner and Stoddard 2004; Zhang and Fan 2001). The objective of this study was to investigate the capabilities and potential of panel-data modeling as a tool for the prediction of groundwater-level fluctuations in the Neishaboor plain, Iran. A thorough review of panel-data history is given by Nerlove (2000), who identified papers by Hildreth (1949 and 1950) as the first published works about the panel-data technique. Interested readers are referred to Baltagi (2005) and Hsiao (2003).

Study area and datasets

Study area

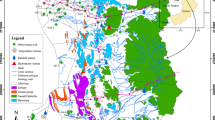
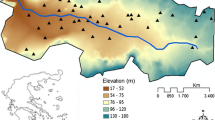
The Neishaboor plain is located between 35°40′ N to 36°39′ N latitude and 58°17′ E to 59°30′ E longitude with semi-arid to arid climate, in the northeast of Iran as shown in Fig. 1. Its hydrological boundaries are with the Yengcheh watershed in the north, the Mashhad and Sang Bast watersheds in the east, the Jolgeh Rokh watershed in the south, and Sabzevar and Soltan Abad watersheds in the west. The total geographical area is 7,350 km², consisting of 3,160 km² mountainous terrain and about 4,190 km² of plain. The maximum elevation is located in Binalood Mountains (3,300 m above sea level), and the minimum elevation is at the outlet of the plain (Hosein Abad Jangal) at 1,050 m above sea level. The average annual precipitation is 234 mm, but this varies considerably from one year to another. The mean annual temperatures at the Bar-Aria station (in the mountainous area) and Mohammad Abad-Fedisheh station (in the plain area) are 13 and 13.8°C, respectively. The annual potential evapotranspiration is about 2,335 mm (Velayati and Tavassloi 1991). According to governmental reports, about 93.5% of the withdrawals in the Neishaboor watershed are consumed by agriculture, mostly in irrigation. Moreover, the share of surface-water resources in total withdrawals is about 4.2%. It means that groundwater is a primary source of water for different purposes and surface water plays a minor role in providing water supply services in the Neishaboor watershed. Therefore, crop evapotranspiration (ET_c)— evapotranspiration from disease-free, well fertilized crops, grown in large fields, under optimum soil water conditions, and achieving full reduction under the given climatic conditions—is responsible for about 90% of water-resources consumption (Hoseini et al. 2005).

Fig. 1

Location of the study area in Khorasan-Razavi province in northeastern Iran

During the last decade, the Neishaboor plain has faced a severe problem of depletion of groundwater resources, which has resulted in the general prohibition, since 1986, of any further water-resources development in this area by the Iranian Energy Ministry (Hoseini et al. 2005). There are many unauthorized wells in the plain and pumping is not regulated, resulting in over-exploitation of the aquifer, which has caused an annual decline in groundwater level of about 0.90 m in recent years. Moreover, some recent studies have revealed an increasing trend in long-term mean annual precipitation (Ghahraman 2006; Ghahraman and Taghvaeian 2008). These studies have also revealed a similar and more quickly increasing trend in evapotranspiration. This has resulted in an increase in irrigation water requirement and subsequently greater deficiency in agricultural water resources. More conflicts and complexities are bound to occur over the plain, unless some profound water-resources management programs are put into action.

Description of datasets

With respect to the aquifer conceptual model, the relationship between independent and dependent variables can be described as follows:

$$ {H_{{{\text{i}} + 1}}} = f\left( {{H_{{\text{i} - \ldots }}},{P_{{{\text{i}} - \ldots }}},E{T_{{{\text{i}} - \ldots }}}} \right) $$

(1)

where H is groundwater level for each month as measured in observation wells (m asl), P is monthly precipitation (mm), ET is monthly reference evapotranspiration (mm) and i is the time step (monthly). Therefore, i + 1 refers to the next month, while i-… refers to current and previous months.

The monthly averages of precipitation and temperature were derived from data collected from the available stations within and outside the Neishaboor plain (Fig. 1). The temperature values were used to compute reference evapotranspiration (ET₀)—evapotranspiration from a reference surface—using the method of Hargreaves and Samani (1982), which was chosen because of its simplicity and the general availability of data. The Penman-Monteith (Allen et al. 1998) and Blaney and Criddle (1950) methods could not be used because of insufficient data. Precipitation and ET₀ were selected as surrogates of groundwater recharge and withdrawal respectively. The use of these parameters has been widely reported in the literature for groundwater-level predictions (Coppola et al. 2003; Coulibaly et al. 2001; Daliakopoulos et al. 2005). The raw data for all these parameters were available for the period 1992–2003. Missing values (9 monthly values) within the collected data were interpolated from the existing measurements with the help of a cubic-spline method (Daliakopoulos et al. 2005).

For the verification of observation well records, available length of record and distance from external influences were taken into account. External influences include: rivers, mountains and agricultural wells, which can all affect the groundwater-level fluctuations. It was obvious that groundwater-level fluctuations for any observation well near agricultural wells and/or rivers were higher than other places in the plain. It means that groundwater-level fluctuations are affected by the mentioned external influences and groundwater-level of these observation wells is not reliable. To assure the validity of data from the observation wells, water-resources experts were consulted in order to capture their experience. In conclusion, observation wells for which the length of record was too short were omitted, and out of 54 observation wells in the study area, only 39 were selected (Fig. 2; Table 1).

Fig. 2

Existing and selected observation wells in the Neishaboor plain

Table 1 Names and codes of the selected observation wells in Neishaboor plain (locations shown on Fig. 2)

Methodology

This study was undertaken in four steps, namely: (1) clustering of the observation wells; (2) data preparation for each clustered zone; (3) groundwater-level modeling via panel-data and ANN models; and (4) a comparison between the results of the two models. These steps are briefly described in this section, while a thorough review of panel-data theory is given in section Theory of panel-data regression modeling. Four measures to compare the results are discussed at the end of this section. Comparison between the results of the two models is presented in section Analysis of modeling results.

Cluster analysis classifies a set of observations into two or more mutually exclusive unknown groups based on combinations of interval variables (David 1997). To reduce the number of contributing observation wells and to give equal weights to each zone, cluster analysis was applied in this study. The 11 average monthly groundwater-level datasets were used for clustering. Being a popular technique, Ward’s clustering method was employed using Minitab 15.0 software (www.minitab.com/education). In this process, cluster membership is assessed by calculating the total sum of squared deviations from the mean of a cluster. The criterion for fusion is that it should produce the smallest possible increase in the error sum of squares (Ward 1963):

$$ TSSDM = \sum\limits_{{k = 1}}^{K} {\sum\limits_{{j = 1}}^{m} {\sum\limits_{{i = 1}}^{{{N_{{\text{k}}}}}} {{{\left( {y_{{{\text{ij}}}}^{{\text{k}}} - y_{{ \bullet {\text{j}}}}^{{\text{k}}}} \right)}^{2}}} } } $$

(2)

$$ y_{{ \bullet {\text{j}}}}^{{\text{k}}} = \frac{{\sum\limits_{{i = 1}}^{{{N_{{\text{k}}}}}} {y_{{{\text{ij}}}}^{{\text{k}}}} }}{{{N_{{\text{k}}}}}} $$

(3)

where TSSDM is the total sum of squared deviations from the mean, k, j and i denotes the clusters, time-series and cross-section dimension, respectively, K is the number of clusters, m is the number of variables (11 average monthly groundwater levels), N _K is the number of members (observation wells) within each cluster, $y_{{ \bullet {\text{j}}}}^{{\text{k}}}$ is the dimensionless mean value of water table fluctuations for month j in cluster K and $y_{{{\text{ij}}}}^{{\text{k}}}$ is the dimensionless value of j related to i in cluster K.

After clustering, data preparation for each zone was performed. An observation well was assigned as cluster representative for each cluster. For this reason, the sum of squared deviations from the mean of a cluster (SSDM) for all observation wells in that cluster were computed. Then, for each cluster, the observation well with the least SSDM was selected as its representative. Finally, values of monthly precipitation and temperature, as independent variables, were estimated by the inverse-distance method (Alsaaran 2005; Tabios and Salas 1985) for each zone, according to the coordinates of each cluster’s representative observation well. At this stage, for both types of model (panel-data and ANN), available data were divided into two sub-sets for training (parameter estimation) over the period 1992 to 2002, and validation over the period 2002 to 2003.

To avoid a lengthy explanation, only a few important facts about ANNs are included here. A “generalized feed-forward” network was used in this study because this type of network has been widely applied for groundwater prediction and forecasting (Coppola et al. 2003; Coulibaly et al. 2001; Daliakopoulos et al. 2005; Nayak et al. 2006). This type of network was suggested by Maier and Dandy (2000) because: (1) it has been found to perform well in comparison with recurrent networks in many practical applications; (2) it has been used almost exclusively for the prediction and forecasting of water-resources variables; and (3) its processing speed “is among the fastest of all models currently in use” (Masters 1993). Also, sigmoidal-type transfer functions (in the hidden layers) and linear transfer functions (in the output layer) were employed, as suggested by numerous researchers (Kaastra and Boyd 1995; Karunanithi et al. 1994).

For the panel-data model, Chow ( 1960), Breusch-Pagan Lagrange Multiplier (LM) (Breusch and Pagan 1980) and Hausman-Wu (Hausman 1978) tests were applied to select the best model in the training phase (1992–2002). A Chow test is simply a test of whether the coefficients estimated over one group of the data are equal to the coefficients estimated over another. The Breusch-Pagan test fits a linear-regression model to the residuals of a linear-regression model and rejects the model if too much of the variance is explained by the additional explanatory variables. The Hausman-Wu specification test is the classical test of whether a fixed or random-effects model should be used. Then, using the best selected model, groundwater levels were predicted for the validation phase (2002–2003).

Four different criteria were used in order to evaluate the effectiveness of the model and its ability to make predictions, as well as to compare the two models. These included Coefficient of Determination (R ²), root mean square error (RMSE), maximum error (ME) and mean normalized error (MNE). MNE was employed because the range of groundwater-level fluctuation in the validation period was different for each observation well, and it seemed that the normalized error value would be more helpful. The MNE for each observation well was calculated as follows:

$$ {\text{MNE}} = \frac{{\sum {\left| {\frac{{{h_{{\text{m}}}} - {h_{{\text{e}}}}}}{{\Delta h}}} \right|} }}{N} $$

(4)

where h _m and h _e are the measured and estimated groundwater levels, respectively, ∆h is the range of groundwater-level fluctuation in the period under consideration, and N is the number of measured values.

Theory of panel-data regression modeling

Introduction

As already mentioned, panel-data analysis endows regression analysis with both a spatial and temporal dimension. The spatial dimension pertains to a set of cross-sectional units of observation. The temporal dimension pertains to periodic observations of a set of variables characterizing these cross-sectional units over a particular time-span. Such models can be viewed as follows (Arellano 2003; Mundlak 1978; Wooldridge 2002; Yaffee 2003):

$$ \begin{array}{*{20}{c}} {{{\mathbf{y}}_{{{\text{it}}}}}{\mathbf{ = \alpha + \beta }}{{\mathbf{X}}_{{{\text{it}}}}}{\mathbf{ + }}{{\mathbf{u}}_{{{\text{it}}}}}} \hfill & {{\text{i}}{\mathbf{ = 1,2, \ldots ,}}{\text{N}}{\mathbf{;}}\;{\text{t}}{\mathbf{ = 1,2, \ldots ,}}{\text{T}}} \hfill \\ \end{array} $$

(5)

where i and t denotes the cross-section and time-series dimension, respectively, N is the number of cross-sections, T is the length of the time-series for each cross-section, y is a dependent-variable vector, X is an independent-variable matrix, α is a scalar, β is the coefficient of the independent-variable matrix and u is the error component in the model.

The performance of any estimation procedure for the model regression parameters depends on the statistical characteristics of the error components in the model. The panel-data procedure estimates the regression parameters in the preceding model under several common error structures. These error structures consist of one and two-way fixed and random-effects models. If the specification is dependent only on the cross-section to which the observation belongs, such a model is referred to as a model with one-way effects. A specification that depends on both the cross section and the time-series to which the observation belongs is called a model with two-way effects. Therefore, the specifications for the one-way model are (Baltagi 2005; Hsiao 2003; Wooldridge 2002):

$$ {u_{{{\text{it}}}}} = {\mu _{{\text{i}}}} + {\nu _{{{\text{it}}}}} $$

(6)

where μ _i denotes the unobservable individual-specific effect and ν _it denotes the remainder disturbance. Note that μ _i is time-invariant and it accounts for any individual-specific effect that is not included in the regression. The remainder disturbance ν _it varies with individuals and time and can be thought of as the usual disturbance in the regression. Similarly, the specifications for the two-way model are:

$$ {u_{{{\text{it}}}}} = {\mu _{{\text{i}}}} + {\lambda _{{\text{i}}}} + {\nu _{{{\text{it}}}}} $$

(7)

where λ _t denotes the unobservable time-specific effect. Note that λ _t is individual-invariant and it accounts for any time-specific effect that is not included in the regression.

Apart from the possible one-way or two-way nature of the effect, the other dimension of difference between the possible specifications is that of the nature of the cross-sectional or time-series effect. The models are referred to as fixed-effects models if the effects are non-random and as random-effects models otherwise (Baltagi 2005; Hsiao 2003; Wooldridge 2002).

The one-way fixed-effects model

In this case, the μ _i are assumed to be fixed parameters to be estimated and the remainder disturbances stochastic with ν _it independent and identically distributed $IID\left( {0,\sigma_{\nu }^2} \right)$. Note that $\sigma_{\nu }^2$ is variance of the remainder disturbance. The X _it are assumed independent of the ν _it for all i and t (Baltagi 2005; Hall 1987; Hsiao 2003; Kangasharju 2000). Then Ordinary Least Squares (OLS) estimator (Leng et al. 2007) is performed on Eq. (5) to get estimates of α, β and μ. If N is large, Eq. (5) will include too many individual dummies, and the matrix to be inverted by OLS is large and of dimension N + k, where k is the number of independent variables. In fact, since α and β are the parameters of interest, the least squares dummy variables (LSDV) estimator can be obtained from Eq. (5), by pre-multiplying the model by Q and performing OLS on the resulting transformed model (Qy = QXβ + Qν) to get the coefficients. Note that Q is a matrix which obtains the deviations from individual means.

The one-way random-effects model

In this case, ${\mu _{{\text{i}}}}\sim IID\left( {0,\sigma _{\mu }^{2}} \right),{\nu _{{{\text{it}}}}}\sim IID\left( {0,\sigma _{\nu }^{2}} \right)$ and the μ _i are independent of the ν _it. In addition, the X _it are independent of the μ _i and ν _it., for all i and t. From Eq. (5), the variance–covariance matrix of error can be computed (Baltagi 2005; Hsiao 2003; Wooldridge 2002):

$$ \Omega = E\left( {uu\prime } \right) = {Z_{\mu }}E\left( {\mu \mu \prime } \right)Z_{\mu }^{\prime } + E(\nu \nu \prime ) $$

(8)

Note that Ω is variance–covariance matrix of error, $\bf{Z_{\mu }} = {I_{{\text{N}}}} \otimes {l_{{\text{T}}}}$; where I _N is an identity matrix of dimension N, l _T is a vector of ones of dimension T and ⨂ denotes the Kronecker product (Liu 1999; Trenkler 1995). Indeed, Z _μ is a selector matrix of ones and zeros, or simply the matrix of individual dummies that may be included in the regression to estimate the μ _i if those are assumed to be fixed parameters.

In order to obtain the generalized least square (GLS) estimator (Browne 1974) of the regression coefficients, the Ω ^–1 is required. This is a huge matrix for typical panels and is of dimension (NT + NT). After calculating Ω ^–1 using a method developed by Wansbeek and Kapteyn (1982, 1983), GLS can be used as a weighted least-squares estimator to obtain coefficients for Eq. (5). For more information on the derivation of these equations, refer to Baltagi (2005), page 16.

The two-way fixed-effects model

If the μ _i and λ _t are assumed to be fixed parameters to be estimated and the remainder disturbances stochastic with ${\nu _{{{\text{it}}}}}\sim IID\left( {0,\sigma _{\nu }^{2}} \right)$, then Eq. (7) represents a two-way fixed-effects-error-component model. The X _it are assumed independent of the ν _it for all i and t. One, would perform the regression of ỹ = Qy on $\tilde{X} = QX$ to get ${{\tilde{\beta }}_{{{\text{OLS}}}}} = {\left( {X\prime QX} \right)^{{ - 1}}}X\prime Qy$.

The two-way random-effects model

If ${\mu _{{\text{i}}}}\sim IID\left( {0,\sigma _{\mu }^{2}} \right),{\lambda _{{\text{t}}}}\sim IID\left( {0,\sigma _{\lambda }^{2}} \right)$ and ${\nu _{{{\text{it}}}}}\sim IID\left( {0,\sigma _{\nu }^{2}} \right)$ independent of each other, then this is the two-way random-effects model. In addition, X _it is independent of μ _i, λ _t and ν _it for all i and t. From Eq. (7), the variance–covariance matrix of error can be computed as follows (Arellano 2003; Baltagi 2005; Hsiao 2003; Wooldridge 2002):

$$ \Omega = E\left( {uu\prime } \right) = {Z_{\mu }}E\left( {\mu \mu \prime } \right)Z_{\mu }^{\prime } + {Z_{\lambda }}E\left( {\lambda \lambda \prime } \right)Z_{\lambda }^{\prime } + \sigma _{\nu }^{2}{I_{{{\text{NT}}}}} $$

(9)

where Z _λ is the matrix of time dummies that may be included in the regression to estimate the λ _t if they are fixed parameters and I _NT is an identity matrix of dimension NT. In order to obtain the GLS estimator of the regression coefficients, the Ω ^–1 is required. After calculating Ω ^–1 using a method developed by Hsiao (2003), GLS can be used as a weighted least-squares estimator to obtain coefficients. For more information on the derivation of these equations, refer to Baltagi (2005), p. 36.

Fixed or random effects model

Having discussed the fixed-effects and the random-effects models and their underlying assumptions, the question now arises of which one to choose. To answer this question, the following steps were taken. Firstly, data “poolability” must be examined. The critical assumption behind pooling data into a panel is that the regression coefficients are constant across individuals (either all coefficients in the vector δ or at least the slope coefficients β). The pooled model therefore has constant coefficients. The Chow test (Chow 1960), was used to examine data poolability, as follows:

H ₀ :

No individual fixed effects (the pooled model) (${\delta _{1}} = {\delta _{2}} = \ldots = {\delta _{{\text{N}}}} = \delta$)

H ₁ :

Individual fixed effects exist (${\delta _{1}} \ne {\delta _{2}} \ne \ldots \ne {\delta _{{\text{N}}}}$)

It is notable that the appropriate statistic for this hypothesis is the F-statistic:

$$ {F_{{\left[ {\left( {{\text{n}} - 1} \right)\left( {{\text{k}} + 1} \right),{\text{n}}\left( {{\text{T}} - \left( {{\text{k}} + 1} \right)} \right)} \right]}}} = \frac{{\left( {R_{0}^{2} - R_{1}^{2}} \right)/\left( {n - 1} \right)\left( {k + 1} \right)}}{{R_{0}^{2}/n\left( {T - \left( {k + 1} \right)} \right)}} $$

(10)

where $R_0^2$ is the Sum Square Error (SSE) of the pooled model and $R_1^2$ is the SSE of the fixed effects model. If F is larger than a critical (tabulated) value, then the null hypothesis is rejected. It reveals the existence of fixed effects between unobservable individual-specific effects and regressors. After understanding the existent effect between individuals, it is necessary to find whether there are any random effects between individuals. With regard to this objective, different tests are proposed.

For the random two-way error-component model, Breusch and Pagan (1980) suggested the Lagrange Multiplier (LM) test. The assumptions follow:

H ₀ :

No random effects (the pooled model) ($\sigma_{\mu }^2 = \sigma_{\lambda }^2 = 0$)

H ₁ :

Random effects exist ($\sigma_{\mu }^2 \succ 0$ and $\sigma_{\mu }^2 \succ 0$)

The LM test statistic is given by:

$$ LM = L{M_{1}} + L{M_{2}} = \frac{{nT}}{{2\left( {T - 1} \right)}}{\left[ {1 - \frac{{\tilde{u}\prime \left( {{I_{{\text{N}}}} \otimes {J_{{\text{T}}}}} \right)\tilde{u}}}{{\tilde{u}\prime \tilde{u}}}} \right]^{2}} + \frac{{nT}}{{2\left( {N - 1} \right)}}{\left[ {1 - \frac{{\tilde{u}\prime \left( {{J_{{\text{N}}}} \otimes {I_{{\text{T}}}}} \right)\tilde{u}}}{{\tilde{u}\prime \tilde{u}}}} \right]^{2}} $$

(11)

where ũ is the SSE of the pooled model and J is a matrix of ones of dimension T or N. LM is asymptotically distributed as a χ ². If LM is larger than the critical value, then the null hypothesis is rejected. It means that there are random effects between unobservable individual-specific effects and regressors.

The Hausman specification test (Hausman 1978) is another classical test of whether the fixed- or random-effects model should be used. The main question here is whether there is significant correlation between the unobserved individual-specific random effects and the regressors. If there is no such correlation, then the random effects model may be more powerful. If there is such a correlation, the random effects model would be inconsistently estimated, and the fixed effects model would be the model of choice, as follows:

H ₀ :

$E\left( {{X_{{{\text{it}}}}}{\mu _{{\text{i}}}}} \right) = 0 \to$ No correlation; random effects consistent and efficient

H ₁ :

$E\left( {{X_{{{\text{it}}}}}{\mu _{{\text{i}}}}} \right) \ne 0 \to$ Correlation exists; fixed effects consistent

Hence, the Hausman test statistic is given by:

$$ m = \left( {{{\tilde{\beta }}_{{{\text{GLS}}}}} - {{\tilde{\beta }}_{{{\text{OLS}}}}}} \right)\prime {\left[ {{\text{var}}\left( {{{\tilde{\beta }}_{{{\text{GLS}}}}} - {{\tilde{\beta }}_{{{\text{OLS}}}}}} \right)} \right]^{{ - 1}}}\left( {{{\tilde{\beta }}_{{{\text{GLS}}}}} - {{\tilde{\beta }}_{{{\text{OLS}}}}}} \right) $$

(12)

The statistic m is asymptotically distributed as $\chi _{{\text{k}}}^{2}$ where k denotes the number of regressors. If m is larger than the critical value, then the null hypothesis is rejected and the fixed effects model is selected. To implement the theory and estimate or analyze panel-data models, SAS software ver. 9.1 was used.

In summary, panel-data analysis is a method of studying a particular subject within multiple sites, periodically observed over a defined time frame. Moreover, with spatial observations and enough cross-sections, panel-data analysis permits the researcher to study the dynamics of change with time-series.

Analysis of modeling results

Cluster analysis

As stated earlier, the Ward method was used for cluster analysis. The tree diagram (dendogram) of clustering is shown in Fig. 3. Regarding physical facts, 90% similarity is considered for clustering the observation wells. The cluster analysis identified 6 homogeneous zones. After clustering, for each zone, the observation well with the least SSDM was selected as its representative. The representative wells are Soltan Abad, Filkhaneh, Aman Abad, Arazie Mohandes, Amir Abad and Jonobe Hosein Abad, for zones 1–6 respectively.

Fig. 3

Dendogram for cluster analysis of the existing observation wells (the six zones are numbered on the dendogram)

After the selection of representative wells, the results were discussed with local water resources officers and experts. In two cases the selected observation wells were not considered suitable, due to some local considerations. Therefore, two other wells, within the same clusters, were nominated as representative wells. Moreover, it should be mentioned that the change was made after a detailed check on ward-clustering results and on behavior resemblance for each pair of observation wells. Figure 4 shows the existing observation wells, the six zones, and representative wells (shown with bold symbols). The important thing to note is that Fig. 4 is just a schematic representation. Obviously, each clustering zone has a region of influence which is the sum of regions of influence of its consistent observation wells. Usually, the region of influence for each observation well is represented by Thiessen polygons. However, the real region of influence, from the point of view of groundwater behavior may be different. For areas near watershed boundaries, where there are no observation wells, no clustering was performed. It should be noted that agricultural wells were not used as a complementary set, because of incomplete data and poor data quality. Finally, for each zone, values of independent variables were estimated by inverse-distance method.

Fig. 4

The selected observation wells in the Neishaboor plain, the six zones from the cluster analysis (numbered in red), and their representative wells

ANN model

Inputs of panel-data and ANN models were the same. Table 2 shows the architectural description of the ANN model. Input variables were selected using sensitivity analysis. Sensitivity analysis using the p-values at the 95%-significance level showed that ET₀ and groundwater-level variables had significant effect until 4 antecedent time lags, but precipitation had significant effect until 5 antecedent time lags. The number of input variables used in the network was 16. The number of hidden nodes in the hidden layer was obtained using trial and error. The statistical adequacies of the applied ANN model for forecasts 1 month ahead are summarized in Table 3, from which it can be seen that the model performance is good, except for Filkhaneh and Amir-Abad observation wells. Also, the maximum error for these observation wells is not within the ±0.5 m that is suggested by Daliakopoulos et al. (2005). Figure 5 shows the prediction results for 1-month ahead for the six selected observation wells, from which it can be seen that the ANN model cannot recognize the behavior of groundwater levels in Filkhaneh, Aman-Abad and Amir-Abad observation wells.

Table 2 Architectural description of the ANN model^a

Table 3 Performance indices during validation period for different clusters, comparing the panel-data and ANN models

Fig. 5

Plots of observed and computed groundwater levels during the validation period for a Soltan Abad, b Filkhaneh, c Aman Abad, d Arazie Mohandes, e Amir Abad and f Jonobe Hosein Abad, the representative wells for clusters 1–6, respectively

“Panel-data” model

As stated earlier, the groundwater level, precipitation and temperature at some antecedent monthly time lags were considered to be independent variables, and groundwater level for a subsequent period as a dependent variable. At first, the one-way and two-way fixed and random effects were trained. Sensitivity analysis revealed that some variables had no significant effect (i.e. the p-value was more than 0.05), meaning that these variables were not significant at the 95%- significance level. The resulting selected variables are shown in Table 4.

Table 4 Selected independent variables using 95% p-value

After training and determining the structures of all models (over the period 1992–2002), the Chow and Hausman tests were applied to find the best model. Firstly, the Chow test was performed; and the fixed-effects model was found to be superior to the pooled model. Then, the results of the Hausman test showed that the two-way fixed-effects model was again superior to the random-effects model. Table 5 shows the computed and critical values for the Chow and Hausman tests. The computed values were obtained using SAS software. Consequently, the two-way fixed-effects model was selected as being the best model. This result is logical, since the groundwater levels at observation wells at different locations and time periods are indeed influencing each other.

Table 5 Computed and critical values of the Chow and Hausman tests

Validation of model

As mentioned earlier, the two-way fixed-effects model was selected as the best model in the training phase. Consequently, groundwater levels were predicted in the test phase (2002–2003) for validation of the model. According to the performance indicators (RMSE, R ², ME and MNE) the model predicted the water levels well, as demonstrated by Table 3. The correlation statistic (R ²), that evaluates the linear correlation between the observed and the computed groundwater levels, is in a good range; except for Amir Abad observation well. The RMSE statistic, which is a measure of the global goodness of fit between the computed and observed groundwater levels, was good, as is evidenced by a low RMSE value (<0.5 m). The ME statistic, which shows the maximum error between the observed and the computed groundwater levels, was good, as it was less than the value suggested by Daliakopoulos et al. (2005). Since the range of groundwater-level fluctuation during the validation period is different for each observation well, it seems that the normalized error value would be more helpful. The normalization for each observation well was calculated with regard to its range of fluctuation. The range of fluctuation during the validation period for Soltan Abad, Filkhaneh, Aman Abad, Arazie Mohandes, Amir Abad and Jonobe Hosein Abad observation wells were 2.64, 3.45, 0.4, 3.11, 2.36 and 1.70 m, respectively. It is obvious from Table 3 that the panel-data model is superior to the ANN model for this dataset. Spatial correlation was not found to be the source of variation of regression errors. However, it seems that the error is less if the observation well is near to recharge boundaries and/or extraction focal points. More research is needed to identify the reason for error variations.

Figure 5 compares the observed groundwater levels against the computed values in the test phase for all the representative wells of the clusters. It can be seen from Fig. 5 that the Soltan Abad, Arazie Mohandes, Aman Abad and Jonobe Hosein Abad tend to underpredict, but Filkhaneh, and Amir Abad tend to underpredict and overpredict at various different times. Note that overprediction denotes more negative depth than the observed, whereas underprediction means an observation depth more than the computed one. In this case, overprediction is preferred, because it offers more reliability in judgments (Coulibaly et al. 2001). The results suggest that the two-way fixed-effects model can offer a reliable framework for the prediction of water-level fluctuations.

As all performance evaluation measures employed so far were global, they do not reveal any information about the errors during the validation period. Figure 6 shows the behavior of errors during the validation period. Note that in this figure a positive sign indicates underestimation and a negative sign indicates overestimation by the model. It can be seen from Fig. 6 that the prediction error for the whole range of water levels is mostly within ±0.5 m. Only for some clusters such as Amir Abad and Filkhaneh, can larger errors be seen.

Fig. 6

The error plots during the validation period. Legend: a Soltan Abad, b Filkhaneh, c Aman Abad (on the left-hand graph), and d Arazie Mohandes, e Amir Abad and f Jonobe Hosein Abad (on the right-hand graph), the representative wells for clusters 1–6 respectively

Comparison of ANN and panel-data models

The results of panel-data models were compared with those of ANN models. The comparison showed that the panel-data model had a better performance over the ANN for this particular dataset. However, the relative performance of the two models was close and both can be considered to have good performance in predicting groundwater levels. However, the panel-data model can be applied in preference to the ANN model for the purpose of water-resources management, because: (1) it is able to consider spatial and temporal dimensions for several observation wells simultaneously; (2) it has a simpler theory than ANN; and (3) it represents a lucid model where variables are related simply via a mathematical function, just like any other regression.

Summary and conclusion

In this study, the application of panel-data modeling as a useful, robust and efficient technique for the prediction of groundwater levels was investigated for the Neishaboor plain. A significant advantage of this type of model is that it can provide satisfactory predictions while considering several observation wells simultaneously. That is to say, panel-data analysis endows regression analysis with both spatial and temporal dimensions. It was found that the two-way fixed-effects model is the most suitable for groundwater level modeling in Neishaboor plain (for this particular dataset) with regard to Chow and Hausman tests. Figure 7 shows the historical behavior of groundwater levels in the six observation wells. It can be seen from this figure that during the period 1992–2003 (132 months) a certain relationship between the groundwater levels in the six observation wells always applies, namely: a > b > d > c > e > f; which is the observed reality of the regional water table. Figure 8 gives the simulated behavior of groundwater levels for the 24-month validation period (2002–2003), for the six observation wells. The same relationship between the observation wells is evident in this figure, too. The general resemblance between the behaviors shown in Figs. 7 and 8 demonstrate that the model has captured the physical phenomena of groundwater in Neishaboor plain. The performance evaluation criteria, namely the R ², RMSE, MNE and ME, were found to be good in both the training and validation phases. Soltan Abad and Aman Abad respectively showed the best and worst fits to the model in the test phase. Furthermore, the prediction error during the validation period was within the reasonable limits. In addition, the results of the panel-data model were compared with the results of an ANN model, with the panel-data model considered to be superior to the ANN model, for this dataset.

Fig. 7

The plots of observed groundwater levels. Legend: a Soltan Abad, b Filkhaneh, c Aman Abad, d Arazie Mohandes, e Amir Abad and f Jonobe Hosein Abad, the representative wells for clusters 1–6 respectively

Fig. 8

The plots of simulated groundwater levels during the validation period. Legend: a Soltan Abad, b Filkhaneh, c Aman Abad, d Arazie Mohandes, e Amir Abad and f Jonobe Hosein Abad, the representative wells for clusters 1–6 respectively

The application of panel-data modeling to water-resources management is new, not having been previously applied for that purpose. Its successful application in this study suggests that there is a promising future for the application of this type of model in different fields of water resources. In this study, complete panels or a balanced panel were used (referring to the individuals that have the same temporal length over the entire sample period). In contrast, incomplete panels are more likely to be the norm in typical cases of water resources and hydrological systems, because hydrological data from different stations usually differ in temporal length. Additionally, when panel data include auto regressive components, they are called dynamic panel data, and are able to deal with dynamic systems. Obviously, many water resources and hydrological systems are dynamic in nature, and therefore researchers can employ this technique to better understand the dynamics of phenomena. Hence, the application of incomplete and dynamic panels to the field of water resources can be the focus of future research.