Exact and approximate analytical solutions of groundwater response to tidal fluctuations in a theoretical inhomogeneous coastal confined aquifer

Abstract

The influence of hydraulic conductivity heterogeneity on tide-induced head fluctuations is presented for a theoretical coastal confined aquifer. The conceptual model assumes that the hydraulic conductivity increases linearly with the distance from the coastline. This type of heterogeneity has been observed in many alluvial coastal aquifers. An exact analytical solution that predicts induced head fluctuations is obtained in terms of a Hankel function. The exact solution can be approximated by a simple mathematical expression, valid for small rates of increase of hydraulic conductivity. Both exact and approximate solutions show significant differences from the classical solution obtained for a homogeneous aquifer. Near the coastline the amplitude of the induced head fluctuation is damped but it is enhanced as the distance to the coast increases. The time-lag between sea tide and induced head fluctuation in the aquifer is not linear; it behaves as a square-root type function leading to a faster transmission of the tidal fluctuation. Hypothetical examples show that the influence of hydraulic conductivity heterogeneity can be significant and should be considered for a correct description of the groundwater response.

Résumé

L’influence de l’hétérogénéité de la perméabilité sur les fluctuations piézométriques induites par la marée est présentée pour un aquifère captif côtier théorique. Le modèle conceptuel suppose que la perméabilité augmente linéairement avec la distance au littoral. Ce type d’hétérogénéité a été observé dans de nombreux aquifères côtiers alluviaux. Une solution analytique exacte qui prédit les fluctuations piézométriques induites est obtenue sous la forme d’une fonction de Hankel. La solution exacte peut être approchée par une expression mathématique simple, valide pour de faibles taux d’augmentation de la perméabilité. Les deux solutions, approchée et exacte, montrent des différences significatives avec la solution classique obtenue pour un aquifère homogène. Près du littoral, l’amplitude des fluctuations piézométriques est atténuée, mais elle amplifiée lorsque la distance au littoral augmente. Le déphasage entre la marée marine et les fluctuations piézométriques induites dans l’aquifère n’est pas linéaire. Il se comporte comme une fonction de type racine carrée, ce qui implique une transmission plus rapide de la fluctuation de marée. Des exemples hypothétiques montrent que l’influence de l’hétérogénéité de la perméabilité peut être significative et doit être prise en considération pour une description correcte de la réponse de l’aquifère.

Resumen

Se analiza el efecto de la heterogeneidad de la conductividad hidráulica en las fluctuaciones inducidas por mareas en un acuífero costero confinado teórico. El modelo conceptual supone que la conductividad hidráulica aumenta linealmente con la distancia a la costa. Este tipo de heterogeneidad ha sido observada en numerosos acuíferos costeros aluviales. Se deriva una solución analítica exacta que predice las fluctuaciones inducidas en términos de la función de Hankel. La solución exacta puede aproximarse mediante una simple expresión matemática que es válida para pequeños incrementos de la conductividad hidráulica. Las soluciones exacta y aproximada muestran diferencias significativas con la solución clásica derivada para un acuífero homogéneo. La amplitud de la fluctuación inducida está atenuada cerca de la línea de costa pero aumenta a medida que la distancia a la costa se incrementa. El defasaje en tiempo entre la marea oceánica y la fluctuación inducida en el acuífero no es lineal, sino que se comporta como una función de tipo raíz cuadrada que produce una transmisión más rápida de la onda de marea. Ejemplos hipotéticos muestran que el efecto de la heterogeneidad en la conductividad hidráulica puede ser importante y debería considerarse para una correcta descripción de la respuesta de las aguas subterráneas.

摘要

本文介绍一个理论海岸承压含水层中渗透系数非均质性对潮汐诱发的水头波动的影响。概念模型假定渗透系数随着距海岸线的距离线性增加。这种非均质的类型在许多冲积海岸含水层中都已观察到。获得的以汉克尔函数形式的精确解析解可用于预测诱发水头波动。这个精确解析解可由一个简单的数学表达式近似,允许渗透系数的小量增加。精确解和近似解都显示了与通过均质含水层获得的传统解的显著差异。靠近海岸带,诱发水头波动的幅度衰减,但是随着据海岸带距离的增加而增强。海水潮汐与含水层中诱发的水头波动之间的延时不是线性的;类似于方根类型的函数,导致对潮汐波动更快的传导。假设例子显示渗透系数非均质性的影响是显著的,应该在对地下水响应的正确描述上加以考虑。

Resumo

A influência da heterogeneidade da condutividade hidráulica nas flutuações do nível piezométrico induzida pelas marés é apresentada para um aquífero costeiro confinado teórico. O modelo concetual assume que a condutividade hidráulica aumenta linearmente com a distância ao litoral. Este tipo de heterogeneidades tem sido observado em muitos aquíferos costeiros aluviais. Uma solução analítica exata que prevê flutuações induzidas do nível piezométrico é obtida em termos de uma função de Hankel. A solução exata pode ser aproximada através de uma expressão matemática simples, válida para pequenas taxas de aumento da condutividade hidráulica. Tanto a solução exata como a aproximada apresentaram diferenças significativas em relação à solução clássica obtida para um aquífero homogéneo. Perto da linha de costa, a amplitude de flutuação do nível piezométrico é amortecida, mas é reforçada com o aumento da distância à costa. O lapso de tempo entre a maré e a flutuação de nível induzida no aquífero não é linear; comportando-se como uma função do tipo raiz quadrada e levando a uma transmissão mais rápida das flutuações das marés. Exemplos hipotéticos mostram que a influência da heterogeneidade da condutividade hidráulica pode ser significativa e que deve ser considerada para uma descrição correta da resposta das águas subterrâneas.

Introduction

The interaction between groundwater and seawater induced by tidal fluctuations has been extensively analyzed through both analytical and numerical methods. Since the 1950s, many analytical solutions to describe this interaction have been derived. Jacob (1950) and Ferris (1951) were the first to obtain an analytical equation for a single homogeneous confined aquifer. Due to its simplicity, this equation has been widely used to estimate hydraulic parameters in coastal aquifers (e.g., Carr and van der Kamp 1969; Drogue et al. 1984; Serfes 1991; Erskine 1991; Millham and Howes 1995; Trefry and Johnston 1998; Jha et al. 2003). In recent years, more complex analytical solutions have been obtained for two-layer systems consisting of an aquifer confined by a semipermeable layer. These analytical solutions allow for the study of leakage and storage effects on the tide-induced head fluctuations (e.g., Jiao and Tang 1999; Li and Jiao 2001a,b; Li and Jiao 2002a,b; Li et al. 2002; Jeng et al. 2002; Li and Jiao 2003b; Song et al. 2007; Li et al. 2008; Sun et al. 2008). All the aforementioned theoretical results are obtained under the assumption of homogeneity of the aquifer system layers. This assumption has significant discrepancy from real aquifers, which usually exhibit inhomogeneity and anisotropy in their hydraulic properties (Li and Jiao 2003a; Trefry and Bekele 2004).

The study of heterogeneity on tide-induced head fluctuations using analytical solutions has been addressed by several researchers. Trefry (1999) presented comprehensive solutions for a finite aquifer consisting of an arbitrary number of contiguous homogeneous zones subjected to sinusoidal linear boundary conditions. Guo et al. (2010) derived an analytical solution for a semi-infinite single aquifer comprising two different homogeneous zones. Chuang et al. (2010) extended this conceptual model to a leaky aquifer system divided into a finite number of horizontal regions. Li et al. (2007), Guo et al. (2007), Xia et al. (2007), Rotzoll et al. (2008) and Geng et al. (2009) included the effect of an outlet capping in submarine aquifer systems. However, to the authors’ knowledge, there are no analytical solutions that consider a continuous variation of the hydraulic properties with distance. In particular, an analytical solution that considers a continuous increase of hydraulic conductivity can be useful for studying alluvial coastal aquifers. In alluvial aquifers, progressively finer sediments are usually deposited on the downstream part of the depositional zone, giving as a result a continuous increase of hydraulic conductivity with the distance to the coastline (Freeze and Cherry 1979; Lunt et al. 2004; Carol et al. 2009; Cardenas 2010; Chuang et al. 2010). In some cases, the rate of increase of hydraulic conductivity can be significant. Montalto et al. (2006) have reported linear variations of approximately two orders of magnitude along transects of 50 m in a flooded tidal marsh in the Hudson River estuary, USA.

The objective of this technical note is to present both exact and approximate analytical solutions for tide-induced head fluctuations in a coastal confined aquifer with hydraulic conductivity that linearly increases with the distance to the coastline. Hypothetical examples are designed to test the analytical solutions and to analyze the effect of the hydraulic conductivity heterogeneity on tide-induced head fluctuations.

Mathematical model and exact analytical solution

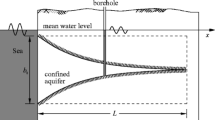
Consider a coastal aquifer laying between two impermeable layers as shown in Fig. 1. Both the aquifer and the impermeable layers end at the coastline and extend landward infinitely. Layers are horizontal and the seaward boundary is assumed to be vertical. For the mathematical description of the problem, let the x-axis be perpendicular to the coastline, horizontal and positive landward, with its origin at the coastline. The datum of the induced head fluctuation is chosen to be the mean water level.

Fig. 1

Schematic representation of the confined coastal aquifer. The x-axis is represented by a dashed line

In order to derive an analytical solution, the following assumptions are made: the flow in the confined aquifer is horizontal and obeys Darcy’s law; the effect of density variations on water flow is neglected; the hydraulic conductivity increases with the horizontal distance; the specific storativity is constant. According to the aforementioned assumptions, the governing equation for the head fluctuations within the confined aquifer can be written as (Bear 1988):

$$ \frac{\partial }{{\partial x}}\left( {K(x)\frac{{\partial h}}{{\partial x}}} \right) = {S_s}\frac{{\partial h}}{{\partial t}} $$

(1)

where h(x,t) is the groundwater head [L], S _s the specific storativity [L^–1] and K(x) the hydraulic conductivity [LT^–1], x the distance to the coastline [L], and t the time [T]. Note that Eq. (1) applies strictly to a confined aquifer. However when the fluctuations in h are small compared to the aquifer thickness, it can also be applied to unconfined aquifers (Bear 1988; Townley 1995, Guo et al. 2010).

The boundary condition at the interface of the sea and the aquifer is expressed as:

$$ h(0,t) = A\cos (\omega t) $$

(2)

where h(0,t) is the head at x = 0, A the tidal amplitude [L] and ω the tidal angular frecuency [T^–1]. At infinity, the following no-flow boundary condition is used:

$$ \mathop{{\lim }}\limits_{{x \to \infty }} K(x)\frac{{\partial h}}{{\partial x}} = 0 $$

(3)

Here, only the periodic solution is considered, so –∞ < t < ∞ and no initial conditions are needed.

Assume a linear increase of the hydraulic conductivity with the distance x:

$$ K(x) = {K_0}(1 + bx) $$

(4)

where K ₀ [LT^–1] is the hydraulic conductivity of the aquifer at x = 0 and b [L^–1] is the rate of increase (b ≥ 0). A linear model for K(x) could be considered arbitrary, but is an initial step towards a more realistic description of some type of heterogeneous aquifers. For example, Cardenas (2010) uses Eq. (4) for describing some features of groundwater dynamics in a fluvial island that can not be accurately represented by a constant hydraulic conductivity. It is also worth mentioning that the hydraulic conductivity given by Eq. (4) tends to infinity when x tends to infinity. This is an unrealistic value for K; however, the analytical solution is not affected by the values of hydraulic conductivity far away from the coast, as will be shown in the next section.

The exact analytical solution of the boundary value problem Eqs. (1)–(4) is presented in the Appendix and further expanded in the electronic supplementary material (ESM), and is given by:

$$ h(x,t) = {\rm Re} \left[ {A\frac{{H_0^{{(1)}}(2\Lambda \sqrt {{1 + bx}} )}}{{H_0^{{(1)}}(2\Lambda )}}{e^{{i\omega t}}}} \right] $$

(5)

where Re denotes the real part of the expression, H ⁽¹⁾₀ is the first kind Hankel function of zero order, Λ = a(–1 + i) /b, and a [L^–1] the tidal propagation parameter defined as:

$$ a = \sqrt {{\frac{{\omega {S_s}}}{{2{K_0}}}}} . $$

(6)

For a homogeneous aquifer (K(x) = K ₀), the inverse of a is the characteristic dampening distance for which the amplitude of the induced head fluctuation decays to A/e~0.36A.

Discussion of the exact analytical solution

To explore the influence of the hydraulic conductivity heterogeneity on tide-induced head fluctuations, the following hypothetical example is designed. The hydraulic parameters of the confined aquifer are assumed to be K ₀ = 1 m/h, S _s = 10^–5 m^–1 and b = 10^–2 m^–1. The sea tide is considered semidiurnal (period of 12.4 h) with an amplitude A of 1 m. The tidal propagation parameter computed using Eq. (6) is a = 1.59 10^–3 m^–1. For the sake of simplicity distances are expressed in dimensionless form multiplying x by a.

Figure 2 shows the sea tide and head fluctuations for both heterogeneous and homogeneous aquifers at two representative points located near (ax = 0.25) and far (ax = 2.0) from the coast. At ax = 0.25 the induced head fluctuation for the heterogeneous aquifer (curve for b in Fig 2a) has a smaller amplitude than the homogeneous one. However, far from the coast (ax = 2.0), the amplitude of the fluctuation given by Eq. (5) is greater than the homogeneous case and a significant time-lag between both responses is also observed. This simple example shows that the effect of heterogeneity on head fluctuations is significant and strongly depends on the distance to the coast.

Fig. 2

Tide-induced head fluctuation versus time at different observation points: a a = 0.25 and b a = 2.0

For a better understanding of the influence of heterogeneity on induced head fluctuations, both the amplitude and time-lag as functions of the dimensionless distance ax are analyzed. The amplitude (h _max) and time-lag (t _lag) of head fluctuations have the following expressions:

$$ {h_{{\max }}}(x) = {A} \sqrt {{B_r^2 + B_i^2}} $$

(7)

$$ {t_{{lag}}}(x) = - \frac{1}{\omega }{\tan^{{ - 1}}}\left( {\frac{{{B_i}}}{{{B_r}}}} \right) $$

(8)

where:

$$ {B_r} = {\rm Re} \left[ {\frac{{H_0^{{(1)}}(2\Lambda \sqrt {{1 + bx}} )}}{{H_0^{{(1)}}(2\Lambda )}}} \right]{ },{ }{B_i} = {\rm Im} \left[ {\frac{{H_0^{{(1)}}(2\Lambda \sqrt {{1 + bx}} )}}{{H_0^{{(1)}}(2\Lambda )}}} \right] $$

(9)

Figure 3 shows the amplitudes computed using Eq. (7) for three different rates of increase of hydraulic conductivity b = 10^–1, 10^–2, 10^–3 m^–1. As a reference, the figure includes the amplitude of a homogeneous aquifer which has the following analytical expression: Ae ^–ax (Jacob 1950). In comparison with the homogeneous model, the linear heterogeneity produces more damped amplitudes for distances less than approximately 1/a (characteristic dampening distance). In this region near the coast, the damping effect increases with the values of b. An opposite behavior is observed for increasing inland distances: the amplitudes of the heterogeneous aquifer are enhanced, leading to larger intrusion of induced fluctuations in the aquifer. This enhancing effect significantly increases with the inland distance, particularly for large values of b.

Fig. 3

Amplitude versus dimensionless distance ax in log scale for different rates of increase of hydraulic conductivity

The time-lag between the sea tide and the induced head fluctuation on the heterogeneous aquifer can be computed from Eq. (8). Figure 4 shows time-lags as a function of ax for b = 10^–1, 10^–2, 10^–3 m^–1. Time-lags of the heterogeneous aquifers are smaller than the time-lag of the homogeneous aquifer, which show a linear increase with distance. The time-lag of the heterogeneous aquifer behaves as a square-root type function, giving as a result a faster transmission of the tidal fluctuation. As it would be expected, the propagation velocity of the induced tide in the aquifer increases with b.

Fig. 4

Time-lag versus dimensionless distance ax for different rates of increase of hydraulic conductivity

In order to analyze the effect of unrealistic values of K predicted by Eq. (4) when x tends to infinity, an analytical solution for a finite aquifer of extension L is derived. In this case, Eq. (1) is solved in a finite domain with the tidal condition Eq. (2) and the following no-flow boundary condition in the right edge of the aquifer:

$$ K(x)\frac{{\partial h}}{{\partial x}} = 0,{ }in{ }x = L $$

(10)

Based on a similar reasoning to derive Eq. (5), it can be shown that the analytical solution of the boundary value problem defined by Eqs. (1), (2) and (10) is given by:

$$ h(x,t) = {\rm Re} \left[ {A\left( {{C_1}{J_0}(2\Lambda \sqrt {{1 + bx}} ) + {C_2}{Y_0}(2\Lambda \sqrt {{1 + bx}} )} \right){e^{{i\omega t}}}} \right] $$

(11)

where

$$ {C_1} = \frac{{ {{Y'}_0}(2\Lambda \sqrt {{1 + bL}} )}}{{{J_0}(2\Lambda ){{Y'}_0}(2\Lambda \sqrt {{1 + bL}} ) - {Y_0}(2\Lambda ){{J'}_0}(2\Lambda \sqrt {{1 + bL}} )}} $$

(12)

$$ {C_2} = \frac{{{{J'}_0}(2\Lambda \sqrt {{1 + bL}} )}}{{{J_0}(2\Lambda ){{Y'}_0}(2\Lambda \sqrt {{1 + bL}} ) - {Y_0}(2\Lambda ){{J'}_0}(2\Lambda \sqrt {{1 + bL}} )}} $$

(13)

with J ₀ and Y ₀ being the first and second kind Bessel functions of zero order.

Figure 5 shows how the amplitudes of induced head fluctuations change with the distance to the coast for both an infinite aquifer and finite aquifers of dimensionless extension aL = 10 and 30. In all cases, the hydraulic parameters of the aquifer are the same as those used in Fig. 2. It can be seen that with increasing of the extension aL, the amplitudes predicted by Eq. (11) quickly tend to the amplitude of the infinite aquifer given by Eq. (5). This test demonstrates that induced head fluctuations are mainly determined by the values of hydraulic conductivity near the coast and Eq. (5) is valid even though the values of K predicted by Eq. (4) are unrealistic.

Fig. 5

Amplitude versus dimensionless distance ax in log scale for finite and infinite aquifers

Asymptotic approximation of the exact solution

In this section, an approximate expression of the exact solution (Eq. 5) is obtained for relatively small rates of increase of hydraulic conductivity. The approximate analytical solution is valid for:

$$ b < < {2^{{7/2}}}a \approx 10a $$

(14)

For these values of b the arguments of the Hankel function of Eq. (5) satisfy:

$$ \left| {2\Lambda \sqrt {{1 + bx}} } \right| > > \frac{1}{4}{ },\quad \left| {2\Lambda } \right| > > \frac{1}{4} $$

(15)

and the following asymptotic approximations of H ⁽¹⁾₀ hold (Arfken and Weber 2005):

$$ H_0^{{(1)}}(2\Lambda \sqrt {{1 + bx}} ) \approx {\left[ {\pi \Lambda \sqrt {{1 + bx}} } \right]^{{ - 1/2}}}{e^{{i\left[ {2\Lambda \sqrt {{1 + bx}} - \frac{1}{4}\pi } \right]}}} $$

(16)

$$ H_0^{{(1)}}(2\Lambda ) \approx {\left[ {\pi \Lambda } \right]^{{ - 1/2}}}{e^{{i\left[ {2\Lambda - \frac{1}{4}\pi } \right]}}} $$

(17)

By replacing Eqs. (16) and (17) in Eq. (5), the following approximate solution is obtained:

$$ h(x,t) = A\frac{{{e^{{ - 2\frac{a}{b}\left( {\sqrt {{1 + bx}} - 1} \right)}}}}}{{{{\left( {1 + bx} \right)}^{{\frac{1}{4}}}}}}\cos \left[ { - 2\frac{a}{b}\left( {\sqrt {{1 + bx}} - 1} \right) + \omega t} \right] $$

(18)

Although the validity of Eq. (18) is limited to values of b given by Eq. (14), its mathematical expression is simple and can be used for a qualitative analysis of induced head fluctuations.

When the heterogeneity of the hydraulic conductivity is negligible, i.e., b → 0 it can be shown that Eq. (18) becomes:

$$ h(x,t) = A{e^{{ - ax}}}\cos \left[ { - ax + \omega t} \right] $$

(19)

which is the analytical solution obtained by Jacob (1950) for a homogeneous confined aquifer.

Figures 6 and 7 show the amplitudes and phase-lags, respectively, of exact and approximate solutions (Eqs. 5 and 18) for two different magnitudes of the rate of increase of hydraulic conductivity b. As it is expected, for a relatively small rate of increase (b = 10^–3 m^–1), the values of amplitude and phase-lag predicted by Eq. (18) are in excellent agreement with the ones of the exact solution Eq. (5). On the other hand, for b = 10^–1 m^–1, the condition (Eq. 14) is not satisfied and significant discrepancies are observed between values predicted by both analytical solutions.

Fig. 6

Amplitude of exact and approximate analytical solutions versus dimensionless distance ax

Fig. 7

Phase-lags of exact and approximate analytical solutions versus dimensionless distance ax

Conclusions

This technical note investigates tide-induced head fluctuations in a confined coastal aquifer whose hydraulic conductivity linearly increases with the distance to the coast. An exact analytical solution that predicts head fluctuations is derived in terms of a Hankel function. For small rates of increse of hydraulic conductivity, an approximate analytical solution with a simple mathematical expression is also obtained. In general terms, it can be concluded that the linear heterogeneity in hydraulic conductivity produces the following effects on the induced head fluctuations: (1) dampened amplitudes for distances less than the characteristic dampening distance 1/a, (2) enhanced amplitudes for increasing inland distances (x > 1/a) and (3) a faster transmission of the tidal effect with a time-lag that can be approximated with a square-root type function. Hypothetical examples show that the influence of the hydraulic conductivity heterogeneity can be significant and should be included in the study of coastal aquifers where this type of heterogeneity has been reported.

Appendix

Let H(x,t) be the solution of the following boundary value problem:

$$ \frac{\partial }{{\partial x}}\left( {{K_0}\left( {1 + bx} \right)\frac{{\partial H}}{{\partial x}}} \right) = {S_s}\frac{{\partial H}}{{\partial t}} $$

(20)

$$ H(0,t) = A{e^{{i\omega t}}} $$

(21)

$$ \mathop{{\lim }}\limits_{{x \to \infty }} K(x)\frac{{\partial H}}{{\partial x}} = 0 $$

(22)

Then, the solution of Eqs. (1)–(4) satisfies:

$$ h(x,t) = {\rm Re} \left[ {H(x,t)} \right] $$

(23)

where Re denotes the real part of the followed complex expression. In order to verify the boundary condition Eq. (21), H(x,t) must be expressed as:

$$ H(x,t) = AX(x){e^{{i\omega t}}} $$

(24)

where X(x) is a complex function.

Substituting Eq. (24) in Eqs. (20)–(22), the following boundary value problem is obtained:

$$ \frac{d}{{dx}}\left( {\left( {1 + bx} \right)\frac{{dX}}{{dx}}} \right) + {b^2}{\Lambda^2}X = 0 $$

(25)

$$ X(0) = 1 $$

(26)

$$ \mathop{{\lim }}\limits_{{x \to \infty }} (1 + bx)\frac{{dX}}{{dx}} = 0 $$

(27)

where:

$$ {\Lambda^2} = - i\frac{{\omega {S_s}}}{{{b^2}{K_0}}} = - i{ }2{\left( {\frac{a}{b}} \right)^2} $$

(28)

In order to find the general solution of Eq. (25), the following change of variables is proposed:

$$ u = 2\Lambda \sqrt {{1 + bx}} $$

(29)

where Λ = a(−1 + i) /b. Replacing Eq. (29) in Eq. (25) gives:

$$ {u^2}\frac{{{d^2}X}}{{d{u^2}}} + u\frac{{dX}}{{du}} + {u^2}X = 0 $$

(30)

The ordinary differential Eq. (30) is the zero order Bessel equation and its general solution can be written as (Abramowitz and Stegun 1965):

$$ X(u) = {C_1}{ }{J_0}(u) + {C_2}{ }{Y_0}(u) $$

(31)

where J ₀ and Y ₀ are the first and second kind Bessel functions of zero order, and C ₁ and C ₂ are complex constants.

Using asymptotic expressions for the derivatives of J ₀ and Y ₀ (Arfken and Weber 2005), it can be shown that the boundary condition Eq. (27) is satisfied when:

$$ \left( {{C_1} + i{C_2}} \right) = 0 $$

(32)

Then:

$$ X(u) = {C_1}{ }\left( {{J_0}(u) + i{ }{Y_0}(u)} \right) = {C_1}H_0^{{(1)}}(u) $$

(33)

where H ⁽¹⁾₀ is the Hankel function of zero order and first kind (Abramowitz and Stegun 1965). Now, imposing the boundary condition Eq. (26) to Eq. (33) yields:

$$ {C_1}{ = }{\left( {H_0^{{(1)}}(2\Lambda )} \right)^{{ - 1}}} $$

(34)

Then the solution of the boundary value problem Eqs. (25)–(27) is:

$$ X(x) = \frac{{H_0^{{(1)}}(2\Lambda \sqrt {{1 + bx}} )}}{{H_0^{{(1)}}(2\Lambda )}} $$

(35)

Finally, in virtue of Eqs. (23) and (24):

$$ h(x,t) = {\rm Re} \left[ {A\frac{{H_0^{{(1)}}(2\Lambda \sqrt {{1 + bx}} )}}{{H_0^{{(1)}}(2\Lambda )}}{e^{{i\omega t}}}} \right] $$

(36)

which is the exact analytical solution for the boundary value problem Eqs. (1)–(4).