Groundwater response to tidal fluctuations in wedge-shaped confined aquifers

Abstract

Most of the analytical solutions to describe tide-induced head fluctuations assume that the coastal aquifer has a constant thickness. These solutions have been applied in many practical problems ignoring possible changes in aquifer thickness, which may lead to wrong estimates of the hydraulic parameters. In this study, a new analytical solution to describe tide-induced head fluctuations in a wedge-shaped coastal aquifer is presented. The proposed model assumes that the aquifer thickness decreases with the distance from the coastline. A closed-form analytical solution is obtained by solving a boundary-value problem with both a separation of variables method and a change of variables method. The analytical solution indicates that wedging significantly enhances the amplitude of the induced heads in the aquifer. However, the effect on time lag is almost negligible, particularly near the coast. The slope factor, which quantifies the degree of heterogeneity of the aquifer, is obtained and analyzed for a number of hypothetical scenarios. The slope factor provides a simple criterion to detect a possible wedging of the coastal aquifer.

Résumé

La plupart des solutions analytiques destinées à décrire les variations de charge hydraulique induites par la marée supposent que l’aquifère côtier a une épaisseur constante. Ces solutions ont été appliquées à de nombreux problèmes pratiques en ignorant les possibles variations de l’épaisseur de l’aquifère, qui peuvent conduire à des estimations erronées des paramètres hydrodynamiques. Dans cette étude, une nouvelle solution analytique est présentée pour décrire les variations de charge hydraulique induites par la marée dans un aquifère côtier en forme de biseau. Le modèle proposé suppose que l’épaisseur de l’aquifère décroît avec la distance depuis le littoral. Une solution analytique de forme fermée est obtenue en résolvant un problème de valeur à la limite avec à la fois une méthode de séparation des variables et une méthode de changement de variables. La solution analytique indique que le biseau augmente significativement l’amplitude des charges hydrauliques induites dans l’aquifère. Cependant, l’effet sur le déphasage temporel est presque négligeable, particulièrement près du littoral. Le facteur de pente, qui quantifie le degré d’hétérogénéité de l’aquifère, est obtenu et analysé pour de nombreux scénarios hypothétiques. Le facteur de pente fournit un critère simple pour détecter un possible biseau de l’aquifère côtier.

Resumen

La mayoría de las soluciones analíticas para describir las fluctuaciones de la carga hidráulica inducidas por mareas asume que el acuífero costero posee un espesor constante. Estas soluciones han sido utilizadas en numerosos problemas prácticos, ignorando posibles cambios en el espesor del acuífero que pueden conducir a estimaciones erróneas de los parámetros hidráulicos. En este estudio, se presenta una nueva solución analítica para describir las fluctuaciones de la carga hidráulica inducidas por mareas en un acuífero costero acuñado. El modelo propuesto asume que el espesor del acuífero decrece con la distancia a la línea de costa. Una solución analítica cerrada se obtiene resolviendo un problema de contorno con los métodos de separación y de cambio de variables. La solución analítica muestra que el acuñamiento aumenta significativamente la amplitud de las carga hidráulicas inducidas en el acuífero. Sin embargo, el efecto sobre el desfasaje temporal es casi despreciable, particularmente cerca de la costa. El factor de pendiente, que cuantifica el grado de heterogeneidad del acuífero, se calcula y analiza para varios escenarios hipotéticos. Este factor provee un criterio simple para detectar un posible acuñamiento del acuífero costero.

摘要

大多数描述潮汐引起的水头波动的解析方法假定沿海含水层具有恒定的厚度。这些解决方法应用于许多实际问题中,忽略了含水层厚度的可能变化,可能导致错误的水力参数估算结果。在本研究中,介绍了一种新的描述楔形沿海含水层潮汐引起的水头波动的解析方法。提出的模型假定含水层厚度随着离开海岸线的距离而降低。通过采用变量分离法和变量变化法解决边界值问题获取了封闭式的解析方法。解析方法表明,楔入大大增强了含水层诱发水头的幅度。然而,时间滞后的影响几乎可以忽略,特别是在海岸附近。针对若干假设方案获取和分析了量化含水层非均质性程度的坡度因子。坡度因子提供了一个探测沿海含水层可能的楔入简单的标准。

Resumo

A maioria das soluções analíticas para descrever flutuações de carga induzidas por marés assumem que os aquíferos costeiros têm uma espessura constante. Essas soluções têm sido aplicadas em muitos problemas práticos, ignorando possíveis mudanças na espessura do aquífero, o que pode levar a estimativas errôneas dos parâmetros hidráulicos. Nesse estudo, uma nova solução analítica para descrever flutuações de carga induzidas por marés em um aquífero costeiro em forma de cunha é apresentada. O modelo proposto assume que a espessura do aquífero diminui com a distância da linha costeira. Uma solução analítica de forma fechada é obtida pela resolução de um problema de valores de contorno com ambos os métodos de separação de variáveis e mudança de variáveis. A solução analítica indica que o encunhamento aumenta significativamente a amplitude das cargas induzidas no aquífero. Entretanto, o efeito na defasagem do tempo é quase negligenciável, particularmente próximo à costa. O fator de inclinação, que quantifica o grau de heterogeneidade do aquífero, é obtido e analizado por vários cenários hipotéticos. O fator de inclinação fornece um critério simples para detectar um possível encunhamento do aquífero costeiro.

Introduction

The tide-induced method has become a very useful and practical tool for the estimation of hydraulic parameters in coastal aquifers (Carr and van der Kamp 1969; Trefry and Johnston 1998; Jha et al. 2003; Zhou 2008; Rotzoll et al. 2013; Zhou et al. 2015). Basically, this method consists of estimating the hydraulic diffusivity (hydraulic conductivity divided by specific storage) from the measurement and analysis of groundwater fluctuations induced by sea tides in wells located near the coastline. The tide-induced method is non-invasive and can be applied in coastal aquifers which are significantly affected by seawater intrusion or are located in highly polluted zones (Jha et al. 2003; Chattopadhyay et al. 2015). In these critical scenarios, the tide-induced method becomes an attractive alternative to the commonly used pumping tests. The interaction between coastal groundwater and sea tides has been extensively analyzed through analytical solutions. In the last decades, many analytical solutions to describe tide-induced head fluctuations have been obtained for a number of simplified aquifer models. Jacob (1950) and Ferris (1951) were the first to derive an analytical solution for a homogeneous confined aquifer that extends landward infinitely. This solution is simple and has been widely used for estimating hydraulic parameters in coastal aquifers (e.g. Carr and van der Kamp 1969; Rotzoll and El-Kadi 2008; Rotzoll et al. 2013; Zhou et al. 2015). However, the assumption of homogeneity of the aquifer has significant discrepancy from real aquifers, which may have spatial variations of the hydraulic properties or complex geometries of the aquifer layer (Li and Jiao 2003; Trefry and Bekele 2004).

The study of the heterogeneity of the hydraulic properties on tide-induced head fluctuations has been addressed by several researchers. Basically, three types of approaches have been employed in order to study such effects. The first approach, referred to as the sub-region model, assumes that the heterogeneous aquifer can be represented by homogeneous sub-regions (Wang et al. 2015). Trefry (1999) presented comprehensive solutions for an aquifer consisting of an arbitrary number of contiguous homogeneous zones subjected to sinusoidal linear boundary conditions. Guo et al. (2010) obtained an analytical solution for an aquifer comprising two homogeneous contiguous zones and fit the observed data in a heterogeneous coastal aquifer in Dongzhai Harbor, China. In contrast, the second approach to handle aquifer heterogeneity assumes a continuous function to describe spatial variations of hydraulic properties. In two recent works (Monachesi and Guarracino 2011; Guarracino and Monachesi 2014) analytical solutions for alluvial aquifers where the hydraulic conductivity increases linearly and quadratically with the distance to the coastline were derived. The third approach considers statistically stationary random fields and can provide estimates of the correlation scale and variance of aquifer transmissivity or conductivity distributions (e.g. Trefry et al. 2011).

Most analytical solutions assume a single aquifer (one layer) or an aquifer system composed of two or more layers with simple geometries. Li and Jiao (2001) study the effect of storage in an aquifer system consisting of a confined aquifer overlain by a semi permeable layer that terminates at the coastline. Li et al. (2008) solved the same problem for an aquifer system that extends infinitely under the sea. Geng et al. (2009) considered a single confined aquifer that extends a finite distance under the sea with its submarine outlet covered by a thin layer. More recently, Guarracino et al. (2012) analyzed the mechanical effects on tide-induced head fluctuation in a coastal aquifer system that extends a finite distance under the sea.

All the aforementioned works assume that the aquifer (or aquifer system) has a constant thickness. This hypothesis is not always valid because nonuniformity in aquifer thickness is commonly reported (Rotzoll et al. 2013; Masterson et al. 2015). Hantush (1962a) developed an approximate theory to describe water flow in aquifers of varying thickness showing that the effect of heterogeneity could be significant. To the authors’ knowledge, there are no analytical solutions that describe tide-induced head fluctuations in aquifers which have a non-uniform thickness.

In the case of volcanic islands or continental coastlines with shallow crystalline basement, sediments can be deposited near the coast forming wedge-shaped aquifers. These aquifers have a finite length and a thickness that increases from inland to coastline (e.g. Rotzoll et al. 2013; Trapp 1992). In general terms, the way in which the aquifer thickness decreases will depend on the deposition pattern and coastal morphology—for example, Hantush (1962b, c) proposes both linear and exponential laws to describe aquifer thickness in groundwater flow equations.

In this article, a finite wedge-shaped aquifer having a thickness that decreases quadratically with the distance to the coastline is assumed. An analytical solution that predicts the tide-induced head fluctuations is derived by solving a boundary-value problem combining the separation of variables method and the change of variables method. In order to explore the influence of the wedging on tide-induced head fluctuations, hypothetical examples are designed and analyzed. The degree of heterogeneity of the aquifer is quantified by calculating the slope factor, which provides a simple criterion to detect a possible wedging.

Mathematical model and analytical solution

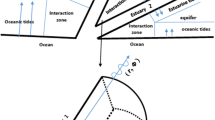
Let us consider a wedge-shaped confined aquifer of length L in contact with the sea as shown in Fig. 1. For the mathematical description of the problem, let the x-axis be perpendicular to the coastline, horizontal and positive landward, with the origin at the coastline. The datum of the induced head fluctuations is the mean water level. As it is mentioned in the ‘Introduction’, linear and exponential laws have been proposed to describe aquifer thicknesses (Hantush 1962b, c). In this study a quadratic law is proposed, which can be considered an intermediate between linear and exponential decreasing of the aquifer thickness. The quadratic law also allows to obtain a closed-form analytical solution for the tide-induced head fluctuation. The aquifer thickness b(x) (0 ≤ x < L) is assumed to decrease with the distance to the coastline according to the following law:

$$ b(x)={b}_{\mathsf{0}}{\left(1-\frac{x}{L}\right)}^2 $$

(1)

where b ₀ is the aquifer thickness at the coastline (x = 0).

Fig. 1

Schematic profiles of a wedge-shaped confined aquifer and a box-shaped confined aquifer (dashed line)

In order to derive an analytical solution, the following assumptions are made: the flow in the confined aquifer is horizontal and obeys Darcy’s law; the effect of density variations on water flow is neglected; the hydraulic conductivity K _s (LT⁻¹) and the specific storativity S _s (L⁻¹) are constant. According to these assumptions, tide-induced head fluctuations are described by the equation (Bear 1972):

$$ \frac{\partial }{\partial x}\left( T(x)\frac{\partial h}{\partial x}\right)= S(x)\frac{\partial h}{\partial t} $$

(2)

where h(x, t) is the groundwater head (L), t the time (T), T(x) = K _s b(x) the transmissivity (L²T⁻¹) and S(x) = S _s b(x) the storativity (−). Assuming that the sea tide can be described by a sinusoidal function, the boundary condition at the sea-aquifer interface (x = 0) can be expressed as:

$$ h\left(0, t\right)= A \cos \left(\omega t\right) $$

(3)

where A is the tidal amplitude (L) and ω the tidal angular frequency (T⁻¹). It is important to remark that since the differential problem is linear, solutions for multiple-constituents tides can be obtained using the superposition principle. At the inland edge of the aquifer (x = L) the following no-flow boundary condition is imposed:

$$ \underset{x\to L}{ \lim}\left( T(x)\frac{\partial h}{\partial x}\right)=0 $$

(4)

The exact analytical solution of Eqs. (2)–(4) can be obtained by re-writing the equations in complex form and using the separation of variables method and change of variables method. The exact analytical solution is as follows:

$$ \begin{array}{c} h\left( x, t\right)=\frac{Ap}{\left(1- x/ L\right)}\left\{{e}^{a x} \cos \left(\omega t+ a x\right)-{e}^{a\left(2 L- x\right)} \cos \left[\omega t+ a\left(2 L- x\right)\right]\right\}-\\ {}\kern1em \frac{Aq}{\left(1- x/ L\right)}\left\{{e}^{a x} \sin \left(\omega t+ a x\right)-{e}^{a\left(2 L- x\right)} \sin \left[\omega t+ a\left(2 L- x\right)\right]\right\}\end{array} $$

(5)

where

$$ p=\frac{1-{e}^{2 aL} \cos \left(2 aL\right)}{1-{e}^{2 aL} \cos \left(2 aL\right)+{e}^{4 aL}},\kern1em q=\frac{e^{2 aL} \sin \left(2 aL\right)}{1-{e}^{2 aL} \cos \left(2 aL\right)+{e}^{4 aL}} $$

(6)

being $a=\sqrt{\frac{\omega {S}_{\mathrm{s}}}{2{K}_{\mathrm{s}}}}$ the tidal propagation parameter (Li and Jiao 2001). The derivation of Eq. (5) is presented in detail in Appendix 1.

In the next section, the derived solution of Eq. (5) is discussed and compared with the analytical solution for a finite aquifer of constant thickness. Note that, taking the limit L → ∞ in Eqs. (5) and (6), h(x, t) tends to:

$$ h\left( x, t\right)= A{e}^{- ax} \cos \left(\omega t- ax\right) $$

(7)

which is the analytical solution obtained by Jacob for a constant thickness aquifer of infinite length.

Results and discussion

To explore the effect of wedging on tide-induced head fluctuations, hypothetical examples are designed and analyzed. As a first example, the predicted responses of the proposed model are compared with the ones obtained for an aquifer of the same length but with a constant thickness (box-shaped aquifer). A schematic profile of a box-shaped confined aquifer is shown in Fig. 1.

The exact analytical solution for this case is as follows:

$$ \begin{array}{c} h\left( x, t\right)= Ap\left\{{e}^{- a x} \cos \left(\omega t- a x\right)+{e}^{- a\left(2 L- x\right)} \cos \left[\omega t- a\left(2 L- x\right)\right]\right\}-\\ {} Aq\left\{{e}^{- a x} \sin \left(\omega t- a x\right)+{e}^{- a\left(2 L- x\right)} \sin \left[\omega t- a\left(2 L- x\right)\right]\right\}\end{array} $$

(8)

where

$$ p=\frac{1+{e}^{-2 aL} \cos \left(2 aL\right)}{1+{e}^{-2 aL} \cos \left(2 aL\right)+{e}^{-4 aL}},\kern1em q=\frac{e^{-2 aL} \sin \left(2 aL\right)}{1+{e}^{-2 aL} \cos \left(2 aL\right)+{e}^{-4 aL}} $$

(9)

Appendix 2 contains a detailed derivation of the analytical solution of Eq. (8).

In order to test Eqs. (5) and (8), it is assumed that both wedge-shaped and box-shaped aquifers have a length L = 150 m, hydraulic conductivity K _s = 50 m day⁻¹, specific storativity S _s = 3 × 10⁻³ m⁻¹ and hydraulic diffusivity D = K _s/S _s = 5 × 10⁴ m² day⁻¹. The sea tide is assumed to be semi-diurnal (period of 12.4 h) with amplitude A = 1 m. Figure 2 shows time variations of the tide-induced head fluctuations computed for three different distances from the coastline: x = 30 m, x = 75 m and x = 120 m. It can be observed that, in the three cases, the head fluctuations induced in the wedge-shaped aquifer have larger amplitudes than in the box-shaped aquifer. The effect on time-lags between sea tides and induced heads is less significant, but smaller time-lags are obtained in the wedge-shaped aquifer. Also note that the difference between the head fluctuations predicted by both models increases with the distance to the coast.

Fig. 2

Time variations of the tide-induced head fluctuations estimated for three different distances from the coastline. Sea tide is included in the figure

The previous example demonstrates that the effect of wedging on head fluctuations could be important and should be considered in order to correctly assess the hydraulic behavior of the aquifer. For a better understanding of this effect, the amplitude h _max and time lag t _lag as functions of the distance to the coastline are computed using the following expressions:

$$ {h}_{\max }(x)=\sqrt{y_{\mathrm{r}}^2(x)+{y}_{\mathrm{i}}^2(x)} $$

(10)

$$ {t}_{\mathrm{lag}}(x)=-\frac{1}{\omega}{ \tan}^{-1}\left(\frac{y_{\mathrm{i}}(x)}{y_{\mathrm{r}}(x)}\right) $$

(11)

where y _r(x) and y _i(x) are respectively the real and imaginary parts of the complex solution y(x) defined in Appendix 1 (solution of the differential problem Eqs. 18–20).

Figure 3 shows the amplitude and time lag for six different aquifer lengths using Eqs. (10) and (11). As a reference, the figure includes the curves of the Jacob model which is valid for a homogeneous aquifer of constant thickness and infinite length. As can be observed, the shorter the length of the aquifer, the higher the amplitude of the induced tide. The amplitude curves tend progressively to the Jacob model as the length of the aquifer increases. On the other hand, time-lag curves converge to the Jacob model near the coast. The range of convergence increases with the length of the aquifer (for example for L = 250 m, the predicted curve fits the Jacob model between 0 and 175 m).

Fig. 3

a Amplitude and b time lag versus distance to the coastline for different aquifer lengths. Jacob’s solution is represented by a red line

It is important to remark that, although the time-lag curves are coincident with the Jacob model near the coast, the amplitude curves of both models are significantly different (see Fig. 3). This behavior would lead to inconsistencies if diffusivity values are estimated from amplitude and time-lag data using the classical procedure based on Jacob model.

In order to quantify these inconsistencies, Trefry and Bekele (2004) introduce the slope factor (SF) defined by the following expressions:

$$ \mathrm{S}\mathrm{F}(x)=\sqrt{\frac{D_{\mathrm{amp}}}{D_{\mathrm{pha}}}} $$

(12)

$$ {D}_{\mathrm{amp}}=\frac{x^2\omega}{2{ \ln}^2\left[{h}_{\max }(x)\right]} $$

(13)

$$ {D}_{\mathrm{pha}}=\frac{x^2}{2\omega {t}_{\mathrm{lag}}^2(x)} $$

(14)

where D _amp and D _pha are the hydraulic diffusivities obtained from amplitude and time-lag data, respectively. For a homogeneous aquifer, tide-induced heads are described by the Jacob model, so the diffusivities D _amp and D _pha are equivalent and SF(x) is constant and equal to 1. For an inhomogeneous aquifer, the slope factor deviates from 1 and then it can be considered a measurement of the heterogeneity degree of the aquifer. Based on the analysis of different sets of data, Trefry and Bekele (2004) reported slope factor values that range from 0.3 to 2.1.

Figure 4 shows slope factor values obtained from Eqs. (12)–(14) for six different wedge-shaped aquifer lengths as functions of x. As a reference, the figure includes the slope factor curve for the Jacob model. It can be seen that, in all cases, slope factor values are greater than 1 and increase with the distance to the coastline. The slope factor curves gradually approach the Jacob model as the aquifer length increases. The use of the classical method in wedge-shaped aquifers can lead to significant errors in the estimation of hydraulic diffusivity—for example, for an aquifer length of 250 m, at x = 100 m, a difference of 86% in the estimation of diffusivity from time-lag and amplitude data is obtained.

Fig. 4

Slope factors versus distance to the coastline for different aquifer lengths. The Jacob solution is represented by a red line

Conclusions

In this study, a new analytical solution to describe the effect of the aquifer wedging on tide-induced head fluctuations has been derived. The aquifer is assumed to be finite with a thickness that decreases quadratically with the distance to the coastline. For this particular geometry, a simple closed-form analytical solution is obtained. This solution is compared with analytical solutions for both finite and infinite constant thickness aquifer models. The wedging produces a significant enhancement of the amplitude of tide-induced heads but a minor effect on time lag which remains linear near the coast. This behavior in amplitude and phase signals could be attributed to the common case of an aquifer of constant thickness (Jacob model) and may lead to a wrong estimation of hydraulic parameters. In these cases, the value of the slope factor can be used to predict a possible wedging of the aquifer.

Appendices

Appendix 1

Let H(x,t) be a complex function that satisfies the following boundary value problem:

$$ \frac{\partial }{\partial x}\left( T(x)\frac{\partial H}{\partial x}\right)= S(x)\frac{\partial H}{\partial t} $$

(15)

$$ H\left(0, t\right)= A{e}^{i\omega t} $$

(16)

$$ \underset{x\to L}{ \lim}\left( T(x)\frac{\partial H}{\partial x}\right)=0 $$

(17)

Because h(x,t) is the solution of Eqs. (2)–(4), it follows that h(x, t) = ℜ[H(x, t)], where ℜ denotes the real part of the complex expression. Substituting H(x, t) = y(x)e ^iωt into Eqs. (15)–(17) yields:

$$ \left(1-\frac{x}{L}\right)\frac{d^2 y}{{d x}^2}-\frac{2}{L}\frac{ d y}{ d x}- i2{a}^2\left(1-\frac{x}{L}\right) y=0 $$

(18)

$$ y(0)= A $$

(19)

$$ \underset{x\to L}{ \lim }{\left(1-\frac{x}{L}\right)}^2\frac{dy}{dx}=0 $$

(20)

where y(x) is a complex function.

In order to find the general solution of Eq. (18), the following change of variables is proposed:

$$ v(x)=\left(1-\frac{x}{L}\right) y(x) $$

(21)

Replacing Eq. (21) into Eqs. (18)–(20) gives:

$$ \frac{d^2 v}{{d x}^2}-2 i{a}^2 v=0 $$

(22)

$$ v(0)= A $$

(23)

$$ \underset{x\to L}{ \lim}\left(1-\frac{x}{L}\right)\frac{dv}{dx}+\frac{v(x)}{L}=0 $$

(24)

By solving Eqs. (22)–(24), one obtains Eq. (5) as the solution of the initial differential problem (Eqs. 2–4).

Appendix 2

In case of having a constant thickness aquifer of finite length, the problem stated by Eqs. (2), (3) and (4) reduces to:

$$ \frac{\partial^2 h}{\partial {x}^2}=\frac{S_s}{K_s}\frac{\partial h}{\partial t} $$

(25)

$$ h\left(0, t\right)= A \cos \left(\omega t\right) $$

(26)

$$ \underset{x\to L}{ \lim}\left(\frac{\partial h}{\partial x}\right)=0 $$

(27)

The solution h(x, t) can be obtained as h(x, t) = ℜ[H(x, t)], where H(x, t) satisfies:

$$ \frac{\partial^2 H}{\partial {x}^2}=\frac{S_s}{K_s}\frac{\partial H}{\partial t} $$

(28)

$$ H\left(0, t\right)= A{e}^{i\omega t} $$

(29)

$$ \frac{\partial H}{\partial x}=0 $$

(30)

Let us define H(x, t) = y(x)e ^iωt. In this case y(x) must verify:

$$ \frac{d^2 y}{d{ x}^2}-2 i{a}^2 y=0 $$

(31)

$$ y(0)= A $$

(32)

$$ \underset{x\to L}{ \lim}\frac{dy}{dx}=0 $$

(33)

The solution of the boundary value problem (Eqs. 31–33) is:

$$ y(x)= A\frac{\left({e}^{-2\left(1+ i\right) aL}{e}^{\left(1+ i\right) ax}-{e}^{-\left(1+ i\right) ax}\right)}{1+{e}^{-2\left(1+ i\right) aL}} $$

(34)

Finally, the following solution for the initial differential problem (Eqs. 25–27) is obtained:

$$ \begin{array}{c} h\left( x, t\right)= Ap\left\{{e}^{- a x} \cos \left(\omega t- a x\right)+{e}^{- a\left(2 L- x\right)} \cos \left[\omega t- a\left(2 L- x\right)\right]\right\}-\\ {} Aq\left\{{e}^{- a x} \sin \left(\omega t- a x\right)+{e}^{- a\left(2 L- x\right)} \sin \left[\omega t- a\left(2 L- x\right)\right]\right\}\end{array} $$

(35)

where

$$ p=\frac{1+{e}^{-2 aL} \cos \left(2 aL\right)}{1+{e}^{-2 aL} \cos \left(2 aL\right)+{e}^{-4 aL}},\kern1em q=\frac{e^{-2 aL} \sin \left(2 aL\right)}{1+{e}^{-2 aL} \cos \left(2 aL\right)+{e}^{-4 aL}} $$

(36)

Note that, as in the case of the wedge-shaped aquifer, taking the limit L → ∞, h(x, t) leads to Jacob’s solution (Eq. 7).