Introduction

From the hydrogeological point of view, tunnel construction brings two kinds of problems: the first is related to the forecast of water inflow location, and the second is related to the forecast of the drainage processes, discharge rate and water-table drawdown. Moreover, drained water can interfere with the superficial aquifers and cause water-table drawdown (Dematteis et al. 2001; Loew 2002), consolidation settlements (Zangerl et al. 2008a), extinction of springs and/or wells (Gisotti and Pazzagli 2001), changes in groundwater quality (Civita et al. 2002), changes in vegetation, changes in conditions of slope stability (Picarelli et al. 2002), and changes in the regime and quality of thermal waters (Gargini et al. 2008) and in the hydrological balance at basin scale (Gattinoni and Scesi 2006). When tunnels are drilled in fractured rock masses, it is difficult to forecast the water-inflow location or the drainage processes, because the hydraulic behaviour is neither homogeneous nor isotropic and the water flow is controlled by joint features (i.e. aperture, filling, roughness), joint dip and dip direction, fracturing degree (i.e. joint spacing, frequency and persistence, rock quality designation - RQD, unit rock volume - URV; Scesi and Gattinoni 2009; Gattinoni and Scesi 2007; Lee and Farmer 1993; Min et al. 2004; Snow 1969; Louis 1974), discontinuity connectivity (Long and Witherspoon 1985; Rouleau and Gale 1985; Meyer and Einstein 2002), and the lithostatic load (also depending on the tunnel depth), which can bring about great changes to the apertures of joints (Bandis et al. 1983; Bai et al. 1999; Liu et al. 2000).

Analytical solutions play an important role in the first and quick estimation of tunnel-inflow methods from the mirror image method proposed by Harr 1962 and the simple equation by Goodman et al. 1965, to the more complex ones by El Tani 2003 and Park et al. 2008, which consider a variable hydraulic load along the tunnel border. Yet, the analytical formulas are generally valid for homogeneous and isotropic aquifers. Cesano et al. (2003) proposed a heterogeneity index allowing a qualitative evaluation of tunnel inflows, whereas Perrochet and Dematteis (2007) proposed an extension for heterogeneous aquifers, but not anisotropic. However, rock masses are typically anisotropic and heterogeneous media, for which the traditional analytical solutions do not accurately predict tunnel drainage (Zhang and Franklin 1993; Fernandez and Moon 2010). Therefore, numerical simulations can help to analyse more complicated scenarios (Dunning et al. 2004; Gattinoni et al. 2008; Molinero et al. 2002; Hwang and Lu 2007; Zangerl et al. 2008b). Another alternative consists of integrating the two approaches (analytical and numerical) with the aim of modifying the traditional analytical methods for properly taking into account the rock-mass complexity, as recently done by Moon and Fernandez (2009), and providing an analytical method for estimating groundwater-inflow rate taking into account the water-table drawdown.

This study uses numerical model results in order to define correction factors applicable to most commonly used analytical formulas using the rock mass geo-structural properties. To this end, groundwater flow in the presence of tunnel drainage is initially simulated using a discrete fractures network approach (Cacas et al. 1990; Therrien and Sudicky 1996; Blessent et al. 2009). In particular, the distinct element numerical code UDEC (Itasca 2001) is used which facilitates a mechanical-hydraulic study in which the rock matrix is considered impermeable and the joints’ permeability depends on the mechanical deformation, which, in turn, is influenced by the water pressure inside the fractures. The simulation results allowed the analysis of the tunnel inflow and the water-table drawdown for different geo-structural characteristics (the number of joint sets and their orientation, spacing, aperture and persistence) and hydrogeological conditions (tunnel depth in comparison to the water table).

Afterwards, for the same configurations used in the numerical model, tunnel flow rates were calculated using the analytical formulas of Goodman et al. (1965) and El Tani (2003), valid for an infinite, homogeneous and isotropic aquifer. Modelling results and analytical formulas are compared; the latter generally greatly overestimate tunnel inflow, because they do not take into account the medium’s anisotropy and heterogeneity. Therefore some corrective coefficients are suggested, and applied to analytic formulas, so as to consider the geological-structural setting. This new empirical relation is then applied in the study of a case history concerning a medium-depth open tunnel, excavated in sedimentary rock masses.

Model description and implementation

To simulate the drainage processes in a fractured medium, an artificial rock mass was considered (consisting of a paragneiss lithotype or a sedimentary rock that is not fractured and karstified very much), crossed by 1–4 joint sets having variable orientations, spacing and apertures (Table 1). A rectangular domain was chosen (150 × 250 m2), to the right side of which a tunnel having a radius of 5 m and N–S direction (Fig. 1) was positioned. It is clear that this type of hypothesis implies the symmetry of the system. For each geo-structural setting considered in the simulations (Table 1), the hydraulic conductivity tensor \( \overline{\overline K} \) (Kiraly 1969) was calculated:

$$ \overline{\overline K} = \sum\limits_{{{\rm{i}} = 1}}^{m} {\frac{{a_{{\rm{i}}}^{3}{f_{{\rm{i}}}}}}{{12\mu }}} \overline{\overline {{A_{{\rm{i}}}}}} $$
(1)

where: m is the number of joint sets; a i, f i and \( \overline{\overline {{A_{{\rm{i}}}}}} \) are, respectively, the aperture (m), the average frequency (number of discontinuities per length unit in L/m) and the orientation tensor of the i-th joint set, μ is the water dynamic viscosity at 20°C (10–3 Pa × s). The hydraulic conductivity tensor allowed for better visualization of the medium’s anisotropy (Fig. 1), as well as calculation of the equivalent hydraulic conductivity (Louis 1974):

$$ {K_{{{\rm{eq}}}}} = {\left( {{K_{1}} \cdot {K_{2}} \cdot {K_{3}}} \right)^{{1/3}}} $$
(2)

where K 1, K 2 and K 3 are the principal components of the hydraulic conductivity tensor, previously defined.

Table 1 Joint dip direction/dip used in the modelling. K eq (m/s) is the equivalent hydraulic conductivity calculated for aperture at the land surface = 1.62 × 10–04 m and spacing = 8 m; K min /K max is the anisotropy ratio in the cross sections of the modelling domain; θ min the angle between K min direction and the horizontal plane
Full size table
Fig. 1
figure 1

Examples of modelling domains for some of the geo-structural settings listed in Table 1: a E/0°–W/90°, b E/45°–W/45°, c E/30°–W/30°, d E/60°–W/60°, e W/45°–W/80°, f E/0°–W45°, g E/30°–E/60°–W/30°–W/60°, h E/30°–W/30°–W10°. In the figure are shown: the tunnel position along the right border of the modelling domain, the joints (as dark lines), the hydraulic conductivity tensor ellipses (in light blue) with the corresponding main components K min and K max belonging to the same plane of the cross section

Full size image

The simulations were carried out using the UDEC code (Universal Distinct Element Code; Itasca 2001), a two-dimensional numerical program based on a distinct element method that simulates the response of discontinuous media subjected to static or dynamic loads, flows and thermal gradients. It is based on a Lagrangian calculation scheme, in which the rock mass is represented by a set of blocks interacting with each other only at the contact points; the behaviour of the whole is governed by the characteristics of the contacts (considered in the present study to be deformable) and of the block’s mechanical properties (considered in the present study to be rigid). To simulate the deformable nature of the contacts, a system of springs (having a known stiffness both in the normal and in tangential direction) is interposed between the rigid blocks. The UDEC code assumes blocks to be impermeable and the groundwater flows only through fractures. The groundwater flow in a joint depends on its hydraulic aperture a, which is, in turn, affected by pore-water pressure within the joint (hydro-mechanically coupled):

$$ a = {a_{0}} + {u_{{\rm{n}}}} $$
(3)

where a 0 is the joint hydraulic aperture at zero normal stress (i.e. in the surface) and u n the joint normal displacement. The algorithm matches the mechanical and hydraulic behaviour of the system: in fact, the aperture, and then the joint permeability, is related to the mechanical deformation, which, in turn, is influenced not only by the lithostatic load but also by water pressure in fractures. Generally, a minimum value a res is assumed for the aperture, below which mechanical closure does not affect the joint permeability. The flow rate is calculated (for edge-edge contact) using the following cubic law:

$$ q = - \frac{{{a^3}}}{{12\mu }} \cdot \frac{{\Delta p}}{l} $$
(4)

where μ is the dynamic water viscosity; a is the joint hydraulic aperture; l is the contact length; ∆p is the pressure change along the contact.

The parameters used for modelling are listed in Table 2. In the modelling, the joint stiffness values are considered independent from the effective normal stress, as the research was mainly oriented to study middle depth tunnels (at an average depth equal to 50 m corresponding to an average normal effective stress in the order of 1.5 MPa). However, the joint stiffness values were considered high enough to preclude differential joint displacement between blocks, which could bring about a local joint closure and a consequent uncontrolled rock-bridge formation (Zangerl et al. 2008c).

Table 2 Parameters used for modelling study
Full size table

The following boundary conditions were applied:

  • Impermeable boundary along the bottom and along the border of the tunnel location (right vertical boundary)

  • Constant load on the opposite side as regards the tunnel location (left vertical boundary)

  • No displacements on the bottom and along the groundwater supply boundary

  • Free hydraulic boundary conditions at the upper boundary of the modelling domain, simulating dry weather conditions

The following initial conditions were considered:

  • Lithostatic load with lateral (horizontal) pressure coefficient equal to 0.5

  • Hydrostatic load depending on the applied constant head boundary condition and complete saturation below the water table

The numerical simulations were carried out through a fully hydraulic-mechanical coupled approach. Because, in the present study, only the final steady-state conditions are of interest, a steady-flow option was chosen for the simulation, which therefore does not consider unsaturated flow. A no-flow boundary condition was applied to the tunnel, but the pore pressure (and the total radial stress too) along the tunnel is reduced to zero by the tunnel opening. This perturbation induces a drainage process into the discrete fractures network around the tunnel, bringing about a water-table drawdown, which is determined only from pore pressure.

Before carrying out the tunnel-inflow simulations, the dimension of the representative elementary volume (REV) was assessed (Bear and Berkowitz 1987). With this aim in mind, considering a constant hydraulic gradient, the water flow along fractures was simulated using UDEC code, varying the domain dimension. For each simulation, the steady-state flow rate was calculated and then the corresponding equivalent porous-medium hydraulic conductivity was calculated. In Fig. 2 an example of the obtained results is shown. It is possible to highlight that, after some initial fluctuations, the hydraulic conductivity reaches an asymptotic value, which corresponds to an average REV dimension (e.g. equal to 75 m for the cases in Fig. 2), always lower than the modelling domain dimension. By considering all the previously listed parameters and their related range of variation (Tables 1 and 2), more than 500 simulations were performed.

Fig. 2
figure 2

Example of the equivalent hydraulic conductivity of the whole domain, varying the domain dimension, for different geo-structural settings and spacings S (considering the same aperture equal to 2.04 × 10–4 m)

Full size image

Analysis of modelling results

During the modelling exercise, both the tunnel pre and post-excavation conditions were simulated until the steady-state condition was reached. At the end of each simulation, groundwater tunnel inflow and water-table drawdown along the tunnel axis were obtained. It is important to highlight that no recharge was considered in the numerical model, therefore the simulated radius of influence connected to the tunnel drainage process always coincides with the model domain dimension. In the following, the modelling results are discussed, analysing the influence of geo-structural parameters on the drainage processes and evaluating the sensitivity of the tunnel-water inflow and drawdown with respect to different parameters.

Influence of number of joint sets and their orientation

The simulation results (Fig. 3) show that for the same equivalent permeability, the tunnel water inflows vary with the varying number of joint sets and structural conditions (Fig. 3). In particular, the number of joint sets governs the degree of fracturing (Fig. 3a): for only one joint set the average unitary rocky volume (URV) is between 50 and 1,200 m3/m, while for two joint sets, the average URV comes down to values between 10 and 300 m3/m. Moreover, from one to several joint sets, the interconnection degree (as defined by Rouleau and Gale 1985) increases: with a single joint set the interconnection degree is obviously zero, while with two joint sets, with a spacing equal to 20 m, interconnection degree is higher than unity.

Fig. 3
figure 3

Trend of the tunnel inflow versus the equivalent hydraulic conductivity (K eq ) of the rock mass for different joint sets and orientations, considering the water table at 50 m above the tunnel. In a geo-structural settings having a different number of joint sets are shown, whereas in b only the influence of joint orientation is shown (for a number of joint sets always equal to two). The graphs show that for the same K eq of 10–7 m/s, the simulated water inflows range from values less than 10–10 m3/s in the presence of a single joint set, to values of 5 × 10–7 m3/s in the presence of two conjugate joint sets having a dip equal to 80°, to values higher than 10–6 m3/s for two conjugate joint sets having a dip of 30°

Full size image

It is also clear that the joints’ orientation plays an essential role in that:

  • It governs the orientation of the permeability tensor because, in saturated media, the tunnel water inflow has a predominantly horizontal trend and discontinuities with a very low dip favour the drainage processes thereby increasing the tunnel water inflow (Figs. 3b and 4).

  • It influences the degree of fracture interconnection. In the examples given in Fig. 3a, the interconnection degree of families having a dip equal to 30° is triple that of the interconnection degree where there are two families with a dip equal to 80° (spacing being equal).

Fig. 4
figure 4

Trend of the a tunnel inflow and b water-table drawdown along the tunnel axis versus the discontinuity frequency (surface aperture kept constant) for several symmetrical geo-structural settings, characterized by two joint families with different dips. Discontinuities with very low dip favour the drainage processes thereby increasing the tunnel-water inflow, but for joint dips lower than 30° (i.e. E/10°–W/10° and E/20°–W/20°) the flow rates decrease, as a consequence of the decrease of the degree of interconnection of the joint sets. On the other hand, joints having an orientation approximately perpendicular to the direction of the water flow (sub-vertical) cause a decrease of flow rates, associated with a greater drawdown

Full size image

Influence of joint spacing

The sensitivity analysis, carried out in relation to the discontinuity spacing, shows that by increasing the degree of fracturing (high frequency and low spacing), both tunnel inflow and drawdown obviously increase (Figs. 4 and 5). This pattern confirms the validity of the model. The most interesting result is that, for the same joint aperture, the growth rate of the discharge with the frequency substantially depends on the discontinuities’ orientation (Fig. 4).

Fig. 5
figure 5

Trend of the tunnel inflow versus: a the joint frequency, for several values of aperture at the land surface (a in m) in the case of two conjugate joint families having dip equal to 30° (The red dotted line indicates a joint frequency corresponding to a spacing equal to the tunnel radius), and b the joint aperture at the land surface for several values of spacing (s in m) in the case of two joint families having a dip respectively equal to 0 and 90°. The points are the simulated values, for which the lines show the trend. The growth in part b follows a power law, which is closely related to the equivalent permeability increasing with the aperture, as well as with the joint spacing

Full size image

Influence of joint aperture and tunnel depth

The simulations show the increase in tunnel-water inflow with the increase of maximum joint aperture at the land surface (Fig. 5b). The hydro-mechanical coupled simulations carried out showed that the hydraulic aperture, defined in Eq. (3), and then the tunnel inflows decrease with depth following a typical exponential law, whose pattern also depends on the geo-structural characteristics of the rock mass (Fig. 6).

Fig. 6
figure 6

a Aperture and b tunnel inflow, decreasing with the depth for several geo-structural settings, considering the same joint spacing (equal to 8 m). The drainage process was simulated for varying tunnel depth, always maintaining the same initial piezometric load above the tunnel axis

Full size image

In particular, for small depths (less than 150 m), the tunnel-inflow trend is well approximated to a linear function, while for greater depths the reduction of the hydraulic joint aperture also determines a sharp reduction of the discharge, until reaching an asymptotic value, having a magnitude depending on the chosen value of the residual hydraulic aperture (in Fig. 6 , a res = 0.6 × 10–04 m).

Influence of hydraulic load

Many simulations were realized by keeping a constant water table, coinciding with the soil surface, along the left domain boundary and by varying the tunnel depth. In this way, it was possible to assess simultaneously the influence of the hydraulic and the lithostatic load. The numerical results showed that the increasing of the water inflows and of the water-table drawdown with greater hydraulic load is strongly influenced by the geo-structural conditions (Fig. 7). In particular, for geo-structural conditions characterized by a high permeability in the horizontal direction, the tunnel-water inflow reaches a peak value at depth of about 100 m (Fig. 7a). Then it slightly decreases, maybe because of the aperture reduction due to the lithostatic load.

Fig. 7
figure 7

Trend of a the tunnel inflow and b the water-table drawdown with the hydraulic load increase, with reference to different geo-structural settings (for the same joint aperture and spacing). The red dotted line in Fig. 7b shows a water-table drawdown equal to the initial water-table level above the tunnel

Full size image

As regards the trend of the water-table drawdown (Fig. 7b), despite the upward trend for increasing hydraulic loads, it is important to note that the values obtained from numerical modelling are well below those assumed by traditional analytical formulas (primarily the relation of Goodman), which consider a drawdown equal to the initial hydrostatic load above the tunnel. In more detail, for high hydraulic loads (greater than 60–70 m), the simulated water-table drawdown is between 65 and 80% of the initial load, while for lower loads, the simulated water-table drawdown is of the order of 25–60% compared to the initial one. The greatest drawdown is observed in the geo-structural conditions characterized by a high permeability along the vertical direction, especially for lower hydraulic loads.

Influence of joint persistence

In the UDEC code, the persistence is controlled through the two following joint set parameters:

  • The trace length of joint segment of the i-th family l i

  • The gap length between joint segments (corresponding to the rock bridge length) of the same i-th family g i

The joint persistence of the i-th family can be then calculated using the following relation:

$$ persistenc{e_{{\rm{i}}}} = \frac{{{l_{{\rm{i}}}} - {g_{{\rm{i}}}}}}{{{l_{{\rm{i}}}}}} $$
(5)

The trace and the gap length are defined both in terms of mean geometric properties and in terms of standard deviation of random fluctuation about the mean. In particular, a standard deviation equal to 20% of the mean value was considered to be a uniform probability distribution.

Sometimes, especially for high values of the gap length and low values of the joint trace length, the generated joint network was characterized by no joints intersecting the tunnel, so that the tunnel inflow was equal to zero. The problem was evidently related to the randomness of the generated joint network. Finally, to have results comparable to each other, a completely interconnected sub-domain (having gap equal to zero) was inserted around the tunnel. The dimension of this sub-domain (equal to 15 × 20 m2) was chosen on the basis of a sensitivity analysis, minimizing its influence on the simulated tunnel inflow (Fig. 8).

Fig. 8
figure 8

Tunnel inflow versus the completely connected sub-domain dimension for a geo-structural setting having two conjugate joint sets (E/30°–W/30°), spacing equal to 8 m, joint length equal to 80 m and gap equal to 8 m. In the figure, a great increase of the tunnel inflow for an increasing of the sub-domain dimension from 0 to 10 m is evident, whereas for a larger sub-domain dimension, only a small fluctuation of the tunnel-inflow values can be observed

Full size image

Simulation results show that the tunnel inflow decreases with the gap length increase and the joint trace length decrease (Fig. 9), corresponding to a decrease in joint persistence. Yet, from a hydraulic point of view, the flow rate in a fractured network is mainly controlled by joint connectivity, depending not only on joint spacing and orientation, but also on joint persistence. For this reason, an interconnectivity probability p from the percolation theory was also considered. This latter was calculated as the ratio between the node’s number in the partially connected domain and the corresponding node’s number for a fully interconnected domain having the same geo-structural characteristics (Berkowitz and Balberg 1993). Obviously, the tunnel inflow increases with the interconnectivity probability, with a trend approximately linear (Fig. 10). The tunnel inflows show an abrupt change in their values (even for several orders of magnitude) for an interconnectivity probability between 0.5 and 0.6, corresponding to the critical probability p c. Below this percolation threshold the flow can be considered localised and, then, it no longer contributes to the tunnel inflow.

Fig. 9
figure 9

Trend of the tunnel inflow: a versus the joint gap for different values of joint trace length expressed in m (gap equal to zero corresponds to a completely interconnected fractures network); b versus the joint trace length for different values of the gap. All the results correspond to a geo-structural setting characterized by two conjugate joint sets (E/30°–W/30°) and spacing equal to 8 m

Full size image
Fig. 10
figure 10

Trend of the tunnel inflow versus the interconnectivity probability for different geo-structural settings, considering a spacing equal to 8 m

Full size image

Comparison between numerical modelling and analytical formulas

For the same configurations used in the numerical modelling, the tunnel water inflow was calculated using the analytical formulas of Goodman et al. (1965) and El Tani (2003):

$$ Q = \frac{{2\pi KL\left( {H - h} \right)}}{{\ln \left( {\frac{{2H - 2h}}{r}} \right)}} $$
(6)

(Goodman et al. 1965)

$$ Q = 2\pi KL\frac{{{\lambda^2} - 1}}{{{\lambda^2} + 1}} \cdot \frac{{\left( {H - h} \right)}}{{\ln \lambda }} $$
(7)

(El Tani 2003)where:

$$ \lambda = \frac{{\left( {H - h} \right)}}{r} - \sqrt {{\frac{{{{\left( {H - h} \right)}^2}}}{{{r^2}}}}} - 1 $$
(8)

K is the equivalent hydraulic conductivity, L the tunnel length, H the depth of the tunnel centre from the water table, h the hydraulic head into the tunnel, and r the tunnel radius. The applicable conditions of these equations, similar to those imposed in the numerical model, are then compared with results obtained from the parametric modelling. In order to apply these equations, the equivalent hydraulic conductivity of the rock mass at the tunnel depth was considered—calculated with Eq. (2). The comparison showed that the El Tani equation provides a better estimate than the more simplified Goodman’s relation, but the trend of the two equations is very similar; for this reason only the Goodman’s equation results are discussed in the following.

Fully interconnected-joints network

The comparison between the modelling results and those obtained through the use of the Goodman analytical formula shows that the Goodman results significantly overestimate the tunnel-water inflow and that the greater this overestimation, the higher the joint dip (Fig. 11). As it is possible to observe in the graph of Fig. 11, the simulated water inflow can be fitted as a function of the tunnel-water inflow calculated with the analytical relations. To achieve this, an exponential function has to be defined whose coefficients depend on the geo-structural characteristics.

Fig. 11
figure 11

The points represent the simulated (UDEC) tunnel inflow versus the inflow calculated with the Goodman equation for different geo-structural settings (characterized by two joint families and changing dip). The continuous lines arise from the power regression of the simulated values. The corresponding regression coefficients (R 2) and hydraulic conductivity ellipses are shown in the graph. The black dotted line indicates a perfect correlation

Full size image

Therefore, only the results obtained from a comparison of flow rates simulated by UDEC and those calculated with the Goodman’s analytic formula are reported. Based on this comparison, an empirical relation able to estimate the tunnel water inflow was pointed out, with particular reference to the case of depth below 150 m. For this depth it is possible to observe an increasing dependence of the drainage processes on the structural setting.

Based on the exponential performance highlighted in Fig. 11, the following relation was defined:

$$ Q = {\hbox{a}}Q_{{\rm{G}}}^{{\rm{b}}} $$
(9)

where Q (m3/s) is the actual tunnel inflow, Q G (m3/s) is the tunnel inflow calculated with the Goodman’s equation, a and b are empirical dimensionless coefficients depending on:

  • The joint dip

  • The hydraulic conductivity anisotropy ratio

  • The orientation of the hydraulic conductivity tensor

To determine the coefficients a and b the following parameter F was empirically defined:

$$ F = \frac{{\sum\limits_{{{\rm{i}} = 1}}^{{\rm{m}}} {\cos {\alpha _{i}}} }}{m}{\left( {\frac{{{K_{{\min }}}}}{{{K_{{\max }}}}}} \right)^{{0.5\varphi }}} $$
(10)

where m is the number of joint sets, α i is the dip of the i-th discontinuity set, K min and K max are respectively the minimum and maximum components of the hydraulic conductivity tensor, while φ can assume the following values:

$$ \phi = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { - 1} & {i\begin{array}{*{20}{c}} f & {{\theta _{{\min }}} > 45^\circ } \\\end{array} } \\\end{array} } \\{\begin{array}{*{20}{c}} 1 & {i\begin{array}{*{20}{c}} f & {{\theta _{{\min }}} \leqslant 45^\circ } \\\end{array} } \\\end{array} } \\\end{array} } \right. $$
(11)

where θ min is the angle between the K min direction and the horizontal plane. The empirical dimensionless coefficients a and b are then defined as a function F (Fig. 12):

$$ b = \ln 3.463{F^{{0.0342}}} $$
(12)
$${\text{a}} = \left\{ {\begin{array}{*{20}c} {{\begin{array}{*{20}c} {{3.448F^{{0.8834}} }} & {{\begin{array}{*{20}c} {{if}} & {{F < 0.737}} \\ \end{array} }} \\ \end{array} }} \\ {{\begin{array}{*{20}c} {{3.2411F^{{0.6805}} }} & {{\begin{array}{*{20}c} {{if}} & {{F \geqslant 0.737}} \\ \end{array} }} \\ \end{array} }} \\ \end{array} } \right.$$
(13)

whereas, the empirical equation thus obtained was verified considering both symmetric and asymmetric geo-structural setting conditions, with an average overestimation less than 10% (Fig. 13).

Fig. 12
figure 12

Trend of the empirical coefficient a a and b b versus the coefficient F. Simulations refer to the results of numerical simulations used to set out the coefficients a and b. The simulations 1 and simulation 2 series are the numerical results for values of F, respectively, less and more than 0.737. Verification series refers to numerical simulations carried out to verify the results of the empirical formula both in symmetric and asymmetric geo-structural conditions

Full size image
Fig. 13
figure 13

Trend of the tunnel inflow calculated through the empirical formula compared to the tunnel inflow obtained by the numerical modelling in several geo-structural conditions (both symmetrical and asymmetrical)

Full size image

Partially interconnected-joints network

Afterwards, the empirical formula obtained for the fully interconnected-joints network was extended to partially interconnected networks, on the basis of the interconnectivity probability p previously defined:

$$ Q = {p^{{\rm{n}}}}{\hbox{a}}Q_{{\rm{G}}}^{{\rm{b}}} $$
(14)

where a and b are the same coefficients defined for the fully interconnected network, p the interconnectivity probability previously defined and n an empirical coefficient set out from the numerical results. The comparison between numerical results for the partially interconnected network and the tunnel inflow calculated with the empirical formula for different values of the exponent n highlighted that the best estimation is achieved for n = 2 (Fig. 14). Equation (11) is valid only for p ≥ 0.6; actually, when p is lower than this percolation threshold (p < p c), the flow is localised and it does not contribute to the tunnel inflow.

Fig. 14
figure 14

Trend of the tunnel inflow in a partially interconnected-fractures network calculated through the empirical formula, considering an exponent n = 2, compared to the corresponding tunnel inflow obtained by the numerical modelling in several geo-structural conditions

Full size image

Application to a real case

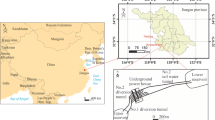
The empirical equation obtained from the analysis of the numerical modelling results was later applied in a real case (Bergamo District, northern Italy). A small diameter tunnel, located at a medium depth, and drilled within sedimentary rocks (mainly flysch of the Lombardy Series), characterized by a medium-low hydraulic conductivity, was analyzed. The open tunnel is below the water table for a length of 5.5 km and it was divided into eight hydrogeological and geo-structural homogeneous stretches (Fig. 15). For each one, the hydraulic conductivity tensor and the corresponding surface equivalent hydraulic conductivity, relative to saturated rock mass, were calculated based on the geo-structural survey (Table 3).

Fig. 15
figure 15

Geological cross section along the tunnel (shown as the dark line) in Bergamo District, northern Italy. The blue line is the water table. The numbers 1–8 indicate the homogeneous stretches in which the tunnel was divided, for which the hydraulic conductivity ellipses (in the plane orthogonal to the tunnel axes) are shown

Full size image
Table 3 Main characteristics of the different stretches in which the tunnel in Bergamo District (northern Italy) was divided, useful for the following estimation of the water inflows. 1–8 refers to the divisional stretches
Full size table

Integrating this information with the results of 20 pumping tests (carried out in transient state and with a constant rate at different depths), it was also possible to consider the decrease of permeability with depth. For the tunnel-inflow calculation, the equivalent hydraulic conductivity at the tunnel depth was then considered. The hydraulic conductivity ellipses (Fig. 15), in the vertical plane (orthogonal to the tunnel direction), were determined by projecting the main hydraulic conductivity directions of the hydraulic conductivity tensor previously calculated. They show a considerable medium anisotropy, in particular, in stretches 2, 4 and 6; the main component of the hydraulic conductivity is almost vertical.

From the geo-structural and hydraulic characterization of the medium, it was possible to calculate the tunnel-water inflow in each homogeneous stretch, both with the Goodman’s equation and with the new empirical relation previously described. The results were compared with the tunnel-monitoring data, arising from the flow rate measured in the tunnel channel at different tunnel distances.

The monitoring data allowed for calculation of the tunnel inflow in the different stretches as the difference between the channel flow rate in the upstream and downstream sections. The results comparison (Fig. 16) showed that the Goodman’s equation provides highly overestimated values of the tunnel-water inflow, especially in those sections where the rock mass anisotropy is higher, with maximum hydraulic conductivity in the direction close to the vertical.

Fig. 16
figure 16

Comparison between the tunnel inflows observed during the monitoring at the Bergamo tunnel (in green), the ones calculated through the Goodman equation (in blue) and through the empirical relation (in red)

Full size image

This overestimation is effectively corrected by using the empirical relation proposed, which, in the case study, provides values comparable to those actually observed in the tunnel (Fig. 16). These results confirm the importance of considering the discontinuous nature of the medium, with particular reference to its structural setting.

Conclusions

The study aimed to define correction factors applicable to most commonly used analytical formulas for tunnel-inflow assessment, taking into account the rock-mass geo-structural setting. The flow parametric model allowed for identification and quantification of the influence of different parameters (number and orientation of joint sets, joint spacing and aperture, tunnel depth, hydraulic load) on the tunnel-water inflow and water-table drawdown. The results show that the joint spacing and aperture are the parameters that mainly control the tunnel discharge; this dependency can still be efficiently reproduced in a single parameter, that is, the equivalent hydraulic conductivity, which is dependent on the joint spacing and aperture.

But the most interesting result is the observation that the tunnel inflow depends on the geo-structural setting of the rock mass, even if the REV (representative elementary volume) is smaller than the modelling domain size. In particular, the faster the tunnel-flow rate increases with the equivalent hydraulic conductivity of the rock mass, the lesser is the joint set dip. This trend can be fitted with a linear equation, characterized by a growing rate dependent on the geo-structural setting. It is, therefore, obvious that one of the factors that most influences the drainage process, but that is rarely included with a traditional analytical approach, is the geo-structural setting. According to these observations, the numerical modelling results were compared with the results obtained by the more traditional analytical formulas, and a method to adapt the simple analytical equations to the geo-structural characteristics of the rock mass was derived.

In order to achieve the project objective, a large number of numerical simulations, performed for different geological and structural conditions, was needed, which allowed for a database large enough to calibrate a correction to the Goodman’s relation, and to define a new empirical equation in which the tunnel-inflow explicitly depends on the geological and structural setting of the rock mass. This equation has, so far, been calibrated considering an average tunnel depth equal to 50 m, corresponding to an average normal effective stress in the order of 1 – 2 MPa, and a rock mass having high joint stiffness values, in which the complete closures of the joints is prevented. The equation, obtained for a fully interconnected-fractures network, was also extended to a partially interconnected network, through a multiplicative coefficient related to the interconnectivity probability. Finally, it was possible to compare the results obtained using the defined relation and the traditional formulas in a case history with the tunnel monitoring data. The conclusion reached was that the results obtained using the defined relation correspond very well to the monitoring data, especially in the tunnel stretches where the rock mass is greatly anisotropic.

The research offers starting points for further development and in-depth studies such as:

  • Evaluation of the influence of joint stiffness (and thus the joints closure), which in this phase of the study was considered constant with depth (not dependent on the normal effective stress) and particularly high

  • Analysis of the tunnel inflow in transient state, which requires a continuous monitoring of the flow rates for the calibration of the numerical model