Empirical model for estimating groundwater flow into tunnel in discontinuous rock masses

Abstract

The high volume of water inflow into tunnel plays a significant role in the design of drainage systems and exerts bio-environmental effects. In engineering practice, analytical and empirical methods that are commonly used to estimate water inflow in sedimentary rock masses, lack sufficient accuracy. The geostructural anisotropy in a fractured rock has a great impact on water inflow. In discontinuous media, anisotropy and heterogeneity of the fractured rock masses are highlited. Hence, these methods are not efficient to calculate water inflow to tunnel in such media, due to the assumed isotropic hydraulic coefficient. In this regard, an empirical formula is developed in this study for hydraulic conductivity in the fractured rock masses for analytical methods, alternately used to predict water inflow. To achieve this, a discrete network flow model was performed. The simulation resulted in a dataset that is helpful in developing hydraulic conductivity empirical formula for well-known Goodman equation. The geostructural parameters, such as the joint orientation, aperture, spacing and joint interconnectivity were included to determine this formula. The acquired empirical equation was utilized in the evaluation of groundwater inflow to middle-depth Amirkabir tunnel in north of Iran. In comparison to the observerd flow, analytical methods resulted in higher overestimation, especially in the sites with high anisotropy. However, empirical model led to a better estimation of water inflow to tunnel.

Introduction

Water inflow into tunnels is one of the most challenging issues in rock tunneling, which flows through initial discontinuities and/or is created in tunnel walls. This causes some impediments in progress of tunneling, such as decrease in rock mass stability, extra pressure exerted on permanent and temporary stability systems, destructive effects on geo-mechanical condition of rock, and finally physical and economical disasters (Holmoy and Nilsen 2014). According to Palmstrom and Stille (2007), water inflow is the main issue in the underground excavation, and many factors such as the rock mass permeability and environmental conditions play important roles in this scenario.

As it is impossible to identify all the factors that affect water inflow into tunnels, especially during drilling, it is difficult to anticipate the exact amount of seepage into tunnels. Therefore, analytical methods are mostly used to calculate seepage rate into tunnels because of simplifying assumptions. Some important investigations have been carried out to calculate water inflow into tunnels. Specific solutions have also been used effectively to manage different situations. Ribacchi et al. (2002), for example, introduced a solution for lining tunnel, providing that the hydrostatic load is constant along the tunnel border. Considering the Jacob and Lohman (1952) solution, Marechal and Perrochet (2003) modelled transient groundwater discharge into deep tunnels. El-Tani (2003) used a Mobius transformation and Fourier series to present an analytical solution for a semi-infinite isotropic and homogeneous aquifer drained by a circular tunnel. Park et al. (2008) presented a closed-form analytical solution for the steady-state groundwater inflow into a drained circular tunnel with focus on different boundary conditions. Also, El-Tani (2010) deliberated an analytical equation for a semi-infinite aquifer drained by a circular tunnel in different heterogeneous aquifer settings using a modified Helmholtz equation.

Analytical equations are developed based on the Darcy’s Law and mass conservation (Liu et al. 2012). They consist of parameters like rock mass permeability, water table, tunnel radius, etc. These solutions are invalid under the following conditions:

• 1. Water inflow around the tunnel is vertical,

• 2. Rock mass bedding around the tunnel is very variable,

• 3. Rock mass permeability cannot be exactly identified.

Although still the analytical equations are universally valid for homogeneous and isotropic aquifers but Cesano et al. (2003) proposed a heterogeneity index allowing a qualitative evaluation of groundwater flow into tunnel, whereas Perrochet and Dematteis (2007) recommended an extension for heterogeneous aquifers. However, rock masses are typically anisotropic and heterogeneous media, for which the traditional analytical solutions do not accurately predict water inflow (Zhang and Franklin 1993; Fernandez and Moon 2010). Nevertheless, Gattinoni and Scesi (2010) using numerical simulation and defining special geometrical characteristics of the tunnel and model developed an empirical correction to the analytical formula (Goodman equation) for estimating groundwater flow into tunnel in fractured rock.

In spite of analytical methods, which are a total estimation of seepage, with attention to basic equations of seepage flow and site characteristics, with applications of numerical methods such as Finite Element Method FEM and Discrete Element Method DEM, water inflow into tunnel can be modeled and then seepage into tunnel in various situations in site can be calculated (Coli and Pinzani 2012).

Unlike analytical methods, these methods are difficult in calculation. Also, they require comprehensive data about the site. Moreover, there are less simplifications and assumptions in these methods. Numerical methods are very complex and application of them is time consuming, however, the results are more precise in comparison to Analytical methods. Numerical simulations, therefore, can help to analyse more complicated situations (Dunning et al. 2004; Gattinoni et al. 2008; Molinero et al. 2002; Hwang and Lu 2007; Zangerl et al. 2008; Gattinoni and Scesi 2010; Butscher 2012; Garzonio et al. 2014).

In this study, numerical model results were used in order to define an empirical relation for calculation of equivalent hydraulic conductivity for the most commonly used analytical formulas using the rock mass geostructural properties. To do this, a discrete fractures network approach was used to simulate the groundwater flow into the tunnel (Cacas et al. 1990; Therrien and Sudicky 1996; Blessent et al. 2009).

In order to facilitate mechanical hydraulic study, the universal distinct element code UDEC (Itasca 2011) was used. The distict element code has the capability to perform the analysis of fluid flow through the fractures of a system of impermeable blocks. A fully coupled hydraulic mechanical analysis could be performed in which fracture conductivity is dependent on mechanical deformation and, conversely, fracture water pressure affect mechanical behavior (Alejano 2014). The simulation results allowed the analysis of the tunnel inflow for different geostructural characteristics (joint sets orientation, spacing, aperture, length and gap) and hydrogeological conditions (tunnel depth in comparison to the water table).

Afterwards, for the same configurations used in the numerical model, tunnel groundwater inflow rates were calculated using the analytical formula of Goodman et al. (1965), valid for an infinite, homogeneous and isotropic aquifer. Model results and analytical formula are compared; not taking into account the anisotropy and heterogeneity of the media, the latter greatly overestimates tunnel inflow. Therefore modified hydraulic conductivity formula should be applied to analytic solutions while considering the geological structural setting.

Materials and methods

General

2-D and 3-D simulation of the flow of each single discontinuity is possible by means of disceret models (Long and Witherspoon 1985; Robinson 1982; Hung and Evans 1985; Rasmussen 1988; Andersson and Dverstorp 1987; Dverstorp and Andersson 1989) using the Navier–Stokes equation (Bear 1993), Kirchoff’s laws for electric circuits (Kraemer and Haitjema 1989) or the model with hydraulically connected circular disks (Cacas et al. 1990). Simulation of the flow in the presence of a series of interconnected bond in two-dimensional model is the simplest form in which the hydraulic head of each site is computed as a weight average of the adjacent sitesʼ hydraulic head, each one multiplied by a transmissivity coefficient N _ij which is related to the flow between the site i and the site j (Fig. 1):

$$H_{0} = \left( {N_{10} H_{1} + N_{20} H_{2} + N_{30} H_{3} + N_{40} H_{4} } \right)/\left( {\Delta N} \right)$$

(1)

If transmissivity T ₁ is equal to T ₂

$$N_{12} = T_{1} = T_{2}$$

(2)

Assuming T ₁ as infinite

$$N_{12} = 2T_{1}$$

(3)

N ₁₂ is the harmonic mean of T ₁ and T ₂, if their values are different:

$$N_{12} = \left( {2T_{1} T_{2} } \right)/\left( {T_{1} + T_{2} } \right)$$

(4)

Numerical modeling of the flow within the single discontinuity is actually performed irrespective of the effects produced by the presence of real shear zones. Numerical distinct element simulation of the groundwater flow requires a comprehensice set of data about the underground and it is frequently used for the investigation of tunnel inflow (Papini et al. 1994; Molinero et al. 2002). UDEC is one the best examples of the existing mathematical models simulate waterflow within discontinuities using distinct element method. A hydro-mechanical simulation can also be performed where the joint hydraulic conductivity depends on the mechanical deformation which in turn is influenced by the water pressure inside the discontinuities (Fig. 2) (Itasca 2011).

Fig. 1

A 2-D discrete flow model schematixation on a plan (a) and in cross section (b) (Croci et al. 2003)

Fig. 2

Schematization of the solid–fluid interaction within discontinuities: a water discharge; b mechanical effects induced by stresses affecting the aperture; and c pressure change in the sites (Itasca 2011)

Detailed data about the discontinuities characteristics must be imported into the numerical distinct element model so that satisfactory results can be obtained. Hence, it is suitable for simulation of local phenomena or detailed scale processes (Samardzioska and Popov 2005).

UDEC is frequently used for simulation of fluid flow through jointed rock media (Herbert 1996; Zhang et al. 1996; Liao and Hencher 1997). Rock blocks surrounded by discontinuities are simulated as rigid or deformable material. In fluid flow simulation, joint conductivity is directly related to the mechanical deformation which is associated with the joint water pressures. Mechanical interaction between blocks is established in where each domain, which is filled with water, is separated by contact points.

In UDEC, fluid flow governing equation for steady laminar flow is calculated based on cubic law for a planar fracture as:

$$Q = - \frac{{a^{3} }}{12\mu }.\frac{\Delta p}{l}$$

(5)

The hydraulic aperture (a) is given, in this analysis, by:

$$a = a_{0} + u_{n}$$

(6)

In Fig. 3, the variation of aperture with normal stress on the joint is demonstrated. Opening and closure of joint aperture can be inferred by arithmetic positive and minus signs in Eq. 6, respectively (Itasca 2011).

Fig. 3

Hydraulic aperture (a) relation with joint normal stress (n _σ ) in UDEC (Itasca 2011)

Numerical modeling procedure

For modeling groundwater flow in a discontinuous media, a rock block was cosidered (formed from a sedimentary rock or a paragneiss lithotype which is low fractured and karstified) that is crossed by two joint sets with varying orientations, spacing and apertures (Table 1).

Table 1 Joint dip direction/dip used for modeling

The two-dimensional numerical model used in this study includes an assembly of intact rock blocks, different tunnel radiuses, hydraulic head above the tunnel, joint spacing and different joint dip/dip directions.

An intact rock block interacts with adjacent blocks through contacts that are located along two conjugate persistents and equally spaced-joint sets, and the tunnel is intersected by joints as shown in Fig. 4. The initial groundwater table is located immediately below the ground surface. A rectangular domain was chosen (100 × 200 m²) and a tunnel with N–S direction was positioned at its center. For each geo-structural setting considered in the simulations (Table 1), the matrix of permeability tensor [K] based on cubic law (Snow 1969) was calculated:

$$\left[ K \right] = \left[ {\begin{array}{*{20}c} {1 - \cos a_{x} \cos a_{x} } & {\cos a_{x} \cos a_{y} } & {\cos a_{x} \cos a_{z} } \\ {\cos a_{y} \cos a_{x} } & {1 - \cos a_{y} \cos a_{y} } & {\cos a_{y} \cos a_{z} } \\ {\cos a_{z} \cos a_{x} } & {\cos a_{z} \cos a_{y} } & {1 - \cos a_{z} \cos a_{z} } \\ \end{array} } \right]$$

(7)

a _i (i = x, y, z) is the included corner of normal direction of fracture and coordinate axis. If combined actions of all fracture groups are considered, the total rock mass cubic law can be deduced as follows:

$$\left[ K \right] = \mathop \sum \limits_{m = 1}^{n} \frac{{ga_{m}^{3} }}{{12b_{m} \vartheta }}\left[ {\begin{array}{*{20}c} {1 - n_{x}^{m} n_{x}^{m} } & {n_{x}^{m} n_{y}^{m} } & {n_{x}^{m} n_{z}^{m} } \\ {n_{y}^{m} n_{x}^{m} } & {1 - n_{y}^{m} n_{y}^{m} } & {n_{y}^{m} n_{z}^{m} } \\ {n_{z}^{m} n_{x}^{m} } & {n_{z}^{m} n_{y}^{m} } & {1 - n_{z}^{m} n_{z}^{m} } \\ \end{array} } \right]$$

(8)

where i is the cluster number of fracture; n is the total number of the cluster; n (i = x, y, z) is the normal direction cosine of normal direction of fractures; ϑ is the kinematics viscosity of fissured water 20 °C (10⁻³ Pa × s); a is the fracture aperture and b is the spacing interval of fractures.

Fig. 4

Schematic section of the model domain, with the simulated joint sets

For a more precise and accurate visualization of the rock anisotropy and equivalent hydraulic conductivity calculation, hydraulic conductivity tensor is used (Louis 1974):

$$K_{\text{eq}} = \left( {K_{1} \cdot K_{2} \cdot K_{3} } \right)^{{\frac{1}{3}}}$$

(9)

where K ₁, K ₂ and K ₃ are the principal components of the hydraulic conductivity tensor, previously defined.

The universal distinct element code (UDEC) was used to evaluate the groundwater inflow into the tunnel. UDEC simulates a rock mass as a composition of discrete blocks separated by joints that are represented by interfaces (Alejano 2014). The parameters used for model implementation are listed in Table 2. In the model, the joint stiffness values were considered independent from the effective normal stress, because the research mainly aimed to study middle-depth tunnels (at an average depth equal to 150 m corresponding to an average normal effective stress in the order of 3 MPa).

Table 2 Model parameters used in this study

For the groundwater flow, the following boundary conditions were applied:

• 1. A stress boundary condition is created along the top of boundary, with a fixed ratio, k, is defined as the ratio of horizontal to vertical normal boundary stresses. The ratio, k, in this condition is set to be 1.

• 2. No pore pressure along the top boundary surface as the groundwater table coincides with the top boundary surface. Constant water pressure along the bottom boundary, and linearly increasing the fluid pressure along the left and right vertical surfaces.

The groundwater level above the tunnel can be defined by changing the head assigned to the vertical boundaries. By specifying a constant hydraulic head at these boundaries, drawdown of the groundwater table is balanced by the groundwater recharge in the models as a result of the tunnel inflow. In this study, the groundwater flow into the tunnel was considered to be steady flow.

In the UDEC program, the blocks are assumed to be impermeable and the groundwater flows only through the fractures between the impermeable blocks. The groundwater flow in a joint depends on the aperture of the joint, the dip/dip direction joint, the joint spacing that is, in turn, affected by the pore water pressure within the joint (hydro-mechanically coupled). The solution for approximating the fluid flow rate through a joint relies on the classic Cubic Law, modified for the non-parallel wedge-shaped fractures. From the numerical simulations applying the above-mentioned boundary conditions, a conceptual model for a fully coupled hydro-mechanical discontinuity system can be derived.

Assessment of hydrogeological parameters impact on groundwater inflow

Due to the uncertainties in the measurement and analysis of rock mass characteristics, research on the impact of the uncertainty seems inevitable in the rate of flow through the rock masses. In line with this requirement, a more accurate concept of problem was obtained by the sensitivity analysis on parameters affecting the water inflow on tunnel in order to determine the simulation permeability tansor and estimating the tunnel inflow in fractured rocks. Hence, in order to evaluate the uncertainty in measurements, any effective parameter increases by 10 and 20 % in each stage, while other parameters are constant and the impact of the increase on the rate of water flow into tunnel was investigated (Fig. 5). As shown in Fig. 5, increasing joint aperture and overburden have the maximum and minimum impacts on the water flow in the tunnel, respectively. Moreover, the effect of joint spacing is inverse. In other words, as the joint spacing increases, the rate of water inflow into the tunnel from the rock masse is decreased. In continue, sensitivity analyses of geo-structural parameters on the water inflow and the modeling results are discussed below.

Fig. 5

Effect of increasing parameters on the groundwater inflow to the tunnel

Sensitivity analyses

By considering all the previously listed parameters and their related range of variation (Tables 1, 2), more than 750 simulations were carried out in relation to the joint set spacing, the tunnel radius, the hydraulic head, the dip direction/dip, joint aperture, joint trance and gap (Figs. 6, 7, 8). Results show that by increased degree of fracture (high frequency and low spacing), the tunnel inflow obviously increases. The simulations correctly reproduce the tunnel drainage in a rock mass. Also, for the same joint aperture, the growth rate of the discharge substantially depends on the orientation of discontinuities. It is noteworthy that the orientation of discontinuities significantly influences the direction of water flow: (1) when the hydraulic gradient is perpendicular to plane of the discontinuity, the discontinuity plane acts as an impermeable barrier and there is no water flow and, (2) the water flow is maximum along the gradient direction, if the plane of the discontinuity is parallel to the hydraulic gradient. The simulations revealed increase in the tunnel-water inflow with the increase of hydraulic head.

Fig. 6

Effect of significant parameters on groundwater flow into tunnel (hydraulic head W. H.: 10, 50, 100 m; tunnel radius T. R.: 1, 3, 5 m; joint set spacing J. S. S.: 1, 2, 5, 10 m; dip direction/dip: E/30°–W/30°, E/45°–W/45°, E/60°–W/60°, E/0°–W/90°; joint aperture: 1 × 10⁻⁴, 1 × 10⁻³, 1 × 10⁻² m)

Fig. 7

Trend of the tunnel inflow versus the joint gap for different values of joint trace length (L in legend) expressed in m and the joint trace length for different values of the gap (G in legend). All the results correspond to a geo-structural setting characterized by two conjugate joint sets (E/30°–W/30°) and spacing equal to 5 m

Fig. 8

Trend of the tunnel inflow versus the interconnectivity probability for different geo-structural settings, considering the joint spacing equal to 5 m. The gray band represents the critical probability P _c and in its left side, P < P _c, the flow will be localised, while in the right side, P > P _c, water inflow will be interconnected

Many simulations were done by a constant joint aperture, coinciding with the soil surface. In this way, however, it was possible to simultaneously assess the influence of the joint aperture. The sensitivity analysis results showed significant effect of variations of this factor on the water inflow and that increased joint aperture results in sudden increase in the flow rate. As the tunnel radius decreases, the water flow rate decreases due to the reduced connected joint number. The study on geo-structural conditions showed that variations of the joint dip have significant impact on the water flow into the tunnel. In particular, the joint spacing is less, while the hydraulic head above the tunnel is high.

Connectivity of joint networks

Joint connectivity is the key characteristic affecting the fluid flow in the jointed rock and refers to the degree of interconnection of a joint population (Long and Witherspoon 1985). Independent fractures behave as isolated bonds which do not have any contribution to the shift of the fluid mass. Interconnected discontinuities, on the contrary, have influence on the conductivity and the water flow through a fracture network formed by connected series of bonds (Scesi and Gattinoni 2009). The geometric connectivity depends on the length, orientation and density of the fractures. The simulation results showed that the tunnel inflow decreases as the gap length increases and the joint trace length decreases (Fig. 7). Crossing and abutting fractures will increase the connectivity, blind or dead-end fractures. Connectivity can be quantified in terms of percolation theory. Network percolation is the conductance of random networks of conductors. Each of the conductors in the network can be opened or closed depending on a probability (Bruines 2003).

Therefore, an interconnectivity probability P from the percolation theory was also considered. It was calculated as the ratio between the node’s number in the partially-connected domain and the corresponding node’s number for a fully interconnected domain with similar geo-structural characteristics (Berkowitz and Balberg 1993). Obviously, the tunnel inflow increases with the interconnectivity probability through an approximately exponential trend (Fig. 8). For an interconnectivity probability between 0.5 and 0.6, abrupt changes are observed in tunnel inflows (even for several orders of magnitude), corresponding to the critical probability P _c. Below this P _c, the system was not connected and the flow was considered to be local (no longer contributes to the tunnel inflow). However, above the P _c, there is a percolating cluster that spans the whole system and the flow is interconnected.

Analyses and discussions

Definition of empirical model

According to the sensitivity analysis presented in previous section, it is found that hydraulic conductivity has a major impact on groundwater inflow to tunnels. Hence, for obtaining an empirical model in discontinuous media or in other word for modifying of analytical methods, hydraulic conductivity parameter should be modified according to geo-structural properties using numerical simulations. Therefore, for the same configurations used in the numerical model, the tunnel water inflow was calculated using the Goodman formula.

Goodman et al. (1965), considering a source and a sink for simulation of a draining tunnel in a homogeneous semi-infinite aquifer, obtained an analytical equation. They applied the equations of Polubarinova (1962) that are identical to the equations developed by Muskat (1937). Experimental tests were performed on tunnel driving in water tanks. One of the interesting points mentioned by Goodman et al. (1965) is the slight increase of water inflow with an increase in tunnel diameter. This equation is developed based on the following assumptions; the radius flow, no bedding in the rock, and accurate prediction of equivalent permeability (Kong 2011):

$$Q = 2\pi K\frac{H}{{2.3\log \left( {\frac{2h}{r}} \right)}}$$

(10)

In order to apply this equation, the equivalent hydraulic conductivity of the rock mass at the tunnel depth was calculated by Eq. (9). Comparison between the model results and those obtained through the Goodman analytical formula showed that the Goodman results significantly overestimate the tunnel-water inflow, and that the greater this overestimation, the lower the joint dip will be (Fig. 9). As shown in Fig. 9, the simulated water inflow can be fitted as a function of the tunnel-water inflow, calculated by the analytical relations. To achieve this, a conditional function has to be defined in which the simulation of hydraulic conductivity depends on the geo-structural characteristics. Based on this comparison, an empirical relation was proposed to estimate the tunnel water inflow, with particular reference to the case of depth below 150 m. For this depth and laminar regime, an increased dependence of the drainage process on the structural setting can be seen. Based on the Goodman equation, the following relation was defined:

$$Q_{\text{em}} = 2\pi k_{\text{sim}} \frac{H}{{2.3 \log \left( {\frac{2h}{r}} \right)}}$$

(11)

where Q _em (m³/s) is the empirical tunnel inflow, and k _sim is the empirical hydraulic conductivity, used instead of k _eq in the analytical formula and depends on:

Fig. 9

The results of numerical analysis (UDEC) versus analytical prediction of groundwater inflow in different geostructural settings are demonstrated by coloured points. Continuous lines are drawn based on linear regression. The regression coefficients as well as the red dotted line indicate the perfect correlation

• 1. The joint dip,

• 2. The orientation of the hydraulic conductivity tensor.

To determine the K _sim, the following parameter λ was empirically defined:

$$\lambda = \left\{ {\begin{array}{*{20}l} {K_{\hbox{min} } \sqrt {\frac{{K_{\hbox{min} } }}{{K_{\hbox{max} } }}} .\left( {1 - \cos \left( {\theta_{\hbox{min} } } \right) + \cos \left( {\frac{\pi }{4}} \right)} \right)^{{\text{Sin} \left( {\theta_{\hbox{min} } } \right)}} , } \hfill & {\emptyset_{\hbox{min} } \le \frac{\pi }{4}} \hfill \\ {K_{\hbox{min} } \sqrt {\frac{{K_{\hbox{max} } }}{{K_{\hbox{min} } }}} .\tan \left( {\theta_{\hbox{min} } } \right), } \hfill & {\emptyset_{\hbox{min} } > \frac{\pi }{4}} \hfill \\ \end{array} } \right.$$

(12)

where K _sim and K _max are the minimum and maximum components of the hydraulic conductivity tensor, θ _min is the minimum joint dip and ∅_min is the angle between the K _min direction and the horizontal plane. λ is a conditional function based on the dip orientation. According to the regression analyses, the empirical K _sim defined as a function of λ:

$$\begin{aligned} K_{\text{sim}} & = 0.055 - 1.64\frac{\lambda }{Ln\left( \lambda \right)} - 0.055{\text{e}}^{\lambda } \\ R & = 0.9765, \, R^{2} = 0.9535 \\ \end{aligned}$$

(13)

The statistics R and R ² in the model Eq. (13) were in an acceptable range. Hence, the empirical equation (Eq. 11) was obtained considering geo-structural setting conditions (Fig. 10).

Fig. 10

Trend of the tunnel inflow using UDEC programe versus the inflow calculated through the empirical formula for several geo-structural conditions (characterized by two joint families and changing dip). The continuous lines arise from the linear regression of the simulated values. The corresponding regression coefficients (R ²) and the red dotted line indicate a perfect correlation

The fully interconnected-joints networks’ empirical formula was extended to partially interconnected networks based on previously defined interconnectivity probability P:

$$Q_{\text{em}} = P^{n} 2\pi k_{\text{sim}} \frac{H}{{2.3 \log \left( {\frac{2h}{r}} \right)}}$$

(14)

where P is the probability of interconnectivity, previously defined and n is an empirical coefficient set out from the numerical results. The numerical results for the partially interconnected network and the tunnel inflow were compared with the empirical formula for different values of the exponent and it was revealed that the best estimation was achieved for n = 2.5. Equation (14) is valid only for P ≥ 0.5. In fact, when P is lower than this percolation threshold (P < P _c), the flow is localized and it does not contribute to the tunnel inflow.

Model validation

After the model was acquired through the regression analyses, its accuracy Eq. (11) was evaluated on 30 % of the initial data, because the test data were excluded. Figure 11 shows the results of the Q empirical formula versus the Q numerical for the test data. As can be seen, the R ² has an acceptable value; thus, the equation can be considered valid.

Fig. 11

The points represent the Q empirical formula versus the inflow calculated with the Q UDEC for the test data

Application to a real case

Numerical modeling of groundwater inflow to a tunnel could provide the best and precise results; however, it requires a detailed conceptual model of the hydrogeological condition, high costs and time-consuming simulations. As there are very limited amount of data in the preliminary geotechnical investigation of the site, it is better to define a simple equation that is able to consider the fractures network. This empirical equation, which is obtained based on parametrical modeling, makes the prediction of groundwater inflow as a function of joint characteristics available. The initial evaluation of the tunnel inflow is useful in determination of the highly risk areas from groundwater inflow point of view, where detailed investigations are necessary.

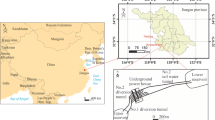
The results of the empirical equation were later applied to a real case (Amirkabir Tunnel, northern Iran). In geological studies, the tunnel intercept 14 geological units, which generally encompass various sedimentary-volcanic sets of Karaj formation. Its petrology contains layers of tuff, sandstone, fine-grained conglomerate, siltstones, lava and agglomerate. In this study, we investigated the groundwater inflow to tunnel from kilometers 3.1 to 14.1. Tunnel is divided to 9 engineering geological sections: Gta2 (sandstone and tuff layers), Gta3 (sandstone layers, tuff, and micro conglomerate), Gta4-1 (sandstone, tuff), Gta4-2 (tuff, in sandstone sections and micro conglomerate), Sts1 (tuff, siltstone, layers of sandstone and micro conglomerate), Sts2-1 (tuff, limestone), Sts2-2 (tuff, limestone, shale and siltstone), Tsh-1 (Sandstone, Shale, Silt stone) and Cz (tuff, sandstone, and micro conglomerate) (Figs. 12, 13). Detailed description of geological units along the tunnel is presented in Table 3 and its geological profile is shown in Fig. 12 (SCE Company 2006).

Fig. 12

Location (a) and geological section (b) of Amirkabir tunnel path (km 3.1–14.1) (SCE Company 2006)

Fig. 13

Unit sequences from U₆ to U₁₀ in the study area showing different morphology of the tunnel site (SCE Company 2006)

Table 3 Description of the tunnel site’s geological units (SCE company 2006)

For each tunnel section, Table 4 presents the hydraulic conductivity tensor. The corresponding surface equivalent hydraulic conductivity was calculated based on the geo-structural survey. This information was integrated with the results of 11 pumping tests (carried out in transient state with a constant rate at different depths). To measure the tunnel inflow using a flowmeter, the outflow was measured daily with synchronous advancing of drilling. Then, the tunnel inflow was calculated in different levels as the difference between the channel flow rate in the upstream and downstream levels. Calculation of tunnel water inflow was a possible task in each section with both Goodman’s equation and the new previously described empirical relation. A comparison was then performed between obtained results and the tunnel-monitoring data, arising from the flow rate measured in the tunnel channel at different tunnel distances. Considering the comparison results (Fig. 14), it is concluded that the tunnel water inflow is highly overestimated using Goodman equation, especially in sections with higher rock mass anisotropy. The maximum hydraulic conductivity was in the direction close to the vertical. This overestimation was effectively corrected through the proposed empirical relation that provides values comparable to those actually observed in the tunnel. For example, “Materials and methods” section is derived in the intensely fractured area with the high rate of anisotropy. The comparison of the water inflow values obtained through Goodman and empirical equations with the observed water inflow rate show that the calculated groundwater inflow rate using the empirical equation is closer than the inflow value computed by Goodman equation to the observed water inflow rate with the relative differences of 38 and 493 %, respectively. In other words, accurate estimation of hydraulic conductivity tensor in fractured and heterogenous zones has a main impact on accuracy and precision of groundwater inflow prediction. These results confirm the importance of considering the discontinuous nature of the media, with particular reference to its structural setting.

Table 4 Main characteristics of different sections in Amirkabir tunnel (northern Iran), useful for the estimation of water inflows (1–12 refers to the divisional sections); (SCE company 2005)

Fig. 14

Comparison between observed water inflow at amirkabir tunnel (in green), calculated using Goodman equation (in blue) and the empirical relation (in red). The percentage values on the chart demonstrate the relative difference of the inflow rates calculated using the Goodman and empirical formulas with the observed water inflow rates in each section

Conclusions

In the recent decades, accurate prediction of groundwater inflow to the tunnel is of great interest in the engineering practice, especially for assessment of environmental impact and designation of tunnel drainage system. In this regard, various analytical equations exist in the technical literature; however, they do not accurately reflect the real phenomena since they are developed based on simplifying assumptions such as homogeneous aquifer, which is in contrast to the fractured nature of the rock masses in the perimeter of the tunnel.

The study aimed to define corrective hydraulic conductivity applicable to Goodman formula for tunnel inflow assessment. The rock-mass geo-structural setting was taken into account. The numerical flow model enabled identifying and quantifying the influence of different parameters (orientation of joint sets, joint spacing and aperture, tunnel radius, and hydraulic head) on the tunnel water inflow. The results show that the joint spacing and aperture mainly control the tunnel discharge. This dependency can still be efficiently reproduced by a single parameter, that is the equivalent hydraulic conductivity. The most interesting result is that the tunnel inflow depends on the geo-structural setting of the rock mass, especially when the joint spacing is less and the hydraulic head above tunnel is high. In particular, the faster the rate of tunnel flow increases with the equivalent hydraulic conductivity of the rock mass, the lesser is the joint set dip. Obviously, the geo-structural setting is one of the factors with highest influence on the drainage process, but it is rarely included in analytical approach. Hence, the only parameter covering aperture, orientation and spacing of the fractures is hydraulic conductivity which has a special role in prediction of groundwater inflow to tunnel. Thus, for obtaining an empirical model in discontinuous media or in other word for modifying of analytical methods, hydraulic conductivity parameter should be modified according to geo-structural properties using numerical simulations.

Numerical model results and analytical formulas were compared and a method was obtained to adapt the simple analytical equations of Goodman to the geo-structural characteristics of the rock mass. To achieve the project aim, numerical simulation was done and a sufficient data set was developed to calibrate Goodman equation and/or define empirical relation according to various structural and geological conditions. This equation was calibrated with respect to average depth of the tunnel, equal to 150 m and normal effective stress of 2–3 MPa. This equation was acquired for fully interconnected fractures network and then, was extended to partially interconnected network, considering the interconnectivity probability. Finally, the empirical and analytical relations were used to estimate the water inflow into Amirkabir tunnel as a case study and was compared to the monitoring data. Some sections of this case study were derived on intensely fractured rock mass. The outcomes of empirical relation corresponded to the monitoring data, especially in those tunnel sections with high anisotropy of rock mass. Therefore, of particular note is that according to geostructural properties of discontinuous media using modified hydraulic conductivity in Goodman solution, a more precise prediction of groundwater inflow to tunnel and as a consequence, a lower relative difference in comparison to the observed inflow rate is reasonable.