Abstract
The groundwater tidal prism is defined as the volume of water that inundates a porous medium, forced by one tidal oscillation in surface water. The pressure gradient that generates the prism acts on the subterranean estuary. Analytical models for the groundwater tidal prism and associated benthic flux are presented. The prism and flux are shown to be directly proportional to porosity, tidal amplitude, and the length of the groundwater wave; flux is inversely proportional to tidal period. The duration of discharge flux exceeds the duration of recharge flux over one tidal period; and discharge flux continues for some time following low tide. Models compare favorably with laboratory observations and are applied to a South Atlantic Bight study area, where tide generates an 11-m3 groundwater tidal prism per m of shoreline, and drives 81 m3 s −1 to the study area, which describes 23% of an observational estimate. In a marine water body, the discharge component of any oscillatory benthic water flux is submarine groundwater discharge. Benthic flux transports constituents between groundwater and surface water, and is a process by which pollutant loading and saltwater intrusion may occur in coastal areas.
Résumé
Le prisme de marée d’eaux souterraine est défini comme le volume brut d’eau qui inonde le milieu poreux, contraint par une oscillation de marée de la masse d’eau de surface. Le gradient de pression qui engendre le prisme agit sur l’estuaire souterrain. Des modèles analytiques du prisme de marée d’eaux souterraine et du flux benthique associé sont présentés. Il est montré que prisme et flux sont directement proportionnels à la porosité, à l’amplitude de la marée et à la longueur de la vague d’eau souterraine; le flux est inversement proportionnel à la période de la marée. La durée du flux de vidange excède celle du flux de recharge au cours d’un cycle de marée ; et un flux de vidange se produit encore quelque temps après la marée basse. La confrontation des modèles aux observations de laboratoire est favorable. Ces modèles sont appliqués à une zone d’étude de la Baie Atlantique Sud où la marée génère un prisme de marée d’eau souterraine de 11 m3 par mètre de côte, et pousse 81 m3 s−1 vers la zone d’étude, ce qui rend compte de 23% d’une estimation issue de l’observation. Dans une masse d’eau marine, la composante de vidange d’un flux oscillatoire d’eau benthique est une vidange sous-marine d’eau souterraine. Le flux benthique transporte des éléments entre eaux souterraines et eaux de surface: il s’agit d’un processus par lequel pollution et intrusion d’eau de mer en zone côtière peuvent se produire.
Resumen
El prisma de marea de agua subterránea se define como un volumen total de agua que inunda el medio poroso, forzado por una oscilación de marea en un cuerpo de agua de superficie. El gradiente de presión generado por el prisma actúa en el estuario subterráneo. Se presentan modelos analíticos para el prisma de marea de aguas subterráneas y el flujo bentónico asociado. Se demuestra que el prisma y los flujos son directamente proporcionales a la porosidad, amplitud de la marea y la longitud de la onda del agua subterránea; el flujo es inversamente proporcional al período de marea. La duración del flujo de descarga excede la duración del flujo de recarga sobre un período de marea; y un flujo de descarga es inducido para un período siguiente de bajamar. Los modelos se comparan favorablemente con las observaciones de laboratorio y son aplicados al South Atlantic Bight donde la marea genera un prisma de marea de agua subterránea de 11-m3, por metro de costa, y fuerza 81 m3 s−1 al área de estudio, lo cual describe el 23% de una estimación observacional. En un cuerpo de agua marino, el componente de una descarga de un flujo de agua bentónico oscilatorio es la descarga submarina subterránea. El flujo bentónico transporta componentes entre agua subterránea y agua superficial, y es un proceso por el cual la carga de contaminantes y la intrusión de agua salina pueden ocurrir en las áreas costeras.
摘要
地下水纳潮量为地表水体一次潮汐振动作用下淹没多孔介质的水的总体积。产生纳潮量的压力梯度作用于地下河口。本文提出了地下水纳潮量和相关海底水通量的解析模型。研究表明, 纳潮量和水通量与孔隙度、潮汐幅度以及地下水波长成正比关系 ; 通量与潮汐周期成反比。一次潮汐周期中, 排泄通量的持续时间超过补给通量的持续时间 ; 且落潮后排泄通量会持续一段时间。模型与实验观测表现出很好的一致性, 且已应用于南大西洋海湾研究区, 该区每米海岸线潮汐能产生11m3的地下水纳潮量, 驱使水以81 m3 s−1至研究区, 相当于观测估计量约23%的。在海水中, 一次振荡的海底水通量中的排泄量部分就是海底地下水的排泄量。海底通量使组分在地下水和地表水之间迁移, 这也是造成滨海地区污染物累积和海水入侵的过程之一。
Resumo
O prisma de maré de água subterrânea é definido como sendo o volume de água que invade o meio poroso, em consequência de uma oscilação da maré num corpo de água superficial. O gradiente de pressão que origina o prisma intervém no estuário subterrâneo. São apresentados modelos analíticos para cálculo de prismas de maré de água subterrânea e escoamentos bênticos associados. Mostra-se que, tanto o prisma como o fluxo, são directamente proporcionais à porosidade, à amplitude da maré e ao comprimento da onda da água subterrânea; o fluxo é inversamente proporcional ao período da maré. A duração do fluxo de descarga excede a duração do fluxo de recarga num período de maré; e um fluxo de descarga acontece durante algum tempo após o período de maré baixa. Os resultados dos modelos foram comparados favoravelmente com observações laboratoriais e foram aplicados num caso de estudo em Bight (Atlântico Sul), onde a maré provoca um prisma de maré de água subterrânea de 11-m3 por metro de costa, ocasionando um caudal de 81 m3 s−1 na área de estudo, descrevendo 23% do fenómeno observado. Num corpo de água marinho, a componente de descarga de um fluxo hídrico bêntico oscilatório corresponde à descarga submarina de água subterrânea. Os fluxos bênticos transportam componentes entre a água subterrânea e a água superficial, e correspondem a um processo pelo qual a poluição e a intrusão salina podem ocorrer nas áreas costeiras.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Benthic pressure gradients forced by numerous mechanisms drive a benthic flux q bf of water and constituents between surface water and a porous medium. With periodic forcing, q bf can oscillate between a benthic discharge flux q bd, by which water and constituents are transported from a porous medium to surface-water, and a benthic recharge flux q br, by which water and constituents are transported from surface-water to the porous medium, such that
The units of q bf depend on the property under consideration. For example, \( \left[ {{L^3}{T^{ - 1}}{L^{ - 2}}} \right] = \left[ {L{T^{ - 1}}} \right] \) for a benthic volume flux, where [L] is the length dimension and [T] is the time dimension.
The groundwater tidal prism P is the volume of water that inundates a porous medium, forced by one tidal oscillation in surface water. Tidal forcing generates a long wave in the porous medium, which is physically coupled with the changing tidal elevation in surface water. Both tidal forcing and the groundwater wave generate benthic pressure gradients.
The net volume of water exchanged between idealized surface water and a porous medium, forced by one tidal oscillation, is zero. Still-water elevation is the water-surface elevation that would occur with a cessation of all forcing (US Army Corps of Engineers 2002; Dean and Dalrymple 2002). In the idealized water body, still-water elevation and tidal amplitude are statistically stationary—they do not change when shifted in time or space. The mean elevation of a forced system is a function of the type of forcing; therefore, still-water elevation may not be equal to mean elevation. In a natural system, a statistically non-stationary still-water elevation or tidal amplitude may cause the net volume of water exchanged between surface water and a porous medium to deviate from zero.
Objectives of the present work are to (1) define the groundwater tidal prism; (2) present analytical models for the groundwater tidal prism and associated benthic flux; (3) show that the models compare favorably with laboratory observations; and (4) apply the models to the South Atlantic Bight (the continental shelf along the east coast of the United States, between Cape Hatteras, North Carolina and West Palm Beach, Florida).
Benthic water flux and tidal prism
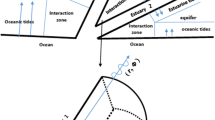
The groundwater tidal prism is analogous to the (surface-water) tidal prism Ω: the volume of water that flows from an ocean into an estuary or bay, between low tide and high tide. Although terrestrial groundwater fluxes to an estuary contribute to the force balance that exists between freshwater and saltwater wedges within a porous medium, freshwater volumes associated with terrestrial groundwater fluxes do not contribute directly to P. Forces that generate P drive chemical and biological fluxes between surface water and the subterranean estuary. For example, q bf driven by the forces that generate P (shown in Fig. 1, and denoted as P-forced benthic flux, or q bf.P) can transport pollutants to both groundwater and surface water (deSieyes et al. 2008; Robinson et al. 2009), and can cause natural constituents such as saltwater, to intrude into groundwater (Cartwright and Nielsen 2001).
Conceptual, vertical, x–z oriented section showing benthic discharge flux q bd.P vectors (red, oriented from the bed into the surface-water domain); benthic recharge flux q br.P vectors (blue, oriented from the bed into the groundwater domain); phreatic surfaces at high tide (blue) and low tide (red); water surfaces at high tide (blue) and low tide (red); and the bed of the water body. This figure is not drawn to scale
Other mechanisms such as terrestrial hydraulic gradient (Bokuniewicz 1992; Younger 1996), density gradient (Moore and Wilson 2005), or wave-related mechanisms (Li et al. 1999; Cartwright et al. 2004a; King et al. 2009), also generate benthic pressure gradients and force q bf, but do not directly contribute to P. Submarine groundwater discharge (SGD) is a benthic water discharge flux to a marine water body. SGD is exclusively a marine process; in the present work, the more general q bf is used in place of SGD to avoid this limitation, with the exception of references to work by others that specifically relate to SGD.
Numerous investigators describe characteristics of tidally influenced groundwater systems. Nielsen (1990) developed an analytical solution for the phreatic surface of a tidally forced groundwater wave inside a beach with an inclined bed. Moore (1999) defined a coastal mixing zone within a porous medium, between fresh, terrestrial water and more saline sea water. He identified this zone as the subterranean estuary, drawing an analogy with the estuarine mixing and transition zone in surface water, which exists between freshwater sources and the ocean. Li et al. (1999) parsed total SGD into three components: SGD forced by the terrestrial hydraulic gradient, tide, and wave setup. They also presented a simple model to quantify the mass of constituents transported by SGD from a porous medium to surface water. Mango et al. (2004) used a Hele-Shaw analog to induce circulation between laboratory cells that represent a coastal aquifer and tidally forced surface water. Michael et al. (2005) identified seasonality in the freshwater-saltwater interface of the subterranean estuary as a mechanism that drives saline discharges, which lag inland recharges, to surface-water. They identify a perched saline zone near the mean tidal elevation, which is shoreward of a fresher discharge zone. Prieto and Destouni (2005) used numerical models to show that tidal forcing enhances the recirculation of seawater through a porous medium, for relatively low rates of SGD; where SGD rates are relatively high, tidal forcing has a lesser effect on recirculation. Colbert et al. (2008) characterized residence time of water and flow dynamics at a tidally forced field site using geochemical tracers and observations of the phreatic-surface elevation. Robinson et al. (2007a, b) and Li et al. (2008) used numerical models and dimensional analyses to investigate relationships between tidal forcing, terrestrial recharge, and recirculation of seawater through a porous medium. These generalized characteristics (phreatic surface dynamics, mixing zone, SGD parsed into components, SGD as a transport mechanism, tidally induced recirculation in a porous medium, seasonality, residence times, relationship between recharge and recirculation) partially describe the subterranean estuary. The groundwater tidal prism is an extension of Moore’s (1999) estuary analogy. It characterizes a flux of water and constituents between surface water and the subterranean estuary.
Nielsen’s tidally-forced, phreatic surface
The well-known Boussinesq equation
governs a transient, one-dimensional phreatic surface h(x,t) within a two-dimensional, x–z oriented domain of porous media, where x is the horizontal, Cartesian, offshore dimension; z is the vertical, Cartesian dimension; t is time; K is hydraulic conductivity; and n is porosity. Nielsen (1990) solved a boundary value problem governed by Eq. (2), where one side of the finite-depth, homogeneous domain is bounded at a free-water surface by an inclined bed, or sloping beach face, with slope \( {s_{\text{b}}} = \tan \beta = \hat z/\hat x \); the other side is unbounded; β is the angle between the inclined bed and the impermeable, horizontal base of the unit; and \( \hat z \) and \( \hat x \) are coordinates on the inclined bed (Fig. 2). The domain is forced by tide
on the inclined bed, where A is tidal amplitude; \( \sigma = 2\pi /T \) is radial tidal frequency; T is tidal period; z = 0 is still-water elevation in surface water; z = η is the elevation of the free-water surface; and z = −H is the elevation of the horizontal, impermeable base of the hydrogeologic unit. Boundary conditions are \( \partial h\left( {x \to \infty, t} \right)/\partial t = 0 \), and \( h\left( {\eta (t)/{s_{\text{b}}},t} \right) = \eta (t) \).
Vertical x–z oriented sections showing a the phreatic surface h(x,t) (blue surface) at time t, and reference volumes \( {\hat V_{{\text{gw}}.1}} \) (yellow volume), \( {\hat V_{{\text{gw}}.2}} \) (blue volume), and \( {\hat V_{{\text{gw}}.3}} \) (gray volume); and b phreatic surfaces h(x,t 1) (red surface) and h(x,t 2) (blue surface) at time t 1 and time t 2, and reference volumes \( {\hat V_{{\text{gw}}.4}} \) (blue volume) and \( {\hat V_{{\text{gw}}.5}} \) (yellow volume)
A graphical representation of Nielsen’s (1990) solution
is shown in Fig. 3 for high tide, low tide, mean tide during ebb or falling tide, and mean tide during flood or rising tide, where \( \lambda = 2\pi /L \) is the wave number in the porous medium, L is the length of the tidally forced groundwater wave in the porous medium,
is a perturbation parameter, and \( \sum {O\left( {{\varepsilon^m}} \right)} \) represents the sum of power-series terms in εm, raised to powers of m ≥ 2. Where \( \beta = \pi /2 \), the wave number in the porous medium λ is a function of n, σ, K, and H. Nielsen (1990) used a perturbation technique, in which an approximate solution (Eq. 4) is developed—from an exact solution to a similar problem (a textbook solution to Eq. 2)—by introducing the perturbation parameter (Eq. 5) into the exact solution, and developing a power series in terms of the perturbation parameter. (Li et al. (2000) and Teo et al. (2003) subsequently developed more robust variants of Nielsen (1990)). In the present work, power-series terms of O(ε2) and higher are truncated in Eq. (4), and Nielsen’s (1990) origin is relocated from the intersection of the inclined bed and the base of the unit, to the intersection of the inclined bed and the still-water elevation. The relocated origin is shown in Figs. 2 and 3.
Vertical x–z oriented section showing phreatic surfaces at high tide (blue surface), mean (ebb) tide (gray surface), low tide (red surface), and mean (flood) tide (green surface). The origin is located at the intersection of the still-water surface and the inclined bed. The inclined bed (black plane) separates the porous medium on the right from the tidal water body on the left. Phreatic surfaces in this figure are true graphical representations of Eq. (4)
High and low tides occur at t = 0 and \( t = T/2 \), respectively. The shape of the phreatic surface at mean tide during ebb is different than the shape of the phreatic surface at mean tide during flood, as shown in Fig. 3. The surface asymptotically approaches a constant, over-height elevation z = d ts at x → ∞, as shown in Fig. 2. Nielsen (1990) assumed that the elevation of the phreatic surface and the tidal elevation are coupled on the inclined bed, and stated that if “decoupling occurs, analytical solution [for h(x,t)] is probably impractical.” Decoupling of the phreatic surface and the tidal surface forms a seepage face, in which q bd.P is realized as a surface flow along the exposed beach face, from the elevated phreatic surface, to the tidal surface at a lower elevation.
Benthic water flux associated with the groundwater tidal prism model
The volume of water in the hydrogeologic unit (\( {\hat V_{\text{gw}}} \)) at time t, per unit length of shoreline, is
where \( {\hat V_{{\text{gw}}.1}},{\hat V_{{\text{gw}}.2}},\,\,{\text{and}}\,\,{\hat V_{{\text{gw}}.3}} \) are volumes shown in Fig. 2a and evaluated in the Appendix.
Substitute Eqs. (23)–(27), into Eq. (6) to yield
Differentiate Eq. (8) with respect to time to yield
Since
Equation (9) can be expressed as
where
and Φ is dimensionless q bf.P integrated across the inclined bed (Fig. 4), from the intersection of the inclined bed and the free-water surface at high tide, to a point offshore at which the forces that generate P cease to drive q bf.P. (The offshore point cannot be estimated with Eq. 11).
a Dimensionless tidal elevation z/A above the still-water surface versus dimensionless time t/T; and b dimensionless benthic flux Φ versus dimensionless time t/T, for Nielsen’s (1990) perturbation parameter ε = 0.1 (red line), ε = 0.2 (green line), ε = 0.4 (black line)
The existence of ∞ in Eq. (8) is seemingly problematic. To develop Eq. (4), Nielsen (1990) imposed a landward boundary condition \( \partial h\left( {x \to \infty, t} \right)/\partial t = 0 \) on Eq. (2). Volume calculations in the present and following sections must include ∞ to accurately represent this boundary condition in the calculations. Fortunately, the existence of ∞ in Eq. (8) is not problematic because ∞ drops out of the solution when Eq. (8) is differentiated, to yield Eq. (9).
Groundwater tidal prism model
The volume of water issuing out of the hydrogeologic unit (\( \Delta {\hat V_{\text{gw}}} \)) between t 1 and t 2 is
where \( {\hat V_{{\text{gw}}.4}} \) and \( {\hat V_{{\text{gw}}.5}} \) are volumes shown in Fig. 2b and evaluated in the Appendix; t
1 and t
2 are two arbitrary points in time within the same ebb tide, such that \( 0 \leqslant {t_2} < {t_1} \leqslant T/2 \); and \( {\hat x_2} \) and \( {\hat x_1} \) are x-coordinates of intersections of free-water surfaces and the inclined bed at t
2 and t
1, respectively, corresponding to \( {\hat x_2} > {\hat x_1} \). With respect to Fig. 3, if \( {t_1} = T/2 \) and t
2 = 0, then  and
and  , where
, where  and
and  are x-coordinates of intersections of the inclined bed, at low and high tides, respectively.
are x-coordinates of intersections of the inclined bed, at low and high tides, respectively.
Substitute Eqs. (28) and (29) into Eq. (13), and solve in non-dimensional form
Note that ∞ in Eq. (14) is not problematic because \( {e^{ - \infty }} \to 0 \) in Eq. (29). Equation (15) can be expressed as

where subscripts 0.1 and 0.2 denote flood tide and ebb tide roots, respectively, of Eq. (9) (Fig. 5), such that \( \Delta {\hat V_{\text{gw}}} = P \); and  is the dimensionless groundwater tidal prism (Fig. 6). For example, where ε = 0.1: Φ = 0 at t
0.2/T = 0.121 and t
0.1/T = 0.630 (Figs. 4 and 5); then
is the dimensionless groundwater tidal prism (Fig. 6). For example, where ε = 0.1: Φ = 0 at t
0.2/T = 0.121 and t
0.1/T = 0.630 (Figs. 4 and 5); then  (Fig. 6) and P = 2.830nA/2λ.
(Fig. 6) and P = 2.830nA/2λ.
Dimensionless time t/T for ebb and flood tide roots to Eq. (9) versus Nielsen’s (1990) perturbation parameter ε. The ebb tide root (blue line) is described by the ordinate on the left-hand side of the figure; the flood tide root (red line) is described by the ordinate on the right-hand side of the figure
Dimensionless groundwater tidal prism  versus Nielsen’s (1990) perturbation parameter ε
versus Nielsen’s (1990) perturbation parameter ε
Discussion
In a two-dimensional idealized system, q bf.P integrates to zero across the inclined bed, over one T
Equation 17 does not imply that q bf.P integrates to zero at all points on the inclined bed
At a point on the inclined bed, q bd.P integrated over 0 to T may exceed q br.P, such that a net q bd.P exists at the point. However, to ensure mass balance required by Eq. (17), q br.P integrated over 0 to T must exceed q bd.P at another point on the inclined bed.
It is possible for the q
bf.P distribution across the inclined bed to locally exhibit flux in one direction, when the profile integrated flux is in the other direction. For example, although dimensionless benthic flux Φ is in discharge at low tide (Φ > 0 at t/T = 0.5 in Fig. 4b), water locally recharges the hydrogeologic unit in the region of  , as shown in Fig. 3, immediately following the occurrence of low tide.
, as shown in Fig. 3, immediately following the occurrence of low tide.
Equations (9), (15) and (17) describe q bf.P within a two-dimensional, x–z domain. In a natural system, where input parameters such as K, n, or H may not be constant in x, q bf.P may not sum to zero across the inclined bed. Restated in equation form
for all y, where y is the coordinate parallel to shore. However, for the idealized three-dimensional system, mass conservation requires that q bf.P sum to zero across the inclined bed. Restated in equation form
The two-dimensional, idealized, homogeneous system defined in Eq. (17) permits the zero-sum mass balance over one tidal cycle. A two-dimensional, natural, heterogeneous system may not yield a zero-sum mass balance over one tidal cycle. However, an idealized, three-dimensional, natural, heterogeneous system must yield a zero-sum mass balance over one tidal cycle. Statistical non-stationarity in the still-water elevation or tidal amplitude may not yield a zero-sum mass balance over one tidal cycle, independent of the dimensionality of the system under consideration.
Benthic flux oscillates between discharge (Φ > 0) and recharge (Φ < 0) conditions (Eq. 1, Fig. 4b). Intuitively, one may expect that an oscillatory q bf.P system should exhibit a discharge condition during ebb tide (\( 0 < t/T < 0.5 \)), as pore water exits the porous medium across the inclined bed; and a recharge condition during flood tide (\( 0.5 < t/T < 1 \)), as pore water enters the porous medium across the inclined bed. Figure 4b shows that this expectation is not correct, in a global sense, across the entire inclined bed. At high tide, where t/T = 0 (or t/T = 1), q bf.P is in a recharge condition, which persists until t/T ≈ 0.125. Restated, the q bf.P system remains in the recharge condition for approximately the first 25% of ebb tide. A similar situation occurs for approximately the first 25% of flood tide, where the q bf.P system is in the discharge condition while the tidal elevation increases. Mathematically, the π/4 phase lag in Eq. (4) causes the \( t/T \approx 0.125 = \pi /4 \) phase lag between tidal elevation extrema (Fig. 4a) and null points in q bf.P (Fig. 4b).
The phase lag is due to the dynamics of the phreatic surface, away from the inclined bed. Consider the low tide and mean tide (flood) expressions of Eq. (4), in Fig. 3. As tide rises, pore volume is flooded near the inclined bed. This inundation is due to local-scale q br.P. Inland, away from the inclined bed, however, the phreatic surface decreases as tide rises. Pore volume is evacuated by a downward flow from regions close to the inland phreatic surface, into deeper regions in the unit and across an offshore reach of the inclined bed. A global q bd.P persists for approximately the first 25% of flood tide because the decreasing landward portion of the phreatic surface generates a larger, positive contribution to \( \partial {\hat V_{\text{gw}}}/\partial t \) than the negative contribution from the near-bed portion of the phreatic surface. Complementary physical descriptions explain the persistence of q br.P for approximately the first 25% of ebb tide.
Nielsen (1990) observed that the phreatic surface rises faster than it falls, and reasoned that this occurs because a porous medium is inundated more efficiently during flood tide than the medium drains during ebb tide. He suggested that this efficiency of recharge generates the constant, over-height elevation z = d ts at x → ∞, as shown in Fig. 2. This reasoning explains why the magnitude of peak recharge is greater than peak discharge, for perturbation parameter ε < 0.43 (Fig. 7). For larger ε, the previously described, low-tide dynamics of the phreatic surface away from the inclined bed cause a relatively more intense maximum Φ near low tide (Φbd.max near t/T = 0.5 in Fig. 4b for ε = 0.4, as compared to ε = 0.1). This causes peak discharge to be greater than peak recharge for perturbation parameter ε > 0.43 (Fig. 7). The transition to a condition in which peak discharge dominates peak recharge is shown in Fig. 8, where the dimensionless time t/T of peak discharge transitions from a nearly constant value of 0.375 for ε < 0.15, to approximately 0.5 for ε → 0.5. This transition and the existence of double maxima for ε = 0.4 in Fig. 4 are governed by the dynamics of the phreatic surface away from the inclined bed. The dimensionless time of peak recharge occurs at t/T = 0.876, independent of ε, for ε < 0.5 (Fig. 8). This suggests that phreatic-surface dynamics that govern peak recharge do not change with ε.
Maxima for dimensionless benthic flux Φ versus Nielsen’s (1990) perturbation parameter ε
Dimensionless time t/T of peak discharge (blue line) and recharge (red line), both versus Nielsen’s (1990) perturbation parameter ε. Dimensionless time of peak discharge is described by the ordinate on the left-hand side of the figure; dimensionless time of peak recharge is described by the ordinate on the right-hand side of the figure
The percentage of the tidal cycle T over which q bf.P is in the discharge condition exceeds the percentage of the tidal cycle T over which q bf.P is in the recharge condition (\( \Delta {t_{\text{bd}}}/T > \Delta {t_{\text{br}}}/T \) in Fig. 9). This temporal imbalance is persistent over 0 < ε ≤ 0.5, and is partially explained by Eq. (17) and the observation that peak recharge exceeds peak discharge for ε < 0.43 (Fig. 7). The largest temporal imbalance occurs for ε = 0.32, at which q bd.P integrated across the inclined bed persists for 51.8% of the tidal cycle (Δt/T = 0.518), and q br.P integrated across the inclined bed persists for the remaining 48.2% of the tidal cycle (Δt/T = 0.482), as shown in Fig. 9. Where the perturbation parameter becomes very small (ε → 0), the duration of q bd.P and q br.P are in balance, such that Δt/T → 0.5 for both conditions. This occurs when tidal amplitude becomes very small (A → 0), wave length in a porous medium becomes very large (L → ∞), or the inclined bed becomes steeper (s b → ∞). The temporal imbalance is enhanced when tidal amplitude becomes very large (A → ∞), wave length in a porous medium becomes very small (L → 0), or the inclined bed becomes flatter (s b → 0).
Dimensionless duration Δt/T of discharge (orange line, Φ > 0) and recharge (green line, Φ < 0) versus Nielsen’s (1990) perturbation parameter ε
Li et al. (1999) used an approach that is similar to Eq. (14) to model SGD forced by tide as the integrated difference between the highest and mean phreatic surfaces. Li et al. (1999) did not detail the derivation; it is unclear whether Eq. (14) and Li et al.’s (1999) model address identical, or related but different problems.
Assumptions and limitations
Abstraction of prototype systems requires assumptions that can lead to notable limitations. The present models characterize a system that is forced by tide alone. It would not be appropriate to apply the present models alone to estimate total benthic discharge flux q bf to a system forced by numerous mechanisms, such as tides, waves, and terrestrial hydraulic gradients.
The present models are based on work by Nielsen (1990). The assumptions and limitations inherent in Nielsen’s (1990) model also apply to the present models. Specifically, a simple sinusoidal tide described by Eq. (3) is the only mechanism forcing the system. The phreatic and tidal surfaces are coupled on the inclined bed, such that a seepage face does not exist. Flow in the porous medium is normal to shore and described by Darcy’s Law. The shore is long and straight. Flow velocity is horizontal, such that the pressure distribution is hydrostatic. The porous medium is bounded by a horizontal, impermeable base, as shown in Fig. 2. The porous medium is homogeneous and isotropic, and can be described by K and n. Fluid is of a constant density. Boundary conditions \( \partial h\left( {x \to \infty, t} \right)/\partial t = 0 \) and \( h\left( {\eta (t)/{s_{\text{b}}},t} \right) = \eta (t) \) exist and are valid. Tidal amplitude A is considerably less than the depth H from the still-water surface to the impermeable base of the porous medium. Finally, the sum of terms of O(ε2) and higher, shown in Eq. (4), is considerably less than the sum of terms of O(ε0) and O(ε). Nielsen (1990) showed that error associated with neglecting terms of O(ε2) and higher is not significant.
The present models cannot be used to estimate the distribution of q bf.P in the offshore direction. Vector trends shown in Fig. 1, from higher magnitude near the intersection of the phreatic surface and the water surface to lower magnitude in the offshore direction, are qualitative and based on conclusions in Robinson et al. (2007a) and Li et al. (2008).
Comparison with Cartwright et al.’s (2004b) laboratory observations
Cartwright et al. (2004b) conducted a laboratory experiment (also detailed in Cartwright 2004) in which an inclined bed of uniformly-packed 0.2 mm sand was forced from the left by a simulated tide to investigate harmonics at the interface and in the porous medium. The laboratory tank was 9 m long by 1.5 m high by 0.14 m wide. Experiment parameters are given in Table 1; tide was a simple harmonic described by Eq. (3).
Cartwright et al. (2004b) plotted the phreatic surface in the porous medium as a function of 24 observations over T, at five locations: x = −0.6, 0.4, 1.4, 2.4, and 4.4 m; and tabulated the mean and the phase for first, second, and third harmonics at x = 6.3 m and 7.2 m. The seven piezometers they used were all located at elevation z = −0.209 m. (In the present work, the origin of the x–z coordinate system is shifted to the intersection of the inclined bed and the still-water surface, from Cartwright et al.’s (2004b) position at the lower left hand corner of the laboratory tank).
Equation (4) is fit to Cartwright et al.’s (2004b) observations by adjusting λ to minimize the χ2 goodness-of-fit parameter. Both the model representation and observations are shown in Fig. 10 for high tide (t/T = 0) and near low tide (t/T = 0.47). Minimum χ2 occurs at λ = 0.450 m−1; χ2 ranges from 6 × 10−3 m to 3 × 10−1 m for the 24 observations. Correlation coefficients range from 0.870 to 0.999, with an average value of 0.977.
Phreatic-surface elevation z with respect to the still-water surface, versus distance x from intersection of the inclined bed and the still-water surface for Eq. (4) (red and blue lines) best-fit with a 0.450-m−1 wave number λ to Cartwright et al.’s (2004b) laboratory observations at high tide (blue square, dimensionless time t/T = 0), and near low tide (red circle, dimensionless time t/T = 0.47). The black line that passes through the origin (x = 0 m, z = 0 m) represents the inclined bed
Equations (9) and (15) are applied to Cartwright et al.’s (2004b) experiment; results are shown in Fig. 11. Equation (9) is a continuous representation of q bf.P, integrated across the inclined bed. Equation (15) is discretized at a temporal resolution equivalent to Cartwright et al.’s (2004b) observations, with an average Δt/T step of 0.037. The ratio of \( \Delta {\hat V_{\text{gw}}} \) calculated with Eq. (15) to the Δt used to calculate \( \Delta {\hat V_{\text{gw}}} \) yields the dashed line for Eq. (15) in Fig. 11. The correlation coefficient between the representations of Eqs. (9) and (15) in Fig. 11 is greater than 0.9999. Equation (9) is a continuous representation of discrete Eq. (15); the favorable agreement between these continuous and discrete equations is then a necessary condition for the validity of both equations.
Benthic flux observations associated with the groundwater tidal prism, developed from Cartwright et al. (2004b), and continuous (∂V/∂t, solid line) and discrete (ΔV/Δt, dashed line) models, both versus dimensionless time t/T
A data set of phreatic surfaces is developed, which includes Cartwright et al.’s (2004b) 24 observations, best-fit to Eq. (4) with λ = 0.450 m−1 (as described in the present section); two expressions of Eq. (4) at the roots of Eq. (9); and one additional expression of Eq. (4) at low tide. Observations plotted in Fig. 11 are derived from this data set by calculating the ratio of a trapezoidal-slice \( \Delta {\hat V_{\text{gw}}} \) approximation between successive phreatic surfaces in the data set, to the duration of time between the occurrence of each surface. The 26 points shown in Fig. 11 are plotted in time at the temporal midpoint of successive surfaces in the data set. Trapezoidal-slice width is 0.01 m; the average Δt/T between the occurrence of each surface in the data set is 0.037. The correlation between data points in Fig. 11 and both Eqs. (9) and (15) is greater than 0.99.
While Cartwright (2004) noted that sources of error may cause his laboratory observations to deviate from theory, the favorable correlation between observations in Fig. 11 and both Eqs. (9) and (15) suggest that these errors are small. Specifically, Cartwright (2004) identified measurement error, instrument error, the formation of a small seepage face, non-uniform flow across the flume in the along-shore direction due to the formation of rivulets in the seepage face, non-hydrostatic pressure near the inclined bed at high tide, and vertical flow effects in the finite-depth porous medium.
Comparison with other studies
Characteristics of the present models are in qualitative agreement with previous investigations. Prieto and Destouni (2005) used numerical models to quantify the influence of tide on SGD. Their models showed that SGD “oscillates with the same period but with a phase lag relative to the tidal oscillation.” While they do not quantify the phase lag, the statement is in agreement with the present models. Robinson et al. (2007b) used a numerical model forced by tide and a terrestrial hydraulic gradient to show that q br “occurs predominantly on the late stages of the rising tide and over high tide,” and that q bd “dominates during the ebbing tide and continues over the early stages of the rising tide.” Their observations qualitatively agree with Fig. 4.
Mango et al. (2004) used a Hele-Shaw device to observe “a strongly asymmetric pattern of fluid exchange” between laboratory cells that represent a tidally forced surface-water body and a porous medium, in which the cells were separated by an inclined bed representing a sloping beach face. Mango et al. (2004) did not force the device with an analog to the terrestrial hydraulic gradient, and they did not consider the role that density variation plays in forcing q bf. They observed that q bd.P is strongest near low tide, and that q bf.P is not symmetrical. Both observations are in agreement with the present models. Specifically, Fig. 4 shows that q bd.P is strongest near low tide; and Fig. 9 shows that q bf.P is asymmetrical for any inclined bed, where ε > 0. They also showed that q bf.P does not integrate to zero at all points on the inclined bed, which is in agreement with Eq. (18).
Colbert et al. (2008) used geochemical tracers and observations of the phreatic-surface elevation on a beach near Catalina Harbor in California (USA) to investigate tidally forced flow dynamics and residence times of water. They observed that during flood tide, “the water table near the beach face rose, while the inland water table fell.” This observation is in agreement with the behavior of Eq. (4); Figs. 1, 3, and 10; and the description on the dynamics of the phreatic surface away from the inclined bed (see Discussion section). They also observed that the “greatest flux of water into the beach occurred during” flood tide. This observation is in agreement with Fig. 4.
Robinson et al. (2007b) showed that q br is dominated by tidal forcing, when the system is driven by both tide and a terrestrial hydraulic gradient, and that the intensity of tidal forcing “is the primary parameter controlling tide-induced recirculation rates.” These observations attest to P and q bf.P as appropriate descriptors of tidally driven exchange between a porous medium and tidally driven surface water.
Li et al. (2008) observed that the “amount of seawater” infiltrating into a porous medium, where the system is driven by both tide and a terrestrial hydraulic gradient, is directly proportional to permeability. Equation (16) shows that P is inversely proportional to λ, which is inversely proportional to hydraulic conductivity K. Since K is directly proportional to permeability, P as well is directly proportional to the latter quantity.
Robinson et al. (2007b) parsed q bf into a tidally-driven recirculation percentage and a density-driven recirculation percentage, in which both quantities are expressed as a function of terrestrial, fresh, groundwater inflow. It is therefore not possible to quantitatively compare the present models, in which terrestrial, fresh groundwater inflow is not considered, to Robinson et al. (2007b).
Application to the South Atlantic Bight
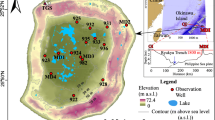
Equations (9) and (15) are now applied to a region of the South Atlantic Bight. Moore (1996) described the delivery of 226Ra to the inner-shelf study area shown in Fig. 12, between July 8 and 11, 1994. Moore (1996) quantified the flux of 226Ra into and out of the study area by numerous pathways, and deduced that a 347 m3 s−1 q bd must exist to transport 226Ra to the study area and balance other 226Ra fluxes.
Moore’s 1996 South Atlantic Bight study area
The National Oceanic and Atmospheric Administration (NOAA) predicted a semi-diurnal tide with an amplitude of approximately 0.8 m at Charleston, South Carolina, between July 7 and July 12, 1994. Benthic water flux to the study area modeled with Eq. (9) is shown in Fig. 13. In the absence of field data to develop a more rigorous estimate of λ, the present analysis, and a similar analysis of the same study area by Li et al. (1999), estimate λ with the Boussinesq wave number (Nielsen 1990)
A field estimate of λ may improve the application. Additional inputs are detailed in Table 2.
a Tide elevation z above the still-water surface in meters, versus dimensionless time t/T; b benthic flux integrated across the inclined bed \( \partial {\hat V_{\text{gw}}}/\partial t \) in cubic meters per second per meter of shoreline for a typical South Atlantic Bight section between Cape Fear and the Savannah River, versus dimensionless time t/T
Several conclusions can be drawn with the present models. The groundwater tidal prism is 11 m3 per m of shoreline, or 3.5 × 106 m3 for the entire 320-km-long study area. Benthic discharge flux associated with P is 2.5 × 10−4 m3 s−1 per m shoreline, or 81 m3 s−1 over the entire study area. In idealized surface water, q bf.P integrated across the study area and over T is zero, such that Eq. (17) holds.
Benthic flux is recharging (q bf.P < 0) for 48.3% of T and discharging (q bf.P > 0) for 51.7% of T. Benthic flux continues to recharge for the first 24.7% of ebb tide, and to discharge for the first 28.1% of flood tide. Peak q br.P integrated across the bed (8.0 × 10−4 m3 s−1 per m of shoreline) exceeds peak q bd.P integrated across the bed (7.3 × 10−4 m3 s−1 per m of shoreline). Equation (17) and the discharge-recharge temporal imbalance (Fig. 9) require this exceedance.
Benthic discharge flux q bf.P to the study area describes \( \left( {81\,{{\text{m}}^3}{{\text{s}}^{ - 1}}} \right)/\left( {347{{\text{m}}^3}{{\text{s}}^{ - 1}}} \right) = 23\% \) of Moore’s (1996) observation. The unexplained 77% remains to be described by other forcing mechanisms, such as terrestrial hydraulic gradient, wave setup, wave-induced groundwater pulse, density gradients, or wave-forced q bf; or possibly by error and/or uncertainty in the observation, or error associated with the abstraction of the natural system with simple models.
Conclusions
Benthic flux q bf.P integrates to zero over one tidal period T in an idealized two-dimensional x–z oriented system. Locally, q bf.P may exhibit in one direction, while the profile-integrated q bf.P exhibits transport in the other direction. A π/4 phase lag exists between tidal extrema and null points in the q bf.P signal. This phase lag is driven by the dynamics of the phreatic surface away from the inclined bed. These dynamics also cause a double q bd.P maxima, such that q bd.P peaks twice, with a lower peak near dimensionless time t/T ≈ 0.25 and a higher peak near t/T ≈ 0.5. The duration of discharge exceeds the duration of recharge over 0 < ε ≤ 0.5.
Two dimensionless numbers allow direct estimation of the groundwater tidal prism P, and characterization of associated benthic flux q bf.P. Specifically, the benthic flux q bf.P is directly proportional to tidal frequency σ, porosity n, and tidal amplitude A; and inversely proportional to the wave number λ in the porous medium. Higher amplitude tides, an increase in medium porosity, shorter tidal periods, or longer groundwater waves increase the amplitude of q bf.P. It is shown that P is also directly proportional to both porosity n and tidal amplitude A, and inversely proportional to the wave number λ in the porous medium. Higher amplitude tides, an increase in medium porosity, or longer groundwater waves increase the groundwater tidal prism P.
The present models reinforce conclusions made by other investigators. Tidally forced benthic flux oscillates between discharge and recharge conditions, and the flux signal lags the tidal signal. The inland phreatic surface is out of phase with the phreatic surface closer to surface water. The benthic flux signal is not symmetrical, such that benthic discharge and benthic recharge exhibit different durations and peak magnitudes. Peak benthic recharge occurs during flood tide. Benthic flux does not integrate to zero over one tidal cycle, at all points on the bed.
The present models quantify the role that tide plays in mixing surface-water, groundwater, and associated constituents within coastal zones. For example, the present models can be used to estimate the role that tide plays in estuarine pollutant loading. The present models provide insight into the relative effect of benthic forcings that drive mixing processes, when used in combination with other models driven by different forcing mechanisms such as waves or terrestrial hydraulic gradient.
Abbreviations
- 226 Ra :
-
Radium-226
- A :
-
Tidal amplitude [L]
- H :
-
Depth to base of the hydrogeologic unit [L]
- K :
-
Hydraulic conductivity [LT −1]
- L :
-
Wave length in a porous medium [L]
- P :
-
Groundwater tidal prism [L 3]
-
 :
: -
Dimensionless groundwater tidal prism
- T :
-
Wave period [T]
- \( {\hat V_{\text{gw}}} \) :
-
Volume of water in a hydrogeologic unit [L 3]
- \( \Delta {\hat V_{\text{gw}}} \) :
-
Volume of water fluxing into or out of a hydrogeologic unit between t 1 and t 2 [L 3]
- \( \partial {\hat V_{\text{gw}}}/\partial t \) :
-
qbf.P integrated across the inclined bed [L3T−1]
- d ts :
-
Inland over-height elevation [L]
- h :
-
Elevation of the phreatic surface within the porous medium [L]
- q bd :
-
Benthic discharge flux, property specific units: for example \( \left[ {{L^3}{T^{ - 1}}{L^{ - 2}} = L{T^{ - 1}}} \right] \) for a benthic volume discharge flux, [M 3 T −1 L −2] for a benthic mass discharge flux
- q bf :
-
Benthic flux, property specific units
- q br :
-
Benthic recharge flux, property specific units
- q bd.P :
-
P-forced benthic discharge flux [LT−1]
- q bf.P :
-
P-forced benthic flux [LT−1]
- q br.P :
-
P-forced benthic recharge flux [LT−1]
- s b :
-
Slope of inclined bed [LL −1]
- t :
-
Time [T]
- t/T :
-
Dimensionless time
- x :
-
Cartesian horizontal (offshore) dimension [L]
- \( \hat x \) :
-
x-coordinate on the inclined bed [L]
-
 :
: -
x-coordinate on the inclined bed at high tide [L]
-
 :
: -
x-coordinate on the inclined bed at low tide [L]
- y :
-
Cartesian horizontal (along-shore) dimension [L]
- z :
-
Cartesian vertical dimension [L]
- \( \hat z \) :
-
Vertical coordinate on the inclined bed [L]
- Φ:
-
Dimensionless q bf.P integrated across the inclined bed
- Ω:
-
(Surface-water) tidal prism [L 3]
- β:
-
Angle of inclined bed, with respect to horizontal
- ε:
-
Nielsen’s (1990) perturbation parameter
- η:
-
Elevation of the free-water surface in the tidally-forced, surface-water body [L]
- λ:
-
Wave number in a porous medium, \( \lambda = 2\pi /L \) [L −1]
- λ B :
-
Boussinesq wave number in a porous medium [L −1]
- λr :
-
Real component of wave number in a porous medium [L −1]
- λι :
-
Imaginary component of wave number in a porous medium [L −1]
- n :
-
Porosity [L 3 L −3]
- σ:
-
Radial tidal frequency, \( \sigma = 2\pi /T \) [T −1]
-
 :
: -
High tide
-
 :
: -
Low tide
- P:
-
Related to the groundwater tidal prism
- bd:
-
Benthic discharge
- bf:
-
Benthic flux
- br:
-
Benthic recharge
- 0:
-
Roots of Eq. (9)
References
Bokuniewicz HJ (1992) Analytical descriptions of subaqueous groundwater seepage. Estuaries 15(4):458–464
Cartwright N (2004) Groundwater dynamics and the salinity structure in sandy beaches. PhD Dissertation, University of Queensland, Australia
Cartwright N, Nielsen P (2001) Groundwater dynamics and salinity in coastal barriers. First international conference on saltwater intrusion and coastal aquifers: monitoring, modeling, and management, Essaouira, Morocco, 23–25 April 2001
Cartwright N, Li L, Nielsen P (2004a) Response of the salt-freshwater interface in a coastal aquifer to a wave-induced groundwater pulse: field observations and modeling. Adv Water Resour 27(3):297–303
Cartwright N, Nielsen P, Li L (2004b) Experimental observations of watertable waves in an unconfined aquifer with a sloping boundary. Adv Water Resour 27(10):991–1004
Colbert SL, Berelson WM, Hammond DE (2008) Radon-222 budget in Catalina Harbor, California: 2. flow dynamics and residence time in a tidal beach. Limnol Oceanogr 53(2):659–665
Dean RG, Dalrymple RA (2002) Coastal processes with engineering applications. Cambridge University Press, New York
deSieyes NR, Yamahara KM, Layton BA, Joyce EH, Boehm AB (2008) Submarine discharge of nutrient-enriched fresh groundwater at Stinson Beach, California is enriched during neap tides. Limnol Oceanogr 53(4):1434–1445
King JN, Mehta AJ, Dean RG (2009) Generalized analytical model for benthic water flux forced by surface gravity waves. J Geophys Res 114:C04004
Li L, Barry DA, Stagnitti F, Parlange JY (1999) Submarine groundwater discharge and associated chemical input to a coastal sea. Water Resour Res 35(11):3253–3259
Li L, Barry DA, Stagnitti F, Parlange JY, Jeng DS (2000) Beach water table fluctuations due to spring-neap tides: moving boundary effects. Adv Water Resour 23(8):817–824
Li HL, Boufadel MC, Weaver JW (2008) Tide-induced seawater-groundwater circulation in shallow beach aquifers. J Hydrol 352(1–2):211–224
Mango AJ, Schmeeckle MW, Furbish DJ (2004) Tidally induced groundwater circulation in an un-confined coastal aquifer modeled with a Hele-Shaw cell. Geology 32(3):233–236
Michael HA, Mulligan AE, Harvey CF (2005) Seasonal oscillations in water exchanges between aquifers and the coastal ocean. Nature 436:1145–1148
Moore WS (1996) Large groundwater inputs to coastal waters revealed by Ra-226 enrichments. Nature 380(6575):612–614
Moore WS (1999) The subterranean estuary: a reaction zone of ground water and sea water. Mar Chem 65(1–2):111–125
Moore WS, Wilson AM (2005) Advective flow through the upper continental shelf driven by storms, buoyancy, and submarine groundwater discharge. Earth Planet Sci Lett 235(3–4):564–576
Nielsen P (1990) Tidal dynamics of the water-table in beaches. Water Resour Res 26(9):2127–2134
Prieto C, Destouni G (2005) Quantifying hydrological and tidal influences on groundwater discharges into coastal waters. Water Resour Res 41:W12427
Robinson C, Li L, Barry DA (2007a) Effect of tidal forcing on a subterranean estuary. Adv Water Resour 30:851–865
Robinson C, Li L, Prommer H (2007b) Tide-induced recirculation across the aquifer-ocean interface. Water Resour Res 43:W07428
Robinson C, Brovelli A, Barry DA, Li L (2009) Tidal influence on BTEX biodegradation in sandy coastal aquifers. Adv Water Resour 32:16–28
Teo HT, Jeng DS, Seymour BR, Barry DA, Li L (2003) A new analytical solution for water table fluctuations in coastal aquifers with sloping beaches. Adv Water Resour 26(12):1239–1247
US Army Corps of Engineers (2002) Coastal Engineering Manual. Engineering Manual 1110-2-1100, US Army Corps of Engineers, Washington, DC
Younger PL (1996) Submarine groundwater discharge. Nature 382(6587):121–122
Acknowledgements
Comments from L.K. Brakefield-Goswami, P.A. Howd, D.F. Payne, C.G. Smith, and three anonymous reviewers improved the manuscript. C.I. Voss, E. Abarca Cameo, M.G. Deacon, S.C. Cooper, S. Duncan, and S. Schemann edited the manuscript. This work was partially funded by the US Geological Survey, Water Resources Discipline.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Elements of Eq. (6)
Volume \( {\hat V_{{\text{gw}}.1}} \) is the volume per meter of shoreline between the phreatic surface h(x,t) and the still-water surface, from point \( \hat x \) on the inclined bed to x → ∞, as shown in Fig. 2a.
Each term in Eq. (22) is evaluated separately:
Volume \( {\hat V_{{\text{gw}}.2}} \) is the volume per meter of shoreline between the inclined bed and the base of the hydrogeologic unit, from point \( \hat x \) on the inclined bed to the intersection of the inclined bed and the impermeable base of the hydrogeologic unit, as shown in Fig. 2a.
Volume \( {\hat V_{{\text{gw}}.3}} \) is the volume per meter of shoreline between the still-water surface and the impermeable base of the hydrogeologic unit, from point \( \hat x \) on the inclined bed to x → ∞, as shown in Fig. 2a.
Elements of Eq. (14)
Volume \( {\hat V_{{\text{gw}}.4}} \) is the volume per meter of shoreline between the inclined bed and the phreatic surface h(x,t 1), from point \( {\hat x_1} \) to point \( {\hat x_2} \), both located on the inclined bed, as shown in Fig. 2b.
Volume \( {\hat V_{{\text{gw}}.5}} \) is the volume per meter of shoreline between the phreatic surfaces h(x,t 1) and h(x,t 2), from point \( {\hat x_2} \) on the inclined bed to x → ∞, as shown in Fig. 2b.
Rights and permissions
About this article
Cite this article
King, J.N., Mehta, A.J. & Dean, R.G. Analytical models for the groundwater tidal prism and associated benthic water flux. Hydrogeol J 18, 203–215 (2010). https://doi.org/10.1007/s10040-009-0519-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10040-009-0519-y
















 :
: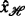 :
: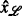 :
: :
: :
: