Assessing the Hydraulic Conductivity Anisotropy and Skin-Effect Based on Data of Slug Tests in Partially Penetrating Wells

Abstract

A semianalytic and approximate analytical solution is given to the problem of slug test in a partially penetrating well in a confined or unconfined anisotropic aquifer. An asymptotic solution is given to the problem of slug test in a partially penetrating well in an unconfined aquifer. The latter solution, unlike the semiempiric Bouwer–Rice method, takes into account hydraulic conductivity anisotropy and skin effect. Levenberg–Marquardt algorithm was used to develop a method for determining hydraulic conductivity anisotropy and skin effect based on data of slug tests in partially penetrating wells in confined or unconfined aquifer.

INTRODUCTION

Slug tests are the most rapid and economically efficient methods for determining the hydraulic characteristics of aquifers. They are based on an abrupt change of water level in a well (with the use of an instantaneous addition or pumping out, compression, short-time pumping, etc.) followed by recording the curve of level (pressure) recovery. An important feature of the slug tests is their short duration in time and no need to measure the flow rate. The estimates of aquifer characteristics obtained by the interpretation of such tests commonly refer to the zone nearest to the well.

The hydraulic conductivity is often determined by the data of slug tests processed by graphical analytic methods proposed by Hvorslev, Bouwer and Rice, Dagan, etc. [14]. Such methods are based on the model of incompressible fluid flow and differ by the method used to calculate the form factor, which depends only on hydraulic conductivity anisotropy and thegeometrical parameters of well screen and drainage domain [29]. The drawbacks of graphical analytic methods include the relatively low accuracy of hydraulic conductivity estimates, especially, in the case of screen clogging [7, 19, 20].

The first analytical solution to the problem of water level recovery in a vertical well after instantaneous charge of water was obtained by S.G. Kamenetskii [2, 4]. This solution was used to construct type curves and propose a method for the analysis of slug-test data [1, 5]. Later, H. Cooper, J.D. Bredehoeft, and I.S. Papadopulos obtained an analogous solution of the problem and constructed a set of type curves of water level recovery in a vertical well [16]. In the more general formulation, the problem of instantaneous pumping out from a vertical well was discussed by N.I. Gamayunov and B.S. Sherzhukov [3, 12], who took into account the flow through a low-permeability interlayer from an aquifer with a constant head. An analytical solution of the problem of instantaneous pumping out from a vertical well with skin-effect taken into account and sets of appropriate type curves are given in [2, 11, 24, 26]. Later, many other analytical solutions were obtained for the problem of slug tests, in particular, for the case of vertical wells in heterogeneous formations and in double-porosity formations [14], for partially penetrating vertical wells [17, 20, 27], horizontal wells [8, 25], etc.

Along with obvious advantages, the slug tests have some drawbacks. The slug tests are known to give ambiguous estimates of aquifer characteristics in some cases when wells with low-permeability skin effect are involved [7, 14]. The problem of joint estimation of hydraulic conductivity, compressibility, and skin effect based on the data of a single slug test can hardly be solved unless any a priori data on these characteristics are available [2, 11, 14]. The uncertainty of the characteristics to be sought for can be reduced by head measurements in observation wells or piezometer located near the perturbation well [14]. Slug tests can be combined with studies of interference in the vertical direction [21]. In that case, the head is measured by high-accuracy pressure transducers in the tested and observed intervals in the well, isolated from one another by inflatable packers. Successive interval slug tests in a single well at different depths can be used to estimate the heterogeneity of the hydraulic conductivity anisotropy and compressibility in a formation over its thickness [21].

The solution of the problems of fluid flow to partially penetrating wells faces difficulties associated with specifying mixed boundary conditions on the cylindrical surface of the well: a constant-head condition is specified within the penetration zone, and a no-flow condition, in the cased borehole section. Problems of this type with mixed boundary conditions, sometimes referred to as Gilbert problems, are among complex problems of mathematical physics. For example, an accurate solution of the problem of steady-state fluid flow to a partially penetrating well, obtained by M.M. Glogovskii, leads to a system of an infinite number of equations with an infinite number of variables [6]. Starting from the work of A.L. Khein [10], the majority of analytical solutions of the problems of transient fluid flow to a partially penetrating vertical well were derived from the assumption that the flux is uniformly distributed across the well screen [2, 18]. The model of a partially penetrating well with flux uniformly distributed across the well screen leads to a nonuniform distribution of head within this interval. A more physically sound is the model of infinite-conductivity well with constant head within the well screen . An approximate approach is also used with a uniform flux across the well screen and weighted-mean head calculated there [17, 20, 27]. In studies [9, 15, 23], the problem of transient water flow to a partially penetrating well is reduced to a system of integral equations describing the flux distribution across the well screen , which is next solved numerically. The condition of constant head within the well screen , as well as some other complicating factors, such as the heterogeneity of the formation, clogging, the presence of free free water surface , can be taken into account in numerical simulation of slug tests in partially penetrating wells [7].

SEMIANALYTICAL SOLUTION OF THE PROBLEM OF SLUG TEST IN A PARTIALLY PENETRATING WELL

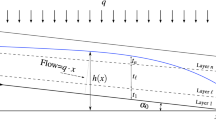
Consider a transient water flow in an infinite anisotropic formation after an instantaneous change in the level in a partially penetrating well by s₀ (Fig. 1). The level in the well s(t) will be rising (dropping), approaching its initial value, because of water inflow (outflow) with a discharge rate $C\frac{{\partial s}}{{\partial t}}$ ($C = \pi r_{c}^{2}$ is the wellbore storage coefficient , r_c is the internal radius of the pipe). The objective is to determine the function of head change $h\left( {r,z,t} \right)$ within the flow domain $r > {{r}_{w}}$, $0 \leqslant z \leqslant b$, and the function s(t), describing level change in the well at $t > 0$. In the dimensionless form, the change in the head in the formation can be described by the piezoconductivity equation:

$$\frac{1}{{{{r}_{d}}}}\frac{\partial }{{\partial {{r}_{d}}}}\left( {{{r}_{d}}\frac{{\partial {{h}_{d}}}}{{\partial {{r}_{d}}}}} \right) + \frac{1}{{b_{d}^{2}}}\frac{{{{\partial }^{2}}{{h}_{d}}}}{{\partial z_{d}^{2}}} = \frac{{\partial {{h}_{d}}}}{{\partial {{t}_{d}}}}$$

(1)

with the initial

$${{h}_{d}}\left( {{{r}_{d}},{{z}_{d}},0} \right) = 0,\,\,\,\,{{s}_{d}}\left( 0 \right) = 1,$$

(2)

and boundary conditions

$${{h}_{d}}\left( {\infty ,{{z}_{d}},{{t}_{d}}} \right) = 0,$$

(3)

$${{\left. {\frac{{\partial {{h}_{d}}}}{{\partial {{z}_{d}}}}} \right|}_{{{{z}_{d}} = 0}}} = 0,\,\,\,\,{{\left. {\frac{{\partial {{h}_{d}}}}{{\partial {{z}_{d}}}}} \right|}_{{{{z}_{d}} = 1}}} = 0,$$

(4)

$${{\left. {\frac{{\partial {{h}_{d}}}}{{\partial {{r}_{d}}}}} \right|}_{{{{r}_{d}} = 1}}} = 0,\,\,\,\,0 \leqslant {{z}_{d}} < {{z}_{{1d}}},\,\,\,\,{{z}_{{2d}}} < {{z}_{d}} \leqslant 1,$$

(5)

$$\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {q\left( {{{z}_{d}},{{t}_{d}}} \right)} d{{z}_{d}} = - {{C}_{d}}\frac{{\partial {{s}_{d}}\left( {{{t}_{d}}} \right)}}{{\partial {{t}_{d}}}},$$

(6)

$${{s}_{d}}\left( {{{t}_{d}}} \right) = {{h}_{d}}\left( {1,{{z}_{d}},{{t}_{d}}} \right) - Sq\left( {{{z}_{d}},{{t}_{d}}} \right),\,\,\,\,{{z}_{{1d}}} \leqslant {{z}_{d}} \leqslant {{z}_{{2d}}},$$

(7)

where ${{h}_{d}} = \frac{h}{{{{s}_{0}}}}$, ${{s}_{d}} = \frac{s}{{{{s}_{0}}}}$, ${{t}_{d}} = \frac{{{{k}_{r}}t}}{{{{S}_{s}}r_{w}^{2}}}$, ${{r}_{d}} = \frac{r}{{{{r}_{w}}}}$, ${{z}_{d}} = \frac{z}{b}$, ${{b}_{d}} = \frac{b}{{{{r}_{w}}}}\sqrt {\frac{{{{k}_{r}}}}{{{{k}_{z}}}}}$, ${{C}_{d}} = \frac{C}{{2\pi b{{S}_{s}}r_{w}^{2}}}$, $q\left( {{{z}_{d}},{{t}_{d}}} \right) = - {{\left. {\left( {{{r}_{d}}\frac{{\partial {{h}_{d}}}}{{\partial {{r}_{d}}}}} \right)} \right|}_{{{{r}_{d}} = 1}}}$, h is the head; k_r, k_z are the hydraulic conductivities in the horizontal and vertical directions; b is formation thickness; S_s is the compressibility; r_w is screen radius; S is skin-factor.

Fig. 1.

Schematic partially penetrating well.

Applying Laplace transform with respect to time and finite Fourier cosine-transform with respect to coordinate z_d to (1)‒(7) [9, 23], we obtain

$$\begin{gathered} {{{\bar {h}}}_{d}}\left( {{{r}_{d}},{{z}_{d}},u} \right) = F\left( {{{r}_{d}},u} \right)\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)d\xi } \\ + \,\,2\sum\limits_{m = 1}^\infty {F\left( {{{r}_{d}},{{\lambda }_{m}}} \right)\cos \left( {\pi m{{z}_{d}}} \right)\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)\cos \left( {\pi m\xi } \right)d\xi } } , \\ \end{gathered} $$

(8)

where u is Laplace transform parameter; ${{\lambda }_{m}} = u + \frac{{{{\pi }^{2}}{{m}^{2}}}}{{b_{d}^{2}}}$; $F\left( {x,y} \right) = \frac{{{{K}_{0}}\left( {x\sqrt y } \right)}}{{\sqrt y {{K}_{1}}\left( {\sqrt y } \right)}}$; K₀(x), K₁(x) are modified Bessel functions of the second kind, zero and first orders, respectively.

The functions describing the variations of water level and inflow density within the screen interval are determined by solving the system of integral equations:

$$\begin{gathered} {{{\bar {s}}}_{d}} = F\left( {1,u} \right)\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)d\xi } \\ + \,\,2\sum\limits_{m = 1}^\infty {F\left( {1,{{\lambda }_{m}}} \right)\cos \left( {\pi m{{z}_{d}}} \right)\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)\cos \left( {\pi m\xi } \right)d\xi } } \\ + \,\,S\bar {q}\left( {{{z}_{d}},u} \right), \\ \end{gathered} $$

(9)

$$\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)d\xi } = {{C}_{d}}\left( {1 - u{{{\bar {s}}}_{d}}} \right).$$

(10)

For the case of a partially penetrating well in an unconfined aquifer, we assume that, during the test period, the free surface remains undisturbed and the well screen is not drained. Replacing the second boundary condition in (4) by ${{h}_{d}}\left( {{{r}_{d}},1,{{t}_{d}}} \right) = 0$ and applying to (1)‒(7) Laplace transform with respect to time and modified finite Fourier sine-transform with respect to coordinate z_d [23], we obtain the following system of integral equations:

$$\begin{gathered} {{{\bar {s}}}_{d}} = 2\sum\limits_{m = 1}^\infty {F\left( {1,{{\mu }_{m}}} \right)\cos \left( {\frac{{\pi \left( {2m - 1} \right){{z}_{d}}}}{2}} \right)} \\ \times \,\,\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)\cos \left( {\frac{{\pi \left( {2m - 1} \right)\xi }}{2}} \right)d\xi } + S\bar {q}\left( {{{z}_{d}},u} \right), \\ \end{gathered} $$

(11)

$$\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)d\xi } = {{C}_{d}}\left( {1 - u{{{\bar {s}}}_{d}}} \right),$$

(12)

where ${{\mu }_{m}} = u + \frac{{{{\pi }^{2}}{{{\left( {2m - 1} \right)}}^{2}}}}{{4b_{d}^{2}}}$.

For numerical solution of the systems of integral equations (9), (10) and (11), (12), the screen interval is divided into segments and it is assumed that water inflow to each segment is uniform. This yields a system of linear algebraic equations for determining Laplace transforms of variations of water head and flux across the screen interval :

$$\left[ {\begin{array}{*{20}{c}} {{{A}_{{11}}} + S}& \cdots &{{{A}_{{1m}}}}&{ - 1} \\ \vdots &{}& \vdots & \vdots \\ {{{A}_{{m1}}}}& \cdots &{{{A}_{{mm}}} + S}&{ - 1} \\ {\Delta {{\zeta }_{1}}}& \cdots &{\Delta {{\zeta }_{m}}}&{{{C}_{d}}u} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\bar {q}}}_{1}}} \\ \vdots \\ {{{{\bar {q}}}_{m}}} \\ {{{{\bar {s}}}_{d}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ \vdots \\ 0 \\ {{{C}_{d}}} \end{array}} \right],$$

(13)

where ${{A}_{{ij}}} = F\left( {1,u} \right)\Delta {{\zeta }_{i}}$ + $2\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\lambda }_{m}}} \right)}}{{\pi m}}\sin \left( {\frac{{\pi m\Delta {{\zeta }_{i}}}}{2}} \right)} \times$$\cos \left( {\pi m{{{\bar {\zeta }}}_{i}}} \right)\cos \left( {\pi m{{{\bar {\zeta }}}_{j}}} \right)$ for confined aquifer; ${{A}_{{ij}}} = 4\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\mu }_{m}}} \right)}}{{\pi \left( {2m - 1} \right)}}\sin \left( {\frac{{\pi \left( {2m - 1} \right)\Delta {{\zeta }_{i}}}}{4}} \right)}$ × $\cos \left( {\frac{{\pi \left( {2m - 1} \right){{{\bar {\zeta }}}_{i}}}}{2}} \right)\cos \left( {\frac{{\pi \left( {2m - 1} \right){{{\bar {\zeta }}}_{j}}}}{2}} \right)$ for unconfined aquifer; $\Delta {{\zeta }_{i}} = {{\zeta }_{i}} - {{\zeta }_{{i - 1}}}$, ${{\bar {\zeta }}_{i}} = {{\left( {{{\zeta }_{i}} + {{\zeta }_{{i - 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\zeta }_{i}} + {{\zeta }_{{i - 1}}}} \right)} 2}} \right. \kern-0em} 2}$, $i = 1, \ldots ,m$, ${{z}_{{1d}}} = {{\zeta }_{0}} < {{\zeta }_{0}} < \ldots < {{\zeta }_{m}} = {{z}_{{2d}}}$. The system of linear algebraic equations is solved by stabilized biconjugate-gradient method BiCGStab with preconditioning. The inverse Laplace transform is performed numerically using Stehfest algorithm [9].

APPROXIMATE SOLUTION OF THE PROBLEM OF SLUG TEST IN A PARTIALLY PENETRATING WELL

Suppose that the distribution of water inflow over the screen interval is uniform. Integrating equations (9) and (11) with respect to z_d and considering (10), (12), we find the change of the weighted-mean head within the screen interval of a partially penetrating well:

$${{\bar {s}}_{d}} = \frac{{{{C}_{d}}\left( {u{{{\bar {h}}}_{d}} + \frac{S}{{{{l}_{d}}}}} \right)}}{{1 + u{{C}_{d}}\left( {u{{{\bar {h}}}_{d}} + \frac{S}{{{{l}_{d}}}}} \right)}}.$$

(14)

Here ${{l}_{d}} = {{z}_{{2d}}} - {{z}_{{1d}}}$; ${{\bar {h}}_{d}} = \frac{{F\left( {1,u} \right)}}{u} + \frac{2}{{ul_{d}^{2}}}$ × $\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\lambda }_{m}}} \right)}}{{{{\pi }^{2}}{{m}^{2}}}}{{{\left[ {\sin \left( {\pi m{{z}_{{2d}}}} \right) - \sin \left( {\pi m{{z}_{{1d}}}} \right)} \right]}}^{2}}}$ is the Laplace transform of the weighted-mean head within the screen interval of a partially penetrating well operated with constant pumping rate in a confined aquifer [9]; ${{\bar {h}}_{d}} = \frac{8}{{ul_{d}^{2}}}\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\mu }_{m}}} \right)}}{{{{\pi }^{2}}{{{\left( {2m - 1} \right)}}^{2}}}}}$ × ${{\left[ {\sin \left( {\frac{{\pi \left( {2m - 1} \right){{z}_{{2d}}}}}{2}} \right) - \sin \left( {\frac{{\pi \left( {2m - 1} \right){{z}_{{1d}}}}}{2}} \right)} \right]}^{2}}$ for unconfined aquifer. If a partially penetrating well penetrates an isotropic confined aquifer, then (14) coincides with the solution obtained by D. Dougherty and D. Babu [17]. For a fully penetrating well in a confined aquifer (${{z}_{{1d}}} = 0$, ${{z}_{{2d}}} = 1$, l_d = 1), expression (14) reduces to the solution of the problem from studies [11, 24], and at S = 0, to the solution of S.G. Kamenetskii [4]. Note that the solution proposed by Z. Hyder et al. [14, 20], known as KGS (Kansas Geological Survey) model, uses a model of finite-thickness skin-effect. A similar model of skin-effect is used in the solution of H. Yeh et al. [27] and in the solution of T. Perina and T. Lee [23].

Now we study the behavior of solution (14) for large values of ${{t}_{d}}$ in the case of unconfined aquifer. Applying to [14] the inverse Laplace transform at $u \to 0$, which corresponds to ${{t}_{d}} \to \infty$, we obtain the following asymptotic solution to the problem of slug test in unconfined formation :

$${{s}_{d}}\left( {{{t}_{d}}} \right) = \exp \left[ { - \frac{{{{t}_{d}}}}{{{{C}_{d}}\left( {{{S}_{p}} + \frac{S}{{{{l}_{d}}}}} \right)}}} \right],$$

(15)

where ${{S}_{p}} = \frac{2}{{l_{d}^{2}b_{d}^{2}}}\sum\nolimits_{m = 1}^\infty {\frac{{{{K}_{0}}\left( {{{\sigma }_{m}}} \right)}}{{\sigma _{m}^{3}{{K}_{0}}\left( {{{\sigma }_{m}}} \right)}}}$ × ${{\left[ {\sin \left( {\frac{{\pi \left( {2m - 1} \right){{z}_{{2d}}}}}{2}} \right) - \sin \left( {\frac{{\pi \left( {2m - 1} \right){{z}_{{1d}}}}}{2}} \right)} \right]}^{2}}$ is pseudoskin-factor, ${{\sigma }_{m}} = \frac{{\pi \left( {2m - 1} \right)}}{{2{{b}_{d}}}}$. The total skin-factor ${{S}_{p}} + \frac{S}{{{{l}_{d}}}}$ in (15) is a characteristic of the degree of well penetration. Note that the value of pseudoskin-factor S_p is inversely proportional to the form factor of a partially penetrating well in an unconfined formation [29].

Another way to take into account the skin-effect is to replace the screen radius r_w by the effective radius ${{\tilde {r}}_{w}} = {{r}_{w}}\exp \left( { - S} \right)$ [2, 11, 14]. With this change, the expression (15) becomes

$${{s}_{d}}\left( {{{{\tilde {t}}}_{d}}} \right) = \exp \left[ { - \frac{{{{{\tilde {t}}}_{d}}}}{{{{{\tilde {C}}}_{d}}{{{\tilde {S}}}_{p}}}}} \right],$$

(16)

where the tilde implies that, in dimensionless parameters, screen radius r_w is replaced by the effective radius ${{\tilde {r}}_{w}}$. Calculations by formulas (15) and (16) have shown that both methods used to account for skin-effect give the same results.

Unlike Bouwer–Rice semiempiric approach [13], the asymptotic solution (15) allows taking into account the hydraulic conductivity anisotropy and skin-effect. V. Zlotnik [28] proposed a modification of Bower–Rice approach for taking into account the hydraulic conductivity anisotropy with the use of the replacement of screen radius r_w by effective radius $r_{w}^{*} = {{r}_{w}}\sqrt {\frac{{{{k}_{z}}}}{{{{k}_{r}}}}}$.

Formula (15) can be used to readily show that skin-effect in Bower–Rice method can be taken into account through replacing the form factor P by 1/(1/P + S). According to modified Bower–Rice method and asymptotic solution (15), the plot of changes in water level in coordinates ln s ‒ t is a straight line with a slope depending on the hydraulic conductivity anisotropy and skin-effect. This demonstrates that the application of graphical–analytical methods to interpret slug tests in partially penetrating wells without the use of a priori information about the hydraulic conductivity anisotropy and skin-effect can cause errors in estimates of hydraulic conductivity [7, 14, 19, 28].

AN ANALYTICAL SOLUTION TO THE PROBLEM OF INTERVAL SLUG TEST OF A VERTICAL WELL

Consider a problem of evaluating the head in test and observation intervals of a well (Fig. 2) after an instantaneous change in the head in the test interval by a value of s₀. In such case, the formulation of problem (1)‒(7) is supplemented by a boundary condition for the observation interval

$$\begin{gathered} \int\limits_{{{z}_{{3d}}}}^{{{z}_{{4d}}}} {q\left( {{{z}_{d}},{{t}_{d}}} \right)d{{z}_{d}}} = - {{C}_{{2d}}}\frac{{\partial {{s}_{{2d}}}\left( {{{t}_{d}}} \right)}}{{\partial {{t}_{d}}}}, \\ {{s}_{{2d}}}\left( {{{t}_{d}}} \right) = {{h}_{d}}\left( {1,{{z}_{d}},{{t}_{d}}} \right) - {{S}_{2}}q\left( {{{z}_{d}},{{t}_{d}}} \right),\,\,\,\,{{z}_{{3d}}} \leqslant {{z}_{d}} \leqslant {{z}_{{4d}}}, \\ \end{gathered} $$

(17)

${{C}_{{2d}}} = \frac{{{{C}_{2}}}}{{2\pi b{{S}_{s}}r_{w}^{2}}}$ is the dimensionless coefficient reflecting the wellbore storage effect of the observation interval, S₂ is the skin-factor of the observation interval.

Fig. 2.

Schematic slug test of a well for interference in the vertical direction (z₁–z₂ and z₃–z₄ are the tested and observation intervals).

Suppose that the distribution of water inflow in the test and observation intervals is uniform. Now the Laplace transform of the averaged heads over the length of the intervals have the form:

$${{\bar {s}}_{{1d}}} = \frac{{{{U}_{1}}{{I}_{2}} - {{U}_{2}}{{Y}_{2}}}}{{{{I}_{1}}{{I}_{2}} - {{Y}_{2}}{{Y}_{1}}}},\,\,\,\,{{\bar {s}}_{{2d}}} = \frac{{{{U}_{2}}{{I}_{1}} - {{U}_{1}}{{Y}_{1}}}}{{{{I}_{1}}{{I}_{2}} - {{Y}_{2}}{{Y}_{1}}}},$$

(18)

where ${{I}_{i}} = 1 + {{C}_{{id}}}{{u}^{2}}{{\bar {h}}_{{ii}}} + \frac{{{{S}_{i}}{{C}_{{id}}}u}}{{{{l}_{{id}}}}}$; ${{Y}_{i}} = {{C}_{{id}}}{{u}^{2}}{{\bar {h}}_{{12}}}$; ${{U}_{2}} = {{C}_{{1d}}}u{{\bar {h}}_{{12}}}$; ${{U}_{1}} = {{C}_{{1d}}}u{{\bar {h}}_{{11}}} + \frac{{{{S}_{1}}{{C}_{{1d}}}}}{{u{{l}_{{1d}}}}}$; ${{\alpha }_{1}} = {{z}_{{1d}}}$; ${{\beta }_{1}} = {{z}_{{2d}}}$; ${{\alpha }_{2}} = {{z}_{{3d}}}$; ${{\beta }_{2}} = {{z}_{{4d}}}$; ${{\bar {h}}_{{ij}}} = \frac{{F\left( {1,u} \right)}}{u} + \frac{2}{u}\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\lambda }_{m}}} \right)}}{{{{\pi }^{2}}{{m}^{2}}}}{{\Psi }_{i}}} {{\Psi }_{j}}$ for a confined aquifer, $i,j = 1,2$; and ${{\bar {h}}_{{ij}}} = \frac{8}{u}\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\mu }_{m}}} \right)}}{{{{\pi }^{2}}{{{\left( {2m - 1} \right)}}^{2}}}}} {{\Omega }_{i}}{{\Omega }_{j}}$ for an unconfined aquifer, $i,j = 1,2$; ${{\Psi }_{i}} = \frac{{\sin \left( {\pi m{{\beta }_{i}}} \right) - \sin \left( {\pi m{{\alpha }_{i}}} \right)}}{{{{l}_{{id}}}}}$, ${{\Omega }_{i}} = \frac{1}{{{{l}_{{id}}}}}\left[ {\sin \left( {\frac{{\pi \left( {2m - 1} \right){{\beta }_{i}}}}{2}} \right) - \sin \left( {\frac{{\pi \left( {2m - 1} \right){{\alpha }_{i}}}}{2}} \right)} \right]$, ${{l}_{{id}}} = {{\beta }_{i}} - {{\alpha }_{i}}$, $i = 1,2$ (i = 1 is for the test interval, i = 2 is for the observation interval).

The coefficient of the wellbore storage effect in observation interval is ${{C}_{2}} = {{V}_{2}}{{C}_{w}}{{\rho }_{w}}{\text{g}}$ (V₂ is the volume of the observation interval, C_w is water compressibility, ${{\rho }_{w}}$ is water density, g is gravitational acceleration ). Considering that the value of C₂ is small compared with C₁ and assuming in (18) ${{C}_{{2d}}} \approx 0$, we obtain:

$$\begin{gathered} {{{\bar {s}}}_{{1d}}} = \frac{{{{C}_{{1d}}}\left( {u{{{\bar {h}}}_{{11}}} + \frac{{{{S}_{1}}}}{{{{l}_{{1d}}}}}} \right)}}{{1 + u{{C}_{{1d}}}\left( {u{{{\bar {h}}}_{{11}}} + \frac{{{{S}_{1}}}}{{{{l}_{{1d}}}}}} \right)}}, \\ {{{\bar {s}}}_{{2d}}} = \frac{{{{C}_{{1d}}}u{{{\bar {h}}}_{{12}}}}}{{1 + u{{C}_{{1d}}}\left( {u{{{\bar {h}}}_{{11}}} + \frac{{{{S}_{1}}}}{{{{l}_{{1d}}}}}} \right)}}. \\ \end{gathered} $$

(19)

In this case, the expression for head variations in the test interval coincides with (14), i.e., the observation interval has no effect on variations in the head in the test interval.

CALCULATION RESULTS

Figure 3a gives drawdown plots for a partially penetrating well , simulated with the semianalytic solution (13) (full lines), approximate analytical solution (14) (dashed lines), and a numerical solution of the problem by finite-element method (symbols). The simulations were carried out with the following parameter values: s₀ = 3 m, k_r = 5 × 10^–6 m/s, k_z = 10^–6 m/s, S_s = 10^–5 m^–1, C = 5 × 10^–4 m², S = 0, r_w = 0.1 m, b = 10 m, z₁ = 4 m, z₂ = 8 m. Figure 3b gives transformed drawdown plots with the use of relationships [22]:

$$\frac{{\partial {{h}_{d}}\left( {{{t}_{d}}} \right)}}{{\partial \ln {{t}_{d}}}} = \frac{{{{t}_{d}}{{s}_{d}}\left( {{{t}_{d}}} \right)}}{{{{C}_{d}}}},\,\,\,\,I\left( {{{s}_{d}}} \right) = \frac{1}{{{{C}_{d}}}}\int\limits_0^{{{t}_{d}}} {{{s}_{d}}\left( \tau \right)d\tau } .$$

(20)

Fig. 3.

(a) Drawdown plots and (b) transformed drawdown plots for a partially penetrating well ((1, 3) confined and (2, 4) unconfined aquifers).

As can be seen from Fig. 3b, the transformed drawdown plots are similar to the type drawdown and drawdown derivative plots for a well operating at constant rate. The unit slope of the transformed drawdown plots at small times can be used to diagnose the wellbore storage effect . At large times, the zero slope of curve 3 characterizes the radial regime of flow toward a partially penetrating well in a confined aquifer, while the negative slope of curve 4 shows the effect of the upper boundary of an unconfined aquifer.

The solution of an inverse problem for determining the unknown parameters ${{k}_{r}}$, ${{k}_{z}}$ and $S$ is constructed by the minimization of objective function:

$$J = \mathop \sum \limits_{i = 1}^N {{\left( {{{s}_{{{\text{exp}}}}}\left( {{{t}_{i}}} \right) - {{s}_{{{\text{sim}}}}}\left( {{{t}_{i}}} \right)} \right)}^{2}},$$

(21)

where ${{s}_{{{\text{exp}}}}}\left( {{{t}_{i}}} \right)$, ${{s}_{{{\text{sim}}}}}\left( {{{t}_{i}}} \right)$ are the observed and calculated values of water level variations in a well at time moments ${{t}_{i}}$, $i = 1,..,N$. The objective function (21) is minimized with the use of Levenberg–Marquardt algorithm.

Figure 4 gives an example of the interpretation of field data of slug test in a partially penetrating well in an unconfined aquifer. The calculations were carried out with the use of the following input data [14]: s₀ = 0.671 m, C = 1.28 × 10^–2 m², S_s = 2 × 10^–4 m^–1, r_w = 0.125 m, b = 47.87 m, z₁ = 29.58 m, z₂ = 31.1 m. The solution of the inverse problem yielded the following parameter estimates: k_r= 3.97 × 10^–5 m/s, k_z= 3.34 × 10^–5 m/s, S = ‒0.49. Note that the estimates of skin-factor and hydraulic conductivity anisotropy are sensitive to the compressibility of formation. For example, an increase in the compressibility of formation by a factor of two leads to the following parameter estimates: k_r= 3.42 × 10^–5 m/s, k_z= 9.07 × 10^–5 m/s, S = ‒0.28. Estimating the hydraulic conductivity by Bower–Rice method and KGS model yielded 4 × 10^–5 and 4.87 × 10^–5 m/s, respectively [14], which is in good agreement with the results of calculations by the proposed method.

Fig. 4.

(a) (symbols) Observed and (full lines) calculated drawdowns and (b) transformed drawdowns in a partially penetrating well.

Figure 5 gives an example of processing an interval slug test in a vertical well in an unconfined aquifer. The calculations were made with the following input data [21]: s₀= 2.79 m, C₁= 5 × 10^–4 m², r_w= 0.0254 m, b = 12 m, z₁= 7.4 m, z₂= 8 m, z₃= 6.5 m, z₄= 6.8 m. In the solution of inverse problem, the objective function for minimization was taken to be the sum of root-mean-square difference between the observed and calculated head values in the observation and test intervals. Solving the inverse problem yielded the following parameter estimates: k_r= 1.45 × 10^–5 m/s, k_z= 4.16 × 10^–8 m/s, S_s= 3.6 × 10^–5 m^–1, S₁= ‒0.25. The obtained estimates are in agreement with the results of interpretation of interval slug-test given in [21]: k_r= 2.1 × 10^–5 m/s, k_z= 1.3 × 10^–8 m/s, S_s= 1.1 × 10^–5 m^–1.

Fig. 5.

(a) (symbols) Observed and (full lines) calculated drawdowns and (b) transformed drawdowns in test and observation intervals.

CONCLUSIONS

A semianalytical solution was obtained for the problem of slug-test in a partially penetrating well in a confined or unconfined anisotropic aquifer, taking into account the skin-effect and the conditions of uniform head distribution in the screen interval. With the water inflow distribution within the screen interval assumed uniform, an approximate analytical solution of the problem was obtained. An asymptotic solution was given to the problem of slug-test in a partially penetrating well in an unconfined aquifer, and it was shown that the reliable estimate of the hydraulic conductivity by graphical analytical method requires a priori data on the anisotropy of conductivity and skin-effect. An approximate analytical solution was obtained for the problem of interval slug-test in a vertical well in a confined or unconfined anisotropic aquifer. Levenberg–Marquardt algorithm was used to develop a method for determining hydraulic conductivity anisotropy and skin-effect based on data of slug test in partially penetrating wells and interval slug-tests in vertical wells.