Friction in inertial granular flows: competition between dilation and grain-scale dissipation rates

Abstract

Friction plays an important role in the behavior of flowing granular media. The effective friction coefficient is a description of shear strength in both slow and rapid flows of these materials. In this paper, we study the steady state effective friction coefficient $\mu$ in a granular material in two steps. First, we develop a new relationship between the steady state effective friction coefficient, the shear rate, the solid fraction, and grain-scale dissipation processes in a simple shear flow. This relationship elucidates the rate- and porosity-dependent nature of effective friction in granular flows. Second, we use numerical simulations to study how the various quantities in the relationship change with shear rate and material properties. We explore how the relationship illuminates the grain-scale dissipation processes responsible for macroscopic friction. We examine how the competing processes of shearing dilation and grain-scale dissipation rates give rise to rate-dependence. We also compare our findings with previous investigations of effective friction in simple shear.

1 Introduction

Granular flows are ubiquitous in nature and technology [1]. Geologic events such as landslides and earthquakes occur because granular materials are able to transition from a solid state to a flowing state. Industrial processes such as hopper flows and powder transport involve the flow of food and pharmaceutical particles. Defense applications of brittle ceramics rely on the flow of a pulverized bulk material for energy dissipation. All of these applications demonstrate the need to understand granular flows at a fundamental level. Effective friction describes the shear resistance of a flowing granular medium and, in continuum simulations of these events, encodes information about grain-scale and contact-scale processes in a single parameter (see Fig. 1).

Fig. 1

Friction encodes contact-scale and grain-scale information in a single parameter for continuum analysis

Granular flows can be classified as quasi-static, inertial (also referred to as dense), or rapid based on a dimensionless shear rate known as the inertial number [2, 3]. The quasi-static behavior of granular media is typically modeled using critical state soil mechanics [4]. Rapid granular flows are similar in some respects to gases and have therefore been extensively modeled using kinetic theories (e.g. [5, 6]). The intermediate regime of inertial granular flows has, unlike the quasi-static and rapid cases, eluded a unified modeling approach. Nevertheless, researchers have made important progress in understanding inertial granular flows in recent years.

The inertial flow regime corresponds to flows with an inertial number, $I = \dot{\gamma }d/\sqrt{P/\rho _g}$, between approximately 0.001 and 1. Here, $\dot{\gamma }$ is the shear rate ($|\dot{\gamma }|$ in 3D), $d$ is the grain diameter, $P$ is the confining pressure, and $\rho _g$ is the grain density. The inertial number is the ratio of the particle relaxation time $d/\sqrt{P/\rho _g}$ to the macroscopic shear time $\dot{\gamma }^{-1}$, as illustrated in Fig. 2 [2, 7]. This interpretation will be revisited when we develop a new friction relationship in Sect. 2.

Fig. 2

The two timescales associated with the inertial number, $I=T_c/T_{\dot{\gamma }}$

Researchers studying the inertial flow regime have developed empirical relationships between $I$ and the steady state effective friction coefficient $\mu$, the solid fraction $\phi$, and the coordination number $Z$ [2, 8]. For instance, da Cruz et al. [2] proposed a linear relationship between $\mu$ and $I$ given by $\mu = a+bI$ for 2D simple shear flows, where $a$ and $b$ are empirical constants. Jop et al. [8] have proposed the nonlinear relationship $\mu = \mu _1+(\mu _2-\mu _1)/(I_0/I+1)$ for 3D flows where $\mu _1, \mu _2$, and $I_0$ are empirical constants. Jop et al. [8] have also developed a constitutive law for predicting the stress distribution and flow profile for well developed granular flows, using the empirical friction law described above. Other local and non-local continuum models have been developed for inertial flows. Each model takes advantage of one of the empirical friction laws described above [9–11]. These models have provided promising tools for predicting the behavior of granular media in a variety of flow configurations. However, investigative studies of inertial granular flows continue on a more basic level in an effort to understand the processes underlying frictional rate-dependence and the microstructure that develops during an inertial flow [12].

da Cruz et al. [2] studied the evolution of forces and anisotropy in inertial granular flows, showing that the anisotropy of the contact network can be explicitly related to friction. Azema and Radjai similarly showed that a classical stress-force-fabric relation holds for inertial flows, demonstrating another link between friction and contact network anisotropy [13, 14]. Hatano and Kuwano [15] provided another interpretation of friction, using an energy balance equation to derive a steady state friction law very similar to that of rate-and-state theory. Jenkins [16] has provided interesting links between friction and various attributes of inclined plane flows by extending hydrodynamic equations valid for rapid flows to the inertial regime. Sun et al. [17] have studied the energy characteristics of inertial granular flows and revealed a number of correlations between the friction coefficient and energy ratios. All of these studies have provided valuable insight into the nature of effective friction in inertial granular flows.

In this paper, we intend to contribute an additional interpretation of effective friction in granular flows by explicitly relating it to the inertial number, the coordination number, the solid fraction, and grain-scale dissipation rates. In Sect. 2, we develop the friction relationship for steady state simple shear flows by performing an energy balance and a simple statistical analysis. We discuss the resulting picture of friction as a competition between dilation and grain-scale dissipation rates. In Sect. 3, we discuss numerical simulations of simple shear flows and present results showing the accuracy of the proposed friction relation. Simulation results are used to illustrate how the effective friction coefficient can be decomposed into contributions from grain-scale dissipation mechanisms. An analysis of the scaling of each of each term in the friction relationship elucidates the mechanisms controlling rate-strengthening. In Sect. 4, we briefly compare our friction law with others proposed in past research. Finally, Sect. 5 offers concluding remarks.

2 The Friction law for simple shear

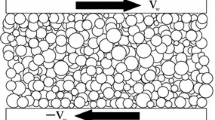
This section provides a derivation of our steady state friction relationship for simple shear flows. Fig. 3a illustrates such a well-developed flow in which the velocity profile in the direction of flow is quasi-linear.

Fig. 3

a A rendering of the simple shear flows featured in this paper. The top-most and bottom-most particles are used as rough boundaries. Colors indicate the magnitude of velocity, where $v_x$ is the imposed wall velocity. b Coefficient of restitution $e$ in a two-particle collision with normal velocity $v_c\sqrt{\rho _g/k_n}$ for data set 1 (dashed line) and data set 2 (solid line) (color figure online)

Similar to past analyses of simple shear flows [15, 18], our starting point is the energy balance relationship

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}(T+U) = D_{ij}\sigma _{ji}-\Gamma \end{aligned}$$

(1)

where $T$ and $U$ are the kinetic and potential energy densities, respectively, $D_{ij} = \partial u_i/\partial x_j$ is the velocity gradient tensor, and $\Gamma$ is the dissipation rate per unit volume. In steady state simple shear flows, only one component of the velocity gradient tensor is nonzero ($D_{xy} = \dot{\gamma }$ in our case), and a time average of Eq. (1) yields

$$\begin{aligned} \overline{\dot{\gamma }\sigma _{yx}} = \overline{\Gamma } \end{aligned}$$

(2)

where the $\overline{(\cdot )}$ indicates a time-average. Defining the effective friction coefficient as $\mu = \overline{\sigma }_{yx}/\overline{\sigma }_{yy}$ and assuming dissipation occurs only at grain contact points, Eq. (2) can be rewritten as

$$\begin{aligned} \overline{\dot{\gamma }\mu \sigma _{yy}} = \overline{\frac{N_c\langle \Gamma _c \rangle }{V}} \end{aligned}$$

(3)

where $N_c$ is the number of grain contacts in the system, $V$ is the volume of the system, and $\langle \Gamma _c \rangle$ is the average dissipation rate at grain contacts in the system. We have made use of the fact that $\sum _{c=1}^{N_c} \Gamma _c = N_c \langle \Gamma _c \rangle$.

Numerical simulations to be described in the next section demonstrate that there is less than a 1 % correlation in the fluctuations in the terms in Eq. (3). We will therefore assume averages of products can be written as products of averages and we will drop all time-averaging symbols. Variables in all following equations should be assumed to be time-averaged unless otherwise noted. Equation (3) becomes

$$\begin{aligned} \mu = \frac{N_c\langle \Gamma _c \rangle }{\sigma _{yy}\dot{\gamma }V} \end{aligned}$$

(4)

We can further simplify Eq. (4) by noting: (1) the number of contact points is related to the coordination number by $N_c = ZN_p/2$ where $N_p$ is the number of particles in the flow; (2) the number of particles can be related to the solid volume of grain material $V_s$ by defining $d$ such that $N_p(4/3)\pi d^{3}/8 = V_s$; (3) $V_s/V = \phi$ where $\phi$ is the solid fraction. The definition of $d$ to satisfy (2) is consistent with $d$ being the grain diameter in the case of monodisperse spheres, an average grain diameter in the case of polydisperse spheres, and a characteristic grain size in flows of complex shaped grains.

Combining the simplifications described above, Eq. (4) becomes

$$\begin{aligned} \mu = \frac{Z\phi }{I}\left( \frac{3\sqrt{\rho _g}}{\pi d^2 \sigma _{yy}^{3/2}} \right) \langle \Gamma _c \rangle \end{aligned}$$

(5)

where the quantity $\pi d^2 \sigma _{yy}^{3/2}/(3\sqrt{\rho _g})$ is a pressure dependent term with units of energy dissipation rate. We therefore call this quantity $\tilde{\Gamma }$ and rewrite Eq. (5) as

$$\begin{aligned} \mu = \frac{Z\phi }{I}\,\frac{\langle \Gamma _c \rangle }{\tilde{\Gamma }} \end{aligned}$$

(6)

Equation (6) is the most general form of our friction relationship. This expression makes no assumption of contact law or grain properties and only imposes the restrictions that the flow is in steady state and energy dissipation occurs at contact points. This assumption does not prohibit the incorporation of material plasticity or fracture so long as such processes are assumed to arise because of contact between grains. In Sect. 3, Eq. (6) will be applied to a specific contact law to discuss the results of numerical simulations.

Before discussing numerical simulations, we can provide a physical interpretation of Eq. (6). The coordination number $Z$ and solid fraction $\phi$ convey the connectivity and compactness of the granular material. Both of these quantities, as well as $Z\phi /I$ taken together, can be assumed to decrease during shearing dilation, a process by which the packing expands at higher shear rates. In contrast, the grain-scale dissipation rates $\langle \Gamma _c \rangle$ may be expected to increase with shear rate due to higher inter-particle forces and collision velocities. The term $\tilde{\Gamma }$ remains constant when the confining pressure is held fixed.

The friction law in Eq. (6) therefore conveys a competition between dilation and microscopic dissipation rates. At low shear rates, $Z\phi /I$ is large and $\langle \Gamma _c \rangle /\tilde{\Gamma }$ is small. At high shear rates, $Z\phi /I$ is small and $\langle \Gamma _c \rangle /\tilde{\Gamma }$ is large. The result of this competition dictates whether the material is rate-strengthening or rate-weakening and highlights the role of dilation in effective friction. This interpretation of effective friction is closely related to the interpretation of the inertial number given in Fig. 2. The same time scales at work in the inertial number, those of confinement and macroscopic shear, are at work in determining the effective friction coefficient. The confinement time scale dictates the value of $Z\phi /I$ while the macroscopic shear time scale dictates the frequency and intensity of particle collisions.

3 Numerical simulations of simple shear

In this section, we discuss numerical simulations of simple shear flows. The simulations explore the behavior of the variables in Eq. (6) and elucidate the competing roles of dilation and microscopic dissipation rates during simple shear at a variety of imposed shear rates. The numerical code used for the simulations is first discussed, followed by a discussion of results.

3.1 Description of code

We use a discrete element code [19] to study the various components of Eq. (6) in the inertial flow regime. Our simulations use a modified version of the granular module from the molecular dynamics code LAMMPS [20], called LIGGGHTS (http://www.liggghts.com). Details of the LIGGGHTS code base are discussed in [21]. Grains are modeled as spheres and interact with a Hertzian contact model. The normal force, $\varvec{F}_n = \varvec{F}_n^m + \varvec{F}_n^v$, has a mechanical portion, $\varvec{F}_n^m = R^*k_n\delta ^{3/2}\varvec{n}_{ij}$, and a viscous portion $\varvec{F}_n^v = \sqrt{\delta }R^*m_\text {eff}\gamma _n\varvec{v}_n$, where $R^* = \sqrt{R_iR_j/(R_i+R_j)}, k_n$ is a spring constant, $\delta$ is the particle overlap, $\varvec{n}_{ij}$ is a vector from the centroid of particle $j$ to the centroid of particle $i, m_\text {eff} = m_im_j/(m_i+m_j), \gamma _n$ is a damping coefficient, and $\varvec{v}_n$ is the normal component of the relative velocity vector. The tangential force, $\varvec{F}_t = \text {min}(\varvec{F}_t^m,\mu _p|\varvec{F}_n|)$, has a mechanical portion, $\varvec{F}_t^m = -\sqrt{\delta }R^*k_t\varvec{\Delta }_s$, and a Coulomb slider enforcing $|\varvec{F}_t^m| < \mu _p|\varvec{F}_n|$ where $k_t$ is a spring constant, $\varvec{\Delta }_s$ is the accumulated tangential displacement of the grains, and $\mu _p$ is the inter-particle friction coefficient. The accumulated tangential displacement of the grains is frozen when grains are sliding. The constants $k_n$ and $k_t$ have units of force per area, consistent with the model presented in [22] and discussed in [21]. Thus, $k_n$ and $k_t$ are material properties that are independent of grain size and can be explicitly linked to grain properties if desired [23]. The constant $\gamma _n$ prescribes a velocity-dependent coefficient of restitution of a binary collision, consistent with experiments [24, 25].

Simple shear is achieved by compressing approximately 10,000 bidisperse spheres between rough boundaries made of grains and moving the boundaries at a specified velocity in opposite directions, as shown in Fig. 3a. Grain radii are (1$\pm$0.2)$\tilde{d}$ where $\tilde{d}$ is specified. The height of the flow $h$ is chosen such that $h/\tilde{d}\ge 20$. The rough boundaries are moved in the $y$ direction to maintain a constant confining pressure throughout each simulation. Periodic boundary conditions are used in the $x$ and $z$ directions.

Confining pressure and grain stiffness is chosen such that $(k_n/\sigma _{yy})^{2/3} \ge 10^4$, making the grains “rigid” as described in [2]. The parameter $k_t$ is chosen to be 1/2 of $k_n$. Our primary data (DS1) set features 26 simulations across the inertial flow regime in which $\mu _p=0.3$ and $\gamma _n$ is set to prescribe the coefficient of restitution $e$ shown as the dashed line in Fig. 3b. The inter-particle friction coefficient of $\mu _p=0.3$ is chosen to provide a balance between lower values found in recent experiments [26] and slightly higher values used in recent simulations [2, 13]. We found that changing this inter-particle friction coefficient has minimal qualitative influence on the results, and mainly acts to shift the $\mu (I)$ curve up or down as reported in [2]. A secondary data set (DS2) features 18 simulations throughout the inertial flow regime with $\mu _p=0.3$ and $\gamma _n$ set to prescribe $e$ as the solid line in Fig. 3b. This data set is only referred to in order to illustrate how grain viscoelasticity influences the material response. Unless otherwise specified, data should be assumed to belong to the primary data set. We leave an in-depth study of the effects of varying $\mu _p, \gamma _n$, particle size distribution, and contact laws for future work.

Stress is measured using the equation

$$\begin{aligned} \sigma _{ij} = \frac{1}{V}\sum _{c=1}^{N_c} l_i^c f_j^c \end{aligned}$$

(7)

where $V$ is volume, $c$ are contact point labels, $N_c$ is the number of contacts in the material, $l_i^c$ is a branch vector pointing from the centroid of particle $j$ to the centroid of particle $i$, and $f_j^c$ is the force vector from particle $j$ to $i$ [27]. The effective friction coefficient is computed using $\mu = \overline{\sigma }_{yx}/\overline{\sigma }_{yy}$, where averages are carried out over several thousand stress calculations once a steady state velocity profile has been reached.

Figure 4 compares $\mu$ and $\phi$ found in our simulations (using DS1) with available data from contact dynamics simulations [13] and 3D annular shear cell experiments [3, 12]. Our simulations show an excellent collapse with the other data sets both in terms of effective frictional response and solid fraction. The effective friction coefficient increases from its quasi-static value throughout the inertial flow regime, approaching a plateau at the transition to the rapid flow regime. The solid fraction decreases approximately linearly throughout the inertial flow regime from a maximum quasi-static value of 0.59.

Fig. 4

A comparison of a effective friction and b solid fraction from our simulations and available data sets taken from the literature. Blue squares are from contact dynamics simulations [13]. Black triangles are from 3D annular shear cell experiments [3, 12]. Error bars indicate standard deviations in time of measured quantities. The dashed line shows the fit $\mu = \mu _0 + (\mu _1-\mu _0)/(1+I_0/I)$ from [8] (color figure online)

In Fig. 4, as in all figures in this paper, plotted quantities are obtained as follows. First, a quantity of interest (e.g., coordination number) is computed at periodic times (approximately $5\times 10^4$ times) once steady state flow has been achieved. The total strain over which quantities are extracted is taken such that averages over larger strains do not change the results. Next, the average of these quantities is used to obtain the plotted data points. Finally, the sample standard deviation is used to obtain the error bars. Error bars are typically omitted from inset plots for clarity.

3.2 Results: validity of friction law

Figure 5 displays the effective friction coefficients for our primary data set computed using the friction relationship in Eq. (6) and the stress formula in Eq. (7). The figure demonstrates that the proposed friction law excellently approximates the effective friction coefficient throughout the inertial flow regime. We have confirmed that a similarly accurate fit exists for other grain properties.

Fig. 5

A comparison of the effective friction coefficient calculated from proposed friction relationship in Eq. (6) and the stress formula in Eq. (7)

3.3 Results: grain-scale dissipation mechanisms

The contact law discussed in Sect. 3.1 implies that Eq. (6) can be written as

$$\begin{aligned} \mu = \frac{Z\phi }{I}\,\frac{\langle \Gamma _n\rangle + \langle \Gamma _s\rangle }{\tilde{\Gamma }} \end{aligned}$$

(8)

where $\langle \Gamma _n \rangle = \langle \varvec{F}_n \cdot \varvec{v}_n\rangle$ is the average viscoelastic dissipation rate, averaged over all contacts, and $\langle \Gamma _s \rangle = \langle |\varvec{F}_t| |\varvec{v}_t|\rangle$ is the average dissipation rate from grain sliding, averaged only over sliding contacts. An additive decomposition of Eq. (8) into $\mu = \mu _n + \mu _s$ yields

$$\begin{aligned} \mu _n = \frac{Z\phi }{I}\,\frac{\langle \Gamma _n \rangle }{\tilde{\Gamma }} \quad \text {and} \quad \mu _s = \frac{Z\phi }{I}\,\frac{\langle \Gamma _s \rangle }{\tilde{\Gamma }} \end{aligned}$$

(9)

The effective friction coefficient can thus be written in a form that clearly decouples contributions from the two grain-scale dissipation mechanisms, viscoelasticity and grain sliding.

Figure 6a illustrates how the two terms in Eq. (9) evolve throughout the inertial flow regime. At low shear rates, dissipation from grain sliding is the primary contributor to effective friction. At higher shear rates, the contribution from grain sliding remains constant or declines as the contribution from viscoelastic dissipation becomes increasingly prominent.

Fig. 6

a The two terms $\mu _n = Z\phi \langle \Gamma _n \rangle /(I\tilde{\Gamma })$ and $\mu _s = Z\phi \langle \Gamma _s \rangle /(I\tilde{\Gamma })$ in the additive decomposition of effective friction given in Eq. (9) for the primary data set (dashed lines) labeled DS1 and the secondary data set (solid lines) labeled DS2. b The total effective friction for the two data sets as a function of $I$. Error bars are omitted from inset plots for clarity

3.4 Influence of material properties

In order to highlight how grain properties influence the relative contributions of microscopic dissipation mechanisms, results from the secondary data set are also shown in Fig. 6 (the solid lines). We recall that the primary data set (DS1) features the same grain properties as the secondary data set (DS2) except for a lower coefficient of restitution, as shown in Fig. 3b.

Figure 6a compares how the two terms in Eq. (9) evolve as a function of shear rate for each data set. Compared to DS1, DS2 features a larger effective friction contribution from grain sliding and a smaller contribution from viscoelasticity throughout most of the inertial flow regime. This occurs because grain viscoelasticity dissipates less energy for a given particle collision in DS2, leaving more kinetic energy in the system to be dissipated by grain sliding. Despite the difference in the grain-scale contributions to effective friction, both data sets feature similar values for $\mu$ until $I\approx 0.4$, as shown in Fig. 6b.

In past work [2, 13], some researchers have ignored the influence of the coefficient of restitution $e$ in shear flows because of the similarity of the effective friction coefficient when measured in systems using different values of $e$. Simulations are therefore often carried out using $e=0$ [13]. The finding in Fig. 6 illustrates that although effective friction may be similar, the grain-scale dissipation mechanism responsible for friction is different in systems with different values of $e$. It may be interesting to explore the range of grain-scale behaviors that emerge from varying $\mu _p$ and $e$ and the reason that they have such a minor influence on effective friction below $I\approx 0.4$. We leave such an investigation as future work.

Increasing or decreasing the inter-particle friction coefficient has the effect of shifting the effective friction curves in Fig. 6b up or down, respectively, but does not significantly affect their shape or the magnitude of viscoelastic dissipation. Thus, the inter-particle friction coefficient primarily sets the baseline magnitude of effective friction while the coefficient of restitution controls the grain-scale contributions.

3.5 Results: dilation and dissipation rates

The evolution of each term in Eq. (6) is shown in Fig. 7. Shearing dilation is captured in the evolution of $Z, \phi$, and $Z\phi /I$ in Fig. 7a, b and d, respectively. At low shear rates, $Z$ and $\phi$ maintain maximum quasi-static values that depend upon properties such as the inter-particle friction coefficient and particle shape. For our primary data set, these quasi-static values are approximately 4 and 0.59 for $Z$ and $\phi$, respectively. As shear rates increase throughout the inertial flow regime, both $Z$ and $\phi$ decrease as the material dilates. At all shear rates investigated, $Z$ is well described by

$$\begin{aligned} Z \approx Z_1 + \frac{Z_2}{b+I} \end{aligned}$$

(10)

and $\phi$ is well described by

$$\begin{aligned} \phi \approx \phi _\text {max}-mI \end{aligned}$$

(11)

where $Z_1, Z_2, b, \phi _\text {max}$, and $m$ are constants. These approximations hold for both data sets set discussed here and for simulations with different values of $\mu _p$ and $\gamma _n$, and different particle size distributions which we do not discuss here.

Fig. 7

a The coordination number $Z$ as a function of inertial number. The dashed line is the fit from Eq. (10). b The solid fraction $\phi$ as a function of inertial number. The dashed line is the fit from Eq. (11). c The average grain-scale dissipation rates $\langle \Gamma _n \rangle /\tilde{\Gamma }$ and $\langle \Gamma _s \rangle /\tilde{\Gamma }$ as a function of inertial number. The dashed lines are power-law fits, with $\langle \Gamma _n\rangle /\tilde{\Gamma }\propto I^{2.4}$ and $\langle \Gamma _s\rangle /\tilde{\Gamma } \propto I^{1.87}$ d The quantity $Z\phi /I$ as a function of inertial number. The dashed lines represent the two regimes of behavior in which $Z\phi /I\propto I^{-1}$ and $Z\phi /I\propto I^{-2}$. Error bars in d are negligibly small

When combined, Eqs. (10) and (11) suggest the two scaling regimes of $Z\phi /I$ shown in Fig. 7d. The scaling $Z\phi /I \propto I^{-1}$ arises because $Z$ and $\phi$ maintain quasi-static values at the low end of the inertial regime. The scaling $Z\phi /I \propto I^{-2}$ arises because $Z$ and $\phi$ decrease in agreement with Eqs. (10) and (11) at higher shear rates. This decreasing contribution of $Z\phi /I$ in Eq. (6) reflects a decrease in both number of contact points and total solid fraction as shearing dilation increases. From an energy perspective, this decay conveys the decrease in internal surface area over which the material can dissipate energy.

While $Z\phi /I$ decreases with shear rate due to shearing dilation, average grain-scale dissipation rates increase as shown in Fig. 7c. Both viscoelastic and grain sliding dissipation rates approximately follow a power-law dependence on $I$ throughout the inertial flow regime, with $\langle \Gamma _n \rangle /\tilde{\Gamma } \propto I^{2.4}$ and $\langle \Gamma _s \rangle /\tilde{\Gamma } \propto I^{1.87}$, as shown in the inset of Fig. 7c. We generally expect $\langle \Gamma _n \rangle /\tilde{\Gamma }$ to scale at least as fast as $I^2$ for our chosen contact law because collision velocities scale approximately with $I$ and viscous normal contact forces scale with collision velocity. Surprisingly, we also find $\langle \Gamma _n \rangle /\tilde{\Gamma }$ to scale at least as fast as $I^2$ when we impose sub-linear dependence of viscous normal forces on grain collision velocities. This likely occurs because the correlation between collision velocities and viscous normal contact forces implies that $\langle \Gamma _n \rangle \propto \overline{\langle \varvec{F}_n^v \cdot \varvec{v}_n\rangle } > \overline{\langle \varvec{F}_n^v\rangle }\,\overline{\langle \varvec{v}_n\rangle } \propto I^2$.

We have not found a similar argument for the scaling of $\langle \Gamma _s \rangle / \tilde{\Gamma }$ with shear rate, but we have always observed this term to scale slower than $\langle \Gamma _n \rangle / \tilde{\Gamma }$.

3.6 Results: rate-dependent friction

When combined, the competing processes of shearing dilation and grain scale dissipation rates give rise to a rate-strengthening effective friction coefficient in our data sets, as shown in Fig. 6b. Rate-strengthening seems to occur because $Z\phi /I$ never decays faster than $I^{-2}$ while $\langle \Gamma _n \rangle / \tilde{\Gamma }$ increases at least as fast as $I^2$ in the inertial regime.

Data sets using other values for $\mu _p$ and $\gamma _n$, as well as other simple contact laws (linear springs or nonlinear dependence of viscous normal force on collision velocity) have been investigated and yield similar results: $Z\phi /I$ never decays faster than $I^{-2}$ and $\langle \Gamma _n \rangle /\tilde{\Gamma }$ always increases at least as fast as $I^2$ in the inertial regime. Velocity-strengthening therefore appears to be a generic system response for bidisperse spheres interacting with many viscoelastic contact models in the inertial regime. We have not observed a transition to rate-weakening friction at low shear rates as observed in some recent experiments [15]. Given the variety of grain properties and particle size distributions we have studied (but not discussed here), we suspect such a crossover, if it exists, to be caused by processes not captured by the current viscoelastic contact model, such as flash heating [15].

In Fig. 7c, dissipation rates approach 0 as $I\rightarrow 0$. This seems to suggest effective friction also approaches 0 as $I\rightarrow 0$; however, $I$ appears in the denominator of Eq. (6). The scaling of dissipation rates with $I$ is therefore the quantity controlling the approach to a quasi-static value of effective friction, not the absolute value of dissipation rates. To clarify this, we enlarge the inset of Fig. 7c in Fig. 8. At the transition from inertial to quasi-static flow, close to $I=10^{-3}$, both dissipation rates trend toward scaling as $\langle \Gamma _i \rangle /\tilde{\Gamma }\propto I$. In the quasi-static regime below $I=10^{-3}$, both dissipation rates reach this scaling. When this occurs, the effective friction coefficient reaches a quasi-static value and the strength is rate-independent. This transition is significant for understanding the onset of rate-dependent behavior and deserves further investigation in future work.

Fig. 8

The inset of Fig. 7c, showing the average grain-scale dissipation rates as a function of inertial number on a log-log scale. The dashed lines illustrate the scaling of each dissipation rate discussed in the text, as well as the scaling proportional to $I$ at the transition to quasi-static flow

4 Discussion

The primary finding of the past two sections are: (1) effective friction in inertial granular shear flows can be interpreted as a competition between shearing dilation and grain-scale dissipation rates; and (2) rate-strengthening effective friction occurs in the inertial flow regime for many viscoelastic contact models and grain properties because grain-scale dissipation rates win the competition with shearing dilation. Although the first finding may seem intuitive, Eq. (6) provides a quantitative means of studying it. Equation (9) also provides a method of tracing macroscopic frictional energy loss down to the grain-scale.

The interpretation of steady state effective friction given in this paper complements interpretations offered by past work [2, 13]. In these past works, researchers explicitly linked friction to the anisotropy of the contact network. An increase in normal force anisotropy was implicated with causing rate-strengthening. This interpretation offers an understanding of how the structural organization of grains may influence macroscopic frictional response. The interpretation of friction in the current paper, however, makes no mention of structural organization and rather relies upon energy dissipation to explain changes in the macroscopic frictional response. That each interpretation can independently explain the change in effective friction as a function of shear rate is interesting and deserves further investigation.

Several other interesting behaviors were observed during the simulations carried out for this work. Many of these behaviors warrant future investigation. First, a similarity in the effective friction coefficient was observed for simulations using different values for the coefficient of restitution $e$. This similarity persisted even while differences were observed in the grain-scale contributions to friction (see Fig. 6). This behavior has been noted by previous authors [2, 13] and has not yet been explained. A number of interesting changes in behavior behavior were also observed to occur near $I\approx 0.1$. Authors in [13] noted a number of topological transitions occurring at this shear rate. In this paper, we observe the transition from $Z\phi /I\propto I^{-1}$ to $Z\phi /I\propto I^{-2}$ close to $I\approx 0.1$. We also observe a dramatic increase in the fraction of sliding contacts at $I\approx 0.1$, regardless of the inter-particle friction coefficient $\mu _p$ used in simulations. Finally, we have observed that Eq. (6) holds for other contact laws and holds locally in layers of roughly constant inertial number in systems and flow configurations where the inertial number varies spatially. It would be useful to investigate such systems in more detail in future work to determine whether the quantitative results of this paper persist.

5 Conclusion

We have presented a relationship between steady state effective friction, the inertial number, coordination number, solid fraction, and grain-scale dissipation rates in a granular shear flow. This relationship elucidates the rate- and porosity-dependent nature of effective friction in granular flows. Numerical simulations of simple shear flows have been used to illustrate how effective friction is furnished by grain-scale dissipation mechanisms. Rate-strengthening was seen to occur because terms encompassing shearing dilation decay more slowly with shear rate than terms encompassing grain-scale dissipation rates increase. We discussed how our findings compare with other interpretations of effective friction and mentioned several observations that warrant future investigation.