Energy dissipation from particulate systems undergoing a single particle crushing event

Abstract

The energy dissipation from particulate systems undergoing particle crushing is often assumed to scale solely with the increase in surface area, irrespective of the strain energy stored in the surrounding media. By analyzing idealized particulate systems undergoing a single particle crushing event, this assumption is questioned and proven invalid. Two analysis types are considered. One represents the particulate system as an idealized assembly and then represents particle contact forces as members belonging to a periodic lattice. The other treats the particulate system as an elastic continuum. Different sizes of two and three dimensional particulate systems are considered, as well as isotropic and anisotropic confining stress states. The overall dissipation is shown to depend strongly on the dimensionality of the system, the anisotropy of the confining stress state and the elastic properties of the system. The ratio between dissipation due to stored elastic energy redistribution from surrounding media and dissipation by fracture surface energy is calculated. The ratio is found to diminish with the increasing dimensionality of the system. It is also shown that this ratio is independent of the fracture surface energy of the material. The most relevant analysis of a three dimensional particulate system to accurately estimate this ratio seems to be a one dimensional analysis of the force chain containing the most heavily loaded particles.

1 Introduction

The energetics of crushing in particulate systems has been studied for many decades. The earliest work includes that of von Rittinger [1] who proposed that energy dissipation arising from crushing is directly proportional to the increased surface area of the particles. More recently, dissipation has been attributed to creation of new surface area as well as friction, for example by geophysicists in studies of particulate fault gouge during earthquakes (e.g., [2, 3]), and in geomechanics studies on work balance and stress-strain behaviour of granular geomaterials exhibiting particle crushing [4, 5].

The energy balance equation for idealized isothermal rate independent processes is generally given by:

$$\begin{aligned} \Delta W=\Delta \Psi +\Delta \Phi , \quad \Delta \Phi \ge 0 \end{aligned}$$

(1)

where $\Delta \Psi$ is the change of free energy and is attributed to change of stored elastic energy in the system, $\Delta W$ is the work added to the system and $\Delta \Phi$ is the incremental internal mechanical dissipation, which is always non-negative.

In geomechanics, using conventional $p-q$ notations, this can be rewritten as:

$$\begin{aligned} p\text{ d }\varepsilon _v +q\text{ d }\varepsilon _s =p\text{ d }\varepsilon _v^e +q\text{ d }\varepsilon _s^e +\frac{\Delta \Phi }{V} \end{aligned}$$

(2)

in which ${\Delta W}/V=p\text{ d }\varepsilon _v+q\text{ d }\varepsilon _s$ is the external work put into the geomaterial per volume and ${\Delta \Psi }/V=p\text{ d }\varepsilon _v^e +q\text{ d }\varepsilon _s^e$ is the amount of work input converted to stored elastic energy per volume causing elastic deformation. $p,\,q,\,\text{ d }\varepsilon _v$ and $\text{ d }\varepsilon _s$ are the mean effective stress, the shear stress, volumetric strain increment and shear strain increment, respectively. A superscript $e$ attached to the strain increment indicates the elastic component. When particle crushing does not occur, it is common to attribute ${\Delta \Phi }/V$ entirely to dissipation due to friction. When particle crushing does occur, an additional dissipation mechanism is often lumped into ${\Delta \Phi }/V$ to reflect dissipation via creation of surface (e.g., [4]). Accordingly, McDowell et al. [4] proposed the following work balance equation:

$$\begin{aligned} p\text{ d }\varepsilon _v^p +q\text{ d }\varepsilon _s^p =Mp\left| {\text{ d }\varepsilon _s^p} \right| +\Gamma ^{*}\text{ d }S \end{aligned}$$

(3)

Note that $p\text{ d }\varepsilon _v^p+q\text{ d }\varepsilon _s^p$ on the left hand side of Eq. (3) is the increment of plastic work put into the system per volume and is equal to the total work put in less the part converted to elastic stored energy $(\left( {\Delta W-\Delta \Psi }\right) /V)$. A superscript $p$ attached to the strain increment indicates the plastic component. The right hand side of Eq. (3) includes two dissipation types, one due to friction $(\Delta \Phi _{\textit{friction}}/V=Mp\left| \text{ d }\varepsilon _s^p\right| )$, in which $M$ is a friction coefficient, and the other representing fracture surface energy $(\Delta \Phi _{\textit{fracture}}/V=\Gamma ^{*}\text{ d }S)$, in which $\text{ d }S$ is a surface area increment. For a geomaterial with a solid volume $V_s$, and a void ratio $e$, the link between dissipation and creation of new surface area is given by the ‘specific fracture surface energy’, $\Gamma ^{*}=\Gamma /{\left( {V_s(1+e)}\right) }$, employing a putative material constant, the ‘fracture surface energy’ $\Gamma$ (having units of N/m).

It is important to distinguish between fracture surface energy and surface free energy. The surface free energy of an ideal solid is the work needed to produce a unit of new surface by a reversible process yielding an equilibrium surface [6]. The surface free energy is indeed a material constant. But with many granular materials and real loading environments, especially granular soils being subjected to high stresses in engineering applications, fracture of a particle occurs uncontrollably. When uncontrollable fracture occurs it is fracture surface energy that is mostly considered.

In experiments fracture surface energy is derived by measurements of the force needed to initiate extension of pre-existing cracks or develop new cracks in a specimen of known geometry under known loading conditions [7]. Therefore, unlike the surface free energy, the fracture surface energy is state dependent and not a material constant. Moreover, uncontrolled fracture is associated with micro cracking and difficult to measure surface roughness and area. There is also an amount of energy dissipation at the newly created surface when uncontrolled fracturing occurs, which is also very difficult to measure. Crystallographic orientation along the surface is also unknown and adds uncertainty. Furthermore, the advancement of a crack is influenced by micro structural inhomogeneities. For these reasons, fracture surface energy is larger than the surface free energy by a factor of at least 2, and often by a factor of 10 or more [7].

In view of this, fracture surface energy $\Gamma$ (rather than surface free energy) is linked directly to the particle crushing event in this study and features in the energy balance equations.

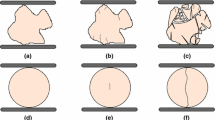
There is another and less often considered dissipation mechanism when particle crushing occurs. It is due to the redistribution of stored elastic energy in the particulate system surrounding the crushed particle, which is separate from the ${\Delta \Psi }/V=p\text{ d }\varepsilon _v^e+q\text{ d }\varepsilon _s^e$ term defined above. The concept is illustrated in Fig. 1 (after Einav and Nguyen [8]). The idea that part of the stored elastic energy contributes to plasticity and dissipation processes is not new. For example, Collins [9] explains how part of the stored elastic energy becomes frozen and unrecoverable in many situations in which geomaterials deform, and as a consequence plastic energy is stored and is recoverable. The proportion of the stored elastic energy that is frozen depends on the nature and magnitude of the plastic deformations which occur.

Fig. 1

Three distinct dissipation modes follow the crushing of a single particle (after Einav and Nguyen [8]): a a particle is about to crush, delivering a given network of contact forces represented by lines thickened in proportion to their magnitude; b new surface area is suddenly liberated that reduces the energy of the individual crushed particle (i.e., associated with the fracture surface energy by newly formed area); however, the inability of that particle to carry loads is responsible for additional redistribution of forces in the surrounding neighbourhood (i.e., dissipation from strain energy redistribution); c reorganisation of the fragments and their neighbouring particles, leading to plastic volumetric dissipation associated with friction. This paper deals with the two modes of dissipation associated with b

To explore the significance of this type of redistribution dissipation, Nguyen and Einav [10] developed a simple 1D model of springs in series that was connected in parallel, in its middle, with another ‘crushable’ spring-connector. Such a simple model does not introduce plastic volumetric dissipation due to friction. Nevertheless, it does demonstrate that once the connector particle crushes the energy dissipated from the system comes primarily from the force variations along the neighboring springs in the series, and may be significantly larger than the dissipation from the connector itself associated with the fracture of the individual particle. The dissipation from the crushed connector particle did not require knowledge of the fracture surface energy $\Gamma$, as it could be linked directly to the amount of energy stored in that connector particle prior to its crushing.

Acknowledging this contribution of energy redistribution to the overall dissipation budget, and maintaining the use of the constant $\Gamma$, Russell [11] examined a slight modification to the work equation hypothesis stated above:

$$\begin{aligned} p\text{ d }\varepsilon _v^p +q\text{ d }\varepsilon _s^p =Mp\left| {\text{ d }\varepsilon _s^p}\right| +\Gamma ^{*}\text{ d }S\left( {1+R}\right) \end{aligned}$$

(4)

$R$ was introduced as a non-dimensional factor to represent the additional contribution of dissipation arising from the energy redistribution $(\Delta \Phi _{\textit{redist}} =R\Delta \Phi _{\textit{fracture}} =R\Gamma ^{*}\text{ d }S)$. Notice that $R=\Delta \Phi _{\textit{redist}}/\Delta \Phi _{\textit{fracture}}$ is assumed to be independent of $\Gamma$ in Eq. (4). Also, Eq. (4) does not include the rate of dissipation arising from plastic volumetric dissipation and friction associated with newly created fragments. Subscripts ‘fracture’ and ‘redist’ distinguish between incremental dissipations due to fracture surface energy and energy redistribution in the surrounding media, respectively.

The 1D spring model by Nguyen and Einav [10] motivates a factor $R$ at the order of the number of particles involved in a typical force chain $(\sim 5-20)$. By analyzing published experimental data for a quartz sand undergoing crushing in oedometric compression using Eq. (4), Russell [11] confirmed this order of magnitude of $R$ once a limiting compression behaviour had been reached (note that a subscript ‘surface’ was used to denote fracture surface energy in [11]).

Here we explore whether $R$, which is a non-dimensional ratio between two energy dissipation types, could be state sensitive. In other words, do different loading paths correspond to different $R$ values? Accordingly, should $R$ depend on $S$, confining stress anisotropy (through $p$ and $q$) or any other material variables? To answer this question the simple 1D model view of Nguyen and Einav [10] is built on to analyze 2D and 3D systems. Two types of analyses are conducted. The first represents particulate systems as idealized assemblies of particles and then represents particle contact forces as forces in members belonging to periodic lattices. The second, referred to as continuum analyses, treats the particulate systems as isotropic linear elastic materials shaped like a cylinder (2D) or sphere (3D). Different sizes of systems are considered, as are isotropic and anisotropic (biaxial for 2D and triaxial for 3D) confining stress states. In both analysis types stored and dissipated energy terms are derived relevant to a single particle crushing event. It is noted that lattice and continuum analyses may only be compared to each other using the elastic constants relevant to the lattice geometry. There are very few lattice geometries which have isotropic structures (thus permit isotropic linear elasticity to be used in continuum analyses) and which can be shaped so that their outer boundary approximately resembles a cylinder or sphere.

The analysis methods used are highly idealized, but useful to study particle scale properties and loading conditions influencing energy balance. For the uncrushed particles we treat their energy entirely as elastic stored energy and we assume negligible their changes to surface area resulting from deformations due to load changes. In real particulate systems the redistribution of stored elastic energy in the system surrounding the crushed particle will depend very much on what happens locally around the particle that crushes and whether its fragments can carry load. So, to simplify the analyses, we assume that the crushing event and the attainment of a new quasi-static system takes place during an infinitesimal time increment, fragments of the crushed particle are completely unloaded and that the sum of the strain energies stored in the fragments is zero. This way $\Delta \Phi _{\textit{fracture}}$ may be linked directly to the loads acting on the particle causing it to crush and the stored strain energy in the particle under those loads.

2 Energy considerations

What follows are detailed analyses of energy dissipation mechanisms in an idealized particulate system accompanying a single crushing event, which includes the crushing event itself plus all of the associated changes in the surrounding state immediately after crushing. The energy dissipation is assumed to occur during a very short time increment $\Delta t$ and that a new quasi-static steady state is reached while the external boundaries of the system do not move.

Since the external boundaries do not move, the incremental work applied on the particulate system can be neglected, leading to:

$$\begin{aligned} \Delta W=\Delta \Psi +\Delta \Phi =0 \end{aligned}$$

(5)

The incremental energy dissipation takes on its maximum possible value (energy dissipation is maximized when the system is closed). In real particulate systems, if crushing occurs quickly with insufficient time for the system boundary to move, then dissipation will also be maximized. However, if the system boundary moves at the same time that crushing occurs, smaller energy dissipations would be calculated.

The maximized incremental energy dissipation during the crushing event in an idealized particulate system is assumed to be divided into two parts. Firstly, each particle in the system before it crushes has a certain amount of elastic strain energy, and when a particle crushes it breaks into many fragments. Its strain energy is dissipated which is analogous to the energy associated with the creation of surface area due to uncontrolled fracture of that particle only, i.e. its fracture surface energy. No other new surfaces are created in the particulate system. Secondly, when a particle crushes, a force redistribution (and associated internal displacement) of the surrounding particulate system occurs. This is associated with strain energy dissipation in the system surrounding the crushed particle. Although this strain energy dissipation arises when a particle crushes, in the formulations below it is treated separately to the dissipation of the stored elastic energy in the crushed particle. Therefore:

$$\begin{aligned} \Delta \Psi =\Psi _2 -\Psi _1\quad \quad \quad \quad \Delta \Phi =\Delta \Phi _{\textit{fracture}} +\Delta \Phi _{\textit{redist}} \end{aligned}$$

(6)

where subscript ‘1’ denotes association with the state of the original particulate system (before particle crushing); subscript ‘2’ denotes association with the state of the modified particulate system after $\Delta t$ has passed and any residual internal kinetic energy has been converted to changes in the elastic strain energy.

By considering both Eqs. (5) and (6):

$$\begin{aligned} \Delta \Phi _{\textit{redist}} =\Psi _1 -\Psi _2 -\Delta \Phi _{\textit{fracture}} \end{aligned}$$

(7)

It is assumed that the fragments of the crushed particle are completely unloaded and that the sum of the strain energies stored in the fragments is zero. $\Delta \Phi _{\textit{fracture}}$ is then equal to the elastic strain energy in the particle immediately before it crushes. Therefore $\Delta \Phi _{\textit{redist}}$ is calculated using strain energies in systems which are subtly different before and after the crushing event. It is not correct to think of $\Delta \Phi _{\textit{redist}}$ as a change to strain energy as it also captures changes to the particulate system geometry (the creation of an inner cavity) and load carrying mass. Indeed the elastic changes to the particulate system geometry, the creation of an inner cavity and the change to load carrying mass are the mechanisms which cause $\Delta \Phi _{\textit{redist}}$ to exist, even when ’plastic’ rearrangement of particles does not occur. This dissipation relates to a move from an initial state, just prior to crushing, to a second quasi-static state reached through damping relaxation [10]. The source of this damping in [10] is external (e.g. heat transfer through conduction and radiation to the surrounding fluid, acoustic emission, friction with surrounding molecules), and not because of inter-particle friction or inelastic collisions. In that respect, here the rearrangement of particles is purely elastic and not derived from non-affine sliding or collisions.

The ratio ${R=\Delta \Phi _{\textit{redist}}}/{\Delta \Phi _{\textit{fracture}}}$ is an important focus in this study as it distinguishes Eqs. (3) and (4). It is emphasized that the dissipation assumed in Eq. (6) does not reflect volumetric plastic rearrangements that may follow crushing. This is reasonable for the idealized systems studied below, and is not intended to represent the full complexity in natural particulate materials.

It is noted that some time after the crushing event, when the external boundary has had time to move, plastic rearrangement will have occurred, that there will be further changes to the elastic stored energy throughout the particulate system, that there will be changes to external work put into the system, and that energy will have been dissipated due to friction/sliding etc. But this study focuses just on the energy balance immediately before and after the sudden crushing of a particle, prior to these continuing processes, to highlight there is more to dissipation than just energy required to create surface or plastic particle rearrangements.

3 Evaluating energy dissipation in a particulate system by treating it as a periodic lattice

In this section the energetics of a particle crushing event is studied by treating a particulate system as a hexagonal packing of particles (cylinders) (Fig. 2a) of diameters $D$ and unit widths. The unit cell of the lattice is an equilateral triangle of side length $D$. One lattice member contributes to a volume of ${\sqrt{3}D^{2}}/6$. Plane strain conditions are assumed.

Fig. 2

A lattice analogy to represent the energy mechanisms associated with particle crushing. Notice that $\Delta \Phi _{\textit{fracture}}=0.5 \sigma ^{2}D^{3}/E_{s}A$, and $\Delta \Phi _{\textit{redist}}=\Psi _{1}-\Psi _{2}-\Delta \Phi _{\textit{fracture}}=1.02 \sigma ^{2}D^{3}/E_{s}A$. a Hexagonal packing of cylindrical particles overlaid by a periodic lattice. The force carried by a member of the lattice represents the contact force between two particles. b An isotropic macroscopic stress of $\sigma$ is applied to the lattice so that the forces in each member are the same and equal to $f=\surd 3\sigma D/3$. c Once the member forces $f=\surd 3 \sigma D/3$ are imposed throughout the lattice, displacement is prevented at the external boundary and six-half members radiating from the central point are removed to represent crushing of a single particle. d The six half-members removed from the lattice have a strain energy representing the strain energy belonging to one particle immediately before it crushes, and is dissipated by the crushing event. This strain energy is associated with the creation of surface area

Before particle crushing, the particles are packed so their centres form a periodic lattice of equilateral triangles of side length $D$. The force carried by a member of the lattice represents the contact force between two particles. It is assumed that a member stiffness is linearly elastic, and therefore that the stiffness between two contacting particles is also linearly elastic. For simplicity it is assumed that all members of the lattice are connected by pin joints. The lattice members have a modulus $E_s$, thickness $t_s$ and cross sectional area per unit width $A_s =1t_s$. All energy terms $W,\,\Phi$ and $\Psi$ computed therefore represent energies per unit width.

Initially in this section attention is given to the lattice with a hexagonal external boundary with side lengths $3D$, so the distance between opposite corners of the external boundary is $6D$ (Fig. 2b). Later other lattice sizes are considered.

Figure 2b represents the lattice before particle crushing. The lattice is subjected to external punctual forces at the pin joints on the external boundary so that each lattice member carries an equal force. $f$ denotes the member force per unit width. Since the geometry of the lattice is isotropic, and the member forces are equal, the loading action of the external punctual forces is equivalent to the loading action of an externally applied isotropic confining stress $\sigma$. $f$ is related to $\sigma$ by:

$$\begin{aligned} f=\frac{\sqrt{3}\sigma D}{3} \end{aligned}$$

(8)

$f$ causes a member displacement $x$ and member strain $\varepsilon$ given by:

$$\begin{aligned} x=\frac{fD}{E_s A_s }\quad \varepsilon =\frac{f}{E_s A_s } \end{aligned}$$

(9)

The mechanical work input associated with the externally applied load is $W_{1}$. It is assumed that no energy dissipation occurs due to this loading, so the mechanical work input is converted to strain energy (stored energy), and $W_1=\Psi _1$. The associated strain energy for a single lattice member is found using the expression:

$$\begin{aligned} \psi =\int \limits _0^x {f\text{ d }x} =\int \limits _0^f {\frac{fD}{E_s A_s }\text{ d }f=} \frac{1}{6}\frac{\sigma ^{2}D^{3}}{E_s A_s} \end{aligned}$$

(10)

The total strain energy (total stored energy) of the original lattice $(\Psi _1)$ is the sum of the strain energies for the internal members and half of the strain energies for the members making up the external boundary. This is because the strain energy of the triangular unit cell is the sum of half of the strain energy in each of the three members used to form it. In a lattice where unit cells adjoin, internal members belong to two unit cells so their full amount of strain energy is used, but external members belong to only one unit cell so half of their strain energy is used. It follows that:

$$\begin{aligned} \Psi _1 =\sum _\mathrm{internal} \psi +\frac{1}{2}\sum _\mathrm{boundary} \psi =\frac{27}{2}\frac{\sigma ^{2}D^{3}}{E_s A_s} \end{aligned}$$

(11)

To simulate the crushing of a single particle six half-members of the lattice radiating from the central pin joint are removed (Fig. 2c). It is assumed that the external boundary of the lattice is fixed (once the member forces of loading situation in Fig. 2b are imposed) to simplify the analogy as there will be no changes to the mechanical work applied, even when changes to the stresses applied at the external boundary occur. The modified lattice, with the fixed outer boundary and parts of internal members removed, undergoes an internal force and strain redistribution. The new strain energy is $\Psi _2$. It and the two other energy terms which represent dissipative processes will now be quantified.

To find $\Psi _2$ the new member forces in the modified lattice were calculated (using a structural analysis) and then the strain energies for each member were summed (taking only half the energies for members on the external boundary) giving:

$$\begin{aligned} \Psi _2 =\frac{1653}{138}\frac{\sigma ^{2}D^{3}}{E_s A_s } \end{aligned}$$

(12)

It follows that:

$$\begin{aligned} \Delta \Psi =\left( {\frac{1653}{138}-\frac{27}{2}} \right) \frac{\sigma ^{2}D^{3}}{E_s A_s }=-\frac{35}{23}\frac{\sigma ^{2}D^{3}}{E_s A_s } \end{aligned}$$

(13)

The energy dissipation term $\Delta \Phi _{\textit{fracture}}$ represents the loss of strain energy that was stored within the removed six half-members (Fig. 2d). This strain energy is dissipated due to the creation of surface area. $\Delta \Phi _{\textit{fracture}}$ is simply six times half the energy for a full length member:

$$\begin{aligned} \Delta \Phi _{\textit{fracture}} =6\frac{\psi }{2}=\frac{1}{2}\frac{\sigma ^{2}D^{3}}{E_s A_s} \end{aligned}$$

(14)

The energy dissipation term $\Delta \Phi _{\textit{redist}}$ represents dissipation associated with the force and strain redistribution in the modified lattice. $\Delta \Phi _{\textit{redist}}$ may be evaluated using Eq. (7) as $\Psi _1,\,\Psi _2$ and $\Delta \Phi _{\textit{fracture}}$ are already known.

$$\begin{aligned} \Delta \Phi _{\textit{redist}} =\left( {\frac{35}{23}-\frac{1}{2}} \right) \frac{\sigma ^{2}D^{3}}{E_s A}=\frac{47}{46}\frac{\sigma ^{2}D^{3}}{E_s A_s} \end{aligned}$$

(15)

The ratio ${\Delta \Phi _{\textit{redist}}}/{\Delta \Phi _{\textit{fracture}}}$ is then:

$$\begin{aligned} \frac{\Delta \Phi _{\textit{redist}} }{\Delta \Phi _{\textit{fracture}} }=\frac{47}{23} \end{aligned}$$

(16)

Energy terms for other lattice sizes, including a general term for a lattice of size 2nD between opposite corners, are given in Table 1. The values of $\Psi _{1},\,\Psi _{2},\,\Delta \Phi _{\textit{redist}},\,\Delta \Phi _{\textit{fracture}}$ and $-\Delta \Psi$ are plotted against lattice size in Fig. 3. The results indicate that energy dissipation due to load redistribution in surrounding particles may be (at least) of the same order of magnitude as that due to the fracture surface energy of the individual particle undergoing crushing and should be included in an energy balance equation.

Table 1 Energies for (a) two dimensional hexagonal lattices and (b) elastic continua of different sizes. The tabulated energy values have to be multiplied by $\sigma ^{2}D^{3}/E_{s}A_{s}$. A Poisson’s ratio of $\mu$ = 0.25 was used

Fig. 3

Energies $\Psi _{1},\,\Psi _{2},\,\Delta \Phi _{\textit{redist}},\,\Delta \Phi _{\textit{fracture}}$ and $(-\Delta \Psi )=\Delta \Phi$ evaluated using the lattice analysis and elastic continuum analysis plotted against lattice size. To get the full energy terms the values on the vertical axes have to be multiplied by $\sigma ^{2}D^{3}/E_{s}A_{s}$. A Poisson’s ratio of $\mu =0.25$ was used

4 Evaluating energy dissipation in a two-dimensional particulate system by treating it as an elastic continuum

Now the particulate system is treated as a linear elastic continuum. For ease of analysis, and to maintain an approximate similarity to the hexagonal geometry used in deriving the lattice solutions, the continuum is assumed to have a cylindrical outer boundary, and as well as a cylindrical inner boundary which encloses a cavity created by a crushed particle (analogous to removing the six-half members in the lattice). In the first case considered it is supposed that loads acting on boundaries are uniformly distributed radial pressures (Fig. 4). In the second case it is supposed that an anisotropic (biaxial) pressure distribution is present on an infinite boundary. The relevant energy terms are evaluated using closed form analytic functions as detailed below.

Fig. 4

Inner and outer boundaries of the elastic continuum and their similarity to a hexagonal lattice with internal half-members removed from the central point

4.1 General expressions

The general term for strain energy in a continuum, per unit of volume, is:

$$\begin{aligned} \psi \left( {\sigma ,\varepsilon } \right) =\int \limits _\varepsilon {\sigma _{ij} \text{ d }\varepsilon _{ij}} \end{aligned}$$

(17)

The absolute strain energy for a volume $V$ is then:

$$\begin{aligned} \Psi =\int \limits _V {\psi \left( {\sigma ,\varepsilon } \right) \text{ d }V} =\int \limits _V {\int \limits _\varepsilon {\sigma _{ij} \text{ d }\varepsilon _{ij} \text{ d }V}} \end{aligned}$$

(18)

which can be simplified for isotropic, homogenous and linear elastic materials:

$$\begin{aligned} \Psi =\frac{1}{2}\int \limits _V {\sigma _{ij} \varepsilon _{ij} \text{ d }V} \end{aligned}$$

(19)

To evaluate $\Psi$ the stresses and strains throughout the continuum need to be defined.

4.2 Analysis to consider an isotropic confining stress state

For an isotropic confining stress state, at a radius $r$ from the centre of the continuum, the major and minor principal stresses are the radial stress $\sigma _r$ and tangential stress $\sigma _\theta$. The equilibrium equation is:

$$\begin{aligned} \frac{\text{ d }\sigma _r }{\text{ d }r}+\frac{\sigma _r -\sigma _\theta }{r}=0 \end{aligned}$$

(20)

The radial strain $\varepsilon _r$ and tangential strain $\varepsilon _\theta$ are given by:

$$\begin{aligned} \varepsilon _r =-\frac{\text{ d }u}{\text{ d }r}\quad \varepsilon _\theta =-\frac{u}{r} \end{aligned}$$

(21)

where $u$ is the radial displacement at $r$. $\varepsilon _r$ and $\varepsilon _\theta$ may be expressed in terms of $\sigma _r$ and $\sigma _\theta$:

$$\begin{aligned} \varepsilon _r&= \frac{\left( {1+\mu } \right) \left( {1-\mu } \right) }{E}\left[ {\sigma _r -\frac{\mu }{1-\mu }\sigma _\theta } \right] \nonumber \\&\varepsilon _\theta =\frac{\left( {1+\mu } \right) \left( {1-\mu } \right) }{E}\left[ {-\frac{\mu }{1-\mu }\sigma _r +\sigma _\theta } \right] \end{aligned}$$

(22)

where $E$ and $\mu$ are the Young’s modulus and Poisson’s ratio of the continuum.

The stresses within the continuum have the general form:

$$\begin{aligned} \sigma _r =A+\frac{B}{r^{2}}\quad \sigma _\theta =A-\frac{B}{r^{2}} \end{aligned}$$

(23)

where the constants $A$ and $B$ are evaluated by integration and invoking boundary conditions. For the boundary condition when a radial pressure $p_b$ is applied at the outer boundary of radius $b$, and the inner boundary of radius $a$ is not loaded, the stresses are defined by Timoshenko and Goodier [12]:

$$\begin{aligned} \sigma _r =p_b \frac{\left( {1-\frac{a^{2}}{r^{2}}} \right) }{\left( {1-\frac{a^{2}}{b^{2}}}\right) }\quad \sigma _\theta =p_b \frac{\left( {1+\frac{a^{2}}{r^{2}}} \right) }{\left( {1-\frac{a^{2}}{b^{2}}}\right) } \end{aligned}$$

(24)

The expression for $\Psi$ in terms of $a,\,b$ and $p_{b}$ is then:

$$\begin{aligned} \Psi \!&= \!\frac{1}{2}\int \limits _V {\left( {\sigma _r \varepsilon _r \!+\!\sigma _\theta \varepsilon _\theta } \right) \text{ d }V}=\pi \int \limits _a^b {\left( {\sigma _r \varepsilon _r \!+\!\sigma _\theta \varepsilon _\theta } \right) r\text{ d }r}\nonumber \\ \!&= \frac{\pi p_b ^{2}b^{2}\left( {\left( {1\!+\!\mu } \right) \left( {1\!-\!2\mu } \right) \!+\!\frac{a^{2}}{b^{2}}\left( {1\!+\!\mu } \right) } \right) }{E\left( {1\!-\!\frac{a^{2}}{b^{2}}} \right) } \end{aligned}$$

(25)

$\Psi _1$ is the stored strain energy in the continuum prior to crushing and is found by setting $a=0$ and $p_b=\sigma$ in Eq. (25) to give:

$$\begin{aligned} \Psi _1 =\frac{\pi \sigma ^{2}b^{2}\left( {1+\mu } \right) \left( {1-2\mu } \right) }{E} \end{aligned}$$

(26)

$\Psi _2$ is the stored strain energy in the continuum after crushing with an unloaded inner boundary and a fixed external boundary. $\Psi _2$ is found by setting $p_b =[{\left( {1-2\mu } \right) \left( {b^{2}-a^{2}} \right) }$ $/{\left( {a^{2}+\left( {1-2\mu } \right) b^{2}} \right) }]\sigma$ (where $p_b$ was found by ensuring $\varepsilon _\theta =0$ at $b$, meaning there is no displacement at the external boundary due to the inner cavity being created, and $p_b$ has reduced slightly from $\sigma$). It follows that:

$$\begin{aligned} \Psi _2 =\frac{\pi \sigma ^{2}b^{2}\left( {1-\frac{a^{2}}{b^{2}}} \right) \left( {1+\mu } \right) \left( {1-2\mu } \right) ^{2}}{E\left( {1-2\mu +\frac{a^{2}}{b^{2}}} \right) } \end{aligned}$$

(27)

$\Delta \Phi _{\textit{fracture}}$ is the stored strain energy in a volume that would neatly fill the inner cavity of radius $a$ when subjected to a confining stress $\sigma$ and is:

$$\begin{aligned} \Delta \Phi _{\textit{fracture}} =\frac{\pi \sigma ^{2}a^{2}\left( {1+\mu } \right) \left( {1-2\mu } \right) }{E} \end{aligned}$$

(28)

$\Delta \Phi _{\textit{redist}}$ is then found using Eqs. (7), (26), (27) and (28):

$$\begin{aligned} \Delta \Phi _{\textit{redist}} =\frac{\pi \sigma ^{2}a^{2}\left( {1-\frac{a^{2}}{b^{2}}} \right) \left( {1+\mu } \right) \left( {1-2\mu }\right) }{E\left( {1-2\mu +\frac{a^{2}}{b^{2}}} \right) } \end{aligned}$$

(29)

When the external boundary of the continuum is of infinite extent $\Delta \Phi _{\textit{redist}}$ can be found by letting $b$ approach infinity and is:

$$\begin{aligned} \Delta \Phi _{redist,\infty } =\frac{\pi \sigma ^{2}a^{2}\left( {1+\mu }\right) }{E} \end{aligned}$$

(30)

The energy ratios ${\Delta \Phi _{\textit{redist}}}/{\Delta \Phi _{\textit{fracture}}}$ and ${\Delta \Phi _{\textit{redist},\infty }}/{\Delta \Phi _{\textit{fracture}}}$ are then:

$$\begin{aligned} \begin{aligned}&\frac{\Delta \Phi _{\textit{redist}} }{\Delta \Phi _{\textit{fracture} }}=\frac{\left( {1-\frac{a^{2}}{b^{2}}} \right) }{\left( {1-2\mu +\frac{a^{2}}{b^{2}}} \right) }\\&\frac{\Delta \Phi _{\textit{redist},\infty } }{\Delta \Phi _{\textit{fracture} }}=\frac{1}{1-2\mu } \end{aligned} \end{aligned}$$

(31)

4.3 Comparisons with lattice analysis

Before the energy terms can be evaluated and compared with those determined using the lattice analysis, equivalent elastic properties for the continuum need to be established. Wang and Mora [13] analyzed a number of periodic lattices. Using their results for the 2D triangular periodic lattice and plane strain, and setting the shear stiffness to be zero at the particle contacts in their results, the macroscopic stresses and strains are given by:

$$\begin{aligned} \varepsilon _r =\frac{\sqrt{3}}{2K_n }\left[ {\sigma _r \!-\!\frac{1}{3}\sigma _\theta } \right] \quad \varepsilon _\theta =\frac{\sqrt{3}}{2K_n }\left[ {-\frac{1}{3}\sigma _r \!+\!\sigma _\theta }\right] \end{aligned}$$

(32)

where ${K_n =E_s A_s}/D$ is the stiffness of the lattice members. It follows that the equivalent elastic properties of the continuum for plane strain conditions (found by comparing Eqs. (22) and (32)) are:

$$\begin{aligned} \mu =\frac{1}{4}\quad E=\frac{5\sqrt{3}}{8}K_n =\frac{5\sqrt{3}}{8}\frac{E_s A_s }{D} \end{aligned}$$

(33)

The input parameters to Eq. (25) which provide a relevant solution for $\Psi _1$ of the original hexagonal lattice in Fig. 2b are $a=0,\,b=\sqrt{{27\sqrt{3}}/{2\pi }}D$ and $p_b =\sigma$ ($b$ defines the radius of a cylinder having the same volume as the hexagonal lattice) to give:

$$\begin{aligned} \Psi _1 =\frac{27}{2}\frac{\sigma ^{2}D^{3}}{E_s A_s } \end{aligned}$$

(34)

which is exactly the same as that calculated earlier (Eq. (11)). $\Delta \Phi _{\textit{fracture}}$ is found by setting $a=\sqrt{{\sqrt{3}}/{2\pi }}D$:

$$\begin{aligned} \Delta \Phi _{\textit{fracture}} =\frac{1}{2}\frac{\sigma ^{2}D^{3}}{E_s A_s} \end{aligned}$$

(35)

which is exactly the same as from the lattice analysis (Eq. (14)). Note that $a$ defines the radius of a cylindrical cavity having the same volume as that lost by removing the six half members.

For zero displacement at the outer boundary (Eq. (27)), again using $b=\sqrt{{27\sqrt{3}}/{2\pi }}D$ and $a=\sqrt{{\sqrt{3}}/{2\pi }}D,\,\Psi _{2}$ is:

$$\begin{aligned} \Psi _2 =\frac{351}{29}\frac{\sigma ^{2}D^{3}}{E_s A_s } \end{aligned}$$

(36)

The $\Delta \Phi _{\textit{redist}}$ term can now be evaluated (Eq. (7)):

$$\begin{aligned} \Delta \Phi _{\textit{redist}} =\frac{26}{29}\frac{\sigma ^{2}D^{3}}{E_s A_s} \end{aligned}$$

(37)

and the ratio ${\Delta \Phi _{\textit{redist}}}/{\Delta \Phi _{\textit{fracture}}}$ is:

$$\begin{aligned} \frac{\Delta \Phi _{\textit{redist}} }{\Delta \Phi _{\textit{fracture}} }=\frac{52}{29} \end{aligned}$$

(38)

The terms in Eqs. (37) and (38) are 13.96 % smaller than the terms calculated above for the lattice (Eqs. (15) and (16)). Modest differences are expected, as the forces in the removed half-members of the lattice can not be represented exactly by a uniform radial pressure acting on the cylindrical inner boundary of the continuum.

Similar calculations were performed for different extents of the outer boundary for comparisons with analyses of lattices of different sizes. The results are presented in Table 1. For an original lattice having a distance $4D$ between opposite corners on the external boundary, $\Delta \Phi _{\textit{redist}}={9\sigma ^{2}D^{3}}/{10E_s}A_s$ is given by the lattice analysis whereas $\Delta \Phi _{\textit{redist}}\!=\!{11\sigma ^{2}D^{3}}/{14E_s}A_s$ is given by the continuum analysis, corresponding to a difference of 14.55 %. For a lattice that has a distance $8D$ between opposite corners, the difference between the two analysis methods is 13.94 %, and for $10D$ the difference is 13.93 %. The values of $\Psi _{1},\,\Psi _{2},\,\Delta \Phi _{\textit{redist}}$ and $-\Delta \Psi$ evaluated using the lattice analysis and continuum analysis are plotted against size in Fig. 3.

The $\Psi _{1}$ values are the same for both analysis methods. The differences between $\Psi _{2}$ values obtained using the two analysis methods are very small, being about 2.5 % for $4D$ and reducing to 0.40 % for $10D$. However, it is observed that a small difference in $\Psi _2$ translates to a larger difference in $\Delta \Phi _{\textit{redist}}$ and therefore ${\Delta \Phi _{\textit{redist}}}/{\Delta \Phi _{\textit{fracture}}}$. It is also observed that $\Delta \Phi _{\textit{redist}}$ and ${\Delta \Phi _{\textit{redist}}}/{\Delta \Phi _{\textit{fracture}}}$ values for the elastic continuum analysis stay around 14 % smaller than corresponding values for the lattice analysis as the lattice becomes increasingly large.

Increasing lattice size has little effect on reducing the differences between $\Delta \Phi _{\textit{redist}}$ and ${\Delta \Phi _{\textit{redist}}}/{\Delta \Phi _{\textit{fracture}}}$ values for the two analysis types. This is because the stresses and strains near the inner cylindrical boundary (or around where the half-members were removed in the lattice) most significantly contribute to calculations of $\Delta \Phi _{\textit{redist}}$ and ${\Delta \Phi _{\textit{redist}} }/{\Delta \Phi _{\textit{fracture}} }$ for all lattice sizes.

Evidently, $\Delta \Phi _{\textit{redist}}$ and ${\Delta \Phi _{\textit{redist}} }/{\Delta \Phi _{\textit{fracture}}}$ due to the removal of the six members from the lattice can be approximated moderately well using the analysis of an elastic continuum with cylindrical boundaries.

4.4 Analysis to consider a far field biaxial confining stress state

The influence of biaxial stresses far from the inner cylindrical boundary of radius $a$ is now considered for the linear elastic material. The far field orthogonal principal stresses are denoted as $p_{xb}$ and $p_{yb}$ (Fig. 5). The subscript $b$ is adopted here to represent an association with the far field to maintain consistency with notations used earlier, even though the far field is of infinite extent. The sudden emergence of the inner cavity does not cause any displacements or stress changes at an infinite external boundary. However, the problem when the continuum is of finite extent is not considered, as difficulties appear when attempting to fix the external boundary once the inner cavity is created. Anisotropy of the far field stress state exists when the ratio ${p_{yb}}/{p_{xb}}$ is not equal to unity.

Fig. 5

A cylindrical cavity of radius $a$ in a continuum of infinite extent, with principal stresses applied at the far field denoted $p_{xb}$ and $p_{yb}$

An equivalent set of stresses at the far field boundary are [12, 14]:

$$\begin{aligned} \left. {\sigma _r } \right| _{r=b}&= \frac{p_{xb} +p_{yb} }{2}+\frac{p_{xb} -p_{yb} }{2}\cos \left( {2\theta }\right) \end{aligned}$$

(39a)

$$\begin{aligned} \left. {\tau _{r\theta } } \right| _{r=b}&= -\frac{p_{xb} -p_{yb} }{2}\sin \left( {2\theta }\right) \end{aligned}$$

(39b)

Supposing that the inner boundary of radius $a$ is not loaded, expressions for the stresses in the continuum surrounding the inner surface that extends to infinity are given by the classical Kirsch solution (e.g., see Jaeger and Cook [15]):

$$\begin{aligned} \sigma _r&= \frac{p_{xb} +p_{yb} }{2}\left( {1-\frac{a^{2}}{r^{2}}} \right) \nonumber \\&+\frac{p_{xb} -p_{yb} }{2}\left( {1+\frac{3a^{4}}{r^{4}}-\frac{4a^{2}}{r^{2}}} \right) \cos \left( {2\theta } \right) \end{aligned}$$

(40a)

$$\begin{aligned} \sigma _\theta&= \frac{p_{xb} +p_{yb} }{2}\left( {1+\frac{a^{2}}{r^{2}}} \right) \nonumber \\&-\frac{p_{xb} -p_{yb} }{2}\left( {1+\frac{3a^{4}}{r^{4}}} \right) \cos \left( {2\theta } \right) \end{aligned}$$

(40b)

$$\begin{aligned} \tau _{r\theta }&= -\frac{p_{xb} -p_{yb} }{2}\left( {1-\frac{3a^{4}}{r^{4}}+\frac{2a^{2}}{r^{2}}} \right) \sin \left( {2\theta } \right) \end{aligned}$$

(40c)

Due to the stress anisotropy $\sigma _r$ and $\sigma _\theta$ are no longer principal stresses.

Equation (22) may be applied to evaluate $\varepsilon _r$ and $\varepsilon _\theta$ anywhere around the inner cavity. The shear strain is found using:

$$\begin{aligned} \varepsilon _{r\theta } =\frac{\left( {1+\mu } \right) }{E}\tau _{r\theta } \end{aligned}$$

(41)

Since the continuum is of infinite extent, $\Psi _{1}$ and $\Psi _{2}$ must be equal to infinity. Even so, $\Delta \Phi _{\textit{fracture}}$ and $\Delta \Phi _{redist,\infty }$ have finite values, and expressions defining them were determined using the procedure outlined below.

First, $\sigma$ is used to denote the far field mean confining stress applied to the system $\sigma ={\left( {p_{xb} +p_{yb} } \right) }/2$, and dimensionless parameters $K_x$ and $K_y$ (which always satisfy $K_x +K_y =2$) represent ratios between the far field principal stresses and the mean stress, respectively, ${K_x =p_{xb} }/\sigma ,\,{K_y =p_{yb}}/\sigma$.

Within the particle immediately before it crushes the principle stresses are everywhere $p_{xb}$ and $p_{yb}$ and the $\Delta \Phi _{\textit{fracture}}$ term is found by evaluating:

$$\begin{aligned} \Delta \Phi _{\textit{fracture}} =\frac{1}{2}\int \limits _V {\left( {p_{xb} \varepsilon _x +p_{yb} \varepsilon _y } \right) \text{ d }V} \end{aligned}$$

(42)

to give:

$$\begin{aligned} \Delta \Phi _{\textit{fracture}} \!=\!\frac{\pi \sigma ^{2}a^{2}\left( {1\!+\!\mu } \right) \left( {\left( {1\!-\!\mu } \right) \left( {K_x ^{2}\!+\!K_y ^{2}} \right) \!-\!2\mu K_x K_y } \right) }{2E}\nonumber \\ \end{aligned}$$

(43)

Next $\Psi$ is defined as:

$$\begin{aligned} \Psi&= \frac{1}{2}\int \limits _V \left( {\sigma _r \varepsilon _r +\sigma _\theta \varepsilon _\theta +2\tau _{r\theta } \varepsilon _{r\theta } } \right) \text{ d }V\nonumber \\&= \frac{1}{2}\int \limits _a^b {\int \limits _0^{2\pi } {\left( {\sigma _r \varepsilon _r +\sigma _\theta \varepsilon _\theta +2\tau _{r\theta } \varepsilon _{r\theta } } \right) r\text{ d }\theta \text{ d }r} } \end{aligned}$$

(44)

in which the integration limit $b=\infty$ is not imposed just yet. Expanding Eq. (44) gives the expression for $\Psi _{2}$ which is very long so is not presented. Setting the integration limit $a=0$ before expanding Eq. (44) gives the expression for $\Psi _{1}$:

$$\begin{aligned} \Psi _1 =\frac{\pi \sigma ^{2}b^{2}\left( {1+\mu } \right) \left( {\left( {1-\mu } \right) \left( {K_x ^{2}+K_y ^{2}} \right) -2\mu K_x K_y } \right) }{2E}\nonumber \\ \end{aligned}$$

(45)

Then, Eq. (7) is applied, and the limit $b=\infty$ imposed, to give the expression for $\Delta \Phi _{redist,\infty }$:

$$\begin{aligned}&\Delta \Phi _{redist,\infty }\nonumber \\&=\frac{\pi \sigma ^{2}a^{2}\left( {1\!+\!\mu } \right) \left( {\left( {1\!-\!\mu } \right) \left( {K_x ^{2}\!+\!K_y ^{2}} \right) \!-\!\left( {1\!-\!2\mu } \right) K_x K_y } \right) }{E}\nonumber \\ \end{aligned}$$

(46)

The ratio ${\Delta \Phi _{redist,\infty }}/{\Delta \Phi _{\textit{fracture}}}$ is:

$$\begin{aligned} \frac{\Delta \Phi _{redist,\infty } }{\Delta \Phi _{\textit{fracture}} }\!=\!\frac{2\left( {\left( {1\!-\!\mu } \right) \left( {K_x ^{2}\!+\!K_y ^{2}} \right) \!-\!\left( {1\!-\!2\mu } \right) K_x K_y } \right) }{\left( {1\!-\!\mu } \right) \left( {K_x ^{2}\!+\!K_y ^{2}} \right) \!-\!2\mu K_x K_y }\nonumber \\ \end{aligned}$$

(47)

Both $\Delta \Phi _{redist,\infty }$ and $\Delta \Phi _{\textit{fracture}}$ are affected by the anisotropic confining stress state and, for a given $\mu$, increase as the stress state becomes more anisotropic, that is as ${K_y }/{K_x}$ (or ${K_x }/{K_y }$) increases (Fig. 6). Variations of the ratio ${R=\Delta \Phi _{redist,\infty } }/{\Delta \Phi _{\textit{surface}}}$ with ${K_y }/{K_x}$ (which is interchangeable with ${K_x }/{K_y })$ are shown in Fig. 7 for $\mu =0.1, 0.2, 0.3$ and 0.4. When $K_x=K_y =1$ Eqs. (43), (46) and (47) become the same as Eqs. (28), (30) and (31). When $\mu =0.25$, $R$ is equal to 2 (the same as would be obtained using Eq. (31)) for all values of $K_x$ and $K_y$ so is unaffected by the anisotropy. Also, when $\mu =0.5,\,R$ becomes infinitely large for all values of $K_x$ and $K_y$, and when $\mu =0,\,R$ becomes equal to 1 for all values of $K_x$ and $K_y$. For all other values of $\mu , R$ is affected by $K_x$ and $K_y$. In general, if $0.25<\mu <0.5$, then $R$ decreases as the stress state becomes more anisotropic, and if $0<\mu <0.25,\,R$ increases as the stress state becomes more anisotropic.

Fig. 6

Normalized energy dissipations ${\Delta \Phi _{\textit{fracture}} E}/{\pi \sigma ^{2}a^{2}}$ and ${\Delta \Phi _{redist,\infty } E}/{\pi \sigma ^{2}a^{2}}$ plotted against stress anisotropy $K_{y}/K_{x}$ for two Poisson’s ratios $\mu$

Fig. 7

Energy dissipation ratio ${\Delta \Phi _{redist,\infty }}/{\Delta \Phi _{\textit{fracture}}}$ plotted against $K_{y}/K_{x}$ for a range of Poisson’s ratios $\mu$

5 Evaluating energy dissipation in a three-dimensional particulate system by treating it as an elastic continuum

In this section the above elastic continuum analysis is extended to a 3D system. It is supposed that the crushing of a particle can be represented by the creation of a spherical cavity (instead of a cylindrical cavity for the 2D problem). In the first case considered it is supposed that loads acting on boundaries are uniformly distributed radial pressures. In the second case it is supposed that an anisotropic triaxial pressure distribution acts on an infinite boundary. The relevant energy terms can then be evaluated using closed form analytic functions as detailed below.

5.1 Analysis to consider an isotropic stress state

For an isotropic confining stress state, the stress equilibrium around the inner boundary can be written as:

$$\begin{aligned} \frac{\text{ d }\sigma _r }{\text{ d }r}+2\frac{\left( {\sigma _r -\sigma _\theta } \right) }{r}=0 \end{aligned}$$

(48)

The radial stress $\sigma _r$ is again the major principal stress and the tangential stress $\sigma _\theta$ represents both the intermediate and minor principal stress due to radial symmetry. The radial strain $\varepsilon _r$ and tangential strain $\varepsilon _\theta$ are given by:

$$\begin{aligned} \varepsilon _r \!=\!\frac{1}{E}\left[ {\sigma _r\! -\!2\mu \sigma _\theta } \right] \;\quad \varepsilon _\theta \!=\!\frac{1}{E}\left[ {-\mu \sigma _r \!+\!\left( {1\!-\!\mu } \right) \sigma _\theta } \right] \end{aligned}$$

(49)

For the case when a radial pressure $p_b$ is applied at the outer boundary of radius $b$, and the inner cavity of radius $a$ is not loaded, the stresses are defined by Timoshenko and Goodier [12]:

$$\begin{aligned} \sigma _r =p_b \frac{\left( {1-\frac{a^{3}}{r^{3}}} \right) }{\left( {1-\frac{a^{3}}{b^{3}}} \right) }\;\quad \sigma _\theta =\frac{p_b }{2}\frac{\left( {2+\frac{a^{3}}{r^{3}}} \right) }{\left( {1-\frac{a^{3}}{b^{3}}} \right) } \end{aligned}$$

(50)

Noting that:

$$\begin{aligned} \Psi&= \frac{1}{2}\int \limits _V {\left( {\sigma _r \varepsilon _r +2\sigma _\theta \varepsilon _\theta } \right) \text{ d }V}\nonumber \\&= \frac{1}{2}\int \limits _a^b {\int \limits _0^{2\pi } {\int \limits _0^\pi {\left( {\sigma _r \varepsilon _r +2\sigma _\theta \varepsilon _\theta } \right) r^{\text{2 }}\text{ sin }\theta \text{ d }\theta }}} \text{ d }\phi \text{ d }r \end{aligned}$$

(51)

$\Psi _1$ is found by setting $a=0$ and $p_b =\sigma$:

$$\begin{aligned} \Psi _1 =\frac{2\pi \sigma ^{2}b^{3}\left( {1-2\mu } \right) }{E} \end{aligned}$$

(52)

$\Psi _2$ is found by setting $p_b =[ 2{( {1-2\mu })( {b^{3}-a^{3}} )}/$ ${( {a^{3}( {1+\mu })+2( {1-2\mu } )b^{3}} )} ]\sigma$ (ensuring no displacement at the external boundary):

$$\begin{aligned} \Psi _2 =\frac{4\pi \sigma ^{2}b^{3}\left( {1-\frac{a^{3}}{b^{3}}} \right) \left( {1-2\mu } \right) ^{2}}{E\left( {2\left( {1-2\mu } \right) +\left( {1+\mu } \right) \frac{a^{3}}{b^{3}}} \right) } \end{aligned}$$

(53)

The $\Delta \Phi _{\textit{fracture}},\,\Delta \Phi _{\textit{redist}}$ and $\Delta \Phi _{redist,\infty }$ terms are then:

$$\begin{aligned} \Delta \Phi _{\textit{fracture}} =\frac{2\pi \sigma ^{2}a^{3}\left( {1-2\mu } \right) }{E} \end{aligned}$$

(54)

and:

$$\begin{aligned}&{\Delta \Phi _{\textit{redist}} =\frac{2\pi \sigma ^{2}a^{3}\left( {1-\frac{a^{3}}{b^{3}}} \right) \left( {1+\mu } \right) \left( {1-2\mu } \right) }{E\left( {2\left( {1-2\mu } \right) +\left( {1+\mu } \right) \frac{a^{3}}{b^{3}}} \right) }}\nonumber \\&{\Delta \Phi _{\textit{redist},\infty } =\frac{\pi \sigma ^{2}a^{3}\left( {1+\mu } \right) }{E}} \end{aligned}$$

(55)

The energy ratios ${\Delta \Phi _{\textit{redist} }}/{\Delta \Phi _{\textit{fracture}} }$ and ${\Delta \Phi _{\textit{redist},\infty }}/{\Delta \Phi _{\textit{fracture}} }$ are then:

$$\begin{aligned}&{\frac{\Delta \Phi _{\textit{redist} }}{\Delta \Phi _{\textit{fracture}} }=\frac{\left( {1-\frac{a^{3}}{b^{3}}} \right) \left( {1+\mu } \right) }{\left( {2\left( {1-2\mu } \right) +\left( {1+\mu } \right) \frac{a^{3}}{b^{3}}} \right) }}\nonumber \\&{\frac{\Delta \Phi _{\textit{redist},\infty } }{\Delta \Phi _{\textit{fracture}} } =\frac{1+\mu }{2\left( {1-2\mu } \right) }} \end{aligned}$$

(56)

5.2 Analysis to consider a far field triaxial confining stress state

The influence of triaxial confining stresses far from the inner spherical boundary of radius $a$ is now considered. The far field orthogonal triaxial principal stresses are denoted as $p_{xb},\,p_{yb}$ and $p_{zb}$. Again, the subscript $b$ is adopted to represent an association with the far field, even though it is of infinite extent. The problem with the continuum being of finite extent is not considered for the reasons mentioned in the 2D analysis. An anisotropy of the far field stress state exists when either of the ratios ${p_{yb}}/{p_{xb}},\,{p_{zb}}/{p_{xb}}$ and ${p_{zb}}/{p_{yb}}$ are not equal to unity.

The full expressions for the stresses and strains throughout an infinite continuum around a spherical cavity when a triaxial stress state is applied in the far field are very long. They are not presented here for brevity. They were found by building on the basic solution given in Eq. (57) (Barber [16]), which is for a single stress $\sigma _i$ acting along the $i$ axis (where $i$ can be either $x,\,y$ or $z$) at the infinite boundary of the continuum containing the spherical cavity. $a$ defines the radius of the spherical cavity, and spherical coordinates $r,\,\phi$ and $\theta$ are defined in Fig. 8. Minor typing errors in Barber’s equation (24.15) have been corrected in their representation here in Eq. (57), and the corrected equation is in agreement with that in Timoshenko and Goodier [12] written using different notations. Equation (57) was derived following a very long procedure which is fully outlined in Barber [16] (Section 24.1.2) so is not presented here for brevity.

Fig. 8

Spherical coordinates used in the basic stress solution for a uniaxial stress $\sigma _i$ acting along the $i$ axis at the infinite boundary (Eq. (57))

$$\begin{aligned}&\sigma _r \nonumber \\&\quad \!=\!\sigma _i \left( {\text{ cos }^{2}\theta \!+\!\frac{\left( {6\!-\!25\text{ cos }^{2}\theta \!+\!5\mu \text{ cos }^{2}\theta } \right) \left( {\frac{a}{r}} \right) ^{3}\!+\!\left( {\!-\!6\!+\!18\text{ cos }^{2}\theta } \right) \left( {\frac{a}{r}} \right) ^{5}}{7\!-\!5\mu }} \right) \nonumber \\ \end{aligned}$$

(57a)

$$\begin{aligned}&\sigma _\theta \nonumber \\&\quad \!=\!\sigma _i \left( {\text{ sin }^{2}\theta \!+\!\frac{\left( {4\!-\!5\mu \!+\!5\text{ cos }^{2}\theta \!-\!10\mu \text{ cos }^{2}\theta } \right) \left( {\frac{a}{r}} \right) ^{3}\!+\!\left( {9\!-\!21\text{ cos }^{2}\theta } \right) \left( {\frac{a}{r}} \right) ^{5}}{2\left( {7\!-\!5\mu } \right) }} \right) \nonumber \\ \end{aligned}$$

(57b)

$$\begin{aligned}&\sigma _\phi \!=\!\sigma _i \left( {\frac{3\left( {\!-\!2\!+\!5\mu \!+\!5\text{ cos }^{2}\theta \!-\!10\mu \text{ cos }^{2}\theta } \right) \left( {\frac{a}{r}} \right) ^{3}\!+\!3\left( {1\!-\!5\text{ cos }^{2}\theta } \right) \left( {\frac{a}{r}} \right) ^{5}}{2\left( {7\!-\!5\mu } \right) }} \right) \nonumber \\ \end{aligned}$$

(57c)

$$\begin{aligned}&\tau _{r\theta } \!=\!\sigma _i \left( {\!-\!1\!+\!\frac{\left( {\!-\!5\!-\!5\mu } \right) \left( {\frac{a}{r}} \right) ^{3}\!+\!12\left( {\frac{a}{r}} \right) ^{5}}{\left( {7\!-\!5\mu } \right) }} \right) \text{ cos }\theta \text{ sin }\theta \end{aligned}$$

(57d)

$$\begin{aligned}&\tau _{r\phi } \!=\!0\end{aligned}$$

(57e)

$$\begin{aligned}&\tau _{\theta \phi } \!=\!0 \end{aligned}$$

(57f)

For a triaxial stress state, the full expressions for $\sigma _{r},\, \sigma _{\theta },\,\sigma _{\varphi },\,\tau _{r\theta },\,\tau _{r\varphi }$ and $\tau _{\theta \varphi }$ are found by applying Eq. (57) to the three principal stresses acting on the infinite boundary. The resulting stress terms are transformed to a common reference coordinate system and then superimposed. Corresponding strains are found using the standard elastic stress-strain relationship.

Since the continuum is of infinite extent, $\Psi _{1}$ and $\Psi _{2}$ must be equal to infinity. However, as for the 2D problem, $\Delta \Phi _{\textit{fracture}}$ and $\Delta \Phi _{redist,\infty }$ have finite values, and defining expressions may be determined using the procedure outlined below.

First, similar to the 2D problem, $\sigma$ is used to denote the far field mean confining stress applied to the system $\sigma ={\left( {p_{xb} +p_{yb} +p_{zb} } \right) }/3$, and dimensionless parameters $K_x,\,K_y$ and $K_z$ (which always satisfy $K_x +K_y +K_z =3)$ represent ratios between the far field principal stresses and the mean stress, respectively, ${K_x \!=\!p_{xb}}/\sigma ,\,{K_y \!=\!p_{yb}}/\sigma ,\,{K_z \!=\!p_{zb} }/\sigma$.

Within the particle immediately before it crushes the principle stresses are everywhere $p_{xb},\,p_{yb}$ and $p_{zb}$ and the $\Delta \Phi _{\textit{fracture}}$ term is found by evaluating:

$$\begin{aligned} \Delta \Phi _{\textit{fracture}} =\frac{1}{2}\int \limits _V {\left( {p_{xb} \varepsilon _x +p_{yb} \varepsilon _y +p_{zb} \varepsilon _z} \right) \text{ d }V} \end{aligned}$$

(58)

to give:

$$\begin{aligned}&\Delta \Phi _{\textit{fracture}}\nonumber \\&\!=\!\frac{2\pi \sigma ^{2}a^{3}\left( {K_x ^{2}\!+\!K_y ^{2}\!+\!K_z ^{2}\!-\!2\mu \left( {K_x K_y \!+\!K_x K_z \!+\!K_y K_z } \right) } \right) }{3E}\nonumber \\ \end{aligned}$$

(59)

Next $\Psi$ is defined as:

$$\begin{aligned} \Psi&= \frac{1}{2}\int \limits _V \left( \sigma _r \varepsilon _r +\sigma _\theta \varepsilon _\theta +\sigma _\phi \varepsilon _\phi \right. \nonumber \\&\left. +2\tau _{r\theta } \varepsilon _{r\theta } +2\tau _{r\phi } \varepsilon _{r\phi } +2\tau _{\theta \phi } \varepsilon _{\theta \phi } \right) \text{ d }V\nonumber \\&= \frac{1}{2}\int \limits _a^b \int \limits _0^{2\pi } \int \limits _0^\pi \left( \sigma _r \varepsilon _r +\sigma _\theta \varepsilon _\theta +\sigma _\phi \varepsilon _\phi \right. \nonumber \\&\left. +2\tau _{r\theta } \varepsilon _{r\theta } +2\tau _{r\phi } \varepsilon _{r\phi } +2\tau _{\theta \phi } \varepsilon _{\theta \phi }\right) r^{\text{2 }}\text{ sin }\theta \text{ d }\theta \text{ d }\phi \text{ d }r\nonumber \\ \end{aligned}$$

(60)

in which the integration limit $b=\infty$ is not imposed just yet. Expanding Eq. (60) gives the expression for $\Psi _{2}$ which is very long so is not presented. Setting the integration limit $a=0$ before expanding Eq. (60) gives the expression for $\Psi _{1}$:

$$\begin{aligned} \Psi _1 \!=\!\frac{2\pi \sigma ^{2}b^{3}\left( {K_x ^{2}\!+\!K_y ^{2}\!+\!K_z ^{2}\!-\!2\mu \left( {K_x K_y \!+\!K_x K_z \!+\!K_y K_z } \right) } \right) }{3E}\nonumber \\ \end{aligned}$$

(61)

Then, Eq. (7) is applied, and the limit $b=\infty$ imposed, to give the expression for $\Delta \Phi _{\textit{redist},\infty }$:

$$\begin{aligned} \Delta \Phi _{\textit{redist},\infty }&= \frac{\pi \sigma ^{2}a^{3}\left( {1+\mu } \right) }{3\left( {7-5\mu } \right) E}\nonumber \\&\quad \times \left( \begin{array}{ll}\left( {13-15\mu } \right) \left( {K_x ^{2}+K_y ^{2}\!+\!K_z ^{2}} \right) +\\ \left( {-6+10\mu } \right) \left( {K_x K_y +K_x K_z +K_y K_z } \right) \end{array} \right) \nonumber \\ \end{aligned}$$

(62)

The ratio ${\Delta \Phi _{\textit{redist},\infty }}/{\Delta \Phi _{\textit{fracture}}}$ is:

$$\begin{aligned}&\!\!\!\frac{\Delta \Phi _{\textit{redist},\infty } }{\Delta \Phi _{\textit{fracture}} }\nonumber \\&\quad =\frac{\left( {1+\mu } \right) \left( \begin{array}{ll}\left( {13-15\mu } \right) \left( {K_x ^{2}+K_y ^{2}+K_z ^{2}} \right) +\\ \left( {-6+10\mu } \right) \left( {K_x K_y +K_x K_z +K_y K_z } \right) \end{array} \right) }{2\left( {7-5\mu } \right) \left( {K_x ^{2}+K_y ^{2}+K_z ^{2}-2\mu \left( {K_x K_y +K_x K_z +K_y K_z } \right) } \right) }\nonumber \\ \end{aligned}$$

(63)

Again both $\Delta \Phi _{\textit{redist},\infty }$ and $\Delta \Phi _{\textit{fracture}}$ are affected by the anisotropic confining stress state. Equations (54), (55) and (56) for the isotropic confining stress state are recovered when $K_x=K_y=K_z=1$.

Variations of normalized energy dissipations ${\Delta \Phi _{\textit{fracture}} E}/ {\pi \sigma ^{2}a^{3}}$ and ${\Delta \Phi _{\textit{redist},\infty } E}/{\pi \sigma ^{2}a^{3}}$ with $K_{y}/K_{x}$ and $K_{z}/K_{x}$ and two Poisson’s ratios $\mu$ are presented in Fig. 9. In general, both types of energy dissipation increase as the stress state becomes more anisotropic. More specifically, for $\mu =0.1$, and when $K_{x}\!=\!1, K_{y}\!=\!5/3$ and $K_{z}\!=\!1/3$, the normalized quantities of ${\Delta \Phi _{\textit{fracture}} E}/{\pi \sigma ^{2}a^{3}}$ and ${\Delta \Phi _{\textit{redist},\infty } E}/{\pi \sigma ^{2}a^{3}}$ are 2.25 and 1.80, respectively, compared to 1.60 and 1.10 for an isotropic stress state. For $\mu \!=\!0.4$, and when $K_{x}\!=\!1,\,K_{y}\!=\!5/3$ and $K_{z}\!=\!1/3$, the normalized quantities of ${\Delta \Phi _{\textit{fracture}} E}/{\pi \sigma ^{2}a^{3}}$ and ${\Delta \Phi _{redist,\infty } E}/{\pi \sigma ^{2}a^{3}}$ are 1.39 and 2.19, respectively, compared to 0.4 and 1.40 for an isotropic stress state.

Fig. 9

Normalized energy dissipations ${\Delta \Phi _{\textit{fracture}} E}/{\pi \sigma ^{2}a^{3}}$ and ${\Delta \Phi _{\textit{redist},\infty } E}/{\pi \sigma ^{2}a^{3}}$ plotted against $K_{y}/K_{x}$ for a range of $K_{z}/K_{x}$ and two Poisson’s ratios $\mu$

Variations of the ratio ${\Delta \Phi _{\textit{redist},\infty }}/{\Delta \Phi _{\textit{fracture}} }$ with ${K_y }/{K_x }$ and ${K_z }/{K_x}$ for a range of Poisson’s ratios $\mu$ are presented in Fig. 10. When $\mu =0.2$ the ratio ${R=\Delta \Phi _{redist,\infty } }/{\Delta \Phi _{\textit{fracture}}}$ is equal to 1 for all values of $K_x,\,K_y$ and $K_z$ (the same as would be obtained using Eq. (56)) so is unaffected by the anisotropy. Also, when $\mu =0.5$ and $K_x =K_y =K_z =1,\,R$ becomes infinitely large.

Fig. 10

Energy dissipation ratio ${\Delta \Phi _{\textit{redist},\infty } }/{\Delta \Phi _{\textit{fracture}}}$ plotted against $K_{y}/K_{x}$ for a range of $K_{z}/K_{x}$ and Poisson’s ratios $\mu$

6 Discussion

For highly idealized particulate systems, expressions have been derived for the energy dissipated by fracturing of a single particle and by load redistribution in the surrounding particles. It has been shown that ratio $R$ between the two energy dissipations depends mainly on the elastic properties of the particulate system and the anisotropy of the stress state applied at the system boundary. To a lesser extent it depends on the size of the system relative to the particle size.

Although the fracture surface energy $\Gamma$ does not appear in the calculations, the energy dissipated by crushing of a single particle will be directly proportional to $\Gamma$. The amount of work put into the system to generate sufficiently large contact forces for the particle to crush must also be directly proportional to $\Gamma$. The energy dissipated by load redistribution in the surrounding particles must then also be directly proportional to $\Gamma$. As a result, when one energy dissipation term is divided by the other, the dependence on $\Gamma$ is removed. $R$ is thus independent of $\Gamma$.

The analyses have also shown that $R$ values were generally larger for the 2D plane strain case than the 3D case. For $\mu =0.2,\,R$ ranges between 1.67 and 2 for all stress states in the 2D case, and $R$ is equal to 1 for all stress states in the 3D case. In the 2D and 3D systems $\Delta \Phi _{\textit{redist}}$ and $R$ depend on the size of the particulate system only in a small way (there is a slight influence of the size of $b$ relative to $a$ in Eqs. (31) and (56) and diminishes as $b$ becomes very large compared to $a$). The load redistribution and associated internal deformation is suppressed by compressive loads developed in ‘arches’ around the created cavity. In the 1D case of Nguyen and Einav [10], however, arching is not possible, and complete unloading of the particulate system occurs after crushing meaning $R$ is quite large and linked heavily to the number of particles in (or size of) the system. There seems to be a diminishment of $R$ with the increasing dimensionality of the system.

So what $R$ value is most relevant to real particulate systems? To answer this question consider the work of Russell [11] in which Eq. (4) was used to back calculate an $R$ value of about 16 in a quartz sand compressed to very high stresses in an oedometer. Also, Russell et al. [17] found through a study of individual particle stress fields that it is the largest contact force which causes crushing. Since force chains in real particulate systems typically act along a string of 5–20 particles [18], the most relevant analysis to estimate $R$ seems to be an analysis of the force chain containing the most heavily loaded particles. Such an analysis would be quite similar to the 1D analysis of Nguyen and Einav [10]. It is noted, however, that as a force chain collapses in a real particulate system there may still be a small amount of arching and suppression of load redistribution that can not be captured in a 1D analysis.

The authors hope that this study motivates others to focus on crushing of particles in heavily loaded force chains. It is well known that force chains are aligned closely with the major principal compressive stress, and that as a soil is loaded and deforms, or as particles crush, some force chains collapse while others are formed (e.g., [18–20]). What is not known, however, is how much of the significant energy stored in heavily loaded force chains is dissipated and how much is transferred to neighboring particles to form a new static equilibrium and form new or strengthen existing force chains. The challenge is to understand the energy balance during these processes.

7 Conclusion

Two analyses of particulate systems that quantify the energy redistribution and energy dissipation due to crushing of a single particle are presented. Fixing the external boundary of the system during the crushing event not only simplifies the analyses but also ensures that the calculated energy dissipation is maximized.

In the first analysis type a 2D particulate system is idealized in its assembly. Particle contact forces are represented as forces in members belonging to a periodic lattice. It is found that the energy dissipation due to stored elastic energy redistribution is generally as large as or a few times larger than fracture surface energy representing the dissipation from the crushed particle. The second analysis type, when the particulate system is treated as a 2D elastic continuum, produces similar results. Applying isotropic and anisotropic stresses at the boundary of the elastic continuum highlights that Poisson’s ratio and the stress anisotropy significantly influence the ratio between dissipation due to redistribution and dissipation due to fracture surface energy, denoted $R$.

The elastic continuum analysis applied to a three dimensional particulate system also highlights that Poisson’s ratio and the amount of stress anisotropy significantly influence $R$.

The ratio $R$ is of interest as it appears in a recently proposed energy balance equation of particulate materials undergoing particle crushing.

The results of these and other analyses indicate that there is a diminishment of $R$ with the increasing dimensionality of the system being analysed. For a typical Poisson’s ratio 0.2, $R$ is about 2 for all stress states in the 2D case, 1 for all stress states in the 3D case, and ranges from 5 to 20 for a 1D case. In view of this, and a back-calculated $R = 16$ for a quartz sand experiencing crushing, the most relevant analysis of a 3D particulate system to accurately estimate $R$ seems to be a 1D analysis of the force chain containing the most heavily loaded particles.