Quaternionic multistate Hopfield neural network with extended projection rule

Abstract

The aim of this paper is to investigate storing and recalling performances of embedded patterns on associative memory. The associative memory is composed of quaternionic multistate Hopfield neural network. The state of a neuron in the network is described by three kinds of discretized phase with fixed amplitude. These phases are set to discrete values with arbitrary divide size. Hebbian rule and projection rule are used for storing patterns to the network. Recalling performance is evaluated through storing random patterns with changing the divide size of the phases in a neuron. Color images are also embedded and their noise tolerance is explored.

1 Introduction

Research on complex-valued and hypercomplex-valued extensions for neural networks has been gaining much interest [1, 2]. Natural treatment for multi-dimensional data on neural networks, such as phase and amplitude in a signal, can be achieved by this kind of extensions. Complex-valued multistate neural network (CVMNN) is a complex-valued Hopfield-type neural network, and the state of a neuron is encoded by a distinct point on a unit circle in the complex plane, i.e., the discretized phase [3]. Multi-level values, such as pixel values of images, can be easily represented using this type of encoding, and thus associative memory that is capable of storing gray-scaled images can be constructed. For CVMNNs there are several studies for the learning schemes that embed patterns to the networks [4, 5].

The use of quaternions, which are four-dimensional hypercomplex numbers, is expected to extend CVMNN so that multi-dimensional vectors with discretized values can be accepted. In this respect, quaternionic multistate neural network (QMNN) has been proposed [6], and several learning schemes have also been formulated [5, 7]. QMNNs enable three-dimensional patterns, such as color images or three-dimensional body images, to be embedded in the network using phasor representation of quaternions. Though these learning schemes for QMNNs are available, the applicability and performances using memory patterns have not yet been investigated.

In this paper, we investigate the performances of QMNNs through storing to and retrieving patterns from the networks. The Hebbian rule and the extended projection rule for QMNN are used for storing memory patterns to the networks. First experiment is to ensure the projection rule actually works, i.e., random patterns can be stably embedded. In the second experiment, the noise robustness of QMNN with the projection rule is also investigated from the viewpoints of discretized level, the number of memory patterns in the network, and noise-affected patterns for the initial configuration of the network. Third experiment is to demonstrate that color images can be stored to and retrieved from a QMNN using the projection rule. Three images with many pixels and with high resolution of the pixel level are used for the memory patterns, and the robustness of the noises for the input patterns is explored.

This paper is organized as follows. Section 2 gives preliminaries, such as the definitions and representations of quaternion and quaternionic multistate neural network. Then, the learning schemes are described in Sect. 3. This is followed in Sect. 4 by showing the experimental results. We finish with conclusions in Sect. 5.

2 Preliminaries

2.1 Definition of quaternions

Quaternions form a class of hypercomplex numbers that consist of a real number and three kinds of imaginary number, ${\varvec{i}}$, ${\varvec{j} }$, ${\varvec{k} }$. Formally, a quaternion is defined as a vector in a four-dimensional vector space,

$$\begin{aligned} \varvec{x}={{x}^{(e)}}+{{x}^{(i)}}{\varvec{i}}+{{x}^{(j)}}{\varvec{j} }+{{x}^{(k)}}{\varvec{k} }\end{aligned}$$

(1)

where ${{x}^{(e)}}$, ${{x}^{(i)}}$, ${{x}^{(j)}}$ and ${{x}^{(k)}}$ are real numbers. The multiplication rules between the three imaginary numbers are:

$$\begin{aligned} {\begin{matrix} {\varvec{i}}^2={\varvec{j} }^2={\varvec{k} }^2={\varvec{i}}{\varvec{j} }{\varvec{k} }=-1,\\ {\varvec{i}}{\varvec{j} }=-{\varvec{j} }{\varvec{i}}={\varvec{k} },\;{\varvec{j} }{\varvec{k} }=-{\varvec{k} }{\varvec{j} }={\varvec{i}},\;{\varvec{k} }{\varvec{i}}=-{\varvec{i}}{\varvec{k} }={\varvec{j} }. \end{matrix}} \end{aligned}$$

(2)

It is also written using 4-tuple or 2-tuple notations as follows:

$$\begin{aligned} \varvec{x}&=\left( {{x}^{(e)}},{{x}^{(i)}},{{x}^{(j)}},{{x}^{(k)}}\right) =\left( {{x}^{(e)}},\vec {x}\right) , \end{aligned}$$

(3)

where $\vec {x}=({{x}^{(i)}}, \, {{x}^{(j)}}, \, {{x}^{(k)}})$. In this representation ${{x}^{(e)}}$ is the scalar part of x, and $\vec {x}$ forms the vector part.

Now, we define the operation between quaternions, $\varvec{p}$ and $\varvec{q}.$ The addition and subtraction of quaternions are defined in the same manner as those of complex numbers or vectors by

$$\begin{aligned} \varvec{p}\pm \varvec{q}&=\left( {{p}^{(e)}}\!\pm {{q}^{(e)}}, \, \vec {p}\pm \vec {q}\right) \end{aligned}$$

(4)

$$\begin{aligned}&=\left( {{p}^{(e)}}\!\pm {{q}^{(e)}}, \; {{p}^{(i)}}\!\pm {{q}^{(i)}}, \; {{p}^{(j)}}\!\pm {{q}^{(j)}},{{p}^{(k)}}\!\pm {{q}^{(k)}}\right) . \end{aligned}$$

(5)

The product of $\varvec{p}$ and $\varvec{q}$, denoted as $\varvec{p}\varvec{q}$, is calculated by Eq. (2) as

$$\begin{aligned} \varvec{p}\varvec{q}=\left( {{p}^{(e)}}{{q}^{(e)}}-\vec {p}\cdot \vec {q}, \; {{p}^{(e)}}\vec {q}+{{q}^{(e)}}\vec {p}+\vec {p}\times \vec {q}\right) . \end{aligned}$$

(6)

where $\vec {p} \cdot \vec {q}$ and $\vec {p}\times \vec {q}$ denote the dot and cross products respectively between three-dimensional vectors $\vec {p}$ and $\vec {q}$.

The quaternion conjugate is defined as

$$\begin{aligned} {\varvec{x}}^{*}=\left( {{x}^{(e)}},-\vec {x}\right) ={{x}^{(e)}}-{{x}^{(i)}}{\varvec{i}}-{{x}^{(j)}}{\varvec{j} }-{{x}^{(k)}}{\varvec{k} }. \end{aligned}$$

(7)

The conjugate of product holds the relation of ${(\,\varvec{p}\varvec{q}\,)}^{*}\! = {\varvec{q}}^{*}{\varvec{p}}^{*}$.

The quaternion norm of $\varvec{x}$, notation $|\varvec{x}|$, is defined by

$$\begin{aligned} |\varvec{x}|=\sqrt{\varvec{x}{\varvec{x}}^{*}}=\sqrt{{{x}^{(e)}}^2+{{x}^{(i)}}^2+{{x}^{(j)}}^2+{{x}^{(k)}}^2}. \end{aligned}$$

(8)

The multiplication between scalar $a = (a, \vec {0})$ and quaternion $\varvec{x}$ is given by

$$\begin{aligned} a\varvec{x}&= \left( a{{x}^{(e)}}, a\vec {x}\right) = \left( a{{x}^{(e)}}, a{{x}^{(i)}}, a{{x}^{(j)}}, a{{x}^{(k)}}\right) . \end{aligned}$$

(9)

2.2 Phasor representation of quaternions

A complex number in the form $\varvec{c}={{c}^{(e)}}+{{c}^{(i)}}{\varvec{i}}$ can be represented in phasor form by $\varvec{c}=r{\mathrm {e} }^{{\varvec{i}}\theta }$, where $r=\sqrt{{{c}^{(e)}}^2+{{c}^{(i)}}^2}$, and $\theta =\arctan {({{c}^{(i)}}/{{c}^{(e)}})}$. Similarly, every quaternion can be represented in the phasor form. The phasor form of quaternions [8] adopted in this paper is as follows:

$$\begin{aligned} \varvec{q}=|\varvec{q}|{\mathrm {e} }^{{\varvec{i}}{\varphi }}{\mathrm {e} }^{{\varvec{k} }\psi }{\mathrm {e} }^{{\varvec{j} }\theta }, \;\;\mathrm {where}\; {\left\{ \begin{array}{ll} {\mathrm {e} }^{{\varvec{i}}{\varphi }}=\cos {\varphi }+{\varvec{i}}\sin {\varphi }\\ {\mathrm {e} }^{{\varvec{j} }\theta }=\cos \theta +{\varvec{j} }\sin \theta \\ {\mathrm {e} }^{{\varvec{k} }\psi }=\cos \psi +{\varvec{k} }\sin \psi \end{array}\right. }. \end{aligned}$$

(10)

${\varphi },\theta$, and $\psi$ are the phases of $\varvec{q}$, and they are defined in the ranges of $\left[ -\uppi ,\uppi \right) , \left[ -{\uppi }/{2},{\uppi }/{2}\right)$, and $\left[ -{\uppi }/{4},{\uppi }/{4}\right]$, respectively.

3 Quaternionic multistate Hopfield neural network

We describe the quaternionic multistate Hopfield neural network model in this section [6]. All the variables in the model are described by quaternions, i.e., neuron states and connection weights. The state of a neuron p is represented using three phases ${\varphi }_p$, $\psi _p$, and $\theta _p$ as

$$\begin{aligned} \varvec{u}_p&= {\mathrm {e} }^{{\varvec{i}}{\varphi }_p}{\mathrm {e} }^{{\varvec{k} }\psi _p}{\mathrm {e} }^{{\varvec{j} }\theta _p} \end{aligned}$$

(11)

where $|\varvec{u}_p|=1$. The action potential of the neuron p at a discrete time t is defined as

$$\begin{aligned} \varvec{h}_{p}(t)&=\sum _{q} {\varvec{w}_{pq} \varvec{u}_{q}(t)}\nonumber \\&=\sum _{q} {\varvec{w}_{pq} {{\mathrm {e} }^{{\varvec{i}}{\varphi }_q(t)}} {{\mathrm {e} }^{{\varvec{k} }\psi _q(t)}} {{\mathrm {e} }^{{\varvec{j} }\theta _q(t)}}} \end{aligned}$$

(12)

where $\varvec{w}_{pq}$ is the connection weights between neuron q to neuron p. The output state of the neuron p at the time $(t+1)$ is determined by

$$\begin{aligned} \varvec{u}_{p}(t+1)&={\text {qsign}}\left( \varvec{h}_p(t)\right) , \end{aligned}$$

(13)

where

$$\begin{aligned} {\text {qsign}}\left( \varvec{h}\right) = \; &{\text {qsign}}\left( {{\mathrm {e} }^{{\varvec{i}}{\varphi }}}{{\mathrm {e} }^{{\varvec{k} }\psi }}{{\mathrm {e} }^{{\varvec{j} }\theta }}\right) \end{aligned}$$

(14)

$$\begin{aligned} = \; &{\text {csign}}_A\Big ({{\mathrm {e} }^{{\varvec{i}}{\varphi }}}\Big ) {\text {csign}}_B\left( {{\mathrm {e} }^{{\varvec{k} }\psi }}\right) {\text {csign}}_C\left( {{\mathrm {e} }^{{\varvec{j} }\theta }}\right) . \end{aligned}$$

(15)

The update is conducted for each of phases in $\varvec{h}$, i.e., ${\varphi }$, $\psi$, $\theta$. The function ${\text {csign}}_A$ is used for updating ${\varphi }$, and it is defined as

$$\begin{aligned}&{\text {csign}}_A\left( {{\mathrm {e} }^{{\varvec{i}}{\varphi }}}\right) =\nonumber \\&{\left\{ \begin{array}{ll} \varvec{q}_0^{({\varphi })} &{} \quad \mathrm {for}\; -\!\uppi \le \arg \left( {{\mathrm {e} }^{{\varvec{i}}{\varphi }}}\right) < -\uppi + {\varphi }_0\\ \varvec{q}_1^{({\varphi })} &{} \quad \mathrm {for}\; -\!\uppi +{\varphi }_0 \le \arg \left( {{\mathrm {e} }^{{\varvec{i}}{\varphi }}}\right) < -\uppi + 2{\varphi }_0\\ &{} \quad \vdots \\ \varvec{q}_{A-1}^{({\varphi })} &{} \quad \mathrm {for}\; -\!\uppi +(A\!-\!1){\varphi }_0 \le \arg \left( {{\mathrm {e} }^{{\varvec{i}}{\varphi }}}\right) \! <\! -\uppi + \!A{\varphi }_0\\ \end{array}\right. }, \end{aligned}$$

(16)

where A is the phase resolution for ${\varphi }$, and ${\varphi }_0$ defines a quantization unit which is represented by ${\varphi }_0=2\uppi /A$. $\varvec{q}_a^{({\varphi })}$ is a distinct point on a unit circle which is defined as $\varvec{q}_a^{({\varphi })}=\exp ({\varvec{i}}{(-\uppi +a{\varphi }_0+\frac{{\varphi }_0}{2}}))$. Therefore, the function ${\text {csign}}_A$ outputs the closest quaternion in $\{\varvec{q}_0^{({\varphi })},\dots ,\varvec{q}_{A-1}^{({\varphi })}\}$ corresponding to the input. Similarly, the function ${\text {csign}}_B$ for updating $\psi$ and the function ${\text {csign}}_C$ for updating $\theta$ are defined as follows:

$$\begin{aligned}&{\text {csign}}_B\left( {{\mathrm {e} }^{{\varvec{k} }\psi }}\right) =\nonumber \\&{\left\{ \begin{array}{ll} \varvec{q}_0^{(\psi )} \!&{} \quad \mathrm {for}\;-\!\frac{\uppi }{4} \le \arg \left( {{\mathrm {e} }^{{\varvec{k} }\psi }}\right) < -\frac{\uppi }{4} + \psi _0\\ \varvec{q}_1^{(\psi )} \!&{} \quad \mathrm {for}\;-\!\frac{\uppi }{4}+\psi _0 \le \arg \left( {{\mathrm {e} }^{{\varvec{k} }\psi }}\right) < -\frac{\uppi }{4} + 2\psi _0\\ \!&{} \quad \vdots \\ \varvec{q}_{B-1}^{(\psi )} \!&{} \quad \mathrm {for}\;-\!\frac{\uppi }{4}+(B\!-\!1)\psi _0 \le \arg \left( {{\mathrm {e} }^{{\varvec{k} }\psi }}\right) \! <\! -\frac{\uppi }{4} +\! B\psi _0\\ \end{array}\right. }, \end{aligned}$$

(17)

$$\begin{aligned}&{\text {csign}}_C\left( {{\mathrm {e} }^{{\varvec{j} }\theta }}\right) =\nonumber \\&{\left\{ \begin{array}{ll} \varvec{q}_0^{(\theta )}&{} \quad \mathrm {for}\;-\!\frac{\uppi }{2} \le \arg \left( {{\mathrm {e} }^{{\varvec{j} }\theta }}\right) < -\frac{\uppi }{2} + \theta _0\\ \varvec{q}_1^{(\theta )}&{} \quad \mathrm {for}\;-\!\frac{\uppi }{2}+\theta _0 \le \arg \left( {{\mathrm {e} }^{{\varvec{j} }\theta }}\right) < -\frac{\uppi }{2} + 2\theta _0\\ &{} \quad \vdots \\ \varvec{q}_{C-1}^{(\theta )}&{} \quad \mathrm {for}\;-\!\frac{\uppi }{2}+(C\!-\!1)\theta _0 \le \arg \left( {{\mathrm {e} }^{{\varvec{j} }\theta }}\right) \!<\!-\frac{\uppi }{2} +\!C\theta _0\\ \end{array}\right. }, \end{aligned}$$

(18)

where B and C are the phase resolutions for ${\varphi }$ and $\theta$, respectively. The quantization units $\psi _0$ and $\theta _0$ are defined by $\psi _0=\uppi /2B$ and $\theta _0=\uppi /C$, respectively. $\varvec{q}_b^{(\psi )}$ and $\varvec{q}_c^{(\theta )}$ are also defined as follows: $\varvec{q}_b^{(\psi )}=\exp (\,{\varvec{j} }{(-\frac{\uppi }{4}+b\psi _0+\frac{\psi _0}{2}}))$, $\varvec{q}_c^{(\theta )}=\exp ({\varvec{k} }{(-\frac{\uppi }{2}+c\theta _0+\frac{\theta _0}{2}})).$

From the above equations, the quaternionic neuron takes a total of $A\times B \times C$ states. An example of the quantized output points of the quaternionic neuron is shown in Fig. 1, where $A=4,B=2$, and $C=3$.

Fig. 1

An example of quantized output points in the quaternionic multistate neuron $(A=4,B=2,C=3)$

The energy function of the network with N quaternionic neurons is given as:

$$\begin{aligned} \varvec{E}(t) = -\frac{1}{2}\sum _{p=1}^N \sum _{q=1}^N {\varvec{u}}^{*}_p(t) \varvec{w}_{pq}\varvec{u}_q(t). \end{aligned}$$

(19)

$\varvec{E}$ takes real value $(\varvec{E}={\varvec{E}}^{*})$ when the connection weights $\varvec{w}_{pq}$ satisfy the following conditions:

$$\begin{aligned} \varvec{w}_{pq}={\varvec{w}}^{*}_{qp},\; \varvec{w}_{pp}={\varvec{w}}^{*}_{pp}=({{\varvec{w}}^{(e)}},\mathbf {0}),\;{{\varvec{w}}^{(e)}}\ge 0 \end{aligned}$$

(20)

The function monotonically decreases under the conditions $|\Delta {\varphi }|<{\varphi }_0$, $|\Delta \psi |<\psi _0$, and $|\Delta \theta |<\theta _0$. In these conditions, $\Delta {\varphi }$, $\Delta \psi$, and $\Delta \theta$ are a phase difference between the state at time $(t+1)$ and the action potential at time t for the neuron undergoing its update [6].

4 Learning schemes

4.1 Hebbian rule

Let $({\xi }^\mu _{{\varphi },1},\dots ,{\xi }^\mu _{{\varphi },N})$, $({\xi }^\mu _{\psi ,1},\dots ,{\xi }^\mu _{\psi ,N})$, and $({\xi }^\mu _{\theta ,1},\dots ,{\xi }^\mu _{\theta ,N})$ be multistate memory patterns. Here, $\xi ^\mu _{\varphi }\in \{0,\dots ,A\!-\!1\}$, $\xi ^\mu _\psi \in \{0,\dots ,B\!-\!1\}$, $\xi ^\mu _\theta \in \{0,\dots ,C\!-\!1\}$, and $\mu$ denotes pattern index. These three patterns can be represented as a quaternionic pattern $(\varvec{\epsilon }^\mu _1,\dots ,\varvec{\epsilon }^\mu _N)$, where $\varvec{\epsilon }^\mu ={{\mathrm {e} }^{{\varvec{i}}(\xi _{{\varphi }}^\mu {\varphi }_0+\frac{{\varphi }_0}{2})}}$ ${{\mathrm {e} }^{{\varvec{k} }(\xi _{\psi }^\mu \psi _0+\frac{\psi _0}{2})}}$ ${{\mathrm {e} }^{{\varvec{j} }(\xi _{\theta }^\mu \theta _0+\frac{\theta _0}{2})}}$.

A straightforward way to embed patterns into the associative memory is the use of Hebbian rule. The Hebbian rule is represented as

$$\begin{aligned} \varvec{w}_{pq} = \sum _{\mu =1}^P \varvec{\epsilon }^\mu _p {\varvec{\epsilon }^\mu _q}^{*}, \end{aligned}$$

(21)

where P is the number of embedded patterns, and $\varvec{\epsilon }_p^\mu$ denotes the state of the neuron p about $\mu$-th memory pattern.

The connection weights calculated by Eq. (21) satisfies the condition Eq. (20), thus the network with these connections is stable. In this scheme, the memory patterns can be stable points in the network when the memory patterns are orthogonal to each other [9].

4.2 Projection rule

Projection rule [10–12] is a learning scheme that can embed non-orthogonal (correlated) memory patterns in a network. A key idea of the projection rule is that non-orthogonal patterns are first projected onto orthogonal ones, and then the Hebbian rule is applied to these projected patterns.

Quaternionic extended projection rule [7] is given as follows:

$$\begin{aligned}&\tilde{\varvec{w}}_{pq}=\sum _{\nu ,\mu }^{P}{\varvec{\epsilon }_p^\mu }{\left( \varvec{Q}^{-1}\right) }_{\!\mu \nu }{\varvec{\epsilon }_q^\nu }^{*},\;\;\; \varvec{Q}_{\mu \nu }=\sum _{p=1}^N{\varvec{\epsilon }_p^\mu }^{*}{\varvec{\epsilon }_p^\nu }, \end{aligned}$$

(22)

where $\varvec{Q}^{-1}$ denotes the pseudo inverse matrix of $\varvec{Q}$. By the use of orthogonalization of correlated patterns, the number of patterns that can be stored in the network equals to the number of neurons in the network.

5 Simulations

5.1 Stability of stored patterns

We first evaluate the stability of the embedded memory patterns which are stored into QMNNs using the Hebbian rule and the projection rule. In this experiment, the patterns with randomly generated values are used as memory patterns. The size of the patterns, which is the number of neurons in the network, is set to 100, and the phase resolutions are set as follows: $(A, B, C)=(4, 1, 2)$, (8, 2, 4), (16, 4, 8), (32, 8, 16), (64, 16, 32). In these conditions, the quantization units ${\varphi }_0$, $\psi _0$, and $\theta _0$ are the same size. The number of the memory patterns, denoted by P, varies such that $P=1,2,\dots ,100$.

The stability of the patterns is investigated by the following procedure. First, for given A, B, C, and P, memory patterns are generated and stored into the network. Next, each of the memory patterns is set to the network as its initial states, then the states for all neurons are updated. If the network state does not change, this stored pattern can be regarded as stable.

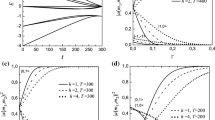
Figure 2 shows P dependency of the retrieval success rates against various phase resolutions. The retrieval success rates are calculated from 1000 trials. From Fig. 2, we find that the memory patterns are hardly embedded to the network using the Hebbian rule. The memory patterns tend to be more unstable with increases of the phase resolutions and the number of stored patterns. If the phase resolutions (A, B, C) are set to (32, 8, 16) or (64, 16, 32), only one pattern is stable in the network as shown in Fig. 2. In other words, two or more memory patterns cannot to be stable in the network using the Hebbian rule for large phase resolutions. On the other hand, the projection rule can store up to 99 patterns in the network regardless of the phase resolutions as shown in Fig. 3. In this figure, the retrieval success rate is $0\;\%$ in the case of $P=100$. It is due to that the self-connection weights, $\tilde{\varvec{w}}_{pp}s$, are set to 0. If these weights are set to positive values, the retrieval success rate becomes $100\;\%$. From these results, all the stored patterns are local minima in the network using the projection rule. Therefore, the memory patterns stored using the projection rule have higher stability than those using the Hebbian rule in QMNN.

Fig. 2

Stability of the memory patterns stored by Hebbian rule

Fig. 3

Stability of the memory patterns stored by projection rule

5.2 Noise robustness of projection rule

We have shown the stabilities of the stored patterns by retrieving stored patterns from the network. In this section, we show the retrieval performance by retrieving patterns from noisy patterns, i.e., the patterns modified from the stored patterns. This evaluates the basins of attractors (stored patterns) produced by the projection rule. We set the experimental conditions for the number of neurons and phase resolutions with the same ones in the previous section.

Figures 4 and 5 show the retrieval success rates when noisy patterns are used as initial configurations of the network. A noisy input pattern is generated from one of the stored patterns with each pixel value being changed with probability r (noise rate). In the case of Fig. 4, the number of stored patterns is set to $P=10$ and the noise rate of the input pattern varies from 0.1 to 1.0. In the case of Fig. 5, the noise rate is fixed to 0.3 and the number of stored patterns is changed from 1 to 40. From these results, we find that the retrieval success rate is decreased with increasing the number of stored patterns. The success rate is also decreased with increasing the phase resolutions.

The deterioration of noise robustness is caused by spurious patterns, i.e., mixture patterns, inverted patterns and rotated patterns of memory patterns. These spurious patterns increase with increasing the number of stored patterns and the phase resolutions. Therefore, the noise robustness of QMNN depends on the number of stored patterns and phase resolutions.

Fig. 4

Retrieval success rate of the stored patterns against the noise rate ($P=10$)

Fig. 5

Retrieval success rate of the stored patterns against the number of stored patterns ($r\;=\;0.3$)

5.3 Image retrieval task

We have explored the performances of QMNN with the projection rule and Hebbian rule in the previous sections, and found that the projection rule could successfully work for storing random patterns. In this section, we investigate the performances of QMNNs by storing and retrieving natural images that have more intensity resolutions in each pixel from the viewpoint of practical applications such as color image database.

Figure 6 shows three types of memory patterns to be embedded to the network. These images consist of $64\times 64=4096$ pixels and each pixel value is represented by 8 bits (256 levels) of three channels. The three channels, which are red, green, and blue, are assigned to ${\varphi }, \theta$, and $\psi$ of a quaternion in phasor representation. Thus, the phase resolutions are set to $A=B=C=256$. The number of neurons in the network is the same as the number of pixels of the images, i.e., $N=4096$. These memory patterns are embedded to the networks with the Hebbian rule and the projection rule.

Figure 7 shows input images and their corresponding output images from the networks. The images on the top rows are the input images, and the pixel values on these images are affected by noises with probability r. The images on the second and third rows are the output images from the networks with patterns being embedded by the Hebbian rule and the projection rule, respectively. From the output images, the network with the Hebbian rule cannot retrieve the stored pattern, even if the original memory pattern is input to the network. Thus the three color images are not stable in the network using the Hebbian rule. On the other hand, the network with the projection rule successfully retrieves stored patterns from the noisy images. Therefore, for a large-scaled network with high resolution of phases, the patterns can be stored by the projection rule.

This experimental result shows that QMNN can store natural images each of which has some correlation to each other and it can retrieve the stored images from noisy input. In this case, loading rate, which is a ratio of the number of stored patterns (P) with respect to the number of neurons (N) in the network, is low ($P=3/N=4096$). When the loading rate for the network gets higher, the retrieval of images tends to be failed, as shown in Figs. 4 and 5. This is due to the spurious patterns in the QMNN caused by the memory patterns.

Fig. 6

Memory patterns for the image retrieval experiment ($64\times 64$ pixels, 24 bit color)

Fig. 7

Image retrieval results (Lenna)

6 Conclusion

In this paper, the stabilities of embedded patterns are investigated in the quaternionic associative memories. The associative memory is based on quaternionic multistate Hopfield neural network. The Hebbian rule and the projection rule are used for embedding memory patterns.

The stability of stored memory patterns has been explored with randomly generated patterns with changing the phase resolutions. From the experimental results, the Hebbian rule hardly stores the memory patterns with increasing the phase resolutions. In contrast, the projection rule can stabilize all the memory patterns into the network regardless of phase resolutions. The noise robustness of the retrieval patterns is also investigated and it is found that the performance from noisy input depends on the phase resolutions of the quaternionic neuron states and the number of stored memory patterns. The practical experimental results show that the color images can be embedded to the network by utilizing the projection rule. Three types of color images are embedded (by the projection rule) and they are retrieved from noisy input images successfully.

To obtain better performances in embedding patterns, we will explore encoding schemes for representing pixel values of images for practical applications. The experimental results show that the QMNNs with the projection rule can store correlated patterns such as natural images successfully, but also show that the retrieval performances become lower when the number of patterns is higher or the resolutions in the neuron are higher. This is due to the spurious patterns by the memory patterns. This problem also lies in CVMNNs, but another type of CVMNN, which has a combination of real-valued and complex-valued neurons in a network, could overcome this problem [13]. It is possible to extend this CVMNN to QMNN for improving the noise robustness. This remains for our future work.