1 Introduction

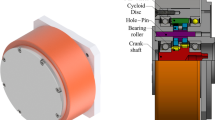
The cycloid planetary gear reducers are important drives for power and/or precision motion transmission. The gear mechanism designed in the type of two-stage eccentric differential, i. e. the so-called “RV-drive”, is today widely applied in automation machinery. As the structural diagrams in Fig. 1 show, this gear drive type consists of an involute planetary stage and a cycloid planetary stage with two disks. Each involute planet is mounted on a crank shaft to generate the revolution motion of the cycloid disk. Such the design configuration has not only the advantages of high gear ratio, but also good performances in load sharing and shock absorbing ability because of multiple tooth pairs in contact. Nevertheless, the trend in designing the gear reducers today is to enlarge the power density, besides the requirements on precise motion. To this purpose, the loads acting on the contact tooth pairs and the cranks must be reduced.

Fig. 1
figure 1

Structure of cycloid planetary gear drive [1]

Full size image

Among various measures, the design concept by using a larger tooth number difference (abbr. TND) can give a possibility to improve the loaded contact characteristics. In other words, the TND of the cycloid gear pair can be selected as two, not as one that is often used in the conventional application. The gear drives with TND of two (∆z = 2) are often applied in the transmission of small reduction ratios in the practice, but they are rarely used in the cases with a higher ratio. Therefore it is interesting to evaluate the feasibility of such the alternative drive concept. The influences of the design parameters on the loaded contact characteristics and the comparison with the conventional drives should be explored.

The essential work for the load analysis is to derive the geometrical and kinematic relations. The study on the mathematic model of the cycloid profile can be found in many literatures. The gear mesh can be also analyzed based on the theory of gearing or the kinematic methods, e. g. the instant center method [2, 3]. Another evaluation criterion of the drives is the sliding characteristics between the engaged teeth. The damages on the tooth flanks, e. g., pitting, wear or scoring, can be predicted by the ratio of specific sliding. However, the related research is often found in some articles on trochoidal gear pumps [4], and is less mentioned in the field of the cycloid gear reducer.

Additionally, the load analysis is also an important issue for evaluating the feasibility of the gear drives with ∆z = 2. The often applied method for analysis of the contact stress of the cycloid gear drives is FEM, e. g. [5,6,7,8,9]. Another approach for load analysis is developed based on analytical methods. For example, Dong et al. [10] proposed a calculation approach for the acting forces on the rolling bearings for supporting the cycloid disks. Blanche and Yang [11, 12] focused on the influences of the manufacturing errors on the transmitted load and transmission errors. Hidaka et al. [13] analyzed the influences of manufacturing errors on the dynamic load behaviors based on the assumption of contact mesh stiffness of tooth action. Gorla et al. [14] conducted an experiment to analyze the contact stress so as to validate the theoretical analysis results from the analytical approach. The authors have developed an numerical loaded tooth contact analysis (LTCA) approach based on the influence coefficient method [15]. This approach is also successfully applied for analysis of the cycloid tooth pairs [2, 3] and also the complete tooth contact considering the bearing stiffness and the friction [16].

The aim of the paper is therefore to study systematically the influences of the design parameters on the contact and loading characteristics of such the alternative drive concept. A set of essential equations for the cycloid profile, tooth contact and the specific sliding of the cycloid stage with ∆z = 2 are at first derived in the paper. A new load analysis approach is extended from the developed LTCA model [12]. The influences of the design parameters on the contact characteristics are further systematically analyzed. Namely, the contact ratio, the specific sliding, the load sharing, the contact stress and the periodical time-variant bearing loads are discussed in the paper. These results are also compared with the conventional drive having ∆z = 1.

2 Fundamentals of the analysis methods for cycloid planetary gear drives

2.1 Construction of the cycloid disk for tooth number difference (TND) of two

(1) Definition of the base tooth profiles.

The tooth profile of the planetary cycloid stage with ∆z = 2 can be regarded as combination of two disks with the same base cycloid profile rotated against each other with an angle τ C, which is equal to τ C0/2 of the base cycloid profile., see Fig. 2. The essential design parameters for the cycloid profile are as follows,

  • the pitch circle radius R C of the pin-wheel,

  • the radius r P of the pins,

  • the eccentricity e of the crank,

  • the gear ratio u of the drive, here equal to z P/∆z.

Fig. 2
figure 2

Construction of the cycloid disc with ∆z = 2

Full size image

The base cycloid profile is in accordance with the cycloid profile with the same design parameters but with ∆z = 1, i. e., owns the coordinates [2], see Fig. 3:

$$x_{\mathrm{C}}=R_{\mathrm{C}}\cdot \cos \theta - e\cdot \cos \left (u\cdot \theta \right )- r_{\mathrm{P}}\cdot \cos \left (\theta - \psi \right )$$
(1)
$$y_{\mathrm{C}}=R_{\mathrm{C}}\cdot \sin \theta - e\cdot \sin \left (u\cdot \theta \right )- r_{\mathrm{P}}\cdot \sin \left (\theta - \psi \right )$$
(2)

with the pressure angle

$$\psi =\arctan \left [\frac{u\cdot e\cdot \sin \left [\left (u- 1\right )\cdot \theta \right ]}{R_{\mathrm{C}}- u\cdot e\cdot \cos \left [\left (u- 1\right )\cdot \theta \right ]}\right ]$$
(3)

or with the factor k = u e/R C

$$\psi =\arctan \left [\frac{k\cdot \sin \left [\left (u- 1\right )\cdot \theta \right ]}{1- k\cdot \cos \left [\left (u- 1\right )\cdot \theta \right ]}\right ]$$
(4)
Fig. 3
figure 3

Definition of the base cycloid profile

Full size image

The profile variable θ for the cycloid curve is defined from the rotation of the generating circle, as the relation shown in Fig. 3. The gear ratio u of the base profile is equal to z P0. In the case of ∆z = 2, the gear ratio u is equal to z P/2, also equal to z P0. The curvature radius ρ of the tooth profile can be obtained [2] as

$$\rho =\frac{R_{\mathrm{C}}\cdot \left [1+k^{2}- 2\cdot k\cdot \cos \left (\left (u- 1\right )\cdot \theta \right )\right ]^{3/2}}{1+u\cdot k^{2}- \left (1+i_{\mathrm{C}}\right )\cdot k\cdot \cos \left [\left (u- 1\right )\cdot \theta \right ]}- r_{\mathrm{P}}$$
(5)

The inflection point on the cycloid profile owns the property of the infinite curvature radius, i. e., the corresponding variable θ inf must be equal to

$$\theta _{\inf }=\frac{1}{u- 1}\arccos \left [\frac{1+u\cdot k^{2}}{\left (1+u\right )\cdot k}\right ]$$
(6)

(2) Intersecting point of the two base cycloid profiles.

In general, the pointing tip of the tooth profile in the case ∆z > 1 is usually rounded with a circular arc. In order to simplify the analysis, the case of rounding is not considered in the study. Based on the symmetrical relation, the separation angle of the intersection point Ypt of the two base cycloid profiles to the x‑axis is equal to a half-pitch angle τC/2, as the relation shown in Fig. 2. The corresponding profile variable θ pt of the point Ypt can be determined with the equation,

$$\arctan \left [\frac{y_{\mathrm{C}}\left (\theta _{\text{pt}}\right )}{x_{\mathrm{C}}\left (\theta _{\text{pt}}\right )}\right ]=\frac{\tau _{\mathrm{C}}}{2}=\frac{\pi }{z_{\mathrm{C}}}$$
(7)

2.2 Gear meshing analysis

The cycloid gear mesh can be analyzed considering the disk as stationary, while the center of the pin wheel OP moves around the center of the disk OC relatively with the crank-shaft angle φ C, and the pin wheel itself rotates also with an angle φ P (=φ C/u). The relative motion can be illustrated with the geometric relation shown in Fig. 4. Some related issues are discussed as follows.

Fig. 4
figure 4

Basic geometric relation for tooth contact of the cycloid disc with ∆z = 2

Full size image

(1) Determination of contact points.

The contact points of the cycloid-pin tooth pairs P i can be determined with aid of the instant center of velocity. In general the analysis can be based on each of the two cycloid profiles respectively, here the terms “odd-numbered” and “even-numbered flanks” are used for distinction. As the relation in Fig. 4 shows, the equations of the profile variables θ for the contact points on both the cycloid flanks are listed in Table 1.

Table 1 Essential equations for determination of tooth contact
Full size table

(2) Theoretic contact ratio.

Because the variable θ of the cycloid profile is linearly associated with the rotation angle φ C of the crank, the meshing period is thus equal to θ pt for the case with ∆z > 1. The theoretic contact ratio ε, which is defined as the average number of contact tooth pairs during gear meshing, can be expressed as

$$\varepsilon =\frac{\theta _{\text{pt}}}{\Delta \tau }$$
(8)

where the pitch angle ∆τ is equal to the relation

$$\Delta \tau =\frac{4\cdot \pi }{z_{\mathrm{P}}\cdot z_{\mathrm{C}}}$$
(9)

(3) Transmission angle.

The conversion of the loaded displacements from the angular displacement of the cranks as well as the decomposition of the acting forces are based on the transmission angle γ i between the normal of the contact tooth pair and the line OPOC. As the relation in Fig. 4 shows, the transmission angle γ i for odd-numbered flanks can be determined as

$$\gamma _{i-\mathrm{I}}=\left (\theta _{i-\mathrm{I}}- \psi _{i-\mathrm{I}}\right )- \varphi _{\mathrm{C}}- \pi$$
(10)

while for even-numbered flanks is

$$\gamma _{i-\text{II}}=\left (\theta _{i-\text{II}}- \psi _{i-\text{II}}\right )- \left (\varphi _{\mathrm{C}}- \tau _{\mathrm{C}}\right )- \pi$$
(11)

(4) Equivalent displacement.

is defined as the compliance of a contact tooth pair along its contact normal due to the translational displacement e ⋅ δ φ of the cycloid disc under loading. This displacement e ⋅ δ φ is caused by the motion of the cranks with an angular displacement δ φ at each instant. The equivalent displacement δ eq i- I(II) of odd-/even-numbered tooth pair i can be determined with the transmission angle γ i (see Eqs. 10 or 11) from Fig. 4, i. e.,

$$\delta _{\text{eq}i-\mathrm{I}\left (\text{II}\right )}=- e\cdot \delta _{\phi }\cdot \sin \gamma _{i-\mathrm{I}\left (\text{II}\right )}$$
(12)

(5) Determination of active contact tooth pairs.

In order to calculate the acting force, it is essential to determine which tooth pairs are in contact. The following relations can be applied:

  • if the cranks rotate in the counter-clockwise direction, the tooth pairs with positive δ eq i are in contact, see Eq. 12; otherwise,

  • if the cranks rotate in the clockwise direction, the tooth pairs with negative δ eq i are in contact.

(6) Sliding velocity.

on the contact point plays an important role for evaluation of tooth scuffing. The sliding velocity of the ith contact tooth pair can be determined based on the instant center IC. According to the geometric relation in Fig. 5, the sliding velocity at the instant contact point M i is equal to the multiple of the rotation speed of the pin-wheel with the distance ICM i ,

$$v_{\mathrm{P}_{i}\mathrm{C}}=\omega _{\mathrm{P}}\cdot \left [R_{\mathrm{C}}\cdot \sqrt{1+k^{2}- 2\cdot k\cdot \cos \left (\theta _{i}- \phi _{\mathrm{C}}\right )}- r_{\mathrm{P}}\right ]$$
(13)
Fig. 5
figure 5

Velocity relation for the cycloid disc

Full size image

The specific sliding ζC i of the driving cycloid disc is calculated by the expression:

$$\zeta _{\mathrm{C}i}=\frac{v_{\mathrm{P}_{i}\mathrm{C}}}{v_{\mathrm{C}}\cos \gamma _{i}}=\frac{\sqrt{1+k^{2}- 2k\cos \left (\theta _{i}- \phi _{\mathrm{C}}\right )}- r_{\mathrm{P}}/R_{\mathrm{C}}}{k\cos \gamma _{i}}$$
(14)

while the specific sliding ζP i of the driven pin is equal to

$$\zeta _{\mathrm{P}i}=\frac{\zeta _{\mathrm{C}i}}{\zeta _{\mathrm{C}i}- 1}$$
(15)

The specific sliding ζC i will become infinitely great, and ζP i  = 1, if the transmission angle γ i is equal to π/2.

2.3 Typical tooth profile for TND of two

Because the base cycloid profile consists of both concave and convex profile, two profile types, i. e., either concave or concave-convex profile, can be found in the case of ∆z > 1. These two type of the cycloid profile are divided according to the relation between the location of the inflection point and tip pointing, i. e.,

  • concave profile, θ inf ≥ θ pt;

  • concave-convex profile, θ inf < θ pt.

In general, the concave profile is good for tooth contact, but the contact ratio is reduced accordingly.

2.4 Loaded tooth contact analysis

(1) Basic LTCA model for cycloid stage.

The contact problem of multiple tooth pairs under loading is statically indeterminate. The shared loads on the tooth pairs can be solved by using two types of equations, namely the equations of load equilibrium as well as the equations of loaded deformation and displacement [15]. To this end, a numerical approach for loaded tooth contact analysis of cycloid planetary gear drives is developed by the authors. This approach is based on the influence coefficient method to express the relation of the deformation of any specific point i on the engaged flanks due to the influence of all the distributed pressures p j , i. e.,

$$w_{i}=\sum _{j=1}^{n}\left (f_{i- j}\cdot p_{j}\right )$$
(16)

where f i−j is the influence coefficient for the condition, that the deformation on point i is caused by a load acting on the point j.

The relations of displacement-deformation is thus valid for the specific point Y i

$$w_{i}+h_{i}=\delta _{\text{eq}i}$$
(17)

where h i is the separation distance between the engaged flanks at the discrete point, more detail see [2].

Another relation for the loaded tooth contact is the load equilibrium equation, i. e., the sum of all the acting forces in the tangential direction (see Fig. 6) must be equal to the equivalent force T/(u ⋅ e), i. e.,

$$\sum _{i=1}^{n}\left (s\cdot q_{i}\cdot \sum _{j=1}^{m}p_{i- j}\right )=\frac{T}{u\cdot e}$$
(18)

where the factor q i is equal to \(q_{i}=\sin \gamma _{i}\).

Fig. 6
figure 6

Relation of acting forces on the cycloid disk

Full size image

The set of the deformation-displacement equations and the load equilibrium equation can be summarized in a form of matrix equation [2], as the expression:

$$\left [\begin{array}{ccccc} \boldsymbol{A}_{1} & \mathbf{0} & \cdots & \mathbf{0} & - q_{1}\mathbf{I}\\ \mathbf{0} & \boldsymbol{A}_{2} & \cdots & \mathbf{0} & - q_{2}\mathbf{I}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \mathbf{0} & \mathbf{0} & \cdots & \boldsymbol{A}_{n} & - q_{n}\mathbf{I}\\ q_{1}s_{1}\mathbf{I} & q_{2}s_{2}\mathbf{I} & \cdots & q_{n}s_{n}\mathbf{I} & 0 \end{array}\right ]\left [\begin{array}{c} \boldsymbol{P}_{1}\\ \boldsymbol{P}_{2}\\ \vdots \\ \boldsymbol{P}_{n}\\ e\delta _{\phi } \end{array}\right ]=\left [\begin{array}{c} - \boldsymbol{H}_{1}\\ - \boldsymbol{H}_{2}\\ \vdots \\ - \boldsymbol{H}_{n}\\ T/\left (u\cdot e\right ) \end{array}\right ]$$
(19)
$$\left [\begin{array}{cc} \mathbf{A} & \mathbf{Q}\\ \mathbf{S} & 0 \end{array}\right ]\left [\begin{array}{c} \mathbf{P}\\ e\delta _{\phi } \end{array}\right ]=\left [\begin{array}{c} - \mathbf{H}\\ T/\left (u\cdot e\right ) \end{array}\right ]$$
(20)

The sub-matrices in Eqs. 19 and 20 are defined as follows:

  • A i contains all the influence coefficients f P i for the tooth pair i; all these sub-matrices are summarized in the matrix A in Eq. 20.

  • I is either the column or the row unit vector.

  • P i as a column vector contains all the contact stresses on the discrete units of the tooth pair i; all these sub-vectors are summarized in a column vector P in Eq. 20.

  • H i as a column vector contains all the separation distances between the engaged tooth flanks of the tooth pair i according to the discrete points; all these sub-vectors are summarized in a column vector H in Eq. 20.

  • S in Eq. 20 combines all the row vectors with a value of q i s i .

Because the contact region of two engaged flanks are divided into small discretized areas for load analysis, the actual contact pattern and distributed contact stresses can be simulated. More details can be found in [2, 3, 15, 16].

(2) Conversion of the basic LTCA model for the case with ∆z = 2.

Considering two disks with a separation angle of τC, the LTCA model for analysis of the case of ∆z = 2 can be expanded by the expression:

$$\left [\begin{array}{ccc} \boldsymbol{A}_{\mathrm{I}} & \mathbf{0} & \mathbf{Q}_{\mathrm{I}}\\ \mathbf{0} & \boldsymbol{A}_{\text{II}} & \mathbf{Q}_{\text{II}}\\ \boldsymbol{S}_{\mathrm{I}} & \mathbf{S}_{\text{II}} & 0 \end{array}\right ]\left [\begin{array}{c} \mathbf{P}_{\mathrm{I}}\\ \mathbf{P}_{\text{II}}\\ e\delta \end{array}\right ]=- \left [\begin{array}{c} - \mathbf{H}_{\mathrm{I}}\\ - \mathbf{H}_{\text{II}}\\ T/e \end{array}\right ]$$
(21)

The contact areas with distributed stresses of the contact tooth pairs based on Eqs. 19 or 21 are solved iteratively until the convergent condition is fulfilled, i. e., all the contact stresses are positive.

(3) Load sharing of the drive

is distinguished between the load sharing among the tooth pairs at a specific angular position as well as the shared loads distributed on an individual tooth flank within a meshing cycle. The normal load F N i −I,II acting on the ith odd/even-numbered contact tooth pair is determined as the sum of all the distributed contact stresses which are solved from the LTCA approach based on Eq. 21, namely,

$$F_{\mathrm{N}i-\mathrm{I},\text{II}}=\sum _{j=1}^{m_{n}}s_{i}p_{i-j}$$
(22)

(4) Bearing loads

on the cranks can be divided into three types of forces based on the load equilibrium conditions, see Fig. 6 and [2, 10]:

  • Force equilibrium,

$$F_{\mathrm{r}}=\sum _{i}^{m}\left [q_{\mathrm{r}i}\cdot F_{\mathrm{N}i}\right ]/3$$
(23)
$$F_{\mathrm{t}}=- \sum _{i}^{m}\left [q_{\mathrm{t}i}\cdot F_{\mathrm{N}i}\right ]/3$$
(24)

  • Moment equilibrium, the circumferential force:

$$F_{\mathrm{c}}=- \sum _{i}^{m}\left [q_{\mathrm{t}i}\cdot F_{\mathrm{N}i}\right ]\cdot \left (u- 1\right )\cdot e/\left (3\cdot r_{R}\right )$$
(25)

where the factors q r i and q t i in the above equation are determined as follows,

$$q_{\mathrm{r}i}=\sin \gamma _{i}$$
(26)
$$q_{\mathrm{t}i}=\cos \gamma _{i}$$
(27)

The result radial forces F CRr and tangential forces F CRt acting on the crank j are equal to the following relations respectively, see Fig. 7,

$$F_{\text{CRr}-j}=F_{r}+F_{\mathrm{c}}\cdot \sin \left [\phi _{\mathrm{C}}+2\pi \left (j- 1\right )/3\right ]$$
(28)
$$F_{\text{CRt}-j}=F_{\mathrm{t}}- F_{\mathrm{c}}\cdot \cos \left [\phi _{\mathrm{C}}+2\pi \left (j- 1\right )/3\right ]$$
(29)
Fig. 7
figure 7

Relation of acting forces on the crank

Full size image

Because the tangential F t and circumferential force F c are directly associated with the output torque T out, i. e.,

$$F_{\mathrm{t}}=\frac{T_{\text{out}}}{3\cdot u\cdot e}$$
(30)
$$F_{\mathrm{c}}=\frac{T_{\text{out}}\cdot \left (u- 1\right )}{3\cdot u\cdot r_{\mathrm{R}}}$$
(31)

only the radial force F r can be changed by using suitable design parameters so as to reduce the bearing loads.

3 Overview of the numerical example

In order to analyzed the influences of the design parameter, the essential gear data are listed in Table 2. The design parameters considered in the paper are the pin radius r P and the eccentricity e, the corresponding values used for the analysis are listed Table 3. A larger pin radius is not considered here, because the available space for installation of the pins in the pin wheel is limited.

Table 2 Essential gearing data for numerical analysis
Full size table
Table 3 Design parameters for influence analysis
Full size table

4 Influence analysis of the design parameters

4.1 Tooth profile and contact ratio

The influences of the design parameters e and r P on the location of tip pointing and the contact ratio are represented in Fig. 8. Because the contact ratio is linearly associated with the profile variable θ pt for tooth pointing, the curves in the diagram illustrate both the two factors at the same time. In general, the cycloid drive with ∆z = 2 having smaller pins and a larger eccentricity owns a larger contact ratio. In such the case, the cycloid profile has a convex and concave portion. On the other hand, a larger pin radius, e.g, r P = 7, lowers the contact ratio with an increased eccentricity.

Fig. 8
figure 8

Influence of e and r P on the location of tip pointing and the contact ratio ε

Full size image

How these parameters affect the profile can be further identified from Fig. 9. A larger pin radius r P under the same eccentricity e causes a smaller tooth thickness t C of cycloid flank and a closer location of the inflection point Yinf and the pointing tip Ypt. On the other hand, the eccentricity e affects the shape of the tooth profile strongly. The tooth depth h C is enlarged with an increased eccentricity e.

Fig. 9
figure 9

Influence of e and r P on the profile

Full size image

4.2 Specific sliding

The influences of the pin radius r P and the eccentricity e on the specific sliding are illustrated in Figs. 10 and 11, respectively. The specific sliding of the cycloid disk ζC is much larger than that of the pin ζP. The specific sliding ζP increases monotonously from the begin A to the end E of contact. The specific sliding ζC, by contrast, decreases at first monotonously, and then asymptotically to −∞ nearby the singular point, where the transmission angle γ i is equal to π/2. As the tooth pair engages further, ζC decreases with change of the sign from +∞ to the a local extremum on the tip E [4].

Fig. 10
figure 10

Influences of the pin radius r P on the specific sliding

Full size image
Fig. 11
figure 11

Influences of the eccentricity e on the specific sliding

Full size image

The pin radius has almost no influences as the curves in Fig. 10 show. The eccentricity e, by contrast, affects the specific sliding strongly (Fig. 11). Namely, as the eccentricity e decreases, the point with infinitely great specific sliding ζC will shift in the direction to the tip E, and the values of ζC in other segments are enlarged, ζP are reduced accordingly.

4.3 Shared loads among the contact tooth pairs

Because the transmission angles γ of the active contact tooth pairs are different, the normal loads are also shared unevenly among the contact tooth pairs, as the analysis results in Figs. 12 and 13 show. The pin radius has less effect on the load sharing. A smaller eccentricity, by contrast, causes unevenly shared loads.

Fig. 12
figure 12

Influences of the pin radius r P on the load sharing among the contact tooth pairs

Full size image
Fig. 13
figure 13

Influences of the eccentricity e on the load sharing among the contact tooth pairs

Full size image

4.4 Shared load on an individual cycloid flank

The distribution of the normal forces acting on an individual cycloid flank is illustrated in Figs. 14 and 15. Some findings from these diagrams are listed as follows:

  • There is no load at the begin of contact A, but a larger load remains at the end of contact E.

  • The shared load varies with several periodical jumps due to the change of the numbers of contact tooth pairs, and the presence of a phase angle for tooth profile.

  • The eccentricity e affects the variation of the load sharing stronger than the pin radius, not only because of the tooth profile, but also because of the transmission angle γ.

  • A small eccentricity e causes a reduced contact ratio and enlarged shared loads, while a small pin radius causes an enlarged contact ratio and reduced shared loads.

Fig. 14
figure 14

Influences of the pin radius r P on the shared load on an individual flank

Full size image
Fig. 15
figure 15

Influences of the eccentricity e on the shared load on an individual flank

Full size image

4.5 Contact stress on an individual cycloid flank

The variation of the contact stress on the flank is similar to that of the shared load, but the stress increases more slowly on the segment after begin of contact A due to the concave profile. The jumping phenomenon is also found in the variation of contact stresses, because of the suddenly changed load. The pin radius r P changes only the value of the contact stress, but not the variation shape, see Fig. 16. By contrast, the eccentricity e affects not only the shape, but also the value of stress variation, Fig. 17. A larger eccentricity has a positive effect on the distribution of the contact stress.

Fig. 16
figure 16

Influences of the pin radius r P on the distributed contact stress on flanks

Full size image
Fig. 17
figure 17

Influences of the eccentricity e on the distributed contact stress on flanks

Full size image

The proposed approach can also simulate the concentrated contact stress on the flank due to the edge effect. Fig. 18 shows the contact pattern with distributed contact stresses of two tooth pairs, respectively. A saddle-shaped distribution of contact stress can be identified in the contact of the 11th tooth pair (Fig. 18a), while a strong stress concentration due to edge contact occurs on the flanks of the 24th tooth pair (Fig. 18b).

Fig. 18
figure 18

Distribution of the contact stress on the flank of the different tooth pair: a normal contact; b edge contact with stress concentration

Full size image

4.6 Bearing loads on the cranks

Among the three types of bearing loads acting on the cranks for supporting the cycloid disks, Eqs. 23, 24 and 25, only the radial forces can be affected by both the eccentricity e and the center radius of the bearings r R. Because the influence of the pin radius on the shared load is not significant, only the eccentricity is considered here for analysis. Fig. 19 shows the variation of the radial forces with three different values of eccentricity. It is obvious to recognize that a larger eccentricity than a certain value causes a larger radial bearing force. Although a certain value of eccentricity will reduce the radial bearing force F r to zero, a larger tangential force F t and less contact points are present due to a smaller eccentricity.

Fig. 19
figure 19

Influences of the eccentricity e on the result radial force due to the sum of normal forces

Full size image

5 Comparison with the TND of one

In order to compare the transmission characteristics, the eccentricity e of the drive with ∆z = 1 and 2 is selected as the same value, while the pin radii r P are different, see Table 4.

Table 4 Additional design parameter for analysis
Full size table

5.1 Load sharing

(1) The shared loads among the contact tooth pairs

for the case of ∆z = 1 and 2 are illustrated in Fig. 20. The loads acting in the drive with ∆z = 2 vary more evenly than those with ∆z = 1, while the maximum load is about half the value in the disk with ∆z = 1.

Fig. 20
figure 20

Loads shared by various contact tooth pairs in the drive with ∆z = 1 and 2

Full size image

(2) The shared loads on an individual flank

in the case of ∆z = 2 vary also evenly, while the shared load is also reduced, Fig. 21. The differences come from that the profile portion having the transmission angle γ smaller than π/2 is less in the case of ∆z = 1.

Fig. 21
figure 21

Comparison of the shared loads acting on the cycloid flank for the drive with ∆z = 1 and 2

Full size image

5.2 Contact stress

Although the pin radius is smaller in the case of ∆z = 2, the high contact stress on the cycloid flank in the case of ∆z = 1 is significantly reduced to about 2/3, Fig. 22. On the other hand, the contact stress varies along the flank also in a type of jumping compared with the case of ∆z = 1. This phenomenon is significant in the concave profile segment because of the sensitive change of the mesh stiffness. In other words, the gradient of the relative curvature in this segment is larger than the other convex segment.

Fig. 22
figure 22

Comparison of the contact stress on the cycloid flank for the drive with ∆z = 1 and 2

Full size image

5.3 Bearing loads

Although the normal loads acting on the cycloid disk with ∆z = 2 are reduced, the result loads F t and F c in the tangential and circumferential direction (see Fig. 6) remains constant during rotation of the crank with a constant output torque T out. The result radial load F r, on the other hand, is affected by the transmission angle γ. The influence can be recognized from Fig. 23. The radial force F r in the case of ∆z = 2 is reduced with about half the value of the normal drive. However, the lowered radial force F r, is still much smaller than the circumferential force F c, which is equal to a constant value 14,444 N, see Eq. 31. In other words, The effect by using ∆z = 2 to reduce the bearing force (F CRr and F CR) is small, as the results in Fig. 24 show. Only 2% of the maximum bearing force is reduced.

Fig. 23
figure 23

Comparison of the radial forces for the cycloid disk with ∆z = 1 and 2

Full size image
Fig. 24
figure 24

Comparison of the bearing support loads for the cycloid disk with ∆z = 1 and 2

Full size image

6 Conclusion and outlook

In order to improve the transmission performances of the cycloid planetary gear drive with a high gear ratio, the concept with tooth number difference of two (∆z = 2) is proposed. The loaded contact characteristics of this drive type are explored with aid of a developed loaded tooth contact analysis model based on the influence coefficient method. No only the influences of the design parameters, here the eccentricity and the pin radius, but also the comparison with ∆z = 1 is analyzed. The comparison of the analysis results are summarized in Table 5.

Table 5 Comparison of the analysis results
Full size table

The analysis results enable us to draw the following conclusions:

  • The theoretical contact ratio of the cycloid drives with ∆z = 2 can be increased by using suitable design parameters, where a smaller pin radius and a larger eccentricity are expected for use.

  • The eccentricity affects significantly the specific sliding. With a larger eccentricity, the point with infinitely great specific sliding ζC will shift in the direction to the tooth root the cycloid profile, and the values of ζC are reduced, but ζP are enlarged accordingly.

  • The shared acting load and contact stress on the contact flanks with ∆z = 2 can be significantly reduced with respect to the case ∆z = 1. A smaller pin radius and a larger eccentricity are suitable for designing such the drive.

  • The variation of the shared load and the contact stress on flanks with ∆z = 2 performs in cyclic jumping type, similarly to the phenomenon in involute spur gearing.

  • The effect by using ∆z = 2 to reduce the bearing loads on the cranks is small, because the influence of the circumferential force is much stronger.

However the modified cycloid profile is applied in practical application, not the theoretical profile, because of the necessary backlash. For further design of flank modification of the cycloid drive with ∆z = 2, the presented results can be still good references and the proposed analysis approach is also an efficient tool.