Using Turbocharger maps in gas exchange simulation and engine control units

Abstract

Characterisation of turbocharger performance is important in gas exchange simulation and engine control unit calibration. Compressor and turbine performance maps are measured on a hot-gas test bed. As a result their performance maps have a large dependence on heat transfer. Gas exchange simulation software assumes adiabatic compressor and turbine maps. The direct use of measured maps leads to defective simulation results. The power balance of compressor and turbine in steady state operation leads to limited turbine performance maps. The acceleration of compressor and turbine are not covered in those maps. In gas exchange simulation the performance maps are extrapolated to cover the entire range of operation. Simulations using the extrapolated maps do not correlate with empirical results. This paper presents methods for reconciling results derived from maps with those observed in the real world over the same extrapolated operating range. The methods use existing maps without additional information to construct performance maps relevant for operation on internal combustion engines. A recipe approach for the application to measured maps is developed and applied to examples. Compared to mathematical extrapolation, the presented methods yield empirically sound extrapolations and improve the quality of gas exchange simulation results.

Zusammenfassung

Die Beschreibung der Eigenschaften von Turboladern ist wichtig für die Ladungswechselrechnung und die Bedatung von Motorsteuergeräten. Verdichter- und Turbinenkennfelder werden auf Heißgasprüfständen gemessen. Wärmeströme in Verdichter und Turbine haben einen großen Einfluss auf die gemessenen Verdichter- und Turbinenkennfelder. Software zur Ladungswechselrechnung geht meist von adiabat vermessenen Verdichter- und Turbinenkennfeldern aus. Die direkte Verwendung solcher Kennfelder führt zu fehlerhaften Simulationsergebnissen. Die Leistungsbilanz zwischen Verdichter und Turbine im stationären Betrieb schränkt die Kennfelder auf diese Bereiche ein. Die Beschleunigung von Verdichter und Turbine wird in diesen Kennfeldern nicht berücksichtigt. In der Software zur Ladungswechselrechnung werden die Kennfelder in den instationären Bereich extrapoliert. In dem extrapolierten Bereich kommt es zu nicht physikalischen Ergebnissen. In dieser Veröffentlichung werden Methoden zur Korrektur der Kennfelder bzgl. Wärmestrom vorgestellt. Die gemessenen Kennfelder können ohne zusätzliche Informationen zur Erstellung von Kennfeldern für den gesammten Motorprozess verwendet werden. Mit den detailliert dargestellten Arbeitsschritten lassen sich die Methoden auf gemessen Kennfelder anwenden. Die vorgestellten Methoden werden auf Beispiele angewendet. Im Vergleich zu rein mathematischen Extrapolationen werden mit den vorgestellten Methoden physikalisch sinnvolle Extrapolationen erstellt und die Qualität von Ladungswechselrechnungen kann entsprechend gesteigert werden.

List of symbols

c _s m/s Spouting velocity

c _slip m/s Slip velocity compressor

c _p J/(kgK) Specific heat capacity at constant pressure

c _v J/(kgK) Specific heat capacity at constant volume

$\dot{m}_{C}$ kg/s Compressor mass flow rate

$\dot{m}_{T}$ kg/s Turbine mass flow rate

$M_{u2}$ - Compressor blade speed mach number

$M_{u4}$ - Turbine blade speed mach number

Nu - Nusselt number

p ₁ Pa Pressure at compressor inlet

p ₂ Pa Pressure at compressor outlet

p ₃ Pa Pressure at turbine inlet

p ₄ Pa Pressure at turbine outlet

P _C W Compressor power

P _M W Mechanical power

P _T W Turbine power

Pr - Prandl number

Re - Reynolds number

T ₁ K Temperature at compressor inlet

T ₂ K Temperature at compressor outlet

T ₃ K Temperature at turbine inlet

T ₄ K Temperature at turbine outlet

u ₂ m/s Circumferential speed compressor wheel

u ₄ m/s Circumferential speed turbine wheel

$\dot{V}_{C}$ m ³/s Compressor volume flow rate

$\beta_{2}$ - Compressor exit blade angle

$\Delta h$ J/kg Specific enthalpy difference

$\Delta h_{is}$ J/kg Specific isentropic enthalpy difference

κ - Ratio of specific heat

λ - Work coefficient

$\eta_{c}$ - Compressor efficiency

$\eta_{cq}$ - Adiabatic compressor efficiency

$\eta_{m}$ - Mechanical efficiency

$\eta_{t}$ - Turbine efficiency

$\phi,\phi_{2}$ - Flow coefficient

ψ - Head coefficient

$\Pi_{C}$ - Ratio of compressor outlet to inlet pressure

$\Pi_{T}$ - Ratio of turbine inlet to outlet presssure

1 Introduction

Turbocharger maps measured on a hot gas test stand serve several purposes. They are necessary

• – turbocharger development process i.e. they serve for comparison with design points and Computational Fluid Dynamics (CFD),

• – for comparison to other turbocharger products,

• – for turbocharger matching to the engine,

• – for application in engine control units (ECU),

• – as a necessary input to gas exchange simulation (GES).

Turbocharger maps are usually measured according to the predefined procedures described in the Turbocharger Gas Stand Test Code [23] and the Turbocharger Nomenclature and Terminology [24]. These test procedures assume an adiabatic measurement and do not take into account effects like

• – heat transfer to and from the compressor,

• – heat transfer from the turbine,

• – bearing and disc friction.

As a consequence compressor and turbine efficiencies are not isentropic efficiencies but diabatic efficiencies due to heat transfer. Furthermore, bearing friction affects the turbine efficiency. These effects along with extrapolation errors are a major cause for the poor predictive capability of transient turbocharger operations. Although the contents are applicable to use in engine control units, this paper focuses more specifically on GES use.

The turbocharger maps are represented as parameterized two dimensional maps in the gas exchange simulation models. In the simulation process, operating points are interpolated in the corresponding lookup tables. As the complete compressor map is measured on a hot gas stand, the two dimensional compressor maps are sufficient for the calculation. Even in non-stationary pulsating gas exchange, as the typical time scale of the pressure gradients is large compared to the rotational time scale of the compressor wheel, the compressor maps are, with one exception, sufficient: Compressor surge is a phenomenon that depends not only on the compressor, but due to pressure oscillations, it also depends on the downstream installation. On a typical hot-gas stand the compressor measurement is diabatic. The heat flux alters the compressor exit temperature and thus the measured efficiency. Based on dimensional analysis and some relations for convective heat transfer a model to correct for the heat flux is presented. In particular, the model uses a non-dimensional representation of compressor maps that can be used in GES and ECU. The non-dimensional representation can even be used to construct simple turbocharger compressor maps, if such maps are not readily available.

Turbine maps are less well represented, as the pulsating flow from the engine makes the turbine wheel operate under conditions that can not be obtained by a steady state hot gas stand measurement. GES software typically extrapolates the turbine maps in a mathematical way. This extrapolation is often poor and does not allow to perform a predictive transient engine operation without tuning the efficiencies. Similar to the case of the compressor, dimensional analysis (see Barenblatt [2]) and some basic relations for heat transfer and bearing friction can be used to construct a simple model to extrapolate the mass flow and efficiencies on a empirical basis. Artificial maps for the compressor and the turbine can not replace the measured maps from a hot gas stand, but they are able to serve as a first order approximation for building a model in the case of lacking data.

One difficulty for engineers performing GES is preparing the turbocharger maps, so that the simulations become predictive. In particular transient simulations and simulations in the range of high mean effective pressure and low engine speed do not compare well to experimental results from the test bench if turbocharger maps are implemented as measured from the hot gas stand.

In the following sections simple analysis procedures for compressor and turbine maps are presented and applied to sample measured maps. For the turbine, the procedure is applied to a standard waste-gate automotive turbocharger, but can also be extended to variable nozzle geometry turbines.

2 Hot gas test bed measurement

Abb. 1

Hot Gas Test Bed with measured quantities

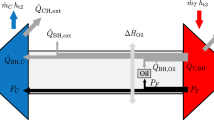
On a turbocharger test rig the turbocharger is measured in steady state under controlled conditions. Inlet static temperature T ₁, inlet static pressure p ₁, inlet mass flow rate $\dot{m}_{C}$, outlet static temperature T ₂ and outlet static pressure p ₂ are measured for the compressor. The corresponding total state quantities are typically computed. The turbine is outfitted with sensors for inlet static temperature T ₃, inlet static pressure p ₃, outlet static temperature T ₄ and outlet static pressure p ₄. The turbine mass flow rate $\dot{m}_{T}$ is typically taken as the mass flow rate to the combustion chamber. A sketch for the instrumented test rig is shown in Fig. 1.

3 Compressor maps

The interpolation of compressor maps is necessary in gas exchange simulation of turbocharged internal combustion (IC) engines. Some mathematical interpolation methods, such as a two dimensional polynomial interpolation as used by Skopil [21] for example, perform well in the interpolation range but perform poorly in the case of extrapolation. Empirical extrapolation methods that mimic the physical behavior in the extrapolation region should be used preferentially.

The compressor inlet state is marked by the subscript 1 and the compressor outlet state is marked by the subscript 2.

A physical approach is the use of non-dimensional quantities for the representation of a compressor map. A review on the non-dimensional quantities for turbocharger compressors is given by Casey and Robinson [5].

For simplicity, the difference between total and static flow quantities is not made at this point. All quantities are assumed to be total quantities. The extension to total-to-static efficiencies typically used is straight forward. The laws for a calorically perfect ideal gas are applied, i.e. heat capacities $c_{p}, c_{v}$ and its ratio $\kappa = c_{p}/c_{v}$ are assumed constant.

3.1 Dimensional representation of compressor maps

Compressor characteristics are mapped as a function of pressure ratio $\Pi_{c} = p_{2}/p_{1}$ and mass flow rate $\dot{m}_{c}$ or volume flow rate $\dot{V}_{C}$. A sample compressor map sketch is shown in Fig. 2. Several iso speed lines (line) and contours of constant efficiency (dashed lines) are displayed in one single figure. These maps differ depending on compressor size and type.

Abb. 2

Dimensional compressor map

A non dimensional representation yields almost identical maps for geometrically similar compressors. This makes the non dimensional representation attractive.

3.2 Non-dimensional representation of compressor maps

A non-dimensional representation of the compressor flow rate is given by the flow coefficient φ.

$$\phi = \frac{\dot{V}_{c}}{d_{2}^{2} u_{2}}$$

(1)

The flow coefficient φ normalizes the volume flow rate $\dot{V}_{c}$ to the compressor wheel size d ₂ and circumferential wheel speed u ₂. Therefore this quantity is independent of the compressor size when comparing geometrically similar compressors.

A non-dimensional representation of the compressor pressure ratio $\Pi_{c} = p_{2}/p_{1}$ is given by the head coefficient ψ.

$$\psi = \frac{\Delta h_{is}}{u_{2}^{2}} = \frac{c_{p} T_{1}}{u_{2}^{2}} \left(\Pi_{c}^{(\kappa-1)/\kappa} -1\right)$$

(2)

The work coefficient λ is the proportionality factor between circumferential wheel speed u ₂ and the work input $\Delta h$ from the compressor wheel to the gas.

$$\lambda = \frac{\Delta h}{u_{2}^{2}} = \frac{c_{p} T_{1}}{\eta_{c} u_{2}^{2}} \left(\Pi_{c}^{(\kappa-1)/\kappa} -1\right)$$

(3)

$\Delta h_{is}$ is the isentropic enthalpy rise. $\Delta h$ is the enthalpy rise including non-isentropic effects. Head coefficient and work coefficient only differ by the isentropic efficiency $\eta_{c} = \Delta h_{is}/\Delta h$.

$$\psi = \eta_{c} \lambda$$

(4)

Flow coefficient, head coefficient and work coefficient are the natural coordinates for the compressor [5]. For a simplified compressor, all speed lines collapse to a single line for the work coefficient. The iso-speed lines form a bundle in case of the head coefficient due to the different efficiencies.

This transfer of a compressor map from pressure ratio over volumetric flow rate to work coeffient and head coefficient over flow coefficient is shown in Fig. 3. Following the reasoning of Casey and Fesich [6], the work coefficient can be interpreted with the geometric parameters of the compressor wheel (outlet blade angle $\beta_{2}$) and the slip velocity c _s .

$$\lambda = \left(1+\frac{k}{\phi_{2}}\right) \left(1-\frac{c_{s}}{u_{2}}+\phi_{2} \tan \beta_{2} \right)$$

(5)

The slip velocity c _s can be modeled by a slip factor $\mu_{slip}$ (see Whitfield and Baines [25]).

$$c_{s} = (1 - \mu_{slip}) u_{2}$$

(6)

This leads to a simple model for the work coefficient.

$$\lambda = \left(1+\frac{k}{\phi_{2}}\right) \left(1-(1-\mu_{slip})+\phi_{2} \tan \beta_{2} \right)$$

(7)

Note that the flow coefficient $\phi_{2}$ is based on the outlet condition of the compressor. k is a small constant and the blade angle $\beta_{2}$ is in general negative. This leads to the decrease of work coefficient with increasing flow coefficient. In Fig. 3 a turbocharger compressor map expressed in the non dimensional quantities φ, ψ and λ is shown. The dashed lines are the work coefficient λ iso speed lines of the compressor. The highest three lines correspond to the lowest three lines in Fig. 2. The continous lines are the load coefficient ψ iso speed lines of the compressor. Theoretically, for a simple compressor, the λ lines should collapse to one single line. The fact that some λ values exceed 1 is due to heat transfer as identified by Casey and Fesich [6] and others. The range of flow coefficients, head coefficients and work coefficients is identical for geometrically similar compressors of different sizes. For similar radial compressors as in automotive turbochargers, the coefficients are all in one range. Therefore this representation is convenient for the use in lookup tables and maps.

Abb. 3

Small automotive turbocharger compressor map expressed in φ, ψ and λ

3.3 Heat transfer in the compressor

In automotive turbochargers for spark-ignition engines the bearing housing is typically water cooled. Therefore the heat flux from the turbine side goes to a great extent to the cooling water. For diesel engine application the water cooling is generally omitted since the heat flux is much smaller as exhaust gas temperatures are significantly lower. In the present analysis the bearing housing is assumed to have a constant temperature. As the compressor housing is mounted to the bearing housing, heat conduction takes place due to the temperature gradient. For small pressure ratios the adiabatic temperature rise results in temperatures smaller than the compressor housing temperature. This results in a heat flux from the compressor housing walls to the compressed gas. For large pressure ratios the adiabatic temperature rise results in gas temperatures larger than the compressor housing temperature. A heat flux from the gas to the compressor housing is the result.

Heat transfer to the compressor, using experiments and CFD, has clearly been identified in the past. See for example the work of Bohn [4], Baines et al. [1], Shaaban and Seume [20] and the references cited in those publications. Since measurement of heat flux in a turbocharger is expensive in resources and time, it can not be performed for every type of turbocharger. It is therefore important to come up with simple models that allow for compensation of heat transfer in compressor maps obtained from a hot gas stand. Casey and Fesich [6] describes the theory on how to identify the heat transfer to the compressor. Here a similar method is developed to come up with a simple three parameter model to correct the compressor map.

The non-dimensional representation of the work coefficient is well suited to identify the heat transfer. Following the argument of Casey and Fesich [6] the enthalpy transfer to the gas can be divided into work done by the compressor wheel w ₁₂ and heat transferred to the gas q ₁₂. The work coefficient can be written as $\lambda_{q}$.

$$\lambda_{q} = \frac{\Delta h_{q}}{u_{2}^{2}} = \frac{w_{12}}{u_{2}^{2}} + \frac{q_{12}}{u_{2}^{2}} = \lambda + \frac{q_{12}}{u_{2}^{2}}$$

(8)

Therefore the work coefficient of a flow with heat transfer should be significantly larger at low φ than the work coefficient with the wheel work input only. Casey and Fesich [6] shows that this is the case especially for lower wheel speeds.

This corresponds to the lowest wheel speed lines with large work coefficient λ in Fig. 3. In the following section a simple model is presented, that can correct λ for the heat transfer.

3.4 Correction for heat transfer to the compressor

The compression process is sketched in a T-S diagram in Fig. 4. The adiabatic Temperature increase due to the work input of the compressor wheel goes from T ₁ to T ₂. Here, for simplicity, the heat transfer is assumed to be at constant total pressure. This assumption is however no restriction to the general model. The heat transfer results in a temperature increase from T ₂ to $T_{2q}$. Neglecting the difference between static and total temperature at the wheel exit, the temperature difference between air exiting the compressor wheel at T ₂ and the compressor housing T _W results in a heat flux $\dot{Q}$ from the compressor housing to the gas when $T_{W}> T_{2}$. Modeling the heat transfer to the gas by forced convection with a heat transfer coefficient α the heat flux becomes

$$\dot{Q} = \alpha A \left(T_{W}-T_{2}\right).$$

(9)

Abb. 4

Compressor T-S diagram with ($T_{1}\rightarrow T_{2q}$) and without ($T_{1}\rightarrow T_{2}$) heat flux

The heat transferred to the gas is convected by the gas mass flow and results in an enthalpy flux increase.

$$\dot{H}_{2q} - \dot{H}_{2}= \dot{Q} = \dot{m}_{c} c_{p} \Delta T$$

(10)

This enthalpy increase contributes to the temperature increase of the gas.

$$\Delta T = T_{2q} - T_{2}$$

(11)

Solving Eq. 9 and Eq. 10 a simple model for the temperature difference is obtained.

$$\Delta T = \frac{\alpha A_{c} \left(T_{W}-T_{g}\right)}{\dot{m}_{C} c_{p}}$$

(12)

As the temperature measured at the compressor exit $T_{2q}$ includes the heat transfer, the compressor efficiency containing the heat flux is typically caculated by

$$\eta_{cq} = \frac{\Pi_{c}^{(\kappa -1)/\kappa}-1}{T_{2q}/T_{1}-1}.$$

(13)

With knowledge of the temperature increase due to heat flux $\Delta T$ the efficiency expression can be rewritten using the unknown adiabatic temperature T ₂.

$$\eta_{cq} = \frac{\Pi_{c}^{(\kappa -1)/\kappa}-1}{T_{2}/T_{1}-1 + \Delta T/T_{1}}$$

(14)

The target is a relation between the diabatic efficiency $\eta_{cq}$ and the adiabatic efficiency $\eta_{c}$.

The compressor power can be determined as function of pressure ratio and efficiency.

$$P_{c} = \dot{m}_{c} c_{p} T_{1}/\eta_{c} \left(\Pi_{c}^{(\kappa -1)/\kappa}-1\right) = \dot{m}_{c} \Delta h_{c}$$

(15)

This leads to an expression for the inverse of the diabatic efficiency $\eta_{cq}$.

$$\frac{1}{\eta_{cq}} = \underbrace{\frac{T_{2}/T_{1}-1}{\Pi_{c}^{(\kappa -1)/\kappa}-1}}_{1/\eta_{c}} + \underbrace{\frac{\Delta T/T_{1}}{\Pi_{c}^{(\kappa -1)/\kappa}-1}}_{\alpha A (T_{W}-T_{2})/(\eta_{c} P_{c})}$$

(16)

At this point the temperature difference from Eq. 12 can be inserted into the expression leading to a correction factor for the compressor efficiency $\eta_{c}$.

$$\frac{\eta_{c}}{\eta_{cq}} = 1 + \frac{\alpha A (T_{W}-T_{2})}{P_{c}}$$

(17)

Here a model for the adiabatic temperature at the wheel exit T ₂ is needed. The total temperature rise corresponds to the work input of the compressor wheel $c_{p} (T_{2}-T_{1}) = \Delta h_{c} = \lambda u_{2}^{2}$.

$$T_{2} = T_{1} + \frac{\Delta h_{c}}{c_{p}} = T_{1} + \frac{\lambda u_{2}^{2}}{c_{p}}$$

(18)

The compressor power can be expressed by the mass flow and enthalpy difference (Eq. 15).

$$\frac{\eta_{c}}{\eta_{cq}} = 1 + \frac{\alpha A (T_{W}-T_{1})}{\phi \rho_{1} d_{2}^{2}u_{2}^{3}\lambda} - \frac{\alpha A \lambda}{\phi \rho_{1} d_{2}^{2}u_{2} c_{p}}$$

(19)

Using arguments from dimensional analysis, the Nusselt number for convective heat transfer is proportional to the Reynolds number to some power n and the Prandtl number to some power k.

$$Nu \propto Re^{n} Pr^{k} \qquad Re = \frac{u_{2}l_{c}}{\nu}$$

(20)

This allows the expression of heat transfer coefficient α by Reynolds and Prandtl numbers. Especially for low volume flow rates the diffuser velocity is proportional to the exit wheel speed. Therefore the Reynolds number is based on the compressor wheel speed.

This link allows to formulate a dependence of heat transfer coefficient α from the circumferential wheel speed u ₂.

$$\begin{array}{ll} \alpha &= Nu \lambda_{Gas}/l_{c} \propto Re^{n} Pr^{k} \lambda_{Gas}/l_{c} \\\alpha &\approx u_{2}^{n} l_{c}^{n-1} \nu^{-n} Pr^{k}\end{array}$$

(21)

Combination with a geometry factor for the wetted area of the compressor housing where heat transfer occurs $A \propto d_{2}^{2}$ elminates the effects from the correction factor. Lumping the remaining quantities into a single constant c ₁, a simple expression for the correction factor is obtained.

$$\frac{\eta_{c}}{\eta_{cq}} = 1 + \frac{c_{1}}{c_{p}\phi u_{2}^{1-n}} \left(\frac{c_{p}(T_{W}-T_{1})}{\lambda u_{2}^{2}}-1 \right)$$

(22)

In this equation unknown quantities remain when applied to compressor maps from the test bed. The temperature difference between the compressor housing T _W and the compressor inlet temperature T ₁, as well as the constants $c_{1},n$ need to be estimated. The model is simplifies much of the underlying physics, but has the advantage on relying on only 3 fitted parameters.

Furthermore, the fraction in the bracket can easily be interpreted: When $c_{p}(T_{W}-T_{1})> \lambda u_{2}^{2}$, the temperature of the compressor housing is larger than the temperature of the gas due to the work input of the compressor. Thus there is a resulting heat flux to the gas. The constant c ₁ is dependent on geometry and the fluid properties of the gas as viscosity, thermal conductivity and a characteristic length scale. Typical values for a small downsizing engine turbocharger without water cooled bearing housing are:

$$\begin{array}{ll} c_{1} &= 50 \, m^{-(n+1)}s^{n+1}K^{-1}\\(T_{W}-T_{1}) &= 70 \, K\\n &= 0,5\end{array}$$

(23)

A sketch of the heat flux correction factor (Eq. 22) for the parameters given in Eq. 23 is given in Fig. 5. At a low circumferential speed and thus low power input the thermal correction is large due to the large temperature difference. With increasing flow coefficient the effect becomes smaller. At high circumferential speed u ₂ the power input is much larger yielding higher pressure ratios and higher temperatures than the compressor housing. A heat flux from the gas to the compressor housing results in a correction factor smaller than one.

Abb. 5

Heat flux correction factor $\eta_{c}/\eta_{cq}$ at different wheel speed u ₂

3.5 Application of correction factor to a measured map

For illustration the procedure is applied to a small turbocharger compressor in use for small diesel downsizing engines without a water cooled bearing housing, up to an engine power of 75 kW. In such a case, the fraction of wetted area to volume flow rate is large compared to larger turbochargers and the effect is much larger. As shown in Fig. 6 the work coefficients $\lambda_{q}$ and λ differ especially for the low speed lines. This is consistent with the leading factor $u_{2}^{n-1}$ in the correction term. Furthermore the difference becomes smaller with increasing flow coefficient φ. Again this is consistent with the proposed empirical correction function. Fitting the 3 constants $c_{1}, (T_{W}-T_{1})$ and n, one obtains a a corrected form of the work coefficient $\lambda_{corr}$.

$$\lambda = \lambda_{q} \frac{\eta_{cq}}{\eta_{c}}$$

(24)

Abb. 6

Load coefficient ψ, work coefficient with heat transfer $\lambda_{q}$ and work coefficient corrected for heat transfer λ against flow coefficient φ

The corrected lines (continuous) in Fig. 6 almost converge with the work coefficients of the other iso speed lines. Application of the correction factor to the measured efficiencies $\eta_{cq}$ yields an estimate of the compressor efficiencies without heat transfer.

Application of the correction is shown in Fig. 7. This correction of compressor efficiencies for heat transfer results in improved GES results at low flow rates and low pressure ratios and thus transient time-to-torque simulations.

Abb. 7

Compressor efficiency including heat transfer $\eta_{cq}$ and for heat transfer corrected efficiency $\eta_{c}$ against flow coefficient φ for the lowest speed lines

3.6 Extrapolation of compressor maps

In general compressor maps are measured for the entire range of iso-speed lines from surge to choke and there is no need for extrapolation. If the information on the compressor is however poor, the equation for the work coefficient λ (Eq. 5) given by Casey is useful for extrapolation.

Although Eq. 5 is strictly only valid in this form for the flow coefficient based on compressor exit conditions $\phi_{2}$, the correlation can be used to fit for the flow coefficient defined in Eq. 1. The possible work flow for the preparation of extrapolated maps is:

• 1. Transfer the compressor map to the non-dimensional coordinates $\phi,\, \psi,\, \lambda$ by Eqs. 1, 2 and 3.

• 2. Fit the work coefficient (Eq. 26) to the higher speed lines as they are less effected by heat transfer via the coefficients $c_{1},\, \mu_{slip}$ and c _beta .

• 3. Evaluate the correction factor $\eta_{c}/\eta_{cq}$ for all operating points by fitting the parameters $c_{1}, \, (T_{W}-T_{1}), \, n$

• 4. Fit the efficiency to Eq. 27 by the six constants $\eta_{cw,max}$, c ₂, $u_{2max}$, c ₃, $\eta_{{cw},max}$ and c ₄.

• 5. choose a suitable range for the compressor extrapolation $\phi, u_{2}$.

• 6. Compute pressure ratio $\Pi_{c}$ by Eq. 30, and efficiencies by Eq. 27.

3.7 Compressor map scaling

In some cases there is a lack of compressor and turbine maps for a first turbocharger simulation. In such a case it is common practice to scale the maps of an existing compressor with a known compressor map to the desired mass flow rate. When the compressor is geometrically similar this is a good estimate. Mass flow rate scales as the square of compressor inlet area. For geometrically similar compressors the wheel exit diameter is then used as the reference length.

$$\begin{aligned}\dot{V}_{c,new} &\approx& \frac{d_{2,new}^{2}}{d_{2,org}^{2}} \dot{V}_{c,org}\end{aligned}$$

(25)

$$\begin{aligned}n_{c,new} &\approx& \frac{d_{2,org}}{d_{2,new}} n_{c,org} \nonumber\\\Pi_{c,new} &\approx& \Pi_{c,org} \nonumber\\\eta_{c,new} &\approx& \eta_{c,org} \nonumber\end{aligned}$$

Pressure ratio depends on the square of the circumferential speed u ₂. When RPM are scaled accordingly, pressure ratio remains the same. Efficiency is similiar for geometrically similar compressors as well. When scaling to smaller sizes, efficiency tends to decrease due to the increase in wetted area compared to volume and thus proportionally increase friction effects. Furthermore tip gap increases proportionally and leads to larger losses. Changes in efficiency are small as long as the size difference is some percent. When large scaling factors are applied, revaluation including tip gap effects and Reynolds numbers (Re) should be applied.

3.8 Artificial compressor maps

If no compressor maps are available at all, models from open literature (Swain [22], Whitfield and Baines [25]) can be used to construct artificial compressor maps from scratch. A cookbook approach is given to construct a new compressor map with a few parameters in a spreadsheet.

• 1. Assume a work coefficient correlation depending on φ:

  The approximation given by the equation of Casey (Eq. 5) in a range of flow coefficient φ in [0.03..0.16] is valid.

  $$\lambda = \left(1+\frac{k}{\phi}\right) \left(1-(1-\mu_{slip}) + c_{\beta} \phi\right)$$

  (26)

  Sample values for the constants are:

  $$\begin{aligned}k &=& 0.004 \nonumber\\\mu_{slip} &=& 0.85 \nonumber\\c_{\beta} &=& - 2.5 \nonumber\end{aligned}$$

• 2. Construct an efficiency depending on flow coefficient φ and wheel speed u ₂:

  Swain [22] gives a suitable correlation for a efficiency.

  A different approach yielding good results models the compressor wheel efficiency $\eta_{w}$ and diffuser/volute efficiency $\eta_{d}$ separately. In the case of the compressor wheel, maximum efficiency is reached at the design point for flow angle and thus at constant flow coefficient φ. Compressor wheel efficiency decreases with increasing friction and other related losses.

  $$\begin{aligned}\eta_{w} &=& \eta_{cw,max}\left(1-c_{2}\left(\frac{u_{2}}{u_{2max}}\right)^{2}\right)\end{aligned}$$

  (27)
  $$\begin{aligned}&& \qquad - c_{3} \left(1-\left(\frac{\phi}{\phi_{\eta_{cw},max}}\right)\right)^{2} \nonumber\\\eta_{d} &=& \eta_{d,max}\left(1-\left(\frac{\phi}{(\phi_{max}-c_{4}(u_{2}/u_{2max})^{4})}\right)^{4}\right) \nonumber\\\eta_{c} &=& \eta_{w} \cdot \eta_{d} \nonumber\end{aligned}$$

  Sample values for the constants are:

  $$\begin{array}{llllll} \phi_{max} &=& 0.18 \qquad & c_{2} &=& 0.05 \\\phi_{\eta_{cw},max} &=& 0.12 \qquad & c_{3} &=& 0.4 \\u_{2,max} &=& 560 \,m/s \qquad & c_{4} &=& 0.02 \\\eta_{cw,max} &=& 0.85 &&& \\\eta_{d,max} &=& 0.85 &&&\end{array}$$

  (28)

  Abb. 8

  

  Model for compressor wheel efficiency $\eta_{w}$, compressor diffuser and volute efficiency $\eta_{d}$ and resulting compressor efficiency $\eta_{c}$

  Efficiencies as modeled by Eq. 27 with the constants given in Eq. 28 is shown in Fig. 8.

• 3. Compute the load coefficient $\psi(\phi,u_{2})$:

  $$\psi(\phi,u_{2}) = \lambda(\phi) \cdot \eta(\phi,u_{2})$$

  (29)

• 4. Compute the pressure ratio $\Pi_{c}$:

  $$\Pi_{c} = \left(1+\frac{\psi(\phi,u_{2}) u_{2}^{2}}{c_{p}T_{1}} \right)^{\kappa/(\kappa-1)}$$

  (30)

• 5. Choose a compressor wheel diameter d ₂ and compute the volume flow rate $\dot{V}_{c}$.

  $$\dot{V}_{c} = \phi d_{2}^{2} u_{2}$$

  (31)

This procedure of artificial maps is of limited use if precise results are to be produced. They are useful for setting up a first gas exchange simulation or engine calibration if no maps are available.

Abb. 9

Artificial compressor maps, top: pressure ratio against volume flow rate, bottom efficiency against volume flow rate

As an example artificial compressor maps with pressure ratio and efficiency are given in Fig. 9. It is clearly visible that there is not a realistic surge line in the artificial compressor map. Surge needs to be modeled separately. For small pressure ratios up to $\Pi_{C} \approx 2$ surge is determined by flow seperation at the compressor inlet tip and the flow angle at the compressor wheel exit entering the diffuser. Since flow angle translates directly to flow coefficient φ, surge occurs for fixed values of flow rate $\phi \approx 0.03$ for lower pressure ratios.

For engine control units, a work coefficient correlation and an efficiency correlation may be obtained by the methods described in the previous sections. Once stored in the engine control unit, the equations presented above can be used.

4 Turbine maps

Turbocharger turbine maps are measured by recording the inlet temperature T ₃, inlet pressure p ₃, exit temperature T ₄ and exit pressure p ₄. As the mass flow through the turbine depends on flow speed and inlet density, a reduced mass flow rate $\dot{m} \sqrt{T_{3}}/p_{3}$ is used to characterize the turbine mass flow rate. The reduced mass flow rate would be a non-dimensional quantity, if the flow area A and gas properties $R,\kappa$ would be included. On the hot gas stand those quantities usually do not vary, and are thus omitted. When it comes to engines with varying equivalence ratio as in diesel engines, the gas properties vary and the mass flow rate should be corrected for the changes. The reduced mass flow rate $\dot{m} \sqrt{T_{3}}/p_{3}$ is usually plotted against the expansion ratio $\Pi_{t} = p_{3}/p_{4}$ of the turbine (see Fig. 11).

Since compressor and turbine are measured simultaneously, turbine characteristics are represented by iso speed lines. The turbine measurement is limited by the power balance with the compressor in steady state operation.

The mass flow rate may change with turbine wheel speed. Radial turbines with typical reaction rates show decreasing mass flow rates with increasing wheel speeds. This effect will be accounted for in a mass flow model proposed in the following section.

Turbine wheel efficiencies $\eta_{t}$ are often plotted against expansion ratio $\Pi_{t}$. A different representation plotting the efficiency $\eta_{t}$ against blade speed ratio $u_{4}/c_{s}$ is also used (see Fig. 13). Here u ₄ is the circumferential speed of the turbine wheel and $c_{s} = \sqrt{2 \Delta h_{t}}$ the spouting velocity.

4.1 Modeling reduced turbine mass flow

A simple model of a radial turbine consists of a static nozzle followed by a nozzle in a rotating reference frame. In this case the pressure ratio across the turbine can be split into the product of the pressure ratio in the fixed nozzle $\Pi_{f}$ times the pressure ratio across the rotating nozzle $\Pi_{r}$.

$$\Pi_{t} = \Pi_{f} \Pi_{r} = \frac{p_{3}}{p_{d}} \frac{p_{d}}{p_{4}} \qquad \Pi_{f} = \frac{p_{3}}{p_{d}} \qquad \Pi_{r}=\frac{p_{d}}{p_{4}}$$

(32)

The reduced mass flow rate through a fixed nozzle with pressure ratio $\Pi_{f}$ is given by the usual expression for the St.Venant–Wantzel equation.

$$\frac{\dot{m}_{t} \sqrt{T_{3}}}{p_{3}} = A \sqrt{\frac{\kappa}{R} \frac{2}{(\kappa_{t}-1)}} \sqrt{\Pi_{f}^{-2/\kappa} - \Pi_{f}^{-\left(\kappa+1\right)/\kappa}}$$

(33)

At this point one essential assumption is made: The expansion ratio of the turbine is always split in the same proportion, independent on pressure ratio. Then the pressure ratio through the nozzle can be estimated by:

$$\Pi_{f} \approx \Pi_{t}^{t_{2}}$$

(34)

Assuming that the nozzle needs to speed up the gas to the speed of the turbine rotor and assuming that the flow enters without deviation angle in the relative reference frame into the wheel, the velocity triangle is given in Fig. 10.

Abb. 10

Turbine inlet velocity triangle

This velocity triangle represents the idealized case. In most operating points, the inlet relative velocity w ₄ will not be perpendicular to the circumferential velocity u ₄. Seeking a simple model, the deviating effects are neglected. The relative velocity can then be expressed as $w = \sqrt{c_{4}^{2}-u_{4}^{2}}$. The circumferential speed of the turbine wheel can be expressed by the blade speed mach number $Mu_{4} = u_{4}/\sqrt{\kappa R T_{3}}$. Combining the previous equations, a model for the mass flow through the turbine wheel accounting for the turbine wheel speed can be formulated.

$$\begin{aligned}\frac{\dot{m}_{t} \sqrt{T_{3}}}{p_{3}} &=& t_{1} \sqrt{\frac{\kappa}{R} \frac{2}{(\kappa_{t}-1)}} \end{aligned}$$

(35)

$$\sqrt {(\Pi _t^{ - 2{t_2}/\kappa } - \Pi _t^{ - {t_2}\left({\kappa + 1} \right)/\kappa }) - {t_3}\Pi _t^{ - 2/\kappa }M_u^2} {\rm{ }}$$

In this model three unknown parameters $t_{1}, \, t_{2}, \, t_{3}$ must be fitted to the given turbine mass flow data. All parameters have a physical significance. t ₁ represents the nozzle effective area. t ₂ is the fraction of the expansion ratio of the turbocharger in the nozzle and thus related to the turbine degree of reaction. t ₃ is the effect of the wheel speed on necessary nozzle flow. Therefore t ₂ and t ₃ need to be adapted simultaneously.

The parameter t ₁ depends explicitly on the turbine nozzle size. Typical values for the remaining parameters are:

$$\begin{array}{lll} t_{2} = 0,55 \qquad &t_{2} \, in \, &[0,2..0,8] \\t_{3} = 0,8 \qquad &t_{2} \, in \, &[0,25..1,5]\end{array}$$

(36)

Abb. 11

Measured and extrapolated reduced turbine mass flow

Figure 11 shows the experimental turbine flow data together with the reduced mass flow modeled by Eq. 35. The advantage of this model is to take into account the effect of the turbine wheel speed on the mass flow rate.

4.2 Turbine efficiency

The isentropic turbocharger turbine efficiency is defined as

$$\eta_{t,is} = \frac{1-T_{4}/T_{3}}{1-1/\Pi_{t}^{(\kappa-1)/\kappa}}.$$

(37)

An application of this equation to hot gas test bed measurements yields efficiencies larger than 100 %. This is due to the large heat flux from the turbine to the environment. Therefore turbocharger efficiencies are typically evaluated using the compressor. Turbine power drives the compressor and is lost in bearing friction $P_{t} = P_{c} + P_{m}$. The mechanical efficiency of the bearing system is defined as $\eta_{m} = P_{c}/P_{t}$. Using the definition of the mechanical efficiency, the product of mechanical and turbine efficiency is determined.

$$\eta_{m} \cdot \eta_{t} = \frac{P_{c}}{\dot{m}_{t} c_{pt} T_{3q} \left(1 - 1/\Pi_{t}^{(\kappa-1)/\kappa}\right)}$$

(38)

A closer look to the power balance and the definition of the mechanical efficiency reveals that mechanical efficiency is dependent on pressure ratio of compressor and turbine expansion ratio.

$$\eta_{m} = \frac{P_{c}}{P_{t}} = \frac{P_{c}}{P_{c}+P_{m}} = \frac{P_{t}-P_{m}}{P_{t}}$$

(39)

Therefore it is not sensible to interpolate or extrapolate the efficiency product $\eta_{m} \eta_{t}$. Due to the pressure pulsations in engine application, the turbine never operates under the steady conditions of the test bed and thus never reproduces those operating points. It is therefore absolutely necessary to separate the effects of mechanical power loss in the bearing system from the actual turbine efficiency.

In Eq. 38 the turbine efficiency is dependent on inlet temperature T ₃. Since there is a large heat flux between turbine inlet temperature measurement and the actual turbine wheel inlet, the heat flux needs to be accounted for when interested in the turbine rotor efficiency. For GES and for ECU application it is important to note, that the temperature T ₃ needs to be modeled according to the heat loss at the operating point. During transients with a lower housing temperature the heat loss may be much greater. This reduces the enthalpy available for expansion at turbine inlet.

4.3 Heat transfer in the turbine

The effect of the heat transfer from the hot gas to the turbine casing is illustrated in the T-S diagram in Fig. 12. After temperature measurement $T_{3q}$ a heat transfer occurs, neglecting friction, at constant total pressure to the turbine inlet. At the turbine inlet this results in a smaller total temperature T ₃. For the turbine efficiency the temperature T ₃ is the thermodynamically relevant temperature.

Abb. 12

Turbine T-S Diagram with ($T_{3q}\rightarrow T_{4q}$) and without ($T_{3}\rightarrow T_{4}$) heat flux

Assuming a forced convective heat transfer from the gas to the turbine casing, the identical procedure from the compressor can be used. The temperature $\Delta T_{t}$ decrease is modeled.

$$\Delta T_{t} = T_{3q} - T_{3} = \frac{\alpha A \left(T_{3q} - T_{3} \right)}{\dot{m}_{t} c_{pt}}$$

(40)

Assuming a turbulent convection as in the case of the compressor and a Reynolds number based on the nozzle velocity, the temperature difference $\Delta T_{t}$ can be accounted for.

$$\begin{array}{ll} \frac{T_{3}}{T_{3q}} &=1 - \frac{\alpha A (1-T_{w}/T_{3q})}{\dot{m}_{t}c_{p}} \\&= 1 - a_{1} \dot{m}_{t}^{n-1}\end{array}$$

(41)

In theory and measurement from large turbines, the radial turbine efficiency $\eta_{t}$ has a parabolic like shape (see Moustapha et al. [15]). Extrapolation beyond measurement points should therefore be based on such an approach.

The measured efficiencies $\eta_{m} \cdot \eta_{t}$ differ significantly due to the mechanical efficiency. Scharf et al. [18] and Lüddecke et al. [13] measured mechanical efficiencies and proposed to correct for heat transfer and mechanical losses. Since measurement of mechanical losses is difficult and costly, it can not be performed for every turbocharger. With some knowledge of the underlying physics the mechanical efficiency can still be modeled.

4.4 Mechanical efficiency and bearing friction

Mechanical losses may be split into three groups:

• – Radial bearing friction:

  Radial bearing friction is proportional to the square of the angular frequency and may be modeled as such.

• – Axial bearing friction:

  Axial bearing friction depends on the axial thrust and linearly on angular frequency

• – Disc wheel friction:

  Disc wheel friction scales with the third power of angular frequency [3], [11].

Putting all effects together, a simple mechanical power model has the form described by Eq. 42.

$$\begin{aligned}P_{f} &=& f_{1} \left| \Pi_{c} - \Pi_{t} \right| \left(\frac{\omega}{\omega_{max}}\right) + \end{aligned}$$

(42)

$$\begin{aligned}&& f_{2} \left(\frac{\omega}{\omega_{max}}\right)^{2} + f_{3} \left(\frac{\omega}{\omega_{max}}\right)^{3} \nonumber\end{aligned}$$

Here $f_{1},\, f_{2}$ and f ₃ are constants that need to be estimated. Formulating the power loss function as in Eq. 42 allows to estimate the maximum power loss individually due to the effect. In some compressor design literature disc wheel friction is estimated to be some order of 3 % of the compressor power at maximum wheel speed. This allows for a fixed constant f ₃. In the case of hydrodynamic bearings, the radial bearing loss may take up to $5\,\%$ of the compressor power at maximum wheel speed. This gives a rough estimate for the coefficient f ₂. The axial bearing loss is typically smaller and may be on the order of 1–3 %. This gives an estimate for the coefficient f ₁.

4.5 Correction of turbine efficiency

Once the friction power P _f is known the turbine wheel efficiency can be obtained from the following equation.

$$\eta_{t} = \frac{P_{c}+P_{f}}{\dot{m}_{t} c_{pt} T_{3} \left(1-1/\Pi_{t}^{(\kappa-1)/(\kappa)}\right)}$$

(43)

The different efficiencies $\eta_{t}$, $\eta_{m}$ and the product $\eta_{t}\eta_{m}$ are shown in Fig. 13 for a small automotive turbocharger.

Abb. 13

$\eta_{t}\cdot\eta_{m}$, $\eta_{m}$ and $\eta_{t}$ by Eq. 43 against $u_{4}/c_{s}$

The efficiency $\eta_{t}$ obtained by Eq. 43 shows a similar shape compared to radial turbine efficiencies from other installations (see Moustapha et al. [15], Fig. 9.5). The efficiency of the sole turbine wheel may be modeled by Eq. 44.

$$\eta_{t,m} = \eta_{t,max} - e_{1} \left(e_{2} - \frac{u_{4}}{c_{s}} \right)^{2}$$

(44)

This efficiency model requires three physical parameters: The maximum efficiency of the turbine $\eta_{t,max}$, the value e ₂ at which the $u_{4}/c_{s}$ maximum occurs and the rate of decrease e ₁. A fit to a small automotive turbocharger gives the following values for the parameters:

$$\begin{array}{ll} \eta_{t,max} &= 0,8 \\e_{1} &= 5,2 \\e_{2} &= 0,65\end{array}$$

(45)

There is no need for a direct model of the product $\eta_{t}\eta_{m}$ since the mechanical power loss P _m is modeled directly.

4.6 Extrapolation of turbine maps

Extrapolation of turbine maps is necessary in most cases for GES and ECU. Due to the power balance $P_{t} = P_{C} + P_{m}$ only short ranges in expansion ratio $\Pi_{t}$ are measured under steady state conditions. Exhaust pressure amplitudes for downsizing engines may require modeling for expansion ratios well beyond the measured range.

A possible work flow for the extrapolation of the turbine map is:

• 1. Compute wheel speed u ₄ and blade speed Mach number Mu ₄.

• 2. Fit the coefficients $t_{1},t_{2}$ and t ₃ to get the reduced mass flow rate $\dot{m}\sqrt{T_{3}}/p_{3}$ for the required range.

• 3. Compute spouting velocity c _s and blade speed ratio $u_{4}/c_{s}$.

• 4. Compute compressor power P _c and correct for heat transfer effects.

• 5. Estimate friction coefficients f ₁, f ₂ and f ₃.

• 6. Compute the turbine efficiency using Eq. 43.

• 7. Fit the coefficients e ₁, e ₂ and $\eta_{t,max}$ in Eq. 44 to extrapolate turbine wheel efficiency to the desired range.

In most GES software the product $\eta_{t}\eta_{m}$ is extrapolated over the necessary range. With the previous arguments, this approach is not satisfactory since losses in the axial bearing are not represented correctly. If there is however not the option for separation of mechanical losses and turbine efficiency, it is necessary to be aware of the possible errors in the computational results.

4.7 Turbine map scaling

As in the case of the compressor, it is possible to scale existing turbine maps for mass flow rate. Reduced turbine mass flow rate scales with the turbine inlet area. For geometrically similar turbines, reduced mass flow rate may be scaled as the ratio of turbine wheel diameters.

When expressed in $u_{4}/c_{s}$ efficiency maps do not need to be scaled.

$$\begin{aligned}\left.\frac{\dot{m}\sqrt{T_{3}}}{p_{3}} \right._{new} &\approx& \frac{d_{4,new}^{2}}{d_{4,org}^{2}} \left.\frac{\dot{m}\sqrt{T_{3}}}{p_{3}} \right._{org} \end{aligned}$$

(46)

$$\begin{aligned}n_{t,new} &\approx& \frac{d_{2,org}}{d_{2,new}} n_{t,org} \nonumber\\\Pi_{t,new} &\approx& \Pi_{t,org} \nonumber\\\eta_{t,new} &\approx& \eta_{t,org} \nonumber\end{aligned}$$

(47)

When scaling turbine maps, care has to be taken to match the turbine to the compressor map. Compressors and turbines are linked by transmitted torque and RPM.

4.8 Accounting for transient filling and emptying effects

Under steady state operations, the size of volumes after pressure measurement is unimportant for determining the turbine map. When exhaust pulses need to fill up volumes before entering the turbine wheel some mass flow is needed to build up the pressure on the turbine wheel. Those effects can only be accounted for if the missing volumes are included in GES and ECU models.

4.9 Artificial turbine maps

If no turbine maps are available at all, models from open literature (see Whitfield and Baines [25]) can be used to construct artificial turbine maps from scratch. A cookbook approach to obtain an artificial turbine map in a spread sheet is obtained by the following steps.

• 1. Define turbine wheel circumferential speeds u ₄.

• 2. Define turbine expansion ratios $\Pi_{t}$.

• 3. Compute the spouting velocity $c_{s} = c_{s}(\Pi_{t})$.

• 4. Compute blade speed ratio $u_{4}/c_{s}$.

• 5. Compute blade speed mach number Mu ₄.

• 6. Compute reduced mass flow rate $\dot{m}\sqrt{T_{3}}/p_{3}$ by Eq. 35.

• 7. Compute turbine efficiency $\eta_{t}$ by Eq. 44.

• 8. Find the corresponding compressor operating points with RPM and power balance.

• 9. Compute the mechanical power loss P _m by Eq. 42.

Abb. 14

Modeled turbine efficiency $\eta_{t}$, mechanical efficiency $\eta_{m}$ as obtained by Eq. 39 and $\eta_{t} \eta_{m}$ for a sample compressor map.

An example of an artificial turbine efficiency map is given in Fig. 14. Note that the efficiency product $\eta_{t}\eta_{m}$ can only be obtained when a corresponding compressor map is available. Further, the product $\eta_{t}\eta_{c}$ is only valid under steady state conditions. Under pulsating conditions, as in IC engine applications, the functions may look significantly different.

5 Summary

The intention of the paper is to provide a recipe apoproach to utilizing map information provided by turbocharger manufacturers for the purpose of GES and ECU simulations performed in extrapolated operating regions.

Turbocharger compressor and turbine maps obtained from a hot gas test bed are dependent on influences from heat transfer and bearing friction. For GES and ECU application it is important to analyze these depencies and to come up with simple corrections to obtain more accurate results in GES and reduce application effort in ECU.

A simple model for the correction of compressor heat flux is presented in Sect. 3.3. The heat transfer dependence on turbine efficiency is discussed in Sect. 4.3.

Measurement on the hot gas test bed is limited to the power balance between the compressor and the turbine. This results in limited information concerning turbine mass flow rate over expansion ratio and limited information on the product of turbine efficiency and mechanical efficiency $\eta_{t}\eta_{m}$. If the number of measured speed lines is few, even the information on the compressor may be poor, and extrapolation must be done for GES and ECU application.

In Sect. 3.6 an extrapolation procedure for compressor maps is proposed. In Sect. 4.6 a procedure for the extrapolation of turbine maps is proposed.

Application of the procedures to a small turbocharger used in downsized diesel engines shows the benefit of the empirical extrapolation methods.

Knowledge of the typical coefficients in the parameter models allows one to construct artificial turbine maps if no information is available at all. Such maps need to be used with caution as they do not rely on a empirically measured turbocharger but maybe helpful in setting up a first GES or ECU calibration.