Introduction

Composites play an increasingly relevant role in the field of functional materials, since heterogeneous systems consisting of a mixture of at least two solid phases are very suitable for the optimization of, e.g., electrical, transport, and mechanical properties. Especially, a sound knowledge of the transport properties of mixed ionically–electronically conducting composites [1] is crucial for the development of novel electroceramic materials for application as, e.g., oxygen separation membranes and cathodes in solid oxide fuel cells [2, 3].

The mass and charge transport in ceramic composites can be strongly affected by interfaces, comprising surface exchange reactions as well as transport across/along grain and interphase boundaries. The permeation of oxygen through densely sintered polycrystalline membranes consisting of perovskite-related materials, such as SrCo0.8Fe0.2O3−δ [4] and La0.5Sr0.5FeO3−δ [5], seems to be enhanced at grain boundary regions. Recently, the oxygen surface exchange reaction has been reported to increase considerably at heterointerfaces of (La,Sr)CoO3/(La,Sr)2CoO4 composite ceramics [6, 7]. Moreover, fast ionic conduction has been observed in nano-sized multilayer heterostructures owing to space charge effects [8] or structural disorder at incoherent heterophase boundaries [9].

It is the aim of this contribution to model phenomenologically the oxygen exchange between a ceramic composite and the surrounding atmosphere after the oxygen partial pressure has been changed instantaneously. The re-equilibration process, i.e., oxidation or reduction of the mixed conducting electroceramics, involves both surface exchange reaction and diffusion of oxygen in the composite consisting of two randomly distributed phases. Special emphasis is laid on fast diffusion of oxygen along grain boundaries as well as heterointerfaces. The microstructure of the composite is described by means of a square grain model and the diffusion equations are solved numerically by application of the finite element method [10, 11]. The composition of the composite is restricted to a dilute distribution of inclusions in a matrix (host) phase, such that percolation phenomena [12, 13] can be neglected. Relaxation curves for the total amount of exchanged oxygen are discussed in terms of effective medium diffusion within the framework of the Maxwell–Garnett approach [14–20]. In the case of extremely fast transport along the grain and interphase boundaries, the relaxation process shows two different time constants. Analytical approximations are provided for this case as well as for blocking interphase boundaries, introducing two separate relaxation times. It should be mentioned that re-equilibration processes of single crystals may even show two relaxation times, when the transport of two chemical components on separate sub-lattices is kinetically de-coupled, e.g., different relaxation kinetics of cation and anion sub-lattices [21]. This situation is not taken into account in the present work, i.e., exclusively the effect of the microstructure on relaxation processes is investigated assuming local equilibrium in the individual phases of the composite. Moreover, conductivity relaxation curves are predicted by coupling diffusion and dc conduction in the present finite element model.

Theoretical aspects

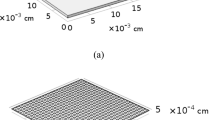
Based on a finite element model published previously [19], the present approach represents an extension with respect to fast diffusion along grain boundaries as well as heterointerfaces. Additionally, finite element simulations of dc conductivity relaxation curves are facilitated within the present model by coupling diffusion and dc conduction. In the following, the extended model will be outlined in detail. The microstructure of a ceramic composite can be described by employing a square grain model, as shown in Fig. 1. The composite is composed of two different phases with individual diffusion coefficients and surface exchange coefficients. The amount of phase 2 may be restricted to values fairly below the percolation threshold, such that the composite is a dilute and random dispersion of inclusions (phase 2) in a polycrystalline matrix (host phase 1). The particles of both phases are considered to be square grains of equal size, d = 0.1 μm. The interfaces (grain boundaries) between grains of phase 1 are assumed to be thin slabs of uniform thickness, δ = 0.5 nm. The interphase (heterophase) boundaries between the inclusions (phase 2) and grains of the matrix (host phase 1) may likewise consist of thin slabs with uniform thickness, δ = 0.5 nm. The kinetic parameters of both grain (homophase) and interphase (heterophase) boundaries may differ considerably from those of the bulk (grains) of phases 1 and 2.

Fig. 1
figure 1

Square grain model for a possible microstructure of the composite consisting of a random distribution of inclusions in a host phase (matrix). The particles of both phases are squares with equal side length d = 0.1 μm. Both the grain boundaries between grains of the host phase and the interphase boundaries between the inclusions and particles of the matrix are thin slabs of uniform thickness δ = 0.5 nm. The volume fraction of inclusions amounts to 10% (g = 0.1)

Full size image

In the case of spatially uniform diffusion coefficients, the transient behavior of transport processes in both phases of the composite as well as the grain and interphase boundaries can be described phenomenologically by

$$ \frac{{\partial {c_1}}}{{\partial t}} = {D_1}{\nabla^2}{c_1} $$
(1a)
$$ \frac{{\partial {c_2}}}{{\partial t}} = {D_2}{\nabla^2}{c_2} $$
(1b)
$$ \frac{{\partial c{\prime}}}{{\partial t}} = D{\prime}{\nabla^2}c{\prime} $$
(1c)
$$ \frac{{\partial c{\prime}{\prime}}}{{\partial t}} = D{\prime}{\prime}{\nabla^2}c{\prime}{\prime} $$
(1d)

where D 1, D 2, D′, and D″ and c 1, c 2, c′, and c″ denote the pertinent diffusion coefficients and diffusant concentrations of phase 1, phase 2, grain boundaries, and heterointerfaces, respectively. The surface of the mixed conducting composite (x = 0) may be exposed to an oxygen containing gas phase (diffusion source). The instantaneous change of the oxygen partial pressure in the surrounding gas phase gives rise to oxygen exchange reactions at the surface of the composite material. In the case of small variations of the oxygen activity (partial pressure), the fluxes at the surface for incorporation or release of oxygen into/from the ceramic composite can be written as (x = 0)

$$ {J_1} = - {k_1}({c_1} - {c_{{1,\infty }}}) = - {D_1}\frac{{\partial {c_1}}}{{\partial x}} $$
(2a)
$$ {J_2} = - {k_2}({c_2} - {c_{{2,\infty }}}) = - {D_2}\frac{{\partial {c_2}}}{{\partial x}} $$
(2b)
$$ J{\prime} = - k{\prime}(c{\prime} - {c{\prime}_{\infty }}) = - D{\prime}\frac{{\partial c{\prime}}}{{\partial x}} $$
(2c)
$$ J{\prime}{\prime} = - k{\prime}{\prime}(c{\prime}{\prime} - {c{\prime}{\prime}_{\infty }}) = - D{\prime}{\prime}\frac{{\partial c{\prime}{\prime}}}{{\partial x}} $$
(2d)

within the limits of linear response. The quantities k 1, k 2, k′, and k″ and c 1,∞, c 2,∞, \( {c{\prime}_{\infty }} \), and \( {c{\prime}{\prime}_{\infty }} \) refer to the surface exchange coefficients and diffusant concentrations at the end of the re-equilibration process (t → ∞) of phase 1, phase 2, grain boundaries, and heterointerfaces, respectively. The surface at x = L may be a diffusion barrier for the diffusing species

$$ \frac{{\partial {c_1}}}{{\partial x}} = \frac{{\partial {c_2}}}{{\partial x}} = \frac{{\partial c{\prime}}}{{\partial x}} = \frac{{\partial c{\prime}{\prime}}}{{\partial x}} = 0, x = L $$
(3)

with L being the thickness of the composite. For symmetry reasons the boundaries at y = ± L/2 are likewise reflecting, i.e. vanishing fluxes,

$$ \frac{{\partial {c_1}}}{{\partial y}} = \frac{{\partial {c_2}}}{{\partial y}} = \frac{{\partial c{\prime}}}{{\partial y}} = \frac{{\partial c{\prime}{\prime}}}{{\partial y}} = 0, y = \pm L/2 $$
(4)

In the case of conductivity relaxation experiments oxygen exchange reactions usually occur at both surfaces (x = 0 and x = 2 L) of a disk-shaped sample with thickness 2 L, such that boundary condition (3) is still fulfilled.

The boundary conditions at the contact between a grain of phase 1 and a grain boundary are given by

$$ {D_1}\frac{{\partial {c_1}}}{{\partial n}} = D{\prime}\frac{{\partial c{\prime}}}{{\partial n}} $$
(5a)
$$ c{\prime} = s{\prime}{c_1}. $$
(5b)

At the contact between phase 1 and the heterointerface the boundary conditions read

$$ {D_1}\frac{{\partial {c_1}}}{{\partial n}} = D{\prime}{\prime}\frac{{\partial c{\prime}{\prime}}}{{\partial n}} $$
(6a)
$$ c{\prime}{\prime} = {s{\prime}{\prime}_1}{c_1}, $$
(6b)

while for phase 2 one arrives at

$$ {D_2}\frac{{\partial {c_2}}}{{\partial n}} = D{\prime}{\prime}\frac{{\partial c{\prime}{\prime}}}{{\partial n}} $$
(7a)
$$ c{\prime}{\prime} = {s{\prime}{\prime}_2}{c_2}. $$
(7b)

The symbols \( s{\prime} \), \( {s{\prime}{\prime}_1} \), and \( {s{\prime}{\prime}_2} \) correspond to the segregation factors for phase 1, phase 2, and grain boundaries as well as heterointerfaces, respectively, and the operator ∂/∂n denotes differentiation along the normal of the interface [22]. In the case of 18O tracer exchange measurements the segregation factors are unity, \( s{\prime} = {s{\prime}{\prime}_1}{ } = {s{\prime}{\prime}_2} = 1. \) Regarding chemical diffusion (conductivity relaxation) experiments the quantities \( s{\prime} \), \( {s{\prime}{\prime}_1} \), and \( {s{\prime}{\prime}_2} \) refer to ratios of the oxygen nonstoichiometry changes of the pertinent phases and interfaces which corresponds to \( s{\prime} = \left( {\partial \mu /\partial {c_1}} \right)/\left( {\partial \mu /\partial c{\prime}} \right) \), \( {s{\prime}{\prime}_1} = \left( {\partial \mu /\partial {c_1}} \right)/\left( {\partial \mu /\partial c{\prime}{\prime}} \right) \), and \( {s{\prime}{\prime}_2} = \left( {\partial \mu /\partial {c_2}} \right)/\left( {\partial \mu /\partial c{\prime}{\prime}} \right) \) for small driving forces (linear response) with μ being the chemical potential of the mobile neutral component (oxygen) in accordance with Ref. [18]. It should be mentioned that in the case of conductivity relaxation experiments, the kinetic parameters are related to chemical diffusion coefficients and chemical surface exchange coefficients, while for 18O exchange studies tracer diffusion coefficients and tracer surface exchange coefficients are involved.

The diffusion Eqs. 1a–1d subject to boundary conditions (2)–(7) have been solved numerically by application of the finite element method using the software package COMSOL Multiphysics® 3.5a. Relaxation curves for the time dependence of the total amount of exchanged oxygen, m(t)/m(∞), are obtained from

$$ \frac{{m(t)}}{{m(\infty )}} = \frac{1}{{{L^2}}}\int\limits_0^L {\int\limits_{{ - L/2}}^{{ + L/2}} {\frac{{c - {c_0}}}{{{c_{\infty }} - {c_0}}}{ }} } {\hbox{d}}y{\hbox{d}}x, $$
(8)

as outlined in detail previously [19, 20]. The quantities c 0 and c ∞ in Eq. 8 denote the initial (t = 0) and final (t → ∞) values of the average (effective) diffusant concentrations.

Additional boundary conditions are required in order to simulate conductivity relaxation curves, see Fig. 1. A constant voltage, U, may be applied at electronically conducting electrodes (y = ±L/2). The remaining surfaces (x = 0, L) may be electrically insulating. The applied voltage, U, corresponds to the difference of the electrochemical potential of the electronic charge carriers in the matrix, inclusions, and grain and interphase boundaries, respectively,

$$ {\tilde{\mu }_{{e,1}}} = {\tilde{\mu }_{{e,2}}} = {\tilde{\mu }{\prime}_e} = {\tilde{\mu }{\prime}{\prime}_e} = - FU,\quad y = + L/{2} $$
(9a)
$$ {\tilde{\mu }_{{e,1}}} = {\tilde{\mu }_{{e,2}}} = {\tilde{\mu }{\prime}_e} = {\tilde{\mu }{\prime}{\prime}_e} = 0,\quad y = - L/{2} $$
(9a)

with F denoting the Faraday constant. If the electronic transport number of the mixed conducting ceramic composite, including both phases as well as the grain and interphase boundaries, is assumed to be almost equal to one (t e  ≈ 1), the total current densities are given by

$$ {j_1} = \frac{{{\sigma_{{e,1}}}}}{F}{\hbox{grad}}{\tilde{\mu }_{{e,1}}} $$
(10a)
$$ {j_2} = \frac{{{\sigma_{{e,2}}}}}{F}{\hbox{grad}}{\tilde{\mu }_{{e,2}}} $$
(10b)
$$ j{\prime} = \frac{{{{\sigma {\prime}}_e}}}{F}{\hbox{grad}}{\tilde{\mu }{\prime}_e} $$
(10c)
$$ j{\prime}{\prime} = \frac{{{{\sigma {\prime}{\prime}}_e}}}{F}{\hbox{grad}}{\tilde{\mu }{\prime}{\prime}_e} $$
(10d)

where σ e,1, σ e,2, \( {\sigma {\prime}_e} \), and \( {\sigma {\prime}{\prime}_e} \) refer to the pertinent (local) electronic conductivities which are a function of space and time during the diffusion experiment. The local conductivities are assumed to vary linearly with the diffusant concentrations (oxygen nonstoichiometry), i.e., \( \Delta {\sigma_e} \propto \Delta c \). The present finite element model enables the coupling of diffusion and dc conduction. The continuity equation

$$ \nabla \cdot {j_1} = \nabla \cdot {j_2} = \nabla \cdot j{\prime} = \nabla \cdot j{\prime}{\prime} = 0 $$
(11)

subject to boundary conditions (9a) and (9b) as well as Eqs. 1a–1d taking account of boundary conditions (2)–(7) are solved simultaneously (COMSOL Multiphysics® 3.5a), yielding the total current I(t) that is obtained by integrating the current density along the boundary at \( y = - L/{2 }\left[ {I(t) = \int_{{x = 0}}^L {j{\hbox{d}}x} \;,y = - L/{2}} \right] \). The normalized electronic conductivity of the composite is finally given by

$$ {\sigma_{{norm}}} = \frac{{\sigma - {\sigma_0}}}{{{\sigma_{\infty }} - {\sigma_0}}} = \frac{{I(t) - I(0)}}{{I(\infty ) - I(0)}} $$
(12)

where σ 0, I(0) and σ ∞, I(∞) are the initial and final values for the conductivity and the total current at the beginning and the end of the conductivity relaxation experiment, respectively.

Results and discussion

Typical examples of calculated relaxation curves for the total amount of exchanged oxygen are depicted in Fig. 2. The numerical simulations coincide remarkably well with the analytical solution for effective medium diffusion [23]

$$ \frac{{m(t)}}{{m(\infty )}} = 1 - 2{\left( {\frac{{{k_{\rm{eff}}}}}{{{D_{\rm{eff}}}}}} \right)^2}\sum\limits_{{n = 0}}^{\infty } {\frac{{\exp \left( { - \alpha_{\rm{n}}^2{D_{\rm{eff}}}t} \right)}}{{\alpha_{\rm{n}}^2\left( {k_{\rm{eff}}^2{L^2}/D_{\rm{eff}}^2 + {k_{\rm{eff}}}L/{D_{\rm{eff}}} + {L^2}\alpha_{\rm{n}}^2} \right)}}} $$
(13)

where the parameters α n are given by the roots of the transcendental equation \( {\alpha_n}\tan ({\alpha_n}L) = {k_{\rm{eff}}}/{D_{\rm{eff}}} \). According to the Maxwell–Garnett approach [15, 18], the effective diffusion coefficient for a two-dimensional homogeneous medium can be written as

$$ {D_{\rm{eff}}} = \frac{{{{D{\prime}}_1}}}{{1 - g + sg}}\left[ {1 + \frac{{2(s{{D{\prime}}_2} - {{D{\prime}}_1})g}}{{s{{D{\prime}}_2} + {{D{\prime}}_1} + ({{D{\prime}}_1} - s{{D{\prime}}_2})g}}} \right]. $$
(14)

with g denoting the volume fraction of inclusions. The symbol s is defined as the ratio of the effective (average) diffusant concentrations (oxygen nonstoichiometries in the case of chemical diffusion) of the matrix including the grain boundaries, \( {c{\prime}_1} \), and the inclusions including the interphase boundaries, \( {c{\prime}_2} \),

$$ s = \frac{{{{c{\prime}}_2}}}{{{{c{\prime}}_1}}} $$
(15a)
$$ {c{\prime}_1} = g{\prime}c{\prime} + (1 - g{\prime}){c_1} $$
(15b)
$$ {c{\prime}_2} = g{\prime}{\prime}c{\prime}{\prime} + (1 - g{\prime}{\prime}){c_2}, $$
(15c)

where g′ refers to the volume fraction of the grain boundaries in the matrix, \( g{\prime} = 2\delta /d \), and g″ is given by \( g{\prime}{\prime} = 4\delta /d \). The thickness of both grain and interphase boundaries, δ, is assumed to be much smaller than the grain size, d, of the polycrystalline matrix as well as the inclusions. The factor s is related to \( s = (\partial \mu /\partial {c{\prime}_1})/(\partial \mu /\partial {c{\prime}_2}) \) in analogy to the segregation factors for the respective phases and interfaces as outlined in the previous section. It is worth mentioning that in the case of small driving forces (linear response) and negligible storage capacity of both grain and interphase boundaries \( {(}s{\prime}g{\prime},{s{\prime}{\prime}_2}g{\prime}{\prime} < < {1)} \), the parameter s reads

$$ s \approx \frac{{(\partial \mu /\partial {c_1})}}{{(\partial \mu /\partial {c_2})}}. $$
(16)

The effective diffusion coefficient of the polycrystalline matrix (including the grain boundaries) can be expressed as

$$ {D{\prime}_1} = \frac{{\varepsilon s{\prime}D{\prime} + (1 - \varepsilon ){D_1}}}{{1 - g{\prime} + s{\prime}g{\prime}}}{, } $$
(17)

while the effective diffusion coefficient for the inclusions including the interphase boundaries is given by

$$ {D{\prime}_2} = \frac{{2\varepsilon {{s{\prime}{\prime}}_2}D{\prime}{\prime} + (1 - 2\varepsilon ){D_2}}}{{1 - g{\prime}{\prime} + {{s{\prime}{\prime}}_2}g{\prime}{\prime}}}{ } $$
(18)

with ε denoting the area fraction of grain and interphase boundaries, ε = δ/d. A detailed derivation of Eqs. 17 and 18, which are valid for fast grain and interphase boundary diffusion (D′, D′ >> D 1, D 2), can be found in the appendix. Analogously to the relations for the effective diffusivity, the effective surface exchange coefficient can be written as

$$ {k_{\rm{eff}}} = \frac{{sg{{k{\prime}}_2} + (1 - g){{k{\prime}}_1}}}{{1 - g + sg}} $$
(19a)
$$ {k{\prime}_1} = \frac{{\varepsilon s{\prime}k{\prime} + (1 - \varepsilon ){k_1}}}{{1 - \varepsilon + \varepsilon s{\prime}}} $$
(19b)
$$ {k{\prime}_2} = \frac{{2\varepsilon {{s{\prime}{\prime}}_2}k{\prime}{\prime} + (1 - 2\varepsilon ){k_2}}}{{1 - 2\varepsilon + 2\varepsilon {{s{\prime}{\prime}}_2}}}. $$
(19c)

The relaxation time for the re-equilibration process is obtained from the slope of the semi-logarithmic plot \( { \ln }[1 - m(t)/m(\infty )] \) versus time, see Fig. 2b, \( {\tau_{\rm{eff}}} = - {({\hbox{slope)}}^{{ - {1}}}} = {(\alpha_1^2{D_{\rm{eff}}})^{{ - 1}}} \) [α 1 is the first root of the transcendental equation \( {\alpha_1}\tan ({\alpha_1}L) = {k_{\rm{eff}}}/{D_{\rm{eff}}} \)]. More details can be found elsewhere [19, 24, 25].

Fig. 2
figure 2

Variation of the total amount of exchanged oxygen with time. The lines are obtained from the present finite element model. The symbols are based on analytical expressions for effective medium diffusion. L = 2.06 μm, d = 0.1 μm, δ = 0.5 nm, g = 0.1, \( s{\prime} = {s{\prime}{\prime}_1} = {s{\prime}{\prime}_2} = 1 \). Solid line: D 1 = 10−11 cm2 s−1, D 2 = 10−10 cm2 s−1, D′ = 2 × 10−9 cm2 s−1, D″ = 3 × 10−8 cm2 s−1, k 1 = 10−7 cm s−1, k 2 = 3 × 10−6 cm s−1, k′ = 10−4 cm s−1, k″ = 4 × 10−4 cm s−1. Dashed line: D 1 = 10−10 cm2 s−1, D 2 = 10−9 cm2 s−1, D′ = 2 × 10−8 cm2 s−1, D″ = 3 × 10−7 cm2 s−1, k 1 = 10−6 cm s−1, k 2 = 3 × 10−7 cm s−1, k′ = 10−4 cm s−1, k″ = 4 × 10−4 cm s−1. a Relaxation curves. b Semi-logarithmic plots

Full size image

Effective medium diffusion is observed only if the time constant τ eff is much higher than the individual relaxation times for the transport processes in the phases and interfaces of the composite, \( {\tau_{\rm{eff}}} > > {\tau_1},{\tau_2},\tau {\prime},\tau {\prime}{\prime} \). On the contrary, when the relaxation time for diffusion in phase 1 and/or phase 2 is much longer than that for transport in the effective medium, the relaxation process shows two separate time constants. The overall re-equilibration process of the two-dimensional square grain model can be described by the analytical approximation

$$ \begin{gathered} \frac{{m(t)}}{{m(\infty )}} = 1 - \frac{{1 - g}}{{1 - g + sg}}{\left\{ {\frac{8}{{{\pi^2}}}\sum\limits_{{n = 0}}^{\infty } {\frac{{\exp [ - {\pi^2}{{(2n + 1)}^2}{D_1}t/{d^2}]}}{{{{(2n + 1)}^2}}}} } \right\}^2} \\- \frac{{sg}}{{1 - g + sg}}{\left\{ {\frac{8}{{{\pi^2}}}\sum\limits_{{n = 0}}^{\infty } {\frac{{\exp [ - {\pi^2}{{(2n + 1)}^2}{D_2}t/{d^2}]}}{{{{(2n + 1)}^2}}}} } \right\}^2}{ }{.} \\\end{gathered} $$
(20)
  1. (a)

    In the case of extremely fast diffusion along the grain boundaries of a homogeneous ceramic material (single phase material), i.e. , \( s{\prime}\varepsilon D{\prime}/(4{L^2}) > > 2{D_1}/{d^2} \), the analytical approximation for the re-equilibration process is likewise given by Eq. 20 with g = 0. A typical example for a relaxation curve of the total amount of exchanged oxygen is depicted in Fig. 3, where the insert shows the corresponding semi-logarithmic plot. The rate-determining step is slow bulk diffusion from the grain boundaries into the grains. At long diffusion times, the slope of the straight line of the semi-logarithmic plot enables the determination of the diffusion coefficient for the grains, D 1, as reported in detail elsewhere [20, 24, 25]. It should be noted that only one relaxation time can be observed in Fig. 3, assuming a negligible storage capacity of the grain boundaries of the polycrystalline single phase material.

    Fig. 3
    figure 3

    Variation of the total amount of exchanged oxygen with time for extremely fast diffusion along the grain boundaries of a single phase (homogeneous) material. The lines are obtained from the present finite element model. The symbols are based on the analytical approximation Eq. 20 with g = 0. L = 2.06 μm, d = 0.1 μm, δ = 0.5 nm, \( s{\prime} = {s{\prime}{\prime}_1} = {s{\prime}{\prime}_2} = 1 \), D 1 = D 2 = 10−15 cm2 s−1 (bulk diffusivity), D′ = D″ = 10−5 cm2 s−1 (grain boundary diffusivity), and k 1 = k 2 = k′ = k″ = 10−4 cm s−1. Insert is the pertinent semi-logarithmic plot

    Full size image
  2. (b)

    Extremely fast diffusion along the grain and interphase boundaries is assumed and the diffusion coefficient of phase 1 (grains of the matrix) is higher than that for the inclusions (phase 2), i.e., \( s{\prime}\varepsilon D{\prime}/(4{L^2}),{s{\prime}{\prime}_2}\varepsilon D{\prime}{\prime}/(4{L^2}) > > 2{D_1}/{d^2} > 2{D_2}/{d^2} \). Relaxation curves for this case are shown in Fig. 4. Two different slopes can be observed in Fig. 4b, which are related to separate relaxation times. The grain and interphase boundaries are re-equilibrated instantaneously, such that the rate-determining diffusion processes occur from the grain and interphase boundaries into the grains of phase 1 and subsequently into the inclusions because of the lower diffusivity of oxygen in phase 2 compared to the matrix. Hence, the first relaxation time (slope of the semi-logarithmic plot in Fig. 4b) reads

    Fig. 4
    figure 4

    Variation of the total amount of exchanged oxygen with time for extremely fast diffusion along the interfaces of the composite and D 1 > D 2. The lines are obtained from the present finite element model. The symbols are based on the analytical approximation Eq. 20. L = 2.06 μm, d = 0.1 μm, δ = 0.5 nm, g = 0.1, \( s{\prime} = {s{\prime}{\prime}_1} = {s{\prime}{\prime}_2} = 1 \), k 1 = 10−6 cm s−1, k 2 = 3 × 10−7 cm s−1, and k′ = k″ = 10−4 cm s−1. a Relaxation curves. b Semi-logarithmic plots

    Full size image
$$ {\tau_{\rm{I}}} = \frac{{{d^2}}}{{2{\pi^2}{D_1}}} $$
(21)

and the second slope in Fig. 4b refers to the time constant for diffusion into the inclusions

$$ {\tau_{\rm{II}}} = \frac{{{d^2}}}{{2{\pi^2}{D_2}}} $$
(22)

in accordance with Eq. 20.

  1. (c)

    The situation of extremely fast diffusion along the grain and interphase boundaries, with a higher diffusivity in phase 2 than in phase 1, is illustrated in Fig. 5, i.e. \( s{\prime}\varepsilon D{\prime}/(4{L^2}),{s{\prime}{\prime}_2}\varepsilon D{\prime}{\prime}/(4{L^2}) > > 2{D_2}/{d^2} > 2{D_1}/{d^2} \). Again, the new equilibrium activity of oxygen is established instantaneously in the grain and interphase boundaries and two different relaxation processes can be distinguished, see Fig. 5b. The first (faster) relaxation process is related to diffusion from the interphase boundaries into the inclusions with the time constant

    Fig. 5
    figure 5

    Variation of the total amount of exchanged oxygen with time for extremely fast diffusion along the interfaces of the composite and D 1 < D 2. The lines are obtained from the present finite element model. The symbols are based on the analytical approximation Eq. 20. L = 2.06 μm, d = 0.1 μm, δ = 0.5 nm, g = 0.1, \( s{\prime} = {s{\prime}{\prime}_1} = {s{\prime}{\prime}_2} = 1 \), k 1 = 10−6 cm s−1, k 2 = 3 × 10−7 cm s−1, and k′ = k″ = 10−4 cm s−1. a Relaxation curves. b Semi-logarithmic plots

    Full size image
$$ {\tau_{\rm{I}}} = \frac{{{d^2}}}{{2{\pi^2}{D_2}}}, $$
(23)

whereas the second transport process corresponds to diffusion into the grains of phase 1 with the relaxation time

$$ {\tau_{\rm{II}}} = \frac{{{d^2}}}{{2{\pi^2}{D_1}}}. $$
(24)

Alternatively, re-equilibration processes with two separate relaxation times are expected, when the time constant for interfacial diffusion exceeds considerably that for effective medium diffusion, i.e., \( {\tau_{\rm{eff}}} < < \tau {\prime},\tau {\prime}{\prime} \). For the sake of simplicity, the discussion is restricted to blocking interphase boundaries (\( D{\prime}{\prime}/\delta < < {D_2}/d,{D_1}/d \))

$$ \begin{gathered} \frac{{m(t)}}{{m(\infty )}} = 1 - \frac{{1 - g}}{{1 - g + sg}} \times 2{\left( {\frac{{{{k{\prime}}_1}}}{{{{D{\prime}}_1}}}} \right)^2}\sum\limits_{{n = 0}}^{\infty } {\frac{{\exp ( - \beta_{\rm{n}}^2{{D{\prime}}_1}t)}}{{\beta_{\rm{n}}^2(k{\prime}_1^2{L^2}/D{\prime}_1^2 + {{k{\prime}}_1}L/{{D{\prime}}_1} + {L^2}\beta_{\rm{n}}^2)}}} - \\\frac{{sg}}{{1 - g + sg}} \times \exp \left( { - \frac{{4D{\prime}{\prime}}}{{d\delta }}t} \right) \\\end{gathered} $$
(25)

provided that the thickness of the heterointerfaces is much smaller than the grain size of the inclusions, δ << d, such that D″/δ corresponds to the mass transfer coefficient for transport across the interphase boundary. The parameters β n are defined by the roots of the transcendental equation \( {\beta_n}\tan ({\beta_n}L) = {k{\prime}_1}/{D{\prime}_1} \). The transport across heterophase boundaries is generally blocked, when depletion (space charge) layers, impurities, or detrimental side reactions arise at the interface. According to Eq. 25, a fast transport process is anticipated in the polycrystalline matrix, resulting in the first relaxation time

$$ {\tau_{\rm{I}}} = \frac{1}{{\beta_1^2{{D{\prime}}_1}}}, $$
(26)

where β 1 is the first root of \( {\beta_1}\tan ({\beta_1}L) = {k{\prime}_1}/{D{\prime}_1} \). The effective kinetic parameters of the matrix (\( {D{\prime}_1} \) and \( {k{\prime}_1} \)) are given by Eqs. 17 and 19b. The second relaxation process involves transport across the blocking heterointerfaces into the inclusions with the time constant for the two-dimensional square grain model

$$ {\tau_{\rm{II}}} = \frac{{d\delta }}{{4D{\prime}{\prime}}}. $$
(27)

Relaxation curves for various volume fractions of inclusions are displayed in Fig. 6. The two separate relaxation processes with different time constants are clearly visible in the semi-logarithmic plots of Fig. 6b, where the relaxation curves exhibit two different slopes.

Fig. 6
figure 6

Time dependence of the total amount of exchanged oxygen for various volume fractions of the inclusions. The lines are obtained from the present finite element model. The symbols are based on the analytical approximation Eq. 25. L = 2.06 μm, d = 0.1 μm, δ = 0.5 nm, \( s{\prime} = {s{\prime}{\prime}_1} = {s{\prime}{\prime}_2} = 1 \), D 1 = 10−10 cm2 s−1, D 2 = 10−11 cm2 s−1, D′ = 2 × 10−8 cm2 s−1, D″ = 3 × 10−18 cm2 s−1 (blocking interphase boundaries), k 1 = 10−6 cm s−1, k 2 = 3 × 10−7 cm s−1, k′ = 10−4 cm s−1, and k″ = 4 × 10−4 cm s−1. a Relaxation curves. b Semi-logarithmic plots

Full size image

Basically, the total amount of exchanged oxygen can be measured as a function of time by employing, among others, thermogravimetry [26] and carrier gas coulometry [27, 28]. In the case of conductivity relaxation experiments [28–30], the quantity m(t)/m(∞) is related to the normalized electronic conductivity \( {\sigma_{\rm{norm}}} = (\sigma - {\sigma_0})/({\sigma_{\infty }} - {\sigma_0}) \). The relation \( m(t)/m(\infty ) = {\sigma_{\rm{norm}}} \) is fulfilled, if the re-equilibration process can be described by effective medium diffusion, i.e., one single (effective) relaxation time is required. On the contrary, when two separate time constants are necessary for the description of the relaxation process, the time dependence of the total amount of exchanged oxygen may differ significantly from the relaxation curve for the electronic dc conductivity.

The discussion of conductivity relaxation curves will be restricted to the following case of two different relaxation times. If the diffusion coefficient of the grains of the matrix is higher by several orders of magnitude than that for the inclusions, a fast transport process will arise in the effective medium of the polycrystalline matrix and the second relaxation process is related to diffusion from the matrix into the inclusions. High diffusivities and conductivities of the grain boundaries and heterointerfaces are assumed, i.e., non-blocking interfaces. This situation has been outlined in detail recently with respect to the total amount of exchanged oxygen [19, 20]. Typical relaxation curves for the total amount of exchanged oxygen as well as the electronic conductivity are shown in Fig. 7. Various ratios of the dc conductivities of the inclusions and the host phase have been taken into account. The re-equilibration process of the matrix is given by

$$ {\left. {\frac{{m(t)}}{{m(\infty )}}} \right|_{\rm{matrix}}} = 1 - 2{\left( {\frac{{{{k{\prime}}_1}}}{{{{D{\prime}}_1}}}} \right)^2}\sum\limits_{{n = 0}}^{\infty } {\frac{{\exp ( - \beta_n^2{{D{\prime}}_1}t)}}{{\beta_n^2(k{\prime}_1^2{L^2}/D{\prime}_1^2 + {{k{\prime}}_1}L/{{D{\prime}}_1} + {L^2}\beta_n^2)}}}, $$
(28)

where the effective diffusion coefficient and the effective surface exchange coefficient of the matrix can be expressed as

$$ {D{\prime}_1} = \frac{{\varepsilon [(1 - 2g)s{\prime}D{\prime} + 2g{{s{\prime}{\prime}}_1}D{\prime}{\prime}] + (1 - \varepsilon ){D_1}}}{{1 - g{\prime} + [(1 - 2g)s{\prime} + 2g{{s{\prime}{\prime}}_1}]g{\prime}}}{ } $$
(29)

and

$$ {k{\prime}_1} = \frac{{\varepsilon [(1 - 2g)s{\prime}k{\prime} + 2g{{s{\prime}{\prime}}_1}k{\prime}{\prime}] + (1 - \varepsilon ){k_1}}}{{1 - \varepsilon + [(1 - 2g)s{\prime} + 2g{{s{\prime}{\prime}}_1}]\varepsilon }}. $$
(30)

The second relaxation process refers to diffusion into the inclusions

$$ {\left. {\frac{{m(t)}}{{m(\infty )}}} \right|_{\rm{inclusions}}} = 1 - {\left\{ {\frac{8}{{{\pi^2}}}\sum\limits_{{n = 0}}^{\infty } {\frac{{\exp [ - {\pi^2}{{(2n + 1)}^2}{D_2}t/{d^2}]}}{{{{(2n + 1)}^2}}}} } \right\}^2}{ } $$
(31)

and the two separate relaxation times are given by Eqs. 26 and 22. Assuming a linear correlation between the oxygen nonstoichiometry and the conductivity changes, the variation of the conductivity of the matrix (host phase 1) with time can be written as

$$ {\sigma_1} = {\sigma_{{1,0}}} + ({\sigma_{{1,\infty }}} - {\sigma_{{1,0}}}){\left. {\frac{{m(t)}}{{m(\infty )}}} \right|_{\rm{matrix}}}, $$
(32)

while the relaxation of the conductivity of the inclusions (phase 2) reads

$$ \sigma _{2} = \sigma _{{2,0}} + {\left( {\sigma _{{2,\infty }} - \sigma _{{2,0}} } \right)}\frac{{m{\left( t \right)}}} {{m{\left( \infty \right)}}}\left| {_{{{\text{inclusions}}}} } \right. $$
(33)

with σ 1,0, σ 2,0 and σ 1,∞, σ 2,∞ denoting the initial and final conductivities of the matrix and inclusions at the beginning (t = 0) and the end (t → ∞) of the relaxation experiment, respectively. Taking account of Eqs. 32 and 33, the conductivity of the composite is given by

$$ \sigma (t) = {\sigma_1}\left[ {1 + \frac{{2({\sigma_2} - {\sigma_1})g}}{{{\sigma_1} + {\sigma_2} + ({\sigma_1} - {\sigma_2})g}}} \right] $$
(34)

in accordance with the two-dimensional Maxwell–Garnett equation. The overall re-equilibration process of the composite with regard to the total amount of exchanged oxygen can be written as

$$ \frac{{m(t)}}{{m(\infty )}} = 1 - \frac{{1 - g}}{{1 - g + sg}} \times {\left. {\frac{{m(t)}}{{m(\infty )}}} \right|_{\rm{matrix}}} - \frac{{sg}}{{1 - g + sg}} \times {\left. {\frac{{m(t)}}{{m(\infty )}}} \right|_{\rm{inclusions}}}. $$
(35)

From Fig. 7, one can deduce that the relaxation curves obtained from the present finite element model concur satisfactorily with analytical approximations based on Eq. 34 for the conductivity relaxation curves and Eq. 35 for the time dependence of the total amount of exchanged oxygen. It should be noted that the finite element simulations for σ(t) differ from the analytical approximation based on Eq. 34 by approximately 1%, when σ 1,0 ≠ σ 2,0 and σ 1,∞ ≠ σ 2,∞. Interestingly, the conductivity relaxation curves deviate from that for the total amount of exchanged oxygen, even if the initial and final conductivities of the matrix and inclusions are equal, i.e., σ 1,0 = σ 2,0 and σ 1,∞ = σ 2,∞ [σ 1(t) ≠ σ 2(t) due to different time constants for phases 1 and 2]. In the case of effective medium diffusion, the coupled simulation of diffusion and dc conductivity relaxation revealed no deviation of m(t)/m(∞) from the normalized conductivity regardless of the relationship between diffusant concentration (oxygen nonstoichiometry) and local conductivity, such that effective kinetic parameters can be obtained from conductivity relaxation experiments by application of Eq. 13.

Fig. 7
figure 7

Relaxation curves for the normalized conductivity, \( {\sigma_{\rm{norm}}} = (\sigma - {\sigma_0})/({\sigma_{\infty }} - {\sigma_0}) \), as well as the total amount of exchanged oxygen, m(t)/m(∞). L = 2.06 μm, d = 0.1 μm, δ = 0.5 nm, g = 0.1, \( s{\prime} = {s{\prime}{\prime}_1} = {s{\prime}{\prime}_2} = 1 \), D 1 = 10−10 cm2 s−1, D 2 = 10−17 cm2 s−1, D′ = 3 × 10−8 cm2 s−1, D″ = 2 × 10−7 cm2 s−1, k 1 = 10−6 cm s−1, k 2 = 3 × 10−7 cm s−1, k′ = 10−4 cm s−1, and k″ = 4 × 10−4 cm s−1. The lines are obtained from the present finite element model. The symbols are based on the analytical approximations (Eqs. 34 and 35)

Full size image

Conclusions

Surface exchange reactions and diffusion of oxygen in a ceramic composite have been modeled numerically by employing the finite element technique. The composite may be composed of a random and dilute distribution of inclusions in a polycrystalline matrix. The microstructure is described by a square grain model including grain boundaries of the matrix (host phase) as well as interphase boundaries between the inclusions and grains of the matrix. Relaxation curves for the total amount of exchanged oxygen due to an instantaneous change of the oxygen partial pressure of the surrounding gas phase are calculated, emphasizing fast diffusion along the grain and interphase boundaries. Analytical approximations are given for effective medium diffusion, provided that the relaxation time for effective medium diffusion is much higher than the time constants for the transport process in the individual phases and interfaces of the composite. Appropriate relations for the effective diffusion coefficient and the effective surface exchange coefficient are introduced. On the contrary, two different relaxation times are required for the description of the re-equilibration process regarding both extremely fast diffusion along the interfaces and blocking interphase boundaries. Analytical approximations and appropriate relations for the two separate time constants are provided for these limiting cases.

In addition, conductivity relaxation curves have been simulated by coupling diffusion and dc conduction in the present finite element model. No deviation between relaxation curves for the total amount of exchanged oxygen and the normalized conductivity is predicted, when the re-equilibration process of the composite can be described by effective medium diffusion. On the contrary, in the case of separate relaxation processes in different phases of the composite the time dependence of the dc conductivity deviates remarkably from that for the total amount of exchanged oxygen. Analytical approximations have been derived which may be suitable for an advanced interpretation of experimental results obtained from conductivity relaxation experiments as well as for the extraction of kinetic parameters of the phases and interfaces in the composite.