Modeling the final sintering stage of doped ceramics: mutual interaction between grain growth and densification

Abstract

Applying the thermodynamic extremal principle, a model for grain growth and densification in the final stage of sintering of doped ceramics was derived, with segregation-dependent interfacial energies and mobilities (or diffusivities). The model demonstrated an interdependence between the driving forces of grain growth and densification during sintering evolution, observed because the surface energy contributes positively to the driving force of grain growth while the GB energy negatively to the driving force of densification. The model was tested in alumina as a host system, and calculations demonstrate that dopants with more negative GB (or surface) segregation enthalpy or which cause lower GB diffusion coefficient can induce higher relative densities at a given grain size. Comparatively studying yttria- and lanthana-doped alumina, the lanthana doping showed significantly enhanced sintering attributed to the larger La³⁺ radius causing a more negative GB segregation energy. This present model is expected to help dopant designing to improve control over sintering.

Introduction

The usage of solid solution additives, or in other words, dopants, is able to bring dramatically microstructural benefits for ceramics, such as microstructural refinement [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] to substantially improve mechanical properties. In principle, a dopant is capable of operating on the grain growth and densification in sintering. A dopant can act thermodynamically to reduce the grain boundary (GB) energy and the surface energy [11, 12, 16], and kinetically by altering the GB mobility and the diffusivity of rate-determining species [14, 15, 17], both effects caused by the dopant segregation at GBs and free surfaces around pores [18, 19].

Efforts have been made to theoretically describe the dependence of grain growth or densification, i.e. pore elimination, on dopant segregation at both GB and surface of ceramics during sintering. In this case, grain growth is generally considered to be affected by two parameters [20, 21], namely the solute drag due to the interaction between GB and dissolved solutes, and the pore drag due to the interaction between GB and pores situated along it. For the solute drag effect, Cahn’s theory [22] is most commonly used to explain the retardation by doping. For the pore-drag effect, a theory of grain growth controlled by migration of pores was developed by incorporating the formulated pore-drag force (dependent on mass transport) into the curvature-driven grain growth equation [17, 23,24,25,26,27,28]. While considering the densification, a mass diffusion flux with composition-dependent diffusion coefficient was derived by applying chemical potential gradients of various constituents obtained using grand partition function, showing certain effects of dopants on the densification rate (closely associated with the mass flux) [29, 30]. Following previous works, the evolution of grain size and relative density in the final stage of sintering of magnesia-doped alumina were plotted by Brook [17] through coupling the (pore-drag-limited) grain growth and the (diffusion-mediated) densification equations with the experimental values of diffusion coefficients (as equation parameters) to qualitatively explain the role of magnesia. Brook’s work was further developed in our recently published paper [31], where, with well-formulated segregation-dependent thermodynamic and kinetic parameters, the grain growth and densification equations were modified separately and then coupled to describe the evolution of grain size (or relative density) with time.

So far, the theoretical framework for grain growth and densification of doped ceramics (especially in the final sintering stage) has been initially established, particularly for a coupling of these two processes. As far as the authors know, however, the previous theoretical works suffer from a certain shortcoming, that is, a significantly mutual interaction between grain growth and densification is ignored, as is shown in Fig. 1. From Fig. 1a, the densification occurs by removal of matter from the GB to the pores, leaving the reduced cross-sectional region of pores on the GB plane to be occupied by the newly formed GB to maintain the stability of the pore-grain structure; this increases the total GB energy. Previously, such effect was not considered when deriving the pore-drag-limited grain growth equation. In addition, as shown in Fig. 1b, due to the GB migration (if grain growth occurs), the pores in various GB regions are moving close to each other, contacting and eventually merging; this process can also be called “self-similar coarsening of pores” [32] which reduces the surface area and then the total surface energy. This effect was also ignored when deriving the diffusion-mediated densification equation.

Figure 1

Schematic of a the shrinkage of a pore situated in a GB upon densification and b the coalescence of pores caused by the GB migration upon grain growth

Obviously, grain growth and densification upon sintering affect the respective driving force of each other due to interfacial energies changes. If one considers them as independent phenomena, upon modeling the two processes, ignoring the mutual interaction will underestimate the driving force for grain growth but overestimate that for densification. Consequently, the actual driving forces when describing effects of doping are not accurate; thus, a reliable assessment for the dopant effect on grain growth and densification cannot be reliably made.

On this basis, a modified theoretical description for the final sintering stage of sintering of doped ceramics (generally considered as the most important stage when targeting fully dense ceramics) is here presented by considering such mutual interaction. To enable a more comprehensive description, grain growth and densification are treated as a whole rather than two separate processes so that the mutual interaction can be naturally incorporated. Model calculations were carried out to explore the thermodynamic and kinetic effects in terms of the parameters reflecting inherent properties affected by the dopant. Thereafter, the model was applied to alumina as a model system to test its validity. This work shows enhanced thermo-kinetic effect on grain growth and densification caused by larger dopant cationic radius and, meanwhile, helping to establish more efficient protocols for the selection of dopants designed to improve sintering control to help achieve fully dense nanocrystalline/ultrafine-grained ceramics.

Model derivation

Thermodynamic extremal principle (TEP) [33], has been intensively applied in modeling dynamic processes involved in material science, e.g., grain growth [34,35,36] and solid-state phase transformation [28, 32, 37,38,39]. As TEP is based on the energy evolution of the process as whole than in single sub-processes, multiple sub-processes are no longer treated separately. A global formulation of TEP can be mainly divided into [33]: (1) to introduce characteristic parameters for proper description of the state and evolution of the system (“Basic model assumptions” section); (2) to derive the evolution equations under certain constraints among the characteristic parameters (“Derivation of evolution laws” section).

Basic model assumptions

In this work, singly doped systems with molecular formula (A, B)_mC_n are solely concerned, in which A, B and C denote, respectively, the host cation, the dopant cation and the anion, and m:n is the stoichiometric ratio; this means that the host and the dopant have same valence state. Such treatment is designed to avoid additional cation/anion vacancies (to maintain the electrical neutrality) due to aliovalent doping, thus minimizing the effect of doping on the defect balance and the resultant effects on the thermodynamic state and the evolution of the system.

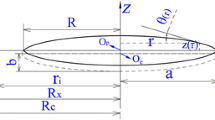
Coble’s geometrical assumption of sintering compacts [40] for the final sintering stage is used here; see Supplementary materials I for details. Accordingly, sintering compacts can be well defined in terms of two main geometrical parameters, i.e., the grain size (R) and the relative density (ρ). Moreover, the solute distribution in the matrix (including the bulk, GBs and free surface layers around pores) should also be one of the main characteristics of the system. Note that, the actual polycrystalline material often possesses many different types of GBs and some free surfaces with different crystal orientations. As a consequence, the solute content in different GBs/free surfaces will also be different. For simplicity, in this paper, we adopt Hillert’s interface phase description [41], thereby ignoring the specific structure of GBs, but treating all GBs in the polycrystalline material as a thermodynamic phase of constant thickness that has its specific composition, isotropic GB energy and diffusivity/mobility. The “GB phase” defined here can be considered to be the average of all GBs. The current model would be suitable for the general polycrystalline material with low- and high-angle GBs, which should not have obvious texture or intergranular films. Using a similar approach, the specific crystal orientation of the free surface layers is also ignored and they are also treated as a thermodynamic phase of constant thickness.

Therefore, the grain size, the relative density, and the solute contents at the bulk (x ^bulk_B ), the GBs (x ^GB_B ) and the free surfaces (x ^s_B ) are considered as the characteristic parameters for TEP application. All the parameters involved are summarized in Table 1. For simplicity, it is assumed that steady-state solute diffusion [34, 42] is maintained at every moment in the evolution of the system, regardless of the solute redistribution. This assumption will be reflected when deriving the dissipation associated with solute diffusion; see Supplementary materials II.

Table 1 Parameters and the corresponding meanings in the modeling process

Derivation of evolution laws

Gibbs energy and total dissipation

Different from metals, the crystal structure of ceramic materials is often more complex, with multiple sub-lattices, and more types of defects and defect complexes. Accordingly, the GBs/free surfaces of ceramic materials are also more complex than those of metals. The system will be further complicated when dopants are introduced as it largely affects the defect balance. Therefore, certain simplification and idealization of the research system would be required to achieve an intelligible thermodynamic description. As elucidated above, the effect of doping on the defect balance is reduced as much as possible taking into account only binary isovalent doped systems. Moreover, the intrinsic defect concentration is assumed negligible, such that both the bulk and the interface phases are assumed as ideal lattice with strict stoichiometric ratios, implying the electric neutrality in the entire matrix.

The molar Gibbs free energy of the system, G, can thus be expressed as a volume fraction-weighted average¹ of the molar Gibbs free energy for the bulk, the GBs and the free surface layers, taking the following form:

$$ G = \left\{ \begin{array}{l} \left( {1 - f_{\text{GB}} - f_{\text{s}} } \right)\left[ {\left( {1 - x_{\text{B}}^{\text{bulk}} } \right)\mu_{\text{A}}^{\text{bulk}} + x_{\text{B}}^{\text{bulk}} \mu_{\text{B}}^{\text{bulk}} + \frac{n}{m}\mu_{\text{C}}^{\text{bulk}} } \right] \hfill \\ +\,f_{\text{GB}} \left[ {\left( {1 - x_{\text{B}}^{\text{GB}} } \right)\mu_{\text{A}}^{\text{GB}} + x_{\text{B}}^{\text{GB}} \mu_{\text{B}}^{\text{GB}} + \frac{n}{m}\mu_{\text{C}}^{\text{GB}} } \right] + f_{\text{s}} \left[ {\left( {1 - x_{\text{B}}^{\text{s}} } \right)\mu_{\text{A}}^{\text{s}} + x_{\text{B}}^{\text{s}} \mu_{\text{B}}^{\text{s}} + \frac{n}{m}\mu_{\text{C}}^{\text{s}} } \right] \hfill \\ \end{array} \right\} $$

(1)

where the superscripts “GB,” “bulk” and “s” distinguish the bulk, the GB and the surface, respectively, f is the volume fraction occupied by the interface (see Supplementary materials I), and x and μ are the molar fraction and chemical potential of the component, respectively.

The total energy dissipation, Q, should consist of the following four contributions:

$$ Q = Q_{\text{M}} + Q_{\text{tr}} + Q_{\text{D}} + Q_{\text{P}} $$

(2)

where the subscripts “M,” “tr,” “D” and “P” represent the intrinsic GB migration, the solute trans-GB diffusion, the diffusion along the GB and the pore migration with the GB, respectively. The above four different types of dissipation can be simply written as [33] (see Eqs. 3–6):

$$ Q_{\text{M}} = \int_{{{\text{GB}}\;{\text{area}}}} {\frac{{v^{2} }}{{M_{\text{intr}} }}{\text{d}}A_{\text{GB}} } $$

(3)

$$ Q_{\text{tr}} = \int_{{{\text{GB}}\;{\text{volume}}}} {\frac{{R_{\text{g}} TJ_{\text{tr}}^{2} }}{{c_{\text{B}}^{\text{GB}} D_{\text{B}}^{\text{GB}} }}{\text{d}}V_{\text{GB}} } $$

(4)

$$ Q_{\text{D}} = \int_{{{\text{GB}}\;{\text{diffusion}}\;{\text{area}}}} {\left( {\frac{{R_{\text{g}} TJ_{\text{A}}^{2} }}{{c_{\text{A}}^{\text{GB}} D_{\text{A}}^{\text{GB}} }} + \frac{{R_{\text{g}} TJ_{\text{B}}^{2} }}{{c_{\text{B}}^{\text{GB}} D_{\text{B}}^{\text{GB}} }} + \frac{{R_{\text{g}} TJ_{\text{C}}^{2} }}{{c_{\text{C}}^{\text{GB}} D_{\text{C}}^{\text{GB}} }}} \right)dV_{\text{GB}} } $$

(5)

$$ Q_{\text{P}} = \int_{{{\text{Pore}}\;{\text{number}}}} {\frac{{v^{2} }}{{M_{\text{P}} }}{\text{d}}N} $$

(6)

where v is the rate of GB migration, M _intr the intrinsic GB mobility, and A _GB the GB area per unit mole of matter; R _g is the mole gas constant, T the temperature (in unit of K), J _tr the steady-state trans-GB diffusive flux of solute atoms, c ^GB_B the solute (dopant cation) concentration at GBs, D ^GB_B the diffusion coefficient of solute atoms at GBs, and V _GB the GB volume per unit mole of matter; J _A, J _B and J _C are the diffusion flux of components “A,” “B” and “C” along GBs, respectively, c ^GB_A and c ^GB_C are the concentration of component “A” and “C” at GBs, and D ^GB_A and D ^GB_C are the diffusion coefficients of components “A” and “C” at GBs of the doped system; N is the number of pores per unit mole of matter, equivalent to the number of pores possessed by each grain multiplied by the number of grains per unit mole of matter, and M _P is the pore mobility. See Supplementary materials II for the specific derivations of Q _M, Q _tr, Q _D and Q _P. The total dissipation is then derived by summing each contribution as (see Eq. 7):

$$ Q = \left\{ \begin{array}{l} A_{\text{GB}} \left[ {\frac{1}{{M_{{\text{int}\, {\text{r}}}} }} + \frac{1}{{{{V_{\text{m}} D_{\text{B}}^{\text{GB}} } \mathord{\left/ {\vphantom {{V_{\text{m}} D_{\text{B}}^{\text{GB}} } {\delta_{\text{GB}} R_{\text{g}} T}}} \right. \kern-0pt} {\delta_{\text{GB}} R_{\text{g}} T}}}}\frac{{\left( {x_{\text{B}}^{\text{GB}} - x_{\text{B}}^{\text{bulk}} } \right)^{2} }}{{x_{\text{B}}^{\text{GB}} }} + \frac{N}{{A_{\text{GB}} }}\frac{1}{{{{3V_{\text{m}} \delta_{\text{s}} D_{\text{s}} } \mathord{\left/ {\vphantom {{3V_{\text{m}} \delta_{\text{s}} D_{\text{s}} } {2\pi R_{\text{g}} Tr^{4} }}} \right. \kern-0pt} {2\pi R_{\text{g}} Tr^{4} }}}}} \right]\left( {\dot{R}} \right)^{2} \hfill \\ + \frac{1}{66}\frac{q\left( w \right)}{{\left( {1 - w} \right)^{2} }}\frac{{R_{\text{g}} T}}{{\delta_{\text{GB}} D_{\text{GB}} }}\frac{{R^{3} }}{{\rho^{4} }}\left( {\dot{\rho }} \right)^{2} \hfill \\ \end{array} \right\} $$

(7)

where the superimposed dot “·” represents the time derivative, δ _GB the width of GB diffusion layer, V _m the molar volume, x ^GB_B and x ^bulk_B the solute contents at the GB and the bulk, respectively, q(w) a function of w that is dependent on ρ (Eq. (S20) in Supplementary materials II), D _GB is the GB self-diffusion coefficient, δ _s the width of surface diffusion layer, D _s the surface self-diffusion coefficient, and r the pore radius.

Note that, Eq. (4), representing the solute drag effect and directly reflecting the contribution of dopant cations to GB migration and system evolution, is directly adopted from metals. Although ceramic materials present more complex GB structure as compared to metals, the idealization and simplification of the research system here and the previous successful application of solute drag idea (in conjunction with the segregation thermodynamics) from the metal system to the ceramic system [15, 20,21,22, 43,44,45,46,47,48] suggest that the above treatment should be reasonable.

Constraints and evolution equations

The evolution path of a system corresponds to the maximum of the total dissipation, Q, constrained by the premise of TEP [33],

$$ \dot{G} + Q = 0 $$

(8)

and the conservation relation of solute amount, i.e.,

$$ \left( {1 - f_{\text{GB}} - f_{\text{s}} } \right)x_{\text{B}}^{\text{bulk}} + f_{\text{GB}} x_{\text{B}}^{\text{GB}} + f_{\text{s}} x_{\text{B}}^{\text{s}} = x_{\text{B}} $$

(9)

with x _B the total solute content. Then, taking the derivatives of both sides in Eq. (9) with respect to time leads to:

$$ - \left( {\dot{f}_{\text{GB}} + \dot{f}_{\text{s}} } \right)x_{\text{B}}^{\text{bulk}} + \dot{f}_{\text{GB}} x_{\text{B}}^{\text{GB}} + \dot{f}_{\text{s}} x_{\text{B}}^{\text{s}} + \left( {1 - f_{\text{GB}} - f_{\text{s}} } \right)\dot{x}_{\text{B}}^{\text{bulk}} + f_{\text{GB}} \dot{x}_{\text{B}}^{\text{GB}} + f_{\text{s}} \dot{x}_{\text{B}}^{\text{s}} = 0 $$

(10)

The necessary conditions for the constraint are thus given by:

$$ \frac{\partial }{{\partial \dot{R}}}\left\{ {Q + \alpha \left( {\dot{G} + Q} \right) + \beta \left[ \begin{array}{l} - \left( {\dot{f}_{\text{GB}} + \dot{f}_{\text{s}} } \right)x_{\text{B}}^{\text{bulk}} + \dot{f}_{\text{GB}} x_{\text{B}}^{\text{GB}} + \dot{f}_{\text{s}} x_{\text{B}}^{\text{s}} \hfill \\ + \left( {1 - f_{\text{GB}} - f_{\text{s}} } \right)\dot{x}_{\text{B}}^{\text{bulk}} + f_{\text{GB}} \dot{x}_{\text{B}}^{\text{GB}} + f_{\text{s}} \dot{x}_{\text{B}}^{\text{s}} \hfill \\ \end{array} \right]} \right\} = 0 $$

(11a)

$$ \frac{\partial }{{\partial \dot{\rho }}}\left\{ {Q + \alpha \left( {\dot{G} + Q} \right) + \beta \left[ \begin{array}{l} - \left( {\dot{f}_{\text{GB}} + \dot{f}_{\text{s}} } \right)x_{\text{B}}^{\text{bulk}} + \dot{f}_{\text{GB}} x_{\text{B}}^{\text{GB}} + \dot{f}_{\text{s}} x_{\text{B}}^{\text{s}} \hfill \\ + \left( {1 - f_{\text{GB}} - f_{\text{s}} } \right)\dot{x}_{\text{B}}^{\text{bulk}} + f_{\text{GB}} \dot{x}_{\text{B}}^{\text{GB}} + f_{\text{s}} \dot{x}_{\text{B}}^{\text{s}} \hfill \\ \end{array} \right]} \right\} = 0 $$

(11b)

$$ \frac{\partial }{{\partial \dot{x}_{\text{B}}^{\text{bulk}} }}\left\{ {Q + \alpha \left( {\dot{G} + Q} \right) + \beta \left[ \begin{array}{l} - \left( {\dot{f}_{\text{GB}} + \dot{f}_{\text{s}} } \right)x_{\text{B}}^{\text{bulk}} + \dot{f}_{\text{GB}} x_{\text{B}}^{\text{GB}} + \dot{f}_{\text{s}} x_{\text{B}}^{\text{s}} \hfill \\ + \left( {1 - f_{\text{GB}} - f_{\text{s}} } \right)\dot{x}_{\text{B}}^{\text{bulk}} + f_{\text{GB}} \dot{x}_{\text{B}}^{\text{GB}} + f_{\text{s}} \dot{x}_{\text{B}}^{\text{s}} \hfill \\ \end{array} \right]} \right\} = 0 $$

(11c)

$$ \frac{\partial }{{\partial \dot{x}_{\text{B}}^{\text{GB}} }}\left\{ {Q + \alpha \left( {\dot{G} + Q} \right) + \beta \left[ \begin{array}{l} - \left( {\dot{f}_{\text{GB}} + \dot{f}_{\text{s}} } \right)x_{\text{B}}^{\text{bulk}} + \dot{f}_{\text{GB}} x_{\text{B}}^{\text{GB}} + \dot{f}_{\text{s}} x_{\text{B}}^{\text{s}} \hfill \\ + \left( {1 - f_{\text{GB}} - f_{\text{s}} } \right)\dot{x}_{\text{B}}^{\text{bulk}} + f_{\text{GB}} \dot{x}_{\text{B}}^{\text{GB}} + f_{\text{s}} \dot{x}_{\text{B}}^{\text{s}} \hfill \\ \end{array} \right]} \right\} = 0 $$

(11d)

$$ \frac{\partial }{{\partial \dot{x}_{\text{B}}^{\text{s}} }}\left\{ {Q + \alpha \left( {\dot{G} + Q} \right) + \beta \left[ \begin{array}{l} - \left( {\dot{f}_{\text{GB}} + \dot{f}_{\text{s}} } \right)x_{\text{B}}^{\text{bulk}} + \dot{f}_{\text{GB}} x_{\text{B}}^{\text{GB}} + \dot{f}_{\text{s}} x_{\text{B}}^{\text{s}} \hfill \\ + \left( {1 - f_{\text{GB}} - f_{\text{s}} } \right)\dot{x}_{\text{B}}^{\text{bulk}} + f_{\text{GB}} \dot{x}_{\text{B}}^{\text{GB}} + f_{\text{s}} \dot{x}_{\text{B}}^{\text{s}} \hfill \\ \end{array} \right]} \right\} = 0 $$

(11e)

where both α and β are the Lagrange multipliers. Whether the chemical potential is well defined or not, the derivative of Gibbs energy with respect to time will not be affected, as the contributions from the derivatives of chemical potentials offset according to the Gibbs–Duhem relation. Each term in Eqs. (11a–11e) is multiplied by each parameter rate, and these five equations can be further summarized as:

$$ 2Q + \alpha \left( {\dot{G} + 2Q} \right) + \beta \left[ \begin{array}{l} - \left( {\dot{f}_{\text{GB}} + \dot{f}_{\text{s}} } \right)x_{\text{B}}^{\text{bulk}} + \dot{f}_{\text{GB}} x_{\text{B}}^{\text{GB}} + \dot{f}_{\text{s}} x_{\text{B}}^{\text{s}} \hfill \\ + \left( {1 - f_{\text{GB}} - f_{\text{s}} } \right)\dot{x}_{\text{B}}^{\text{bulk}} + f_{\text{GB}} \dot{x}_{\text{B}}^{\text{GB}} + f_{\text{s}} \dot{x}_{\text{B}}^{\text{s}} \end{array} \right] = 0 $$

(12)

Comparing Eq. (12) with Eqs. (8) and (10) gives:

$$ \left( {2 + \alpha } \right)Q = 0 \Rightarrow \alpha = - 2 $$

(13)

Substituting the value of α and the expressions of total Gibbs energy and dissipation into Eqs. (11c–11e) leads to,

$$ \beta = 2\left( {\mu_{\text{B}}^{\text{bulk}} - \mu_{\text{A}}^{\text{bulk}} } \right) = 2\left( {\mu_{\text{B}}^{\text{GB}} - \mu_{\text{A}}^{\text{GB}} } \right) = 2\left( {\mu_{\text{B}}^{\text{s}} - \mu_{\text{A}}^{\text{s}} } \right) $$

(14)

which is known as the “parallel tangent rule,” proposed by Hillert [41] for describing the equilibrium between the bulk and the interface phases. Substituting the value of α, and the expressions of β and total Gibbs energy and dissipation into Eqs. (11a) and (11b) yields

$$ \begin{aligned} \sum\limits_{{i = {\text{GB}},{\text{s}}}} { - \frac{{\partial f_{i} }}{\partial R}\left\{ \begin{array}{l} \left[ {\left( {1 - x_{\text{B}}^{i} } \right)\mu_{\text{A}}^{i} + x_{\text{B}}^{i} \mu_{\text{B}}^{i} + \frac{n}{m}\mu_{\text{C}}^{i} } \right] \hfill \\ - \left[ {\left( {1 - x_{\text{B}}^{\text{bulk}} } \right)\mu_{\text{A}}^{\text{bulk}} + x_{\text{B}}^{\text{bulk}} \mu_{\text{B}}^{\text{bulk}} + \frac{n}{m}\mu_{\text{C}}^{\text{bulk}} } \right] - \left( {x_{\text{B}}^{i} - x_{\text{B}}^{\text{bulk}} } \right)\left( {\mu_{\text{B}}^{\text{bulk}} - \mu_{\text{A}}^{\text{bulk}} } \right) \hfill \\ \end{array} \right\}} \hfill \\ = A_{\text{GB}} \left[ {\frac{1}{{M_{\text{intr}} }} + \frac{1}{{{{V_{\text{m}} D_{\text{B}}^{\text{GB}} } \mathord{\left/ {\vphantom {{V_{\text{m}} D_{\text{B}}^{\text{GB}} } {\delta_{\text{GB}} R_{\text{g}} T}}} \right. \kern-0pt} {\delta_{\text{GB}} R_{\text{g}} T}}}}\frac{{\left( {x_{\text{B}}^{\text{GB}} - x_{\text{B}}^{\text{bulk}} } \right)^{2} }}{{x_{\text{B}}^{\text{GB}} }} + \frac{N}{{A_{\text{GB}} }}\frac{1}{{{{3V_{\text{m}} \delta_{\text{s}} D_{\text{s}} } \mathord{\left/ {\vphantom {{3V_{\text{m}} \delta_{\text{s}} D_{\text{s}} } {2\pi R_{\text{g}} Tr^{4} }}} \right. \kern-0pt} {2\pi R_{\text{g}} Tr^{4} }}}}} \right]\mathop R\limits^{ \bullet } \hfill \\ \end{aligned} $$

(15a)

and

$$ \begin{aligned} &\sum\limits_{{i = {\text{GB}},{\text{s}}}} { - \frac{{\partial f_{i} }}{\partial \rho }\left\{ \begin{array}{l} \left[ {\left( {1 - x_{\text{B}}^{i} } \right)\mu_{\text{A}}^{i} + x_{\text{B}}^{i} \mu_{\text{B}}^{i} + \frac{n}{m}\mu_{\text{C}}^{i} } \right] \hfill \\ - \left[ {\left( {1 - x_{\text{B}}^{\text{bulk}} } \right)\mu_{\text{A}}^{\text{bulk}} + x_{\text{B}}^{\text{bulk}} \mu_{\text{B}}^{\text{bulk}} + \frac{n}{m}\mu_{\text{C}}^{\text{bulk}} } \right] - \left( {x_{\text{B}}^{i} - x_{\text{B}}^{\text{bulk}} } \right)\left( {\mu_{\text{B}}^{\text{bulk}} - \mu_{\text{A}}^{\text{bulk}} } \right) \hfill \\ \end{array} \right\}} \hfill \\ & \quad =\frac{1}{66}\frac{q\left( w \right)}{{\left( {1 - w} \right)^{2} }}\frac{{R_{\text{g}} T}}{{\delta_{\text{GB}} D_{\text{GB}} }}\frac{{R^{3} }}{{\rho^{4} }}\dot{\rho } \hfill \\ \end{aligned} $$

(15b)

Further employing Hillert’s definition of interface energy [41] and inserting expressions of volume fractions occupied by GBs and free surface layers (see Eqs. (S6) and (S7) in Supplementary materials I), Eqs. (15a) and (15b) can be rewritten as:

$$ \dot{R} = \frac{{M\left[ {\gamma_{\text{GB}} + \lambda \left( \rho \right)\gamma_{\text{s}} } \right]}}{R} $$

(16)

where the GB mobility is expressed by

$$ M = \left[ {\frac{1}{{M_{\text{intr}} }} + \frac{1}{{{{V_{\text{m}} D_{\text{B}}^{\text{GB}} } \mathord{\left/ {\vphantom {{V_{\text{m}} D_{\text{B}}^{\text{GB}} } {\delta_{\text{GB}} R_{\text{g}} T}}} \right. \kern-0pt} {\delta_{\text{GB}} R_{\text{g}} T}}}}\frac{{\left( {x_{\text{B}}^{\text{GB}} - x_{\text{B}}^{\text{bulk}} } \right)^{2} }}{{x_{\text{B}}^{\text{GB}} }} + \frac{N}{{A_{\text{GB}} }}\frac{1}{{{{3V_{\text{m}} \delta_{\text{s}} D_{\text{s}} } \mathord{\left/ {\vphantom {{3V_{\text{m}} \delta_{\text{s}} D_{\text{s}} } {2\pi R_{\text{g}} Tr^{4} }}} \right. \kern-0pt} {2\pi R_{\text{g}} Tr^{4} }}}}} \right]^{ - 1} $$

(17)

and λ following

$$ \lambda \left( \rho \right) = \frac{{24\pi \left( {1 - \rho } \right)^{{\frac{2}{3}}} }}{{\left( {3 + 6\sqrt 3 } \right)\left( {\frac{\pi }{\sqrt 2 }} \right)^{{\frac{2}{3}}} - 11\pi \left( {1 - \rho } \right)^{{\frac{2}{3}}} }} $$

(18)

and

$$ \dot{\rho } = \frac{{\theta \left( \rho \right)V_{\text{m}} \delta_{\text{GB}} D_{\text{GB}} \left[ {\eta \left( \rho \right)\gamma_{\text{GB}} + \gamma_{\text{s}} } \right]}}{{R_{\text{g}} TR^{4} }} $$

(19)

where the parameter θ is dependent on ρ by the following relationship

$$ \theta \left( \rho \right) = 132\sqrt[3]{6}\frac{{\left( {1 - w} \right)^{2} }}{q\left( w \right)}\rho^{2} \left( {\frac{1 - \rho }{\rho }} \right)^{{ - \frac{1}{3}}} $$

(20)

and η following

$$ \eta \left( \rho \right) = \frac{1}{{8\sqrt[3]{2\pi }}}\left( {1 + 2\sqrt 3 } \right)\left( {1 - \rho } \right)^{{\frac{1}{3}}} - \frac{11}{24} $$

(21)

Therein, γ _GB and γ _s are the GB energy and surface energy, respectively.

As the evolution equations for R [Eq. (16)] and ρ [Eq. (19)] are derived, corresponding work for the solute contents at the bulk, GBs and free surfaces, needs to be completed. As elucidated above, Eq. (14), namely the “parallel tangent rule,” stipulates the equilibrium between the bulk and the interface phases (for a given interface area), at which the equilibrium solute distribution is achieved [41]. Accordingly, a modified version [16] of the Langmuir–Mclean isothermal segregation theory [49, 50], which addresses the coexistence of GB and free surface, is used to assess the equilibrium solute distribution among the bulk, the GBs and the free surfaces:

$$ \frac{{x_{\text{B}}^{\text{GB}} }}{{1 - x_{\text{B}}^{\text{GB}} }}{ = }\frac{{x_{\text{B}}^{\text{bulk}} }}{{1 - x_{\text{B}}^{\text{bulk}} }}\exp \left( { - \frac{{\Delta H_{\text{seg}}^{\text{GB}} }}{{R_{\text{g}} T}}} \right) $$

(22a)

$$ \frac{{x_{\text{B}}^{\text{s}} }}{{1 - x_{\text{B}}^{\text{s}} }}{ = }\frac{{x_{\text{B}}^{\text{bulk}} }}{{1 - x_{\text{B}}^{\text{bulk}} }}\exp \left( { - \frac{{\Delta H_{\text{seg}}^{\text{s}} }}{{R_{\text{g}} T}}} \right) $$

(22b)

where ΔH ^GB_seg and ΔH ^s_seg are the GB- and the surface-segregation enthalpies, respectively. Combining Eqs. (22a) and (22b) with the conservation equation of solute amount [Eq. (9)], x ^bulk_B , x ^GB_B and x ^s_B for a given total solute content and temperature can be solved as functions of the grain radius and the relative density. Since the composition redistribution during the sintering process is not the focus of this work, then evolution of the three solute contents over time will not be displayed below.

Note that Eq. (16) has a mathematical form similar to the classical curvature-driven grain growth equation (i.e., dR/dt = Mγ _GB/R) except for the term γ _GB + λγ _s. This means a different constituent of driving force involved in the grain growth with the densification proceeding; the surface energy also contributes to the driving force of grain growth, in contrast with the conventional viewpoint that the GB energy is the only constituent [51]. Analogously, Eq. (19) has a mathematical form similar to the widely used GB-diffusion-mediated densification equation [52] (i.e., dρ/dt∝V _m δ _GB D _GB γ _s/R _g TR ⁴) except for the scale factor θ(ρ) and the term ηγ _GB + γ _s. The different constituents of driving force involved in the densification means that the GB energy also contributes to the driving force of densification when grain growth occurs, in contrast with the conventional viewpoint that the surface energy is the only constituent [40, 52,53,54,55]. The different scale factors imply different diffusion gradients utilized for deriving diffusion flux along the GB, J _D; see Eq.(S19) in Supplementary materials II.

Segregation-dependent interface energy and interface diffusivity

To assess the five characteristic parameters derived in section “Constraints and evolution equations,” in the case of dopant-cation segregation, the segregation dependence of several thermodynamic and kinetic parameters, including the GB energy (γ _GB), the surface energy (γ _s), the GB self-diffusion coefficient (D _GB), the surface self-diffusion coefficient (D _s), the GB diffusion coefficient of dopant cation (D ^GB_B ) and the intrinsic GB mobility (M _intr), must be known.

• (1) Interface energy

As formulated by Gibbs [56], the effect of solute segregation on interface energy can be expressed as

$$ {\text{d}}\gamma_{j} = - \varGamma_{j} {\text{d}}\mu_{\text{B}}^{\text{bulk}} $$

(23)

where j is the interface type, Γ _j the Gibbs excess of solute at the interface j. Subsequently, a lot of work [57,58,59,60,61,62,63] has been developed to give analytical expressions of segregation-dependent interface energy. One of them [60], assuming negligible entropic contributions, is well accepted, exhibiting the interface energy directly associated with the interface segregation enthalpy and the solute excess, i.e.,

$$ \gamma_{j} = \gamma_{j0} + \varGamma_{j} \Delta H_{\text{seg}}^{j} \approx \gamma_{j0} + \frac{{m_{j} x_{j} }}{{\varOmega^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} N_{\text{Avg}} }}\Delta H_{\text{seg}}^{j} $$

(24)

where γ _j0 is the interface energy for a pure host system, Γ _j the Gibbs solute excess, Ω the average volume per molecule, and m _j the average number of the atomic layers at interface j (i.e., 3 for GB [49] and 1 for free surface [11, 12]).

Note that, Eq. (24) was originally derived using the Hillert’s polycrystalline material free energy map and the parallel tangent rule [41]. Although the configurational entropy term is ignored compared with the widely used Weissmüller’s interface energy model [57], Eq. (24) can also be used to relatively accurately assess the effect of segregation on GB (surface) energy, as previously demonstrated [11, 13, 16, 31, 64]. In fact, although the configurational entropy affects the level of segregation and the interface energy to a certain extent, segregation enthalpy plays a more important role.

It should be noteworthy that the energy contribution from elastic distortion due to size misfit could considerably influence segregation and the interface energy, which has been widely recognized in other research works [62, 63, 65,66,67,68]. In the current work, differently, no explicit elastic energy term appears in Eq. (24). However, the elastic energy term, in fact, has been implicitly included in the physical quantity, namely segregation enthalpy ΔH ^j_seg .

• (2) Self-diffusion coefficient/mobility

As the segregation proceeds, the increased availability of solute atoms at the interface allows the sites of high compression and tension to be removed so that the net energy of the interface is reduced, which is expected according to the Gibbs adsorption isotherm theory [Eq. (23)] [56]. Consequently, the materials at the interface become more like the bulk from the diffusion viewpoint. This concept has been formulized by Borisov [69] to give a semi-empirical relationship between the GB energy and the GB self-diffusion coefficient. Borisov’s semi-empirical relationship [69] was combined with the segregation-dependent GB energy [Eq. (24)] to quantitatively describe the dependence of GB self-diffusion coefficient on segregation level, which was further extended to the case of surface diffusion [31]:

$$ D_{j} = D_{j0} \exp \left( {\frac{{\alpha \Delta H_{\text{seg}}^{j} }}{{R_{\text{g}} T}}x_{j} } \right) $$

(25)

where D _j0 is the self-diffusivity of interface j, and α denotes the diffusion mechanism (2 for vacancy diffusion and 1 for interstitial diffusion).

Based on the reaction rate theory [70] that describes the relationship between the intrinsic GB mobility and the GB self-diffusion coefficient, i.e., M _intr = V _m D _GB/aR _g T, the intrinsic GB mobility affected by segregation can be derived by incorporating the segregation-dependent GB self-diffusion coefficient [Eq. (25)] [31]:

$$ M_{\text{intr}} = M_{\text{intr0}} \exp \left( {\frac{{\alpha \Delta H_{\text{seg}}^{\text{GB}} }}{{R_{\text{g}} T}}x_{\text{GB}} } \right) $$

(26)

with M _intr0 = V _m D _GB0/aR _g T.

• (3) GB diffusion coefficient of solute

To the authors’ knowledge, the dependence of the GB diffusion coefficient of dopant cation in the host, D ^GB_B , on the segregation level has rarely been reported. As proposed for metal/alloys [71], the solute atoms have nearly the same activation energy of GB diffusion as the solvent atoms because the changed environment around the atom diffusion path due to segregation will apply to both, so that the GB diffusion of solute exhibits similar segregation dependence to that of solvent, as shown in Eq. (25). Considering that only isovalent doping is concerned in this work,² it is assumed that Eq. (25) applies to the case of ionic compounds. Then we have:

$$ D_{\text{B}}^{\text{GB}} = D_{{{\text{B}}0}}^{\text{GB}} \exp \left( {\frac{{\alpha \Delta H_{\text{seg}}^{\text{GB}} }}{{R_{\text{g}} T}}x_{\text{GB}} } \right) $$

(27)

where D ^GB_B0 is the GB diffusion coefficient of dopant cation in the case of dilute limit of solution.

Modified equations for grain growth and densification in sintering

Substituting Eqs. (24–27) into Eqs. (16), (17) and Eq. (19), we obtain

$$ \begin{aligned} \dot{R} & = \frac{{\left[ {\left( {\gamma_{{{\text{GB}}0}} + \frac{{m_{\text{GB}} x_{\text{GB}} }}{{\varOmega^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} N_{\text{Avg}} }}\Delta H_{\text{seg}}^{\text{GB}} } \right) + \lambda \left( \rho \right)\left( {\gamma_{{{\text{s}}0}} + \frac{{m_{\text{s}} x_{\text{s}} }}{{\varOmega^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} N_{\text{Avg}} }}\Delta H_{\text{seg}}^{\text{s}} } \right)} \right]}}{R} \\ & \quad \times \left[ \begin{array}{l} \frac{1}{{M_{{{\text{intr}}0}} }}\exp \left( { - \frac{{\alpha \Delta H_{\text{seg}}^{\text{GB}} }}{{R_{\text{g}} T}}x_{\text{GB}} } \right) + \frac{1}{{{{V_{\text{m}} D_{{{\text{B}}0}}^{\text{GB}} } \mathord{\left/ {\vphantom {{V_{\text{m}} D_{{{\text{B}}0}}^{\text{GB}} } {\delta_{\text{GB}} R_{\text{g}} T}}} \right. \kern-0pt} {\delta_{\text{GB}} R_{\text{g}} T}}}}\frac{{\left( {x_{\text{B}}^{\text{GB}} - x_{\text{B}}^{\text{bulk}} } \right)^{2} }}{{x_{\text{B}}^{\text{GB}} }}\exp \left( { - \frac{{\alpha \Delta H_{\text{seg}}^{\text{GB}} }}{{R_{\text{g}} T}}x_{\text{GB}} } \right) \hfill \\ + \frac{N}{{A_{\text{GB}} }}\frac{1}{{{{3V_{\text{m}} \delta_{\text{s}} D_{{{\text{s}}0}} } \mathord{\left/ {\vphantom {{3V_{\text{m}} \delta_{\text{s}} D_{{{\text{s}}0}} } {2\pi R_{\text{g}} Tr^{4} }}} \right. \kern-0pt} {2\pi R_{\text{g}} Tr^{4} }}}}\exp \left( { - \frac{{\alpha \Delta H_{\text{seg}}^{\text{s}} }}{{R_{\text{g}} T}}x_{\text{s}} } \right) \hfill \\ \end{array} \right]^{ - 1} \\ \end{aligned} $$

(28)

and

$$ \begin{aligned} \dot{\rho } & = \frac{{\theta \left( \rho \right)V_{\text{m}} \delta_{\text{GB}} D_{{{\text{GB}}0}} }}{{R_{\text{g}} TR^{4} }} \\ & \quad \times \left[ {\eta \left( \rho \right)\left( {\gamma_{{{\text{GB}}0}} + \frac{{m_{\text{GB}} x_{\text{GB}} }}{{\varOmega^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} N_{\text{Avg}} }}\Delta H_{\text{seg}}^{\text{GB}} } \right) + \left( {\gamma_{{{\text{s}}0}} + \frac{{m_{\text{s}} x_{\text{s}} }}{{\varOmega^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} N_{\text{Avg}} }}\Delta H_{\text{seg}}^{\text{s}} } \right)} \right]\exp \left( {\frac{{\alpha \Delta H_{\text{seg}}^{\text{GB}} }}{{R_{\text{g}} T}}x_{\text{GB}} } \right) \\ \end{aligned} $$

(29)

Equations (28) and (29) are the modified equations of grain growth and densification after considering segregation. Among all the parameters of these two equations, the GB- and the free-surface-segregation enthalpies (ΔH ^GB_seg and ΔH ^s_seg ), and the GB diffusion coefficient of dopant cation in the case of dilute limit of solution (D ^GB_B0 ), are closely related to the dopant itself. Therein, ΔH ^GB_seg directly influences the GB energy, the GB self-diffusion coefficient and the intrinsic GB mobility while ΔH ^s_seg acting directly on the surface energy and the surface self-diffusion coefficient; ΔH ^GB_seg and D ^GB_B0 operate together to impact the GB diffusion coefficient of dopant cation. On this basis, effects of the dopant on the grain growth and the densification, in terms of ΔH ^GB_seg , ΔH ^s_seg and D ^GB_B0 , as well as the calculation procedure for obtaining the evolution of grain radius and relative density, are schematically shown in Fig. 2, from which, it is clear that the mutual interaction bridges the dopant and the grain growth/densification.

Figure 2

Schematic of how dopants affect the grain growth and densification during sintering process, also showing the calculation procedure for obtaining the evolution of grain radius and relative density over time

Model calculation and demonstration

The mutual interaction between grain growth and densification illustrated in “Introduction” enables us to shine light on the situation where both the GB energy and the surface energy contribute to the driving forces of gain growth and densification, so that the real equations governing the evolution of R and ρ can be re-derived. Here, model calculations for a certain system will be performed, to show the microstructure evolution affected by doping while considering the mutual interaction between grain growth and densification.

Selection of research system

Alumina, which has wide industrial application due to its excellent mechanical and physical properties [72], is chosen as the research system. Values of model parameters are listed in Table 2. Therein, the initial values for grain radius R ₀ and relative density ρ ₀ are set as 0.2 µm and 90%,³ respectively. The sintering temperature T is given as 1300 °C, which is within the range of widely used temperatures for the sintering of Al₂O₃. The dopant content x _B is set as 1 × 10⁻³. The molecule volume Ω (of AlO_3/2) is 2.11 × 10⁻²⁹ m³ [17], and then the average interatomic distance a is according to a = Ω^1/3 calculated as 2.76 × 10⁻¹⁰ m. The GB energy (γ ^GB0) and the surface energy (γ ^s0) for pure Al₂O₃ are set as 0.34 J/m² [52] and 0.71 J/m² [52], respectively. δ _GB D _GB0 is selected to follow the relationship 8.6 × 10⁻¹⁰ exp(−418 × 10³/R _g T) [52], while D _s0 follows 0.09 exp(−322 × 10³/R _g T) [17].

Table 2 Values of some model parameters used for calculation

Driving forces for grain growth and densification

As shown in section “Constraints and evolution equations,” the mutual interaction between grain growth and densification is reflected in the constituents of driving force for the two processes, cf. Equations (16) and (19). For simplicity, the driving forces of grain growth and densification in pure Al₂O₃ as a function of ρ are calculated using the data given in Table 2, see Fig. 3a. As ρ increases, the driving force of grain growth decreases and eventually returns to the GB energy at ρ = 100%. For densification, the driving force is always smaller than the surface energy, also decreasing with ρ. The above evolutions are compatible with the evolutions of λ and η with ρ (Fig. 3b) calculated using Eqs. (18) and (21), respectively. As ρ increases, λ systematically decreases from 1.06 to 0 while η decreases from −0.32 to −0.44. Obviously, the surface energy serves a positive role in lifting the driving force of grain growth, which decreases with ρ and eventually vanishes as ρ achieves 100%, where all the pores are eliminated and a full densification is attained. On the contrary, the negative η indicates that the GB energy operates to reduce the driving force of densification. The decreasing η with ρ implies a continuously enhanced effect which reaches its maximum at full densification.

Figure 3

Evolution of a the driving forces for grain growth and densification in pure Al₂O₃ and of b two dimensionless parameters, λ and η as a function of relative density

Note that, the two dimensionless parameters, λ and η, are only dependent on ρ, which means the above mutual interaction comes naturally as a result of grain-pore structure, regardless of doping or not. Similar results also occur for the case of doping and are therefore not displayed here.

Effects of GB- and surface-segregation enthalpies and dopant-cation GB diffusivity

Considering the mutual interaction, it is desirable to obtain physically realistic driving forces of grain growth and densification, so that, for the case of doping, the evolution of microstructure during sintering can be described, and a more reliable assessment of the action of dopants is allowed, with the help of segregation-dependent interface energies and diffusivities/mobilities.

GB segregation enthalpy

As a first analysis, ΔH ^s_seg is set to be −40 kJ mol⁻¹, which corresponds to a relatively moderate segregation behavior; D ^GB_B0 is assumed to be 0.02D _GB0, enabling an observable solute drag effect.⁴ Then, by combining the calculation procedures (Fig. 2) with the parameters listed in Table 2, the evolution of R and ρ over t and the trajectory of R versus ρ are calculated for ΔH ^GB_seg (= −20, −40, and −60 kJ mol⁻¹ corresponding to the cases of relatively weak, moderate and strong GB segregation), see Fig. 4. With increasing ΔH ^GB_seg (the absolute value), a smaller R at the same t is achieved, suggesting a suppressed grain growth (Fig. 4a), while a higher ρ is presented except for the initial stage, corresponding to an accelerated densification (Fig. 4b). For a given R, an enhanced GB segregation exhibits a higher ρ (Fig. 4c), indicating a promoted sintering behavior.

Figure 4

a Grain radius and b relative density calculated as a function of time and c trajectory of grain radius versus relative density, at T = 1300 °C and x _B = 0.001 for different values of GB segregation enthalpy (ΔH ^GB_seg  = −20, −40, −60 kJ mol⁻¹) with the model parameters of ΔH ^s_seg  = −40 kJ mol⁻¹ and D ^GB_B0  = 0.02D _GB0. The arrow marks the direction of decreasing ΔH ^GB_seg (the absolute value)

Since the modified grain growth equation [Eq. (16)] seems associated with the dopant itself and ρ, then the grain growth is directly affected by the dopant-cation segregation and indirectly by the feedback from densification; the modified densification equation [Eq. (19)] implies an analogous physics. So, the evolution of both R and ρ is governed by both the direct action of dopant-cation segregation and the mutual feedback between grain growth and densification.

With increasing the GB segregation level, reflected by the absolute value of ΔH ^GB_seg , a decreased GB energy and a consequently reduced driving force of grain growth are thermodynamically exhibited, see Fig. 5a and Figs. S1a and S1b in Supplementary materials III. Kinetically, a decreased intrinsic GB mobility and an enhanced solute drag effect (due to reduced D ^GB_B ) arise, both of which act together to create a decreased GB mobility at the initial stage, see Fig. 5a and Figs. S1c to S1f in Supplementary materials III. Thereby, a sluggish grain growth is yielded (Fig. 4a) with respect to ΔH ^GB_seg , due to the thermodynamically reduced driving force and the kinetically reduced GB mobility. From Fig. 5b, the direct effect of ΔH ^GB_seg on densification, thermodynamically, decreases the GB energy (Fig. S1a in Supplementary materials III) but increases the driving force of densification (Fig. S2a in Supplementary materials III), while, kinetically, decreasing the GB self-diffusion coefficient (Fig. S2b in Supplementary materials III). Since the densification is delayed at the initial stage with respect to ΔH ^GB_seg (Fig. 4b), then it can be concluded that the reduced GB self-diffusion coefficient influences the densification much stronger than the increased driving force of densification does.

Figure 5

Logical sequence showing how the increasing GB segregation enthalpy (absolute value) affects a grain growth and b densification, and c the feedback from grain growth on densification and d the feedback from densification on grain growth. The up and down arrows represent the increase and decrease in a parameter, respectively, the symbol “Asterisk” marks the change that plays the dominant role, and the symbols “Question mark” marks that the parameter change is not sure. The meanings of these symbols always apply throughout this article

As the sintering proceeds, the feedback between grain growth and densification must be considered. Since the densification rate is inversely proportional to the biquadrate of grain radius [cf. Eq. (19)], the grain growth will suppress the densification process (Fig. 5c). With progressing the densification (Fig. 5d), thermodynamically, a decreased driving force of grain growth is predicted due to its dependence on ρ (Fig. 3a and Fig. S3a in Supplementary materials III), and kinetically, an increased pore mobility and a decreased GB-pore density (N/A _GB) would be expected due to their relationships with ρ (see the description regarding Fig. S3 in Supplementary materials III), thus weakening the pore drag and enhancing the GB mobility. This is not consistent with the evolution of GB mobility with ρ (Figs. S1f and S3f in Supplementary materials III). On this basis, we put our attentions upon the change of GB mobility with respect to segregation enthalpy, i.e., an initially decreased but later increased GB mobility with the increase of ΔH ^GB_seg (the absolute value) (Figs. S1f and S3f in Supplementary Materials III), arising from a transition of GB mobility-dominant factor from the intrinsic and solute drag (directly from ΔH ^GB_seg ) to the pore drag (indirectly from densification).

As ΔH ^GB_seg increases, the always retarded grain growth upon sintering (Fig. 4a) is thus explained as follows. The direct action of ΔH ^GB_seg , decreasing both the driving force of grain growth and the GB mobility (Fig. 5a), governs the initial stage of grain growth and, together with the feedback from densification that decreases the driving force but increases the GB mobility (Fig. 5d), affects the later stage. The initially suppressed but later accelerated densification with increasing ΔH ^GB_seg (the absolute value) (Fig. 4b) implies a transition from the direct action of ΔH ^GB_seg (enhancing the driving force of densification but reducing the GB self-diffusion coefficient more) (Fig. 5b) to the feedback from grain growth (Fig. 5c). Clearly, both the suppressed grain growth and the enhanced densification (except for the initial stage) contribute positively to the sintering, thus leading to the promoted sintering behavior (Fig. 4c).

Surface segregation enthalpy

Following the GB segregation, the evolution of R and ρ over t and the trajectory of R versus ρ for ΔH ^s_seg (= −20, −40, and −60 kJ mol⁻¹) at ΔH ^GB_seg  = −40 kJ mol⁻¹ and D ^GB_B0  = 0.02D _GB0 are calculated and shown in Fig. 6. With increasing ΔH ^s_seg (the absolute value), both the grain growth and the densification are initially suppressed but later accelerated (Fig. 6a, b), while a promoted sintering behavior (Fig. 6c) is observed; see Figs. S4–S7 in Supplementary Materials III.

Figure 6

a Grain radius and b relative density as a function of time, and c trajectory of grain radius versus relative density at T = 1300 °C and x _B = 0.001 for different values of surface segregation enthalpy (ΔH ^s_seg  = −20, −40, −60 kJ mol⁻¹) with the model parameters of ΔH ^GB_seg  = −40 kJ mol⁻¹ and D ^GB_B0  = 0.02D _GB0

Dopant-cation GB diffusion

Analogous to section “GB segregation enthalpy,” the evolution of R and ρ over t and the trajectory of R versus ρ for D ^GB_B0 (= 0.05D _GB0, 0.02D _GB0, 0.01D _GB0, corresponding to the cases of relative weak, moderate and strong solute drag effect) at ΔH ^GB_seg  = ΔH ^s_seg  = −40 kJ mol⁻¹, are calculated and shown in Fig. 7. With decreasing D ^GB_B0 , a reduction of R is observed at the initial stage, followed by its increase at the later stage (Fig. 7a), exhibiting an accelerated grain growth behavior (except for the initial stage). For densification, a higher ρ is attained at a smaller D ^GB_B0 (Fig. 7b). Accordingly, a displacement of R versus ρ trajectory to smaller R for a given ρ is exhibited (Fig. 7c), indicating a promotion of sintering behavior, see Figs. S8–S10 in Supplementary Materials III.

Figure 7

a Grain radius and b relative density as a function of time, and c trajectory of grain radius versus relative density, at T = 1300 °C and x _B = 0.001 for different values of the GB diffusion coefficient of dopant cation (D ^GB_B0  = 0.05D _GB0, 0.02D _GB0, 0.01D _GB0) with the model parameters of ΔH ^GB_seg  = ΔH ^s_seg  = −40 kJ mol⁻¹

Accordingly, it is concluded that the dopant with a more negative GB (or surface) segregation enthalpy or a lower GB diffusion coefficient can achieve a higher relative density at the same grain size. This confirms our viewpoint that dopants play a role in stabilizing the microstructure of ceramics, and moreover, this enhanced stabilization caused by more negative GB (or surface) segregation enthalpy or lower dopant-cation GB diffusivity seems analogous to that in nano-scale alloys caused by more negative GB segregation enthalpy or slower solute diffusivity; see section “Enhanced thermo-kinetic effects due to oversized dopant cation.”

Application and discussions

Model application in sintering of doped alumina

The final-stage of sintering of Al₂O₃ doped with 1000 ppm Y₂O₃ or La₂O₃ was investigated at 1350 °C [4]. Accordingly, the trajectory of grain size to relative density during this isothermal process was recorded, as shown in Fig. 8. Obviously, the addition of La₂O₃ brought about a smaller grain size at the same relative density compared to that of Y₂O₃.

Figure 8

Comparison between the model calculation and the experimental result for the trajectory of grain radius to relative density in yttria- or lanthana-doped alumina annealed at 1350 °C

Before applying the model, it is necessary to determine the fitting parameters; see Supplementary materials IV. Applying the segregation enthalpy (for both GB and surface segregation) and the dopant-cation GB diffusion coefficient (in the case of dilute limit of solution) as the fitting parameters, the current model is used to describe well the evolution of grain radius with relative density for Al₂O₃ individually doped with 1000 ppm Y₂O₃ and La₂O₃ (Fig. 8). For Y³⁺ (La³⁺) doping, the segregation enthalpy and the dopant-cation GB diffusion coefficient (in the case of dilute solution limit) are fitted to be −56.3 ± 0.2 kJ mol⁻¹ and −60.8 ± 0.2 kJ mol⁻¹; and (0.102 ± 0.003)·D _GB0 and 0.078 ± 0.003)·D _GB0 for yttria and lanthana, respectively. La³⁺ doping corresponds to a more negative segregation enthalpy and a slower GB diffusion coefficient as compared to the Y³⁺ doping, consistently with the correspondingly promoted sintering behavior. Furthermore, we performed the fitting using three parameters (i.e., ΔH ^GB_seg , ΔH ^s_seg and D ^GB_B0 ) and also obtained good agreement between the model and the experiment; see Supplementary materials IV. For the La³⁺ (Y³⁺) doping, we note there is certain difference between the fittings using two and three parameters; however, the relative contrast between the two cases of doping always holds, that is, the promoted sintering behavior is always consistent with the increased segregation enthalpy (absolute value) and the decreased dopant-cation GB diffusion coefficient, irrespective of using two- or three-parameter fitting.

While the model is well-behaved in the tested experimental data, this is hardly a full proof of credibility and universal applicability. From the point view of modeling, while the theoretical framework used here, i.e., TEP was certainly demonstrated to be applicable for describing dynamic processes involved in material science, the model itself is limited by system constrains used in the model development, such as GB-diffusion-mediated pore shrinkage and surface-diffusion-mediated pore migration. Although such mechanisms have previously been shown to account for a number of the real situations, these are certainly not overreaching mechanisms.

Enhanced thermo-kinetic effects due to oversized dopant cation

As is well known, the segregation tendency and diffusion of solute atoms would be closely associated with the misfit strain due to their introduction into the solvent matrix. Generally, the segregation enthalpy (absolute value) and the work required to overcome the diffusion barrier for large atoms are thought to greatly exceed those of small atoms [49], as a result of large strain energy. Moreover, for ionic compounds, the electrostatic interaction between the dopant cation and the host space charge layer exerts an additional force on itself and then impacts its diffusion and segregation process. In the case of isovalent doping, however, the effect of electrostatic interaction is minimized [13], so that the cationic radius mismatch would play the dominant role. As such, the cationic radius of the dopant would probably become the determining factor influencing its segregation and diffusion.

Thermodynamically, the dopant acts in sintering through a concurrent segregation of its cation to GBs and free surfaces to reduce the GB energy and the surface energy. That is to say, the dopants play a role in stabilizing the microstructure of sintering compacts, which is similar to the case of nanocrystalline alloys [59], where the thermal stability of the system is improved due to the reduced GB energy by segregation of solute atoms to the GBs. Actually, this similarity originates from an intrinsic correlation of thermodynamics and kinetics, that is, the smaller driving force (caused by more negative segregation enthalpy) and the higher activation energy (caused by lower dopant-cation/solute diffusivity) are correlated with each other. A summary of this concept is described in Supplementary materials V.

Therefore, it is inferred that isovalent dopant cations having a larger ionic radius would be able to produce a more negative segregation enthalpy and a slower GB diffusion coefficient in the host, thus promoting the sintering behavior. This is consistent with the situation presented in section “Model application in sintering of doped alumina,” where compared with Y³⁺, La³⁺, which has larger radius, exhibits a promoted sintering behavior, with more negative GB- and surface-segregation enthalpies and lower GB diffusion coefficient. We believe this conclusion would also apply to other ionic systems besides alumina and may be considered as a guideline for selection of the dopant species.

Conclusion

The main conclusions can be summarized as follows:

• 1. Applying the thermodynamic extremal principle, the evolution equations, for the grain size and the relative density in the final-stage of sintering of doped ceramics were derived with segregation-dependent interface energy and diffusivity/mobility. The mutual interaction between grain growth and densification was considered, and essentially depends on the driving forces of the concurrent processes: the surface energy contributes positively to the driving force of grain growth while the GB energy negatively to the driving force of densification.

• 2. Increased GB (or surface) segregation enthalpy and/or decreased GB diffusion coefficient of dopant cation leads to a promoted sintering behavior in Al₂O₃ system, i.e., a higher relative density at the same grain size, due to enhanced thermodynamic and/or kinetic effect.

• 3. As compared with the doping of Y₂O₃, the significantly enhanced sintering behavior by La₂O₃ is consistent with the more negative GB- and surface-segregation enthalpies and the slower dopant-cation GB diffusion coefficient. This suggests that an isovalent dopant with a larger cationic radius presents a more negative segregation enthalpy and a lower GB diffusion coefficient, which can be considered as a guideline for selecting the dopant species for targeting full dense, nanocrystalline or ultrafine-grained ceramics.