Abstract
Calculations of acidities of molecules with multiple tautomeric and/or conformational states require adequate treatment of the relative energetics of accessible states accompanied by a statistical-mechanical formulation of their contribution to the macroscopic pKa value. Here, we demonstrate rigorously the formal equivalence of two such approaches: a partition function treatment and statistics over transitions between molecular tautomeric and conformational states in the limit of a theory that does not require adjustment by empirical parameters correcting energetic values. However, for a frequently employed correction scheme, linear scaling of (free) energies and regression with respect to reference data taking an additive constant into account, this equivalence breaks down if more than one acid or base state is involved. The consequences of the resulting inconsistency are discussed on our datasets developed for aqueous pKa predictions during the recent SAMPL6 challenge, where molecular state energetics were computed based on the “embedded cluster reference interaction site model” (EC-RISM). This method couples integral equation theory as a solvation model to quantum-chemical calculations and yielded a test set root mean square error of 1.1 pK units from a partition function ansatz. For all practical purposes, the present results indicate that a state transition approach yields comparable accuracy despite the formal theoretical inconsistency, and that an additive regression intercept, which is strictly constant in the limit of large compound mass only, is a valid approximation.

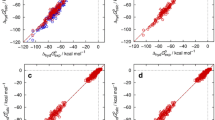
Embedded cluster reference interaction site model-derived vs. experimental pKa for the test set calculated with either the partition function (blue) or the state transition approach (red), using m as a free parameter
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Calculations of acidity constants, Ka, are important not only for practical purposes but also serve as important benchmarks for testing solvation models used in conjunction with quantum-chemical calculations, particularly in an aqueous environment [1]. Without loss of generality, and specializing to water as a solvent, the constitutive reaction equation
is characterized thermodynamically by the relation between equilibrium constant, activities a, standard Gibbs energy of reaction ΔrG0 and standard chemical potentials μ0 via
where β is an inverse temperature. The standard chemical potentials in solution are commonly referenced to a standard state of 1 bar and a formal concentration of c0 = 1 M at the specified temperature (hereinafter assumed to be 298.15 K) under the assumption of infinite dilution.
Quantum calculations of these quantities, for instance by employing a continuum solvation approach, usually model such an ideal solution state by construction, approximating the standard chemical potential of a compound i in a given, fixed conformational and tautomeric state j, for instance, by [2,3,4,5].
It is given by the sum of an ideal (“id”) part, which contains the explicit reference to the standard concentration to be specified below, and an interaction component, termed \( {G}_j^0(i) \) here. The latter can be approximated by adding an electronic energy in solution, \( {E}_j^{0,\mathrm{sol}}(i) \), an excess chemical potential, \( {\mu}_j^{0,\mathrm{ex}}(i) \), that represents the Gibbs energy of solvation upon transferring a solute in the “frozen” structural and electronic solution state from the (ideal) gas phase into the solvent (assuming identical formal gas and solution phase concentrations), and potentially a “rigid rotor, harmonic oscillator” (RRHO) model of rotational and vibrational contributions to the Gibbs energy. As the standard condition of infinite dilution is implicitly assumed by constructing the Hamiltonian, the superscript “0” at the interaction terms \( {G}_j^0(i) \) can be dropped for simplicity.
For treating multistate species comprising an ensemble of distinct tautomeric and conformational states, two strategies are available. One approach is to sum over states by defining, in a more or less ad hoc manner, a canonical partition function while ignoring pressure-volume contributions [3,4,5], to end up for the protonation equilibrium with
where we sum over M base and N acid states. The fourth term on the right hand side (r.h.s.) represents the Gibbs energy of hydration of the “proton” (again assuming identical gas phase and solution state concentrations) [6, 7] and otherwise only ideal terms that are usually assumed to be an additive constant. Therefore, on the decadic pK scale we finally obtain the expression for the partition function (PF) approach,
with
where the terms assumed to be constant in total (i.e., ideal gas and proton) are contained in b and, additionally, computational flexibility is offered by introducing a parameter m, which, ideally, is 1. The parameters m and b are typically adjusted by fitting to experimental reference data, as was done by us [3, 4, 8] and others [5, 9, 10] (the latter reference also representing an early example of a PF-type treatment), to name just a few.
The alternative is to connect all base and acid states by individual transition equilibria as
for which straightforward reduction of Eq. (5) would give
The individual state-to-state equilibrium constants can then be assembled to yield the macroscopic form from mass balance,
as [11].
where “ST” denotes the state transition approach. Here, in contrast to the analysis by Bochevarov et al. [11], who distinguish between “micro- “(i.e., tautomeric) and “nano- “(i.e., conformational) states, which leads to another layer in the continued fraction expansion, we need no such discrimination as the concepts of tautomers and (underlying) conformers is purely semantic, though pragmatically useful for certain models [11]. Physically, tautomers and conformers for a certain ionization state refer to different local minima of the (free) energy surface derived from one and the same molecular Hamiltonian, whereas the Hamiltonians of acid and base forms differ. Hence, we simply refer to “states” between which transitions can occur in the equilibrium mixture.
Though plausible, as the information content of both the PF and the ST approaches in terms of the state-specific Gibbs energies is identical, it is not immediately obvious under which circumstances both methods yield identical results. The goal of the present work was therefore to elucidate the formal equivalence both analytically and numerically. As will be shown below, both methods agree only in the limiting cases of a regression “slope” parameter m being exactly 1, i.e., for ideal (and usually inapplicable) models that do not require any form of empirical scaling of energies, or, trivially, in situation where only single acid and base states are considered. Numerically, this conclusion will be illustrated and discussed by re-analysis of our previous results obtained during the recent SAMPL6 (“Statistical Assessment of the Modeling of Proteins and Ligands”) challenge [4, 12] on blindly predicting aqueous pKa values for a number of kinase inhibitor fragments with multiple protonation states and considerable conformational flexibility.
Theory
Formal correspondence of the PF and ST approaches can be proved if the mass balance equation leading to the continued fraction representation (10) can be derived on the same statistical-mechanical footing as Eq. (5) and its reduction to Eq. (8). We therefore start with the fundamental expression for the chemical potential of a molecule (omitting index i for notational simplicity) composed of distinct states j such that the approximation (3) and the assumption of negligible pressure-volume work hold,
Here, G is the excess (interaction) part of the total chemical potential as in Eq. (3), V represents the volume, NM is the number of solute molecules which is 1 at infinite dilution, Z is the partition function, and Λ denotes the thermal wavelength given by
with molecular mass mM and Planck’s constant h. The statistical-mechanical chemical potential should be equivalent to the macroscopic thermodynamic definition
with total solute concentration c, split into state contributions cj according to mass balance, and activity coefficients γj that approach 1 at infinite dilution. By noting that the probability of a state j can be written as
where we inserted 1 = c0/c0, and inserting 1 = ∑jpj as denominator in G of Eq. (11) we have
We recover the concentration dependence of (13) as the last term on the r.h.s., and the standard chemical potential therefore becomes
which, by also noting that c → 1/V at infinite dilution, finally yields
For the protonation equilibrium in the partition function derivation we then ultimately find from inserting the expressions for the standard chemical potential for the reacting species into Eq. (2) and taking the negative decadic logarithm
Comparison with Eq. (5) shows that both relations are equivalent (for m = 1), showing that mass balance leads directly to the partition function approach. It is, however, important to note that the regression intercept b, i.e., the sum of the first two terms in the latter equation is actually not a constant as it depends not only on the mass of proton but also on the mass ratio of acid and base forms via the thermal wavelengths, though not on the particular state. Unless the mass-dependent terms are grouped with the Boltzmann factors the intercept can be interpreted as essentially constant only in the limit of much larger molecular mass of the compound compared to the proton, which, however, holds true in most situations. In this limit, the first term becomes −4.39 kcal mol−1 (see also [13]) compared to the much larger Tissandier value for the Gibbs solvation energy of the proton of −265.89 kcal mol−1 [6] (assuming identical gas and solution phase concentrations). For, e.g., HF, the first quantity would change by 7.5%, corresponding to ca. 0.24 pK units. Very accurate calculations should, therefore, take this effect into account. Note that this result holds not only within the quantum-statistical formalism invoked for the chemical potential, but also in a classical framework, where integration over momentum space yields the identical dependence of the standard chemical potential on molecular mass and standard concentration (see Eq. (8) in [14]).
To close the proof of equivalence, mass balance also leads to the continued fraction expansion (10) where Eq. (8) can be inserted to show under which conditions Eqs. (5) and (18) arise. Mass balance according to Eq. (9) for the protonation equilibrium readily leads to the continued fraction expansion (10) as derived in [11]. Rewriting Eq. (8) on the energy scale and inserting into (10) yields
In the innermost sum, the j-dependent denominator is constant for all k such that we obtain
in the ST form. In contrast, the corresponding PF result derived from Eq. (5) reads
which clearly shows that both expressions can only be identical if either m = 1 for multistate mixtures or if only one state per acid and base form exists while b is unaffected.
Numerical illustration
To demonstrate the effect of slope parameters m ≠ 1 on the relative performance of both the PF and ST models for a realistic prediction problem, here we re-analyze training and test set data obtained during the SAMPL6 challenge [4], where the PF model was employed exclusively. Briefly, we tested EC-RISM [2] theory for treating aqueous solvation in conjunction with quantum-chemical calculations, and were able to show that root mean square errors (RMSE) of ca. 1.0 pK units could be achieved for a well-known training set [15]. About the same error (1.1 pK units) was obtained for the independent test set composed of kinase inhibitor fragments, whose microstates were provided as part of the SAMPL6 challenge where the task was to blindly predict their pKa values. The challenge was explicitly designed to cover molecules with multiple protonation sites, ionization states, and high conformational freedom, which necessitated adequate conformational sampling based on a large reference set of tautomers provided by the organizers. It is therefore not immediately clear that the PF and the ST approaches should perform similarly, as a non-unity slope together with large state ensembles suggests discrepancies (see derivation and discussion above).
We confine our re-analysis to the best-performing quantum-chemical level of theory and solvation model, termed “MP2/6-311+G(d,p)/φopt/copt2” in [4], where we used the two best-ranked conformations per tautomeric state (“copt2”) with an optimized model to compute electrostatic solute-solvent interactions (“φopt”) in combination with the 6-311+G(d,p) basis set within MP2 calculations. As a consistency check, besides the “2par” regression models (m and b variable), we additionally tested the PF and the ST models with a fixed slope of m = 1 (“1par”), not only to demonstrate the resulting equivalence, but also to analyze the impact on predictive performance. All statistical regression and metrics data are found in Tables 1 (training set) and 2 (test set), while the individual correlations of calculated and experimental data for the various methods are depicted in Fig. 1. Note that, unlike the linear regression problem of the PF approach, the ST model requires nonlinear optimization of a loss function defined by the sum of squared residuals.
Embedded cluster reference interaction site model (EC-RISM-)derived vs. experimental pKa for training [15] (top row) and test set [4] (bottom row) calculated with either the partition function (PF; blue) or the state transition (ST) approach (red, mostly overlaying blue symbols). The charge state of the molecular species involved in the transition is reflected by different symbols: squares acids (training set)/anionic transition (test set), triangles bases (training set)/cationic transition (test set). Anionic and cationic refer to the sum over the charges of all species involved in a reaction which is negative or positive, respectively. Pairs of calculated and experimental data points are collected in Online Resource 1, raw data underlying the regression analysis was taken from Online Resources to [4]. a, c using m as a free parameter and b, d: using a fixed m = 1.
Training both models in 1par and 2par variants showed the expected results. While the trained parameters and the resulting statistical metrics are identical in the 1par case, as mathematically required, there is a small but almost negligible difference in the results for the 2par models, which is mainly a result of the limited amount of tautomeric and conformational freedom in the training data set (see Online Resources in [4]). The same holds true when applying the trained models to the test dataset from the SAMPL6 challenge. Despite the drastically differing diversity, the results are in line with the results from the training set. One has to keep in mind, though, that the 1par models are substantially inferior regarding performance (training set), and even more so in terms of predictivity (test set), which emphasizes the importance of scaling (free) energies by the slope parameter. Surprisingly, since the differences between PF and ST models are so small, it is in practice almost irrelevant which approach is preferred for acidity predictions.
Concluding remarks
In summary, we addressed a conceptual problem for practical pKa calculations that results from the necessity to include an energy scaling parameter m into the prediction model that is typically adjusted empirically. To this end, we derived the rigorous statistical-mechanical expressions for the acidity constants for two variants of multistate calculations, which revealed the source of an inconsistency when used within regression analysis.
From a mathematical perspective, the issue boils down to the inequality (x + y)m ≠ xm + ym for arbitrary m ≠ 1 where x and y represent non-zero Boltzmann factors of different tautomeric or conformational states of a given molecule. This finding is an example of a case in which formal equivalence of two approaches does not necessarily translate into equivalence in practical applications where numerical model adjustments turn out to be necessary. One might have expected significant differences between the partition function (l.h.s.) and the state transition (r.h.s.) approaches as the regression results indicate significant deviations from 1. However, for the training set the largest difference between PF and ST results is on the order of 0.1 pK units with our slope parameter of 0.74. Even with a smaller m of 0.5, this difference would not exceed approximately 0.2 pK units. This means that both models are quantitatively very similar for practical purposes, at least as long as a sufficiently accurate methodology is applied as in this work, and there is no obvious reason to prefer one method over the other.
Another result of the rigorous derivation was that the regression constant is actually variable, though with limited, and, in practice, mostly negligible range, as it depends, strictly speaking, on the mass ratio between acid and base form, which approaches unity only in the limit of large molecules. Taken together, these findings could be useful to the community as they clarify potential sources of controversy.
References
Alongi KS, Shields GC (2010) Theoretical calculations of acid dissociation constants: a review article. Ann Rep Comput Chem 6:113–138
Kloss T, Heil J, Kast SM (2008) Quantum chemistry in solution by combining 3D integral equation theory with a cluster embedding approach. J Phys Chem B 112:4337–4343
Tielker N, Tomazic D, Heil J, Kloss T, Ehrhart S, Güssregen S, Schmidt KF, Kast SM (2016) The SAMPL5 challenge for embedded-cluster integral equation theory: solvation free energies, aqueous pK a, and cyclohexane–water log D. J Comput Aided Mol Des 30:1035–1044
Tielker N, Eberlein L, Güssregen S, Kast SM (2018) The SAMPL6 challenge on predicting aqueous pK a values from EC-RISM theory. J Comput Aided Mol Des 32:1151–1163
Pracht P, Wilcken R, Udvarhelyi A, Rodde S, Grimme S (2018) High accuracy quantum-chemistry-based calculation and blind prediction of macroscopic pK a values in the context of the SAMPL6 challenge. J Comput Aided Mol Des 32:1139–1149
Tissandier MD, Cowen KA, Feng AY, Gundlach E, Cohen MH, Earhart AD, Coe JV (1998) The Proton’s absolute aqueous enthalpy and Gibbs free energy of solvation from cluster-ion solvation data. J Phys Chem A 102:7787–7794
Zhang H, Jiang Y, Yan H, Cui Z, Chunhua Y (2017) Comparative assessment of computational methods for free energy calculations of ionic hydration. J Chem Inf Model 57:2763–2775
Heil J, Tomazic D, Egbers S, Kast SM (2014) Acidity in DMSO from the embedded cluster integral equation quantum solvation model. J Mol Model 20:2161
Klamt A, Eckert F, Diedenhofen M, Beck ME (2003) First principles calculations of aqueous pK a values for organic and inorganic acids using COSMO-RS reveal an inconsistency in the slope of the pK a scale. J Phys Chem A 107:9380–9386
Beck ME, Bürger T (2003) Predicting acidity for agrochemicals. In: Ford M, Livingstone D, Dearden J, Van deWaterbeemd H (eds) Euro-QSAR 2002: designing drugs and crop protectants. Blackwell, Oxford, pp 446–450
Bochevarov AD, Watson MA, Greenwood JR (2016) Multiconformation, density functional theory-based pK a prediction in application to large, flexible organic molecules with diverse functional groups. J Chem Theory Comput 12:6001–6019
https://drugdesigndata.org/about/sampl6. Accessed 13 February 2019; see also special issue of J Comput Aided Mol Design (2018) 32(10)
Rebollar-Zepeda A, Galano A (2016) Quantum mechanical based approaches for predicting pK a values of carboxylic acids: evaluating the performance of different strategies. RSC Adv 6:112057
Gilson MK, Given JA, Bush BL, McCammon JA (1997) The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys J 72:1047–1069
Klicić JJ, Friesner RA, Liu SY, Guida WC (2002) Accurate prediction of acidity constants in aqueous solution via density functional theory and self-consistent reaction field methods. J Phys Chem A 106:1327–1335
Acknowledgments
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2033 – Projektnummer 390677874, and under the Research Unit FOR 1979. We also thank the IT and Media Center (ITMC) of the TU Dortmund for computational support and, of course, Tim Clark for the continuous fruitful collaborations and discussions over the years.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper belongs to the Topical Collection Tim Clark 70th Birthday Festschrift
Rights and permissions
About this article
Cite this article
Tielker, N., Eberlein, L., Chodun, C. et al. pKa calculations for tautomerizable and conformationally flexible molecules: partition function vs. state transition approach. J Mol Model 25, 139 (2019). https://doi.org/10.1007/s00894-019-4033-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00894-019-4033-4