Introduction

Fungi are highly resistant organisms responsible for many kinds of diseases. Most are resistant to the action of antimicrobial drugs. Recently, the frequency of systemic infections has increased dramatically along with the number of invasive, mostly opportunistic, fungal species carrying infectious diseases. Fungal infections are important causes of morbidity and mortality in hospitalized patients [1]. None of the existing systemic antifungals satisfies the medical need completely; there are weaknesses in spectrum, potency, safety, pharmacokinetic properties, etc.

Infections due to Candida species are the most common of the fungal diseases [2]. Candida species produce a broad range of infections, ranging from nonlife-threatening muco–cutaneous illnesses to invasive processes that may involve virtually any organ [3]. Few substances have been discovered that exert an inhibitory effect on the fungi pathogenic for man, and most of these are relatively toxic [4]. Many effective antimicrobial drugs possess heterocyclic systems in their structure, like imidazoles [5], quinazolines [6], benzazoles [7–9] and oxazolo(4,5-b)pyridines [10].

Computer simulation techniques potentially offer a further means to probe structure–activity relationships. Quantitative structure–activity relationships (QSAR) represent the most effective computational approaches in drug design [11]. Several reports of QSAR studies over antifungal compounds have been developed in the last years. Yalcin and co-workers [12] correlated structural indicator parameters and physicochemical properties with growth inhibitory activity against Candida albicans for heterocyclic ring derivatives. The molecular topology formalism was applied for García-Domenech and co-workers to search of QSAR relations for a group of substituted carbazoles, furans and bezimidazoles [13]. Hasegawa and co-workers [14] obtained a neural network model for a small data set of antifungal azoxy derivatives employing physicochemical parameters. Neural network analysis was also employed by Mghazli and co-workers [15] for constructing QSAR models of relationships between structure and antifungal activity of substituted imidazoles.

In the present work, we treated a set of 96 heterocyclic ring derivatives (Fig. 1): 2,5,6-trisubstituted benzoxazoles, 2,5-disubstituted benzimidazoles, 2-substituted benzothiazoles and 2-substituted oxazolo(4,5-b)pyridines both with multiple linear regression (MLR) and Bayesian-regularized artificial neural network (BRANN) analysis [16]. Three-dimensional molecular descriptors were used for encoding the structural information of the compounds studied. Optimum variable subsets of six descriptors were selected using linear and nonlinear genetic algorithm (GA) searches. Both MLR and BRANN techniques were used for modeling the observed antifungal activity of the training set (80 compounds). The adequacy of the models was examined by means of their statistic significances, the statistic of the leave-one-out (LOO) cross-validation and the prediction of a test set (16 compounds), which represent 1/6 of the total data set. In addition, the capacity of the selected variables to differentiate the data was evaluated by means of the unsupervised training of a Kohonen self-organizing neural network (KNN).

Fig. 1
figure 1

General structure of heterocyclic ring derivatives

Full size image

Materials and methods

Dataset: source and prior preparation

The in vitro inhibitory activities against Candida albicans (log(1/C); C = minimum inhibition concentration expressed in M), of 96 heterocyclic ring derivatives were collected from two previous reports [9, 12]. A twofold serial dilution technique was employed to carry out the activity assays. The chemical structures along with experimental antifungal activity data of the compounds used in this study are shown in Table 1.

Table 1 Structures and in vitro antifungal activities of the analyzed compounds against C. albicans
Full size table

Geometry optimization calculations for each compound of this study were carried out using the quantum chemical semiempirical method PM3 [17] included in Mopac 6.0 [18].

Molecular descriptors

The 3D descriptors from the Dragon software [19, 20] were calculated for each compound: aromacity indices [21, 22], randic molecular profiles [23], geometrical descriptors [20], RDF descriptors [24], 3D-MoRSE descriptors [25], WHIM descriptors [26] and GETAWAY descriptors [27]. In total, 721 descriptors were calculated. Descriptors that stayed constant or almost constant were eliminated and pairs of variables with a correlation coefficient greater than 0.95 were classified as intercorrelated, and only one of these was included in the model. Finally, 322 descriptors were obtained.

Selection of training and test sets

The k-means cluster analysis (k-MCA) was used to divide the entire data in two subsets [28] (training and test sets) so that general characteristics appear in both sets. To ensure a statistically acceptable data partition into several clusters, we took into account the number of members and the standard deviation of the variables in each cluster (as low as possible). The quality of the model was determined by examining the standard deviation between and within clusters, the respective Fisher ratio and their P level of significance.

Particular characteristics of all compounds are represented in each cluster derived from k-MCA. Selection was carried out by taking, in a random way, compounds belonging to each cluster. Finally, the data was divided: 16 compounds were selected for the test set and the 80 remaining compounds were incorporated to the training set.

GA variable selection

We used both linear and nonlinear modeling of the antifungal activity of some heterocyclic ring derivatives. Since 322 molecular descriptors were available for the QSAR analysis and only a subset of them is statistically significant in terms of correlation with biological activities, deriving an optimal QSAR model through variable selection must be addressed. Six variables are adequate for an 80-target model. In this sense, feature selection approaches were carried out by means of a GA [29] in such a way that optimum linear and neural network models are obtained.

Genetic algorithm is a class of methods based on biological evolution rules. The first step is to create a population of linear regression models. These regression models mate with each other, mutate, crossover, reproduce and then evolve through successive generations toward an optimum solution. The distinctive aspect of a GA is that it investigates many possible solutions simultaneously, each of which explores different regions in parameter space [24].

The GA implemented in this paper is a version of the So and Karplus report [30] and was programmed within the Matlab environment using the GA and neural network toolboxes [31]. Inside the GA framework, we implemented two routines, one to select optimum subsets of six variables for multivariate linear regression of the activity (MLR–GA) and another for neural network training using six variables as BRANN inputs and the antifungal activity as target outputs (BRANN–GA).

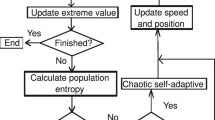
An individual in the population is represented by a string of integers that indicate the numbering of the columns in the data matrix. In the original study, the fitness of the individual was determined by a variety of fitness functions proportional to the residual error of the training set, the test set, or even the cross-validation set from the neural network simulations. In our approach, we tried the MSE of data fitting for linear and BRANN models, as the case may be, as the individual fitness function. The basic design of the implemented GA is summarized in the flow diagram shown in Fig. 2. The first step is to create a gene pool (population) of N individuals. Each individual encodes the same number of descriptors; the descriptors are chosen randomly from a common data matrix, and in a way such that (1) no two individuals can have exactly the same set of descriptors and (2) all descriptors in a given individual must be different. The fitness of each individual in this generation is determined by the MSE of the model and scaled using a scaling function. A top scaling fitness function scaled a top fraction of the individuals in an equal population; these individuals have the same probability to be reproduced while the rest are assigned the value 0 [32].

Fig. 2
figure 2

Flow diagram describing the strategy for the genetic algorithm. See Fig. 3 for the detailed descriptions of the reproduction strategy

Full size image

In the next step, a fraction of children of the next generation is produced by crossover (crossover children) and the rest by mutation (mutation children) from the parents. Sexual and asexual reproductions take place so that the new offspring contains characteristics from two or one of its parents (Fig. 3). In a sexual reproduction, two individuals are selected probabilistically on the basis of their scaled fitness scores and serve as parents. Next, in a crossover, each parent contributes a random selection of half of its descriptor set and a child is constructed by combining these two halves of the “genetic code.” Finally, the rest of the individuals in the new generation are obtained by asexual reproduction when parents selected randomly are subjected to a random mutation in one of its genes, i.e., one descriptor is replaced by another.

Fig. 3
figure 3

Schematic diagram describing the reproduction strategy in GA algorithm

Full size image

Similarly to So and Karplus [30], we also included elitism, which protects the fittest individual in any given generation from crossover or mutation during reproduction. The genetic content of this individual simply moves on to the next generation intact. This selection, crossover and mutation process is repeated until all of the N parents in the population are replaced by their children [32]. The fitness score of each member of this new generation is again evaluated, and the reproductive cycle is continued until a 90% of the generations showed the same target fitness score [33].

Multiple linear regression

This method was used to generate a six-variable linear model between the antifungal activity (log(1/C)) and the selected molecular descriptors. The validity of the model was proven by the square multiple correlation coefficient (r 2), the standard deviation (s) and the F test value.

Bayesian-regularized artificial neural network

In contrast to common statistical methods, artificial neural networks (ANNs) are not restricted to linear correlations or linear subspaces [34]. They can take into account nonlinear structures and structures of arbitrarily shaped clusters or curved manifolds. As biological phenomena are considered nonlinear by nature, the ANN technique was used in order to discover the possible existence of nonlinear relationships between antifungal activity and molecular descriptors that are ignored for the linear model.

When parameters (weights and biases) increase, the network loses its ability to generalize. The error on the training set is driven to a very small value, but when new data is presented to the network the error is large. The predictor has memorized the training examples, but it has not learned to generalize to new situations; the network overfits the data.

Typically, training aims to reduce the sum of squared errors:

$$F = {\rm MSE} = \frac{1}{N}{\sum\limits_{i = 1}^N {(Y_{i} - A_{i})^{2}}}$$
(1)

Bayesian regularization involves modifying the performance function (F). It is possible to improve generalization by adding an additional term [16].

$$F = \beta \times {\rm MSE} + \alpha \times {\rm MSW}$$
(2)
$${\rm MSW} = \frac{1}{n}{\sum\limits_{j = 1}^n {w^{2}_{j}}}$$
(3)

In these equations, F is the network performance function, MSE is the mean of the sum of squares of the network errors, N is the number of compounds, Y i is the predicted biological activity of the compound, i,A i is the experimental biological activity of the compound, i, MSW is the mean of the sum of the squares of the network weights, w j are the weights of the neuron, j, n is the number of network weights and α and β are objective function parameters.

The relative size of the objective function parameters dictates the emphasis for training obtaining a smoother network response. MacKay’s Bayesian regularization automatically sets the correct values for the objective function parameters [16], in the sense that the regularization is optimized. In the Bayesian framework, the weights of the network are considered random variables. After the data is taken, the density function for the weights can be updated according to Bayes’ rule:

$$P(\left. w \right|D,\alpha, \beta, M) = \frac{{P(\left. D \right|w,\beta, M) \times P(\left. w \right|\alpha, M)}}{{P(\left. D \right|\alpha, \beta, M)}}$$
(4)

where D represents the data set, M is the particular neural network model used and w is the vector of network weights. P(w|D, α, β, M) is the posterior probability, that is the plausibility of a weight distribution considering the information of the data set in the model used. P(w|α, M) is the prior density, which represents our knowledge of the weights before any data is collected. P(D|w, β, M) is the likelihood function, which is the probability of the data occurring, given the weights. P(D|α β, M) is a normalization factor, which guarantees that the total probability is 1.

Considering that the noise in the training set data is Gaussian and that the prior distribution for the weights is Gaussian, the posterior probability fulfils the relation:

$$P(\left. w \right|D,\alpha, \beta, M) = \frac{1}{{Z_{F}}}\hbox{exp} (- F)$$
(5)

where Z F depends on objective function parameters. Thus, under this framework, minimization of F is identical to finding the (locally) most probable parameters [16].

Bayesian regularization overcomes the remaining deficiencies of neural networks [35]. Bayesian methods produce predictors that are robust and well matched to the data which make optimal predictions.

Model validation

The quality of the fit of the training set by a specific model was measured by its r 2,

$$r^{2}=1 - \frac{{{\sum\nolimits_{i=1}^N {(Y_{i} - A_{i})^{2}}}}}{{{\sum\nolimits_{i = 1}^N {(Y_{i} - \ifmmode\expandafter\bar\else\expandafter\=\fi{A})^{2}}}}}$$
(6)

where N is the number of compounds, Y i and A i are the predicted and experimental biological activities of i compound respectively, \(\ifmmode\expandafter\bar\else\expandafter\=\fi{A}_{i} \) is the average experimental activity.

However, a most important measure is the prediction quality of models. An internal LOO cross-validation process was carried out calculating q 2 and of LOO cross-validation. A data point is removed (left out) from the set, and the model refitted; the predicted value for that point is then compared to its actual value. This is repeated until each datum has been omitted once. The sum of squares of these deletion residuals can then be used to calculate q 2, an equivalent statistic to r 2.

$$q^{2} = 1 - \frac{{{\sum\nolimits_{i=1}^N {(Y_{i} - A_{i})^{2}}}}}{{{\sum\nolimits_{i=1}^N {(Y_{i} - \ifmmode\expandafter\bar\else\expandafter\=\fi{A})^{2}}}}}$$
(7)

where N is the number of compounds, Y i and A i are the predicted and experimental biological activities of i left-out compound respectively, \(\ifmmode\expandafter\bar\else\expandafter\=\fi{A}_{i} \) is the average experimental activity of left-in compounds that are different to i.

The predictive power of the models was also measured by an external validation process that consists in predicting the activity of unknown compounds forming the test set. In this case r 2 of the test-set fitting is calculated.

Kohonen self-organizing neural network

KNN [36] has the special property of effectively creating a spatially organized internal representation of various features of input signals and their abstractions, following an unsupervised and competitive process. In a self-organizing neural network, the neurons are arranged in a 2D array to generate a 2D feature map such that similarity in the data is preserved. If two input data vectors are similar, they will be mapped into the same neuron or into neurons close together in the 2D map. Similar features in output vectors will be grouped if adequate variables are selected.

Learning in a self-organizing feature map occurs for one vector at a time. First the network identifies the winning neuron, then the weights of the winning neuron and the other neurons in its neighborhood are moved closer to the input vector at each learning step. The winning neuron’s weights are altered proportional to the learning rate. The weights of neurons in its neighborhood are altered proportional to half the learning rate. The learning rate and the neighborhood distance used to determine which neurons are in the winning neuron’s neighborhood are altered during training through two phases; an ordering phase that decreases the distances between neurons until the tuning neighborhood distance and the tuning phase that tunes the network, keeping the ordering learned in the previous phase.

Results and discussion

MLR analysis

MLR–GA analysis was performed on the training set selected by k-Means clustering described in Table 1. We included all 80 molecules of the training set for the model generation. After collecting the data, six parameters that give the “best” regression were selected by GA. The model is shown in Eq. 8

$$\begin{aligned} \hbox{log} \left (\frac{1}{C}\right) = & (4.533 \pm 0.228)\\ & \quad + (1.060 \pm 0.245)\hbox{\it Mor13v} \\ & \quad - (0.502 \pm 0.203)\hbox {\it Mor19v} \\ & \quad + (1.302 \pm 0.370)\hbox {\it Mor27v} \\ & \quad +(2.835 \pm 0.548)\hbox {\it Mor29v} \\ & \quad + (1.441 \pm 0.341)\hbox {\it H8u} \\ & \quad + (1.423 \pm 0.473)\hbox {\it H5m} \\ n=& 80\\ r^{2}=& 0.746 \\ s=& 0.115 \\ F=& 35.842 \\ \end{aligned} $$
(8.)

where n is the number of compounds included in the model, r 2 is the square correlation coefficient, s is the standard deviation of the regression and F is the Fisher ratio.

Equation 8 shows that the six descriptor model includes four Molecule Representation of Structures based on Electron diffraction (3D-MoRSE) descriptors (Mor13v, Mor19v, Mor27v and Mor29v) and two GETAWAY descriptors (H8u and H5m). It is noteworthy that there is no significant intercorrelation between these descriptors, as shown in Table 2. Table 3 shows statistic quantities for this model. Since the q 2 value was about 0.692, the model was considered to be a good predictive one, according to Wold [37] (q 2 >0.5). In addition, the external validation showed r 2 values for the test set of 0.780.

Table 2 Correlation matrix of the descriptors selected by linear GA
Full size table
Table 3 Statistic parameters of the linear and nonlinear models for the antifungal activity of the heterocyclic derivatives
Full size table

The 3D-MoRSE [25] code considers a molecular transform, derived from an equation used in electron diffraction studies. Electron diffraction does not yield atomic coordinates directly but provides diffraction patterns from which the atomic coordinates are derived by mathematical transformations. The 3D-MoRSE code is applied by Eq. 9:

$$I(s) = {\sum\limits_{i = 2}^N {{\sum\limits_{j = 2}^{i - 1} {A_{i} A_{j} \frac{{\sin sr_{{ij}}}}{{sr_{{ij}}}}}}}}$$
(9)

In this equation A i and A j are atomic properties of atoms i and j,r ij represents the interatomic distances and s measures the scattering angle. The value of s (0, ..., 31.0 Å−1) is considered only at discrete positions within a certain range. Values of Is) are defined at 32 evenly distributed values of s in the range of 0–31.0 Å−1 . These 32 values constitute the 3D-MoRSE code of the 3D structure of a molecule. Different atomic properties Ai were used, like atomic mass, atomic van der Waals volumes, residual atomic Sanderson electronegativities and atomic polarizabilities. The possibility for choosing an appropriate atomic property gives great flexibility to the 3D-MoRSE code for adapting it to the problem under investigation. In this work, 3D-MoRSE selected descriptors are weighted by atomic van der Waals volumes (Mor13v, Mor19v, Mor27v and Mor29v), this code can express the appropriate distribution of the size of the molecules for having a certain activity.

On the other hand, in Eq. 8 H8u and H5m descriptors belong to Geometry, Topology and Atom-Weight AssemblY [27] (GETAWAY) descriptors that are based on a molecular influence matrix (MIM) similar to that defined in statistics for regression diagnostics and calculated from the molecular matrix M as:

$${\rm MIM} = M \times (M^{T} \times M)^{{- 1}} \times M^{T} $$
(10)

GETAWAY descriptors match the 3D molecular geometry provided by the MIM and atom relatedness by molecular topology, with chemical information. The diagonal elements h ii of the MIM, called leverages, encode atomic information and represent the “influence” of each molecule atom in determining the whole shape of the molecule; in fact, mantle atoms always have higher h ii values than atoms near the molecule center. Each off-diagonal element h ij represents the degree of accessibility of the jth atom to interactions with the ith atom.

Specifically, H8u and H5m are H indices from H-GETAWAY descriptors based on Moreau-Brotto autocorrelation descriptors [38]. In such descriptors, geometrical information provided by leverage values is combined with atomic weightings, accounting for specific physicochemical properties of molecule atoms. H indices consider the MIM off-diagonal elements, which provide information on the degree of interaction between atom pairs, modifying the Moreau-Broto autocorrelations. H k (w) is defined as:

$$H_{k} (w) = {\sum\limits_{i = 1}^{A - 1} {{\sum\limits_{j > 1} {h_{{ij}} \times w_{i} \times w_{j} \times \delta (k;d_{{ij}} ;h_{{ij}})}}}}$$
(11)

where k (1, 2, ..., d) is the path length (lag) in the molecular graph, d ij is the topological distance between atoms i and j, while w i and w j are the A-dimensional property vector of the atoms i and j. The function δ (k; dij; hij) is a Dirac-delta function defined as

$$\delta = (k;d_{{ij}} ;k_{{ij}}) = {\left\{{\begin{array}{*{20}c} {{1\;{\rm if}\;d_{{ij}} \; = \;k\quad{\rm and}\;h_{{ij}} \; > \;0}} \\ {{0\;{\rm if}\;d_{{ij}} \ne k\quad{\rm or}\;h_{{ij}}\;\leq \;0}} \\ \end{array}} \right\}}$$
(12)

As indicated by the δ function, only positive h ij values are considered. Negative signs of the off-diagonal elements mean that the two atoms occupy opposite molecular regions with respect to the center and hence their mutual degree of accessibility should be low.

Bayesian-regularized artificial neural network analysis.

Artificial neural network (ANN) training was carried out according to the Levengerg-Marquardt optimization [39]. The initial value for μ was 0.005 with decrease and increase factors of 0.1 and 10, respectively. The training was stopped when μ became larger than 1010.

We used the following architecture:

  • The input layer included the selected descriptors (six descriptors).

  • One hidden layer with sigmoid transfer function was included. The hidden layer’s architecture was varied from 4 to 7 neurons.

  • The output layer had a linear transfer function and one neuron, representing the antifungal activity. The input and output values were normalized.

Analysis of the hidden-layer architecture showed that results were stable between 4 and 7 neurons because the Bayesian regularization avoids overfitting. Finally, a 6-5-1 architecture was chosen.

In a first approach, BRANN was generated using the same descriptors that appeared in the MLR–GA model as network inputs in order to improve the fit of the linear model. Afterward, by running the BRANN–GA routine until 90% of the generations reached the same fitness values, an optimum neural network model, BRANN–GA, was obtained (see Materials and methods).

Statistics for the BRANN model appear in Table 3. This nonlinear model was superior to the MLR–GA one by fitting the training set with a higher r 2 of 0.889, in comparison with 0.746 for the linear model. Nevertheless, the two models exhibited similar predictive power measured by internal and external validation processes. Linear and nonlinear values of q 2 of LOO cross-validation were 0.692 and 0.625 for the internal validation, respectively, while the external validation showed r 2 values for the test set of 0.780 and 0.811, respectively (Table 3). These results agreed with previous reports, in which ANNs trained with variables selected by linear search routines were superior to linear models by increasing data fitting, but the predictors did not exhibit a remarkable improvement in predictive power [40, 41].

The BRANN–GA approach yielded an optimum variable subset that was more diverse in comparison with the descriptor subset of the linear model. The BRANN–GA predictor includes four kinds of molecular descriptors, two RDF descriptors (RDF055u and RDF085m), two 3D-MoRSE descriptors (Mor10u and Mor25p), one WHIM descriptor (E1u) and one GETAWAY descriptor (H8v). Similarly to the variables selected by MLR–GA, there is no significant intercorrelation between these descriptors, as shown in Table 4.

Table 4 Correlation matrix of the descriptors selected by nonlinear GA
Full size table

RDF descriptors are calculated from the radial distribution function of an ensemble of N atoms that can be interpreted as the probability distribution of finding an atom in a spherical volume of radius r. Eq. 13 represents the radial distribution function code:

$$g(r) = f{\sum\limits_i^{N - 1} {{\sum\limits_{j > 1}^N {A_{i} A_{j} {\text e}^{{- B(r - r_{{ij}})^{2}}}}}}}$$
(13)

where f is a scaling factor, N is the number of atoms, A i and A j are atomic properties of atoms i and j,r ij represents the interatomic distances and B is an smoothing parameter, which defines the probability distribution of the individual distances. g(r) was calculated at a number of discrete points with defined intervals. In the BRANN–GA model, RDF055u and RDF085m take into account the atoms inside virtual spheres of 5.5 and 8.5 Å of diameter, excluding atoms at the most external spheres (heterocyclic ring-derivative diameters varied from 10 to 15 Å).

Another descriptor in the BRANN–GA model is the WHIM index E1u. The weighted holistic invariant molecular (WHIM) indices are invariant to roto-translation descriptors obtained for each molecular geometry [26]. They are calculated by transforming Cartesian coordinates weighted by atomic properties and centering the coordinates to obtain invariance to translation. Then, a principal components analysis (PCA) leads to three principal component axes and new coordinates are obtained by projecting the old ones onto the PCA axes, obtaining three score column vectors t 1, t 2 and t 3. Four kinds of descriptor are calculated from the first to fourth order of t m scores, related to molecular size, shape, symmetry and atom distribution. The WHIM descriptor E1u is that given by the kurtosis, calculated from the fourth order moments of the t m scores. It is related to the atom distribution along the principal axes for the unweighted scheme.

An improvement in the reliability on the modeling of the antifungal activity was achieved by the BRANN–GA procedure. BRANN–GA fitted the training set with an r 2 value of 0.937, its internal validation exhibited a q 2 value of LOO cross-validation of 0.689 and r 2 value of 0.874 was obtained for test-set fitting (Table 3). When comparing this predictor with the previous models developed in this paper, we found that, besides the improvement on the fitting of training set, the most remarkable result is the increment in predictive power. Although BRANN–GA exhibits a similar q 2 of LOO cross-validation in comparison to the MRL–GA model, a remarkable increase in the quality of the prediction of the external test set was obtained. In this regard, several authors have suggested that independent q 2 values, the only way to estimate the true predictive power of a QSAR model is to compare the predicted and observed activities of a (sufficiently large) external test set of compounds that was not used for training [42]. Table 5 shows predicted and experimental activities for the test set. Plots in Fig. 4 depict the fitting of the training and test sets for MLR–GA, BRANN and BRANN–GA models. In the light of this result, the superiority of this BRANN model is well addressed by its significantly higher r 2 value of 0.874 in comparison with 0.780 and 0.811 for the MLR–GA and BRANN models, respectively. Similarly, the plots of the residual antifungal activities depicted in Fig. 5 confirm the higher accuracy of BRANN–GA model. Figure 5c showed that, contrary to linear GA-derived models, the BRANN–GA predicts the whole test set with a residual lower than 0.2, included compound 96, which was an outlier for the other models.

Table 5 Predicted log(1/C) values of compounds from test set compared with their observed values by MLR–GA, BRANN and BRANN–GA models
Full size table
Fig. 4
figure 4

Predicted versus experimental activities for the data set. a MLR (filled circle) training set; (open circle) test set. b BRANN (filled circle) training set; (open circle) test set. c BRANN–GA (filled circle) training set; (open circle) test set

Full size image
Fig. 5
figure 5

Residuals for predictions in data set compounds. (a) MLR. (b) BRANN. (c) BRANN–GA

Full size image

KNN analysis.

In order to achieve data differentiation using the six descriptors in the best predictor BRANN–GA, a KNN with 12×12 neurons was mapped with these descriptors as input vectors and both training and test sets were included in the training process. Neurons were initially located at a gridtop topology map. The ordering phase was realized in 1,000 steps with learning rate = 0.9 until the tuning neighborhood distance (1.0) was achieved. The tuning phase learning rate was 0.02. Training was performed for a period of 2,000 epochs in an unsupervised manner.

Figure 6 depicts the KNN map of the data, 66 of a total of 144 neurons were occupied, 8 neurons are considered as conflictive. As can be seen, compounds with a similar range of activity were grouped into neighboring areas. The most active compounds are grouped in the upper-left zone, the rest of the active compounds (log(1/C) > 4.2) are fundamentally grouped at the upper right. The less active compounds were organized in clusters through the entire map. The fact that most and less active compounds were located in several islands confirms that the descriptors chosen distinguish the data quite well.

Fig. 6
figure 6

A KNN map for the data set using the selected six descriptors (model BRANN–GA). More than one compound for neuron is indicated. Underlined number means conflictive neuron. Squares at right decode the ranges of antifungal activities (log1/C)

Full size image

Model interpretation

3D descriptors have found many applications in the performance of QSAR studies. Moreover the results are better when models combine several groups of descriptors [43]. The most obvious way for coding the 3D structure of a molecule by specifying the Cartesian or internal coordinates of the atoms is unfavorable for most applications because the number of 3D coordinates is intimately tied to the number of atoms in a molecule. This drawback is eradicated when using 3D descriptors.

Several reports have been published about linear QSAR of the antifungal activity of heterocyclic compounds. Specifically, Yalcin et al. [12] reported a MLR equation using local descriptors and Verloop’s STERIMOL parameters to describe the antifungal activity of a subset of 68 compounds included in the current study, dividing them in a 61-member training set and 7-member test set. In spite of the good results achieved by these authors, some remarks should be addressed. The authors reported an irrational r 2 of 0.980 considering the implicit uncertainty of the twofold serial dilution technique employed in the activity assays. Although a q 2 of LOO cross-validation of 0.670 is similar to the values reported here and the model explains 83.7% of the external validation predictions, the test set was bounded to the most inner compounds, including neither more active (>4.36) nor less active (<4.01) antifungal heterocyclic ring derivatives. Regarding this, the test set is not a representative sample of the whole set of 68 compounds. In addition, the significance of this model in comparison with our approach is limited since local descriptors consider molecules like frames with isolated devices, while 3D global descriptors relate all physicochemical properties in an integral frame, allowing some interpretation of the study phenomena.

The ANN approach has been applied successfully in antifungal QSAR studies. Hasegawa et al. [14] reported modeling of the antifungal activity of a small data set of 30 azoxy compounds using back-propagation neural networks and physicochemical parameters. Similarly Mghazli et al. [15] used these networks in a QSR study of 1-[2-(substituted phenyl)allyl]imidazole derivatives using physicochemical parameters. Their results revealed a nonlinear influence of the molecular hydrophobicity on the antifungal activity. Both of these previous studies lacked any feature-selection algorithm to search among a pool of descriptors encoding different molecular properties for variables having relevant relationships with the antifungal activity.

In this paper, two sets of six 3D molecular descriptors were selected from a pool of 721 descriptors for modeling the antifungal activity of 96 heterocyclic compounds. The linear GA results were framed in 3D-MoRSE and H-GETAWAY descriptors weighted by atomic van der Waals volumes and atomic masses. Otherwise, the nonlinear GA found a more complex and reliable solution including 3D-MoRSE, RDF, WHIM and H-GETAWAY descriptors weighted by the same properties and adding atomic polarizabilities.

The 3D-MoRSE selected descriptors are weighted by atomic van der Waals volumes (Mor13v, Mor19v, Mor27v and Mor29v). This code can express the appropriate distribution of the size of the molecules for having a certain activity. On the other hand, H8u, the unweighted H index of lag 8, has a positive influence in the MLR–GA. Atoms at d ij =8 in opposite molecular regions would be discarded, therefore H8u adopts larger values for long molecules and stretched conformations. Similarly, H5m has a positive influence and increases when one-side fifth path lengths are present, but it also takes into account atomic masses.

The BRANN–GA results are clearly different with regard to the linear ones. The role of the descriptors in the nonlinear models is not amenable to analysis because of the black-box nature of the BRANN methodology. The BRANN–GA model retains the H index of lag 8, but weighted by atomic van der Waals volumes (H8v). In addition, the nonlinear relation changes the code in the 3D-MoRSE descriptors, introducing the effect of atomic polarizabilities (Mor10u and Mor25p) and the WHIM descriptor E1u is related to the atom distribution along the principal axes for the unweighted scheme.

Despite the fact that interpreting QSAR models is always a difficult task, we can conclude that the linear and nonlinear models obtained here showed that the distribution of van der Waals atomic volumes and atomic masses have a large influence on the antifungal activities of the compounds studied. This suggests that molecular size and shape play an important role in the antifungal activity modeled. Also, the BRANN–GA model included the influence of atomic polarizability that could be associated with the capacity of the antifungal compounds to be deformed when interacting with biological macromolecules. These facts agree well with reports in which the capacity of the active molecule to transfix fungi cellular wall is considered a key factor for adequate antifungal activity [1].

Conclusions

Biological activities are complex in nature. A QSAR study on antifungal activity was performed by means of MLR and BRANN techniques. The GA approach was used for selecting optimum subsets of descriptors for linear and nonlinear modeling of the antifungal activity of 96 heterocyclic derivatives. The highest linear correlation between six descriptors and the activity had r 2 values of 0.746 and 0.780 for training and test sets, respectively. The use of variables selected by a linear GA approach for training neural networks did not produce a more predictive model. However, the combination of BRANN and GA techniques yielded the best predictors able to describe about 94% of the training set and 87% of the test set. Our models suggest there are high influences of molecular size, shape and deformability in the antifungal activity. On the other hand, the antifungal compounds were well differentiated regarding their antifungal potency in a KNN map built using the descriptors present in BRANN–GA predictor.