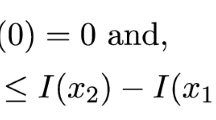Abstract
In this paper, we consider an optimal insurance problem from the perspective of a risk-averse individual who faces an insurable risk as well as some background risk and wants to maximise the expected utility of his/her final wealth. To reduce ex post moral hazard, we follow Huberman et al. (Bell J. Econ. 14:415–426 1983) to assume that alternative insurance contracts satisfy the principle of indemnity and the no-sabotage condition. When the insurance premium is calculated by the expected value premium principle, a necessary and sufficient condition for the optimality of an insurance contract is established under a general dependence structure between insurable and background risks. By virtue of this condition, some qualitative properties of optimal contracts are developed, a scheme is provided to improve any suboptimal insurance strategy, and optimal insurance forms are derived explicitly for some dependence structures of interest. These forms are not always piecewise linear.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
When facing an insurable risk, an individual may choose to share this risk with an insurer by purchasing an insurance contract. Generally, the insured has to make a balance between the risk transfer and the insurance premium paid, with the goal of maximising his/her satisfaction. This naturally elicits the study of optimal insurance design for the insured. In the formulation of an optimal insurance problem, there are many different premium principles and risk measures to choose, which stimulates different streams of research on this topic.
In the pioneering work of Arrow [1] who analyses the optimal insurance problem under the expected utility (EU) framework (von Neumann and Morgenstern [34, Chap. I]), the optimality of stop-loss insurance, which is full insurance above a deductible, is established for maximising the EU of the insured’s final wealth when the insurance premium is calculated by the expected value principle. Later this result is generalised mainly in two directions. In one direction, different premium principles are used to price insurance contracts. For instance, Raviv [26], Young [36], Kaluszka [17] and Kaluszka and Okolewski [18] investigate the optimal insurance design under the principle of equivalent utility, Wang’s premium principle, mean–variance premium principles and the maximal possible claims principle, respectively. Another direction is to generalise the EU framework. Van Heerwaarden et al. [32] and Gollier and Schlesinger [14] extend Arrow’s result by considering a general optimisation criterion preserving second degree stochastic dominance. Bernard et al. [4] and Xu et al. [35] instead obtain optimal insurance strategies explicitly under the framework of rank-dependent expected utility (RDEU). The optimal insurance demand under prospect theory is investigated in Sung et al. [31] and Schmidt [29]. See e.g. Balbás et al. [2] and Kiesel and Rüschendorf [19] for the optimal contract design under general risk measures.
Notably, the aforementioned studies are restricted to the single-risk framework. In practice, however, an individual may face multiple sources of risks, where one major risk is to be insured and other risks such as investment risk, economic risk and operational risk are either uninsurable or not to be insured. These risks are often combined together and treated as background risk in insurance economics. It is noteworthy that many different dependence structures between background risk and insurable risk exist in insurance practice. We refer to Vercammen [33] and Dana and Scarsini [10] for a detailed discussion.
The optimal insurance design with background risk has attracted great attention from academics. Mayers and Smith [24] investigate the optimal proportion rate of quota-share insurance together with the demand of financial assets, while Doherty and Schlesinger [11] analyse the optimal deductible level of the stop-loss insurance when the insured’s initial wealth is random. Eeckhoudt and Kimball [12] investigate how the presence of background risk affects the demand for quota-share insurance and stop-loss insurance, assuming that the background risk increases with respect to the insurable risk in the sense of third increasing convex order and that the insured is risk-averse and prudent. However, these analyses are confined to some special types of insurance contracts and thus lack generality. Gollier [13] instead considers a large range of alternative possible insurance contracts which are asked to satisfy the principle of indemnity. That is, the indemnity is nonnegative but less than the insurable loss. Assuming that the insurance premium only depends on the expected indemnity, he shows that the optimal contract is stop-loss insurance if background risk and insurable risk are independent, and changes to disappearing deductible when the background risk becomes stochastically increasing with respect to the insurable risk in the sense of convex order. The optimality of disappearing deductible is also obtained in Mahul [23] and Dana and Scarsini [10] who extend the insurance model of Raviv [26] by taking background risk into consideration. However, this optimal insurance contract allows the marginal indemnity to be strictly larger than 1, and hence the insured has an incentive to benefit himself/herself by overstating the actual loss, described as ex post moral hazard by Huberman et al. [16]. As a result, the insurance contract of this type is seldom used in practice.
To reduce ex post moral hazard, Huberman et al. [16] suggest that both the insured and the insurer should pay more for a larger realisation of the insurable loss. Equivalently, the marginal indemnity should be nonnegative and less than 1. This is also referred to as the no-sabotage condition (Carlier and Dana [6]). After imposing this condition and the principle of indemnity on insurance contracts, Lu et al. [21] obtain the same result as Arrow [1] in favor of stop-loss insurance under the assumption that the background risk is stochastically increasing in the insurable risk. This result is further extended by Chi and Wei [9] to a weaker positive dependence structure. More specifically, they obtain the optimality of stop-loss insurance for the insured with the risk preference preserving \((n+1)\)th degree stochastic dominance when the background risk is right tail increasing with respect to the insurable risk in \(n\)th stochastic order.
Clearly, a positive dependence of this kind cannot capture the full spectrum of the relationship between background risk and insurable risk. In addition to positive dependence, Dana and Scarsini [10] introduce several other types of dependence structures that frequently appear in insurance practice. Motivated by their study, it is natural to ask what is the optimal insurance form for a general dependence structure between background risk and insurable risk when ex post moral hazard is excluded like in Huberman et al. [16]. To the best of our knowledge, there is little literature tackling this problem. Our objective is to fill the gap and shed some light on the study of this problem.
In this paper, we revisit the optimal insurance problem with background risk by assuming a general dependence structure between background risk and insurable risk. To exclude ex post moral hazard, we follow the way of Huberman et al. [16] to assume that alternative insurance contracts satisfy the principle of indemnity and the no-sabotage condition. As in the literature, the insurance premium is calculated by the expected value principle with a safety loading coefficient \(\rho \). We show that the optimal insurance contract always exists and is often unique. However, it is quite difficult to be derived explicitly because of the general dependence assumption and the no-sabotage condition. We instead use the approach of the calculus of variations to get a necessary and sufficient condition for the solution, which provides a sketchy way to characterise solutions. More specifically, the marginal indemnity of an optimal insurance contract should be either 0 or 1, with some exceptions at critical points, depending upon the comparison between the function \(\Phi _{f^{*}}(x)\) defined in (3.4) and \(1+\rho \). By virtue of this condition, we can design a better insurance strategy based on any suboptimal contract, and derive optimal insurance forms explicitly for some interesting dependence structures. The main contributions of this paper are threefold:
First, a necessary and sufficient condition is provided for the optimality of any insurance strategy satisfying the principle of indemnity as well as the no-sabotage constraint. This condition plays a fundamental role in our analysis. It can be used to develop useful characteristics of optimal contracts. In particular, the optimal insurance contract often involves a deductible if the safety loading coefficient \(\rho \) is positive, regardless of the dependence structure between insurable risk and background risk. In addition, for any suboptimal insurance strategy, a scheme is developed to enhance the strategy, which results in a strict increase in the EU of the insured’s final wealth. Furthermore, it is very helpful in deriving optimal contracts explicitly for some dependence structures including not only positive dependence but also negative dependence and even mixed dependence. It is quite different from Lu et al. [21] and Chi and Wei [9] who derive explicit optimal insurance contracts only for the positive dependence case. Although a few general dependence structures have been studied in Lu et al. [22], their analysis is restricted to the optimality of some piecewise linear insurance contracts. However, we find that optimal insurance forms are not always piecewise linear, especially for some moderate negative dependence and mixed dependence. Therefore, our analysis significantly complements the research of optimal insurance design with background risk by taking into account more dependence structures and establishing the optimality of new insurance forms.
Second, we find that the optimal insurance design with background risk usually changes significantly once the no-sabotage condition is imposed. More specifically, we show that optimal contracts satisfying this condition are very different from those without imposing this condition (Dana and Scarsini [10]), as illustrated in Table 1. This finding is quite different from the result obtained by Carlier and Dana [7], who show that in the absence of background risk the optimal insurance contract always satisfies the no-sabotage condition under the majority of EU or non-EU based models. Notably, Xu et al. [35] have a finding similar to ours under the RDEU framework when background risk is not taken into consideration.
Third, we revisit Mossin’s theorem in the presence of background risk. Mossin’s theorem states that in the absence of background risk (equivalently, background risk is a constant), full insurance is optimal if and only if the safety loading coefficient \(\rho \) is equal to 0. However, in the presence of background risk, we show that Mossin’s theorem may be violated. In particular, the optimality of full insurance heavily relies on the dependence between background and insurable risk and need not hold even if \(\rho \) is 0. One special example is that the sum of background and insurable risks is negatively quadrant dependent with the insurable risk, and the no-insurance strategy is always optimal for this case (Corollary 4.2).
The rest of the paper is organised as follows. In Sect. 2, we formulate an optimal insurance model with background risk and introduce some dependence notions. In Sect. 3, a necessary and sufficient condition is established for the optimality of any given insurance strategy, and a scheme is developed to improve any suboptimal insurance strategy under an arbitrary dependence structure. In Sects. 4–6, optimal insurance contracts are derived explicitly for some categories of positive, moderate negative and strong negative dependence. Section 7 extends the analysis to some mixed dependence structures by assuming that the insured exhibits constant absolute risk aversion (CARA). Some concluding remarks are provided in Sect. 8. Finally, the appendix collects three useful lemmas.
2 Preliminaries
2.1 Model formulation
Suppose that within a fixed time period, an insured endowed with initial wealth \(w\) is facing two sources of risks \(X\) and \(Y\), where \(X\) is insurable and nonnegative and \(Y\) is a background risk and may be negative. Both \(X\) and \(Y\) are defined on a probability space \((\Omega ,\mathcal{F},\mathbb{P})\), and \(X\) is assumed to be bounded with the support
Denote by \(M\) the essential supremum of \(X\); then \(M= \sup S(X)<\infty \). The assumption of a bounded insurable risk is commonly used in insurance economics. See for example Dana and Scarsini [10] and Schlesinger [28].
In order to reduce the risk exposure, the insured seeks to purchase an insurance contract, in which an amount \(f(X)\) of risk is ceded to an insurer and the residual risk \(I_{f}(X)=X-f(X)\) is retained. The functions \(f(x)\) and \(I_{f}(x)\) are usually called the insured’s ceded and retained loss functions, respectively. In insurance economics, it is widely accepted that the insurance contract should satisfy the principle of indemnity. That is, the ceded loss should be nonnegative but not exceed the original loss. However, it is insufficient to impose only this constraint on insurance contracts. To preclude ex post moral hazard, we follow Huberman et al. [16] to further assume that alternative insurance contracts satisfy the no-sabotage condition, which asks both the insured and the insurer to pay more for a larger realisation of the insurable loss. Mathematically, \(f(x)\) and \(I_{f}(x)\) should be increasing functions. It is necessary to point out that the terms “increasing” and “decreasing” used in this paper mean “nondecreasing” and “nonincreasing”, respectively. Using ℭ to represent the set of admissible ceded loss functions, we have
Note that \(f \in \mathfrak{C}\) is equivalent to that \(f(x)\) is increasing and Lipschitz-continuous in the sense that
Thus any admissible ceded loss function \(f(x)\) is differentiable with \(0\le f'(x)\le 1\) almost everywhere.
To cover the potential insurable loss for the insured, the insurer will need to collect a premium. Following the majority of the literature, we assume that the insurer is risk-neutral and calculates the insurance premium by the expected value principle. Using \(\pi (\cdot )\) to represent the premium principle, we have
for some nonnegative safety loading coefficient \(\rho \). It is worthwhile to point out that the assumption of the expected value premium principle plays an important role in this paper. Specifically, the linearity of this principle is necessary in establishing Theorem 3.3, which is the foundation of many results in later sections. Admittedly, there are many alternatives beyond the expected value premium principle. Readers are referred to Young [37] for a comprehensive review of premium principles. Despite the existence of alternative premium principles, not many of them have been used in the study of optimal insurance design under the EU framework. This is mainly due to the mathematical challenge. For example, Raviv [26] and Young [36] have studied the optimal insurance problem under the principle of equivalent utility and Wang’s premium principle, respectively, and neither has obtained explicit solutions even in the absence of background risk. Therefore, we stick to the expected value premium principle to avoid complications.
With an insurance arrangement, the insured’s final wealth \(W_{f}(X,Y)\) can be represented by
because \(I_{f} (X) = X-f(X) \geq 0\) and \(\pi (f(X)) \geq 0\) as \(f(X) \geq 0\). Following the classical EU framework, the objective is to maximise the EU of the insured’s final wealth. Mathematically, the optimisation problem can be formulated as
where \(u(\cdot )\) is a strictly increasing concave utility function with \(u'(\cdot )>0\) and \(u''(\cdot )<0\). The chosen utility function reflects the attitude of the insured’s risk aversion. For technical convenience, we make the following assumption throughout the paper:
Assumption 2.1
\(-\infty <\mathbb{E}\big [u\big (w-Y-X-(1+\rho )\mathbb{E}[X]\big ) \big ]<\mathbb{E} [u(w-Y) ]<\infty \).
It is worth mentioning that the above mathematical model is also applicable to analyse the optimal insurance problem with random initial wealth and an insurable risk. More specifically, by regarding the negative of the wealth as a background risk, the analysis is equivalent to solving the optimisation problem (2.3).
2.2 Dependence notions
The solution to problem (2.3) heavily depends on the dependence structure between background and insurable risks. In order to study this problem, we introduce below some useful dependence notions.
Definition 2.2
A random variable \(Z_{1}\) is said to be stochastically increasing (resp. stochastically decreasing) in a random variable \(Z_{2}\), denoted as \(Z_{1}\uparrow _{\mathrm{st}} Z_{2}\) (resp. \(Z_{1}\downarrow _{\mathrm{st}} Z_{2}\)), if \(x \mapsto \mathbb{E}[v( {Z_{1}})| {Z_{2}}=x]\) is increasing (resp. decreasing) over the support of \({Z_{2}}\) for any increasing function \(v(\cdot )\) such that \(\mathbb{E}[|v( {Z_{1}})|]<\infty \).
The notion of stochastic increasingness was proposed by Lehmann [20]. Clearly, \(Y\uparrow _{\mathrm{st}} X\) indicates a positive dependence structure between \(X\) and \(Y\). On the other hand, stochastic decreasingness implies a negative dependence structure. These two notions have been widely used in insurance economics; see for example Dana and Scarsini [10], Cai and Wei [5] and Lu et al. [21].
In addition to stochastic increasingness, Lehmann [20] also introduced the notion of positive quadrant dependence, which was described in terms of joint distribution functions. Later, Shaked and Shanthikumar [30, Sect. 9.A.1] provided an equivalent characterisation by using joint survival functions, which is characterised by Definition 2.3 below.
Definition 2.3
Two random variables \(Z_{1}\) and \(Z_{2}\) are positively (negatively) quadrant dependent, denoted as \(Z_{1}\sim _{\,\mathrm{PQD}} Z_{2}\) (\(Z_{1}\sim _{\,\mathrm{NQD}} Z_{2}\)), if
Further, we introduce the notion of right tail increasingness, which was proposed by Barlow and Proschan [3, Chap. 5] and whose applications in optimal insurance problems can be found in Chi and Wei [9].
Definition 2.4
A random variable \(Z_{1}\) is right tail increasing (resp. right tail decreasing) in a random variable \(Z_{2}\), denoted as \(Z_{1}\uparrow _{\mathrm{rt}} Z_{2}\) (resp. \(Z_{1}\downarrow _{\mathrm{rt}} Z_{2}\)), if \(x \mapsto \mathbb{E}[v( {Z_{1}})| {Z_{2}}>x]\) is increasing (resp. decreasing) over the support of \({Z_{2}}\) for any increasing function \(v(\cdot )\) such that \(\mathbb{E}[|v( {Z_{1}})|]<\infty \).
It is not difficult to establish that \(Y\downarrow _{\mathrm{st}} X\) (resp. \(Y\downarrow _{\mathrm{rt}} X\), \(Y \sim _{\,\mathrm{NQD}} X\)) if and only if \(-Y\uparrow _{\mathrm{st}} X\) (resp. \(-Y\uparrow _{\mathrm{rt}} X\), \(-Y \sim _{\,\mathrm{PQD}} X\)). Furthermore, we have among these notions the implications
All these notions indicate some kind of positive dependence, with PQD being the weakest one. It should be pointed out that the notion of PQD is symmetric (that is, \(Y\sim _{\,\mathrm{PQD}} X\Longleftrightarrow X\sim _{\,\mathrm{PQD}} Y\)), while the other two notions are not.
3 Insurance design under an arbitrary dependence structure
In this section, we study problem (2.3) under an arbitrary dependence structure. Specifically, we first discuss the existence and uniqueness of a solution and then establish a necessary and sufficient condition for the optimality of any given insurance strategy.
Proposition 3.1
(i) There exists at least one solution to problem (2.3).
(ii) The solution is unique in the sense that \(f_{1}(X) = f_{2}(X)\)a.s. for any two solutions \(f_{1}, f_{2}\)to problem (2.3) if one of the following conditions is satisfied: (a) \(\rho >0\); (b) \(0\in S(X)\).
Proof
(i) Define \(\mathfrak{M}=\sup _{f\in \mathfrak{C}}\mathbb{E}[u(W_{f}(X,Y))]\). There exists a sequence \((f_{n})_{n\ge 1}\subseteq \mathfrak{C}\) such that
where the inequality follows from (2.2). Since \(X\) is bounded by \(M\), the \((f_{n}(X))_{n\ge 1}\) are uniformly bounded by \(M\) as well. Furthermore, all the \((f_{n})_{n\ge 1}\) are Lipschitz-continuous with a common Lipschitz constant, namely 1. According to the Arzelà–Ascoli theorem (Rudin [27, Theorem 7.25]), there exists a subsequence \((f_{n_{k}})_{k\ge 1}\) that uniformly converges to a continuous function \(f^{*}\) on the closed interval \([0, {M}]\). Define \(f^{*}(x)=f^{*}({M})\) for any \(x> {M}\). Following from (2.1), it is easy to verify that \({f^{*}(x)\in \mathfrak{C}}\). Furthermore, \(W_{f_{n_{k}}}(X,Y) \to W_{f^{*}}(X,Y)\) a.s. Because \({W_{f_{n_{k}}}(X,Y) \leq w-Y}\) by (2.2) and \(u\) is increasing, using first the continuity of \(u(\cdot )\) and then Fatou’s lemma implies
which in turn implies \(\mathfrak{M} \le \mathbb{E}[u(W_{f^{*}}(X,Y))]\). Since \(\mathfrak{M} \ge \mathbb{E}[u(W_{f^{*}}(X,Y))]\) according to the definition of \(\mathfrak{M}\), we have \(\mathfrak{M}=\mathbb{E}[u(W_{f^{*}}(X,Y))]\). Therefore, \(f^{*}(x)\) is a solution to problem (2.3).
(ii) If both \(f_{1}\) and \(f_{2}\) are solutions to problem (2.3), it immediately follows that
For any \(p\in (0,1)\), \(pf_{1}+(1-p)f_{2} \in \mathfrak{C}\) and hence \(\mathbb{E} [u(W_{pf_{1}+(1-p)f_{2}}(X,Y)) ] \le \mathfrak{M}\). On the other hand, the concavity of \(u(\cdot )\) leads to
Therefore, the equality in (3.1) must be obtained. Noting that \(u''(\cdot )< 0\), this equality holds only if \(W_{f_{1}}(X,Y) = W_{f_{2}}(X,Y)\) a.s., or equivalently,
If \(\rho > 0\), taking expectations on both sides of (3.2) yields \(\mathbb{E}[f_{1}(X)]=\mathbb{E}[f_{2}(X)]\), which in turn implies \(f_{1}(X)=f_{2}(X)\) a.s. This proves case (a).
If \(\rho =0\), consider case (b): \(0\in S(X)\). It follows from (3.2) that the equation \(\mathbb{E}[f_{2}(X)]-\mathbb{E}[f_{1}(X)]=f_{2}(X)-f_{1}(X)\) holds almost surely. In other words, we have \(\mathbb{P}[X\in \mathcal{B}]=1\) with \(\mathcal{B}=\{x\in [0, M]:\mathbb{E}[f_{2}(X)]-\mathbb{E}[f_{1}(X)]=f_{2}(x)-f_{1}(x) \}\). If \(0\in \mathcal{B}\), then \(\mathbb{E}[f_{2}(X)]-\mathbb{E}[f_{1}(X)]=f_{2}(0)-f_{1}(0)=0\) and thus it holds for all \(x\in {\mathcal{B}}\) that \(f_{2}(x)-f_{1}(x) = \mathbb{E}[f_{2}(X)]-\mathbb{E}[f_{1}(X)]=0\). This implies \(f_{1}(X)= f_{2}(X)\) a.s. since \(\mathbb{P}[X\in \mathcal{B}]=1\). Otherwise, consider the case \(0\notin \mathcal{B}\). Because \(0\in S(X)\), there must exist a sequence \((x_{n})_{n\ge 1}\) such that \(x_{n}\in \mathcal{B}\) and \(\lim _{n\to \infty }x_{n}=0\). Therefore, we have \(\mathbb{E}[f_{2}(X)]-\mathbb{E}[f_{1}(X)]=\lim _{n\to \infty }f_{2}(x_{n})-f_{1}(x_{n})=0\), which in turn implies \(f_{1}(X) = f_{2}(X)\) a.s. from (3.2). □
Remark 3.2
Note that the solutions to problem (2.3) need not be unique if \(\rho =0\) and \(0\notin S(X)\). For example, if \(f^{*}(x)\) is a solution to (2.3) with \(f^{*}(\operatorname*{{\mathrm{ess}\inf}}X)>0\), where \(\operatorname*{{\mathrm{ess}\inf}}X=\inf S(X)\), then \(\tilde{f}(x)=(f^{*}(x)-f^{*}(\operatorname*{{\mathrm{ess}\inf}}X))^{+}\) is also a solution to problem (2.3) because \(W_{f^{*}}(X,Y) = W_{\tilde{f}}(X,Y)\) a.s. Although the solutions are not unique in this case, it should not be a major concern. For one thing, we can see that the two optimal ceded loss functions differ only by a constant shift on \(S(X)\) and they produce the same final wealth in the sense of ℙ-a.s. For another, the insurable loss in practice usually possesses a positive probability mass at zero and the insurer usually sets a positive safety loading coefficient to calculate the insurance premium. Therefore, we can safely conclude the uniqueness of the solution in most situations of practical interest.
Without a specific assumption on the dependence between \(X\) and \(Y\), it is generally difficult to find the solution explicitly. Below, we derive a necessary and sufficient condition for the optimality of any given ceded loss function.
Theorem 3.3
The ceded loss function \(f^{*}(x)\)is a solution to problem (2.3) if and only if it satisfies
almost everywhere on \([0, M)\), where \(\Phi _{f}(x)\)is defined as
Proof
(i) (Necessity) We assume that \(f^{*}(x)\) is a solution to problem (2.3). For any \(f(x)\in \mathfrak{C}\) and \(p\in [0,1]\), if \(f_{p}(x):=pf^{*}(x)+(1-p)f(x)\), then \(f_{p}(x) \in \mathfrak{C}\). The optimality of \(f^{*}(x)\) implies \(\frac{\partial \mathbb{E}[u(W_{f_{p}}(X,Y))]}{\partial p}|_{p=1} \ge 0\), which is equivalent to
where the first equality follows from the fact that \(f(x)=\int _{0}^{\infty }f'(t)\mathbb{I}_{\{x>t\}}dt\) and \(\mathbb{I}_{A}\) is the indicator function of the event \(A\). Note that the above inequality holds true for any \(f\in \mathfrak{C}\). Below we prove by contradiction that this implies (3.3).
If (3.3) is not satisfied, there exists a set \(E \subseteq [0, M)\) with positive Lebesgue measure such that either \({f^{*}}'(x)<1\) and \(\Phi _{f^{*}}(x)>1+\rho \) for any \(x\in E\) or \({f^{*}}'(x)>0\) and \(\Phi _{f^{*}}(x)<1+\rho \) for any \(x\in E\). In the first case, we can construct a ceded loss function \(f\) such that \(f'(x)=1\) for any \(x\in E\) and \(f'(x) = {f^{*}}'(x)\) elsewhere. Then the last integral in (3.5) reduces to
Recalling that \(u'(\cdot )>0\), \(\mathbb{P}[X>x]>0\) and \((\Phi _{f^{*}}(x)-(1+\rho ) ) ({f^{*}}'(x)-1 )<0\) for any \(x\in E\), we conclude that the above integral value is negative. This contradicts (3.5). A similar contradiction can be obtained in the second case.
(ii) (Sufficiency) If (3.3) is satisfied, then for any \(f\in \mathfrak{C}\), we have
where the first inequality is due to the concavity of the utility function \(u(\cdot )\). As a consequence, \(f^{*}(x)\) is a solution to problem (2.3). The proof is thus completed. □
For a ceded loss function \(f^{*}\) to be optimal, \(f^{*}\) should satisfy (3.3) almost everywhere. Note that values of \({f^{*}}'\) on a set with zero Lebesgue measure do not affect the value of \(f^{*}\). Henceforth, whenever \({f^{*}}'(x)\) is used to describe the optimal marginal ceded loss function, we shall not mention the term “almost everywhere”. Note that \(\mathbb{E}[u'(W_{f^{*}}(X,Y))]<\infty \) under Assumption 2.1, and hence \(\Phi _{f^{*}}(x)\) is well defined.
The above theorem provides a necessary and sufficient condition to characterise the optimal insurance strategy. We remark that this result does not require any specific assumption on the dependence structure between \(X\) and \(Y\). Although Theorem 3.3 does not explicitly solve the problem, it provides insights on what form the optimal insurance strategy should take. Specifically, the marginal indemnity should be either 0 or 1, with some exceptions at the critical point(s) (where \(\Phi _{f^{*}}(x) = 1+\rho \)). This is very useful in developing characteristics of optimal insurance contracts.
Corollary 3.4
If \(f^{*}(x)\)is a solution to problem (2.3), then
where \(\nu _{\rho }=\inf \{x\ge 0:\, \mathbb{P}[X>x]\le \frac{1}{1+\rho }\}\).
Proof
Note that \(\mathbb{P}[X>x] > \frac{1}{1+\rho }\) if and only if \(x< {\nu _{\rho }}\). For any \(f\in \mathfrak{C}\), we have
for any \(x< {\nu _{\rho }}\). Therefore, it follows from Theorem 3.3 and (2.1) that \({f^{*}}(x)=0\) for any \(x< {\nu _{\rho }}\). □
Remark 3.5
Corollary 3.4 suggests that the insured should always fully retain the risk below the level \({\nu _{\rho }}\), regardless of the dependence structure between \(X\) and \(Y\). In other words, the dependence structure between \(X\) and \(Y\) does not affect the existence of a deductible in the optimal insurance arrangement, provided that \({\nu _{\rho }}>0\). Notably, when \(\rho =0\), \(\nu _{\rho }\) becomes 0 and the statement of Corollary 3.4 trivially holds true.
Theorem 3.3 is also useful in improving the insurance strategy. More specifically, for any \(f\in \mathfrak{C}\), we define
If \(f\) is an optimal ceded loss function, then Theorem 3.3 implies that the sets \(\mathfrak{B}_{-}^{f}\) and \(\mathfrak{B}_{+}^{f}\) have Lebesgue measure 0. Otherwise, if \(f\) is suboptimal, the Lebesgue measure of \(\mathfrak{B}_{-}^{f}\cup \mathfrak{B}_{+}^{f}\) is positive. To enhance the strategy \(f\), we can reduce the marginal indemnity at points with \(\Phi _{f}(t)<1+\rho \) and increase the marginal indemnity at points with \(\Phi _{f}(t)>1+\rho \) to some degree. Specifically, based on \(f\), a sequence of ceded loss functions can be constructed by
Obviously, \(f_{p}^{s}\in \mathfrak{C}\) for any \(p\in [0,1]\) and \(f_{0}^{s}(x)=f(x)\).
Proposition 3.6
For any suboptimal ceded loss function \(f\in \mathfrak{C}\), there exists some \(p^{*}\in (0,1]\)such that
Proof
Assume that \(f\) is not a solution to (2.3). It is easy to see that \(\mathbb{E}[u(W_{f_{p}^{s}}(X,Y))]\) is a concave function of \(p\) with
Recall that \(|\mathfrak{B}_{-}^{f}\cup \mathfrak{B}_{+}^{f}|>0\). The above equation together with the definitions of \(\mathfrak{B}_{-}^{f}\) and \(\mathfrak{B}_{+}^{f}\) implies that \(\frac{\partial \mathbb{E}[u(W_{f_{p}^{s}}(X,Y))]}{\partial p} |_{p=0}>0\), which in turn implies
where \(p^{*}=\operatorname*{{\mathrm{arg}\max}}_{p\in [0,1]}\mathbb{E}[u(W_{f_{p}^{s}}(X,Y))]\in (0,1]\). □
Proposition 3.6 provides a practical scheme to enhance the insurance design. When seeking an optimal insurance contract, a decision maker could first design a ceded loss function \(f\) based on the past experience, then he/she should check whether the selected strategy satisfies (3.3). If yes, then \(f\) is the optimal insurance strategy. Otherwise, it is suboptimal and can be enhanced according to the scheme described in Proposition 3.6. In principle, it is possible to reach the optimal insurance strategy by repeating the enhancement scheme. However, we admit that the repetition (especially for many times) of the enhancement scheme may encounter practical challenges and thus need not deliver the optimal contract as expected.
In general, it remains challenging to explicitly derive the optimal insurance strategy. In the following three sections, we study the optimal insurance problem under several categories of dependence structures between \(X\) and \(Y\): (i) positive dependence, \(Y\sim _{\,\mathrm{PQD}}X\), which includes \(Y\uparrow _{\mathrm{rt}} X\) and \(Y\uparrow _{\mathrm{st}} X\) as special cases; (ii) strong negative dependence, \((Y+X)\sim _{\,\mathrm{NQD}}X\), which includes \((Y+X)\downarrow _{\mathrm{rt}} X\) and \((Y+X)\downarrow _{\mathrm{st}} X\) as special cases; and finally (iii) moderate negative dependence, \((Y+X)\uparrow _{\mathrm{st}} X\) and \(Y\downarrow _{\mathrm{st}} X\). Dependence structures in these categories have very different nature and thus lead to different optimal insurance contracts. Note that the moderate negative dependence is characterised by the notion of stochastic increasingness, which is stronger than that used in the other two categories. This is because the case of the moderate negative dependence structure is generally more difficult to analyse. A similar categorisation of dependence structures has been considered by Dana and Scarsini [10] to study optimal insurance design in a different setup. Further discussion on the comparison between their results and ours is given in Sect. 8.
4 Strong negative dependence
We focus on the strong negative dependence structure \((Y+X)\sim _{\,\mathrm{NQD}} X\) in this section. Intuitively, the insurable risk \(X\) is fully hedged by the background risk \(Y\), and there is no need to purchase any insurance coverage for \(X\). In this section, we confirm this intuition through rigorous proofs.
Proposition 4.1
No-insurance is optimal if and only if
In particular, if \(x \mapsto \mathbb{E}[u'(w-Y-X)|X\ge x]\)is decreasing over \([{\nu _{\rho }}, {M})\), then no-insurance is the solution to problem (2.3).
Proof
The necessity and sufficiency of (4.1) for the optimality of no-insurance follow directly from Theorem 3.3 and Corollary 3.4.
In particular, if \(x \mapsto \mathbb{E}[u'(w-Y-X)|X\ge x]\) is decreasing over \([{\nu _{\rho }}, {M})\), then
for any \(x\in [{\nu _{\rho }}, {M})\), where the last inequality follows from (3.6). As a consequence, no-insurance is optimal. □
Proposition 4.1 can be easily interpreted. Intuitively, (4.1) means that the insurance cost (safety loading coefficient \(\rho \)) is quite high, and thus it makes sense not to purchase any insurance coverage. A stronger sufficient condition for the optimality of no-insurance, which is independent of the specific expression of the insured’s utility function, is provided below.
Corollary 4.2
If \((Y+X)\sim _{\,\mathrm{NQD}} X\), then the no-insurance strategy is a solution to problem (2.3).
This corollary follows from Proposition 4.1 and Lemma A.1 by noting that \(u'(\cdot )\) is a decreasing function. Recall from (2.4) that each of \((Y+X) \downarrow _{\mathrm{rt}} X\) and \(X\downarrow _{\mathrm{rt}}(Y+X)\) implies \((Y+X)\sim _{\,\mathrm{NQD}} X\). Each of \((Y+X) \downarrow _{\mathrm{rt}} X\) and \(X\downarrow _{\mathrm{rt}}(Y+X)\) is also a sufficient condition for the optimality of no-insurance. It is worth mentioning that the optimality of no-insurance with background risk has been studied by Lu et al. [22] under the assumption of \((Y+X)\downarrow _{\mathrm{st}} X\), which is stronger than the assumption of Corollary 4.2. In this sense, Corollary 4.2 extends their result to a more general setting of negative dependence.
5 Positive dependence
In this section, we investigate the optimal insurance design under positive dependence \(Y\sim _{\,\mathrm{PQD}}X\), as well as its special case \(Y\uparrow _{\mathrm{rt}} X\). It is worth pointing out that the classical single risk model falls into this category, with the background risk \(Y\) degenerating to a constant. In the single-risk framework, Arrow [1] has already demonstrated that stop-loss insurance is optimal. In this section, we shall find out whether stop-loss insurance preserves its optimality under a general positive dependence. We also derive conditions for full insurance to be optimal and thus generalise Mossin’s theorem [25].
5.1 Optimality of stop-loss insurance
Proposition 5.1
If \(Y\uparrow _{\mathrm{rt}} X\), then stop-loss insurance is a solution to problem (2.3).
Proof
Consider a stop-loss insurance strategy \(f^{\mathrm{sl}}_{d}(x)= (x-d)^{+}\) for \(d\ge 0\) and evaluate \(\Phi _{f_{d}^{\mathrm{sl}}}(d)\), where \(\Phi _{f}(x)\) is defined in (3.4). As a function of \(d\), \(\Phi _{f^{\mathrm{sl}}_{d}}(d)\) depends on \(d\) through two sources. We rewrite it as \(\Psi (d; f^{\mathrm{sl}}_{d})\) to emphasise this implicit relation,
where \(x\wedge y=\min \{x,y\}\). Since \(Y\uparrow _{\mathrm{rt}}X\), according to Proposition 5.1 in Chi and Wei [9], \(\Phi _{f^{\mathrm{sl}}_{d}}(d)\) is increasing in \(d\) over \([{\nu _{\rho }}, {M})\). With \(\inf \emptyset = \infty \) by convention, define
If \(d^{*}<\infty \), then \(\Psi (d^{*}; f^{\mathrm{sl}}_{d^{*}}) \ge 1+\rho \) since \(\Psi (d; f^{\mathrm{sl}}_{d})\) is a right-continuous function of \(d\) and \(\Psi (t; f^{\mathrm{sl}}_{t}) \le 1+\rho \) for any \(t< d^{*}\). Since \(u''(\cdot )<0\) and \(Y\uparrow _{\mathrm{rt}}X\), for any \(x\ge d^{*}\), it holds that
On the other hand, for any \(x \in [{\nu _{\rho }}, d^{*})\), we have
where the first inequality follows from Lemma A.2. The above two equations together with Theorem 3.3 imply that \(f_{d^{*}}^{\mathrm{sl}}(x)\) is a solution to problem (2.3).
If \(d^{*} =\infty \), we must have \(\Psi (d; {f_{d}^{\mathrm{sl}}}) <1+ \rho \) for all \(d \in [{\nu _{\rho }}, {M})\), which in turn implies
where the last inequality follows from Lemma A.2 together with the dependence assumption on \(X\) and \(Y\). Thus it follows from Proposition 4.1 that the optimal insurance strategy is no-insurance, which is a special form of stop-loss insurance. □
Chi and Wei [9, Proposition 4.7] have established the same result as Proposition 5.1 by using a different approach. We reprove this result for two reasons. First, the proof demonstrates the application of Theorem 3.3. More importantly, following the proof presented above, the assumption of \(Y\uparrow _{\mathrm{rt}}X\) can be weakened to “\(\mathbb{E}[v(Y)|X>x]\) is increasing in \(x\in [{\nu _{\rho }}, {M})\) for all increasing functions \(v(\cdot )\)”, which is not covered by Chi and Wei [9, Proposition 4.7]. The result of Proposition 5.1 is interpreted as follows. In the single-risk model, stop-loss insurance is the optimal strategy in the sense that it provides full indemnification above the deductible and thus completely eliminates the right-tail risk. When adding a positively dependent (in the sense of \(Y\uparrow _{\mathrm{rt}}X\)) background risk, the insurance demand for the right-tail risk is not reduced at all. Therefore, the stop-loss insurance is still needed.
Motivated by Proposition 5.1, it is natural to ask what is the optimal insurance strategy under the dependence structure of \(Y\sim _{\,\mathrm{PQD}}X\), which is a weaker assumption than that used in Proposition 5.1. While this question is generally challenging to answer, some results can be derived when the insurance premium becomes actuarially fair, as discussed in the next subsection.
5.2 Optimality of full insurance
Proposition 5.2
Full insurance is optimal if and only if
Furthermore, if the insurable loss \(X\)is positive almost surely, i.e., \(\mathbb{P}[X>0]=1\), then full insurance is optimal if and only if
Proof
The necessity and sufficiency of (5.1) for the optimality of full insurance directly follow from Theorem 3.3. Thus it remains to prove the equivalence between (5.1) and (5.2) for a positive insurable risk. Clearly, (5.2) implies (5.1). On the other hand, a combination of (3.6) and (5.1) yields that \({\nu _{\rho }} =0\), which implies \(\rho =0\) since \(X\) is positive almost surely. Therefore, (5.1) implies (5.2). □
Proposition 5.2 suggests that it is rational to purchase full insurance only when the insurance cost is relatively low, as described by (5.1). It should be noted that full insurance is an unusual choice, as evidenced by (5.2) as well as Corollary 3.4. Especially if the insurable loss \(X\) is positive almost surely, (5.2) indicates that in order to guarantee the optimality of full insurance, the insurance premium has to be actuarially fair, i.e., \(\rho =0\). In other words, if the safety loading coefficient \(\rho \) is positive, then full insurance is usually suboptimal. This result has been established by Mossin [25] for the single risk model, as stated below.
Corollary 5.3
Consider a single-risk insurance model, i.e., set \(Y=0\)in problem (2.3). The full-insurance strategy is optimal if and only if \(\rho =0\).
Proof
The conclusion directly follows from (5.1) by noting that the expression on the left-hand side of (5.1) reduces to 1 with the assumption \(Y=0\). □
Note that the necessary and sufficient condition for the optimality of full insurance in the single-risk model is much simpler than those in the presence of background risk. In particular, with background risk, \(\rho =0\) is not necessarily a sufficient condition for the optimality of full insurance. For example, if \(Y=-X\), it immediately follows from (4.1) that no-insurance is optimal, regardless of the value of \(\rho \), intuitively because \(X\) is perfectly hedged by \(Y\). Thus full insurance is suboptimal in this case.
Proposition 5.4
Full insurance is a solution to problem (2.3) for all increasing concave utility functions if and only if \(\rho =0\)and \(Y\sim _{\,\mathrm{PQD}}X\).
Proof
(Sufficiency) If \(\rho =0\) and \(Y\sim _{\,\mathrm{PQD}}X\), then the result is a direct corollary of Proposition 5.2 and Lemma A.1 by noting that \(u'(w-y-(1+\rho )\mathbb{E}[X])\) is increasing in \(y\) for any increasing concave utility function \(u(\cdot )\).
(Necessity) If full insurance is a solution to problem (2.3) for all increasing concave utility functions, we immediately get \(\rho =0\) by setting \(u(x)\equiv x\) in (5.1). Define \(v(y)=u'\big (w-y-(1+\rho )\mathbb{E}[X]\big )\) for any real \(y\). With \(\rho =0\), (5.1) reduces to \(\mathbb{E}[v(Y)|X>x] \ge \mathbb{E}[v(Y)]\) for any \(x\in [0,M)\) and any increasing function \(v(\cdot )\), which implies \(Y\sim _{\,\mathrm{PQD}} X\) according to Lemma A.1. □
Notably, Hong et al. [15] use the notion of positive expectation dependence, which is weaker than PQD, to study the optimal insurance problem with background risk. However, they focus only on the quota-share insurance. Specifically, they show that the insured should purchase less (more) than full insurance if and only if the insurable risk \(X\) is negatively (positively) expectation dependent with the background risk \(Y\). This problem is revisited by Lu et al. [22] by assuming the admissible strategy set of ℭ. [22, Proposition 4.2] obtains the optimality of full insurance under the assumption of \(Y\uparrow _{\mathrm{st}} X\) and \(\rho =0\). Note that \(Y\uparrow _{\mathrm{st}} X\) implies \(Y\sim _{\,\mathrm{PQD}}X\). In this sense, Proposition 5.4 extends the result of [22, Proposition 4.2].
More importantly, Proposition 5.4 reveals the relationship between the dependence structure and the optimality of full insurance. Mossin’s theorem (Corollary 5.3) establishes that full insurance is optimal if and only if \(\rho =0\) in the single-risk model. In the presence of background risk, the condition \(\rho =0\) is no longer sufficient for full insurance to be optimal, as evidenced by the remarks immediately after Corollary 5.3. It is the dependence structure that matters. Now Proposition 5.4 indicates that among different positive dependence notions, PQD is the minimal requirement to guarantee the full-insurance strategy to achieve the uniform optimality.
6 Moderate negative dependence
In this section, we investigate the optimal insurance design under the moderate negative dependence structure \((Y+X)\uparrow _{\mathrm{st}} X\) and \(Y\downarrow _{\mathrm{st}} X\). Intuitively, this dependence structure means that the background risk provides a partial, but not full, hedge for the insurable risk. Therefore, it is reasonable to anticipate that partial insurance coverage above a deductible would be needed. In order to avoid a tedious technical discussion, we make the following assumption
Assumption 6.1
(1) The conditional distribution of \(X\) given \(X > 0\) is continuous and \(S(X)=[0, M]\);
(2) \({\nu _{\rho }}>0\).
Under the above assumption, we must have \(\rho >0\), and hence the solution to problem (2.3) is unique according to Proposition 3.1. We should note that Assumption 6.1 does not exclude the possibility that the insurable loss \(X\) possesses a positive probability mass at zero. In that case, due to the definition of \(\nu _{\rho }\) in Corollary 3.4, the probability mass should satisfy \(\mathbb{P}[X=0]< \frac{\rho }{1+\rho }\). Furthermore, the assumption of \({\nu _{\rho }}>0\) together with (3.6) implies that \(\Phi _{f}({\nu _{\rho }})< 1+\rho \) for any \(f\in \mathfrak{C}\).
Proposition 6.2
Under Assumption 6.1, when \((Y+X)\uparrow _{\mathrm{st}} X\)and \(Y\downarrow _{\mathrm{st}} X\), \(f^{*}\in \mathfrak{C}\)is the solution to problem (2.3) if and only if it satisfies
for some \(d\in (\nu _{\rho },M]\).
Proof
(Sufficiency) Assume \(f\in \mathfrak{C}\) satisfies (6.1). Denote
Then \(\Phi _{{f}}(x)= \frac{\mathbb{E}[V_{f}(X)|X>x]}{\mathbb{E}[V_{f}(X)]}\) and hence \(\mathbb{E}[V_{f}(X)|X>x]=(1+\rho )\mathbb{E}[V_{f}(X)]\) for \(x\in (d,M)\) due to the second case in (6.1). This, together with the continuity of \(V_{f}(x)\) implied by Assumption 6.1, further leads to
Since \(f(x)=0\) for \(x\in [0,d]\), \((Y+X)\uparrow _{\mathrm{st}} X\) implies that \(V_{f}(x)\) is increasing over \([0,d]\). Therefore, for any \(x\in [0,d]\), we have
According to Theorem 3.3, \(f\) is the solution to problem (2.3).
(Necessity) Assume \({f^{*}}\) is the solution to problem (2.3). Recall that \(\Phi _{f^{*}}(x) < 1+\rho \) for any \(x\le {\nu _{\rho }}\) and that \(\Phi _{f^{*}}(x)\) is continuous over \((0,M)\) under Assumption 6.1. If \(\Phi _{f^{*}}(x) < 1+\rho \) for all \(x\in (0,M)\), then Theorem 3.3 implies that the solution is no-insurance, which satisfies (6.1) with \(d=M\). Otherwise, there exists a \(d\in (\nu _{\rho },M)\) such that
Consequently, we have \(f^{*}(x) =0\) for all \(x\in [0, d]\) due to Theorem 3.3. In the following, we show by contradiction that \(\Phi _{f^{*}}(x)=1+\rho \) for all \(x\in [d,M)\). Consider two cases:
(i) There exists an \(x_{0}\in (d,M)\) such that \(\Phi _{f^{*}}(x_{0})>1+\rho \). The continuity of \(\Phi _{f^{*}}(x)\) implies that there exist \(x_{\ell }\) and \(x_{u}\) such that
It follows from Theorem 3.3 that \({f^{*}}'(x)=1\) and hence \(V_{f^{*}}(x)\) is decreasing over \((x_{\ell }, x_{u})\) because \(Y\downarrow _{\mathrm{st}} X\). If \(x_{u}=M\), then \(\Phi _{f^{*}}(x)\) is decreasing over \([x_{\ell }, M)\) and thus \(1+\rho <\Phi _{f^{*}}(x_{0})\le \Phi _{f^{*}}(x_{\ell })=1+\rho \), leading to a contradiction. Otherwise, if \(x_{u}< M\), then \(\Phi _{f^{*}}(x_{u})=1+\rho \). Using an argument similar to case (i)(b) of Lemma A.3, a contradiction can be derived.
(ii) There exists an \(x_{1}\in (d,M)\) such that \(\Phi _{f^{*}}(x_{1})<1+\rho \). A contradiction can also be derived by using a similar argument to case (i).
Combining cases (i) and (ii) yields \(\Phi _{f^{*}}(x)= 1+\rho \) for any \(x\in (d,M)\). □
Remark 6.3
In (6.1), \(d\) is a parameter to be determined. According to (3.6), \(d\) should fall in the set \(({\nu _{\rho }},M]\). Proposition 3.1 has established the existence and uniqueness of the solution to problem (2.3). Therefore, Proposition 6.2 indicates that the solution to (6.1) exists and is unique within the set ℭ. It is possible that (6.1) has other solutions not belonging to ℭ. However, this can be excluded by adding some regularity condition such as the existence of a joint density function of the random vector \((X, Y)\).
Proposition 6.2 shows that the optimal insurance strategy \(f^{*}\) satisfies \({f^{*}}(x) =0\) for \(x\in [0,d]\) and \({f^{*}}'(x) \in [0,1]\) for \(x\in (d,M)\). In other words, the optimal insurance strategy is partial coverage above a deductible under the assumption that \(Y\downarrow _{\mathrm{st}} X\) and \((Y+X) \uparrow _{\mathrm{st}} X\). This makes sense because \(Y\downarrow _{\mathrm{st}} X\) indicates that the background risk \(Y\) is negatively dependent with \(X\) and thus provides a hedge to some extent. On the other hand, \((Y+X) \uparrow _{\mathrm{st}} X\) indicates that the hedge for \(X\) provided by \(Y\) is not adequate and the unhedged portion still calls for insurance coverage.
Below, we derive another equation for the solution based on (6.1), which can be used to develop a numerical solution scheme.
Corollary 6.4
Under Assumption 6.1, when \((Y+X)\uparrow _{\mathrm{st}} X\)and \(Y\downarrow _{\mathrm{st}} X\), \(f^{*}\in \mathfrak{C}\)is the solution to problem (2.3) if and only if it satisfies
where \(\tau =\mathbb{E}[f^{*}(X)]\), \(K_{\tau }(x,t)=\mathbb{E} [u'' (w-Y-X-(1+\rho )\tau +t )|X=x ]\)and the parameter \(d\in ({\nu _{\rho }},M]\)is determined by
with \(\chi _{\tau }(x)=\mathbb{E} [u' (w-Y-X-(1+\rho )\tau ) |X=x ]\).
Proof
Due to Proposition 6.2, it suffices to verify that (6.1) and (6.4) are equivalent.
“(6.1) ⟹ (6.4)” If (6.1) holds, then we have (6.3), i.e.,
where \(V_{f}(x)\) is defined in (6.2). Note that \(V_{f^{*}}(x)=\chi _{\tau }(x)\) for all \(x\in [0,d]\). (6.6) implies that \(V_{f^{*}}(x)=V_{f^{*}}(d)\) and thus \(V_{f^{*}}(x)= \chi _{\tau }(d)\) for all \(x\in [d,M)\). Since \((Y+X)\uparrow _{\mathrm{st}} X\), then \(\chi _{\tau }(x)\) is increasing in \(x\) and thus \(V_{f^{*}}(x) = \chi _{\tau }(x) \wedge \chi _{\tau }(d)\), which together with (6.6) yields (6.5). On the other hand, noting that
we have
which implies the first case in (6.4) by recalling \(V_{f^{*}}(x)=\chi _{\tau }(d)\) for all \(x\in [d,M)\).
“(6.4) ⟹ (6.1)” Note that (6.7) generally holds true. Combining it with the first case of (6.4), we have \(V_{f}^{*}(x) = \chi _{\tau }(d)\) for all \(x\in [d,M)\). Following the same argument as in the first part, we have \(V_{f^{*}}(x) = \chi _{\tau }(x) \wedge \chi _{\tau }(d)\), which together with (6.5) implies (6.6). Thus \(\Phi _{f^{*}}(x) = 1+\rho \) for all \(x\in (d,M)\) and (6.1) is verified. □
It is worth noting that the dependence structure \(Y \downarrow _{\mathrm{st}} X\) and \((Y+X)\uparrow _{\mathrm{st}} X\) has been considered by Dana and Scarsini [10] for analysing the optimal insurance design. Their study is merely qualitative, concluding that the solution \(f^{*}\) should fall in ℭ even if the no-sabotage condition is removed. The results derived in this section make solid progress towards completely solving the optimal insurance problem under this dependence structure. Specifically, Proposition 6.2 quantitatively identifies the form of the optimal insurance, and Corollary 6.4 provides a scheme to numerically derive the optimal insurance strategy. Below, we illustrate the general idea to find the numerical solution but omit the details of implementation:
-
(i)
Choose a value from \([0, \mathbb{E}[X]]\) and assign it to \(\tau \).
-
(ii)
For the chosen \(\tau \), solve (6.5) for \(d\).
-
(iii)
Derive an expression for \(f(x)\) based on (6.4).
-
(iv)
Check whether the equation \(\tau =\mathbb{E}[f(X)]\) and \(f\in \mathfrak{C}\) hold.
-
(v)
If yes, the obtained \(f\) is the desired solution. Otherwise, let \(\tau \) run through all the values in \([0, \mathbb{E}[X]]\) (with a small step) and repeat (ii)–(iv) until the conditions in (iv) are satisfied (up to some precision criterion).
7 CARA utility functions
In this section, we focus on a CARA utility function, i.e.,
for some \(\gamma >0\). With this utility function, the objective function can be rewritten as
for any \(f\in \mathfrak{C}\), where
Therefore, solving problem (2.3) is equivalent to solving the optimisation problem
Note that problem (7.1) can be treated as a special case of the original optimisation problem (2.3), with \(Y+X=m(X)\). Therefore, all the results derived in previous sections can apply to problem (7.1).
Motivated by the equivalence between problems (2.3) and (7.1) under the CARA assumption, we use \(m(x)\) to categorise the dependence structure between insurable and background risks in this section. The dependence structures discussed in the previous sections can be connected to the behavior of \(m(x)\) in the following way:
-
(i)
If \(Y+X \downarrow _{\mathrm{st}} X\), then \(m'(x)\le 0\).
-
(ii)
If \(Y \uparrow _{\mathrm{st}} X\), then \(m'(x)\ge 1\).
-
(iii)
If \(Y+X \uparrow _{\mathrm{st}} X\) and \(Y \downarrow _{\mathrm{st}} X\), then \(0 \le m'(x)\le 1\).
Scenarios (i) and (ii) correspond to a special case of strong negative dependence and positive dependence as discussed in Sects. 4 and 5, respectively, under which the solutions have been explicitly derived. Scenario (iii) corresponds to the moderate negative dependence structure discussed in Sect. 6. Recall that Sect. 6 has not obtained an explicit solution under this dependence structure. The following proposition shows that problem (7.1) as a special form of problem (2.3) can be explicitly solved in that case.
Proposition 7.1
If \(0 \le m'(x) \le 1\), then the solution to problem (7.1) is given by \(f^{*}(x) = (m(x)-m(d^{*}))^{+}\)for some nonnegative \(d^{*}\in [{\nu _{\rho }}, M]\).
Proof
The proof is similar to that of Proposition 5.1 and thus omitted. □
In view of Proposition 7.1 and the discussion before it, problem (7.1) has been explicitly solved under the dependence structures of (i) \(m'(x) \le 0\), (ii) \(m'(x) \ge 1\), and (iii) \(0 \le m'(x) \le 1\). It should be noted that these three dependence structures cannot capture the full spectrum of the relationship between background and insurable risks. It is necessary to analyse the optimal insurance design under other types of dependence. In the rest of this section, we study the following mixed dependence structures, for some \(x_{0}\in (0, M)\):
Case 1. \(m'(x)\le 0\) for \(0 \le x\le x_{0}\) and \(0\le m'(x) \le 1\) for \(x>x_{0}\).
Case 2. \(0\le m'(x)\le 1\) for \(0\le x\le x_{0}\) and \(m'(x) \le 0\) for \(x>x_{0}\).
Case 3. \(m'(x) \ge 1\) for \(0 \le x\le x_{0}\) and \(0\le m'(x) \le 1\) for \(x>x_{0}\).
Case 4. \(0\le m'(x) \le 1\) for \(0 \le x\le x_{0}\) and \(m'(x) \ge 1\) for \(x>x_{0}\).
In order to avoid a tedious technical discussion, we carry out the analysis under Assumption 6.1, and hence the solution to problem (2.3) is unique. The same holds for problem (7.1). It will be solved for these four cases in the following propositions.
Proposition 7.2
In Case 1, the solution to problem (7.1) is given by
for some \(d^{*}_{1}\ge x_{0}\vee {\nu _{\rho }}\), where \(x\vee y=\max \{x, y\}\).
Proof
Define
for \(d\ge x_{0}\vee {\nu _{\rho }}\), where \(m_{d}^{T}(X)=(m(X)-m(d))^{+}\mathbb{I}_{\{X>x_{0}\}}\). By simple calculation, we have
where the last inequality is derived by \(m'(d)\ge 0, u'(\cdot )>0, u''(\cdot )<0\) and
In other words, \(d \mapsto L(d)\) is increasing over \([x_{0}\vee {\nu _{\rho }}, M )\).
Noting that \(m(x)\ge m(x_{0})\) for any \(x\ge 0\), it holds almost surely that
Since \(u'(\cdot )\) is decreasing, we conclude that \(L(x_{0})\le 1\). If \({\nu _{\rho }}>x_{0}\), we can get from (3.6) and Assumption 6.1 that \(L({\nu _{\rho }})\le 1+\rho \). Therefore, we can define
If \(d^{*}_{1}<\infty \), then for any \(x\ge d^{*}_{1}\), we have
where \(\Phi _{f}(x)\) is defined in (3.4) with \(Y+X=m(X)\). We prove \(\Phi _{f^{*}}(x)\le 1+\rho \) for any \(0\le x< d^{*}_{1}\), and hence \(f^{*}\) is the solution to problem (7.1) according to Theorem 3.3. Specifically, the proof is divided into two cases:
(i) If \(m(d^{*}_{1}) \ge m(0)\), then \(m(d^{*}_{1}) \ge m(x)\) for any \(0\le x\le d^{*}_{1}\). For notational convenience, we rewrite \(W_{f}(X,m(X)-X)\) as \(W_{f}(X)\). For each \(x\in [0, d^{*}_{1}]\), noting that \(f^{*}(x) = 0\), we have
Since \(W_{f^{*}}(x) = W_{f^{*}}( d_{1}^{*})\) for any \(x \ge d^{*}_{1}\), it holds for any \(x \ge 0\) that
where the equality follows from the fact that \(L(d^{*}_{1})=1+\rho \). As a consequence, we have \(\Phi _{f^{*}}(x) \le 1+\rho \) for all \(x\in [0, d_{1}^{*}]\).
(ii) If \(m(d_{1}^{*}) < m(0)\), there exists an \(x_{1}\in [0,x_{0}]\) such that \(m(x) \ge m({d}^{*}_{1})\) for any \(x\in [0, x_{1}]\) and \(m(x) \le m({d}^{*}_{1})\) for any \(x\in [x_{1}, {d}^{*}_{1})\). For any \(x \in [x_{1}, {d}^{*}_{1})\), similarly to (7.2), we can conclude that \(W_{f^{*}}(x) \ge W_{f^{*}}(d_{1}^{*})\) and thus
which implies \(\Phi _{f^{*}}(x) \le 1+\rho \). For any \(x\in [0, x_{1}]\), since \(m(x) \ge m(d_{1}^{*})\), we get
On the other hand, note that
Combining (7.3) and (7.4), we obtain \(\mathbb{E}[u'(W_{f^{*}}(X))|X>x] \le \mathbb{E}[u'(W_{f^{*}}(X))]\). Therefore, \(\Phi _{f^{*}}(x) = \frac{\mathbb{E}[u'(W_{f^{*}}(X))|X>x]}{\mathbb{E}[u'(W_{f^{*}}(X))]} \le 1 \le 1+\rho \) for any \(x\in [0,x_{1})\). This ends the case \(d_{1}^{*} < \infty \).
If \(d_{1}^{*}=\infty \), we have \(f^{*}(X)=0\) and
for any \(t\in [x_{0}, M)\), where the last inequality is derived by the fact \(m'(x)\ge 0\) for all \(x\ge x_{0}\). Thus we have \(\Phi _{f^{*}}(t)= \frac{\mathbb{E} [u'(w-m(X))|X>t ]}{\mathbb{E} [u'(w-m(X)) ]}\le 1+\rho \) for all \(t\in [x_{0},M)\). We prove that this inequality also holds for each \(t\in [0, x_{0})\), and hence \(f^{*}(x)\equiv 0\) (the no-insurance strategy) is the solution according to Theorem 3.3. Specifically, the proof is divided into two cases:
(i) If \(u'(w-m(0))\le (1+\rho )\mathbb{E} [u'(w-m(X)) ]\), then for any \(0\le t< x_{0}\),
where the first inequality is derived by the fact that \(m'(x)\le 0\) for \(x\le x_{0}\).
(ii) If \(u'(w-m(0))> (1+\rho )\mathbb{E} [u'(w-m(X)) ]\), there must exist a \(t_{0}\in (0, x_{0})\) such that \(u'(w-m(t_{0}))=(1+\rho )\mathbb{E} [u'(w-m(X)) ]\). Using a similar argument, we have \(\frac{\mathbb{E} [u'(w-m(X))|X>t ]}{\mathbb{E} [u'(w-m(X)) ]}\le 1+ \rho \) for any \(t\in [t_{0}, x_{0})\). On the other hand, noting that \(u'(w-m(x))\) is decreasing on \([0, t_{0}]\) and by virtue of (7.3) and (7.4), we have
for any \(t\in [0,t_{0})\). As a consequence, \(\frac{\mathbb{E} [u'(w-m(X))|X>t ]}{\mathbb{E} [u'(w-m(X)) ]}\le 1+ \rho \) for any \(t\in [0, x_{0})\). This ends the case \(d_{1}^{*}= \infty \). □
Proposition 7.3
In Case 2, the solution to problem (7.1) is given by
for some \({\nu _{\rho }}\wedge x_{0}\le d_{2}^{L} \le d_{2}^{U} \le x_{0}\).
Proof
Let \(f^{*}\) be the solution to problem (7.1). Under Assumption 6.1, it follows from (3.6) that \(\Phi _{f^{*}}(x) < 1+\rho \) for any \(0\le x\le {\nu _{\rho }}\). Furthermore, for each \(x\in [{\nu _{\rho }}, M)\), Lemma A.3 (iii) implies \(\Phi _{f^{*}}(x) \le 1+ \rho \) since \(m'(x)\le 1\). Therefore, \(\Phi _{f^{*}}(x) \le 1+ \rho \) for all \(x\in [0,M)\).
If \(\Phi _{f^{*}}(x) < 1+\rho \) for all \(x\in [0,M)\), it follows from Theorem 3.3 that the solution is no-insurance, which is a special case of (7.5) by setting \(d_{2}^{L}=d_{2}^{U}\).
Otherwise, define
We have \(\Phi _{f^{*}}(d_{2}^{L}) = \Phi _{f^{*}}(d_{2}^{U})=1+\rho \) and \({\nu _{\rho }}< d_{2}^{L}\le d_{2}^{U}\).
If \(d_{2}^{U}\le x_{0}\), recalling that \(0\le m'(x)\le 1\) for all \(x\in [d_{2}^{L}, d_{2}^{U}]\), we get from Lemma A.3 (i)(c) that \(\Phi _{f^{*}}(x) =1+\rho \) for any \(x \in [d_{2}^{L}, d_{2}^{U}]\) and \(\Phi _{f^{*}}(x)<1+\rho \) elsewhere, due to the definitions of \(d_{2}^{L}\) and \(d_{2}^{U}\). This implies that \(f^{*}(x)\) admits the form (7.5) according to Theorem 3.3 and Lemma A.3 (ii).
If \(d_{2}^{U} > x_{0}\), then \(\Phi _{f^{*}}(x) \ge \Phi _{f^{*}}(d_{2}^{U})=1+\rho \) for any \(x\in [x_{0}, d_{2}^{U}]\) since \(m(x)-f^{*}(x)\) is decreasing on \([x_{0}, {M})\). Recalling that \(\Phi _{f^{*}}(x) \le 1+\rho \) for all \(x\in [0,M)\), it must hold that \(\Phi _{f^{*}}(x)=1+\rho \) for all \(x\in [x_{0}, d_{2}^{U}]\). According to Lemma A.3 (i)(c), we also have \(\Phi _{f^{*}}(x)= 1+\rho \) for all \(x\in [d_{2}^{L}, x_{0}]\) since \(0\le m'(x)\le 1\) for \(x\in [d_{2}^{L}, x_{0}]\). Due to the definitions of \(d_{2}^{L}\) and \(d_{2}^{U}\), we conclude that \(\Phi _{f^{*}}(x)<1+\rho \) for any \(x < d_{2}^{L}\) or \(x>d_{2}^{U}\).
As a consequence, we have \({f^{*}}'(x)=0\) for any \(x< d_{2}^{L}\) or \(x> d_{2}^{U}\) according to Theorem 3.3 and \({f^{*}}'(x)=m'(x)\) for any \(x \in (d_{2}^{L}, d_{2}^{U})\) according to Lemma A.3 (ii). For each \(x\in (x_{0}, d_{2}^{U}) \subseteq (d_{2}^{L}, d_{2}^{U})\), noting that \({f^{*}}'(x)\ge 0\ge m'(x)\), it must hold that \({f^{*}}'(x)=m'(x)=0\). Therefore, \(f^{*}(x)\) still admits the form given in (7.5). □
Proposition 7.3 identifies the optimal insurance form when background risk \(Y\) and insurable risk \(X\) follow the dependence structure specified in Case 2. Intuitively, when \(X>x_{0}\), the combined risk \(m(X)\) is decreasing in \(X\), meaning that the increment of \(X\) is completely hedged by \(Y\) and thus no-insurance is needed. When \(X\in [0,x_{0}]\), the combined risk \(m(X)\) can be treated as a single one and a one-layer insurance form is applied to \(m(X)\). We remark that if \(x_{0} \le {\nu _{\rho }}\), it is easy to conclude that the optimal strategy is no-insurance, which is a special case of (7.5) by setting \(d_{2}^{L}= d_{2}^{U}\).
Proposition 7.4
In Case 3, the solution \(f^{*}(x)\)to problem (7.1) admits one of the following forms:
(a) \(f^{*}(x) = (m(x) - m(d_{3}^{U}))^{+}\)for some constant \(d_{3}^{U}\)with \(x_{0}\le d_{3}^{U} \le M\);
(b) \(f^{*}(x) = (x-d_{3}^{L})^{+} \mathbb{I}_{\{x\le d_{3}^{U}\}} + (m(x) - m(d_{3}^{U}))^{+}\)for some constants \(d_{3}^{L}, d_{3}^{U}\)with \(0\le d_{3}^{L} \le x_{0} \le d_{3}^{U}\le M\).
Proof
First, consider the case \(\Phi _{f^{*}}(x_{0})< 1+\rho \). Since \(m'(x)\le 1\) for any \(x\ge x_{0}\), it follows from Lemma A.3 (iii) that \(\Phi _{f^{*}}(x) \le 1+\rho \) for all \(x\ge x_{0}\). Define
We have \(\Phi _{f^{*}}(x)< 1+\rho \) for any \(x\in [x_{0}, d^{U}_{3})\) and \(\Phi _{f^{*}}(x) = 1+\rho \) for any \(x \in [d^{U}_{3},M)\) according to Lemma A.3 (iii′). Therefore \(m(x) -f^{*}(x)\) is increasing on \([x_{0}, d_{3}^{U}]\) and constant on \([d_{3}^{U}, M)\) according to Theorem 3.3 and Lemma A.3 (ii). Recalling that \(m'(x) \ge 1\) for any \(x\le x_{0}\), it follows from (2.1) that \(m(x)-f^{*}(x)\) is increasing over \([0, x_{0}]\). Therefore \(m(x)-f^{*}(x)\) is increasing over \([0, M)\), which implies that \(\Phi _{f^{*}}(x)\) is increasing and thus \(\Phi _{f^{*}}(x) \le \Phi _{f^{*}}(x_{0}) < 1+\rho \) for any \(x\le x_{0}\). According to Theorem 3.3, we have \({f^{*}}'(x)=0\) for any \(x \le d_{3}^{U}\) and \(m'(x)={f^{*}}'(x)\) on \([d_{3}^{U}, M)\). That is, \({f^{*}}(x)\) admits the form (a).
Second, consider the case \(\Phi _{f^{*}}(x_{0}) > 1+\rho \). Define
Under Assumption 6.1, it is easy to see that \({\nu _{\rho }}< d_{3}^{L}< x_{0}< d_{3}^{U}\), \(\Phi _{f^{*}}(d_{3}^{L}) = 1+\rho \) and \(\Phi _{f^{*}}(x) > 1+\rho \) for any \(x\in (d_{3}^{L}, d_{3}^{U})\). Recalling that \(m'(x)\ge 1\) for \(x\in [0, x_{0}]\), we get that \(u'(W_{f^{*}}(x))\) is increasing on \([0, x_{0}]\) and hence
which is equivalent to \(\frac{ u'(W_{f^{*}}(d_{3}^{L}))}{\mathbb{E}[u'(W_{f^{*}}(X))]}<1+ \rho \). Consequently, for any \(x\in [0,d_{3}^{L})\),
If \(d_{3}^{U} <{M}\), then \(\Phi _{f^{*}}(d_{3}^{U})=1+\rho \) due to the continuity of \(\Phi _{f^{*}}(x)\). According to Lemma A.3 (iii′), we have \(\Phi _{f^{*}}(x)=1+\rho \) for any \(x\in [d_{3}^{U}, M)\). If \(d_{3}^{U} ={M}\), then \(\Phi _{f^{*}}(x) > 1+\rho \) for any \(x\in (d_{3}^{L}, M)\) due to the definitions of \(d_{3}^{L}\) and \(d_{3}^{U}\). Either way, we conclude that \(\Phi _{f^{*}}(x) < 1+\rho \) for any \(x\in [0, d_{3}^{L})\), \(\Phi _{f^{*}}(x) > 1+\rho \) for any \(x\in (d_{3}^{L}, d_{3}^{U})\), and \(\Phi _{f^{*}}(x) = 1+\rho \) for any \(x\in [d_{3}^{U}, M)\). According to Theorem 3.3 and Lemma A.3 (ii), we have \({f^{*}}'(x)=0\) for any \(x\in [0, d_{3}^{L})\), \({f^{*}}'(x)=1\) for any \(x\in (d_{3}^{L}, d_{3}^{U})\) and \({f^{*}}'(x)=m'(x)\) for any \(x\in (d_{3}^{U}, M)\). Therefore \(f^{*}(x)\) admits the form (b) for this case.
Finally, we consider the case \(\Phi _{f^{*}}(x_{0}) = 1+\rho \). Recalling that \(0\le m'(x)\le 1\) for \(x>x_{0}\), we have \(\Phi _{f^{*}}(x)=1+\rho \) for any \(x\in [x_{0}, M)\) according to Lemma A.3 (iii′), and thus \(m'(x)={f^{*}}'(x)\) for \(x\in (x_{0}, {M})\) due to Lemma A.3 (ii). Since \(m'(x)\ge 1\) for any \(x\in (0, x_{0})\), then \(m(x) - f^{*}(x)\) is increasing on \([0, x_{0}]\) and thus on \([0, M)\). Therefore \(\Phi _{f^{*}}(x)\) is increasing on \([0,M)\), and so \(\Phi _{f^{*}}(x)\le \Phi _{f^{*}}(x_{0})=1+\rho \) for any \(x\le x_{0}\). Define \(x_{3}=\inf \{x\in [0, x_{0}]: \Phi _{f^{*}}(x)=1+\rho \}\). We have \(\Phi _{f^{*}}(x)<1+\rho \) for any \(x\in [0, x_{3})\) and \(\Phi _{f^{*}}(x_{3})=1+\rho \) due to the continuity of \(\Phi _{f^{*}}(x)\). Then the increasing property of \(\Phi _{f^{*}}(x)\) implies that \(\Phi _{f^{*}}(x)=1+\rho \) for any \(x\ge x_{3}\). Using Theorem 3.3 and Lemma A.3 (ii), we get \({f^{*}}'(x)=0\) for \(x\in (0, x_{3})\) and \({f^{*}}'(x)=m'(x)\) for \(x\in (x_{3}, M)\). On the other hand, for any \(x\in (x_{3}, x_{0})\), noting that \({f^{*}}'(x)\le 1\le m'(x)\), we must have \({f^{*}}'(x)=m'(x)=1\). Therefore \(f^{*}\) admits the form (b) with \(d_{3}^{L}=x_{3}\) and \(d_{3}^{U}=x_{0}\). □
Proposition 7.5
In Case 3, the solution to (7.1) is given by \(f^{*}(x)= (m(x) - m(d_{3}))^{+}\)for some \(d_{3}\in [x_{0},M]\)if \(\Phi _{f^{0}_{x_{0}}}(x_{0}) \le 1+\rho \), where \(f^{0}_{x_{0}}(x) = (m(x) - m(x_{0}))^{+}\).
Proof
If \(x_{0}\le {\nu _{\rho }}\), it follows from (3.6) that \(\Phi _{f^{*}}(x_{0}) < 1+\rho \) under Assumption 6.1. Therefore, similarly to the proof of Proposition 7.4, we can conclude that \(f^{*}(x)= (m(x) - m(d_{3}))^{+}\) for some \(d_{3}\in [x_{0},M]\). If \(x_{0}> {\nu _{\rho }}\), using a proof similar to that of Chi and Wei [9, Proposition 5.1], we can show that \(d \mapsto \Phi _{f^{0}_{d}}(d)\) is increasing over \([x_{0}, {M})\). Note that \(\lim _{d\uparrow {M}} \Phi _{f^{0}_{d}}(d) = \frac{u'(w-m({M}))}{\mathbb{E}[u'(w-m(X))]}\).
If \(\lim _{d\uparrow {M}} \Phi _{f^{0}_{d}}(d) \ge 1+ \rho \), there exists a \(d_{3}\in [x_{0}, M]\) such that \(\Phi _{f^{0}_{d_{3}}}(d_{3}) = 1+ \rho \), because \(d \mapsto \Phi _{f^{0}_{d}}(d)\) is continuous and it is assumed that \(\Phi _{f^{0}_{x_{0}}}(x_{0}) \le 1+\rho \). In Case 3, it is easy to see that \(x \mapsto -W_{f^{0}_{d_{3}}}(x)\) is increasing over \([0, d_{3}]\) and constant afterwards. So is \(x \mapsto \mathbb{E}[u'(W_{f^{0}_{d_{3}}}(X))|X>x]\). Thus, \(\Phi _{f^{0}_{d_{3}}}(x)=1+\rho \) for \(x \ge d_{3}\) and \(\Phi _{f^{0}_{d_{3}}}(x) \le 1+\rho \) for \(x \le d_{3}\). According to Theorem 3.3, \(f^{0}_{d_{3}}(x) =(m(x)-m(d_{3}))^{+}\) is a solution.
If \(\frac{u'(w-m({M}))}{\mathbb{E}[u'(w-m(X))]} < 1+ \rho \), noting that \(x \mapsto u'(w-m(x))\) is increasing gives
According to Proposition 4.1, the solution is no-insurance, which is a special form of \(f^{*}(x) = (m(x)-m(d))^{+}\) with \(d=M\). □
Remark 7.6
From the above result, we can see that in Case 3, the optimal insurance admits the form \(f^{*}(x)= (m(x) - m(d_{3}))^{+}\) for some \(d_{3} \in ({\nu _{\rho }}, M]\) when \(x_{0}\le {\nu _{\rho }}\).
Proposition 7.7
In Case 4, the solution \(f^{*}(x)\)to problem (7.1) admits one of the following forms:
(a) \(f^{*}(x) = (x - d_{4}^{U})^{+}\)for some constant \(d_{4}^{U}\)with \(d_{4}^{U} \in [x_{0}, {M}]\);
(b) \(f^{*}(x) = (m(x) - m(d_{4}^{L}))^{+}\mathbb{I}_{\{x\le d_{4}^{M}\}} + (x-d_{4}^{M})^{+}\)for some constants \(d_{4}^{L}, d_{4}^{M}\)with \(0\le d_{4}^{L} \le d_{4}^{M} \le x_{0}\).
Proof
First, consider the case \(\Phi _{f^{*}}(x_{0}) \ge 1+\rho \). According to Lemma A.3 (iv), we have \({f^{*}}'(x)=1\) for any \(x> x_{0}\). If \(\Phi _{f^{*}}(x_{0}) = 1+\rho \), set \(d_{4}^{M}=x_{0}\). Otherwise, let
Under Assumption 6.1, we have \(d_{4}^{M} >{\nu _{\rho }}\) and \(\Phi _{f^{*}}(d_{4}^{M}) =1+\rho \). By Theorem 3.3, we have \({f^{*}}'(x)=1\) for any \(x\in (d_{4}^{M}, x_{0})\). Further, if we define
then \({\nu _{\rho }}< d_{4}^{L}\le d_{4}^{M}\) and \(\Phi _{f^{*}}(d_{4}^{L}) =1+\rho \) due to the continuity of \(\Phi _{f^{*}}(x)\). From Lemma A.3 (i)(c) and (ii), we have \(\Phi _{f^{*}}(x) = 1+\rho \) and thus \(m'(x)={f^{*}}'(x)\) for \(x\in (d_{4}^{L}, d_{4}^{M})\). According to the definition of \(d_{4}^{L}\), we have either \(\Phi _{f^{*}}(x) > 1+\rho \) for all \(x < d_{4}^{L}\) or \(\Phi _{f^{*}}(x) < 1+\rho \) for all \(x < d_{4}^{L}\). Since \({\nu _{\rho }}< d_{4}^{L}\) and \(\Phi _{f^{*}}({\nu _{\rho }})<1+\rho \), the latter case must hold, i.e., \(\Phi _{f^{*}}(x) < 1+\rho \) for all \(x < d_{4}^{L}\). This implies \({f^{*}}'(x)=0\) for \(x< d_{4}^{L}\) according to Theorem 3.3. In summary, when \(\Phi _{f^{*}}(x_{0}) \ge 1+\rho \), we have
That is, the solution \(f^{*}\) admits the form (b).
Second, consider the case \(\Phi _{f^{*}}(x_{0}) <1+\rho \). Define
Clearly, \(\Phi _{f^{*}}(x) < 1+\rho \) and thus \({f^{*}}'(x)=0\) for \(x\in (x_{4}, d_{4}^{U})\). Furthermore, it can be concluded that \(x_{4} = 0\). Otherwise, we have \(0< x_{4}< x_{0}\), and thus \(\Phi _{f^{*}}(x_{4}) = 1+\rho \) and \(\Phi _{f^{*}}(x) < 1+\rho \) for any \(x\in (x_{4}, x_{0}]\). According to Theorem 3.3, we have \({f^{*}}'(x)=0\) on \((x_{4}, x_{0}]\); then \(m(x)-f^{*}(x)\) is increasing on \([x_{4}, M)\) and so is \(\Phi _{f^{*}}(x)\). Therefore, we get \(\Phi _{f^{*}}(x_{4}) \le \Phi _{f^{*}}(x_{0}) < 1+\rho \), which contradicts \(\Phi _{f^{*}}(d_{4}^{L}) = 1+\rho \). If \(d_{4}^{U} ={M}\), then \(\Phi _{f^{*}}(x) < 1+\rho \) for any \(x \in [0, M)\) and hence the solution is no-insurance, which is a special case of form (a). If \(d_{4}^{U} < {M}\), then \(\Phi _{f^{*}}(d_{4}^{U})=1+\rho \). Since \(m'(x)\ge 1\) for any \(x>d_{4}^{U}\), Lemma A.3 (iv) implies \({f^{*}}'(x)=1\) for any \(x>d_{4}^{U}\). Recalling that \({f^{*}}'(x)=0\) for any \(x\in (0, d_{4}^{U})\), we conclude that the solution \(f^{*}\) admits the form (a). □
Remark 7.8
Proposition 7.7 gives two possible forms for the solution to problem (7.1) in Case 4. Note that both suggest that the insured should cede all the tail risk. This makes sense because with the structure specified in Case 4, the background risk becomes stochastically increasing with the insurable risk when the insurable loss exceeds \(x_{0}\). Similarly to Remark 7.6, we note that the solution to problem (7.1) in Case 4 must admit the form (a) if \(x_{0}\le {\nu _{\rho }}\). Further, we develop a weaker sufficient condition to decide when the solution takes the form (a) in the following proposition.
Proposition 7.9
In Case 4, the stop-loss insurance \(f^{\mathrm{sl}}_{d_{4}}(x)=(x-d_{4})^{+}\)for \(d_{4} \ge x_{0}\)is the solution to problem (7.1) if \(\Phi _{f^{\mathrm{sl}}_{x_{0}}}(x_{0}) \le 1+\rho \).
Proof
The proof is very similar to that of Proposition 7.5 and thus omitted. □
While the preceding analysis is restricted to CARA utility functions, it is also applicable to any other increasing concave utility function if the dependence structure between \(X\) and \(Y\) is of some special form.
Proposition 7.10
If \(Y+X=m(X)+\epsilon \)for some function \(m(x)\)and a random variable \(\epsilon \)independent of \(X\), the results of Propositions 7.1–7.5, 7.7and 7.9still hold true for any risk-averse insured.
Proof
Defining \(\hat{u}(w)=\mathbb{E}[u(w-\epsilon )]\), we have \(\hat{u}'(\cdot )>0\) and \(\hat{u}''(\cdot )<0\). Since \(\epsilon \) is independent of \(X\), the analysis of problem (2.3) with \(Y+X=m(X)+\epsilon \) is equivalent to solving the maximisation problem
But that is the same as problem (7.1), only with a different insured’s utility function. Therefore, we obtain the desired results by using the same arguments. □
Interestingly, Proposition 7.4 shows that the optimal ceded loss function may satisfy \({f^{*}}'(x)=1\) while \(m'(x)\le 1\) for some \(x\in [x_{0},d_{3}^{U})\) in Case 3. That is, the optimal strategy may overinsure this part of the insurable risk. The following example is used to justify the existence of such an over-insurance situation.
Example 7.11
In this example, we assume that \(X\) is uniformly distributed on \([0,1]\) and \(Y+X=m(X)\), where
We choose the safety loading coefficient \(\rho = 0.1\) and we use the utility function \(u(z) = -0.5(w-z)^{2}\) with \(z\le w\), where \(w\) is the insured’s initial wealth. This utility function is often called the quadratic utility function in the literature, and it is applicable for our setting because
for any \(f\in \mathfrak{C}\), where the inequality uses \(m(x)\ge x\ge f(x)\) for all \(x\in [0,1]\).
In this setting, problem (2.3) is equivalent to problem (7.1). Consider the stop-loss insurance form \(f_{d}(x) =(x-d)^{+}\) for \(d\in [0,1]\). Note that \({\mathbb{E}[f_{d}(X)]=0.5(1-d)^{2}}\), \(u'(z) = w-z\) and \(W_{f_{d}}(X) = w- m(X) + f_{d}(X) -(1+\rho )\mathbb{E}[f_{d}(X)]\). For \(0\le d<0.9\), simple calculations yield that
Set \(d^{*}= 0.123525\). It is easy to verify that \(\Phi _{f_{d^{*}}}(d^{*}) = 1+\rho \). Furthermore, \(x \mapsto u'(W_{f_{d^{*}}}(x))\) is increasing over \([0,0.9]\) and decreasing afterwards with
Similarly as in the proof of Proposition 7.2, it can be shown that \(\Phi _{f_{d^{*}}}(x) <1+\rho \) for \(x < d^{*}\) and \(\Phi _{f_{d^{*}}}(x) >1+\rho \) for \(x > d^{*}\). Therefore, \(f_{d^{*}}\) is the solution to problem (7.1) according to Theorem 3.3. Notably, \(f'_{d^{*}}(x)=1\) while \(m'(x) =0.9<1\) on the interval \([0.9,1]\), indicating an over-insurance situation.
8 Concluding remarks
In this paper, we study an optimal insurance problem in the presence of background risk, where alternative insurance contracts are asked to satisfy the principle of indemnity and the no-sabotage condition. We first establish in Theorem 3.3 a necessary and sufficient condition for the optimality of any given admissible ceded loss function and then provide a way to enhance any suboptimal insurance strategy under an arbitrary dependence structure. Theorem 3.3 suggests that the optimal ceded loss function should roughly possess a multilayer form. With the help of this result, we show the optimality of insurance forms of general interest and also solve the optimal insurance problem under different types of dependence structures.
We mainly focus on three categories of dependence structures: (i) positive dependence \(Y\sim _{\,\mathrm{PQD}}X\), which includes \(Y\uparrow _{\mathrm{st}} X\) as a special case; (ii) strong negative dependence, i.e., \((Y+X)\sim _{\,\mathrm{NQD}}X\), which includes \((Y+X)\downarrow _{\mathrm{st}} X\) as a special case; and (iii) \((Y+X)\uparrow _{\mathrm{st}} X\) and \(Y\downarrow _{\mathrm{st}} X\). In each category, we derive the optimal insurance strategy, and the results align with intuition. Specifically, strong negative dependence implies that the background risk provides a full hedge for the insurable risk and thus requires no-insurance coverage. On the other hand, a positively dependent background risk provides hardly any hedge for the insurable risk and thus requires stop-loss insurance coverage under the expected value premium principle. In between, a moderately negatively dependent background risk provides a partial hedge for the insurable risk and thus requires some insurance coverage for the unhedged portion. Some results concerning the positive and strong negative dependence structures have been established in the literature, and this paper generalises and extends those results. There are few studies in the literature regarding the moderate negative dependence case. To the best of our knowledge, we are the first to conduct a quantitative analysis on the optimal insurance strategy for this dependence case under the EU framework.
It is worth pointing out that the no-sabotage condition plays an important role in the optimal insurance design with background risk. In the absence of that condition, Dana and Scarsini [10] investigate the qualitative properties of optimal insurance contracts for three cases: (i) \(Y\uparrow _{\mathrm{st}} X\), (ii) \((Y+X)\downarrow _{\mathrm{st}} X\), and (iii) \(Y\downarrow _{\mathrm{st}} X\) and \((Y+X)\uparrow _{\mathrm{st}} X\). In Table 1, we compare our optimal insurance strategies with those of [10]. Notably, for case (iii), [10] conclude that the optimal ceded loss function should fall in ℭ (without giving an explicit solution). Consequently, the optimal insurance strategies with and without the no-sabotage condition must turn out to be the same, as given by Corollary 6.4. However, for the other two cases, Table 1 illustrates that optimal contracts are quite different. Therefore, as in Chi and Tan [8], we emphasise that adding the no-sabotage constraint is quite necessary for the optimal insurance design in the presence of background risk, especially for positive and strong negative dependence structures. Even in the absence of background risk, this constraint plays a critical role in the optimal insurance design under the RDEU framework, as pointed out by Xu et al. [35].
It should be noted that the approach developed in this paper to solve the optimal insurance problem is innovative. It consists of two steps. First, a necessary and sufficient condition is established for the optimality of an insurance contract; then this condition is applied to derive explicit solutions in different cases. As demonstrated in the paper, this approach is powerful and is applicable in a wide range of scenarios. It is also promising to apply it in other types of optimal insurance problems where classical methods fail to work.
There are still unsolved problems. Our ultimate goal is to find the optimal insurance strategy under an arbitrary dependence structure between background risk and insurable risk. This problem is of interest to both academics and practitioners. In practice, it is usually difficult to precisely identify the dependence structure, and practitioners need to know the optimal contracts under different scenarios for the purpose of robust decision-making. On the other hand, this problem is very challenging because of its generality. Fortunately, the study in this paper has shed some light on the ultimate solution. First of all, Theorem 3.3 reveals the general form of the optimal insurance contract, and Proposition 3.6 provides a way to enhance any suboptimal insurance strategy. Furthermore, the analysis on different categories of dependence structures and their mixtures in Sects. 4–7 reveals how the dependence structure affects the insurance demand and thus provides a foundation for further research.
References
Arrow, K.J.: Uncertainty and the welfare economics of medical care. Am. Econ. Rev. 53, 941–973 (1963)
Balbás, A., Balbás, B., Heras, A.: Optimal reinsurance with general risk measures. Insur. Math. Econ. 44, 374–384 (2009)
Barlow, R.E., Proschan, F.: Statistical Theory of Reliability and Life Testing: Probability Models. Holt, Rinehart & Winston, New York (1975)
Bernard, C., He, X., Yan, J.-A., Zhou, X.Y.: Optimal insurance design under rank-dependent expected utility. Math. Finance 25, 154–186 (2015)
Cai, J., Wei, W.: Optimal reinsurance with positively dependent risks. Insur. Math. Econ. 50, 57–63 (2012)
Carlier, G., Dana, R.-A.: Pareto efficient insurance contracts when the insurer’s cost function is discontinuous. Econ. Theory 21, 871–893 (2003)
Carlier, G., Dana, R.-A.: Rearrangement inequalities in non-convex insurance models. J. Math. Econ. 41, 483–503 (2005)
Chi, Y., Tan, K.S.: Optimal incentive compatible insurance with background risk. Working paper (2015). Available online at https://ssrn.com/abstract=2589438
Chi, Y., Wei, W.: Optimum insurance contracts with background risk and higher-order risk attitudes. ASTIN Bull. 48, 1025–1047 (2018)
Dana, R.-A., Scarsini, M.: Optimal risk sharing with background risk. J. Econ. Theory 133, 152–176 (2007)
Doherty, N.A., Schlesinger, H.: The optimal deductible for an insurance policy when initial wealth is random. J. Bus. 56, 555–565 (1983)
Eeckhoudt, L., Kimball, M.: Background risk, prudence, and the demand for insurance. In: Dionne, G. (ed.) Contributions to Insurance Economics, pp. 239–254. Springer, New York (1992)
Gollier, C.: Optimum insurance of approximate losses. J. Risk Insur. 63, 369–380 (1996)
Gollier, C., Schlesinger, H.: Arrow’s theorem on the optimality of deductibles: A stochastic dominance approach. Econ. Theory 7, 359–363 (1996)
Hong, S.K., Lew, K.O., MacMinn, R., Brockett, P.: Mossin’s theorem given random initial wealth. J. Risk Insur. 78, 309–324 (2011)
Huberman, G., Mayers, D., Smith, C.W. Jr: Optimal insurance policy indemnity schedules. Bell J. Econ. 14, 415–426 (1983)
Kaluszka, M.: Optimal reinsurance under mean–variance premium principles. Insur. Math. Econ. 28, 61–67 (2001)
Kaluszka, M., Okolewski, A.: An extension of Arrow’s result on optimal reinsurance contract. J. Risk Insur. 75, 275–288 (2008)
Kiesel, S., Rüschendorf, L.: On the optimal reinsurance problem. Appl. Math. 40, 259–280 (2013)
Lehmann, E.L.: Some concepts of dependence. Ann. Math. Stat. 37, 1137–1153 (1966)
Lu, Z.Y., Liu, L.P., Zhang, J.Y., Meng, L.L.: Optimal insurance under multiple sources of risk with positive dependence. Insur. Math. Econ. 51, 462–471 (2012)
Lu, Z.Y., Meng, S.W., Liu, L.P., Han, Z.: Optimal insurance design under background risk with dependence. Insur. Math. Econ. 80, 15–28 (2018)
Mahul, O.: Optimal insurance design with random initial wealth. Econ. Lett. 69, 353–358 (2000)
Mayers, D., Smith, C.W. Jr.: The interdependence of individual portfolio decisions and the demand for insurance. J. Polit. Econ. 91, 304–311 (1983)
Mossin, J.: Aspects of rational insurance purchasing. J. Polit. Econ. 76, 553–568 (1968)
Raviv, A.: The design of an optimal insurance policy. Am. Econ. Rev. 69, 84–96 (1979)
Rudin, W.: Principles of Mathematical Analysis, 3rd edn. McGraw-Hill, New York (1976)
Schlesinger, H.: The theory of insurance demand. In: Dionne, G. (ed.) Handbook of Insurance, pp. 167–184. Springer, New York (2013)
Schmidt, U.: Insurance demand under prospect theory: A graphical analysis. J. Risk Insur. 83, 77–89 (2016)
Shaked, M., Shanthikumar, J.G.: Stochastic Orders. Springer, Berlin (2007)
Sung, K.C.J., Yam, S.C.P., Yung, S.P., Zhou, J.H.: Behavioral optimal insurance. Insur. Math. Econ. 49, 418–428 (2011)
Van Heerwaarden, A.E., Kaas, R., Goovaerts, M.J.: Optimal reinsurance in relation to ordering of risks. Insur. Math. Econ. 8, 11–17 (1989)
Vercammen, J.: Optimal insurance with nonseparable background risk. J. Risk Insur. 68, 437–448 (2001)
von Neumann, J., Morgenstern, O.: Theory of Games and Economic Behavior. Princeton University Press, Princeton (1944)
Xu, Z.Q., Zhou, X.Y., Zhuang, S.C.: Optimal insurance under rank-dependent utility and incentive compatibility. Math. Finance 29, 659–692 (2019)
Young, V.R.: Optimal insurance under Wang’s premium principle. Insur. Math. Econ. 25, 109–122 (1999)
Young, V.R.: Premium principles. In: Teugels, J., Sundt, B. (eds.) Encyclopedia of Actuarial Science, vol. 3, pp. 1323–1331. John Wiley & Sons, West Sussex (2004)
Acknowledgements
Both authors are grateful to two anonymous reviewers for their valuable comments, which greatly improved the presentation of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Chi’s work was supported by grants from National Natural Science Foundation of China (No. 11971505), the MOE (China) Project of the Key Research Institute of Humanities and Social Sciences at Universities (No. 16JJD790061) and the 111 Project of China (No. B17050). Wei acknowledges the financial support from the Research and Creative Activities Support (AAC2253) of the University of Wisconsin-Milwaukee.
Appendix A: Useful lemmas
Appendix A: Useful lemmas
Lemma A.1
The notions of PQD and NQD have the following equivalent characterisations:
(i) \(Y \sim _{\,\mathrm{PQD}} X\)if and only if \(\mathbb{E}[v(Y)|X>x] \ge \mathbb{E}[v(Y)]\)for all \(x\)and any increasing function \(v(\cdot )\)such that \(\mathbb{E}[|v(Y)|]<\infty \).
(ii) \(Y \sim _{\,\mathrm{NQD}} X\)if and only if \(\mathbb{E}[v(Y)|X>x] \le \mathbb{E}[v(Y)]\)for all \(x\)and any increasing function \(v(\cdot )\)such that \(\mathbb{E}[|v(Y)|]<\infty \).
Proof
It suffices to prove (i). The conclusion of (ii) can be obtained through the relationship that \(Y \sim _{\,\mathrm{PQD}} X\) if and only if \(-Y \sim _{\,\mathrm{NQD}} X\).
Note that \(Y \sim _{\,\mathrm{PQD}} X\) is equivalent to \(\mathbb{P}[Y>y|X>x]\ge \mathbb{P}[Y>y]\) for any \(x\) and \(y\). This is further equivalent to saying that the conditional distribution of \(Y\) given \(X > x\) is larger than the distribution of \(Y\) in the usual stochastic order. The desired characterisation immediately follows from the functional characterisation of the usual stochastic order; see Shaked and Shanthikumar [30, Sect. 1.A.1]. □
Lemma A.2
If \(x \mapsto \mathbb{E}[v(Y)|X>x]\)is increasing over \([{\nu _{\rho }}, M)\)for any increasing function \(v(\cdot )\), then \(x \mapsto \mathbb{E}[w(Y+X\wedge t)|X>x]\)is increasing over \([{\nu _{\rho }}, {M})\)for any increasing function \(w(\cdot )\)and nonnegative \(t\).
Proof
For any \({\nu _{\rho }}\le x_{1}< x_{2}<{M}\), we have
If \(\mathbb{P}[x_{1}< X\le x_{2}]=0\), then \(\mathbb{E}[w(Y+X\wedge t)|X>x_{2}]=\mathbb{E}[w(Y+X\wedge t)|X>x_{1}]\). Otherwise, if \(\mathbb{P}[x_{1}< X\le x_{2}]>0\), the above equation implies that
where the first inequality is derived by the increasingness of \(w(\cdot )\) and the second follows from the assumption. □
Lemma A.3
Let \(f^{*}\)be the solution to problem (7.1). Under Assumption 6.1, \(\Phi _{f^{*}}(x)\)in (3.4) possesses the following properties:
(i) Assume there exist \(s_{1}, s_{2}\in (0, {M})\)such that \(s_{1}< s_{2}\)and
(a) If \(m(x)\)is increasing over \([s_{1}, s_{2}]\), then \(\Phi _{f^{*}}(x) \ge 1+\rho \)for all \(x\in [s_{1}, s_{2}]\).
(b) If \(m'(x) \le 1\)on \([s_{1}, s_{2}]\), then \(\Phi _{f^{*}}(x) \le 1+\rho \)for all \(x\in [s_{1}, s_{2}]\).
(c) If \(0 \le m'(x) \le 1\)on \([s_{1}, s_{2}]\), then \(\Phi _{f^{*}}(x) = 1+\rho \)for all \(x\in [s_{1}, s_{2}]\).
(ii) If \(\Phi _{f^{*}}(x) = 1+\rho \)for any \(x \in [s_{1}, s_{2}]\), then \(m(x)-f^{*}(x)\)is constant on \([s_{1}, s_{2}]\).
(iii) If there exists \(s_{0}\in [0,{M})\)such that \(\Phi _{f^{*}}(s_{0}) \le 1+\rho \)and \(m'(x)\le 1\)for \(x\in [s_{0}, {M})\), then \(\Phi _{f^{*}}(x) \le 1+\rho \)for all \(x\in [s_{0}, {M})\).
(iii′) If there exists \(s_{1}\in [0,{M})\)such that \(\Phi _{f^{*}}(s_{1}) =1+\rho \)and \(0\le m'(x)\le 1\), then \(\Phi _{f^{*}}(x) =1+\rho \)for any \(x\in [s_{1}, {M})\).
(iv) Assume there exists \(s_{0}\in [0,{M})\)such that \(\Phi _{f^{*}}(s_{0})\ge 1+\rho \). If \(m'(x) \ge 1\)for any \(x\ge s_{0}\), then \({f^{*}}'(x)=1\)for any \(x\in (s_{0},{M})\).
Proof
(i)(a) Assume the result does not hold, i.e., there exists \(x_{1} \in (s_{1}, s_{2})\) such that \(\Phi _{f^{*}}(x_{1}) < 1+\rho \). Due to the continuity of \(\Phi _{f^{*}}(x)\), we conclude that there exist \(s_{3}, s_{4}\) such that \(s_{1} \le s_{3} < x_{1} < s_{4} \le s_{2}\), \(\Phi _{f^{*}}(s_{3})=\Phi _{f^{*}}(s_{4})=1+\rho \) and \(\Phi _{f^{*}}(x) < 1+\rho \) for all \(x \in (s_{3}, s_{4})\). It follows from Theorem 3.3 that \({f^{*}}'(x)=0\) on \((s_{3}, s_{4})\). This in turn implies that \(m(x)-f^{*}(x)\) is increasing over \([s_{3}, s_{4}]\), and so is \(u'(W_{f^{*}}(x))\). Recalling that \(s_{3} < x_{1} <s_{4}\), we have
which in turn implies
On the other hand, using a similar argument, we have
Therefore we must have \(u'(W_{f^{*}}(x_{1}))<(1+\rho )\mathbb{E}[u'(W_{f^{*}}(X))]\), which contradicts (A.1). Thus the desired conclusion must hold.
(i)(b) Assume the conclusion does not hold, i.e., there exists \(x_{1} \in (s_{1}, s_{2})\) such that \(\Phi _{f^{*}}(x_{1}) > 1+\rho \). Use the same argument as in (i)(a), we can get a contradiction and thus prove the desired conclusion.
(i)(c) This is a combination of the conclusions from (i)(a) and (i)(b).
(ii) If \(\Phi _{f^{*}}(x) = 1+\rho \) for all \(x \in [s_{1}, s_{2}]\), a simple calculation gives
for any \(s_{1}\le x_{1}< x_{2}\le s_{2}\). Under Assumption 6.1, it is easy to get from the above equation that \(u'(W_{f^{*}}(x))=(1+\rho )\mathbb{E}[u'(W_{f^{*}}(X))]\) for any \(x\in [s_{1}, s_{2}]\). As a result, \(m(x)-f^{*}(x)\) is constant over \([s_{1}, s_{2}]\).
(iii) Assume there exists \(x_{1} \in (s_{0}, {M})\) such that \(\Phi _{f^{*}}(x_{1}) > 1+\rho \). Note that \(x \mapsto \Phi _{f^{*}}(x)\) is continuous on \([s_{0}, {M})\) under Assumption 6.1. Define
Clearly, we have \(s_{0}\le x_{L} < x_{1} <x_{U}\), \(\Phi _{f^{*}}(x_{L}) = 1+\rho \) and \(\Phi _{f^{*}}(x) > 1+\rho \) for all \(x \in (x_{L}, x_{U})\), which together with Theorem 3.3 implies that \({f^{*}}'(x)=1\) and thus \(m(x)-f^{*}(x)\) is decreasing on \((x_{L}, x_{U})\). If \(x_{U} ={M}\), then \(m(x)-f^{*}(x)\) is decreasing on \([x_{L}, {M})\), and so is \(\Phi _{f^{*}}(x)\). Therefore, we have \(\Phi _{f^{*}}(x_{L}) \ge \Phi _{f^{*}}(x_{1}) >1+\rho \), which contradicts \(\Phi _{f^{*}}(x_{L}) = 1+\rho \). If \(x_{U} <{M}\), then by the continuity of \(\Phi _{f^{*}}(x)\), we have \(\Phi _{f^{*}}(x_{U}) = 1+\rho \). According to (i)(b), we have \(\Phi _{f^{*}}(x) \le 1+\rho \) for all \(x\in (x_{L}, x_{U})\), which contradicts \(\Phi _{f^{*}}(x_{1}) > 1+\rho \). As a result, there cannot exist \(x_{1} \in [s_{0}, {M})\) with \(\Phi _{f^{*}}(x_{1}) > 1+\rho \). In other words, we must have \(\Phi _{f^{*}}(x)\le 1+\rho \) for any \(x \in [s_{0}, {M})\).
(iii′) According to (iii), we must have \(\Phi _{f^{*}}(x) \le 1+\rho \) for any \(x\in [s_{1},{M})\). Define \(y_{U}=\sup \{t\in [s_{1}, {M}): \Phi _{f^{*}}(t)=1+\rho \}\). We have \(s_{1}\le y_{U}\le M\) and \(\Phi _{f^{*}}(y_{U})=1+\rho \). If \(y_{U}< M\), the definition of \(y_{U}\) and the continuity of \(\Phi _{f^{*}}(t)\) imply \(\Phi _{f^{*}}(t)<1+\rho \) for all \(t\in (y_{U}, M)\). Using Theorem 3.3, we get \({f^{*}}'(t)=0\), and hence \(m(x)-f^{*}(x)\) is increasing over \((y_{U}, M)\). Consequently, we have \(1+\rho >\Phi _{f^{*}}(t) \ge \Phi _{f^{*}}(y_{U})=1+\rho \) for all \(t\in (y_{U}, M)\), which leads to a contradiction. Therefore, we must have \(y_{U}=M\) and the result follows by using (i)(c).
(iv) If \(m'(x)\ge 1\) for \(x\ge s_{0}\), (2.1) implies that \(m(x)-f^{*}(x)\) is increasing on \([s_{0}, {M})\). So is then \(\Phi _{f^{*}}(x)\). If \(\Phi _{f^{*}}(s_{0})>1+\rho \), then \(\Phi _{f^{*}}(x) \ge \Phi _{f^{*}}(s_{0})>1+\rho \) for any \(x \ge s_{0}\), and thus \({f^{*}}'(x)=1\) for any \(x>s_{0}\) according to Theorem 3.3. Otherwise, if \(\Phi _{f^{*}}(s_{0})=1+\rho \), let \(s_{1}= \sup \{x \in [s_{0}, {M}): \Phi _{f^{*}}(x) = 1+\rho \}\). Then the increasing property of \(\Phi _{f^{*}}(x)\) implies
Therefore we have \({f^{*}}'(x)=1\) for any \(x\in (s_{1},{M})\), and (ii) implies that \(m(x)-f^{*}(x)\) is constant on \([s_{0}, s_{1}]\), which in turn implies that \({f^{*}}'(x) = m'(x)=1\) on \((s_{0}, s_{1})\) because \(m'(x) \ge 1\ge {f^{*}}'(x)\). As a consequence, \({f^{*}}'(x)=1\) for any \(x\in (s_{0},{M})\). □
Rights and permissions
About this article
Cite this article
Chi, Y., Wei, W. Optimal insurance with background risk: An analysis of general dependence structures. Finance Stoch 24, 903–937 (2020). https://doi.org/10.1007/s00780-020-00429-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00780-020-00429-0
Keywords
- Background risk
- General dependence structures
- Mossin’s theorem
- No-sabotage condition
- Optimal insurance design