Abstract
We study a novel pricing operator for complete, local martingale models. The new pricing operator guarantees put-call parity to hold for model prices and the value of a forward contract to match the buy-and-hold strategy, even if the underlying follows strict local martingale dynamics. More precisely, we discuss a change of numéraire (change of currency) technique when the underlying is only a local martingale, modelling for example an exchange rate. The new pricing operator assigns prices to contingent claims according to the minimal cost for superreplication strategies that succeed with probability one for both currencies as numéraire. Within this context, we interpret the lack of the martingale property of an exchange rate as a reflection of the possibility that the numéraire currency may devalue completely against the asset currency (hyperinflation).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We propose to modify the notion of a contingent claim price in the setting where the source of uncertainty is a strict local martingale rather than a martingale. More precisely, we propose to use as a pricing operator for contingent claims the minimal cost for superreplicating a given contingent claim simultaneously under two probability measures. In the case of foreign exchange markets with X modelling the exchange rate (for example, the price of one Euro in dollars), the two measures can be thought of as a “dollar measure” and a “Euro measure” corresponding to the choice of dollars or Euros as numéraires. The two measures are not equivalent if X is a strict local martingale (that is, a local martingale that is not a martingale). In this case, the cost for joint superreplication is higher than the expected value under the local martingale measure.
Our main result is Theorem 3.4, which provides a formula for the minimum joint superreplication cost in a complete market. This approach restores put-call parity and international put-call equivalence for model prices, and gives the price X 0 for the contingent claim that pays X T at time T. Our pricing formula agrees with the proposals of other authors (Lewis [25], Madan and Yor [26], Andersen [1]); the novelty is the rigorous justification of this formula as a hedging cost.
The mathematical contribution of this paper is mainly contained in Sect. 2 and the Appendix. We show how to construct the measure corresponding to a numéraire that is allowed to vanish. Towards this end, we construct the Föllmer measure for nonnegative local martingales, extending the corresponding results for strictly positive local martingales. We also develop a stochastic calculus for the suggested change of measure, in which neither measure dominates the other one.
Section 3 contains the main financial results of the paper. Our approach uses two numéraires simultaneously, which requires us to re-introduce the notions of market completeness and superreplication. We introduce a model of the market and define trading strategies and contingent claim replication. After proving our main result on the minimal replicating price, we give numerous corollaries and examples.
In Sect. 4, we consider a physical measure under which both currencies might completely devalue against the other. In such a situation, an equivalent probability measure under which the exchange rate follows local martingale dynamics cannot exist. Instead, each risk-neutral measure is only absolutely continuous with respect to the physical measure. However, as one may use both currencies as hedging instruments, superreplication of contingent claims might still be possible. We provide a set of conditions under which replicating strategies exist, and we show in Proposition 4.2 how the minimal cost for such a strategy is exactly given by the pricing operator of this paper.
This point of view gives us an interpretation of the lack of the martingale property of an exchange rate under a risk-neutral probability measure, as the positive probability of complete devaluations of currencies (corresponding to explosions of the exchange rate) occurring under some dominating probability measure. We remark that this dominating probability measure usually does not correspond to the Föllmer measure, which we shall discuss below, but is equivalent to the sum of the Föllmer measure and the original measure.
1.1 Related literature
We now link our financial results to relevant literature:
Strict local martingales, that is, local martingales that are not martingales, have recently been introduced in the financial industry to model exchange rates under the risk-neutral measure. This is due to the fact that they are able to well capture observed features of the market such as implied volatility surfaces and that they are easily analytically tractable. An important example is the class of “quadratic normal volatility” models, a family of local martingales which are studied for example in Andersen [1] and in our companion paper Carr et al. [2]. There is a vast literature on pricing options in strict local martingale models, often coined “bubbles”. For an overview of this literature, we refer the interested reader to the recent survey by Protter [31]. Heston et al. [18] were among the first to point out that put-call parity usually does not hold in strict local martingale models. For a discussion of these models specifically in the context of foreign exchange, we refer the reader to Jarrow and Protter [21]. Further models in which strict local martingales appear can be found among the class of stochastic volatility models; Sin [40] was among the first to point this out. For example, in the log-normal SABR model, if the asset price process is positively correlated with the stochastic volatility process, then it follows strict local martingale dynamics; see Example 6.1 in Henry-Labordère [17].
Several papers suggest adjustments to the pricing of contingent claims by expectations in strict local martingale models in order to address the lack of put-call parity:
Lewis [25] proposes to add a correction term to the price of a call. However, this approach lacks a clear economic motivation. As his starting point is exactly put-call parity for model prices, it is not clear how other contingent claims should be priced. Cox and Hobson [4] suggest to consider collateral requirements when pricing contingent claims; such collateral requirements correspond to a constraint on the class of admissible trading strategies. This leads to a higher contingent claim price, but usually does not restore put-call parity for model prices.
Madan and Yor [26] propose to take the limit of a sequence of prices obtained from approximating the asset price by true martingales as the price for a contingent claim. This approach also restores put-call parity for model prices. However, one might criticize that the limit of the approximating prices usually does not agree with the classical price in the case that the underlying is a true martingale. For instance, consider an arbitrage-free, complete market with corresponding risk-neutral measure \(\mathbb {Q}\), a standard \(\mathbb {Q}\)-geometric Brownian motion X=(X t ) t∈[0,T] as underlying, and a contingent claim that pays \(\mathbf {1}_{\{X_{T} \in \mathbb {N}\}} / q_{X_{T}}\) at maturity T, where \(q_{y} = \mathbb {Q}(\max_{t \in[0,T]} X_{t} \geq y)\) for all \(y \in \mathbb {R}\). This claim should have price zero as \(X_{T} \notin \mathbb {N}\) almost surely. However, if one approximates X with versions that are stopped at hitting times of integers, as in Madan and Yor’s approach, then one obtains a price of one for that claim.
We here suggest to take an economic point of view based on a replicating argument and derive a pricing operator that restores put-call parity, and therefore assigns model prices that correspond to observed market prices. We thus not only justify Lewis’ pricing operator by an economic argument, but also generalize it to a wider class of models and contingent claims.
The approach taken here can be interpreted as a link between classical pricing and pricing under Knightian uncertainty. Pricing in the classical sense corresponds to the choice of one probability measure under which a contingent claim is superreplicated. This choice implies a strong assumption on the chosen nullsets, that is, by assumption a set of events is determined to be not relevant for computing a replicating trading strategy. If the modeler were to consider another probability measure, other events would be selected, leading to a different replicating price and strategy. Indeed, one would like that the choice of probability measure should not have a large impact on the price (or, more importantly, on the hedging strategy), or at least should be quantifiable.
We remark that Delbaen and Schachermayer [7] work out the connection of strict local martingales and changes of numéraires. While we understand a change of numéraire as a combination of a change of currency and the corresponding change of measure, they start by looking at the change of currency only. Their results imply that in an arbitrage-free model, a change of currency leads to the existence of arbitrage if the corresponding exchange rate is a strict local martingale under a unique risk-neutral measure. We circumvent the appearance of arbitrage here by associating the change of numéraire with the introduction of a new probability measure that is not equivalent to the old one. It is exactly this lack of equivalence which avoids the arbitrage after the change of currency.
2 Change of measure with a nonnegative local martingale
In this section, given a probability measure \(\mathbb {Q}\), we construct and discuss a new probability measure \(\widehat{\mathbb {Q}}\) corresponding to a density process that follows local martingale dynamics only and is allowed to hit zero. It is helpful to interpret the notation of this section in a financial context. Towards this end, we interpret X as an exchange rate, for example, the price of one Euro in dollars. Then \(\mathbb {Q}\) represents the risk-neutral measure corresponding to the dollar-numéraire and \(\widehat{\mathbb {Q}}\) the risk-neutral measure corresponding to the Euro-numéraire.
The mathematical finance literature has utilized the techniques developed by Föllmer [12] and Meyer [27] to construct probability measures with a strict local martingale as density process mostly in the context of arbitrage and bubbles; see for example Delbaen and Schachermayer [6], Pal and Protter [28], Fernholz and Karatzas [11], Ruf [34], and, parallel to the present work, Kardaras et al. [23]. Here, we slightly extend this literature by allowing the local martingale to hit zero. On the other hand, true martingales possibly hitting zero as density processes have been studied by Schönbucher [39] within the area of credit risk. Schönbucher [39] terms the corresponding measure a “survival measure”. We extend this direction of research by allowing the change of measure to be determined by a local martingale only.
Throughout this section, we fix a time horizon T∈(0,∞], a stochastic basis \((\varOmega, \mathcal {F}_{T}, (\mathcal {F}_{t})_{t \in[0, T]}, \mathbb {Q})\), and a nonnegative \(\mathbb {Q}\)-local martingale X=(X t ) t∈[0,T]. We assume that x 0:=X 0>0 is deterministic, that \((\mathcal {F}_{t})_{t \in[0, T]}\) is right-continuous, and that X(ω) has right-continuous paths for all ω∈Ω; see also Lemma 1.1 in Föllmer [12] for the construction of a right-continuous version if this assumption does not hold.
Any nonnegative random variable, such as X T , is explicitly allowed to take values in [0,∞]. For a nonnegative random variable Z and some set \(A \in~\mathcal {F}_{T}\), we write Z 1 A to denote the random variable that equals Z whenever ω∈ A, and otherwise is zero. For any stopping time τ, we denote the stochastic process that arises from stopping a process N=(N t ) t∈[0,T] at time τ by \(N^{\tau}= (N_{t}^{\tau})_{t \in [0,T]}\); that is, \(N^{\tau}_{t} := N_{t \wedge\tau}\) for all t∈[0,T]. For any measure \(\mathbb {P}\) on \((\varOmega , \mathcal {F}_{T})\), we denote the corresponding expectation operator by \(\mathbb {E}^{{\mathbb {P}}}\).
We define the stopping times
for all \(i \in \mathbb {N}\), set R:=lim i↑∞ R i and S:=lim i↑∞ S i , with the convention that \(\inf\emptyset:= \mathfrak{T}\) for some transfinite time \(\mathfrak{T} > \infty\); see Appendix A for details. Define the process Y=(Y t ) t∈[0,T] by Y t :=1/X t 1 {R>t} for t∈[0,T] and the stopping times
again with \(\inf\emptyset:= \mathfrak{T}\). We observe that \(S_{i} = S_{i}^{Y}\) for all \(i \in \mathbb {N}\) if X (R+t)∧T =∞ for all t≥0. We assume that \((\mathcal {F}_{t} \cap \mathcal {F}_{R-})_{t \in[0, T]}\) is the right-continuous modification of a standard system; see Appendix B for notation and a discussion of this assumption.
The next theorem states the main result of this section: for the nonnegative \(\mathbb {Q}\)-local martingale X, there exists a probability measure under which X serves as the numéraire. We remark that we only specify the new measure on \((\varOmega, \mathcal {F}_{R-})\) and not on \((\varOmega, \mathcal {F}_{T})\). This is due to the fact that the original measure \(\mathbb {Q}\), by assumption, does not “see” any events after the stopping time R. However, a measure on \((\varOmega, \mathcal {F}_{T})\) satisfying the properties of the next theorem could be easily constructed by arbitrarily, but consistently, extending the measure \(\widehat{\mathbb {Q}}\) from \(\mathcal {F}_{R-}\) to \(\mathcal {F}_{T}\). Observe that Z 1 {R>τ∧T} is \(\mathcal {F}_{R^{-}}\)-measurable if Z is an \(\mathcal {F}_{\tau\wedge T}\)-measurable random variable for some stopping time τ.
Theorem 2.1
(Change of measure with a nonnegative local martingale)
There exists a unique probability measure \(\widehat{\mathbb {Q}}\) on \((\varOmega, \mathcal {F}_{R-})\) such that
holds for all stopping times τ and for all \(A \in \mathcal {F}_{\tau\wedge T}\). This measure also satisfies \(\widehat{\mathbb {Q}}(R_{i} \wedge T<R) = 1\) for all \(i \in \mathbb {N}\). Moreover, we have
and
for all stopping times τ and \(\mathcal {F}_{\tau\wedge T}\)-measurable random variables Z∈[0,∞].
The process Y satisfies
furthermore, we have
if and only if the process X is a (uniformly integrable) \(\mathbb {Q}\)-martingale. Moreover:
-
1.
Y is a \(\widehat{\mathbb {Q}}\)-supermartingale;
-
2.
Y is a local \(\widehat{\mathbb {Q}}\)-martingale if and only if \({\mathbb {Q}}(S>S_{i} \wedge T) = 1\) for all \(i \in \mathbb {N}\); then \((S_{i}^{Y})_{i \in \mathbb {N}}\) is, under \(\widehat{\mathbb {Q}}\), a localizing sequence for Y;
-
3.
Y is a \(\widehat{\mathbb {Q}}\)-martingale if and only if \({\mathbb {Q}}(S > T) = 1\).
Proof
Without loss of generality, assume throughout the proof that x 0=1. Observe that \(X^{R_{i}}\) is a nonnegative martingale by Lemma A.3 in the Appendix; thus, it generates a measure \(\mathbb {Q}_{i}\) on \((\varOmega, {\mathcal {F}}_{R_{i}-})\) by \(\mathrm {d}\mathbb {Q}_{i} := X^{R_{i}}_{T} \,\mathrm {d}\mathbb {Q}\) for all \(i \in \mathbb {N}\). Observe that the family of probability measures \((\mathbb {Q}_{i})_{i \in \mathbb {N}}\) is consistent, that is, \(\mathbb {Q}_{i+j}|_{{\mathcal {F}}_{R_{i}-}} = \mathbb {Q}_{i}\) for all \(i,j \in \mathbb {N}\), and that \({\mathcal {F}}_{R-} = \bigvee_{i \in \mathbb {N}} {\mathcal {F}}_{R_{i}-}\). Now, the extension Theorem V.4.1 in Parthasarathy [29] yields the existence of a probability measure \(\widehat{\mathbb {Q}}\) on \((\varOmega, {\mathcal {F}}_{R-})\) such that \(\widehat{\mathbb {Q}}|_{{\mathcal {F}}_{R_{i}-}} = \mathbb {Q}_{i}\); see Appendix B for an argument that the assumptions of that theorem hold.
Observe that for all \(A \in \mathcal {F}_{\tau\wedge T}\) and stopping times τ,
This yields (2.1). Now, with τ=R i and A=Ω we obtain that \(\widehat{\mathbb {Q}} (R > R_{i} \wedge T ) = 1\) for all \(i \in \mathbb {N}\). This identity implies that \(\widehat{\mathbb {Q}}(A) = \widehat{\mathbb {Q}} (A \cap \{R > R_{i} \wedge T \} ) = \mathbb {E}^{\mathbb {Q}}[X^{R_{i}}_{T} \mathbf {1}_{A} ]\) for all \(A \in \mathcal {F}_{R_{i}-}\) and \(i \in \mathbb {N}\). Since \({\mathcal {F}}_{R-} = \bigvee_{i \in \mathbb {N}} \mathcal {F}_{R_{i}-}\) and \(\bigcup_{i \in \mathbb {N}} \mathcal {F}_{R_{i}-} \) is a π-system, this yields uniqueness of \(\widehat {\mathbb {Q}}\) on \((\varOmega, \mathcal {F}_{R-})\). Then (2.2) follows from (2.1) by applying the monotone convergence theorem, and (2.3) follows from (2.2) by using the fact that \(\mathbb {Q}(R>T)=1\) and formally applying (2.2) to \(Z \mathbf {1}_{\{R > \tau\wedge T\}} Y^{\tau}_{T}\) instead of Z, where τ and Z are as in the theorem.
Observe that \(\{\inf_{t \in[0,T]} Y_{t} < 0\} = \bigcup_{i \in \mathbb {N}} \{\inf_{t \in[0,R_{i})}Y_{t} < 0\}\) \(\widehat{\mathbb {Q}}\)-almost surely and conclude that Y is \(\widehat{\mathbb {Q}}\)-almost surely nonnegative by dominated convergence and applying (2.1) with τ=R i and \(A = {\{ \inf_{t \in[0,R_{i})} Y_{t} < 0\} }\) for all \(i \in \mathbb {N}\). Next, (2.1) with τ=T and A={inf t∈[0,T] Y t >0} yields that \(\widehat{\mathbb {Q}}(\{\inf_{t \in[0,T]} Y_{t} > 0\} ) = \mathbb {E}^{\mathbb {Q}}[X_{T}]\), which shows the equivalence of the positivity of Y under \(\widehat{\mathbb {Q}}\) and the martingale property of X under \(\mathbb {Q}\).
Observe that
by applying (2.3) twice (with Z=1 A and τ=t the first time and τ=s the second time), for all t∈[0,T], s∈[0,t] and \(A \in \mathcal {F}_{s}\). Thus, the process Y is a \(\widehat{\mathbb {Q}}\)-supermartingale. This implies for all stopping times τ that Y τ is a \(\widehat {\mathbb {Q}}\)-martingale if and only if \(\mathbb {Q}(S > \tau\wedge T ) = 1\), since \(\mathbb {Q}(S > \tau\wedge T ) = \mathbb {E}^{\widehat{\mathbb {Q}}} [Y_{T}^{\tau}]\) again by (2.3) with Z=1. Using τ=T yields that Y is a \(\widehat{\mathbb {Q}}\)-martingale if and only if \(\mathbb {Q}(S >T ) = 1\), and using \(\tau= S^{Y}_{i}\) yields that for all \(i \in \mathbb {N}\), \(Y^{S_{i}^{Y}} \) is a \(\widehat{\mathbb {Q}}\)-martingale if and only if \(\mathbb {Q}(S >S_{i} \wedge T ) = 1\), since \(\mathbb {Q}(S_{i}^{Y} = S_{i})=1\). We conclude by applying (i) and the equivalence of (a.1) and (a.2) in Lemma A.3 in the Appendix. □
It is important to note that the measures \(\mathbb {Q}\) and \(\widehat{\mathbb {Q}}\) are usually not absolutely continuous with respect to each other; in particular, we can have \(\widehat{\mathbb {Q}}(R \leq T) > 0 = \mathbb {Q}(R \leq T)\). Furthermore, note that the indicators in (2.2) and (2.3) can be omitted if Z is finite or \(\mathbb {Q}(S \leq T) = 0\) or \(\widehat{\mathbb {Q}}(R \leq T) = 0\), respectively. In general, however, the indicators are necessary as the example \(Z=1/X^{S}_{T}\) illustrates.
Remark 2.2
(Duality of martingale property and positivity of density processes)
Observe that we have proved the equivalence of the following statements in Theorem 2.1:
-
1.
Y is a (uniformly integrable) \(\widehat{\mathbb {Q}}\)-martingale on [0,T];
-
2.
\(\mathbb {Q}(S>T) = 1\).
We have also proved the equivalence of the following statements:
-
1.
X is a (uniformly integrable) \({\mathbb {Q}}\)-martingale on [0,T];
-
2.
\(\widehat{\mathbb {Q}}(R>T) = 1\).
We emphasize the symmetry of these two equivalences.
This duality of the martingale property of a nonnegative local martingale under one measure and its non-explosiveness under another measure has been utilized to provide conditions for the martingale property of local martingales; see in particular Cheridito et al. [3] and Ruf [35, 37].
We next derive properties of the change of measure in Theorem 2.1. In particular, we focus on understanding which of the martingale properties of stochastic processes survive the change of measure, possibly after modifying the processes. The discussion here involves local martingales on stochastic intervals. This notion generalizes the definition of local martingales; its precise definition can be found in Appendix A.
Proposition 2.3
(Equivalence of (local) martingales)
Assume the notation of Theorem 2.1 and let τ denote a stopping time and N=(N t ) t∈[0,T] a progressively measurable stochastic process taking values in [0,∞] and such that N t =N t 1 {R>t} for all t∈[0,T]. The following statements then hold:
-
(i)
The process \((N^{\tau}_{t} \mathbf {1}_{\{S > \tau\wedge t\}})_{t \in [0,T]}\) is a \(\mathbb {Q}\)-martingale if and only if N τ Y τ is a \(\widehat{\mathbb {Q}}\)-martingale.
-
(ii)
The process (N t 1 {S>t}) t∈[0,T] is a \(\mathbb {Q}\)-local martingale on [0,S) (equivalently, on [0,R∧S)) if and only if NY is a \(\widehat{\mathbb {Q}}\)-local martingale on [0,R) (equivalently, on [0,R∧S)).
-
(iii)
If \((N_{t}^{S_{i}} \mathbf {1}_{\{S>S_{i} \wedge t\}})_{t \in [0,T]}\) is a \(\mathbb {Q}\)-martingale for all \(i \in \mathbb {N}\), then NY is a \(\widehat{\mathbb {Q}}\)-local martingale.
The proof of Proposition 2.3 is based on an extended version of Bayes’ formula and can be found in Appendix C. Applying (i) to N≡1 and to N=X with τ=T yields exactly the equivalences of Remark 2.2. Applying (ii) to N≡1 yields that Y is a \(\widehat{\mathbb {Q}}\)-local martingale on [0,R∧S) if and only if S is announced under \(\mathbb {Q}\) (for example, if X does not jump to zero under \(\mathbb {Q}\)). The example X=Y≡1 shows that the reverse direction in (iii) in Proposition 2.3 usually does not hold.
In order to better understand the change of measure suggested in this section, it is instructive to study an extreme case where the measures \(\mathbb {Q}\) and \(\widehat{\mathbb {Q}}\) are not only not absolutely continuous with respect to each other, but even singular:
Example 2.4
(Singular measures)
Assume that T∈(0,∞) and let X be defined by
where W=(W t ) t∈[0,T] denotes a \(\mathbb {Q}\)-Brownian motion and \(\widetilde {S} = S\) the first hitting time of −1 by \(( \int_{0}^{t} 1/\sqrt{T-u}\, \,\mathrm {d}W_{u})_{t \in[0,T)}\). Since X corresponds to a deterministically time-changed Brownian motion, we have \(\mathbb {Q}(S < T) = 1\) and thus \(\mathbb {Q}(X_{T} = 0) =1\).
Under the measure \(\widehat{\mathbb {Q}}\) of Theorem 2.1, note that Y=(Y t ) t∈[0,T], defined by Y t :=1/X t 1 {R>t} for all t∈[0,T], has the dynamics
for all t∈[0,R) and some \(\widehat{\mathbb {Q}}\)-Brownian motion \(W^{\widehat{\mathbb {Q}}} :=(W_{t}^{\widehat{\mathbb {Q}}})_{ t \in[0,R) }\). Thus, Y is just a time-change of the reciprocal of a three-dimensional \(\widehat{\mathbb {Q}}\)-Bessel process Z starting in one. To see this, define the processes Z=(Z u ) u≥0 and B=(B u ) u≥0 by Z u :=Y T(1−exp(−u)) and
Then observe that \(\mathrm {d}Z_{u} = -Z_{u}^{2} \,\mathrm {d}B_{u}\) and 〈B〉 u =u for all u≥0 and conclude by applying Lévy’s theorem; see Theorem 3.3.16 in Karatzas and Shreve [22]. We then get Y t =Z log(T/(T−t)) and \(\widehat{\mathbb {Q}}(Y_{t} > 0 \mbox{ for all } t \in [0,T)) = 1 = \widehat{\mathbb {Q}}(Y_{T} = 0) \); see Sect. 3.3 of Karatzas and Shreve [22]. Indeed, note that
Thus, the two measures are singular with respect to each other on \(\mathcal {F}_{T}\) since we have \(\mathbb {Q}(R=T) = 0 < 1 = \widehat{\mathbb {Q}}(R=T)\); however, \(\widehat{\mathbb {Q}}\) is absolutely continuous with respect to \(\mathbb {Q}\) on \(\mathcal {F}_{t}\) for all t∈[0,T) since Y is a strictly positive, strict \(\widehat{\mathbb {Q}}\)-local martingale; see Remark 2.2. We also note that X t is a true \(\mathbb {Q}\)-martingale for all t∈[0,T), but X=X T is a strict \(\mathbb {Q}\)-local martingale.
The next example is a slight modification of the example in Delbaen and Schachermayer [9]. It here illustrates that the equivalence of two probability measures \(\mathbb {Q}\) and \(\mathbb {Q}^{Z}\) on \((\varOmega, \mathcal {F}_{T})\), under which X is a nonnegative right-continuous local martingale, does not necessarily imply the equivalence of the corresponding probability measures \(\widehat{\mathbb {Q}}\) and \(\widehat{\mathbb {Q}}^{Z}\), constructed as in Theorem 2.1. This observation is one reason why we shall assume complete markets later on.
Example 2.5
(Lack of equivalence)
Fix T∈(0,∞) and let \(\mathcal{X} = (\mathcal{X}_{t}) _{t \in [0,T]}\) and \(\mathcal{Z} = (\mathcal{Z}_{t})_{t \in [0,T]}\) denote two independent processes with the same distribution as the process X in Example 2.4. Define the stopping time
with \(\inf\emptyset:= \mathfrak{T}\), and similarly \(\tau^{\mathcal{Z} }\). Define now the processes \(X := \mathcal{X}^{\tau^{\mathcal{X} } \wedge\tau^{\mathcal{Z} } }\) and \(Z := \mathcal{Z}^{\tau ^{\mathcal{X} } \wedge\tau^{\mathcal{Z}}}\). Since the stopping time \(\tau^{\mathcal{Z} }\) is independent from \(\mathcal{X}\) and satisfies \(\mathbb {Q}(\tau^{\mathcal{Z} } < T) = 1\), the process X is a strictly positive true \(\mathbb {Q}\)-martingale by a conditioning argument; and similarly, so is Z.
Define now a new probability measure \(\mathbb {Q}^{Z}\) by \(\mathrm {d}\mathbb {Q}^{Z} = Z_{T} \,\mathrm {d}\mathbb {Q}\) and observe that \(\mathbb {Q}\) and \(\mathbb {Q}^{Z}\) are equivalent and that the process X is a strict \(\mathbb {Q}^{Z}\)-local martingale since
where we have used the definitions of \(\mathbb {Q}^{Z}, \tau^{\mathcal{X}}\) and \(\tau^{\mathcal{Z} }\), the facts that \(\mathbb {Q}( \tau^{\mathcal{X} }=\tau ^{\mathcal{Z} }) =0\) and that X and Z have the same distribution under \(\mathbb {Q}\), and the martingale property of X under \(\mathbb {Q}\).
Let \(\widehat{\mathbb {Q}}\) and \(\widehat{\mathbb {Q}}^{Z}\) now denote the probability measures of Theorem 2.1 with X as density process. These two measures cannot be equivalent since X is a strictly positive true \(\mathbb {Q}\)-martingale, but only a strict \(\mathbb {Q}^{Z}\)-local martingale. Thus, the measures \(\mathbb {Q}\), \(\mathbb {Q}^{Z}\) and \(\widehat{\mathbb {Q}}\) are all equivalent, but only absolutely continuous with respect to \(\widehat{\mathbb {Q}}^{Z}\).
To elaborate on this, under both measures \(\widehat{\mathbb {Q}}\) and \(\widehat{\mathbb {Q}}^{Z}\), the process 1/X is a martingale and follows the same dynamics as the process Y in (2.5), stopped at time \(\tau:= {\tau}^{\mathcal{X} } \wedge{\tau}^{\mathcal{Z} } \). However, the distribution of τ is different under the two measures. More precisely, under \(\widehat{\mathbb {Q}}\), the stopping time \(\tau\leq{\tau}^{\mathcal{Z} }\) is bounded by the first time that the nonnegative \(\widehat{\mathbb {Q}}\)-local martingale \(\mathcal{Z}\) starting in 1 hits 1/2, thus \(\widehat{\mathbb {Q}}({\tau} <T) =1\); see also (ii) of Proposition C.3 in the Appendix. However, both 1/X and 1/Z are \(\widehat{\mathbb {Q}}^{Z}\)-martingales and the event that neither of these hits 2 has positive probability under \(\widehat{\mathbb {Q}}^{Z}\); thus \(\widehat{\mathbb {Q}}^{Z}(\tau> T) > 0\). This yields \(\widehat{\mathbb {Q}}(R \leq T) = 0 < \widehat{\mathbb {Q}}^{Z}(R \leq T)\), despite \({\mathbb {Q}}\) and \({\mathbb {Q}}^{Z}\) being equivalent.
3 Minimal joint replication price
In this section, we derive and discuss a representation of a contingent claim price, which we define as the minimal cost of replicating the contingent claim’s payoff under two probability measures simultaneously; specifically, the measure under which the underlying follows local martingale dynamics (\(\mathbb {Q}^{\$}\)) and the measure that corresponds to the change of numéraire ( ). We interpret a nonnegative \(\mathbb {Q}^{\$}\)-local martingale X as the current market value of one Euro in dollars, and the process Y:=1/X under the measure
). We interpret a nonnegative \(\mathbb {Q}^{\$}\)-local martingale X as the current market value of one Euro in dollars, and the process Y:=1/X under the measure  , derived from \(\mathbb {Q}^{\$}\) via the density process X (see Theorem 2.1), as the current market value of one dollar in Euros under its corresponding numéraire measure.
, derived from \(\mathbb {Q}^{\$}\) via the density process X (see Theorem 2.1), as the current market value of one dollar in Euros under its corresponding numéraire measure.
Remark 3.1
(Arbitrage and strict local martingales)
Modelling asset prices with strict local martingales usually leads to features of contingent claim prices that, on the first look, seem to imply simple arbitrage opportunities and do not reflect our economic understanding of financial markets. To elaborate on this issue, we remind the reader of the standard definition of a contingent claim price in a complete market framework as the minimal (super-)replicating cost of this contingent claim; here the replication occurs almost surely under the unique risk-neutral measure.
Using such contingent claim prices then usually results in the loss of standard put-call parity in strict local martingale models; see for example Cox and Hobson [4]. Even more disturbingly, the minimal replicating price for an asset modelled as a strict local martingale in a complete market is below its current value. Yet, due to an admissibility constraint on trading strategies, these models do not yield arbitrage opportunities; see also Delbaen and Schachermayer [5, 8]. For example, the strategy of shorting the asset modelled by a strict local martingale and replicating its payoff for a lower cost is not admissible, as it might lead to unbounded negative wealth before the strategy matures; more details on this argument are discussed in Ruf [36].
Throughout this section, we again assume a time horizon T∈(0,∞] and a filtered probability space \((\varOmega, \mathcal {F}_{T}, (\mathcal {F}_{t})_{t \in [0,T]}, \mathbb {Q}^{\$})\) that satisfies the technical conditions of Appendix B. We fix a nonnegative \(\mathbb {Q}^{\$}\)-local martingale X with almost surely càdlàg paths (and right-continuous for all ω∈Ω), define the stopping times \((R_{i})_{i \in \mathbb {N}}\), \((S_{i})_{i \in \mathbb {N}}\), S , and R as in Sect. 2, and assume that \(\mathbb {Q}^{\$}(S>S_{i} \wedge T) = 1\) for all \(i \in \mathbb {N}\); that is, X is assumed not to jump to zero. As above, we define a process Y=(Y
t
)
t∈[0,T] by Y
t
:=1/X
t
1
{R>t} for all t∈[0,T]. As illustrated in Theorem 2.1, there exists a probability measure  , which corresponds to the probability measure with X as numéraire, symbolically
, which corresponds to the probability measure with X as numéraire, symbolically  . We then extend the measure
. We then extend the measure  , currently defined on \((\varOmega, \mathcal {F}_{R-})\), to a measure on \((\varOmega, \mathcal {F}_{T})\), which we again denote, with a slightly misuse of notation, by
, currently defined on \((\varOmega, \mathcal {F}_{R-})\), to a measure on \((\varOmega, \mathcal {F}_{T})\), which we again denote, with a slightly misuse of notation, by  ; see Appendix B.
; see Appendix B.
For some \(d \in \mathbb {N}\), we assume the existence of d+1 tradable assets with nonnegative almost surely càdlàg price processes (and right-continuous for all ω∈ Ω), denoted by S
$=(S
$,(i))
i=0,1,…,d
in dollars and by S
€=(S
€,(i))
i=0,1,…,d
in Euros, with \(S^{\$, (i)} = (S^{\$, (i)}_{t})_{t \in [0,T]}\) and  for all i=0,1,…,d. We assume that the processes S
$,(i) have \(\mathbb {Q}^{\$}\)-local martingale dynamics and S
€,(i) have
for all i=0,1,…,d. We assume that the processes S
$,(i) have \(\mathbb {Q}^{\$}\)-local martingale dynamics and S
€,(i) have  -local martingale dynamics for all i=0,1,…,d. Moreover, we assume that these price processes describe the same assets and are consistent; that is, we assume that
-local martingale dynamics for all i=0,1,…,d. Moreover, we assume that these price processes describe the same assets and are consistent; that is, we assume that  for all t∈[0,T] and i=0,1,…,d. Thus, given a dollar price process S
$,(i) for the ith asset, the process S
€,(i) denotes the price for the same asset in Euros for all i=0,1,…,d, as it is the dollar price multiplied by the price of one dollar in Euros. This relationship holds up to time R∧S; any event “beyond” that has probability zero under one of the two measures.
for all t∈[0,T] and i=0,1,…,d. Thus, given a dollar price process S
$,(i) for the ith asset, the process S
€,(i) denotes the price for the same asset in Euros for all i=0,1,…,d, as it is the dollar price multiplied by the price of one dollar in Euros. This relationship holds up to time R∧S; any event “beyond” that has probability zero under one of the two measures.
By combining Proposition 2.3 and Proposition A.4 in the Appendix, given the \(\mathbb {Q}^{\$}\)-dynamics of S
$, we can always construct  -local martingales S
€ which satisfy \(S^{\$, (i)}_{t} \mathbf {1}_{\{R \wedge S>t\}} = S^{\$, (i)}_{t} \mathbf {1}_{\{R \wedge S>t\}}Y_{t}\) for all t∈[0,T] and i=0,1,…,d. More precisely, the equivalence in (ii) of Proposition 2.3 and our standing assumption that \(\mathbb {Q}^{\$}(S>S_{i} \wedge T)=1\) for all \(i \in \mathbb {N}\) first yield that S
$,(i)
Y is a
-local martingales S
€ which satisfy \(S^{\$, (i)}_{t} \mathbf {1}_{\{R \wedge S>t\}} = S^{\$, (i)}_{t} \mathbf {1}_{\{R \wedge S>t\}}Y_{t}\) for all t∈[0,T] and i=0,1,…,d. More precisely, the equivalence in (ii) of Proposition 2.3 and our standing assumption that \(\mathbb {Q}^{\$}(S>S_{i} \wedge T)=1\) for all \(i \in \mathbb {N}\) first yield that S
$,(i)
Y is a  -local martingale on [0,R∧S). Secondly, since R∧S is foretellable under
-local martingale on [0,R∧S). Secondly, since R∧S is foretellable under  , by Theorem 2.1, any
, by Theorem 2.1, any  -local martingale on [0,R∧S) can be extended to a local martingale on [0,R∧S], and then of course to a local martingale on [0,T] in an arbitrary manner after R∧S since the dynamics under one measure only determine the dynamics under the other measure up to the stopping time R∧S.
-local martingale on [0,R∧S) can be extended to a local martingale on [0,R∧S], and then of course to a local martingale on [0,T] in an arbitrary manner after R∧S since the dynamics under one measure only determine the dynamics under the other measure up to the stopping time R∧S.
We suppose that S
$,(0) and S
€,(1) denote the dollar and Euro money market account, each assumed to pay zero interest; that is, S
$,(0)≡1≡S
€,(1). Thus, S
$,(1)=X denotes the price of one Euro in dollars and S
€,(0)=Y the price of one dollar in Euros. More generally, part (iii) of Proposition 2.3 yields that if S
$,(i) is a \(\mathbb {Q}^{\$}\)-martingale for some i=1,…,d, then  for all t∈[0,T]; in other words, the martingale property of S
$,(i) under \(\mathbb {Q}^{\$}\) forces S
€,(i) to hit zero under
for all t∈[0,T]; in other words, the martingale property of S
$,(i) under \(\mathbb {Q}^{\$}\) forces S
€,(i) to hit zero under  at time R∧S. Vice versa, if S
€,(i) is a
at time R∧S. Vice versa, if S
€,(i) is a  -martingale for some i=1,…,d, then \(S^{\$, (i)}_{t} \mathbf {1}_{\{ S \leq t\}} = 0\) for all t∈[0,T].
-martingale for some i=1,…,d, then \(S^{\$, (i)}_{t} \mathbf {1}_{\{ S \leq t\}} = 0\) for all t∈[0,T].
We now are ready to define a trading strategy, relying on stochastic integrals with respect to the (d+1)-dimensional local martingales S
$ and S
€. We refer to Sects. I.4d and III.4a in Jacod and Shiryaev [20] for a discussion of stochastic integrals when the filtration does not satisfy the “usual assumptions’’, in the case of d=1 or all price processes being continuous, and to Jacod [19] for the general case. We denote by L(S
$) and L(S
€) the space of all predictable processes that are integrable with respect to S
$ and S
€, respectively, under the corresponding measures \(\mathbb {Q}^{\$}\) and  .
.
Stochastic integration is used in the following definition:
Definition 3.2
(Trading strategy)
A trading strategy is an \(\mathbb {R}^{d+1}\)-valued process η∈L(S $)∩L(S €) such that
-
its corresponding dollar wealth process \(V^{{\$}, \eta} = (V^{{\$ }, \eta}_{t}) _{t \in [0,T]}\) and Euro wealth process
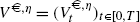 defined by
defined by 
stay nonnegative almost surely under the corresponding measure \(\mathbb {Q}^{\$}\) and
 , respectively, and
, respectively, and -
the self-financing condition holds, that is,

where the dynamics are computed under the corresponding measure \(\mathbb {Q}^{\$}\) and
 .
.
We say that η is a trading strategy for initial capital v∈[0,∞) expressed in dollars if
holds; and similarly for initial capital v expressed in Euros.
Thus, at any time t∈[0,T], each component of η t determines the current number of shares of each asset held at that point of time. Note that

Thus, the nonnegativity condition on V
$,η implies the one on  , but only up to the stopping time R. Moreover, a simple application of Itô’s rule yields that the self-financing condition under \(\mathbb {Q}^{\$}\) implies the one under
, but only up to the stopping time R. Moreover, a simple application of Itô’s rule yields that the self-financing condition under \(\mathbb {Q}^{\$}\) implies the one under  , but again only up to the stopping time R; see also Geman et al. [14].
, but again only up to the stopping time R; see also Geman et al. [14].
We call any pair of \(\mathcal {F}_{T}\)-measurable random variables (D
$,D
€) a contingent claim if D
€
1
{R∧S>T}=D
$
1
{R∧S>T}
Y
T
. The random variable D
$ (D
€) corresponds to the dollar (Euro) price of a contingent claim, as seen by the dollar (Euro) investor. We remind the reader that the event {S≤T} has zero  -probability, but might have positive \(\mathbb {Q}^{\$}\)-probability, and the converse statement holds for the event {R≤T}.
-probability, but might have positive \(\mathbb {Q}^{\$}\)-probability, and the converse statement holds for the event {R≤T}.
We represent a contingent claim as a pair of random variables so that we can exactly express its payoff both in dollars and in Euros including in the event of X hitting infinity. For example, the contingent claim (X
T
,1) pays off one Euro at maturity, while the contingent claim (X
T
,1
{R>T}) pays off one Euro if the price of one Euro in dollars did not explode. For K≥0, the claims \(D^{C,\$}_{K} := ((X_{T}-K)^{+}, (1-K Y_{T})^{+})\) and \(D^{P,\$}_{K} := ((K-X_{T})^{+},(K Y_{T}-1)^{+})\) are called call and put, respectively, on one Euro with strike K and maturity T. Equivalently, by exchanging the first with the second component and X
T
with Y
T
, we define calls and puts on one dollar and denote them by  and
and  . In foreign exchange markets, self-quantoed calls are traded, defined as \(D^{\mathrm{SQC},\$}_{K} := X_{T} D^{C,\$}_{K} = (X_{T}(X_{T}-K)^{+}, (X_{T}-K)^{+})\) for some K≥0.
. In foreign exchange markets, self-quantoed calls are traded, defined as \(D^{\mathrm{SQC},\$}_{K} := X_{T} D^{C,\$}_{K} = (X_{T}(X_{T}-K)^{+}, (X_{T}-K)^{+})\) for some K≥0.
We shall assume that the market is complete both for the dollar investor and for the Euro investor; that is, for any contingent claim (D $,D €) with D $, D € taking values in [0,∞), there exist trading strategies η $ and η € such that

and such that \(V^{\$, \eta^{\$}}\) is a \(\mathbb {Q}^{\$}\)-martingale and  is a
is a  -martingale. The replicability of any contingent claim under \(\mathbb {Q}^{\$}\) does not necessarily imply that any contingent claim can be replicated under
-martingale. The replicability of any contingent claim under \(\mathbb {Q}^{\$}\) does not necessarily imply that any contingent claim can be replicated under  , since the two measures are not equivalent in general.
, since the two measures are not equivalent in general.
Remark 3.3
(A seeming paradox)
Let the exchange rate X be a strict \(\mathbb {Q}^{\$}\)-local martingale hitting zero with positive probability. Then Y is a strict  -local martingale and we have the following paradox. Under the dollar measure, one can replicate the payoff of one Euro less than one Euro; simultaneously, under the Euro measure, one can replicate the payoff of one dollar for less than one dollar. To conclude, the exchange rate reflects an overly high price (compared to their replicating cost) both for the dollar and for the Euro; thus it is at the same time too high and too low for the dollar. This paradox can be explained by recalling that the two measures \(\mathbb {Q}^{\$}\) and
-local martingale and we have the following paradox. Under the dollar measure, one can replicate the payoff of one Euro less than one Euro; simultaneously, under the Euro measure, one can replicate the payoff of one dollar for less than one dollar. To conclude, the exchange rate reflects an overly high price (compared to their replicating cost) both for the dollar and for the Euro; thus it is at the same time too high and too low for the dollar. This paradox can be explained by recalling that the two measures \(\mathbb {Q}^{\$}\) and  are not equivalent; and therefore the investors are concerned with different events when replicating a Euro or a dollar.
are not equivalent; and therefore the investors are concerned with different events when replicating a Euro or a dollar.
The next theorem constitutes the core result of this section; we recall our standing assumption that \(\mathbb {Q}^{\$}(S>S_{i} \wedge T) = 1\) for all \(i \in \mathbb {N}\).
Theorem 3.4
(Minimal joint replicating price)
Define the dollar and Euro pricing operators as


for a contingent claim D=(D $,D €). Whenever D is nonnegative, the minimal joint Q $- and Q €-replicating price expressed in dollars (Euros) is p $(p €). More precisely, there exists a trading strategy η for initial capital p $(D) (expressed in dollars) with

and there exist no \(\widetilde{p} < p^{\$}(D)\) and no trading strategy \(\widetilde{\eta}\) for initial capital \(\widetilde{p}\) (expressed in dollars) such that (3.4) holds with η replaced by \(\widetilde{\eta}\).
Proof
The second equality in (3.3) follows directly from Theorem 2.1. Since the market is assumed to be complete, there exist trading strategies ν for initial capital \(p^{(1)} := \mathbb {E}^{ \mathbb {Q}^{\$}}[D^{\$}]\) (in dollars) and θ for initial capital  (in Euros) such that V
$,ν is a \(\mathbb {Q}^{\$}\)-martingale,
(in Euros) such that V
$,ν is a \(\mathbb {Q}^{\$}\)-martingale,  is a
is a  -martingale, and
-martingale, and

To show (3.4), we now prove that the trading strategy η:=ν+θ replicates D
$ under \(\mathbb {Q}^{\$}\) and D
€ under  ; the initial cost for η, expressed in dollars, is exactly p
$=p
(1)+x
0
p
(2). Moreover, note the identities \(V^{{\$},\eta}_{T} = V^{{\$},\nu}_{T} + V^{{\$},\theta}_{T}\) and
; the initial cost for η, expressed in dollars, is exactly p
$=p
(1)+x
0
p
(2). Moreover, note the identities \(V^{{\$},\eta}_{T} = V^{{\$},\nu}_{T} + V^{{\$},\theta}_{T}\) and  . In order to prove that η is a trading strategy, it suffices to prove that (a) \(\mathbb {Q}^{\$}(V^{{\$},\theta}_{T} > 0) = 0\) and (b)
. In order to prove that η is a trading strategy, it suffices to prove that (a) \(\mathbb {Q}^{\$}(V^{{\$},\theta}_{T} > 0) = 0\) and (b)  .
.
For (a), note that \((V^{\$,\theta}_{t} \mathbf {1}_{\{S > t\}})_{t \geq0}\) is a \(\mathbb {Q}^{\$}\)-local martingale by (i) in Proposition 2.3 with \(N = (V^{\$,\theta}_{t} \mathbf {1}_{\{R > t\}})_{t \geq0}\) and τ=R i for all \(i \in \mathbb {N}\). By taking differences, so is \((V^{\$,\theta}_{t} \mathbf {1}_{\{S \leq t\}})_{t \geq0}\), which implies \(\mathbb {Q}^{\$}(\{V^{{\$},\theta}_{T} > 0\} \cap\{S \leq T\}) = 0\). Observe next that

by (2.3) and (3.1) for all \(i \in \mathbb {N}\), which yields (a).
For (b), it suffices to show that  is a (nonnegative)
is a (nonnegative)  -local martingale. Since
-local martingale. Since  is one, it only remains to show, by (3.1), that NY with \(N := (V^{{\$},\nu}_{t} \mathbf {1}_{\{R > t\}})_{t \in [0,T]}\) is also a
is one, it only remains to show, by (3.1), that NY with \(N := (V^{{\$},\nu}_{t} \mathbf {1}_{\{R > t\}})_{t \in [0,T]}\) is also a  -local martingale. However, this follows directly from (iii) in Proposition 2.3 since N was assumed to be a \(\mathbb {Q}^{\$}\)-martingale.
-local martingale. However, this follows directly from (iii) in Proposition 2.3 since N was assumed to be a \(\mathbb {Q}^{\$}\)-martingale.
Next, we show that η corresponds to the cheapest trading strategy. To that end, let \(\widetilde{p} \in [0, \infty)\) and \(\widetilde{\eta}\) be a trading strategy for initial capital \(\widetilde{p}\) (expressed in dollars) that superreplicates D
$ under \(\mathbb {Q}^{\$}\) and D
€ under  . Then \(\widetilde{p} = M_{0} + N_{0}\), where M and N are the martingale and strict local martingale part of the Riesz decomposition \(V^{{\$},\widetilde{\eta}} = M + N\) under \(\mathbb {Q}^{\$}\) with \(\mathbb {Q}^{\$}(N_{T} = 0) = 1\). More explicitly, \(M_{t} := \mathbb {E}^{ \mathbb {Q}^{\$}}[V^{{\$},\widetilde{\eta}}_{T}\, |\, \mathcal {F}^{0}_{t}]\) and \(N_{t} := V^{{\$},\widetilde{\eta}}_{t} - M_{t}\) for all t∈[0,T]; see Theorem 2.3 of Föllmer [13] for the case of a not completed filtration.
. Then \(\widetilde{p} = M_{0} + N_{0}\), where M and N are the martingale and strict local martingale part of the Riesz decomposition \(V^{{\$},\widetilde{\eta}} = M + N\) under \(\mathbb {Q}^{\$}\) with \(\mathbb {Q}^{\$}(N_{T} = 0) = 1\). More explicitly, \(M_{t} := \mathbb {E}^{ \mathbb {Q}^{\$}}[V^{{\$},\widetilde{\eta}}_{T}\, |\, \mathcal {F}^{0}_{t}]\) and \(N_{t} := V^{{\$},\widetilde{\eta}}_{t} - M_{t}\) for all t∈[0,T]; see Theorem 2.3 of Föllmer [13] for the case of a not completed filtration.
Note that \(M = V^{{\$},\widetilde{\nu}}\) and \(N = V^{{\$},\widetilde {\theta}}\) for some trading strategies \(\widetilde{\nu}\) and \(\widetilde {\theta}\) with \(\widetilde{\eta} = \widetilde{\nu} + \widetilde{\theta}\). Since \(\widetilde{\nu}\) superreplicates D
$ under \(\mathbb {Q}^{\$}\), we obtain \(M_{0} \geq \mathbb {E}^{ \mathbb {Q}^{\$}}[D^{\$}]\). As in (b) in the first part of the proof, we have  . Thus, \(\widetilde{\theta}\) superreplicates D
€ under
. Thus, \(\widetilde{\theta}\) superreplicates D
€ under  . This implies that
. This implies that  , which yields that \(\widetilde{p} = M_{0} + N_{0} \geq p^{\$}(D)\). □
, which yields that \(\widetilde{p} = M_{0} + N_{0} \geq p^{\$}(D)\). □
Theorem 3.4 yields the smallest amount of dollars (Euros) needed to superreplicate a claim D under both measures \(\mathbb {Q}^{\$}\) and  . The corresponding replicating strategy is, as the proof illustrates, a sum of two components. The first component is the standard strategy that replicates the claim under one of the two measures; the second component replicates the claim under the events that only the other measure can “see”.
. The corresponding replicating strategy is, as the proof illustrates, a sum of two components. The first component is the standard strategy that replicates the claim under one of the two measures; the second component replicates the claim under the events that only the other measure can “see”.
The next few corollaries are direct implications of the last theorem. We usually formulate them only in terms of the dollar pricing operator p $, but they symmetrically also hold for the Euro pricing operator p €.
Corollary 3.5
(Linearity of pricing operator)
The pricing operator
p
$
of (3.2) is linear on its domain: for any claims
 and
and
 and any
\(a \in \mathbb {R}\)
such that
D
1
and
D
2
are both in the domain of
p
$, we have
and any
\(a \in \mathbb {R}\)
such that
D
1
and
D
2
are both in the domain of
p
$, we have
where
 .
.
Proof
The statement follows directly from the linearity of expectations. □
Corollary 3.6
(Martingale property of wealth process)
The wealth process V $,η of Theorem 3.4 is a \(\mathbb {Q}^{\$}\)-local martingale and thus does not introduce an arbitrage opportunity. It is a strict \(\mathbb {Q}^{\$}\)-local martingale if and only if the \(\mathbb {Q}^{\$}\)-local martingale X is a strict \(\mathbb {Q}^{\$}\)-local martingale and

Similarly, the wealth process
 is a
is a
 -local martingale. It is a strict
-local martingale. It is a strict
 -local martingale if and only if the
-local martingale if and only if the
 -local martingale
Y
is a strict
-local martingale
Y
is a strict
 -local martingale and
-local martingale and
Proof
The local martingale property of the wealth processes under the corresponding measures follows directly from their definition. The lack of martingale property follows from checking when the quantities p
$(D) and p
€(D) in (3.2) and (3.3) satisfy \(p^{\$}(D) > E^{ \mathbb {Q}^{\$}}[D^{\$}]\) and  , respectively. □
, respectively. □
Corollary 3.7
(Price of a Euro)
The minimal joint
\(\mathbb {Q}^{\$}\)- and
 -superreplicating price of (X
T
,1) is
x
0 (expressed in dollars) or 1 (expressed in Euros).
-superreplicating price of (X
T
,1) is
x
0 (expressed in dollars) or 1 (expressed in Euros).
Proof
Recall (2.2), which implies the identity  . □
. □
The corresponding replicating strategy is the buy-and-hold strategy of one Euro.
Corollary 3.8
(Put-call parity)
The prices of puts and calls simplify under the pricing operator p $ to

moreover, the put-call parity
holds, where \(K \in \mathbb {R}\) denotes the strike of the call \(D^{C,\$}_{K}\) and put \(D^{P,\$}_{K}\).
Proof
The statement follows directly from (3.2) and the linearity of expectations. □
We refer to Madan and Yor [26] for alternative representations of the call price in (3.5).
Giddy [15] introduces the notion of international put-call equivalence which relates the price of a call in one currency with the price of a put in the other currency; see also Grabbe [16].
Corollary 3.9
(International put-call equivalence)
The pricing operators p $ and p € satisfy international put-call equivalence: for all K>0,

Proof
We obtain

where we have used the identities of Corollary 3.8 and (2.3). The second equivalence follows in the same way or from the put-call parity for model prices in (3.6). □
The next remark discusses how our result motivates and generalizes Lewis’ generalized pricing formulas.
Remark 3.10
(Lewis’ generalized pricing formulas)
Within Markovian stochastic volatility models, Lewis [25] derives call and put prices which exactly correspond to (3.2) when applied to the call payoff \(D^{C,\$}_{K}\) or put payoff \(D^{P,\$}_{K}\). Lewis starts from the postulate that put-call parity holds, and then shows that the correction term that is added to the expected payoff under \(\mathbb {Q}^{\$}\) corresponds to the probability of some process exploding under another measure (corresponding here to  ). We start here instead from an economic argument by defining the price as the minimal superreplicating cost for a contingent claim under two possibly non-equivalent measures that arise from a change of numéraire. We then show that this directly implies put-call parity for model prices. This approach also yields a generalization of Lewis’ pricing formula to arbitrary, possibly path-dependent contingent claims.
). We start here instead from an economic argument by defining the price as the minimal superreplicating cost for a contingent claim under two possibly non-equivalent measures that arise from a change of numéraire. We then show that this directly implies put-call parity for model prices. This approach also yields a generalization of Lewis’ pricing formula to arbitrary, possibly path-dependent contingent claims.
Example 3.11
(Singular measures (continued))
We continue here our discussion of Example 2.4 with \(\mathbb {Q}^{\$}= \mathbb {Q}\) and  . Although the exchange rate X is a \(\mathbb {Q}^{\$}\)-local martingale, from the classical point of view of a dollar investor, the minimal superreplicating price of one Euro at time T is zero because under \(\mathbb {Q}^{\$}\) there are only paths under which this contingent claim becomes worthless. However, by means of the correction term, (3.2) yields a price p
$((X
T
,1))=x
0 when considering the minimal joint \(\mathbb {Q}^{\$}\)- and
. Although the exchange rate X is a \(\mathbb {Q}^{\$}\)-local martingale, from the classical point of view of a dollar investor, the minimal superreplicating price of one Euro at time T is zero because under \(\mathbb {Q}^{\$}\) there are only paths under which this contingent claim becomes worthless. However, by means of the correction term, (3.2) yields a price p
$((X
T
,1))=x
0 when considering the minimal joint \(\mathbb {Q}^{\$}\)- and  -superreplicating price of one Euro. For the self-quantoed call \(D^{\mathrm{SQC},\$}_{K}\), the classical price would again be zero; however, considering also the paths that the Euro investor under
-superreplicating price of one Euro. For the self-quantoed call \(D^{\mathrm{SQC},\$}_{K}\), the classical price would again be zero; however, considering also the paths that the Euro investor under  can see, Theorem 3.4 suggests a price \(p^{\$}(D^{\mathrm{SQC},\$}_{K})=\infty\) since
can see, Theorem 3.4 suggests a price \(p^{\$}(D^{\mathrm{SQC},\$}_{K})=\infty\) since  .
.
In many applications, however, the measures \(\mathbb {Q}^{\$}\) and  do not become singular. Often, one of them is absolutely continuous with respect to the other. In this case, the formulas for computing p
$(D) and p
€(D) simplify:
do not become singular. Often, one of them is absolutely continuous with respect to the other. In this case, the formulas for computing p
$(D) and p
€(D) simplify:
Corollary 3.12
(Absolutely continuous measures)
If
\(\mathbb {Q}^{\$}(S>T) = 1\), that is, if
Y
is a
 -martingale, then
p
€
can be computed as
-martingale, then
p
€
can be computed as

If
 , that is, if
X
is a
\(\mathbb {Q}^{\$}\)-martingale, then
, that is, if
X
is a
\(\mathbb {Q}^{\$}\)-martingale, then

Proof
Assume that \(\mathbb {Q}^{\$}(S>T) = 1\). Then Remark 2.2 implies that \(\mathbb {Q}^{\$}\) is absolutely continuous with respect to  . Thus, if a trading strategy superreplicates D
€
. Thus, if a trading strategy superreplicates D
€
 -almost surely for a Euro investor, then it also superreplicates D
$
\(\mathbb {Q}^{\$}\)-almost surely for a dollar investor. The second statement can be shown analogously. □
-almost surely for a Euro investor, then it also superreplicates D
$
\(\mathbb {Q}^{\$}\)-almost surely for a dollar investor. The second statement can be shown analogously. □
Example 3.13
(Reciprocal of the three-dimensional Bessel process)
We set d=T=1 and let X denote a nonnegative \(\mathbb {Q}^{\$}\)-local martingale distributed as the reciprocal of a three-dimensional Bessel process starting in 1; in particular, there exists a Brownian motion W=(W t ) t∈[0,T] such that
It is well known that X is strictly positive and that Y is a  -Brownian motion stopped when it hits zero; see for example Delbaen and Schachermayer [6]. Since X is strictly positive, the discussion in Remark 2.2 yields that \(\mathbb {Q}^{\$}\) is absolutely continuous with respect to
-Brownian motion stopped when it hits zero; see for example Delbaen and Schachermayer [6]. Since X is strictly positive, the discussion in Remark 2.2 yields that \(\mathbb {Q}^{\$}\) is absolutely continuous with respect to  ; thus, Corollary 3.12 applies.
; thus, Corollary 3.12 applies.
Let us study the self-quantoed call \(D^{\mathrm{SQC},\$}_{K}\). Since Brownian motion hits 0 in any time interval with positive probability, we obtain that X hits ∞ with positive  -probability. This yields directly a minimal joint \(\mathbb {Q}^{\$}\)- and
-probability. This yields directly a minimal joint \(\mathbb {Q}^{\$}\)- and  -superreplicating price of \(p^{\$ }(D^{\mathrm{SQC},\$}_{K}) =\infty\). It is interesting to note that as in Example 3.11, the classical price is finite; in fact,
-superreplicating price of \(p^{\$ }(D^{\mathrm{SQC},\$}_{K}) =\infty\). It is interesting to note that as in Example 3.11, the classical price is finite; in fact,

for all K≥0, where we have plugged in the density of killed Brownian motion; see Exercise III.1.15 in Revuz and Yor [32].
We remark that as a corollary of Remark 2.2, our setup contains only positive “bubbles” under the corresponding measure. A bubble is usually defined as the difference of the current price and the expectation of the terminal value of an asset, that is, \(x_{0} - \mathbb {E}^{ \mathbb {Q}^{\$}}[X_{T}]\) and  , respectively. It is possible that both bubbles are strictly positive; however, negative bubbles cannot occur by the supermartingale property of the asset price processes under the corresponding measure. This contrasts Jarrow and Protter [21], where negative bubbles are discussed, however only when considering the dollar measure \(\mathbb {Q}^{\$}\), which is not the risk-neutral measure of a Euro investor.
, respectively. It is possible that both bubbles are strictly positive; however, negative bubbles cannot occur by the supermartingale property of the asset price processes under the corresponding measure. This contrasts Jarrow and Protter [21], where negative bubbles are discussed, however only when considering the dollar measure \(\mathbb {Q}^{\$}\), which is not the risk-neutral measure of a Euro investor.
In the next section, we provide an interpretation of a bubble (lack of the martingale property of the exchange rate) as the possibility of a hyperinflation under some dominating “real-world” measure \(\mathbb {P}\). If for both currencies such hyperinflations have positive \(\mathbb {P}\)-probability, then X and Y both have a positive bubble.
4 A physical measure
In this section, we start by specifying a physical probability measure \(\mathbb {P}\) instead of a risk-neutral probability measure \(\mathbb {Q}^{\$}\). We again assume a time horizon T∈(0,∞] and a filtered probability space \((\varOmega, \mathcal {F}_{T}, (\mathcal {F}_{t})_{t \in [0,T]}, \mathbb {P})\) that satisfies the technical conditions of Appendix B. Let X=(X
t
)
t∈[0,T] denote a process taking values in [0,∞] with right-continuous paths for all ω∈Ω. Define the stopping times \((R_{i})_{i \in \mathbb {N}}, (S_{i})_{i \in \mathbb {N}}, S\) and R as in Sect. 2 and assume that \(\mathbb {P}(S_{i} \wedge T< S) = 1\) for all \(i \in \mathbb {N}\), X
(R+t)∧T
=∞ if R≤T and X
(S+t)∧T
=0 if S≤T for all t≥0. In particular, this assumption implies that no oscillations can occur; that is, the events H
$:={R≤T} and H
€:={S≤T} are disjoint. Suppose that \(\mathbb {P}(H^{\$}) <1\) and  . Define again Y=(Y
t
)
t∈[0,T] by Y
t
:=1/X
t
1
{R>t} for all t∈[0,T].
. Define again Y=(Y
t
)
t∈[0,T] by Y
t
:=1/X
t
1
{R>t} for all t∈[0,T].
Under the physical probability measure \(\mathbb {P}\), the events H $ and H € may both have positive probability. We interpret these events as the complete devaluation (hyperinflation) of the dollar or Euro currency with respect to the other. Such hyperinflations have been observed; for example, the exchange rate between the American and German currencies changed by a factor of 1010 from January 1922 to December 1923, as described in Sargent [38]. During a hyperinflation, the interest rate of the inflating currency tends to become very large, and so far, we have assumed zero interest rates. We may reinterpret X T as the forward exchange rate of dollars per Euro at time T, as opposed to a spot exchange rate. This is consistent with various interest rate assumptions, including the possibility that the dollar (respectively Euro) interest rate should explode when the dollar (respectively Euro) experiences a hyperinflation.
If \(\mathbb {P}(H^{\$}) > 0\) and  , then no risk-neutral measure equivalent to \(\mathbb {P}\) can exist such that either X or Y follow local martingale dynamics. Nevertheless, pricing and hedging of contingent claims might still be possible. Towards this end, let us introduce the two artificial measures
, then no risk-neutral measure equivalent to \(\mathbb {P}\) can exist such that either X or Y follow local martingale dynamics. Nevertheless, pricing and hedging of contingent claims might still be possible. Towards this end, let us introduce the two artificial measures

where we have conditioned the physical measure \(\mathbb {P}\) on the events \(H^{\$^{c}}\) and  that no hyperinflation occurs. Note that both measures \(\mathbb {P}^{\$}\) and
that no hyperinflation occurs. Note that both measures \(\mathbb {P}^{\$}\) and  are absolutely continuous with respect to \(\mathbb {P}\) and that \(\mathbb {P}\) is absolutely continuous with respect to their average
are absolutely continuous with respect to \(\mathbb {P}\) and that \(\mathbb {P}\) is absolutely continuous with respect to their average  .
.
As in Sect. 3, for some \(d \in \mathbb {N}\), we assume the existence of d+1 tradable assets with nonnegative price processes, denoted by S
$=(S
$,(i))
i=0,1,…d
in dollars and by S
€=(S
€,(i))
i=0,1,…d
in Euros; as before, with \(S^{\$, (i)} = (S^{\$, (i)}_{t})_{t \in [0,T]}\) and  for all i=0,1,…,d. We also assume again that
for all i=0,1,…,d. We also assume again that  for all t∈[0,T] and i=0,1,…,d and that S
$,(1)=X and S
€,(0)=Y. Moreover, we assume that S
$ and S
€ have càdlàg paths \(\mathbb {P}^{\$}\)- and
for all t∈[0,T] and i=0,1,…,d and that S
$,(1)=X and S
€,(0)=Y. Moreover, we assume that S
$ and S
€ have càdlàg paths \(\mathbb {P}^{\$}\)- and  -almost surely, respectively.
-almost surely, respectively.
Suppose that there exists exactly one probability measure \(\mathbb {Q}^{\$}\) ( ) that is equivalent to \(\mathbb {P}^{\$}\) (
) that is equivalent to \(\mathbb {P}^{\$}\) ( ) and under which the processes S
$ (S
€) are local martingales. Consider the condition of no obvious hyperinflations (NOH):
) and under which the processes S
$ (S
€) are local martingales. Consider the condition of no obvious hyperinflations (NOH):
-
(NOH)
The probability measures \(\mathbb {P}^{\$}\) and
 are equivalent on \(\mathcal {F}_{(R_{i} \wedge S_{j})-}\) for all \(i, j \in \mathbb {N}\).
are equivalent on \(\mathcal {F}_{(R_{i} \wedge S_{j})-}\) for all \(i, j \in \mathbb {N}\).
This condition corresponds to an environment in which at no time, one knows that a certain hyperinflation will occur \(\mathbb {P}\)-almost surely; that is, hyperinflations occur as a surprise. To see this, assume that the condition (NOH) does not hold. Then there exist \(i,j \in \mathbb {N}\) and a set \(A \in \mathcal {F}_{(R_{i} \wedge S_{j})-}\) such that for example \(\mathbb {P}^{\$ }(A) = 0\) and  , which implies A⊂H
$ (modulo \(\mathbb {P}\)). Thus, for some paths one knows that a hyperinflation will occur before it occurs. As the next lemma shows, the condition (NOH) brings us back to the framework of Theorems 2.1 and 3.4.
, which implies A⊂H
$ (modulo \(\mathbb {P}\)). Thus, for some paths one knows that a hyperinflation will occur before it occurs. As the next lemma shows, the condition (NOH) brings us back to the framework of Theorems 2.1 and 3.4.
Lemma 4.1
((NOH) and change of numéraire)
The following two conditions are equivalent:
-
(i)
The condition (NOH) holds.
-
(ii)
The equality in (2.1) of Theorem 2.1 holds for all stopping times τ and \(A \in \mathcal {F}_{\tau\wedge T}\) with \(\widehat{\mathbb {Q}}\) replaced by
 and
\(\mathbb {Q}\)
replaced by
\(\mathbb {Q}^{\$}\).
and
\(\mathbb {Q}\)
replaced by
\(\mathbb {Q}^{\$}\).
The proof of this equivalence is based on the assumption that  is the unique probability measure equivalent to
is the unique probability measure equivalent to  such that S
€ are
such that S
€ are  -local martingales. It is contained in Appendix D.
-local martingales. It is contained in Appendix D.
The next proposition yields that the minimal cost (expressed in dollars) for replicating a contingent claim D=(D
$,D
€) \(\mathbb {P}\)-almost surely is given by (3.2) in Theorem 3.4 if condition (NOH) holds. More precisely, one can find a trading strategy η, in the sense of Definition 3.2, such that the corresponding terminal wealth satisfies  . Since \(\mathbb {P}\) and
. Since \(\mathbb {P}\) and  are equivalent, we interpret η as a replication strategy under the physical measure \(\mathbb {P}\).
are equivalent, we interpret η as a replication strategy under the physical measure \(\mathbb {P}\).
Proposition 4.2
(Minimal replication cost under \(\mathbb {P}\))
Assume that the condition (NOH) holds. Then the minimal replicating cost for a contingent claim D=(D $,D €) under \(\mathbb {P}\) is exactly the one computed in Theorem 3.4.
Proof
Theorem 3.4 yields the minimal joint replicating cost of a claim under \(\mathbb {Q}^{\$}\) and under any extension of the corresponding measure after a change of numéraire. However, Lemma 4.1 shows that  is exactly such an extension if (NOH) holds. This yields the assertion since \(\mathbb {Q}^{\$}\) and
is exactly such an extension if (NOH) holds. This yields the assertion since \(\mathbb {Q}^{\$}\) and  are equivalent to \(\mathbb {P}^{\$ }\) and
are equivalent to \(\mathbb {P}^{\$ }\) and  , respectively. □
, respectively. □
We also obtain an interpretation of the lack of martingale property of X under the risk-neutral measure \(\mathbb {Q}^{\$}\) as the possibility of an explosion under the physical measure \(\mathbb {P}\):
Corollary 4.3
(Interpretation of the lack of the martingale property)
Assuming the condition (NOH), we have
\(\mathbb {P}(H^{\$}) > 0\)
if and only if
X
is a strict
\(\mathbb {Q}^{\$}\)-local martingale; equivalently, we have
 if and only if
Y
is a strict
if and only if
Y
is a strict
 -local martingale.
-local martingale.
Proof
Note that \(\mathbb {P}(H^{\$}) > 0\) if and only if  , which is equivalent to
, which is equivalent to  . Lemma 4.1 and Remark 2.2 then yield the first equivalence of the assertion. The second follows in the same manner. □
. Lemma 4.1 and Remark 2.2 then yield the first equivalence of the assertion. The second follows in the same manner. □
If the condition (NOH) does not hold, then Theorem 3.4 still provides an upper bound for the minimal replicating cost of a contingent claim. However, as the next example shows, the expression in (3.2) usually does not give the smallest minimal replicating cost under \(\mathbb {P}\).
Example 4.4
(Condition (NOH) not satisfied)
We fix d=1 and T=1. Let U denote an \(\mathcal {F}_{0}\)-measurable random variable taking values in {−1,1} with \(\mathbb {P}(U = 1) \in(0,1)\). Furthermore, define X=(X t ) t∈[0,T] by X t :=(Z t )U for all t∈[0,1], where Z=(Z t ) t∈[0,T] has the same distribution as the process in (2.4). Thus H $={U=−1} and H €={U=1}, and the condition (NOH) is not satisfied.
Consider the contingent claim D=(1,1), which pays either one dollar if the dollar does not hyperinflate or otherwise one Euro. Then (3.2) yields a price (in dollars) of p $(D)=1+1=2. However, at time zero, it is already known which of the two currencies defaults, as U is \(\mathcal {F}_{0}\)-measurable. Thus, the trading strategy η=(1 {U=1},1 {U=−1}), holding one unit of the corresponding currency, perfectly replicates the contingent claim at an initial cost of only one dollar.
5 Conclusion
Based on a replication argument, we have introduced a novel pricing operator for contingent claims that restores put-call parity and international put-call equivalence for model prices. If the underlying is a true martingale, our pricing operator is just the classical replication price. Furthermore, we have interpreted the lack of the martingale property of an underlying price process under the risk-neutral probability as the positive probability of an explosion (hyperinflation) under some dominating physical measure.
Two directions of future research arise. First, we have focused on the case of two currencies, corresponding to one exchange rate only. It would be interesting to extend the results of this paper to multiple currencies and to find a consistent way to describe devaluations of currencies with respect to several other currencies. The numéraire-free approach taken in Yan [41] might be very useful. Second, throughout this paper we have relied on the assumption that markets are complete. Again, it would be interesting to consider incomplete markets and to develop a theory of joint superreplication in such markets.
References
Andersen, L.: Option pricing with quadratic volatility: a revisit. Finance Stoch. 15, 191–219 (2011)
Carr, P., Fisher, T., Ruf, J.: Why are quadratic normal volatility models analytically tractable? SIAM J. Financ. Math. 4, 185–202 (2013)
Cheridito, P., Filipović, D., Yor, M.: Equivalent and absolutely continuous measure changes for jump-diffusion processes. Ann. Appl. Probab. 15, 1713–1732 (2005)
Cox, A., Hobson, D.: Local martingales, bubbles and option prices. Finance Stoch. 9, 477–492 (2005)
Delbaen, F., Schachermayer, W.: A general version of the fundamental theorem of asset pricing. Math. Ann. 300, 463–520 (1994)
Delbaen, F., Schachermayer, W.: Arbitrage possibilities in Bessel processes and their relations to local martingales. Probab. Theory Relat. Fields 102, 357–366 (1995)
Delbaen, F., Schachermayer, W.: The no-arbitrage property under a change of numéraire. Stoch. Stoch. Rep. 53, 213–226 (1995)
Delbaen, F., Schachermayer, W.: The fundamental theorem of asset pricing for unbounded stochastic processes. Math. Ann. 312, 215–250 (1998)
Delbaen, F., Schachermayer, W.: A simple counterexample to several problems in the theory of asset pricing. Math. Finance 8, 1–11 (1998)
Dellacherie, C.: Ensembles aléatoires. I. In: Dold, A., Eckmann, B. (eds.) Séminaire de Probabilités, III. Lecture Notes in Mathematics, vol. 88, pp. 97–114. Springer, Berlin (1969)
Fernholz, D., Karatzas, I.: On optimal arbitrage. Ann. Appl. Probab. 20, 1179–1204 (2010)
Föllmer, H.: The exit measure of a supermartingale. Z. Wahrscheinlichkeitstheor. Verw. Geb. 21, 154–166 (1972)
Föllmer, H.: On the representation of semimartingales. Ann. Probab. 1, 580–589 (1973)
Geman, H., El Karoui, N., Rochet, J.: Changes of numéraire, changes of probability measure and option pricing. J. Appl. Probab. 32, 443–458 (1995)
Giddy, I.: Foreign exchange options. J. Futures Mark. 3, 143–166 (1983)
Grabbe, J.: The pricing of call and put options on foreign exchange. J. Int. Money Financ. 2, 239–253 (1983)
Henry-Labordère, P.: Analysis, Geometry, and Modeling in Finance. Advanced Methods in Option Pricing. Chapman & Hall, Boca Raton (2009)
Heston, S., Loewenstein, M., Willard, G.: Options and bubbles. Rev. Financ. Stud. 20, 359–390 (2007)
Jacod, J.: Intégrales stochastiques par rapport à une semimartingale vectorielle et changements de filtration. In: Azéma, J., Yor, M. (eds.) Séminaire de Probabilités, XIV. Lecture Notes in Mathematics, vol. 784, pp. 161–172. Springer, Berlin (1980)
Jacod, J., Shiryaev, A.N.: Limit Theorems for Stochastic Processes, 2nd edn. Springer, Berlin (2003)
Jarrow, R., Protter, P.: Foreign currency bubbles. Rev. Deriv. Res. 14, 67–83 (2011)
Karatzas, I., Shreve, S.E.: Brownian Motion and Stochastic Calculus, 2nd edn. Springer, New York (1991)
Kardaras, C., Kreher, D., Nikeghbali, A.: Strict local martingales and bubbles. Preprint arXiv:1108.4177 (2012)
Lenglart, E.: Transformation des martingales locales par changement absolument continu de probabilités. Z. Wahrscheinlichkeitstheor. Verw. Geb. 39, 65–70 (1977)
Lewis, A.L.: Option Valuation under Stochastic Volatility. Finance Press, Newport Beach (2000)
Madan, D., Yor, M.: Itô’s integrated formula for strict local martingales. In: Émery, M., Yor, M. (eds.) Séminaire de Probabilités, XXXIX. Lecture Notes in Mathematics, vol. 1874, pp. 157–170. Springer, Berlin (2006)
Meyer, P.: La mesure de H. Föllmer en théorie de surmartingales. In: Dold, A., Eckmann, B. (eds.) Séminaire de Probabilités, VI. Lecture Notes in Mathematics, vol. 258, pp. 118–129. Springer, Berlin (1972)
Pal, S., Protter, P.E.: Analysis of continuous strict local martingales via h-transforms. Stoch. Process. Appl. 120, 1424–1443 (2010)
Parthasarathy, K.: Probability Measures on Metric Spaces. Academic Press, New York (1967)
Perkowski, N., Ruf, J.: Conditioned martingales. Electron. Commun. Probab. 17, 1–12 (2012)
Protter, P.: A mathematical theory of financial bubbles. In: Henderson, V., Sircair, R. (eds.) Princeton Lectures on Mathematical Finance, Paris, pp. 1–108. Springer, Cham (2013)
Revuz, D., Yor, M.: Continuous Martingales and Brownian Motion, 3rd edn. Springer, Berlin (1999)
Ruf, J.: Optimal trading strategies under arbitrage. Ph.D. thesis, Columbia University, New York, USA (2011) http://academiccommons.columbia.edu/catalog/ac:131477
Ruf, J.: Hedging under arbitrage. Math. Finance 23, 297–317 (2013)
Ruf, J.: The martingale property in the context of stochastic differential equations. Preprint (2013). arXiv:1306.0218
Ruf, J.: Negative call prices. Ann. Finance 9, 787–794 (2013)
Ruf, J.: A new proof for the conditions of Novikov and Kazamaki. Stoch. Process. Appl. 123, 404–421 (2013)
Sargent, T.J.: The ends of four big inflations. In: Hall, R.E. (ed.) Inflation: Causes and Effects, pp. 41–98. University of Chicago Press, Chicago (1982)
Schönbucher, P.J.: A Libor market model with default risk. Preprint, available at SSRN (2000). http://ssrn.com/abstract=261051 or doi:10.2139/ssrn.261051
Sin, C.: Complications with stochastic volatility models. Adv. Appl. Probab. 30, 256–268 (1998)
Yan, J.A.: A new look at the fundamental theorem of asset pricing. J. Korean Math. Soc. 35, 659–673 (1998)
Acknowledgements
We thank Sara Biagini, Zhenyu Cui, Pierre Henry-Labordère, Ioannis Karatzas, Kostas Kardaras, Martin Klimmek, Alex Lipton, and Nicolas Perkowski for their helpful comments on an early version of this paper. In particular, we are deeply indebted to Sergio Pulido for his careful reading of this paper and for several helpful discussions. We are grateful to two anonymous referees, an Associate Editor, and Martin Schweizer for very helpful suggestions, which substantially improved this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
The views represented herein are the authors’ own views and do not necessarily represent the views of Morgan Stanley or its affiliates and are not a product of Morgan Stanley research.
Appendices
Appendix A: Local martingales on stochastic intervals
In this appendix, we provide some technical results for stochastic processes that satisfy the local martingale property up to a stopping time. Such stochastic processes appear throughout this paper.
Similarly to Perkowski and Ruf [30], we consider the time set \(\mathcal{T}:= [0,\infty] \cup\{\mathfrak{T}\}\), where \(\mathfrak{T}\) represents a time “beyond horizon”; the natural ordering is extended to \(\mathcal{T}\) by \(t < \mathfrak{T}\) for all t∈[0,∞]. For any \(t \in\mathcal{T}\) and any sequence \((t_{i})_{i \in \mathbb {N}}\) with \(t_{i} \in\mathcal{T}\) for all \(i \in \mathbb {N}\), we write lim i↑∞ t i =t if either \(t = \mathfrak{T}\) and \(\inf_{i \geq j} t_{i} = \mathfrak{T}\) for some \(j \in \mathbb {N}\), or if \(t < \mathfrak{T}\), \(\sup_{i \geq j} t_{i} < \mathfrak{T}\) and lim i↑∞;i≥j t i =t for some \(j \in \mathbb {N}\).
Throughout this appendix, we fix a time horizon T∈(0,∞], an arbitrary stochastic basis \((\varOmega, \mathcal {F}_{T}, (\mathcal {F}_{t})_{t \in[0, T]}, \mathbb {P})\), and a process N=(N t ) t∈[0,T] taking values in [−∞,∞]. For a \(\mathcal{T}\)-valued random variable τ, we define the stopped stochastic process \(N^{\tau}= (N_{t}^{\tau})_{t \in[0,T]} :=(N_{t \wedge\tau})_{t \in[0,T]}\). Throughout this appendix, we fix a stopping time τ, which is a map \(\tau: \varOmega\rightarrow\mathcal{T}\) such that \(\{\tau\leq t\} \in \mathcal {F}_{t}\) for all t∈[0,T]. If not specified further, all (in)equalities are interpreted in the \(\mathbb {P}\)-almost sure sense.
We start with a definition.
Definition A.1
(Local martingale on a stochastic interval)
We call N:
-
(1)
a local martingale on [0,τ] if there exists a nondecreasing sequence of stopping times \((\tau_{i})_{i \in \mathbb {N}}\) with lim i↑∞ τ i >τ∧T such that \(N^{\tau_{i} \wedge\tau}\) is a martingale for all \(i \in \mathbb {N}\);
-
(2)
a local martingale on [0,τ) if there exists a nondecreasing sequence of stopping times \((\tau_{i})_{i \in \mathbb {N}}\) with lim i↑∞ τ i =τ such that \(N^{\tau_{i}}\) is a martingale for all \(i \in \mathbb {N}\).
In particular, if T=τ=∞, then a local martingale on [0,τ) corresponds exactly to the usual notion of a local martingale. Observe that if N is a local martingale on [0,τ], then it is a local martingale on [0,τ). If the definition of a local martingale on [0,τ) required additionally the assumption that τ i <τ for all \(i \in \mathbb {N}\) (something that Definition A.1 does not require), this implication would in general not hold true; consider for example a compensated Poisson process and τ the time of its first jump. Observe also that if \(\widetilde{\tau}\) is a stopping time with \(\widetilde{\tau} \wedge T < \epsilon\vee\tau \) for all ϵ>0, then any local martingale on [0,τ) is also a local martingale on \([0,\widetilde{\tau}]\).
In the following, we repeatedly use the fact that
is a (local) martingale if \(N^{{\eta_{1}} }\) and \(N^{ \eta_{2}}\) are (local) martingales for some stopping times η 1 and η 2. The next lemma is useful in several of the proofs in this paper.
Lemma A.2
(Localization sequence for a local martingale on a stochastic interval)
The following two statements are equivalent:
-
(a.1)
N is a local martingale on [0,τ].
-
(a.2)
There exists a nondecreasing sequence of stopping times \((\tau_{i})_{i \in \mathbb {N}}\) such that lim i↑∞ τ i >τ∧T and that N is a local martingale on [0,τ i ∧τ] for all \(i \in \mathbb {N}\).
The following three statements are equivalent:
-
(b.1)
N is a local martingale on [0,τ).
-
(b.2)
There exists a nondecreasing sequence of stopping times \((\tau_{i})_{i \in \mathbb {N}}\) such that lim i↑∞ τ i =τ and that N is a local martingale on [0,τ i ] for all \(i \in \mathbb {N}\).
-
(b.3)
There exists a nondecreasing sequence of stopping times \((\tau_{i})_{i \in \mathbb {N}}\) such that lim i↑∞ τ i =τ and that N is a local martingale on [0,τ i ) for all \(i \in \mathbb {N}\).
Proof
For the first part, we only need to show the implication from (a.2) to (a.1). Thus, assume (a.2), which yields that there exists for all \(i \in \mathbb {N}\) a stopping time η i with \(\mathbb {P}({\eta}_{i} \leq\tau_{i} \wedge\tau\wedge T) \leq2^{-i}\) such that \(N^{{\eta}_{i} \wedge{\tau}_{i} \wedge\tau}\) is a martingale. For all \(i \in \mathbb {N}\), define \(\widetilde{\tau}_{i} = \max_{j \in\{1, \ldots, i\}} ({\eta}_{j} \wedge{\tau}_{j})\) and observe that \(N^{\widetilde{\tau}_{i} \wedge\tau}\) is a martingale for all \(i \in \mathbb {N}\) and that \(\lim_{i \uparrow\infty} \widetilde {\tau}_{i} > \tau\wedge T\). This shows that (a.1) holds.
For the second part, we only need to show the implication from (b.3) to (b.1). Assume now (b.3). Then there exists a nondecreasing sequence of stopping times \(({\eta}_{i})_{i \in \mathbb {N}}\) such that
and \(N^{\eta_{i}}\) is a martingale for all \(i \in \mathbb {N}\). Define \(\widetilde{\tau}_{i} := \tau\wedge\max_{j \in\{1, \ldots, i\}} \eta_{i} \) and observe that \(N^{\widetilde{\tau}_{i}}\) is a martingale for all \(i \in \mathbb {N}\) and that \(\lim_{i \uparrow\infty} \widetilde{\tau}_{i} = \tau\), which yields (b.1). □
For the next lemma, observe that the random times
with \(\inf\emptyset:= \mathfrak{T}\) for all \(j \in \mathbb {N}\) take values in \([0,\tau\wedge T] \cup\mathfrak{T}\) and are stopping times if the underlying filtration \((\mathcal {F}_{t})_{t \in[0,T]}\) is right-continuous and N(ω) is a right-continuous path for all ω∈Ω; see for example Problem 1.2.6 in Karatzas and Shreve [22].
Lemma A.3
(Localization sequence for a nonnegative local martingale)
Assume that the underlying filtration \((\mathcal {F}_{t})_{t \in[0,T]}\) is right-continuous and N(ω) is a right-continuous path taking values in [0,∞] for all ω∈Ω. Define the stopping times \((\rho_{j})_{j \in \mathbb {N}}\) as in (A.1) and ρ:=lim j↑∞ ρ j . Then the following statements hold:
-
(i)
If \(N^{\rho_{j} \wedge\tau}\) is a supermartingale for all \(j \in \mathbb {N}\) (in particular, if N τ is a supermartingale), then \(\rho= \mathfrak{T}\).
-
(ii)
If \(N^{\rho_{j} \wedge\tau_{i}^{(j)}}\) is a supermartingale for all \(i,j \in \mathbb {N}\) for some nondecreasing sequences of stopping times \((\tau_{i}^{(j)})_{i \in \mathbb {N}}\) with \(\lim_{i \uparrow\infty} \tau_{i}^{(j)} = \tau\) for all \(j \in \mathbb {N}\), then ρ≥τ.
The following statements are equivalent:
-
(a.1)
N is a local martingale on [0,τ].
-
(a.2)
\(N^{\rho_{j} \wedge\tau}\) is a uniformly integrable martingale for all \(j \in \mathbb {N}\).
-
(a.3)
\(N^{\rho_{j}}\) is a local martingale on [0,τ] for all \(j \in \mathbb {N}\).
The following statements are equivalent:
-
(b.1)
N is a local martingale on [0,τ).
-
(b.2)
\(N^{\rho_{j} \wedge\tau_{i}}\) is a uniformly integrable martingale for all \(i,j \in \mathbb {N}\) for some nondecreasing sequence of stopping times \((\tau_{i})_{i \in \mathbb {N}}\) with lim i↑∞ τ i =τ.
-
(b.3)
\(N^{\rho_{j}}\) is a local martingale on [0,τ) for all \(j \in \mathbb {N}\).
Proof
Assume that \(N^{\rho_{j} \wedge\tau}\) is a nonnegative supermartingale and note that \(N^{\rho_{j} \wedge\tau}_{T} \geq j\) if ρ j ≤τ∧T; thus \(\mathbb {P}(\rho_{j} \leq\tau\wedge T) \leq N_{0} / j\) for all \(j \in \mathbb {N}\), which yields (i). Next, assume that there exist sequences of stopping times \((\tau _{i}^{(j)})_{i \in \mathbb {N}}\) such that \(N^{\rho_{j} \wedge\tau_{i}^{(j)}}\) is a supermartingale for all \(i,j \in \mathbb {N}\). Fix a sequence (i j ) j∈N so that
Then we have \(N_{0} \geq \mathbb {E}[ N^{\rho_{j} \wedge\tau_{i_{j}}^{(j)}}_{T}] \geq j \mathbb {P}(\rho_{j} \leq\tau_{i_{j}}^{(j)} \wedge T)\) and thus
for all \(j \in \mathbb {N}\), which yields (ii).
Now assume (a.1) and observe that \(\sup_{t \in[0,T]} N_{t}^{\rho_{j} \wedge\tau} \leq j + N_{T}^{\rho_{j} \wedge\tau}\) and that \(N_{T}^{\rho_{j} \wedge\tau}\) is integrable for all \(j\in \mathbb {N}\) since N τ is a supermartingale. This observation in conjunction with dominated convergence shows (a.2). Next, assume (a.3) and observe that \(N^{\rho _{j}}\) is a supermartingale on [0,τ] for all \(j \in \mathbb {N}\), and thus \(\rho=\mathfrak{T}\) by (i). The first part of Lemma A.2 then yields (a.1).
Now assume (b.1), which gives the existence of a nondecreasing sequence of stopping times \((\tau_{i})_{i \in \mathbb {N}}\) with lim i↑∞ τ i =τ such that N is a local martingale on [0,τ i ] for all \(i \in \mathbb {N}\). Using the implication of (a.1) to (a.2) with τ replaced by τ i for all \(i \in \mathbb {N}\), we observe that (b.2) holds. Next, assume (b.3). Then (ii) yields that ρ≥τ and the second part of Lemma A.2 then yields (b.1). □
Note that the implication of (b.3) to (b.1) in Lemma A.3 with T=τ=∞ yields that any nonnegative right-continuous process N is automatically a local martingale (on [0,∞)) if \(N^{\rho_{j}}\) is a local martingale (on [0,∞)) for all \(j \in \mathbb {N}\). Furthermore, by (ii), \(N^{\rho_{j}}\) is a supermartingale for all \(j \in \mathbb {N}\) if and only if N is a supermartingale.
We call the stopping time τ foretellable if there exists a nondecreasing sequence of stopping times \((\tau_{i})_{i \in \mathbb {N}}\) such that lim i↑∞ τ i =τ (in particular, there exists some \(i(\omega) \in \mathbb {N}\) with \(\tau_{i(\omega)}(\omega) = \mathfrak{T}\) if \(\tau(\omega) = \mathfrak{T}\)) and τ i ∧T<τ∨ϵ for all \(i \in \mathbb {N}\) and ϵ>0. We then call \((\tau_{i})_{i \in \mathbb {N}}\) an announcing sequence for τ.
The following result illustrates that a nonnegative local martingale on a half-open stochastic interval (with respect to a foretellable stopping time) can be extended to one on a closed interval. For example, if N is defined by N t :=1 {t<τ} for all t∈[0,T], then N can be extended to a process M=(M t ) t∈[0,T] with M t :=1 for all t∈[0,T], representing a local martingale on [0,T].
Proposition A.4
(Extension of local martingales on a stochastic interval)
Suppose that the assumptions of Lemma A.3 hold and assume that τ is foretellable and that N is a local martingale on [0,τ). Then there exists a unique local martingale M=(M t ) t∈[0,T] on [0,T] such that M=M τ, (M t 1 {t<τ}) t∈[0,T]=(N t 1 {t<τ}) t∈[0,T], M 0=N 0 and, moreover, lim s↑τ(ω) M s (ω)=M t (ω) for all ω∈Ω with \(\tau(\omega) \notin\{ 0,\mathfrak{T}\}\). The process M has nonnegative and right-continuous paths.
Proof
The uniqueness of M follows directly from its left-continuity at time τ. Let \((\tau_{i})_{i \in \mathbb {N}}\) denote an announcing sequence for τ and \((\widetilde{\tau}_{i})_{i \in \mathbb {N}}\) a nondecreasing sequence of stopping times such that \(N^{\widetilde{\tau}_{i}}\) is a martingale for all \(i \in \mathbb {N}\) and \(\lim_{i \uparrow\infty} \widetilde{\tau}_{i} = \tau\). We assume without loss of generality that \(\tau_{i} = \tau_{i} \wedge \widetilde{\tau}_{i}\) for all \(i \in \mathbb {N}\). Observe that \(N^{\tau_{i}}\) is a nonnegative supermartingale for all \(i \in \mathbb {N}\). By imitating the proof of Theorem 1.3.15 in Karatzas and Shreve [22] based on Doob’s up- and down-crossing inequalities (replace therein n by τ n for all \(n \in \mathbb {N}\) and ∞ by τ), we obtain that \(M_{t} := \lim_{i \uparrow\infty} N_{t}^{\tau_{i}}\) for all t∈[0,T] exists.
We need to show that M defined in this way is a local martingale on [0,T]. By Lemma A.3, it suffices to show that \(M^{\widetilde{\rho}_{j}}\) is a martingale for all \(j\in \mathbb {N}\), where \(\widetilde{\rho}_{j} := \inf\{t \in[0,T] : {M}_{t} > j\}\) with \(\inf\emptyset:= \mathfrak{T}\). Fix an arbitrary \(j \in \mathbb {N}\) and observe that by dominated and monotone convergence
which yields the statement since by Fatou’s lemma, \(M^{\widetilde{\rho }_{j}}\) is a supermartingale. □
We warn the reader that usually \(M_{T}^{\tau}\neq N^{\tau}_{T}\), even if N is a martingale on [0,τ], since N need not be left-continuous at τ. We also refer the reader to the related Exercise IV.1.48 in Revuz and Yor [32], where the case of not necessarily nonnegative local martingales is treated.
Appendix B: Conditions on the filtration in Sects. 2–4
In this appendix, we discuss the technical assumptions on the underlying filtration that are necessary for the results in Sects. 2–4. Throughout this appendix, we fix a time horizon T∈(0,∞] and denote a set of states by Ω≠∅ and a filtration by \(({\mathcal {F}}_{t})_{t \in[0,T]}\).
We refer to Appendix A for the definition of a stopping time. For any stopping time τ, we define
and
if \(({\mathcal {F}}_{t})_{t \in[0,T]}\) is the right-continuous modification of a filtration \(({\mathcal {F}}_{t}^{0})_{t \in[0,T]}\); see p. 156 in Föllmer [12].
In Sect. 2, we are constructing a probability measure on \((\varOmega, \mathcal {F}_{R-})\) for a certain stopping time R:=lim i↑∞ R i , where \((R_{i})_{i \in \mathbb {N}}\) is a sequence of nondecreasing stopping times, defined in Sect. 2. This construction is based on an extension theorem, more precisely on Theorem V.4.1 in Parthasarathy [29], and thus requires certain technical assumptions on the filtration \(({\mathcal {F}})_{t \in[0,T]}\). Specifically, we require in Sects. 2–4 that
-
(i)
\(({\mathcal {F}}_{t})_{t \in[0,T]}\) be the right-continuous modification of a filtration \(({\mathcal {F}}_{t}^{0})_{t \in[0,T]}\), and
-
(ii)
\(({\mathcal {F}}_{R_{i}-})_{i \in \mathbb {N}}\) be a standard system, as defined in Sect. 6 of Föllmer [12].
Furthermore, in Sect. 3, we require that
-
(iii)
any probability measure \(\mathbb {P}\) on \((\varOmega, \mathcal {F}_{R-})\) can be extended to a probability measure \(\widetilde{\mathbb {P}}\) on \((\varOmega , \mathcal {F}_{T})\).
A sufficient condition for requirement (ii) is that
is the right-continuous modification of a standard system (RCMSS); see Remark 6.1.1 in Föllmer [12], applied to the filtration \((\mathcal{G}_{t})_{t \geq0}\) with \(\mathcal{G}_{t} := {\widehat {\mathcal {F}}}_{1/(1-t) - 1}\) if T=∞, and \(\mathcal{G}_{t} := {\widehat{\mathcal {F}}}_{t T}\) otherwise, for all t∈[0,1], and \(\mathcal{G}_{t} = {\widehat{\mathcal {F}}}_{T}\) for all t>1. We remark that \((\widehat{\mathcal {F}}_{t})_{t \in[0,T]}\) then usually does not satisfy the “usual conditions” as it is not completed under some probability measure. Observe that if \(({\mathcal {F}}_{t}^{0})_{t \in[0,T]}\) is a standard system, then so is \(({\mathcal {F}}^{0}_{t} \cap{ \mathcal {F}}_{R-})_{t \in[0,T]}\).
In the following, we provide a canonical example for Ω and for a filtration \(({\mathcal {F}}_{t})_{t \in[0,T]}\), such that \(({\mathcal {F}}_{t} \cap{ \mathcal {F}}_{R-})_{t \in[0,T]}\) is an RCMSS. This example provides a sufficiently rich structure so that one might as well assume, throughout this paper, that the underlying filtered measurable space is of that form.
Towards this end, let E denote any locally compact space with countable base (for instance, \(E=\mathbb {R}^{n}\) for some \(n \in \mathbb {N}\)), and let Ω denote the space of right-continuous paths ω:[0,T]→[0,∞]×E whose first component ω (1) satisfies ω (1)(R(ω)+t)=∞ for all t≥0, and that have left limits on (0,R(ω)), where R(ω) denotes the first time that ω (1)=∞. Let \(({\mathcal {F}}_{t}^{0})_{t \in[0,T]}\) denote the filtration generated by the paths and \((\mathcal {F}_{t})_{t \in [0,T]}\) its right-continuous modification. Then it follows as in Dellacherie [10], Meyer [27] and Example 6.3.2 of Föllmer [12] that \(({\mathcal {F}}_{t} \cap{ \mathcal {F}}_{R-})_{t \in[0,T]}\) is an RCMSS. We identify the process X(ω), which appears in Sect. 2, with the first coordinate of ω.
Observe that in the canonical setup of the last paragraph, the extension of requirement (iii) always exists. To see this, define \(\widetilde{\mathbb {P}}(A) := \mathbb {P}(\omega^{R-} \in A)\) for all \(A \in \mathcal {F}_{T}\), where ω R−∈Ω is given for all ω∈Ω by
for some e∈E for all t∈[0,T]. This specific construction then yields one extension \(\widetilde{\mathbb {P}}\) on \((\varOmega, \mathcal {F}_{T})\).
Appendix C: Proof of Proposition 2.3 and further statements concerning the change of measure in Sect. 2
In this appendix, we provide additional statements on the change of measure suggested in Sect. 2 and on the proof of Proposition 2.3. We refer to Appendix A for the definition of a stopping time.
Below, we shall rely on the next lemma:
Lemma C.1
(Convergence of stopping times)
Assume the setup of Theorem 2.1 and fix a stopping time τ. Then we have \(\mathbb {Q}(S>\tau) = 0\) if and only if \(\widehat{\mathbb {Q}}(R>\tau) = 0\).
Proof
Without loss of generality, we set x 0=1. Then (2.1) yields that
which yields one direction of the statement. The other direction follows from (2.3) in the same manner. □
Next, we formulate a generalized version of Bayes’ formula. If X is a \(\mathbb {Q}\)-martingale, this formula is well known; see for example Lemma 3.5.3 in Karatzas and Shreve [22]. If X is a strictly positive continuous \(\mathbb {Q}\)-local martingale, Bayes’ formula has been derived in Ruf [33].
Proposition C.2
(Bayes’ formula)
Assume the setup of Theorem 2.1 and fix two stopping times ρ,τ with ρ≤τ \(\mathbb {Q}\)- and \(\widehat{\mathbb {Q}}\)-almost surely and an \(\mathcal {F}_{\tau\wedge T}\)-measurable random variable Z∈[0,∞]. Then we have the Bayes’ formula
This equality holds \(\mathbb {Q}\)- and \(\widehat{\mathbb {Q}}\)-almost surely.
Proof
Without loss of generality, assume that x 0=1. Then (C.1) holds \(\widehat{\mathbb {Q}}\)-almost surely since \(\widehat{\mathbb {Q}}(S > \rho\wedge T) = 1\) and for all \(A \in \mathcal {F}_{\rho}\),
Moreover, (C.1) holds \(\mathbb {Q}\)-almost surely since \(\mathbb {Q}(R>\rho \wedge T) = 1\) and
for all \(A \in \mathcal {F}_{\rho}\). □
Bayes’s formula yields a simple proof of Proposition 2.3:
Proof of Proposition 2.3
The statement in (i) is a corollary of Proposition C.2 if we replace τ by τ∧t and use \(Z=N_{t}^{\tau}\) and ρ=τ∧s in (C.1) for all t∈[0,T] and s∈[0,t].
Assume now that (N t 1 {S>t}) t∈[0,T] is a \(\mathbb {Q}\)-local martingale on [0,S). Then there exists a nondecreasing sequence of stopping times \((\tau_{i})_{i \in \mathbb {N}}\) with \(\mathbb {Q}(\lim_{i \uparrow\infty} \tau_{i} = S) = 1\) and such that \((N^{\tau_{t}} \mathbf {1}_{\{S > \tau_{i} \wedge t\}})_{t \in [0,T]}\) is a \(\mathbb {Q}\)-martingale for all \(i \in \mathbb {N}\). Now, (i) implies that \(N^{\tau_{i}} Y^{\tau_{i}}\) is a \(\widehat{\mathbb {Q}}\)-martingale. An application of Lemma C.1 with τ:=lim i↑∞ τ i yields that NY is a \(\widehat{\mathbb {Q}}\)-local martingale on [0,R). The reverse direction follows in the same manner. This yields (ii).
Assume next that \((N_{t}^{S_{i}} \mathbf {1}_{\{S>S_{i} \wedge t\}})_{t \in [0,T]}\) and thus \((N_{t}^{S_{i}^{Y}} \mathbf {1}_{\{S>S_{i}^{Y} \wedge t\}})_{t \in [0,T]}\) are \(\mathbb {Q}\)-martingales for all \(i \in \mathbb {N}\). Then the statement in (iii) follows from (i) and the fact that \(\widehat{\mathbb {Q}}(\lim_{i \uparrow\infty} S^{Y}_{i} > T) = 1\) by (i) in Lemma A.3. □
We conclude this appendix by providing a Girsanov-type result. Towards this end, denote the quadratic covariation process of two \(\mathbb {Q}\)-semimartingales N (1) and N (2) with càdlàg paths by [N (1),N (2)]=([N (1),N (2)] t ) t∈[0,T]. If X has càdlàg paths, the process \(N^{S_{i}}\) is a \(\mathbb {Q}\)-semimartingale with càdlàg paths and \([N,X]^{S_{i}} := [N^{S_{i}},X]\) has \(\mathbb {Q}\)-integrable variation for all \(i \in \mathbb {N}\), then the quadratic covariation process [N,X] has a compensator “up to time S”, that is, there exists a process 〈N,X〉=(〈N,X〉 t ) t∈[0,T] such that \(\langle N,X\rangle^{S_{i}}\) is the compensator of \([N,X]^{S_{i}}\) for all \(i \in \mathbb {N}\); see Theorem III.3.11 of Jacod and Shiryaev [20]. For any càdlàg stochastic process Z=(Z t ) t∈[0,T], we define Z t−:=lim s↑t Z s for all t∈(0,T) and Z 0−:=Z 0.
Proposition C.3
(Girsanov-type theorem)
Assume the setup of Theorem 2.1 and let N=(N t ) t∈[0,T] denote a progressively measurable stochastic process taking values in [−∞,∞] such that N t =N t 1 {R>t} for all t∈[0,T] and such that \(N^{S_{i}}\) is a \(\mathbb {Q}\)-semimartingale with càdlàg paths for all \(i \in \mathbb {N}\). Suppose that X has càdlàg paths. We then have the following statements:
-
(i)
The process \(N^{R_{i}}\) is a \(\widehat{\mathbb {Q}}\)-semimartingale with càdlàg paths for all \(i \in \mathbb {N}\).
-
(ii)
If N is a \(\mathbb {Q}\)-local martingale on [0,S) (equivalently, on [0,R∧S)) and if \([N,X]^{S_{i}}\) has \(\mathbb {Q}\)-integrable variation for all \(i \in \mathbb {N}\), then \(\widetilde{N} =(\widetilde{N} _{t})_{t \in [0,T]}\) defined by
$$\begin{aligned} \widetilde{N} _t := N_t - \int_0^{t} Y_{s-} \,\mathrm {d}\langle N,X \rangle _s\quad\textit{for all } t \in[0,T] \end{aligned}$$is a \(\widehat{\mathbb {Q}}\)-local martingale on [0,R) (equivalently, on the interval [0,R∧S)).
-
(iii)
If N is a \(\mathbb {Q}\)-local martingale on [0,S) (equivalently, on [0,R∧S)) and if we have \(\mathbb {Q}(S>S_{i} \wedge T) = 1\) for all \(i \in \mathbb {N}\), then \(\widehat{N} =(\widehat{N} _{t})_{t \in [0,T]}\) defined by
$$\begin{aligned} \widehat{N} _t := N_t - \int _0^{t \wedge S} Y_s \,\mathrm {d}[ N,X ]_s\quad \textit{for all } t \in[0,T] \end{aligned}$$is a \(\widehat{\mathbb {Q}}\)-local martingale on [0,R) (equivalently, on the interval [0,R∧S)).
Proof
The proof is based on a simple localization argument. Observe that
so that \(\widehat{\mathbb {Q}}\) is absolutely continuous with respect to \({\mathbb {Q}}\) on \(\mathcal {F}_{R_{i}} \cap \mathcal {F}_{R-}\) for all \(i \in \mathbb {N}\). Thus (i) corresponds directly to Theorem III.3.13 in Jacod and Shiryaev [20]. By Theorems III.3.11 in Jacod and Shiryaev [20], the process \(\widetilde{N}^{R_{i}}\) is a \(\widehat{\mathbb {Q}}\)-local martingale; thus \(\widetilde{N}\) is a \(\widehat{\mathbb {Q}}\)-local martingale on [0,R i ) for all \(i \in \mathbb {N}\). Lemma A.2 then yields (ii). Similar reasoning yields that \(\widehat{N}\) is a \(\widehat{\mathbb {Q}}\)-local martingale on [0,R) by applying Theorem 3 in Lenglart [24], after observing that the proof therein also works for probability spaces that do not satisfy the usual assumptions. □
Remark C.4
(Lack of martingale property in Proposition C.3)
One might wonder whether (ii) or (iii) of Proposition C.3 can be strengthened by replacing each “local martingale” by “martingale”. Example 2.5 illustrates that such a statement would be false, even in the case of X being a strictly positive, true \(\mathbb {Q}\)-martingale. To see this, replace \(\widehat{\mathbb {Q}}\) by \(\mathbb {Q}^{Z}\) and the processes N by X and X by Z in Proposition C.3. Then N is a true \(\mathbb {Q}\)-martingale, but \(\widetilde{N} = \widehat{N} = N\) is only a strict \(\mathbb {Q}^{Z}\)-local martingale.
Appendix D: Proof of Lemma 4.1
In this appendix, we provide the
Proof of Lemma 4.1
The fact that (ii) implies (i) follows directly from (2.2) and (2.3) with Z=1
A
and τ=R
i
∧S
j
for all \(A \in \mathcal {F}_{R_{i} \wedge S_{j}}\) and \(i,j \in \mathbb {N}\), since  .
.
For the reverse direction, fix a stopping time τ and note that it suffices to show (2.1) for events \(A \in \mathcal {F}_{\tau\wedge T}\) that satisfy
since  as Y is a
as Y is a  -local martingale and thus cannot explode. Therefore, we may assume without loss of generality that \(A \in \mathcal {F}_{(R \wedge S)-}\). Let \(\widehat{ \mathbb {Q}^{\$}}\) denote the unique probability measure on \((\varOmega, \mathcal {F}_{R-})\) that was constructed in Theorem 2.1 with \(\mathbb {Q}\) replaced by \(\mathbb {Q}^{\$}\). We need to show the identity
-local martingale and thus cannot explode. Therefore, we may assume without loss of generality that \(A \in \mathcal {F}_{(R \wedge S)-}\). Let \(\widehat{ \mathbb {Q}^{\$}}\) denote the unique probability measure on \((\varOmega, \mathcal {F}_{R-})\) that was constructed in Theorem 2.1 with \(\mathbb {Q}\) replaced by \(\mathbb {Q}^{\$}\). We need to show the identity  .
.
Since \(\bigcup_{i,j \in \mathbb {N}} \mathcal {F}_{(R_{i} \wedge S_{j})-}\) is a π-system that generates \(\mathcal {F}_{(R \wedge S)-}\), it suffices to show that  for all \(i,j \in \mathbb {N}\). Next, fix \(i, j \in \mathbb {N}\) and note that by (i), \(\widehat{ \mathbb {Q}^{\$}}\) and
for all \(i,j \in \mathbb {N}\). Next, fix \(i, j \in \mathbb {N}\) and note that by (i), \(\widehat{ \mathbb {Q}^{\$}}\) and  are equivalent on \(\mathcal {F}_{(R_{i} \wedge S_{j})-}\). Therefore, the
are equivalent on \(\mathcal {F}_{(R_{i} \wedge S_{j})-}\). Therefore, the  -martingale Z=(Z
t
)
t∈[0,T] with
-martingale Z=(Z
t
)
t∈[0,T] with  for all t∈[0,T] is well defined. We need to show that Z
T
=1. Observe that the measure
for all t∈[0,T] is well defined. We need to show that Z
T
=1. Observe that the measure  defined by
defined by  is also equivalent to
is also equivalent to  and the processes S
€ are
and the processes S
€ are  -local martingales; see also Proposition 2.3. Since
-local martingales; see also Proposition 2.3. Since  was assumed to be unique among these measures, we conclude. □
was assumed to be unique among these measures, we conclude. □
Rights and permissions
About this article
Cite this article
Carr, P., Fisher, T. & Ruf, J. On the hedging of options on exploding exchange rates. Finance Stoch 18, 115–144 (2014). https://doi.org/10.1007/s00780-013-0218-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00780-013-0218-3
Keywords
- Foreign exchange
- Pricing operator
- Put-call parity
- Strict local martingales
- Föllmer measure
- Change of numéraire
- Hyperinflation




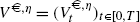 defined by
defined by 
 , respectively, and
, respectively, and
 .
. are equivalent on
are equivalent on  and
and