Abstract
Modern search engines employ advanced techniques that go beyond the structures that strictly satisfy the query conditions in an effort to better capture the user intentions. In this work, we introduce a novel query paradigm that considers a user query as an example of the data in which the user is interested. We call these queries exemplar queries. We provide a formal specification of their semantics and show that they are fundamentally different from notions like queries by example, approximate queries and related queries. We provide an implementation of these semantics for knowledge graphs and present an exact solution with a number of optimizations that improve performance without compromising the result quality. We study two different congruence relations, isomorphism and strong simulation, for identifying the answers to an exemplar query. We also provide an approximate solution that prunes the search space and achieves considerably better time performance with minimal or no impact on effectiveness. The effectiveness and efficiency of these solutions with synthetic and real datasets are experimentally evaluated, and the importance of exemplar queries in practice is illustrated.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Traditional query answering is about finding the structures in a data repository that satisfy the query conditions [2, 8, 9, 15, 24, 48]. Simpler, less structured and less specific queries [7] have attracted considerable attention because users may not always be accustomed to the technicalities and capabilities of the query language. To capture the elements of interest given the vague specifications of such queries, techniques like query relaxation [33], semantic enhancements [6], statistics-driven query answering [19] and log-based analysis [10, 37] were developed. Yet, these techniques assume that the user is aware of the characteristics of the structures of interest and can (at least partially) describe them in the query.
We advocate here that there are many practical scenarios in which the user may not know how to describe the specifications of the items of interest, but does know one of them, i.e., one of those elements that are expected to be in the result set. Here, we study ways to infer the result set using the known item as a seed. In other words, the user “query” works as an example of what the elements of interest are. We call this novel query paradigm exemplar queries to emphasize its different nature and the new evaluation methods it requires. Exemplar queries find application, amongst others, in cases of a student a curious citizen, an investigator, a lawyer or a reporter that needs to perform a study on a topic to which she may not be familiar with, but has as a starting point an element from those related to the topic.
The notion of exemplar queries reminisces the notion of query by example (QBE) [53], yet it is fundamentally different. In QBE, the query is an instance of the intended conditions and works as a wildcard query. An exemplar query, on the other hand, indicates the type of elements that are expected to be in the results. These elements may have characteristics different from those mentioned in the example, simply because their similarity to the example that the user query provides may be based on characteristics that are not explicitly stated in the query (i.e., the example). Our approach is also different from query relaxation [33, 36], which aims at producing more generic versions of a query, for a similar reason.
Motivating example: Consider a student who wants to perform a study on company acquisitions in the Bay area, without being an expert in the field, nor familiar with the related terminology. Issuing a query with the terms “acquisitions” and “Bay Area” will return documents about acquisitions and also mentioning the Bay area. Yet, an article on the takeover of Tumblr by Yahoo! may not be returned if the terms “acquisition” and “Bay area” are not explicitly mentioned in the text.
The student knows that a good example for the type of acquisition she is looking for is the one of YouTube by Google. Thus, she issues the query: “Google founded-in Menlo Park acquired YouTube”. The search engine typically responds with results related to Google, Menlo Park and YouTube, but will not return anything related to the acquisition of Tumblr by Yahoo! If many users have performed similar searches in the past, an analysis of the query logs may reveal that information, and the search engine (based on log analysis) may propose, in the related searches section, queries on Yahoo! and Tumblr (A simple test in existing search engines reveals that this is not actually happening.). Relaxing one or more of the query conditions does not help in a significant way, since the results are still focused around the term “Google.”
Consider now a second candidate answer for the user query: Paramount that was acquired by CBS. Between the Yahoo!–Tumblr and CBS–Paramount answers, it is more likely that the former is among the company acquisitions that the user is interested in and not the latter. This is because even though Yahoo! was founded in a different city than Google, that city is still in California (just like with Google), while the city that CBS was founded is in New York. Furthermore, the example of Google–YouTube that the user provided is about IT companies and so is the Yahoo!–Tumblr pair, while CBS–Paramount belongs to the broadcasting industry.
Therefore, there is a need to devise methods for inferring the set of elements that the user is interested in from a sample (of that set), which may be provided by the user. Exemplar queries can form the basis of a new form of search engines that use them as the main query evaluation mechanism, or they can be used to enhance the services that search engines are currently offering.
In particular, in parallel to the query evaluation a search engine performs, the query can also be seen as an exemplar query and be evaluated as such. These results can be appended to the results the search engine generates, increasing the probability to capture the user’s intent. Alternatively, the results of the exemplar query evaluation can be modeled as a set of queries and then appended in the list of “related/additional queries” that most modern search engines are currently suggesting to their users.
Proposed approach: Evaluating an exemplar query is a two-step approach. The first identifies in the data the elements mentioned in the user query. These elements may be in the form of documents, entities, tuples or web pages, and they constitute the user sample, which is the input to our approach. The second step examines the database and finds elements similar to the user sample: Those are the elements belonging to the desired result set. These elements constitute the solutions, which are eventually ranked and presented to the user. A high-level overview of a system employing the exemplar query paradigm to answer keyword queries on a knowledge graph can be seen in Fig. 1.
We highlight that the notion of exemplar queries is generic and can be applied to any data model. In this study though, we focus on the case where data is represented using a graph with labeled edges, e.g., a knowledge graph. Therefore, the samples and the solutions are substructures of the graph, namely subgraphs. Regarding the first step, that is, the interpretation of the user query within the database, there exist several solutions that have been proposed in the literature [26, 27, 41]. Thus, in this work, we focus on the second step, that of searching for relevant subgraphs, using two alternative measures that we call congruence relations: graph isomorphism and strong simulation. Furthermore, we are interested in the efficient retrieval of the k most relevant results. Traditional query answering on graphs [28, 29, 52] focuses on finding the best subset of nodes matching a given graph query and offers no straightforward and time-efficient adaptation for the retrieval of the top-k most relevant subgraphs based on our form of congruence. (The brute-force solution is exponential in nature.)
Example 1
In order to illustrate these ideas, consider the knowledge graph depicted in Fig. 2 and the exemplar query “Google founded-in Menlo Park acquired YouTube”, represented by graph Q1 at the top-left corner of the figure. The evaluation of this query on the database results to the user sample that is indicated in the database with the dashed box labeled S. Searching for structures that are (edge-isomorphic) congruent to the user sample results to the two structures indicated with the dotted line boxes labeled A1 and A2, which refer to companies founded in some city that have acquired other companies. These are the answers to the exemplar query, and in this particular example, we would like to have the “Yahoo!–Santa Clara–Tumblr” answer ranked higher than “CBS–NYC–Paramount,” since the former is closer to the subject of the exemplar query (they are all, California-based IT companies).
While we introduced Exemplar Queries in a previous work [34], here we present its complete formalization, and study two alternative congruence relations. Moreover, we propose an efficient pruning schema for both relations, which precomputes a compact representation of each node in terms of neighbor nodes at a fixed distance from it. We demonstrate that this algorithm is exact, i.e., it preserves the correctness of the final answers, while significantly reducing computation time. We also propose an approximate algorithm, which effectively restricts the search space. We also propose an approximate algorithm, which can effectively prune the search space. We show that this heuristic works very well in practice, with no significant compromise on the quality of the results. The effectiveness of this result has also been showcased in practice [35]. As a trade-off between efficiency and quality we study a top-k algorithm, that stops exploring the search space as soon as the k best answers are found.
Contributions: In this paper, we make the following contributions:
-
1.
We introduce and formally define a novel form of query answering, referred to as exemplar queries that treats a query as a sample from the desired result set.
-
2.
We study exemplar queries for graph-based edge-labeled models and devise two congruence relations, based on subgraph isomorphism and strong simulation, which effectively answer exemplar queries in this context. In addition, we provide a theoretical analysis for our relations, proving their correctness, and we demonstrate that the two proposed relations capture different, yet interesting use cases.
-
3.
We propose two algorithms to compute the exact solution: a straightforward solution and an optimized algorithm that can prune the search space. We also introduce an efficient top-k algorithm based on our proposed ranking function. Furthermore, we describe an approximate algorithm with significant efficiency gains and minimal effect on the final ranking, which can be used for real-time query answering.
-
4.
We perform a thorough experimental evaluation, using the largest multigraph ever used (Freebase [20]) in this field. We experimentally show that existing approaches either fail to produce correct exemplar query evaluations, or they do so in a much longer time, which makes them inapplicable for online applications. In contrast, the experiments demonstrate the efficiency of our solutions, and a user study validates the usefulness of exemplar queries.
Paper structure: The remainder of this paper is structured as follows. Section 2 presents the related work, and Sect. 3 formally defines our problem. Section 4 introduces the generic exact algorithm and the two specific congruence relations studied in the paper. Algorithmic solutions for isomorphic structures are described in Sect. 5 and for strong simulation in Sect. 6. Section 7 summarizes the proposed approach, explaining how to combine the algorithms and how to rank the results. We present the experimental evaluation in Sect. 8, and finally, we conclude in Sect. 9.
2 Related work
Searching the web has been studied for a long time and the task of understanding the user queries is vital in many scenarios. In this area, several solutions have been proposed, all starting from the same premise: The user is looking for a particular resource, but does not know how to express it. In this light, we review the work in the areas of query refinement and query diversification, as well as in that of query answering on graphs, and highlight the differences to our problem.
Query modification: Many different works study ways to provide the user with answers that may be of interest even if they were not explicitly requested in the query. Query refinement [33] extends the user query in order to retrieve more precise results [2, 8, 42, 48] using some external knowledge. In our work, we are not trying to alter the query, but only use it as a sample that can lead us to additional queries generating resources of interest. Query relaxation [33, 36], on the other hand, relaxes an overspecified query that returns no answers to allow a non-empty answer set to be produced. Our approach is somehow similar; however, query relaxation is driven by the conditions in the query. It will not include results that are similar to those the user query generates, unless they are satisfying a subset of these conditions. A recent work [23] proposes a method to perform semantic exploration of the knowledge graph. This is in line with the query relaxation works in which the information need of the user is not clear from the beginning. In contrast, our approach adds additional results by using similarities at the data level. Related queries deal with the discovery of queries generating results of possible interest to a user based on a query that the user has already posed. Their discovery is based on information like query logs [2, 48], document corpuses [8], knowledge bases [38] or wikis [10]. Since our work can be used to suggest related queries as explained in the introduction, it can be seen as complementary to these approaches, offering a new way of generating related queries.
Another group of works that do not try to extend or improve the query results with new data, but only to organize them in some way that is more comprehensive to the user, is the one of faceted search [15] and query categorization [46]. Despite the fundamental difference from our approach, these works are also aiming at increasing the user satisfaction.
Query answering on graphs: Most works on finding a graph structure in a large graph exploit graph edit distance that measures similarity between subgraphs [18]. Computing the graph edit distance is NP-hard, and numerous indexing and pruning techniques have been proposed to improve the performance [47, 50]. Traditionally, graph search has been solved efficiently. Our solution is mainly related to approximate query answering on graphs. Approximate search can be performed when the user does not know the exact keywords to formulate the query, formulating an incomplete or imprecise query. In graphs, p-homomorphism [16] enables similarity structure search instead of the strict isomorphism. Likewise, NeMa [29] introduces the notion of node neighborhood (i.e., the set of nodes reachable from a source node in a limited number of steps) to match nodes and edges approximately, which is relevant to our approach. One recent work, SLQ [51], elaborates over the latter including a ranking model for a set of fixed textual/topological transformations from query to answer nodes in a graph. Similarly, strong simulation [32], which we employ in our study, finds approximate answers to a graph query. Nevertheless, all these works subsume that the user is able to express the query conditions, even though partially. This is not true in our case.
3 Problem statement
The first step for retrieving the answers to an exemplar query can be easily achieved using traditional query evaluation techniques. We denote the results of this type of evaluation of a query Q as \({\text {eval}}(Q)\) and refer to it as the user sample.
The second step is to find the remaining structures of interest for the user, based on the structure that has been identified in the first step. Note that there exists a query that describes all these structures that the user is looking for, it is just that she is not aware of that query, or is not in a position to describe it. Thus, it is natural to assume that all the structures of interest have some commonalities among them, and especially with the one that the user provided as an indicative example. As such, we are interested in finding similar structures to the results of the first step and return these results as an answer to the user-provided query. We refer to this new query paradigm as exemplar queries, and the results of their evaluation as exemplar answers, or simply answers.
Definition 1
The evaluation of an exemplar query Q on a database \(D\), denoted as xmpEval(Q), is the set \(\{a | \exists \)s s.t. \(s\in eval(Q) \wedge a{\approx }s\}\), where a and s are structures in D and \(\approx \) indicates a congruence relation.
In the definition above, we refer to the concept of congruence relation as a binary relation defined over the elements of the database, with the following semantics: Given an element from the database, it tests its membership to the desired answer set that is implied by the element in eval(Q) (i.e., the sample element provided by the user). Intuitively, a congruence relation defined this way acts as a similarity check, i.e., deciding whether the two structures are similar or not.
Note that the definition of exemplar queries above is independent of the data model, the query form, the retrieved results, and the congruence relation. As long as there is a standard query evaluation methodology and some congruence relation that can be used to fit a specific use case, exemplar queries can be answered. This leads to flexibility and the ability to use exemplar queries in a wide range of different applications. Nonetheless, while Definition 1 adapts to many application scenarios and data models, the congruence relation should be carefully selected based on the domain and the expected results. A proper congruence relation should be able to infer from the user sample and the data the conditions that represent the desired result set. Indeed, recent studies employ (although not explicitly) the notion of Exemplar Query Answering for the relational model [13, 44], where the congruence relation is represented by the select–project–join query that generates the user samples. Therefore, in their case, two elements belong to the same desired result set if they satisfy the same query conditions.
On the contrary, we are interested in applying exemplar queries in cases where the data are highly heterogeneous, involving relaxed structures. This is notably the case of knowledge graphs that represent entities as labeled nodes with attributes and relationships as labeled edges. For this reason, in our current study, we have chosen to employ this flexible data model, a simple query form with a traditional query evaluation that is based on subgraph matching, and two very generic congruence relations that are based on edge label-preserving similarity on graphs.
As mentioned above, for the representation of the data we consider an entity-based data model [14] that can represent various forms of heterogeneous knowledge. In particular, we assume an infinite set of labels \(\mathcal {L}\) and of values \(\mathcal {V}\). The set \(\mathcal {V}\) consists of an infinite set of atomic values \(\mathcal {T}\) and of object identifiers \(\mathcal {O}\), i.e., \(\mathcal {V}=\mathcal {T}\cup \mathcal {O}\). An object is a representation of a real-world entity or concept and is modeled through an object identifier and a set of attributes for that identifier modeling characteristic properties of the real-world entity or concept. An attribute of an object \(o\in \mathcal {O}\) is a triple \(\langle o,\ell ,v\rangle \), where \(\ell \in \mathcal {L}\) and \(v\in \mathcal {V}\).
A database is a finite collection of objects, alongside a finite set of attributes for these objects. The attributes are either connecting the objects or specify some characteristic properties of them.
Definition 2
A database is a pair \(D:\langle O, A \rangle \) where \(O\subseteq \mathcal {O}\) and \(A\subset O\times \mathcal {L}\times (O\cup \mathcal {T})\), both finite.
A database can be represented as a graph where every object, or atomic value in the database, is represented as a node and every attribute as a labeled edge from the node representing the object of the attribute to the node representing its value. Thus, we can equivalently say that a database \(\langle O, A \rangle \) is a graph G(N, E), also denoted as \(\langle N, E \rangle \), where the set of nodes \(N\) is the set \(\{n\mid n\in O \vee \exists (n',\ell ,n)\in A\}\) and the set of edges \(E\) is the set \(\{n\overset{\ell }{\rightarrow }n'\mid (n,\ell ,n')\in A\}\). The expression \(n\overset{\ell }{\rightarrow }n'\) denotes an edge from node n to node \(n'\) labeled \(\ell \). We also say that two nodes \(n_1\), \(n_2\) are equivalent and denote it as \(n\equiv n'\), if they represent the same atomic value or the same object, i.e., the identifiers of the objects they, respectively, represent are the same.
A query is traditionally an expression describing a set of objects alongside a set of conditions they need to satisfy. These conditions describe certain characteristics of these objects and the relationships they may have among them. We make the natural assumption that the objects referenced in a query are somehow all connected; otherwise, the query expression would actually constitute two independent queries. Since a query describes a set of objects with attributes, i.e., properties and relationships among them, it can also be seen as a database and consequently represented as a connected graph. Answering a query on a database means finding the database structures that satisfy the query specification. By the term database structures, we mean a set of objects and a set of attributes for these objects. In graph terms, answering a query means finding the subgraphs in the database that have a structure matching the graph representation of the query. The set of these subgraphs constitutes the answer set of the query.
Definition 3
A query Q is a database whose graph representation is a connected graph \(Q : \langle N_Q, E_Q \rangle \). An answer to a query \(Q : \langle N_Q, E_Q \rangle \) on a database \(D\) is any connected subgraph \(D' : \langle N_{D'}, E_{D'} \rangle \) of \(D\) matching the query Q, i.e., there exists a binary relation \(\mathcal {R}\), such that \(\forall n_{Q} \in N_{Q}, \exists n_{D'} \in N_{D'} : n_Q\mathcal {R}\; n_{D'}\). The set of all such subgraphs, denoted as eval(Q), is referred to as the answer set of the query.
Query Q is finally evaluated as an exemplar query according to Definition 1. Finally, we note that we are interested in returning a ranked list of results and in particular the top-k most similar and relevant structures. Then, given a query Q evaluated as an exemplar query, in this work we address the following problem.
Problem 1
(Exemplar Query Answering) Given an exemplar query Q and a parameter k, find the top-k answers \(a \in D\) such that \(a \in xmpEval(Q)\) for a chosen congruence relation \(\approx \) and a ranking function \(\rho \).
In the next paragraphs, we provide insights about suitable similarity and ranking functions for the case of knowledge graphs.
Congruence relation: Even though several different congruence relations can be used, we are interested in those that are able to preserve user intent by generalizing the set of conditions that can be derived by the sample. Hence, we consider two alternatives based on edge-preserving subgraph matching relations: (a) a congruence relation based on the notion of subgraph isomorphism [12], and (b) a more elastic relation, based on the recently introduced strong simulation [32]. While subgraph isomorphism is a natural method for identifying perfect matches of an input query graph in the database, strong simulation offers the ability to group-matching nodes based on nearby edge labels. As we discuss in more detail later on, strong simulation relaxes the strict requirements of isomorphism, while preserving the topology and the semantics of the original query. The motivations for a less rigid congruence relation are twofold: compactness and expressiveness. Compactness allows us to aggregate several answers in a single graph (e.g., all the acquisitions from Google), while expressiveness allows for some freedom in the structure matched. The following example motivates the need for the strong simulation congruence relation.
Example 2
Consider the example described in Sect. 1 and the portion of the database illustrated in Fig. 2. Consider query Q2, shown at the top- left corner of the figure, where the user additionally asks for companies that own a Web site. The query evaluates to the same sample S. Then the only perfect match is A2, which is semantically further away than A1. In this case, strict equality may not best serve the intentions of the user, who may be interested in companies with at least one acquisition and one Web site. Therefore, the congruence relation should allow some degree of freedom. Using simulation, both A1 and A2 are returned as answers (Tumblr serving both as an acquisition and a Web site).
Ranking function: An exemplar query is an implicit indication of the structure and the kind of results the user expects. Therefore, an ideal ranking function should be able to distinguish answers that have characteristics similar to the user sample and at the same time penalize results that are semantically unrelated to the query. We explain this intuition with an example (a formal discussion is included in Sect. 7).
Example 3
Consider again the database illustrated in Fig. 2 and the user (exemplar) query Q1, shown at the top-left corner of the figure. The evaluation of this query on the database results to the user sample shown in the database with the dashed box labeled S, and the structures that are (edge-isomorphic) similar to the user sample are indicated with the dotted line boxes labeled A1 and A2. These are the answers to the exemplar query. We observe that A1 has around itself more nodes and edges in common to the user sample S (for instance, the IT Company, Search Engine and California) than A2. Therefore, A1 should be ranked higher than A2.
Since the first step of the exemplar query evaluation is a standard search in a graph for a subgraph matching the user query and many solutions have already been studied [26, 27, 41], we will not discuss this problem further. Instead, we focus on the implementation of the second step, which is to devise a method that given such subgraph (the user sample) finds other edge-isomorphic (or alternatively simulating) subgraphs (the exemplar answers) and ranks them based on their similarity to nodes around the query, as well as their position within the query neighborhood. One of the challenging parts of this is that there is no clear limit on how large a query neighborhood to consider, apart from the entire database, i.e., how far from the user sample a congruent answer can still be considered relevant to the query. In our implementation, we use Freebase, which is one of the largest knowledge graphs available nowadays. Existing works on graph similarity concentrate the effort of searching on a large number of small graphs, but searching on a very large graph in the form and size we consider here has not been considered before, even though there is an increasing interest for such application [31].
4 The basic algorithm
Once the user query has been evaluated and the sample S has been identified in the database \(D\), the set of congruent structures will have to be discovered. To do so, the user sample S will have to be compared with every other subgraph in the database. Instead of considering the exponential number of subgraphs in the database, by following a typical backtracking approach [45], a node \(n_s\) from S is randomly selected to serve as a seed. Then all the nodes in the database \(D\) are considered, one at a time. For each such node n, we check whether a subgraph congruent to S can be constructed when mapping \(n_s\) to n. If such a graph is found, then it is added in the set of exemplar answers. At the end of this procedure, the exemplar answers are sorted and returned to the user (all of them or only the top-k) as the result to the exemplar query (The sorting task is studied in detail in Sect. 7.).
The pseudocode of the above steps is described in Algorithm 1. The construction of the matching subgraphs (line 5 in Algorithm 1) is done by initially considering a graph G consisting only from the node \(n_s\) and a subgraph T consisting only from node n, and assuming that congruence relation maps \(n_s\) to n. Then the algorithm iteratively tries to expand the subgraphs G and T with edges from S and \(D\), respectively, such that the resulting subgraphs remain congruent (based on the selected congruence relation). If (after a number of steps) the graph G becomes equal to S, then T is one of the answers.

Searching for possible matches of the user sample in the entire database, as the Algorithm XQ requires, is an expensive operation. Thus, one of the main challenges is how to effectively and efficiently reduce the search space preserving quality guarantees on the answers. In what follows, we propose solutions based on structural properties of the database that adapt to different congruence relations.
4.1 Instantiations of the congruence relation
The XQ algorithm requires the definition of a congruence relation to find the answers to an exemplar query. Although different congruence relations could fit the definition, we are interested in those that preserve the semantic properties of the user query. In a knowledge graph, a candidate similarity function should preserve the edge labels of the user sample and the (basic) layout of connections between nodes, since these are the elementary features that constitute the user sample. We identify two compelling congruence relations, based on: (1) subgraph isomorphism, which finds exact matches and is known to be \(\mathbf {NP}\)-hard, and (2) strong similarity, a weaker notion of subgraph matching that admits a cubic-time solution in the size of the query [32].
In the following, we formally define the two congruence relations we selected, and discuss their properties.
4.1.1 Subgraph isomorphism
The most natural definition of congruence to the query terms is strict equality. In graph terms, this means finding structures that are subgraph isomorphic to the user sample. While subgraph isomorphism is defined over node and edge labels, matching node labels means referring to the exact same object, which is too strict for the exemplar query scenario. Therefore, we define edge-preservingFootnote 1 isomorphism as follows:
Definition 4
A database \(D\) is edge-preserving isomorphic to a database \(D'\), denoted as \(D\simeq D'\), if there is a bijective function \(\mu \) from the nodes of \(D\) to the nodes of \(D'\) such that for every edge \(n_1 \overset{\ell }{\rightarrow } n_2\) in \(D\), the edge \({\mu }(n_1) \overset{\ell }{\rightarrow } {\mu }(n_2)\) is in \(D'\).
Edge-preserving isomorphism is a very restrictive congruence relation, in that it recognizes only exact structures. We acknowledge that this level of precision could be desired in some cases but detrimental in other settings. Consider, for instance, the query Q2 and the two graphs S and A2 from Example 2. They are conceptually very close; S is an IT Company that has bought another company, owns a Web site and was founded in California. A1 on the other hand differs from S, because Tumblr is a Web site and also an acquisition of Yahoo. However, the user could be interested in A1 and may want it included in the results. To allow more flexibility in our congruence relation, we propose simulation [40], and in particular strong simulation [32], which we discuss next.
4.1.2 Strong simulation
In simulation, we say that a candidate answer graph simulates a query graph if the former contains the same edge sequences of the latter and preserves sequences of edge labels in the same order. In practice, this translates to checking if every sequence of edge labels in the query is contained in the candidate answer. Since the subgraph match is performed in a sequence-wise fashion, this notion preserves the semantics of the query, yet allows for some freedom in the structure. This can be seen in Example 2, where A1 is not isomorphic to Q2, yet it is simulating.
This flexibility though has some significant shortcomings. First, graph simulation does not consider parent–child relationships, since it only requires that nodes in the relation match the outgoing edges of the query. Second, the matched graph is not bounded, in that any sequence of edges with the same label can be matched to a single edge in the query. These issues are illustrated in the following example, where we show two graphs that are matched by simulation, but not by strong simulation, and do not satisfy the user intention.
Example 4
Consider the scenario in Fig. 3. The user is asking for IT companies, such that one acquired the other with a focus on the Investors. She provides the example “Sequoia Capital invested in IT company YouTube acquired by IT company Google.” This is depicted as the sample S in the figure, and we then search for congruent graphs using simulation. Searching for structures simulating the query results in G1 and G2. G1 simulates S because both Google and Yahoo! have an outgoing acquired edge, YouTube and Tumblr have an isA edge, IT Company matches with both IT Company and Web site in G1, and Sequoia and Spark have an investor edge. However, the fundamental property that YouTube and Tumblr are both IT Companies is lost, since simulation does not require to match nodes with the same parent. Note that also G2 simulates S, since Google is matched by Microsoft and CBS, YouTube is matched by Paramount, IT Company is matched by Publishing and IT Company in G2, and Sequoia is matched by InterWest. Intuitively, every edge sequence in S is matched by some sequence in G2. Simulation disregards the locality of the match, finding possible answers in any part of the graph. Consequently, even though G1 and G2 are correctly simulating the sample, they both prove to be unsatisfying answers.
Motivated by the above discussion, we adopt a more stringent congruence relation called strong simulation. Strong simulation requires the definition of dual simulation. Dual simulation is a bidirectional simulation that checks both the incoming and outgoing edges of each query node.
Definition 5
(Dual simulation) Let  and \(D: \langle N, E \rangle \) be two databases represented as graphs. \(D\) dual simulates \(S\), denoted as \(S\trianglelefteq _DD\), if there exists a relation \(\mathcal {R}\), such that for every node
and \(D: \langle N, E \rangle \) be two databases represented as graphs. \(D\) dual simulates \(S\), denoted as \(S\trianglelefteq _DD\), if there exists a relation \(\mathcal {R}\), such that for every node  and \(n \in N\) for which
and \(n \in N\) for which  :
:
-
1.
for all
 , exists \(n'\) such that \(n \overset{\ell }{\rightarrow }n'\) and
, exists \(n'\) such that \(n \overset{\ell }{\rightarrow }n'\) and 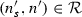 , and
, and -
2.
for all
 , exists \(n''\) such that \(n'' \overset{\ell }{\rightarrow }n\) and
, exists \(n''\) such that \(n'' \overset{\ell }{\rightarrow }n\) and  .
.
While dual simulation admits answers of any diameter, strong simulation is bounded to the diameter of the query. Strong simulation is based on the notion of reachable nodes. We call d-hop node of a node n a node that is reachable from n in at most d hops, i.e., the shortest path from n to this node is no longer than d.
Definition 6
(d-hop) Let \(n \in N\) be a node of a database \(D:\langle N, E \rangle \). The node \(n_i \in N\) is a d-hop node of n if there exists a path from n to \(n_i\) of length at most d. The d-hop node set of n, denoted as \(\mathbb {N}_d(n)\), is the set of d-hop nodes of n. The d-graph of n, denoted as \(D[n,d]\), is the subgraph of \(D\) inducedFootnote 2 by the nodes in \(\mathbb {N}_d(n)\).
Strong simulation defines bounds on the size of the simulation. Moreover, as proved in [32], the size of the maximum dual simulation relation is bounded by the diameter of the query. Recall that the diameter of a query is the length of the longest shortest path.
Definition 7
(Strong simulation) A database \(D:\langle N, E \rangle \)
strong simulates a database  , denoted as \(S\trianglelefteq _SD\), if there exist a node \(n \in N\) and a d-graph \(D[n,d]\) such that:
, denoted as \(S\trianglelefteq _SD\), if there exist a node \(n \in N\) and a d-graph \(D[n,d]\) such that:
-
1.
d is equal to the diameter of the database \(S\).
-
2.
\(S\trianglelefteq _DD[n,d]\) with the maximal dual simulation (i.e., any other dual simulation of \(S\) in \(D[n,d]\) is contained in the maximal).
This definition embodies the two important properties of bounding the simulation relation size within the d-graph and preserving the parent–child relationships. Looking back at Example 2, we observe that using Definition 7, the query returns both A1 and A2 as results. At the same time, both G1 and G2 (shown in Fig. 3) are rejected, which is the desired behavior.
Note that, differently from the seminal work [32], our definition matches edge labels instead of node labels. In Sect. 6, we describe how the existing algorithms for this case, providing analytical results on the correctness of this adaptation.
The following sections introduce algorithmic solutions for both congruence relations. Section 5 introduces approximate and exact algorithms to evaluate exemplar queries with isomorphism, while Sect. 6 describes our strong simulation algorithms, designed for the case of exemplar queries.
5 Finding subgraph isomorphic answers
Since subgraph isomorphism is an \(\mathbf {NP}\)-hard problem, we need to carefully design our algorithmic solutions in order to be efficient in practice. This becomes particularly important when the database size is large. In this section, we present the methods, and the ideas behind them, that we devised to efficiently answer exemplar queries using isomorphism as the congruence relation.
5.1 An efficient exact solution
To improve the performance, we propose an effective way to prune the search space, i.e., the list of database nodes we have to match to the nodes of the user sample in order to find isomorphic structures, leading to a new algorithm: FastXQ. The FastXQ algorithm is divided into two steps: First we use the query to drive a process that will restrict and prune the search space, and then, we apply XQ to the resulting restricted spaced. To prune the space, we devise an efficient technique for comparing nodes and an algorithm for effectively rejecting pairs of nodes that are bound to not participate in any isomorphic mapping. We call this algorithm IterativePruning. Although this technique does not remove all non-matching subgraphs, the schema is effective and reduces significantly the search space and therefore the total number of isomorphic checks. The false positives are subsequently removed by running the traditional isomorphic verification algorithm on them.
To compare nodes (and inspired by [28]), we devise a technique that is meant to represent the part of the graph around them in a compact way and to match the nodes in advance without the need to examine all the nodes in the graph. More specifically, the idea is to store a compact representation of nodes and edges that are at a fixed distance d from each node. This provides an effective way to compare nodes, allowing the pruning to remove the non-matching nodes without having to actually visit any part of the graph around them.
A basic concept of our approach is also the notion of d-hop nodes introduced in Definition 6. For every node in the database, we compute a table consisting of the number of nodes that are reachable from that node at some specific distance and with a path ending with a label \(\ell \). In other words, for a node n, for every label \(\ell \) and for every distance i, we keep the cardinality of the set \(W_{n,\ell ,i}\), where
In practice, since doing so for every node in the database is expensive in terms of time, we implement an approach similar to an inverted index. We use an index structure that for every label and for every distance can provide a list of all the nodes that have a label \(\ell \) at the respective distance and the number of edges with such labels. The index is a hash table, in which keys are edge labels and values are two-dimensional matrices. For a label \(\ell \), the matrix contains in position i, j all the nodes n, such that \(|W_{n,\ell ,i}| = j\), for each \(j > 0\).
Note that, once computed for each label \(\ell \) and each \(i \le d\), W compactly represents the portion of the graph around a node. For this reason, if we compute W for the nodes of the user sample as well, we can compare nodes in the database and nodes in the user sample, in order to know in advance which nodes can be pruned. We denote the d-hop nodes set of a node  of graph \(S\) by
of graph \(S\) by  . A node \(n \in N\) of \(D: \langle N, E \rangle \) matches a node
. A node \(n \in N\) of \(D: \langle N, E \rangle \) matches a node  in the user sample and therefore is not pruned, if the following property holds (ref. to Theorem 1 for a formal proof).
in the user sample and therefore is not pruned, if the following property holds (ref. to Theorem 1 for a formal proof).
Property 1
For each label \(\ell \) and a distance \(i \le d\),  .
.
Using the ability to compare nodes through the compact representation of the part of the graph around them, we devise a way of fast eliminating pairs of the user sample and database nodes, respectively, which do not participate in an isomorphism match. Traditional techniques that compute isomorphisms compute matches of the different nodes independently and then try to combine the results. We show that this process can be optimized further, if the comparison of the nodes takes into consideration the previously computed matches. To implement this idea, we exploit dual simulation. Note that in this case, simulation is used to prune nodes in advance and not as a congruence relation as in Sect. 6.
Deciding whether one graph dual simulates another graph is known to be solvable in polynomial time with respect to the size of the graph [22]. The main idea of our approach is to check whether a subgraph can dual simulate the user sample on the database graph, while iteratively pruning nodes that cannot possibly match.
5.1.1 Matching algorithm with iterative pruning
The algorithm works as follows. First, it calculates the d-hop nodes for each node of the user sample. Then, a user sample node is selected as starting node. Although any node is a valid starting node, we propose to pick the node with the lowest selectivity among the user sample nodes, with the hope to reduce the number of candidate matches between the user sample and database nodes. The selectivity is an estimate of the number of possible matches generated from a user sample node. The idea is to consider the number of adjacent nodes of a user sample node and the frequency of the labels of the edges connected to it. The selectivity of a node n is
where the frequency \({\text {freq}}(n)\) of a node n is defined as the sum of the number of outgoing and incoming edges. The selectivity favors nodes in which both the degree and the frequency of the labels are high. Furthermore, the further the edges are from the node n, the less important the frequencies are, which explains the \(i^{-1}\) factor.
We similarly define the frequency of a label \(\ell \) as the number of edges in the graph having label \(\ell \) and we denote it as \(|E^{\ell }|\). The less probable the combination of labels at a certain distance is, the lower the selectivity and the higher is the expected pruning power.
After having selected the starting node \(n_{{\text {min}}}\), the algorithm retrieves the nodes in the database that match the node \(n_{{\text {min}}}\) and marks them as candidate mappings \(\mu (n_{{\text {min}}})\), where \(\mu \subseteq N_S \times N\) is the mapping between user sample and database nodes that the algorithm will compute. Then the algorithm iteratively checks, for each user sample node \(n_S\) not yet visited, that each adjacent edge of \(n_S\) matches the edges adjacent to the nodes \(n \in \mu (n_S)\), verifying the label and the direction of the edge. If it does not match, then n is removed from \(\mu (n_S)\); otherwise, we consider a node \(n_1\) adjacent to n a candidate for the user sample node \(n_S'\) adjacent to \(n_S\), i.e., we insert it into \(\mu (n_S)\), if the condition described by Theorem 1 holds. Finally, the user sample node \(n_S\) is marked as visited and removed from the candidate list. The steps of the algorithm are described in pseudocode in Algorithm 2.

In the worst case, Algorithm 2 will have to traverse the entire database for each node. Thus, the complexity of the algorithm is \(\mathcal {O}(|E| * (|N_S| + |E_S|))\). Since the user sample is typically very small, the algorithm is, for the majority of practical cases, quadratic to the number of nodes. In the implementation, in order to reduce the time computation of \(\mu \), we used a hash map for storing the nodes of the user sample and their partial mappings.
The set of candidate mappings computed by Algorithm 2 is used to eliminate those nodes of the database that will never participate in an isomorphism with the user sample nodes.
5.1.2 Algorithm correctness and complexity
The following theorem guarantees that Algorithm 2 does not falsely discard any node while traversing the user sample nodes. However, it may introduce false positives, i.e., nodes that match the user sample nodes but are not included in an isomorphism.Footnote 3
Theorem 1
Given a database \(D: \langle N, E \rangle \) and a user sample \(S\), let \(\mathbb {N}_d\) and \(\mathbb {N}_d^S\) be the d-hop nodes set of \(D\) and \(S\), respectively. If there exists a subgraph isomorphism \(\mu : N_S \rightarrow N\), then \(\forall n_S \in N_S, \mathbb {N}_d^S(n_S) \subseteq \mathbb {N}_d(n), n \in N, n \in \mu (n_S)\)
Proof
(by contradiction) Suppose that \((n_S,n) \in \mu \), but \(\mathbb {N}_d^S(n_S)\) \(\not \subseteq \mathbb {N}_d(n)\), then there exists \(i, 1\le i \le d\) and a label \(\ell \) such that Property 1 does not hold, i.e., \(|W_{n_S,\ell ,i}|>|W_{n,\ell ,i}|\). For this reason, we can say that there exists \(n_S' \in W_{n_S,\ell ,i}\), connected to \(n_S''\in \mathbb {N}_{i-1}(n_S)\) by \(\ell \), i.e., \(n_S'\overset{\ell }{\rightarrow }n_S''\). The latter assumption holds since \(\mu \) is a subgraph isomorphism. However, there does not exist any \(\mu (n_S')\overset{\ell }{\rightarrow }\mu (n_S'')\), which contradicts the subgraph isomorphism hypothesis. \(\square \)
Additionally, a guarantee that the algorithm is complete, namely it does not discard any simulating answer, is offered by the following theorem.
Theorem 2
Given a user sample \(S\) and a database \(D: \langle N, E \rangle \), if a node \(n \in N\) is pruned by Algorithm 2, then n does not belong to any dual simulation of S in \(D\).
Proof
In order to prove the theorem, we need to prove that a node n discarded by the algorithm cannot participate in any simulation of the sample S. Recall that a node is discarded by Algorithm 2 if one of the following conditions holds
-
(a)
\(\mathbb {N}_d^S(n_S') \nsubseteq \mathbb {N}_{d}(n_{1} )\) (line 9)
-
(b)
\(n_S \overset{\ell }{\rightarrow } n_S'\), but
 (line 8)
(line 8)
If (a) holds, then it follows immediately from Theorem 1 that the node cannot participate in an isomorphism; thus, we conclude. Conversely, if (b) holds, then \(n_S\) has an \(\ell \) edge, but n does not. In this case, from the definition of simulation, n cannot simulate \(n_S\). On the other hand, node n cannot be part of any other simulation, since it has been previously considered in a matching path from \(n_{min}\) to \(n_S\). Therefore, there exists a path in S that is not matched by n. This concludes the proof. \(\square \)
5.2 An approximate solution
In the previous subsection, we describe an exact solution to prune the search space, removing nodes that cannot possibly match the user sample. That approach reduces the total number of isomorphism tests, while ensuring that all the subgraph isomorphic graphs (and only those) will be returned as answers. In this subsection, we propose an additional method that removes in advance portions of the graph that are likely to not be relevant to the user, i.e., not to contain answers that will be ranked among the top-k. The idea is based on the observation that the user is not always interested in all the answers, but only in the portion more closely related to the sample. We call this method ApFastXQ.
We aim at restricting in advance the search space in order to search for solutions, i.e., to search for isomorphic structures, only in the portion of the graph that is more likely to contain answers that are also the most relevant to the user. Consequently, some of the solutions will be discarded in advance because they are not likely to rank among the top-k most relevant answers. As already mentioned previously (Fig. 2), both pairs CBS–Paramount and Yahoo!–Tumblr are part of the solution space, but the pair Yahoo!–Tumblr is more relevant to the user, and therefore, we would like to restrict our search only to the subgraph that is containing the second but not the first.
In the following, we describe how we model this portion of the graph, which we call Query Neighborhood (Sect. 5.2.1). That portion is the subset of nodes with higher proximity to the nodes of the user sample. The intuition behind this is that nodes in the graph that are located far from the user sample will be also semantically distant from the user’s intention as expressed in the exemplar query. Hence, even if such nodes will form an answer, such answers will be considered not interesting by the user.
We model a relatedness measure based on the distance in the graph, and we use it to prune away nodes that are far away from the user sample before even looking for isomorphic structures among them.
It is clear that, while the approach described in the previous subsection is exact (does not discard any valid answers), this second approach is approximate: Some correct answers could potentially be filtered out as they fall out of the Query Neighborhood. For this reason, we propose a principled way of measuring the relatedness and for pruning the graph, aimed at discarding only irrelevant solutions. We implement a function that iteratively retrieves the Query Neighborhood without traversing the entire graph (Sect. 5.2.2). As we show later (Sect. 8), thanks to the SelectQueryNeighborhood algorithm, by operating in this special portion of the graph, we can effectively reduce the search space. The restricted search space can then be given as input to XQ in Algorithm 1, without sacrificing the quality of the results. We can still apply on this subgraph the pruning techniques presented in the previous subsection and then look for isomorphic structures on a much smaller database. Hence, the ApFastXQ algorithm first applies the SelectQueryNeighborhood algorithm and then FastXQ.
5.2.1 Identifying relevant answers
Given the set of exemplar answers \(\mathfrak {Q}= {\text {xmpEval}}(Q_e)\), we aim at restricting our search to the subset \(\mathfrak {Q}_{\rho } \subseteq \mathfrak {Q}\) that contains only the answers that are more relevant to the user, i.e., those that are more likely to rank among the top-k when considering the ranking function \({\rho }\). Since the only evidence of the user’s intent is the input query Q and the corresponding user sample \(S\), we assume a measure of relevance \(\rho _{S}\) of each answer to the sample:
Definition 8
(Relevance measure) Given a user sample \(S\), the relevance measure \(\rho _{S}\) is a function \(\rho _{S}:\mathfrak {Q}~\mapsto ~\mathbb {R}^{+}\) that, given an answer \(A \in \mathfrak {Q}\), returns the relevance \(\rho _{S}(A)\) of A to \(S\).
Note that given a second answer \(A' \in \mathfrak {Q}\), if \(\rho _{S}(A) > \rho _{S}(A')\), then we say that A is more relevant than \(A'\) with respect to \(S\). We can now define the set of relevant exemplar answers as
where the threshold \(\tau > 0\) is data dependent and can be provided by the user. The idea is that such set should then contain the top-k answers.
Since \(\mathfrak {Q}_{\rho }\) is a set of subgraphs of \(D\), we say that the set of solutions \(\mathfrak {Q}_{\rho }\) is contained in the subgraph \(D_{\rho } \subseteq D\), which is any subgraph of \(D\) that contains all the relevant exemplar answers \(\mathfrak {Q}_{\rho }\) and none of the remaining irrelevant exemplar answers \(\overline{\mathfrak {Q}}_{\rho } = \mathfrak {Q}\backslash \mathfrak {Q}_{\rho }\). This portion of the graph is the subgraph induced by the subset of nodes \(N_{\rho } \subseteq N\), called the relevant nodes. In the following, we assume that for an answer to be considered relevant, all its nodes should be relevant, i.e., they should satisfy the minimum relevance threshold \(\tau \) (otherwise, we would be admitting answers that are only partially relevant).
Therefore, we consider a relevance measure \(\rho _{N_{S}}: N\mapsto \mathbb {R}^{+}\) to be applicable to any node in the graph. Then, relevant nodes are the nodes whose relevance measure is above the threshold \(\tau \), i.e., \(N_{\rho } = \{ n \in N| \rho _{N_{S}}(n) > \tau \}\). Hence, an answer A is relevant when all its nodes are relevant. In practice, we first identify the set of relevant nodes \(N_{\rho }\), and we then use only these nodes to construct the subgraph \(D_{\rho } \subseteq D\).
In our solution, we implement \(\rho _{N_{S}}\) as a distance measure on the graph, such that it measures the distance of every node from the nodes of the sample \(N_{S}\), and we keep only nodes that are within a certain distance threshold from the sample. For this reason, we call \(D_{\rho }\) the Query Neighborhood of the sample \(S\). In order to compute this distance, we propose the Adaptive Personalized PageRank Vector (APPV), an extension of the Personalized PageRank Vector (PPV), designed to exploit the properties of our problem. This is implemented by the SelectQueryNeighborhood algorithm.
5.2.2 The SelectQueryNeighborhood algorithm

Our solution models the computation of the Personalized PageRank Vector (PPV) [25] which is used as an estimate of the distances of the nodes in the graph from the subset of nodes in the user sample. In the literature, Personalized PageRank (PPR) [21, 25] is a well-known technique that computes the PageRank biased toward the preferences of the user. The problem is defined as follows: given an input graph \(G:\langle N, E \rangle \) with \(|N|\) vertices, and a preference vector \(\varvec{p} \in \mathbb {R}^{|N|}\), output the PPV \(\varvec{v} \in \mathbb {R}^{|N|}\) containing the PPR scores for all vertices of G with respect to the preference vector \(\varvec{p}\). We use \(\varvec{p}[n]\) to denote the personalized preference value for node \(n \in N\), and \(\varvec{v}[n]\) to denote its PPR score. In our case, user preferences are expressed through the query Q, and for this reason, we initialize the preference vector according to the nodes in the user sample S, which models the query Q in the database. Finally, we say that the relevance measure \(\rho _{N_{S}}(n)\) of a node n is its corresponding Personalized Page Rank value \(\varvec{v}[n]\).
The main difference between the original PPV model and our solution, APPV, lays on the semantic of edges. Traditionally, edges between nodes are treated equally as they usually represent just a link from one webpage to another (i.e., they are all of the same kind). In contrast, our model adapts to the various edges and their labels, according to S. In particular, the edges in our model may represent different kinds of relationships. It is therefore natural to differentiate transition probabilities based on the information carried by each single edge, as some relationships are more informative than others [11, 49]. Moreover, labels that do appear in the user query should be given more importance when computing the PageRank, since they represent the user preference.
Figure 4 depicts the output of the computation on the graph of our running example. Here all the nodes have been assigned the weights from the final APPV, computed using the set of nodes in the sample as initial preferences.
The set \(N_{\rho }\), which satisfies the selectivity requirement, consists of nodes with Personalized PageRank score higher than a minimum threshold \(\tau \), \(0<\tau <1\).
To compute the transition probabilities in the APPV model, assume a model of the database \(D: \langle N, E \rangle \), and let \(A^{D}\) be the adjacency matrix of this graph. If \(\left| N\right| \) is the number of nodes in the database, then \(A^{D}\) is an \(\left| N\right| \times \left| N\right| \) square matrix. In this matrix, we have that \(0<A_{ij}^{D}\le 1\) if and only if the node i has a relationship \(e^{\ell }_{ij}\) with node j with label \(\ell \); otherwise, we have \(A_{ij}^{D}=0\). In this way, the element \(A_{ij}^{D}\) models the amount of information that is transferred from node i to node j by the edge \(e^{\ell }_{ij}\) as a function of its label \(\ell \). In our solution, the values in \(A^{D}\) are proportional to the amount of information [43] carried by the edge \(e^{\ell }_{ij}\), which is:
where \(E^{\ell }\) is the set of edges with label \(\ell \). Note that the frequency of a label can be easily pre-computed in the database.
In order to account for the importance of the edges in the user sample, we additionally define matrix \(A^{S}\), which is constructed from the adjacency matrix of the database, but where only entries for edges whose label appears also in S are assigned a nonzero value. In other words, we construct an \(\left| N\right| \times \left| N\right| \) square matrix with \(0 < A^{S}_{ij} \le 1\) if the nodes i and j are connected by an edge and that edge has a label \(\ell \) that appears as label of one edge in the user sample S and with \(A^{S}_{ij}=0\) otherwise.
We then combine the two matrices into the matrix \(\bar{A} = A^{D} + A^{S}\) and normalize it. Under this transformation, \(\bar{A}\) becomes the transition probability matrix for the knowledge base graph, where more relevance is given to edges carrying more information, as well as to edges with labels that appear in the query. We also define \(\varvec{p}\), an \(\left| N\right| \times 1\) column vector, which serves as the normalized preference vector for which \(\varvec{p}[n] \ne 0\text { iff }n \in N_{S}\), i.e., \(0 < \varvec{p}[n] \le 1\) if and only if the node i is in S. Given the column normalized transition probability matrix \(\bar{A}\), the teleportation probability c, and the preference vector \(\varvec{p}\), our technique adheres to the Personalized PageRank semantics [11, 25]. Thus, the APPV \(\varvec{v}\) is defined as the stationary distribution of the Markov chain with state transition given by the matrix
where the teleportation probability \(c \in (0,1)\) is typically \(\approx 0.15\), with small changes in this value having little effect in practice [39].
The exact computation of this vector typically requires \(\mathcal {O}(|N|^2)\) time and space. Performing the computation through power iteration requires \(\mathcal {O}(|N|t)\) time, where t is the number of iterations to be performed. Nevertheless, this computation is still not practical for very large graphs.
In order to compute this value fast, we extend the template proposed in [3] and apply an approach similar to the weighted particle filtering procedure proposed in [30] but extended to correctly take into account the teleportation probability and to consider the non-uniform edge weights that we previously introduced. The extension is shown in Algorithm 4.

Algorithm 4 simulates a set of \(1/\tau \) floating particles (line 2) starting from each node with a nonzero value in \(\varvec{p}\). At each iteration (lines 6–15), they split among the neighbors of the node they are currently visiting, but we prevent them to split to arbitrarily small sizes, limiting them to have minimum size \(\tau \) (lines 12–13). When spreading the particles among the neighbors, the algorithm gives preference to the edges with higher weights. The restart probability c will dissipate part of the particles at every iteration (line 7), and the algorithm will stop when no more particles are floating around.
At the end of the algorithm, we return the APPV containing the scores that have been accumulated through each iteration on every node. We then keep the subset of the graph containing only those nodes with a score higher than some threshold and the edges connected to them (line 6–7 in Algorithm 3). Since we are dealing with an iterative approximation, we keep only those nodes that have been visited by at least one particle, which means that we discard all nodes, whose value is not greater than \(\tau \).
6 Finding simulating answers
In its original formulation, strong simulation is node label preserving [32], meaning that the query and the database have labels on the nodes (instead of the edges). On the contrary, our definition is strictly based on edge labels: We require to preserve the relationships among nodes, ignoring the node labels. The adaptation of strong simulation from node label preserving to edge label preserving is possible, albeit non-trivial. We discuss the details in the following paragraphs. We also show that it is possible to use the same strong simulation algorithms [5] in our setting. The solution we propose includes the translation of our graph into an expanded graph.
Definition 9
(Expanded graph) For a given graph \(G: \langle N, E \rangle \), the expanded graph is a graph \(G^+:\langle N^+, E^+ \rangle \), where each \(n_1 \overset{\ell }{\rightarrow } n_2, (n_1,n_2) \in E\) is substituted with two edges \(n_1 \overset{}{\rightarrow } n^\ell \) and \(n^\ell \overset{}{\rightarrow } n_2\), where \(n^\ell \) is a new uniquely identified node with label \(\ell \). The path \(n_1 \overset{}{\rightarrow } n^\ell \overset{}{\rightarrow } n_2\) is called expanded edge and \(n^\ell \) is called edge node.
Clearly, \(N^+ = N\cup \{n^\ell \mid \exists ~n_1,n_2 \in N, n_1 \overset{\ell }{\rightarrow } n_2\}\) and \(E^+ = \{(n_1,n^\ell ),(n^\ell ,n_2)\mid n_1,n_2 \in N\wedge n_1 \overset{\ell }{\rightarrow } n_2\}\).
Figure 5 represents an edge \(n_1 \overset{\ell }{\rightarrow } n_2\) and its expansion. Note that the nodes \(n_1\) and \(n_2\) in the expansion have no labels. We now prove that the definition of dual simulation in [32] is equivalent to ours when applied to the expanded graph. Recall that in a node-labeled graph, simulation is defined as follows.
Definition 10
(Node label dual simulation) A node-labeled graph \(D_1: \langle N_1, E_1 \rangle \) dual simulates another graph \(D_2: \langle N_2, E_2 \rangle \), denoted as \(D_1 \trianglelefteq _D^ND_2\), if there exists a relation \(\mathcal {R}\), such that for each \((n_1^\ell ,n_2^\ell ) \in \mathcal {R}\): (1) for all \(n_1 \rightarrow n_1'\), exists \(n_2'\) such that \(n_2 \overset{}{\rightarrow } n_2'\) and \((n_1',n_2') \in \mathcal {R}\), (2) for all \(n_1'' \rightarrow n_1\), exists \(n_2''\) such that \(n_2'' \rightarrow n_2\) and \((n_1'',n_2'') \in \mathcal {R}\).
We need to prove that edge label strong simulation is equivalent to node label simulation on expanded graphs. We first prove the following lemmas.
Lemma 1
Given two databases  and \(D: \langle N, E \rangle \), \(S\trianglelefteq _DD\)
\(\Leftrightarrow \)
\(S^+ \trianglelefteq _D^ND^+\).
and \(D: \langle N, E \rangle \), \(S\trianglelefteq _DD\)
\(\Leftrightarrow \)
\(S^+ \trianglelefteq _D^ND^+\).
Proof
The structure of the proof is as follows. We prove both directions separately constructing another dual simulation starting from the one existing by hypothesis.
(\(\Rightarrow \)): Given a dual simulation relation \(\mathcal {R}_D\) from  to D, we construct a relation
to D, we construct a relation
where  . Note that for the generality of \(s_1,s_2,n_1,n_2\), \(\mathcal {R}_D^+\) contains edges in both directions. \(\mathcal {R}_D'\) is, in fact, a dual simulation from \(S^+\) to \(D^+\). Suppose \(\mathcal {R}_D'\) is not a dual simulation, then it must exist
. Note that for the generality of \(s_1,s_2,n_1,n_2\), \(\mathcal {R}_D^+\) contains edges in both directions. \(\mathcal {R}_D'\) is, in fact, a dual simulation from \(S^+\) to \(D^+\). Suppose \(\mathcal {R}_D'\) is not a dual simulation, then it must exist  such that it for any \(n \in N^+\), \((s,n) \notin \mathcal {R}_D\). We have two cases:
such that it for any \(n \in N^+\), \((s,n) \notin \mathcal {R}_D\). We have two cases:
-
1.
\(s \in N\). This is a contradiction, since \(\mathcal {R}_D\) is a dual simulation it exists a n, such that \((s,n) \in \mathcal {R}_D\).
-
2.
\(s \in N^+ \setminus N\). This means that s is an edge node and exists a label \(\ell \) and
 , such that \(s_1 \overset{\ell }{\rightarrow } s_2\). By hypothesis exists \(n_1, n_2 \in N\) such that \((s_1, n_1) \in \mathcal {R}_D\), and \((s_2,n_2) \in \mathcal {R}_D\). However, in the expanded graph \(n_1 \overset{}{\rightarrow } n^\ell \overset{}{\rightarrow } n_2\), implying that \((s_\ell ,n_\ell ) \in \mathcal {R}_D'\) contradicting the hypothesis.
, such that \(s_1 \overset{\ell }{\rightarrow } s_2\). By hypothesis exists \(n_1, n_2 \in N\) such that \((s_1, n_1) \in \mathcal {R}_D\), and \((s_2,n_2) \in \mathcal {R}_D\). However, in the expanded graph \(n_1 \overset{}{\rightarrow } n^\ell \overset{}{\rightarrow } n_2\), implying that \((s_\ell ,n_\ell ) \in \mathcal {R}_D'\) contradicting the hypothesis.
(\(\Leftarrow \)): The proof is similar to the forward arrow, noticing that \(\mathcal {R}_D= \mathcal {R}_D' \setminus \mathcal {R}_D^+,\) and will be omitted. \(\square \)
We are now ready to prove the following theorem.
Theorem 3
Given two databases  and \(D: \langle N, E \rangle \), \(S\trianglelefteq _SD\)
\(\Leftrightarrow \)
\(S^+ \trianglelefteq _S^ND^+\).
and \(D: \langle N, E \rangle \), \(S\trianglelefteq _SD\)
\(\Leftrightarrow \)
\(S^+ \trianglelefteq _S^ND^+\).
Proof
Recall that from Definition 7, two graphs are strongly similar if there exists a node \(n \in N\) and a \(d-\)graph \(D[n,d]\) such that (1) d is equal to the diameter of \(S\) and (2) \(S\trianglelefteq _DD[n,d]\) with the maximal dual simulation. If \(S\trianglelefteq _SD\), by Lemma 1 follows that \(S^+ \trianglelefteq _D^ND^+[n,d]\) and it easy to see that d is the diameter of \(S^+\). It also follows that \(S^+ \trianglelefteq _D^ND^+[n,d]\) with the maximal relation, since the relation as defined in Lemma 1 contains all the pairs plus the pairs included in the expanded edges. \(\square \)
Theorem 3 states that it is sufficient to run the Match algorithm from [32] on an expanded graph and then remove all the edge nodes and the matching from the expanded graph to obtain valid strong-simulating results for the original graph. Algorithm 5 shows the pseudocode of the strong simulation algorithm. First, the graphs \(S\) and \(D\) are expanded using the procedure Expand (lines 1, 2); then, the Match algorithm is used to find strong-simulating answers \(\mathfrak {Q}^+\) in the expanded graphs \(S^+\) and \(D^+\) (Line 4). Finally, all the results in \(\mathfrak {Q}^+\) are contracted using the Contract function to remove the expanded edges (lines 5–7).

Algorithm complexity: The Match algorithm on \(D^+\) runs in \(\mathcal {O}(|N^+|(|N^+|+(|N_s^+| + |E_s^+|)(|N^+| + |E^+|)))\) as shown in [32]. Since the size of the user sample is small, \(|N_s^+|\) is bounded by a small constant and we can consider Match to run in \(\mathcal {O}(|N^+|(|N^+|+(|N^+| + |E^+|)))\). On the other hand, \(|N^+| = |N| + |E|\) since for each edge we add a node and \(|E^+| = 2|E|\). Therefore, since both Expand and Contract execute in \(\mathcal {O}(|E|)\) time, the overall complexity is dominated by Match, which runs in \(\mathcal {O}(|N|^4)\) for expanded graphs.
Applying pruning techniques: Algorithm 5 works with any kind of graph, but expanding the entire database may be time-consuming. A legit question then is whether IterativePruning can be applied to simulation. Indeed, this is possible by relaxing the constraint in Property 1. It easily follows from Theorem 1 and Definition 5 that in a database \(D: \langle N, E \rangle \), a node \(n \in N\) matches a node  in the user sample \(S\), so it is not pruned, if for each label \(\ell \) and a distance \(i \le d\), if
in the user sample \(S\), so it is not pruned, if for each label \(\ell \) and a distance \(i \le d\), if  then \(|W_{n,\ell ,i}| > 0\). We refer to this algorithm as IterativePruning
\(^*\).
then \(|W_{n,\ell ,i}| > 0\). We refer to this algorithm as IterativePruning
\(^*\).
We call FastXQSim the algorithm that derives from XQ when instantiated with the StrongSimSearch congruence relation described in Algorithm 5 and the pruning algorithm IterativePruning \(^*\).
Regarding the restriction of the search space presented in Sect. 5.2, we note that no changes are needed to SelectQueryNeighborhood. Therefore, for the case of strong simulation, we can use the ApFastXQ algorithm by first applying the SelectQueryNeighborhood algorithm presented above and then the FastXQSim with IterativePruning \(^*\). We refer to this new algorithm as ApFastXQSim.
7 Solution workflow
In the following, we first summarize how the various algorithms we have presented combine to solve our problem. Then we explain how we can rank the results produced by these solutions and present the user with the top-k among them.
7.1 Choice of algorithms
The first solution (refer to Fig. 6) is to adopt the exact and exhaustive XQ algorithm (Algorithm 1). In Algorithm 1, we can either instantiate the FindSimilarSubgraphs function with an exploratory isomorphic search or use strong simulation by replacing lines 3–9 with StrongSimSearch (Algorithm 5) to obtain the XQSim algorithm.
In order to improve the running time of XQ and XQSim, we first prune the search space by applying IterativePruning (Algorithm 2) and its variation IterativePruning \(^*\), respectively. This leads to the FastXQ and FastXQSim algorithms, respectively, which are both exact, i.e., the final list of top-k results corresponds to the actual top-k exemplar answers.
A further improvement in terms of time performance is possible using the SelectQueryNeighborhood function (Algorithm 3). This function can be used without changes with both isomorphism and strong simulation and leads to the ApFastXQ and ApFastXQSim algorithms, respectively. In this case, we are just reducing the total amount of subgraph isomorphism (or simulation) checks needed, but all answers returned are still the result of an exact isomorphism (or simulation). These algorithms simply trade off effectiveness for efficiency, returning a meaningful subset of the results.
7.2 Ranking query answers
Once the answers have been computed from the user sample, they need to be ranked in order to either be returned sorted to the user that posed the query, or to select only the k most promising candidates, i.e., the top-k. To do this, we introduce a novel ranking function that is a linear combination of two scores, namely the structural similarity score \(\mathcal {S}\) based on the d-hop nodes set and the amount of information as provided by the APPV vector, which indicates the relevance of nodes with respect to the sample nodes. The score of each answer is computed by using the above two parameters to compare the answer to the user sample.
Most node similarity measures proposed in the literature are based on the concept of graph similarity and isomorphism. This is the case for graph edit distance [18], which is computed with a reduction to graph isomorphism, and is therefore inapplicable to our problem, due to its high time complexity. A different method is proposed in [28] and is based on a vectorial representation of nodes. This idea seems suitable for our settings; thus, we extended it in order to capture the differences among nodes that emerge when taking into account the edge labels connecting the d-hop nodes. We also embed distance information aiming at giving different weights to nodes based on their distance from the sample (for the reasons presented in Sect. 5.2). Thus, for every node n, we build a vector containing a value for every label \(\ell \in L\) in the graph, and we compute this score as
The value \(I(\ell )\) represents the amount of information [43] described in Sect. 5.2.2—Eq. 3 which quantifies the importance of an edge label. The \(i^{2}\) term is a quadratic decay factor to the importance of an edge at distance i from the current considered node. Intuitively, the further you go from the node, the less important is the edge you encounter.
Given the vectorial representation of two nodes, we compute the node similarity \(\mathcal {S}\) using a metric for vectors, such as the Jaccard, Euclidean distance or cosine similarity. Note that our vectorial representation contains already the computed score \(\sigma \). In our experiments, we use cosine similarity, but any other similarity metrics can also be used. Therefore, the structural similarity between a node \(n_s\) of the user sample and any matching node n is computed as follows:
The structural similarity above does not take into account the proximity measure of the results with respect to the user sample. Therefore, we consider a linear combination, parametrized by \(\lambda \), between the node similarity (structural) and the Personalized PageRank (proximity) as follows.
where \(\varvec{v}[n]\) is the APPV defined in Sect. 5.2.1. We then compute the average of \(\rho (n_s,n)\) over the number of nodes matching the user sample nodes in the similarity relation \(\mathcal {R}\) and sum over all nodes in the sample:
Note that the choice of \(\lambda \) (in Eq. 8) is data dependent. A value \(\lambda \) close to 1 favors results that share more edges with the d-hop nodes of the user sample. On the other hand, a value close to 0 will take into account only solutions that are close to the original query. For this reason, we can see \(\lambda \) as a diversification parameter that depends on the user and on the data. This is also the approach taken by most diversification models [1].
7.3 Top-k answering with TopKXQ
The approximate approach we presented above first computes all the answers within the Query Neighborhood and then ranks them. Hence, answers outside this neighborhood are disregarded. Although this approach is particularly suited when the most relevant answers are expected to be close to the user sample, it might not find k answers in case the relevance threshold \(\tau \) is set too low. The only answers that will be incorrectly discarded by applying the APPV approximation are those that are far away from the sample, but still achieve structural similarity higher than the proximity value of all the answers near the sample. Even though in practice the number of answers lost is negligible (refer to Sect. 8), in what follows we propose a more rigorous approach.
The key idea is to implement an exact top-k algorithm that we call TopKXQ, which explores the graph until k answers are found, and all the other candidate answers are guaranteed to be worse (i.e., rank lower) than those. This algorithm is based on the computation of an upper bound on the ranking value for the answers that have not been considered so far. It implements an iterative process that explores the graph around the sample in circles of increasing radius. Starting from an empty answer set, the algorithm finds answers that are progressively further away from the sample. The search stops when the upper bound of any remaining candidate answer is lower than the value of the lowest ranked answer in the top-k candidates. Thus, this approach ensures that there are no false negatives.
7.3.1 Computing an upperbound for top-k answering
The stopping condition of the algorithm determines what is the highest score that can be obtained if an answer exists outside the nodes explored so far and compares it with the score of the current kth answer. To devise an upper bound on the rank value of the nodes, we note that Eq. 9 can be rewritten as
In this equation, we observe that the second term depends on the position of the answer with respect to the user sample, since it is averaging over the APPV values of the nodes in the answer. As such, it decreases proportionally to the distance of an answer from the user sample. Therefore, answers outside the current neighborhood necessarily achieve lower scores for this value.
On the other hand, the first term takes into account the structural similarity between each node in the query and each corresponding node in the answer. Thus, it depends only on the labels of edges around the two.
Given the above two observations, we can compute the maximum value for the similarity score achievable by any candidate answer outside the current neighborhood. In particular, given a sample S, we compute an upper bound for the structural similarity value \(\mathcal {S}(n_s,n)\) between all nodes \(n_s \in N_s\) and \(n \in N\setminus N_{\rho }\), where \(N_{\rho }\) is the set of nodes in the current portion of the graph, where answers have already been computed.
Therefore, the sum of the best structural similarity value for each sample node is the highest possible structural similarity achievable by an answer outside the neighborhood.
We then use this value to determine whether there exists any candidate answer \(\overline{N}_s \subseteq N\setminus N_{\rho }\), such that the value of \(\sum _{\bar{n}_s\in \bar{N}_s}{\mathcal {S}(n_s,\bar{n}_s)}\) is high enough to fall into the top-k answers. The application of the neighborhood algorithm produces only answers for which all nodes are within the distance measure; hence, answers that are not completely contained in the neighborhood are disregarded. Thus, for the stopping condition to be correct, we take into account also answers that lie across the boundary of the current neighborhood.
7.3.2 The TopKXQ algorithm

The above process is described in Algorithm 6, TopKXQ, which starts by expanding the Query Neighborhood and searching for answers in that portion of the graph. Then, if less than k answers are found, the algorithm proceeds by expanding further the neighborhood. The expansion process is similar to what is presented in Algorithm 3, by using decreasing values for the threshold \(\tau \). Then, it also performs a BFS exploration following only edges with labels appearing in the query, in order to include borderline solutions. Eventually, when k or more answers have been found, the algorithm computes the upper bound for the structural similarity. The search only continues in the case where the score for the kth answer is lower than the upper bound, which means that a better answer may exist in the graph.
The UpperBound method is described in Algorithm 7. This function retrieves the node \(\bar{n} \in N\setminus N_{\rho }\), with the highest similarity value \(\mathcal {S}(n_s,\bar{n})\), for each node \(n_s\) in the sample S. Given a node \(n_s \in N_{S}\), \(\bar{n} = {\text {*}}{argmax}_{n \in N \setminus N_\rho } \mathcal {S}(n_s,n)\).

With such nodes, it builds a mock solution that maximizes the structural similarity score, while containing only nodes that are outside the current neighborhood. The computation can be improved further considering only nodes in \(N \setminus N_\rho \) that are connected through edges with the same labels of the sample nodes.
Figure 7 depicts the TopKXQ algorithm, based on the graph isomorphism congruence relation. If we want a version of the algorithm that works with the strong simulation congruence relation, then we simply have to replace algorithms 1 and 2 with algorithms 5 and 2*, respectively. Note that TopKXQ is an optimal algorithm: It always produces the correct top-k answers.
8 Experimental evaluation
In this section, we experimentally validate our solution by measuring its performance and comparing it to other approaches.
Queries We extracted 100 real queries entailing a user need expressible with an exemplar query from the AOL query log,Footnote 4 and mapped them to the knowledge base.Footnote 5 Words in each query were manually associated with the most appropriate node, and relationships were similarly translated into an edge or a path. An example of such a mapping can be seen in Table 1.
Furthermore, we built 100 synthetic queries by selecting 100 nodes at random among those that have at least 2 outgoing or ingoing edges. Then, we run for each of them one undirected random walk with restart with teleportation and halting probability, sampled between 0.05 and 0.35. In our experimental evaluation, we used these queries in addition to the 100 queries from the AOL log, for a total of 200 queries. The samples obtained in this way are highly heterogeneous in terms of size and frequency of edge labels. Each query has between 2 and 11 edges and diameter up to 10, with more than 200 different edge labels overall in each set, while the average diameter is 2.8, in line with real-world queries [17]. In order to test our algorithms with different query shapes, we made sure our queries contain cycles, single paths, trees, and complete graphs. Although we have used both the AOL queries and the 100 synthetic queries, we report only the graphs for the AOL queries, since the results of the experiments on both sets are almost identical.
Datasets: We downloaded the full Freebase knowledge base [20] in April 2014, obtaining a connected graph of 76M nodes and 314M edges, with about 4.5K distinct edge types. We refer to this dataset as Real. To the best of our knowledge, this is the biggest graph used in this context in the literature and the first time that the entire Freebase graph is used for this purpose. While related works [28, 47, 50] use a small part of Freebase, we explored solutions that scale to its full size. Based on Real, we generated 10 synthetic datasets, embedding 20 samples of the test set in different points of the graph: We performed a breadth-first traversal from a fixed starting node and randomly chose to embed an answer according to a distribution that decreases exponentially with the distance from the starting node (thus modeling answers at varying distances). For the scalability tests, we generated graphs having 0.5, 1, 5, 10 and 20 M nodes and 1K embedded queries. We denote them as GSize-x, where x is the graph size. Similarly, we generated graphs with 10 M nodes and 0.5, 1, 2, 5 and 10 K embedded answers. We denote them as QSize-x, where x is the number of generated answers.
Experimental setup: In our experiments, we use \(d=2\) since we verified that it leads to low memory requirements for storing the d-hop nodes set, without sacrificing time performance (see Sect. 8.3). We also observed that \(\lambda = 0.3\) (see Sect. 7) is a good compromise for retrieving diverse and qualitative results. In Sect. 8.4, we study the effect of varying the threshold parameter \(\tau \) (see Sect. 5.2.2), for which we set the default value to 0.003. All the reported results are averages over 5 consecutive runs. We implemented our solution in Java 1.8 and ran the experiments on a i686 Intel Xeon E52440 2.40 GH machine with 12 cores in hyper-threading and 188 Gb RAM, over Linux kernel v3.13.0. The graphs are loaded into main memory using our graph library available under open-source license.Footnote 6
Implemented Algorithms: Apart from FastXQ, ApFastXQ, FastXQSim and ApFastXQSim, we implemented three additional algorithms from related works:
QueryReformulation: An algorithm that produces query reformulations by mining sessions from query logs in a term-level fashion [48]. The model is trained on the AOL query log, and the suggestions are based on our query test set.
EQ-Graph: Entity-query graph is a model that computes serendipitous suggestions starting from entity mentions in a page [10]. For our queries to work in this setting, we associated to each node the corresponding Wikipedia page (or the best Wikipedia page that represents the node). The model is trained on a big query log from the Yahoo! Search Engine.
NeMa: This algorithm [29] and other previous works are based on the assumption that there exists a truly small set of correct answers to a graph query, which is not true in our case. Therefore, we implemented their technique taking into account edge label matches instead of node matches. The authors kindly provided us a C++ implementation (compiled using gcc v4.4.3).
Summary of results: Our user studies demonstrate that 92 % of the users believe that exemplar queries are relevant and useful for search tasks and that existing approaches are not able to provide effective solutions to our problem. The user studies also show that our method identifies meaningful results with 81 % precision. We observe that the IterativePruning algorithm leads to graphs up to 80 % smaller, decreasing the running time by 30 %, with even higher improvements when we choose starting nodes with low selectivity. Overall, more than 50 % of the queries take less than 1 second for \(\tau \ge 0.003\). The set of results measuring performance demonstrates the scalability of our approach to the largest knowledge graph available in the field (76M nodes, 314M edges), while maintaining interactive response times. Finally, the results show that strong simulation leads to richer answer sets than isomorphism, retrieving 34 % more nodes (i.e., entities).
8.1 Usefulness
In order to assess the quality of the proposed solution, we conducted the following user study. We used Amazon Mechanical Turk (http://mturk.com) and asked 94 users (with no restriction with respect to education level, age and country) to evaluate our system. For each query in the test set, we provided an explanation of the topic, the query intention and the top-10 results in our answer set obtained using isomorphism as congruence relation and ranked according to our ranking function. We asked each user to rate each result as irrelevant, weakly related or very related with respect to the topic and the expressed query intention. Each user evaluated between 2 and 10 queries (on average 8).
The users provided 4540 marks in total (see Fig. 9): 81 % of our results are marked as relevant (weakly or strongly) and only 19 % of them are not considered relevant suggestions. Out of the 427 suggestions we produced, 172 (40 %) are judged highly relevant by more than 50 % of the users, while each exemplar query contains at least one relevant (weakly or strongly) result for 99 % of the users. Note that the answers judged irrelevant were still graphs with the same structure of the user query, but were simply not related enough to the specific user information need.
Moreover, each user expressed her opinion with respect to (a) the idea of using examples as a search paradigm, (b) whether she already had the need of searching using exemplar queries and (c) the usefulness of the system in general. As shown in Fig. 10, 92 % of the users considers the exemplar queries paradigm and the overall system useful for retrieving additional and relevant information. Furthermore, 62 % of the people interviewed declared that they already had the need to perform this kind of exemplar queries search in the past (but there was no system to support them).
8.2 Comparison to previous work
In the following, we compare our method against two different approaches: (a) algorithms that produce related queries and (b) an approximate query answering technique for graphs.
Related queries: We implemented and compared with the methods QueryReformulation and EQ-Graph mentioned earlier, through a user study similar to the one presented in Sect. 8.1. For each query in the test set, we presented to users three groups of suggestions: one produced with our method and one produced by each one of the two methods above. We then asked users which of the three groups of suggestions they considered the most helpful for each query task.
The results, depicted in Fig. 8, show that in 64 % of the cases the users preferred our solution to the other two. Furthermore, for 78 % of the queries that received more than 2 marks, the majority of users preferred our solution. In 18 % of the cases, none of the proposed solutions were satisfying, neither the answers proposed by our model nor those produced by the other algorithms. Overall, the two competing approaches together were preferred by less than 30 % of the users, none of them choosing the two approaches in all the queries.
Approximate query answering on graphs: We now present the comparison between our approach and NeMa [29], a state-of-the-art technique for answering approximate queries on graphs. Since on Real a single query takes NeMa more than 13 h to process, we test NeMa on graphs obtained after applying SelectQueryNeighborhood on our query test set, thus giving it an advantage. The results in Fig. 11 show that NeMa is almost three orders of magnitude slower than our algorithm. This suggests that a query answering technique for graphs is not applicable to our setting.
We also provide anecdotal evidence comparing the top-5 results from our method and NeMa. Tables 2 and 3 show the top-5 results of NeMa for two different exemplar queries compared with the results of our algorithm, shown in Tables 4 and 5 (for our algorithm, we report the top-2 results containing query terms, the top-2 results not containing query terms and for reference, the lowest ranking result).
We observe that if the structure of the exemplar query is complex (e.g., it contains cycles), NeMa fails to find the correct answers, mapping different query nodes on the same graph node as depicted in Table 3-row 3, where the same graph node, “Oral Transmission,” is used twice. Actually, 87 % of the answers produced by NeMa are not isomorphic to the test queries, producing results that contain the same node more than once and, thus, leading to poor results. Furthermore, the top answers proposed by NeMa for Q2 contain diseases that are not sexually transmitted (e.g., diabetes that is ranked 2nd), a situation that does not occur with our algorithm.
For strong simulation, Tables 6 and 7 report the top-2 results containing query terms, the top-2 results not containing query terms and the result with the lowest ranking score. Note that, with strong simulation, some answers include more nodes than those in the query. For instance, the first result in Table 6 lists all the acquisitions made by GoogleFootnote 7 and also Menlo Park. This is the result of the maximality enforced by strong simulation, which compresses several isomorphic answers in one single simulating answer. Similarly, the third result (that does not contain any node of the query) represents all the acquisitions by Yahoo, along with the Santa Clara node. Contrary to isomorphism, strong simulation correctly groups answers having the same root node (e.g., Yahoo). Table 7 shows how the maximality condition reduces the size of similar answers. Indeed, all the results that are in the first two rows of Table 5 are condensed in the first result in Table 7 that represents all the risk factors and prevention methods for sexually transmitted infections. We observe that some nodes are still repeated among different results, concluding that strong simulation does not necessarily collapse all the redundant information in one single answer. Nonetheless, we still obtain good clusters of answers. Note that Table 7, in rows 3 and 4, presents relevant answers about other contagious infections not related to sex, thus offering a richer, more diverse answer set. These results are also present in the isomorphic answers, but in much lower-ranked positions.
8.3 Pruning effectiveness
We now study the impact of pruning on query time and the effect of selectivity on pruning time.
Pruning impact: We perform a batch of experiments using repeatedly the query test set, comparing the query time with and without applying IterativePruning, and depict the results in Fig. 12. The parameter d of IterativePruning (Sect. 5.1) determines how large is the d-hop nodes set of each node and it is compared to the similar representation for each node of the query.
By definition, a higher value of d causes a more aggressive pruning of the search space. We note that, as discussed in Sect. 5.1, our pruning technique does not modify the quality of the final result set, nor does it discard any relevant result. Nonetheless, Theorem 1 suggests that values of d larger than the query diameter (i.e., 3 or greater for our queries) have no impact on pruning power. Fig. 13 validates this claim, showing that the added benefit with \(d=3\) is minimal. In practice, these results show that graph structures captured by the node’s 3-hop nodes (i.e., for nodes at distance 3) have insignificant additional discriminative power. Therefore, building d-hop node tables for \(d=3\), or more, would not be beneficial in terms of pruning and would instead be detrimental in terms of performance.
Overall, pruning results in querying time reductions between 3 and 99 %. Interestingly, for 17 % of the queries, pruning does not affect query time. The reason is that pruning is more effective when the the frequencies in the graph of the sample edge-labels are low, since a large part of the graph is eliminated with fewer operations. This observation allows us to run the IterativePruning on demand. On average, IterativePruning reduces query time by 30 % and the graph size by 80 % (by removing non-matching edges). This entire batch of experiments takes 17 minutes to run with pruning and 38 without, saving 55 % of the total time.
Pruning selectivity: We study the performance of pruning in terms of time as a function of the selectivity of the starting node in the sample. Remember that low selectivity means better pruning (see Eq. 1). We run experiments measuring the correlation between time and selectivity, selecting the different nodes of the sample as starting nodes. The results show a positive correlation of 0.57 between selectivity and time performance, which is statistically significant at the 0.01 significance level. We conclude that starting from a low selective node positively impacts the pruning time, with savings up to 87 %.
8.4 Calibrating
We study the effect of \(\tau \) on SelectQueryNeighborhood in terms of time and quality of the results. The parameter \(\tau \) of SelectQueryNeighborhood determines the degree of approximation of the estimation of PPV of each node and is directly related to the number of answers retrieved and to the running time. In Fig. 15c, f, we plot the size of the neighborhoods (counts of vertices and edges from the graph) visited for increasing values of \(\tau \) (from 0.001 to 0.01) and the number of answers retrieved in each case. We refer to visited vertices/edges as the vertices/edges retrieved by our SelectQueryNeighborhood algorithm. We then search for relevant answers in the graph containing only such nodes and edges. In general, we see in Fig. 14 that, for values of \(\tau \) equal or greater than 0.005, the vast majority of queries run in less than 1 s. On the other hand, when we use values of \(\tau \) equal or smaller than 0.003, we see that some queries start taking more than 10 seconds.
Study of the average (top) and median (bottom) time and number of results (count) as a function of the threshold \(\tau \), comparing isomorphism and simulation with the ApFastXQ/ApFastXQSim algorithms, a average neighbor and pruning time, b average total time, c average count in terms of number of answers and visited edges/nodes, d median neighbor and pruning time, e median total time, f median count in terms of number of answers and visited edges/nodes
We witness an exponential decay in the number of visited nodes and edges as \(\tau \) increases, which is proportional to the number of answers retrieved. This is mirrored in Fig. 15a, d by a decrease in the time needed to retrieve the query neighborhood and to prune it. In line with this, Fig. 15b, e shows that with larger values of \(\tau \), the total time needed to compute the results decreases in the same manner. Thus, with a larger neighborhood, we find more answers to the query, at the expense of higher execution times.
We observe that the average time required by strong simulation to compute the set of maximal d-graphs is higher than isomorphism (Fig. 15b), but as the median result demonstrates (Fig. 15e), this is only true for very few large and complex queries. There is also a noticeable difference in the number of answers retrieved by strong simulation and isomorphism (see Fig. 15c, f). This is a natural consequence of the strong simulation algorithm and a desirable effect, because all the results are grouped in fewer but larger answers. Fig. 16 validates this claim, showing that even though strong simulation retrieves less answers, those involve between 22 % (for \(\tau =0.01\)) and 48 % (for \(\tau =0.0003\)) more distinct nodes than isomorphism. As expected, we found that for every query the answer set retrieved with strong simulation is a superset of the one retrieved with isomorphism.
In order to better understand the time performance behavior of our approach, we measured the correlation between search time and a number of query characteristics: diameter, density, number of repeated edge labels and average label frequency. With isomorphism as congruence relation, the number of repeated edge labels positively correlates with the running time, as shown in Fig. 17. This correlation is statistically significant with p value <0.001. We also observed a weak correlation (p value <0.01) between the average number of times a label appears in the query and the search time.
Note that these observations do not hold for strong simulation. The performance of strong simulation depends only on the size of the graph, since the Match algorithm is not affected by the characteristics of the queries [32].
We now evaluate the quality of the answers produced by ApFastXQ, by measuring precision at 1,5,10, 50,100, where precision at k (abbreviated P@k) is defined as the fraction of results produced by FastXQ that are also produced by ApFastXQ in the first k positions. Table 8 shows that overall precision is high, especially for the top positions. Any value of \(\tau \) between 0.003 and 0.005 is a reasonable choice, leading to high precision and an average query time of less than 2.4 seconds. Evidently, the choice of this parameter depends on the application. In a biological setting, where precision is more important than time, \(\tau =0.002\) could be a reasonable choice, producing very precise answers in about 10 seconds. On the web, where timely answers are needed, \(\tau =0.005\) can still offer precise answers in the top positions, in <1 s. In our experiments, we use \(\tau =0.003\).
8.5 Top-k results
We now study the performance of the TopKXQ algorithm and compare it against both FastXQ and AppFastXQ. We measure the portion of the graph explored by each solution, counting the number of nodes and edges used during the isomorphic test. In this experiment, we use GSize-10 and look for the top-10 answers. We report the results in Fig. 18.
We can see that FastXQ explores the entire graph, while TopKXQ visits more than an order of magnitude less nodes and edges. This considerable improvement is possible, because TopKXQ directly computes the top-k answers, while FastXQ has to first compute all the answers, and then rank them.
The AppFastXQ algorithm explores the smallest portion of the graph, namely four and three orders of magnitude less than FastXQ and TopKXQ, respectively. This speedup is due to the fact that the answer set produced by AppFastXQ is approximate, while the other two algorithms always provide the optimal answers. Nevertheless, as we discussed earlier (refer to Table 8), this approximate set of answers overlaps almost completely with the optimal set of answers, and they always contain the same top-1 answer.
8.6 Scalability
We present the scalability experiments as a function of the number of answers and the size of the database. Figure 19 shows the number of visited edges and nodes, and the number of results when the number of embedded answers increases (recall that QSize-x contains exactly x answers for each exemplar query). Figure 20 depicts the time of ApFastXQ, broken down in the times required by the three components of the algorithm. We observe that using SelectQueryNeighborhood as the number of answers increases from 60 to 100, the number of explored nodes remains almost the same. This is expected, since SelectQueryNeighborhood does not explore more nodes as long as the structure of the graph remains almost unchanged, but it finds more answers embedded in the same subgraph.
Conversely, if the size of the dataset increases and the number of answers is fixed, it is less likely to find answers close to the exemplar query. As expected, since the number of nodes explored is almost the same (see Fig. 21), the time remains constant (see Fig. 22), even though we move from 500 k to 20 M nodes. This supports our design choice, since changes in the peripheral part of the graph do not affect APPV.
9 Conclusions
In this paper, we introduce and define a novel query paradigm called exemplar queries and describe how it is applied in the case of knowledge graphs, where it requires the search for subgraph isomorphism in order to evaluate a query. We also propose a more flexible congruence relation, based on strong simulation. For both congruence relations, we propose an exact solution based on an effective and theoretically sound pruning technique, a fast algorithm for the search of top-k relevant exemplar answers and an efficient approximation algorithm. We evaluated our approach using in its entirety (for the first time in the literature) one of the biggest multigraphs available and coupled our results with a user study, demonstrating the efficiency and usefulness of the proposed system.
Notes
In the rest of the document, we will be dropping the part “edge-preserving.”
A subgraph induced by a set of nodes \(N\) is the subgraph whose edges have both endpoints in \(N\).
Note that those nodes will be removed later, when the actual isomorphic check will be performed.
List of queries: http://www.mi.parisdescartes.fr/~themisp/exemplarquery-ext/ .
For ease of exposition, we do not report the complete list of entities in the answer.
References
Agrawal, R., Gollapudi, S., Halverson, A., Ieong, S.: Diversifying search results. In: WSDM (2009)
Anagnostopoulos, A., Becchetti, L., Castillo, C., Gionis, A.: An optimization framework for query recommendation. In: WSDM (2010)
Baeza-Yates, R., Boldi, P., Castillo, C.: Generalizing pagerank: damping functions for link-based ranking algorithms. In: SIGIR (2006)
Bedini, I., Elser, B., Velegrakis, Y.: The trento big data platform for public administration and large companies: use cases and opportunities. In: PVLDB, vol. 6(11) (2013)
Beeri, C., Milo, T.: Schemas for integration and translation of structured and semi-structured data. In: ICDT. Springer, Berlin (1999)
Bergamaschi, S., Domnori, E., Guerra, F., Trillo Lado, R., Velegrakis, Y.: Keyword search over relational databases: a metadata approach. In: SIGMOD (2011)
Bergamaschi, S., Guerra, F., Rota, S., Velegrakis, Y.: A hidden markov model approach to keyword-based search over relational databases. In: ER (2011)
Bhatia, S., Majumdar, D., Mitra, P.: Query suggestions in the absence of query logs. In: SIGIR (2011)
Boldi, P., Bonchi, F., Castillo, C., Vigna, S.: Query reformulation mining: models, patterns, and applications. Inf. Retr. 14(3), 257 (2011)
Bordino, I., De Francisci Morales, G., Weber, I., Bonchi, F.: From machu_picchu to rafting the urubamba river: anticipating information needs via the entity-query graph. In: WSDM (2013)
Chakrabarti, S.: Dynamic personalized pagerank in entity-relation graphs. In: WWW (2007)
Cook, S. A.: The complexity of theorem-proving procedures. In: Symposium on Theory of Computing (1971)
Dimitriadou, K., Papaemmanouil, O., Diao, Y.: Explore-by-example: an automatic query steering framework for interactive data exploration. In: SIGMOD (2014)
Dong, X., Halevy, A.Y., Madhavan, J.: Reference reconciliation in complex information spaces. In: SIGMOD (2005)
Dou, Z., Hu, S., Luo, Y., Song, R., Wen, J.: Finding dimensions for queries. In: CIKM, pp. 1311–1320 (2011)
Fan, W., Li, J., Ma, S., Wang, H., Wu, Y.: Graph homomorphism revisited for graph matching. PVLDB 3(1–2), 1161 (2010)
Gallego, M.A., Fernández, J.D., Martínez-Prieto, M.A.: and P. de la Fuente. An empirical study of real-world SPARQL queries. In USEWOD Workshop-WWW (2011)
Gao, X., Xiao, B., Tao, D., Li, X.: A survey of graph edit distance. Pattern Anal. Appl. 13(1), 113 (2010)
Gauch, S., Smith, J.B.: Search improvement via automatic query reformulation. TOIS 9(3), 249–280 (1991)
Google. Freebase data dumps. https://developers.google.com/freebase/data (2014)
Haveliwala, T. H.: Topic-sensitive pagerank. In: WWW (2002)
Henzinger, M. R., Henzinger, T. A., Kopke, P. W.: Computing simulations on finite and infinite graphs. In: FOCS (1995)
Hogan, A., Mellotte, M., Powell, G., Stampouli, D.: Towards fuzzy query-relaxation for rdf. In: The Semantic Web: Research and Applications, pp. 687–702. Springer, Berlin (2012)
Jansen, B., Booth, D., Spink, A.: Determining the informational, navigational, and transactional intent of web queries. Inf Process Manag 44, 1251 (2008)
Jeh, G., Widom, J.: Scaling personalized web search. In: WWW (2003)
Kargar, M., An, A.: Keyword search in graphs: Finding r-cliques. Proc VLDB Endow 4(10), 681 (2011)
Kasneci, G., Ramanath, M., Sozio, M., Suchanek, F.M., Weikum, G.: Star: Steiner-tree approximation in relationship graphs. In: ICDE (2009)
Khan, A., Li, N., Yan, X., Guan, Z., Chakraborty, S., Tao, S.: Neighborhood based fast graph search in large networks. In: SIGMOD (2011)
Khan, A., Wu, Y., Aggarwal, C.C., Yan, X.: Nema: Fast graph search with label similarity. In: PVLDB (2013)
Lao, N., Cohen, W.W.: Fast query execution for retrieval models based on path-constrained random walks. In: KDD (2010)
Lissandrini, M., Mottin, D., Palpanas, T., Papadimitriou, D., Velegrakis, Y.: Unleashing the power of information graphs. SIGMOD Rec. 43(4), 21 (2015)
Ma, S., Cao, Y., Fan, W., Huai, J., Wo, T.: Strong simulation: capturing topology in graph pattern matching. TODS 39(1), 4 (2014)
Mishra, C., Koudas, N.: Interactive query refinement. In: EDBT (2009)
Mottin, D., Lissandrini, M., Velegrakis, Y., Palpanas, T.: Exemplar queries: give me an example of what you need. Proc. VLDB Endow. 7(5), 365 (2014)
Mottin, D., Lissandrini, M., Velegrakis, Y., Palpanas, T.: Searching with XQ: The Exemplar Query Search Engine. In: Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, pp. 901–904. ACM, NY, USA
Mottin, D., Marascu, A., Roy, S.B., Das, G., Palpanas, T., Velegrakis, Y.: A probabilistic optimization framework for the empty-answer problem. Proc. VLDB Endow. 6(14), 1762–1773 (2013)
Mottin, D., Palpanas, T., Velegrakis, Y.: Entity Ranking Using Click-Log Information. Intel. Data Anal. J. 17(5), 837 (2013)
Ngo, V. M., Cao, T. H.: Ontology-based query expansion with latently related named entities for semantic text search. In: IJIIDS (2010)
Page, L., Brin, S., Motwani, R., Winograd, T.: The pagerank citation ranking: bringing order to the web. TR 1999-66, Stanford InfoLab (November)
Park, D.: Concurrency and Automata on Infinite Sequences. Springer, Berlin (1981)
Pound, J., Hudek, A. K., Ilyas, I. F., Weddell, G.: Interpreting keyword queries over web knowledge bases. In: CIKM (2012)
Qiu, Y., Frei, H.-P.: Concept based query expansion. In: SIGIR (1993)
Shannon, C.E.: A mathematical theory of communication. SIGMOBILE Mob. Comput. Commun. Rev. 5(1), 3–55 (2001)
Shen, Y., Chakrabarti, K., Jones, M.: Discovering queries based on example tuples. In: SIGMOD (2014)
Ullmann, J.R.: An Algorithm for Subgraph Isomorphism. J ACM. 23(1), 31–42 (1976)
Vallet, D., Zaragoza, H.: Inferring the most important types of a query: a semantic approach. In: SIGIR, pp. 857–858 (2008)
Wang, X., Ding, X., Tung, A. K. H., Ying, S., Jin, H.: An efficient graph indexing method. In: ICDE, pp. 210–221 (2012)
Wang, X., Zhai, C.: Mining term association patterns from search logs for effective query reformulation. In: CIKM, pp. 479–488 (2008)
Xing, W., Ghorbani, A.: Weighted pagerank algorithm. In: CNSR, pp. 305–314 (2004)
Yan, X., Yu, P. S., Han, J.: Graph indexing: a frequent structure-based approach. In: SIGMOD (2004)
Yang, S., Wu, Y., Sun, H., Yan, X.: Schemaless and structureless graph querying. Proc. VLDB Endow. 7(7), 565 (2014)
Zhao, P., Han, J.: On graph query optimization in large networks. VLDB J. 3(1–2), 340–351 (2010)
Zloof, M. M.: Query by example. In: AFIPS NCC, pp. 431–438 (1975)
Acknowledgments
This work was partially supported by the Trento RISE Big Data Project [4] and the Keystone COST action IC1302. We would like to thank the authors of [10], NeMa [29] and strong simulation [32] for kindly providing us their code. We thank Paola Quaglia for the valuable discussion and suggestions about simulation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Y. Velegrakis was partially supported by the ERC grant Lucretius and the KEYSTONE Cost Action.
Rights and permissions
About this article
Cite this article
Mottin, D., Lissandrini, M., Velegrakis, Y. et al. Exemplar queries: a new way of searching. The VLDB Journal 25, 741–765 (2016). https://doi.org/10.1007/s00778-016-0429-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00778-016-0429-2








 , exists
, exists 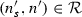 , and
, and , exists
, exists  .
. (line 8)
(line 8)

 , such that
, such that 















