Graph similarity search on large uncertain graph databases

Abstract

Many studies have been conducted on seeking an efficient solution for graph similarity search over certain (deterministic) graphs due to its wide application in many fields, including bioinformatics, social network analysis, and Resource Description Framework data management. All prior work assumes that the underlying data is deterministic. However, in reality, graphs are often noisy and uncertain due to various factors, such as errors in data extraction, inconsistencies in data integration, and for privacy-preserving purposes. Therefore, in this paper, we study similarity graph containment search on large uncertain graph databases. Similarity graph containment search consists of subgraph similarity search and supergraph similarity search. Different from previous works assuming that edges in an uncertain graph are independent of each other, we study uncertain graphs where edges’ occurrences are correlated. We formally prove that subgraph or supergraph similarity search over uncertain graphs is $\#$P-hard; thus, we employ a filter-and-verify framework to speed up these two queries. For the subgraph similarity query, in the filtering phase, we develop tight lower and upper bounds of subgraph similarity probability based on a probabilistic matrix index (PMI). PMI is composed of discriminative subgraph features associated with tight lower and upper bounds of subgraph isomorphism probability. Based on PMI, we can filter out a large number of uncertain graphs and maximize the pruning capability. During the verification phase, we develop an efficient sampling algorithm to validate the remaining candidates. For the supergraph similarity query, in the filtering phase, we propose two pruning algorithms, one lightweight and the other strong, based on maximal common subgraphs of query graph and data graph. We run the two pruning algorithms against a probabilistic index that consists of powerful graph features. In the verification, we design an approximate algorithm based on the Horvitz–Thompson estimator to fast validate the remaining candidates. The efficiencies of our proposed solutions to the subgraph and supergraph similarity search have been verified through extensive experiments on real uncertain graph datasets.

1 Introduction

Graphs have been used to model various data in a wide range of applications, such as bioinformatics, social network analysis, and Resource Description Framework (RDF) data management. Furthermore, in these real applications, due to noisy measurements, inference models, ambiguities of data integration, and privacy-preserving mechanisms, uncertainties are often introduced in the graph data. For example, in a protein–protein interaction (PPI) network, the pairwise interaction is derived from statistical models [5, 6, 23], and the STRING database (http://string-db.org) is such a public data source that contains PPIs with uncertain edges provided by statistical predictions. In a social network, probabilities can be assigned to edges to model the degree of influence or trust between two social entities [2, 17, 31]. In a RDF graph, uncertainties/inconsistencies are introduced in data integration where various data sources are integrated into RDF graphs [21, 30].

To model the uncertain graph data, a probabilistic graph model is introduced [21, 24, 30, 35, 58]. In this model, each edge is associated with an edge existence probability to quantify the likelihood that this edge exists in the graph, and edge probabilities are independent of each other. However, the proposed probabilistic graph model is invalid in many real scenarios. For example, for uncertain PPI networks, authors in [10, 36] first establish elementary interactions with probabilities between proteins, then use machine learning tools to predict other possible interactions based on the elementary links. The predictive results show that interactions are correlated, especially with high dependence of interactions at the same proteins. Given another example, in communication networks or road networks, an edge probability is used to quantify the reliability of a link [8] or the degree of traffic jam [19]. Obviously, there are correlations for the routing paths in these networks [19], i.e., a busy traffic path often blocking traffic in nearby paths. Therefore, it is necessary for a probabilistic graph model to consider correlations existing among edges or nodes.

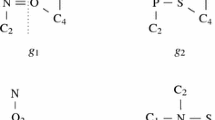
Clearly, it is unrealistic to model the joint distribution for the entire set of nodes in a large graph, i.e., road and social networks. Thus, in this paper, we introduce joint distributions for local nodes. For example, in graph 001 of Fig. 2, we give a joint distribution to measure interactions (neighbor edges¹) of the three nodes in a local neighborhood. The joint probability table (JPT) shows the joint distribution, and a probability in JPT (the second row) is given as $Pr(e_1=1,e_2=1,e_3=0)=0.2$, where “1” denotes existence while “0” denotes nonexistence. For larger graphs, we have multiple joint distributions of nodes in small neighborhoods (in fact, these are marginal distributions). In real applications, these marginal distributions can be easily obtained. For example, authors in [19] use sampling methods to estimate a traffic joint probability of nearby roads, and point out that the traffic joint probability follows a multi-gaussian distribution. For PPI networks, authors in [10, 36] establish marginal distributions using a Bayesian prediction.

In this paper, we study similarity graph containment search (i.e., subgraph similarity search and supergraph similarity search) over uncertain graphs due to the wide usage of similarity graph containment search in many application fields, such as answering SPARQL queries (graph) in RDF graph data [1, 21], predicting complex biological interactions (graphs) [10, 43], and identifying vehicle routings (graphs) in road networks [8, 19]. Below is a motivation example.

Motivation example In bioinformatics, interactions between proteins are modeled as a graph, namely a PPI network, where vertices represent proteins and edges represent interactions between proteins. Figure 1 shows a real PPI network of yeast in the STRING database [44]. A weight is assigned to each edge to represent the reliability of high-throughput protein interactions. In the STRING database, the reliability of PPIs is identified through experimental annotations in the Open Biological Ontology (OBO) [40]. Biologists use a subgraph query to discover a diseased yeast. To achieve this, the complex (subgraph) of a diseased yeast is used to match the PPI network of an examined yeast. If the matching is successful, the examined yeast very likely has such a disease. However, a query hardly has an exact match in a PPI network, due to the false positives generated in biological experiments [6, 23]. In Fig. 1, the subgraph query cannot find any exact match in the PPI network. Thus, a subgraph similarity search is more desirable. If we relax the edge ($a,c$) of the subgraph query, we can find an exact match ($a,b,c$) in the PPI network. On the contrary, the supergraph query is used to identify the properties that an unknown PPI network has. To achieve this, biologists use the unknown PPI network (supergraph) to match many small size of known PPI networks (a database). As a result, biologists can predict that the unknown PPI network has the properties of known PPI networks in the query answers. The supergraph similarity search is also crucial in querying PPI networks, e.g., the supergraph query contains the PPI network exactly only after the PPI network relaxes an edge ($d,e$).

Fig. 1

Motivation example of querying uncertain PPI networks

Fig. 2

Uncertain graph database and query graph

In biology analysis, we should consider not only the structural containment, but also the probabilistic information (reliability) provided by these real uncertain PPI networks. The probabilities of different edges can be treated as independent or correlated. Many approaches have shown that the protein interactions behave strong local correlations [6, 9]. For example, the clique ($b,d,e$) in the PPI network shows the local correlations. In the experiments, we show that more accurate PPI predictions can be obtained in the correlated data model than in the independent data model. Therefore, in this paper, we study similarity graph containment search over uncertain graphs with local correlations.

In the following, we provide the query semantics, our solutions, and contributions for probabilistic subgraph similarity search and probabilistic supergraph similarity search, respectively.

1.1 Probabilistic subgraph similarity matching

1.1.1 Query semantics

In this paper, we focus on threshold-based probabilistic subgraph similarity matching (T-PS) over a large set of uncertain graphs. Specifically, let $D=\{g_1,g_2,\ldots ,g_n\}$ be a set of uncertain graphs where edges’ existences are not independent, but are given explicitly by joint distributions, $q$ be a query graph, and $\epsilon$ be a probability threshold, and then, a T-PS query retrieves all graphs $g\in D$ such that the subgraph similarity probability (SUBP) between $q$ and $g$ is at least $\epsilon$. We will formally define SUBP later (Definition 9).

We employ the possible world semantics [13, 42], which have been widely used for modeling probabilistic databases, to explain the meaning of returned results for subgraph similarity search. A possible world graph (PWG) of an uncertain graph is a possible instance of the uncertain graph. It contains all vertices and a subset of edges of the uncertain graph, and it has a weight which is obtained by joining joint probability tables of all neighbor edges. Then, for a query graph $q$ and an uncertain graph $g$, the probability that $q$ subgraph similarly matches $g$ is the summation of the weights of those PWGs, of $g$, to which $q$ is subgraph similar. If $q$ is subgraph similar to a PWG $g'$, $g'$ must contain a subgraph of $q$, say $q'$, such that the difference between $q$ and $q'$ is less than the user-specified error tolerance threshold $\delta$. In other words, $q$ is subgraph isomorphic to $g'$ after $q$ is relaxed with $\delta$ edges.

Example 1

Consider graph 002 in Fig. 2, and edges are attached with labels, i.e., $a,b,c\ldots$ $JPT_1$ and $JPT_2$ give joint distributions of neighbor edges $\{e_1,e_2,e_3\}$ and $\{e_3,e_4,$ $e_5\}$, respectively. Figure 3 lists partial PWGs of uncertain graph 002 and their weights. The weight of PWG (1) is obtained by joining $t_1$ of $JPT_1$ and $t_2$ of $JPT_2$, i.e., $Pr(e_1=1,e_2=1,e_3=1,e_4=1,e_5=0)=Pr(e_1=1,e_2=1,e_3=1)\times Pr(e_3=1,e_4=1,e_5=0)=0.3\times 0.25=0.075$. Suppose the similarity threshold is 1. To decide if $q_1$ subgraph similarly matches uncertain graph 002, we first find all of 002’s PWGs that contain a subgraph whose difference to $q_1$ is less than 1. The results are PWGs (1), (2), (3), and (4), as shown in Fig. 3, since we can delete edge $a$, $b$ or $c$ of $q_1$. Next, we add up the probabilities of these PWGs: $0.075+0.045+0.075+0.045+\cdots =0.45$. If the query specifies a probability threshold of 0.4, then graph 002 is returned since $0.45 > 0.4$.

Fig. 3

Partial possible world graphs of uncertain graph 002

The above example gives a naive solution, to T-PS query processing, that needs to enumerate all PWGs of an uncertain graph. This solution is very inefficient due to the exponential number of PWGs. Therefore, in this paper, we propose a filter-and-verify method to reduce the search space.

1.1.2 Challenges and contributions

Given a set of uncertain graphs $D=\{g_1,\ldots ,g_n\}$ and a query graph $q$, our solution performs T-PS query processing in three steps, namely structural pruning, probabilistic pruning, and verification. In the structural pruning step, we conduct $q$ on each deterministic graph $g_i^c$, which removes uncertainty from $g_i$ ($g_i\in D$), and get a match candidate set $SC^q$. In the probabilistic pruning, we first obtain upper and lower bounds of SUBP via a pre-computed index. Next, we refine the set of candidates in $SC_q$, by pruning those potential uncertain graphs whose upper bound is smaller than $\epsilon$ or whose lower bound is larger than $\epsilon$. In the index, we compute frequent subgraph features $\{f\}$ and store the upper and lower bounds of the subgraph isomorphism probability (SIP) of $f$ to $g$. We calculate bounds of SUBP through the bounds of SIP. In the verification phase, we validate each candidate uncertain graph remaining after the previous steps to determine the final answer set. There exist several challenges in the above steps. In the following, we give the challenges and our solutions.

Challenge 1: Determine best bounds of SUBP

As we will see, there are many features satisfying pruning conditions; thus, we can obtain a large number of bounds of SUBP based on the bounds of SIP. In this paper, we convert the problem of computing the best upper bound into a set cover problem. Our contribution is to develop an efficient randomized algorithm to obtain the best lower bound using integer quadratic programming.

Challenge 2: Compute an effective index

An effective index should consist of tight upper and lower bounds whose values can be computed efficiently. As we will show later, calculating an SIP is $\#$P-hard, which increases the difficulty of computing an effective index. To address this challenge, we make a contribution to derive tight bounds of SIP by converting the problem of computing bounds into a maximum clique problem and propose an efficient solution by combining the properties of probability conditional independence and graph theory.

Challenge 3: Find the features that maximize pruning

Frequent subgraphs (mined from $D^c$) are commonly used as features in graph matching. However, it would be impractical to index all of them. Our goal is to maximize the pruning capability with a small number of features. To achieve this goal, we consider two criteria in selecting features, the size of the feature and the number of disjoint embeddings that a feature has. A feature of small size and many embeddings is preferred.

Challenge 4: Compute SUBP efficiently

Though we are able to filter out a large number of uncertain graphs, computing the exact SUBP in the verification phase may still take quite some time and become the bottleneck in query processing. To address this issue, we develop an efficient sampling algorithm, based on the Monte Carlo theory, to estimate SUBP with a high quality.

1.2 Probabilistic supergraph similarity matching

1.2.1 Query semantics

Similar to subgraph similarity matching, probabilistic supergraph similarity matching retrieves uncertain graphs $\{g\}$ from $D=\{g_1,g_2,\ldots ,g_n\}$ such that the supergraph similarity probability (SUPP) between $q$ and $g$ is at least $\epsilon$. For a query graph $q$ and an uncertain graph $g$, the value of SUPP is the summation of the weights of those possible worlds, of $g$, to which $q$ is supergraph similar. If $q$ is supergraph similar to a possible world $g'$, $q$ must contain a subgraph of $g$, say $q'$, such that the difference between $g$ and $q'$ is less than the user-specified distance threshold $\delta$. In other words, $g'$ is subgraph isomorphic to $q$ after $g'$ is relaxed with $\delta$ edges.

Example 2

Consider uncertain graph 001 and query $q_2$ in Fig. 2 and $001$’s possible worlds in Fig. 4. Assume the distance threshold is 1. To decide whether $q_2$ supergraph similarly matches uncertain graph 001, we first find all of 001’s PWGs $\{g'\}$ such that $q_2$ contains a subgraph $q_2'$ whose difference between $g'$ is less than 1. The results are PWGs (1), (2), (3), and (4), as shown in Fig. 4. Next, we add up the probabilities of these PWGs: $0.1+0.2+0.1+0.1=0.5$. If the query specifies a probability threshold of 0.6, then graph 001 is a false answer since $0.5 < 0.6$.

Fig. 4

Partial possible world graphs of uncertain graph 001

1.2.2 Challenges and contributions

We can also employ the filter-and-verify framework to answer the supergraph similarity query. However, compared with the subgraph similarity query, each step in the query processing of supergraph matching is more complex and difficult. For example, we may attempt to obtain a structural pruning condition for supergraph similarity matching by modifying the structural pruning condition for subgraph similarity matching as follows:

If $q$ is not supergraph similar to $g^c$, then the SUPP of $q$ to $g$ is 0.

However, this pruning condition does not work correctly for the supergraph similarity matching. For example, in Example 2, $q_2$ is not supergraph similar to $001^c$, but the SUPP is 0.5 which does not equal 0. The reason is as follows: Though $q$ is not supergraph similar to $g^c$, $q$ may be supergraph similar to a possible world $g'$ of $g$ ($g'$ is a subgraph of $g$). In this case, the SUPP of $q$ to $g$ is not 0 and the probabilities of such possible worlds should be summarized.

Also, the probabilistic pruning rules cannot be applied to supergraph similarity matching. To address these problems, we propose novel pruning and verification algorithms to answer the probabilistic supergraph similarity matching efficiently. We summarize the following contributions.

• 1. We propose a lightweight probabilistic pruning condition (graph feature based) that can quickly remove unqualified uncertain graphs. We prove a formula that calculates the exact value of SUPP. Based on the formula, we also give a strong pruning condition (graph feature based) that can filter out most unqualified uncertain graphs.

• 2. Frequent subgraphs are commonly used as features in graph matching. However, it would be impractical to index all of them. Our goal is to maximize the pruning capability with a small number of features. To achieve this goal, we start with frequent subgraphs as our features. We denote them as $F_0$. We devise a model to estimate query costs. Then, we select the best feature set $F\subset F_0$ that optimizes the cost model. We prove that solving the exact optimization problem is hard, and we propose a $c$-approximate approach. This enables us to derive an index of small size and powerful pruning capability.

• 3. We design a basic sampling algorithm to verify the candidates, so that we avoid the hard problem of computing SUPP. To speed up the basic algorithm, we propose an advanced sampling algorithm, based on unequal probability sampling techniques, that samples many possible worlds together during one sampling process.

• 4. We carry out extensive experiments on real uncertain graph data to evaluate the overall performance and the effectiveness of pruning and verification algorithms.

1.3 Paper organization

The remainder of this paper is organized as follows. We formally define the subgraph similarity query and the supergraph similarity query over uncertain graphs and give the complexity of the problems in Sect. 2. In Sect. 3, we give pruning and verifying algorithms for subgraph similarity query. In Sect. 4, we focus on developing algorithms for supergraph similarity query. We discuss the results of performance tests in Sect. 5 and the related work in Sect. 6. Finally, in Sect. 7, we draw our conclusions.

2 Problem definition and complexity

In this section, we define some necessary concepts and show the complexity of our problem. Table 1 summarizes the notations used in this paper.

Table 1 Notations

2.1 Problem definition

Definition 1

(Deterministic Graph) An undirected deterministic graph² $g^c$ is denoted as $(V, E,\Sigma ,L)$, where $V$ is a set of vertices, $E$ is a set of edges, $\Sigma$ is a set of labels, and $L:V\cup E\rightarrow \Sigma$ is a function that assigns labels to vertices and edges. A set of edges are neighbor edges, denoted by $ne$, if they are incident to the same vertex or the edges form a triangle in $g^c$.

For example, consider graph 001 in Fig. 2. Edges $e_1$, $e_2$, and $e_3$ are neighbor edges, since they form a triangle. Consider graph 002 in Fig. 2. Edges $e_3$, $e_4$, and $e_5$ are also neighbor edges, since they are incident to the same vertex.

Definition 2

(Uncertain Graph) An uncertain graph is defined as $g = (g^c, X_E)$, where $g^c$ is a deterministic graph and $X_E$ is a binary random variable set indexed by $E$. An element $x_e\in X_E$ takes values 0 or 1, and it denotes the existence possibility of edge $e$. A joint probability density function $Pr(x_{ne})$ is assigned to each neighbor edge set, where $x_{ne}$ denotes the assignments restricted to the random variables of a neighbor edge set, $ne$.

An uncertain graph has uncertain edges but deterministic vertices. The probability function $Pr(x_{ne})$ is given as a joint probability table of random variables of $ne$. For example, the uncertain graph 002 in Fig. 2 has two joint probability tables associated with two neighbor edge sets, respectively.

Definition 3

(Possible World Graph) A possible world graph $g' = (V' ,E',\Sigma ', L')$ is an instantiation of an uncertain graph $g = ((V, E, \Sigma , L), X_E)$, where $V'=V$, $E'\subseteq E$, $\Sigma '\subseteq \Sigma$. We denote the instantiation from $g$ to $g'$ as $g \Rightarrow g'$.

Both $g'$ and $g^c$ are deterministic graphs. But an uncertain graph $g$ corresponds to one $g^c$ and multiple PWGs. We use $PWG(g)$ to denote the set of all PWGs derived from $g$.

Definition 4

(Conditional Independence) Let $X$, $Y$, and $Z$ be sets of random variables. $X$ is conditionally independent of $Y$ given $Z$ (denoted by $X\perp Y|Z$) in distribution Pr if:

$$\begin{aligned} \begin{aligned} Pr(X = x;Y = y|Z = z)=Pr(X = x|Z = z)\\Pr(Y = y|Z = z) \end{aligned} \end{aligned}$$

for all values $x\in dom(X)$, $y\in dom(Y)$ and $z\in dom(Z)$.

Following real applications [10, 19, 21, 36], we assume that any two disjoint subsets of Boolean variables, $X_{A}$ and $X_B$ of $X_E$, are conditionally independent given a subset $X_C$ ($X_A\perp X_B|X_C$), if there is a path from a vertex in $A$ to a vertex in $B$ passing through $C$. Then, the probability of a possible world graph $g'$ is given by:

$$\begin{aligned} Pr(g\Rightarrow g')=\prod _{ne\in NS}Pr(x_{ne}) \end{aligned}$$

(1)

where $NS$ is all the sets of neighbor edges of $g$.

For example, in uncertain graph 002 of Fig. 2, $\{e_1,$ $e_2\}\perp \{e_4,e_5\}|e_3$. Clearly, for any possible world graph $g'$, we have $Pr(g\Rightarrow g')>0$ and $\sum _{g'\in PWG(g)}$ $Pr(g\Rightarrow g')=1$, that is, each PWG has an existence probability, and the sum of these probabilities is 1.

Definition 5

(Subgraph Isomorphism) Given two deterministic graphs $g_1= (V_1, E_1, \Sigma _1, L_1)$ and $g_2=( V_2, E_2, \Sigma _2,$ $L_2)$, we say $g_1$ is subgraph isomorphic to $g_2$ (denoted by $g_1\subseteq _{iso} g_2$), if and only if there is an injective function $f : V_1\rightarrow V_2$ such that:

• for any $(u,v)\in E_1$, there is an edge $(f(u),f(v))\in E_2$;

• for any $u\in V_1$, $L_1(u)= L_2(f(u))$;

• for any $(u,v)\in E_1$, $L_1(u,v)= L_2(f(u),f(v))$.

The subgraph $(V_3,E_3)$ of $g_2$ with $V_3=\{f(v)|v\in V_1\}$ and $E_3=\{(f(u),f(v))|(u,v)\in E_1\}$ is called the embedding of $g_1$ in $g_2$.

When $g_1$ is subgraph isomorphic to $g_2$, we also say that $g_1$ is a subgraph of $g_2$ and $g_2$ is a super-graph of $g_1$.

Definition 6

(Subgraph Isomorphism Probability) For a deterministic graph $f$ and an uncertain graph $g$, we define their subgraph isomorphism probability (SIP) as

$$\begin{aligned} Pr(f\subseteq _{iso} g)=\sum _{g'\in SUB(f,g)}Pr(g\Rightarrow g') \end{aligned}$$

(2)

where $SUB(f,g)$ is $g$’s possible worlds that are supergraphs of $f$, that is, $SUB(f,g)=\{g' \in PWG(g) | f\subseteq _{iso} g'\}$.

Definition 7

(Maximum Common Subgraph—MCS) Given two deterministic graphs $g_1$ and $g_2$, the maximum common subgraph of $g_1$ and $g_2$ is the largest subgraph of $g_2$ that is subgraph isomorphic to $g_1$, denoted by $mcs(g_1, g_2)$.

Definition 8

(Subgraph Distance) Given two deterministic graphs $g_1$ and $g_2$, the subgraph distance is $dis(g_1, g_2) = |g_1|-|mcs(g_1, g_2)|$. Here, $|g_1|$ and $|mcs(g_1, g_2)|$ denote the number of edges in $g_1$ and $mcs(g_1, g_2)$, respectively. For a distance threshold $\delta$, if $dis(g_1, g_2)\le \delta$, we call $g_1$ is subgraph similar to $g_2$ or $g_2$ is supergraph similar to $g_1$.

Note that, in this definition, subgraph distance only depends on the edge set difference, which is consistent with pervious works on similarity search over deterministic graphs [18, 39, 49]. The operations on an edge consist of edge deletion, relabeling, and insertion.

Definition 9

(Subgraph Similarity Probability) For a given query graph $q$, an uncertain graph $g$ ³, and a subgraph distance threshold $\delta$, we define their subgraph similarity probability as,

$$\begin{aligned} Pr(q\subseteq _{sim} g)=\sum _{g'\in SUB(q,g)}Pr(g\Rightarrow g') \end{aligned}$$

(3)

where $SUB(q,g)$ is $g$’s possible world graphs and $q$ has subgraph distance to each $g'\in SUB(q,g)$ no larger than $\delta$, that is, $SUB(q,g)=\{g' \in PWG(g$ $) |$ $dis(q,g')\le \delta \}$.

Probabilistic Subgraph Similarity Query Given a set of uncertain graphs $D=\{g_1,\ldots ,g_n\}$, a query graph $q$, and a probability threshold $\epsilon$ ($0 < \epsilon \le 1$), a subgraph similarity query returns a set of uncertain graphs $\{g|Pr(q\subseteq _{sim} g)\ge \epsilon , g\in D\}$.

Definition 10

(Supergraph Similarity Probability) For a given query graph $q$, an uncertain graph $g$, and a subgraph distance threshold $\delta$, we define their supergraph similarity probability as,

$$\begin{aligned} Pr(q\supseteq _{sim} g)=\sum _{g'\in SUP(q,g)}Pr(g\Rightarrow g') \end{aligned}$$

(4)

where $SUP(q,g)$ is $g$’s possible world graphs that have subgraph distance to $q$ no larger than $\delta$, that is, $SUP(q,g)=\{g' \in PWG(g$ $) |$ $dis(g',q)\le \delta \}$.

Probabilistic Supergraph Similarity Query Given a set of uncertain graphs $D=\{g_1,\ldots ,g_n\}$, a query graph $q$, and a probability threshold $\epsilon$ ($0 < \epsilon \le 1$), a supergraph similarity query returns a set of uncertain graphs $\{g|Pr(q\supseteq _{sim} g)\ge \epsilon , g\in D\}$.

2.2 Problem complexity

From the problem statement, we know that in order to answer a probabilistic subgraph or supergraph similarity query efficiently, we need to calculate the subgraph similarity probability (SUBP) or supergraph similarity probability (SUPP) efficiently. We now show the time complexities of calculating SUBP and SUPP.

Theorem 1

It is $\#$P-hard to calculate the subgraph similarity probability.

Proof Sketch

Here, we just highlight the major steps here. We consider a probabilistic graph whose edge probabilities are independent from each other. This probabilistic graph model is a special case of the probabilistic graph defined in Definition 2. We prove the theorem by reducing an arbitrary instance of the $\#$P-complete DNF counting problem [16] to an instance of the problem of computing $Pr(q\subseteq _{sim}g)$ in polynomial time. Figure 5 illustrates an reduction for the DNF formula $F=(y_1\wedge y_2)\vee (y_1\wedge y_2\wedge y_3)\vee (y_2\wedge y_3)$. In the figure, the graph distance between $q$ and each possible world graph $g'$ is 1 (delete vertex $w$ from $q$). Each truth assignment to the variables in $F$ corresponds to a possible world graph $g'$ derived from $g$. The probability of each truth assignment equals to the probability of $g'$ that the truth assignment corresponds to. A truth assignment satisfies $F$ if and only if $g'$, the truth assignment corresponds to, is subgraph similar to $q$ (suppose graph distance is 1). Thus, $Pr(F)$ is equal to the probability, $Pr(q\subseteq _{sim} g)$. $\square$

Similarly, we obtain the time complexity of calculating SUPP as follows.

Fig. 5

The uncertain graph $g$ and query graph $q$ constructed for $(y_1\wedge y_2)\vee (y_1\wedge y_2\wedge y_3)\vee (y_2\wedge y_3)$

Theorem 2

It is $\#$P-hard to calculate the supergraph similarity probability.

3 Probabilistic subgraph similarity query processing

3.1 Framework of our approach

3.1.1 Structural pruning

The idea of structural pruning is straightforward. If we remove all the uncertainty in an uncertain graph, and $q$ is still not subgraph similar to the resulting graph, then $q$ cannot subgraph similarly match the original uncertain graph.

Formally, for $g\in D$, let $g^c$ denote the corresponding deterministic graph after we remove all the uncertain information from $g$. We have

Theorem 3

If $q\nsubseteq _{sim} g^c$, $Pr(q\subseteq _{sim} g)=0$.

Based on this observation, given $D$ and $q$, we can prune the database $D^c=\{g_1^c,\ldots ,g_n^c\}$ using conventional deterministic graph similar matching methods. In this paper, we adopt the method in [49] to quickly compute results. [49] uses a multi-filter composition strategy to prune large number of graphs directly without performing pairwise similarity computation, which makes [49] more efficient compared to other graph similarity search algorithms [18, 54]. Assume the result is $SC_q^c=\{g^c|q\subseteq _{sim} g^c,g^c\in D^c \}$. Then, its corresponding uncertain graph set, $SC_q=\{g|g^c\in SC_q^c\}$, is the input for uncertain subgraph similarity matching in the next step.

3.1.2 Probabilistic pruning

To further prune the results, we propose a probabilistic matrix index (PMI) that will be introduced later, for probabilistic pruning. For a given set of uncertain graphs $D$ and its corresponding set of deterministic graphs $D^c$, we create a feature set $F$ from $D^c$, where each feature is a deterministic graph, i.e., $F \subset D^c$. In PMI, for each $g\in SC_q$, we can locate a set $D_{g}=\{\langle LowerB(f_j), UpperB(f_j)\rangle |f_j\subseteq _{iso} g^c, 1\le j\le$ $|F|\}$ where $LowerB(f)$ and $UpperB(f)$ are the lower and upper bounds of the subgraph isomorphism probability of $f$ to $g$ (Definition 6). If $f$ is not subgraph isomorphic to $g^c$, we have $\langle 0\rangle$.

In the probabilistic filtering, we first determine the remaining graphs after $q$ is relaxed with $\delta$ edges, where $\delta$ is the subgraph distance threshold. Suppose the remaining graphs are $\{rq_1,\ldots ,rq_i,\ldots , rq_a\}$. For each $rq_i$, we compute two features $f_i^1$ and $f_i^2$ in $D_g$ such that $rq_i\supseteq _{iso} f_i^1$ and $rq_i\subseteq _{iso} f_i^2$. Then, we can calculate upper and lower bounds of $Pr(q\subseteq _{sim}g)$ based on the values of $UpperB(f_i^1)$ and $LowerB(f_i^2)$ for $1\le i\le a$, respectively. If the upper bound of $Pr(q\subseteq _{sim}g)$ is smaller than probability threshold $\epsilon$, $g$ is pruned. If the lower bound of $Pr(q\subseteq _{sim}g)$ is not smaller than $\epsilon$, $g$ is in the final answers.

3.1.3 Verification

In this step, we calculate $Pr(q\subseteq _{sim} g)$ for query $q$ and candidate answer $g$, after probabilistic pruning, to make sure $g$ is really an answer, i.e., $Pr(q\subseteq _{sim} g)\ge \epsilon$.

3.2 Probabilistic pruning

As mentioned in the last subsection, we first conduct structural pruning to remove uncertain graphs that do not approximately contain the query graph $q$, and then, we use probabilistic pruning techniques to further filter the remaining uncertain graph set, named $SC_q$.

3.2.1 Pruning conditions

We first introduce an index structure, PMI, to facilitate probabilistic filtering. Each column of the matrix corresponds to an uncertain graph in the database $D$, and each row corresponds to an indexed feature. Each entry records $\{LowerB(f),UpperB(f)\}$, where $UpperB(f)$ and $LowerB(f)$ are the upper and lower bounds of the subgraph isomorphism probability of $f$ to $g$, respectively.

Example 3

Figure 6 shows the PMI of uncertain graphs in Fig. 2. Note that the upper or lower bounds in PMI are derived from the methods proposed in Sect. 3.3.

Fig. 6

Probabilistic matrix index (PMI) and features of uncertain graph database in Fig. 2

Given a query $q$, an uncertain graph $g$, and subgraph distance $\delta$, we generate a graph set, $U=\{rq_1,\ldots ,rq_a\}$, by relaxing $q$ with $\delta$ edge deletions or relabelings.⁴ Here, we use the solution proposed in [49] to generate $\{rq_1,\ldots ,rq_a\}$. Suppose, we have built the PMI. For each $g\in SC_q$, in PMI, we locate

$$\begin{aligned} D_{g}=\{\langle LowerB(f_j), UpperB(f_j)\rangle |f_j\subseteq _{iso} g^c,\quad 1\le j\le |F|\} \end{aligned}$$

For each $rq_i$, we find two graph features in $D_{g}$, $\{f_i^1,f_i^2\}$, such that $rq_i\supseteq _{iso} f_i^1$ and $rq_i\subseteq _{iso} f_i^2$, where $1\le i \le a$. Then, we have probabilistic pruning conditions as follows.

• Sub-Pruning 1 Given a probability threshold $\epsilon$ and $D_{g}$, if $\sum _{i=1}^a UpperB(f_i^1)<\epsilon$, then $g$ can be safely pruned from $SC_q$.

• Sub-Pruning 2 Given a probability threshold $\epsilon$ and $D_{g}$, if $\sum _{i=1}^a LowerB(f_i^2)-\sum _{1\le i,j\le a}UpperB(f_i^2)UpperB(f_j^2)$ $\ge \epsilon$, then $g$ is in the final answers, i.e., $g\in A_q$, where $A_q$ is the final answer set.

Before proving the correctness of the above two pruning conditions, we first introduce a lemma about $Pr(q\subseteq _{sim} g)$, which will be used for the proof. Let $Brq_i$ be a Boolean variable where $1\le i\le a$, $Brq_i$ is true when $rq_i$ is subgraph isomorphic to $g^c$, and $Pr(Brq_i)$ is the probability that $Brq_i$ is true. We have

Lemma 1

$$\begin{aligned} Pr(q\subseteq _{sim} g)=Pr(Brq_1\vee \cdots \vee Brq_a). \end{aligned}$$

(5)

Proof Sketch

From Definition 9, we have

$$\begin{aligned} Pr(q\subseteq _{sim} g)=\sum _{g'\in SIM(q,g)}Pr(g\Rightarrow g') \end{aligned}$$

(6)

where $SMI(q,g)$ is a set of PWGs that have subgraph distance to $q$ no larger than $\delta$. Let $d$ be the subgraph distance between $q$ and $g^c$. We divide $SIM(q,g)$ into $\delta -d+1$ subsets,⁵ $\{SM_0,\ldots ,SM_{\delta -d}\}$, such that a PWG in $SM_i$ has subgraph distance $d+i$ with $q$. Thus, from Eq. 6, we get

$$\begin{aligned}&Pr(q\subseteq _{iso} g)=\sum _{g'\in SM_1\cup \cdots \cup SM_{\delta -d}}Pr(g\Rightarrow g')\nonumber \\&\quad =\sum _{0\le j_1\le \delta -d}\sum _{g'\in SM_{j_1}}Pr(g\Rightarrow g')\nonumber \\&\qquad -\sum _{0\le j_1<j_2\le \delta -d}\sum _{g'\in SM_{j_1}\cap SM_{j_2}}Pr(g\Rightarrow g')+\cdots \nonumber \\&\qquad + (-1)^{i}\sum _{0\le j_1<\cdots < j_i\le \delta -d}\sum _{g'\in SM_{j_1}\cap \cdots \cap SM_{j_i}} Pr(g\Rightarrow g')\nonumber \\&\qquad +\cdots + (-1)^{\delta -d}\sum _{g'\in SM_{j_1}\cap \cdots \cap SM_{j_{\delta -d}}} Pr(g\Rightarrow g'). \end{aligned}$$

(7)

Let $L_i$, $0\le i\le \delta -d$, be the graph set after $q$ is relaxed with $d+i$ edges and $BL_i$ be a Boolean variable, when $BL_i$ is true, it indicates at least one graph in $L_i$ is a subgraph of $g^c$. Consider the $i$th item on the RHS in Eq. 7, let $A$ be the set composed of all graphs in $i$ graph sets, and $B=BL_{j_1}\wedge \cdots \wedge BL_{j_i}$ be the corresponding Boolean variable of $A$. The set $g'\in SM_{j_1}\cap \cdots \cap SM_{j_i}$ contains all PWGs that have all graphs in $A$. Then, for the $i$th item, we get,

$$\begin{aligned} \begin{aligned}&(-1)^{i}\sum _{0\le j_1<\cdots < j_i\le \delta -d}\sum _{g'\in SM_{j_1}\cap \cdots \cap SM_{j_i}}Pr(g\Rightarrow g')\\&\quad =(-1)^{i}\sum _{0\le j_1<\cdots < j_i\le \delta -d}Pr(BL_{j_1}\wedge \cdots \wedge BL_{j_i}). \end{aligned} \end{aligned}$$

(8)

Similarly, we can get the results for other items. By replacing the corresponding items with these results in Eq. 7, we get

$$\begin{aligned}&Pr(q\subseteq _{iso} g)=\sum _{0\le j_1\le \delta -d}Pr(BL_j)\nonumber \\&\quad - \sum _{0\le j_1<j_2\le \delta -d}Pr(BL_{j_1}\wedge BL_{j_2})+\cdots \nonumber \\&\quad + (-1)^{i}\sum _{0\le j_1<\cdots < j_i\le \delta -d}Pr(BL_{j_1}\wedge \cdots \wedge BL_{j_i})+\cdots \nonumber \\&\quad + (-1)^{\delta -d}Pr(BL_{j_1}\wedge \cdots \wedge BL_{j_{\delta -d}}). \end{aligned}$$

(9)

Based on the inclusion–exclusion principle [33], the RHS of Eq. 9 is $Pr(BL_0\vee \cdots \vee BL_{\delta -d})$. Clearly, $BL_0\subseteq \cdots \subseteq BL_{\delta -d}$, then

$$\begin{aligned}&Pr(BL_0\vee \cdots \vee BL_{\delta -d})=Pr(BL_{\delta -d})\\&\quad =Pr(Brq_1\vee \cdots \vee Brq_a) \end{aligned}$$

$\square$

Lemma 1 gives a method to compute SUBP. Intuitively, the probability of $q$ being subgraph similar to $g$ equals the probability that at least one graph of the graph set $U=\{rq_1,\ldots ,rq_a\}$ is a subgraph of $g$, where $U$ is the remaining graph set after $q$ is relaxed with $\delta$ edges. With Lemma 1, we can formally prove the two pruning conditions.

Theorem 4

Given a probability threshold $\epsilon$ and $D_{g}$, if $\sum _{i=1}^a$ $UpperB(f_i^1)<\epsilon$, then $g$ can be safely pruned from $SC_q$.

Proof Sketch

Since $rq_i\supseteq _{iso} f_i^1$, we have $Brq_1\vee \cdots \vee Brq_a\subseteq Bf_1^1\vee \cdots \vee Bf_{a}^1$, where $Bf_i^1$ is a Boolean variable denoting the probability of $f_i^1$ being a subgraph of $g$ for $1\le i\le a$. Based on Lemma 1, we obtain

$$\begin{aligned} \begin{aligned} Pr(q\subseteq _{sim} g)&=Pr(Brq_1\vee \cdots \vee Brq_{a})\\&\le Pr\left( Bf_1^1\vee \cdots \vee Bf_{a}^1\right) \\&\le Pr\left( Bf_1^1\right) +\cdots +Pr\left( Bf_a^1\right) \\&\le UpperB(f_1^1)+\cdots +UpperB\left( f_a^1\right) \!<\!\epsilon . \end{aligned} \end{aligned}$$

Then, $g$ can be pruned. $\square$

Theorem 5

Given a probability threshold $\epsilon$ and $D_{g}$, if $\sum _{i=1}^a L$-$owerB(f_i^2)-\sum _{1\le i,j\le a}UpperB(f_i^2)UpperB(f_j^2)\ge \epsilon$, then $g\in A_q$, where $A_q$ is the final answer set.

Proof Sketch

Since $\vee _{i=1}^a Brq_i\supseteq \vee _{i=1}^a Bf_i^2$, we can show that

$$\begin{aligned} \begin{aligned} Pr(q\subseteq _{sim} g)&=Pr(Brq_1\vee \cdots \vee Brq_{a})\\&\ge Pr\left( Bf_1^2\vee \cdots \vee Bf_{a}^2\right) \\&\ge \sum _{i=1}^a Pr\left( Bf_i^2\right) -\sum _{1\le i,j\le a}Pr\left( Bf_i^2\right) \\&\quad Pr\left( Bf_j^2\right) \ge \sum _{i=1}^a LowerB(f_i^2)\\&\quad -\sum _{1\le i,j\le a}UpperB(f_i^2)UpperB(f_j^2)\\&\ge \epsilon . \end{aligned} \end{aligned}$$

Then, $g\in A_q$. $\square$

Note that the pruning process needs to address the traditional subgraph isomorphism problem ($rq\subseteq _{iso} f$ or $rq\supseteq _{iso} f$). In our work, we implement the state-of-the-art method VF2 [12].

3.2.2 Obtain tightest bounds of subgraph similarity probability

In pruning conditions, for each $rq_i$ ($1\le i\le a$), we find only one pair of features $\{f_i^1,f_i^2\}$, among $|F|$ features, such that $rq_i\supseteq _{iso} f_i^1$ and $rq_i\subseteq _{iso} f_i^2$. Then, we compute the upper bound, $U_{sim}(q)=\sum _{i=1}^a UpperB(f_i^1)$ and the lower bound $L_{sim}(q)=\sum _{i=1}^a LowerB(f_i^2)-\sum _{1\le i,j\le a}UpperB(f_i^2)$ $UpperB(f_j^2)$. However, there are many $f_i^1$s and $f_i^2$s satisfying conditions among $F$ features, therefore, we can compute a large number of $U_{sim}(q)$s and $L_{sim}(q)$s. For each $rq_i$, if we find $x$ features meeting the needs among $|F|$ features, we can derive $x^a$ $U_{sim}(q)$s. Let $x=10$ and $a=10$, then there are $10^{10}$ upper bounds. The same holds for $L_{sim}(q)$. Clearly, it is unrealistic to determine the best bounds by enumerating all the possible ones; thus, in this section, we give efficient algorithms to obtain the tightest $U_{sim}(q)$ and $L_{sim}(q)$.

Obtain Tightest $U_{sim}(q)$

For each $f_j$ ($1\le j\le |F|$) in PMI, we determine a graph set, $s_j$, that is a subset of $U=\{rq_1,\ldots ,rq_a\}$, such that $rq_i\in s_j$ s.t. $rq_i\supseteq _{iso} f_j$. We also associate $s_j$ with a weight, $UpperB(f_j)$. Then, we obtain $|F|$ sets $\{s_1,\ldots ,s_{|F|}\}$ with each set having a weight $w(s_j)=UpperB(f_j)$ for $1\le j\le |F|$. With this mapping, we transform the problem of computing the tightest $U_{sim}(q)$ into a weighted set cover problem defined as follows.

Definition 11

(Tightest $U_{sim}(q)$) Given a finite set $U=\{rq_1,$ $\ldots ,rq_a\}$ and a collection $S=\{s_1,\ldots ,s_j,\ldots ,s_{|F|}\}$ of subsets of $U$ with each $s_j$ attached a weight $w_{s_j}$, we compute a subset $C\subseteq S$ to minimize $\sum _{s_j\in C}w(s_j)$ s.t. $\bigcup _{s_j\in C}s_j$ $=U$.

It is well known that the set cover problem is NP-complete [16]; hence, we use a greedy approach to approximate the tightest $U_{sim}(q)$. Algorithm 1 gives detailed steps. Assume the optimal value is OPT, the approximate value is within $OPT\cdot ln|U|$ [14].

Example 4

In Fig. 2, suppose we use $q_1$ to query uncertain graph 002, and the subgraph distance is 1. The relaxed graph set of $q$ is $U=\{rq_1,rq_2,rq_3\}$ as shown in Fig. 7. Given indexed features $\{f_1,f_2,f_3\}$, we first determine $s_1=\{rq_1,rq_2\}$, $s_2=\{rq_2,rq_3\}$, and $s_3=\{rq_1,rq_3\}$. We use the $UpperB(f_j)$, $1\le j\le 3$, as weight for three sets, and thus, we have $w(s_1)=0.4$, $w(s_2)=0.1$ and $w(s_3)=0.5$. Based on Definition 11, we obtain three $U_{sim}(q)$s, which are 0.4+0.1=0.5, 0.4+0.5=0.9, and 0.1+0.5=0.6. Finally, the smallest (tightest) value, 0.5, is used as the upper bound, i.e., $U_{sim}(q)=0.5$.

Fig. 7

Obtain tightest $U_{sim}(q)$

Obtain Tightest $L_{sim}(q)$

For lower bound $L_{sim}(q)$, the larger (tighter) $L_{sim}(q)$ is, the better the probabilistic pruning power is. Here, we formalize the problem of computing the largest $L_{sim}(q)$ as an integer quadratic programming problem and develop an efficient randomized algorithm to solve it.

For each $f_i$ ($1\le i\le |F|$) in PMI, we determine a graph set, $s_i$, that is a subset of $U=\{rq_1,\ldots ,rq_a\}$, such that $rq_j\in s_i$ s.t. $rq_j\subseteq _{iso} f_i$. We associate $s_i$ with a pair weight of $\{LowerB(f_i), Upper$ $B(f_i)\}$. Then, we obtain $|F|$ sets $\{s_1,\ldots ,s_{|F|}\}$ with each set having a pair weight $\{w_L(s_i),w_U$ $(s_i)\}$ for $1\le i\le |F|$. Thus, the problem of computing tightest $L_{sim}(q)$ can be formalized as follows.

Definition 12

(Tightest $L_{sim}(q)$) Given a finite set $U=\{rq_1, \ldots ,rq_a\}$ and a collection $S=\{s_1,\ldots ,s_{|F|}\}$ of subsets of $U$ with each $s_i$ attached a pair weight $\{w_L(s_i),w_U(s_i)\}$, we compute a subsect $C\subseteq \{s_1,\ldots ,s_{|F|}\}$ to maximize

$$\begin{aligned}&\sum _{s_i\in C}w_L(s_i)-\sum _{s_i,s_j\in C} w_U(s_i)w_U(s_j)\\&\quad \hbox {s.t. }\bigcup _{s_i\in C}s_i=U. \end{aligned}$$

Associate an indicator variable, $x_{s_i}$, with each set $s_i\in S$, which takes value 1 if set $s_i$ is selected, and 0 otherwise. Then, we want to:

$$\begin{aligned} \begin{aligned} \hbox {Maximize }&\sum _{s_i\in C}x_{s_i}w_L(s_i)-\sum _{s_i,s_j\in C}x_{s_i}x_{s_j}w_U(s_i)w_U(s_j)\\ \quad \hbox {s.t. }&\sum _{rq\in s_i}x_{s_i}\ge 1 ~~~\forall rq\in U,\\&x_s \in \{0, 1\}. \end{aligned} \end{aligned}$$

(10)

Equation 10 is an integer quadratic programming problem which is a hard problem [16]. We relax $x_{s_i}$ to take values within $[0,1]$, i.e., $x_{s_i} \in [0, 1]$. Then, the equation becomes a standard quadratic programming (QP) problem. Clearly, this QP is convex, and there is an efficient solution to solve the programming [28]. Since all feasible solutions for Eq. 10 are also feasible solutions for the relaxed quadratic programming, the maximum value $QP(I)$ computed by the relaxed QP provides an upper bound for the value computed in Eq. 10. Thus, the value of $QP(I)$ can be used as the tightest lower bound. However, the proposed relaxation technique cannot give any theoretical guarantee on how tight $QP(I)$ is to Eq. 10 [14].

Now following the relaxed QP, we propose a randomized rounding algorithm that yields an approximation bound for Eq. 10. Algorithm 2 shows the detailed steps. According to Eq. 10, it is not difficult to see that the more elements in $U$ are covered, the tighter $L_{sim}(q)$ is. The following theorem states that the number of covered elements of $U$ has a theoretical guarantee.

Theorem 6

When Algorithm 2 terminates, the probability that all elements are covered is at least $1-\frac{1}{|U|}$.

Proof Sketch

For an element $rq\in U$, the probability of $rq$ is not covered in an iteration is

$$\begin{aligned} \prod _{rq\in s}\left( 1-x_s^*\right) \le \prod _{rq\in s}e^{-x_s^*}\le e^{-\sum _{rq\in s}x_s^*}\le \frac{1}{e}. \end{aligned}$$

Then, the probability that $rq$ is not covered at the end of the algorithm is at most $e^{-2log|U|}\le \frac{1}{|U|^2}$. Thus, the probability that there is some $rq$ that is not covered is at most $|U|\cdot 1/|U|^2= 1/|U|.$ $\square$

Example 5

In Fig. 2, suppose we use $q_1$ to query uncertain graph 002, and the subgraph distance is 1. The relaxed graph set of $q$ is $U=\{rq_1,rq_2,rq_3\}$ shown in Fig. 8. Given indexed features $\{f_1,f_2\}$, we first determine $s_1=\{rq_1\}$ and $s_2=\{rq_1,rq_2,rq_3\}$. Then, we use $\{LowerB(f_i),$ $UpperB(f_i)\}$, $1\le i\le 2$, as weights, and thus, we have $\{w_L(s_1)=0.28, w_U(s_1)=0.36\}$, $\{w_L(s_2)=0.08, w_U(s_2)$ $=0.15\}$. Based on Definition 12, we assign $L_{sim}(q)=0.31$.

Fig. 8

Obtain tightest $L_{sim}(q)$

3.3 Probabilistic matrix index

In this section, we discuss how to obtain tight $\{LowerB(f),$ $UpperB(f)\}$ and generate features used in the PMI.

3.3.1 Bounds of subgraph isomorphism probability

LowerB(f)

Let $Ef=\{f_1,\ldots ,f_{|Ef|}\}$ be the set of all embeddings⁶ of feature $f$ in the deterministic graph $g^c$, $Bf_i$ be a Boolean variable for $1\le i\le |Ef|$, which indicates whether $f_i$ exists in $g^c$ or not, and $Pr(Bf_i)$ be the probability that the embedding $f_i$ exists in $g$. Similar to Lemma 1, we have

$$\begin{aligned} Pr(f\subseteq _{iso} g)=Pr(Bf_1\vee \cdots \vee Bf_{|Ef|}). \end{aligned}$$

(11)

According to Theorem 1, it is not difficult to see that calculating the exact $Pr(f\subseteq _{iso} g)$ is NP-complete. Thus, we rewrite Eq. 11 as follows

$$\begin{aligned} \begin{aligned} Pr(f\subseteq _{iso} g)&=Pr(Bf_1\vee \cdots \vee Bf_{|Ef|})\\&=1-Pr(\overline{Bf_1}\wedge \cdots \wedge \overline{Bf_{|Ef|}})\\&\ge 1-Pr(\overline{Bf_1}\wedge \cdots \wedge \overline{Bf_{|IN|}}\mid \\&\overline{Bf_{|IN|+1}}\wedge \cdots \wedge \overline{Bf_{|Ef|}}) . \end{aligned} \end{aligned}$$

(12)

where $IN=\{Bf_{1},\ldots ,Bf_{|IN|}\}\subseteq Ef$.

Let the corresponding embeddings of $Bf_{i}$, $1\le i\le |IN|$, not have common parts (edges). Since $g^c$ is connected, these $|IN|$ Boolean variables are conditionally independent given any random variable of $g$. Then, Eq. 12 is written as

$$\begin{aligned}&Pr(f\subseteq _{iso} g)\\&\quad \ge 1-Pr\left( \overline{Bf_1}\wedge \cdots \wedge \overline{Bf_{|IN|}}\mid \overline{Bf_{|IN|+1}}\wedge \cdots \wedge \overline{Bf_{|Ef|}}\right) \nonumber \\&\quad =1-\prod _{i=1}^{|IN|}\left[ 1-Pr\left( Bf_i\mid \overline{Bf_{|IN|+1}}\wedge \cdots \wedge \overline{Bf_{|Ef|}}\right) \right] .\nonumber \end{aligned}$$

(13)

For variables $Bf_x, Bf_y\in \{Bf_{|IN|+1},\ldots , Bf_{|Ef|}\}$, we have

$$\begin{aligned} Pr(Bf_i|Bf_x\wedge Bf_y)&= \frac{Pr(Bf_i\wedge Bf_x\wedge Bf_y)}{Pr(Bf_x\wedge Bf_y)}\nonumber \\&= \frac{Pr(Bf_i\wedge Bf_x\wedge Bf_y)/Pr(Bf_y)}{Pr(Bf_x\wedge Bf_y)/Pr(Bf_y)}\nonumber \\&= \frac{Pr(Bf_i\wedge Bf_x|Bf_y)}{Pr(Bf_x|Bf_y)}. \end{aligned}$$

(14)

If $Bf_i$ and $Bf_x$ are conditionally independent given $Bf_y$, then

$$\begin{aligned} Pr(Bf_i\wedge Bf_x|Bf_y)=Pr(Bf_i|Bf_y)Pr(Bf_x|Bf_y). \end{aligned}$$

(15)

By combining Eqs. 14 and 15, we obtain

$$\begin{aligned} Pr(Bf_i| Bf_x\wedge Bf_y)=Pr(Bf_i|Bf_y). \end{aligned}$$

(16)

Based on this property, Eq. 14 is reduced to

$$\begin{aligned} \begin{aligned} Pr(f\subseteq _{iso} g)&\ge 1\!-\prod _{i\!=1}^{|IN|}\left[ 1\!-\!Pr\left( Bf_i\mid \overline{Bf_{|IN|+1}}\wedge \cdots \wedge \overline{Bf_{|Ef|}}\right) \right] \\&=1-\prod _{i=1}^{|IN|}\left[ 1-Pr\left( Bf_i\mid \overline{Bf_{1}}\wedge \cdots \wedge \overline{Bf_{|C|}}\right) \right] \\&=1-\prod _{i=1}^{|IN|}[1-Pr(Bf_i|COR)] \end{aligned} \end{aligned}$$

(17)

where $COR=\overline{Bf_{1}}\wedge \cdots \wedge \overline{Bf_{|C|}}$, and the corresponding embedding of $Bf_j\in C=\{Bf_1,\ldots ,Bf_{|C|}\}$ overlaps with the corresponding embedding of $Bf_i$.

For a given $Bf_i$, $Pr(Bf_i|COR)$ is a constant, since the number of embeddings overlapping with $f_i$ in $g^c$ is constant. Now, we obtain the lower bound of $Pr(f\subseteq _{iso} g)$ as

$$\begin{aligned} LowerB(f)=1-\prod _{i=1}^{|IN|}[1-Pr(Bf_i|COR)], \end{aligned}$$

(18)

which is only dependent on the selected $|IN|$ embeddings that do not have common parts with each other.

To compute $Pr(Bf_i|COR)$, a straightforward approach is the following. We first join all the joint probability tables (JPT) and, meanwhile, multiply joint probabilities of joining tuples in JPTs. Then, in the join result, we project on edge labels involved in $Bf_i$ and $COR$, and eliminate duplicates by summing up their existence probabilities. The summarization is the final result. However, this solution is clearly time inefficient for the sake of join, duplicate elimination, and probability multiplication.

In order to calculate $Pr(Bf_i|COR)$ efficiently, we use a sampling algorithm to estimate its value. Algorithm 3 shows the detailed steps. The main idea of the algorithm is as follows. We first sample a possible world $g'$. Then, we check the condition, in Line 4, that is used to estimate $Pr(Bf_i \wedge COR)$, and the condition, in Line 7, that is used to estimate $Pr(COR)$. Finally, we return $n_1/n_2$ which is an estimation of $Pr(Bf_i \wedge COR)/Pr(COR)=Pr(Bf_i|COR)$. The cycling number $m$ is set to $(4ln\frac{2}{\xi })/\tau ^2$ ($0<\xi <1$, $\tau >0$) used in Monte Carlo theory [33].

Example 6

In Fig. 6, consider $f_2$, a feature of uncertain graph 002 shown in Fig. 2. $f_2$ has three embeddings in 002, namely $EM1$, $EM2$, and $EM3$ as shown in Fig. 9. In corresponding $Bf_i$s, $Bf_1$, and $Bf_3$ are conditionally independent given $Bf_2$. Then, based on Eq. 18, we have $LowerB(f)=1-[1-Pr(Bf_1|\overline{Bf_2})][1-Pr(Bf_3|\overline{Bf_2})]=0.26$.

Fig. 9

Embeddings and $fG$ of feature $f_2$ in the uncertain graph 002

As stated early, $LowerB(f)$ depends on embeddings that do not have common parts. However, among all $|Ef|$ embeddings, there are many groups which contain disjoint embeddings and lead to different lower bounds. We want to get a tight lower bound in order to increase the pruning power. Next, we introduce how to obtain the tightest $LowerB(f)$.

Obtain tightest lower bound We construct an undirected graph, $fG$, with each node representing an embedding $f_i$, $1\le i\le |Ef|$, and a link connecting two disjoint embeddings (nodes). Note that, to avoid confusions, nodes and links are used for $fG$, while vertices and edges are for graphs. We also assign each node a weight, $-\ln [1-Pr(Bf_i|COR)]$. In $fG$, a clique is a set of nodes such that any two nodes of the set are adjacent. We define the weight of a clique as the sum of node weights in the clique. Clearly, given a clique in $fG$ with weight $v$, $LowerB(f)$ is $1-e^{-v}$. Thus, the larger the weight, the tighter (larger) the lower bound. To obtain a tight lower bound, we should find a clique whose weight is largest, which is exactly the maximum weight clique problem. Here, we use the efficient solution in [7] to solve the maximum clique problem, and the algorithm returns the largest weight $z$. Therefore, we use $1-e^{-z}$ as the tightest value for $LowerB(f)$.

Example 7

Following Example 6, as shown in Fig. 9, $EM1$ is disjoint with $EM3$. Based on the above discussion, we construct $fG$, for the three embeddings, shown in Fig. 9. There are two maximum cliques, namely $\{EM1, EM3\}$ and $EM2$. According to Eq. 18, the lower bounds derived from the two maximum cliques are 0.26 and 0.11, respectively. Therefore, we select the larger (tighter) value 0.26 to be the lower bound of $f_2$ in 002.

UpperB(f)

Firstly, we define Embedding Cut: For a feature $f$, an embedding cut is a set of edges in $g^c$ whose removal will cause the absence of all $f$’s embeddings in $g^c$. An embedding cut is minimal if no proper subset of the embedding cut is an embedding cut. In this paper, we use minimal embedding cut.

Denote an embedding cut by $c$ and its corresponding Boolean variable (same as $Bf$) by $Bc$, where $Bc$ is true indicating that the embedding cut $c$ exists in $g^c$. Similar to Eq. 11, it is not difficult to obtain,

$$\begin{aligned} \begin{aligned} Pr(f\subseteq _{iso} g)&=1-Pr(Bc_1\vee \cdots \vee Bc_{|Ec|})\\&=Pr(\overline{Bc_1}\wedge \cdots \wedge \overline{Bc_{|Ec|}}) \end{aligned} \end{aligned}$$

(19)

where $Ec=\{c_1,\ldots ,c_{|Ec|}\}$ is the set of all embedding cuts of $f$ in $g^c$. Equation 19 shows that the subgraph isomorphism probability of $f$ to $g$ equals the probability of all $f$’s embedding cuts disappearing in $g$.

Similar to the deduction from Eq. 11 to 18 for $Lower$ $B(f)$, we can rewrite Eq. 19 as follows

$$\begin{aligned} \begin{aligned}&Pr(f\subseteq _{iso} g)=Pr\left( \overline{Bc_1}\wedge \cdots \wedge \overline{Bc_{|Ec|}}\right) \\&\quad \le Pr\left( \overline{Bc_1}\wedge \cdots \wedge \overline{Bc_{|IN'|}}|\overline{Bc_{|IN'|+1}}\wedge \cdots \wedge \overline{Bc_{|Ec|}}\right) \\&\quad =\prod _{i=1}^{|IN'|}\left[ 1-Pr\left( Bc_i|\overline{Bc_{|IN'|+1}}\wedge \cdots \wedge \overline{Bc_{|Ec|}}\right) \right] \\&\quad =\prod _{i=1}^{|IN'|}\left[ 1-Pr\left( Bc_i|\overline{Bc_{1}}\wedge \cdots \wedge \overline{Bc_{|D|}}\right) \right] \\&\quad =\prod _{i=1}^{|IN'|}[1-Pr(Bc_i|COM)] \end{aligned} \end{aligned}$$

(20)

where $IN'=\{Bc_1,\ldots ,Bc_{|IN'|}\}$ is a set of Boolean variables whose corresponding cuts are disjoint, $COM=\overline{Bc_{1}}\wedge \cdots \wedge \overline{Bc_{|D|}}$, and the corresponding cut of $Bc_{j}\in D=\{Bc_1,\ldots , Bc_{|D|}\}$ has common parts with the corresponding cut of $Bc_i$.

Finally, we obtain the upper bound as

$$\begin{aligned} UpperB(f)=\prod _{i=1}^{|IN'|}[1-Pr(Bc_i|COM)]. \end{aligned}$$

(21)

The upper bound only relies on the picked embedding cut set in which any two cuts are disjoint.

The value of $Pr(Bc_i|COM)$ is estimated using Algorithm 3 by replacing embeddings with cuts. Similar to the lower bound, computing the tightest $UpperB(f)$ can be converted into a maximum weight clique problem. However, different from the lower bound, each node of the constructed graph $fG$ represents a cut and has a weight of $-ln[1-Pr(Bc_i|COM)]$ instead. Thus, for the maximum weight clique with weight $v$, the tightest value of $UpperB(f)$ is $e^{-v}$.

Now, we discuss how to determine embedding cuts in $g^c$.

Calculation of embedding cuts We build a connection between embedding cuts in $g^c$ and cuts for two vertices in a deterministic graph.

Suppose $f$ has $|Ef|$ embeddings in $g^c$, and each embedding has $k$ edges. Assign $k$ labels, $\{e_1,\ldots ,e_k\}$, for edges of each embedding (the order is random.). We create a corresponding line graph for each embedding by (1) creating $k+1$ isolated nodes, and (2) connecting these $k+1$ nodes to be a line by associating $k$ edges (with corresponding labels) of the embedding. Based on these line graphs, we construct a parallel graph, $cG$. The node set of $cG$ consists of all nodes of the $|Ef|$ line graphs and two new nodes, $s$ and $t$. The edge set of $cG$ consists of all edges (with labels) of the $|Ef|$ line graphs. In addition, one edge (without label) is placed between an end node of each line graph and $s$. Similarly, there is an edge between $t$ and the other end node of each line graph. As a result, $|Ef|$ embeddings are transformed into a deterministic graph $cG$.

Based on this transformation, we have

Theorem 7

The embedding cut set of $g^c$ is also the cut set (without edges incident to $s$ and $t$) from $s$ to $t$ in $cG$.

In this work, we determine embedding cuts using the method in [25].

Example 8

Figure 10 shows the transformation for feature $f_2$ in graph 002 in Fig. 2. In $cG$, we can find cuts $\{e_2,e_4\}$, $\{e_1,e_3,$ $e_4\}$, and $\{e_2,e_3\}$ which are clearly the embedding cuts of $f_2$ in 002.

Fig. 10

Transformation from embeddings of $f_2$ to parallel graph $cG$

3.3.2 Feature generation

We would like to select frequent and discriminative features to construct a PMI.

To achieve this, we consider $UpperB(f)$ given in Eq. 21, since the upper bound plays a most important role in the pruning capability. According to Eq. 21, to get a tight upper bound, we need a large disjoint cut set and a large $Pr(Bc_i|COM)$. Suppose the cut set is $IN''$. Note that $|IN''|=|IN'|$, since a cut in $IN''$ has a corresponding Boolean variable $Bc_i$ in $IN'$. From the calculation of embedding cuts, it is not difficult to see that a large number of disjoint embeddings leads to a large $|IN''|$. Thus, we would like a feature that has a large number of disjoint embeddings. Since $|COM|$ is small, a small size feature results in a large $Pr(Bc_i|COM)$. In summary, we should index a feature, which complies with following rules:

• Rule 1 Select features that have a large number of disjoint embeddings.

• Rule 2 Select small size features.

To achieve rule 1, we define the frequency of feature $f$ as $frq(f)$ $=\frac{|\{g|f\subseteq _{iso} g^c, |IN|/|Ef|\ge \alpha , g\in D \}|}{|D|}$, where $\alpha$ is a threshold of the ratio of disjoint embeddings among all embeddings. Given a frequency threshold $\beta$, a feature $f$ is frequent iff $frq(f)\ge \beta$. Thus, we would like to index a frequent feature. To achieve rule 2, we control a feature size used in Algorithm 4. To control feature number [38, 48], we also define the discriminative measure as: $dis(f)=|\bigcap \{D_{f'}|$ $f'\subseteq _{iso} f\}|/|D_f|$, where $D_f$ is the list of uncertain graphs $g$ s.t. $f\subseteq _{iso} g^c$. Given a discriminative threshold $\gamma$, a feature $f$ is discriminative, iff $dis(f)>\gamma$. Thus, we should also select a discriminative feature.

Based on the above discussion, we select frequent and discriminative features, which is implemented in Algorithm 4. In this algorithm, we first initial a feature set $F$ with single edge or vertex (lines 1–4). Then, we increase feature size (number of vertices) from 1, and pick out desirable features (lines 6–9). $maxL$ is used to control the feature size, and guarantees picking out a small size feature satisfying rule 2. $frq(f)$ and $dis(f)$ are used to measure the frequency and discrimination of feature. The controlling parameters $\alpha$, $\beta$, and $\gamma$ guarantee picking out a feature satisfying rule 1. The default values of the parameters are usually set to 0.1 [48, 49].

3.4 Verification

In this section, we present the algorithms to compute subgraph similarity probability (SUBP) of a candidate uncertain graph $g$ to $q$.

Equation 5 is the formula to compute SUBP. By simplifying this equation, we have

$$\begin{aligned} Pr(q\subseteq _{sim} g)\!=\!\sum _{i=1}^{a}(\!-1)^{i}\sum _{J\subseteq \{1,\ldots ,a\},|J|\!=\!i}Pr\left( \wedge _{j=1}^{|J|}Brq_j\right) .\nonumber \\ \end{aligned}$$

(22)

Clearly, we need an exponential number of steps to perform the exact calculation. Therefore, we develop an efficient sampling algorithm to estimate $Pr(q\subseteq _{sim}g)$.

By Eq. 5, we know there are totally $a$ $Brq$s that are used to compute SUBP. By Eq. 11, we know $Brq=Bf_1\vee \cdots \vee Bf_{|Ef|}$. Then, we have

$$\begin{aligned} Pr(q\subseteq _{sim}g)=Pr(Bf_1\vee \cdots \vee Bf_m) \end{aligned}$$

(23)

where $m$ is the number of $Bf$s contained in these $a$ $Brq$s.

Assume $m$ $Bf$s have $x_1,\ldots ,x_k$ Boolean variables for uncertain edges. Algorithm 5 gives detailed steps of the sampling algorithm. In this algorithm, we use a junction tree algorithm to calculate $Pr(Bf_i)$ [20].

4 Probabilistic supergraph similarity query processing

4.1 Compared to subgraph similarity search

In subgraph similarity search, we propose to effectively filter uncertain data graphs (i.e., prune false answers and validate true answers) without computing subgraph similarity probability. Specifically, we give structural and probabilistic pruning rules to filter out uncertain graphs. However, these pruning rules have no indication on $Pr(q\supseteq _{sim} g)$.

We first examine the structural pruning rule: If $q\nsupseteq _{sim} g^c$, $Pr(q\supseteq _{sim} g)=0$. This rule does not work correctly for probabilistic supergraph similarity search. Below is an example.

Example 9

We examine the uncertain graph $001$ and the query graph $q_2$ with $\delta =1$ shown in Fig. 2. $q_2\nsupseteq _{sim} 001^c$, since any resulting graph (deleting one edge from $001^c$) is not subgraph isomorphic to $q_2$. But $Pr(q\supseteq _{sim} g)\ne 0$. To see this, Fig. 4 gives PWGs and $q_2$ is supergraph similar to these PWGs [i.e., (1), (2), (3), and (4)]. We summarize the probabilities of these PWGs and get $Pr(q\supseteq _{sim} g)=0.5$.

We next examine the probabilistic pruning rule. Given a query $q$ and a distance threshold $\delta$, we generate a graph set, $U=\{rq_1,\ldots ,rq_a\}$, by relaxing $q$ with $\delta$ edges. For each $rq_i$, we find a graph feature $f_i$ such that $rq_i\supseteq _{iso} f_i$, where $1\le i \le a$. Then, we have: If $\sum _{i=1}^a UpperB(f_i^1)<\epsilon$, $Pr(q\supseteq _{sim} g)<\epsilon$.

This rule is not correct for the probabilistic supergraph search either. Below is an example.

Example 10

Figure 11 shows a graph set $U=\{rq_1,rq_2,rq_3\}$ with $q_2$ (in Fig. 2) relaxed by one edge.⁷ Figure 11 also gives graph features $f_i$ (mined from graph $001^c$) such that $rq_i\supseteq _{iso} f_i$ for $1\le i\le 3$. Suppose $\epsilon =0.4$, we compute $\sum _{i=1}^3 Upper$ $B(f_i)=0.13+0.13+0.13=0.39<\epsilon$. However, against the pruning condition $Pr(q\supseteq _{sim} g)<\epsilon$, $g$ is a true answer ($Pr(q\supseteq _{sim} g)=0.5>\epsilon$). The same conclusion can also be drawn for the validating rule, i.e., $Pr(q\supseteq _{sim} g)\ge LowerBound>\epsilon$.

Fig. 11

Invalid probabilistic pruning rules for supergraph similarity query

We conclude that probabilistic supergraph similarity matching are inherently different from the subgraph similarity matching. Novel filtering and verification techniques are required for probabilistic supergraph similarity query processing.

4.2 Lightweight filtering techniques

In this section, we propose a feature-based probabilistic pruning condition that is easy to implement and can filter out false uncertain graphs quickly. Next, we give a feature generation algorithm that can pick out powerful graph features.

4.2.1 Pruning rules

Theorem 8

Given an uncertain graph $g$, a query $q$, and a graph feature $f$ of $g^c$, suppose that $f\nsubseteq _{sim} q$. Then, $Pr(q\supseteq _{sim} g)\le 1-Pr(f\subseteq _{sim} g)$.

Proof Sketch

Let $A$ denote the set of PWGs $g'$ of $g$ such that $g'\subseteq _{sim} q$, and $B$ denote the set of PWGs $g'$ of $g$ such that $f\subseteq _{sim} g'$. Since $g'\subseteq _{sim} q$ and $f\nsubseteq _{sim} q$, $f\nsubseteq _{sim} g'$ and $A=\{g'|g'\subseteq _{sim} q, f\nsubseteq _{sim} g'\}$. Then $A\subseteq PWG(g)-B$, and we have:

$$\begin{aligned} \begin{aligned} Pr(q\supseteq _{sim} g)&=\sum _{g'\in A}Pr(g')\\&\le \sum _{g'\in PWG(g')}Pr(g')-\sum _{g'\in B}Pr(g')\\&= 1-Pr(f\subseteq _{sim} g) ~~~~~~~~ \end{aligned} \end{aligned}$$

(24)

$\square$

If we use the Inequality in 24 as a pruning rule, we should calculate $Pr(q\subseteq _{sim} g)$ efficiently. However, according to Theorem 1, it is NP-hard to calculate $Pr(f\subseteq _{sim} g)$. To solve the problem, we incorporate the lower bound of $Pr(f\subseteq _{sim} g)$ given in Theorem 5 into Inequality 24. Then, we have the following probabilistic pruning rule.

• Super-Pruning 1 Given an uncertain graph $g$, a query $q$, a threshold $\epsilon$, and a graph feature $f$ such that $f\nsubseteq _{sim} q$, if $Pr(q\supseteq _{sim} g)\le 1-Pr(f\subseteq _{sim} g)\le 1-\sum _{i=1}^a LowerB(f_i^2)$ $+\sum _{1\le i,j\le a}UpperB(f_i^2)UpperB(f_j^2)<\epsilon$, then $g$ can be safely pruned from the database $D$.

To strength the pruning condition, we can use Algorithm 2 to obtain the tightest upper bound for $Pr(f\subseteq _{sim} g).$

Regarding Super-Pruning 1, we obtain the corresponding deterministic graph database $D^c$ from uncertain graph database $D$, and then, we mine a set of discriminative frequent subgraphs $F$ from $D^c$ using the technique in [48]. The feature-based index $I=\{(f,D_f)|f \in F \}$ consists of the features in $F$ and their corresponding invited list $D_f$, where $D_f$ is represented as follows.

$$\begin{aligned} D_f=\{\langle g,UpperB(Pr(q\subseteq _{sim} g))\rangle |g\in D, f\subseteq g^c)\} \end{aligned}$$

(25)

where $UpperB(Pr(q\subseteq _{sim} g))=1-\sum _{i=1}^a LowerB(f_i^2) +\sum _{1\le i,j\le a}UpperB(f_i^2)UpperB(f_j^2)$

4.2.2 Feature generation

The feature-based index $I$ consists of frequent subgraphs $F$ from $D^c$. However, there might exist thousands or millions of features, and it would be unrealistic to index all of them. Thus, our goal is to maximize the pruning capability of $I$ with a small number of indexed features. Motivated by machine learning methods for query processing [37, 41], in this section, we employ a model, which uses a query log as the training data, to select features offline. Based on the model, we develop an optimal selection mechanism to remove useless features so that $I$ can have a great pruning capability.

Let $C_q$ be the candidate set after probabilistic pruning.

The naive solution $SCAN$, to the supergraph similarity search problem examines the database $D$ sequentially and computes SUPP for each uncertain graph to decide whether its SUPP is not smaller than $\epsilon$. For a query $q$, we define the gain, $J$, of indexing a graph feature set $F$ as the number of SUPP computations that can be saved from $SCAN$:

$$\begin{aligned} \begin{aligned} J&=|D|-|C_q|\\&=|\cup _{q\doteq CND}\{g|g\in D\}| \end{aligned} \end{aligned}$$

(26)

where $CND\triangleq UpperB<\epsilon$.

To obtain more effective features, we use a set of queries $\{q_1, q_2,\ldots ,q_a\}$ instead of a single query. In this case, an optimal index should maximize the total gain

$$\begin{aligned} J_{total} =\sum _{l=1}^{a}|\cup _{q_l\doteq CND}\{g|g\in D\}| \end{aligned}$$

(27)

which is the summation of the gain in Eq. 26 over all queries.

We map the problem of maximizing Eq. 27 to the maximum coverage as follows.

Definition 13

(Feature Generation) Given a set of supergraph queries $Q=\{q_1,\ldots ,q_a\}$ and its corresponding set of uncertain graph databases $\{D_1,\ldots ,D_a\}$, we relate a feature $f$ in the frequent subgraph set $F_0=\{f_1,\ldots ,f_b\}$ to a set of uncertain graphs $G_f=\{g|f\subseteq _{iso}g, g\in D_i for 1\le i\le a\}$, if the uncertain graph $g$ (indexed by $f$) is pruned in the probabilistic pruning (i.e., $CND$). We want to select $F\subset F_0$ such that $|\cup _{f\in F}G_f|$ is maximized.

The transformation shows that maximizing $|\cup _{f\in F}G_f|$ means maximizing $J_{total}$. Usually, there is a memory constraint that avoids a very large index. To implement this, we set a fixed $K$ and choose the best $K$ features. In practice, we can set $K$ according to the space capacity of the system. To solve the maximum coverage problem, we set integer variables $x_i=1$ iff $f_i$ is selected in $F_0$ and $y_j=1$ iff $g_j$ in $G_f$ is covered. Then, the optimal feature selection is an integer program:

$$\begin{aligned}&\hbox {Maximize } \sum _{j=1}^{a}y_j\\&\quad \hbox {s.t. } \sum _{i=1}^{b}x_{i}\le K, \quad y_j \le \sum _{\{i|g_j\in G_{f_i}\}}x_i,\quad x_i, y_j\in \{0, 1\}\nonumber \end{aligned}$$

(28)

Although the integer program gives an optimal solution to the problem, it is impractical to compute the exact solution as it is NP-complete [16]. We transform the integer program to linear program by relaxing the constraints to be $0<x_i,y_j\le 1$. We can efficiently solve the linear program [11] and get a solution $(x^*,y^*)$, where $0<x^*,y^*\le 1$. Next, we select each $f_i\in F_0$ independently with probability $x_i^*$. Let $OPT$ be the maximum value returned by the integer program, then the relaxed technique will return the approximation given by $(1-1/e)$ $OPT$ [14].

4.3 Strong filtering techniques

The filtering technique given in Super-Pruning 1 can remove false uncertain graphs efficiently. But we do not know how close the upper bound in Pruning 1 comes to the true value. In other words, we do not know how effective the pruning power is. Thus, in this section, we prove a formula that can calculate the true value of SUPP. Next, we give a strong pruning condition derived from the formula.

We first define maximal common subgraph. When two graphs have subgraphs that are isomorphic, then these subgraphs are called common subgraphs. A maximal common subgraph (MCS) is a common subgraph which has the maximal number of edges, in other words, if $s$ is a common subgraph of graphs $h_1$ and $h_2$, and there is no other common subgraph which has more edges than $s$, then $s$ is a maximal common subgraph of $h_1$ and $h_2$. Note that two graphs may have many MCSs. For example, Fig. 12 shows two graphs $g$ and $q$, and Fig. 13 gives four MCSs between $g$ and $q$.

Fig. 12

Uncertain graph and supergraph query

Fig. 13

Maximal common subgraphs between $g$ and $q$ in Fig. 12

Next, for a MCS $MG$ between $q$ and $g^c$, we define a Boolean variable $Bmg$. $Bmg$ is true if $MG$ appears in the graph $g^c$, and $Pr(Bmg)$ is the probability that $Bmg$ is true. Let $w$ be the number of all MCSs between $q$ and $g^c$. For SUPP, we have

Lemma 2

$$\begin{aligned} Pr(q\supseteq _{sim} g)=Pr(Bmg_1\vee Bmg_2\vee \cdots \vee Bmg_w) \end{aligned}$$

(29)

Proof Sketch

From Definition 10, we have

$$\begin{aligned} Pr(q\supseteq _{sim} g)=\sum _{g'\in SUP(q,g)}Pr(g\Rightarrow g') \end{aligned}$$

(30)

where $SUP(q,g)$ is a set of PWGs that are subgraph similar to $q$. We divide $SUP(q,g)$ into $|E(g)|+1$ subsets, $\{SM_0,\ldots ,SM_{|E(g)|}\}$.

Thus, from Eq. 30, we get

$$\begin{aligned} \begin{aligned}&Pr(q\supseteq _{sim} g)=\sum _{g'\in SM_0\cup \cdots \cup SM_{|E(g)|}}Pr(g\Rightarrow g')\\&\quad =\sum _{0\le j_1\le |E(g)|}\sum _{g'\in SM_{j_0}}Pr(g\Rightarrow g')\\&\quad \quad -\sum _{0\le j_1<j_2\le |E(g)|}\sum _{g'\in SM_{j_1}\cap SM_{j_2}}Pr(g\Rightarrow g')+\cdots \\&\quad \quad +(-1)^{i}\sum _{0\le j_1<\cdots < j_i\le |E(g)|}\\&\quad \quad \sum _{g'\in SM_{j_1}\cap \cdots \cap SM_{j_i}}Pr(g\Rightarrow g')+\cdots \\&\quad \quad + (-1)^{|E(g)|}\sum _{g'\in SM_{j_1}\cap \cdots \cap SM_{j_{|E(g)|}}} Pr(g\Rightarrow g'). \end{aligned} \end{aligned}$$

(31)

We denote $A$ be a subgraph of $g^c$, composed of $i$ MCS, and $B=Bmg_{j_1}\wedge \cdots \wedge Bmg_{j_i}$ be the corresponding Boolean variable of $A$. Note that a PWG $g'$ in $SM_0$ is subgraph similar to $q$. Thus, $A$ is a MCS of $q$ and $g'$. Then, the set $g'\in SM_{j_0}\cap \cdots \cap SM_{j_i}$ contains all PWGs that have all graphs in $A$. In other words, these PWGs are subgraph similar to $q$. Then, for the $i$th item, we get,

$$\begin{aligned} \begin{aligned}&(-1)^{i}\sum _{0\le j_1<\cdots < j_i\le |E(g)|}\sum _{g'\in SM_{j_1}\cap \cdots \cap SM_{j_i}}Pr(g\Rightarrow g')\\&\quad =(-1)^{i}\sum _{0\le j_1<\cdots < j_i\le |E(g)|}Pr(Bmg_{j_1}\wedge \cdots \wedge Bmg_{j_i}). \end{aligned} \end{aligned}$$

(32)

Similarly, we can get the results for other items. By replacing the corresponding items with these results in Eq. 31, we get

$$\begin{aligned}&Pr(q\supseteq _{sim} g)=\sum _{0\le j_1\le |E(g)|}Pr(Bmg_j)\nonumber \\&\quad - \sum _{0\le j_1<j_2\le |E(g)|}Pr(Bmg_{j_1}\wedge Bmg_{j_2})+\cdots \nonumber \\&\quad + (-1)^{i}\sum _{0\le j_1<\cdots < j_i\le |E(g)|}Pr(Bmg_{j_1}\wedge \cdots \wedge Bmg_{j_i})\nonumber \\&\quad +\cdots + (-1)^{|E(g)|}Pr(Bmg_{j_1}\wedge \cdots \wedge Bmg_{j_{|E(g)|}}). \end{aligned}$$

(33)

Based on the inclusion–exclusion Principle [33], the RHS of Eq. 33 is $Pr(Bmg_0\vee \cdots \vee Bmg_{|E(g)|})$.

The PWGs of $g$ that have fewer edges may be subgraph similar to $q$, though $g^c$ is not subgraph similar to $q$. Thus, the MCS $MG_i$ may not appear in $g^c$, in other words, $Bmg_i$ may be false. Recall that $w$ is the total number of MCSs. Then, we have $Bmg_0\vee \cdots \vee Bmg_{|E(g)|}=Bmg_1\vee \cdots \vee Bmg_{|w|}$. From the above equation, we can obtain the conclusion. $\square$

Lemma 2 gives a method to compute SUPP. The intuition is as follows: For the uncertain supergraph matching, each possible graph $g'$ of $g$ relaxes a distance threshold into a set of graphs $g''$, and then, $g''$ subgraph matches query $q$. Note that both $g''$ and $g'$ are subgraphs of $g$. A result of $g''$ subgraph matches $q$, say $r$, is a subgraph of $q$. Thus, $r$ is a MCS of $q$ and $g'$. If all possible graphs of $g$ conduct the above process, we obtain all MCSs between $q$ and $g$. Therefore, the probability of $q$ being supergraph similar to $g$ equals the probability that at least one MCS between $q$ and $g^c$ appears in $g$. Figure 12 shows an uncertain graph $g$ and a query $q$. The four MCSs shown in Fig. 13 contribute to SUPP, i.e., $Pr(q\supseteq _{sim} g)=Pr(MCS_1\vee MCS_2 \vee MCS_3 \vee MCS_4)$.

Lemma 2 indicates a major difference between calculating SUBP and SUPP. We give an example to illustrate this. For SUBP, if $q$ is not subgraph similar to $g^c$, the value of SUBP is 0 (in this case, $q$ is not subgraph similar to any PWG of $g$). In contrast to SUPP, if $q$ is not supergraph similar to $g^c$, the value of SUPP may be larger than 0 (In this case, many PWGs of $g$ may be subgraph similar to $q$). In fact, the MCSs between $q$ and $g$ contribute to SUPP in the case of $q\nsupseteq _{sim} g^c$. The example also shows that the value of SUPP is usually large. In conclusion, MCS leads to difficulties of computing SUPP.

Based on Lemma 2, we obtain the following pruning rules in analogy to subgraph similarity search.

Given a query $q$, an uncertain graph $g$ and a distance threshold $\delta$, we generate the MCS set, $U=\{MG_1,\ldots ,MG_a\}$ between $q$ and $g^c$. Here, we use the solution proposed in [26] to generate $\{MG_1$ $,\ldots ,MG_a\}$. We also use the index, PMI, for subgraph similarity search (Sect. 3.3). Then for each $g\in D$, in PMI, we locate $D_{g}=\{\langle LowerB(f_j), UpperB(f_j)\rangle$ $|f_j\subseteq _{iso} g^c, 1\le j\le |F|\}$. For each $MG_i$, we find two graph features in $D_{g}$, $\{f_i^1,f_i^2\}$, such that $MG_i\supseteq _{iso} f_i^1$ and $MG_i\subseteq _{iso} f_i^2$, where $1\le i \le a$. Then, we have novel pruning conditions as follows.

• Super-Pruning 2 Given a probability threshold $\epsilon$ and $D_{g}$, if $\sum _{i=1}^a UpperB(f_i^1)<\epsilon$, then $g$ can be pruned from $D$.

• Super-Pruning 3 Given a probability threshold $\epsilon$ and $D_{g}$, if $\sum _{i=1}^a LowerB(f_i^2)-\sum _{1\le i,j\le a}U$ $pperB(f_i^2)UpperB(f_j^2)$ $\ge \epsilon$, then $g$ is in the final answers, i.e., $g\in A_q$, where $A_q$ is the final answer set.

To strengthen the two pruning rules, we use the techniques in Sect. 3.3 to obtain tight $UpperB(f)$ and $Lower$-$B(f)$.

To obtain effective features for Super-Pruning 2 and 3, we extend the feature generation algorithm for Super-Pruning 1. In Super-Pruning 1, one graph feature is used to prune an uncertain graph, but in Super-Pruning 2 and 3, a set of graph features is used to filter out an uncertain graph. Therefore, in Definition 13, we can use a set of features instead of one feature to obtain the new feature generation algorithm.

Definition 14

(Sets of Features Generation) Given a set of supergraph queries $Q=\{q_1,\ldots ,q_a\}$ and its corresponding set of uncertain graph databases $\{D_1,\ldots ,D_a\}$, we relate a set of features $F'=\{f_1,\ldots ,f_a\}\subset F_0=\{f_1,\ldots ,f_b\}$ to a set of uncertain graphs $G_{F'}$, if the uncertain graph $g\in G_F'$ is pruned in the probabilistic pruning (i.e., Super-Pruning 2 and 3). We want to select a collection $C$ of subsets of $F_0$ such that $|\cup _{F'\in C}G_{F'}|$ is maximized.

We use the solution to Eq. 29 to compute $C$. Finally, we obtain graph features: $\bigcup _{F'\in C} F'$.

4.4 Verification

In this section, we present the algorithms to compute $Pr(q\supseteq _{sim} g)$ for each $g\in C_q$. Then, we can obtain the query answers, i.e., $A_q=\{g|Pr(q\supseteq _{sim} g)\ge \epsilon \}$. As shown in Theorem 2, calculating SUPP is a #P-hard problem, so we use sampling methods to get an approximate result.

4.4.1 Basic sampling

In this subsection, we give a basic sampling algorithm based on Monte Carlo theory.

During the sampling process, we sample $N$ possible world graphs, $g_1$, $g_2$, $\dots$, $g_N$, according to $Pr(x_{ne})$ of each neighbor edge set. Then, on each sampled possible world graph $g_i$, we check whether $q$ is supergraph similar to $g_i$. We set a flag $y_{i}$ for each $g_i$, so that

$$\begin{aligned} y_{i}=\left\{ \begin{array}{ll} 1 &{} \quad \mathrm{if}\, q\, \text {is supergraph similar to}\, g_i\\ 0 &{} \quad \mathrm{otherwise} \end{array} \right. \end{aligned}$$

Thus, the estimator $\widehat{\theta }$ equals to,

$$\begin{aligned} \widehat{\theta }=\widehat{Pr\left( q\supseteq _{sim} g\right) }=\frac{\sum _{i=1}^N y_{i}}{N} \end{aligned}$$

(34)

For any sampling method, the Mean Square Error (MSE) incorporates both bias and precision of an estimator $\widehat{\theta }$ into a measure of overall accuracy. It is calculated as,

$$\begin{aligned} MSE(\widehat{\theta })=E[(\widehat{\theta }-\theta )^2]=Var(\widehat{\theta })+Bias(\widehat{\theta },\theta ) \end{aligned}$$

The bias of an estimator is given by,

$$\begin{aligned} Bias(\widehat{\theta })=E(\widehat{\theta })-\theta . \end{aligned}$$

An estimator of $\theta$ is unbiased if its bias is $0$ for all values of $\theta$, that is, $E(\widehat{\theta })=\theta$. As the estimator of Monte Carlo method is unbiased [15], thus,

$$\begin{aligned} MSE(\widehat{\theta }) = Var(\widehat{\theta }) =\frac{1}{N}\theta (1-\theta )\approx \frac{1}{N}\widehat{\theta }(1-\widehat{\theta }) \end{aligned}$$

(35)

where $\theta =Pr(q\supseteq _{sim} g)$.

4.4.2 Advanced sampling

In the basic sampling, we should increase the value of $N$ if we want to guarantee an accurate answer. But as a consequence, the calculation will take a long time. To solve the problem, in this subsection, we propose an advanced sampling algorithm that can obtain an accurate answer efficiently.

The main idea of the advanced sampling is to sample a lot of PWGs together in one sampling. Thus we can reduce $N$ compared with the basic sampling. Below, we use an example to show the idea.

Example 11

Figure 12 shows an uncertain graph $g$ and a query $q$ with distance threshold $\delta =1$. Figure 14 shows five PWG that are subgraph similar to $q$. These PWGs contain the graph $e_1e_2$ or its subgraphs $e_1$ and $e_2$. The graph $e_1e_2$ is a MCS between $q$ and $g^c$. According to Lemma 2, the MCS $e_1e_2$ contributes to the SUPP of $q$ to $g$. In the advanced sampling, we apply the MCS detection algorithm to sample edges $e_1e_2$, and the 5 PWGs are totally the PWGs that contain $e_1e_2$ or its subgraphs $e_1$ and $e_2$. Thus, our advanced sampling algorithm only needs one sampling process that samples all these 5 PWGs together. But in the basic sampling algorithm, it takes 5 times to sample them. In other words, sampling once in the advanced algorithm has the same effect with sampling 5 times in the basic algorithm. Thus, by together sampling the PWGs containing the same MCS, the advanced sampling algorithm can effectively reduce the sample size $N$.

Fig. 14

Advantage of advanced sampling method

As indicated in the above example, the main idea of our advanced sampling algorithm is to sample the edges at the same time with the process of the MCS detection algorithm. The pseudocode is shown in Algorithm 6. In the algorithm, we first sample the current neighbor edges and then run the MCS detection algorithm McsAlgo [26] along with the existent edges after the sampling. We finish one sampling process when McsAlgo detects one MCS.

After describing the algorithm, let us see how to estimate SUPP (Line 10). Here, we cannot use the estimator $\sum _{i=1}^N y_i/N$ in the basic sampling. The reason is as follows: $\sum _{i=1}^N y_i/N$ requires that two different sampling results are independent [15], but there are dependencies between different sampling results in Algorithm 6.

Taking this into consideration, we resort to Unequal Probability Sampling, since it allows for any dependence between different samples [29]. Unequal probability sampling is that some units in the population have probabilities of being selected from others. Suppose a sample of size $N$ is selected randomly from a population $S$ but that on each draw, unit $i$ is sampled according to any probability $q_i$, where $\sum _{i=1}^{S}q_i=1$ [29].

We apply the Horvitz–Thompson (H–T) estimator in unequal probability sampling method, since the H–T estimator is a general estimator, which can be used for any probability sampling plan, including both sampling with and without replacement [29]. Then, the H–T estimator of $Pr(q\supseteq _{sim} g)$ can be calculated as

$$\begin{aligned} \widehat{\theta }=\widehat{Pr(q\supseteq _{sim} g)}=\frac{1}{N}\sum _{i=1}^N\frac{Pr_{mcs}\cdot y_{i}}{\pi _i} \end{aligned}$$

(36)

where $Pr_{mcs}$ is the probability of the sampled PWGs containing a MCS between $q$ and $g^c$, which can be calculated as

$$\begin{aligned} Pr_{mcs}=\prod _{1\le i\le m_{samp}} Pr(e_i) \end{aligned}$$

(37)

where $m_{samp}$ is the number of sampled edges in one sampling process.

In Eq. 36, $\pi _i=1-(1-q_i)^N$ is the probability that each of different sampling results is sampled. We set $q_i=Pr_{mcs}$ which is given by Eq. 37.

The H–T estimator is unbiased, i.e., $E(\widehat{\theta })=\theta$ [29]. In the following, we analyze the variance of the estimator, i.e., $Var(\widehat{\theta })$. Let $\pi _{ij}=1-(1-q_i)^N-(1-q_j)^N-(1-q_i-q_j)^N$, which is the probability that $\pi _i$ and $\pi _j$ are in the result set at the same time, then the variance of this estimator is

$$\begin{aligned} \begin{aligned} Var(\widehat{\theta })&= \sum _{i\in v}\left( \frac{1-\pi _i}{\pi _i}\right) \left( Pr_{mcs}^i\right) ^2 \\&\quad \, +\sum _{\begin{array}{c} i,j\in v, i\ne j \end{array}}\left( \frac{\pi _{ij}-\pi _i\pi _j}{\pi _i\pi _j}\right) Pr_{mcs}^i Pr_{mcs}^j \end{aligned} \end{aligned}$$

(38)

where $v$ is a sampling result.

Since we set $q_i=Pr_{mcs}$, $Var(\widehat{\theta })$ gets its minimum value. Moreover, at this time, it can be shown that $Var(\widehat{\theta _{H\hbox {--}T}})$ $\le Var(\widehat{\theta _{B}})$. In other words, the H–T estimator obtains a more accurate answer than the basic one. In conclusion, the advanced sampling algorithm is more efficient and obtains a more accurate estimator than the basic sampling algorithm.

5 Performance evaluation

In this section, we report the effectiveness and efficiency test results of our new proposed techniques for probabilistic subgraph and supergraph similarity search. Our methods are implemented on a Windows XP machine with a Core 2 Duo CPU (2.8 and 2.8 GHz) and 4 GB main memory. Programs are compiled by Microsoft Visual C++ 2005.

5.1 Probabilistic subgraph similarity search

5.1.1 Experimental setting

In the experiments, we use a real uncertain graph dataset.

(1) Real uncertain graph dataset The real uncertain graph dataset is obtained from the STRING database⁸ that contains the PPI networks of organisms in the BioGRID database.⁹ A PPI network is an uncertain graph where vertices represent proteins, edges represent interactions between proteins, the labels of vertices are the COG functional annotations of proteins¹⁰ provided by the STRING database, and the existence probabilities of edges are provided by the STRING database. We extract 5K uncertain graphs from the database. The uncertain graphs have an average number of 385 vertices and 612 edges. Each edge has an average value of 0.383 existence probability. According to [10], the neighbor PPIs (edges) are dominated by the strongest interactions of the neighbor PPIs. Thus, for each neighbor edge set $ne$, we set its probabilities as: $Pr(x_{ne})=max_{1\le i\le |ne|}$ $Pr(x_i)$, where $x_i$ is a binary assignment to each edge in $ne$. Then, for each $ne$, we obtain $2^{|ne|}$ probabilities. We normalize those probabilities to construct the probability distribution, of $ne$, that is the input into our algorithms. Each query set $qi$ has 100 connected query graphs and query graphs in $qi$ are size-$i$ graphs (the edge number in each query is $i$), which are extracted from corresponding deterministic graphs of uncertain graphs randomly, such as $q50$, $q100$, $q150$, $q200$ and $q250$. In scalability test, we randomly generate 2K, 4K, 6K, 8K, and 10K data graphs.

(2) Parameter setting The setting of experimental parameters is set as follows: the probability threshold is 0.3–0.7, and the default value is 0.5; the subgraph distance is 2–6, and the default value is 4; the query size is 50–250, and the default value is 150. In feature generation, the value of $maxL$ is 50–250, and the default value is 150; the values of $\{\alpha ,\beta ,\gamma \}$ are 0.05–0.25, and the default value is 0.15.

(3) Algorithms As introduced in Sect. 3.1, we implement the method in [49] to do structural pruning. This method is called Structure in the experiments. In probabilistic pruning, the method using bounds of subgraph similarity probability is called SUBPBound, and the approach using the best bounds is called OPT-SUBPBound. To implement SUBPBound, for each $rq_i$, we randomly find two features satisfying conditions in the PMI. The method using bounds of subgraph isomorphism probability is called SIPBound, and the method using the tightest bound approach is called OPT-SIPBound. In verification, the sampling algorithm is called SMP, and the method given by Eq. 22 is called Exact. Since there are no pervious works on the topic studied in this paper, we also compare the proposed algorithms with Exact that scans the uncertain graph databases one by one. The complete proposed algorithm of this paper is called PMI. We report average results in following experiments.

5.1.2 Experimental results

Exp-1 In the first experiment, we demonstrate the efficiency of SMP against Exact in the verification step. We first run structural and probabilistic filtering algorithms against the default dataset to create candidate sets. The candidate sets are then verified for calculating SSP using the proposed algorithms. Figure 15a reports the result, from which we know SMP is efficient with an average time less than 3 s, while the curve of Exact decreases exponentially. The approximation quality of SMP is measured by the precision and recall metrics with respect to the query size shown in Fig. 15b. Precision is the percentage of true uncertain graphs in the output uncertain graphs. Recall is the percentage of returned uncertain graphs in all true uncertain graphs. The experimental results verify that SMP has a very high approximation quality with precision and recall both larger than 90 %. We use SMP for verification in following experiments.

Fig. 15

Scalability to query size. a Runtime, b query quality

Exp-2 Figure 16 reports candidate sizes and pruning time of SUBPBound, OPT-SUBPBound, and Structure with respect to probability thresholds. Recall that SUBPBound and OPT-SUBPBound are derived from upper and lower bounds of SIP. Here, we feed them with OPT-SIPBound. From the results, we know that the bars of SUBPBound and OPT-SUBPBound decrease with the increase of the probability threshold, since larger thresholds can remove more false graphs with low confidences. As shown in Fig. 16a, the candidate size of OPT-SUBPBound is very small (i.e., 15 on average) and is smaller than that of SUBPBound, which indicates that our derived best bounds are tight enough to have a great pruning power. As shown in Fig. 16b, OPT-SUBPBound has a short pruning time (i.e., less than 1s on average) but takes more time than SUBPBound due to more subgraph isomorphic tests during the calculation of OPT-SUBPBound. Obviously, probabilities do not have impacts on Structure, and thus both bars of Structure hold constant.

Fig. 16

Scalability to probability threshold. a Candidate size, b runtime

Exp-3 Figure 17 shows candidate sizes and pruning time of SIPBound, OPT-SIPBound, and Structure with respect to subgraph distance thresholds. To examine the two metrics, we feed SIPBound and OPT-SIPBound to OPT-SUBPBound. From the results, we know that all bars increase with the increase of the subgraph distance threshold, since larger thresholds lead to a large remaining graph set which is input into the proposed algorithms. Both OPT-SIPBound and SIPBound have a small number of candidate graphs, but OPT-SIPBound takes more time due to additional time for computing tightest bounds. From Figs. 16a and 17a, we believe that though Structure remains a large number of candidates, the probabilistic pruning algorithms can further remove most falsely identified graphs with efficient runtime. This observation verifies our algorithmic framework (i.e., structure pruning–probabilistic pruning–verification) is effective to process queries on a large uncertain graph database.

Fig. 17

Scalability to subgraph distance threshold. a Candidate size, b runtime

Exp-4 Figure 18 examines the impact of parameters $\{maxL,$ $\alpha ,\beta ,\gamma \}$ for feature generation. Structure holds constant in the 4 results, since the feature generation algorithm is used for probabilistic pruning. From Fig. 18a, we know that the larger $maxL$ is, the more candidates SUBPBound and OPT-SUBPBound have. The reason is that the large $maxL$ generates large sized features, which leads to loose probabilistic bounds. From Fig. 18b, we see that all bars of probabilistic pruning first decrease and then increase, and reach lowest at the values 0.1 and 0.15 of $\alpha$. As shown in Fig. 18c, d, both bars of OPT-SIPBound decrease as the values of the parameters increase, since either large $\beta$ or large $\gamma$ results in fewer features.

Fig. 18

Impact of parameters for feature generation. a $maxL$, b $\alpha$, c $\beta$, d $\gamma$

Exp-5 Figure 19 reports the total query processing time with respect to different graph database sizes. PMI denotes the complete algorithm, that is, a combination of Structure, OPT-SUBPBound (feed OPT-SIPBound) and SMP. From the result, we know PMI has quite an efficient runtime and avoids the huge cost of computing SSP (#P-hard). PMI can process queries within 10 s on average. But the runtime of Exact grows exponentially and has gone beyond 1,000 s at the database size of 6k. The result of this experiment validates the designs introduced in this paper.

Fig. 19

Total query processing time

Exp-6 Figure 20 examines the quality of query answers based on probability correlated and independent models. The query returns uncertain graphs if the uncertain graphs and the query (subgraph) belong to the same organism of PPI networks. We say the query and uncertain graph belong to the same organism if the subgraph similarity probability is not less than the threshold. In fact the STRING database has given real organisms of the uncertain graphs. Thus we can use the precision and recall to measure the query quality. Precision is the percentage of real uncertain graphs in the returned uncertain graphs. Recall is the percentage of returned real uncertain graphs in all real uncertain graphs. To determine query answers for the probability independent model, we multiply probabilities of edges in each neighbor edge set to obtain joint probability tables (JPT). Based on the JPTs, we use $PMI$ to determine query answers for the probability independent model. Each time, we randomly generate 100 queries and report average results. In the examination, $COR$ and $IND$ denote the probability correlated and probability independent models, respectively. In the figure, precision and recall decrease as probability threshold is larger, since large thresholds make query and graphs more difficult to be categorized into the same organism. We also know that the probability correlated model has much higher precision and recall than the probability independent model. The probability correlated model has average precision and recall both larger than 85 %, while the probability independent model has values smaller than 60 % at threshold larger than 0.6. The result indicates that our proposed model behaves more accurate biological properties than the probability independent model.

Fig. 20

Query quality comparison (COR vs. IND)

5.2 Probabilistic supergraph similarity search

5.2.1 Experimental setting

In experiments, we use a real uncertain graph dataset.

(1) Real uncertain graph dataset In this subsection, we also use the real uncertain graph dataset: the STRING database. We extract 5K uncertain graphs from the database. The uncertain graphs have an average number of 105 vertices and 183 edges. Each edge has an average value of 0.412 existence probability. For each neighbor edge set $ne$, similar to the subgraph matching, we also set its probabilities as: $Pr(x_{ne})=max_{1\le i\le |ne|}$ $Pr(x_i)$, where $x_i$ is a binary assignment to each edge in $ne$. Finally, we normalize these probabilities to construct the joint probability distribution. In scalability test, we randomly generate 2K, 4K, 6K, 8K, and 10K uncertain data graphs. We vary the vertex number of uncertain graphs as 50, 100, 150, 200, or 250.

(2) Parameter Settings Each query set $qi$ has 100 query graphs and $qi$ is $q100$, $q150$, $q200$, $q250$, or $q300$ (the default is $q200$). The probability threshold is 0.3–0.7, and the default value is 0.5. The graph distance threshold is 2–6, and the default value is 4.

(3) Algorithms For sampling algorithms, the basic one is called BS and the advanced one is AS. For pruning algorithms, the lightweight one is called LW and the strong one is ST.

5.2.2 Experimental results

Exp-1 First, we demonstrate the efficiency of BS and AS in the verification step. We first run the filtering algorithms against the default dataset to create candidate sets. The candidate sets are then verified for calculating SUPP using the proposed algorithms. Figure 21a reports the efficiency results, in which all curves grow with the increase of the query size. The reason is that, the larger the size of a query is, the more MCSs are detected. On average, AS runs 9.3 more efficient than BS, which validates our design that sampling once in AS has the same effect as sampling many times in BS. In Fig. 21b, we use the precision and recall metrics to measure the approximation quality of the sampling algorithms, i.e., AS-Pre, AS-Rec, BS-Pre, and BS-Rec. The experimental result verifies that both AS and BS have very high approximation qualities with precision and recall larger than 90 %. To compare with the method of sampling equation 29 (IE), we first compute all MCSs of $q$ and $g$, then use the same randomized algorithm as Algorithm 5 to estimate SUPP. From the figure, we observe that IE has takes much more time than AS but less time than BS. The estimation quality of IE is between AS and BS. The result shows that AS is also a very effective algorithm compared to IE. We use AS for verification in the following experiments.

Fig. 21

Scalability to query size. a Running time, b query quality

Exp-2 Second, we examine the pruning power and pruning efficiency in Fig. 22 with respect to probability thresholds. The pruning power is examined using the candidate size after pruning, and the pruning efficiency is examined using the running time of the pruning algorithms. From the results, we know that all curves decrease with the increase of the probability threshold, since larger thresholds can remove more false graphs with low confidences. As shown in Fig. 22a, the candidate size of ST-Prune is very small (i.e., 15 on average) and is much smaller than that of LW-Prune, which indicates that our derived bounds of ST-Prune are tight enough to have a great pruning power. But as shown in Fig. 22b, ST-Prune takes more time than LW-Prune due to much time being taken to detect MCSs.

Fig. 22

Scalability to probability threshold. a Candidate size, b running time

Exp-3 Third, we show the candidate sizes and pruning time of LW-Prune and ST-Prune in Fig. 23 with respect to subgraph distance thresholds. In the figure, all values increase as the subgraph distance threshold increases, since a larger threshold leads to a large remaining graph set which is input into the proposed algorithms. ST-Prune has a smaller number of candidate graphs compared to LW-Prune, but ST-Prune has higher costs than LW-Prune due to additional time for computing MCSs. This result shows that, though ST-Prune takes a bit more time, ST-Prune can remove most false graphs. Thus, the overall running time for ST-Prune is efficient.

Fig. 23

Scalability to subgraph distance threshold. a Candidate size, b running time

Exp-4 Fourth, we report the pruning power and pruning efficiency of LW-Prune and ST-Prune in Fig. 24 with respect to database sizes. As shown in Fig. 24a, both LW-Prune and ST-Prune have short running time, i.e., the average results of LW-Prune and ST-Prune are 0.83 and 4.1 s, respectively. In Fig. 24b, we observe that the candidate size of ST-Prune is small (i.e., less than 100 on average) and LW-Prune also remains a few uncertain graphs. We also observe that both running time and candidate size increase little as the database size increases, which indicates that our proposed techniques are scalable.

Fig. 24

Scalability to database size. a Candidate size, b running time

Exp-5 Fifth, we examine the performance of index for LW and ST in Fig. 25 with respect to vertex number of uncertain graph. We feed optimal features to the index through a query log as follows: In each experiment, we divide a database $D$ to a query log set $\gamma$ ($\frac{4}{5}|D|$) and a testing query set $q$ ($\frac{1}{5}|D|$). Figure 25a gives the index size of ST-Index and LW-Index, from which we observe that they both take little space costs. This is because ST-Index and LW-Index mine most effective features for the index and the size of these features is small. The small size of the index comes at the cost of somewhat higher index building cost as shown in Fig. 25b. The reason is that we should train a query log in constructing index. ST-Index takes more building time and space costs than LW-Index, since ST-Index first selects best feature sets and then unions the sets to obtain the features.

Fig. 25

Performance of index. a Index size, b building time

Exp-6 Sixth, we present the total query processing time in Fig. 26 with respect to different graph database sizes and vertex numbers. In this examination, we equip LW and ST with AS, i.e., LW+AS and ST+AS. In the result, LW+AS outperforms ST+AS by several orders of magnitude due to the great pruning power of ST. ST+AS can process queries within 10 s on average. The result shows that by combining our pruning and sampling techniques, the query processing can be conducted very efficiently.

Fig. 26

Total query processing time. a Regarding to database size, b regarding to vertex number

Exp-7 Finally, Fig. 27 examines the qualities of probability correlated model and independent model on supergraph similarity search. Similar to the subgraph similarity search, we test whether a query graph and a data graph belong to the same organism by verifying SUPP$\ge \epsilon$. We also use the precision and recall to measure the query quality based on the given ground truths in the STRING database. In the examination, COR and IND denote the probability correlated model and probability independent model, respectively. In the figure, precision and recall decrease as the probability threshold is larger, since large thresholds make query and graphs more difficult to be categorized into the same organism. We also observe that the probability correlated model has higher precision and recall than the those of the probability independent model. On average, the precision or recall of COR is 20 % greater than that of IND. The experimental results again verify that the local correlated model behaves more accurate biological properties than the independent model.

Fig. 27

Query quality comparison (COR vs. IND)

5.3 Case study

This paper studies the subgraph similarity and supergraph similarity search on uncertain graphs with edge correlations (denoted by SUBS-COR and SUPS-COR), which includes many subproblems, i.e., subgraph similarity matching with edge independence (denoted by SUBS-IND), subgraph matching with edge correlations (denoted by SUBE-COR), subgraph matching with edge independence (denoted by SUBE-IND), supergraph similarity matching with edge independence (denoted by SUPS-IND), supergraph matching with edge correlations (denoted by SUPE-COR) and supergraph matching with edge independence (denoted by SUPE-IND). In this testing, we examine each subproblem in the same platform and report the total query processing time of these subproblems on the real uncertain PPI networks. It is easy to implement these subproblems by extending our proposed algorithm, i.e., setting the distance threshold with 0 for the exact matching and calculating the independence probability for the edge independence model.

Figure 28 shows the results on the subgraph (similarity) and supergraph (similarity) matching. From the results, we observe that the similarity matching takes more running time than the exact matching, since the similarity matching consists of many exact matching. We also observe that the independent model needs less query costs than the correlated model because of efficient calculations on the independent probabilities. All algorithms are efficient, i.e., on average, the exact matching takes less than 5 s on either subgraph or supergraph search, and the similarity matching takes less than 10 s on average. The subgraph matching, however, incurs less costs than the supergraph matching due to the absence of structural pruning in supergraph matching. This experimental result shows that our defined query is a very general problem and our solution to the general problem is also rather effective at each subproblem.

Fig. 28

Total query processing time. a Subproblems of the subgraph similarity matching, b subproblems of the supergraph similarity matching

6 Related work

In this paper, we study similarity search over uncertain graphs, which is related to uncertain and graph data management. Readers who are interested in general uncertain and graph data management please refer to [3, 4], respectively.

The topic most related to our work is similarity search in deterministic graphs. Yan et al. [49] proposed to process subgraph similarity queries based on frequent graph features. They used a filtering-verification paradigm to process queries. He et al. [18] employed an R-tree like index structure, organizing graphs hierarchically in a tree, to support $k$-NN search to the query graph. Jiang et al. [22] encoded graphs into strings and converted graph similarity search into string matching. Williams et al. [46] aimed to find graphs with the minimum number of miss-matchings of vertex and edge labels bounded by a given threshold. Zeng et al. [54] proposed tight bounds of graph edit distance to filter out false graphs in similarity search, based on which, Wang et al. [45] developed an indexing strategy to speed up query. Shang et al. [39] studied super-graph similarity search, and proposes top-down and bottom-up index construction strategy to optimize the performance of query processing. SAPPER [55] and Tspan [56] are the only two works with the aim to efficiently generate all similarity matches of a query in a large data graph.

Another related topic is querying uncertain graphs. Potamias et al. [35] studied $k$-nearest neighbor queries ($k$-NN) over uncertain graphs, i.e., computing the $k$ closest nodes to a query node. Zou et al. [57, 58] studied frequent subgraph mining on uncertain graph data under the probability and expectation semantics, respectively. Moustafa et al. [34] incorporated node uncertainty and edge uncertainty into identity uncertainty, and studied subgraph pattern matching over uncertain graphs with identity uncertainty. Yuan et al. [51, 53] study the exact and similarity subgraph matching on probabilistic graphs. Yuan et al. [52] also develop efficient algorithms to process keyword queries over a large uncertain graph data. In another work, Yuan et al. [50] and Jin et al. [24] studied shortest path query and distance-constraint reachability query in a single uncertain graph. Hua et al. [19] studied several path queries in an uncertain road network. Kollios et al. [27] studied clustering uncertain graphs based on the expected graph distance, while Liu et al. [32] studied the problem of reliable clustering on uncertain graphs based on the graph entropy. The above works define uncertain graph models with independent edge distributions and do not consider edge correlations. Moreover, their proposed queries are completely different the query studied in this paper. Therefore, the techniques in these works cannot be used to process graph similarity queries on uncertain graph data.

7 Conclusion

This is the first work to answer the similarity graph containment queries (subgraph and supergraph similarity queries) on large uncertain graphs with correlation on edge probability distributions. Though it is an NP-hard problem to answer the subgraph or supergraph similarity query, we employ a filter-and-verify methodology to answer the two queries efficiently. During the filtering phase, for the subgraph similarity query, we first propose a PMI with tight upper and lower bounds of subgraph isomorphism probability. Then, based on PMI, we derive upper and lower bounds of the subgraph similarity probability, while for supergraph similarity query, we compute effective bounds of supergraph similarity probability based on maximal common subgraphs of query and uncertain graph. Therefore, we are able to filter out a large number of uncertain graphs without calculating the subgraph and supergraph similarity probabilities. During verification to fast validate final answers, we use the inclusion–exclusion principle to develop sampling algorithms for the subgraph similarity query, while we develop sampling algorithms based on the Horvitz–Thompson estimator for supergraph queries. Finally, we confirm our designs for the two queries through an extensive experimental study.