Dynamic monitoring of optimal locations in road network databases

Abstract

Optimal location (OL) queries are a type of spatial queries that are particularly useful for the strategic planning of resources. Given a set of existing facilities and a set of clients, an OL query asks for a location to build a new facility that optimizes a certain cost metric (defined based on the distances between the clients and the facilities). Several techniques have been proposed to address OL queries, assuming that all clients and facilities reside in an $L_p$ space. In practice, however, movements between spatial locations are usually confined by the underlying road network, and hence, the actual distance between two locations can differ significantly from their $L_p$ distance. Motivated by the deficiency of the existing techniques, this paper presents a comprehensive study on OL queries in road networks. We propose a unified framework that addresses three variants of OL queries that find important applications in practice, and we instantiate the framework with several novel query processing algorithms. We further extend our framework to efficiently monitor the OLs when locations for facilities and/or clients have been updated. Our dynamic update methods lead to efficient answering of continuous optimal location queries. We demonstrate the efficiency of our solutions through extensive experiments with large real data.

1 Introduction

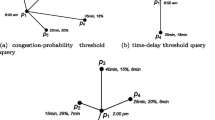
An optimal location (OL) query concerns three spatial point sets: a set $F$ of facilities, a set $C$ of clients, and a set $P$ of candidate locations. The objective of this query is to identify a candidate location $p\in P$, such that a new facility built at $p$ can optimize a certain cost metric that is defined based on the distances between the facilities and the clients. OL queries find important applications in the strategic planning of resources (e.g., hospitals, post offices, banks, retail facilities) in both public and private sectors [2, 6, 29]. As an example, we illustrate three OL queries based on different cost metrics.

Example 1

Julie would like to open a new supermarket in San Francisco that can attract as many customers as possible. Given the set $F$ ($C$) of all existing supermarkets (residential locations) in the city, Julie may look for a candidate location $p$, such that a new supermarket on $p$ would be the closest supermarket for the largest number of residential locations.

Example 2

John owns a set $F$ of pizza shops that deliver to a set $C$ of places in Gotham city. In case that John wants to extend his business by adding another pizza shop, a natural choice for him is a candidate location that minimizes the average distance from the points in $C$ to their respective nearest pizza shops.

Example 3

Gotham city government plans to establish a new fire station. Given the set $F(C)$ of existing fire stations (buildings), the government may seek a candidate location that minimizes the maximum distance from any building to its nearest fire station.

Several techniques [2, 6, 26, 29] have been proposed for processing OL queries under various cost metrics. All those techniques, however, assume that $F$ and $C$ are point sets in an $L_p$ space. This assumption is rather restrictive because, in practice, movements between spatial locations are usually confined by the underlying road network, and hence, the commute distance between two locations can differ significantly from their $L_p$ distance. Consequently, the existing solutions for OL queries cannot provide useful results for practical applications in road networks.

1.1 Problem formulation

This paper presents a novel and comprehensive study on OL queries in road network databases. We consider a problem setting as follows. First, any facility in $F$ or any client in $C$ should locate on an edge in an undirected connected graph $G^{\circ }= (V^{\circ }, E^{\circ })$, where $V^{\circ }\; (E^{\circ })$ denotes the set of vertices (edges) in $G^{\circ }$. Second, every client $c \in C$ is associated with a positive weight $w(c)$ that captures the importance of the client. For example, if each client point $c$ represents a residential location, then $w(c)$ may be specified as the size of the population residing at $c$. Third, there should exist a user-specified set $E^{\circ }_c$ of edges in $E^{\circ }$, such that a new facility $f$ can be built on any point on any edge in $E^{\circ }_c$, as long as $f$ does not overlap with an existing facility in $F$. $E^{\circ }_c$ can be arbitrary, e.g., we can have $E^{\circ }_c = E^{\circ }$. We define $P$ as the set of points on the edges in $E^{\circ }_c$ that are not in $F$, and we refer to any point in $P$ as a candidate location. For example, Fig. 1 illustrates a road network that consists of five vertices and eight edges. The squares (crosses) in the figure denote the facilities (clients) in the road network. The highlighted edges are the user-specified set $E^{\circ }_c$ of edges where a new facility may be built.

Fig. 1

Example of $G^{\circ }$

We investigate three variants of OL queries as follows:

• 1. The competitive location query asks for a candidate location $p \in P$ that maximizes the total weight of the clients attracted by a new facility built on $p$. Specifically, we say that a client $c$ is attracted by a facility $f$ and that $f$ is an attractor for $c$, if the network distance $d(c, f)$ between $c$ and $f$ is at most the distance between $c$ and any facility in $F$. In other words, the competitive location query ensures that

  $$\begin{aligned} p&= \mathop {\hbox {argmax}}\limits _{p\in P}\sum _{c \in C_p} w(c), \end{aligned}$$

  (1)

  where $C_p = \{ c \mid c \in C \; \wedge \; \forall f \in F, d(c, p) \le d(c, f)\}$, i.e., $C_p$ is the set of clients attracted by $p$. Example 1 demonstrates an instance of this query.

• 2. The MinSum location query asks for a candidate location $p \in P$ on which a new facility can be built to minimize the total weighted attractor distance (Wad) of the clients. In particular, the Wadof a client $c$ is defined as $\widehat{a}(c)=w(c) \cdot a(c)$, where $a(c)$ denotes the distance from $c$ to its attractor (referred as the attractor distance of $c$). That is, the MinSum location query requires that

  $$\begin{aligned} p&= \mathop {\hbox {argmin}}\limits _{p\in P}\sum _{c \in C} w(c) \cdot \min \Big \{d(c, f) \mid f \in F \cup \{p\}\Big \}\nonumber \\&= \mathop {\hbox {argmin}}\limits _{p\in P}\sum _{c \in C} \widehat{a}(c). \end{aligned}$$

  (2)

  Example 2 shows a special case of the MinSum location query where all clients have the same weight.

• 3. The MinMax location query asks for a candidate location $p\in P$ to construct a new facility that minimizes the maximum Wadof the clients, i.e.,

  $$\begin{aligned} p&= \mathop {\hbox {argmin}}\limits _{p\in P} \Bigg ( \max _{c \in C} \Big \{\widehat{a}(c) \mid F=F\cup \{p\} \Big \}\Bigg ). \end{aligned}$$

  (3)

  Example 3 illustrates a MinMax location query.

One fundamental challenge in answering an OL query is that there exists an infinite number of candidate locations in $P$ where the new facility may be built, i.e., $P$ is a continuous domain on the edges of the network (Recall that $P$ contains all points on the edges in the user-specified set $E^{\circ }_c$, except the points where existing facilities are located.). This necessitates query processing techniques that can identify query results without enumerating all candidate locations. Another complicating issue is that the answer to an OL may not be unique, i.e., there may exist multiple candidate locations in $P$ that satisfy Eqs. 1, 2, or 3. We propose to identify all answers for any given optimal location query and return them to the user for final selection. This renders the problem even more challenging, since it requires additional efforts to ensure the completeness of the query results.

Lastly, in some applications, it is common that clients or existing facilities have moved on the road network after the last execution of OL queries. Instead of computing the OLs again from scratch, we expect to monitor the query results in an incremental fashion, which may dramatically reduce the query cost (compared to the naive approach of recomputing the OLs after location updates for facilities and clients).

1.2 Contributions

In this paper, we propose a unified solution that addresses all aforementioned variants of optimal location queries in road network databases. Our first contribution is a solution framework based on the divide-and-conquer paradigm. In this framework, we process a query by first (i) dividing the edges in $G^{\circ }$ into smaller intervals, then (ii) computing the best query answers on each interval, and finally (iii) combining the answers from individual intervals to derive the global optimal locations. A distinct feature of this framework is that most of its algorithmic components are generic, i.e., they are not specific to any of the three types of OL queries. This significantly simplifies the design of query processing algorithms and enables us to develop general optimization techniques that work for all three query types.

Secondly, we instantiate the proposed framework with a set of novel algorithms that optimize query efficiency by exploiting the characteristics of OL queries. We provide theoretical analysis on the performance of each algorithm in terms of time complexity and space consumption.

Thirdly, we present extensions to our framework to enable the incremental monitoring of the query results from OL queries, when the locations of facilitates or clients have changed.

Last, we demonstrate the efficiency of our algorithms with extensive experiments on large-scale real datasets. In particular, our algorithms can answer an OL query efficiently on a commodity machine, in a road network with 174,955 vertices and 500,000 clients. Furthermore, the query result can be incrementally updated in just a few seconds after a location update for either a client or a facility.

2 Related work

The problem of locating “preferred” facilities with respect to a given set of client points, referred to as the facility location problem, has been extensively studied in past years (see [8, 20] for surveys). In its most common form, the problem (i) involves a finite set $C$ of clients and a finite set $P$ of candidate facilities and (ii) asks for a subset of $k\; (k > 0)$ facilities in $P$ that optimizes a predefined metric. The problem is polynomial-time solvable when $k$ is a constant, but is NP-hard for general $k$ [8, 20]. Furthermore, existing solutions do not scale well for large $P$ and $C$. Hence, existing work on the problem mainly focuses on developing approximate solutions.

OL queries can be regarded as variations of the facility location problem with three modified assumptions: (i) $P$ is an infinite set, (ii) $k=1$, i.e., only one location in $P$ is to be selected (but all locations that tie with each other need to be returned), and (iii) a finite set $F$ of facilities has been constructed in advance. These modified assumptions distinguish OL queries from the facility location problem.

Previous work [2, 6, 26, 29] on OL queries considers the case when the transportation cost between a facility and a client is decided by their $L_p$ distance. Specifically, Cabello et al. [2] and Wong et al. [26] investigate competitive location queries in the $L_2$ space. Du et al. [6] and Zhang et al. [29] focus on the $L_1$ space and propose solutions for competitive and MinSum location queries, respectively. None of the solutions developed therein is applicable when the facilities and clients reside in a road network.

There also exist two other variations of the facility location problem, namely the single facility location problem [8, 20] and the online facility location problem [9, 17], that are related to (but different from) OL queries. The single facility location problem asks for one location in $P$ that optimizes a predefined metric with respect to a given set $C$ of clients. It requires that no facility has been built previously, whereas OL queries consider the existence of a set $F$ of facilities.

The online facility location problem assumes a dynamic setting where (i) the set $C$ of clients is initially empty, and (ii) new clients may be inserted into $C$ as time evolves. It asks for a solution that constructs facilities incrementally (i.e., one at a time), such that the quality of the solution (with respect to some predefined metric) is competitive against any solutions that are given all client points in advance. This problem is similar to OL queries, in the sense that they all aim to optimize the locations of new facilities based on the existing facilities and clients. However, the techniques [9, 17] for the online facility location problem cannot address OL queries, since those techniques assume that the set $P$ of candidate facility locations is finite; in contrast, OL queries assume that $P$ contains an infinite number of points, e.g., $P$ may consist of all points (i) in an $L_p$ space (as in [2, 6, 26, 29]) or (ii) on a set of edges in a road network (as in our setting).

In the preliminary version of this paper [27], we investigated the static version of optimal location queries. Compared with the preliminary version, this paper presents a new study on handling updates in the locations of facilities and clients. In particular, we present novel incremental methods to identify OLs after updates for all three types of optimal location queries. We also include an extensive experiments that demonstrate the efficiency of the incremental update methods over the naive approach of recomputing OLs from scratch after each update (using the static methods from our preliminary version [27]).

Ghaemi et al. [10–12] studied static and dynamic versions of competitive location queries. Their solutions, however, are not applicable for MinSum and MinMax location queries. In contrast, we present a uniform framework for all three variants of optimal location queries. Furthermore, as will be shown in Sect. 10, our solution for competitive location queries has a much lower memory consumption than Ghaemi et al.’s while only incurring a slightly higher computation cost.

Lastly, there is a large body of the literature on query processing techniques for road network databases [3, 4, 15, 16, 19, 21–24, 28]. Most of those techniques are designed for the nearest neighbor (NN) query [16, 21, 22] or its variants, e.g., approximate NN queries [23, 24], aggregate NN queries [28], continuous NN queries [19], and path NN queries [3]. None of those techniques can address the problem we consider, due to the fundamental differences between NN queries and OL queries. Such differences are also demonstrated by the fact that, despite the plethora of solutions for $L_p$-space NN queries, considerable research effort [2, 6, 26, 29] is still devoted to OL queries in $L_p$ spaces.

3 Solution overview

We propose one unified framework for the three variants of OL queries. In a nutshell, our solution adopts a divide-and-conquer paradigm as follows. First, we divide the edges in $E^{\circ }$ into smaller intervals, such that all facilities and clients fall on only the endpoints (but not the interior) of the intervals. As a second step, we collect the intervals that are segments of some edges in $E^{\circ }_c$, i.e, all points in such an interval are candidate locations in $P$. Then, we traverse those intervals in a certain order. For each interval $I$ examined, we compute the local optimal locations on $I$, i.e., the points on $I$ that provide a better solution to the OL query than any other points on $I$. The global optimal locations are pinpointed and returned, once we confirm that none of the unvisited intervals can provide a better solution than the best local optima found so far.

In the following, we will introduce the basic idea of each step in our framework; the details of our algorithms will be presented in Sects. 4–8. For convenience, we define $n$ as the maximum number of elements in $V^{\circ },\; E^{\circ },\; C$, and $F$, i.e., $n = \max \{|V^{\circ }|, |E^{\circ }|, |C|, |F|\}$. Table 1 summarizes the notations frequently used in the paper.

Table 1 Frequently used notations

3.1 Construction of road intervals

We divide the edges in $E^{\circ }$ into intervals, by inserting all facilities and clients into the road network $G^{\circ }= (V^{\circ }, E^{\circ })$. Specifically, for each point $\rho \in C \cup F$, we first identify the edge $e\in E^{\circ }$ on which $\rho$ locates. Let $v_l$ and $v_r$ be the two vertices connected by $e$. We then break $e$ into two road segments, one from $v_l$ to $\rho$ and the other from $\rho$ to $v_r$. As such, $\rho$ becomes a vertex in the network. Once all facilities and clients have been inserted into $G^{\circ }$, we obtain a new road network $G = (V, E)$, where $V = V^{\circ }\cup C \cup F$. For example, Fig. 2 illustrates a road network transformed from the one in Fig. 1. Transforming $G^{\circ }$ to $G$ requires only $O(n)$ space and $O(n)$ time, since $|C|=O(n),\; |F|=O(n)$, and it takes only $O(1)$ time to add a vertex in $G^{\circ }$. In the sequel, we simply refer to $G$ as our road network.

Fig. 2

Example of $G$

3.2 Traversal of road intervals

After $G$ is constructed, we collect the set $E_{c}$ of edges in $E$ that are partial segments of some edges in $E^{\circ }_c$. For example, the highlighted edges in Fig. 2 illustrate the set $E_c$ that correspond to the set $E^{\circ }_c$ of highlighted edges in Fig. 1. As a next step, we traverse $E_{c}$ to look for the optimal locations. A straightforward approach is to process the edges in $E_{c}$ in a random order, which, however, incurs significant overhead, since the optimal locations cannot be identified until all edges in $E_{c}$ are inspected. Section 6 addresses this issue with novel techniques that avoid the exhaustive search on $E_{c}$. The idea is to first divide $E_{c}$ into subsets and then process the subsets in descending order of their likelihood of containing the optimal locations.

3.3 Identification of local optimal locations

In Sect. 4, we will present algorithms for computing the local optimal locations on any edge $e \in E_{c}$, based on (i) the attractor distance of each client and (ii) the attraction set $\mathcal {A}(v)$ of each endpoint $v$ of $e$. Specifically, the attraction set $\mathcal {A}(v)$ contains entries of the form $\langle c, d(c, v) \rangle$, for any client $c$ such that $d(c, v) \le a(c)$. That is, $\mathcal {A}(v)$ records the clients that are closer to $v$ than to their respective attractors (i.e., the respective nearest facilities). The attraction sets of $e$’s endpoints are crucial to our algorithm, since they capture all clients that might be affected by a new facility built on $e$ (see Sect. 4 for a detailed discussion). We will present our algorithms for computing attraction sets and attractor distances in Sect. 5.

3.4 Updates of facilities and clients

In Sects. 7 and 8, we present algorithms for incrementally monitoring the results of OL queries when there are updates in the locations of facilities and/or clients. The basic idea of our algorithms is to (i) maintain auxiliary information about the solutions to OL queries and (ii) utilize the auxiliary information to accelerate the re-computation of query results in case of updates.

4 Local optimal locations

This section presents our initial algorithms for computing local optimal locations on any edge $e \in E_c$, given the attraction sets of $e$’s endpoints, and the attractor distances of the clients. For ease of exposition, we will elaborate our algorithms under the assumption that none of $e$’s endpoints is an existing facility in $F$, i.e., both endpoints of $e$ are candidate locations in $P$. We will discuss how our algorithms can be extended (for the general case) in the end of the discussion for each query type.

4.1 Competitive location queries

Recall that a competitive location query asks for a new facility that maximizes the total weight of the clients attracted by it. Intuitively, to decide the optimal locations for such a new facility on a given edge $e \in E_c$, it suffices to identify the set of clients that can be attracted by each point $p$ on $e$. As shown in the following lemma, the clients attracted by any $p$ can be easily computed from the attraction sets of $e$’s endpoints.

Lemma 1

A client $c$ is attracted by a point $p$ on an edge $e \in E_c$, iff there exists an entry $\langle c, d(c, v) \rangle$ in the attraction set of an endpoint $v$ of $e$, such that $d(c, v) + d(v, p) \le a(c)$.

Proof

Observe that $d(c, p) \le d(c, v) + d(v, p)$. Hence, when $d(c, v) + d(v, p) \le a(c)$, we have $d(c, p) \le a(c)$, i.e., $c$ is attracted by $p$. Thus, the “if” direction of the lemma holds.

Now consider the “only if” direction. Since $p$ is a point on $e$, the shortest path from $p$ to $c$ must go through an endpoint $v$ of $e$. Observe that $d(p, c) \ge d(v, c)$. Therefore, if $c$ is attracted by $p$, we have $a(c) \ge d(p, c) \ge d(v, c)$, which indicates that $\langle c, d(c, v) \rangle$ must be an entry in $\mathcal {A}(v)$.$\square$

Based on Lemma 1, we propose the CompLoc algorithm (in Fig. 3) for finding local competitive locations on an edge $e \in E_c$. We illustrate the algorithm with an example.

Fig. 3

The CompLoc Algorithm

Example 4

Suppose that we apply CompLoc on an edge $e_0$ with a length $\ell = 5$. Figure 4a illustrates $\mathcal {A}(v_l)$ and $\mathcal {A}(v_r)$, where $v_l$ ($v_r$) is the left (right) endpoint of $e_0$. Assume that each client $c$ has a weight $w(c)=1$ and an attractor distance $a(c) = 5$.

CompLoc starts by creating a one-dimensional plane $R$. After that, it identifies those clients that appear in $\mathcal {A}(v_l)$ but not $\mathcal {A}(v_r)$. By Lemma 1, for any $c$ of those clients, if $c$ is attracted to a point $p$ on $e_0$, then $d(p, v_l) \in [0, a(c) - d(c, v_l)]$, and vice versa. To capture this fact, CompLoc creates in $R$ a line segment $[0, a(c) - d(c, v_l)]$ and assigns a weight $w(c) = 1$ to the segment. In our example, $c_1$ is the only client that appears in $\mathcal {A}(v_l)$ but not $\mathcal {A}(v_r)$, and $a(c_1) - d(c_1, v_l) = 1$. Hence, CompLoc adds in $R$ a segment $s_1 = [0, 1]$ with a weight $w(c_1) = 1$, as illustrated in Fig. 4b.

Next, CompLoc examines the only client $c_2$ that is contained in $\mathcal {A}(v_r)$ but not $\mathcal {A}(v_l)$. By Lemma 1, a point $p \in e_0$ is an attractor for $c$, if and only if $d(p, v_l) \in [\ell - a(c_2) + d(c_2, v_r), \ell ]$. Accordingly, CompLoc inserts in $R$ a segment $s_2 = [\ell - a(c_2) + d(c_2, v_r), \ell ]$ with a weight $w(c_2) = 1$.

After that, CompLoc identifies the clients $c_3$ and $c_4$ that appear in both $\mathcal {A}(v_l)$ and $\mathcal {A}(v_r)$. For $c_3$, we have $\ell \le 2 \cdot a(c_3) - d(c_3, v_l) - d(c_3, v_r)$, which (by Lemma 1) indicates that any point on $e_0$ can attract $c_3$. Hence, CompLoc creates in $R$ a segment $[0, 5]$ with a weight $w(c_3) = 1$. On the other hand, since $\ell > 2 \cdot a(c_4) - d(c_4, v_l) - d(c_4, v_r)$, a point $p$ on $e_0$ can attract $c_4$, if and only if $d(p, v_l) \in [0, a(c_4) - d(c_4, v_l)]$ or $d(p, v_l) \in [\ell - a(c_4) + d(c_4, v_r), \ell ]$. Therefore, CompLoc inserts in $R$ two segments $s_4 = [0, 2]$ and $s'_4 = [4, 5]$, each with a weight 1 (see Fig. 4b).

As a next step, CompLoc scans through the line segments in $R$ to compute the local competitive locations on $e_0$. Let $p$ be any point on $e_0$, and $o$ be the point in $R$ whose coordinate equals the distance from $p$ to $v_l$. Observe that, a client $c \in C$ is attracted by $p$, if and only if there exists a segment $s$ in $R$, such that (i) $s$ is constructed from $c$ and (ii) $s$ covers $o$. Therefore, to identify the local competitive locations on $e_0$, it suffices to derive the intervals $I$ in $R$, such that (i) $I \subseteq [0, \ell ]$, and (ii) $I$ maximizes the total weight of the line segments that fully cover $I$. Such intervals can be computed by applying a standard plane sweep algorithm [1] on the line segments in $R$. In our example, the local competitive locations on $e_0$ correspond to two intervals in $R$, namely $[0, 1]$ and $[4, 5]$, each of which is covered by three segments with a total weight 3. Finally, CompLoc terminates by returning the two intervals $[0, 1]$ and $[4, 5]$, as well as the weight 3.$\square$

Our discussion so far assumes that no facility in $F$ locates on an endpoint of the given edge $e$. Nevertheless, CompLoc can be easily extended for the case when either of $e$’s endpoints is a facility. The only modification required is that, we need to exclude the facility endpoint(s) of $e$, when we construct the line segment(s) on $R$ that corresponds to each client. For example, if we have a line segment $[0, 5]$ and the left endpoint of $e$ is a facility, then we should modify segment as $(0, 5]$ before we compute the local competitive locations on $e$. The case when the right endpoint of $e$ is a facility can be handled in a similar manner.

Fig. 4

Demonstration of CompLoc. a Edge $e_0$, b Plane $R$

CompLoc runs in $O(n \log n)$ time and $O(n)$ space. First, constructing line segments in $R$ takes $O(n)$ time and $O(n)$ space, since (i) there exist $O(n)$ clients in the attraction sets of the endpoints of $e$, (ii) at most two segments are created from each client. Second, since there are only $O(n)$ line segments in $R$, the plane sweep algorithm on the segments runs in $O(n \log n)$ time and $O(n)$ space.

4.2 MinSum location queries

For any candidate location $p$, we define the merit of $p$ (denoted as $m(p)$) as

$$\begin{aligned} m(p) = \sum _{c \in C} w(c) \cdot \max \{0, a(c) - d(c, p)\}. \end{aligned}$$

That is, $m(p)$ captures how much the total Wadof all clients may reduce, if a new facility is built on $p$. A point is a local MinSum location on an edge $e \in E_c$, if and only if it has the maximum merit among all points on $e$. Interestingly, the merit of the points on any edge $e$ is always maximized at one endpoint of $e$, as shown in the following lemma.

Lemma 2

For any point $p$ in the interior of an edge $e \in E$, if $m(p)$ is larger than the merit of one endpoint of $e$, then $m(p)$ must be smaller than the merit of the other endpoint.

Proof

Let $v_l$ ($v_r$) be the left (right) endpoint of $e$. Recall that $C_p$ is the set of clients attracted by $p$. First of all,

$$\begin{aligned} m(v_l)&= \sum _{c \in C} w(c) \cdot \max \{0, a(c) \! - \! d(c, v_l)\}\nonumber \\&\ge \sum _{c \in C_p} w(c) \cdot \big ( a(c) - d(c, v_l) \big ),\mathrm{and \,similarly,}\nonumber \\ m(v_r)&\ge \sum _{c \in C_p} w(c) \cdot \big ( a(c) - d(c, v_r) \big ). \end{aligned}$$

(4)

Assume w.l.o.g. that $m(p) > m(v_l)$. We have

$$\begin{aligned} m(p)&= \sum _{c \in C_p} w(c) \cdot \big ( a(c) - d(c, p) \big ) \\&\ge m(v_l)\ge \sum _{c \in C_p} w(c) \cdot \big ( a(c) - d(c, v_l) \big ), \end{aligned}$$

which leads to

$$\begin{aligned} \sum _{c\in C_p}w(c)(d(c,v_l)-d(c,p))>0. \end{aligned}$$

(5)

Let $C_p^l\;(C_p^r)$ be the subset of clients $c$ in $C_p$, such that the shortest path from $c$ to $p$ passes through $v_l$ ($v_r$). Clearly, $C_p^r=C_p - C_p^l$, and $d(c, p) = d(c, v_l) + d(v_l, p)$ for any $c \in C_p^l$. By Eq. 5,

$$\begin{aligned}&\!\!\!\sum _{c \in C_p^r} w(c) \cdot \big ( d(c, v_l) - d(c, p) \big ) \nonumber \\&\!\!\!\!\quad >\sum _{c \in C_p^l} w(c) \cdot \big ( d(c, p) - d(c, v_l) \big )= d(v_l, p) \cdot \sum _{c \in C_p^l} w(c).\nonumber \\ \end{aligned}$$

(6)

Since $d(c, v_l) \le d(c, p) + d(v_l, p)$ for any $c \in C_p^r$, we have

$$\begin{aligned} d(v_l,p)\cdot \sum _{c\in C_p^r} w(c) \ge \mathrm LHS of (6) \ge d(v_l,p)\cdot \sum _{c\in C_p^l} w(c), \end{aligned}$$

which means that

$$\begin{aligned} \qquad \sum _{c \in C_p^r} w(c)&> \sum _{c \in C_p^l} w(c). \end{aligned}$$

(7)

Note that $d(c, p) = d(c, v_r) + d(v_r, p)$ for any $c \in C_p^r$, and $d(c, v_r) \le d(c, p) + d(v_r, p)$ for any $c \in C_p^l$. By Eq. 4 & 5,

$$\begin{aligned}&\!\!\! m(v_r) \! - \! m(p) \! \ge \! -m(p) \! + \! \sum _{c \in C_p} \! w(c) \! \cdot \! ( a(c) \!-\! d(c, v_r)) \nonumber \\&\!\!\!\quad = \sum _{c \in C_p^l} \! w(c) \! \cdot \! \big ( d(c, p) - d(c, v_r) \big ) \nonumber \\&\!\!\!\qquad + \sum _{c \in C_p^r} \! w(c) \! \cdot \! \big ( d(c, p) - d(c, v_r) \big ) \nonumber \\&\!\!\! \quad \textstyle \ge d(v_r, p) \cdot \Big ( - \sum _{c \in C_p^l} w(c) + \sum _{c \in C_p^r} w(c) \Big ) \end{aligned}$$

(8)

By Eqs. 7 and 8, $m(v_r) - m(p) \ge 0$. Hence, the lemma is proved.$\square$

By Lemma 2, if the endpoints of an edge $e \in E_c$ have different merits, then the endpoint with the larger merit should be the only local MinSum location on $e$. But what if the merits of the endpoints are identical? The following lemma provides the answer.

Lemma 3

Let $e$ be an edge in $E$ with endpoints $v_l,\; v_r$, such that $m(v_l)=m(v_r)$. Then, either all points on $e$ have the same merit, or $v_l$ and $v_r$ have larger merit than any other points on $e$.

Proof

First of all, by Lemma 2, for any point $\rho$ on $e$, it must satisfy $m(\rho )\le m(v_l)=m(v_r)$, given that $m(v_l)=m(v_r)$. Now, assume on the contrary that there exist two points $p$ and $q$ on $e$, such that $m(v_l) = m(v_r) = m(p) \ne m(q)$. This indicates that $m(q) < m(v_l) = m(v_r) = m(p)$. Assume without loss of generality that $d(v_l, p) < d(v_l, q)$. We will prove the lemma by showing that $m(p) = m(v_l)$ cannot hold given $m(p) > m(q)$.

Let $C_p$ be the set of clients attracted by $p$. We divide $C_p$ into three subsets $C_1,\; C_2$, and $C_3$, such that

$$\begin{aligned} C_1&= \{c \in C_p \mid d(c, p) = d(c, q) - d(p, q)\}, \\ C_2&= \{c \in C_p \mid d(c, p) = d(c, q) + d(p, q)\}, \\ C_3&= C_p - C_1 - C_2. \end{aligned}$$

It can be verified that, for any client $c \in C_3$, the shortest path from $c$ to $p$ must go through $v_l$. This indicates that,

$$\begin{aligned} d(c, v_l) = d(c, p) - d(v_l, p), \forall c\in C_3. \end{aligned}$$

(9)

Given $m(p) > m(q)$ and $C_p \subseteq C$, we have

$$\begin{aligned}&\!\!\!\sum _{c \in C_1} w(c) \cdot \big ( d(c, q) - d(c, p) \big )\nonumber \\&\quad \!\!\! - \sum _{c \in C_2} w(c) \big ( d(c, p) - d(c, q) \big ) \\&\!\!\!\quad +\sum _{c \in C_3} w(c) \cdot |d(c, q) - d(c,p)| > 0. \end{aligned}$$

This leads to

$$\begin{aligned} \sum _{c \in C_1 \cup C_3} w(c) - \sum _{c \in C_2} w(c) > 0 \end{aligned}$$

(10)

On the other hand, we have

$$\begin{aligned} m(v_l) \!-\! m(p) \!&\ge \!\sum _{c \in C_1 \cup C_3} w(c) \cdot \big ( d(c, p) - d(c, v_l) \big ) \nonumber \\&{} - \sum _{c \in C_2} w(c) \cdot \big ( d(c, v_l - d(c, p) \big ) \nonumber \\&= d(v_l, p) \cdot \Big (\sum _{c \in C_1 \cup C_3} w(c) - \sum _{c \in C_2} w(c)\Big ) \nonumber \\&> 0. \qquad \text { (By Equation~10)} \end{aligned}$$

(11)

Thus, the lemma is proved.$\square$

By Lemmas 2 and 3, we can identify the local MinSum locations on any given edge $e$ as follows. First, we compute the merits of $e$’s endpoints based on their attraction sets. If the merits of the endpoints differ, then we return the endpoint with the larger merit as the answer. Otherwise (i.e., both endpoints of $e$ have the same merit $\gamma$), we inspect any point $p$ in the interior of $e$ and derive $m(p)$ using the attraction sets of the endpoints. If $m(p) < \gamma$, both endpoints of $e$ are returned as the result; otherwise, we must have $m(p)=\gamma$, in which case we return the whole edge $e$ as the answer. In summary, the local MinSum locations on $e$ can be found by computing the merits of at most three points on $e$, which takes $O(n)$ time and $O(n)$ space given the attraction sets of $e$’s endpoints.

Note that the above algorithm assumes that both endpoints of $e$ are candidate locations. To accommodate the case when either endpoint of $e$ is a facility, we post-process the output of our algorithm as follows. If the set $S$ of local MinSum locations returned by our algorithm contains a facility endpoint, we set $S = \emptyset$; otherwise, we keep $S$ intact. To understand this post-processing step, observe that the merit of any facility point is zero, since building a new facility on any point in $F$ does not change the attractor distance of any client. Hence, if $S$ contains a facility point, then the maximum merit of all points on $e$ should be zero. In that case, the global MinSum location must not be on $e$, and hence, we can ignore the local MinSum locations found on $e$.

4.3 MinMax location queries

Next, we present our solution for finding the local MinMax locations on any edge $e \in E_c$, i.e., the points on $e$ where a new facility can be built to minimize the maximum Wadof all clients. Our solution is based on the following observation: For any client $c$, the relationship between the Wadof $c$ and the new facility’s location can be precisely captured using a piecewise linear function.

For example, consider the edge $e_0$ in Fig. 4a. Assume that there exist only $4$ clients $c_1,\; c_2,\; c_3$, and $c_4$, as illustrated in the attraction sets in Fig. 4a. Further assume that (i) the clients’ attractor distances are as shown in Fig. 5a, and (ii) all clients have a weight $1$. Then, if we add a new facility on $e_0$ that is $x$ ($x \in [0, 5]$) distance away from the left endpoint $v_l$ of $e_0$, the Wadof $c_3$ can be expressed as a piecewise linear function:

$$\begin{aligned} g_3(x) = \left\{ \begin{array}{ll} x + 1, &{}\quad \mathrm if x \in [0, 3] \\ 7 - x, &{}\quad \mathrm if x \in (3, 5] \end{array} \right. \end{aligned}$$

We define $g_3$ as the Wad function of $c_3$. Similarly, we can also derive a Wadfunction $g_i$ for each of the other client $c_i\; (i=1, 2, 4)$. Figure 5b illustrates $g_i\; (i \in [1, 4])$.

Fig. 5

Representing attractor distances as functions of the location of the new facility. a Attractor distances without the new facility, b Piecewise linear functions

Let $g_{up}$ be the upper envelope [1] of $\{g_i\}$, i.e., $g_{up}(x) = \max _{i} \{g_i(x)\}$ for any $x \in [0, 5]$ (see Fig. 5b). Then, $g_{up}(x)$ captures the maximum Wadof the clients when a new facility is built on $x$. Thus, if the point (on $e_0$) that is $x$ distance away from $v_l$ is a local MinMax location, then $g_{up}$ must be minimized at $x$, and vice versa. As shown in Fig. 5b, $g_{up}$ is minimized when $x \in [0, 0.5]$. Hence, the local MinMax locations on $e_0$ are the points $p$ on $e_0$ with $d(p, v_l) \in [0, 0.5]$.

In general, to compute the local MinMax locations on an edge $e$, it suffices to first construct the upper envelope of all clients’ Wadfunctions and then identify the points at which the upper envelope is minimized. This motivates our MinMaxLoc algorithm (in Fig. 6) for computing local MinMax locations.

Fig. 6

The MinMaxLoc algorithm

Given an edge $e \in E_c$, MinMaxLoc first retrieves two attraction sets $\mathcal {A}(v_l)$ and $\mathcal {A}(v_r)$, where $v_l$ ($v_r$) is the left (right) endpoint of $e$. After that, it creates a two-dimensional plane $R$, in which it will construct the Wadfunctions of some clients. Specifically, MinMaxLoc first identifies the set $C_-$ of clients that appear in neither $\mathcal {A}(v_l)$ nor $\mathcal {A}(v_l)$. By Lemma 1, for any client $c \in C_-$, the attractor distance of $c$ is not affected by a new facility built on $e$. Hence, the Wadfunction of $c$ can be represented by a horizontal line segment in $R$. Observe that, only one of those segments may affect the upper envelope $g_{up}$, i.e., the segment corresponding to the client $c^*$ with the largest Wadin $C_-$. Therefore, given $C_-$, MinMaxLoc only constructs the Wadfunction of $c^*$, ignoring all the other clients in $C_-$.

Next, MinMaxLoc examines each client $c \in C - C_-$ and derives the Wadfunction of $c$ based on $\mathcal {A}(v_l)$ and $\mathcal {A}(v_r)$. In particular, each Wadfunction is represented using at most three line segments in $R$. Finally, MinMaxLoc computes the upper envelope $g_{up}$ of the Wadfunctions in $R$ and then identifies and returns the points at which $g_{up}$ is minimized.

MinMaxLoc can be implemented in $O(n \log n)$ time and $O(n)$ space. Specifically, given the attractor distances of the clients in $C$, we can identify the client $c^*$ with $O(n)$ time and space. After that, it takes only $O(n)$ time and space to construct the Wadfunctions of clients, since each function is represented with $O(1)$ line segments. As there exist $O(n)$ segments in $R$, the upper envelope $g_{up}$ should contain $O(n)$ linear pieces and can be computed in $O(n \log n)$ time and $O(n)$ space [13]. Finally, by scanning the $O(n)$ linear pieces of $g_{up}$, we can compute the local MinMax locations on $e$ in $O(n)$ time and space.

In addition, MinMaxLoc can also be extended to handle the case when either endpoint of $e$ is a facility in $F$. In particular, if the left endpoint $v_l$ of $e$ is a facility, then MinMaxLoc excludes $v_l$ when it computes the upper envelope $g_{up}$ of the Wadfunctions. That is, the domain of $g_{up}$ is defined as $(0, \ell ]$ instead of $[0, \ell ]$. The case when the right endpoint of $e$ is a facility can be addressed similarly.

5 Computing attraction sets and attractor distances

Our algorithms in Sect. 4 require as input (i) the attractor distances of all clients in $C$, and (ii) the attraction sets of the endpoints of the given edge $e \in E_c$. The attractor distances can be easily computed using the algorithm by Erwig and Hagen [7]. Specifically, Erwig and Hagen’s algorithm takes as input a road network $G$ and a set $F$ of facilities. With $O(n \log n)$ time and $O(n)$ space, the algorithm can identify the distance from each vertex $v$ in $G$ to its nearest facility in $F$. In the following, we will investigate how to compute the attraction sets of the vertices in $G$, given the attractor distances derived from Erwig and Hagen’s algorithm.

5.1 The blossom algorithm

By definition, a client $c$ appears in the attraction set of a vertex $v$, if and only if $d(c, v)$ is no more than the attractor distance $a(c)$ of $c$. Therefore, given the attractor distances of all clients, we can compute the attraction sets of all vertices in $G$ in a batch as follows. First, we set the attraction set of every vertex in $G$ to $\emptyset$. After that, for each client $c \in C$, we apply Dijkstra’s algorithm [5] to traverse the vertices in $G$ in ascending order of their distances to $c$. For each vertex $v$ encountered, we check whether $d(c, v) \le a(c)$. If $d(c, v) \le a(c),\; c$ is inserted into the attraction set of $v$. Otherwise, $d(c, v') > a(c)$ must hold for any unvisited vertex $v'$, i.e., none of the unvisited vertices can attract $c$. In that case, we terminate the traversal and proceed to the next client. Once all clients are processed, we obtain the attraction sets of all vertices in $G$. We refer to the above algorithm as Blossom, as illustrated in Fig. 9.

Blossom has an $O(n^2 \log n)$ time complexity, since it invokes Dijkstra’s algorithm once for each client, and each execution of Dijkstra’s algorithm takes $O(n \log n)$ time in the worst case [5]. Blossom requires $O(n^2)$ space, as it materializes the attraction set of each vertex in $G$, and each attraction set contains the information of $O(n)$ clients. Such space consumption is prohibitive when $n$ is large. To remedy this deficiency, Sect. 5.2 proposes an alternative solution that requires only $O(n)$ space.

5.2 The OTF algorithm

The enormous space requirement of Blossom is caused by the massive materialization of attraction sets. A natural idea to reduce the space overhead is to avoid storing the attraction sets and derive them only when needed. That is, whenever we need to compute the local optimal locations on an edge $e \in E_c$, we compute the attraction sets of $e$’s endpoints on the fly and then discard the attraction sets once the local optimal locations are found. But the question is, given a vertex $v$ in $G$, how do we construct the attraction set $\mathcal {A}(v)$ of $v$? A straightforward solution is to apply Dijkstra’s algorithm to scan through all vertices in $G$ in ascending order of their distances to $v$. In particular, for each client $c$ encountered during the scan, we examine the distance $d(v, c)$ from $c$ to $v$. If $d(v, c) < a(c)$, we add $c$ into $\mathcal {A}(v)$; otherwise, $c$ is ignored. Apparently, this solution incurs significant computation overhead, as it requires traversing a large number of vertices. Is it possible to compute $\mathcal {A}(v)$ without an exhaustive search of the vertices in $G$? The following lemma provides us some hints.

Lemma 4

Given two vertices $v$ and $v'$ in $G$, such that $d(v, v')$ is larger than the distance from $v'$ to its nearest facility $f'$. Then, $\forall c\in \mathcal {A}(v)$, the shortest path from $v$ to $c$ must not go through $v'$.

Proof

Assume on the contrary that the shortest path from $v$ to $c$ goes through $v'$. Then, we have

$$\begin{aligned} d(v, c)&= d(v, v') + d(v', c) > d(v', f') + d(v', c) \\&\ge d(f', c). \end{aligned}$$

This contradicts our assumption that $c$ is attracted by $v$.$\square$

Consider for example the road network in Fig. 7, which contains three subgraph $G_1,\; G_2$, and $G_3$ that are connected by a facility $f_1$ and two vertices $v_1$ and $v_2$. In addition, $d(v_1, v_2) = 2$, $d(v_2, f_1) = 1$, and $f_1$ is the facility closest to $v_2$. Since $d(v_1, v_2) > d(v_2, f_1)$, by Lemma 4, $v_2$ must not be on the shortest path from $v_1$ to any client attracted by $v_1$. This means that no client in $G_2$ or $G_3$ can be attracted by $v_1$, because all paths from $v_1$ to $G_2$ or $G_3$ go through $v_2$. Therefore, if we are to compute $\mathcal {A}(v_1)$, it suffices to examine only the clients in $G_1$.

Fig. 7

Example of Lemma 4

Based on Lemma 4, we propose the OTF (On-The-Fly) algorithm (in Fig. 10) for computing the attraction set of a vertex $v$ in $G$. Given $v$, OTF first sets $\mathcal {A}(v) = \emptyset$ and then applies Dijkstra’s algorithm to visit the vertices in $G$ in ascending order of their distances to $v$. For each vertex $v'$ visited, OTF retrieves the distance $\lambda$ from $v'$ to its closest facility (recall that $\lambda$ is computed using Erwig and Hagen’s algorithm [7]). If $d(v, v') \le \lambda$ and $v'$ is a client, then OTF adds $v'$ into $\mathcal {A}(v)$. On the other hand, if $d(v, v') > \lambda$, then OTF ignores all edges adjacent to $v'$ when it traverses the remaining vertices in $G$. This does not affect the correctness of OTF, since, by Lemma 4, deleting $v'$ from $G$ does not change the shortest path from $v$ to any client attracted by $v$. After $v$ is processed, OTF checks whether any of the unvisited vertices in $G$ is still connected to $v$. If none of those vertices is connected to $v$, OTF terminates by returning $\mathcal {A}(v)$; otherwise, OTF proceeds to the unvisited vertex that is closest to $v$.

It is not hard to verify that OTF runs in $O(n \log n)$ time and $O(n)$ space. Therefore, if we employ OTF to compute the local optimal locations on every edge in $G$, then the total time required for deriving the attraction sets would be $O(n^2 \log n)$, and the total space needed is $O(n)$ (as OTF does not materialize any attraction sets). In contrast, computing the attraction sets with Blossom incurs $O(n^2 \log n)$ time and $O(n^2)$ space overhead. Hence, OTF is more favorable than Blossom in terms of asymptotic performance.

6 Pruning of road segments

Given the algorithms in Sects. 4 and 5, we may answer any OL query by first enumerating the local optima on each edge in $E_c$ and then deriving the global optimal solutions based on the local optima. This approach, however, incurs a significant overhead when $E_c$ contains a large number of edges. To address this issue, in this section we propose a fine-grained partitioning (FGP) technique to avoid the exhaustive search on the edges in $E_c$.

6.1 Algorithm overview

At a high level, FGP works in four steps as follows. First, we divide $G$ into $m$ edge-disjoint subgraphs $G_1, G_2, \ldots , G_m$, where $m$ is an algorithm-specific parameter. Second, for each subgraph $G_i$ ($i \in [1, m]$), we derive a potential client set $C_i$ of $G_i$, i.e., a superset of all clients that can be attracted by a new facility built on any edge in $G_i$.

As a third step, we inspect each potential client set $C_i$ ($i \in [1, m]$), based on which we derive an upper bound of the benefit of any candidate location $p$ in $G_i$. Specifically, for competitive location queries, the benefit of $p$ is defined as the total weight of the clients attracted by $p$; for MinSum (MinMax) location queries, the benefit of $p$ is quantified as the reduction in the total (maximum) Wadof all clients, when a new facility is built on $p$.

Finally, we examine the subgraphs $G_1, G_2, \ldots , G_m$ in descending order of their benefit upper bounds. For each subgraph $G_i$, we apply the algorithms in Sects. 4 and 5 to identify the local optimal locations in $G_i$. After processing $G_i$, we inspect the set $S$ of best local optima we have found so far. If the benefits of those locations are larger than the benefit upper bounds of all unvisited subgraphs, we terminate the search and return $S$ as the final results; otherwise, we move on to the next subgraph.

The efficacy of the above framework rely on three issues, namely (i) how the subgraphs of $G$ are generated, (ii) how the potential client set $C_i$ of each subgraph $G_i$ is derived, and (iii) how the benefit upper bound of $G_i$ is computed. In the following, we will first clarify how FGP derives benefit upper bounds, deferring the solutions to the other two issues to Sect. 6.2. We begin with the following lemma.

Lemma 5

Let $G_i$ be a subgraph of $G,\; C_i$ be the potential client set of $G_i$, and $p$ be a candidate location in $G_i$. Then, for any competitive location query, the benefit of $p$ is at most $\sum _{c \in C_i} w(c)$. For any MinSum location query, the benefit of $p$ is at most $\sum _{c \in C_i} \widehat{a}(c)$. For any MinMax location query, the benefit of $p$ is at most $\max _{c \in C} \widehat{a}(c) - \max _{c \in C - C_i} \widehat{a}(c)$.

Proof

The lemma follows from the facts that (i) $C_i$ contains all clients that can be attracted by $p$, and (ii) for any client in $C_i$, its Wadis at least zero after a new facility is built on $p$.$\square$

The benefit upper bounds in Lemma 5 require knowledge of all clients’ attractor distances, which, as mentioned in Sect. 5, can be computed in $O(n \log n)$ time and $O(n)$ space using Erwig and Hagen’s algorithm [7]. We can further sort the attractor distances in a descending order with $O(n \log n)$ time and $O(n)$ space. Observe that, given the sorted attractor distances and the potential client set $C_i$ of a subgraph $G_i$, the benefit upper bound of $G_i$ (for any OL query) can be computed efficiently in $O(|C_i|)$ time and $O(n)$ space.

6.2 Graph partitioning

We are now ready to discuss how FGP generates the subgraphs from $G$ and computes the potential client set of each subgraph. In particular, FGP generates subgraphs from $G$ by applying an algorithm called GPart (as illustrated Fig. 11), which takes as input $G$ and a user defined parameter $\theta \in (0, 1]$. GPart first identifies the set $V$ of vertices in $G$ that are adjacent to some edges in $E_c$. As a second step, GPart computes a random sample set $V_\Delta$ of the vertices in $V$ with a sampling rate $\theta$, after which it splits $G$ into subgraphs based on $V_\Delta$.

Specifically, GPart first constructs $|V_\Delta |$ empty subgraphs and assigns each vertex in $V_\Delta$ as the “center” of a distinct subgraphs. After that, for each vertex $v$ in $G$, GPart identifies the vertex $v' \in V_\Delta$ that is the closest to $v$ and computes $d(v, v')$. This step can be done by applying Erwig and Hagen’s algorithm [7], with $G$ and $V_\Delta$ as the input. Next, for each edge $e$ in $G$, GPart checks the two endpoints $v_l$ and $v_r$ of $e$ and inserts $e$ into the subgraph whose center $v'$ minimizes $\min \{d(v', v_l), d(v', v_r)\}$. After all edges in $G$ are processed, GPart terminates by returning all subgraphs constructed. For example, if $G$ equals the graph in Fig. 8 and $V_\Delta = \{v_1, v_2, v_3\}$, then GPart would construct three subgraphs $\{e_1, e_2, e_3\},\; \{e_4, e_5, e_6\}$, and $\{e_7, e_8\}$, whose centers are $v_1,\; v_2$, and $v_3$, respectively. In summary, GPart ensures that the edges in the same subgraph form a cluster around the subgraph center. As such, the edges belonging to the same subgraph tend to be close to each other. This helps tighten the benefit upper bounds of the subgraph because, intuitively, points in proximity to each other have similar benefits. Regarding asymptotic performance, it can be verified that GPart runs in $O(n \log n)$ time and $O(n)$ space.

Fig. 8

Example of GPart

Fig. 9

The Blossom algorithm

Fig. 10

The OTF algorithm

Fig. 11

The GPart algorithm

Given a subgraph $G_i$ obtained from GPart, our next step is to derive the potential client set for each $G_i$. Let $E_{G_i}$ be the set of edges in $G_i$ that also appear in $E_c$, and $V_{G_i}$ be the set of endpoints of the edges in $E_{G_i}$. By Lemma 1, for any candidate location $p$ on an edge $e$ in $G_i$, the set of clients attracted by $p$ is always a subset of the clients in the attraction sets of $e$’s endpoints. Therefore, the potential client set of $G_i$ can be formulated as the set of all clients that appear in the attraction sets of the vertices in $V_{G_i}$. In turn, the attraction sets of the vertices in $V_{G_i}$ can be derived by applying either the Blossom algorithm or the OTF algorithm in Sect. 5. In particular, if Blossom is adopted, then we feed the graph $G$ as the input to Blossom.¹ In return, we obtain the attraction sets of all vertices in $G$, based on which we can compute the potential clients set of all subgraphs in $G$. In addition, the attraction sets can be reused when we need to compute the local optimal locations on any edge in $G$.

On the other hand, if OTF is adopted, then we feed each vertex in $V_{G_i}$ to OTF to compute its attraction set, after which we collect all clients that appear in at least one of the attraction sets. The drawback of this approach is that it requires multiple executions of OTF, which leads to inferior time efficiency. To remedy this drawback, we propose the P-OTF algorithm (in Fig. 12) for computing the potential client set of a subgraph $G_i$. Given the graph $G$, P-OTF first creates a new vertex $v_0$ in $G$ and then constructs an edge between $v_0$ and each vertex in $V_{G_i}$, such that the edge has a length $0$. After that, P-OTF invokes OTF once to compute the attraction set of $v_0$ in $G$. Observe that, if a client $c$ is attracted by $v_0$, then there must exist a vertex in $V_{G_i}$ that attracts $c$, and vice versa. Hence, the potential client set of $G_i$ should be equal to the set of clients in the attraction set $\mathcal {A}(v_0)$ of $v_0$. Therefore, once $\mathcal {A}(v_0)$ is computed, P-OTF terminates by returning all clients in $\mathcal {A}(v_0)$. In summary, P-OTF computes the potential client set of $G_i$ by invoking OTF only once, which incurs $O(n \log n)$ time and $O(n)$ space overhead.

Fig. 12

The P-OTF algorithm

Before closing this section, we discuss how we set the input parameter $\theta$ of GPart. In general, a larger $\theta$ results in smaller subgraphs, which in turn leads to tighter benefit upper bounds. Nevertheless, the increase in $\theta$ would also lead to a larger number of subgraphs, which entails a higher computation cost, as we need to derive the potential client set for each subgraph. Ideally, we should set $\theta$ to an appropriate value that strikes a good balance between the tightness of the benefit upper bounds and the cost of deriving the bounds. We observe that, when the potential client sets of the subgraphs are computed using Blossom, $\theta$ should be set to $1$. This is because, Blossom derives potential client sets by computing the attraction sets of all vertices, regardless of the value of $\theta$. As a consequence, the computation cost of the benefit upper bounds is independent of $\theta$. Hence, we can set $\theta =1$ to obtain the tightest benefit upper bounds without sacrificing time efficiency. On the other hand, if P-OTF is adopted, then the overhead of computing potential client sets increases with the number of subgraphs. To ensure that this computation overhead does not affect the overall performance, $\theta$ should be set to a small value. We suggest setting $\theta =1\,\permille$ across the board.

7 Recomputation of local optimal locations after updates

In this section, we present solutions for efficiently monitor the local OLs given continuous updates in the locations of facilities and clients. This problem setting can be illustrated with following example.

Example 5

John owns a set of trucks for food service in San Francisco, and he would like to position his trucks to attract the largest number of clients against competition from other food service trucks. Given that the locations of clients and other competing trucks may change as time evolves, John would like to continuously monitor the optimal locations for positioning his trucks.

The updates of facilities and/or clients on a road network are natural and common operations. For users who would like to track optimal location(s) in the face of updates over a time period, our dynamic monitoring techniques are essential. Note that tracking optimal location(s) over a period of time, rather than finding an optimal location in a given time-instance and building a facility there right away, often is a natural choice for many business operations. For example, a corporation would like to monitor the optimal location for their business to build a new facility in a chosen time period, before making the final decision. This gives them the opportunity to carry out market analysis, learn how other facilities may update their locations, and more importantly, how clients may move on the road network over a period of time.

Furthermore, our dynamic monitoring techniques can be used to answer continuous optimal location queries (COLQ) efficiently, where a service provider needs to answer a sequence of optimal location queries from different users, and very naturally, updates may take place in between any two OLQs. Instead of always answering an OLQ from scratch, it is obviously desirable to answer them in an incremental and monitoring fashion.

In what follows, we will first present an overview of our solutions for handling updates (Sect. 7.1) and then discuss detailed algorithms for the three variants of optimal location queries (Sects. 7.2–7.4).

7.1 Overview

We consider four types of updates to the locations of clients and facilities:

• 1. Insertion of a client $c$ (denoted as $AddC(c)$);

• 2. Deletion of a client $c$ (denoted as $DelC(c)$);

• 3. Insertion of a facility $f$ (denoted as $AddF(f)$);

• 4. Deletion of a facility $f$ (denoted as $DelF(f)$).

A straightforward method for handle such updates is to adopt our algorithms in Sects. 3–6, i.e., we recompute the OLs from scratch after each update. Intuitively, this method is highly inefficient as it performs a large amount of redundant computation in the identification of OLs. To address this issue, we extend our unified framework in Sect. 3 and enables it to incrementally process updates.

First, for each edge $e \in E_c$, we maintain the set $I_0$ of local OLs on $e$, as well as the benefit $m_0$s of those OLs. For the competitive location query, the benefit $m_0$ is the total weights of clients attracted by a facility built on the OLs. For the MinSum location query, $m_0$ is the merit of the OLs. For the MinMax location query, $m_0$ is the maximum WAD of all clients. Given an update of clients or facilities, we process the update in four steps as follows:

• 1. Step 1: We compute a set $V_c$ of clients whose attractor distances are affected by the update.

• 2. Step 2: For each client $c\in V_c$, we identify its previous attractor distance $a^0(c)$ and new attractor distance $a'(c)$, and we construct two sets $\mathcal {U}_c^-$ and $\mathcal {U}_c^+$, where

  $$\begin{aligned} \mathcal {U}_c^-&= \{ \langle v, d(c,v)\rangle | d(c,v)<a^0(c) \}, \\ \mathcal {U}_c^+&= \{ \langle v, d(c,v)\rangle | d(c,v)<a'(c) \}. \end{aligned}$$

• 3. Step 3: We update $I_0$ and $m_0$ for each edge $e$, based on the sets $V_c,\; a^0(c),\; a'(c),\; \mathcal {U}_c^-$, and $\mathcal {U}_c^+$ associated with each client $c \in V_c$.

• 4. Step 4: We derive and return the global OLs when none of the unvisited $e \in E_c$ can provide a better solution than the best optima found so far.

To explain, recall that the local OLs on an edge $e$ are decided by (i) the attraction sets for the endpoints of $e$ and (ii) the attractor distances of the clients. Therefore, if we are to derive the new $I$ and $m$ for each edge, we can first identify the changes in the aforementioned attraction sets and attractor distances. Steps $1$ and $2$ serve this purpose since (i) for any client $c$, the change in the attractor distance of $c$ can be derived from $a^0(c)$ and $a'(c)$, and (ii) the change in the attraction sets of $e$’s endpoints can be derived given $\mathcal {U}_c^-$ and $\mathcal {U}_c^+$ for each $c$. In the following, we will first discuss how Steps 1 and 2 can be implemented for the four types of updates, namely $AddC(c),\;DelC(c),\; AddF(f)$, and $DelF(f)$.

$\pmb {AddC(c)}$ and $\pmb {DelC(c)}$: Given a client $c$ to be inserted or deleted, we can easily perform Step $1$ by setting $V_c=\{c\}$. For Step $2$, we employ the Dijkstra’s algorithm to traverse the vertices in $G$ in ascending order of their distances to $c$, until we reach the facility $f$ nearest to $c$. Then, we set $a_0(c)=0$ and $a'(c)=d(c,f)$ if $f$ is just inserted; otherwise (i.e., $f$ is just deleted), we set $a_0(c)=d(c,f')$ and $a'(c)=d(c,f)$. Finally, for each vertex $v$ visited by Dijkstra’s algorithm, we insert an entry $\langle v, d(c,v)\rangle$ into $\mathcal {U}_c^+$.

$\pmb {AddF(f)}$ and $\pmb {DelF(f)}$: When a facility $f$ is inserted or deleted, the set $V_c$ of clients in Step $1$ is exactly the set $\mathcal {A}(f)$, i.e., the attraction set of $f$. To compute $\mathcal {A}(f)$, we can use either the Blossom algorithm in Sect. 5.1 or the OTF algorithm in Sect. 5.2. After that, we can perform Step $2$ as follows. For each client $c \in \mathcal {A}(f)$, we employ Dijkstra’s algorithm to traverse the vertices in $G$ in ascending order of their distances to $c$, until we reach a facility $f' \ne f$. Then, we set $a_0(c)=d(c,f')$ and $a'(c)=d(c,f)$. Finally, for each vertex $v$ visited Dijkstra’s algorithm, we insert an entry $\langle v, d(c,v)\rangle$ into $\mathcal {U}_c^-$ if $d(c, v) \le d(c, f)$; otherwise, we insert an entry $\langle v, d(c,v)\rangle$ into $\mathcal {U}_c^+$.

Next, we clarify how Step 3 can be implemented. In our solution, for each $c \in V_c$, we update the local OLs for each edge using the change in attractor distances and attraction sets caused by $c$, which can be derived from $a^0(c)$, $a'(c)$, $\mathcal {U}_c^-$ and $\mathcal {U}_c^+$. Note that not all edges’ local OLs can be affected by a client $c$. In other words, when we update local OLs for each edge with the effect of $c$, we can initially identify a set of edges whose $I$ and $m$ will remain unchanged. Therefore, for each $c \in V_c$, we first prune this set of edges and then update the local OLs for remaining edges. In the following, we will clarity how we can perform the pruning of edges and the update of the local OLs, for each of the three variants of OL queries.

7.2 Competitive location queries

Figure 13 shows the algorithm for updating local OLs for a competitive location query, given a client $c \in V_c$. The algorithm first prunes the edges whose $I$ and $m$ will not change (Lines 1–4 in Fig. 13. Specifically, if an edge’s endpoints cannot attract $c$ either before the update or after the update, its local OLs will not change. The reason is that, when we compute local OLs on $e(v_l,v_r)$ (see Sect. 4.1), we use $\mathcal {A}(v_l)$, $\mathcal {A}(v_r)$ and $a(c)$s only if $c$ appears in $\mathcal {A}(v_l)$ or $\mathcal {A}(v_r)$.

Fig. 13

The CompLoc_ClientUpdate Algorithm

As a next step, we update the local OLs for each of the remaining edges $(E_c)$. First, we construct the set $I^-$ of points on $e$ that attracts $c$ before the update, and the set $I^+$ of points on $e$ that attracts $c$ after the update (lines 6–16), in a similar fashion as what we do in the CompLoc Algorithm (Fig. 3) for each client. There are three possible cases:

• 1. $I^-=I^+$, i.e., the set of points that attracts $c$ remains unchanged. In this case, we keep $I_0$ and $m_0$ as new local OLs and their benefits of $e$.

• 2. $I^-\subset I^+$, i.e., there is a new set of points that can attract $c$. Let $I'=I^+-I^-$. In this case, we compute $I_0 \cap I'$. If $I_0 \cap I' = \emptyset$, then we recompute the new local OLs. If $I_0 \cap I' \ne \emptyset$, then $I_0 \cap I'$ must be the the new local OLs, in which case we update $m$ accordingly.

• 3. $I^+\subset I^-$, i.e., there is a set of points that can attract $c$ before the update but cannot attract $c$ any more after the update. Let $I^* = I^- - I^+$. In this case, if $I^*$ fully covers $e$, then the local OLs remain the same, and $m=m_0-w(c)$. Otherwise, we compute $I_0 - I^*$. If $I_0 - I^*$ is not empty, the OLs will be $I_0-I'$ (lines $30$ and $31$). On the other hand, if $I_0 - I^*$ is empty, then we recompute the local optima using the CompLoc Algorithm in Fig. 3.

Note that one of the three cases must occur since we have $I^-\subset I^+$ whenever $a^0(c)\le a'(c)$, and $I^+\subset I^-$ otherwise.

Given the CompLoc_ClientUpdate Algorithm, we can implement Step 3 in Sect. 7.1 as follows. For $AddC(c)$ and $DelC(c)$, we have $V_c=\{c\}$, and hence, we only need to invoke CompLoc_ClientUpdate once, with $c$ as the input. For $AddF(f)$ and $DelF(f)$, we need to apply CompLoc_ClientUpdate once for each client in $V_c =\{ c | \langle c,d(c,v) \rangle$ $\in \mathcal {A}(f)\}$. Such multiple execution of the algorithm may lead to repeated computation of the local OLs on an edge $e$. To avoid this unnecessary overhead, when handling $AddF(f)$ and $DelF(f)$, we will first identify the edges whose local OLs need to be updated, and we compute the local OLs for each of those edge in a batch, without any redundant computation.

7.3 MinSum location queries

Recall that, to compute the local OLs for a MinSum location query, we only need the merit value of an edge’s two endpoints, $m(v_l)$ and $m(v_r)$. Hence, we only need to update the merit value for each vertex $v$, which can attract those clients affected by the update (i.e., $V_c$). There are three conditions in which a vertex’s merit value has to be updated. In the first case, $v$ can attract $c$ before the update but cannot attract $c$ after the update. In this case, we should subtract $w(c)\cdot (a^0(c)-d(v,c))$ away from $m(v)$. Secondly, $v$ can now attract $c$; thus, we should add $w(c)\cdot (a'(c)-d(v,c))$ to $m(v)$. The last condition is that $v$ can attract $c$ both before and after the update but $a(c)$ has changed. In this case, we should update $m(v)$ with the difference between $a^0(c)$ and $a'(c)$. The details of the MinSumLoc_ClientUpdate Algorithm are shown in the Fig. 14. To achieve step $3$ during an update for a MinSum location query, we execute the MinSumLoc_ClientUpdate Algorithm for each $c\in V_c$.

Fig. 14

The MinSumLoc_ClientUpdate Algorithm

7.4 MinMax location queries

Recall that the local MinMax locations on an edge $e$ are the points $x$ on $e$ at which $g_{up}(x)$ is minimized (see Sect. 4.3). Therefore, for any edge $e$, if $m_0$ is larger than both $\widehat{a}^0(c)$ and $\widehat{a}'(c)$, then $e$ would not be affected by the change in the attractor distance of $c$. In that case, we can omit $e$ when processing the update.

On the other hand, if $m_0$ is smaller than either $\widehat{a}^0(c)$ or $\widehat{a}'(c)$, then we first check whether the previous $g_c(x)$ can affect $e$’s $g_{up}(x)$. If it does, we should evaluate how removing $g_c(x)$ can affect $e$’s $I$ and $m$. Secondly, we check whether the new $g_c(x)$ can affect $e$’s $g_{up}(x)$. If it does, we should evaluate how adding $g_c(x)$ can affect $e$’s $I$ and $m$. Here the previous $g_c(x)$ can be easily derived from $a^0(c)$ and $\mathcal {U}_c^-$, while the new $g_c(x)$ can be derived from $a'(c)$ and $\mathcal {U}_c^+$ (see Sect. 4.3).

To evaluate how removing $g_c(x)$ from $e$ can affect $I$ and $m$, if the maximum value of $g_c(x)$ is less than $m_0$, the local MinMax locations remain the same; otherwise, we recompute them using the MinMaxLoc algorithm in Fig. 6. To evaluate how adding $g_c(x)$ to $e$ may affect $I$ and $m$, we compute the envelope of $g(x)=m_0$ and $g_c(x)$ as $g_{up}'(x)$. After that, if there exist points in $I_0$ where $g_{up}'(x)$ is minimized with value $m_0$, we return those points with local optima $m_0$. Otherwise, we recompute the local MinMax locations using the MinMaxLoc algorithm. The details of the MinMaxLoc_ClientUpdate Algorithm are shown in Fig. 15.

Fig. 15

The MinMaxLoc_ClientUpdate Algorithm

To implement Step 3 during an update for a MinMax location query, we execute the MinMaxLoc_ClientUpdate Algorithm for each $c\in V_c$. If the type of update is $AddF(f)$ or $DelF(f)$, we can delay the recomputation operation to the end of update in order to avoid redundant computations, as we discussed in Sect. 7.2.

8 Updates with FGP

In this section, we discuss how the FGP technique proposed in Sect. 6 can be incorporated with the solutions in Sect. 7 to efficiently monitor the global optimal locations in the event of updates.

At a high level, handling updates with FGP works as follows. We maintain a list of subgraphs obtained in Sect. 6 by FGP. Note that in Sect. 6, the FGP method may only compute the local optima for each edge in some of the subgraphs, which have larger upper bounds than others. We denote those subgraphs as $computed$ and $uncomputed$, those have not executed the local optima computation due to relatively smaller upper bounds.

When there is an update, we compute the set of affected subgraphs and update their upper bounds. If an affected subgraph $G_i$ is $computed$, we update the local optima for its edges by applying the algorithms in Sect. 7; otherwise, we keep it in the group of $uncomputed$. The update of upper bounds for all four types of update operation can be easily achieved according to Lemma 5. The next step is similar to the last step of FGP. Specifically, we examine the subgraphs in descending order: for $uncomputed$ subgraphs, we sort them by their upper bounds; for $computed$ subgraphs, we sort them by their local optima. For each examined $G_i$, if it is $uncomputed$, we apply the algorithm in Sects. 4 and 5 to identify the local optima in $G_i$ and move it to $computed$; if it is $computed$, we take its local optima. If the current global optima is larger than the local optima (upper bound for $uncomputed$ subgraphs) of the next subgraph, we terminate the search.

The benefit of incorporating FGP for updates is that we do not need to maintain the local optima for all edges; this saves both running time and memory consumption. However, a potential limitation with the above algorithm is that the number of $computed$ subgraphs will never decrease. This may lead to a situation where most subgraphs will become $computed$ after many update operations, which eliminates the benefit of FGP. To avoid this problem, we propose to control the number of $computed$ subgraphs since we need to maintain the local optima for all edges in $computed$ subgraphs. Specifically, once we obtain the global optima, we change those unexamined $computed$ subgraphs, whose upper bound is less than the global optima, to $uncomputed$.

9 Continuous optimal location queries

Another important and interesting contribution made by our dynamic OLQ methods is the enabling of COLQ. Note that in numerous applications in spatial databases, the continuous monitoring of query results is desirable, and sometimes a critical requirement. The reason is that spatial objects often are moving, and updates to their locations are fairly common in many applications. For example, extensive efforts have been devoted to this topic, such as continuous nearest neighbor queries [11, 19], continuous skyline computations [14, 18], and many others. To that end, we will show that our dynamic update techniques enable the efficient execution of continuous optimal location queries (continuous OLQ).

Consider the following application scenario. The city office wants to answer optimal location queries to different business users as where the optimal location is for them to build their new facility. Once an optimal location has been identified, a business user is like to go ahead and build a new facility at that location. Without our dynamic update methods, the city needs to answer the next optimal location query from another business user from scratch. However, with our dynamic monitoring techniques, the city office can now continuously answer a sequence of optimal location queries, amid a number of updates in between. Note that in this process, not only a new facility can be inserted, an existing facility may be removed. Furthermore, clients on the road network may also have changed their locations over a period of time. These challenges must be addressed by our dynamic monitoring techniques. We denote this problem as the continuous optimal location queries. Formally, a user supplies a ordered sequence of operations, where an operation could be an optimal location query (any one of three types OLQs that we have studied), or an updates on either facilities and/or clients. The goal is to be able to continuously produce answers to these optimal location queries in an incremental fashion. Between any two optimal location queries in the sequence, there could be a (large) number of update operations on both facilities and clients.

That said, our proposed dynamic methods can be easily adapted to answer COLQs, where both clients and facilities may update their positions arbitrarily on the road network. We assume a client and/or a facility will issue an update with a new location (and an old location which is his/her current location on the network, if it is an existing client or facility), whenever a change has been made.

The first optimal location query from the sequence of operations can be answered using our static algorithms discussed in Sects. 4, 5, and 6. Subsequently, we can continuously monitor the optimal locations for subsequent OLQs in the input sequence by treating any update operation as a deletion (if an old location exists) followed by an insertion (of either a client or a facility), which is done using the recomputation methods proposed in Sects. 7 and 8.

10 Experiments

This section experimentally evaluates the proposed solutions. For each type of OL queries, we examine two approaches for traversing the edges in $E_c$, (i) the Basic approach that computes the local optimal locations on every edge in $E_c$ before returning the final results and (ii) the Fine-Grained Partitioning (FGP) approach. For each approach, we combine it with two different techniques for deriving attraction sets, i.e., Blossom and OTF. We implement our algorithms in C++ and perform all experiments on a Linux machine with an Intel Xeon $2$GHz CPU and $4$GB memory.

Our implementation uses the widely adopted road network representation proposed by Shekhar and Liu [25]. Besides the road network, in the dynamic scenario, we also maintain a list of local optimal locations and additional information for getting attraction sets. Specifically, for Basic approach, we maintain a list of all edges’ local optimal locations; for FGP approach, we maintain a list of subgraphs, and each subgraph contains a list of local optimal locations for its edges. In addition, for Blossom method, we maintain the attraction sets for all vertices in $G$, while for OTF method, we maintain the nearest facility for each vertex in $G$ as well as the distance between them.

The running time reported in our OLQ computation experiments includes the cost of all algorithmic components of our framework, including the overhead for computing attractor distances using Erwig and Hagen’s algorithm [7] (see Sect. 5). The running time for updates reports the cost after the OLQ computation.

Datasets We use two real road network datasets, SF and CA, obtained from the Digital Chart of the World Server. In particular, SF (CA) captures the road network in San Francisco (California) and contains 174,955 nodes and 223,000 edges (21,047 nodes and 21,692 edges). We obtain a large number of real building locations in San Francisco (California) from the OpenStreetMap project and use random sample sets of those locations as facilities and clients on SF (CA). We synthesize the weight of each client by sampling from a Zipf distribution with a skewness parameter $\alpha > 1$.

We also generate a synthetic dataset(denoted as UN), which has SF as its underlying road network and facilities and clients in uniform distribution. For the facilities and clients which are not located on road network edges, we snapped them to the closest edge.

Default settings For the computation of all three types of OL queries, we vary five parameters in our experiments: (i) the number of facilities $|F|$, (ii) the number of clients $|C|$, (iii) the percentage $\tau = |E^{\circ }_c| / |E^{\circ }|$ of edges (in the given road network) where the new facility can be built, (iv) the input parameter $\theta$ of the FGP algorithm (see Fig. 11), and (v) the skewness parameter $\alpha$ of the Zipf distribution from which we sample the weight of each client. For the updates, we vary two parameters: $|F|$ and $|C|$. For $AddC(c)$ and $DelC(c)$, we randomly generate 1,000 updates, and for $AddF(f)$ and $DelF(f)$, we randomly generate $50$ updates. Unless specified, we set $|F|=\hbox {1,000}$ and $|C|=300,000$, so as to capture the likely scenario in practice where the number of clients is much larger than the number of facilities. We also set $\tau =100\%$, in which case the OL queries are most computationally challenging, since we need to consider every point in the road network as a candidate location. The default value of $\theta$ is set to 100 % $(1\permille )$ when Blossom (OTF) is used to derive attraction sets, as discussed in Sect. 6.2. Finally, we set $\alpha = +\infty$ by default, in which case all clients have a weight 1.

10.1 The OLQ computation in the static case

We first investigate the efficiency and scalability of various methods for different OLQ queries in the static case.

Effect of $\theta$. Our first sets of experiments focus on competitive location queries (CLQ). Figure 16 shows the effect of $\theta$ on the running time of our solutions that incorporate FGP. Observe that, when Blossom is adopted to compute attraction sets, our solution is most efficient at $\theta = 1$. This is consistent with the analysis in Sect. 6.2 that $\theta = 1$ (i) leads to the tightest benefit upper bounds, and thus, (ii) facilitates early termination of edge traversal. In contrast, when OTF is adopted, $\theta = 1$ results in inferior computational efficiency. This is because, when OTF is employed, a larger $\theta$ leads to a higher cost for deriving benefit upper bounds, which offsets the efficiency gain obtained from the tighter upper bounds. On the other hand, $\theta = 1\permille$ strikes a good balance between the overhead of upper bound computation and the tightness of the upper bounds, which justifies our choice of default values for $\theta$. Note that another possible way of identifying a good $\theta$ value is to run tests on a (small) random sample of the dataset on the given network.

Fig. 16

Running time versus $\theta$ (CLQ). a $SF$, b $CA$

The OTF-based solution outperforms the Blossom-based approach in both cases. The reason is that, regardless of the value of $\theta$, the Blossom-based approach requires computing the attraction sets of all vertices. In contrast, the OTF-based solution only needs to derive the attraction sets of the vertices in each subgraph it visits. Since the OTF-based solution visits only subgraphs whose benefit upper bounds are large, it computes a much smaller number of attraction sets than the Blossom-based approach does, and hence, it achieves superior efficiency.

For brevity, in the following we focus on the larger SF dataset. The results on CA are qualitatively similar.

Effect of $\alpha$. Figure 17 shows the effect of $\alpha$ on the performance of our solutions, varying $\alpha$ from 2 to $+\infty$. Evidently, the memory consumption and running time of our solutions are insensitive to the clients’ weight distributions. The reason is that, for Basic approach, the change of $\alpha$ does not change the complexity of our solution. And for FGP approach, the distribution of weights is independent with the clients’ locations, so the distribution of benefit upper bounds of subgraphs will not be affected by $\alpha$, which indicates that the performance of FGP approach is also insensitive to the weight distribution.

Fig. 17

Effect of $\alpha$ (CLQ on SF). a Memory consumption, b running time

Effect of $|F|$. Next, we vary the number of facilities $(|F|)$ from 32 to 4,000. Figures 18a illustrates the memory consumption of our solutions on SF. The methods based on Blossom incur significant space overheads and run out of memory when $|F| < \hbox {1,000}$. This is due to the $O(n^2)$ space complexity of Blossom. In contrast, the memory consumption of OTF-based methods are always below 20MB, since OTF incurs only $O(n)$ space overhead.

Fig. 18

Effect of $|F|$ (CLQ on SF). a Memory consumption, b running time

Figure 18b shows the running time of each of our solutions as a function of $|F|$. The methods that incorporate FGP outperform the approaches with Basic in all cases, since FGP provides much more effective means to avoid visiting the edges that do not contain optimal locations. In addition, when FGP is adopted, the OTF-based approach is superior to the Blossom-based approach, as is consistent with the results in Fig. 16. Finally, the running time of all solutions decreases with the increase in $|F|$. The reason is that, when $|F|$ is large, each client $c$ tends to have a smaller attractor distance $a(c)$. This reduces the number of road network vertices that are within $a(c)$ distance to $c$, and hence, $c$ should appear in a smaller number of attraction sets. Therefore, the attract set of each vertex in the road network would become smaller, in which case that Blossom and OTF can be executed in shorter time. Consequently, the overall running time of our solutions is reduced.

Effect of $|C|$. The next set of experiments investigate the scalability of our solutions by varying the number of clients, $|C|$, from 100,000 to 500,000. Figure 19a, b shows the space consumption (running time) of our solutions as functions of $|C|$. As in the previous experiments, Blossom-based approaches consume enormous amounts of memory, while the method that incorporates both FGP and OTF consistently outperform all the other methods in terms of both space and time. The running time of all solutions increases with $|C|$, because a larger $|C|$ leads to (i) more edges in the transformed network $G$ and (ii) more clients in each attraction set, both of which complicate the computation of optimal locations. We also conduct the same experiment on UN dataset. Figure 20 shows the result. As we can see, the data distribution does not affect the performance of the proposed methods. In particular, with a uniform spatial distribution of facilities and clients, our FGP approach still has the best performance. That is because, the sizes of subgraphs generated by FGP approach are different, so the upper bounds of different subgraphs can be various, which indicates that the FGP approach is still effective when the spatial distribution of facilities and clients is uniform.

Fig. 19

Effect of $|C|$ (CLQ on SF). a Memory consumption, b running time

Fig. 20

Effect of $|C|$ (CLQ on UN). a Memory consumption, b running time

Effect of $\tau$. Figure 21 illustrates the memory consumption and running time of our solutions when $\tau$ changes from 1% to 100%. Blossom-based approaches require less memory when $\tau$ decreases, since (i) a smaller $\tau$ leads to fewer edges in $E_c$ and (ii) Blossom stores only the attraction sets of the endpoints of the edges in $E_c$. In contrast, the space overheads of OTF-based methods do not change with $\tau$, since they always compute attraction sets on the fly, regardless of the value of $\tau$.

Fig. 21

Effect of $\tau$ (CLQ on SF). a Memory consumption, b running time

On the other hand, the running time of Blossom-based approaches is not affected by $\tau$. This is because, Blossom computes attraction sets, by invoking Dijkstra’s algorithm for each client $c \in C$ and putting $c$ in the attraction set of every vertex $v \in V$ such that $d(c, v) \le a(c)$. Observe that, even if we require only a single attraction set of a vertex $v_0 \in V$, Blossom still needs to execute Dijkstra’s algorithm once for each client $c$; otherwise, it is impossible to decide whether $d(c, v_0) \le a(c)$ holds or not. As a consequence, the efficiency of Blossom-based approaches does not improve with the decrease in $\tau$. In contrast, OTF-based solutions incur much less computation overhead when $\tau$ is reduced, since they compute attraction sets by invoking OTF only on the vertices of the edges in $E_c$. The decrease in $\tau$ renders $|E_c|$ smaller, in which case the OTF-based solutions require fewer executions of the OTF algorithm, and hence, their running time decreases.

Comparison with method in [10]. Figure 22 compares the memory consumption and running time of our solution with the method proposed in [10], which is denoted as ONLQ for convenience. In order to compare the performance fairly, we re-implemented ONLQ using C++ and perform all experiments on a Linux machine with the previously mentioned configurations. Our (the OTF with FGP) method has a less memory consumption but longer running time compared to the ONLQ method when we vary $|C|$. This observation can also be found when we vary $|F|$.

Fig. 22

Comparison with ONLQ in [10] (on SF). a Memory consumption, b running time

MinSum and MinMax location queries The rest of our experiments evaluate the performance of our solutions for MinSum location queries (MinSumLQ) and MinMax location queries (MinMaxLQ). In general, the experimental results are mostly similar to those for competitive location queries. This is not surprising, because our solutions for the three types of queries follow the same framework and adopt the same algorithmic components (e.g., Blossom and OTF).

Figures 23 and 24 show the effects of $|F|$ and $|C|$ on the performance of our solutions for MinSum location queries. Again, the method that combines FGP and OTP achieves the best space and time efficiency in all cases. In addition, Blossom-based approaches entails excessively high memory consumption, especially when $|F| < \hbox {1,000}$ or $|C| > \hbox {300,000}$.

Fig. 23

Effect of $|F|$ (MinSumLQ on SF). a Memory consumption, b running time

Fig. 24

Effect of $|C|$ (MinSumLQ on SF). a Memory consumption, b running time

Figures 25 and 26 plot the memory consumption and running time of our solutions for MinMax location queries. The relative performance of each method remains the same as in Figs. 23 and 24. Interestingly, each method incurs a higher computation time for MinMax location queries than for the other two types of OL queries. This is caused by the fact that our solutions identify local MinMax locations on any given edge $e$, by computing the upper envelope of a set of Wadfunctions (see Sect. 4.3). This procedure is more costly than computing the local competitive (MinSum) locations on $e$.

Fig. 25

Effect of $|F|$ (MinMaxLQ on SF). a Memory consumption, b running time

Fig. 26

Effect of $|C|$ (MinMaxLQ on SF). a Memory consumption, b running time

Summary Our results show that the solutions incorporating FGP and OTF consistently achieve the best performance for all three types of OL queries, in terms of both space and time. In particular, they require less than 20MB memory and 200 seconds to answer OL queries in a road network with 174,955 nodes, 223,000 edges, up to 500,000 clients, and down to 32 facilities (recall that the performance of the solutions improves with the number of facilities). We also recommend that setting $\theta =1\permille$ for these solutions, so as to optimize the overall running time.

10.2 Incremental OLQ queries under updates

We next examine the impacts of updates and the efficiency of our incremental methods for answering OLQ queries in an event of update. As shown in default settings, in each experiment, we continuously add or delete 1,000 clients or 50 facilities, and we show the average running time unless otherwise specified.

10.2.1 Effect of $|F|$

The first set of experiments focuses on competitive location queries (CLQ). We vary the number of facilities $(|F|)$ from 32 to 4,000. Figure 27a shows the memory consumption of $AddC(c)$ as a function of $|F|$. Clearly, Blossom-based methods consume enormous amounts of memory due to the $O(n^2)$ space overhead for maintaining the attraction sets of all vertices. For OTF-based methods, the memory consumption is slightly larger than that of the OLQ computation in the static case due to the maintaining of local optimal locations, but still very small. The memory consumption in other three operations has similar trends, so we omit them for brevity.

Fig. 27

Memory consumption of $AddC(c)$ (CLQ on SF). a Effect of $|F|$, b effect of $|C|$

Figure 28 shows that the running time of all solutions decreases with the increase in $|F|$. The reason is that, when $|F|$ is larger, a client will have a smaller attractor distance and a facility will attract a smaller set of clients. This reduces the effective range of a client and the computation cost when the optimal locations on an edge need to be recomputed. Furthermore, the running time of an update is much (at least $2$ to $3$ orders of magnitude) less than that of the OLQ computation from Sect. 10.1. That is because each update only takes effect on a part of the road network in all of the proposed incremental update algorithms.

Fig. 28

Update running time: effect of $|F|$ (CLQ on SF). a $AddC(c)$, b $DelC(c)$, c $AddF(f)$, d $DelF(f)$

In particular, Fig. 28a, b show the running time of the $AddC(c)$ and $DelC(c)$ operations. Clearly, the FGP approaches always outperform the Basic approaches, since with FGP we do not need to maintain local optimal locations for all edges. Moreover, the method that does incorporate FGP and OTF outperforms the other three approaches.

Figure 28c, d show the running time for the $AddF(f)$ and $DelF(f)$ operations. In this case, the FGP approaches are quite similar to the Basic approaches. That is because adding or deleting a facility will cause the changes of attractor distances for many clients, which may lead to the change of the upper bounds for many subgraphs. As a result, the amount of edges that need to be maintained will be large and there is a relatively high chance that at least one previously $uncomputed$ subgraph will be fully computed during the update operation, which may cause a high computation overhead. The OTF-based methods slightly outperform the Blossom-based methods in $AddF(f)$, but are much slower than Blossom-based methods in $DelF(f)$. That is because, in OTF-based methods, we need to maintain the distance from each vertex to its nearest facility (see Sect. 5) and when deleting a facility $f$, we must find the new nearest facility for each of the vertices that previously take $f$ as its nearest facility, which takes $O(n \log n)$ time and is a significant computation overhead for updates.

10.2.2 Effect of $|C|$

Next, we vary the number of clients ($|C|$) from 100,000 to 500,000. Figure 27b shows the memory consumption of $AddC(c)$ as a function of $|C|$. Same as the discussion for the effect of $|F|$, the memory consumption is also similar to that in the static OLQ computation. Similar trends were also observed for the memory consumption of other three types of updates, which are omitted for brevity.

Figure 29 shows the running time as a function of $|C|$. The running time of all solutions increases as $|C|$ goes up. That is because, when $|C|$ is large, $|E|$ is also large and there are more clients in each attraction set, which will increase the computation complexity. Nevertheless, all incremental methods under different update operations are much more efficient when compared to computing OLQs from scratch using the static OLQ methods from Sect. 10.1.

Fig. 29

Update running time: effect of $|C|$ (CLQ on SF), a $AddC(c)$, b $DelC(c)$, c $AddF(f)$, d $DelF(f)$

Figure 30 shows the effect of $|C|$ on UN dataset. As we can see, the trends are similar to those in Fig. 29. These figures shows that the proposed methods are insensitive to the distribution of facilities and clients. The same conclusion is observed for other variants of OLQ.

Fig. 30

Update running time: effect of $|C|$ (CLQ on UN), a $AddC(c)$, b $DelC(c)$, c $AddF(f)$, d $DelF(f)$

Effect of growth of updates Next we investigate the stability of our solution when updates grows over time. Figure 31 shows the running time of each update operation in a series of continuous updates (1,000 clients updates and 50 facilities updates). In Fig. 31a, b, we show the average running time of every continuous 100 clients updates. In Fig. 31c, d, we show the average running time of every continuous 5 facilities updates. It can be seen that the running time for all four update operations is stable with the growth of number of updates. For basic approach, it is because we maintain local optimal locations for all edges and the time of updates will not affect anything in the framework. For FGP approach, since we develop a method to avoid the number of subgraphs that need to be maintained to become larger and larger with more updates, as discussed in the last paragraph in Sect. 8, the updating time is still stable.

Fig. 31

Update running time: growth of updates (CLQ on SF). a $AddC(c)$, b $DelC(c)$, c $AddF(f)$, d $DelF(f)$

Comparison with method in [11]. Fig. 32 compares the memory consumption and running time of the OTF-FGP method with the method proposed in [11], which is denoted as CMRNQ for convenience. The OTF-FGP method has a less memory consumption but longer running time compared to the CMRNQ method when we vary $|C|$. We omit the figures for varying $|F|$ as they have the similar trends.

Fig. 32

Comparison with CMRNQ in [11] (on SF). a $AddF(f)$, b $DelF(f)$, c $AddF(f)$, d $DelF(f)$

MinSum and MinMax location queries The rest of our experiments evaluates the performance of proposed incremental solutions on updates for MinSumLQ and MinMaxLQ queries. These results are shown in Figs. 33, 34, 35, 36, 37, and 38, and they generally report similar trends as that in the CLQ problem discussed above.

Fig. 33

Memory consumption of $AddC(c)$ (MinSumLQ on SF). a Effect of $|F|$, b effect of $|C|$

Fig. 34

Memory consumption of $AddC(c)$ (MinMaxLQ on SF). a Effect of $|F|$, b effect of $|C|$

Fig. 35

Update running time: effect of $|F|$ (MinSumLQ on SF). a $AddC(c)$, b $DelC(c)$, c $AddF(f)$, d $DelF(f)$

Fig. 36

Update running time: effect of $|C|$ (MinSumLQ on SF). a $AddC(c)$, b $DelC(c)$, c $AddF(f)$, d $DelF(f)$

Fig. 37

Update running time: effect of $|F|$ (MinMaxLQ on SF). a $AddC(c)$, b $DelC(c)$, c $AddF(f)$, d $DelF(f)$

Fig. 38

Update running time: effect of $|C|$ (MinMaxLQ on SF). a $AddC(c)$, b $DelC(c)$, c $AddF(f)$, d $DelF(f)$

In particular, Figs. 33 and 34 show that our best incremental update methods (i.e., the ones that incorporate both FGP and OTF) for MinSumLQ and MinMaxLQ enjoy small memory footprints for the $AddC(c)$ operation. The memory consumption of these methods for other three types of update operations is similar and were omitted for brevity.

Figures 35 and 36 investigate the effect of $|F|$ and $|C|$ on the running time under different types of update operations for the MinSumLQ queries, respectively. In general, larger $|F|$ leads to smaller update cost and larger $|C|$ on the other hand introduces higher update cost, for similar reasons as we have explored for the CLQ queries. Nevertheless, compared to the running time of the corresponding static OLQ methods from Sect. 10.1, our incremental update methods are much more efficient (faster by at least 3–4 orders of magnitude).

Similar experiments were carried out in Figs. 37 and 38, to investigate the effect of $|F|$ and $|C|$ on the running time under different types of update operations for the MinSumLQ queries, respectively. And not surprisingly, we have observed similar trends, where the incremental update methods’ running time are at least 3–4 orders of magnitude smaller compared to that in the naive approach (if we were to run the static OLQ computations from scratch after every update using the static methods from Sect. 10.1).

Summary Our results show that the incremental update methods are highly effective, efficient, and scalable. In particular, solutions incorporating both FGP and OTF achieve the best performance for all three types of OL queries on all update operations. Last but not least, our framework for handling updates can incrementally answer and monitor OL queries in a much faster fashion than the baseline approach of re-computing the OLs from scratch after each update using the static methods from Sect. 10.1.

10.3 Continuous optimal location queries

In this section, we investigate the performance of adapting our update algorithms to answer the COLQ. We set up the sequence of operations in a continuous optimal location query as follows.

In between any two optimal location queries, a percentage $f_F$ $(f_C)$ of the facilities (clients) will change their locations, where $f_F\; (f_C)$ is called the facility (client) agility. For any facility or client that is selected to issue an update, its new location is given as follows. This facility or client will perform a random walk on the road network with a fixed distance $d_F$ $(d_C)$ to determine its new location.

That said, here we only showed the results of the CLQ variant (competitive location query). The results for the other two types of optimal location queries, MinSumLQ and MinMaxLQ, have exhibited similar trends. Hence, we omitted them for brevity.

In the following experiments, the default values of $|F|$ and $|C|$ is the same as that in the previous experiments, i.e., $1,000$ and 300,000, respectively. The $f_F$ ($f_C$) is set to 1% (0.1%) by default, which means that 10 facilities and 300 clients will issue updates between two OLQs. The default value of $d_F$ ($d_C$) is set to the average edge length. We measured the average running time of answering every OLQ query from a continuous OLQ.

Figure 39a examines the effect of the $|F|$. With the increasing number of facilities, the running time for the COLQ has decreased. When $|F|=4,000$, the COLQ can be answered in several seconds using the blossom based methods under the default setup. In this case, more facilities imply that the attraction distance of each client will be reduced, leading to faster dynamic update time. On the other hand, the running time has increased with more clients, as shown in Fig. 39b. Note that the update time for each client is almost constant. The reason for the increase in query time in Fig. 39b is because that we set the client agility to a percentage of $|C|$, i.e., there are more clients moving when $|C|$ becomes larger.

Fig. 39

COLQ Running time: effect of $|F|$ and $|C|$ (CLQ on SF). a Effect of $|F|$, b effect of $|C|$

Figure 40a shows that the running time of COLQ increases linearly to the facility agility. But the running time only increases slightly when we increase the client agility as shown in Fig. 40b. This is because that the running time of the facility update operations is the dominating factor, although there are more client updates in each experiment.

Fig. 40

COLQ Running time: effect of agility (CLQ on SF). a Effect of $f_F$, b effect of $f_C$

Finally, we vary the moving distance of the facilities and clients. As we can see in Fig. 41, the running time is not affected by either $d_F$ or $d_C$. This is because that our method answers COLQ for each facility (client) by a deletion and an insertion, which are insensitive to the moving distance of the facility (client).

Fig. 41

COLQ Running time: effect of moving distance (CLQ on SF). a Effect of $d_F$, b effect of $d_C$

11 Conclusion

This work presents a comprehensive study on optimal location queries in large, disk-resident road network databases, closing the gap between previous studies and practical applications in road networks. Our study covers three important types of optimal location queries and introduces a unified framework that addresses all three query types efficiently. We have also extended our framework to handle updates efficiently in an incremental fashion.

Extensive experiments on real datasets demonstrate the scalability of our solution in terms of running time and space consumption. An interesting direction for future work includes the optimal location queries for moving objects in road networks.