1 Introduction and survey of previous relevant published work

With the development of electronic technology and navigation technology, unmanned ship technology could play an important role in a wide range of activities like marine exploration, development and monitoring. And the outstanding hydrodynamic characteristic of the unmanned ship is the guarantee of its safety.

Compared to sailing in calm water, a ship advancing in waves experiences six degrees of freedom motions and dissipates more energy. The extra induced loss of energy is termed as added resistance due to sea waves. The motions and added resistance in waves of a ship can be analyzed using the boundary element method based on potential theory. Based on the three-dimensional (3D) Green’s function provided by Wehausen and Laitone [1], the velocity potential of diffracted/radiated waves is expressed in terms of a system of pulsating sources, distributed all over the wetted surface of the floating structure[2]. For zero forward speed issue, the leading commercial 3D diffraction/radiation software AQWA[3],has already been widely used in the offshore industry[4,5,6],which is also developed using the pulsating sources technique. And in the case of a ship advancing in waves, some authors [7, 8] employed the translating-pulsating source Green’s function which the linearized free surface condition with a forward speed was automatically satisfied. However, compared with the issue of zero forward speed case, the translating–pulsating source Green’s function under non-zero forward speed is always difficult to compute. To overcome this difficulty, a correction for the forward speed is usually made to the zero forward speed solution. This is in a manner similar to that used by Salvesen et al. in their frequency domain strip theory work [9]. In cases where low speeds are considered, the differences are negligible and small compared to the pulsating source method with the translating–pulsating source method based on forwards speed Green’s function [10]. Recently, RANS simulations based on computational fluid dynamics (CFD/RANS simulation) have also been used to predict ship resistance and wave-induced ship motions [11,12,13].

According to previously published work, it is noted here that suitably designed flapping foils have the ability to extract energy from their generated vortices [14] as well as free-surface waves [15, 16] and uniform flows [17]. In their experimental studies, Anderson et al. [18], and Read et al. [19] have shown that propulsive performance of a harmonically oscillating foil in uniform flow is dependent on the following parameters, which are the heave amplitude, Strouhal number, angle of attack and the phase angle between heave and pitch. According to work published by Read et al. [19], the optimum efficiency was obtained at Strouhal number between 0.25 and 0.4. Also, in this regard, using computational fluid dynamics software FLUENT, De Silva andYamaguchi [20] performed a numerical analysis on a two-dimensional active oscillating hydrofoil in wavy flow based on the Reynolds-averaged Navier–Stokes equation. It was found that when the wave has a − 90° phase difference with foil heave motion (when the wave elevation is at the wave crest and the foil is at its bottommost position), the efficiency and thrust reached their maximum values due to the high utilization of wave orbital velocity. An unsteady boundary element method was developed by Filippas and Belibassakis [21] and applied to the analysis of two-dimensional flapping hydrofoils in waves when operating beneath the free surface. The hydrodynamic performance of tandem oscillating foils in regular head waves has been investigated by Xie et al.[22].In this study, two fixed horizontal hydrofoils were mounted beneath the keel of an unmanned ship, one at the bow and the other at the stern. Two cases were considered, one case is the hydrofoils mounted to a fixed ship type structure and another case mounted to a floating ship. It was concluded that the thrust produced by the bow foil is higher than that of stern foil for the case of hydrofoils mounted to a floating ship. And the thrust produced by the bow foil on a ship is much larger than the case of foils mounted to a fixed offshore structure with no oscillating motions.

For the case of a ship with hydrofoils encountering a wave, the hydrofoils follow the hull of the ship to perform heaving and pitching motions, and it could produce the forward thrust on these hydrofoils. According to the published studies [23,24,25,26], employing a hydrofoil at the bow of a ship, whether the foils are fixed or actively controlled, have the effect of an auxiliary propulsion for the ship, and also reduce the vertical wave-induced motions of the ship. The experimental results obtained by Terao [27] show that a hydrofoil installed under the catamaran hull of a floating wind turbine system has the effects on reducing the wave drift forces and the pitch motion. And in theory, the motion and resistance in waves of a ship with hydrofoils can be obtained using linear seakeeping analysis in conjunction with foil model based on quasi-steady lifting line approximation [23, 25, 28].

In this paper, the hydrodynamics of a novel unmanned catamaran ship completely driven by hydrofoils are investigated by numerical simulations. The concept design of this unmanned ship is illustrated in Fig. 1. As a full-time mobile ocean observation platform in the sea, the ship could completely driven by two fixed hydrofoils at low speed, which are employed in the bow and stern, respectively. And the electronic power from the photovoltaic (PV) panels could guarantee the normal operation of navigation system, position system and other shipboard equipment. In this way, this unmanned ship can operate in the sea for a very long time without any supplements. Figure 2 is the photograph of this kind of unmanned ship in a sea trail at Zhuhai, China [29].

Fig. 1
figure 1

The illustration of the unmanned catamaran ship

Full size image
Fig. 2
figure 2

The photograph of the unmanned catamaran ship completed driven by hydrofoils

Full size image

First, the potential theory and the CFD method based on FLUENT [30] for ship motion analysis are introduced. Next, the validation of the two numerical methods is carried out by comparing the results of heave and pitch motions of the catamaran model without hydrofoils. Finally, the motions of the catamaran type unmanned ship fitted with hydrofoils in head regular waves are analyzed using unsteady Reynolds-averaged Navier–Stokes solver in FLUENT, and the effects of hydrofoils on motion response of the unmanned ship are discussed.

2 Motions of low-speed unmanned catamaran ship without hydrofoils based on potential flow theory

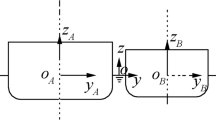
As shown in Fig. 3, three coordinate systems are introduced. The first one is a space fixed right-handed reference axes OXYZ, with the origin O at the mean free surface and Z-axis pointing vertically upwards. The second one is a moving reference axes system oxyz, which is translating with the same velocity as that of the ship forward speed U. Its x-axis points positively in the direction of the bow, and the z-axis points vertically upwards through the centre of gravity of the ship. It is assumed that OXYZ coincide with oxyz initially. The third axis system is adopted for the description of ship motions; here it is convenient to use body-fixed axes Gxbybzb with the origin G at ship’s centre of gravity. The wave direction β is defined in OXY plane of the fixed reference axes, the angle between wave propagating direction and the positive X-axis measure anti-clockwise.

Fig. 3
figure 3

The coordinate system of a ship

Full size image

The linear sinusoidal waves are assumed, and the water is considered incompressible and inviscid and flow is irrotational. The wave amplitude is assumed to be small compared to both the wave length and water depth.

In the fixed reference axes, the water surface elevation at position X and Y can be expressed as

$$\zeta (X,Y,t)=A\cos (kX\cos \beta +kY\sin \beta - \omega t),$$
(1)

where A is the wave amplitude, ω is the wave frequency, k is the wave number, and having the wavelength λ = 2π/k.

As shown in Fig. 1, the axis transformation between the fixed and moving reference frame is

$$X=Ut+x,\,Y=y,\,Z=z.$$
(2)

Substituting Eq. 2 into Eq. 1, the wave elevation in the moving reference frame can be expressed as

$$\zeta (x,y,t)=A\cos (kx\cos \beta +ky\sin \beta - {\omega _{\text{e}}}t),$$
(3)

in which

$${\omega _{\text{e}}}=\omega - kU\cos \beta ,$$
(4)

where ωe is the encounter frequency.

The wave surface elevation, Eq. 3 can also be expressed in complex form as

$$\zeta (x,y,t)=Re\left\{ {A{{\text{e}}^{ik(x\cos \beta +y\sin \beta -{\omega _{\text{e}}}t)}}} \right\}.$$
(5)

In the moving reference frame, the total velocity potential Φ(x, y, z, t) of the flow field due to the forward speed and the oscillating motions of the catamaran can be expressed as

$$\Phi (x,y,z,t)= - Ux+{\phi _{\text{S}}}(x,y,z)+{\phi _{\text{T}}}(x,y,z,t),$$
(6)

where, ϕS(x, y, z) is the steady perturbation potential due to forward motion and ϕT(x, y, z,t) is the first-order velocity potential of the unsteady wave system varies with the encounter frequency and can be expressed as

$${\phi _{\text{T}}}(x,y,z,t)=Re\left\{ {{\varphi _{\text{T}}}(x,y,z){{\text{e}}^{ - {\text{i}}{\omega _{\text{e}}}t}}} \right\},$$
(7)
$${\varphi _{\text{T}}}(x,y,z)={\varphi _{\text{I}}}(x,y,z)+{\varphi _{\text{D}}}(x,y,z)+\sum\limits_{{j=1}}^{6} {{\varphi _j}(x,y,z){\eta _{j0}}} ,$$
(8)
$${\varphi _I}(x,y,z)=\frac{{ - igA}}{\omega }\frac{{\cosh k(z+d)}}{{\cosh kd}}{{\text{e}}^{ik(x\cos \beta +y\sin \beta )}},$$
(9)

where φI is the first-order incident wave potential, φD is the diffraction wave potential, φj0 is the radiation wave potential due to the j-th motion with unit motion amplitude, ηj0 is the complex amplitude of motion of the j-th degree of freedom.

The velocity potential should satisfy Laplace’s equation in the whole fluid domain

$$\frac{{{\partial ^2}{\varphi _{\text{T}}}}}{{\partial {x^2}}}+\frac{{{\partial ^2}{\varphi _{\text{T}}}}}{{\partial {y^2}}}+\frac{{{\partial ^2}{\varphi _{\text{T}}}}}{{\partial {z^2}}}=0.$$
(10)

If the disturbed steady flow is neglected, the linear-free surface equation is satisfied, such that

$${\left( { - i{\omega _{\text{e}}} - U\frac{\partial }{{\partial x}}} \right)^2}{\varphi _{\text{T}}}+g\frac{{\partial {\varphi _{\text{T}}}}}{{\partial z}}=0\quad {\text{on}}\,z=0.$$
(11)

If the forward speed U is considered to be small and a high frequency assumption is made that the encounter frequency of oscillation ωe is much higher than the differential operator \(U{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0pt} {\partial x}}\), then the following approximate free surface boundary condition can be used

$$- \omega _{{\text{e}}}^{2}{\varphi _{\text{T}}}+g\frac{{\partial {\varphi _{\text{T}}}}}{{\partial z}}=0\quad {\text{on}}\,z=0.$$
(12)

The flow should also satisfy the boundary condition on the surface of the body surface SB of the ship, as expressed by the following equation

$$\frac{{\partial {\phi _{\text{D}}}(x,y,z)}}{{\partial n}}= - \frac{{\partial {\phi _{\text{I}}}(x,y,z)}}{{\partial n}},\quad {\text{on }}{S_{\text{B}}},$$
(13a)
$$\frac{{\partial {\varphi _j}(x,y,z)}}{{\partial n}}= - i{\omega _{\text{e}}}{n_j}+U{m_j}\quad {\text{on }}{S_{\text{B}}},$$
(13b)

where

$$({n_1},{n_2},{n_3})={\mathbf{n}},$$
(14a)
$$({n_4},{n_5},{n_6})={\mathbf{r}} \times {\mathbf{n}},$$
(14b)
$$({m_1},{m_2},{m_3})= - \frac{1}{U}({\mathbf{n}} \cdot \nabla ){\mathbf{W}},$$
(14c)
$$({m_4},{m_5},{m_6})= - \frac{1}{U}({\mathbf{n}} \cdot \nabla )({\mathbf{r}} \times {\mathbf{W}}),$$
(14d)

in which, \({\mathbf{n}}\)  is the outward unit normal vector on the body surface and \({\mathbf{r}}\) is the position vector of a point with respect to the ship’s centre of gravity. W is the steady velocity filed,

$${\mathbf{W}}=\nabla [ - Ux+{\phi _{\text{S}}}(x,y,z)].$$
(15)

The catamaran hull considered in this paper is assumed to be slender, then assuming that the steady velocity potential is small, \(\left| {\nabla {\phi _{\text{S}}}} \right|<<U\), a simplified m term can be written as

$$({m_1},{m_2},{m_3})=(0,0,0),$$
(16a)
$$({m_4},{m_5},{m_6})=(0,{n_3}, - {n_2}).$$
(16b)

The boundary condition of the seabed should also be satisfied, as expressed by the equation

$$\frac{{\partial {\phi _{\text{T}}}}}{{\partial z}}=0,\quad {\text{on }}z= - d.$$
(17)

The radiation condition of the outgoing waves must also be satisfied so that as \(\sqrt {{x^2}+{y^2}} \to \infty\) the generalized wave disturbance dies away.

In this case, the frequency domain pulsating Green’s function can be employed together with the body boundary condition given in Eqs. 13a and b to determine the diffraction and radiation potential components. The amplitude Fj0 of wave exciting forces, added mass Ajk, and wave damping Bjk can also be estimated from

$${F_{j0}}= - \rho \iint\limits_{{{{\text{S}}_B}}} {\left( {\text{i}{\omega _e}+U\frac{\partial }{{\partial x}}} \right)}({\phi _{\text{I}}}+{\phi _{\text{D}}}){n_j}{\text{d}}s,$$
(18)
$$\begin{aligned} {F_{jk}} & = - \rho \iint\limits_{{{{\text{S}}_B}}} {\left( {\text{i}{\omega _e}+U\frac{\partial }{{\partial x}}} \right)}{\phi _k}{n_j}{\text{d}}s \\ & =\omega _{e}^{2}{A_{jk}}+\text{i}{\omega _e}{B_{jk}}. \\ \end{aligned}$$
(19)

The unmanned ship is considered as a rigid body and the oscillating motion, referred to the centre of gravity, in the j-th mode in response to regular waves encountered at frequency ωe may be expressed by the equation

$${\eta _j}(t)={\eta _{j0}}{{\text{e}}^{ - i{\omega _{\text{e}}}t}},$$
(20)

where, η1, η2 and η3 are the translational displacements in x, y and z direction respectively, while η4, η5 and η6 denote the rotational motions about the x, y and z directions respectively.

The coupled six degrees of freedom linear differential equations of motion in frequency domain can be expressed by the following equation

$$\sum\limits_{{k=1}}^{6} {[ - \omega _{{\text{e}}}^{2}({M_{jk}}+{A_{jk}}) - i{\omega _{\text{e}}}B_{k}^{{}}+{K_{jk}}} ]{\eta _{k0}}={F_{j0}},$$
(21)

where Mjk is the mass matrix, Kjk is the hydrostatic stiffness matrix.

3 Hydrodynamics of an unmanned ship based on FLUENT

The software AQWA[3] suite has the advantages of fast computational speed. However, the effect of thrust and lift force caused by hydrofoils can not be taken in account by AQWA itself. In this case, the computational fluid dynamics software FLUENT [30] is selected to calculate the motions of the unmanned ship. The turbulent flow around the ship traveling in waves is simulated by solving the incompressible RANS equations with the finite volume method. This is achieved using volume of fluid (VOF) formulation and the open channel boundary condition. The velocities of the ship are calculated from the forces balance on the ship, as done by the six degree of freedom (6DOF) solver. The dynamic mesh model is used to update the volume mesh at each time step based on the new position of the boundaries of the ship.

3.1 The VOF model

The VOF model is used to track the free surface by the solution of a continuity equation for the volume fraction of one of the phases. Two phase incompressible flow combining air and water are considered. The air is defined as the primary phase and the water as the secondary phase, and the volume fraction of each of the fluids in each computational cell is tracked throughout the domain. In the VOF model, a single set of momentum equations is shared by the fluids. Reynolds averaging approach with Shear-Stress Transport (SST) k − ω model is selected for the numerical calculation.

3.2 Open channel wave boundary conditions and numerical beach treatment

Open channel wave boundary conditions in ANSYS Fluent allow us to simulate the propagation of waves through velocity inlet boundary condition. In this work, the first-order Airy wave theory, which is applied to small amplitude waves in shallow to deep water depth ranges, is applied. According to the relative motion theory, the effect of a moving ship could be incorporated with the flow current when the flow is specified relative to the ship.

To avoid wave reflection caused by outlet boundary for passing waves, a damping sink term is added in the momentum equation for the cell zone in the vicinity of the pressure outlet boundary. Numerical beach treatment in ANSYS Fluent uses linear damping in vertical direction along gravity and quadratic damping in flow direction.

3.3 Dynamic meshing with 6DOF solver

The tetrahedron unstructured grid based on spring-based smoothing, local re-meshing and dynamic mesh updating techniques are used to model flow where the shape of the domain is changing with the time due to motion of the ship. The 6DOF solver in ANSYS Fluent is used to compute motions of the center of gravity of the ship. The governing equation for the translational motion of the center of gravity is solved in the inertial coordinate system, and the angular motion is computed using body coordinates. The angular and translational velocities are used in the dynamic mesh calculations to update the rigid body position.

When a ship is moving thought head waves, the dominant motion responses are heaving and pitching motions, while the surge, sway, roll and yaw motions are usually neglected.

3.4 Forces generated by fixed tandem foils in waves

When an unmanned ship equipped with hydrofoils encounters a head wave, the ship undergoes heave and pitch motions, and each fixed horizontal foil follows the ship hull performing a harmonic heave motion hi(t) and pitch motion θi(t), they can be given by

$${h_i}(t)={\eta _3}(t) - {x_{{\text{b}}i}}{\eta _5}(t),\quad i=1,{\text{ }}2,$$
(22)
$${\theta _i}(t{\text{)}}={\eta _5}(t)\quad i={\text{1}},{\text{ 2,}}$$
(23)

where xbi is the longitudinal position along the ship where the i-th foil is located.

Each oscillating foil generates force in waves because of the relative motion between the hydrofoil and water. The hydrodynamic force components can be obtained through pressure integration over the foils

$${F_{ji}}(t)= - \rho \iint\limits_{{{{\text{S}}_{_{i}}}}} {p{n_j}{\text{d}}S}\quad i={\text{1}},{\text{ 2}};\, j={\text{1}},{\text{ 3}},{\text{ 5}}{\text{.}}$$
(24)

If the direction of the horizontal force component F1i(t) points to the bow of the ship, it means the oscillating foil provide thrust and propel the ship to overcome the ship hull resistance and then move with a low forward speed against the wave, and the vertical component F3i(t) acting as the damping force for reducing heave and pitch motions of the ship.

The forces can be non-dimensionalised as follows

$${C_{ji}}(t{\text{)}}=\frac{{{F_{ji}}(t)}}{{\frac{1}{2}\rho {U^2}c}}\quad j={\text{1}},{\text{ 3,}}$$
(25)
$${C_{ji}}(t{\text{)}}=\frac{{{F_5i}(t)}}{{\frac{1}{2}\rho {U^2}{c^2}}}\quad j={\text{5,}}$$
(26)

where c is the chord of the foils, ρ is the density of water.

4 Results and discussion

The model of the catamaran with two fixed horizontal foils is illustrated in Fig. 4. And the principal particulars of the catamaran and the parameters of the foils are listed in Tables 1 and 2, respectively. The mass and inertial moments of pitch for the catamaran with foils are 61.7 kg and 19 kg · m2, respectively.

Fig. 4
figure 4

Geometry of the catamaran model with fixed foils

Full size image
Table 1 Main particulars of catamaran model
Full size table
Table 2 Main particulars of the catamaran model with foils
Full size table

4.1 Motion response of unmanned ship without hydrofoils

Illustration of AQWA meshes for the diffraction/radiation calculations is shown in Fig. 5. A total of 17,134 elements are automatically generated on the catamaran hull, and 8025 panels on the wetted hull. The water depth is 0.695 m, and the wave exciting forces on the catamaran is shown in Fig. 6.

Fig. 5
figure 5

Hull mesh used in AQWA calculation

Full size image
Fig. 6
figure 6

Wave exciting forces on the catamaran

Full size image

The response motions, Eq. 20 can also be expressed as \({\eta _j}(t)=\left| {{\eta _{j0}}} \right|\cos ( - {\omega _{\text{e}}}t+{\varepsilon _j})\), where \(\left| {{\eta _{j0}}} \right|\) is the motion amplitude of j-th mode, and εj is the phase angle relative to the incident wave at centre of gravity of the ship. The heave and pitch motions of the catamaran model without hydrofoils moving at constant forward speed U = 0.1 m/s are shown in Fig. 7. It indicates that when the ratio of wavelength to ship length λ/L > 1.2, the phase angle of the heave motion is relative to the incident wave ε3 ≈ 0°, but the phase angle of the pitch lags behind the wave nearly about 90°. And the pitch motion reaches its maximum value when λ/L ≈ 1.5.

Fig. 7
figure 7

Heave and pitch motion responses of the catamaran without foils (β = 180°, U = 0.1 m/s)

Full size image

The motions are also implemented by 6DOF solver in ANSYS Fluent. The computational domain with x = − 23.5–7.5 m, y = − 2.0–2.0 m, z = − 0.695–1.0 m is used for the case of wavelength λ = 4.0–7.0 m and there are total 1,277,238 tetrahedral cells. Time step size dependency is made for the case of λ = 4.5 m, A = 0.025 m, β = 180°, U = 0.2 m/s and the time series of motion responses are given in Fig. 8, which is shown that the motion amplitudes change with time step size. To return to good results, smaller time step size should be used. For wavelength λ < 4.0 m, the calculation domain is − 13.0 m ≤ x ≤ 4.5 m, − 2.0 m ≤ y ≤ 2.0 m, − 0.695 m ≤ z ≤ 1.0 m, and a total of 858,074 tetrahedral cells are used. Two models, Inviscid and SST k − ω, are selected for the numerical calculation. Inviscid flow analyses neglect the effect of viscosity on the flow, and are appropriate for applications where inertial forces tend to dominate viscous forces. The heave and pitch motions obtained by two models with time step size 0.001 s for the catamaran model without hydrofoils at speed U = 0.2 m/s in regular head waves are shown in Fig. 9, which coincide with the results from 3D diffraction/radiation software AQWA. It demonstrates that the selected time step size 0.001 s, the setting of calculation domain and the grid number are acceptable. Figure 9 also shows that the results obtained from Inviscid model and SST k−ω model are almost the same, so the pressure forces on the ship will dominate the viscous forces for ship’s heave and pitch motions.

Fig. 8
figure 8

Time series of the motion responses (Iinviscid model: U = 0.2 m/s, λ = 4.5 m, A = 0.025 m, β = 180o)

Full size image
Fig. 9
figure 9

Motion responses of the examined catamaran against non-dimensional wave length λ/L (β = 180o)

Full size image

For regular head waves with amplitude A = 0.05 m and wave length λ = 3.5 m, the time histories of heave and pitch motions by ANSYS Fluent SST k − ω model for the catamaran without foils when traveling with no forward speed and low forward speeds (U = 0.1 and 0.2 m/s) are illustrated in Fig. 10. It is shown that the amplitudes of both heave and pitch motions increase with the ship speed.

Fig. 10
figure 10

Time series of the motion responses for the examined catamaran model traveling at low speed in head waves (λ = 3.5 m, A = 0.05 m)

Full size image

4.2 Free running speed of the catamaran model with tandem foils

Free running wave basin test of the catamaran model with passively pitch controlled tandem foils under head wave conditions, was carried out at the wave basin of the South China University, China, as shown in Fig. 11. The dimensions of the catamaran model and the foils were the same as shown in Tables 1 and 2, but the struts used in the experiment was different from the one shown in Fig. 4, and the chord length of each strut was 23 mm. The free running velocities for wave periods T = 1.3 and 1.8 s in head waves versus wave height H are shown in Fig. 12. Under the action of water waves, the catamaran with tandem foils has the ability of autonomous navigation at low speed. For the case of catamaran with passively pitch controlled foils, the numerical prediction of the free running velocities and motions based on multibody dynamics theory should be used, and the simulation will be more complicated. For the case with fixed tandem foils, only one model test (wave period T = 1.8 s) was carried out. From Fig. 12, we found that the free running velocity was slightly smaller than that with passively pitch controlled foils, so no further experimental data were recorded. For simplicity, in the numerical simulations for the catamaran with fixed foils, we imposed a relatively low speed U = 0.1 m/s by comparing with the free running velocities shown in Fig. 12 for the case with passively pitch controlled foils.

Fig. 11
figure 11

Free running wave basin test of the catamaran model with passively pitch controlled foils

Full size image
Fig. 12
figure 12

Free running velocities of the catamaran with tandem foils

Full size image

4.3 The effect of hydrofoils on motion responses of unmanned ship

The effects of tandem foils and struts on the noncirculatory force coefficients, namely the added mass and radiation damping coefficients calculated by AQWA, are shown in Figs. 13 and 14. The effects of the foils on the wave exciting forces on the catamaran are shown in Fig. 15. It is found that the added mass for the catamaran with foils is larger than that of without foils. But the radiation damping is smaller than that of without foils at most wavelength range.

Fig. 13
figure 13

Comparison of the added mass of the catamaran model with and without foils

Full size image
Fig. 14
figure 14

Comparison of the radiation damping coefficients of the catamaran model with and without foils

Full size image
Fig. 15
figure 15

Comparison of the wave exciting forces on the catamaran model with and without foils

Full size image

The computational results from FLUENT for the catamaran model without foils are validated by comparison with the data from AQWA, which is presented in Fig. 9. The motions of a ship with foils can also be found using Reynolds-averaged Navier–Stokes solver. In this case, the CFD software FLUENT is qualified for investigating the effect of hydrofoils on the motions of the unmanned ship. Figure 16 illustrates the generated computational grid with tandem hydrofoils for the case of wave length λ = 3.5 m at starting time t = 0. The computational domain with x = − 13.0–4.5 m, y = − 2.0–2.0 m, z = − 0.695–1.0 m, there are a total of 1,327,071 tetrahedral cells. For the catamaran model with foils, the finer grids are needed in the process of volume mesh updating, which is handled automatically by FLUENT at each time step. And the massive amount grid model takes more computing time compared to the case without foils. As a result, only the comparison of the ship motions for the catamaran model without hydrofoils and with fixed hydrofoils at forward speed U = 0.1 m/s in regular head waves are given, as shown in Fig. 17. It is found that when λ/L < 2.4, the fixed hydrofoils reduces the pitch motion significantly, and when λ/L > 2.4, the pitch motion is slightly larger than that without hydrofoils. The influence of the tandem foils on pitch motions decreases with the increasing wavelength when λ/L > 2.4. The pitch motions calculated by AQWA are much larger than the results obtained by Fluent in the range of λ/L < 2.4, this means that the circulatory forces, namely the vertical component of the lift force caused by foils act as damping force for reducing the heave and pitch motions of the ship.

Fig. 16
figure 16

Overview of computational grid for the case of λ = 3.5 m

Full size image
Fig. 17
figure 17

Heave and pitch motions of the examined catamaran models in head waves

Full size image

The forces acting on the fixed structure in water waves are considered to be the wave exciting forces. When the catamaran model is moving at speed U = 0.1 m/s in regular head waves with A = 0.05 m, λ = 3.5 m, the time series of the wave exciting forces in surge, heave and pitch direction are shown in Figs. 18, 19 and 20. It is found that the wave exciting force acting on the catamaran with foils in surge direction is slightly larger than that without foils, but the amplitudes in heave and pitch directions become a bit smaller.

Fig. 18
figure 18

Time series of wave exciting force in surge direction (λ = 3.5 m, A = 0.05 m, U = 0.1 m/s)

Full size image
Fig. 19
figure 19

Time series of wave exciting force in heave direction (λ = 3.5 m, A = 0.05 m, U = 0.1 m/s)

Full size image
Fig. 20
figure 20

Time series of wave exciting moment in pitch direction (λ = 3.5 m, A = 0.05 m, U = 0.1 m/s)

Full size image

The time series of heave, pitch motions, the resistance and the vertical force acting on the catamaran for wave amplitude A = 0.05 m, wave length λ = 3.5 m are shown in Figs. 21, 22, 23 and 24. The results show that the fixed hydrofoils have not only reduced motions of the catamaran but also changed the phase angle. Referring to Figs. 21 and 22, we observe that the phase angle of the heave and pitch motions with foils lag nearly about 5° and 30°, respectively, compared with the case without foils. Compared with the case without foils, the amplitude of the added resistance acting on the catamaran model has also become smaller. The hydrodynamic performance of tandem oscillating foils in head waves were studied in Ref. [22]. The heave motions of the foils was obtained according to the equations of \({h_i}(t)={\eta _3}(t) - {x_{{\text{b}}i}}{\eta _5}(t)={h_{0i}}\cos ({\omega _{\text{e}}}t+{\psi _i})\), i = 1, 2, where xbi is the longitudinal position along the ship where the i-th foil located, ψi is the phase angle between the heave of the i-th foil and the wave elevation at the origin of moving coordinate system. Numerical simulation of a two-dimensional method was applied to obtain the hydrodynamic performance of the unsteady flow around the tandem oscillating foils in waves. It is assumed that the foils moving towards from right to left, according to the principle of relative motion, the effect of moving object could be incorporated with the flow current from left to foils. The instantaneous horizontal force coefficient was defined as Cxi(t) = C1i(t). Cxi(t) is negative for the thrust force, positive for the resistance force. Figure 25 shows the instantaneous horizontal force coefficients for the bow and stern foils encountered head waves with U = 0.1 m/s, wave period T = 1.5 s (wavelength λ = 3.1 m) and wave amplitude A = 0.05 m. It is found that, the bow foil generates thrust more than 90% of the time in one encounter wave period Te, but the stern foil is only 60%. Figure 25 illustrated that the horizontal components forces acting on the tandem foils provide thrust to propel the unmanned ship. Figure 24 shows that the amplitude of total vertical force acting on the catamaran has really become smaller comparing with the case without foils. So we can conclude that the vertical damping forces on the foils decrease the heave and pitch motions of the ship, and then reduce the wave-added resistance on the ship.

Fig. 21
figure 21

Time series for the heave motion of the catamaran models in head waves (λ = 3.5 m, A = 0.05 m, U = 0.1 m/s)

Full size image
Fig. 22
figure 22

Time series for the pitch motion of the catamaran models in head waves (λ = 3.5 m, A = 0.05 m, U = 0.1 m/s)

Full size image
Fig. 23
figure 23

Time series for the resistance of the catamaran models in head waves (λ = 3.5 m, A = 0.05 m, U = 0.1 m/s)

Full size image
Fig. 24
figure 24

Time series for the vertical force of the catamaran models in head waves (λ = 3.5 m, A = 0.05 m, U = 0.1 m/s)

Full size image
Fig. 25
figure 25

Horizontal force coefficients curve for tandem oscillating foils in head wave (U = 0.1 m/s, β = 180°, A = 0.05 m, T = 1.5 s, encountered wave period Te = 1.43 s)

Full size image

5 Conclusions

The effect of fixed horizontal hydrofoils on the hydrodynamics of an unmanned ship is investigated using numerical method based on Reynolds-averaged Navier–Stokes equation. The simulated results for the unmanned ship without hydrofoils in head regular waves are validated by comparison with that of potential theory. To get larger foil’s heaving motions, two fixed hydrofoils are mounted at the bow and stern under the keel of an unmanned ship. The hydrofoils will follow the hull of the ship to perform oscillating motions and then generate thrust. The fixed hydrofoils not only change the heaving and pitching motions of the unmanned ship but also change their phase angles.