1 Introduction

In deep water, marine risers subject to strong ocean currents, suffer from high-mode vortex-induced vibrations (VIV), when vortex shedding interacts with the structural properties of the riser, resulting in large amplitude vibrations in both in-line (IL) and cross-flow (CF) directions. When the vortex shedding frequency approaches the natural frequency of the marine riser, the cylinder takes control of the shedding process causing the vortices to be shed at a frequency near the natural frequency. This phenomenon is called vortex shedding ‘lock-in’ or synchronization. Under the ‘lock in’ conditions, large resonant oscillations reduce the fatigue life significantly.

Analysis of dynamic response excited by VIV is one of the most important aspects in the design of the offshore oil production risers and pipelines, which connect the fixed facilities on the seabed and the processing equipments on the offshore platforms. To understand the insight of VIV, large work has been done on the evaluation of dynamic response, wake structure and fluid force of rigid and flexible cylinder, see critical reviews from Sarpkaya [1] and Williamson [2]. The drag and lift coefficients of a spring-mounted rigid cylinder has been largely estimated in the literatures [3, 4], but they have not been evaluated well for a long flexible cylinder. The investigation of fluid force along a long flexible cylinder either experimentally or numerically is complicated, see comment from Huera-Huarte et al. [5]. Evangelinos et al. [6] used direct numerical simulation (DNS) to calculate fluid force of flexible cylinders which subjected VIV up to second mode. Huera-Huarte et al. [5] implemented a finite element method model (FEM) to obtain fluid force of a long flexible cylinder which subjected VIV up to 14th mode in in-line and 8th mode in cross-flow. His methodology was using experimental response data obtained in a test program as input to the numerical model, the instantaneous distributed in-line and cross-flow forces acting on a flexible cylinder could be studied successfully. However, there still existed an approximation using the stiffness, mass and damping matrices which were not updated during each time step.

Following the idea to use experimental response data as input by Huera-Huarte et al. [5], an alternative numerical model named as Generalized Integral Transform Technique (GITT) approach is studied here to investigate fluid force distribution of a long flexible cylinder. This computational algorithm, with its intrinsic characteristic of finding solutions with automatic global error control [7–10], opened up an alternative perspective in benchmarking and covalidation for such analyses of dynamic response of beams and plates [11–14]. Gu et al. [15] had used this method to study the fluid force of a long flexible cylinder, the drag and lift coefficients were evaluated by the comparison with previous results to show its reliability and capability. In this paper, we complete those previous results by reporting an accurate solution of fluid force distribution of a long flexible cylinder. The partial differential equations (PDEs) is transferred to ordinary differential equations (ODEs) by GITT, then the convergence behavior is possible to be performed through different truncation order (N = 1, 2, 3, 4, 5, 6, 8, 16 and 32) to evaluate the influence of the different mode number, which obviously cannot be performed in the physical space. The comparison between the numerical results from GITT and the experimental results from load cell shows the performance of GITT solution. The numerical results found that the highest mode will be subject to the greatest uncertainties, and the truncation order N = 4 is adequate for the present experimental cases. Then, the application of proposed GITT to a large-scale experimental program conducted by Trim et al. [16] was implemented to evaluate the fluid force of a long flexible riser during high-mode VIV. Finally, extended discussion of the error and limitation of the proposed method was presented and several conclusions were drawn.

2 Model description

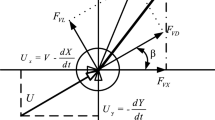
The marine riser model can be idealized as a beam with low flexural stiffness. The deflection of a generic beam is described by means of Euler–Bernoulli beam equation. As shown in Fig. 1, a Cartesian coordinate system with its origin at one end of the cylinder model is used, in which x -axis is parallel to flow velocity, z-axis coincides with spanwise axis of the cylinder model in its undeflected configuration and y -axis is perpendicular to both. Since the governing equations in in-line and cross-flow directions are the same, only the cross-flow deduction is presented here. The equation of transverse displacement Y of the cylinder model is described by:

$$\begin{aligned} m\dfrac{\partial ^{2} Y}{\partial T^{2}}+r_{s}\dfrac{\partial Y}{\partial T}-T_\mathrm{top} \dfrac{\partial ^{2} Y}{\partial Z^{2}}+\mathrm{EI}\dfrac{\partial ^{4} Y}{\partial Z^{4}}=F_L, \end{aligned}$$
(1)

where EI denotes the flexural stiffness, \(T_\mathrm{top}\) the applied axial tension, \(\rho\) the fluid density, U the flow velocity, D the diameter of the cylinder model, \(F_{L}\) the lift force around Strouhal frequency including all the hydrodynamic forces, such as the potential and vortex force components [2, 17]. T the time and Z the coordinate in spanwise direction. The mass m is the mass of cylinder model per unit length, \(r_{s}\) the structural damping [18].

Fig. 1
figure 1

Sketch of the coordinate system

Full size image

By introducing dimensionless time \(t=T\Omega _{f}\), transverse displacement \(y=Y/D\) and span position \(z=Z/L\), the coupled fluid-structure dynamical system yields

$$\begin{aligned} \dfrac{\partial ^{2} y}{\partial t^{2}}+\delta \dfrac{\partial y}{\partial t}-c \dfrac{\partial ^{2} y}{\partial z^{2}}+b \dfrac{\partial ^{4} y}{\partial z^{4}}=f, \end{aligned}$$
(2)

The dimensionless damping \(\delta\), tension c, bending stiffness b and fluid force f are given by:

$$\begin{aligned} \delta&=\dfrac{r_s}{m \Omega _f},\end{aligned}$$
(3a)
$$\begin{aligned} c&=\dfrac{T_\mathrm{top}}{m\Omega _{f}^{2}L^{2}},\end{aligned}$$
(3b)
$$\begin{aligned} b&=\dfrac{\mathrm{EI}}{m\Omega _{f}^{2}L^{4}},\end{aligned}$$
(3c)
$$\begin{aligned} f&=\dfrac{F_L}{m \Omega _f^2 D}, \end{aligned}$$
(3d)

The cylinder model is pin-ended, hence deflections and curvatures equal to zero at each end, giving the following boundary conditions:

$$\begin{aligned}&y(0,t)=0,\end{aligned}$$
(4a)
$$\begin{aligned}&y(1,t)=0,\end{aligned}$$
(4b)
$$\begin{aligned}&\dfrac{\partial ^{2} y(0,t)}{\partial z^{2}}=0,\end{aligned}$$
(4c)
$$\begin{aligned}&\dfrac{\partial ^{2} y(1,t)}{\partial z^{2}}=0, \quad \forall t. \end{aligned}$$
(4d)

3 Integral transform solution

Following the ideas in GITT, the next step is that of selecting eigenvalue problems and proposing eigenfunction expansions. The eigenvalue problem for transverse displacement y(z, t) is chosen as expression:

$$\begin{aligned} \frac{d^4 \phi _i ( z )}{d z^4} = \lambda ^4_i \phi _i ( z ), \quad 0 < z < 1, \end{aligned}$$
(5)

The advantage of the selection of the proposed eigenfunction can eliminate the fourth-order derivative term related to the bending stiffness, then the selection of truncation order could be analyzed to avoid the error mainly induced by the high mode, which cannot be examined in the physical space. The boundary conditions of eigenvalue problem are shown as follows

$$\begin{aligned}&\phi _i ( 0 ) = 0, \end{aligned}$$
(6a)
$$\begin{aligned}&\phi _i ( 1 ) = 0, \end{aligned}$$
(6b)
$$\begin{aligned}&\frac{d^{2} \phi _i ( 0 )}{d z^{2}} = 0, \end{aligned}$$
(6c)
$$\begin{aligned}&\frac{d^{2} \phi _i ( 1 )}{d z^{2}} = 0, \end{aligned}$$
(6d)

where \(\phi _i ( z )\) is the eigenfunction of problem (5), \(\lambda _i\) is the corresponding eigenvalue, they satisfy the following orthogonality property

$$\begin{aligned} \int ^{1}_{0} \phi _i ( z ) \phi _j ( z ) \mathrm{d}z = \delta _{ij} N_i, \end{aligned}$$
(7)

with \(\delta _{ij} = 0\) for \(i \ne j\), and \(\delta _{ij} = 1\) for \(i = j\). The norm, or normalization integral, is written as

$$\begin{aligned} N_i = \int ^{1}_{0} \phi ^2_i ( z ) \mathrm{d}z, \end{aligned}$$
(8)

Problem (5) is readily solved analytically to yield

$$\begin{aligned} \phi _i ( z )= \sin ( \lambda _{i} z), \end{aligned}$$
(9)

and the eigenvalues become

$$\begin{aligned} \lambda _{i} = i \pi , \qquad i=1,2,3,\ldots , \end{aligned}$$
(10)

The eigenvalue problem (5) allows definition of the following integral transform pairs

$$\begin{aligned} \left\{ {{\bar{y}}_i} ( t ) = {\int ^{1}}_{0} {\tilde{\phi }}_{i} ( z ) y ( z , t ) \mathrm{d}z, \quad \text {transform} \right. \end{aligned}$$
(11a)
$$\begin{aligned} \left\{ y ( z , t ) = \sum ^{\infty }_{i = 1} \tilde{\phi }_i ( z ) \bar{y}_i ( t ), \quad \text {inversion} \right. \end{aligned}$$
(11b)
$$\begin{aligned} \left\{ \bar{f}_i ( t ) = \int ^{1}_{0} \tilde{\phi }_i ( z ) f ( z , t ) \mathrm{d}z, \quad \text {transform}\right. \end{aligned}$$
(12a)
$$\begin{aligned} \left\{ f ( z , t ) = \sum ^{\infty }_{i = 1} \tilde{\phi }_i ( z ) \bar{f}_i ( t ), \quad \text {inversion}\right. \end{aligned}$$
(12b)

where \(\tilde{\phi }_i ( z )\) is the normalized eigenfunction

$$\begin{aligned} \tilde{\phi }_i ( z ) = \frac{\phi _i ( z )}{N^{1/2}_i} , \end{aligned}$$
(13)

Now, the next step is thus to accomplish the integral transformation of the original partial differential system. For this purpose, Eq. 5 followed by the boundary conditions given by Eq. 6 are multiplied by \(\int ^{1}_{0} \tilde{\phi }_i ( z ) \mathrm{d}z\), integrated over the domain in z [0,1], and the inverse formula given by Eq. (11b) is employed. After the usual manipulations, the following coupled ordinary differential system results, for the calculation of the transformed \(\bar{y}(t)\):

$$\begin{aligned}& \dfrac{d^{2} \bar{y}_i(t)}{d t^{2}}+\delta \dfrac{d \bar{y}_i(t)}{d t}- c \sum ^{\infty }_{j=1} P_{ij} \bar{y}_i(t) + b \lambda _i^4 \bar{y}_i(t)=\bar{f}_i(t), \hfill \\ &i=1,2,3,\ldots , \end{aligned}$$
(14)

where the coefficient of the ordinary differential system is given by the following expressions:

$$\begin{aligned} {P}_{ij} = \int ^{1}_{0} \tilde{\phi }_i(z) \frac{d^2 \tilde{\phi }_j(z)}{d z^2} \mathrm{d}z, \end{aligned}$$
(15)

The first and second derivative of \(\bar{y}\) with respect to time can be obtained by following integral transform

$$\begin{aligned}&\dfrac{d^{2} \bar{y}_i(t)}{d t^{2}} = \int ^{1}_{0} \tilde{\phi }_i ( z ) \dfrac{\partial ^{2} y(z , t)}{\partial t^{2}} \mathrm{d}z, \end{aligned}$$
(16a)
$$\begin{aligned}&\dfrac{d \bar{y}_i(t)}{d t} = \int ^{1}_{0} \tilde{\phi }_i ( z ) \dfrac{\partial y(z , t)}{\partial t} \mathrm{d}z. \end{aligned}$$
(16b)

The boundary conditions are naturally satisfied by the eigenfunctions. System (14) is now in an appropriate format for numerical solution when the displacement, velocity and acceleration are obtained from experimental response data. Once \(\bar{f}_i ( t )\) has been numerically evaluated, the analytical inversion formula (12b) recovers the dimensionless function f (z, t).

To verify and validate the inverse solution for source term, an experiment of a towed riser model was conducted in uniform flow in present research. The fluid force is extracted from the load cell in the experiment. Since the time-varying shape of the riser can be composed as a series of eigenfunctions or mode shapes [19], theoretically, the series should be infinity. Hence, the maximum mode (truncation order) is determined based on the mode analysis to evaluate the convergence behavior of inverse solution.

4 Experimental details

To calibrate GITT solution, an experiment of a towed riser model in uniform flow was conducted in present research. The experiments were carried out in a towing tank which has a test section 0.75 m in width, 0.72 m in height and 16 m in length, at School of Engineering, Federal University of Rio Grande (FURG), Rio Grande do Sul, Brazil. The sketch of the experimental setup is shown in Fig. 2. The flexible cylinder had an outer diameter of 19.5 mm and was constructed of plastic tube with a 6.4-mm steel core as shown in Fig. 2a. Several nylon pieces were used to clamp the steel core and support the outer plastic tube as shown in Fig. 2b. Strain gages were mounted on the flexible cylinder to measure the responses at five locations (identified as S1, S2, S3, S4 and S5), with the relative positions 0.84, 0.67, 0.50, 0.33, and 0.16 in length from the bottom end, respectively. The load cell was used to extract the supporting force of the flexible cylinder. As for the dynamic system of the flexible cylinder, the supporting force in cross-flow motion is approximately expressed as:

$$\begin{aligned} F_{S}= m\dfrac{\partial ^{2} Y}{\partial T^{2}} - F_{L} . \end{aligned}$$
(17)

where \(F_{S}\) denotes the supporting force in cross-flow motion.

Fig. 2
figure 2

Sketch of the experimental setup. a Cross section view of cylinder; b cylinder model; c side view, d front view

Full size image

The lift coefficient is a dimensionless coefficient that relates the fluid force acting on a reference area associated with the body, which is defined as:

$$\begin{aligned} C_{L}=\dfrac{F_{L}}{\frac{1}{2}\rho U^{2}D}. \end{aligned}$$
(18)

Based on this definition, once the fluid force \(F_{L}\) is evaluated, the lift coefficient can be obtained.

The natural frequency of the flexible cylinder with variable top tension was measured from plunk tests in still water. To find the experimental natural frequencies, the cylinder model was excited at its middle span after setting each different top tension. Table 1 shows the fundamental natural frequencies in terms of different top tensions applied. Since the aspect ratio (\(L/D \approx 74\)) is not large, the natural frequency of second mode was not captured.

Table 1 Summary of main parameters of the experiment
Full size table

More detail of this setup of the experiment could be found in Gu et al. [15]. The summary of the experiments is shown in Table 2. The aspect ratio is defined as \(\Lambda =L/D\); reduced velocity is defined as \(U_r=U/f_n D\); Reynolds number is defined as \(\text{ Re }=\rho U D/ \nu\), \(\nu\) denotes viscosity of the flow.

Table 2 Summary of main parameters of the experiment
Full size table

5 Experimental verification

The present experiment used 5 strain gage stations to capture the displacement of the dynamic vibration, a cubit polynomial fitting method was implemented to yield the displacement of the entire spanwise position of the cylinder model. Figure 3 indicates the instantaneous displacements in CF and IL directions in a time interval t \(\in\) [8 21] s at \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s , \(U_r=5.3\). The left column is the instantaneous CF displacement, the middle column is the IL displacement and the third column is the IL displacement without mean. It is noticed that in all cases the IL mean displacements at \(z/D=0.33\) are larger than the ones at \(z/D=0.84\), this is confirmed by the second column in Fig. 3, due to: (1) the drag force in water is much higher than in air, hence larger drag force exerts on the lower half of the flexible cylinder; (2) lower axial tension force acts on the lower half of flexible cylinder due to its weight.

Fig. 3
figure 3

Instantaneous displacements from cubic polynomial fitting. (1) Left column graph the instantaneous CF deflection; (2) middle column graph IL deflection; (3) right column graph IL deflection without mean. Black lines plotted at every 0.1 s in the time interval t \(\in\) [8 21] s, \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\)

Full size image

The dynamic response results shown above is used as input to calculate fluid force distribution based on GITT, and the verification of the proposed numerical method with experimental results is performed. We chose the maximum mode as 32, which should be sufficient for the present experimental flexible cylinder, since it only can be excited in the low modes (1–3). The maximum mode is set as N = 1, 2, 3, 4, 5, 6, 8, 16 and 32 to evaluate the convergence behavior of integral transform solution.The instantaneous spanwise distribution of lift force coefficient \(C_L\) is shown in Figs. 4 and 5 at \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\), the times are at \(T=6.5\) s and 8.7 s, respectively. It can be observed that in the last graph (\(N=1-32\)) in the Fig. 4, the curves of \(N=4\), \(N=5\) and \(N=6\) are almost overlapped. This means the fluid force has good convergence behavior in the mode number range 4–6; but when \(N \ge 8\), the lift distribution presents the high-mode feature. This phenomenon is induced by the error of high-mode \(\bar{y}_N(t)\), which is proportional to the term \(\lambda ^4\). From the mode analysis shown in Fig. 6, the third mode almost has no contribution to the overall response. Hence, the truncation order \(N=4\) is selected to be adequate in all numerical simulations to avoid the error induced by the high mode.

Fig. 4
figure 4

GITT solutions of spanwise distribution of lift coefficient \(C_L\) with different truncation orders N at time \(T=6.5\) s, \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\)

Full size image
Fig. 5
figure 5

GITT solutions of spanwise distribution of lift coefficient \(C_L\) with different truncation orders N at time \(T=8.7\) s, \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\)

Full size image
Fig. 6
figure 6

Modal weights: CF (left) and IL (right) oscillations up to 3rd mode, from Gu et al. [15]

Full size image

Figure 7 shows the instantaneous spanwise distribution of drag force coefficient \(C_D\) at \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\), the time is at \(T=6.5\) s. It is noted that the error induced by high mode of drag coefficient distribution is not so remarkable as the one of lift coefficient distribution. This phenomenon is due to that the in-line vibration is always happening behind the cylinder model as shown in the middle graph of Fig. 3. From the shape of the in-line motion, it is known that the response of the cylinder is obviously dominated by mode 1 if we do not take out of the mean of the response. In other words, the weight of mode 1 of in-line motion should be much higher than the ones of other mode numbers. Thus, the influence of the high-mode error induced by the term \(\lambda ^{4}\) in in-line motion is much less when compared with the same influence in cross-flow motion. However, the instantaneous spanwise distribution of drag force coefficient after taking the mean IL motion out is shown in Fig. 8. It is depicted that the drag force coefficients after taking the mean IL motion out decrease from about 4 to 1, which is less that the lift force coefficient. The high-mode feature also could be seen when \(N \ge 8\), but it is not so remarkable as in the lift force coefficient distribution.

Fig. 7
figure 7

GITT solutions of spanwise distribution of drag coefficient \(C_D\) with different truncation orders N at time \(T=6.5\) s, \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\)

Full size image
Fig. 8
figure 8

GITT solutions of spanwise distribution of drag coefficient \(C_D\) after taking the mean IL motion out with different truncation orders N at time \(T=6.5\) s, \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\)

Full size image

Figure 9 illustrates instantaneous spanwise distributions of fluid force coefficient at every 0.05 s in the time interval T \(\in\) [6 9] s, \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\). The left column graph represents the instantaneous lift coefficient \(C_L\) and the right column graph represents the instantaneous drag coefficient \(C_D\). It is noticed that the envelope of lift coefficient presents symmetric feature, whereas the envelope of drag coefficient presents the asymmetric feature. The mean of all instantaneous distributions of drag coefficients is plotted as the red line as shown in the right graph. The red curve shows that the drag force is much larger at the lower part than the upper part of the flexible cylinder. The reason is that the fluid force induced by the water is obviously larger than that induced by the air. Since the lift and drag coefficients calculated from GITT are based on the experimental response data as input, they could be presented in spatial and temporal evolutions as shown in Figs. 10 and  11. It is noticed that the lift coefficient varies in positive and negative alternately, whereas the drag coefficient stays only in positive. Meanwhile, the maximum drag coefficient stays around the zone z \(\in\) [0.2 0.4], which proved that the larger fluid force is induced by water.

Fig. 9
figure 9

Instantaneous spanwise distribution of fluid force coefficient. (1) Left column graph the instantaneous lift coefficient \(C_L\); (2) right column graph the instantaneous drag coefficient \(C_D\). Black lines plotted at every 0.05 s in the time interval T \(\in\) [6 9] s, \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\)

Full size image
Fig. 10
figure 10

Spatio-temporal evolution of the instantaneous distribution of lift coefficient \(C_L\) in the time interval T \(\in\) [6 9] s, \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\)

Full size image
Fig. 11
figure 11

Spatio-temporal evolution of the instantaneous distribution of drag coefficient \(C_D\) in the time interval T \(\in\) [6 9] s, \(T_\mathrm{top}=49.0\) N, \(U=0.54\) m/s, \(U_r=5.3\)

Full size image

The comparison of RMS (root mean square) of lift coefficient at different top tension between the proposed approach and the experimental results from load cell is performed to verify the accuracy of GITT solution, as shown in Fig. 12. The blue square and red circle symbols represent the experimental results from load cell and numerical results from GITT, respectively. It is noticed that the numerical results are in good agreement with the experimental results. The maximum lift coefficient is about 3.0, and both the numerical and experimental results have the clear upper and lower branches. When comparing the upper and lower branches of lift coefficient and of the maxima cross-flow amplitude from Gu et al. [15], it is observed that the maximum lift force occurs at the maximum cross-flow amplitude. The comparisons of lift coefficient at \(T_\mathrm{top} = 49\) N in tabular form is given in Table 3, with absolute and relative errors in percentage. It is necessary to point out that in some region where lift coefficients are very small, such as \(U_r\) \(\in\) [8,12] at \(T_\mathrm{top} = 19.6\) N, any uncertain factor will induce the relative errors in percentage which are quite large if we compare them with these small lift coefficients. Hence, the relative errors in percentage represent the absolute error with respect to the maximum value from load cell. From Table 3, the maximum relative errors are less than 20 % and average errors are approaching zero, which shows that the lift coefficients reasonably agree well with the experimental results.

Table 3 Lift coefficient comparisons between the experimental results and GITT at different top tensions
Full size table
Fig. 12
figure 12

Comparison of RMS of lift coefficient \(C_L\) at different top tensions between numerical results by GITT and experimental results from load cell

Full size image

Mean drag coefficients \(C_D\) with respect to the reduced velocity at different top tension are also calculated based on GITT as shown in Fig. 13. The maximum drag coefficient is about 3.5, and the numerical results have the clear upper and lower branches. However, it is observed that when the drag coefficient passes the first peak (maximum value) at reduced velocity around 5.5, it decreases initially and then increases again to format a second peak as shown in the plot at the \(T_\mathrm{top} = 19.6\) N. To explain this phenomenon, the comparison of maxima in-line vibration amplitudes between strain gage station S3 and the results by cubic polynomial fitting is performed as shown in Fig. 14. The green square and pink circle symbols represent the maximum amplitude from strain gage station S3 and the maximum amplitude from the polynomial fitting, respectively. It is shown that when reduced velocity is lower than 5.5, these two lines are quite close. When reduced velocity is around 5.5, both of them have a peak and then decrease. When reduced velocity approaches to 12, the pink line has larger values than that of green line. This difference illustrates that the maximum amplitude does not occur at the strain gage station S3, especially at the higher flow velocity. This also could be confirmed by the middle graph of Fig. 3 which shows clearly that the lower part instantaneous displacements of cylinder are larger than that of the strain gage station S3. From the Fig. 6, it is known that the in-line vibration is dominated by the first mode and the fluid force based on GITT is calculated using the experimental response data as input, thus the dramatical increase of the pink line at higher reduced velocity induces the second peak of the drag coefficient as shown in Fig. 13.

Fig. 13
figure 13

Mean drag coefficient \(C_D\) at different top tensions by GITT

Full size image
Fig. 14
figure 14

Comparison of maxima in-line vibration amplitudes between strain gage station S3 and the results by cubic polynomial fitting

Full size image

6 Application to high-mode VIV

The above discussion verified the capability and availability of the proposed method to evaluate the fluid force of flexible cylinder. Since the eigenfunction is a sinusoidal series expansion, it should have the ability to simulate the high-mode behavior of vortex-induced vibrations. To apply the GITT to evaluate the fluid force of high-mode VIV, the numerical simulation of an experiment on a towed riser model in uniform flow conducted by Trim et al. [16] is carried out. The experimental investigation was performed at Marintek Ocean Basin in Trondheim. The overall layout of the experiments is shown in Fig. 15. The riser model was 38 m in length and 27 mm in diameter with an aspect ratio of 1407. It was equipped with a dense array of high-quality instrumentation, and the flow profile was uniform stepped from 0.3 to 2.4 m/s with an increasing step of 0.1 m/s. The summary of main parameters of the experiments is given in Table 2. The datasets used in present simulation are Test No. 2120 and Test No. 2150 [20], the corresponding flow velocities are 1.4 and 1.7 m/s, respectively.

Fig. 15
figure 15

Overall layout of the VIV experiment with the carriage velocity of 0.3–2.4 m/s at MARINTEK [16]

Full size image

To obtain the displacement of transverse vibration from finite strain gage sensors, Lie and Kaasen implemented modal analysis [19]. This method is based on the assumption that the time-varying shape of riser can be composed as a series of eigenfunctions or mode shapes. But the displacements computed from measured bending strains have errors due to the magnitude of bending strain associated with displacement of a given amplitude in the i th mode is proportional to \(i^2\), which means the lowest modes will be subject to the greatest uncertainties [21]. Therefore, in present cases, mode numbers from 6 to 15 are involved in numerical simulation. Since the participative modes are fewer than strain gage sensors, a least-squares method is used to calculate displacement, then implementing finite difference method to obtain velocity and acceleration. The strain signals are filtered through Meyer wavelet-based denoising to avoid the influence of high-frequency noise.

Based on the modal analysis, the spatio-temporal evolutions of instantaneous displacement Y of Test No. 2120 and Test No. 2150 are shown in Figs. 16 and  17, respectively. It is seen that the maximum amplitude has been found with values up to 0.06 m in Test No. 2120 and 0.08 m in Test No. 2150, respectively. In some region the displacement demonstrates as a traveling wave, which means the instantaneous displacement has no remarkable anti-nodes as shown in Figs. 20a and  21a. The traveling wave was defined by Chaplin et al. [21] with a similar experiment setup. As he explained, in the absence of any knowledge of distribution of added mass, and neglecting the effect of variations in tension, the mode shapes have been assumed to be sinusoids. The fact that all contributing modes defined in this way are neither in phase nor in anti-phase with each other, and the fact that there are no pure nodes in the profiles, indicated that the motion in both directions is a traveling wave.

Fig. 16
figure 16

Spatio-temporal evolution of the instantaneous displacement Y. Test No. 2120

Full size image
Fig. 17
figure 17

Spatio-temporal evolution of the instantaneous displacement Y. Test No. 2150

Full size image

The next step is to use the dynamic response as input and implement GITT to calculate the fluid force distribution of the long flexible riser. Figures 18 and  19 show the spatio-temporal evolutions of lift coefficient \(C_L\) of Test No. 2120 and Test No. 2150, respectively. It is seen that the maxima amplitudes have been found with values up to 2 in Test No. 2120 and No. 2150. The features of the color contours do not follow the spatio-temporal evolutions of instantaneous displacement as shown in Figs. 16 and  17. Figures 20c and  21c show the instantaneous lift coefficient at midpoint in a time interval 0.2 s for these two cases. No pure nodes are depicted in the plots which are the same as the instantaneous displacement, the traveling wave also can be observed in Figs. 18 and  19.

Fig. 18
figure 18

Spatio-temporal evolution of the lift coefficient \(C_L\). Test No. 2120

Full size image
Fig. 19
figure 19

Spatio-temporal evolution of the lift coefficient \(C_L\). Test No. 2150

Full size image

RMS (root mean square) of displacement and lift coefficient is shown in Figs. 20b, d and  21b, d for Test No. 2120 and Test No. 2150, respectively. The profile of RMS of displacement of Test No. 2120 shows the mode number is 8 which is smaller than 9 from Trim et al. [16], this discrepancy may be induced by different participating modal numbers involved in the calculation between present study and study from Trim et al. [16]. Mode number of lift coefficient of Test No. 2120 is 10 as shown in Fig. 20d. As for Test No. 2150, Fig. 21b shows mode number of displacement is 9 which is the same as the study by Trim et al. [16], and mode number of lift coefficient is 9 as shown in Fig. 21d.

Fig. 20
figure 20

Displacement and lift coefficient distribution. Test No. 2120. a Instantaneous displacement in a time interval 0.2 s; b RMS of displacement; c instantaneous lift coefficient in a time interval 0.2 s; d RMS of lift coefficient

Full size image
Fig. 21
figure 21

Displacement and lift coefficient distribution. Test No. 2150. a Instantaneous displacement in a time interval 0.2 s; b RMS of displacement; c instantaneous lift coefficient in a time interval 0.2 s; d RMS of lift coefficient

Full size image

7 Results and discussion

From the results shown above, the GITT method is using the displacement, velocity and acceleration as inputs to obtain each mode contribution of fluid force, thus the accuracy of input plays an important role to such simulation and should be carefully considered. The error in the estimated force can come from two different sources, which are the error of the GITT method itself and the error due to pre-processing the measurements (filtering, modal analysis, etc.).

  • As for the error of the GITT method, if the dynamic response is absolutely accurate, the GITT solution should be more accurate when the truncation order N is higher. Each term of \({\tilde{\phi }_i}\left( z \right)\) satisfies boundary conditions, besides, there is no approximation involved in the analytical derivation of GITT approach, the problem solution represented by the summation of a rapidly converging infinite series (12b) simultaneously satisfies the governing differential equation (2) and the boundary conditions (4). In real calculations, the derived series solution needs to be truncated somewhere for computational evaluation. Theoretically, the solution will be more accurate if the truncation order is higher. In the reality, the response extracted from experiment would have some error due to many uncertainties, such as the turbulence of flow, the noise from towing carriage and noise from acquisition system. There errors will be amplified dramatically by the fourth term \(\lambda ^4\) at the high-mode \(\bar{y}_N(t)\). Hence, the appropriate selection of truncation order should be examined after the modal analysis which could show the dominated modes clearly. Sometimes, in the dominant mode some sort of aliasing may exist, thus the selection zone of truncation order should contain all of the dominated modes.

  • As for the error due to pre-processing the measurements, the strain signals are filtered through Meyer wavelet-based denoising to avoid the influence of high-frequency noise, which is probably different from the denoising technique used by Trim et al. [16]. But the filtering quality is verified during present study, and it is found that the filtered signal is smooth and high-frequency noise is removed.

  • As for the error induced by modal analysis, Trim et al. [16] commented in their study “In order to get accurate results from the modal analysis, the participating mode numbers used as input to the analysis were tuned on a trial and error basis. The results are in some cases sensitive to the participating mode numbers, but are considered in general to be reasonably accurate.” Thus, we have tried several combinations of the participating mode numbers for the present 2 cases, it is found that the participating mode numbers from 6 to 15 are reasonably accurate to represent the dynamic response of the riser model.

Another issue of the approximation is the cubic polynomial fitting method used to capture the spanwise distribution of in-line and cross-flow motions. Since the response of present riser model is dominated mostly by mode 1, the cubic polynomial fitting method is suitable in present experimental verification. Obviously, when a flexible riser suffers high modes, the modal analysis is better to reproduce the dynamic response. In addition, the cubic spline interpolation was performed to compare with the cubic polynomial fitting, and the error of fluid force coefficient between these two methods is less than 1 %, which means that the choice of these two methods is not a matter during the GITT calculation of present experimental verification.

One question of proposed GITT is Can it be applied to sheared flow ? In the shear flow, the profile of displacement may be asymmetric such as the experimental results from Trim et al. [16]. Then the dynamic response (the profile of displacement, velocity and acceleration) would be integrated with eigenfunction from 0 to 1 as shown in Eqs. 11(a) and 16. Then the question will be transformed to Can the dynamic response be perfectly represented as the superposition of the eigenfunction? Theoretically, the Fourier series formalism provides a means to represent any periodic function as a superposition of sinusoidal functions whose frequencies are integral multiples of its fundamental frequency (harmonics). Hence, the dynamic response of the flexible cylinder could be extended as a periodic function, then in every closed interval in which the dynamic response (imagined to be periodically extended) is continuous as well as sectionally smooth, the Fourier series converges uniformly. It concludes that the proposed GITT solution is capable to be applied to sheared flow.

8 Conclusions

A GITT solution capable of evaluating fluid force of a flexible circular cylinder due to VIV has been proposed in this paper. The partial deferential governing equations were transformed to ordinary deferential equations based on the GITT method. The advantage of the selection of the proposed eigenfunction can eliminate the fourth-order derivative term related to the bending stiffness, then the selection of truncation order could be analyzed to avoid the error mainly induced by the high mode, which cannot be examined in the physical space. Then an experiment was carried out in a towing tank. The experimental response was accurately measured and used as input, then implementing GITT to calculate the fluid force distribution of the long flexible cylinder. The truncation order of eigenfunction was examined based on the fluid force spanwise distribution. Due to error induced by the high-order mode, truncation order was 4 for all present experimental verification. The comparison between the numerical results from GITT and the experimental results from load cell verified the capability and availability of the proposed GITT method. If one can use a method for lower modes, then one certainly can extend the method for higher modes. Two experimental cases from the literature were evaluated and good agreement was obtained based on the spatio-temporal evolutions of the lift coefficient and the mode numbers.

However, this integral transform method is using the displacement, velocity and acceleration as inputs to obtain each mode contribution of fluid force, thus the accuracy of input plays an important role to such simulation and should be carefully considered. Since this method is easy to implement, it can be an alternative method to investigate fluid force of such slender structures.