Hull-form optimization using parametric modification functions and particle swarm optimization

Abstract

The focus of this paper is on devising designer-friendly hull-form variations coupled with optimization algorithms. Hull-form variations are carried out through parametric modification functions. Two kinds of representative optimization algorithms are considered here. One is the well-known sequential quadratic programming which is the derivative based. The other is particle swarm optimization which is the derivative free. The results applying these two algorithms to typical hull-form optimization problems are discussed in the paper. The technique using the parametric modification functions has been developed for modifying the ship’s geometry according to the widely recognized naval architect’s design practice. An original geometry can be easily deformed through the change of the variables of the modification functions; and useful information about the effect of the parameters is immediately obtained. Moreover, the variables of the modification functions can be considered as the design variables in the formulation of the optimization problem. For the performance prediction of the hull form, WAVIS version 1.3 is used for the potential-flow and RANS solver. Computational results for both single- and multi-objective problems are presented.

1 Introduction

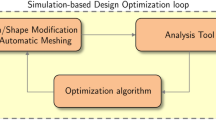
Simulation-based design (SBD) is an emerging engineering tool to deal with complicate optimization problems which come out of diverse technical sectors, including ship hydrodynamics. The developments in CFD and greater computer power offer chances for a more integrated and frequent use of the SBD in the ship design process.

However, the SBD has not been widely used in practical ship design. There are some problems to resolve—robust and automated grid generation and manipulation, and hull-form variation under constraints according to the industrial needs; and the parameterization is one of the issues that must be overcome before the SBD can make a widespread impact on the practice of ship design, which has to be as familiar as possible to the ship designer. Despite the damping effects of reality on the immediate expectations, the potential benefits and pay-offs of the impact of the SBD on the ship design process are so great that the researches on the SBD have been performed to yield promising results, to reveal specific new challenges and to suggest directions of research.

Various types of ships have been optimized to satisfy the objective functions through SBD: Wigley with minimum wave-making resistance [1], bow vertical motion [2]; Series 60 with minimum wave-making resistance in deep water [1, 3] and shallow water [4], bow vertical motion [2], total resistance expressed as the sum of wave-making and viscous resistance [5, 6]; tanker SR221 with minimum delivered power and overshoot angle [7]; Suezmax tanker with minimum wave-making resistance at bow region and viscous pressure resistance at stern region [8]; LPG carrier with minimum total resistance [9]; container ship SR175 with minimum heave motion [10], heave and pitch motion [11]; KCS with minimum wave-making resistance [12]; ultra large container ships with minimum total resistance [9]; ferry with minimum wave height in calm water and absolute vertical acceleration [13]; combatant ship DTMB 5415 with improvement of flow- and wave-field [14], with minimum total resistance obtained from RANS solver [15, 16], total resistance and seakeeping [17, 18]; frigate with minimum total resistance obtained from RANS solver [19], wave-making resistance and seakeeping [20]; catamaran with minimum wave-making resistance [21], and total resistance [22].

There are three core technologies for the SDB: hull-form variation, performance prediction via a flow solver of a varied hull form, and selection of the optimized hull form. These three technologies have each developed to be applied in various ways. Various techniques have been deployed for the hull-form variation—vertex control, modification function, and form-parameter variation.

Vertex control involves expressing the initial hull form as a curved surface such as a B-spline, and shifting the hull form with the vertex as the design parameter [1, 6, 7, 10, 11, 16, 23–25]. The upside to this technique is the flexibility of the hull-form variation, but poor fairness after the variation and the challenging control of the hull form are the downsides. The form-parameter variation defines the hull form with a form parameter for surface modeling [9, 13, 15, 17, 19, 20, 26–28]. It boasts strong flexibility and fairness, and ease-of-use; but the initial hull form is not readily conveyed with a form parameter. Modification (or transformation) function calculates the varied hull-form by reflecting the variation amount that taps into the modification function of the initial hull form, which does not require the initial hull form to be defined by a form parameter [3–5, 8, 14, 21, 22, 29]. Flexibility and fairness are the advantages, while the variation is restricted by the modification function and it is not as easy to manipulate for the designer.

In the field of the CFD prediction for the objective functions (i.e., ship resistance, propulsion, seakeeping and maneuvering performance, etc.), the potential-flow and RANS solvers have been applied. The potential-flow solver has widely used because of the efficiency in evaluating the wave-making resistance [1, 3, 4, 21, 24, 30–32] or the wave height [13] in calm water, in spite of the low physical fidelity. Furthermore, the total resistance in full scale can be obtained by adding the viscous resistance expressed as empirical formula to the wave-making resistance [5, 6, 9, 22]. In the case of small margin of improvement, it is necessary to use the high-fidelity CFD solver, such as RANS solver. The RANS solver has been applied to predict the total resistance in model scale, which includes the automatic grid deformation as a sequel to hull-form variation [12, 14–16, 19, 33–35]. Tahara et al. [7] performed the optimization for the minimum delivered power and the first overshoot angle in 10^o/10^o zig-zag test using the RANS solver. Park et al. [8] optimized the bow and the stern hull forms separately, where the objective functions are the minimum wave-making and viscous resistance for the bow and stern using potential-flow and RANS solvers, respectively. The seakeeping qualities are assessed using either two-dimensional strip theory [2, 11, 13, 20] or three-dimensional panel methods [10].

The objective functions are nonlinear with respect to the design variables, and complex design constraints are imposed. Several techniques based on deterministic or probabilistic algorithms have been applied for solving nonlinear optimization problems with constraints such as genetic algorithms (GA), evolution strategy (ES), sequential quadratic programming (SQP), and particle swarm optimization (PSO). However, no single technique is best for solving all problems. The evolutionary algorithms (EAs), which are inspired by the Darwin’s theory of evolution and the survival of the fittest, are stochastic search techniques that perform a multiple directional search by maintaining a population of potential solutions. GAs and ESs are the most widely used EAs. In the GAs, the whole parent population is replaced by their offspring and their cost value is computed, whereas this happens partly only in the ESs. The EAs are able to avoid local optima as they start from multiple points. The GAs [2, 5, 13, 31] and the ESs [1] have been widely used. Another feature of the GA is that it can be extended to find Pareto optimal solutions in multi-objective optimization, i.e., multi-objective GA [3, 7, 20, 29]. The SQP is the gradient-based technique that taps into the differential value of the objective function or the constraint’s design parameter [4, 6–8, 21, 36]. The advantages are rapid convergence and computational efficiency. However, this is a local optimizer which may prove challenging to employ in local minima and non-connected feasible regions. The SQP is suitable for a single-objective optimization. The PSO is derivative free and suitable for a multi-objective optimization [7, 10, 11, 16, 22, 29, 37, 38]. Peri and Campana [35] suggested two phases of the optimization process by introducing the surrogate models for the reduction of the overall time. Chen et al. [24] proposed the Levenberg–Marquardt method, which is an inverse design algorithm, to determine the optimal shape of the bulbous bow. Campana et al. [15] suggested two alternative ways to reduce the computational expense; the narrow band derivative-free approach using GA and the derivative-based variable-fidelity approach. Tahara et al. [17] proposed the uniform covering (UNICO) approach with variable fidelity for the multi-objective optimization problems. Campana et al. [10] suggested a filled function-based algorithm when the objective function requires high-fidelity models and its first derivatives are not available. Kim et al. [12] applied the variable-fidelity optimization model to the hull-form hydrodynamic optimization problem: minimization of the wave drag of a modern container ship.

In this paper, a designer-friendly hull-form variation technique is proposed. The varied hull forms are coupled with not only a local but also a global optimization algorithm. One is a well-known SQP, which is the derivative-based algorithm. The other is the deterministic particle swarm optimization (DPSO), which is the derivative free. They are the representatives of classes, however, with rather opposite characteristics. The results applying these two algorithms to typical hull-form optimization problems are discussed as well. Issues pertain to bow hull-form optimization for the container ship and the stern for the VLCC. The former is about minimizing wave-making resistance at two ship speeds. The latter is about minimizing viscous resistance and optimizing the wake on the propeller plane. Objective functions are obtained using the potential-flow and RANS solver of WAVIS version 1.3 [39, 40].

2 Problem formulation

The mathematical formulation of the optimization problem is expressed as Eq. 1

$$ {\text{Minimize}}\,[f_{1} (\bar{x}), f_{2} (\bar{x}), \ldots , f_{K} (\bar{x})] $$

(1)

Subject to the equality and inequality constraints

$$ h_{j} (\bar{x}) = 0,\quad j = 1, \ldots , p $$

(2)

$$ g_{j} (\bar{x}) \le 0,\quad j = 1, \ldots , q $$

(3)

where $f_{i} (\bar{x})$ is the objective function, K is the number of objective functions, p is the number of equality constraints, q is the number of inequality constraints and $\bar{x} = (x_{1} ,x_{2} , \ldots , x_{N} ) \subseteq S$ is a solution or design variable. The search space S is defined as an N-dimensional rectangle in $\Re^{N}$ (domains of variables defined by their lower and upper bounds):

$$ x_{i}^{\ell } \le x_{i} \le x_{i}^{u} ,\quad i = 1, \ldots , N $$

(4)

The constraints define the feasible area. This means that if the design variables vector $\bar{x}$ be in agreement with all constraints $h_{j} (\bar{x})$ (equality constraint) and $g_{j} (\bar{x})$ (inequality constraint), it belongs to the feasible area.

In this study design variables vector includes the main parameters (length, breadth, draft) and the hull control points which are limited by the lower and upper bounds. The displacement (V) is an inequality constraint, which is kept within ±1 % of the original value (V ₀), namely 0.99 ≤ V/V ₀ ≤ 1.01.

3 Parameterization approach

A designer-friendly parametric modification tool is adopted for modifying the hull form according to the classical naval architect’s approach as well as the office design practice.

Among a large number of methods available to modify hull forms, ship designers, traditionally, are interested in systematic using of some parameters. The major benefit of this approach is that the original ship geometry can be easily deformed by a limited number of the well-known design parameters. As a consequence, the modified hull form due to the change of the parameters is immediately obtained. Useful information about the effect of the modified hull form on the hydrodynamic characteristics is obtained through CFD analysis. Moreover, the variables of the parameter modification function can be considered as the design variables of an optimization problem. These variables are varied systematically one by one, keeping constant all the others. Then, the design sensitivity can be easily extracted through the CFD analysis for the evaluation of the ship performances.

For a number of reasons, this is not the approach followed by most of the current generation of optimization codes. The geometrical manipulation modules of these codes are indeed typically based on CAD systems (or CAD emulators) and hence make use of mathematical surfaces instead, i.e., describing the ship surface based on non-uniform rational basis spline (NURBS) or splines patches, with a limited number of control points, freely adjustable by the designer, to obtain the required hull shape. As a consequence, the changes of the main hull parameters are computed a posteriori, and they are not the direct output of the code.

This paper, somewhat, goes back to a practical hull-form design approach, in which the hull-form variations are directly related to the design parameters, and the parametric modification is fully integrated with both the geometry modification module and the CFD analysis.

The initial hull surface is represented using the following B-spline surfaces:

$$ Q\left( {u,v} \right) = \mathop \sum \limits_{i = 1}^{{n_{i} + 1}} \mathop \sum \limits_{j = 1}^{{n_{j} + 1}} B_{i,j} N_{i,k} (u)M_{j,\ell } (v) $$

(5)

where the B _i,j are the vertices of a polygon net, N _i,k (u) and M _j,ℓ(v) the B-spline basis function in the bi-parametric u and v directions, respectively.

The parametric modification function is superimposed on the original hull (H _old) to obtain modified geometry (H _new):

$$ H_{\text{new}} (X,Y,Z) = H_{\text{old}} (X,Y,Z) + r^{(\ell )} (X) \cdot s^{(m)} (Y) \cdot t^{(n)} (Z) $$

(6)

where r ^(ℓ)(X), s ^(m)(Y) and t ⁽ⁿ⁾(Z) are the parametric modification functions defined as polynomials along the X, Y and Z directions, respectively. The superscripts $(\ell )$, (m) and (n) are the orders of polynomials. Here, a local coordinate (X, Y, Z) is applied, where the positive X direction goes from the AP to the FP, and the positive Z direction is vertical from the hull bottom. The units of X and ΔX are stations. ΔY and ΔZ are non-dimensionalized by B/2 and T, respectively. The modified geometry is obtained using the perturbation with specific direction depending on the design parameters. Sectional area curve (SAC), section shape and bulb shape are used as modification functions of bow hull form in Table 1.

Table 1 Design parameters for the fore body hull-form optimization

This parametric modification approach can also be applied to grid generation because the modification functions are based on positions only. The smoothness is guaranteed as the modified geometry is constricted by modification functions.

The disadvantage of this approach is that it is not fully flexible and it allows us to obtain the modified geometry according to parametric modification function which is already defined.

3.1 SAC shape parametric modification function

Various hull forms can be derived by parametric modification of SAC. Figure 1 shows the SACs of fore body for the original and the modified hull form using four design variables (X ₀, X ₁, X _c , ΔX ^SAC).

Fig. 1

SACs of fore body for the original and the modified hull form using four design variables

A sixth-order polynomial defined only in x direction as r ⁽⁶⁾(X) can be used as parametric modification function of the SAC shape. To determine the polynomial coefficients of r ⁽⁶⁾(X), the following seven conditions need to be satisfied:

$$ \begin{aligned} r(X_{0} ) = 0\quad r(X_{1} ) = 0\quad \,r(X_{C} ) = 0\quad r^{\prime}(X_{0} ) = 0\quad r^{\prime}(X_{1} ) = 0, \hfill \\ r(0.5X_{0} + 0.5X_{C} ) = \Delta X^{\text{SAC}} ,\quad r(0.5X_{C} + 0.5X_{1} ) = - \Delta X^{\text{SAC}} \hfill \\ \end{aligned} $$

where X ₀ and X ₁ represent the reference range of the modification, X _C a position at which the shape of the ship section is fixed, ΔX ^SAC maximum longitudinal movement of the sections. Note that the section positions for the maximum longitudinal movement are located at X = 0.5(X ₀ + X _C ) and X = 0.5(X ₁ + X _C ), respectively, to preserve the displacement. The modification function r ⁽⁶⁾(X) can be changed by the variations of parameters X ₀, X ₁, X _C and ΔX ^SAC. So, these four parameters can be considered as design variables associated with the parametric modification of the SAC. One can also fix some of the four parameters, and change the others. In the applications presented in the present study, the parameters X ₀, X ₁ and X _C are prescribed, and only parameter ΔX ^SAC is allowed to change, i.e., taken as design variable.

As a result of the modification of the original SAC, the new section shape at any longitudinal position can be obtained by Lackenby method [41]. The new grid point on the hull surface can be obtained by moving the grid point in x direction according to the modification function as follows,

$$ X_{\text{new}} = X_{\text{old}} + r^{(6)} (X) $$

(7)

3.2 Section shape parametric modification function

There are two types of the section shape modification functions: design load water line (DLWL) and U–V type. The DLWL type is the function to modify the section shape associated with the DLWL and the U–V type is the function to modify the section shape into the U- or the V-shaped section.

The parametric modification functions of the section shape are also defined as three polynomials in X, Y and Z directions. The new grid point on the hull surface can be obtained using the perturbation in Y direction, and the amount of perturbation can be obtained by multiplying three modification functions as follows,

$$ Y_{\text{new}} = Y_{\text{old}} + r^{(4)} (X) \cdot s^{(5)} (Y) \cdot t^{(1)/(3)/(2)} (Z) $$

(8)

where r ⁽⁴⁾(X) and s ⁽⁵⁾(Y) are fourth- and fifth-order polynomial defined in X and Y direction, respectively. t ^(1)/(3)/(2) in Z direction is divided into three; a first-order polynomial is used below Z ₀, a third-order between Z ₀ and Z ₁, and a second-order beyond Z ₁. The coefficients of the polynomials are determined from the specified conditions. Note that r ⁽⁴⁾(X) and s ⁽⁵⁾(Y) serve as the weight functions for a given section, and t ^(1)/(3)/(2) defines the change in y, i.e., ΔY as a function of Z for a given section located at X.

The modification function t ^(1)/(3)/(2) can be changed by the variations of the parameters ΔY, Z ₀ and Z ₁, where ΔY represents maximum horizontal movement, denoted as ΔY ^DLWL for the section modification function associated with DLWL type and ΔY ^U–V for that of U–V type, Z ₀ is kept fixed as the draft of the hull, and Z ₁ is the position where horizontal movement is maximum.

Figure 2a shows the distribution of the DLWL type modification functions for ΔY ^DLWL = 0.1, Z ₀ = 0.3 and Z ₁ = 1, and Fig. 2b shows the distribution of the U–V type modification functions for ΔY ^U–V = 0.04, Z ₀ = 0.35 and Z ₁ = 1. The x, y and z in Fig. 2 are non-dimensionalized by LPP. The parameters ΔY ^DLWL, Z ₀ and Z ₁ can be used as design variables in the DLWL type section modification, and ΔY ^U–V, Z ₀ and Z ₁ in the U–V type section modification.

Fig. 2

Distributions of the section shape modification functions

The left and right sides of Fig. 3 show the body plans for the section shape modification function of the DLWL type (ΔY ^DLWL, $Z_{0}^{\text{DLWL}}$ and $Z_{1}^{\text{DLWL}}$ are design variables) and of the U–V type (ΔY ^U–V, Z ^U–V₀ and Z ^U–V₁ are design variables), respectively.

Fig. 3

Original and modified body plans and design variables using section shape modification function of the DLWL and the U–V type

In the present optimization study, both Z ₀ and Z ₁ are prescribed, and only ΔY ^U–V and ΔY ^DLWL are allowed to change (used as design variables) in the DLWL type and U–V type modifications, respectively.

3.3 Bulb shape parametric modification functions

Modification of bulb shape can be conducted by four design parametric functions: bulb area, bulb height, bulb length and bulb size.

Following the similar procedure as the section shape parametric modification, the modified grid point can be obtained by adding the perturbation in each direction, in which the amount of perturbation can be obtained by multiplying three modification functions as follows,

$$ {\text{Bulb area}}:Y_{\text{new}} = Y_{\text{old}} + r^{(2)/(3)} (X) \cdot t^{(5)} (Z) $$

(9)

$$ {\text{Bulb length}}:X_{\text{new}} = X_{\text{old}} + r^{(4)} (X) $$

(10)

$$ {\text{Bulb}}\,{\text{height}}:Z_{\text{new}} = Z_{\text{old}} + r^{(4)} (X) \cdot s^{(1)} (Y) \cdot t^{(5)} (Z) $$

(11)

$$ {\text{Bulb size}}:Z_{\text{new}} = Z_{\text{old}} + r^{(4)} (X) \cdot s^{(1)} (Y) \cdot t^{(6)} (Z) $$

(12)

Note that r ^(2)/(3)(X) of the bulb area is divided into two; a second-order polynomial is used between X ₀ and X ₁, and a third between X ₁ and X ₂, where X ₂ is the location where the bulb ends. These functions can again be obtained from the specified conditions. And r ^(2)/(3)(X) in Eq. 9, r ⁽⁴⁾(X) and s ⁽¹⁾(Y) in Eqs. 10 and 11 serve as weight functions, which can be determined first. The other polynomials in Eqs. 9–12 are defined in terms of some parameters, which can be used as design variables. In the present study, some of these parameters are fixed, and others are allowed to change (used as design variables). Figure 4 shows the original and the modified bulb area, bulb length, bulb height, bulb size, and the corresponding design variables. Δy _BA, Δx _BL, Δz _BH and Δz _BS are chosen as design variables, which denote the variation of bulb area, bulb length, bulb height and bulb size, respectively.

Fig. 4

Four design variables (ΔY ^BA, ΔX ^BL, ΔZ ^BH and ΔZ ^BS) to describe the bulb shape

During each optimization cycle of the hull-form modification, surface grids are generated through the use of the modification function and volume grids are manipulated. The grid manipulations are carried out with an algebraic scheme since the structured grid system is being employed, in reference to the work of Tahara et al. [14].

4 The optimization algorithms

The gradient-based algorithms are widely used in the industrial due to their rapid convergence properties and the computational efficiency when a relatively small number of variables are considered. However, these algorithms are local optimizers, which have difficulties with local minima and non-connected feasible regions. Because of the increase of computer power and the development of efficient global optimization (GO) methods, in recent years, the nongradient-based algorithms have attracted much attention. Furthermore, GO method provides several advantages over local approaches. They are generally easy to program and to parallelize, do not require the continuity in the problem definition, and are generally better suited for finding a global, or a near global, solution. In particular, these algorithms are ideally suited for solving an optimization problem of discrete and/or combinatorial type. In this paper, the gradient-based SQP and the gradient-free PSO are compared, focusing on their effectiveness and efficiency.

4.1 SQP

The SQP is an efficient, gradient-based, local optimization algorithm. The method, based on the iterative formulation and solution of quadratic programming subproblems, obtains subproblems using a quadratic approximation of the Lagrangian and by linearizing the constraints. The equations of 1–3 are approximated with quadratic forms:

$$ \hbox{min} \,{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}d^{T} B \, d + f(x)^{T} d $$

(13)

subject to

$$ h_{i} (x)^{T} d + h_{i} (x) = 0,\quad j = 1, \ldots ,p $$

(14)

$$ g_{i} (x)^{T} d + g_{i} (x) = 0,\quad j = 1, \ldots ,q $$

(15)

where d is search direction vector and B is approximate Hessian matrix of the Lagrangian. During the optimization process, the optimum d is determined and x is updated as expressed in Eq. 14 at each iteration [36].

$$ x^{k + 1} = x^{k} + \alpha^{k} \cdot d^{k} $$

(16)

where k means kth iteration and α represents step size.

4.2 PSO

The PSO is a gradient-free and global optimization algorithm. The PSO to solve distinctive global optimization problems (e.g., ship design) is encouraged by the following appealing features: (1) balance, between the computation involved and the precision of the solution detected; (2) constant computational cost and memory engagement at each iteration; (3) availability of a current approximate solution; (4) derivatives of the objective function not required; (5) easy implementation and parallelization of the method.

The PSO simulates the social behavior of a group of individuals by sharing their information during the exploring of design space. Each particle of the swarm has its own (individual) memory to remember the places visited during the exploration, and the swarm has its own collective memory to memorize the best location ever visited by anyone of the particles. The particles have an adaptable velocity and investigate the design space analyzing their own flying experience, and the one of all the particles of the swarm. Each particle is a potential solution of the optimization problem.

The PSO algorithm assumed that each individual in the particles swarm is composed of three N-dimensional vectors, where N is the dimensionality of the search space. These are the current position $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x}_{i}$, the previous best position $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {p}_{i}$, and the velocity $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{i}$. A particle swarm is composed of Nv number of particles, the position of the number i particle expressed as $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x}_{i} = [x_{i1} ,x_{i2} , \ldots ,x_{iN} ]$, and so the velocity is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{i} = [v_{i1} ,v_{i2} , \ldots ,v_{iN} ]$, the best position find by the number i particle is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {p}_{i} = [p_{i1} ,p_{i2} , \ldots ,p_{iN} ]$, the best position find by the whole particles expressed as $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {p}_{g} = [p_{g1} ,p_{g2} , \ldots ,p_{gN} ]$. The basic algorithm is simple as follows:

• Step 0 (initialize)

Distribute a set of particles inside the design space, using user-defined distributions. Evaluate the objective function in the particles’ position and find the best location (p _b ).

• Step 1 (compute particle’s velocity)

At the step k + 1, calculate the velocity vector v _i for each particle i using the equation:

$$ v_{i}^{k + 1} = \chi [w^{k} v_{i}^{k} + c_{1} r_{1}^{k} (p_{i}^{k} - x_{i}^{k} ) + c_{2} r_{2}^{k} (p_{g}^{k} - x_{i}^{k} )] $$

(17)

where χ is a speed limit and w is the inertia of the particles controlling the impact of the previous velocities onto the current one. The second and third terms, with weights c ₁ and c ₂, are the individual and collective contributions, respectively, and finally r ₁ and r ₂ are random coefficients uniformly distributed in [0, 1].

• Step 2 (update position)

Update the position of each particle:

$$ x_{i}^{k + 1} = x_{i}^{k} + v_{i}^{k} $$

(18)

• Step 3 (check convergence)

Go to Step 1 and repeat until some convergence criterion (e.g., the maximum distance among the particles, a condition on the velocity) is matched.

DPSO is a deterministic version of the basic PSO for constrained single-objective problems which includes several algorithmic improvements. More details are given in Campana et al. [41]. A multi-objective version of the DPSO has been recently presented in Pinto et al. [11] to which the interested reader is referred.

Experimental results indicate that a large value of the inertia w promotes a wide exploration of the global search space. Hence, w is initially set to a high value and then gradually decreased ($w^{k + 1} = K \cdot w^{n}$, with K < 1) to facilitate the fine tuning of the current search area. The set of parameters adopted in the computations is listed in Table 2, in reference to the work of Compana et al. [42]:

Table 2 Parameters for the forebody hull-form optimization algorithm

5 Flow solver

The ship sails at constant speed (U) in calm water. Such condition is assumed to be the same as uniform flow moving downstream at the condition of a fixed ship. The coordinate applied has the flow direction as the axis x (+) and the starboard as the axis y (+), and the opposite direction of the gravitation as the axis z (+). The origin of the coordinate is located where the center plane, midship, and the undisturbed free surface meet.

WAVIS version 1.3 code was utilized, which consists of potential-flow solver and RANS solver. The details and formulations of the numerical methodologies are well described in the works of [39, 40, 43, 44]. Hence, only main features of the methodologies are described.

The potential-flow part uses a panel method based on the raised panel approach for the nonlinear ship wave problem of practical hull forms [39, 40]. The convergence criteria are the residuals for the kinematic and dynamic free-surface boundary conditions. Kim et al. [43] compared and verified the computational results with those of towing-tank experiments of KCS and KVLCC2, which are the present objective ships. The wave-resistance coefficient (C _W) is eventually given by the pressure integral over the wetted hull surface. For the computations, the hull and the free surface have been discretized with 912 and 1690 panels, respectively. During the computation, the ship was free to sink and trim. We apply the linearized free-surface boundary condition on the free surface, since this considerably reduces the computational time without affecting the results.

The RANS solver utilizes the finite volume method to solve the Reynolds-averaged Navier–Stokes equations [39]. The realizable k–ε model is applied for the turbulence closure. Double-body model is used to treat free surface. The computational results of KVLCC2 and KCS are compared and verified with those of towing-tank experiments [40, 44–46].

The accuracy of flow solver has a large impact on the practical implementation. Strictly speaking, the validation and verification of flow solver should be first performed before the optimization. The improvement obtained by the optimization should be larger than the numerical noise of flow solver. However, the uncertainty analysis does not performed in this paper, since the validation and verification were carried out in advance by [47]. Kim et al. [40] showed that WAVIS version 1.3 can predict resistance coefficients and nominal wake fractions with acceptable accuracy compared to the towing-tank model experiment. They also studied grid dependency using three grid systems (83 × 33 × 33, 99 × 41 × 41, 99 × 41 × 41) and revealed that the calculated result with 166,419 (=99 × 41 × 41) grids is almost the same as that with 280,917 (=117 × 49 × 49). In the present work, 290,813 (=173 × 41 × 41) grids are used. This grid size seems to be appropriate to identify the proper trends of the objective functions. Of course, it does not guarantee the accuracy because of the other effects, i.e., turbulence model, free-surface effect, etc. Although the present flow solver is low fidelity, the computational results are seemed to be applicable to the optimization. Each computation requires about 25 min on an Intel Core 2—6600—2.4 GHz.

6 Results

To verify the practicability of the hull-form variation using parametric modification functions, a bow hull-form optimization was carried out for a container ship. Both the SQP and the PSO optimization algorithms are applied to find a proper algorithm. The latter has been used with the two different sizes of swarm population and of the initial distributions illustrated in Sect. 6.1.

The objective ship is the Korea Research Institute of Ships & Ocean Engineering (KRISO) 3600 TEU container ship (KCS) model. Main dimensions are LPP = 230 m, B = 32.2 m, T = 10.8 m. In the case of the single-objective function problem, the goal is a minimum value of wave-resistance coefficient (C _W) at a fixed speed corresponding to F _N  = 0.26 (design speed 24.0 knots). F _N is Froude number based on LPP. The motivation for the choice of C _W is that the focus of this paper is on linking the parametric modification approach with local and global optimizers, and therefore there was no need for using more complicated objective functions. In the potential-flow solver of WAVIS version 1.3, the C _W is calculated using the static wetted surface of the varied hull form. The wave-making resistance is the actual objective function. The C _W in the paper is non-dimensionalized by the static wetted surface of the original hull for convenience. In the case of the multi-objective function problem, the objective functions are the minimum values of C _W at two speeds. For a container ship, the wave-making resistance holds a very large portion of total resistance and is sensitive to not only hull form but also ship speed. Ship owners are interested in slow steaming (or reducing ship speed) to cut down fuel consumption and carbon emissions. Hence, two ship speeds are taken into account; F _N  = 0.26 and 0.24 (22.16 knots).

The keel line is fixed, but bulb profile can be changed. Finally, the design variables are limited by some box constraints. That is the variations of the design variables are restricted at the range from Station 12 to bulb tip. The hull form should be smoothly joined to the original at Station 12.

For the single-objective problem, we will discuss the numerical results of five different cases, consisting of 2–6 numbers of parametric modification functions. The cases are summarized in Table 3. The design variables are described in detail at the previous section of parameterization approach. Initial value is used for 0 (zero), which denotes the original hull form since there is no variation of the design parameter. Problem number N is obtained by adding the corresponding design parameter to those used in the problem number (N − 1).

Table 3 Test cases for the different numbers of parametric modification functions

The more numbers of modification functions, the better an optimal hull form will be, since the more freedom of hull-form variation. However, according to the work of Diez et al. [48], larger design spaces are also more difficult to explore, especially if a global optimum is sought, and therefore a proper tradeoff between space dimensionality and design variation should be carefully considered.

Then, we will discuss the results of a multi-objective case. This problem is evidently a multi-point optimization problem more than a truly multi-objective, but, as stated mentioned before, we have been interested in assessing the performances of the optimizers/parametric approach coupling more than in solving a complicated problem.

6.1 Single-objective tests

The effective number and distribution of the initial particles significantly affect the results in the PSO algorithm. The probability to find an optimum value will increase as the number (of particles) increases with the same number of PSO iterations, however, the computational time rapidly increases. If one has a fixed budget of function evaluations, then there is a tradeoff between the swarm size and the number and iterations. Therefore, it is necessary to find an optimum number and distribution to effectively explore the design space. As the design variables increase, the necessity will increase.

Three kinds of the methods are investigated, that is, PSO-hcf, PSO-hcv, and PSO-sobol.

• PSO-hcf: the swarm particles initially distributed at the center of the hypercube faces. The number of the swarm particles is 2Nv, where Nv is the number of the design variables.

• PSO-hcv: the swarm particles initially distributed at the vertices of the hypercube faces. The number of the swarm particles is 2^Nv.

• PSO-sobol: the swarm particles initially distributed according the Sobol quasi-random sequence). In general, this method does not require a fixed number of the swarm particles. Here, the number is of 2^Nv + 1.

Figure 5 shows the initial distributions of the swarm particles using the above three methods in the case of Nv = 3.

Fig. 5

Initial distribution of the swarm particles in the case using 3 design variables

The initial value of the design parameter is 0 (zero), which denotes the initial hull form. The interesting quantities to be monitored are both the resistance reduction and the number of function evaluations Nf. The C _W reduction ratio (ΔC _W) obtained and Nf are summarized in Table 4. The C _W of the original hull form at F _N  = 0.24 is 0.3544 × 10⁻³. Note that Nf is related to the computational efficiency.

Table 4 Reduction ratios of C _w and number of function evaluations of five problems for single-objective test

Table 4 shows the feasibility of the parametric modification functions, and the optimization using the SQP and the PSO. In the performance aspect, the order is SQP, PSO-hcv, PSO-sobol, and PSO-hcf. In the computational efficiency aspect, the order is SQP, PSO-hcf, PSO-sobol, and PSO-hcv. The SQP demonstrates a fast convergence and a superior performance. The PSO-hcv is computationally the slowest. The PSO-hcf is as efficient as the SQP in the aspect of the computational time, however, inferior to the other methods in the aspect of the performance. Overall, the PSO-sobol shows comparable to the SQP in the aspect of performance and computational efficiency.

Figure 6 shows ΔC _W versus Nv for four methods. All four methods show better performances as the number of design variables increases, which is already shown in Table 4. SQP and PSO-hcv increase linearly their performance with Nv. PSO-sobol shows roughly the same trend, but Nv = 5. In the case of PSO-sobol for Nv = 5, the ΔC _W decreases as the number of the swarm particles increases. This means that it leaves a part of the design space unexplored. Better result will be shown if the swarm particles increase. However, the number was not changed, since the focus is the comparison of the other methods using similar number of swarm particles (2^Nv + 1). PSO-hcf shows approximately a square-root trend.

Fig. 6

C _W reduction ratio as a function of the number of variables

To explain the reason why the SQP shows the best, it is necessary to look at the convergence path of the OPT1 and the OPT2 feasible domains in ℜ² and ℜ³, respectively, as shown in Figs. 7 and 8. The convergence path of the OPT3, the OPT4 and the OPT5 cannot be easily shown, since their domains are in ℜ⁴, ℜ⁵ and ℜ⁶, respectively.

Fig. 7

Iso-contours of C _W and convergence paths of the SQP and the PSO-sobol for the OPT1

Fig. 8

Iso-contours of C _W and convergence paths of the SQP and the PSO-sobol for the OPT2

Figures 7 and 8 show the iso-contours of C _W and the convergence paths of the SQP and the PSO-sobol for the OPT1 and the OPT2, respectively. The shapes of the iso-contours of C _W and the (volume) constraint clearly show that the domain is convex. Hence, this is a unique global optimum. This ensures that even a local optimization algorithm can find the global optimum independently. This is an ideal condition for the fast convergence of any gradient-based approach. It is deduced from the good performances of the SQP for the OPT3, the OPT4 and the OPT5 that the basic features of the set of optimization problems share the same characteristics.

The PSO-hcv shows almost identical C _W reductions with respect to the SQP, but with a much higher Nf (up to one order of magnitude). This is predictable since the PSO is a gradient-free, global optimization algorithm, and the lack of knowledge of the gradient information requires more computational effort. On the other hand, it will work well in cases where any local method would fail. The different behavior between the two methods can be observed in the paths of the SQP and of the PSO-sobol.

It is interesting that both the PSO-sobol and the PSO-hcf show a much reduced Nf comparing that of the PSO-hcv. The values of Nf of the PSO-sobol and the PSO-hcf are very close to that of the SQP (in two cases even less than that of the SQP). These two approaches show, however, different performances with respect to the C _W reduction. The PSO-sobol very close to that by the SQP is to be optimum, although the PSO-hcv gives the best C _W reduction.

In conclusion, the PSO-sobol shows good efficiency in terms of reduced Nf, is attractive when more complex problems have to be solved (e.g., with more complex constraints).

6.2 Multi-objective test #1

As previously mentioned, the objective functions are the minimum values of C _W at F _N  = 0.24 and 0.26. The bow hull form is optimized without altering the stern. Modification functions are the entrance angle in SAC, the section shape (U–V type), the section shape (DLWL type) and the bulb area. That means four design variables are considered, i.e., Nv = 4. The PSO-sobol is implemented. Hence, the number of initial swarm particles is 17(=2⁴ + 1). The initial hull forms and the design spaces are determined through the parametric studies as the same ways of the single-objective tests. Figure 9 shows the distributions of all the swarm particles, the Pareto set after five generation, and the Pareto optimal set. The swarm particles explore a wide range of the domain for the objective functions.

Fig. 9

Pareto set after 5 generation and Pareto optimal set of multi-objective test #1

The Pareto front is reported in the function space in Fig. 10. Figure 10 shows the Pareto optimal set from multi-objective optimization with the PSO-sobol approach and the SQP solutions.

Fig. 10

Pareto optimal set from multi-objective optimization and the SQP solutions

SQP-KSC1 and 2 represent the SQP solution of the two single-objective problems obtained for the two different speeds. The SQP can only deal with a single-objective problem. To deal with a multi-objective one, the SQP can be applied through an aggregated approach, i.e., the problem has to be transformed into a single-objective one by making a linear combination, with some user-defined weights, of all the objective functions. In this way, however, the true nature of the multi-objective problem (i.e., the concept of Pareto front, see as an example in Miettinen [49] is lost. Here, the SQP is used to solve the separated problems at the two speeds. Among the eight Pareto solutions, three solutions are chosen, that is, the PSO-KCS1, 2, and 3. The values of C _W and the reduction ratios comparing to that of the original hull form (ΔC _W) for three Pareto, and two SQP are listed in Table 5.

Table 5 Values and reduction ratios of C _w of the original and the optimized hull forms from the PSO and the SQP at two speeds

The PSO-KCS1 is hull form with a minimum C _W (=0.6129 × 10⁻³) at F _N  = 0.26, which reduces the C _W by 7.8 %. The PSO-KCS3 is hull form with a minimum C _W (=0.2776 × 10⁻³) at F _N  = 0.24, which reduces the C _W by 8.5 %. The PSO-KCS2 is one of the remaining Pareto solutions, which reduces the C _W by 7.6 and 7.5 % at F _N  = 0.26, and 0.24, respectively. The SQP-KCS1 and 2 are the solutions of the SQP optimization for the single-objective function at F _N  = 0.26 and 0.24, respectively. The C _W from the SQP is the lowest, since the optimization is performed at one objective function.

The body plans of the three PSO solutions are present in Fig. 11. The three hull forms show some differences, which are due to their own objective functions. In the case of PSO-KCS1 and KCS3, the section shapes are modified toward increasing the entrance angle and the bulb area; while the variation varies between the two. The section shapes of PSO-KCS2 are modified in the direction of increasing the entrance angle and reducing the bulb area.

Fig. 11

Body plans of three Pareto front solutions (PSO-KCS1, 2 and 3) and the original ones

Note that the multi-optimal problem is taken into consideration in this work. Various hull forms may exist to satisfy similar objective functions. Multi-optimal hull forms can be derived using the PSO since the whole design spaces are explored, whereas the SQP not. All the three hull forms are practical. Therefore, the PSO and parametric modification can efficiently find Pareto optimal set the field of multi-objective hull-form design.

6.3 Multi-objective test #2

The second multi-objective test is the optimization of the stern hull form of the KVLCC2 (second version of the KRISO very large crude-oil carrier). Main dimensions are L = 320 m, B = 58.0 m, T = 20.8 m. The model-ship scale ratio is 58.00, and F _N  = 0.142, R _N  = 4.6 × 10⁶ at ship design speed (V _S = 15.5 knots). R _N is Reynolds number in model scale based on LPP. This test is more complex and expensive.

The final goal of the objective function for the hull-form optimization is minimizing delivered power. This can be done through the use of RANS solver in towing and self-propulsion conditions. It is very time-consuming even at a model scale. The objective functions in this work are to minimize (1) viscous pressure resistance coefficient (C _VPM, or form resistance coefficient) and (2) the mean longitudinal velocity of a selected region on the propeller plane as expressed in Eq. 19

$$ {\text{Mean}}(V_{x} ) = \int_{ - \alpha }^{\alpha } {\int_{{ - r_{0} }}^{{r_{P} }} {V_{x} \cdot r{\text{d}}r{\text{d}}\theta } } $$

(19)

where α is the angle of the selected region (−45^o < α < 45^o) and V _x is non-dimensional longitudinal velocity. We take—Mean(V _x ) as objective function to be minimized, which means maximizing wake velocity. Maximizing wake velocity is related to resistance and propulsion performances. Higher wake velocity (or lower wake fraction) is known for lower viscous resistance and hull efficiency. However, it is not generally applicable. The experimental results of the KVLCC1 which is similar to the KVLCC2, the V-form hull (i.e., higher wake velocity) is superior to both the basic and the U-form hull form (i.e., lower wake velocity) with respect to the resistance and propulsion performance [50]. In this work, maximizing wake velocity is selected as one of the objective functions to take the propulsive performance into consideration. The flow at the selected upper part of propeller plane is also related to propeller performance, that is, maximizing wake velocity makes the inflow velocity distribution on the propeller plane uniform. Therefore, maximizing wake velocity has been one of the important parameters used for ship design.

The C _VPM in the paper is non-dimensionalized by the static wetted surface of the original hull for convenience, which is the same case for C _W as mentioned before.

The stern hull form is optimized without altering the bow, since the objective functions are mainly influenced by the viscous flow of the stern.

The goal of this example is to show the possibility of linking the parameterization technique with volume solvers and to test the effectiveness of the optimizers.

Three design variables have been used: (1) x ₁ = ΔX in the parametric function of the SAC shape (stern region), (2) x ₂ = ΔY in the parametric function of the U–V type section shape and (3) x ₃ = ΔY in the parametric function of the DLWL type section shape. The number of initial swarm particles is 9(=2³ + 1), since the PSO-sobol is implemented. The adopted box constraints are x ₁ ≤ 0.5, x ₂ ≤ 0.07 and x ₃ ≤ 0.07. The range of the aft modification part of the hull is St. 0–St. 8.

A regular sampling of the two objective functions was performed before the test started, so that it has been possible to plot their gross structure and to follow the evolution of the optimization procedure. Figure 12 shows the distribution of the form resistance and mean velocity on the propeller plane as a function of the 3 design variables. The red dots are Pareto solutions. For positive values of x ₁, both the functions show reduced values with respect to the original hull (the point at x ₁ = x ₂ = x ₃ = 0). As to x ₂ (the U–V type section shape), the two functions show opposite trends. Minor changes are produced by x ₃ (DLWL type section shape). The discrete approximation of the Pareto front eventually found by the algorithm is also reported. The solutions are close to the box constraint on x ₁.

Fig. 12

Contours of form resistance and mean velocity on the propeller plane as a function of the 3 design variables

Among these Pareto optimal solutions, three hull forms are considered as samples: PSO-KVLCC1, 2 and 3. Figure 13 displays the performances of the Pareto solutions. The values of the design variables and the objective functions of the original and three Pareto solutions are listed in Table 6. The number of evaluation is 369. The PSO-KVLCC1 is a hull form with a minimum C _VPM(=0.817 × 10⁻³), which reduces the C _VPM by 10.5 % comparing to that of the original(=0.913 × 10⁻³). The PSO-KVLCC3 is hull form with a minimum wake, which increases the mean velocity by 70.9 % comparing to that of the original. The PSO-KVLCC2 is one of the remaining Pareto solutions, which reduces the C _VPM by 6.2 % and the mean velocity by 12.5 % comparing to that of the original.

Fig. 13

The performances of the Pareto solutions

Table 6 Summary of multi-objective test case #2

Their body plans, compared with the original ones, are reported in Fig. 14. The geometrical features of these three solutions are easily identifiable. PSO-KVLCC1 has the highest admissible value of x ₂, and hence shows a V-type stern, whereas PSO-KVLCC3 has the lowest admissible value of x ₂, hence showing a U-type shape. All the three ships display a larger SAC angle (positive x ₁).

Fig. 14

Comparisons of body plans for three different solutions of the multi-objective test case #2

The contours of the axial velocity and velocity vectors on the propeller plane are present in Fig. 15. R _P is non-dimensional radius of propeller. The form drag becomes smaller as the hull form becomes V type (i.e., PSO-KVLCC1). The mean velocity becomes faster as the hull form becomes U type (i.e., PSO-KVLCC3). These are conflicting. Consequently, the optimal hull form to minimize the objective function will be derived in the case of a single-objective problem. However, the various hull forms are derived to reduce the objective functions in the case of the multi-objective problem. For this reason, the multi-objective technique is more effective when the objective functions are conflicting tendency.

Fig. 15

Contour of axial velocity and velocity vector on the propeller plane

7 Conclusions

• 1. This paper introduces the practical hull-form optimization design method utilizing the hull-form parameterization and the deterministic optimization technique of PSO.

• 2. Bow and stern hull-form designs are successfully implemented using the above two methods. The former is to minimize wave-making resistance at two ship speeds. The latter is to minimize viscous resistance and mean longitudinal velocity of a selected region on the propeller plane, where −45^o < α < 45^o.

• 3. In the problem of single-objective function, the SQP is quicker in getting the converged solution than the PSO. In the problem of multi-objective function, the PSO effectively deduces the Pareto optimal set.

• 4. It is possible to cut down on the computational expenses by reducing the design variables through the use of hull-form parameterization method. The practicality of the hull-form optimization is also increased by lessening computational amount through the use of global optimization technique of the PSO.

• 5. However, the hull-form parameterization method has lower autonomy to modify hull form, since the modification is only dependent of the parameterization. This shortcoming will be overcome through developing or adding a little more various parameterization methods.