Abstract
In conventional model-oriented formal refinement, the abstract model is supposed to capture all the properties of interest in the system, in an as-clutter-free-as-possible manner. Subsequently, the refinement process guides development inexorably towards a faithful implementation. However, refinement says nothing about how to obtain the abstract model in the first place. In reality developers experiment with prototype models and their refinements until a workable arrangement is discovered.
Retrenchment is a formal technique intended to capture some of the informal approach to a refinable abstract model in a formal manner that will integrate with refinement. This is in order that the benefits of a formal approach can migrate further up the development hierarchy. The basic ideas of retrenchment are presented, and a simple telephone system feature interaction case study is elaborated. This illustrates not only how retrenchment can relate incompatible and partial models to a more definitive consolidated model during the development of the contracted specification, but also that the same formalism is applicable in a re-engineering context, where the subsequent evolution of a system may be partly incompatible with earlier design decisions. The case study illustrates how the natural method of composing retrenchments can give results that are too liberal in certain cases, and stronger laws of composition are derived for systems possessing suitable properties. It is shown that the methodology can encompass more ad hoc and custom-built techniques such as Zave's layered feature engineering approach to applications exhibiting a feature-oriented architecture (such as telephony).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Formal refinement, in its various guises, has a long and distinguished history. From the early papers [1, 2, 3], it has developed into a large and vibrant field of research. A comprehensive survey would be out of place here, but modern accounts in the spirit of the original work can be found in [4, 5]. In all of these the assumption is that one knows already what the abstract model is, and all one has to do is to refine it to a suitable lower-level model, gaining a high degree of assurance for the development thereby.
But the reality is that in most software development the correct abstract model is by no means obvious at the outset. Anecdotal evidenceFootnote 1 suggests that this is not only true where one would expect it, namely in the development of large and complex real-world critical applications, (undertaken using a formal approach because of the belief in the assurance obtainable, or because legislation mandates it), but is even present in the behind-the-scenes aspects of the development of small textbook or research examples, in which some experimentation is often required before a model that will satisfactorily refine to the desired concrete one is arrived at. (And that last sentence exhibits an undertone that is quite deliberate, because it is frequently true that at the outset one has a firmer idea of what the concrete model looks like than the abstract one, and one reverse engineers the latter from the concrete one to some degree.) The upshot of this is that formal approaches, of the conventionally understood kind, do not help much in the creation of an abstract model that can be contracted to with confidence for further development. Not that they ever claimed to, but in the 'oversold and underused' [6] atmosphere that has often surrounded debate about formal techniques in the past, it is easy to imagine that they might have done.
Retrenchment [7, 8, 9, 10], is a technique that aims to help address this issue by providing a formalism in which the demanding proof obligations (POs) of refinement are weakened, so that models not refinable to the ultimate concrete system, but nevertheless considered useful, can be incorporated into the development in a formal manner. This is not to say that every misconception and blunder that led to the correct abstraction ought to be recorded in some sort of retrenchment audit trail, but that a sanitised accountFootnote 2 of the construction of the abstract model from preliminary but incompleteFootnote 3 precursors that are considered convincing by the domain experts is of benefit.
The stress on the acquiescence of domain experts is vital. To seek to impose from the outside an alien development discipline on an already well-established engineering milieu is doomed to failure. Yet a naive effort to impose refinement as a software development technique can result in exactly that. To be able to successfully discharge the refinement POs can force a development to adopt a structure surprisingly unlike what one might imagine at the outset, especially when interfacing with physical models. Furthermore, engineers with an established track record of successful development are seldom sympathetic to the suggestion that all their familiar working practices must suddenly be abandoned in favour of a way of working forced implicitly by the rigidity of the refinement POs.
Retrenchment is a technique that seeks not to disturb well-entrenched engineering habits, by allowing models to be developed in a manner more in tune with engineering intuitions. Yet it aims to do so in a manner that can ultimately be integrated with refinement. To do so, the POs of retrenchment must be less exigent than those of refinement, but nevertheless have a structure that is close enough to those of the refinement POs to make the reconciliation feasible; we will see the details below. Above all, it is vital that the mathematics of the formalism be the servant and not the master during the development activity.
The development route that retrenchment opens up now appears as follows. In the initial stages of requirements definition and specification design, many preliminary and partial models are built. Some of these may well prove, upon experimentation and further reflection, to be misguided. They can be discarded. Other models will, perhaps after some modifications, contain a sensible account of aspects of the desired behaviour of the intended system. Unfortunately, it is quite likely that not all of these sensible models will be compatible with each other, in that being concerned with only part of the desired behaviour, and above all with clarity and intuitive perspicuity, not all of the complexities of how the part focused on interacts with other parts will have been ironed out. Nor indeed should one expect it to have been. One must understand first the broad intentions before narrowing down on the finer details; details moreover that may only be of concern in limited special cases. On a formal level, the incompatibility we speak of usually manifests itself in the impossibility of accommodating the various models we speak of in a single-refinement based development. Retrenchment, being more forgiving of this kind of incompatibility, offers the possibility of retrenching from such a collection of models to a more complicated model that properly takes into account all the requirements, and that can serve both as the basis of a contract between customer and supplier, and as the basis of a subsequent refinement-based implementation. We call this latter model the contracted model.
The reflective process involved in reconciling the incompatible partial models with the contracted model, which is partially captured in the retrenchment relations and proof obligations between these models, strengthens the confidence that the right contracted model has been decided upon, an activity that would otherwise be completely informal. At worst, this is simply because it is a reflective process. Any kind of reconsideration of such design decisions from a novel standpoint is bound to be helpful to some degree, simply because two perspectives are always better than one. At best, the engineering of the POs of the retrenchments will have brought into sharp focus the most important issues that need to be clarified in firming up the contracted model. One side effect of retrenchment is to provide a formal framework within which such considerations can exist.
What we have just described may be called the utopian view of the utility of retrenchment. However, there is another scenario in which retrenchment may yet come to be accepted as even more useful than in the utopian sense. Suppose we have a developed system, with perhaps some hundreds of millions of installed instances. Technology advances, and it suddenly becomes feasible to enhance the original conception of the system in a multitude of ways. Now, the original system must serve as a sensible precursor in the design of the enhanced system, but not because it was merely conceived as a convenient staging post on the way to the more elaborate design, but because it is there de facto, and no development of the enhanced system can take place without taking due account of the installed system base. The original system is of course a precursor of the upgraded one because it preceded it chronologically, but the intent is no longer that it is in some sense subservient to the development of the newer one. In such situations it is almost inevitable that the new system will not be a straightforward refinement of the old one, and the added flexibility of retrenchment proves much more convenient. The preceding remarks apply with full force in the case of telephony, a case study that forms a thread running through the rest of the paper.
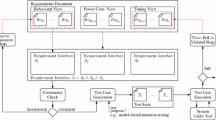
The rest of this paper is now structured as follows. The next section introduces our notation for systems, and gives a toy example. In Sect. 3 we develop a very primitive telephone system model, together with two independent enhancements, call forwarding and call hold. Section 4 reviews the basic ideas of retrenchment in the context of the earlier system notations and toy example. Since there are areas of incompatibility between the primitive telephone system model and the two enhancements (features) introduced, retrenchment is needed to describe the relationships between the primitive model and the enhanced models; Sect. 5 covers this. Section 6 considers how the two features may be combined: again there are areas of incompatibility when both features can be triggered. It is shown that given a design decision about how to resolve the incompatibility, retrenchments can relate the two features to the resulting final model. Section 7 considers the two compositions of the two features along the two routes from the original model to the final model, and compares these to a retrenchment description of a one-step derivation. It is shown that the compositions give safe overestimates for what is permitted, due to the proof technique used. This attests to the solidity of the retrenchment technique. Section 8 describes two stronger laws of composition for retrenchments that overcome the overgenerous provisions of the standard composition. While the first of these is still too weak to cover what takes place in the present case study, the second is better suited to doing so. This illustrates that when disjunctions play a prominent role in a derivation (as they notably do in applications of retrenchment), we should both take care to interpret the results in an appropriate manner, and note that small changes in other parts of the system can significantly affect the said interpretation.
In Sect. 9 we bring into the discussion Zave's layered feature-engineering approach, which proposes an architectural methodology for dealing with feature interactions. This acts as a spur to re-examine our case study from a layered feature-engineering perspective, and the feature models for this approach are described in Sect. 10. Section 11 considers the retrenchments between the layers of this approach and relates them to the ones introduced earlier, thus closing the loop. Section 12 concludes. In an Appendix we describe how an alternative development of the case study based on refinement might run. The pros and cons of the refinement- and retrenchment-based approaches are compared, and we illustrate how the routes available to us via refinement all suffer from undesirable aspects. These discussions are offlined so as not to disturb the retrenchment-oriented flow of ideas in the main body of the paper.
All through the paper, in constructing formal models, we make use of a Z-like notation for standard discrete mathematics notions. Mostly this should be self-explanatory, but we introduce a couple of possibly less familiar notations here.
Let R be a relation from X to Y, a set of (x, y) pairs with x ∈ X, y ∈ Y. Then its domain and range are:
If X = Y then the field of R is:
The domain and range subtraction operators \( \leftsubtractoper \) and \( \rightsubtractoper \) are defined by:
and the domain and range override operators \( \leftoverrideoper \) and \( \rightoverrideoper \) are defined by:
X → Y denotes the total functions from X to Y; X ↣ Y the total injections, and \( {\bf{X}} \rightarrowtailbar {\bf{Y}} \) the partial injections, etc. For a relation R, R + denotes the transitive closure of R. Other notations are introduced in situ.
2 System descriptions
In this paper we will strive to describe systems in the simplest way possible consistent with the mathematical precision necessary for resolving the technical issues we have in mind. Accordingly we work in a pure transition system framework. In this context, a system will be described in the following manner.
The system will possess a set of operations, Ops, with typical element m (and among the various operations there will be a distinguished initialisation operation Init). A typical operation m will act on a current (or before-) state u, in a manner that depends on the current input i, and will accomplish a state transformation yielding a new (or after-) state u′, producing an output value o. The values u and u′ will be drawn from a state space U common to all operations, while the input spaces and output spaces I m and O m can in principle vary from operation to operation, as is indicated by the notation. The transitions of the system (arising from some operation m) can therefore be written \( u\;{\textrm{-}}\!{\left( {i,\;m,\;o} \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;{u}' \). The totality of such transitions makes up the transition or step relation for m, which we write stp m , or stp m (u, i, u′, o) when we want to display the variables involved.
We consider a toy example before moving on to the many more substantial systems contained in the rest of the paper. Aside from the initialisation Init, our system has one further operation Up. We have U = {0, 3}, and I Up = ∅ = O Up . Init sets u to 0, and Up is given by \( 0\;{\textrm{-}}\!{\left( {\varepsilon ,\;Up_{{\rm{A}}} ,\;\varepsilon } \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;3 \), where ε is the empty input and output; this is the only step in stp Up . This completes the description of the toy example, the only transition of which is illustrated in the top arrow of Fig. 1. We will return to this example in Sect. 4 to give an equally toy illustration of retrenchment.
3 Features in a simple telephony model
We will illustrate the potential for retrenchment to capture the evolution of an integrated specification from incomplete and contradictory prior models, using elements of feature interaction in telephone systems as a case study. There is now a substantial literature on this topic, e.g. [11, 12], since the naive combination of novel services on top of the plain old telephone system (POTS) model can be problematic. Since our primary aim is to illustrate the utility of retrenchment and not to advance the state of the art in telephony, our models will be oversimplified in the extreme. Still, they will make the intended points well enough. In this section we start with the simplest model PHONE, and then consider the addition of call forward and call hold facilities, a well-known situation in which the naive combination of extra services does not work.
PHONE
In this system the state space is just the set of active calls, captured in the state variable calls, which is a partial injection on the set of available phones NUM, and in which the domain and range of the active calls relation do not intersect; and with calls initialised empty. (In POTS the same handset cannot be both the instigator of a phone call and the receiver of a phone call at the same time.)
There are just two operations, connect n and break n , the former to dial number i from phone n, and the latter to disconnect phone n. We define \( {{\rm{free}}{\left( n \right)} \equiv n \notin {\rm{fld}}{\left( {calls} \right)} \equiv {\rm{\neg }}\;{\rm{busy}}{\left( n \right)}} \).
Note that (naively speaking) you cannot make a call from a handset already engaged in a phone call, so that free(n) must be a precondition in (6); i.e. it is asserted in the definition of connect n . However, the outcome of a connection attempt made from a free handset depends on the state of the destination handset; therefore free(i) is a guard in a conditional.
In POTS you can't be having a telephone conversation with yourself on the same handset. Now whereas in real life when you pick up a phone and dial your own number you hear the engaged tone, the connect n model in (6) is only sensitive to the state of the calling handset at the instant immediately before the handset is lifted, at which point we have just said that it must be free; therefore in our crude model we must include the (n ≠ i) term in the guard to ensure the invariant in (5) is preserved. For simplicity, this tactic for dealing with the 'calling oneself' scenario is maintained for all the models in this paper.
From this very basic model we now construct enhanced services one at a time: first call forwarding.
PHONE CF
In this system the state space is the set of active calls as before, plus a table fortab, of call forwarding data, the latter being a partial injection on the phones whose transitive closure is acyclic, and also initialised empty:
Two new operations regfor CF,n (i) and delfor n manipulate the table. The former inserts forwarding destinations in the table, the latter removes them.
Note that for simplicity we do not mention parts of the state (i.e. here the part described by the state variable calls) left unaltered by an operation: this is the programming convention on update of state values, in contrast to the logical convention for defining relations, which takes it that any variables not explicitly constrained can be assigned arbitrary values from the appropriate domain. The logical convention is certainly more widely used when defining relations, but in this paper we stress that, for economy, we will adhere to the programming convention when defining transition steps, despite the slightly non-standard nature of the definitions which result. To avoid confusion, we will highlight the relevant facts again at particularly critical points.
Note that regfor CF,n merely (and silently) overwrites any existing information in the table if it is safe to do so. This is certainly a rather naive model.
In the presence of this new service, the connect n and break n operations must be re-examined, as the behaviour required of them potentially changes due to the new functionality we are building. The connect n operation may be re-engineered thus:
while the break n operation, it turns out, is unaltered:
This completes call forwarding. Now we turn our attention to call holding.
PHONE CH
In this system the state space is the set of active calls, plus a table holtab, of call holding data, the latter being a subset of the phones, initialised empty:
Two operations insert and remove elements of this subset. Again for simplicity the operations work silently, giving no feedback.
With this service, connect n and break n need re-examination once more, for the same reason as above. The connect n operation simulates rather primitively the infuriating feedback obtainable from most holding services; however, there is no attempt made to accurately model the resolution of a hold when the call recipient becomes free:
The break n operation is unaltered as before:
which completes the call holding model.
Before going on to consider feature interaction, it is appropriate to ask how the two enhanced models PHONE CF and PHONE CH , are related to PHONE. The natural expectation might be that they would in some sense be refinements of PHONE, but this turns out not to be the case. The reason is that the simple PHONE system prescribes a specific response for the busy(i) case, this being given by the clauses \( {o = NO \wedge {calls}' = calls} \), a naive model of the engaged tone. This is in turn necessitated by the desire to make the PHONE system model complete, as it would need to be if the PHONE system is to be considered a viable specification in its own right. Under the same busy(i) conditions, when suitable supplementary conditions hold, the two enhanced models prescribe different and incompatible behaviour: in PHONE CF a connection can be made to the forward location should there be one and it happens to be free, while in PHONE CH an irritating message drones on interminably should the destination phone be one for which holding is configured. This means that the enhanced models cannot be viewed as straightforward extensions of the PHONE model. But in some sense this would have to be the case if the relationships between PHONE and the enhanced systems were to be refinements.
In the Appendix we outline how one can approach this kind of development via refinement, most particularly as it illustrates the fact that in order to do so we must start with a different formulation of the primitive model PHONE. We examine two possible starting models, PHONE′ and PHONE′′, and we see that in both cases these versions of PHONE are incomplete. In the case of PHONE′ it is a straightforward case of model incompleteness, a problem forestalled in the PHONE model which specifies that if the desired number is not available then a well-defined default behaviour is required. (In particular, the PHONE model does not give the designer unfettered licence to refine the busy(i) case down to completely arbitrary behaviour, as does PHONE′.) In the case of PHONE′′, where an unrestricted set of possible connection outcomes in the busy(i) case is permitted, with the intention that refinement to PHONE CF subsequently narrows it down to a more specific subset, we have requirements incompleteness, since such uncontrolled connection behaviour can never reflect a realistic user-level requirement. (Again, the PHONE model does not give the designer licence to make an arbitrary connection in the busy(i) case.)
Thus the Appendix shows that PHONE models refinable to PHONE CF or PHONE CH display traits that are problematic from the requirements perspective. We curtail further discussion at this juncture, positing firstly that PHONE as described captures completely the natural functional requirements of the POTS model of this paper, and secondly that (as we are about to illustrate) there is no difficulty in casting the relationships between the PHONE model and the enhanced models as retrenchments. But first we must say what retrenchment is.
4 Retrenchment
Retrenchment is a relationship between two systems of the kind we have been dealing with. These will be the abridged system, expressing an idealised but self-consistent view of some part of the desired system, and the completed system, which takes all of (or at least more of) the necessary details into account.Footnote 4
At the abridged level, we have a system as we described in Sect. 2, namely a set of operations Ops A with typical element m A, and state space, input spaces, and output spaces U, I mA, O mA, respectively. The transition relations for typical operations m A are stp mA(u, i, u′, o). Note that we have acquired an extra subscript A to unambiguously indicate the abridged system where necessary.
At the completed level we have an entirely analogous set-up. This time the operation name set, state, input and output spaces are Ops C, V, J mC, P mC, respectively, with values m C, v, j, p, and similar conventions as before, except noting that we write the operation name set and operation names subscripted with C, e.g. m C. We assume each abridged level operation m A, has a corresponding completed level operation m C, but there may also be other completed level operations, so that there is an injection from the set Ops A to Ops C, which associates m A with m C.
We now turn to the relationship between the two levels, which consists of several pieces. Firstly we have the relationship between abridged and completed state spaces, which is given by the retrieve relation G(u, v). Next we demand that the two initialisation operations Init A and Init C at abridged and completed levels establishes G in corresponding after-states (as usual, the free variables are assumed implicitly universally quantified):
Turning to the transition relation for a typical operation m A, beyond the retrieve relation G, we have a within relation P m (i, j, u, v), and concedes relation C m (u′, v′, o, p; i, j, u, v). The punctuation indicates that C m is mainly concerned with after-values, but may refer to before-values too where necessary. These are combined into the retrenchment PO for steps, which says that for each such m A:
This PO affords considerable flexibility in relating different levels of abstraction, see [7, 8, 13, 9] for a discussion.
We return to our previous toy example for a brief illustration. We have seen that the abridged level is given by Init A, and one further operation Up A, with U = {0, 3}, I UpA = ∅ = O UpA; and such that Init A sets u to 0, and Up A is given by the one and only transition \( 0\;{\textrm{-}}\!{\left( {\varepsilon ,\;Up_{{\rm{A}}} ,\;\varepsilon } \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;3 \). At the completed level we have Init C and Up C. The state space is V = {0, 3, X}, and J UpC = ∅, P UpC = {Done, Error}. Init C sets v to 0, and stp UpC has two transitions {\(0\;{\textrm{-}}\!{\left( {\varepsilon ,\;Up_{{\rm{C}}} ,\;Done} \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;3\), \(0\;{\textrm{-}}\!{\left( {\varepsilon ,\;Up_{{\rm{C}}} ,\;Error} \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;X\)}. The non-trivial steps of both systems are illustrated in Fig. 1.
The retrieve relation is given by the inclusion of U into V, i.e. equality of abridged and completed values, and the within relation for Up is U×V (i.e. we have a trivial within relation, where we also remove the empty input spaces).
There is some scope for choosing the concedes relation C Up . The smallest possibility is:
while other possibilities include:
Note that C 2 = C 3 because of the smallness of the spaces involved. These different possibilities indicate some of what can be expressed using retrenchment in a more syntactically based framework, in particular that what goes into the concedes relation is at least partly a question of design, and of the relative importance of various issues as perceived by developers. It is easy to check that the PO (19) holds for each of the C i s. With this under our belts, we turn to the retrenchments of our case study.
5 Retrenchments for the telephony systems
Turning to the retrenchments between the systems of Sect. 3, in each instance we first say which model is the abridged one and which the completed one, and then we give the retrieve relation between the state spaces, and the within and concedes relations for each operation of the abridged model.
PHONE to PHONE CF
We set up the data for the retrenchment as follows, with PHONE as the abridged model and PHONE CF as the completed model:
Showing that the POs of retrenchment hold for these data is easy. The initialisation PO (18) is trivial given that all the sets in the states of both models are initialised empty. Also the operation PO (19) is easy given that the only case where the actions of connect n and connect CF,n differ is precisely the case documented in the concedes relation (25). The two break operations are identical, leading to trivial within and concedes relations.
PHONE to PHONE CH
The abridged model is PHONE as before and PHONE CH is now the completed model:
The POs are as straightforward as previously, and for the same reasons.
6 Feature interaction in telephony
Having built our basic system, and having separately considered the call forwarding and call holding optional enhancements, we now consider combining the two features. Any combination is based on the assumption that the calls state component and the input and output spaces of the two variants of the connect n and break n operations are to be identified insofar as possible. (This precludes constructions that incorporate say two calls state components and then implement call forwarding in one, and call holding in the other. Formally this might work up to a point, but in practice such solutions are not useful models of the real world.) In any event, we stress that whatever method of combining the two features is used, it will require a design decision, and will not just rest on the mechanical application of some standard piece of formalism.
PHONE CF/CH
The state space is calls as before, plus tables of call forwarding and call holding data:
The auxiliary operations to manage the two tables are unchanged:
(The equalities above are to be understood according to the programming convention on values, namely that anything not mentioned is to be left unchanged.) The break operations are also unaltered:
The interest lies of course in the connect CF/CH,n (i) operation. Our design is guided by the following principles. Firstly, if the conditions for neither service enhancement hold, then the system should behave like the plain PHONE service. Secondly, if the conditions for exactly one of the service enhancements hold, then the system should behave according to that enhancement. The third case, when the conditions for both the call forwarding and call hold enhancements are valid, requires a more intrusive design decision. We determine that in this case the caller should have a choice between the two alternatives. To keep things as simple as previously, we do not model the interaction with the caller or the resolution of a hold situation very faithfully, modelling it by issuing a particular message at the output, in line with the unsophisticated nature of all the models in this paper.
It is clearly plausible to infer immediately that refinements will not hold either between the PHONE CF and PHONE CF/CH models, or between the PHONE CH and PHONE CF/CH models; reasons for this are as discussed earlier.
Despite this, we show that retrenchment can give a good account of the situation, due to the more flexible proof obligations that characterise it.
PHONE CF to PHONE CF/CH
In contrast to the two retrenchments given previously, this time PHONE CF is the abridged model and PHONE CF/CH is the completed model, illustrating how in a development hierarchy what is regarded as concrete at one point becomes abstract when one focuses lower down. (This is just as appropriate for the piecewise development of a specification from preliminary models as it is when developing an implementation from an already agreed specification.)
It is clear that the relevant POs hold. Initialisation is trivial as usual, and the operation POs are trivial for all but the connect n operation. In the latter case it is easy to see that in the cases where the abridged and completed models differ, the differences are adequately documented in the concedes clause.
PHONE CH to PHONE CF/CH
Here the abridged model is PHONE CH and PHONE CF/CH plays the part of the completed model.
The POs are as straightforward as previously.
We note that in both of these retrenchments, the concedes clause for the connect n operation has to cater for two exceptional conditions. In the case of the CF>CH retrenchment, when holding is available, the two actions for when forwarding is available or not are both incompatible with the provisions of the PHONE CF model, while in the CH>CF retrenchment, when forwarding is available the two actions for when holding is available or not are both incompatible with the provisions of the PHONE CH model. Aside from these non-trivial cases, we have a greater proliferation of essentially trivial operation POs, arising from the fact that PHONE CF and PHONE CH have management operations for the forward and hold tables respectively, and these are also present in identical fashion in PHONE CF/CH .
7 Compositions of retrenchments and a direct retrenchment design
Given that we have two routes to get from the simple model PHONE to the final model PHONE CF/CH , the first via PHONE CF and the second via PHONE CH , we can examine the compositions of the relevant pairs of retrenchments and compare them, both to each other and to a one-step retrenchment which derives the final design from the original simple PHONE system.
For the formulation of retrenchment used in this paper, the method of composing retrenchments is examined in detail in [9]. For brevity we just sketch the results.
Suppose we have at top level a system given by variables u, i, u′, o (for a typical operation). At intermediate level suppose the variables are v, j, v′, p (for the corresponding operation). And at lowest level suppose the variables are w, k, w′, q (for an operation corresponding to an intermediate level operation with variables v, j, v′, p). Suppose a retrenchment is given from top level to intermediate level with retrieve relation G(u, v), and for a top-level operation m, the within and concedes relations are P m (i, j, u, v), C m (u′, v′, o, p; i, j, u, v). Suppose there is also a retrenchment from intermediate level to lowest level whose retrieve relation is H(v, w), and such that for intermediate-level operation m, the within and concedes relations are Q m (j, k, v, w), D m (v′, w′, p, q; j, k, v, w). In such a case there is a retrenchment from the top level to the lowest level, for which the retrieve relation is:
and for which the within and concedes relations for a top-level operation m are:
This result is confirmed by straightforward predicate calculus as follows. On the basis of the assumed retrenchments and the validity of their POs, we assume we are given u, i and w, k related by (55) and (56), and a lowest-level step \(w\;{\textrm{-}}\!{\left( {k,\;m,\;q} \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;{w}'\). We extract from (55) and (56) the conjunction of the antecedents for the individual POs, and apply them in turn to derive intermediate and highest-level steps, and thence the conjunction of the consequents for the individual POs. Some predicate calculus now manipulates this conjunction into the disjunction of (55) and (56), confirming that (55)–(57) indeed define a valid retrenchment.
We will now calculate the composed quantities (55–57) for the two retrenchment routes from PHONE to PHONE CF/CH . In both cases we only need to check for the top-level operations connect n and break n because the other operations at the intermediate level get filtered out of the composed retrenchment.
For clarity, we will simplify the results as much as possible. This includes, for example, eliminating clauses if they arise anyway from other parts of the PO for the composed retrenchment, or are obvious logical consequences of such parts. Thus we strive not so much for the literal results of (55)–(57) as for answers that are equivalent to them within the context of their intended use, i.e. equivalent under the hypotheses that the antecedents of the PO are true, and that a suitable abridged level step has been inferred from them.
We start with the route via PHONE CF , getting a retrenchment whose data, K, R, E, we label with CF>CH. Starting with the retrieve relation, we plug (23) and a suitably relabelled (37) into (55) and get:
Moving to connect n and the within relation, we likewise plug (23) and (24) and a suitably relabelled (37) and (38) into (56). We note that as far as the use of the resulting relation in the operation PO is concerned, we can discard the term \( {G{\left( {u,v} \right)} \wedge H{\left( {v,w} \right)}} \) which arises via (56) since \( P_{CF,connect_n } (i,\;j,\;u,\;v) \) and \( Q_{CF > CH,connect_n } (j,\;k,\;v,\;w) \) are independent of the state variables u, v, w, and \( {K_{{CF > CH}} (u,\;w)} \) is one of the PO antecedents anyway. Thus we get:
Similarly, for the concedes relation, we plug (23) and (25) and a suitably relabelled (37) and (39) into (57). After some simplification and further manipulation, which we explain below, we get the following, where the individual clauses are labelled for ease of identification later:
In deriving (60), in line with our remarks above, we fully exploited the environment furnished by the context of the intended use of the concedes clause, which consists of the antecedents of the composed retrenchment PO. These state that i = j, j = k hold, and allow us to exploit the properties of G and H, removing the existential quantifications \( {\exists {v}',v,j} \) via the one point rule. Also we identified intermediate-level outputs with higher- or lower-level outputs as appropriate in the clauses containing G or H, allowing us to eliminate the \( {\exists p} \) quantification too. This goes slightly beyond what is expressed in the generic operation PO because outputs are discussed only in the concedes clause.Footnote 5
Now disjuncts [1] and [2] of (60) come from the \( {C \wedge H} \) term in (57). We note that [2] is an artefact in that it applies to a situation in which both forwarding and holding are configured, and prescribes an outcome incompatible with our design decision in (36). This phenomenon is attributable to the insensitivity of H to the means by which the state it is mapping was arrived at, i.e. it allows forwarding behaviour to survive when a subsequent design decision has overridden it. This in turn is a by-product of the proof technique used to establish the soundness of the composed retrenchment, which calculates a composed concedes relation which is safe if possibly overgenerous, purely on the basis of Boolean algebra, and without regard to the underlying behaviour of the composed systems. We look at this issue more closely in the next section.
In like manner [3] and [4] come from \( {G \wedge D} \), with [4] being an artefact which also applies when forwarding and holding are configured, but this time stipulating a different incompatible outcome to [2]. Finally [5] comes from \( {C \wedge D} \), which generates two disjuncts from D; however one of them reduces to false.
The other operation figuring in the retrenchment is break n for which we find, uninterestingly:
Now we can turn our attention to the alternative route to PHONE CF/CH via PHONE CH . Going through the same procedure we get a retrenchment labelled with CH>CF.
The retrieve relation is as before:
Similarly, for connect n , using the same techniques as in (59), we obtain the within relation:
To obtain the concedes relation, we manipulate (28) and (30) and a suitably relabelled (46) and (48) into:
Using the same technical tricks as before, this time [2] and [3] are spurious; with [1], [4], [5] agreeing with [3], [1], [5] respectively of (60). Note that the spurious clauses in the two calculations are not the same. They result from the propagation of inappropriate information in different directions.
As before, for break n we find:
With these calculations completed, we can consider what the details of the retrenchment would look like if we built both enhanced services into the plain PHONE model simultaneously. It is not hard to see that this retrenchment would be given firstly by:
and secondly for connect n we would get the within relation:
while for the concedes relation we would need merely to record the cases in which the simple PHONE model differs from the PHONE CF/CH model, thus:
For break n we would find as usual:
With these formulae in place, we are in a position to compare the various retrenchments we have derived. The only places in which they differ are the various concedes relations for the connect n operation. A little thought shows that \( C_{CH/CF,connect_n } \) is a subrelation of both \( E_{CF > CH,connect_n } \)and of \( E_{CH > CF,connect_n } \)See Fig. 2.
It is not hard to see why this is the case. The law of composition (57) is inclusive, in that all the behaviours permitted by the component concedes relations are effectively preserved and combined in all possible ways in the composed concedes relation. As noted previously, this is a consequence of the proof technique adopted to establish the soundness of the definition of the composed retrenchment, which just manipulates the conjunction of the component PO consequents. This is insensitive to whether in any particular situation there are in fact any before-states, after-states, inputs, outputs and transitions that inhabit all the clauses allowed for in the composition. Inevitably, this can sometimes give more than is needed, as happened here.
The kind of composition of concedes clauses we have used is appropriate for an adequately descriptive approach to system description, in which it is the job of the concedes clauses to place safe constraints on what the systems actually do. In a more prescriptive approach, in which the concedes clauses must define what the systems ought (and ought not) to do, a semantically more incisive law of composition, where spurious behaviour is eliminated, is more appropriate. We describe possible improved composition laws in the next section.
8 Stronger compositions for retrenchments
Suppose we are given three systems: a top-level system with data u, i, u′, o, an intermediate system with data v, j, v′, p, and a lowest-level system with data w, k, w′, q. Let there be a retrenchment from top level to intermediate system characterised by relations G(u, v), P m (i, j, u, v), C m (u′, v′, o, p; i, j, u, v), and a retrenchment from intermediate to lowest-level system characterised by relations H(v, w), Q m (j, k, v, w), D m (v′, w′, p, q; j, k, v, w).
Consider the top-level to intermediate system retrenchment. We define the following predicates for an abstract operation m:
We say that a retrenchment is tidy iff for all abstract operations m:
and
This says that the combinations of before-states and inputs at both levels that characterise the transitions that can re-establish the retrieve relation are disjoint from those that merely establish the concedes relation.
Analogously for the intermediate to lowest-level retrenchment, we have the predicates \( {\text{pre}}^{{{\text{Ret}}}}_{m} {\left( {v,j,w,k} \right)},\;{\text{pre}}^{{{\text{Con}}}}_{m} {\left( {v,j,w,k} \right)},\;{\text{pre}}^{{{\text{RetA}}}}_{m} {\left( {v,j} \right)},\;{\text{pre}}^{{{\text{RetC}}}}_{m} {\left( {w,k} \right)},\;{\text{pre}}^{{{\text{ConA}}}}_{m} {\left( {v,j} \right)},\;{\text{pre}}^{{{\text{ConC}}}}_{m} {\left( {w,k} \right)}. \)
Two adjacent retrenchments like these, which are both tidy, are said to be compatibly tidy iff for all abstract operations m:
and
hold for the intermediate system. In (81) and (82) the antecedent pre clauses come from the intermediate to lowest-level retrenchment, which is subscripted 2 to distinguish it from the top-level to intermediate retrenchment, which is subscripted 1, and from which the consequents come.
Theorem 8.1
With the current notations, two compatibly tidy retrenchments compose to give a single retrenchment given by the data:
Proof
To show that we have a retrenchment, we must show that the POs for the composed retrenchment follow from the POs for the individual ones. The initialisation PO follows immediately by composing the individual initialisation POs.
For the operation PO, we assume the antecedents. These give w, k, v, j, u, i, from (83) and (84), with v, j arising by instantiating the existential quantifier. We also have a step \(w\;{\textrm{-}}\!{\left( {k,\;m,\;q} \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;{w}'\) for some lowest-level operation m corresponding to an abstract operation. Since from (84) we have \( {H{\left( {v,w} \right)} \wedge Q_{m} {\left( {j,k,v,w} \right)}} \), we satisfy the antecedents of the intermediate to lowest-level retrenchment operation PO, which gives an intermediate step \(v\;{\textrm{-}}\!{\left( {j,\;m,\;p} \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;{v}'\), and \( H{\left( {{v}',{w}'} \right)} \vee D_{m} {\left( {{v}',{w}',p,q; \ldots } \right)} \). Now using \( {G{\left( {u,v} \right)} \wedge P_{m} {\left( {i,j,u,v} \right)}} \) from (84), we satisfy the antecedents of the top-level to intermediate retrenchment operation PO, which gives a top-level step \(u\;{\textrm{-}}\!{\left( {i,\;m,\;o} \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;{u}'\) and \( G{\left( {{u}',{v}'} \right)} \vee C_{m} {\left( {{u}',{v}',o,p; \ldots } \right)} \).
Since the intermediate to lowest-level retrenchment is tidy, exactly one of \( {\text{pre}}^{{{\text{RetC}}}}_{m} {\left( {w,k} \right)}_{2} \) or \( {\text{pre}}^{{{\text{ConC}}}}_{m} {\left( {w,k} \right)}_{2} \) will hold, but not both. Suppose the former. Then H(v′, w′) holds as does \( {\text{pre}}^{{{\text{RetA}}}}_{m} {\left( {v,j} \right)}_{2} \). From (81) we deduce \( {\text{pre}}^{{{\text{RetC}}}}_{m} {\left( {v,j} \right)}_{1} \). By the fact that the top-level to intermediate retrenchment is tidy we deduce that \( {\text{pre}}^{{{\text{C}} onC}}_{m} {\left( {v,j} \right)}_{1} \) is impossible, whereupon G(u′, v′) holds, as does \( {\text{pre}}^{{{\text{RetA}}}}_{m} {\left( {u,i} \right)}_{1} \). Thus in this case we have established that K(u′, w′) holds.
Alternatively, suppose that \( {\text{pre}}^{{{\text{ConC}}}}_{m} {\left( {w,k} \right)}_{2} \) is true. Then analogous reasoning establishes in turn D m (v′, w′, p, q; …), \( {\text{pre}}^{{{\text{ConA}}}}_{m} {\left( {v,j} \right)}_{2} \), \( {\text{pre}}^{{{\text{ConC}}}}_{m} {\left( {v,j} \right)}_{1} \), C m (u′, v′, o, p; …), and \( {\text{pre}}^{{{\text{ConA}}}}_{m} {\left( {u,i} \right)}_{1} \). Thus E m (u′, w′, o, q; …) holds. The two cases together verify the operation PO for the composed retrenchment with retrieve, within and concedes relations given by (83)–(85). □
The structure of the above result is very appealing. The data that specifies the combined retrenchment is built in an especially simple way from the component clauses. Despite this, note that the composed retrenchment is not necessarily tidy. Subscripting its pre clauses 12 to distinguish them from those hitherto, we observe that for some w, k, we might have \( {\text{pre}}^{{{\text{RetC}}}}_{m} {\left( {w,k} \right)}_{{12}} \; \wedge \;{\text{pre}}^{{{\text{ConC}}}}_{m} {\left( {w,k} \right)}_{{12}} \) due to the way that the composed data K, R m , E m connected top-level values u, i, u′, o (satisfying stp m (u, i, u′, o)) to lowest-level values w, k, w′, q (satisfying stp m (w, k, w′, q)) using intermediate values v, j, v′, p for which stp m (v, j, v′, p) was simply not valid. We therefore see that this composition is not automatically compositional without additional conditions; evidently it cannot be associative as it stands either.
Let us check whether the provisions of this result apply to the feature interaction case study. Consider any of the retrenchments we have described. In every case the following hold. For a call to the connect n operation, the input data to abridged and completed connect n operations are the same, and the abridged before-state is a part of the completed before-state. The latter means that the retrieve relation is a projection from the completed to abridged state, obtained by discarding the additional data in the completed state. Consequently, for an (almost) arbitrary abridged state, one can conceive an input value for which connection at the abridged level is blocked, and furthermore: (a) there exists a value for the additional data in the completed state for which connection at the completed level is still blocked; (b) there exists a value for the additional data in the completed state for which connection at the completed level (or other successful outcome) is now possible. So in general there will be some u, i for which we can make \( {\text{pre}}^{{{\text{RetA}}}}_{m} {\left( {u,i} \right)}\; \wedge \;{\text{pre}}^{{{\text{ConA}}}}_{m} {\left( {u,i} \right)} \) valid, and the retrenchments will not be tidy. On the other hand, we know that possibilities (a) and (b) are mutually exclusive in the sense that it is always true that different additional data are needed to establish the two different possibilities. We will use this clue to drive a wedge between the possibilities aggregated in \( {\text{pre}}^{{{\text{RetA}}}}_{m} {\left( {u,i} \right)}\; \wedge \;{\text{pre}}^{{{\text{ConA}}}}_{m} {\left( {u,i} \right)} \), deriving an even sharper composition law.
Let us say that a retrenchment is neat iff for all abstract operations m:
The neat condition keeps retrieve relation-preserving behaviour apart from concedes relation-establishing behaviour, as does the tidy condition, but it does it in a technically more fine-grained way. The price we pay for proving the analogue of Theorem 8.1 is that a more complicated structure, requiring contributions from the pre- clauses introduced above, is needed in the combined concedes relation.
Theorem 8.2
With the current notations, two neat retrenchments compose to give a single retrenchment given by (83) and (84) and:
Furthermore, any intermediate-level transition \(v\;{\textrm{-}}\!{\left( {j,\;m,\;p} \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;{v}'\) that witnesses the composed operation PO can validate either at most one of the disjuncts of (87), or the composed retrieve relation (83).
Proof
The proof starts by repeating the first two paragraphs of the proof of Theorem 8.1, after which we argue as follows.
Since the intermediate to lowest-level retrenchment is neat, exactly one of \( {\text{pre}}^{{{\text{Ret}}}}_{m} {\left( {v,j,w,k} \right)}_{2} \) or \( {\text{pre}}^{{{\text{C}} on}}_{m} {\left( {v,j,w,k} \right)}_{2} \) will hold, but not both. Suppose the former. Then H(v′, w′) holds and we call this case Ret-2. (The latter will be case Con-2.)
By the fact that the top-level to intermediate retrenchment is neat we know that exactly one of \( {\text{pre}}^{{{\text{Ret}}}}_{m} {\left( {u,i,v,j} \right)}_{1} \) or \( {\text{pre}}^{{{\text{Con}}}}_{m} {\left( {u,i,v,j} \right)}_{1} \) will hold, but not both. This subdivides case Ret-2 into two subcases, Ret-2/Ret-1 and Ret-2/Con-1 respectively. In Ret-2/Ret-1 we have \( {\text{pre}}^{{{\text{Ret}}}}_{m} {\left( {v,j,w,k} \right)}_{2} \) and \( {\text{pre}}^{{{\text{Ret}}}}_{m} {\left( {u,i,v,j} \right)}_{1} \) and we re-establish the retrieve relation G(u′, v′) in the after-state. In Ret-2/Con-1 we have \( {\text{pre}}^{{{\text{Ret}}}}_{m} {\left( {v,j,w,k} \right)}_{2} \) and \( {\text{pre}}^{{{\text{Con}}}}_{m} {\left( {u,i,v,j} \right)}_{1} \). In this case we establish \( {C_{m} {\left( {{u}',{v}',o,p;i,j,u,v} \right)} \wedge H{\left( {{v}',{w}'} \right)}} \).
In like manner we can consider Con-2 and its two subcases Con-2/Ret-1 and Con-2/Con-1 which respectively establish the other two possibilities permitted by (87). These four cases verify the operation PO for the composed retrenchment with retrieve, within and concedes relations given by (83), (84) and (87).
Moreover, the preceding proof shows that at most one of the four subcases Ret-2/Ret-1, Ret-2/Con-1, Con-2/Ret-1, Con-2/ Con-1 can be witnessed by any intermediate-level step \(v\;{\textrm{-}}\!{\left( {j,\;m,\;p} \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;{v}'\), as postulating that any two or more of them are witnessed by the same \(v\;{\textrm{-}}\!{\left( {j,\;m,\;p} \right)}\!\textrm{-}\raisebox{1pt}{\small${>}$}\;{v}'\) quickly yields a contradiction of the neatness of either the top-level to intermediate, or intermediate to lowest-level retrenchment (or both). □
Corollary 8.3
With the current notations, two neat retrenchments satisfying:
compose to give a single retrenchment given by (83) and (84) and:
Proof
Immediate. □
We observe that just as in the previous case, the notion of neat retrenchment is not compositional, and it is even easier to imagine how the required condition might fail for the composite. Thus for the same u, i, w, k we might both have \( {\text{pre}}^{{{\text{Ret}}}}_{m} {\left( {u,i,w,k} \right)}_{{12}} \) established via subcase Ret-2/Ret-1 above and witnessed by v a, j a, v′ a, p a, and also \( {\text{pre}}^{{{\text{Con}}}}_{m} {\left( {u,i,w,k} \right)}_{{12}} \) established via one of the other subcases and witnessed by v b, j b, v′ b, p b. These different intermediate values get existentially quantified away, and we are left with a failure of (86).
Let us now consider the extent to which the retrenchments of our case study turn out to be neat.
PHONE to PHONE CF
The concedes relation is (25):
We note that for a fixed fortab, if u and v agree on the calls component, and we have i = j, then whenever the concedes relation holds, v′ and v differ in the calls component whereas u′ = u. Consequently v′ and u′ differ in the calls component. Moreover, u′ and v′ agree on the calls component whenever the retrieve relation is re-established. Since both cannot be true simultaneously, the retrenchment is neat.
PHONE to PHONE CH
The concedes relation is (30):
This time for fixed holtab, if u and v agree on the calls component, and we have i = j, then whenever the concedes relation holds, v′ = v and u′ = u, i.e. u′ and v′ agree on the calls component too; the outputs contain the only indication that an abnormal situation obtains. Also u′ and v′ agree on the calls component whenever the retrieve relation is re-established. So we can have both true, and the retrenchment is not neat as it stands.
This is attributable to the lack of sensitivity of (73) to outputs. In the general case we can overcome the problem by using a notion of retrenchment that is sensitive to properties of outputs in the case where the retrieve relation is re-established, as we pointed out in footnote 5. With such an amplification of the notion of 're-establishing the retrieve relation' fed into both the operation PO and (73), all our results concerning tidiness and neatness carry over, and the present retrenchment also becomes neat.
(As we also pointed out in footnote 5, for simplicity we finessed the alternative, of suitably reformulating the concedes relation to also carry the output properties in the well-behaved case, but such a concedes relation becomes universally true in the models of interest (and in the context of the operation PO antecedents). When, as now, we are looking to separate behaviour that re-establishes the retrieve relation from behaviour that establishes the concedes relation, such universal validity of the concedes relation is unhelpful, though even this can be overcome by suitably dissecting the inevitably more complex concedes relation that results. We omit the technical details which would distort this paper unduly.)
PHONE CF to PHONE CF/CH
The concedes relation is (39):
This retrenchment displays both of the behaviours discussed above. In the \( {{u}' = u \wedge {v}' = v} \) alternative we see a difference in the outputs to which the retrieve relation is insensitive, so neatness fails in the strict sense; while in the other alternative we have a bona fide modification of the state component in one model but not the other, so this alternative exhibits neatness.
PHONE CH to PHONE CF/CH
The concedes relation is (48):
This is similar to the preceding case, in having both a neat alternative, and one that is not.
We conclude overall that though some of the retrenchments of our case study are not neat in the strict sense, the deficit would be easy to remedy, and neatness provides a good intuition for understanding the case study's behaviour; we will see just how good in Sects 10 and 11.
Furthermore we can illustrate that the tighter composition of concedes relations for neat retrenchments in (87) has the capacity to eliminate spurious clauses such as those arising in (60) and (65). We do so by examining the one case in which neatness holds unreservedly. This is clause [4] of \( E_{CF > CH,connect_n } \) in (60) which is:
This arises from the \( {G \wedge D} \) term in (57) applied to the composition order in which call forwarding is introduced first. Suppose this term were inhabited in the models of interest. Then we would have to have \( {\text{pre}}^{{{\text{Ret}}}}_{m} {\left( {u,i,v,j} \right)}\; \wedge \;{\text{pre}}^{{{\text{Con}}}}_{m} {\left( {v,j,w,k} \right)} \) true (for the only possible j and a suitable v). Since we know that \( {\text{pre}}^{{{\text{Con}}}}_{m} {\left( {u,i,v,j} \right)} \) holds, because the call forwarding clauses of (11) only hold in the busy(i) case, i.e. when POTS connection is impossible, we would have \( {\text{pre}}^{{{\text{Ret}}}}_{m} {\left( {u,i,v,j} \right)}\; \wedge \;{\text{pre}}^{{{\text{Con}}}}_{m} {\left( {u,i,v,j} \right)} \), which contradicts the neatness of the PHONE to PHONE CF retrenchment. So clause (81) can be safely elided from the composed concedes relation. Similar arguments would deal with the other spurious clauses in (60) and (65) if it were the case that these retrenchments were entirely neat.
9 Layered feature engineering
Zave [14] describes a feature of a software system as 'an optional or incremental unit of functionality' and a feature-oriented description as comprising 'a base description and feature modules'. Telecommunications systems are conventionally given using such descriptions [11, 15], and this is not the only application domain that can be described in terms of features and their composition. In general, features are neither perfectly modular nor perfectly compositional. This is the case in telecommunications practice, where not only must feature interaction be designed for and managed, but it can also be useful to the system specifier.
Zave proposes a formal method for feature-oriented descriptions which she calls feature engineering. Working from partial (and in general inconsistent) requirements, this involves four stages: (a) describe new features as if independent, (b) understand all potential interactions, (c) decide which interactions are desirable and which are not, and (d) adjust features and their composition to select desired interactions and avoid those not desired.
In the remaining sections of this paper we will see that retrenchment offers a stepwise method of 'layering in' partial requirements (features), whilst managing interaction handling. We will therefore suggest that retrenchment offers a feature-engineering approach to feature-oriented applications.
The layering approach to requirements specification is familiar from the object-oriented paradigm: new, consistent requirements on a class are expressed (via the inheritance relation) in the subclass, by adding structure and behaviour in a manner consistent with the superclass.Footnote 6 Layering, in this object-oriented style, is not new in the formal methods world; Back has proposed layering through interpreting inheritance as superposition refinement [16, 17].
10 Feature engineering the case study
In this section we reorganise our telephony case study along feature-engineering lines. Layering emerges as a natural technique in sympathy with retrenchment. We focus in the sequel exclusively on the connect n operation as the only one for which non-trivial issues arise. To lighten the notation, we no longer use 'connect n ' as a subscript, reserving subscripts to distinguish between different variants of the operation. Before we start we introduce a couple of items of notation for combinators on relations.
The relational override combinator \( \leftoverrideoper \) is familiar from the preceding sections and will be used a lot.
The relational 'union asserted disjoint' combinator \( \mathrel{\hbox{\underbar{$\cup$}}} \) is defined for two relations R and S (both from X to Y say) by:
and is otherwise undefined. Thus \( \mathrel{\hbox{\underbar{$\cup$}}} \) asserts (rather than enforces) that R and S are disjoint. (In this respect it is different from conventional disjoint union, which is always well defined, and which in effect enforces the distinctness of its arguments, if necessary by introducing some tagging mechanism behind the scenes, so that the originating set of any element of the disjoint union can always be discerned. In our model-based reasoning, where elements of the model are supposed to correspond to aspects of the real world, such surreptitious tags can have no place and we use the unconventional \( \mathrel{\hbox{\underbar{$\cup$}}} \) to advertise that a union is in fact formed from two disjoint sets.) Note that valid uses of \( \mathrel{\hbox{\underbar{$\cup$}}} \) can always be replaced by \( \leftoverrideoper \), resulting in equivalent if slightly less overtly informative expressions.
Finally we will use conventional union \({ \cup }\) on relations too. This combinator is applicable when the relations in question are in an appropriate sense not in conflict with each other on a non-trivial intersection. (One plausible area for using the conventional union combinator is given by the calling number delivery feature, in which the caller transmits his number to the callee, who may or may not display it and choose to react accordingly. This behaviour may coexist benignly with almost every other feature, making union an appropriate combinator to contemplate.)
We now rebuild the operations we discussed previously out of smaller-grained features. The original operations from the preceding sections will be referred to by using their previous names, e.g. connect n , while the individual features we will discuss will typically be called stp f , where f is the feature name, and we have lifted the general stp notation for transition relations to highlight that we define a feature by giving a presentation of the relevant transition relation. Of particular note is the fact that the original operations must be model complete (as they were before), while the individual features that comprise them need not be.
We start with the PHONE model. In line with our feature-engineering goals, we split the original POTS connect n operation into two features, stp P and \( stp_{\bar P} \), representing respectively the connection capability and the non-connection capability:
so the original POTS connect n operation (6) is given by:
Here we have renamed the connect n of (6) as connect P,n , the P subscript emphasising the POTS aspect. Note that the override combinator is definitely needed in (98) as the non-connection capability is in principle always available.
Now we consider call forwarding. The call forwarding feature stp CF,n can be defined by:
We wish to combine this with the PHONE model of course. The first thing to note is that the state space for PHONE CF is larger than that for PHONE, so we cannot utilise the \( \leftoverrideoper \) and \( \mathrel{\hbox{\underbar{$\cup$}}} \) operations directly to combine stp CF,n with the previous system. This is where our programming convention comes to the fore. As previously, whenever the definition of a state transition operation (via a relation) does not mention some state variables, it is to be understood that the part of the state described by such state variables is to remain unchanged during the transition. This gives us a means of defining the PHONE model's state space in a PHONE CF model's context (since not all of the PHONE CF state is mentioned in a PHONE transition). But this does not cover all that we have to contend with.
We note that the various features we engineer generate outputs not shared by other features, so we have to determine what is to be done about reconciling those output values. Hitherto we have not specified precisely what the various spaces of output values are; we have merely mentioned some individual values as needed. We can thus assume that all such values are already present in a common space of output values.
Finally, we must consider the input values. By implication the input spaces are identical in all cases, as all inputs are arbitrary phone numbers. Therefore no special measures are needed to reconcile these.
To summarise: identical input spaces are trivially identified; output spaces are implicitly identified by considering the union of all values ever used for output; state spaces, which are the Cartesian products of the sets of values permitted for the various state variables, are combined by identifying the state variables themselves where possible. (For example, the state space for an abridged model whose states are just the values for the calls variable can be combined with the state space for a completed model whose states are (pairs of) values for the calls and fortab variables, by identifying the calls variables. This results in an overall state space of pairs of values for the calls and fortab variables, where the value of calls is common, and in the abridged model the value of fortab is irrelevant but unchanged during any abridged state transition.)
With all of this in mind, we can regard (96) and (97) as implicitly defining an extension of stp P,n and \( stp_{\bar P,n} \) to appropriately larger state spaces, in particular to ones including a forwarding table, and to all the necessary output values. Regarding and \( \leftoverrideoper \) \( \mathrel{\hbox{\underbar{$\cup$}}} \) as now referring to these enlarged sets of values also, we can define the call forward connect operation by:
where we define stp P>>CF,n as the contents of the parentheses on the preceding line. The P>CF notation of the subscript of stp P>>CF,n indicates the feature precedence we have in mind. (Note that this is distinct from the CF>CH notation used earlier, which merely indicated temporal order of combination of features.)
It is not hard to see that (100) agrees with the original call forward connect operation (11). It is also easy to see that we are vindicated in our use of \( \mathrel{\hbox{\underbar{$\cup$}}} \), as stp P,n requires free(i) to hold whereas stp CF,n requires busy(i). Of course the override to \( stp_{\bar P,n} \) is still needed as \( stp_{\bar P,n} \) provides a response for all busy(i) cases.
We can deal with call holding similarly. Assuming the same conventions, we define the call holding feature by:
and now we get:
which agrees with (16).
Now when we consider combining the two features, our layering strategy and use of override suggests a possibility not considered before, namely of simply allowing one feature to take precedence over the other when both are applicable. Noting that we will not be able to use \( \mathrel{\hbox{\underbar{$\cup$}}} \) between the two features, and also replacing the previous uses of \( \mathrel{\hbox{\underbar{$\cup$}}} \) by \( \leftoverrideoper \) to simplify the bracketing, we get two models, depending on which order of precedence we select:
As should be clear from the preceding remarks, neither of these operations coincides with the connect CF/CH,n operation of (36) since that operation depended on novel design for cases when call forwarding and call holding both applied. However, an operation like (36) can be handled in our layered feature-engineering approach by inventing a fresh feature for the precise purpose of describing what should happen in the overlapping cases, and then incorporating it into the feature hierarchy at the appropriate point.
This idea forms a key ingredient of the general approach described below. Whenever features are in conflict and a straightforward prioritisation does not give an adequate solution to the problem, we design a new feature: an interaction feature intended to take precedence over both of them, and defining the behaviour required. For features A and B in conflict, we systematically name the relevant interaction feature A+B.
Using the interaction feature strategy, we re-engineer the overlapping call forwarding and call holding case with the interaction feature CF+CH:
With stp CF+CH,n to hand, we recover the connect CF/CH,n operation of (36) by:
In the first line of (106) we have been quite explicit in setting out the layering in a way that exposes the dependencies and independencies between adjacent features in detail (we could, more lazily, have just used override throughout). Thus stp CF+CH,n and stp P,n are combined in union asserted disjoint, because one of them requires busy(i) and the other its negation. These must in turn override stp CH,n and stp CF,n for reasons that have already been discussed. However stp CH,n and stp CF,n must be combined using conventional union rather than \( \mathrel{\hbox{\underbar{$\cup$}}} \), because they are certainly not disjoint. In fact (stp CH,n \({ \cup }\) stp CF,n ) offers a non-deterministic choice in the overlap region, a fact which has no design significance in the context of (106) as the overlap is immediately overridden by the stp CF+CH,n feature.
The preceding leads us to a stepwise method for feature composition with static resolution of interactions in the spirit of the feature engineering of [18].
Procedure 10.1
-
1.
Describe each feature f independently using a relation stp f . Include a default feature f D to ensure model completeness.
-
2.
Choose a precedence order between features.
-
3.
Start with the topmost feature f 0 and the default feature f D, to build the operation \( {op_{0} = stp_{{f_{D} }} \leftoverrideoper stp_{{f_{0} }} } \).
-
4.
For successive i, layer in feature f i after feature f i-1 giving:
$$\eqalign{ & op_i = stp_{f_D } \leftoverrideoper stp_{f_i } \leftoverrideoper stp_{f_{i - 1} } \leftoverrideoper ...\leftoverrideoper stp_{f_0 } \cr & = stp_{f_D } \leftoverrideoper stp_{f_i } \leftoverrideoper stp_{f_0 >> ... >> f_{i - 1} } \cr & = stp_{f_D } \leftoverrideoper stp_{f_0 >> ... >> f_i } \cr} $$(107) -
5.
If feature f i interacts with feature f j for j < i, design an 'interaction feature' f i+j to resolve the problem, giving it precedence over both f i and f j thus:
$$\eqalign{ & op_i = stp_{f_D } \leftoverrideoper stp_{f_i } ...\leftoverrideoper stp_{f_j } \leftoverrideoper stp_{f_{i + j} } \leftoverrideoper...\leftoverrideoper stp_{f_0 } \cr & = stp_{f_D } \leftoverrideoper stp_{f_i } \leftoverrideoper stp_{f_0 >> ...f_{i + j} >> f_j >> ... >> f_{i - 1} } \cr & = stp_{f_D } \leftoverrideoper stp_{f_0 >> ...f_{i + j} >> f_j >> ... >> f_i } \cr} $$(108) -
6.
Repeat until all features have been handled.
Procedure 10.1 only considers the possibility of binary interactions between features, but this is clearly not the only possibility. Ultimately if there are n features, there are up to 2n possible interactions (one for each possible subset of the n). All interactions can give rise to interaction features, and these can be layered in as above. The objective of prioritisation is of course to minimise the number of interactions that have to be handled 'out of line', by choosing an ordering such that the interactions naturally subsume one another as far as possible.
Of course we have not yet related the various layers to one another. The technique for doing this will be retrenchment, and will form the subject of the next section.
11 Layered feature engineering by composition of retrenchments
Now that we have defined the features of interest and their composites, it might be thought that the retrenchments between them are just the ones we have already dealt with. This is almost true, but we must remember that the operations of the last section are defined on subtly different spaces than previously, so we must also adapt our previous retrenchments accordingly.
Our feature layering of the last section simply imposed new functionality on operations so, just as in Sect. 3, we used the same variable names for all the different models. However, just as in Sect. 5, when we come to discuss retrenchments between the models, we must use distinct names for distinct models (but with a tacit understanding of which distinct names are distinct names for the same thing). This is rendered potentially more confusing because, recalling the discussion after (99), all the models are assumed to share the same spaces of values.
Thus all the input spaces are trivially the same; all the outputs are assumed to also belong to the same space of values; and there is a common state space, the Cartesian product of all the sets of values permitted for any of the state variables occurring in any of the models to be considered.
We have remarked that in defining transitions we adhere to the programming convention whereby any variable not explicitly altered by the transition is to remain at its previous value. However, for the retrieve, within and concedes relations of a retrenchment this is not appropriate. These relations do not describe a state change of some system, but comprise the description of the retrenchment relationship between two distinct systems. This is a predicate in the conventional sense, and it is therefore the logical convention that is appropriate here; i.e. any variable not mentioned is unconstrained within its range of permitted values.
With this understood, we can describe the general nature of the retrenchments to come. In all cases the within relations will be of the form:
because the input spaces will always be the same. The retrieve relations will be of the form:
because the state spaces of all models have been extended to be the same.Footnote 7 Since these facts hold for all the systems of interest, we need not mention the retrieve or within relations any more. Finally the concedes relations will feature the variables intrinsic to the models at issue, on the understanding that all other variables are unconstrained.
As an example of the preceding, we consider the retrenchment from \( {connect_{{P,n}} = stp_{{\bar{P},n}} \leftoverrideoper stp_{{P,n}} } \) in (98), to \( {connect_{{CF,n}} = stp_{{\bar{P},n}} \leftoverrideoper stp_{{P > > CF,n}} = stp_{{\bar{P},n}} \leftoverrideoper stp_{{CF,n}} \leftoverrideoper stp_{{P,n}} } \) in (100). Note that we have reverted to using the override combinator throughout, as we will do for the remainder of this section for notational simplicity.Footnote 8
The two models differ only when call forward is enabled, so we can write the concedes clause as:
In (111), (u, i) ∈ (dom(stp CF,n ) – dom(stp P,n )) refers to the part of the abridged before-state and input spaces outside of dom(stp P,n ) but inside dom(stp CF,n ) (the latter viewed through the within and retrieve relations (109 and 110)), and acting as a constraint on \( {stp_{{\bar{P},n}} (u,i,{u}',o)} \); while (v, j) ∈ (dom(stp CF,n ) – dom(stp P,n )) refers to the same thing viewed in the other direction through the within and retrieve relations, and acting as a constraint on stp CF,n (v, j, v′, p), all in line with the semantics of the override combinator. Although (111) is syntactically different from (25), in the intended context of use (i.e. when the retrieve and within relations are assumed, and a completed level step is posited together with a suitable abridged level step inferred from all of these), the two are equivalent. The formulation in (111), while including some redundant clauses, is more systematic, and its structure reflects closely the layering in of features used in the construction of connect CF,n .
Lemma 11.1
Let op l = stp fD \( \leftoverrideoper \) + stp f0>>...>>fl and let op l+1 = stp fD \( \leftoverrideoper \) stp fl+1 \( \leftoverrideoper \) stp f0>>...>>fl be given by layering in feature f l+1 as in Procedure 10.1. Suppose that stp f0>>...>>fl and stp fl+1 have no transitions in common that differ only on outputs (on the common space of values on which they are both defined). Let C fl>>fl+1(u′, v′, o, p; i, j, u, v) be given by:
Then with within and retrieve relations (109 and 110), C fl>>fl+1 defines a neat retrenchment from op l to op l+1.
Proof
We consider first the view in which both op l and op l+1 are regarded as transition relations on the same space of values. Then we can partition the common domain of these relations into three pieces: (1) the set of (u, i) pairs in dom(stp f0>>...>>fl ); (2) the set of (u, i) pairs in (dom(stp fl+1) – dom(stp f0>>...>>fl )); (3) the remainder. On piece (1) both op l and op l+1 behave as stp f0>>...>>fl . On piece (3) both op l and op l+1 behave as stp fD. On piece (2) they differ, op l behaving like stp fD and op l+1 behaving like stp fl+1; moreover, these behaviours are incompatible, having no transitions in common that differ only on outputs, by hypothesis.
Now in the view where op l is the abridged system, and uses variables u, i, u′, o, and op l+1 is the completed system, and uses variables v, j, v′, p, pieces (1) and (3) describe points at which the retrieve relation is re-established, and piece (2) describes points at which the concedes relation (112) is established. Since there are no transitions in common that differ only on outputs starting from points in piece (2), the retrieve relation cannot hold there, and the neatness condition (86) is proved.
Note that the phrase 'no transitions in common that differ only on outputs' is connected with the insensitivity of the re-established retrieve relation to outputs in the present formulation of retrenchment. With a more incisive version, this could be strengthened to 'no transitions in common'.
Lemma 11.2
Let op l and op l+1 be as in Lemma 11.1, and similarly for op l+1 and op l+2. Then condition (88) of Corollary 8.3 holds.
Proof
Considering as before the view in which op l , op l+1 and op l+2 are regarded as transition relations on the same space of values, we can partition the common domain into four pieces: (1) the (u, i) pairs in dom(stp f0>>...>>fl ); (2) the (u, i) pairs in (dom(stp fl+1) – dom(stp f0>>...>>fl )); (3) the (u, i) pairs in (dom(stp fl+2) – dom(stp f0>>...>>fl ) – dom(stp fl+1)); (4) the remainder. On piece (1) op l , op l+1 and op l+2 behave like stp f0>>...>>fl . On piece (4) op l , op l+1 and op l+2 behave like stp fD.
On piece (2) they differ, with op l behaving like stp fD, and op l+1 and op l+2 both behaving like stp fl+1. On piece (3) they also differ, with op l and op l+1 behaving like stp fD, and op l+2 behaving like stp fl+2. Moreover, these behaviours, where different, are incompatible, having no transitions in common that differ only on outputs, by hypothesis.
So on each piece, at least two consecutive operations out of op l , op l+1 and op l+2 behave identically, i.e. in the retrenchment view, on each piece at least one retrenchment re-establishes the retrieve relation. Since both retrenchments are neat, so that we have (86) for both, there can be no triples of transitions from the transition relations of op l , op l+1 and op l+2 which make \( {\text{pre}}^{{{\text{Con}}}}_{{op}} {\left( {u,i,v,j} \right)}\; \wedge \;{\text{pre}}^{{{\text{Con}}}}_{{op}} {\left( {v,j,w,k} \right)} \) true. So we get (88).
The preceding immediately admits the applicability of Corollary 8.3, which declares that the composed concedes relation has the structure \( {{\left( {G \wedge D_{{op}} } \right)} \vee {\left( {C_{{op}} \wedge H} \right)}} \). Noting that all retrieve relations are identities, and using the one point rule to eliminate intermediate variables as previously, we get:
Noting that the retrieve and within relations are identities, and taking advantage of the antecedents of the retrenchment operation PO as we have done before, we manipulate (113) to obtain something not logically equivalent to (113), but equivalent to it in the context of its use, and of a shape that we prefer:
This displays the expected behaviour, namely that in the region of disagreement between op l , op l+1, and op l+2, op l behaves like the default feature stp fD throughout, while op l+2 behaves like stp fl+1 at points in dom(stp fl+1) and like stp fl+2 at points in dom(stp fl+2).
The structure of the general case should now be evident. If we have an operation op n structured by layering features f 1 ... f n into a default stp fD \( \leftoverrideoper \) stp f0 operation, then the transition relation for op n can be displayed as:
where \( \triangleleft \) is domain restriction. The concedes relation from op 1 to op n can now be written as:
Note that unlike the cases covered by Lemmas 11.1 and 11.2, expressions (115) and (116) were built by analogy and are not directly based on the results of Sect. 8. To have attempted to get (115) and (116) formally would have entailed a digression into the multiple compositionality and associativity properties of tidy and neat retrenchments. Given the counterexamples to tidiness and neatness of composed tidy and neat retrenchments indicated in Sect. 8, this would have proved to be a lengthy exercise.
The regular structure of expressions (115) and (116), and the fact that feature interaction can be dealt with by introducing interaction features which are handled just like any other features, means that (115) and (116) can do duty for the general case of interacting features, simply by relabelling the features that occur, in line with (108). The approach just outlined is certainly the simplest method for handling feature interaction in the present layered architecture.
An alternative route to the same thing treats feature interaction not as a fresh feature, but as a new kind of phenomenon, utilising not Corollary 8.3 but the full force of Theorem 8.2. However, a moment's thought reveals that in both approaches ultimately the same process of partitioning the before- and input spaces is going on under different guises, and the lack of a specific 'interaction feature' is counterbalanced by the \( {C \wedge D} \) term in (87) and corresponding manipulations in the remainder of the theory; so we do not pursue this option in detail.
The same insight informs the treatment of the other feature combinators: union, and union asserted disjoint. Arbitrarily complicated feature expressions may be analysed to discern the regions of enabledness of the constituent subexpressions, and from there we partition the before- and input spaces into regions in which a single feature or collection of features is enabled. Furthermore, the same approach will deal with 'partial interaction features', where the desire is to introduce a new feature on only part of the region in which two other features interact, and in the remainder to deal with the interaction by other means, e.g. by prioritisation; one has simply to generate a finer partition. Once the appropriate partition of the before- and input spaces has been arrived at, the definitions of various staged versions the operation of interest, given by adding the behaviour relevant to individual regions one by one, follows readily.
12 Conclusions
Feature interaction in telephony has attracted a fair amount of attention in recent years, e.g. [11, 12]. The burgeoning telecoms industry is always introducing new capabilities into its systems, mainly because of the flexibility afforded by digital electronics and programmed interconnection exchanges. However, even if a telecoms provider can make a rational reconciliation of all of the enhanced services that it provides itself, it is by no means clear that when one provider's network is interfaced to another provider's network, the results will be as either provider envisaged. This kind of thing has posed a challenge to development techniques (both formal and not so formal).
Amongst these various efforts, refinement has been used to address the problem [19], but the use of refinement in an area where previously established properties have to be overridden is frequently an exercise in perversity. One has to search for a way of formulating the problem so that the contradictions inherent in a typical development step do not become exposed during the refinement process, the sophistication of the notion of refinement used notwithstanding. This is principally because refinement allows only the accumulation of properties in a conjunctive manner, a trait which although immensely appealing and mathematically robust is often at odds with real-world experience in system development. The Appendix below illustrates this phenomenon concretely to some extent in a very simple context.
In contrast, the recording of the development decisions made via retrenchment would, we would claim, appear much more natural, and in the preceding sections we have considered a simple illustration of this via a stripped-down telephony case study. By necessity, such a simple example cannot display many of the facets of inconsistency in specification that we claim may be usefully described by retrenchment. Instead we showed in Sect. 6 how a simple functional interaction between features could be resolved by design and described by retrenchment. It is noteworthy that our chosen features can be handled very much in the manner of the prioritised 'busy treatments' of [14], where features available to deal with a call request to a busy subscriber are applied in a guarded and prioritised manner.
The work in this paper represents a new methodological departure for retrenchment. The notion was conceived as a liberalisation of classical refinement for the situation where the idealised description was incompatible with finite, discrete computational models. Retrenchment was thus conceived as an 'approximate' refinement, or refinement with exceptions. In the case of feature-oriented descriptions, the thesis is that retrenchment offers a framework for the stepwise, layered construction of a requirements specification, accounting for both beneficial and harmful interactions. For harmful, or interfering, interactions, the framework allows incorporation of design to resolve the interaction in the layered construction process.
This retrenchment approach to feature interaction can be located in the taxonomy of formal methods for feature interaction in [20] as property-based. That is, the description is in terms of feature properties and their relations to one another. The description is in first-order logic, and as for other property-based approaches, tools such as PVS [21] can be brought to bear to mechanise the process, and to bring the additional assurance that mechanical checking can give.
However, it must be emphasised that since the denial of previously established properties is fraught with danger if adopted in a development path, the use of retrenchment for these purposes must be adopted in a completely transparent and conscious manner. System designers must be aware that the abstract and concrete models in a retrenchment step must coexist in an open dialogue about the evolution of the functional requirements of the desired system, which are recorded via the retrenchment POs. They must not assume, just because the retrenchment technique is formal, that it is therefore some miraculous panacea, the adherence to the formal structure of which automatically guarantees success. In other words, designers must not think that retrenchment absolves them from taking responsibility for design decisions. With such a proviso, retrenchment can help to both document and to justify the design arrived at.
On purely technical grounds, it must be admitted that we were limited somewhat in this paper by the fact that the retrenchments we used related a single step at the upper level to a single step at the lower level. This is certainly the easiest formulation of the retrenchment concept to understand and to work with. However our models were thereby doomed to be rather unrealistic as regards accurately reflecting real-world telephone systems, as we pointed out at the time. In reality, call connection and the other features we alluded to are all multistep operations, and the temporal aspects cannot be neglected in an accurate model. To undertake a more convincing retrenchment-based study of feature interaction, we would have to resort to a formulation of retrenchment that allowed more than one step at a single level to play a role in the retrenchment relationship. Some aspects of such a formulation of retrenchment have been studied in [13], where one abstract step is retrenched to several concrete steps, and a retrenchment version of Schellhorn's m:n refinement would also be relevant in this context [22, 23].
While doing such a more detailed study of feature interaction remains for future work, and would undoubtedly be worthwhile, we have concentrated in this paper on making the case for retrenchment not only as a means of progressing approximate and requirements incomplete models towards a more definitive contracted model, but also as a useful formal tool for re-engineering and design evolution situations (since mathematically, there is little to distinguish the two activities). We used feature interaction as a pertinent illustrative vehicle. We have seen that as well as providing an encompassing milieu for such activity, retrenchment can comfortably accommodate more ad hoc custom approaches such as layered feature engineering. Therefore we regard the case as well made.
Notes
Several private communications.
Taking some liberties with language, we mean not only 'made sanitary' but 'made sane'.
Some comment on the word 'incomplete' is in order. We mean here incomplete in the sense that some of the functional requirements of the system are deliberately being ignored in order to better understand and define the ones being focused on; we call this requirement incompleteness. In other places incompleteness is intended to refer to the lack of viability of a model to serve as a system description in its own right from a user's perspective (irrespective of the totality of requirements that ultimately needs to be captured). In such cases the incompleteness refers to the lack within the model of any defined system response to at least some of what ought to be regarded as legitimate user demands or inputs to the system; we call this model incompleteness; another way of describing this would be lack of input readiness. Such scenarios usually arise when there is an intention to fill in the missing pieces during later refinements: these later refinements can be of such a nature that they are incompatible for technical reasons with natural completions of the abstract model in its own right, thus provoking the incompleteness of the abstract model in the first place (since a suitable extension of an adroitly designed but incomplete abstract model will usually yield a valid refinement).
Most presentations of retrenchment speak of an abstract and a concrete system, in the spirit of moving towards an implementation.
One can accept this situation as it stands; i.e. one can, if a more precise solution is desired, add any necessary information about the outputs in those cases where the retrieve relation is re-established (and the concedes clause is not otherwise verified) as a top-level disjunct in the concedes clause, making it true always; we have finessed this possibility. Alternatively to improve matters regarding outputs, one can move to a more expressive if more complicated formulation of retrenchment, e.g. sharp retrenchment or its close relatives [13, 9]. Among these possibilities, output retrenchment replaces G in the consequent of the operation PO by \( {G \wedge O} \), where O(o, p) relates higher- and lower-level outputs for the case that G is maintained (in our case reducing to just (o = p)). Then a sound law of composition supplements (55)–(57) with the composition of O relations for successive retrenchments.
This is as opposed to inheritance by method overriding, where superclass behaviour is altered, in an inconsistent manner, in the subclass. This alteration could be described using the concedes relation in a retrenchment-based formulation of the inheritance relation.
We could have opted for a variant in which components of the extended common state which are not intrinsic to the model at a given layer were unconstrained, generating retrieve relations which were equalities in some components and universal relations in other components; but (110) is simper and leads to equivalent results.
Readers will be able to rework what follows for operation definitions involving \( \mathrel{\hbox{\underbar{$\cup$}}}\;and\; \cup \) without difficulty.
Actually the location cannot be entirely unspecified. It must be chosen in such a way that the invariant in (121) is preserved. One could add a clause to (125) to ensure this.
References
Wirth N (1971) The development of programs by stepwise refinement. Commun ACM 14:221–227
Dijkstra EW (1972) Notes on structured programming. In: Structured programming. Academic Press, London
Hoare CAR (1972) Proof of correctness of data representations. Acta Inform 1:271–281
de Roever W-P, Engelhardt K (1998) Data refinement: model-oriented proof methods and their comparison. Cambridge University Press, Cambridge
Back RJR, von Wright J (1998) Refinement calculus: a systematic introduction. Springer, Berlin Heidelberg New York
Barroca LM, McDermid JA (1992) Formal methods: use and relevance for the development of safety-critical systems. Comput J 35:579–599
Banach R, Poppleton M (1998) Retrenchment: an engineering variation on refinement. In: Bert D (ed) Proceedings of B-98. Lecture notes in computer science, vol 1393. Springer, Berlin Heidelberg New York, pp 129–147. See also Tech Rep UMCS-99–3-2, http://www.cs.man.ac.uk/cstechrep
Banach R, Poppleton M (2000) Retrenchment, refinement and simulation. In: Bowen JP, Dunne S, Galloway A, King S (eds) Proceedings of ZB-00. Lecture notes in computer science, vol 1878. Springer, Berlin Heidelberg New York, pp 304–323
Banach R, Poppleton M (1999) Sharp retrenchment, modulated refinement and simulation. Form Aspects Comput 11:498–540
Banach R, Poppleton M (2001) Engineering and theoretical underpinnings of retrenchment (submitted) http://www.cs.man.ac.uk/~banach/some.pubs/Retrench.Underpin.ps.gz
Calder M, Magill E (eds) (2000) Feature interactions in telecommunications and software systems VI. IOS Press, Amsterdam
Kimbler K (ed) (1999) Feature interactions in telecommunications and software systems V. IOS Press, Amsterdam
Banach R, Poppleton M (2000) Fragmented retrenchment, concurrency and fairness. In: Liu S, McDermid JA, Hinchey M (eds) Proceedings of ICFEM-00. IEEE Computer Society Press, Los Alamitos, CA
Zave P (2001) Requirements for evolving systems: a telecommunications perspective. In: Proceedings of the 5th IEEE international symposium on requirements engineering, pp 2–9
Kimbler K, Bouma LG (eds) (1998) Feature interactions in telecommunications and software systems V. IOS Press, Amsterdam
Back RJR (2002) Software construction by stepwise feature introduction. In: Bert D, Bowen JP, Henson MC, Robinson K (eds) Proceedings of ZB-02. Lecture notes in computer science, vol 2272. Springer, Berlin Heidelberg New York, pp 162–183
Back RJR, Sere K (1996) Superposition refinement of reactive systems. Form Aspects Comput 8:324–346
Jackson M, Zave P (1998) Distributed feature composition: a virtual architecture for telecommunications services. IEEE Trans Software Eng 24:831–847
Cansell D, Mery D (2000) Playing with abstraction and refinement for managing features interactions. In: Bowen JP, Dunne S, Galloway A, King S (eds) Proceedings of ZB-00. Lecture notes in computer science 1878. Springer, Berlin Heidelberg New York, pp 148–167
Calder M, Kolberg M, Magill E, Reiff-Marganiec S (2001) Feature interaction: a critical review and considered forecast. Comput Networks 41(1):115–141
Crow J, Owre S, Rushby J, Shankar N, Sirvas M (1995) a tutorial introduction to PVS. In: France R, Gerhart S, Larrondo-Petrie M (eds) Proceedings of WIFT-95 workshop on industrial strength formal specification techniques. IEEE Computer Society Press, Los Alamitos, CA
Schellhorn G (1999) Verification of abstract state machines. PhD thesis, University of Ulm Fakultät für Informatik
Schellhorn G (2001) Verification of ASM refinements using generalized forward simulation. J Univers Comput Sci 7:952–979
Acknowledgement
The authors would like to thank Michael Jackson for valuable interaction during the preparation of this paper.
Author information
Authors and Affiliations
Corresponding author
Appendix: PHONE Development via Refinement
Appendix: PHONE Development via Refinement
In this section we examine the prospects for doing at least some of the development of the telephone case study using refinement. We had better start by saying what we mean by refinement in this context.
We are working in a straightforward transition system-based framework. For this reason, notions of potential non-termination and attendant complexities, often taken into account in refinement formalisms, just do not arise: there are transitions that initiate and terminate successfully as described in an operation's transition relation, and there is nothing else. We revert to the usual convention of speaking about an abstract and a concrete system, as is prevalent in the refinement literature.
With the notational conventions we have been using up to now, we define the precondition for say an abstract operation m A, whose transition relation is stp mA, by:
(So pre mA is just what we called dom mA before, but we now conform to the terminology more common in refinement.)
Now we define refinement from an abstract system to a concrete system to be characterised by the following Z-refinement-like conditions:
Note that we are being strict here about I/O. The inputs and outputs must be identical at the two levels of abstraction. This is in line with viewing refinement as an implementation mechanism which can silently replace an abstract model with an implementation, without the user's awareness. (Also it finesses a couple of minor logical niggles.)
What are now the prospects of doing, for example, the PHONE to PHONE CF development step via refinement? Immediately we say nil, because (118) is violated by the additional table management operations of PHONE CF . Let us agree to ignore this for the sake of not falling at the first fence. We next examine one model for PHONE that has prospects for refinement.
PHONE′
In this system the state space is just as for the original PHONE model:
The two operations, connect n and break n , look like:
Note that this differs from PHONE in that the specification of connect n has nothing corresponding to the 'else' clause of (6). It is thus a partial operation since in the \( {{\rm{busy}}{\left( i \right)} \vee {\left( {n = i} \right)}} \) case we are outside the precondition of connect n . Some stratagem like this is forced on us, however, because if PHONE CF 's connect CF,n operation is to be a valid refinement of connect n , then up to the latitude permitted by the retrieve relation (which will continue to be (23) and thus effectively affords no latitude whatsoever), the actions of connect CF,n and connect n must agree in the \( {{\rm{busy}}{\left( i \right)} \vee {\left( {n = i} \right)}} \) case should they both be defined, otherwise (120) will fail. This effect is rendered even more acute when we remember that, in refinement, outputs must agree.
Unfortunately this kind of partiality of operations is not acceptable in a high-level model that purports to capture a coherent set of user requirements, and is a manifestation of the model incompleteness described in the Introduction. User requirements at this level must express a defensively drawn and complete model, as it is quite unreasonable to assume that users can flawlessly adhere to the need to never call a connect n operation from a before-state/input combination for which there exists no connect n transition.
(It is thus clear that model incompleteness is unavoidably a user-level or meta-level issue, not deducible from the mathematics of the model alone. For example, whereas it is certainly the case that there are never any connect n transitions when busy(n) holds, this is not a symptom of model incompleteness due to the different significance of n and i at user level—users accept that it is semantically self-contradictory to expect a transition in the busy(n) case.)
Since this refinement attempt has spawned some unsatisfactory features, we give an alternative construction, exploiting non-determinism rather than partiality this time.
PHONE′′
In this system the state space is just as before:
The operations connect n and break n this time look like:
In this version of events, in the \( {{\rm{busy}}{\left( i \right)} \vee {\left( {n = i} \right)}} \) case, the operation connect n has the capacity to non-deterministically connect to some unspecified location.Footnote 9 The non-determinism is resolved in the refinement to PHONE CF (still using the same retrieve relation), in which the connect CF,n operation specifies when and where a connection can be made in the \( {{\rm{busy}}{\left( i \right)} \vee {\left( {n = i} \right)}} \) case.
The abstract operation is now total, overcoming the objection in the previous version. However, the price for this is the non-deterministic else clause in (125). For sure, the PHONE′′ model is a more abstract entity than the PHONE CF model, but when one asks the question as to what extent PHONE′′ deserves to be called a specification of the POTS model in the sense that PHONE′′ captures a coherent set of functional requirements of the POTS system the answer is less than satisfactory. Is the specific non-determinism present in PHONE′′ a requirement of the POTS model? The answer is surely that it is not. The PHONE′′ model was specifically construed to withhold those features from PHONE CF that could neatly be reinstated by the definition of refinement that we are using; i.e. it was reverse engineered from PHONE CF . Thus the abstract and concrete levels have become entangled in this development, and vestiges of properties of the envisaged lower-level model have had to migrate to the higher-level one in order to satisfy the exigencies of refinement. This is the kind of reverse engineering we alluded to in the Introduction; and while it might not be too problematic in such a small example, in larger systems it can become a serious nuisance. The pollution of the perspicuity of the higher-level models, arising from the forced incorporation of very specific perspectives on inappropriate lower-level detail forced upwards by the demands of refinement, can merely serve to bring an otherwise blameless refinement-based specification development methodology into disrepute among designers.
Thus refinement based-developments of the evolution of a more complex specification from a simpler one (each of which captures a coherent set of functional requirements of the system at a suitable level of abstraction) are replete with difficulties. We have illustrated these just in the case of the PHONE to PHONE CF development step; however, extending the same approach to the other parts of the feature interaction case study would simply cause the illustrated difficulties to proliferate.
Rights and permissions
About this article
Cite this article
Banach, R., Poppleton, M. Retrenching partial requirements into system definitions: a simple feature interaction case study. Requirements Eng 8, 266–288 (2003). https://doi.org/10.1007/s00766-002-0157-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00766-002-0157-6