Electron Spin Resonance in Strongly Correlated Metals

Abstract

Modern technique of electron spin resonance (ESR) measurements and data analysis in strongly correlated metals, which allows finding the full set of spectroscopic parameters including oscillating magnetization, relaxation parameter (line width), and hyromagnetic ratio (g-factor), is described. Application of the considered method is illustrated by such examples as metallic systems CeB₆, Mn_1−xFe_xSi, GdB₆, Ho_xLu_1−xB₁₂, and metallic surface of topological Kondo insulator SmB₆. It is shown that ESR in strongly correlated metals provides a unique tool for studying short-range correlations at the nanoscale of a spin polaron type, electron nematic effects, and spin fluctuation transitions. Application of ESR technique opens new opportunities for observation of quantum critical points, including hidden ones. In many cases, it is just ESR, which either indicates the necessity for clarification or deep revision of the prevailing paradigm, or constitutes the basis for a new concept of magnetic properties of various strongly correlated metals.

1 Introduction

The problem of magnetic resonance in strongly correlated electronic systems (SCES) is multifaceted. It covers materials differing by electrodynamic and magnetic properties: metals, semiconductors, and dielectrics, and, for that reason, studying of electron spin resonance requires special experimental methods and data analysis schemes. In some cases, the use of straightforward cavity technique and commercial spectrometers produces artifacts, resulting in completely misleading physical models. Nevertheless, when ESR is studied and analyzed correctly, it provides unique information about spin dynamics and spin relaxation in SCES, which is not available in static magnetic measurements. For example, ESR opens up a new route for the investigation of quantum critical phenomena, quantum spin chains, and topological insulators.

Strongly correlated metals are probably the most difficult case, as long as correct measurements in this case require specific experimental layout and data analysis schema. The principal difficulty or characteristic feature of metallic SCES is the concentrated nature of the magnetic system. Basically, when magnetic ion is present in each unit cell, any mode of magnetic oscillations is a collective mode, and thus, the standard single-ion physics from the textbooks is not applicable even for electron paramagnetic resonance description, and, strictly speaking, in most cases an adequate microscopic theory is either missing or not adequate. Additional complications may originate from itinerant electrons interacting with localized magnetic moments (LMM). In this situation, we are forced to use semi-classical language implying Landau–Lifshitz equation of motion for dynamic magnetization, but, as we will show, this ansatz, in spite of its general (and to some extent model-free nature), also leads to controversial results. Apparently, no solutions to the rising problems may be found in the ESR Bibles [1, 2], which, from one hand, looks very promising for theoretical studies.

From the over hand, it seems that an opportunity to develop adequate theory for ESR in metallic SCES was not used so much. For that reason, the current review will mainly represent experimentalist’s opinion of current state of the art in this field of research. The paper is organized as follows. At first, we will concentrate on the problem of measurement of ESR in strongly correlated metals. The described technique and it application will be illustrated by such examples as manganites, ferromagnet EuB₆, heavy-fermion metal with orbital ordering CeB₆, quantum critical system Mn_1−xFe_xSi, and metallic surface of strongly correlated topological insulator SmB₆. At the end, some recent experiments on several metallic SCES will be considered. Therefore, in this review, we attempt to bring together the cases of different metals, but we clearly realize that it is not possible to cover a vast field of research. We would also like to apologize to all researchers whose contribution to the ESR problem in strongly correlated metals was not adequately reflected, or was not even mentioned at all, despite its generally recognized importance.

2 Measurement of ESR in Strongly Correlated Metals

These materials are often viewed as the most difficult case for ESR studies. Magnetic concentrated matrix of metallic SCES demonstrates strong spin fluctuations, which are expected to broaden ESR line width to the values of about tenths Tesla [3,4,5,6], practically unobservable in standard spectrometers. Thus, classical approach to the investigation of magneto-optical response in metals is based on consideration of a magnetic impurity, i.e., on single-ion problem in crystal field modified by interaction with band electrons [7]. However, extrapolation of isolated impurity case to the case of concentrated system requires ad hoc assumptions based on more or less common sense, which may bring misleading results.

From the technical point of view, the difficulty of measuring ESR and subsequent interpretation of the data is due to inhomogeneous distribution of microwaves in the sample, when oscillating electromagnetic field is concentrated in a skin layer. To overcome this problem, it is sometimes recommended to measure powder samples consisting of the grains, whose size is about skin depth. The data showed in Fig. 1 for manganite La_1−xCa_xMnO₃ with x = 0.2 strongly prevent from using this prescription. The comparison of the quasi-optical transmission ESR spectra of the powder sample (panel a) and that taken in cavity ESR measurement of individual grain (panel b) clearly indicates that work with  the powder sample results in loosing of the fine structure and related physical information about the state of Mn magnetic ion.

Fig. 1

Comparison of the ESR transmission spectra on a powder sample of La_1−xCa_xMnO₃ (x = 0.2) (a) and cavity spectra for small single crystal of the same material (b). Both types spectra are measured at the same microwave frequency 60 GHz

It is possible to notice that spectra in Fig. 1 demonstrate splitting into two lines with lowering temperature. This behavior was observed many times in many systems and, to the delight of the physicists, was interpreted (and used as a way to study) magnetic phase separation [8, 9]. However, a nice spectra evolution similar to that in Fig. 1 may be merely an artifact. Indeed, boundary conditions to Maxwell equations suggest that, at the sample boundary parallel to the external field, magnitude of the magnetic field is unchanged, whereas, in the sample volume, the local field is changed by adding 4πM (where M is static magnetization). If M value is high enough, the splitting of ESR spectra in two lines will occur due to a combination of the response from the surface and the volume. Apparently, this possibility is most dangerous for the powder samples and small grains, where surface-to-volume ratio increases as inversed grain size.

2.1 The Method and Problems of Studying ESR in Strongly Correlated Metals

The problem of “false line splitting” was studied in detail for the case of EuB₆ [10, 11]. This material is a ferromagnetic metal with Curie temperature at 14 K and relatively low electron concentration ~0.01 n_Eu (here, n_Eu = a⁻³ is Eu concentration in a cubic unit cell of a size a ~ 4 Å). The charge state of Eu is 2 + and related magnetic moment is high ~ 7μ_B [12], so that gradient of the magnetic field in the sample at low temperatures is strong.

Shape of the EuB₆ single crystal was varied in ESR experiment [10, 11] performed in a reflecting cylindrical cavity operating at ~ 60 GHz TE₀₁₁ mode (Fig. 2). External steady magnetic field was aligned parallel to the cavity axis. In the cases 1–4, the sample was placed at the cavity bottom in the region of the maximum of oscillating magnetic field. When the sample shape is close to cubic, the low-temperature spectra exhibit two well-resolved wide lines A and B, the distance between which increases as temperature decreases and scales with the sample magnetization [10] (Fig. 2, lines 1 and 2). For the sample in the form of a thin plate, the amplitude of line B becomes strongly suppressed due to the decrease in the relative contribution of the sample surface part, which is parallel to the external magnetic field (see Fig. 2, line 3). A further decrease in the plate thickness (Fig. 2, line 4) results in the further decrease in the amplitude of this spectral feature, which is transformed to a shoulder of the resonance A.

Fig. 2

Electron spin resonance spectra at 60 GHz for EuB₆ single crystal samples with various shapes and, correspondingly, various inhomogeneities of the magnetic field (see text for details). The sample shapes, as well as the standard experimental geometry (1–4) and geometry with excluded the inhomogeneity of the magnetic field (5), are schematically presented irrespective of the sizes. The external magnetic field is aligned parallel to the [001] crystallographic direction (from Ref. [11])

Apparently, it is not possible to avoid inhomogeneity of the magnetic field in the sample of rectangular form. At the same time, it is possible to use layout, where effects of field inhomogeneity and demagnetization on the ESR spectra will be reduced to minimal value. For that reason, it was suggested [10, 11] making cavity bottom of a thin foil with a hole (diaphragm) located at the position of the maximum of oscillating magnetic field. In contrast to standard ESR geometry, sample closes the hole outside the cavity and fixes with the help of conducting glue to obtain electric contact (see drawing at line 5 in Fig. 2). In this case, the oscillating magnetic field geometry inside the cavity is not strongly affected and only central part of the studied metallic sample is subjected to microwave radiation. As long as hole size is small and closed by the central part of the sample, M = const and internal steady magnetic field acting on spins in the sample may be treated as homogeneous. It is visible that the considered experimental layout results in a noticeable narrowing of the resonance and the complete disappearance of the “surface” line B, because microwaves are no longer interacting with the surface area (Fig. 2, line 5).

This example clearly shows that the first step in correct measurements of the metallic SCES consists in the application of special experimental layout with the sample outside the cavity. Second step consists in the correction of the external field to the factor 4πM to get the steady field the sample, which eliminates artifacts in temperature dependence of the g-factor [11]. Further investigation is based on the quantitative analysis of the ESR line shape in cavity measurements. Below, we will briefly describe this subject following Ref. [13].

The microwave cavity absorption depends on the sample high-frequency magnetic permeability and conductivity in a magnetic field as well as the unloaded cavity losses. According to Young and Uehling [14], the cavity quality factor loaded with metallic sample is given by:

$$Q^{ - 1} = Q_{0}^{ - 1} + Q_{\rm s}^{ - 1} ,$$

(1a)

$$Q_{{\text{s}}} \sim {\text{Re}} \left[ {\frac{i\omega \mu }{\sigma }} \right]^{1/2} ,$$

(1b)

$$\mu = \mu_{1} - i\mu_{2} ,$$

(1c)

here, Q is the total quality factor of the loaded cavity, Q₀ is the quality factor of the empty cavity, Q_s denotes losses introduced by the sample, μ is high-frequency complex magnetic permeability, and σ is the complex conductivity of the sample, which, in the microwave frequency range ω/2π < 100 GHz, is almost equal to dc conductivity.

Thus Eq. (1b) is reduced to:

$$Q_{{\text{s}}} = D \cdot (\rho \mu_{{\text{R}}} )^{1/2} ,$$

(1d)

where ρ stands for sample resistivity, μ_R is effective magnetic permeability, and D is temperature-independent coefficient [11]. Calculation of μ_R could be done in quasi-classical limit by applying Landau–Lifshitz–Gilbert equation:

$$\frac{{\partial M_{0} }}{\partial t} = - \gamma [M_{0} \times H] - \frac{\alpha }{{M_{0} }}[M_{0} \times [M_{0} \times H]],$$

(2)

in which H is vector of external magnetic field, γ is hyromagnetic ratio, and α stands for relaxation parameter. In Eq. (2), M₀ and M₀ denote respectively vector and absolute value of magnetization part, which is responsible for considered ESR mode (below M₀ will be also referred as oscillating or dynamic magnetization). To find μ_R and calculate resonant cavity losses, it is necessary to consider the relation between vectors of the oscillating magnetic induction inside the sample B_ω and oscillating magnetic field outside H_ω [15]. If the field inhomogeneity effects are excluded, this relation is given by:

$${\mathbf{B}}_{\omega } \, = \, \hat{\mu }{\mathbf{H}}_{\omega } ,$$

(3)

where microscopic magnetic permeability tensor $\hat{\mu }$ does not depend on spatial coordinates and possesses the following structure:

$$\hat{\mu } = \left( {\begin{array}{*{20}c} {\mu_{0} } & {i\mu_{\alpha } } & 0 \\ { - i\mu_{\alpha } } & {\mu_{0} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right)$$

(3a)

In the cavity modes similar to TE_01n of cylindrical cavity, vector H_ω is almost linearly polarized at sample location, and electromagnetic field in the sample may be represented as a sum of two circular polarizations described by complex μ_p and μ_m [13,14,15]:

$$\mu_{p1} - i\mu_{p2} = \mu_{0} + \mu_{\alpha } { ;}\quad \mu_{m1} - i\mu_{m2} = \mu_{0} - \mu_{\alpha }$$

(3b)

Assuming that frequency-dependent part of magnetization is small with respect to M₀, Eqs. (2), (3) lead to the following expressions:

$$\mu_{p1} = 1 + 4\pi \frac{{\gamma \cdot M_{0} [(1 + \alpha^{2} )\omega_{0} - \omega ]}}{{(\omega_{0} - \omega )^{2} + \alpha^{2} \omega_{0}^{2} }},\quad \mu_{p2} = 4\pi \frac{{\gamma \cdot M_{0} \alpha \omega }}{{(\omega_{0} - \omega )^{2} + \alpha^{2} \omega_{0}^{2} }},$$

(4a)

$$\mu_{p1} = 1 + 4\pi \frac{{\gamma \cdot M_{0} [(1 + \alpha^{2} )\omega_{0} + \omega ]}}{{(\omega_{0} + \omega )^{2} + \alpha^{2} \omega_{0}^{2} }},\quad \mu_{p2} = 4\pi \frac{{\gamma \cdot M_{0} \alpha \omega }}{{(\omega_{0} + \omega )^{2} + \alpha^{2} \omega_{0}^{2} }}.$$

(4b)

Here:

$$\omega_{0} = \gamma (H - 4\pi M_{0} )$$

(4c)

is the resonant frequency. Effective magnetic permeability in (1d) acquires the form:

$$\mu_{{\text{R}}}^{1/2} = \frac{1}{2}\{ [(\mu_{p1}^{2} + \mu_{p2}^{2} )^{1/2} + \mu_{p2} ]^{1/2} + [(\mu_{m1}^{2} + \mu_{m2}^{2} )^{1/2} + \mu_{m2} ]^{1/2} \} .$$

(5)

The Eqs. (1d) and (4), (5) may be used directly for the analysis of the ESR line shape in the cavity experiment with suggested experimental geometry when the sample is located outside the cavity. Moreover, it is possible to notice that it is possible to calibrate cavity absorption in units of magnetic permeability. Indeed, many strongly correlated metals possess temperature dependence of resistivity at low temperatures where Q₀(T) = const. As long as in zero magnetic field μ_R≡1 [Eq. (5)], formulae (1a) and (1d) suggest a scaling of the loaded cavity quality factor with sample resistivity 1/Q = C + Dρ^1/2 with temperature-independent coefficients C and D, which may be determined from the fitting of Q(T) by ρ(T) dependence. Additionally, Eq. (1d) suggests that at fixed temperature field dependence of the resistivity ρ(H) serves as a background on which magnetic resonance features caused by μ_R(ω, H) are formed. Thus, using field and temperature dependence of the sample resistivity, it is possible to find coefficient D in (1d) and, consequently, obtain μ_R(ω, H) in absolute units without using any reference sample for calibration of ESR spectrometer (see Fig. 3). More details about the data analysis procedure can be found elsewhere [11].

Fig. 3

a Comparison of microwave sample losses in the units of resistivity (curves 1, magnetic resonance) and dc magnetoresistance (curves 2, baseline) at various temperatures for EuB₆. b Field dependencies of the magnetic permeability in EuB₆ at various temperatures obtained from procedure of absolute calibration. For convenience, the curves are shifted consecutively along μ^1/2 axis with respect to the curve for 4.2 K by Δμ^1/2 = 1.1. All data are corrected to the demagnetization effect (from Ref. [11])

Implementation of special geometry of ESR cavity measurements together with absolute calibration of ESR spectra gives way to the fitting of the line shape by Eqs. (4), (5), which allows obtaining the full set of spectroscopic parameters: hyromagnetic ratio γ (g-factor), relaxation parameter α (line width W), and oscillating magnetization M₀ without any additional assumptions. This technique was first suggested in Ref. [11], and up to now, it was successfully applied to single crystals of metallic SCES like EuB₆ [11], CeB₆ [16, 17], MnSi [18, 19], and Mn_1−xFe_xSi [13, 20, 21]. Ideas of considered experimental method occurred to be fruitful for ESR investigation of topological Kondo insulator SmB₆ [22, 23]. At present, we do not see any limitation or disadvantage of using this approach to studying for strongly correlated systems by ESR.

It is worth noting that the modeling of the ESR line shape based on Eqs. (4), (5) can be extended to the case of inhomogeneous the distribution of the magnetic field in the sample located inside the cavity, where “false” splitting of the ESR line may be observed. As the first step, it is necessary to compute the distribution of the magnetic field inside the sample of real shape with real magnetic parameters obtained from static magnetic measurements (Fig. 4a). After that, it is possible to use Eqs. (4), (5) and to obtain ESR response by integration over sample volume. Example in Fig. 4b corresponds to a single magnetic oscillator with g-factor g ≈ 2 and one fitting parameter α. Simulated and experimental spectra demonstrate good coincidence thus providing independent confirmation of the validity of the proposed experimental and data analysis schemes. This type of simulation can be used for estimation of the optimal diaphragm diameter keeping inhomogeneous line broadening (and thus systematic error in fitting parameters) on a desired minimal level.

Fig. 4

Simulation of line shape in EuB₆ single crystal in the standard ESR experiment (sample located inside the cavity at the maximum of oscillating magnetic field). a Distribution of the resonant field inside the sample. b Experimental (solid line) and simulated (dashed line) spectra at 12 K. External magnetic field is located along [100] direction

Although quasi-classical model used for the description of ESR spectra works reasonably well, it is necessary to add some remarks. In standard cases, existing microscopic theories provide expressions for dynamic magnetic susceptibility (or equivalently magnetic permeability), which follow from the quantum mechanical consideration of transitions between energy levels of a magnetic ion split in a magnetic field by the Zeeman effect [1, 2]. To our best knowledge, the “quantum mechanical” dynamic susceptibilities for strongly correlated materials were computed in the case of Kondo-lattice type heavy-fermion metal [5] and one-dimensional (1D) quantum antiferromagnetic spin chain with S = 1/2 [24]. In this situation, one is forced to use quasi-classical model for data analysis if any quantitative results are desired. It is worth noting that consideration of susceptibilities confines us by the case of linear magnetic response, whereas Eq. (4) is derived by linearization of the equation of motion (2) and, consequently, M₀ ≅ M₀(B_res) in Eq. (4), where B_res is the field of magnetic resonance. Thus quasi-classical approach has an advantage for analysis of high-frequency ESR, for which non-linear M₀(B_res) dependence may not be neglected. At the same time, the use of high frequencies may be of crucial importance for the possibility of observation of ESR terminated by spin fluctuations in strongly correlated materials [3,4,5].

Equations (4), (5) give asymmetric line shape, which is often called a “dysonian” one. Apparently, the correct description of cavity absorption is not related to an arbitrary mixing of the real and imaginary parts of magnetic permeability, which is referred sometimes as an “empirical Dyson model”. Moreover, the approach described above is an alternative to classical “Dyson ESR line shape” theory developed by Feher and Kip [25]. In this ansatz, the asymmetric line shape in metals results from competition between spin relaxation time T₂ and spin diffusion time T_D in a skin layer [25], whereas in the considered quasi-classical model, spin diffusion effects are neglected and all magnetic moments (elementary magnetic dipoles) are treated as localized in space. At the same time, spin diffusion effects should become essential when itinerant electrons are contributed to ESR together with localized magnetic moments (LMM).

This problem was investigated in detail in the case of CeB₆, where the contribution from electrons to electron spin resonance cannot be excluded a priori [16]. First of all, it was shown that the assumption about the rapid diffusion (T_D < T₂) does not meet the experimental case. From fitting of the same ESR line by the dysonian line shape [25] and by the model of localized magnetic moments without spin diffusion, it was possible to find that Dyson model reproduces line shape equally well if characteristic times satisfy condition T_D/T₂ > 2 (see Fig. 5). At the same time an independent theoretical estimate of this ratio gives T_D/T₂ ~ 100, which corresponds to a very slow spin diffusion of heavy electrons [16]. Thus, it turned out that any magnetic moments in CeB₆, either electron or Ce³⁺, are “seen” by ESR as LMM having fixed position in space and the quasi-classical description of the ESR line shape [Eqs. (4), (5)] is applicable [16].

Fig. 5

Examples of the line shape modeling for the magnetic resonance in CeB₆. Points correspond to experiment; solid line is calculated in the framework of modification of the localized magnetic moments model. For T = 1.8, the fitting by Dyson model with T_D = 0.1T₂ is shown by dashed line (from Ref. [16])

It is possible to add that the considered approach to ESR line shape analysis may be also valid in the case, when the contribution of itinerant electrons may be merely neglected. Let us consider an ordinary metal, where concentration of itinerant electrons equals concentration of localized magnetic moments. If the field dependence of magnetization is far enough from saturation, the ratio of magnetizations for electrons M_e and LMM M_LMM is about M_e/M_LMM ~ k_BT/E_F ≪ 1 [26], where E_F denotes Fermi energy of electrons. This type of calculation may be extended to the case of strongly correlated metal. For example, the estimate M_e/M_LMM ~ 10^–3 is valid in the case of MnSi, where the magnetic moment is localized on Mn [18, 19], and for quantitative description of ESR in this material, it is sufficient to account for contribution of LMM only. This is well illustrated by Fig. 6, where static and oscillation magnetization for this material are compared. It is clearly visible that in MnSi, the condition M = M₀ holds within experimental accuracy.

Fig. 6

Static magnetization M (white circles), oscillating magnetization M₀ (black circles), and g-factor (triangles) in MnSi. For finding M₀, the procedure of absolute calibration of the cavity absorption was applied from Ref. [19]

From the above consideration, it is possible to conclude, that on one hand, “dysonian” line shape is not so sensitive to spin diffusion and Dyson model [25] gives the same result as LMM model when T_D ~ T₂. From the other hand, when the system of magnetic ion LMM is concentrated as in strongly correlated metals, its magnetic contribution exceeds the possible contribution of itinerant electrons, and thus, ESR will see behavior of LMM without direct accounting of spin diffusion rather than that of electrons with any spin diffusion rate. The latter statement does not mean that itinerant electrons (if any) do not contribute to the ESR picture at all. However, the itinerant electron effects should be discussed in terms of spectroscopic parameters obtained from the data analysis in the framework of LMM model. In this sense, situation may be different from a magnetic impurity in metallic matrix case [7], where impurity and itinerant electrons may have comparable contributions to dynamic magnetic properties. Although the strongly correlated metallic system with strong spin diffusion was not found so far, it is possible to recommend additional modeling of the ESR line shape by Dyson model, which may be useful at least for checking of applicability of the proposed approach.

As a final remark, we wish to point out that the ESR line shape in experimental SCES may be both asymmetric and broad. The ESR line shape in the model given by Eqs. (4), (5) depends on the interplay between various spectroscopic parameters and, if inhomogeneity effects are not excluded, on magnetic field inhomogeneity. For that reason, the application of a rule to a graph aimed at the direct finding of relaxation parameter from the “visible” line width and “direct” determination of the g-factor from the cavity absorption maximum may be misleading [11].

2.2 Further Development of the Experimental Method

The possibility of direct determination of oscillating magnetization in strongly correlated metals described in the previous sections is unique. The price, which should be paid for that, consists in complementary measurements of ESR together with magnetoresistance and static magnetization.

Recently, an additional method for experimental determination of M₀ was purposed [27]. In contrast to the absolute calibration approach developed in Refs. [11, 16] and described in the previous section, the considered technique is based on analysis of the ESR line shift in two different alignments with respect to external magnetic field of the sample loaded cylindrical cavity operating at TE_01n mode. As before, a special sample mounting geometry excluding edge effects and magnetic field inhomogeneity is applied. In the first case, the cavity is aligned in a standard way in superconducting solenoid, as showed in Figs. 1 and 2 i.e., external steady magnetic field is parallel to the cavity axis and is perpendicular to the sample surface. In the second case, the cavity in the solenoid is rotated by 90°, so that the external field is parallel to the sample surface and perpendicular to the cavity axis. The difference of the resonance field in these cases depends on oscillating magnetization M₀ and static magnetization M. When resonant microwave frequency is kept the same and demagnetization factors for both geometries are known, it is possible to show that the difference of the resonant fields allows computing oscillating magnetization without any procedure of the cavity absorption calibration [27]. This technique was checked for EuB₆, where M and M₀ are known to coincide [11], and for CeB₆, where M and M₀ are not equal [16]. For both materials, excellent coincidence of the results obtained by the aforementioned method and by the method of absolute calibration was reported [27].

It is necessary to point out that both methods of finding oscillating magnetization depend on the model for dynamic magnetic permeability. In practice, the “effect” of different analytical expressions obtained so far is not so strong. A detailed discussion of this problem may be found elsewhere [11].

3 Electron Spin Resonance in CeB₆ (‘Exception to Exceptions’)

The “modern history” of ESR studies of strongly correlated metals starts from observation of ESR in strongly correlated heavy-fermion material YbRh₂Si₂ [3]. In this material, an estimate of the spin fluctuations contribution to the line width W gives W ~ 37 T, although narrow ESR line was detected in this material with the help of X-band spectrometer at resonant field about 0.2 T [3]. This discrepancy stimulated an intense search for the physical mechanism, which might lead to narrowing of the ESR line width to observable values. According to the existing theories, resonant line broadening by spin fluctuations may be overcome by ferromagnetic (FM) correlations [5, 6]. On a qualitative level, this result is nothing but the second advent of well-known Korringa mechanism of spin relaxation [7], where ESR line width is inversely proportional to magnetic susceptibility W ~ 1/χ [6]. Indeed, FM correlations enhance χ and thus reduce W.

This clear physical picture was blurred by the discovery of magnetic resonance in cerium hexaboride CeB₆ [28]. This strongly correlated heavy-fermion metal possesses typical for various rare-earth hexaboride crystal structure (Fig. 7a) and is known to be driven by antiferromagnetic (AFM) interactions rather than ferromagnetic ones [29]. Additional difficulty arises from the complicated character of the magnetic phase diagram of CeB₆ (Fig. 7b), consisting of the high-temperature paramagnetic (P) phase and two low-temperature phases, the so-called antiferroquadrupole (AFQ) phase, where ordering of the Ce f-orbitals is expected, and complex antiferromagnetic (AF) phase [29]. It turned out that ESR in CeB₆ detected in AFQ phase was missing in P phase and, therefore, it was supposed that this phenomenon may be somehow caused by orbital ordering effects [28].

Fig. 7

Structure of rare-earth hexaborides (a); magnetic phase diagram of CeB₆ (b) and layout for CeB₆ measurements with rotating external magnetic field (c). In the panel b, the B–T domain where 60 GHz electron spin resonance may be observed is limited by dashed lines . The anisotropic phase boundary for the AF phase is shown for B||[110] direction. c Schematically displays the 4f orbitals of Ce³⁺ magnetic ions

3.1 Ferromagnetic Correlations vs. Antiferromagnetic Interactions in CeB₆.

However, subsequent ESR studies, which implied line shape analysis as described above, have revealed that resonance magnetic oscillations in CeB₆ are caused by oscillating magnetization M₀, which is less than total static sample magnetization M in the case, when external steady magnetic field is aligned along [110] direction [16]. In the paramagnetic phase, T > T_AFQ(B_res) temperature dependence of static magnetization follows AFM Curie–Weiss law:

$$M(T)\sim 1/(T - \theta ),$$

(6)

with paramagnetic temperature θ ≈ − 6 K (line 1a in Fig. 8). The initial experiment [16] and further study by a spectrometer with enhanced sensitivity [17] suggest that the temperature dependence of the oscillating part at the resonance field M₀(B_res, T) is different from M(B_res, T). Just below T_AFQM₀(B_res, T) exhibits clear FM behavior with θ ≈ 2.6–2.8 K (lines 2a and 3a in Fig. 8). Interesting that around T ~ 3 K temperature dependence of oscillating magnetization changes again. Best fit in the range T < 3 K presented in Fig. 8 by line 3b corresponds to Curie–Weiss law with small, but negative paramagnetic temperature θ ≈ − 0.6 K, thus suggesting FM–AFM crossover inside the orbitally ordered antiferroquadrupole phase (Fig. 8).

Fig. 8

Static and oscillating magnetization in CeB₆. 1—static magnetization temperature dependence at the field of magnetic resonance M; 2, 3—experimental data for oscillating magnetization M₀ from Refs. [16, 17], respectively. Lines 1a, 2a, 3a, and 3b are fits by Curie–Weiss law (see text for details). T_AFQ marks the transition from the paramagnetic phase to antiferroquadrupole phase in the resonant field B_res

It is worth noting that after the discovery of the FM component in CeB₆ in ESR experiment [16], this result was later confirmed in neutron scattering experiments [30, 31]. Moreover, the recent comparative study revealed an excellent agreement between the dispersion laws ω(B) for the main gapless resonant mode in the AFQ phase subtracted from the ESR measurements and the neutron scattering in magnetic field data [32]. This mode corresponding to the g-factor g ~ 1.6–1.7 may be traced up to ω/2π ~ 350 GHz for magnetic field aligned along [110] crystallographic direction [32, 33]. However, the situation with the high-frequency ESR experiments in CeB₆ is more complicated as long as for ω/2π > 200 GHz the second mode with the g-factor g ~ 1.2–1.3 is observed simultaneously with the main ESR mode [33].

Therefore, ESR in CeB₆ indicates non-trivial magnetization structure and existence of an oscillating ferromagnetic component in the AF system. On one hand, this observation is in agreement with the ESR mechanism in a strongly correlated system with strong spin fluctuations based on FM correlations [5, 6]. On the other hand, the combination of dynamic magnetic properties revealed by ESR method is very unusual and unexpected from the theoretical point of view [34, 35]. Unique physics of magnetic resonance in CeB₆ allowed calling it “exception to exceptions” [34, 35].

3.2 Magnetic Resonance Anisotropy in CeB₆

It turned out that situation with dynamic magnetic properties in CeB₆ is even more complicated [17]. Experiments with magnetic field aligned along with different crystallographic directions [17] clearly demonstrate selected character of [100] direction (Fig. 9a). For B||[001] ESR line broadens at least two times with respect to B|| [110] and B|| [111] cases, where W(T) almost coincides. Simultaneously, the direction [001] is characterized by strong temperature dependence of the g-factor in contrast to directions [110] and [111], for which g(T)≈const. The most striking behavior is observed in the case of oscillating magnetization M₀ (Fig. 9a). The inequality M₀/M < 1 holds at any temperature studied for B||[110] and B||[111] in agreement with [16]. It is amazing that for B||[001], the oscillating magnetization may exceed total static magnetization (M₀/M > 1, Fig. 9a). This finding is far from ordinary common sense expectations and, to the best of our knowledge, has never been reported in electron spin resonance studies.

Fig. 9

Temperature dependences of spectroscopic parameters for different crystallographic directions (a) and angular dependences of g-factor at different temperatures, reduced oscillating magnetization M₀ at T = 2.65 K and line width W at T = 1.8 K (b). Solid lines at the top of the panel b related represent g-factor theoretical fits (see text). Another lines in the a, b are guides to the eye. Inset shows correlation in polar coordinates between angular dependences of the magnetoresistance (B = 2.8 T ~ B_res) and line width at T = 1.8 K, which manifests electron nematic effect (from Ref. [17])

In addition, there is a difference in the character of temperature dependence of oscillating magnetization for B||[110] and alignments B|| [001] and B||[111]. For [110], the function M₀/M = f(T) is monotonous [16, 17]. In the cases B||[111] and B||[001], temperature dependence M₀/M = f(T) is different (Fig. 9a). In the vicinity of ~ 2.5 K, lowering temperature results in a decrease of M₀(T) and hence of the ratio M₀/M as long as the temperature dependence of the total static magnetization does not show any peculiarities in this temperature range. This quasi-antiferromagnetic behavior correlates with the discussed above FM-AFM crossover for B||[110] presented in Fig. 8.

In experiment with measuring the angular dependences of ESR parameters [17], the studied CeB₆ sample was oriented in a way allowing external field B to pass main crystallographic directions [001], [110] and [111] while sampling rotation (Fig. 7c). Hereafter, the angle θ is measured from the axis [001] (Fig. 7c). Angular dependence of the g-factor g(θ) obtained at temperatures 1.8 K (T < T*) and 2.65 K (T > T*) is weak and coincides except the region Δθ =  ± 30° around [001] direction (Fig. 9b). In this temperature-angle domain, lowering temperature results in noticeable growth of the g-factor up to ~ 13% (Fig. 9b).

The selected character of the [100] direction clearly develops in another ESR parameters. The normalized oscillating magnetization M₀/M₀([100]) = f(θ) jumps just around [100] for T = 2.65 K ~ T* and the line width W(θ) broadening is also related with this specific crystallographic direction (Fig. 9b, lower curves). Note that the magnitude of the M₀(θ) jump and W(θ) enhancement at θ = 0 (B||[100]) reasonably agrees with the data obtained in temperature measurements along different axes (Fig. 9a). Some discrepancies may be attributed to small misalignment of the sample in different ESR setups and the more complicated background in an experiment with the rotating cavity.

3.3 The g-Factor: Theory vs. Experiment

The comparison of the obtained g(θ) dependence with the theoretical predictions [34, 35] was carried out in Ref. [17]. In the orbital ordering model of the AFQ phase used in Refs. [34, 35] and widely accepted [28,29,30,31,32,33,34,35] since early work [29], the ground state of Ce³⁺ ion in CeB₆ is assumed to be Γ₈, which symmetry allows electric quadrupole and magnetic octupole moments [29]. In his theory, Schlottmann qualitatively explained the presence of FM correlations in AFQ phase and found the following expression for the Γ₈ state [34, 35]:

$$g(\theta ,\phi ) = \frac{{g_{ + } + g_{ - } }}{2},$$

(7)

where

$$g_{ \pm } = 2\left\{ {\cos^{2} (\theta )\left( {1 \pm \frac{4}{7}\cos (\phi )} \right)^{2} + \sin^{2} (\theta )\left[ {\left( {1 \mp \frac{2}{7}\cos (\phi )} \right)^{2} + \frac{12}{{49}}\sin^{2} (\phi )} \right]} \right\}^{1/2} .$$

(8)

Here, the angle φ is a free parameter of the model [34, 35], which fixes spatial orientation of the 4f orbitals in the AFQ phase [34, 35]. Equations (1) and (2) suggest that g(θ) should lie within the interval $\min \left\{ {g(\theta ,0),g(\theta ,\pi /2} \right\} \le g(\theta ) \le \max \left\{ {g(\theta ,0),g(\theta ,\pi /2} \right\}$; the corresponding functions g(θ, 0) and g(θ, π/2) are plotted in Fig. 9b.

It is remarkable that the theoretical prediction completely fails with the description of the g-factor magnitude. Indeed, the expected g-factor value is located in the limits 2–2.23, whereas experiment gives g ~ 1.4–1.75 (Fig. 9a, b). Moreover, as long as theoretical expressions [Eqs. (1), (2)] do not depend on temperature directly, the only way for introducing of the g-factor temperature dependence is an assumption concerning temperature dependence of the angle φ = φ(T). However, the strongest temperature variation occurs along [001] direction, for which Eqs. (1), (2) give g ≡ 2 independent of the φ value (Fig. 9b, upper curves). Therefore, the existing theory is unable to account for anomalous temperature dependence of the g-factor along [001] axis.

Later Schlottmann disputed this result [36]. He suggested an alternative data fit, which involved multiplication of Eq. (7) with some empirical factor presumably due to an interaction of Ce³⁺ LMM with itinerant electrons (a kind if Knight shift). Indeed, screening may change amplitude of oscillating elementary magnetic dipole μ* and thus somehow change the resonance conditions. Data in Fig. 8 extrapolated to T = 0 suggest that in CeB₆, the condition μ* ≈ μ_B should hold. The rough estimate μ* = gJμ_B, corresponding to experimental values of the g-factor (Fig. 9) gives μ* ≈  (2.1–2.5)μ_B for effective quantum number J = 3/2 describing Γ₈ quartet in contradiction with experiment. The reasonable values μ* ≈  (0.7–0.9)μ_B are reached for the case J = 1/2 exclusively. The latter quantum number is hardly possible in pure Γ₈ ground state. It is worth noting that the quantitative accounting of experimental data and theory [36] requires relatively high Knight shifts, leading to variation of the g-factor by ~ 20% [35, 36].

It is interesting that experimental g-factor values are located between g-factors for the Γ₈ and Γ₇ ground states for Ce³⁺ ion (Fig. 9b), as long as in the latter case g(Γ₇) ≈ 1.42 [2]. Therefore, assuming mixing of the quartet Γ₈ and doublet Γ₇ as a ground state and following calculations in Refs. [10, 11], it is possible to estimate the effective g-factor:

$$g_{{{\text{eff}}}} \approx x \cdot g(\Gamma_{8} ) + (1 - x) \cdot g(\Gamma_{7} ),$$

(9)

where g(Γ₈) is given by Eqs. (7), (8) and x represents the mixing parameter. Similar to Eq. (7), quantum transitions providing validity of Eq. (8) should be fast enough to make valid a description of ESR with an averaged g-factor. Surprisingly, this naïve relation allows well describing the experimental data magnitude and angular dependence assuming x = 0.3 and φ = π/3 except the anomalous region around [100] (see solid line Γ₇ + Γ₈ in Fig. 9b). The equivalent description of experimental data was suggested in Ref. [17], but the interpretation of the data based on the mixing of Γ₇ and Γ₈ was not considered.

Although Eq. (9) looks too simple to be correct, the weighted sum of the g-factors may be due to a combination of different quantum states and equations of this type are known in the ESR theory [37]. Actually, the same type of equations is used to obtain g-factor in Refs. [34, 36]. If the Eq. (9) is valid and mixing occurs, there should be another ESR line with the g-factor corresponding to different x values. Indeed, two resonances were observed simultaneously in Ref. [33] in the high-frequency range (Fig. 10). Apparently, in the case of the resonance B, it is necessary to assume x ≈ 0 in Eq. (9), because experimental values are somewhat less than the theoretical value for the Γ₇ state. This discrepancy may be attributed to the screening effect suggested by Schlottmann, and the observed difference allows estimating of the correction factor as ~ 0.91. Thus, screening by itinerant electrons reduces g-factor of Γ₇ state in CeB₆ by ~ 9%. Assuming the same reduction factor for the Γ₈ state, it is possible to refine mixing parameter x, which should be ~ 0.5 rather than 0.3.

Fig. 10

The g-factors for two magnetic resonances observed in reflection experiment [33]. Expected g-factors for the mixture of Γ₈ and Γ₇ states and for pure Γ₇ state are shown by dashed lines

This type of analysis of the g-factor values in CeB₆ meets several criticisms. The first and the strongest argument is that symmetry forbids mixing of the Γ₈ and Γ₇ states. However, there are some results, which demonstrate experimentally the lowering symmetry in several dodeca- and hexaborides at temperatures below 100 K [38,39,40,41,42]. If it is also relevant to the case of CeB₆ and lattice distortions similar to those observed in Refs. [38,39,40,41,42] occur the unit cell, the lattice will be no longer cubic in the strict sense. For that reason, the Γ₇ and Γ₈ states may be no longer exact and mixing may be no longer excluded based on symmetry consideration. Thus, the findings [38,39,40,41,42], in principle, can open the way for a complicated ground state in some hexaborides including CeB₆. In addition, orbital ordering at T_AFQ induces a doubling of the lattice period even in zero magnetic field [43] and corresponding lattice distortions at the magnetic transition into AFQ phase are highly probable. Unfortunately at a moment, the structure of CeB₆ was not examined with accuracy comparable with that in Refs. [38,39,40,41,42] and the considered opportunity remains possible but hypothetical.

Schlottmann has suggested an alternative explanation of second resonance in CeB₆, which should be absent in his original model. As long as this resonance was observed at frequencies above 200 GHz (Fig. 10, mode B), he supposes a threshold nature of this extra mode of magnetic oscillations, resulting from a decay of the AFQ phase due to absorption of the quantum of electromagnetic radiation with the energy high enough to destroy collective AFQ phase [35]. However, the idea concerning decay of the AFQ phase is not confirmed by any additional experiments. Moreover, the “threshold” 200 GHz is nothing, but the cut-off frequency of quasi-optical setup used in experiments reported in Ref. [33]. As long as line B typically is more weak than line A in Fig. 10, there is no surprise that it was not observed at lower frequencies without any ad hoc assumptions.

The problem with the [001] direction in the theory [34, 35] was explained in Ref. [36] as a result of AFM anisotropic correlations, which are not taken into account in the considered theory. These correlations may enhance g-factor via changing of the Knight shift. Nevertheless, the question why AFM correlations should be located along [001], although data in Fig. 8 suggest onset of AFM correlations below ~ 3 K for [110] direction as well, remains open. It is worth noting that the g-factor for [110] remains temperature-independent (Fig. 9a) even in the presence of AFM correlations.

To summarize, the situation with an explanation of the g-factor anisotropy in CeB₆ remains controversial and adequate theory in spite of all efforts [34,35,36] seems to be missing. Therefore, it is interesting to revisit the problem of the ground state in CeB₆, which will be done at the end of this section.

3.4 Spin Fluctuations, Line Width, and Oscillating Magnetization

According to [3,4,5,6] ESR line width is the measure of spin fluctuations. The bigger the magnitude of spin fluctuations, the more broad ESR line is observed and vice versa. Typically, AFM correlations lead to broadening of the ESR line, whereas FM correlations lead to narrowing [36]. As it is pointed out in Sect. 3.1, there is a remarkable correlation between angular dependence of the line width and oscillating magnetization (Fig. 9b). Together with the anomalous temperature dependences of the oscillating magnetization and line width for B||[001], this fact means that the same physical mechanism simultaneously contributes in a correlated way to line width and oscillating magnetization. Considering this effect formally, when oscillating magnetization is computed by integration of the resonant magnetoabsorption curve (an analogue to common computation integrated intensity of the ESR line width), it is possible to conclude that variation of the line width provides either noticeable or decisive contribution to the observed dependences of M₀(T, θ). This circumstance is non-trivial, as long as according to the standard method of statistical physics, energy levels of a system must be absolutely sharp when statistical sum and magnetization are calculated [44].

The considered problem in most cases is ignored in ESR studies, where line width is understood as a result of Zeeman level broadening [1] and could not be resolved in semi-classical approach, where relaxation term in the Landau–Lifshitz equation is introduced “by hands”. To our best knowledge, the only case, where a similar situation in a strongly interacting system was resolved correctly, is the Oshikawa–Affleck theory of ESR in S = 1/2 AF quantum spin chain [24]. In this approach, the ESR line shape is represented as an envelope of the infinite set of ESR frequencies corresponding to the anisotropic terms in Hamiltonian, which breaks symmetry of initial problem. In this situation, there is no surprise that the parameters describing ESR line shape are correlated, which was established for the line width and g-factor [45].

When the line shape appears as a kind of distribution function of the magnetic oscillators, the correlation between line width, g-factor, and oscillating magnetization makes no surprise, and in this sense, the data for CeB₆ (Fig. 9) can be explained naturally. However, this step immediately brings us to the necessity of refining “spin fluctuations” contribution to ESR line width [3,4,5,6]. Indeed, ESR line shape may be attributed to either specific interactions in magnetic systems like in Oshikawa–Affleck theory without introducing any fluctuations at all, or to some specific distribution of spin fluctuation rate inside the ESR line contour. Namely, in the latter case, we need to assume that the more spin fluctuations appear in a particular frequency range, the fewer oscillators contribute to ESR line. Consequently, at the center of the ESR line, the spin fluctuations must have less intensity than in the wings. We will return to discussion of the considered dilemma in the next section.

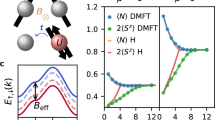
Now, let us discuss the possible reasons for the excess of the oscillating magnetization M₀ with respect to the total static magnetization M in B||[001] direction, where condition M₀ > M, which contradicts to the common sense may hold (Fig. 9a). In a line of discussion in this section, it is possible to suppose that this anomaly results from the use of semi-classical approach to ESR line shape out of the limits of its applicability. However, it is unclear why experimentally observed line shape may be well described in this model. The second possibility is considered in Ref. [17], where the difference in static and dynamic magnetic properties is attributed to a specific term in dynamic magnetic susceptibility expected in Abrahams–Wölfle model and describing interaction between LMM and itinerant electrons. The third option appears in the spin polaron model, considered in Ref. [16]. Here, spin polaron is a quasi-bound state of itinerant electron in the vicinity of Ce³⁺ magnetic ion. If LMM and bound electron spins are parallel, the oscillating magnetization may be enhanced and the magnitude of oscillating magnetic dipole will be higher resulting in increase of the g-factor. Simultaneously, the spin fluctuation rate must be anisotropic, and for B||[001] direction the living time (or the time of coherence) of magnetic oscillators must reach a maximum. To make this model working for an explanation of the M₀ > M inequality, it is necessary to assume that the ESR frequency in experiment [17] is higher than the inversed time of living of the spin polaron state. This model qualitatively explains the origin of spin fluctuations by the transition of an electron between a bound state in spin polaron and itinerant state in the Fermi sea. It is worth noting that FM interactions inside spin polaron do not exclude AF interaction between spin polarons in agreement with the data in Fig. 8. Moreover, the change of magnetic interactions (Fig. 8) may be explained by redistribution of the electron density between itinerant and quasi-bound states. Experimentum crucius for spin polaron model should be an examination of the oscillating magnetization at low frequencies, which, unfortunately, is not done so far.

3.5 Electron Nematic Effect and Spin Fluctuation Transitions in CeB₆

Investigating of spatial anisotropy that is generated spontaneously in the translationally invariant metallic phase, i.e., electron nematic or spin nematic effect, has addressed a great challenge for both experimentalists and theoreticians [46,47,48,49]. Numerous experimental objects like ultra clean quantum Hall systems, ruthenates, high-T_c superconductors [1], and iron-based superconductors [47,48,49] demonstrate unexpected anisotropy in their electronic properties, forbidden by high symmetry of the studied systems. As pointed out in Ref. [46], it looks amazing how point-like electrons demonstrate properties similar to those of liquid crystals, where rod-shaped molecules act as basic blocks to form a nematic phase [50]. Up to now, several theoretical mechanisms were proposed to explain electron nematic effect including Pomeranchuk instability of Fermi liquid or melting of a stripe phase [46, 47, 49]. Another intriguing option for the realization of an electron nematic phase is provided by the crystal with orbital ordering, as long as both orbitally ordered states and electron nematic phases may be considered as systems with broken spatial symmetry [46, 49]. In the quantum spin systems, nematic phases correspond to the case when the spin-rotational symmetry is broken, but no magnetic order is formed [51]. This specific situation is predicted to occur in the phase with quadrupolar order, where the spin fluctuation magnitude varies along different crystallographic directions [51], so that anisotropic spin fluctuations “mimic” molecules in the liquid crystal nematic phase.

Thus, nematic phases in strongly correlated materials bring to consideration new type of magnetic transition, which may be labeled as spin fluctuation transition (SFT). The difference with ordinary magnetic transition is schematically illustrated in Fig. 11. For simplicity, spins are represented by 2D set of magnetic arrows. In the paramagnetic phase, both averaged spin projections <S_x> and <S_y> satisfy conditions <S_x>  =  <S_y>  = 0, and thus, an average spin at each site is zero. Simultaneously, in paramagnetic phase, spin fluctuations are isotropic <S_x²>  =  <S_y²>  ≠ 0. This means that in paramagnetic phase, magnetic arrows are disordered and their directions fluctuate uniformly at each site. When ordinary magnetic transition occurs, some spin projection becomes non-zero (<S_y>  ≠ 0 and <S_x>  = 0 in Fig. 11) and magnetic structure is formed (for example, an FM structure in Fig. 11). In this case, spin fluctuations may be either isotropic or anisotropic, but, in most cases, should freeze at T = 0 forming an ordered ground state altered by zero quantum oscillations. However, a different scenario is possible. For SFT, the condition <S_x>  =  <S_y>  = 0 holds in any phase, but the condition <S_x²>  =  <S_y²> breaks at the transition point and in the spin fluctuating phase <S_x²>  ≠  <S_y²> , so that arrows start to fluctuate in an anisotropic manner rather than uniformly (Fig. 11). Thus a spin nematic transition is a kind of spin fluctuation transition, but, in general case, we will define SFT as any transition at which character of spin fluctuations changes. This approach will be illustrated below for several experimental systems, including CeB₆. It is necessary to add that SFT may correspond to the change of thermodynamical characteristics of a magnetic system as in the case of an ordinary magnetic transition [51].

Fig. 11

Magnetic transitions and spin fluctuation transitions (see text for details)

As we have already mentioned, CeB₆ is the system, where quadrupolar ordering is expected in AFQ phase due to Γ₈ ground state [29], and thus, spin nematic phase may be found in the AFQ phase. However, as stressing in Ref. [51], observations of nematic effects in the quadrupolar or orbital phases are challenging, because they behave as antiferromagnets in thermodynamic studies [51]. The breakthrough in this problem was achieved in the recent studies of CeB₆ [17, 52]. First of all, a perfect correlation between angular dependences of ESR line width and magnetoresistance at B_res was established [17] (see plot in polar coordinates in Fig. 9b; the geometry for both experiments is shown in Fig. 7c). Comparison with the same temperature T = 1.8 K of the magnetoresistance Δρ(B, θ) = ρ(B, θ) − ρ(B = 0) in the field B ~ 2.8 T corresponding to ESR region on the magnetic phase diagram and ESR line width W(θ) shows that normalized to the value for [100] direction magnetoresistance Δρ_n = Δρ(B, θ)/Δρ(B, 0) and line width W_n = W(θ)/W(0) are linked in a simple way 1 − Δρ_n = a(1 − W_n), where a is numerical coefficient a ~ 0.1 [17]. As long as characteristics of magnetic scattering of itinerant electrons (magnetoresistance) and spin rotation (line width) are linked, the only way to obtain consistent picture is to suppose that both effects are driven by spin fluctuations. In view of discussion in Sect. 3.4, it is necessary to admit that this observation favors spin fluctuation-based approach [3,4,5] rather than Oshikawa–Affleck type behavior.

Anisotropic spin fluctuations are a clear sign of possibility of nematic behavior [51]. The detailed investigation carried out in Ref. [52] has completely confirmed the presence of electron nematic effect in AFQ phase of CeB₆. Nematic transition in CeB₆ develops when the magnetic field exceeds some characteristic value ~ 0.3–0.5 T and occurs exactly at the temperature corresponding to the transition between PM and AFQ phases [52]. This finding completely meets theoretical expectations. However, it is not CeB₆, if no “exception” is observed. New transition inside the AFQ phase, which may be associated with the change of the symmetry of magnetic scattering on spin fluctuations, was discovered [52]. At some characteristic temperature T₀(B) < T_AFQ(B), the symmetry of spin fluctuations, scattering on which control magnetoresistance in CeB₆, changes around T₀(B) (see, e.g., data in Fig. 2c), so that the ρ(B, T, θ) pattern rotates at 45°. As long as no magnetic order develops at latter transition, this finding suggests that CeB₆ undergoes two subsequent SFT, where the first one occurs at AFQ-PM phase boundary, whereas the second is not associated with known phase boundaries at the magnetic phase diagram (Fig. 7b). Thus, although CeB₆ really demonstrate behavior expected for solid-state analogues of livid crystals, this liquid crystal appears to be very unusual.

3.6 Magnetic Phase Diagram and the Ground State Problem

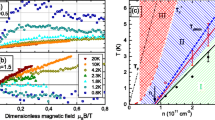
It is instructive to put experimental data for spin fluctuation (nematic) transition [52] and position of the FM–AFM crossover, which follows from our analysis of the oscillating magnetization (Fig. 8), on the standard magnetic phase diagram of CeB₆ (Fig. 12). The SFT, at which symmetry of spin fluctuation changes, demonstrates a remarkable correlation with the crossover region. Moreover, an additional phase boundary in low magnetic fields related to SFT was also found in Ref. [52]. Earlier, some transition in the same region of the magnetic phase diagram was reported in Ref. [53] based on the analysis of field dependence of magnetic susceptibility (line C in Fig. 12).

Fig. 12

Magnetic phase diagram of CeB₆. Lines are subtracted from magnetoresistance data, white circles denotes phase transitions revealed from microwave impedance measurements [6, 7]. Stars mark position of the PM-AFQ boundary, which follows from electron nematic effect study [52]. Investigation of the electron nematic effect suggests new lines inside AFQ phase: T₀(B) corresponding to second SFT transition and transition in low magnetic fields B₀ ≈ const [52]. Vertical dashed lines border FM-AFM crossover area obtained from the data in Fig. 8. Magnetic transition in the low field region observed in Ref. [53] is marked as line C

In view of our analysis based on a complementary set of experimental data, it is no longer possible to ignore the fact that the antiferroquadrupole phase of CeB₆ is not homogeneous and several extra transitions occur inside this region of the magnetic phase diagram (Fig. 12). This is not possible for pure Γ₈ ground state, and therefore, it is necessary to consider this problem in more detail.

There is no doubt that 4f ¹ state of C³⁺ must be splitted to Γ₇ doublet and Γ₈ quartet, if cubic symmetry of the lattice holds [2, 29]. However, symmetry analysis does not tell anything either about distance between these levels or their relative positions. In the early studies, when no orbital physics was involved, the specific heat experimental data “unambiguously” witnessed [54] that the ground state is Γ₇. At that time, the value of Γ₇–Γ₈ splitting was unknown, but it was believed that the energy distance is high enough to exclude influence of Γ₈ state on low-temperature properties of CeB₆ (Fig. 13a).

Fig. 13

Various models for crystal field splitting of Ce³⁺ magnetic ion energy levels in CeB₆ (see text for details)

When orbital ordering in CeB₆ was established and AFQ model appeared on the agenda [55] the Γ₇ was no longer considered as a ground state. Indeed, orbital effects and phase with the quadrupolar order are possible for the Γ₈ rather than for the Γ₇ state. Therefore, there is no surprise that understanding of specific heat data was gradually changed to clear evidence of the Γ₈ ground state (instead of Γ₇ ground state) on demand of developing CeB₆ orbital physics [56].

Historically, the next model for Ce³⁺ state in CeB₆ was developed by Hanzawa and Kasuya [57]. They suggested the levels schema shown in Fig. 13b, where Γ₇ and Γ₈ states are very close, energy splitting is about 10 K and, moreover, the Γ₇ doublet is the lowest in energy (Fig. 13b). This approach allowed accounting orbital ordering effects in the framework of AFQ ansatz. We wish to emphasize that this model is still the only model, which predicts transitions at the magnetic phase diagram at low fields similar to that shown in Fig. 12. In addition, some measurements of specific heat favor the considered energy schema consisting of close Γ₇ and Γ₈ states [58].

The diagram of 4f ¹ state of C³⁺ splitting, which is nowadays widely accepted and treated as a standard one, appeared as a result of important work [59]. In this study, the inelastic neutron scattering allowed determining splitting of some levels as 46 meV (530 K) in CeB₆ matrix. However, these data do not tell anything either about relative positions of Γ₇ and Γ₈ levels, or, strictly speaking, about origin of the transition itself. The latter issue was resolved based on the Raman scattering data [59]. The observed transition was interpreted as just the transition between Γ₇ and Γ₈ levels, because analysis of the Raman data demonstrated the presence of some (but not all) symmetry elements expected for Γ₇–Γ₈ transition [59]. At this point, the correct labeling of the lowest in energy level is not yet possible. An argument, favoring the Γ₈ ground state was deduced from the temperature dependence of a Raman mode located in the diapason 370–380 cm⁻¹ [59]. Namely, this mode demonstrated energy shift, which was interpreted as a splitting of the Γ₈ quartet into two doublets Γ_8.1 and Γ_8.2 separated by ~ 2.6 meV (30 K) [59]. Authors of [59] pointed out that such splitting is unlikely for the Γ₇, so that the split Γ₈ is the ground state. As a result, we are coming to the schema Fig. 13c, which is considered a hundred percent correct and was never revised since its establishment.

The conclusions made in Ref. [59] and their influence on CeB₆ physics deserve some critical comment. First of all, the declared splitting of the Γ₈ was never observed directly up to now. As we see, this unobserved splitting is a cornerstone of the whole construction, as shown in Fig. 13c. Second, the theoretical analysis influence of the Γ₈ structure on the AFQ phase is almost missing, and the majority of studies take simple Γ₈ state for granted [29,30,31,32,33,34,35,36]. And finally, pure Γ₈ state is unable explaining ESR data as we have demonstrated above. If, for a second, one will forget the “consistent” state of the art in CeB₆ studies and will be asked about the most reliable schema for the ground state in view of ESR solely, the answer will be the Hanzawa–Kasuya schema (Fig. 13b). In our opinion, it is hardly possible without assuming the presence of an interaction between Γ₇ and Γ₈ states, which is possible in the studied temperature range when corresponding levels are close. We wish to add that the model [57] allows describing orbitally ordered phase of CeB₆ as an AFQ phase and, thus, does not exclude nematic effects.

This supposition also leaves open questions. If the ground state is a kind of Γ₇ + Γ₈, what is located at 46 meV above? What is the driving force for the mixing mechanism, desired for an explanation of the ESR data? Is it possible to explain Raman scattering data [59] by transitions from the complex Γ₇ +  Γ₈ state to some other excited state? Unfortunately, there are no answers at a moment. Moreover, these answers have no sense if the results of ESR experiments are ignored. But if not, it is worth revisiting the question of Ce³⁺ ground state in CeB₆ on the basis of recent probing of low-energy excitations in this exciting strongly correlated metal by advanced electron spin resonance technique.

4 Topological Kondo Insulator SmB₆ and Electron Spin Resonance

Development of the topological Kondo insulator (TKI) concept [60, 61] has marked a watershed between “old” and “new” physics of mixed-valence compound samarium hexaboride, SmB₆. Now, this area of research is characterized by a flood of publications, mainly focused on specific SmB₆ transport properties, which are presumably due to topologically protected surface characterized by Dirac spectrum of electrons [62,63,64,65,66,67]. For example, these TKI surface states are responsible for the famous resistivity plateau [62, 63], zeroing of the thermopower [68, 69], and may be detected in spectroscopic experiments as some level in the correlation gap [70, 71]. Although TKI approach seems to be widely accepted and demonstrates good potential for consistent interpretation of a variety of low-temperature properties, some recent publications argue that SmB₆ is nothing but trivial surface conductor [72].

Classical old physics of SmB₆ was considering the problem of intragap states as a bulk phenomenon, which may be treated in the either Kondo insulator [73] or in the exciton–polaron model [74]. Several approaches [75,76,77] were suggested to explain the homogeneous mixed-valence state characterized by temperature-dependent ratio of Sm²⁺/Sm³⁺ ions from X-ray absorption spectroscopy data [78, 79]. The valence fluctuating state approach is based on the assumption that charge state of each Sm ion continuously changes between 2 + and 3 + due to quantum transitions involving band electrons. Based on Refs. [80, 81], it is commonly assumed that fluctuation time (i.e., time of living of Sm³⁺ or Sm²⁺ state) is about τ ~ 10^–13 s. It is essential that such fluctuations are expected to persist up to the lowest temperatures constituting a homogeneous fluctuating valence ground state. As long as Sm³⁺ ion is magnetic (S = 1/2) and Sm²⁺ ion is non-magnetic (S = 0), the τ parameter will simultaneously define the spin fluctuation time. Since the charge and spin fluctuation process occur at each Sm site, the effective magnetic moment of the Sm ion μ* will rapidly fluctuate between μ* = 0 and μ* and, therefore, this physical quantity is not well defined.

The fluctuating ground state model was criticized in Ref. [77]. According to [77], the X-ray photoemission data [78, 79] and Mössbauer spectroscopy experiments [82] may be explained in a different uniform way, assuming the formation of a quasi-molecular complex constructed of two Sm³⁺ ions binding one electron corresponding to average valence ν = 2.5 in rough agreement with experimental data [78]. This hypothetical construction must have well-defined effective magnetic moment. The departures from the fixed value ν = 2.5 observed in experiment [78] may be ascribed to some fluctuations of the considered type of ground state, although such effects were not discussed in original paper [77].

Below, we will show how electron spin resonance shed more light on controversial issues in SmB₆ physics, including TKI problem. We wish to emphasize that in most cases, the magnetism of SmB₆ is studied for the samples specially doped with magnetic impurities. Here, we consider the case of pure undoped single crystals of SmB₆.

4.1 Absorption of Microwave Radiation: Bulk vs. Surface

Before starting the discussion of ESR experimental results, it is instructive to analyze peculiarities of microwave radiation absorption in a sample, where surface layer conductivity and bulk conductivity are different. Let us consider SmB₆ sample with finite thickness d. The incident electromagnetic wave is absorbed in the surface layers of the sample having thickness a, as well as in the sample bulk (Fig. 14a). To compute the relative parts P_s and P_b for the power absorbed at the surface and in the bulk, respectively (we assume P_s + P_b = 1), it is necessary to separate bulk and surface conductivity contributing to DC resistivity temperature dependence ρ(T). To estimate, we assume that bulk conductivity in the plateau region follows the law ρ_b(T) ~ exp(E_a/k_BT) denoted by red dashed line in Fig. 14b. For simplicity, we consider temperature-independent conductivity of the surface layer ρ_s(T) = const (the same supposition is often made in the literature [63]). The ρ_s value (black dashed line in Fig. 14b) is found by fitting of experimental data by equation ρ(T) = 1/[1/ρ_s + 1/ρ_b(T)] (the so-called parallel resistor model [63]).

Fig. 14

Absorption of microwave radiation in TKI SmB₆. General schema for calculation of the microwave power P_s absorbed at the surface layers of thickness a and microwave power P_b absorbed in the bulk of a sample having thickness d (a). Temperature dependence of resistivity for SmB₆ sample in the low-temperature region and calculated temperature dependences of P_s(T), P_b(T) and the ratio P_s/P_b (b). Dashed lines in the panel b denote extrapolations for the bulk and surface resistivity in the parallel resistors model (see text for details). Experimental data are taken from [22]

In the calculation, we assume that surface layer depth, a, is small with respect to the sample thickness, d. Indeed, in the topological Kondo insulator model [60, 61], the parameter a is about size of the unit cell. As long as d >>  a, it is possible to consider SmB₆ sample as δ-layer with the conductivity σ_s at the surface covering volume with the conductivity σ_b. For the studied geometry (Fig. 14a), the problem becomes essentially one-dimensional. In the case of semi-infinite sample (d → ∞), the ratio of the microwave power absorbed in the front δ-layer, P_s, to the microwave power absorbed in the sample bulk, P_b, may be derived from a straightforward calculation, which yields P_s/P_b = σ_sa/σ_bδ, where δ_b is the skin depth in the sample volume. The bulk conductivity σ_b(T) = 1/ρ_b(T) can be directly obtained from experimental data, whereas determination of σ_s from ρ_s is not so simple. In the parallel resistor model used for modeling of the ρ(T) temperature dependence, the σ_s must be enhanced with respect to 1/ρ_s by the factor l_eff/a, where macroscopic length l_eff is comparable with the sample sizes and depends on the measurement method. For the standard four-probe schema applied for the sample having the shape of a rectangular parallelepiped, the effective length is the ratio of the sample cross-section square and cross-section perimeter. The final result acquires the form P_s/P_b = ρ_bl_eff/ρ_sδ_b, and the ratio P_s/P_b does not depend on the thickness of the surface layer if the parameters ρ_b and ρ_s, following from experimental resistivity data, ρ_b and ρ_s, are introduced and a ≪ l_eff, δ_b.

The finite sample thickness reduces the magnitude of the power absorbed in the sample bulk by $1 - \exp ( - 2d/\delta_{{\text{b}}} )$. At the same time, in the considered case, the surface at the opposite edge of the sample will contribute to surface absorption as well, which will enhance P_s by $1 + \exp ( - 2d/\delta_{{\text{b}}} )$. This gives:

$$\frac{{P_{{\text{s}}} }}{{P_{{\text{b}}} }} = \frac{{l_{{{\text{eff}}}} }}{{\delta_{{\text{b}}} \tanh (d/\delta_{{\text{b}}} )}}$$

(10)

For an estimate, we have used expression $\delta_{{\text{b}}} = c\sqrt {\rho_{{\text{b}}} /2\pi \omega }$, which, in the plateau region, can be re-written in the form $\delta_{{\text{b}}} = \delta_{0} \cdot f(T)$, where $\delta_{0} = c\sqrt {\rho_{{\text{s}}} /2\pi \omega }$ and $f(T) = \exp [E_{{\text{a}}} (1/T - 1/T_{0} )/2k_{{\text{b}}} ]$. The temperature T₀ denotes the crossing point of asymptotics ρ_s = const and ρ_b ~ exp(E_a/k_BT) (Fig. 14b). Thus, Eq. (10) depends on two dimensionless parameters l_eff/δ₀ and d/δ₀ and resistivity activation energy E_a.

Results of calculation of temperature dependences P_s(T), P_b(T), and P_s/P_b(T) for SmB₆ samples studied in Ref. [22] are shown in Fig. 14b. It is visible that P_s(T) and P_b(T) are equal at T ~ 6 K and lowering of temperature results in the strong enhancement of the surface absorption with respect to the bulk. Namely, for T < 4 K, almost all microwave power is absorbed inside the surface layer. Indeed, the higher the conductivity, the stronger is absorption, and, for that reason, surface effects will dominate at low temperatures.

4.2 Cavity Experiments and ESR

Our consideration suggests that in the case of SmB₆, it is prospective to use recommended above experimental layout, where the sample is located outside the cavity and closes a small hole at the cavity bottom. In contrast to the thick metallic sample, in the studied case, the microwave radiation will leak through a thin surface layer and bulk of the sample. The schema of 60 GHz cavity experiments for probing of [110] surface of SmB₆ used in Ref. [22] is presented in Fig. 15a. In this work, two types of preparation of [110] surface were tested. The first surface was prepared by mechanical polishing (S1) and the second (S2) was obtained by chemical etching of the S1 surface [22]. In zero magnetic field, cavity losses were used to compute microwave resistivity, which may be compared with the DC resistivity [22]. The result is shown in Fig. 15b. It is much unexpected that microwave resistivity demonstrates low-temperature behavior different from that known from DC measurements. The low-temperature microwave resistivity exhibits behavior typical for a metal resistivity decreases with lowering temperature), rather than typically supposed ρ_s(T) = const.

Fig. 15

Experimental layout for microwave cavity measurements of SmB₆ (a) and comparison of microwave (MW) and DC resistivity in the low-temperature region (b) for different surface treatment (from Ref. [22])

The observed discrepancy is a result of dominating microwave power absorption just at the sample surface as it follows from the estimate obtained in the previous section and has two consequences. First of all, it is clear that microwave measurements provide a model-free direct method of probing TKI surface. Second, as long as conductivity in the plateau region is higher than expected in the parallel resistor model applied in Sect. 4.1, the temperature diapason, where surface absorption of microwave radiation dominates, will be enhanced from above.

The ESR spectra from undoped SmB₆ samples were first reported in Ref. [83] for two fixed temperatures 4.2 K and 1.8 K. The detected signal consisted of two close lines and, although the conditions of experiment corresponded to the surface magnetoabsorption, was interpreted as a bulk effect [83]. In this work, the ESR was attributed to some intrinsic defects stabilizing magnetic Sm³⁺ ions [83]. The next step in ESR probing of the SmB₆ surface was done more than 20 years after with the help of advanced equipment developed for studying of the strongly correlated metals [22]. Experimental geometry corresponded to Fig. 15a.

The spectra observed in Ref. [22] are formed by several lines, which include the ESR modes (doublet A, B accompanied by satellites A₁, B₁) and extra line C. The amplitudes of these resonances increase with lowering of temperature, whereas the resonant fields remain constant within experimental accuracy. The position of the main doublet A, B agrees reasonably with the data for two main ESR lines reported previously in Ref. [83]. The investigation of the surface treatment effect on the spectra showed that ESR part of the whole magnetoabsorption signal is almost insensitive to the surface preparation. In contrast, line C magnitude is different for S1 and S2 surfaces [22]. Analysis carried in Ref. [22] indicates that this mode may correspond to cyclotron resonance of surface carriers observed in ESR geometry as a consequence of a coupling between the spin and charge degrees of freedom in topological insulators [84]. Below, we will consider ESR in TKI SmB₆ in more detail.

The ESR absorption in SmB₆ may be well approximated by a sum of four Lorentzian lines (Fig. 16b). This procedure allows finding g-factors, integrated intensities, and line widths for any spectral component [22, 23]. The observed g-factors are very close to 2: g(A₁) = 1.944 ± 0.001, g(A) = 1.926 ± 0.001, g(B) = 1.920 ± 0.001, g(B₁) = 1.911 ± 0.001 and temperature-independent [22]. The most unusual behavior was discovered for integrated intensity [22]. All the lines are not observed at temperatures above 5.5 K (Fig. 16a). Moreover, the integrated intensity for any ESR line can be fitted by a critical behavior [22]:

$$I\left( T \right)\,\sim \,(T^{*} {-}T)^{\nu } ,$$

(11)

with characteristic temperature T* = 5.34 ± 0.05 K and exponent ν = 0.38 ± 0.03 (Fig. 16c). It is worth noting that the temperature T* correlates well with the onset of the surface conductivity. It is shown in Ref. [22] that law (11) is not affected by the effects of redistribution of the absorbed microwave power between sample surface and bulk states. Therefore, the critical behavior of the integrated ESR intensity results from the temperature dependence of the spin susceptibility of paramagnetic centers located at the sample surface and responsible for ESR in SmB₆. This means that these paramagnetic centers do not exist in the range T > T* and emerge in the sample below T* due to some abrupt magnetic transition. These paramagnetic centers do not only exist at the sample surface, but are also robust with respect to surface treatment. Therefore, in view of topologically protected nature of SmB₆ surface, they have intrinsic origin rather than extrinsic [22].

Fig. 16

Magnetic resonance probing of [110] surface of SmB₆ in the state S1 (from [22]). Resonant magnetoabsorption spectra at different temperatures (a), structure and deconvolution of the ESR signal into components (b), and temperature dependences of integrated intensity for different ESR spectral components and total ESR signal (c). In the a, b, the ESR spectrum is formed by four lines A₁, A, B, B₁. The line C in the panel a presumably corresponds to a cyclotron resonance at the sample surface [22]. Absorption scale in the a, b is designed in a way to resemble cavity signal. For that reason, the spectra after subtraction of the base line (b) became formally negative

ESR line width W(T) may be used for estimation of spin relaxation time from relation:

$$\tau (T) = \frac{\hbar }{{\mu^{*} W}} = \frac{\hbar }{{g\mu_{B} J \cdot W(T)}}$$

(12)

Here, J is the quantum number of the ESR centrum and we assume that the effective magnetic moment is given by the standard equation $\mu^{*} = g\mu_{{\text{B}}} J$. As long as in SmB₆, g-factors are known [22], the ESR data allow finding the product $\tau (T)J$. According to [23], in this material, we may expect values J = 5/2 (free Sm³⁺ ion), J = 3/2 (Γ₈ quartet ground state of Sm³⁺ in SmB₆ matrix [85]) and J = 1/2 (some paramagnetic center or Γ₈ state splits into two doublets like in CeB₆). The corresponding estimates are shown in Fig. 17, and the values τ ~ 4 × 10^–9–10^–7 s for spin relaxation may be expected [23].

Fig. 17

Summary of charge and spin relaxation times in SmB₆. Intervals limited by dashed lines correspond to results reported in Refs. [81, 82, 86]. Points denote spin relaxation time for various J obtained in Ref. [23]

Comparison with the charge fluctuation times (which must be equal spin relaxation times [23, 80, 81]) obtained either in the classical works ~ 10^–12–3 × 10^–14 s [80, 81], or with the values (1.6–3) × 10^–14 s following from more recent studies [86], shows that spin relaxation times for paramagnetic centers responsible for ESR is 4–7 orders higher than those reported in the literature [80, 81, 86]. Thus, ESR-active centers in SmB₆ possess an anomalous spin relaxation. It is worth noting that characteristic time ~ 10^–13 s will correspond to line width of 10³ T, which cannot be detected in ESR experiments.

4.3 New Model of SmB₆ Magnetism Based on ESR Data

The observed critical behavior of integrated intensity [Eq. (11)] excludes an explanation of ESR based on some “defects” or chemical impurities, as long as these types of paramagnetic centers exist at any temperature in the sample and unable emerge at some critical temperature [22, 23]. Considering the nature of the magnetic resonance in SmB₆, it is necessary to take into account that it is pure surface phenomenon, and paramagnetic centers responsible for ESR are located at the surface layer [22, 23]. The study of static magnetic properties [87] shows that localized magnetic moments are also located at the sample surface, and total magnetization consists of two terms: magnetization of LMM and Pauli paramagnetism of surface electrons [87]. At the same time, the sample bulk is magnetically silent. This physical picture is in perfect agreement with the Kondo breakdown concept [88], which allows adequately describing the magnetic properties of a topological Kondo insulator like SmB₆ [23, 87].

The first candidate for paramagnetic center could be Sm³⁺ magnetic ion having for some reason enhanced spin relaxation time ~ 10^–8 s rather than 10^–13 s. According to [87], concentration of paramagnetic centers is low and for T = 2.5 K does not exceed 4.5 × 10^–5 of the total concentration of Sm ions. Nevertheless, the paradigm of an isolated Sm³⁺ ion with strongly enhanced spin relaxation time is insufficient for the accounting of experimental data [23]. Both ESR and static magnetization measurements show that LMM, responsible for magnetic resonance and magnetization, does not exist at temperatures T > T* = 5.5 K and appears below this characteristic temperature [22, 87]. Integrated intensity is proportional to spin susceptibility I(T) ~ χ(T) and, as long as in this case g(T) = const and hence μ*(T) = const, the number of these LMM will exhibit critical behavior N(T) ~ (T* − T)^ν [23], which is unlikely for an isolated Sm³⁺ ion.

Hint for elucidation the nature of LMM in SmB₆ may be obtained in the data suggesting anomalously high value of the effective magnetic moment describing field dependence of magnetization in SmB₆M(B, T) ~ φ(μ*B/k_BT) [87, 89]. Here, B denotes magnetic field and function φ(x) satisfies conditions φ(x → 0) ~ x and φ(x → ∞) → 1. In practical, data analysis φ(x) is substituted by Brillouin function B_J, although the exact form of φ(x) is unknown for strongly correlated materials [87, 89]. In the case of paramagnetic centers in SmB₆, the following estimates of effective magnetic moments were obtained: μ* ~ 14μ_B (J = 5/2), μ* ~ 12μ_B (J = 3/2) μ* ~ 7μ_B (J = 1/2) [87]. These values noticeably exceed those expected for an isolated single-ion μ* = gJμ_B (~ 5μ_B, ~ 3μ_B, and ~ μ_B for J = 5/2, J = 3/2, and J = 1/2, respectively).

The considered set of unusual dynamic and static magnetic properties may be a consequence of formation of the many-body spin polaron state [87, 89] driven by AFM interaction. According to [89], this spin polaron may be treated as a ferrimagnetic cluster containing n₁ electrons with the magnetic moments μ₁ and n₂ LMM with the magnetic moments μ₂. The “sublattices” in this ferrimagnet are formed by LMM and electrons, respectively, and it is assumed that μ₁ ≠ μ₂. Magnetic interactions in clusters result in parallel alignment on the sublattice magnetization and local magnetic field vectors for any external magnetic field [89]. This leads to a canted configuration of the sublattices magnetization, and it is supposed that the sum of the sublattices magnetizations always has non-zero projection on the direction of the magnetic field only [89]. The number of LMM and electrons in the cluster is controlled by thermodynamic stability condition, which reduces to μ₁²n₁ = μ₂²n₂, and it is possible to show that such spin cluster behaves as a paramagnetic center with enhanced (with respect to elementary magnetic moments in each sublattice) effective magnetic moment μ* in the field dependence of magnetization. Simultaneously, the dynamic properties of this cluster correspond to rotation at a single frequency with g-factor g = 2 [89].

In the considered model, the value of μ* is given by [89]:

$${\mu}^* = \frac{{{\mu _ + }}}{{\cos \theta - \sqrt {{{({\mu _ + }/{\mu _ - })}^2} - {{\sin }^2}\theta } }} = \frac{{{\mu _ + }}}{{\cos \theta - \sqrt {{{({n_ - }/{n _ + })}} - {{\sin }^2}\theta } }},$$

(13)

where indexes + and − denote two sublattices, which have positive and negative projections of magnetization on external magnetic field direction, respectively. The angle θ in Eq. (13) is the angle between the external magnetic field and magnetization of the sublattice with positive projection. It is visible that if $\mu_{ - } = \mu_{ + } + \Delta \mu$ and $\left| {\Delta \mu } \right| < < \mu_{ + } ,\mu_{ - }$ the Eq. (13) reduces to $\mu^{*} \approx \mu_{ + }^{2} \cos \theta /\Delta \mu$ and paramagnetic response of spin cluster (μ* > 0) is possible when Δμ > 0, and hence, sublattice with the biggest magnetic moments is aligned antiparallel to the external field and contains fewer members due to aforementioned stability condition. For strong enhancement of μ*, it is necessary to have small Δμ or, equivalently, $n_{ + } \approx n_{ - }$ ($n_{ + } < n_{ - }$).

The calculation of μ*(θ) based on spin polaron model [89] was done in Ref. [23] for different numbers of electrons and LMMs in spin cluster, assuming μ₁ = μ_B (Fig. 18a). The requirement of a paramagnetic response (μ* > 0) suggests $n_{ + } = n_{1} = n_{{\text{e}}}$ and $n_{ - } = n_{2} = n_{{{\text{Sm}}^{{{3} + }} }}$; simultaneously, maximization of the effective magnetic moment gives $n_{{\text{e}}} = n_{{{\text{Sm}}^{{{3} + }} }} + 1$. Hereafter, $n_{{\text{e}}}$, $n_{{{\text{Sm}}^{{{3} + }} }}$ denote number of electrons and Sm³⁺ ions in a spin polaron state. The above suppositions also give an estimate of the effective magnetic moment for Sm³⁺, which is about Bohr magneton, and slightly exceeds μ_B for $n_{{\text{e}}} = n_{{{\text{Sm}}^{{{3} + }} }} + 1$ (inset in Fig. 18a). According to [23], the realistic values of μ* matching experimental results [87] may correspond to the numbers comparable with the number of Sm³⁺ in an isolated unit cell (Fig. 18a). An example of spin configuration for $n_{{{\text{Sm}}^{{{3} + }} }} = 8$ and $n_{{\text{e}}} = 9$ is presented in Fig. 18b.

Fig. 18

Spin polaron model predictions for SmB₆ paramagnetic centers: the effective magnetic moment (a) and an example of spin configuration (b). Inset in the panel a shows expected magnetic moment for Sm³⁺ in SmB₆ (from the Ref. [23])

The considered estimate leads to the possible qualitative explanation of the low-temperature magnetic transition with emerging high μ* and anomalous spin relaxation rate. Spin cluster (spin polaron) shown in Fig. 18b may be constructed of $n_{{{\text{Sm}}^{{{3} + }} }}$ Kondo singlets which are binding one excessive electron. These spin states may survive at the sample surface as rare occasions, although the majority of the Kondo singlet states are destroyed in accordance with the Kondo breakdown model [88]. Apparently, the forming of a spin polaron requires several Sm³⁺ ions being closely located to each other. In a regime of mixed valence of τ ≤ 10^–8 s, this may result in freezing of such state if the temperature is low enough and less than the energy of formation of such spin state. Thus, the transition temperature T* may be attributed to the formation of spin polarons, and the spatial fluctuations scenario explains why the concentration of these magnetic centers is so low [22, 87]. The formation of spin polarons requires gain in energy below T*, which may occur due to excessive electron localization. Once spin polaron is formed, it will behave as a paramagnetic center with enhanced μ* in static magnetization field dependence and will cause magnetic oscillation mode close to g-factor g = 2. The many-body nature of the spin polaron state suggests that electron transitions times may be strongly renormalized [23] and therefore, spin relaxation times in an ESR experiment may be different from ordinary charge fluctuation times [80, 81, 86]. In addition, the surface of SmB₆ is enriched by Sm³⁺ states with respect to the sample volume [79], which should favor the applicability of the spin polaron model.

We see that analysis of ESR and static magnetization data leads to a new concept of magnetism of SmB₆. The set of anomalous properties may be attributed to the formation of specific paramagnetic centers—spin polarons driven by antiferromagnetic interaction. As an early prognostic of these states, it is possible to consider the Ref. [77], where many-body stable states of several bound Sm³⁺ ions were first considered. Although spin polaron model may explain most of available to date experimental data, it is too simple to explain the presence of several lines in ESR spectra, and, thus, requires additional clarification. In conclusion to this section, it is possible to add that magnetic centers may lift topological protection of a topological insulator surface due to breaking of time-reversal symmetry. Therefore, ESR data may change the view of the possibility of TKI state realization in SmB₆ at low temperatures.

5 ESR Probing of Quantum Critical Phenomena

By definition, quantum phase transitions are transitions which occur at T = 0. Transition point at the axis of the controlling parameter (which may be pressure, concentration, or magnetic field) is called quantum critical point (QCP) [90]. Quantum critical (QC) behavior may be found in different systems, but hereafter we will confine ourselves by various magnets. From experimental point of view, the presence of a QCP can be detected by anomalies of the physical properties, namely resistivity or magnetic susceptibility, which develops at finite temperatures [90]. An important scenario is a disorder-driven quantum criticality. Theoretically, in the case of the QC regime induced by disorder, the ground state is represented by the Griffiths phase consisting of spin clusters characterized by different values of the exchange integral J [91,92,93]. The magnetic susceptibility in the Griffiths phase at low temperatures obeys power law χ ~ 1/T^ξ (ξ < 1) different from the convenient Curie–Weiss dependence. This law is a consequence of the power distribution function of exchange energy and reflects low-temperature correlations in spin system [91,92,93].

Disorder-driven QC behavior was probed by ESR in various spin chain systems and low-dimensional magnets (see, for example, [94,95,96,97,98,99,100,101,102]). However, in the majority of cases, the ESR was used to monitor spin susceptibility in a QC Griffiths phase, i.e., magnetic resonance methods served technically, as a special “magnetometer”, and thus brought not so much new physics of quantum criticality itself. In addition, the mentioned case is the case of dielectric materials rather than metals. At the same time, just in metals, the proximity to FM quantum critical point and related FM fluctuations are driving the ESR physical picture [3,4,5], and hence, the problem of the relation between quantum criticality and electron spin resonance in strongly correlated metals is on the agenda. As it will be shown below, the considerable progress in studying of QC phenomena by ESR technique was achieved by the investigation of metallic system Mn_1−xFe_xSi.

5.1 Itinerant vs. LMM Picture in MnSi

In Sect. 1, we have already mentioned the case of manganese monosilicide, MnSi. This material was traditionally treated as an archetypical itinerant magnet [103] and, in the old time, Moriya theory served as a basis for the interpretation of ESR in MnSi [104]. However, the application of the line shape analysis schema described above allowed concluding that ESR “sees” oscillating magnetization as a set of localized magnetic moments [18, 19]. In addition, the analysis of the g-factor temperature dependence showed that the idea of a spin density more or less uniformly distributed in the unit cell as requested in Moriya theory is inconsistent with experiment [18]. Moreover, the LDA calculations evidence that spin density in MnSi is localized on Mn ions and Mn effective magnetic moment is about 1.2μ_B [105].

Nevertheless, the straightforward application of the Heisenberg model to the case of MnSi is not possible. Indeed, an effective magnetic moment μ* describing field dependence of magnetization in MnSi M(B, T) = M_sφ(μ*B/k_BT) equals μ* = (5.3–11.6)μ_B depending on the choice of model form for φ(x), whereas saturated magnetization is M_s ~ 0.3μ_B per Mn ion [89]. This discrepancy is believed to be typical just for itinerant magnets, and the qualitative level is explained as a result of spin fluctuations in the case of distributed spin density [103]. The solution to the problem was got in the framework of spin polaron model [18, 19, 89]. This model was briefly described in Sect. 4.3; more details can be found elsewhere [89]. It is essential that spin polaron approach allows describing simultaneously high values of μ* and low magnitude of M_s in quantitative agreement with experiment and predicts magnetic oscillations at a frequency corresponding to g ≈ 2 [89]. For the purpose of the present work, it is sufficient to consider spin polaron as a kind of LMM formed in the vicinity of Mn ion, which has time of living controlled by electron transitions between quasi-bound spin polaron states and continuum band states [18, 19, 89]. These transitions form a mechanism of spin fluctuations alternative to that in Ref. [103]. However, we wish to emphasize that it not possible to underestimate a heuristic significance of Moriya work, which, although neglects spatial correlations between LMM and band electrons, unambiguously shows the importance of itinerant component in magnetic properties of strongly correlated metals.

5.2 Magnetic Phase Diagram of Mn_1−xFe_xSi Solid Solution

The spin polaron concept allowed explaining important characteristics of B–T magnetic phase diagram of MnSi [19] and was successfully generalized to the case of MnSi–FeSi solid solutions, where iron substitutes manganese [106]. In Mn_1−xFe_xSi magnetic moment of spin polaron nature is localized on manganese site, whereas iron acts as non-magnetic diluting agent. In view of above consideration, it is natural to expect that spin fluctuations will take an essential effect on the magnetic phase diagram of this system.

The cubic B20 type structure of Mn_1−xFe_xSi is shown in Fig. 19a. Lattice constant for MnSi equals a = 4.56 Å and in the diapason x < 0.3, where magnetic resonance could be observed, weakly depend on iron concentration. Due to the absence of an inversion center, symmetry of crystal lattice allows Dzyaloshinskii–Moriya (DM) interaction. Assuming the localized nature of magnetic moments on Mn sites, it is possible to use simple model Hamiltonian for the description of magnetic structure:

$$\hat{H} = \hat{H}_{{{\text{ex}}}} + \hat{H}_{{{\text{DM}}}} = - J\sum {\vec{S}_{i} } \cdot \vec{S}_{j} + \vec{D}\sum {\vec{S}_{i} } \times \vec{S}_{j} .$$

(14)

Fig. 19

Crystal structure (a) and the formation of spiral magnetic structure due to a combination of ferromagnetic exchange and Dzyaloshinskii–Moriya interaction (b) in Mn_1−xFe_xSi

The first term in Eq. (14) is standard scalar product of spin variables describing ferromagnetic exchange, whereas the second term given by the vector product corresponds to DM interaction. As a result of the combined action of two different interactions, instead of parallel alignment of spins, magnetic structure acquires spiral form (Fig. 19b). The helix period depends on exchange integral J and DM constant $D = \left| {\vec{D}} \right|$ and equals L ~ aJ/D in the case J >  > D. This simple model surprisingly well describes the magnetic structure of Mn_1−xFe_xSi depicted from neutron scattering experiments [107, 108]. It is established that in zero magnetic field, spirals directions are degenerate and aligned along spatial diagonals in B20 cubic lattice [107]. In finite magnetic field, spirals are oriented along field direction [107,108,109]. In MnSi, helix period equals 180 Å and substitution of manganese by iron results in a noticeable reduction of this parameter up to ~ 100 Å for x = 0.1 [109]. Apparently, the considered description of the magnetic structure is oversimplified and completely neglects itinerant component and spin polaron states. On the other hand, the spin polaron model developed in Ref. [89] does not account effects spiral structure as long as the expected size of spin polaron is about unit cell and much less than the magnetic helix period. In our opinion, development of an adequate theory correctly describing magnetic structure in the presence of interaction between band electrons and Mn LMM appears as a prospective future task in this field of research.

Magnetic T − x phase diagram for Mn_1−xFe_xSi in the region of weak magnetic field where M ~ B was established in Ref. [110] on the basis of magnetic measurements and small-angle neutron scattering (SANS) data. The transition temperature T_c(x) into spiral phase with long-range magnetic order (LRO) is found to decrease linearly from T_c(0) = 29 K with iron concentration and quantum critical point x* ~ 0.11 for which T_c(x*) = 0 (Fig. 20a, b).

Fig. 20

T–x magnetic phase diagram of Mn_1−xFe_xSi for low magnetic fields: experiment (a), theoretical description (b), and a map of the exponent α(T, x) (c). Panel d represents the magnetic phase diagram of Mn_1−xFe_xSi in the resonant field B_res ~ 2.2 T together with a sequence of quantum phase transitions at B ≈  0. Labeling by letters corresponds to various phases, including spiral phase with long-range magnetic order (LRO), phase with short-range magnetic order (SRO), paramagnetic phase (PM), Griffiths phase (GP), and spin-polarized phase (SP). In the b, c, the regions where classical and quantum fluctuations dominate are marked as CF and QF, respectively. Quantum critical points corresponding to suppression of LRO and SRO are indicated as x* and x_c. In the c, digits denote:: 1—T_c(x), 2—T_s(x), 3—T_eq(x), 4—x = x*. From the works [20, 21, 110]

An interesting feature of the considered phase diagram is the presence of some extra phase with a boundary T_s(x), covering LRO phase (Fig. 20a, b). Some theories describe this phase as a magnetic phase with short-range magnetic order (SRO) [111, 112] or a chiral spin liquid phase [111]. This approach was criticized in Ref. [113], where SRO phase was described as a region of spin fluctuations with specific anisotropy. Experimentally in SRO phase, SANS maps [108] much resemble diffraction patterns observed in liquid crystals’ nematic phases [50]. Quantitative theoretical description of T_s(x) phase boundary is based on idea of freezing of two types of co-existing magnetic fluctuations: classical critical (CF) and quantum critical (QF), which are characterized by radii R_cl ~ 1/(T − T_c)^β and R_qc ~ 1/T, respectively [90, 110]. This idea predicts change of regime of spin fluctuations at some line in the paramagnetic phase T_eq(x), which position is fixed when LRO and SRO boundaries are defined from an experiment (Fig. 20b).

In MnSi and Mn_1−xFe_xSi, resistivity is sensitive to magnetic scattering [19, 114] and, therefore, depends on the character of spin fluctuations. At low temperatures, the resistivity in considered system may be described as ρ(T, x) = ρ₀ + A⋅T^α and residual resistivity ρ₀ may be found by extrapolation in the limit T → 0. Therefore, fine details of magnetic scattering may be revealed by considering effective exponent α(T, x) = ln(ρ − ρ₀)/A(T_s, x)ln T, which excludes the effects of ρ₀ variation caused by uncontrollable defects and impurities. The map α(T, x) obtained in Ref. [21] is shown in Fig. 20c. The growth of the exponent α(T, x) in the paramagnetic phase (PM) develops just between lines T_eq(x) and x = x*, where regime of spin fluctuations should change [110].

As long as the line T_eq(x) is a direct consequence of a presence of QCP at x*, experimental data at finite are in agreement (or proves) transition from LRO phase to some other magnetic phase at T = 0. In view of discussion in Sect. 3.5 either transition CF–QF at T_eq(x), or transition into SRO phase at T_s(x), are just kinds of spin fluctuation transitions. Thus SRO phase can be not be only described as a spin liquid phase [111, 114], but possesses a specific regime of magnetic fluctuations [113] typical to spin nematic phase. In this sense, various approaches available in the literature [108, 110,111,112,113,114] elucidate different aspects of magnetic phases with the partial order and spin fluctuation transitions.

Another non-trivial aspect of T − x magnetic phase diagram of Mn_1−xFe_xSi is the onset of a Griffits phase (GP) for x > x_c ~ 0.24 characterized by power law of magnetic susceptibility χ ~ 1/T^ξ with ξ ~ 0.5–0.6 [110]. Simultaneously T_s(x) decreases with x and, hence, the second QCP is expected at x_c for which T_s(x_c) = 0 (Fig. 20a, b). Continue an analogy proposed in Ref. [111]; it is possible to say that at x_c a “liquid” change into a “fog”, where droplets are correlated spin clusters forming Griffiths phase. Thus, the QCP at x_c is likely associated with the change of the system topology. This interpretation was used in the model [110] and allowed a quantitative description of the whole Mn_1−xFe_xSi diagram with the help of one fitting parameter (Fig. 20b). Some anomalies of spin fluctuations presumably associated with the presence of QCP at x_c may be also noticed on α(T, x) map (Fig. 20c).

To summarize, experimental data for Mn_1−xFe_xSi and their theoretical analysis suggest a quantum bicriticality phenomenon, i.e., presence of two QC points x* and x_c corresponding to suppression of the long-range and short-range magnetic orders, respectively. The QCP at x* is closed from the finite temperatures by SRO phase and, thus, may be classified as hidden QCP point [90, 110, 112]. The study of the Hall effect in Mn_1−xFe_xSi revealed the importance of frustration, which, together with the effects of disorder induced by substitution of Mn by Fe, result in the observed form of the magnetic phase diagram including positions of QC points. More details about frustration in Mn_1−xFe_xSi system may be found elsewhere [115].

5.3 ESR Probing of Quantum Critical Phenomena in Mn_1−xFe_xSi

The ESR in strongly correlated metals is a good probe for the investigation of spin fluctuations as it was already demonstrated in the case of CeB₆ (Sect. 3). Therefore, it is reasonable to find access to QC phenomena by ESR technique, as long as the magnetic phase diagram is driven by spin fluctuations (Sect. 5.2). However, the complicated magnetic phase diagram took at resonant field (B_res ~ 2.2 T at 60 GHz) became noticeably different from that considered above [20]. Both LRO and SRO phases are partly substituted at B_res by the so-called spin-polarized (SP) phase (Fig. 20d). In this phase, the itinerant and localized magnetic moments inside each spin polaron acquire parallel alignment keeping total ferrimagnetic configuration [19, 89]. On simplified Heisenberg language of effective LMM system, the SP phase is an analogue of FM phase [19].

In principle, the observed change of the T − x puts into question quantum bicritical scenario based on the sequence of phase transitions LRO → SRO → GP at T = 0 (Fig. 20d). The QC point at x* ~ 0.11, if it still exists, is now hidden inside the SP phase. The phase boundary of SP phase T_SP(x) is changed with respect to T_s(x) in the region x* < x < x_c (Fig. 20a–d), so that position of the second QCP may be altered. Therefore, the possible relation between quantum criticality and ESR in Mn_1−xFe_xSi may be quite complicated.

Examples of ESR spectra after the procedure of absolute calibration in units of effective magnetic permeability μ for the samples with different iron concentration are shown in Fig. 21a. In all cases, μ(B = 0) = 1 and data in these figures are shifted for clarity. Additionally, a scale factor is applied to each μ(B) curve in Fig. 21a. In general case, magnetic resonance can be observed in both paramagnetic and spin-polarized phases and is missing in the Griffiths phase. In that sense, the physical picture of ESR in Mn_1−xFe_xSi is different from that in QC spin chain systems [94,95,96,97,98,99,100,101,102], where ESR is observed in both PM and Griffiths phases.

Fig. 21

ESR spectra for Mn_1−xFe_xSi samples with various x at T = 4.2 K (a). The corresponding scale factors are shown at the right of each curve. Points correspond to the experiment and the lines denote results of model approximation. Magnetic field is parallel to [110] crystallographic direction for all samples studied. Temperature dependences of the line width (b) and scaling behavior (c) in Mn_1−xFe_xSi. Line 1 in panel c is the fitting by the scaling function, the lines 2 and 3 corresponds to the approximation in the NFL model (see text for details). The inset shows concentration dependence of the g-factor (from [20])

It is found that both increase in temperature and x results in broadening of the ESR line and simultaneous decrease of its amplitude [20]. Experimental data (points in Fig. 21a) can be well fitted in the model of oscillating LMM (lines in Fig. 21a). For all samples studied, the oscillating magnetization was within experimental error equal to total static magnetization [20] as in the case of MnSi (Fig. 6).

Except the case x = 0 (pure MnSi) in studied crystals, the g-factor is not dependent on temperature. The increase of iron concentration results in a decrease of the g(x) by ~ 5% in the diapason 0 < x < x* followed by a kink at characteristic concentration x* (inset in Fig. 21b). Further enhancement of x leads to a gradual increase of the g-factor up to the limiting concentration x_c (inset in Fig. 21b). The data obtained in Ref. [20] on the ESR line width are summarized in the main panel Fig. 21b. It is remarkable that the observed W(x, T) variation in Mn_1−xFe_xSi may reach at least the order of magnitude (Fig. 4a), and hence, the strongest effect of iron doping consists in influence on the ESR line width and spin relaxation [20].

As it is shown in Ref. [20], the W(x, T) data can be reduced to the universal scaling dependence W(x, T)/W(T_SP) = f(T − T_SP) for the majority of compositions, (Fig. 21c). The value W(T_SP) was determined either by interpolation or extrapolation of the experimental W(T) dependence either to the T_SP(x) ≠ 0 point, or to T_SP = 0 for 0.19 ≤ x ≤ 0.24 (see Fig. 20d). It follows from Fig. 21c that the universal behavior holds for all iron concentrations, except those corresponding to the QC points x* ~ 0.11 and x_c ~ 0.24. The scaling function f(z) acquires a relatively simple form f(z < 0)≈1 and f (z > 0)≈1 + a₀z², where the coefficient a₀ equals 6.5 × 10^–3 K⁻² (solid line 1 in Fig. 21c).

The discovered in Ref. [20] scaling behavior constitutes anomaly in the spin relaxation of Mn_1−xFe_xSi. Indeed, the classical explanation of the line widths observed in the ESR of magnetic ions in metals is based on Korringa mechanism [7], which means that temperature-dependent part of the line width ΔW(T)should be proportional to inversed spin susceptibility, ΔW(T) ~ 1/χ(T). Assuming the validity of Curie–Weiss law in Mn_1−xFe_xSi, it is natural to expect the dependence ΔW(T) ~ 1/χ(T) ~ (T − T_SP), whereas experiment gives ΔW(T) ~ (T − T_SP)² (Fig. 21c).

In addition to the violation of Korringa relaxation mechanism, there is another anomaly of ESR line width, namely the departures from the universal behavior exactly at characteristic concentrations x* ~ 0.11 and x_c ~ 0.24 (Fig. 21c), which are supposed to correspond to quantum phase transitions. This observation suggests that spin relaxation along the lines x = x* and x = x_c is different from the rest of the T − x magnetic phase diagram and related W(T) dependence appears more weak [20]. The considered anomaly may be qualitatively explained by the theory of the ESR in strongly correlated metals developed by Wölfle and Abrahams [116]. According to [116] in the Fermi-liquid (FL) regime ΔW(T) ~ T², whereas in the non-Fermi-liquid (NFL) regime ΔW(T) ~ T, and hence, the considered anomaly in Mn_1−xFe_xSi may be explained by the onset of non-Fermi-liquid regime in the proximity of the quantum critical points. Taking the temperature-dependent contribution to the line width in the form obtained in Ref. [116], it is possible to come to the model expression [20]:

$$W\left( T \right)\, = \,A \cdot T \cdot {\text{atan}}\left( {T/T_{x} } \right)\, + \,W_{0} ,$$

(15)

where T_x denotes an energy scale for a crossover between FL (T <  < T_x) and NFL (T >  > T_x) regimes. The above equation provides reasonable approximation for the experimental W(T) curves for the samples with x = 0.11 and x = 0.24 assuming T_x ~ 11 K (x = x*, line 2 in Fig. 21b, c) and T_x ~ 0 (x = x_c, line 3 in Fig. 21b, c). In agreement with the magnetic phase diagram (Fig. 1), it is possible to conclude that in both cases, T_x is about transition temperature T_SP.

Thus, the probing of Mn_1−xFe_xSi solid solutions by ESR technique showed [20] that spin relaxation in this system is very unusual and involves two different mechanisms, one of which is responsible for the violation of Korringa-type relaxation and gives the universal scaling behavior. Another mechanism is likely connected with the NFL effects [116] and develops at QC points having positions x* ~ 0.11 and x_c ~ 0.24 determined for B≈0, although the ESR is measured at relatively high magnetic field. These data support the real existence of the hidden QC point x*. Although this QC point is located inside the spin-polarized phase, it gives rise to specific spin relaxation even in the paramagnetic phase. We wish to emphasize that in ESR studies, the anomalies related to QC points are more pronounced than in the case of resistivity (Fig. 20c).

At the end of this section, we would like to comment about a statement in the literature claiming that underlying QC point in Mn_1−xFe_xSi cannot produce observable anomalies at finite temperatures [117]. The examples, presented in this part of the review, unambiguously evidence that this difficulty may be overcome using ESR technique, which is the right tool for “visualization” of quantum critical points, including the hidden ones, on the magnetic phase diagram.

6 Some Latest Developments of ESR in Strongly Correlated Metals

In this section, we will consider some recent experiments, which may be considered as growth points for a better understanding of the ESR problem in strongly correlated metals.

6.1 Single Ion Physics vs. Concentrated Case (Ho_xLu_1−xB₁₂)

High-frequency (60 GHz) ESR in the paramagnetic phase of the rare-earth (RE) dodecaboride Ho_xLu_1−xB₁₂ was recently reported in Ref. [118]. The structure of RB₁₂ is fcc cubic formed by rare earth element R and octahedral clusters B₁₂ (Fig. 22a). In addition, the RE ion can be considered as surrounded by boron cage constructed of 24 atoms (Fig. 22b). This results in reduced coupling of the RE ion inside boron carcass and the appearance of a double-well potential, in which this ion moves (Fig. 22c). In turn, lowering temperature induces random freezing of RE ions in allowed equilibrium positions. For that reason, a disordered glassy state (DGS) is formed below some characteristic temperature T*, which in Ho_xLu_1−xB₁₂ is about 60 K [118].

Fig. 22

RB₁₂ crystal structure (a), part of RB₁₂ structure formed by two truncated cuboctahedrons centered on rare earth ion (b) and schema of double-well potential for Ho³⁺ ions (from [118])

Experiments carried out in the range 0.1 < x < 1 showed that ESR in this strongly correlated metal may be observed just in DGS and magnetic resonance is caused by Ho³⁺ magnetic ions [118]. The g-factor strongly depends on Ho concentration and varies from g = 5.6 (x = 0.1) to g = 4.5 (x = 1). A characteristic feature of the research carried out in Ref. [118] consists in the comparison of the experimental line shape with that simulated in a single-ion approximation, which, to our best knowledge, is the first attempt of this kind. Modeling of the spectra was carried out by Ho³⁺ ions in a cubic crystal field with parameters following from inelastic neutron scattering data [118]. The schema of energy levels is formed from 4f¹⁰ configuration for Ho³⁺ and corresponds to Γ₅ triplet ground state and the closest excited state is located in 84 К higher in energy [118]. Both hyperfine splitting of ESR lines, and random deformations in DGS state were taken into account. As long as in double-well potential dimers, Ho–Ho may be formed, the effects of coupling between Ho³⁺ ions were considered including dipole–dipole and exchange magnetic interactions.

It is instructive to compare calculations in the single-ion model and experimental data in the most diluted case x = 0.1. The results are summarized in Fig. 23. As long as the fine structure of the ESR line is not observed in the ESR experiment, the line shape was simulated as an envelope of hyperfine lines broadened by 3.7 × 10^–3 T [118]. Interestingly, that the considered approximation allows a correct description of the ESR line position and gives asymmetric line in qualitative agreement with experiment.

Fig. 23

Measured ESR absorption spectra (solid lines) of the Ho_0.1Lu_0.9B₁₂ crystal at a frequency of 60 GHz for T = 2 K in three orientations of the magnetic field B||[100, 110], and [111] and the calculated envelopes of electron-nuclear transitions in the spectra of isolated Ho³⁺ ions (panel a; the dotted curve shows the hyperfine structure of the transitions between sublevels of the main triplet in a cubic crystalline field, the dashed line was obtained by taking into account random tetragonal strains of the crystal lattice) and dimers Ho³⁺–Ho³⁺ (b, the dotted and dashed lines correspond to antiferromagnetic- and ferromagnetic-exchange interactions respectively). From the work [118]

However, simulation gives an ESR line, which is narrower than that measured even for x = 0.1 (Fig. 23). Consideration of bigger Ho concentrations makes discrepancies much higher. In the most concentrated case x = 1 (pure HoB₁₂), the ESR line at 60 GHz broadens by ~ 2.5 times and shifts to higher magnetic fields by 0.17 T [118]. It is clear that single-ion modeling is unable to account such effects. This example clearly demonstrates that ESR in strongly correlated metal is a collective effect, and approximation of an isolated magnetic ion in the crystal field has very limited applicability if any. This circumstance constitutes the main difference between magnetic impurities in metallic matrix case considered in classical review [7] and strongly correlated metal with concentrated magnetic subsystem.

6.2 Strong Correlation Between Line Width and g-Factor (GdB₆)

ESR in strongly correlated metal GdB₆ with antiferromagnetic ordering has a long history of studies. Pioneering investigation in X-band diapason revealed ESR signal corresponding to g-factor ~ 2.01 [119]. Recent experiments [120] not only detected magnetic resonance in antiferromagnetic phase T < T_N = 15.5 K for the first time, but also demonstrated unique behavior of ESR parameters in the paramagnetic phase [120].

Traditionally, GdB₆ is described as a material with short-range magnetic correlations, and hence ESR line width in the PM phase should diverge as W(T) ~ 1/(T − T_N)^δ, where exponent δ is about unity. In this, line width increases for T → T_N, but remain finite at T = T_N [120]. Simultaneously, the g-factor with lowering temperature increases, as well. Assuming temperature dependence of this parameter in a form:

$$g(T) = \Delta g(T) + g_{0} ,$$

(16)

where g₀ ~ 2 denotes high-temperature value of the g-factor, it is possible to show that W(T) and Δg(T) are linked by relation:

$$W(T) = a_{0} \cdot \Delta g(T),$$

(17)

(Fig. 24). In Eq. (17), the coefficient a₀ equals ~ 100 kOe [120]. Considered regularity may be reasonably treated as a consequence of collective nature of ESR in GdB₆ when it is necessary to describe physical picture of ESR via evolution of the ESR line shape for which ordinary spectroscopic parameters are no longer independent. Thus, the simple quasi-classical model for magnetic oscillations (Sect. 2), where hyromagnetic ratio and relaxation parameter are totally independent, is not correct in the strict sense.

Fig. 24

Temperature dependences of the line width (filled points) and g-factor (empty points) in the paramagnetic phase of GdB₆. The insert shows a linear relationship between line width and the g-factor temperature shift (from Ref. [120])

The considered situation is likely unique in the case of ESR in strongly correlated metals, but has already been reported for other strongly correlated materials. The universal link between the line width and g-factor shift was established in spin chain system CuGeO₃ doped with magnetic impurities [45]. Doping with magnetic impurities causes the onset of the staggered field in Cu²⁺ spin chains and  basing on Oshikawa–Affleck theory for ESR in S = 1/2 AF quantum spin chains [24] it is possible to derive following universal equation [45]:

$$\frac{W(T)}{{\Delta g(T)}} = 1.99\frac{{k_{{\text{B}}} T}}{{\mu_{{\text{b}}} }},$$

(18)

which, on one hand, does not depend on any characteristics of the staggered field in the sample [45] and, on the other hand, meets experimental situation in CuGeO₃ very well [45]. The validity of Eq. (18) is a direct consequence of the collective nature of ESR on Cu²⁺ spin chains and does not have any classical analogue. It is also possible to conclude that in strongly correlated system, the equations of the type [Eqs. (17), (18)] may be a consequence of presence of some “collective” energy scale, which may be either universal or reflect specific interactions in concentrated spin systems. In our opinion, both theoretical and experimental future investigations of the universal links between line width and g-factor in various SCES will be rewarding.

Interestingly, if we combine Eqs. (17) and (18), it is possible to estimate some “frozen” characteristic temperature $T_{{\text{f}}} = a_{0} \mu_{{\text{B}}} /1.99k_{{\text{B}}}$ for GdB₆: T_f~ 3.5 K. Authors of [120] claim that T_f may be related to spin fluctuation energy, as long as below this temperature fine structure of the magnetic resonance spectra in antiferromagnetic phase become resolved. This idea allows discriminating different types of energy scale assumed by Eqs. (17) and (18). The S = 1/2 AF chain system does not possess any magnetic transition up to T = 0, and thus in this case, energy scale may be just ~ k_BT like in quantum critical systems [90]. At the same time in the systems with magnetic transition at finite temperature like GdB₆, the energy scale responsible for universal linking of ESR parameters ~ k_BT_f may be also finite and corresponds to some effective temperature. Future studies will show whether the above reasoning turns out to be only an unconfirmed hypothesis, or whether they will give a new impetus to the development of EPR physics in strongly correlated electronic systems.

7 Conclusions

A straightforward conclusion of our review is that ESR in strongly correlated metals is promising direction of research (among other promising directions as one may say). We attempted to show that position of ESR in this field of research must be shifted from promising to unique tool for research. The ESR magnifying lens allows finding short-range correlations at the nanoscale of a spin polaron type and observing quantum critical points even hidden at the magnetic phase diagram. In many cases, it is just ESR, which either indicates the necessity for clarification or deep revision of the prevailing paradigm (metallic system with quadrupolar order CeB₆), or constitutes basis for new concept of magnetic properties (metallic surface of topological Kondo insulator SmB₆).

It is important to mention that the problem of choice between itinerant magnetism and description of the magnetic properties by considering localized magnetic moments, which, from time to time, appears in ESR studies of strongly correlated metals, may have an unexpected solution. For example, in the stoichiometric iron pnictides, the same d-electrons form the local moments and participate in the charge and spin transport [121]. On that ground, one cannot preclude the manifestation of the dual role of electrons in the other strongly correlated metallic systems and further theoretical research in this direction may be rewarding.

The ESR opens a window into the interesting and amazing world of electron nematic effects and spin fluctuation transitions. Apart from quadrupolar ordering effects considered in the present work, it is important to keep in mind an alternative scenario for nematicity based on the Fermis surface nesting [122], which provides another inherent mechanism resulting in the creation of charge stripes. The ESR probing of inhomogeneous electronic state of a stripe type in various strongly correlated electronic systems looks very promising.

However, the ESR becomes proper tool then and only then the adequate experimental technique is applied. This technique is more sophisticated than that realized in apparatus commercially available to date and requires additional facilities for measuring static magnetic properties and magnetoresistance as an inseparable part of ESR research. Nevertheless, the use of the correct measuring methods including quantitative line shape analysis forms a watershed between valuable physical results and experimental artifacts. Although we have achieved considerable progress in experimental studies and there are several breakthroughs and very valuable theoretical results, the ESR research on metals with strong electronic correlations is still awaiting Columbus, who will map the new beautiful islands of scientific knowledge.