Probing Spontaneous Spin Magnetization and Two-Phase State in Two-Dimensional Correlated Electron System

Abstract

Strongly interacting two-dimensional (2D) carrier system has a tendency to spontaneous spin magnetization and mass divergence. Numerous experiments aimed to reveal these instabilities were not entirely convincing. In particular, spin susceptibility of itinerant electrons, determined from quantum oscillations, remains finite at the critical density of the 2D metal-insulator transition (MIT), n = n _c . In contrast, the susceptibility and effective mass determined from high field magnetotransport were reported to diverge. Later, it became clear that as interactions grow, the homogeneous 2D Fermi liquid breaks into a two phase state which hampers interpretation of the experimental data. The thermodynamic magnetization measurements have revealed spontaneous formation of the spin-polarized collective electron droplets (“nanomagnets”) in the correlated 2D Fermi liquid, while the spin susceptibility of itinerant electrons in the surrounding 2D “Fermi sea” remains finite. Here, we report how the non Fermi-liquid two-phase state (dilute ferromagnet) reveals itself in magnetotransport and zero field transport. We found in the correlated 2D system a novel energy scale T ^∗<T _F . At T≈T ^∗ the in-plane field magnetotransport and zero field transport exhibit features. Finally, in thermodynamic magnetization, the spin susceptibility per electron, ∂ χ/∂ n changes sign at T≈T ^∗. All three notable temperatures are close to each other, behave critically, $\propto (n-n_{c})$; we associate, therefore, T ^∗ with a novel energy scale caused by interactions in the two-phase 2DE system.

1 Introduction: Spin Magnetization in the In-plane Field

Fig. 1

a, b Spin magnetization ∂ M/∂ n vs. dimensionless field for two densities and at various temperatures, measured in ref. [2]. Vertical arrow depicts n _c =0.88. Densities are in units of 10¹¹ cm ⁻². c Empirical phase diagram of the 2DE system. Dashed areas are (I) – SD in the majority FL phase, (II) – FL in the majority SD phase, (III) – non-degenerate correlated system, blank area – localized phase. Full dots show the kink temperature T _kink in magnetoconductance, open dots – inflection T _infl in ρ(T). Dash-dotted line – bare ( T _F ), dashed line – renormalized ($T_{F}^{*}$) Fermi temperatures. Bold blue dash line is T _{d M/d n} from ref. [2]. Solid lines are guide to the eye. Vertical arrow marks critical density n _c

The low-density two-dimensional (2D) electron system has a tendency to ordering in the spin or charge channels, due to the interplay between Coulomb interaction and Pauli principle. Particularly, as density decreases, the ratio r _s between the interaction and Fermi energies increases pushing the system towards a ferromagnetic instability. In the Hartree-Fock approximation, the Bloch instability was predicted to occur as a first-order phase transition to fully polarized state. In the limit of short-range interactions, the Stoner instability, a second-order phase transition characterized by divergent spin susceptibility, is expected. Numerical simulations for a clean single-valley 2D electron system [1] predict Bloch instability at r _s ≈25 followed by Wigner crystallization at r _s ≈37, whereas clean two-valley system is believed to be stable against spontaneous spin polarization. Numerous experimental attempts to reveal the spin susceptibility divergence were inconsistent. Thermodynamic spin magnetization measurements [2] has clarified the reason of the inconsistency: the 2D interacting electron system experiences a transition from Fermi liquid to a two-phase state, that hampers interpretation of the data.

The spin polarized phase has been revealed in thermodynamic measurements of the spin magnetization M in weak in-plane magnetic fields [2–4]. In these measurements, ∂ M/∂ n=−∂ μ/∂ B was determined from modulation of the 2D layer chemical potential μ in the weak in-plane magnetic field B [4]. The main result of the measurements [2] is the observation of “spin-droplets”—spin polarized collective electron states with a total spin of the order of two [2]. These easily polarized “nanomagnets” exist as a minority phase on the background of the majority Fermi liquid phase even though the density and the dimensionless conductance are high, k _F l≫1; the latter inequality is commonly considered as the criterion of a well-defined Fermi liquid state.

Figure 1a, b shows typical ∂ M/∂ n signal for several densities. For low densities, ∂ M/∂ n is positive, much exceeding the Pauli spin susceptibility (Fig. 1a) at low temperatures. Its magnetic field behavior is reminiscent of that for free spins, $\partial M/\partial n=\mu _{B}\tanh (b)$, where b = μ _B B/T≪1 is the dimensionless magnetic field ($\hbar$ and k _B are set to unity throughout the paper). However, ∂ M/∂ n exceeds Bohr magneton, the fact that evidences for ferromagnetic alignment of spins. For high densities, in the metallic regime, the ratio of the interaction energy to the kinetic Fermi energy is not great. As expected for the Fermi gas with density-independent Pauli spin susceptibility, ∂ M/∂ n in low magnetic fields approaches zero [2]. At intermediate densities, well in the metallic phase (e.g., at n=1.5×10¹¹ cm ⁻² in Fig. 1), ∂ M/∂ n changes sign with temperature. Indeed, negative ∂ M/∂ n is expected in the metallic phase, since increase in density reduces interaction and spin polarization of the 2D system. Thermal fluctuations suppress magnetic ordering; therefore, as temperature increases, ∂ M/∂ n becomes less negative, changes sign and approaches the dependence expected for noninteracting non-degenerate electrons (see Fig. 1b).

Figure 1c shows a phase diagram, based on the experimental results of ref. [2]. Here, the dashed line T _{d M/d n} , corresponding to the sign change of ∂ M/∂ n separates regions (I) with dominating spin droplets, ∂ M/∂ n>0, and (II) Fermi liquid, ∂ M/∂ n<0. In the lower-density phase (II), as density increases, the number of droplets increases, reaching its maximum at the temperature-dependent critical border (dash line). In the high-density phase (I), the spin droplets disappear gradually as density increases. The phase diagram, therefore, shows a critical magnetic behavior for the 2D electron system in the regime of strong interactions [5].

2 Two Phase State and Charge Transport

One may expect that the presence of the localized “spin-droplets” with a non-zero magnetic moment will be seen in transport of the itinerant electrons. However, the effect of droplets is rather delicate. This is discussed in the following sections.

Fig. 2

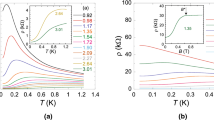
a Temperature dependencies of the prefactor a _σ (T) measured in weak fields B<T at two densities. For clarity, one curve is scaled by 0.1×. The similarity of the two sets of data measured with two different high-mobility samples illustrate a general character of the knee-type dependence. b Zero field temperature dependence of resistivity at low densities measured for sample Si-2. The densities are in 10¹¹ cm ⁻². Dots mark inflection points

2.1 In-plane Field Magnetoresistance

Variations of the conductivity and resistivity with weak in-plane field are parabolic:

$$ \sigma = \sigma_{0} - a_{\sigma} B^{2} + \textit{{o}}\left( B^{2}\right) \qquad \rho = \rho_{0} + a_{\rho} B^{2} + \textit{{o}}\left( B^{2}\right), $$

(1)

where by definition

$$ a_{\sigma} \equiv \left. -\frac{1}{2} \partial^{2}\sigma/\partial B^{2} \right|_{B=0} \qquad a_{\rho} \equiv \left. \frac{1}{2} \partial^{2}\rho/\partial B^{2} \right|_{B=0} . $$

In order to probe true spin effects, the magnetic field g μ _B B should be less than T, (T ² τ), and T _F . The magnetoconductivity in the in-plane field is purely Zeeman effect on the e-e interaction correction [6], and is predicted to follow:

$$\begin{array}{@{}rcl@{}} a_{\sigma}(T) \propto \left\{ \begin{array}{cl} &(1/T)^{2}, \quad T\tau \ll 1 \\ &(1/T), \quad T\tau \gg 1.\\ \end{array} \right. \end{array} $$

(2)

As we found, for low-mobility samples, indeed, a _σ (T) developed in accord with the interaction correction theory [6]. However, for high mobility samples where electron-electron interactions are strong in the dilute regime, the agrement with theory is no longer valid. In Fig. 2, we plotted the prefactor a _σ (T,n) for a high mobility sample versus temperature. One can see that a _σ (T) indeed develops in a ballistic fashion, $\propto (1/T)$, up to temperatures 1.5–2 K which are a factor of 10 higher than the predicted T∼1/τ∼0.2 K, then it sharply changes to the novel unforseen dependence, $a_{\sigma }(T) \propto (1/T)^{2}$, making the overall picture inconsistent with (2). The kink and the overall type of behavior is observed in the wide range of densities and for all studied high mobility samples. Though the high-temperature behavior, $a_{\sigma } \propto T^{-2}$, formally coincides with the upper line of (2), it cannot be associated with the diffusive interactions and in fact is the novel high-temperature phenomenon. As carrier density decreases, the kink in Fig. 2a moves down and the (1/T ²)–regime occupies more and more space and eventually at n = n _c extends down to the lowest explored temperature T≈0.3 K.

2.2 Resistivity in Zero Field

Searching for a manifestation of the two-phase state in zero field transport, we analyze the ρ(T) dependence for high-mobility samples (see Fig. 2b). Its variations are large (up to a factor of 10), making the interaction correction theory inapplicable in this “high temperature” regime. Each ρ(T) curve has two remarkable points: ρ(T) maximum at $T_{\max }$, and inflection at T _infl [7]. Whereas $T_{\max }$ is an order of the renormalized Fermi energy, the inflection happens at lower temperatures, in the degenerate regime. In Fig. 1b, we plotted three temperatures, T _kink, T _infl, and T _{d M/d n} . They all develop critically versus electron density, vanishing $\propto (n-n_{c})$ at the same density n _c ; the latter, within the experimental uncertainty, coincides with the MIT critical density in transport [7, 8]. The proximity of these three notable temperatures (which are inherent to high mobility samples solely) supports the existence of a new energy scale T ^∗ in the correlated 2D system.

2.3 Phenomenological Description of the Data

We suggest below a phenomenological model that links the “high temperature” transport and magnetotransport behavior in a unified picture. One can see from Fig. 2 that ρ(T) follows one and the same additive resistivity functional form over a wide density range:

$$\begin{array}{@{}rcl@{}} \rho(T)&=&\rho_{0} +\rho_{1}\exp(-{\Delta}(n)/T), \\ {\Delta} (n)&=& \alpha (n-n_{c}(B)), \end{array} $$

(3)

where ρ ₁(n,B) is a slowly decaying function of n, and ρ ₀(n,T) includes Drude resistivity and quantum corrections of various origin.

This empiric functional resistivity form fits well the ρ(T) dependence for a number of material systems [9, 10]. It also satisfies the general requirements for transport behavior in the vicinity of a critical point [7, 11–13], and explains the apparent success of the earlier attempts of one-parameter scaling (namely, of the ρ(T) steep rise and the mirror reflection symmetry between ρ(T) and σ(T) on the metallic and insulating sides of the MIT) [8, 13]. Equation (3) correctly describes the inflection in ρ(T) and linear density dependence of the inflection temperature [9]. Obviously, in this model, T _infl=Δ/2. To take magnetic field into account, we include to (Δ/T) all the lowest order in B/T (and even-in-B) terms, as follows:

$$ {\Delta}(T,B,n)/T ={\Delta}_{0}(n)/T - \beta(n) B^{2}/T - \xi(n) B^{2}/T^{2}, $$

(4)

with Δ₀ = α[n−n _c (0)].

Equations (3) and (4) link the magnetoconductance with the zero-field ρ(T) temperature dependence. As a result, the ρ(T,B) dependence becomes as follows:

$$\begin{array}{@{}rcl@{}} \rho(B,T) &=& \left[\sigma_{D} - \delta\sigma \cdot \exp \left( - T/T_{B} \right)\right]^{-1} \\ &&+\rho_{1} \exp \left( - \alpha \frac{n-n_{c}(0)}{T} - \beta \frac{B^{2}}{T} - \xi \frac{B^{2}}{T^{2}}\right) \end{array} $$

(5)

The term in the square brackets includes Drude conductivity and interaction quantum corrections [6, 14]. The latter, δ σ(T) = γ(B ²/T) + η T, was calculated using the experimentally determined Fermi-liquid coupling constants [15, 16], and σ _D was found in the conventional way [17]. In order to cut-off the corrections above a certain temperature [18] and, thus, to disentangle the exponential- and linear-in-T contributions, the calculated interaction correction is cut-off with an exponential crossover function above T _B which for simplicity we set equal to Δ(n)/2.

From (5), the prefactor a _σ =−(1/2)∂ ² σ/∂ B ² is calculated straightforwardly and in Fig. 3 is compared with the experimental data. In the ρ(T) fitting (Fig. 3a, c, e), basically, there is only one adjustable parameter, ρ ₁(n), for each density. Indeed, n _c (0) is determined from the conventional scaling analysis at B=0 [7], and the slope, α=2∂ T _infl(n)/∂ n may be determined from Fig. 1b. At the next step, in the a _σ (T) fitting (Fig. 3b, d, f), we fixed the parameters determined from the ρ(T) fit, and varied β(n) and ξ(n).

Fig. 3

Fitting ρ(T,B=0) dependencies (left panels) and a _σ (T) (right panels) with the same set of the fitting parameters, for three representative densities. Dots are the data, solid curves—fit with (5), dashed lines show calculated quantum corrections in the ballistic regime [6, 14]. Sample Si-2; carrier densities are indicated in 10¹¹ cm ⁻²

One can see that both ρ(T) and a _σ (T) are well-fitted; the model captures correctly the major data features: the steep ρ(T) rise (including the inflection), and the a _σ (T) kink. Within this model, the kink signifies a transition from the low-temperature regime (I), T<T ^∗), where the linear σ(T) temperature dependence dominates, to the high-temperature regime (II), T>T ^∗, governed by the steep exponential ρ(T) rise; both regimes are irrelevant to the diffusive-type interaction.

3 Discussion: Impact on the Transport and Magnetotransport

The additive resistivity form is intrinsic to the two-phase state of the low-density 2D electronic system (Matthiessen’s rule). The phase separation and the two-channel transport are also common in the vicinity of the phase transition [19]. Dealing with the two-phase state, the two channel scattering or additive resistivity approach seems quite adequate to the problem.

The two parallel dissipation channels in our models are presumably (i) ordinary impurity scattering of the itinerant electrons in the 2D Fermi liquid, and (ii) resonant scattering and hybridization of itinerant electrons and collective localized states (“spin-droplets”). The latter may be viewed as quantum dots confining four or more electrons [2]. At low temperatures, the large-sized spin droplets scatter itinerant electrons ineffectively and elastically, and do not contribute to the phase breaking. It might be for this reason we did not see any hysteresis effects that are often observed in the two-phase state in the vicinity of the phase boundary [19, 20]. Besides the low-lying ground energy state, the spin droplets have excited levels which may be temporarily occupied by itinerant electrons at high enough temperatures. Capture and emitting electrons from/to the droplets is a slow process, requiring rearrangement of all electrons inside the dot. Only at temperatures above T ^∗ the hybridization processes become effective and contribute to the DC transport. At these temperatures, however, the phase coherence is lost [18, 21].

In conclusion, we have explored how the spontaneously formed spin-polarized collective droplets affect transport and magnetotransport of itinerant electrons in the correlated 2D electron system. We have found that their effect takes place above a characteristic temperature T ^∗ that sets a novel energy scale in the two-phase electronic system. At the crossover T ^∗(n), the spin magnetization per electron changes sign, the in-plane field magnetoconuctance crosses over from the conventional ballistic type −(B ²/T) to the novel −(B ²/T ²) dependence, and the zero field resistivity ρ(T) exhibits an inflection. The three respective borders develop critically, $\propto (n-n_{c})$, and are rather close to each other. Since the crossover at T ^∗ is related to the transition from the minority to majority SD phase, we conjecture that T ^∗ might be related with the energy of exited levels in the spin droplets.

We suggested a phenomenological description of the transport and magnetotransport data, based on the two scattering channels. Already at this phenomenological level, our results explain why the Fermi-liquid parameters extracted from the σ(B _∥) data scatter significantly in various experiments and why they differ from those obtained from the zero-field σ(T) data. Indeed, by fitting the data in the nominally ballistic regime, one would observe a _σ (and deduce $F_{0}^{\sigma }$ values) dependent on the particular temperature range, above or below the kink temperature. The microscopic mechanism behind the two-scattering model requires a special theoretical consideration.