Abstract
The current theory of three-pulse electron double resonance (PELDOR) has been generalized to the case, when paramagnetic particles (spin labels) in pairs or groups have the electron paramagnetic resonance (EPR) spectra, which overlap essentially or coincide. The PELDOR signal modulation induced by the dipole–dipole interaction between paramagnetic spin ½ particles in pairs embedded in disordered systems has been analyzed comprehensively. It has been shown that the PELDOR signal contains additional terms in contrast to the situation considered in the current theory, when the EPR spectra of the spin labels in the pairs do not overlap. In disordered systems, the pairs of spin labels have the characteristic dipolar interaction frequency. According to the current theory for pairs of spin labels, the PELDOR signal reveals the modulation with this characteristic frequency. The additional terms, which are obtained in this work, do not change the modulation frequency of the PELDOR signal for pairs of spin labels. However, these additional terms should be taken into account when analyzing the amplitude of the PELDOR signal and the amplitude of the modulation of the PELDOR signal. The consistent approach to treating the PELDOR data for the groups containing three or more spin labels has been outlined on the basis of the results for pairs of spin labels. It has been also analyzed how the spin flips and molecular motion or molecular isomerization can affect the manifestation of the interaction between the spin labels in PELDOR experiments. PELDOR experiments for the stable biradicals (biradicals I containing 1-oxyl-2,2,5,5-tetramethylpyrroline-3-yl spin labels and biradicals II containing 3-imidazoline spin labels) have been performed. The results have been interpreted within the theory developed in this work.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Pulse electron–electron double paramagnetic resonance (PELDOR) experiments are widely used for determining distances between spin labels in pairs, and also the number of dipolar-coupled spins in groups, e.g., in spin-labeled proteins, and the distribution of distances between spin labels in groups (see, e.g., [1–7]). The manifestation of the dipole–dipole interaction is detected in these experiments. The dipole–dipole interaction leads to the modulation of the PELDOR signals. The modulation frequencies are determined by the value of the dipole–dipole interaction between spin labels.
The manifestations of the spin–spin interaction between paramagnetic centers in solids in the pulse EPR experiments were studied comprehensively (see [8–13]). The results of these investigations created a basis for the development of PELDOR. It was demonstrated theoretically and experimentally that the exchange and dipole–dipole interactions between partners in pairs of the paramagnetic particles can cause the modulation of the electron spin echo signals [14]. This effect depends on the excitation pattern of the electron spins in the pulse EPR experiment. The echo signal of a given spin is modulated by the interaction between this spin and the spin of the partner paramagnetic particle in the pair in the case, when the partner spin is also excited by the microwave (MW) pulse. The distance between the partners in pairs can be found from the modulation frequency of the echo signal [14, 15]. This modulation effect makes it possible to highlight the spin–spin interaction between particular paramagnetic particles using their selective excitation by the MW pulse. This option is implemented in the PELDOR experiments.
The dipole–dipole interaction between paramagnetic particles distributed over the sample volume causes the spin echo signal decay. The kinetics of this decay depends on the spatial distribution of the paramagnetic particles. This option was widely used when studying the distribution of paramagnetic particles in tracks of ionizing irradiation [8, 10, 11]. The relevant results are important when interpreting the experimental PELDOR data, since the PELDOR signal is affected by the dipole–dipole interaction between the paramagnetic particles distributed over the sample volume, the same as the primary electron spin echo or the stimulated echo signals (see, e.g., [8–11]).
The first theoretical description of the three-pulse ELDOR experiment was presented in [16]. The system of the randomly distributed pairs of the hydrogen atom (spin A) and the hydroquinone radical (spin B), which were produced during the photolysis of frozen solutions at 77 K, was considered. The electron paramagnetic resonance (EPR) spectra of these particles do not overlap and the spins A and B can be selectively excited by the MW pulses in the course of the PELDOR experiment.
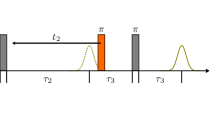
Figure 1 shows the protocol of the three-pulse ELDOR experiment. The amplitude of the PELDOR signal exhibits the modulation described at any fixed interval τ as [16].
Protocol of the three-pulse PELDOR experiment [14]. The spin echo is formed by the MW excitation of the spins A at t = 0 and t = τ. The additional (pump) MW pulse excites the spins B at t = T and affects the spin echo signal. Durations of pulses at t = 0, T and τ are t p1, t p2 and t p3, respectively
where V 0(τ) is the primary spin echo signal without the MW pump pulse, p B is the probability of the inversion of the spins B by the MW pump pulse at t = T, and D is the parameter of the dipole–dipole interaction
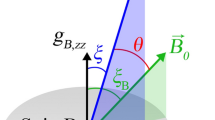
Here, r AB is the distance between spins A and B, θ is the angle between the vector r AB and the direction of the external magnetic field. Here, we assume that the g-tensors of spin labels are practically isotropic. We suppose that the distance between the partner spins in the pair is larger than 1 nm so that the contribution of the short-range exchange interaction between particles can be ignored (the range of distances preferable for PELDOR was discussed in Refs. [5, 17–19]. Possible effects of the exchange interaction on the PELDOR signal were discussed in Refs. [20–22].
Equation (1) describes the well-known effect of the so-called instantaneous spectral diffusion [8–11, 23, 24] induced by the “instant” change of the dipole–dipole interaction when the selective MW pulse inverts the spin projection of partner particles. The instantaneous spectral diffusion in the pulse EPR experiments selectively reveals the dipole–dipole interaction between definite particles (spin labels). With this idea in mind, the pulse EPR methodology was used to obtain information about the spatial distribution of paramagnetic particles [8, 10–13, 16].
The suggestion to use the PELDOR methodology for characterizing complex molecular structures, when several spin labels are inserted and they form groups of spin labels, was presented in Ref. [25]. This approach was developed comprehensively (see, e.g., [26–35]).
Let us assume that there are groups of N spin labels. The current paradigm is to present the PELDOR signal as a product of two terms (see, e.g., [1, 5, 14, 19, 21–23])
where V(T) describes the effect of the spin labels, which are pumped by the MW pulse at the moment t = T (see Fig. 1). V(T) contains the contributions of the dipole–dipole interaction inside the groups of spin labels and between these groups \( V_{\text{intra}} \left( T \right) \) and \( V_{\text{inter}} \left( T \right) \), respectively,
The contribution of the dipole–dipole interaction inside the groups of spin labels will be discussed below (see Sect. 2.5). Here, we present only approximate results to illustrate that PELDOR can give information about the number and the mutual spatial positions of spin labels in groups. Neglecting any correlations of the positions of spin labels in the groups, \( V_{\text{intra}} \left( T \right) \) is presented as (see, e.g., [1, 5, 25, 30, 33, 34])
Here, \( \left\langle \cdots \right\rangle \) means averaging over orientations of the r AB vector and distances between spin labels in these groups. Equation (6) is used for determining the distribution of the inter-pair distances in the group of N spin labels (see, e.g., [36, 37]). It appears that the approximation used in Eq. (6) is not good for the p B that is typical for recent PELDOR work (see [34, 43]).
It is expected that the contribution of the interaction between spin labels inside groups \( V_{\text{intra}} \left( T \right) \) with increasing T tends to
This asymptotic value of the PELDOR signal does not depend on the distances between the spin labels inside the group. It depends only on the number N of spin labels in the group. Equation (7) is used for determining the number N of spin labels in the groups [1–7, 30].
At present, Eqs. (1)–(7) are used for interpreting the PELDOR data in the cases, when the particles in pairs or groups are nitroxide free radicals with overlapping or coinciding EPR spectra. But Eq. (1) was derived for the situation, when partners in the pair are paramagnetic particles with the EPR spectra, which do not overlap, so that these partners can be excited selectively by MW pulses. Therefore, it is necessary to study whether Eq. (1) is applicable to the systems, when both spin labels in pairs are the same nitroxide free radicals or nitroxide free radicals with close magnetic resonance parameters, so that their EPR spectra overlap substantially. Concerning the current paradigm of treating groups of spin labels, it contains several additional assumptions [see, e.g., Eqs. (6), (7)], which may restrict its application to real systems. We will consider these assumptions in more detail below.
In this work, we generalize Eq. (1) and derive the contribution of the intra-pair interaction to the three-pulse ELDOR signal, when the EPR spectra of the partner spin labels in the pair overlap (or even coincide). The results obtained for the pairs are generalized to the case of groups of spin labels. The manifestations of the spin–lattice relaxation and the molecular dynamics in the experimental PELDOR data are also discussed theoretically. The theoretical considerations are compared with the PELDOR experimental data obtained when studying biradicals, which contain the stable nitroxide radical centers: biradicals I containing 1-oxyl-2,2,5,5-tetramethylpyrroline-3-yl spin labels and biradicals II containing 3-imidazoline spin labels.
2 Theoretical Consideration
2.1 Pairs of the Spin ½ Paramagnetic Particles
Let us consider an ensemble of pairs of paramagnetic particles (spin labels) R 1 and R 2 with the electron spins ½, when their EPR spectra g 1(ω) and g 2(ω) overlap or coincide. In the case of nitroxide radicals, the line widths of the EPR spectra are mainly determined by the inhomogeneous broadening induced by the g-tensor anisotropy and hyperfine interactions with magnetic nuclei. Usually, the contribution of the homogeneous broadening of EPR lines is one-two orders of magnitude less than that of the inhomogeneous broadening of the EPR spectra of spin labels [1–7]. This fact makes it possible to excite selectively different parts of the EPR spectra in the course of the PELDOR experiment. Let us assume that the spin echo-forming MW pulses has the frequency ω A and the MW pump pulse has the frequency ω B. In the further consideration, we assume that the EPR spectra of particles R 1 and R 2 are rather broad so that it is possible to excite electron spins R 1 and R 2 selectively in the frequency space. In the PELDOR experiments, the MW pulses with frequencies ω A and ω B excite spins with the resonance frequencies in intervals (ω A − ω 1A, ω A + ω 1A) and (ω B − ω 1B, ω B + ω 1B), respectively. Here, ω 1A and ω 1B denote the Rabi frequencies of the MW pulses. The requirement of the frequency-selective excitation in the course of the PELDOR experiment is fulfilled when
Note that this condition was also assumed in the theory presented in Ref. [16]. But the condition Eq. (8) is not sufficient to justify using Eq. (1) for the case, when the EPR spectra of the partners in pairs overlap.
Let us consider the contribution of a given pair R 1 R 2 to the three-pulse ELDOR signal (Fig. 1). Pulses with frequencies ω A and ω B can rotate the spins of both partners R k , k = 1, 2. Spin dynamics of the two interacting spin labels in the presence of pulses is rather complicated. We consider systems when the interaction between spins in pairs is relatively small, namely, we assume that D 0 < ω 1A, ω 1B. Under this condition, the probability of the spins inversion is calculated straightforwardly. Let us denote the resonance frequency of the spin R k as Ω k and the probability of the reorientation of the spin R k by the MW pulse, which has duration t p , the frequency ω F and the Rabi frequency ω 1F as p(Ω k |ω F, t p ), k = 1, 2, F = A, B. Then,
Let us divide the ensemble of pairs R 1 R 2 into sub-ensembles with the different inversion patterns of spins R 1 and R 2 by the MW pulses at the moments T and τ during the three-pulse ELDOR experiment (Table 1). The shapes of the contributions of different inversion patterns are given in the last column of Table 1. During these calculations, we assumed that the resonance frequencies of two spins Ω 1 and Ω 2 in the pair are independent [see Eq. (11)]. There can be situations when this assumption is not valid.
First, let us consider the contribution of one of the partners in a pair, e.g., spin R 1 , to the PELDOR signal. The first pulse at t = 0 rotates spin R 1 around the x-axis and creates the average spin moment along the y-axis
The patterns of the excitation of spins, which do not contribute to the PELDOR signal, are not given in Table 1. The contribution of the spin R 2 of the pair to the PELDOR signal is given by expressions similar to those given in Table 1 with subscripts 1 and 2 interchanged. The signal observed in the PELDOR experiments is the sum of contributions of spins R 1 and R 2.
In Table 1, the symbol \( \left\langle \cdots \right\rangle \) means averaging over the distributions of the EPR frequencies, which are given by the EPR spectra g 1 (Ω 1) and g 2(Ω 2) of spins R 1 and R 2,
Thus, the contribution of the spin R 1 to the three-pulse ELDOR signal is.
Equation (12) is similar to the expression which describes the observable in the “2 + 1” pulse train electron spin resonance method suggested in Refs. [12, 13]. Only amplitudes P mn in Eq. (12) are different from ones given in Ref. [13] [see Eqs. (4), (6)].
Let us assume that the frequencies ω A and ω B are well separated so that the probability for any spin to be inverted by the MW pulses with both frequencies, ω A and ω B, can be neglected
Below we will estimate quantitatively the validity of this assumption (see Sect. 2.6).
Under this assumption, we obtain
Let us introduce new notations to simplify expressions (14):
Then, the contribution of the spin R 1 to the PELDOR signal is
The contribution of the spin R 2 to the PELDOR signal is given by the expression similar to that for the spin R 1 [see Eq. (16)]
Here, p 1(ω A) and p 1(ω B) are average probabilities of the inversion of the spin R 1 by the corresponding MW pulses with the frequencies ω A and ω B. As expected, Eq. (16) and (16a) coincide if R 1 ≡ R 2.
The comparison of Eq. (16) with Eq. (1) shows that the additional term
appears in the case, when the paramagnetic particles in the pairs have the overlapping EPR spectra. This term reflects the fact that there are pairs, in which both partners are excited by the echo-forming MW pulses, so that the dipole–dipole interaction induces the electron spin echo modulation due to the instantaneous spectral diffusion [8–11]. Equation (16) is reduced to Eq. (1), if the partners in the pair have the EPR spectra, which do not overlap, because in this case, p 2(ω A) = 0.
One of the major aspects of the result presented in Eq. (16) is that in contrast to the current paradigm [see Eq. (1)], the contribution of the intra-pair dipole–dipole interaction to the PELDOR signal V(T, τ) [Eq. (16)] is not a product of the two terms V(T) and V 0(τ),
which gives the contribution of the intra-pair dipole–dipole interaction to the primary spin echo signal in the absence of the MW pump pulse.
If Eq. (1) is valid, then, the ratio of the PELDOR to the primary spin echo signals can be used to subtract the contribution of the additional MW pulse to the PELDOR signal. This is justified when the EPR spectra of the spin labels in the pair do not overlap [16]. In this case, dividing V(T,τ) by V 0(τ), one can obtain \( V\left( {T, \, \tau } \right)/V_{0} \left( \tau \right) = 1 - p_{ 2} (\omega_{\text{B}} )\left( { 1 - \left\langle {{ \cos }\left( {D_{12} T} \right) } \right\rangle } \right) \). This procedure is used in a number of publications when studying the systems of spin labels with overlapping EPR spectra (see, e.g., [1, 25–29]). However, this result is not valid when the EPR spectra of the spin labels overlap. In this case,
where
Equation (18) is formally similar to Eq. (1) but in contrast to Eq. (1), there appears the τ- and p 2(ω A)-dependent parameter p 2eff(τ) instead of the τ-independent parameter p 2(ω B). Note that p 2eff(τ) = p 2(ω B) only if \( p_{ 2} (\omega_{\text{A}} )\left( { 1- \left\langle { { \cos }\left( {D_{12} \tau } \right)} \right\rangle } \right) = 0 \). In the general case, \( p_{2eff} \left( \tau \right) > p_{2} \left( {\omega_{B} } \right) \).
The PELDOR signal normalization given by Eq. (18) is not the only one used when analyzing experimental data. Another suggestion is the normalization using the equation (see, e.g., [40])
where V(T) is the experimental PELDOR signal, \( V_{\infty } \) is the PELDOR signal at a large T, V 0 is the PELDOR signal at T = 0. By substituting Eq. (16) for V(T) and \( V_{\infty } = 1 - p_{2} (\omega_{\text{A}} )\left( {1 - \cos \left( {D\tau } \right)} \right) - p_{2} (\omega_{\text{B}} ) \) into Eq. (20), we obtain that \( V_{n} = \left\langle {\cos \left( {DT} \right) } \right\rangle \). Thus, in the case of the spin-label pairs, the normalization using Eq. (20) eliminates the contribution of the new term p 2(ω A)(1 − cos(Dτ)) introduced in this work from the experimental data. However, this statement for the spin-label pairs is valid only in the limit when the term P 14cos(D(τ − T)) [see Eq. (12)] can be neglected safely. Taking into account all terms in Eq. (12) leads to a more complex expression for V n . Suppose that \( V_{\infty } = 1 - (p_{2} (\omega_{\text{A}} ) - p)\left( {1 - \cos \left( {D\tau } \right)} \right) - p_{2} (\omega_{\text{B}} ) \) and \( V_{0} = 1 - p_{2} (\omega_{\text{A}} )\left( {1 - \cos \left( {D\tau } \right)} \right) \). Then, the normalized signal [Eq. (12)] gives \( V_{n} = \left( {(p_{2} (\omega_{\text{B}} ) - p)\cos \left( {DT} \right) + p\cos \left( {D\left( {\tau - T} \right)} \right)} \right)/\left( {p_{2} (\omega_{\text{B}} ) - p\left( {1 - \cos \left( {D\tau } \right)} \right)} \right) \). When p < p 2(ω B) the normalized signal equals \( V_{n} \approx \left\langle {\cos \left( {DT} \right)} \right\rangle + (p/p_{2} (\omega_{\text{B}} ))\sin \left( {D\tau } \right)\sin \left( {DT} \right) \), where \( p = \left\langle {p(\varOmega_{2} |\omega_{B} ,t_{p2} ) \, p(\varOmega_{2} |\omega_{A} ,t_{p3} )} \right\rangle \) (see Table 1). This estimation shows that correction is small when p < p 2(ω B).
In the case of disordered systems, there is a random distribution of the vector r 12, which connects spin labels in the pair. Therefore, the contribution of the intra-pair interaction given, e.g., by Eq. (16) should be averaged over the random distribution of the polar angle \( \theta \) between the direction of the r 12 vector and the direction of the external magnetic field. In addition, there can be the distribution f(r 12) of the distance r 12 between partners in the pairs, so that Eq. (16) should be averaged over this distribution f(r 12) as well. The average contribution of the intra-pair interaction to the echo signal is [1–7]
Here, V 1(T, τ) is given, e.g., by Eq. (16). The contribution of the spin R 2 to the PELDOR signal can be found analogously using Eq. (16a).
Equation (21) shows that it is necessary to integrate the contributions from the randomly distributed pairs when interpreting the PELDOR data for disordered systems. To this end, it is necessary to find the integral of the form
Each orientation of the pair is characterized by its dipolar frequency ±D 0(1 − 3cos2 θ). When the polar angle θ varies from 0 to π, the frequency Ω = D 0(1 − 3cos2 θ) changes in the interval {−2D 0, D 0}, so that the absolute value of \( \varOmega \) varies in the interval {0, 2D 0}. The frequency \( \varOmega \) = D 0 occurs when θ = π/2. i.e., on the equator of the spherical coordinate system. The statistical weight of equatorial points is the largest one. The distribution function of the \( \varOmega \) value equals.
where
\( g_{1} (\varOmega ) = c/((D_{0} - \varOmega )^{1/2} , \, g_{2} (\varOmega ) = c/(D_{0} + \varOmega )^{1/2} ), \, c = 1/\left( {2\left( {3D_{0} } \right)^{1/2} } \right) \), \( \chi \) is Heaviside function.
Peculiar feature of the Ω distribution is that g 1(Ω) has a singularity of the type \( \frac{1}{{\sqrt {D_{0} - \varOmega } }} \). The distribution of this dipolar frequency is well known: it leads to the characteristic Pake doublet shape of the two-spin spectrum [38]. For further discussion, we present the \( \left| \varOmega \right| \) distribution (Fig. 2). Figure 2 shows that it can be considered qualitatively as a sum of two parts. One is relatively broad and varies rather monotonically; and we denote its integral intensity as p d . The other is a narrow part of the distribution, which includes the singular point; and we denote its integral intensity as p c . Note that p d = 1 − p c . The fractions p d and p c are effective parameters to be specified in more detail below. Note that both terms g 1(Ω) and g 2(Ω) contribute to the p d part of the pairs of spins while only g 1(Ω) term contributes to the p c part of the pairs.
The behavior of the average cosine \( \left\langle {\cos DT} \right\rangle \) [Eq. (22)] calculated for r = 3 nm is shown in Fig. 3. The fast decay at the early stage occurs due to the destructive interference of the contributions of the p d part of pairs, which have the broad distribution of frequencies (Fig. 2). The signal modulation (oscillations) at t > t decay is determined by the contribution of the p c part of pairs, which have the frequencies around the singular value D 0. The amplitude of the second peak of the modulated PELDOR signal has the value of around 0.2. Note that the modulation amplitude decreases slowly, when the time T increases. Similar observations were obtained for all other distances in the interval r{1 nm, 10 nm}.
Due to the singularity of F(Ω), one can expect that the \( \left\langle {\cos DT} \right\rangle \) modulation frequency has to tend to D 0, when \( t \to \infty \). At finite t values, the oscillations of the average cosine \( \left\langle {{ \cos }\left( {D{\text{t}}} \right) } \right\rangle \) always manifest contributions of the pairs with different dipolar frequencies from the narrow p c part of the distribution (Fig. 2). The p c part of the distribution depends on the observation time. Suppose that the frequencies \( \varOmega \) in the p c part of the distribution are in the interval \( \varOmega \{ D_{0} - \delta ,\;D_{0} + \delta \} \). The pairs with the frequencies \( \{ D_{0} - \delta ,\;D_{0} + \delta \} \) contribute to the average cosine \( \left\langle {\cos \left( {\varOmega t} \right) } \right\rangle \) constructively, i.e., are not destroyed due to the destructive interference, if the condition \( \delta t \ll 1 \) is fulfilled. Thus, when the time t (t is T or τ in the PELDOR experiment) increases, the effective width of the constructive part of the frequency distribution should decrease (p c decreases). As a consequence, the oscillation (modulation) amplitude should decrease, when t increases (Fig. 3). The numerical calculations show that the “starting” value of the oscillation amplitude is close to 0.2 for different values of the distance between partners in the pair. On the basis of this observation, we suggest that p c ≤ 0.2. We calculated separately contributions to the average cosine \( \left\langle {{ \cos }\left( {D{\text{t}}} \right) } \right\rangle \) from the pairs around the equatorial plane for the interval of the angle \( \theta \{ \pi /2 - \Delta \theta ,\;\pi /2 + \Delta \theta \} \), i.e., the pairs from the constructive, p c, sub-ensemble of the pairs (see Fig. 2), and the rest pairs with the angle \( \theta \) in the intervals \( \theta \;\{ 0,\pi / 2- \Delta \theta \} \) and \( \theta \;\{ \pi / 2+ \Delta \theta ,\;\pi \} \) , i.e., the pairs from the destructive, p d , sub-ensemble. The calculation results for \( \Delta \theta = 0.2 \) are given in Fig. 4.
Contributions of the pairs with the angle θ in the intervals θ{π/2 − 0.2, π/2 + 0.2} (dotted line) and of the rest pairs with the angle θ in the intervals θ{0, π/2 − 0.2} and θ{π/2 + 0.2, π} (dashed line). The exact dependence for the average cosine \( \left\langle {\cos \left( {DT} \right)} \right\rangle \) calculated for all angles θ{0, π} (solid line, compare with Fig. 3). Calculations were performed for r = 3 nm
When t > t decay, the pairs around the equatorial plane with the angle \( \theta \) in the interval \( \{ \pi / 2- 0. 2,\pi / 2+ 0. 2\} \) produce the oscillation pattern close to that expected from the total ensemble of pairs (compare the dotted and solid lines in Fig. 4). On the basis of this result, we assume that the PELDOR signal observed after the early stage of the fast decay, at t > t decay, is mainly produced by the pairs with the angle \( \{ \pi / 2- 0. 2,\pi / 2+ 0. 2\} \).
The observation that p c ≤ 0.2 is of importance. It means that only 20 % of the pairs excited by the MW pulses in the PELDOR experiments are manifested in the oscillation effect as a result of the constructive interference of their contributions. The contributions of 80 % of the pairs to the PELDOR signal decrease rather fast due to the destructive interference.
Equation (22) can be presented in terms of Fresnel integrals [39]
where y = 6D 0 T/π. Equation (23) has an asymptotic value at \( D_{0} T \gg 1 \).
Asymptotically, the oscillation frequency tends to the singular frequency D 0. Note that the phase of the asymptotic oscillations is shifted by π/4. This phase shift reflects the asymmetry of the frequency distribution with respect to \( \varOmega = D_{0} \) (Fig. 2).
The average cosine \( \left\langle {{ \cos }\left( {DT} \right) } \right\rangle \) gives the contribution of the intra-pair dipole–dipole interaction to the free induction decay signal. It is worth to note that the free induction decay signal of the nuclear magnetization in crystals induced by the dipole–dipole interaction is phenomenologically described by \( \frac{{e^{{ - a^{2} t^{2} /2}} \sin bt}}{bt}\), where a and b are fitting parameters (see [35], Eq. (IV.51)).
Note that \( \left\langle {\cos \left( {D\left( r \right)t} \right)} \right\rangle \) is the kernel of the integral equation for determining the distribution of the distance between spin labels [16]. Keeping this in mind, we found the approximate expression for \( \left\langle {\cos \left( {Dt} \right) } \right\rangle \) (23). We propose to approximate the exact function Eq. (23) by the asymptotic value Eq. (24) in the region t > t*. The value t* is to be specified in more detail. Equation (24) does not describe the behavior of the average cosine \( \left\langle {\cos \left( {Dt} \right) } \right\rangle \) at D 0 t < 1, moreover, it diverges when \( D_{0} t \to 0 \). At t < t*, the PELDOR signal decreases sharply due to the destructive interference of the broad frequency distribution. We suggest to describe the PELDOR signal at t < t* using the phenomenological function
This choice was dictated by the fact that the p d part of the frequency distribution (Fig. 2) consists of the two broad flat distributions in the intervals {0, D 0} and {D 0, 2D 0}. The function [Eq. (25)] is the Fourier transformation of the rectangular distribution with an effective (fitting) width \( \eta D_{0} \): \( f(\varOmega ) = (1/(\eta D_{0} )) \) in the interval \( \varOmega \{ 0,\eta D_{0} \} \).
At the first glance, Eq. (25) gives the time dependence, which is similar to the exact behavior of the average cosine for the pairs in disordered systems Eq. (23). In both cases, there is a sharp decay at the early stage. At t > π/D 0, there are oscillations, the amplitude of which decreases. But these dependences have important differences. According to Eq. (25), the oscillation amplitude decreases much faster than that from the exact calculations. According to Eq. (24), the amplitude of the average cosine \( \left\langle {{ \cos }\left( {\text{Dt}} \right) } \right\rangle \) decreases as \( 1/\sqrt t \), while according to Eq. (25), the amplitude decreases as 1/t. Another important difference concerns the oscillation frequency. Numerical calculations for different values of the fitting parameter \( \eta \) showed that the early stage of the fast decay of the average cosine \( \left\langle {\cos \left( {\varOmega t} \right) } \right\rangle \) is described reasonably well by Eq. (25) at \( \eta = 1. 5 \) (Fig. 5). Thus, at t < t*, we approximate the average cosine in the form of Eq. (25). At t > t*, the average cosine Eq. (23) can be described well by Eq. (24).
Using numerical calculations, we found that the average cosine \( \left\langle {{ \cos }\left( {\text{Dt}} \right) } \right\rangle \) [Eq. (22)] can be approximated with the fitting parameters t* = 2.5/D 0 and \( \eta = 1. 5 \) as
Here, \( \chi \left( T \right) \) is the Heaviside function.
Numerical calculations performed for different distances r between partners in the pair show that the approximate (semi-phenomenological) Eq. (26) coincides reasonably well with the rigorous theoretical result Eq. (23) (compare two curves in Fig. 5).
Several features of the average cosine \( \left\langle {{ \cos }\left( {DT} \right) } \right\rangle \) can be used to find the dipolar frequency D 0 of the pairs from the PELDOR experiments. One option is the oscillation period of the PELDOR signal at t > t*. Another option is the oscillation amplitude. The shape of the fast decay can be used as well to obtain the frequency D 0 (see, e.g., [6]). For example, after the fast decay, the first intersection of the average cosine \( \left\langle {{ \cos }\left( {DT} \right) } \right\rangle \) with the abscissa occurs around t 0 = 2.15/D 0.
To test the accuracy of the approximation Eq. (26), we found the Fourier transformations of Eq. (23) and approximate Eq. (26) functions (Fig. 6). It is seen in Fig. 6 that the Fourier transformations of Eqs. (23) and (26) are in reasonable agreement. Thus, Eq. (26) is a good approximation to the exact function given by Eq. (23).
By substituting Eq. (26) into Eqs. (1), (12), (16)–(18), we obtain the contribution of the intra-pair interaction to the three-pulse ELDOR signal for disordered systems.
In the case of the spin labels R 1 and R 2 with non-overlapping EPR spectra considered in [16] (\( p_{2} \left( {\omega_{A} } \right) = 0 \)), the PELDOR signal can be approximated as
When T > t* = 2.5/D 0, the PELDOR signal [Eq. (27)] is reduced to
where V 0 (τ) describes the primary spin echo signal, and
is the statistical weight of the pairs which continue to interfere constructively. According to Eq. (28), the oscillation amplitude manifested in experiment is determined not only by the probability p B of the spin inversion by the MW pump pulse but also by the statistical weight p c of the pairs, which have the oscillation frequency around the singularity of the frequency distribution.
In the case of pairs R 1 R 2 with the overlapping EPR spectra when \( p_{ 2} (\omega_{\text{A}} ) \ne 0 \), the manifestation of the dipole–dipole interaction in the PELDOR experiments is described by the following equations.
For the spin label R 1 in the pair R 1 R 2 [see Eq. (12)]
When T > t decay, Eq. (30) is reduced to
For the spin label R 2 in the pair R 1 R 2 [see Eq. (16a)], we have the similar result, only the indices 1 and 2 have to be interchanged [compare Eq. (16) and (16a)].
When T > t decay, Eq. (16a) results in
The average oscillation pattern of the primary spin echo signal has the form [see Eq. (17)]
When T > t decay, Eq. (32) is reduced to
It follows from the numerical calculations that the decay time \( t_{\text{decay}} \approx \frac{2\pi }{{3D_{0} }} = \frac{{2\pi r^{3} {\hbar}}}{{3g_{1} g_{2} \beta^{2} }} \) .
It increases as r 3, when the distance between partners in the pair increases. For example, at r = 4 nm \( t_{\text{decay}} \approx \;200 \;ns \), and at r = 8 nm \( t_{\text{decay}} \approx 1 6 {\text{\,00 }}\;{\text{ns}} \).
The results concerning the modulation of the PELDOR signal from the pairs of spin labels allow us to state the following.
In the case of single crystals, the oscillation frequency of the PELDOR signal is angular-dependent [see, e.g., Eqs. (1) and (2)] and the oscillation amplitude normalized to its initial value (at T = 0) is the probability of the spin inversion by the MW pump pulse.
In the case of disordered systems, the PELDOR signals from the randomly oriented pairs of the spin labels interfere. Around 80 % of the pairs exhibit the destructive interference and the rest 20 % contribute to the constructive interference. The oscillation frequency of the PELDOR signal is close to the characteristic value \( D_{0} = \frac{{g_{1} g_{2} \beta^{2} }}{{\hbar{\text{r}}^{3} }} \).
In contrast to the spin labels with non-overlapping EPR spectra [see Eq. (1)], the PELDOR signal \( V\left( {T,\tau } \right) \ne V_{0} \left( \tau \right)V\left( T \right) \) in the case of the spin labels with overlapping EPR spectra.
The oscillations of the PELDOR signal have the phase shift (π/4) [Eq. (33)] (see Fig. 7)
Here, T 0 = 2π/D 0 is the oscillation period. Note that all considerations above were done under the assumption that the MW pulses are “instantaneous”. In a real situation, when the pulses have finite durations, it might be not so straightforward to subtract this phase shift in experiment (see, e.g., [29]).
2.2 Effect of the Interaction Between Pairs on the PELDOR Signal Decay
The inter-pair dipole–dipole interaction between spins in the magnetically diluted solids results in the additional decay of the PELDOR signal. When the EPR spectra of a pair of spin labels R 1 and R 2 do not overlap, the effect of the inter-pair interaction on the PELDOR signal was given in Ref. [16]. Suppose that spins R 1 are excited by the MW pulses with the frequency ω A forming the PELDOR signal and spins R 2 are excited by the MW pump pulse with the frequency ω B. In this case, the effect of the inter-pair interaction was obtained neglecting the spatial correlation of the spin labels in pairs. Under these conditions, the effect of the inter-pair interaction on the PELDOR signal is given as [16].
The term V inter,R1 arises due to the contribution of the inter-pair interaction of spins R 1–R 1* (here two R 1 spin labels belong to different pairs R 1 R 2, see Fig. 8)
Here, g 1 is the g-factor of R 1, C pair is the total concentration of the pairs R 1 R 2. Note that the total concentration C of spin labels is C = 2C pair.
The term V inter,R2 arises due to the contribution of the inter-pair interaction of spins R 1–R 2*
Parameters b A and b B in Eqs. (35, 36) give the echo signal decay rates due to the instantaneous diffusion mechanism induced by the inter-pair interactions. They depend on the concentration of the pairs and on the efficiency of the spin excitation by the MW pulses [8–11, 24].
The results Eqs. (35) and (36) can be rather straightforwardly generalized to the case of the pairs, when the EPR spectra of partners overlap. In this case, each paramagnetic center can be excited by both MW pulses with the frequencies ω A and ω B, and both spin labels contribute to the PELDOR signal. Therefore, we have to calculate separately the contribution of spins R 1 and R 2 to the signal and then to sum them. To simplify the consideration, let us assume that spin labels are identical, and the EPR spectra of R 1 and R 2 coincide. The expressions below in this section are presented for the case of identical spin labels. In this case, g-factors of partner labels are equal and the two spins R 1 and R 2 in a pair give the same contributions to the PELDOR signal. Under these conditions, the effect of the inter-pair interactions on the decay of the PELDOR signal can be presented as [8–10, 16]
where r k is the distance between a given spin and the k-th spin in the sample; the product includes all spins except for two spins in the pair under consideration, and \( \left\langle \ldots \right\rangle \) means averaging over the spatial distribution of spins. The effect of the interaction between the given spin and any pair on the PELDOR signal depends on the spatial correlation of the spin labels in that pair. This problem was discussed in [11]. If this effect of the spatial correlation of spin labels inside pairs is neglected, Eq. (38) can be written as
where N 0 is the total number of spin labels in the sample, V(r, θ) describes the effect of the interaction between two spins on the PELDOR signal, which is given by Eq. (16).
By substituting Eq. (16) into Eq. (38) and using the Markov method [8, 38], one obtains the effect of the inter-pair interaction on the decay of the PELDOR signal [note that we consider the case when g-factors of the labels are equal, g 1 = g 2 = g, p 1(ω A) = p 2(ω A) = p(ω A), p 1(ω B) = p 2(ω B) = p(ω B)]
C = 2C pair is the total concentration of the spin labels.
Here, p(ω F), F = A, B, denotes the probability of the inversion of the identical spins R 1 and R 2 by MW pulses with the frequency ω F [see Eq. (16)].
Equation (39) is derived under the assumption that the spatial correlation of the spin labels in pairs can be ignored. When the spatial correlation is taken into account, the \( V_{\text{inter}} = \left\langle {\mathop \prod \nolimits V(r_{k} ,\theta_{k} )} \right\rangle \) (37) can be treated as follows. Let us assume that different pairs are not correlated in space but the labels are spatially correlated inside pairs. Then, Eq. (37) can be rewritten as
Here, \( V_{\text{pair}} \) presents the effect of the dipole–dipole interaction between the given spin and any pair on the PELDOR signal, N pair is the total number of pairs in the sample. To find \( \left\langle {V_{\text{pair}} } \right\rangle \), let us consider a given spin label, e.g., R 1, of the pair, which interacts with another pair R 1*R 2* in the sample. The effect of this interaction on the PELDOR signal is presented as a product of terms caused by the interactions R 1–R 1* and R 1–R 2* (Fig. 8). Using Eq. (16), the effect of the interaction R 1–R 1*on the PELDOR signal can be written as
In this case, the dipole–dipole interaction is determined by the r 1 vector [see Fig. (8)].
The effect of the interaction R 1–R 2* on the contribution of the spin R 1 to the PELDOR signal is given by the expression similar to Eq. (41)
Note that in this case, the dipole–dipole interaction is determined by the r 2 vector (see Fig. 8).
The total effect of the interaction with the pair R 1*R 2* on the R 1 spin contribution to the PELDOR signal is the product of the expressions given by Eqs. (41) and (42)
Note that when the spin labels R 1 and R 2 are not identical, one has to calculate separately the contribution of both partners in the pair to the PELDOR signal. The effect of the interaction between the spin R 2 and the pair R 1*R 2* on the PELDOR signal caused by the spins R 2 can be written using Eq. (16a) and it is given by the expression similar to Eq. (43). We consider here the situation of the identical spin labels R so that in the case under consideration the average contributions to the signal of the spin labels R 1 and R 2 are equal.
Two vectors r 1 and r 2 are correlated because their destination points should match the condition that the length of the vector r = r 1 − r 2 is fixed. The average value of Eq. (43) \( \langle { V\left( {T,\tau } \right)_{\text{pair}} } \rangle \) is found with allowance for this correlation of r 1 and r 2 . To proceed further, we introduce two vectors: r c = (r 1 + r 2 )/2 and r = r 1 − r 2 . It is shown in Fig. 8 that r c connects the spin R 1 with the middle point between the two spins R 1* and R 2*, while the second vector r connects two partners in the pair R 1*R 2*. These vectors are determined by their lengths and their polar and azimuthal angles
The manifestation of the dipole–dipole interaction in the PELDOR signal Eq. (43) is determined by the lengths of the vectors r 1 and r 2 and cosines of the angles θ 1 and θ 2 between these vectors and the direction of the external magnetic field. Using Eq. (44), we obtain
Using Eq. (45), we find D(r 1 ) and D(r 2 ) in Eqs. (41) and (42)
Using Eqs. (41)–(43), (45), and (46), we find the effect of the inter-pair interaction on the PELDOR signal [see Eq. (40)]
where
The average value of Eq. (47) is
Note that \( \left\langle \ldots \right\rangle \) in Eq. (49) means the integration over θ and α in the interval (0, π), over φ and β in the interval (0, 2π) and the integration over r c values in the interval (\( 0,\infty \)). The total effect of the inter-pair interaction on the PELDOR signal can be presented as [see Eqs. (40), (48), and (49)]
The asymptotic value of (50) at \( N_{\text{pair}} \to \infty \) is
Here, the term \( e^{{ - b\left( {\omega_{\text{A}} } \right)\tau - b\left( {\omega_{\text{B}} } \right)T}} \) describes the effect of the inter-pair interaction on the PELDOR signal, when the spatial correlation effects are neglected [see Eq. (39)].
To compare the contributions of the correlation term w 1 w 2 and the term w 1 + w 2 in the exponent of Eq. (51), we calculated their values averaged over all possible orientations of the vectors r 1 and r 2 at the fixed r c value. Denote the average values \( \left\langle { {\text{w}}_{ 1} + {\text{w}}_{ 2} } \right\rangle = \left( { 1/\left( { 1 6\pi^{ 2} } \right)} \right)\left( {{\text{W}}_{ 1} + {\text{W}}_{ 2} } \right){\text{ and}} \, \left\langle {{\text{w}}_{ 1} {\text{w}}_{ 2} } \right\rangle = \left( { 1/\left( { 1 6\pi^{ 2} } \right)} \right){\text{W}}_{ 1} {\text{W}}_{ 2} , \) where
Here, the term W 1 + W 2 is due to the inter-pair interaction in the absence of the spatial correlation of spin labels inside the pair. The additional term W 1 W 2 appears due to the spatial correlation of spin labels in pairs. The correlation means that the distance r between the two labels in the pair is fixed, while the orientation of the vector r (see Fig. 8) is random. It is expected that this correlation effect should decrease when r c is large enough. To get better insight in the role of the spins spatial correlation, we calculated numerically the W 1 + W 2 and W 1 W 2 values for two r c values: r c = 2r and r c = 5r (Fig. 9). Figure 9c, d shows that in the case r c = 5r, the correlation term W 1 W 2 is two orders of magnitude less than the term W 1 + W 2. Thus, in this case, the correlation effect is negligible. In the case r c = 2r (see Fig. 9a, b), the correlation term W 1 W 2 is only four times less than the term W 1 + W 2 related to the pairs of the spatially non-correlated spin labels. This means that the spatial correlation of the labels in the pairs affects the PELDOR manifestation of the inter-pair dipole–dipole interaction when the distance between the pairs is comparable with the distance between partners inside the pair. We suppose that the concentration of the pairs is low so that the statistical weight of the cases, when two pairs are at the distance comparable with the distance between partners inside the pair, is negligible. Under this condition, it is correct to describe the contribution of the inter-pair interaction to the PELDOR signal by Eq. (39), which was obtained under the assumption that any correlation in the spatial positions of the spin labels in the pairs is neglected. However, this correlation effect is of importance when considering manifestations of the dipole–dipole interaction in the PELDOR signal of the spin labels in groups, since the spin labels in the group have a certain rigid architecture and all distances between spins are comparable with each other. This item will be further discussed below (Sect. 2.5).
2.3 Effect of Random Flips of Spins
In the previous Sects. 2.1 and 2.2, it was assumed that the spatial positions of the spin labels and the distances between labels do not change, and the longitudinal projection S Z of spins during the free spin evolution in the intervals between the MW pulses is conserved. However, in real systems this assumption may be violated due to the spin and/or molecular dynamics. Note that the effect of the dipole–dipole interaction on the free induction decay, primary spin echo and stimulated electron spin echo signals, when the longitudinal projection of spins changes randomly, was studied in [8–13, 24, 41, 42].
Let us consider paramagnetic particles with spins ½. Suppose that the electron spins can flip (flop) with the rate W in a random manner. These spin flips can be induced either by the electron spin–lattice interaction or by the electron spin diffusion. The random flips of the electron spins induce fluctuations of the local magnetic field, i.e., the spectral diffusion, which operates alongside with the instantaneous spectral diffusion induced by the MW pulses which rotate the electron spins. Under these conditions, the dipole–dipole interaction between the spin labels is manifested in the spin echo experiments even without the MW pump pulse (this subject was studied comprehensively in [8–13, 24, 41, 42]).
It was shown in Sect. 2.1 that in the general case, the four excitation patterns contribute to the PELDOR signal (see Table 1). If the MW frequencies \( \omega_{\text{A}} \) and \( \omega_{\text{B}} \) are separated well, the probability for any spin to be inverted by the MW pulses with both frequencies \( \omega_{\text{A}} \) and \( \omega_{\text{B}} \) can be neglected. In this case, only three inversion patterns contribute to the PELDOR signal [see Eq. (14)]. In the presence of spin flips (flops), the same three inversion patterns contribute to the PELDOR signal. But the shapes of the PELDOR signal induced by these inversion patterns change compared to Eq. (14). These patterns and corresponding contributions to the PELDOR signal are summarized in Table 2.
The shapes of the PELDOR signal (Table 2) were obtained using the results of [24], where the kinetic equations were obtained and solved for the spin density of the spin-label pairs in the situation, when the spins randomly flip (flop) due to the spin–lattice interaction [20, Eqs. (9)–(13)].
For the inversion pattern no.1 (Tables 1 and 2), the partner spin in the pair is not inverted by the spin echo-forming pulse at t = τ (Fig. 1). As a result, the dipole–dipole interaction between partners in the pair is not manifested in the spin echo signal in the absence of the random spin flips (flops). Therefore, in this case, the shape of the PELDOR signal is J 1 = 1 (Table 1). In the presence of the random spin flips (flops), the dipole–dipole interaction in the pairs is randomly modulated. As a result, the spectral diffusion occurs and the dipole–dipole interaction is manifested in the spin echo signal [8–13, 24, 41]. The shape of this contribution to the echo signal, J 1(W 2), was calculated in [24, Eq. (16)] (Table 2). It is worth to note that J 1(W 2) reveals the damped oscillations with the dipolar frequency.
For the inversion pattern no. 2 (Tables 1 and 2), the partner spin in the pair is inverted by the spin echo-forming pulse at t = τ (Fig. 1). As a result, the dipole–dipole interaction between partners in the pair is manifested in the spin echo signal even in the absence of the random spin flips. In this case, the shape of the PELDOR signal is J 2 = cos(Dτ) (Table 1). This term reflects the fact that there are pairs, in which both partners are excited by the echo-forming MW pulses, so that the dipole–dipole interaction induces the electron spin echo modulation due to the instantaneous spectral diffusion [8–12, 24]. The spectral diffusion induced by the random modulation of the dipole–dipole interaction in the presence of the random spin flips changes the shape of the echo signal. The shape of this contribution to the signal, J 2(W 2), was calculated in [24, Eq. (17)] (Table 2).
For the inversion pattern no. 3, the shape of the PELDOR signal J 3(W 2) was found in the present work using solutions of the kinetic equations for the spin density matrix of the spin-label pairs [24]. The spin density matrix of the pair ρ in the Liouville presentation was written as
Here, ρ(0) is approximated as \( \rho \left( 0 \right) = \left( {1/4} \right)\left( {1 - \left( {\hbar \omega_{0} /kT_{0} } \right)\left( {S_{1Z} + S_{2Z} } \right)} \right) \) [24], T 0 is temperature, ω 0 is the Zeeman frequency, P 1(π/2) is the super operator of the inversion of the spin R 1, P 12(π) is the super operator of the inversion of spins R 1 and R 2, P 2(π) is the super operator of the inversion of the spin R 2, L 0(t) is the super operator of the free spin evolution between the actions of the MW pulses in the course of the three-pulse ELDOR experiment (Fig. 1). Using the solution of the kinetic equation for the spin density matrix [see [24], Eqs. (12) and (13)], we found the shape J 3(W 2) of the contribution to the PELDOR signal (Table 2). It was calculated as J 3(W 2) = Tr((S 1y ) ρ(2τ)). Note that \( {\text{J}}_{ 1} \Rightarrow 1 \), \( {\it{J}}_{ 2} \Rightarrow { \cos }\left( {{\it{D}}\it{\tau} } \right) \), \( {\it{J}}_{ 3} \Rightarrow { \cos }\left( {{\it{DT}}} \right) \) when \( {\it{W}}_{ 2} \Rightarrow 0 \) (see Table 2).
The contribution of the spin label R 2 to the PELDOR signal can be obtained from Table 2 by interchanging indices 1 and 2.
The PELDOR signal of the pairs R 1 R 2 is
If the EPR spectra of R 1 and R 2 are separated well and do not overlap, so that p 2(ω A) = 0 and v 2 = 0 (we suppose that spins R 1 produce the PELDOR signal), then the PELDOR signal is
These results show that the random spin flips affect modulation of the PELDOR signal induced by the dipole–dipole interaction. The modulation effect should disappear, when the spin flips rate becomes large enough, i.e., when \( W \ge \left| D \right|/ 2 \). In this case of the fast random spin flips, an additional spin flip induced by the MW pump pulse is of no importance, and the PELDOR effect disappears. Under this condition, the intra-pair dipole–dipole interaction gives the additional decay of the PELDOR signal exp(−D 2 τ/(4 W)), which does not contain the dependence on T (here, T is the time when the MW pump pulse is applied in the three-pulse ELDOR experiment, see Fig. 1).
When the spin flips rate is small, i.e., \( W < \left| D \right|/ 2 \), the PELDOR signal oscillation frequency decreases \( \omega_{\text{osc}} \approx D - 2 W^{2} /D \). Due to this red shift of the oscillation frequency, the apparent (determined in PELDOR experiments) distance between partners in the pair can be larger than the real distance. It is well known that the slow variation of the resonance frequency (induced in the case considered by the spin flips) broadens the spectral lines [38] and this line broadening is \( \Delta \omega \approx W \). Accordingly, the increase in the spin flip rate decreases the oscillation amplitude of the PELDOR signal and smears out the oscillations. Note that these distortions of the PELDOR data are similar to the consequences of the distribution of distances between partners in pairs. Note that for the pairs, which are characterized by the magic angle, when 1 − 3cos2θ = 0, the dipole–dipole interaction frequency D = 0.
In the absence of the MW pump pulse, the contribution of the intra-pair interaction to the primary spin echo signal is given by Eq. (53), if \( p_{1} (\omega_{\text{B}} ) = p_{2} (\omega_{\text{B}} ) = 0 \). Then, Eq. (53) is reduced to
Note that the PELDOR signal [Eqs. (53) and (54)] cannot be presented as the product of the primary spin echo signal V 0(τ) and the MW pump effect V(T). These results show that the spin flips can change the oscillation amplitude and shift the oscillation frequency of the PELDOR signal. Figure 10 illustrates how random spin flips can affect the three-pulse PELDOR signal. Calculations were performed using Eq. (54).
Effect of spin flips on the contribution of the dipole–dipole interaction to the PELDOR signal for the pairs when the EPR spectra of partners do not overlap (the distance between partners in pairs r = 4 nm). Dashed line—the static limit, W = 0 (compare with Fig. 4). Solid line—W = 3 × 105 s−1
It can be seen in Fig. 10 that the random spin flips can essentially disturb the oscillation amplitude of the PELDOR signal. In the presence of random spin flips, an additional spin flip induced by the MW pump pulse in the course of the PELDOR experiments becomes of less importance, when the rate of random flips increases. As a result of this effect, the amplitude of the PELDOR signal and the oscillation amplitude become less (see Fig. 10). This decrease in amplitudes was expected.
2.4 Effect of the Conformational Transitions
Due to the molecular motion including the conformational transitions of molecular systems, the dipole–dipole interaction can be randomly modulated as well. This will also affect the manifestation of the dipole–dipole interaction of the spin labels in the PELDOR signal. The conformational transitions produce the random change of the vector r which connects the spin labels in the pair.
Due to the anisotropy of the g-tensor of spin labels, the conformational transitions can change the resonance frequencies. As a result, the same MW pulse can excite different EPR frequency regions of the spin labels in the course of the molecular conformational transitions. This effect is disturbing the PELDOR signal formation. To illustrate how the molecular conformational transitions affect the PELDOR signal, let us consider a simple model situation, when the change of the spin-label resonance frequencies as a result of the conformational transitions can be ignored. This model situation refers to the spin labels which have practically isotropic g-tensors and which have relatively small anisotropic terms in their hyperfine interaction.
Suppose there are random jumps with the average frequency W between two conformations so that the distance r between spin labels and the orientation of the vector r change randomly. In this case, the dipolar frequency D can be considered as a stochastic process D(t). Note that manifestations of the spectral diffusion in stationary and pulse magnetic resonance experiments are described in many reviews and monographs (see, e.g., [8–10, 38]).
Let us assume that the distance between two-spin labels in these configurations is r 1 and r 2. Then, the corresponding dipolar frequencies are
Let us denote
The dipolar frequencies can be written as
Thus, the dipolar frequency can be presented as a sum of the average frequency D 12 and the stochastic process Δ(t)
Due to the conformational transitions, Δ(t) jumps randomly between the values Δ and −Δ with the average frequency W. The random frequency shift Δ(t) (the spectral diffusion process) induced by the conformation transitions is similar to the modulation of the dipolar frequency shift caused by the random spin flips considered in the previous Sect. 2.3. Therefore, we can use the results presented above [Eqs. (53) and (54)].
The PELDOR signal of the pairs R 1 R 2 is
If the EPR spectra of spins R 1 and R 2 do not overlap, the PELDOR signal is (we assume that spins R 1 produce the PELDOR signal)
Here, we introduced the following notations:
where s(t) = −1 in the interval {0, τ}, s (t) = 1 in the interval {τ, 2τ},
where s(t) = 1 in the interval {0, 2τ},
where s(t) = −1 in the interval {0, T}, s(t) = 1 in the interval {T, τ}, s(t) = −1 in the interval {τ, 2τ}.
Here, \( \left\langle \ldots \right\rangle \) means averaging over all realizations of the stochastic process Δ(t). For this particular process of the spectral diffusion, the average values J 1(W) and J 2(W) were calculated in [34, Eqs. (10) and (11)]. The average value J 3(W) was calculated in the present work. The results are
where \( Q^{2} = \left( {\Delta /2} \right)^{2} - W^{2} \).
The ratio of the rate W to the frequency jump \( \left| \Delta \right| \) may differ depending on the distance between the two spin labels in the pair and on the orientation of the pair with respect to the external magnetic field in both conformations.
In the case \( W < \left| \Delta \right| \), Eq. (62) tends to
\( J_{1} \left( W \right) = e^{ - 2W\tau } \),
Thus, in the limit of the relatively slow conformational transitions, the PELDOR signal of the spin-label pairs will exhibit oscillations with the dipolar frequencies of all conformations. The oscillation amplitude is reduced due to the finite lifetime of the conformations of the molecular structure, where the spin labels are embedded. The manifestation of the molecular motion including the conformational transitions in the shape of the EPR spectra is studied well. It is well known that the slow molecular motion leads to the broadening of the EPR spectral lines. Note that there is also the shift of the resonance frequencies.
In the case \( W > \left| \Delta \right| \), Eq. (62) tends to
In the limit of the rather fast molecular transitions, the PELDOR signal oscillates with the frequency, which is the average value of the dipolar frequencies of both conformations. This fact is the manifestation of the well-known exchange narrowing effect in the EPR spectroscopy.
The frequency shift Δ depends on the variation of a length of the vector r between the spin labels and its orientation when the molecular conformation changes. Therefore, the results presented in Eqs. (62)–(64) should be averaged over all these orientations.
The specific manifestations of the molecular transformations in the PELDOR signal can be helpful. Let us assume that two oscillation frequencies were detected in the experiment. Several situations can give this result. Firstly, there may be two sub-ensembles of the spin-label pairs which have different distances between labels. Secondly, there may be triads of spins of the type AB2, which will also induce the oscillations of the PELDOR signal with two distinctive frequencies. Thirdly, two oscillation frequencies may arise due to the existence of two conformations of the molecular system, where a pair of the spin labels is embedded. The conformation transition rate is strongly temperature-dependent. This third option can be, in principle, tested by analyzing the temperature dependence of the PELDOR signal oscillations for spin labels with favorable relaxation behavior.
2.5 Groups of Spin Labels
The distance between two spin labels can be determined by detecting modulation of the PELDOR signal in the disordered system. This distance serves as a constraint condition when choosing the molecular structure [1–7].
It can be expected that more information about the structure of a system can be obtained using more than two spin labels. Then, the number of constraints increases so that the molecular structure under investigation can be specified better. Keeping this in mind, the PELDOR signal for group of spin labels was investigated comprehensively in many publications (the discussion of this problem can be found in Refs. [1–7, 19, 34, 36, 40, 43]). In these works, it was demonstrated that the modulation of the PELDOR signal makes it possible to measure the distances between the spins in groups. It was demonstrated that the determination of these frequencies can be complicated due to the spatial correlation effects [19] and presence of the combination frequencies which lead to the appearance of ghost distances between spin labels in groups [40]. To avoid these potential difficulties, it is recommended to use rather weak MW pump pulses. Naturally, the sensitivity decreases in this case. Note, it was suggested in Ref. [40] also a semiempirical correction of the background-corrected data to attenuate the influence of combination frequencies in the distance distribution.
Nowadays, the PELDOR methodology is commonly used to determine the number of spin labels and the distribution of distances between the spin labels in the group. In principle, the PELDOR data make it possible to determine the inter-spin distances and the angles between vectors connecting the spins in groups (see, e.g., [19, 34, 40]).
The current paradigm of the PELDOR study of the spin-label groups is developed for the spin labels A and B, which have the non-overlapping EPR spectra. In practice, the spin labels are used, the EPR spectra of which overlap. In this section, we extend our results obtained for the pairs of spin labels with the overlapping EPR spectra to the groups of spins.
Let us consider a group of N spin labels with spin S = 1/2. The contribution of the interaction between the spin labels inside the group to the PELDOR signal is given by [25]
where V kn determines the effect on the signal of the chosen k-th spin caused by the interaction with the n-th partner in the group This effect was discussed in Sect. 2.1.
In disordered systems, the PELDOR signal contains the contributions of the spin-label groups with different spatial orientations. We suppose that as a whole the spin group is oriented randomly but the relative orientations of the vectors inside the group, e.g., of two r kn and r km , vectors, are fixed. Therefore, it is necessary to take into account this correlation in the directions of the vectors when averaging V [Eq. (65)] over all possible orientations of the spin groups. The average V value is found as [25]
There is a number of publications (see, e.g., [5, 25] ), where the correlations in the spatial positions of the spins inside groups are neglected and the average V value is presented as the product of the average terms \( V_{kn} \) of the each n-th partner spin label
Equation (67) can be written in the explicit form using the results presented in Sect. 2.1. This approximation can give reasonable results, when the probability of the inversion of the spins by the MW pump pulse is small, \( p\left( {\omega_{\text{B}} } \right) \ll 1 \).
In the general case, the average value [Eq. (66)] depends on the correlation in the mutual spatial positions of the spin labels in groups. Here, we consider the PELDOR signal in two situations.
The first model system Let us consider the situation, when the EPR spectra of the spins R 1 and R 2 do not overlap. This case is comprehensively considered in the current PELDOR theory (see, e.g., [1, 5, 25, 30, 33, 34]). Here, we shortly summarize the known results and present some results of numerical simulations which illustrate some features of spin-label groups PELDOR signal modulation: the appearance of the combined frequencies of the modulation, the manifestation of the spatial correlation of spin labels in the group. These features are relevant to the spin labels with the overlapping EPR spectra as well and the results for this model situation will serve as a reference situation when considering further the PELDOR signal for the spin labels with overlapping EPR spectra.
So let us imagine the spin-label groups of the type AB N − 1: the spin label R 1 is excited by the MW pulses which form the spin echo signal (R 1 is a spin label of the type A [8, 9]) and it is not excited by the MW pump pulse, while the spin label R 2 is excited only by the MW pump pulse (R 2 is the spin label of the type B [8, 9]). In this case, the effect of the n-th spin label R 2 on the PELDOR signal induced by the spin R 1 is given by Eq. (1): \( V_{{ 1 {\text{n}}}} \left( T \right) = 1 - p_{R2} \left( {\omega_{\text{B}} } \right) \, \left( {1 - \cos \left( {D_{{ 1 {\text{{\it{n}}}}}} T} \right)} \right) \).
The effect of the N − 1 spin labels R 2 of a group on the PELDOR signal is described as
We denote p R2(ω B) ≡ p 2. Here, we assume that the MW pump pulse excites all spins R 2 in the group in the same manner. Then, Eq. (68) can be rewritten as a series (see, e.g., [40])
The first term on the right-hand side of Eq. (69) depends on the number N of spins and does not depend on the distances between spin labels. The second term on the right-hand side of Eq. (69) contains the average cosines \( \left\langle {\cos \left( {D_{{1{\text{n}}}} T} \right) } \right\rangle \), which were discussed above in Sect. 2.1 in detail. According to this discussion, at times T larger than the time of the fast decay (TD 01n > 1) the average cosine \( \left\langle { { \cos }\left( {D_{{ 1 {\text{{\it{n}}}}}} T} \right) } \right\rangle \Rightarrow \left( {\pi /\left( { 1 2D_{{0 1 {\text{n}}}} T} \right)} \right)^{ 1/ 2} { \cos }\left( {D_{{0 1 {\text{{\it{n}}}}}} T - \pi / 4} \right) \) [see Eq. (24)]. This term leads to the modulation (oscillations) of the PELDOR signal. There are N − 1 frequencies {D 01n } but some frequencies can be close to each other or coincide if some distances between spin labels are close to each other or equal. The term of the \( \left\langle {\cos \left( {DT} \right) } \right\rangle \) type determines the modulation pattern of the PELDOR signal in the case of spin-label pairs. In the case of the AB N − 1 spin-label groups, the additional (combination) oscillation frequencies appear, which arise from the second (p 22 ), third (p 32 ) and higher order terms in the series [Eq. (69)] containing products of two cosines and other terms containing products of \( 3, \, 4, \ldots ,N - 1 \) cosines, i.e., terms like \( \left\langle {\cos \left( {D_{{1{\it{n}}}} T} \right) \, \cos \left( {D_{{1{\it{k}}}} T} \right)\cos \left( {D_{{1{\it{m}}}} T} \right) } \right\rangle \) (see the comprehensive discussion of this item in Refs. [19, 36, 40]).
The effect on PELDOR signal of the spatial correlation of the spin labels in groups is recognized. Here, we present one more quantitative illustration of the significance of the spatial correlations of spin labels in the PELDOR signal.
Let us consider the average of the product of two cosines [see the third term in Eq. (69)]
This term leads to the additional oscillation frequencies Ω + = (D 1n + D 1k ) and Ω − = (D 1n − D 1k ). As it was demonstrated, e.g., in [19], the distributions of the frequencies Ω + and Ω − depend on the correlation in the mutual spatial orientation of the vectors r 1k and r 1n . Let us denote the angle between these vectors as ϕ and the angle of the rotation of the vector r 1n around the direction of the vector r 1k as ζ. Then, the cosines of the angles between the directions of the external magnetic field and the vectors r 1k and r 1n are given by c k = cos(θ) and c n = cos(θ) cos(ϕ) − sin(θ) sin(ϕ) cos(ζ), respectively [19]. Then, one has
Using Eqs. (71), one can find the distributions of the frequencies Ω + and Ω −. These distributions can be found straightforwardly in the particular case, when the r 1k and r 1n vectors are located on the same line, i.e., the angle ϕ = 0 or π, so that c k = c n = cos(θ). In this case, the distribution of the combination frequencies has singularities at (Ω+)sing. = (D 01n + D 01k ) and (Ω−)sing. = (D 01n − D 01k ). The same singularities are expected for the non-correlated situation. However, in the general case, when the mutual orientation of the r 1k and r 1n vectors is correlated, the distributions of the frequencies Ω +=(D 1n + D 1k ) and Ω − = (D 1n − D 1k ) can change [19]. To illustrate the possible scale of the spatial correlation effect, we calculated the distributions of the frequencies Ω + and Ω − using the Monte Carlo method for several architectures of spin systems. Some results are presented in Fig. 11.
Figure 11 demonstrates that the spatial correlation of the spin labels affects essentially the distribution of the combination frequencies. The distribution of the frequency Ω − manifests a maximum at Ω − = (D 01 − D 02) as it was expected on a basis of the qualitative speculations. The situation is more complicated for the distribution of the frequency Ω + = (D 1 + D 2). In principle, there is always a singularity at Ω + = (D 01 + D 02). But this is not the major feature of this distribution. The pronounced maximum is shifted with respect to the frequency Ω + = (D 01 + D 02). For example, when r 1 = r 2 = 5 nm and the angle between vectors r 1 and r 2 is ϕ = π/2, the pronounced singularity of the distribution of the frequency Ω + occurs not at Ω + = 2D 0 (as it might be expected) but at Ω + = D 0 (Fig. 11a). Note that in this case, the distribution of the combination frequency Ω + = (D 1 + D 2 ) is similar to the distribution of the dipolar frequencies in pairs (compare Figs. 2, 11a). There is only a very “minor” (not pronounced) singularity at Ω + = 2D 0. Note that in this case, the broad part of the distribution has low intensity.
In other two examples shown in Fig. 11b, c, the pronounced maxima of the distribution of the combination frequency Ω + is also shifted considerably to values lower than the D 01 + D 02. Another remarkable feature of these distributions is the relatively small fractions of the systems, which have frequencies around the singular frequencies. In fact, the intensity of the distributions around the singular points is much less pronounced than it was for the dipolar frequencies D in the case of the pairs (compare Figs. 2, 11b, c). Thus, in this case, the fraction of the systems, which contribute to the constructive interference at T > T decay, is much less than that in the case of the spin-label pairs. At the same time, the fraction of the systems, which give the destructive interference, increases, since the broad part of the distribution is of relatively high intensity (Fig. 11b, c).
The distributions in Fig. 11 are in fact the Fourier transforms of the average cosines \( \left\langle {\cos \left( {\left( {D_{1} + D_{2} } \right)T} \right) } \right\rangle \quad {\text{and}} \quad \left\langle { \cos \left( {\left( {D_{1} - D_{2} } \right)T} \right) } \right\rangle \). Direct calculations in the time domain presented in (Fig. 12) are in agreement with expectations on the basis of the distributions (data in the frequency domain) shown in Fig. 11.
Exact average value of \( \left\langle {{ \cos }\left( {{\text{D}}_{ 1} {\text{T}}} \right){ \cos }\left( {{\text{D}}_{ 2} {\text{T}}} \right) } \right\rangle \) (solid curves) and approximate average value of this cosines product calculated as \( \left\langle {{ \cos }\left( {{\text{D}}_{ 1} {\text{T}}} \right) } \right\rangle \left\langle {{ \cos }\left( {{\text{D}}_{ 2} {\text{T}}} \right) } \right\rangle \) (dot curves). Simulations are done for the following parameters: a r 1 = r 2 = 5 nm, ϕ = π/2; b r 1 = r 2 = 5 nm, ϕ = π/3; c) r 1 = 2 nm, r 2 = 3 nm, ϕ = π/2
In time-domain representation, the effect of the spatial correlation can be characterized by the comparison of two quantities: the exact value of the product of two cosine terms, \( J_{\text{corr}} = \left\langle {\cos \left( {D_{1} T} \right)\cos \left( {D_{2} T} \right) } \right\rangle \), taking into account the spatial correlation of the positions of spins, and the approximate value of this product of cosines \( J_{\text{noncorr}} = \left\langle {{ \cos }\left( {D_{1} T} \right) } \right\rangle \left\langle {{ \cos }\left( {D_{2} T} \right) } \right\rangle \) neglecting the spatial correlation effect.
Calculations were performed for the same distances between the spin label A and two spin labels B, r 1 and r 2, and angles ϕ between the vectors r 1 and r 2, which were used in the calculations of the distribution of the combination frequencies (Fig. 11). The calculation results are shown in Fig. 12.
Figure 12 shows that J(T) decays fast in the interval T{0, T decay} and then, at T > T decay it varies non-monotonically and demonstrates a kind of a modulation pattern. The exact J corr and approximate J noncorr average values deviate at T > T decay, after the fast decay. This deviation is the most pronounced in Fig. 12a. Qualitatively, the behavior of J corr and J noncorr is similar to the time dependence of the average cosine \( \left\langle {\cos \left( {DT} \right) } \right\rangle \), i.e., only the small fraction of the triads continues to give the constructive interference contribution to the oscillations of J at T > T decay. Comparison of Figs. 2 and 12 shows that at T > T decay, the modulation amplitude induced by the term \( \left\langle {\cos \left( {D_{1} T} \right)\cos \left( {D_{2} T} \right) } \right\rangle \) does not exceed p cc = 0.1 and it decreases faster than that induced by the term \( \left\langle {\cos \left( {D_{1} T} \right) } \right\rangle {\text{or}} \left\langle {\cos \left( {D_{2} T} \right) } \right\rangle \) (see Sect. 2.1). The deviation between J corr and J noncorr is pronounced most strongly, when the distances between spins are the same, r 1 = r 2, ϕ = π/2 (Fig. 12a). In this case, at T > T decay, the approximate result J noncorr oscillates with the frequency D 10 + D 20 = 2D 0. At the same time, the exact result J corr oscillates not with the frequency 2D 0 but with the frequency close to D 0 in accordance with the distribution of combination frequencies shown in Fig. 11a.
Note that the model situation of the groups with N = 3 was studied comprehensively in Ref. [19]. It was demonstrated that the spatial correlation effect discussed becomes important when the probability of the spin inversion increases. According to [19], the promising strategy of the PELDOR experiments when studying the triads or larger (N > 3) spin-label groups AB N − 1 is the variation of the probability p R2(ω B) of the spin inversion by the MW pump pulse. When \( p_{R2} \left( {\omega_{\text{B}} } \right) \ll 1 \), the linear term \( \sum_{n} \left\langle {\cos \left( {D_{1n} T} \right) } \right\rangle \) dominates in the signal modulation and the PELDOR signal can give a set of frequencies {D 01n }. As a result, it is possible to determine a set of distances between spin labels A and B. Note that for the AB N − 1 groups, the number of the oscillation frequencies is N − 1. When p R2(ω B) increases, many combination frequencies can contribute to the modulation pattern of the PELDOR signal, and the contributions of different harmonics can interfere destructively. As a result, the modulation of the PELDOR signal can be smeared out.
The second model system Let us consider the R N group of identical spin labels R. Thus, this model refers to the spin labels with totally overlapping EPR spectra. In addition, we assume that the EPR spectrum of the spin labels R is wide enough so that it is possible to excite electron spins of R selectively in the frequency space. In PELDOR experiments, the MW pulses with frequencies ω A and ω B excite spins with the resonance frequencies in intervals (ω A − ω 1A , ω A + ω 1A) and (ω B − ω 1B , ω B + ω 1B), respectively. In this case, the contribution of the intra-group dipole–dipole interaction to the three-pulse ELDOR signal is described by Eq. (66), where the n-th spin-label effect on the signal from the k-th spin label is given by Eq. (16). The average contribution of any spin label of the group to the PELDOR signal is given as
Here, the notations \( \Lambda_{kn} = \left\langle {p(\omega_{\text{B}} )} \right\rangle + \left\langle {p(\omega_{\text{A}} )} \right\rangle ( 1 - { \cos }\left( {D_{kn} \tau } \right),p_{\text{B}} = \left\langle {p(\omega_{\text{B}} )} \right\rangle \) are introduced. Note that there are evident relations Λ kn = Λ nk , D kn = D nk , cos(D nk T) = cos(D kn T). The group of the N spin labels has N(N − 1)/2 characteristic frequencies {D 0kn }. Note that the Eq. (72) is reduced to Eq. (8) in Ref. [40] when \( \left\langle {p(\omega_{\text{A}} ) } \right\rangle = 0 \), i.e., when the EPR spectra of the spin labels do not overlap.
The PELDOR signal [Eq. (72)] has the term V 0, which does not depend on T:
The term V 0 depends on the τ value. However, in the PELDOR experiments, τ is long enough so it might be justified to ignore all oscillating terms in Eq. (72). Then,
When the probability p B of the spin-label inversion by the MW pump pulse is small enough, the oscillations of the PELDOR signal induced by the intra-group interaction are mainly determined by the terms in Eq. (72), which are linear in cosine terms
Assuming that \( \Lambda_{kn} \approx \left\langle {p(\omega_{\text{B}} )} \right\rangle + \left\langle {p(\omega_{\text{A}} )} \right\rangle \) and using Eq. (24) at relatively large T values (T > T decay), it is possible to approximate V 1(T) [Eq. (75)] as
There are N (N − 1)/2 characteristic frequencies D 0kn determined by the distances r kn between the spin labels in the R N group. In fact, some distances can be close or even coincide depending on the architecture of the R N group. Let us introduce the distribution function f(r) normalized to 1, which gives the probability for any two partners in the group to have the distance r between them, while \( \int {f\left( r \right)r^{2} {\text{d}}r = 1} \). Then, Eq. (76) can be written as (at T > T decay)
Using Eqs. (74) and (77), the PELDOR signal [Eq. (72)] can be written as
When p B and/or the number N of the spin labels in the group increases, the terms with products of cosines can become more significant.
In the current literature [1–6], the approximate Eq. (79) is used
The comparison of Eq. (78) with the Eq. (79) shows that they predict the same oscillation frequencies. However, Eqs. (78) and (79) predict the relatively different contributions of the non-oscillating and oscillating terms. This subject was already discussed in Sect. 2.1 for spin-label pairs. Thus, the results of our consideration might be important, when the modulation amplitude of the normalized PELDOR signal is used to obtain the number of spin labels in the group.
The results presented for the PELDOR signal modulation induced by the dipole–dipole interaction in the groups of spin labels with overlapping EPR spectra show that the modulation pattern differs, in principle, from the case of the groups of spin labels with non-overlapping EPR spectra (current theory case, see, e.g., Eq. (8) in Ref. [40]), the numerous new terms appear in the expression for the PELDOR signal [see Eq. (72)]. In fact, in both cases (in current theory and the theory presented in this work), a set of the PELDOR signal modulation frequencies is the same, since in both cases, the spin dynamics of the system proceeds with the same spin-Hamiltonian. In both cases, the same characteristic dipolar frequencies and their combinations operate. But the current theory and the present theory predict, in principle, different amplitudes for the contributions with different frequencies.
Thus, the interference picture, the modulation pattern of the observed PELDOR signal can differ in the framework of the present theory compared to the current theoretical description. Note, in the case of the spin-label pairs, it was pointed out that the effect of the new terms in the PELDOR signal of the spin labels with overlapping EPR spectra can be eliminated using the proper signal normalization procedure [Eq. (20)] if the probability to invert the same spin by the both, ω A and ω B frequencies, MW pulses is negligibly small.
2.6 Estimation of the Validity of the Assumption Eq. (13).
It was shown (Table 1) that for the pairs R 1 R 2, when the partners have the EPR spectra, which overlap, the three-pulse ELDOR signal contains the terms with cos(DT) and cos(D(τ − T)). According to Table 1, the amplitude of the cos(DT) term is
and the amplitude of the cos(D(τ − T)) term is
Here, \( p_{2} (\omega_{\text{A}} ,\omega_{\text{B}} )) \equiv \left\langle { p\left( {\varOmega_{2} |\omega_{\text{B}} ,t_{p2} } \right)p\left( {\varOmega_{2} |\omega_{\text{A}} ,t_{p3} } \right) } \right\rangle \) is the average probability that the same spin R 2 with the resonance frequency Ω 2 is inverted by the MW pump pulse with the frequency ω B at the moment T and by the echo-forming pulse with the frequency ω A at the moment τ; \( v_{1} \equiv \left\langle { m1_{y} \left( {\varOmega_{1} } \right)p\left( {\varOmega_{1} |\omega_{\text{A}} ,t_{p3} } \right)\left( {1 - p\left( {\varOmega_{1} |\omega_{\text{B}} ,t_{p2} } \right)} \right)} \right\rangle \) (Table 1).
The exact expression for the PELDOR signal without the assumption Eq. (13) is [compare with approximate expression given by Eq. (16)]
The contribution of the spin R 2 to the PELDOR signal is given by the expression similar to that for the spin R 1 [see Eq. (16a)]
where \( p_{1} (\omega_{A} ,\omega_{B} )) \equiv \left\langle { p\left( {\varOmega_{1} |\omega_{B} ,t_{p2} } \right)p\left( {\varOmega_{1} |\omega_{A} ,t_{p3} } \right) } \right\rangle \).
If R 1 and R 2 are the same spin labels, their total contributions to the PELDOR signal is
Here, \( p(\omega_{{A}} ) = \left\langle {p\left( {\varOmega |\omega_{{A}} ,t_{p3} } \right) } \right\rangle ,p(\omega_{{B}} ) = \left\langle {p\left( {\varOmega |\omega_{{B}} ,t_{p2} } \right) } \right\rangle \).
In Sects. 2.1, 2.2, 2.3, 2.4, 2.5, we assumed that
To estimate the validity of this assumption, the numerical calculations were performed for biradicals I containing 1-oxyl-2,2,5,5-tetramethylpyrroline-3-yl spin labels and biradicals II containing 3-imidazoline spin labels. The structures of these biradicals are presented in Fig. 15.
Using the spectra in Fig. 15b, d, we calculated p(ω A,ω B), p(ω A) and p(ω B). The results are given in Table 3. Note that during these calculations, we use the total EPR spectrum of the biradical. During these calculations, we assumed that the EPR spectra of the spin labels are close to the EPR spectrum of the biradicals studied.
We calculated the parameters relevant to our experiments, which are discussed in Sect. 3 (Table 3, the second and fifth columns). We calculated also the possible contribution of the term \( \left\langle {\cos (D(\tau - T)) } \right\rangle \) which occurs, when the frequency ω B of the MW pump pulse is close to the frequency ω A of the echo-forming MW pulses (Table 3, the third and sixth columns). As it was expected, the p 2(ω A,ω B) value increases, when these two frequencies ωA and ωB come closer, and the p2(ω A,ω B) value becomes negligible, when these frequencies are removed far (Table 3, the fourth and seventh columns). It can be seen that under the conditions in our experiments the inequality \( p_{2} (\omega_{\text{A}} ,\omega_{\text{B}} ) \ll p_{2} (\omega_{\text{B}} ) \) is fulfilled so that the assumption Eq. (13) is justified in the typical experimental situations (see. Table 3, the second and fifth columns).
The excitation of the same spin by the MW pulses with both frequencies ω A and ω B can affect the PELDOR signal in several ways. It decreases the amplitude of the term containing cos(DT) [see Eqs. (80), (82), and (84)]. There appears a new term containing cos(D(τ − T)) [Table 1 and Eqs. (82) and (84)]. This term has an interesting feature. When T increases, dephasing of oscillations with different frequencies D decreases since τ − T decreases (Fig. 13). This possibility was mentioned in Ref. [6]. as well with reference to the “2 + 1” pulse train electron spin echo method [12, 13].
Average cosine \( \left\langle {{ \cos }\left( {{\text{D}}\left( {\tau - {\text{T}}} \right)} \right) } \right\rangle \) calculated for r = 3 nm, D 0 = 11.5 × 106 rad/s, τ = 2,000 ns. The oscillation period is close to T 0 = 2π/D 0 = 547 ns (compare with Fig. 3)
The T-dependences of the average cosine \( \left\langle {\cos \left( {DT} \right) } \right\rangle \) term (Fig. 3) and that of the average cosine \( \left\langle {\cos \left( {D(\tau - T)} \right) } \right\rangle \) term (Fig. 13) are opposite in the interval {0, τ}. To illustrate the manifestation of the average cosine \( \left\langle { \cos \left( {D(\tau - T)} \right) } \right\rangle \) term, we calculated the quantity \( c_{1} \left\langle {\cos \left( {DT} \right)} \right\rangle + c_{2} \left\langle { \cos \left( {D(\tau - T)} \right) } \right\rangle \) and compared it with the average cosine \( \left\langle {\cos \left( {DT} \right) } \right\rangle \) (Fig. 14).
Average cosine \( \left\langle {{ \cos }\left( {\text{DT}} \right) } \right\rangle \) (solid curves) and \( c_{1} \left\langle {\cos \left( {DT} \right) } \right\rangle + c_{2} \left\langle {\cos \left( {D\left( {\tau - T} \right)} \right)} \right\rangle \) (dotted curves) calculated for r = 3 nm, D 0 = 11.5 × 106 rad/s, τ = 2,000 ns: a c 1 = 0.9, c 2 = 0.1; b c 1 = 0.8, c 2 = 0.2
It can be seen that the average cosine \( \left\langle {\cos \left( {D(\tau - T)} \right) } \right\rangle \) term leads to the decrease of the amplitude of the PELDOR signal at T = 0 and to the decrease of the modulation amplitude. This means that average cosine \( \left\langle {\cos \left( {D(\tau - T)} \right) } \right\rangle \) term can affect the amplitude of the normalized PELDOR signal. Thus, when interpreting the PELDOR experimental data, one should keep in mind that due to the excitation of the same spin by MW pulses with both frequencies ω A and ω B, the apparent modulation amplitude of the PELDOR signal is less than that expected disregarding this excitation. The contribution of the average cosine \( \left\langle { \cos \left( {D(\tau - T)} \right) } \right\rangle \) term to the PELDOR signal affects the phase of the signal modulation as well.
3 Experimental Data and Their Analysis
To test the results of our theory, we performed the PELDOR experiments on the biradicals I containing 1-oxyl-2,2,5,5-tetramethylpyrroline-3-yl spin labels and biradicals II containing 3-imidazoline spin labels (Fig. 15). The paramagnetic centers in these biradicals are identical and their EPR spectra overlap completely.
All experiments were performed at Q-band on an Elexsys E-580 spectrometer (Bruker) equipped with a Bruker Flexline probehead EN5107D2. Q-band measurements were performed to eliminate the modulation of the PELDOR signal due to the hyperfine interaction between electron spins and distant protons. Three-pulse ELDOR was carried out using the sequence (π/2) mwA-T-(π) mwB-(τ-T)-(π) mwA-τ-echo for different τ values. The lengths of the π and π/2 pulses were 52 and 26 ns, respectively. All measurements were performed at 80 K. Temperature was controlled using an ER4118CF cryostat and an ITC503 temperature controller (Oxford).
The PELDOR signal V exp(T, τ) at T = 0 is reduced to the primary spin echo signal V exp(τ) obtained without applying the MW pump pulse, V exp(T = 0, τ) = V exp(τ). This fact makes it possible to find the initial amplitude of the PELDOR signal. The normalized PELDOR signal was found as V n = V exp(T, τ)/V exp(τ). According to the discussion in the Sect. 2.1 [see Eqs. (18)–(20) and the discussion around these equations] this particular normalization procedure can be useful to demonstrate a presence of the new terms in the PELDOR signal.
The results of the PELDOR experiments and simulations are shown in Figs. (16) and (17). The simulations were performed using Eq. (18). The simulations according to the current theory [Eq. (1)] were shown as well. To simulate the PELDOR curves, the probabilities p(ω A) and p(ω B) of the spin inversion by the MW pulses are needed. They were found using the EPR spectra (Fig. 15) and Eq. (9) (Table 3, the second and fifth columns). The distances between two spin labels in biradicals were determined from the PELDOR signal modulation frequency. For biradical I, this distance r = 3.8 nm, for biradical II, r = 1.8 nm.
Dependence of the normalized PELDOR signal on the τ value and its simulations for biradicals I: (a) for fitting parameters p f(ω A), p f(ω B); (c) for calculated parameters p theor(ω A), p theor(ω B) and for biradicals II: (b) for fitting parameters p f(ω A), p f(ω B); (d) for calculated parameters p theor(ω A), p theor(ω B). Experimental data are squares and circles. Simulations using Eq. (18) are shown as solid lines. Dashed lines are simulations using Eq. (1). The fitting and calculated parameters p(ω A), p(ω B) are given in the text and Table 3. In the case of biradical I, τ = 1,064 and 1,632 ns, in the case of biradical II, τ = 190 and 252 ns
Normalized experimental PELDOR data (squares) and their simulations for biradicals I (a, c) and II (b, d). Solid lines show simulations using Eq. (18). Dashed lines show simulations using Eq. (1). The (a, b) present the simulations with the theoretically calculated parameters p theor(ω A), p theor(ω B). The (c, d) present the simulations with the fitting parameters p f(ω A), p f(ω B). In the case of biradical I, τ = 2,952 ns, in the case of biradical II, τ = 596 ns
Figure 16a, c shows that in the case of biradical I, the experimental normalized PELDOR signal V n does not manifest the τ-dependence, while in the case of biradical II (Fig. 16b, d) there is the τ-dependence. According to the current PELDOR theory, V n should not depend on τ [Eq. (1)]. But the current theory does not hold, when the EPR spectra of spins in the biradical overlap. When these spectra overlap, the normalized PELDOR signal should demonstrate the τ-dependence [Eq. (18)]. Thus, the experimental data for biradical II are qualitatively in agreement with our theory. According to our theory [Eq. (18)], the τ-dependence of the PELDOR signal should be less pronounced, when p(ω A) decreases [Eq. (19)]. The calculated p(ω A) value (see Table 3) shows that it is about 25 % less for biradical I. There is another reason why the τ-dependence of the normalized PELDOR signal is less pronounced for biradical I than for biradical II. According to Eq. (18), the τ-dependence of the normalized PELDOR signal is determined by the effective parameter p eff(τ),
According to Eq. (24), when D 0 τ > 2π,
In our PELDOR experiments, (π/(12D 0 τ))1/2 is 0.108 and 0.125 for biradicals I and II, respectively. Therefore, the effective value of p(ω A) [Eq. (87)] is about 15 % less for biradical I.
Thus, our theory has a potential to interpret qualitatively the experimental observation concerning the τ-dependence of the normalized PELDOR signals for biradical I and biradical II.
However, the situation is more complicated concerning the quantitative description of the modulation amplitude of the PELDOR signal. According to Eq. (86), the normalized PELDOR signal is
Since p theor(ω A) < 1, then,
It appears that the simulations with the theoretically computed parameters p theor(ω A) and p theor(ω B) do not describe perfectly the PELDOR signals (see Fig. 16c, d). The simulations give even worse results if the effective parameters p eff(ω A) and p eff(ω B) are used since p eff(ω B) > p theor(ω B). To obtain good agreement between simulations and experimental data, the following fitting parameters should be used: p f(ω A) = 0.08, p f(ω B) = 0.072 for biradical I and p f(ω A) = 0.18, p f(ω B) = 0.12 for biradical II. The results of the simulations with these fitting parameters are presented in Fig. 16a, b. We see that good agreement is achieved when the simulations are done with the parameter p(ω B), which is less than the values obtained by the theoretical calculations (Table 3).
To test the fitting parameters p f(ω A) and p f(ω B) obtained from the fitting the τ-dependence of the PELDOR signal (Fig. 16), the PELDOR signals were studied in the extended range of T values (Fig. 17).
Figure 17 shows that the fitting parameters p f(ω A) and p f(ω B) obtained when studying the τ-dependence of the PELDOR signals are reasonably good fitting parameters for the T-dependence of the PELDOR signals as well. The fitting parameters p f(ω A) and p f(ω B) differ from their calculated values p theor(ω A) and p theor(ω B).
The observation that the p f(ω B) value is less than the p theor(ω B) value can be explained as follows. One option is to take into account the possibility of the inversion of a sub-ensemble of spins by the MW pulses of both frequencies, ω A and ω B. This option was discussed in Sect. 2.6. It was shown that under conditions of our experiments, this effect reduces p(ω B) but the reduction is rather small, it is around 0.005–0.01 (a few percents) for our experimental situation. Another option is the effect of the contribution of the term containing \( \left\langle {\cos \left( {D(\tau - T)} \right) } \right\rangle \) to the PELDOR signal. It was shown in Sect. 2.6 (Fig. 14) that this term can reduce the initial amplitude of the PELDOR signal and it decreases the amplitude of the PELDOR signal oscillations. Spectral diffusion induced by the spin–lattice relaxation of spins (Sect. 2.3) and the molecular isomerization (Sect. 2.4) can be also responsible for the reduction of the oscillation amplitude of the PELDOR signal. The discrepancy of the parameters p f(ω B) and p theor(ω B) can also arise from the experimental errors when determining the initial behavior of the PELDOR signal, the initial amplitude of the PELDOR signal. We plan to study this problem separately.
4 Conclusions
Experimental PELDOR data contain information about the architecture of spatial positions of the spin labels. This information is of major importance since it can be used when studying, e.g., structures of proteins and other biologically actual compounds. If the spin labels are site-directed, the spin labels architecture gives a “contour” of these visually disordered molecular (supramolecular) systems, which can serve as constraints when determining the structure of proteins etc.
The PELDOR experiments can be instructive not only concerning the structure of systems studied but also concerning their spin and molecular dynamics. It is better to perform the structural studies at low temperatures, when the molecular motion (including conformational transitions of macromolecules) and spin–lattice relaxation process proceed slowly and do not disturb the PELDOR data. The random spin flips due to the spin–lattice relaxation or the spin diffusion or the molecular mobility can reduce the modulation amplitude and frequencies of the PELDOR signal modulation.
The best PELDOR strategy for studying the architecture of spin groups would be to use the spin labels A and B, which have the non-overlapping EPR spectra. In this case, the current paradigm of the PELDOR application can be successfully used. In practice, the spin labels are used, the EPR spectra of which overlap. In this work, we presented the generalization of the current PELDOR theory for the spin labels with the overlapping EPR spectra. In this work, we extended the three-pulse ELDOR theory for the spin labels in pairs and groups to the case, when the spin labels EPR spectra overlap. The three-pulse ELDOR signal for the spin labels with overlapping EPR spectra was analyzed theoretically in detail.
In the general case, the PELDOR signal has new contributions. One contribution arises from the fact that the spin echo-forming MW pulses can excite both spin labels in pairs and several spin labels in groups. As a result, the conventional primary spin echo modulation effect is manifested in the PELDOR signal. Another contribution is due to the excitation of the same spin label by the MW echo-forming pulse and the pump pulse in the PELDOR experiment. These new contributions interfere with the contribution to the PELDOR signal considered in the current (conventional) theory.
The modulation pattern of the PELDOR signal is a sum of oscillations (harmonics) with characteristic frequencies of the dipole–dipole interactions between spin labels and their linear combinations. A set of possible oscillation frequencies for the spin-label systems considered is the same in the current theory and in the generalized theory presented in this work, since these frequencies are determined by the same spin-Hamiltonian. But relative contributions of different harmonics predicted by the current theory and by the theory presented in this work are, in principle, different. Thus, the current and the generalized here theory can, in principle, lead to different distance distributions. The results of our consideration might be of importance when the modulation amplitude of the PELDOR signal is used, e.g., to obtain the number of spin labels in the groups. For example, neglecting the new terms in the PELDOR signal results in a p 2100 % error when the number of the spin labels in the groups is determined (here, p 2 is the probability of the inversion of the same spin label by the MW echo-forming pulse and the pump pulse in the PELDOR experiment).
It was shown that the manifestation of the intra-pair dipole–dipole interaction in the PELDOR signal cannot be presented as a product of the primary echo signal in the absence of the MW pump pulse and the factor, which describes the effect of the MW pump pulse on the PELDOR signal. This observation affects the strategy of interpreting the experimental data. In fact, when the multiplicative behavior is valid, it is rather straightforward to subtract the contribution of the MW pump pulse to the PELDOR signal from the experimental data. In this case, the PELDOR effect can be characterized by the ratio of the data of the two experiments: PELDOR and primary echo.
In this work, we were focused on the three-pulse ELDOR. At present, the four-pulse ELDOR is widely and successfully exploited. The four-pulse ELDOR theory for the spin labels with overlapping EPR spectra is under development and will be presented in a separate publication.
References
A.D. Milov, A.G. Maryasov, Yu.D. Tsvetkov, Appl. Magn. Reson. 15, 107–143 (1998)
A.G. Maryasov, Yu.D. Tsvetkov, J. Raap, Appl. Magn. Reson. 14, 101–114 (1998)
G. Jeschke, Y. Polyhach, Phys. Chem. Chem. Phys. 9, 1895–1910 (2007)
K. Moebius, A. Savitsky, High-Field EPR Spectroscopy on Proteins and Their Model Systems (RSC Publishing, Cambridge, 2009)
Yu.D. Tsvetkov, A.D. Milov, A.G. Maryasov, Uspekhi Khimii (in Russian) 77, 487–520 (2008)
G. Jeschke, Ann. Rev. Phys. Chem. 63, 419–446 (2012)
A.D. Milov, Yu.D. Tsvetkov, A.G. Maryasov, M. Gobbo, C. Prinzivalli, M. De Zotti, F. Formaggio, C. Toniolo, Appl. Magn. Reson. 44, 495–508 (2013)
K.M. Salikhov, A.G. Semenov, Yu.D. Tsvetkov, Electron Spin Echo and Its Applications (Nauka, Novosibirsk, 1976)
W.B. Mims, in Electron Paramagnetic Resonance, ed. by S. Geschwind (Plenum Press, New York, 1972), pp. 263–351
K.M. Salikhov, Yu.D. Tsvetkov, in Time-Domain ESR Spectroscopy, ed. by L. Kevan, R. Schwartz (Wiley, New York, 1979)
A.M. Raitsimring, K.M. Salikhov, Bull. Magn. Reson. 7, 184–195 (1985)
V.V. Kurshev, A.M. Raitsimring, Yu.D. Tsvetkov, J. Magn. Reson. 81, 441–454 (1989)
V.V. Kurshev, A.M. Raitsimring, T. Ichikawa, J. Phys. Chem. 95, 3564–3568 (1991)
V.F. Yudanov, K.M. Salikhov, G.M. Zhidomirov, Yu.D. Tsvetkov, Theor. Eksper. Khim. 5, 663–668 (1969)
V.V. Konovalov, S.A. Dzuba, A.M. Raitsimring, K.M. Salikhov, Yu.D. Tsvetkov, Khim. Vysokikh Energii. 14, 525–530 (1980)
A.D. Milov, K.M. Salikhov, M.D. Schirov, Fiz. Tverd. Tela (in Russian) 23, 975–982 (1981)
R.E. Martin, M. Pannier, F. Diederich, V. Gramlich, M. Hubrich, H.W. Spiess, Angew. Chem. Int. Ed. Engl. 37, 2834–2837 (1998)
G. Jeschke, A. Koch, U. Jonas, A. Godt, J. Magn. Reson. 155, 72 (2001)
G. Jeschke, M. Sajid, M. Schulte, A. Godt, Phys. Chem. Chem. Phys. 11, 6580–6591 (2009)
A.D. Milov, Yu.D. Tsvetkov, J. Raap, Appl. Magn. Reson. 19, 215–226 (2000)
A.D. Milov, B.D. Naumov, Yu.D. Tsvetkov, Appl. Magn. Reson. 26, 587–599 (2004)
A. Weber, O. Schiemann, B. Bode, T.F. Prisner, J. Magn. Reson. 157, 277–285 (2002)
J.R. Klauder, P.W. Anderson, Phys. Rev. 125, 912–916 (1962)
K.M. Salikhov, S.A. Dzuba, A.M. Raitsimring, J. Magn. Reson. 42, 255–276 (1981)
A.D. Milov, A.B. Ponomarev, Yu.D. Tsvetkov, Chem. Phys. Lett. 110, 67–72 (1984)
A.D. Milov, Yu.D. Tsvetkov, Appl. Magn. Reson. 18, 217–226 (2000)
A.G. Maryasov, Yu.D. Tsvetkov, Appl. Magn. Reson. 18, 583–605 (2000)
M. Benatti, A. Weber, J. Antonic, D.L. Perlstein, J. Robblee, J. Stubbe, J. Am. Chem. Soc. 125, 14988–14989 (2003)
M.K. Bowman, A.G. Maryasov, N. Kim, V.J. Derose, Appl. Magn. Reson. 26, 23–40 (2004)
G. Jeschke, G. Panek, A. Godt, A. Bender, H. Paulsen, Appl. Magn. Reson. 26, 223–244 (2004)
A.D. Milov, R.I. Samoilova, Yu.D. Tsvetkov, F. Formaggio, C. Toniolo, J. Raap, Appl. Magn. Reson. 29, 703–716 (2005)
A.G. Maryasov, M.K. Bowman, Yu.D. Tsvetkov, Appl. Magn. Reson. 30, 683–701 (2006)
V.P. Denisenkov, T.F. Prisner, J. Stubbe, M. Benatti, Appl. Magn. Reson. 29, 375–384 (2005)
G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C.R. Timmel, D. Hilger, H. Jung, Appl. Magn. Reson. 30, 473–498 (2006)
M.K. Bowman, A.G. Maryasov, J. Magn. Reson. 185, 270–282 (2007)
R. Ward, A. Bowman, E. Sozudogru, H. El-Mkami, T. Owen-Hughes, D.G. Norman, J. Magn. Reson. 207, 164–167 (2010)
O.S. Fedorova, Yu.D. Tsvetkov, Acta Naturae. 5, 1–32 (2013)
A. Abragam, The Principles of Nuclear Magnetism (Clarendon, Oxford, 1961)
A.D. Milov, A.D. Ponomarev, Yu.D. Tsvetkov, J. Struct. Chem. 25, 710–713 (1984)
T. Von Hagens, Y. Polyhach, M. Sajid, A. Godt, G. Jeschke, Phys. Chem. Chem. Phys. 15, 5854–5866 (2013)
G.M. Zhidomirov, K.M. Salikhov, ZhETP 56, 1933–1939 (1969)
L.V. Kulik, S.A. Dzuba, I.A. Grigoryev, Yu.D. Tsvetkov, Chem. Phys. Lett. 343, 315–324 (2001)
B.E. Bode, D. Margraf, J. Plackmeyer, G. Duerner, T.F. Prisner, O. Schiemann, J. Am. Chem. Soc. 129, 6736–6745 (2007)
Acknowledgments
We are grateful to Prof. V.F. Tarasov and Dr. V.K. Voronkova for discussions and support. We express our gratitude to Prof. G. Jeschke and Dr. A.G. Maryasov for the fruitful discussion of our results and their comment that the three-pulse ELDOR considered in this work is similar to the “2 + 1” pulse train electron spin echo method. We thank Prof. G. Jeschke and Dr. L. Kulik for the biradicals they provided us with. We are very pleased to thank L.V. Mosina for language editing of our manuscript. This work was supported by the grant for the leading scientific school of the Russian Federation NSh-4653.2014.2.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Salikhov, K.M., Khairuzhdinov, I.T. & Zaripov, R.B. Three-Pulse ELDOR Theory Revisited. Appl Magn Reson 45, 573–619 (2014). https://doi.org/10.1007/s00723-014-0541-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00723-014-0541-7