1 Introduction

Dynamic nuclear polarization (DNP) has gained renewed interest in recent years [1] due to its ability to dramatically increase the NMR signals originating from a large variety of molecules, and its wide applicability. DNP samples typically contain molecules of interest, a solvent, and stable radicals which contain unpaired electrons. These samples are then irradiated continuously by microwave (MW) fields close to the electron resonance frequency for relatively long times (in the timescale of the nuclear relaxation time). This leads to a transfer of the large Boltzmann polarization of the electrons to the nuclei in the sample.

The first DNP mechanism was introduced by Overhauser [2] and was termed the Overhauser effect. This relies on fast cross-relaxation processes between electrons and interacting nuclei, present in liquids and conducting solids. In non-conducting solid samples, such as frozen glass forming solvents, three possible DNP mechanisms are responsible for the polarization transfer: The solid effect (SE) [3, 4], the cross effect (CE) [5, 6, 7], and thermal mixing (TM) [8]. A discussion of the difference between these mechanisms can also be found in some recent publications [9]. Macroscopic rate equations were previously used to phenomenologically describe these DNP processes (see for example Refs. [10, 11]). These equations typically takes into account the characteristic features of the samples such as the nuclear and electron spin relaxation rates and the EPR line-shape of the radicals.

Recently, it was proposed that additional insight into the DNP process can be gained by studying the behavior of microscopic model systems, using quantum mechanical formalisms and numerical simulations [12–16]. The size of these systems are of course limited by computer memory restrictions, although solutions for overcoming these limitations are currently being proposed [17, 18]. Based on such calculations we suggested in a recent publication [12, 15] that the presence of many (core) nuclei, which are directly hyperfine coupled to the electrons taking part in the SE and CE mechanisms, broaden the double quantum (DQ) and zero quantum (ZQ) spectra, and dramatically reduce the end polarization. In the present study we discuss the effects of multi-electron environments on the SE and CE-DNP processes.

The current typical solid DNP setup is at high magnetic fields, where the width of the EPR line is much larger than the excitation bandwidth of the effective MW field. Then, the static SE and CE mechanisms rely on the irradiation of isolated electrons in the EPR spectrum, while leaving most electrons unaffected. These unaffected electrons will however have non-negligible dipolar interactions with their DNP active neighbors when we are dealing with high radical concentrations (i.e. 10–40 mM) typically used during DNP enhancement. Only a small fraction of these electrons are in a condition to create single electron pairs that support CE-DNP processes. For TM-DNP large clusters of electrons that are coupled via dipolar flip-flop terms or electron cross-relaxation and have an intrinsic line-width larger than the nuclear Larmor frequency, must be present [8, 19]. This case is outside the scope of this study.

Here we report on the effect of electrons which are not directly affected by the MW irradiation on the SE- and CE-DNP processes. Using numerical calculations of model multi-electron and multi-nuclear systems we show that these electrons broaden the DQ and ZQ spectra and that relaxation pathways provided by these electrons can restore some of the polarization lost due to the many core nuclei. This study provides another example of the complexity of the DNP processes and emphasizes the necessity to take multi-spin phenomena into account in order to obtain a better understanding of solid state DNP.

2 Interactions and Relaxations

In this publication we consider a static solid sample, composed of N e unpaired electrons (S = 1/2) and N n equivalent nuclei (I = 1/2). The spin dynamics of this system is evaluated using the theoretical model introduced earlier for the description of the SE-DNP and CE-DNP processes in model systems [12, 13, 15]. Its Hamiltonian in the MW rotating frame can be presented as [20]:

$$ H=H_{Z}+H_{hfi}+H_{D}+H_{d}+H_{\rm MW}=H_{0}+H_{\rm MW}, $$
(1)

where

$$ \begin{aligned} H_{Z} &= \sum\limits_{a}\Updelta\omega_{a}S_{z,a}-\omega_{n}\sum\limits_{i}I_{z,i} \\ H_{hfi} &= \sum\limits_{a,i}\left\{A_{z,ai}S_{z,a}I_{z,i}+\frac{1}{2}(A_{ai}^{+}S_{z,a}I_{i}^{+}+A_{ai}^{-}S_{z,a}I_{i}^{-})\right\}\\ H_{D} &= \sum\limits_{a<b}D_{ab}(2S_{z,a}S_{z,b}-\frac{1}{2}(S_{a}^{+}S_{b}^{-}+S_{a}^{-}S_{b}^{+}))\\ H_{d} &= \sum\limits_{i<j}d_{ij}(2I_{z,i}I_{z,j}-\frac{1}{2}(I_{i}^{+}I_{j}^{-}+I_{i}^{-}I_{j}^{+}))\\ H_{\rm MW} &= \omega_{1}\sum\limits_{a}S_{x,a} \end{aligned} $$
(2)

with a, b = 1, …, N e and i, j = 1, …, N n. These terms represent the electron off-resonance and nuclear Zeeman interactions, the secular and pseudo-secular electron–nuclear hyperfine interactions, the electron and nuclear dipolar interactions, and the MW irradiation, respectively.

All interaction coefficients in these terms depend on the geometry of the spin system and its orientation with respect to the direction of the external magnetic field, pointing in the z direction. For example, the dipolar coefficient of the interaction between two electrons is given by:

$$ D_{ab}=D_{e}r_{ab}^{-3}(3 \cos^{2}\,\theta-1), $$
(3)

where \(D_{e}=\frac{\mu_{0}}{8\pi\hbar}g_{a}g_{b}\beta_{e}^{2}, \) r ab is the magnitude of the distance vector between two electrons a and b, and θ the angle between this vector and the external magnetic field. In the same manner the values of the off-resonance coefficients \(\Updelta\omega_{a}\) of the electrons depend on the principal axis system (PAS) g-tensor components (g x , g y , g z ) and orientation with respect to the external magnetic field:

$$ \begin{aligned} \Updelta\omega_{a}&=g(\theta',\phi')\beta_{e}B_{0}/\hbar-\omega_{\rm MW}\\ g(\theta',\phi')&=(g_{x}^{2} \sin^{2}\,\theta' \cos^{2}\,\phi'+g_{y}^{2} \sin^{2}\, \theta' \sin^{2}\,\phi'+g_{z}^{2}\cos^{2}\,\theta')^{1/2}+g_{0}, \end{aligned} $$
(4)

where θ′, ϕ′ are the polar angles of the external magnetic field in the PAS frame and g 0 is the isotropic part of the interaction. ωMW is the frequency of the MW irradiation field. Large differences between the off-resonance values of two strongly interacting electrons a and b can quench their mutual dipolar flip-flop term even when r ab is small.

The dynamics of the spin system is determined by the time independent Hamiltonian of Eq. 1 and by fluctuating interactions which define relaxation rates. The latter are here defined in the diagonalized representation of H 0, \(\Uplambda_{0}=D^{-1}H_{0}D, \) with eigenstates |λ k 〉 and energies λ k . The relaxation mechanisms cause the individual spins to oscillate between states, determining the overall relaxation rates of the ensemble average populations and coherences [21]. Here we introduce effective relaxation parameters T −11,kk′ and T −12,kk′ belonging to the |λ k 〉↔|λ k′〉 transition. In order to evaluate the electron and nuclear polarizations the ensemble average spin density operator ρ(t) is defined, with its diagonal elements in the diagonalized representation given by the populations p κ(t) = 〈λκ|D −1ρ(t)D|λκ〉. At thermal equilibrium these populations are determined by the Boltzmann statistics, resulting in:

$$ \frac{p_{k'}^{\rm eq}}{p_{k}^{\rm eq}}=\varepsilon_{kk'}= \exp\left\{[(\lambda_{k}-\lambda_{k'})+ \omega_{\rm MW}(M_{{e},k}-M_{{e},k^{\prime}})]\hbar/k_{\rm B}T\right\}, $$
(5)

where M e,κ is the total electron angular momentum component in the z direction of |λκ〉. The values of the spin–lattice rates T −11,kk′ , driving the populations to satisfy Eq. 5, are calculated here for simplicity assuming fluctuating interactions proportional to S x,a and I x,i , and using empirical rates T −11a and T −11i , as described in Ref. [12]. The spin–spin relaxation rates T −12,kk′ are introduced by choosing a priori values, without performing any specific frame transformations. For simplicity we consider a single spin–spin relaxation rate T −12MW for all transitions affected by the MW irradiation, and a second rate T −12n for all other transitions.

The required expectation values, such as the nuclear polarization, are determined here from the density operator ρ(t) representing the whole spin system under investigation. In order to propagate the density operator in time we must solve

$$ \begin{aligned} \bar{\rho}^{\Uplambda}(t) &=U(t)\bar{\rho}^{\Uplambda}(0)\\ U (t)&=\exp(-(i\hat{\Uplambda}+\hat{R})t), \end{aligned} $$
(6)

where \(\hat{\Uplambda}\) is the Liouville space representation of the Hamiltonian in the diagonal frame, \(\Uplambda=\Uplambda_{0}+D^{-1}H_{\rm MW}D, \bar{\rho}^{\Uplambda}(t)\) is the vector representation of \(\rho^{\Uplambda}(t)=D^{-1}\rho(t)D, \) and \(\hat{R}\) is the relaxation superoperator. The magnitudes of the polarizations of each nucleus i can then be calculated using

$$ P_{i}(t)=\bar{p}(t)\cdot[[D^{-1}I_{z,i}D]] , $$
(7)

where \(\bar{p}(t)\) is a vector composed of all the p k (t) populations, and [[X]] stand for the vector of diagonal elements of X. The nuclear enhancement can be normalized with respect to the electron thermal polarization, P i (t)/P e (0), with

$$ P_{e}(0)=-\bar{p}(0)\cdot[[D^{-1}S_{z,{e}}D ] ] . $$
(8)

When we are only interested in the steady state enhancement, the density operator \(\rho_{\rm ss}^{\Uplambda}(t)\) can be derived by solving

$$ (i\hat{\Uplambda}+\hat{R})\bar{\rho}_{\rm ss}^{\Uplambda}(t)=0. $$
(9)

Thus \(\bar{\rho}_{\rm ss}^{\Uplambda}\) belongs to the null space of \((i\hat{\Uplambda}+\hat{R}),\) and it is given by \(c_{0}\bar{l}_{0}, \) where c 0 is a scalar and \(\bar{l}_{0}\) is an eigenvector with an eigenvalue of zero. The value of c 0 can be found from the conservation of populations in the system, \(\bar{1}\cdot c_{0}\bar{l}_{0}=1\), where \(\bar{1}\) is a vector representation of the identity matrix. Since \((i\hat{\Uplambda}+\hat{R})\) is a sparse matrix, solving Eq. 9 can be faster than solving Eq. 6, making it also possible to deal with larger spin systems.

When dealing with a SE-DNP process, the effective MW irradiation fields of magnitudes ω1,kk′, equal to the matrix elements 2〈λ k |D −1 H MW D|λ k'〉 and exciting the DQ or ZQ |λ k 〉→|λ k'〉 transitions, are relatively weak. When H 0 of the spin system is diagonalized and the condition \(|\omega_{1,kk{\prime}}|\ll\sqrt{T_{2,kk{\prime}}^{-2}+\Updelta\omega_{kk{\prime}}^{2}}\) is fulfilled, we can reduce the dimension of the calculations by transferring Eq. 6 to a rate equation for \(\overline{p}(t). \) In that case the ω1,kk′’s are replaced by MW rates \(W_{kk{\prime}}=\frac{\omega_{1,kk{\prime}}^{2}T_{2,kk{\prime}}}{1+(\Updelta\omega_{kk{\prime}}T_{2,kk{\prime}})^{2}}, \) as was discussed in Ref. [13], and spin systems can be considered that are larger than those that can be handled by Eqs. 6 and 9.

In the following sections we ignore the dipolar Hamiltonian H d in order to simplify the calculations. This is justified when considering core nuclei. These nuclei i, surrounding an electron a are characterized by |A z,ai  − A z,aj | ≫ |d ij | for all other nuclei j in the sample. For these core nuclei the dipolar flip-flop terms proportional to d ij will be quenched by the hyperfine interactions. We should however not forget that the nuclear dipolar interaction plays an important role in the transfer of polarization from the electrons to the bulk nuclei. The bulk polarization is determined by a dipolar assisted DNP transfer process that is mediated by the core nuclei and its magnitude depends therefore strongly on the ability of the MW irradiation to polarize these core nuclei [13]. In the last Sect. 6.3 we will reintroduce H d into the calculations to examine this polarization transfer to remote bulk nuclei.

Next, model spin systems that can be treated numerically are chosen and the influence of electron and nuclear additions on the nuclear polarization enhancements are characterized.

3 The Electron Spin System

Before choosing the interaction parameters of our model spin systems, we imagine a typical static DNP experiment on a glass forming solution, with randomly distributed single radicals that are surrounded by solvent nuclei of a single type. Such a sample of volume V can be characterized by an unpaired electron concentration C (defined here in units of mM). To characterize the interaction network of these electrons we must estimate the probabilities of finding relatively isolated electrons or small networks of strongly dipolar coupled electrons, in particular electron pairs that can be the source of CE-DNP processes. These probabilities can be estimated for different values of C while taking into account the width of the EPR line-shape.

The average distance from one electron to its nearest neighbor (in units of Å) in the sample is given by \(\bar{r}_{{e}-{e}}=(\frac{\pi}{6}\sigma C)^{-1/3}, \) with \(\sigma\simeq 6.02\times10^{-7}\,[\hbox{mM}^{-1}{\rm{{\AA}}}^ {-3}]\). This was calculated assuming that on average each electron is surrounded by a volume without other electrons of \(\frac{V}{N_{e}}=(\sigma C)^{-1}=\frac{4}{3}\pi\left(\frac{1}{2}\bar{r}_{{e}-{e}}\right)^{3}. \) In general, the value of the average dipolar interaction 〈D ab 〉, obtained by inserting \(\bar{r}_{{e}-{e}}\) into Eq. 3 is in the order of a MHz or less for concentrations of less then 100 mM.

More insight on the spin system can be gained from the microscopic distributions of electrons around single electron spins a. The probability of finding n electrons b within a distance r ab  ≤ r l is:

$$ F_{n\geq1}=1-\exp(-\sigma Cv), $$
(10)

and the probability of finding only one such electron b is:

$$ F_{n=1}=\sigma Cv\exp(-\sigma Cv). $$
(11)

Here \(v=\frac{4}{3}\pi(r_{l}^{3}-r_{0}^{3}), \) where r 0 is some minimal distance between two electrons. Similar expressions for the condition of having a dipolar interaction |D ab | ≥ D l can be derived assuming that r 0 can be neglected, by inserting for v the value \((16\pi/9\sqrt{3})D_{e}/D_{l}. \) When r 0 cannot be neglected we can approximate these probabilities using D e r −3 ≥ D e r −3 l . All these equations are derived in the appendix.

Figure 1 shows two examples of the F n≥1 (black) and F n=1 (gray) probabilities as a function of the radical concentration, using r l equal to 30 Å (solid lines) and 12 Å (dotted lines), respectively, with r 0 = 5Å. The former r l is smaller than the average electron distance even for an electron concentration of 100 mM (or of 60 mM for a cubic lattice), and results in electron dipolar interactions of about 1 MHz or more. This value is in the order of magnitude of the hyperfine coupling between the electrons and neighboring core protons and therefore can not be neglected. The latter can be compared with the distance between the electrons in the TOTAPOL and BT2E bi-radicals, which is about 12.8 Å [22], and corresponds to a dipolar interaction of more than 15 MHz. The probability of finding at least one electron (black lines), or only a single electron (gray lines) with a dipolar interaction larger than D l is shown in Fig. 1b, c for a radical concentration of 40 and 10 mM, respectively. This was calculated using D l ≃ D e r −3 l . For a radical concentration of 40 mM almost all the electrons will have several neighbors with a dipolar interaction of more then 1 MHz. There is about a 24 % chance to find a single neighbor with a dipolar interaction of 15 MHz or more, and about 4 % of finding several such neighbors. For an electron concentration of 10 mM there is a probability of more than 70 % to find at least one neighbor with a dipolar interaction of 1 MHz or more, and about 35 % of only one such neighbor. The probability of finding a single neighbor with a dipolar interaction of more than 15 MHz is about 7 % in this case. Therefore, in most cases a DNP active electron will be dipolar coupled to at least one other electron with a dipolar interaction of more than 1 MHz. In many cases we expect that the differences between nearest and next nearest neighboring distances are significant. The latter case resembles distance distributions in system of bi-radicals.

Fig. 1
figure 1

a The probabilities F n≥1 and F n=1 of finding at least one (black) or only one (gray) additional electron in the neighborhood of an electron, within a distance of r l  = 30Å (solid lines) or of 12 Å (dotted lines), as a function of the mono-radical concentration. b, c The probabilities of finding at least one (black) or only one (gray) additional electron in the neighborhood of an electron with a dipolar interaction larger than D l , for a mono-radical concentration of 40 and 10 mM, respectively. In all cases a minimal electron-electron distance of r 0 = 5 Å was assumed

Full size image

As mentioned above, we will restrict our simulations mainly to core nuclei. The areas occupied by the core nuclei are not well defined as well as their boarders. The global sizes and shapes of the core areas around a single radical depend on the type of nuclei and on their concentration. An example of such a core region with an average radius of about 12–15 Å is illustrated in Ref. [12] . When two neighboring radicals are in close proximity their core areas become connected, as illustrated in Ref. [15]. Because we are interested in the influence of DNP inactive electrons coupled to active ones, we do not restrict ourselves to additional electrons with overlapping core areas.

In order to evaluate the effect of the electron dipolar interactions on the DNP mechanism we must take into account the dispersion of the electron frequencies, as determined by the inhomogeneously broadened EPR line-shape. For example, in order to get substantial dipolar state mixing between neighboring electrons, we require that the difference between their off-resonance frequencies is smaller or of the order of the dipolar interaction between them, \(|\Updelta\omega_{a}-\Updelta\omega_{b}| \leq |D_{ab}|. \)

For an EPR line with a width of a few hundred MHz, as is typically the case for nitroxides at high fields, most neighboring electrons do not satisfy this equality, even for a radical concentration of 40 mM. Therefore it will be rare to find large flip-flop coupled networks of many electrons with significantly dipolar mixed states. It is however important to note that these interactions will still lead to spectral diffusion via electron cross-relaxation [20].

The strength of the dipolar interaction will also determine the probability of finding electrons at the CE condition, since the width of this condition is approximately given by ± |D ab A a,n /2ω n | [15]. As a result electron pairs with strong dipolar interactions are likely to take a significant part in the CE-DNP mechanism, although the probability of finding such pairs is relatively small. It is therefore possible to consider CE-DNP between the low abundant electron pairs even for randomly distributed electrons. Since the width of the CE condition is expected to be smaller than 1 MHz and the CE mechanism requires an EPR linewidth that is larger than the nuclear Larmor frequency, the probability of finding electrons at the CE is very low at high fields.

We can thus conclude that for broad EPR lines, such as nitroxides in fields of a few Tesla or more, only a small fraction of the electrons are directly affected by the MW irradiation and are SE-DNP active, while an even smaller fraction will result in CE-DNP. Because most of the electrons in the sample satisfy \(|\Updelta\omega_{a}-\Updelta\omega_{b}|>|D_{ab}|, \) we do not expect any large state mixing between DNP active electrons and their inactive neighbors. However, these DNP inactive electrons can influence the enhancement processes, as will be discussed in what follows. For radicals with EPR spectra that are tens of MHz wide, such as trityl-type radicals in fields of a few Tesla, the dipolar flip-flop coupled networks can be more extended and the number of DNP inactive electrons will be reduced. As a consequence for such samples with high radical concentrations, coupled multi-electron systems must be considered, possibly exhibiting thermal mixing effects. These effects will not be discussed here and will be left for future studies. We however believe that the mechanism proposed for broad EPR lines will play a role even in these cases.

4 The DQ and ZQ Transitions

It was previously shown that the hyperfine interactions of the core nuclei, coupled to an isolated electron a, determine the width of the DQ and ZQ spectra [12]. MW excitation of part of the transitions composing these spectra leads to a SE-DNP enhancement process. When we consider two interacting electrons a and b, the DQ or ZQ spectrum of electron a can overlap with the SQ spectrum of the second electron b. This can result in CE conditions, where strong product state mixing can result in a CE-DNP enhancement process. These conditions depend on the hyperfine interactions of the core nuclei and on the a − b dipolar interaction, as was previously explained. Once again, here we are interested in the influence of additional electrons c in these systems on these two processes. Referring to the above discussion, we assume that the SQ transitions of electrons c are removed from those of a and b, such that |D ac | ≪ |ω a/b  − ω c |, and from the DQ and ZQ transitions. In this case the effects of the dipolar flip-flop terms between a and c and between b and c can be neglected.

The frequencies of the DQ ai transitions of a single core nucleus i close to a single electron a in a spin system containing additional electrons c is given to zeroth order by:

$$ \begin{aligned} \omega_{{\rm DQ},ai}=\omega_{a}-\omega_{n}+\sum\limits_{j\neq i}(\pm)_{j}\left(\frac{1}{2}A_{z,aj}\right)+\sum\limits_{,{c\neq a}}(\pm)_{c}\left(D_{ac} +\frac{1}{2}A_{z,ci}\right). \end{aligned} $$
(12)

The first sum takes into account the effect of the hyperfine interaction of all the nuclei j ≠ i with electron a, and the second sum the effect of the dipolar interaction of all electrons with electron a and their hyperfine interaction with nucleus i (which is expected to be relatively small). The (± ) x sign is equal to 1 or −1, depending on the spin up or spin down state of x. Similar expressions are obtained for the ZQ ai transition frequencies, after replacing −ω n by +ω n .

When two electrons a and b are coupled to nucleus i and close to their basic CE condition, \( \left( \omega_a - \omega_b \right) \simeq \pm \omega_{n}, \) the additional electrons c and nuclei j cause a shift and result in the CE conditions:

$$ \begin{aligned} (\omega_{a}-\omega_{b})&\simeq \pm\omega_{n}+\sum\limits_{j\neq i}(\pm)_{j}\frac{1}{2}(A_{z,aj}-A_{z,bj})\\ &\quad+\sum\limits_{c\neq a,b}(\pm)_{c}(D_{ac}-D_{bc}+\frac{1}{2}A_{z,ci}). \end{aligned} $$
(13)

Taking these equalities into account, it is now possible to study the effect of additional electrons and nuclei on the polarization enhancement of nucleus i.

5 Polarization Enhancement

In this section we set the stage for calculating the effect of the additional electrons on the basic SE-DNP and CE-DNP processes. To do so we consider the SE polarization enhancement in a simple three-spin system with two electrons a and c and a single nucleus i, which is hyperfine coupled to electron a. The frequencies of the two electrons are far from the CE condition and |ω a  − ω c | ≫ |D ac |. This system has only two DQ ai transitions:

$$ \begin{aligned} &|\alpha_{a},\beta_{c};\alpha_{i}\rangle\leftrightarrow|\beta_{a},\beta_{c};\beta_{i}\rangle\\ &|\alpha_{a},\alpha_{c};\alpha_{i}\rangle\leftrightarrow|\beta_{a},\alpha_{c};\beta_{i}\rangle \end{aligned} $$
(14)

with a frequency difference of about 2D ac . Here we have ignored the small state mixing due to the diagonalization of H 0. When both transitions are simultaneously excited by an effective MW irradiation field, such that both transitions are saturated, the steady state populations p(χ a , χ c ;χ i ) with χ = α, β become:

$$ p(\alpha_{a},\beta_{c};\alpha_{i})=p(\beta_{a},\beta_{c};\beta_{i}) $$
(15)

and

$$ p(\alpha_{a},\alpha_{c};\alpha_{i})=p(\beta_{a},\alpha_{c};\beta_{i}). $$
(16)

The effect of the spin-lattice relaxation of electron a will result in:

$$ \varepsilon_{e}p(\beta_{a},\chi_{c};\chi_{i}) =p(\alpha_{a},\chi_{c};\chi_{i}) $$
(17)

and of electron c results in:

$$ \varepsilon_{e}p(\chi_{a},\beta_{c};\chi_{i}) =p(\chi_{a},\alpha_{c};\chi_{i}) $$
(18)

where \(\varepsilon_{e}\) is the Boltzmann ratio between the electronic states taken from Eq. 5 after removing all energy terms except for the electron Zeeman interaction. Combining these equalities results in this ideal case in a steady state nuclear polarization that is equal to the initial electron polarization [12]

$$ P_{n}(t_{\rm s.s.})=\frac{1}{2}\frac{1-\varepsilon_{e}}{1+\varepsilon_{e}}=P_{e}(0). $$
(19)

Here we assumed that the nuclear relaxation rate is significantly smaller than the electron relaxation rates. The high nuclear polarization in this case is a combined result of the saturation of the DQ transitions by the MW irradiation and the electron spin-lattice relaxation mechanisms.

When only one of these DQ ai transitions is saturated, only Eqs. 15 or 16 are satisfied. Combining this with the effect of T −11,a  ≠ 0 on the spin system (Eq. 17) will result in only half of the previously obtained nuclear polarization \(P_{n}(t_{\rm s.s.})=\frac{1}{2}P_{e}(0). \) If T −11,c would have been zero, the spin system could have been decomposed into two subsystems, one with electron spin c in state |α c 〉 experiencing a MW irradiation and one of the same spin in |β c 〉 without an irradiation. However, because we are dealing with systems with T −11,c  ≠ 0 (Eq. 18), we do not divide the system during the calculations and continue evaluating the ensemble average polarizations as derived from \(\rho^{\Uplambda}(t).\) This results in full nuclear polarization, as in Eq. 19.

This simple example shows that MW irradiation on only a part of the transitions of DQ or ZQ spectra, dipolar broadened by additional electrons, can still result in large nuclear enhancements, due to the spin-lattice relaxation processes of these electrons. In the following sections we will demonstrate this effect by performing numerical simulations on model spin systems.

6 Numerical Simulations

In this section we show results from numerical simulations of nuclear polarizations enhanced by SE-DNP and CE-DNP processes. In Sects. 6.1 and 6.2 we start from simple two-spin {e a  − n 1} and three-spin {e b  − e a  − n 1} systems, and show the polarization of nucleus 1 after the addition of other nuclei and electrons. In these simulations we did not take nuclear dipolar interactions into account. In Sect. 6.3 we present the polarization of the nuclei in a chain, with only one single nucleus hyperfine coupled to the electron and with dipolar couplings between the nuclei. We again consider the effect of the addition of a nucleus and an electron on the DNP polarization. The parameters of all the spin systems used for the simulations are summarized in Tables 1 and 2, unless stated otherwise.

Table 1 Simulation parameters used in Sects. 6.1 and 6.2, for simulations of SE and CE DNP enhancements
Full size table
Table 2 Simulation parameters used in Sect. 6.3, for simulations of nuclear enhancements during dipolar-assisted SE DNP
Full size table

6.1 Solid Effect DNP

To calculate the signal enhancements of the {e a  − n 1} spin system we solve the population rate equations [13]. The steady state frequency swept DNP enhancement of nucleus 1 is shown in Fig. 2a before (dotted line) and after adding one additional electron (solid black lines) or nucleus (gray line). In both cases the single line composing the initial DQ ai spectrum becomes a doublet resulting in the split DNP spectra. When a nucleus is added the maxima in the polarization drops, while the addition of an electron does not reduce these two maxima. The addition of the electron reduces the line-widths by a factor of about \(\sqrt{2}. \) In Fig. 2b the initial polarization buildup curves of nucleus 1 are plotted for these {e a  − n 1}, {e c  − (e a  − n 1)}, and {(e a  − n 1) − n 2} spin systems, with the MW irradiation applied at the frequency of the maxima in the steady state polarization around (ωMW − ω a )/2π≈ − 144 MHz,  − 145.5 MHz, and −145.5 MHz respectively. The steady state values of the latter are shown by the black and gray triangles. All three buildup curves reach their steady state polarizations with two time constants. The first time constants are about equal in all three cases and correspond to the initial saturation of the irradiated DQ transition. The polarization after this time step depends on the fraction of the irradiated DQ transitions. In the two-spin system the second time constant equals to T 1,a and after the addition of the electron this constant becomes longer. The addition of a nucleus reduces the end polarization, and the time constant approaches T 1n [12].

Fig. 2
figure 2

a The normalized SE-DNP steady state polarization of nucleus 1 as a function of the MW irradiation frequency, for a {e a  − n 1} (dotted black line), a {e c  − (e a  − n 1)} (solid black line, with the steady state marked by a black triangle), and a {(e a  − n 1) − n 2} (solid gray line, with the steady state marked by a gray triangle) spin system. The MW irradiation was applied around the DQ transitions. b Polarization buildup curves of nucleus 1 for these three spin systems. The MW irradiation was applied at the maxima of the DNP lines around (ωMW − ω a )/2π =  −144 MHz,  −145.5 MHz, and −145.5 MHz, respectively. All other parameters used in the simulation are given in Table 1

Full size image

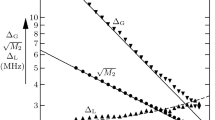
In Fig. 3a, b the steady state DNP spectra of nucleus 1 (black lines) are shown after the addition of three electrons or of three nuclei. The DNP spectra after the addition of seven spins are shown in Fig. 4a. In this case the electron interaction parameters were chosen from a random electron distribution corresponding to a 40 mM radical concentration. To enable an easy comparison between the additions of electrons and nuclei, the dipolar and hyperfine interactions were chosen such that the two additions resulted in similar DQ a1 spectra. This was accomplished by copying the electron configurations and creating corresponding nuclear configurations by scaling all the distances according to \(r_{a-i}=\sqrt[3]{{{\gamma_{n}}/ {\gamma_{{e}}}}}r_{a-c}\simeq r_{a-c}/8.7. \) In all cases the addition of the nuclei results in an end polarization of nucleus 1 that is smaller than after the addition of electrons. The reduction in the widths of the frequency bands in the DNP spectra after the additions of these electrons is approximately given by the square root of the number of added electrons or less.

Fig. 3
figure 3

The normalized SE-DNP steady state polarizations of nucleus 1 as a function of the MW irradiation frequency in a a {3e − (e a  − n 1)}, b a {(e a  − n 1) − 3n}, and c a {3e − (e a  − n 1) − 3n} spin system. The MW irradiation was applied around the DQ transitions, with the simulations performed using a temperature of 100 K (black lines) or 1.5 K (gray lines). d Polarization buildup curves of the systems used in a (solid black line), b (solid gray line) and c (dashed gray line), using a temperature of 100 K. The steady state polarization is marked by solid black, solid gray and empty gray triangle, respectively. The MW irradiation was applied at (ωMW − ω a )/2π =  −141.25 MHz, −141.475 MHz and −141 MHz, respectively. The buildup of the {e a  − n 1} system (dashed black line, with the steady state marked by an empty black triangle) used in Fig. 2b is shown for comparison. All other parameters used in the simulation are given in Table 1

Full size image
Fig. 4
figure 4

a The normalized SE-DNP steady state polarization of nucleus 1, as a function of the MW irradiation frequency, after the addition of seven electrons (black line) or seven nuclei (gray line) to an {e a  − n 1} spin system. The positions of the seven electrons was randomly chosen within a 69.2 Å box aligned with the direction of the magnetic field (z), which corresponds to an electron concentration of about 40 mM. The minimal electron–electron distance was set to 10 Å. Electron a was placed at the center of the box (0,0,0), nucleus 1 was placed at position [3.1, 0, 3.1] Å and the positions of the remaining electrons are: [8.6 12.4 −7.2], [−9.2 33.8 −32.0], [26.7 28.6 20.5], [−27.8 −16.5 −11.4], [12.4 −25.2 15.3], [−27.2 10.6 −0.4], and [19.3 14.9 28.0] Å. The difference between the EPR frequency of these electrons and that of electron a were chosen to be equal to −26,  −21,  −77, 3, 4, 127, and 118 MHz. The positions of the nuclei were determined by scaling of the electron positions by \(\sqrt[3]{{\frac{{\gamma_1{\rm H}}}{{\gamma_e}}}}. \) All other parameters were taken from Table 1. b Polarization buildup curves of nucleus 1 in these spin systems, during a MW irradiation applied at the DNP frequency of (ωMW − ω a )/2π =  −141 MHz. The buildup of the {e a  − n 1} system (dashed black line) used in Fig. 2b is shown for comparison. The steady state polarizations are marked by triangles. All other parameters used in the simulation are given in Table 1

Full size image

Examples of the polarization buildup curves of nucleus 1 in these systems are shown in Figs. 3d and 4b. In all cases the MW irradiation was applied at the frequency band around (ωMW − ω a )/2π≈ −141 MHz in the DNP spectra of Figs. 3 and 4. The steady state polarizations are marked by triangles. In both figures the polarization of the {e a  − n 1} system is drown again, for comparison (note the change of timescale). A comparison between these buildup curves and the buildup curves shown in Fig. 2d shows that as more electrons are added the buildup time becomes slower, which eventually leads to lower steady state polarization. The addition of more nuclei (with a common spin-lattice relaxation time) has little effect on the polarization buildup times.

Now we consider the effect of a simultaneous addition of electrons and nuclei. To do this we first consider a {e c  − (e a  − n 1) − n 2} system, where nucleus 2 reduces the end polarization of nucleus 1. Figure 5 shows the polarization of nucleus 1, after the addition of one electron c. Here the polarization is shown as a function of the MW irradiation frequency and the dipolar interaction D ac between electrons c and a, normalized by the hyperfine interaction A z,a2. For most values of D ac /A z,a2 the maximal polarization stays constant. However, the polarization increases when |D ac /A z,a2| ≈ 0.5 and two of the hyperfine split DQ a1 transitions are irradiated. Another condition leading to increased enhancement is obtained when \(|D_{ac}|\approx\frac{1}{4}|A_{z,a1}\pm A_{z,a2}|, \) so that one of the DQ frequencies of nuclei n 1 and n 2 become equal. This effect can also be seen in Fig. 3c (black lines), where three nuclear and three electron spins are added, with |D ak /A z,ak |≈ 0.5 for k = 2, 3, 4. In general, for SE-DNP on a system containing DNP active electrons a, with core nuclei j and surrounding electrons c, we can expect many such overlaps between DQ aj transitions of the different a − j electron-nuclear spin pairs. MW excitation of these transitions can therefore result in higher polarization enhancements than for similar systems without the c electrons.

Fig. 5
figure 5

The normalized SE-DNP steady state polarization of nucleus 1 in a {e c  − (e a  − n 1) − n 2} spin system, as a function of the MW irradiation frequency and the ratio between the electron dipolar and the A a2 hyperfine interactions. The irradiation was applied around the DQ transitions. All other parameters used in the simulation are given in Table 1

Full size image

Figure 3d (dotted gray line) shows the polarization buildup curve for this system, with the empty gray triangle marking the steady state value. The MW irradiation was applied at (ωMW − ω a )/2π ≈ −141 MHz. The polarization buildup has three time constants: one corresponding to the initial saturation of the DQ transitions, the next to the electron spin lattice relaxation, and the third to the nuclear spin lattice relaxation time. Irradiation at other points in the spectra result in variations in the relative contribution of each time constant (data not shown). For example, irradiation applied at (ωMW − ω a )/2π ≈ −144 will result in a higher end polarization and a timescale close to T 1e , while irradiation at (ωMW − ω a )/2π ≈ −139 MHz results in lower end polarization and a timescale close to T 1n .

So far we considered spin systems at 100 K. Lowering the temperature will lead to population distributions that mainly populate the lower electronic states. A consequence of this change in population distribution is shown in Fig. 3a–c, where the gray lines present the steady state DNP polarizations calculated for a temperature of 1.5 K. Only MW irradiation on the DQ transitions of the low energy states results in substantial DNP enhancements. As before, the addition of several nuclei results in a reduction of the end polarization, and addition of more electrons to this multi-nuclear system yields only limited improvement.

6.2 Cross-Effect DNP

Here we consider the effect of adding nuclei and electrons to a {e b  − e a  − n 1} three-spin system, close to the CE condition. In this case calculations were performed solving Eq. 9. Figure 6a shows the polarization of nucleus 1 as a function of the MW irradiation frequency and of the difference between the electron frequencies, ω b  − ω a , for the three-spin system. The vertical contour lines correspond to irradiation on the DQ a1 transitions, and the horizontal ones are located at the CE conditions. In Fig. 6b and c the same is shown after the addition of an electron c or a nucleus 2, respectively. In both cases the additional spin results in a splitting of the DQ a1 transition and of the CE condition. Here again the dipolar or hyperfine interactions of the added spin were chosen such that this splitting is the same in both cases. The addition of a nucleus results in a decrease in the maximal polarization, while the additional electron leaves the maximal polarization unchanged, but narrows the widths of the SE-DNP enhancement profiles and the widths of the CE conditions. Figure 7d shows the polarization of nucleus 1 after an electron c and a nucleus 2 are both added to the system, with |D ac /A z,a2| ≈ 0.5. This results in three DQ transition and three CE condition contour lines, with a maximal polarization similar to that obtained in Fig. 6a for the three spin system. As in the SE case, reducing the temperature limits this beneficial electron polarizing effect (not shown). The polarization buildup time of these systems is shown in Fig. 7. Here we considered only systems close to the CE condition, with electron frequency and MW irradiation frequency marked by the white circles in Fig. 6. These calculations were performed using Eq. 6. For the isolated {e b  − e a  − n 1} system (dashed black line) the buildup is in the order of T 1e . After the addition of an electron (solid black line) the buildup becomes a bit longer. When another nucleus is added (solid gray line) the buildup has an initial rate in the order of T 1e , followed by a buildup in the order of T 1n . Two polarization buildup curves are shown for this system, after the addition of both an electron and a nucleus: A system with (ω b  − ω a )/2π ≈ −144 MHz and an irradiation around (ωMW − ω a )/2π ≈ −142 MHz (dotted black line), and a system with (ω b  − ω a )/2π ≈ −141 MHz and an irradiation around (ωMW − ω a )/2π ≈ −139 MHz (dotted gray line). The buildups of these systems resemble the buildup of the {e b  − e a  − n 1} system after the addition of an electron or a nucleus, respectively.

Fig. 6
figure 6

a Normalized DNP steady state polarization of nucleus 1 in a {e b  − e a  − n 1} spin system around the CE condition, as a function of the MW irradiation frequency and the electron frequency difference. The results of b were obtained after the addition of an electron {e c  − (e b  − e a  − n 1)}, of c after the addition of a nucleus {(e b  − e a  − n 1) − n 2}, and of d after the addition of both an electron and a nucleus {e c  − (e b  − e a  − n 1) − n 2}. The irradiation was applied around the DQ transitions and electron difference was changed around the ω b  − ω a  ≈ −ω n CE condition, using the parameters of Table 1. The white circles indicate the parameters used in Fig. 7

Full size image
Fig. 7
figure 7

Polarization buildup curves of nucleus 1 for the systems used in Fig. 6a–d, close to the CE condition. The parameters used were (ω b  − ω a )/2π ≈ −143.95 MHz and (ωMW − ω a )/2π ≈ −142 MHz for the {e b  − e a  − n 1} system (dashed black line), (ω b  − ω a )/2π ≈ −142.45 MHz and (ωMW − ω a )/2π ≈ −140.5 MHz for the {e c  − (e b  − e a  − n 1)} (solid black line) and {(e b  − e a  − n 1) − n 2} (solid gray line, with the steady state marked by a filled gray triangle) systems, and (ω b  − ω a )/2π ≈ −143.95 MHz and (ωMW − ω a )/2π ≈ −142 (dotted black line) or (ω b  − ω a )/2π ≈ −141 MHz and (ωMW − ω a )/2π ≈ −139 (dotted gray line, with the steady state marked by an empty gray triangle) for the {e c  − (e b  − e a  − n 1) − n 2} system. These parameters result in the steady state enhancements shown inside the white circles in Fig. 6. All other parameters where taken from Table 1

Full size image

6.3 Dipolar-Assisted DNP

So far we examined the affect of DNP inactive electrons on the polarization of nuclei hyperfine coupled to a single or a pair of DNP active electrons. By ignoring the nuclear dipolar interaction in these calculations we also ignore the transfer of polarization to remote bulk nuclei that are directly or indirectly dipolar coupled to the core nuclei [13]. We now consider a system in which the nuclear dipolar interaction plays an important role in the enhancement of nuclear polarizations. We concentrate on a SE-DNP process polarizing bulk nuclei that are not directly interacting with the DNP active electron. These nuclei experience the MW irradiation via the hyperfine and dipolar interactions. This basic spin system is composed of an electron a, a core nucleus 1, and five bulk nuclei j = 2,…,6. Only nucleus 1 is hyperfine coupled to the electron a. We then add to this system a core nucleus and a DNP inactive electron, and consider their effect on the dipolar-assisted DNP polarization enhancement of the bulk nuclei. To simplify the simulations we assume that A z,a1 = 0 preventing quenching of the dipolar couplings between nucleus 1 and it neighbor. The nuclei are arranged in a chain, with each one dipolar coupled to its nearest neighbors. The temporal evolution of the polarization of these nuclei, during MW irradiation applied at \(\Updelta\omega_{a}=\omega_{n}, \) is shown in Fig. 8a. Because the nuclear T −11n rates are rather slow, all nuclei reach a large polarization close to P e (0). Figure 8b shows the effect on the buildup curves after the addition of a second core nucleus, termed 1’ , with A z,a1' = 3 MHz, and without dipolar interactions to the rest of the nuclei. This nucleus splits the DQ transitions, and a MW irradiation on one of these transitions (\(\Updelta\omega_{a}=\omega_{n}-A_{z,a1'}/2\)) results in a decrease of the maximal polarization. When however in addition an electron c is added, with D ac  = A z,a1'/2, some of the reduced polarizations is restored. This can be seen in Fig. 8c, with the MW field applied again on one of the DQ transitions, namely \(\Updelta\omega_{a}=\omega_{n}. \) This simple model calculation indicates that the bulk polarizations react in a similar manner to the additional electrons and nuclei as the core nuclei.

Fig. 8
figure 8

a The temporal evolution of the nuclear polarizations during DNP, for a linear chain of spins. The gray line corresponds to nucleus 1 which is hyperfine coupled to the electron, and the black lines to the 5 other nuclei with each one dipolar coupled to its neighbors. b The same after the addition of a nucleus 1′, coupled to electron a. c The same after the addition of another electron c which is dipolar coupled to electron a, in addition to nucleus 1′. Only hyperfine interactions between a and 1 and 1′ are considered. All other parameters are given in Table 2

Full size image

7 Conclusions

In this study we examined the influence of electrons that are not directly involved in the DNP enhancement processes during SE- and CE-DNP experiments, on static samples with high concentrations of mono-radicals. For this study we chose simple model spin systems, with parameters that are relevant for real samples, and simulated their nuclear polarizations. In real samples with inhomogeneously broadened EPR lines that have a width much larger than the dipolar interaction between neighboring electrons, there are no networks of strongly dipolar coupled electron. Therefore we expect the nuclear enhancement to be driven mainly by SE- or CE-DNP active electrons, which are surrounded by many DNP inactive electrons. The dipolar interaction between these neighboring electrons can however exceed the average electron dipolar interaction. Thus even at relatively low electron concentrations we can expect to get dipolar interactions in the order of the electron-nuclear hyperfine interaction, and at high enough electron concentrations they can become similar to those found in bi-radicals.

In order to investigate the influence of the inactive electrons, we compared the addition of these electrons to the spin systems with the addition of core nuclei. Earlier we showed that extending the number of core nuclei results in additional splittings of the DQ and ZQ transitions and the CE conditions, which in turn can cause significant reductions of the DNP polarizations. Here we have shown that despite the fact that additional dipolar coupled electrons also split the DQ and ZQ transitions and the CE conditions, their presence results only in a marginal reduction of the maximal polarization. This is a consequence of the spin-lattice relaxation mechanism of these additional electrons. We have also shown that the reduction of the polarization due to the presence of many core nuclei can be partially recovered by the dipolar coupled DNP inactive electrons.

In this work we performed calculations on small isolated spin systems and showed their nuclear enhancements resulting from MW irradiation that excite specific DQ transitions. In real systems the DQ spectra are composed of transitions with an (almost) continuous frequency distribution and one MW field can only partially excite the DQ transitions of many electrons. The success of the DNP experiment relies however on the enhancement of the removed bulk nuclear polarizations surrounding the DNP active electrons. Increasing the electron concentration can have several potential benefits: (1) It will directly increase the number of DNP active electrons, reducing the average number of bulk nuclei polarized by each individual electron; (2) it will increase the probability of finding electron pairs at the CE condition, which can result in more efficient DNP polarization mechanisms; (3) and it will increase the number of electrons interacting with DNP active electrons. These last electrons do not contribute to the DNP enhancement directly, but broaden the range of DQ and ZQ transitions, and as a result the MW irradiation will partially excite more electrons responsible for the bulk polarization. Additionally, as shown in the present study, these electrons can prevent part of the reduction in enhancement due to the presence of the core nuclei, increasing the ability of each of the DNP active electrons to polarize the bulk.

We must, however, realize that the addition of electrons to the system increases the portion of core nuclei, whose NMR signals cannot be observed due to their large hyperfine interactions. Higher electron concentration also results in a decrease of the electron and nuclear spin-lattice relaxation times. While a reduction of T 1e can be beneficial for the polarization process, reduction of the bulk T 1n leads to lowering of the enhancements while decreasing the overall buildup time of the bulk polarization. This may improve the accumulated enhancement of NMR signals measured per unit time [23]. Finally, spectral diffusion between the electrons at significantly high radical concentrations, which was outside the scope of this study, could have a disturbing effect on the bulk DNP enhancement.

The present study demonstrates the complexity of the DNP processes in real samples, and emphasizes the need to further investigate the details of the signal enhancement of the bulk nuclei.