Public capital, health persistence and poverty traps

Abstract

Growth dynamics and health outcomes are studied in a three-period overlapping generations model with public capital. Agents face a non-zero probability of death in adulthood. Parental health affects the health status of their children at birth, and health status in adulthood depends on health in childhood. An autonomous increase in life expectancy has an ambiguous impact on growth, because of an adverse effect on the public–private capital ratio. If life expectancy depends endogenously on health status, multiple equilibria may emerge. A reallocation of public spending toward either health or infrastructure may put the economy on a convergent path to a high-growth, high productivity steady state. However, escaping from a health-induced poverty trap can occur only if the quality of public spending is sufficiently high.

1 Introduction

It is now well recognized that investments in health can influence the pace of economic growth via their effects on a variety of health outcomes and health-related factors, including labor market participation and labor productivity, human capital accumulation, life expectancy, savings, and fertility decisions. Conversely, poor health may impede not only physical strength but also mental abilities, incentives to invest in education, and the ability to provide child care; as a result, it may not only be a cause of persistent poverty, but also an outcome of poverty. There is much evidence to support this two-way causality; Lorentzen et al. (2008), for instance, found a bidirectional link between life expectancy and income. Finlay (2007), in a cross-country study, found that growth, education, and health are all determined simultaneously.

From the perspective of development theorists, a natural implication of the empirical evidence is that growth, development, and health outcomes (as well as their implications for demographic variables) should be studied jointly to understand how stagnation and poverty traps may emerge, and what to do to escape from them.¹ This recognition has led to a number of contributions, based on overlapping generations (OLG) models, in which life expectancy (or more precisely the survival probability) is endogenized. Most noteworthy among them are Blackburn and Cipriani (2002), Kalemli-Ozcan (2003), Chakraborty (2004), Cervellati and Sunde (2005, 2011), Hashimoto and Tabata (2005), Finlay (2006), Hazan and Zoabi (2006), Bhattacharya and Qiao (2007), Tang and Zhang (2007), Castelló-Climent and Doménech (2008), Osang and Sarkar (2008), and De la Croix and Licandro (2013). Chakraborty (2004) for instance developed an OLG model in which labor is inelastically supplied and life expectancy is a linear function of public health expenditures, which are funded by a tax on wage income. In turn, agents’ wage income depends on the society’s rate of capital accumulation, which is increasing in longevity. Interactions between life expectancy and savings generate therefore multiple equilibria and health-income traps: a short life expectancy slows down capital accumulation and economic growth, while a lower income shortens life expectancy—which in turn lowers savings and investment. However, because wages rise continuously with the level of output per worker, health status rises perpetually—a rather unattractive feature of the analysis.

This paper contributes to this literature by developing an OLG model that departs from existing contributions in several important ways. First, it abstracts from human capital accumulation. Instead, the endogeneity of life expectancy is related directly to health status, rather than human capital as for instance in Blackburn and Cipriani (2002), Castelló-Climent and Doménech (2008), or Osang and Sarkar (2008). On the one hand, there is indeed evidence suggesting that better educated individuals are more able to adopt healthy lifestyles and inspire their children to follow the same type of behavior (see Silles 2009; Mullahy and Robert 2010). For instance, Cutler and Lleras-Muney (2010) found that, controlling for several factors, better educated people in the United Kingdom and the United States are less likely to be obese, less likely to smoke, and less likely to be heavy drinkers. On the other, it is possible for causality to go in the other direction—healthier individuals (especially in childhood) do better in school, which in turn promotes health-related knowledge (see Behrman 2009). This mechanism may be particularly important for developing countries, especially the poorest ones. Without taking a stand on the direction of causality between health and education, the focus here is solely on the link between health status and life expectancy.² In addition, and as is made clear later, health is quite distinct from knowledge as a source of human capital because it cannot grow without bounds.

Second, the paper accounts for the fact that parents’ health affects directly the health of their children, and that health outcomes in childhood may affect health outcomes in adulthood. As a result, health status displays persistence, as in De la Croix and Licandro (2013) and Osang and Sarkar (2008). Indeed, there is substantial evidence now to suggest that parental health affects the health of children at birth and that health in late life is the outcome of a cumulative process of exposure to health risks in childhood.³ Cognitive and physical impairments of children often begins in utero, due to inadequate nutrition and poor health of the mother—illustrated most dramatically through mother-to-child transmission of HIV. Health persistence is thus an important source of dynamics in a growth context.

Third, the analysis accounts for externalities associated with public capital, not only in terms of the production of goods, but also in terms of the production of health services. There is a sizable literature by now that emphasizes the importance of access to infrastructure for health outcomes. Studies have found that access to clean water and sanitation plays a critical role in the fight against malnutrition and infant mortality. Because many vaccines require continuous and reliable refrigeration to retain their effectiveness, dependable access to electricity is essential for the functioning of hospitals and the delivery of health services. Getting access to clean energy for cooking (as opposed to smoky traditional fuels) in people’s homes reduces indoor air pollution and the incidence of respiratory illnesses. Improved roads make it easier for qualified medical workers to move between cities and rural areas and for those seeking care to reach hospitals and clinics. Consequently, the paper takes a broader perspective on the relationship between health, infrastructure, and growth, in line with the recent literature on the macroeconomic effects of health services.⁴

The key issue that the paper addresses is the following: in a context where health is an important source of dynamics, by affecting both labor efficiency and life expectancy, and the production of health services depends on access to public capital, under what conditions do “health-induced poverty traps”emerge, and can public policy allow a country to escape from these traps? What role does the health externality of public capital play in this process? The key result is that if health outcomes and life expectancy are endogenously related, multiple equilibria can emerge, not because of the effect of life expectancy on saving and capital accumulation (as in Chakraborty 2004) but rather through its impact on labor supply. In addition, shifting the economy from a path converging to a low-growth trap, to a path converging to a high-growth equilibrium, can be achieved by a sufficiently large increase in spending on either health or infrastructure—provided that spending is efficient enough. In the process, I also show that, in contrast to the existing literature, an autonomous increase in life expectancy may not raise the growth rate of output in the long run, because of an adverse effect on the public–private capital ratio. This result is useful to understand why the empirical literature has found conflicting results on the link between life expectancy and growth.

The paper unfolds as follows. Section 2 presents the model. Section 3 solves for the optimal household decision rules, derives the balanced-growth path under the assumption of a constant survival rate, and discusses the properties of the model—most notably with respect to an increase in life expectancy. Section 4 considers threshold effects associated with health status and the possibility of multiple equilibria. I also address the issue of whether an increase in either type of productive public spending considered in the model (health and infrastructure) may allow a country to escape from a low-growth trap. Section 5 discusses the robustness of the results and the last section of the paper offers some concluding remarks.⁵

2 The model

Consider an OLG economy where one marketed good is produced and individuals live (at most) for three periods: childhood, adulthood and old age. The good can be either consumed in the period it is produced or stored to yield capital at the beginning of the following period. Each individual is endowed with 0 units of time in childhood and in old age, and 1 unit in middle age. The only source of income is therefore wages in the second period of life, which serves to finance consumption in adulthood and old age. Savings can be held only in the form of physical capital. Agents have no other endowments, except for an initial stock of physical capital, $K_{0}^{P}$ at time $t=0$, which is held by an initial generation of retirees. Children depend on their parents for consumption and health care.

The fertility rate is constant. Keeping children healthy involves only a (fixed) time cost, in terms of the parent’s time. Consistent with the evidence mentioned earlier, health status of children depends also on access to infrastructure services and on the parent’s health, whereas health status of adults depends solely on health status in childhood.⁶ There is therefore “state dependence” in health outcomes. Adults decide on the allocation of their time between work and leisure. At the end of the second period of life there is a non-zero probability of dying, which is initially taken as given.

In addition to individuals, the economy is populated by firms and an infinitely-lived government. Firms produce marketed goods using private capital, labor, and public capital as inputs. The government invests in infrastructure and spends on health and some unproductive services. It taxes only the wage income of adults. It cannot borrow and therefore must run a balanced budget in each period. All government services are provided free of charge. Public capital is nonexcludable but partially rival, due to congestion effects. Finally, all markets clear and there are no debts or bequests between generations.

2.1 Households

Let $n\ge 1$ denote the exogenous fertility rate. Raising a child involves a fixed time cost of $\varepsilon ^{R}\in (0,1)$, related to taking care of the child’s health (breast feeding, taking children to medical facilities for vaccines, etc.). Adults also allocate time, in proportion $\varepsilon _{t+1}^{W}$, to working. Leisure is thus defined as $1-\varepsilon _{t+1}^{W}-\varepsilon ^{R}n$. The probability of survival from adulthood to old age (at the end of period $t+1$) is denoted by $p_{m}\in (0,1)$, and is taken as constant for the moment.

Assuming that consumption of children in the first period of life is subsumed in their parents’ consumption, expected lifetime utility at the beginning of period $t+1$ of an agent born at $t$ is specified as

$$\begin{aligned} U=\ln c_{t+1}^{t}+\eta _{L}\ln \left( 1-\varepsilon _{t+1}^{W}-n\varepsilon ^{R}\right) +p_{m}\frac{\ln c_{t+2}^{t}}{1+\rho }, \end{aligned}$$

(1)

where $c_{t+j}^{i}$ denotes consumption of generation $i$ individuals at date $t+j$ and $\rho >0$ the discount rate. For simplicity, health (either in childhood or in adulthood) does not provide direct utility.⁷ Parameter $\eta _{L}>0$ measures the individual’s relative preference for leisure.

In standard fashion, period-specific budget constraints are given by

$$\begin{aligned} c_{t+1}^{t}+s_{t+1}&= (1-\tau )\varepsilon _{t+1}^{W}a_{t+1}w_{t+1},\end{aligned}$$

(2)

$$\begin{aligned} p_{m}c_{t+2}^{t}&= (1+r_{t+2})s_{t+1}, \end{aligned}$$

(3)

where $a_{t+1}$ is individual labor efficiency, $w_{t+1}$ the wage rate, $\tau \in (0,1)$ the tax rate, $r_{t+2}$ the rental rate of private capital, and $s_{t+1}$ saving. Equation (3) indicates that individuals consume at period $t+2$ with a probability $p_{m}$.⁸

Combining these two equations yields the consolidated budget constraint

$$\begin{aligned} c_{t+1}^{t}+\frac{p_{m}c_{t+2}^{t}}{1+r_{t+2}}=(1-\tau )\varepsilon _{t+1}^{W}a_{t+1}w_{t+1}. \end{aligned}$$

(4)

2.2 Firms

There is a continuum of identical firms, indexed by $i\in (0,1)$. They produce a single nonstorable good, which is used either for consumption or investment. Production requires the use of private inputs, effective labor and private capital (which firms rent from the currently old agents), and public capital. Although public capital is nonexcludable, it is partially rival because it is subject to congestion. As in Glomm and Ravikumar (1994), congestion is assumed to depend on both the aggregate private capital stock and the size of the (adult) population.⁹

Assuming a Cobb–Douglas technology, the production function of firm $i$ takes therefore the form

$$\begin{aligned} Y_{t}^{i}=\left[ \frac{K_{t}^{I}}{\left( K_{t}^{P}\right) ^{\phi _{K}}N_{t}^{\phi _{N}}} \right] ^{\alpha }\left( A_{t}\varepsilon _{t}^{W,i}N_{t}^{i}\right) ^{\beta }\left( K_{t}^{P,i}\right) ^{1-\beta }, \end{aligned}$$

(5)

where $K_{t}^{P,i}$ denotes the firm-specific stock of capital, $K_{t}^{P}=\int _{0}^{1}K_{t}^{P,i}\,di$ the aggregate private capital stock, $K_{t}^{I}$ the stock of public capital in infrastructure, $A_{t}$ average, economy-wide labor efficiency (which is the same for all firms), $N_{t}^{i}$ the number of adult workers employed by firm $i, \,N_{t}$ the total number of adults, $\phi _{K},\phi _{N}>0$, $\alpha >0$, and $\beta \in (0,1)$. Thus, production exhibits constant returns to scale in firm-specific inputs, effective labor $A_{t}\varepsilon _{t}^{W,i}N_{t}^{i}$ and capital $K_{t}^{P,i}$.

By contrast, public capital in infrastructure is exogenous to each firm’s production process and affects all individual producers in the same way. However, its productivity effects are diminished by excessive use, as measured by the aggregate private capital stock and the size of the population. For instance, the greater the number of trucks operated by the private sector, the greater the likelihood of traffic jams and lost time for workers. The greater the use of electricity-powered machine equipment by individual firms, the higher the pressure on power grids, and the greater the likelihood of power failures. These are particularly important considerations for low-income countries, where public assets in transportation and energy are, to begin with, limited.

Markets for both private capital and labor are competitive. Each firm’s objective is to maximize profits, $\Pi _{t}^{i}$, with respect to labor services and private capital, taking $A_{t}$ as given:

$$\begin{aligned} \max _{N_{t}^{i},K_{t}^{P,i}}\Pi _{t}^{i}=Y_{t}^{i}-r_{t}K_{t}^{P,i}-w_{t}\varepsilon _{t}^{W}A_{t}N_{t}^{i}, \end{aligned}$$

where $r_{t}$ is the rental rate of private capital.

Profit maximization yields

$$\begin{aligned} w_{t}=\beta Y_{t}^{i}/\varepsilon _{t}^{W}A_{t}N_{t}^{i},\quad \quad r_{t}=(1-\beta )Y_{t}^{i}/K_{t}^{P,i}, \end{aligned}$$

(6)

which implies that private inputs are paid at their marginal product.

Given that all firms and workers are identical, in a symmetric equilibrium these conditions become

$$\begin{aligned} w_{t}=\beta Y_{t}/\varepsilon _{t}^{W}A_{t}N_{t},\quad \quad r_{t}=(1-\beta )Y_{t}/K_{t}^{P}. \end{aligned}$$

(7)

Because the number of firms is normalized to 1, aggregate output is given by

$$\begin{aligned} Y_{t}=\int _{0}^{1}Y_{t}^{i}di=N_{t}^{\beta -\alpha \phi _{N}}\left( k_{t}^{I}\right) ^{\alpha }\left( \varepsilon _{t}^{W}A_{t}\right) ^{\beta }\left( K_{t}^{P}\right) ^{1-\beta +\alpha (1-\phi _{K})}, \end{aligned}$$

(8)

where $k_{t}^{I}=K_{t}^{I}/K_{t}^{P}$ is the public–private capital ratio. As shown below, $k_{t}^{I},\,\varepsilon _{t}^{W},$ and $A_{t}$ are all constant in the steady state. To ensure steady-state growth (linearity of output in the private capital stock) and eliminate the scale effect associated with population requires the following assumptions:

Assumption 1

$\beta -\alpha (1-\phi _{K})=0$, $\phi _{N}=\beta /\alpha$.

Combining these two conditions yields $\phi _{K}+\phi _{N}=1$, a result similar to that established by Glomm and Ravikumar (1994) in a related setting.

Under these assumptions, (8) yields aggregate output as

$$\begin{aligned} Y_{t}=\left( k_{t}^{I}\right) ^{\alpha }\left( \varepsilon _{t}^{W}A_{t}\right) ^{\beta }K_{t}^{P}. \end{aligned}$$

(9)

2.3 Health status and labor efficiency

The health status of a child, $h_{t}^{C}$, depends positively on the parent’s health status, $h_{t}^{A}$, rearing time allocated by the parent, and access to public services:

$$\begin{aligned} h_{t}^{C}=\bar{h}^{C}+\left( h_{t}^{A}\right) ^{\kappa }\left( 1+\varepsilon ^{R}\right) ^{\nu _{C}}\left( H_{t}^{G}\right) ^{1-\nu _{C}}, \end{aligned}$$

(10)

where $\bar{h}^{C}\ge 0$ is health status at birth, $H_{t}^{G}$ the supply of public health services (which is also subject to congestion), and$\ \kappa ,\nu _{C}\in (0,1)$. The fact that a child’s health status depends on the parent’s health may be related, as discussed in the introduction, to in utero effects, or to the impact of parents’ physical ability to take care of their children (which may require walking long distances, on difficult terrain, to take them to medical facilities). In practice, public health services are likely to be subject to congestion related either to total population or, more specifically here, the potential number of children seeking medical attention, $nN_{t}$. For simplicity, however, I abstract from this issue.¹⁰

To capture the idea (discussed in the introduction) that cognitive deficits in early life may be impossible to reverse, the health status of adults is assumed to depend only on their health status in childhood:

$$\begin{aligned} h_{t+1}^{A}=h_{t}^{C}. \end{aligned}$$

(11)

Substituting (10), with $\bar{h}^{C}=0$ for simplicity, in (11) yields

$$\begin{aligned} h_{t+1}^{A}=\left( h_{t}^{A}\right) ^{\kappa }\left( 1+\varepsilon ^{R}\right) ^{\nu _{C}}\left( H_{t}^{G}\right) ^{1-\nu _{C}}. \end{aligned}$$

(12)

Thus, because a parent’s health affects his children’s health, and because adult well-being depends on own health in childhood, there is serial dependence in $h_{t}^{A}$. In the spirit of Grossman’s (1972) approach, health is therefore viewed as a durable stock—which can be increased here by improving access to public health services early in life, in line with the literature on early childhood intervention (see Behrman 2009).

For simplicity, adult labor efficiency is taken to be linearly related to health status:

$$\begin{aligned} a_{t}=h_{t}^{A}. \end{aligned}$$

(13)

2.4 Government

The government taxes adults at the constant rate $\tau$ and spends a total of $G_{t}^{I}$ on infrastructure investment, $G_{t}^{H}$ on health, and $G_{t}^{U}$ on other (unproductive) items.¹¹ It cannot issue bonds and must therefore run a balanced budget:

$$\begin{aligned} G_{t}=G_{t}^{I}+G_{t}^{H}+G_{t}^{U}=N_{t}\tau \varepsilon _{t}^{W}A_{t}w_{t}. \end{aligned}$$

(14)

Shares of spending are constant fractions of revenues:

$$\begin{aligned} G_{t}^{h}=\upsilon _{h}N_{t}\tau \varepsilon _{t}^{W}A_{t}w_{t},\quad \quad h=I,H,U \end{aligned}$$

(15)

where $\upsilon _{h}\in (0,1)$.¹² Combining (14) and (15) therefore yields

$$\begin{aligned} \sum \upsilon _{h}=1. \end{aligned}$$

(16)

The production of public capital requires combining the flow spending on infrastructure and the existing stock of public capital. For instance, to build roads requires public land; to build a power plant requires using roads to carry construction materials, and electricity to operate machine tools and construction equipment.¹³ Assuming full depreciation, the law of motion of the public capital stock in infrastructure is thus given by

$$\begin{aligned} K_{t+1}^{I}=(G_{t}^{I})^{\varkappa }(K_{t}^{I})^{1-\varkappa }, \end{aligned}$$

(17)

where $\varkappa \in (0,1)$ is a technology parameter.¹⁴

The production of health services by the government exhibits constant returns to scale with respect to the (congested) stock of public capital in infrastructure, $K_{t}^{I}$, and the flow of government spending on health services, $G_{t}^{H}$:

$$\begin{aligned} H_{t}^{G}=\left[ \frac{K_{t}^{I}}{\left( K_{t}^{P}\right) ^{\phi _{H}}}\right] ^{\mu }\left( \varphi G_{t}^{H}\right) ^{1-\mu }, \end{aligned}$$

(18)

where $\mu ,\,\varphi \in (0,1)$ and $\phi _{H}>0$. This specification captures the fact that (in addition to spending on health per se) access to infrastructure is critical to the production of health services in poor countries, as noted in the Introduction. Coefficient $\varphi$ is an efficiency parameter that measures the extent to which government spending on health actually helps to produce health services. The proportion $1-\varphi$ measures therefore the fraction of resources “lost” due to poor management or waste—a common weakness of health systems in developing countries (see World Health Organization 2000).

In similar fashion to (5), public capital is also assumed to be subject to congestion, as measured by the private capital stock. To ensure that health status is stationary, the following assumption is imposed on $\phi _{H}$:

Assumption 2

$\phi _{H}=\mu ^{-1}$.

2.5 Market-clearing and equilibrium

The asset market-clearing condition requires tomorrow’s private capital stock to be equal to today’s aggregate savings by adults:

$$\begin{aligned} K_{t+1}^{P}=N_{t}s_{t}. \end{aligned}$$

(19)

The following definition may therefore be proposed:

Definition 1

A competitive equilibrium for this economy is a sequence of consumption, savings and time allocated to market work $\{c_{t+1}^{t},c_{t+2}^{t},s_{t},\varepsilon _{t+1}^{W}\}_{t=0}^{\infty }$ , public and private capital stocks $\{K_{t+1}^{P},K_{t+1}^{I} \}_{t=0}^{\infty }$, prices $\{w_{t},r_{t+1}\}_{t=0}^{\infty }$, health status of children and adults $\{h_{t}^{C},h_{t+1}^{A}\}_{t=0}^{\infty }$, a constant tax rate $\tau$ and constant spending shares $\upsilon _{I}$ and $\upsilon _{H}$, such that, given the initial capital stocks $K_{0}^{P}$ and $K_{0}^{I}>0$, health status $h_{0}^{C}$ and $h_{0}^{A}>0$, individuals maximize utility, firms maximize profits, the product market clears, and the government budget is balanced.

In equilibrium, individual labor efficiency must also be equal to the economy-wide average efficiency level, so that $a_{t}=A_{t}$. The following definition characterizes the balanced growth path:

Definition 2

A balanced growth equilibrium is a competitive equilibrium in which $c_{t}^{t}$, $c_{t+1}^{t}$, $Y_{t}$, $K_{t}^{P}$, and $K_{t}^{I}$, all grow at the constant rate $\gamma$, health status in childhood and adulthood, $h_{t}^{C}$ and $h_{t}^{A}$, are constant, and the rate of return on private capital, $r_{t}$, is also constant.

Assuming that health status is constant in the long-run equilibrium [as in Osang and Sarkar (2008) for instance] is a natural one to make if survival rates are endogenously related to health. Indeed, there are limits in the long run as to how much private behavior and medical science can improve individual health status. The important implication, is that health (unlike knowledge) cannot by itself be an engine of permanent growth.

3 Balanced growth path

Each adult maximizes (1) subject to (4), (10), and (11), with respect to $c_{t+1}^{t}$, $c_{t+2}^{t}$, and $\varepsilon _{t+1}^{W}$, taking $\tau$, $H_{t}^{G}$, as well as $p_{m}$ as given. The solution of the household problem is provided in Appendix. It shows that in equilibrium, with constant population ($n=1$) and with $\varepsilon ^{R}=0$ for simplicity,

$$\begin{aligned}&\displaystyle \sigma =\frac{p_{m}}{(1+\rho )+p_{m}}<1,&\end{aligned}$$

(20)

$$\begin{aligned}&\displaystyle \tilde{\varepsilon }^{W}=\frac{1}{1+\eta _{L}(1-\sigma )}<1,&\end{aligned}$$

(21)

where $\sigma$ is the marginal propensity to save. From these solutions, the following proposition can be established:

Proposition 1

An increase in the survival rate from adulthood to old age, $p_{m}$, increases the savings rate and labor supply.

These results are by now standard in the literature (see, for instance, Blackburn and Cipriani 2002; Zhang and Zhang 2005). Through a life-cycle effect, a higher adult survival rate dictates a need for higher savings to finance consumption in old age, and thereby has a positive effect, ceteris paribus, on the savings rate and labor supply.

The balanced growth rate of the economy is derived in Appendix, where it is shown that the model can be condensed into an autonomous, first-order linear difference equation system in $\hat{h}_{t}^{A}=\ln h_{t}^{A}$ and $\hat{k}_{t}^{I}=\ln k_{t}^{I}$, which can be written as

$$\begin{aligned} \left[ \begin{array}{c} \hat{h}_{t+1}^{A} \\ \hat{k}_{t+1}^{I} \end{array} \right] =\left[ \begin{array}{c} a_{10} \\ a_{20} \end{array} \right] \left[ \begin{array}{cc} \zeta _{1} &{} \zeta _{2} \\ a_{21} &{} a_{22} \end{array} \right] \left[ \begin{array}{c} \hat{h}_{t}^{A} \\ \hat{k}_{t}^{I} \end{array} \right] , \end{aligned}$$

(22)

where $a_{10}$ and $a_{20}$ are constant terms and

$$\begin{aligned} \zeta _{1}&= \kappa +\beta (1-\nu _{C})(1-\mu )>0,\\ \zeta _{2}&= (1-\nu _{C})[\mu +\alpha (1-\mu )]>0,\\ a_{21}&= -\beta (1-\varkappa )<0,\\ a_{22}&= (1-\varkappa )(1-\alpha )>0. \end{aligned}$$

The steady-state values of $h_{t}^{A}$ and $k_{t}^{I}$ are obtained by solving the system

$$\begin{aligned} \tilde{k}^{I}&= \left\{ \frac{(\beta \upsilon _{I}\tau )^{\varkappa }(\varepsilon ^{W})^{-\beta (1-\varkappa )}}{\beta \sigma (1-\tau )}\right\} ^{1/\Pi }(\tilde{h}^{A})^{-\beta (1-\varkappa )/\Pi }, \end{aligned}$$

(23)

$$\begin{aligned} \tilde{k}^{I}&= \big [\varphi \upsilon _{H}\tau \beta \big (\tilde{\varepsilon } ^{W}\big )^{\beta }\big ]^{-(1-\nu _{C})(1-\mu )/\zeta _{2}}\big (\tilde{h}^{A}\big )^{(1-\zeta _{1})/\zeta _{2}}, \end{aligned}$$

(24)

where $\Pi =1-(1-\alpha )(1-\varkappa )\in (0,1)$. To ensure stability (as discussed in Appendix), the following condition is imposed:

Assumption 3

$\zeta _{1}<1$.

Intuitively, this condition implies that the magnitude of the parent-to-child externality measured by $\kappa$ (which also corresponds to the degree of persistence in health status in equilibrium) cannot be too high.

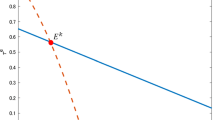
Figure 1 illustrates the determination of the steady-state equilibrium. Equation (23) defines a concave, downward-sloping curve denoted $KK$ . By contrast, the curve defined by Eq. (24), denoted $HH$, is upward-sloping, given Assumption 3. In addition, in the figure $HH$ is shown as concave.¹⁵ $^{,}$ ¹⁶

Fig. 1

Steady-state equilibrium

It is immediately clear from the shape of these curves that there is a unique non-trivial equilibrium located at the point at which they intersect, Point $E$. Health status and labor efficiency are thus both constant in the steady state, together with the public–private capital ratio.¹⁷ If the economy is initially at values $\left( h_{0}^{A},k_{0}^{I}\right)$ corresponding to, say, Point $A$, it will converge monotonically to $E$. At initial values corresponding to Point $B$ instead, the economy may cycle around the equilibrium point.

From (9), (13) and the solution for the growth rate of private capital given in Appendix, the steady-state growth rate of output is

$$\begin{aligned} 1+\gamma =\beta \sigma (1-\tau )\left( \tilde{k}^{I}\right) ^{\alpha }\left( \tilde{\varepsilon } ^{W}\tilde{h}^{A}\right) ^{\beta }, \end{aligned}$$

(25)

where $\tilde{h}^{A}$ and $\tilde{k}^{I}$ are the solutions of (23) and (24).

The equilibrium solution can be used to examine the impact of a variety of parameters and policy variables on long-run growth. Most importantly for the purpose at hand, the following result can be established:

Proposition 2

An increase in the survival rate from adulthood to old age has an ambiguous effect on the steady-state growth rate of output.

An increase in $p_{m}$ affects growth essentially through an increase in the savings rate, $\sigma$, and, through savings, labor supply. As noted earlier, with higher likelihood to surviving to old age, adults save more for late-life consumption and work more. In turn, changes in $\sigma$ affect growth both directly (through higher saving and labor supply), and indirectly, through changes in the steady-state values of the public–private capital ratio and health status. The direct effect, as can be seen in (25), is positive—a higher savings rate raises the rate of private capital accumulation and time allocated to market work.

However, there are also indirect effects, which operate through changes in $\tilde{k}^{I}$ and $\tilde{h}^{A}$. In fact, both the increase in $\sigma$ and $\varepsilon ^{W}$ lead to a reduction in the public–private capital ratio. This does not depend on the assumption that existing public capital is essential in the production of new capital; with $\varkappa =1$, the effects of labor supply on public and private capital accumulation cancel out, but the savings effect remains. It does not depend either on the magnitude of $\mu$, the health externality of public capital. Given these conflicting effects on the public–private capital ratio, the net effect on the steady-state growth rate, $d(1+\gamma )/dp_{m}$, cannot be determined a priori.

This result is illustrated in Fig. 2. For $\tilde{h}^{A}$ given, the increase in $p_{m}$ lowers the steady-state public–private capital ratio as a result of the increase in both the savings rate and labor supply, which combine to increase the private capital stock; $KK$ must therefore shift vertically downward. For $\tilde{k}^{I}$ given, the increase in $p_{m}$ raises steady-state health status as a result of the increase in health expenditure associated with higher labor supply and labor income; $HH$ must therefore shift horizontally rightward. Consequently, the position of the new equilibrium depends on the magnitude of the shift in both curves. If the new equilibrium point is located at $E^{\prime }$, to the Southeast of $E$, the public–private capital ratio is lower but health status is higher. By contrast, if the new equilibrium is at $E^{\prime \prime }$ or $E^{\prime \prime \prime }$, to the Southwest of $E$, both health status and the public–private capital ratio are lower. Because the public–private capital ratio always falls, the net effect on the steady-state growth rate is ambiguous in all cases.¹⁸ Note also that the larger $\mu$ is, the smaller the shift in $HH$, and thus the more likely that health status will deteriorate as a result of the increase in life expectancy. A strong health externality of public capital may lead therefore to a paradox: an increase in life expectancy, through its general equilibrium effects, may lead to a deterioration in health status and to an adverse effect on growth.

Fig. 2

Increase in life expectancy

It is also worth noting that, from (24), if labor supply was assumed constant, or if health services had no impact on childhood health ($\nu _{C}=1$), $HH$ would not shift in response to the increase in the survival rate—as would be the case with $\mu =1$. In such conditions, both the public–private capital ratio and health status would unambiguously deteriorate. Put differently, with $\nu _{C},\mu \in (0,1)$, in the present setting the only reason why health status may improve following the increase in the survival rate is because labor supply is endogenous; by raising output, it also increases the amount of resources that the government can spend on providing health services.

Thus, the foregoing analysis shows that the “standard”view, according to which an increase in the adult survival rate promotes growth [as for instance in Blackburn and Cipriani (2002) and Zhang and Zhang (2005)], does not necessarily hold when the congestion effects of private capital (and, less fundamentally, the health externality of public capital), are taken into account.¹⁹ Moreover, the same results would obtain if congestion effects had been measured in terms of total output, instead of the private capital stock.

4 Poverty traps and public policy

The foregoing analysis focused on the case of constant life expectancy and a unique balanced growth equilibrium. I now examine the case where the survival rate is endogenously related to health outcomes and examine whether multiple equilibria can emerge. I also study the role of public policy in that context.

A natural route to follow in the present setting would be to consider the case where the survival rate is related directly to the individual’s own health status. In solving their optimization problem, parents would then internalize the implications of their time allocation decisions. Unfortunately, given the complexity of the model, endogenizing the survival probability in that way precludes an analytical treatment.

Alternatively, suppose that the survival probability of any particular individual depends on average health status in the economy—which, in equilibrium, is of course the same for all individuals. For instance, if you stop smoking, but you continue to be surrounded by smokers, your health prospects will not necessarily improve. If you quit drinking, but nobody else does, the risk of you getting involved in a car accident involving a drunk driver will not necessarily diminish. In an environment where deadly communicable diseases can spread rapidly (as is often the case in urban slums in developing countries), and vaccines do not completely protect from the risk of getting infected, one individual getting immunized will not change the risk to which he is exposed—unless all individuals get immunized; and so on. In such conditions, it is natural to retain the assumption that agents do not internalize the effect of their time allocation decisions on their own survival probability.²⁰

Suppose then that the adult survival rate is a piece-wise function defined as

$$\begin{aligned} p_{t}=\left\{ \begin{array}{ll} p_{m}&{}\quad \text {for}\quad h_{t}^{A}<h_{L}^{A}, \\ f(h_{t}^{A})&{}\quad \text {for}\quad h_{L}^{A}\le h_{t}^{A}<h_{H}^{A}, \\ p_{M}&{}\quad \text {for}\quad h_{t}^{A}\ge h_{H}^{A}, \end{array} \right. \end{aligned}$$

(26)

where $f^{\prime }>0$ and $f^{\prime \prime }<0$. Thus, if health status is below $h_{L}^{A}$, the likelihood of surviving to old age is $p_{m}$, as before. In the context of poor countries, this could reflect the fact that levels of education are also low, implying that nutritional habits remain the same and prevent at first improvements in health status from translating into higher survival rates.²¹ As health status improves above that threshold, the relationship between $p_{t}$ and $h_{t}^{A}$ is positive and concave over the interval $(h_{L}^{A},h_{H}^{A})$. It becomes constant again at $p_{M}$ and $p_{m}<p_{M}<1$ for values of health status above $h_{H}^{A}$. Put differently, beyond a certain point, further changes in health status have no effect on the probability to survive—perhaps reflecting the fact that there always remains a risk of accidental death.²²

Function (26) is illustrated in the Northeast quadrant of Fig. 3. The Northwest quadrant of the figure shows the (concave) relationship between life expectancy and the savings rate, whereas the Southwest quadrant shows the (convex) relationship the savings rate and time allocated to market work [see (20) and (21)]. The Southeast quadrant shows the reduced-form relationship between health status and labor supply.²³

Fig. 3

Health, life expectancy and labor supply

To illustrate how these threshold effects in health can lead to poverty traps and study the role of public policy in that context, I focus on the case where $\varkappa =1$, that is, the case where public capital is not essential to produce new capital.²⁴ As can be inferred from the results in Appendix, the public–private capital ratio is then constant over time at

$$\begin{aligned} J=\frac{\upsilon _{I}\tau }{\sigma (1-\tau )}. \end{aligned}$$

(27)

The following corollary, which is useful for the discussion below, can be established on the basis of the results in Proposition 1:²⁵

Corollary to Proposition 1 An increase in the survival probability from adulthood to old age lowers the public–private capital ratio.

The behavior of the economy is now determined solely by the dynamics of adult health status. Because time allocated to market work depends endogenously on health status, through the savings rate (see Proposition 1), Appendix shows that this dynamic equation takes the general form, using (27),

$$\begin{aligned} h_{t+1}^{A}=\Phi (h_{t}^{A})=\Gamma \sigma _{t}^{-\zeta _{2}}(\varepsilon _{t}^{W})^{\beta (1-\nu _{C})(1-\mu )}(h_{t}^{A})^{\zeta _{1}}, \end{aligned}$$

(28)

where $\Gamma =(\varphi \upsilon _{H}\tau \beta )^{(1-\nu _{C})(1-\mu )}[\upsilon _{I}\tau /(1-\tau )]^{\zeta _{2}}$ and $\zeta _{1},\zeta _{2}$ are as defined earlier.²⁶

For $h_{t}^{A}<h_{L}^{A}$, $\sigma _{t}$ and $\varepsilon _{t}^{W}$ are constant at the values given in (20) and (21), and the adjustment process in (28) is stable under Assumption 3, that is, $\zeta _{1}<1$. Beyond $h_{L}^{A}$, however, because the savings rate is positively related to the survival probability, which itself depends on health status, and because labor supply depends on the savings rate, both $\sigma _{t}$ and $\varepsilon _{t}^{W}$ depend on health status, as illustrated in Fig. 3. These functional forms can be written as $\sigma _{t}=\sigma (h_{t}^{A})$ and $\varepsilon _{t}^{W}=g(h_{t}^{A})$, with $\sigma ^{\prime },g^{\prime }>0$.²⁷ As a result, Assumption 3 may no longer be sufficient to ensure (monotonic) convergence.

Indeed, using linear approximations to both $\sigma ()$ and $g()$, the following result can be established:

Proposition 3

Health dynamics are unstable in the interval $(h_{L}^{A},h_{H}^{A})$ if $\vert \Phi ^{\prime } \vert =\zeta _{1}+\beta (1-\nu _{C})(1-\mu )-\zeta _{2}>1$.

Using the definitions given earlier of $\zeta _{1}$ and $\zeta _{2}$, this condition can be rewritten as

$$\begin{aligned} \kappa +(1-\nu _{C})\{\beta (1-\mu )-[\mu +\alpha (1-\mu )]\}>1. \end{aligned}$$

(29)

The first point to notice in (29) is that, without the endogenous time allocation effect (that is, the dependence of $\varepsilon ^{W}$ on $\sigma$), multiple equilibria cannot occur. The direct effect of health status through the savings rate, as captured by $\zeta _{2}$, always makes the model more stable, abstracting for oscillatory behavior (that is, as long as $\zeta _{1}>\zeta _{2}$); this is in contrast with Chakraborty (2004). Put differently, the possibility of poverty traps arises solely because of endogenous labor supply. The second point is that if health in childhood does not depend on access to health services ($\nu _{C}=1$), the instability condition is just $\kappa >1$; multiple equilibria cannot occur either. By calculating the derivative of the transition curve, $\vert \Phi ^{\prime }\vert$, with respect to $\mu$, it can be established that

$$\begin{aligned} \text {sg}(\frac{d\vert \Phi ^{\prime }\vert }{d\mu })=\text {sg} [-\beta -(1-\alpha )]<0, \end{aligned}$$

which implies that the stronger the health externality of public capital is, the less likely it is that multiple equilibria will emerge.²⁸ These results can be summarized in the following proposition:

Proposition 4

For multiple equilibria to occur labor supply must be endogenous, $\varepsilon _{t}^{W}=g(h_{t}^{A})$, and health status in childhood must depend on access to health services ($\nu _{C}>0$). The weaker the health externality of public capital is (the lower $\mu$ is), the more likely it is that multiple equilibria will emerge.

Suppose then that condition (29) holds for $h_{t}^{A}\in (h_{L}^{A},h_{H}^{A})$. The steady-state equilibrium may therefore not be unique; there can be up to three possible steady states, two of which at most are stable. Figure 4 describes two cases where there exists a unique steady-state equilibrium.²⁹ By contrast, Fig. 5 describes the case of multiple, locally stable steady-state equilibria; a steady state with either low health status, $\tilde{h}_{1}^{A}$, and high health status, $\tilde{h} _{3}^{A}$. The intermediate equilibrium, $\tilde{h}_{2}^{A}$, is unstable.³⁰ In this case, initial conditions determine the economy’s long-run steady-state equilibrium: economies with a relatively low initial health status may converge to a poverty trap, characterized by poor health outcomes, low labor efficiency, and low growth. For instance, if initial health is such that $0<h_{0}^{A}<\tilde{h} _{2}^{A}$, the economy will converge to $\tilde{h}_{1}^{A}$, whereas if $h_{0}^{A}>\tilde{h}_{2}^{A}$, it will converge to $\tilde{h}_{3}^{A}$.

Fig. 4

Dynamics of health status: unique equilibrium

Fig. 5

Dynamics of adult health status: multiple equilibria

What is the role of public policy then? The impact of an increase at $t=0$ in the share of investment in infrastructure financed by a cut in unproductive outlays ($d\upsilon _{I}+d\upsilon _{U}=0$) is illustrated in Fig. 6. The policy shifts the law of motion $\Phi (h_{t}^{A})$ upward. The key issue is whether, starting from a situation where $h_{0}^{A}$ is positioned to the left of the the unstable equilibrium (which implies that the economy would converge to a low-growth trap at $A^{1}$), the policy shift is large enough to ensure that $h_{0}^{A}$ is now positioned to the right of the unstable equilibrium, thereby ensuring convergence to the high-growth steady state.³¹ This is indeed what is shown in the figure; following the policy shift, the new unstable equilibrium is at $B^{2}$ and the economy converges to the new high-growth steady state at $B^{3}$.

Fig. 6

Escaping a health-induced poverty trap

Can an increase in the share of spending on health, financed also by a cut in unproductive spending ($d\upsilon _{H}+d\upsilon _{U}=0$), achieve the same outcome? It depends on the magnitude of the spending efficiency parameter, $\varphi$, and the elasticity of the production of health services with respect to infrastructure, $\mu$. If $\varphi$ is too low, even a large increase in $\upsilon _{H}$ may not be sufficient to induce an upward shift in $\Phi (h_{t}^{A})$ that is large enough to put the economy on a convergent path to the high-growth equilibrium. If $\mu$ is relatively high, a better strategy may then be to spend more on infrastructure. Indeed, if at the same time $\varphi$ is relatively low and $\mu$ relatively high, paradoxically the best way to improve health outcomes and escape a health-induced poverty trap may involve reducing spending on health services to create room for higher investment in infrastructure.³² In fact, even if $\mu$ is relatively low, a higher spending share on infrastructure (offset by a reduction in the share of spending on health) may still be preferable if the production externality associated with public capital (as measured by $\alpha$) is high, because it entails a higher level of public spending on health through the impact of output on tax revenues.

But of course, spending on infrastructure could be subject to the same efficiency issues that characterize other components of government spending, including health outlays. In fact, there is now robust evidence to suggest that there are serious quality issues associated with infrastructure spending in the poorest countries in the developing world.³³ Thus, to the extent that there is an inverse correlation between the quality of government spending (be it on health or infrastructure) and the level of corruption, escaping from a poverty trap through higher public expenditure may also require deep institutional reforms.

5 Robustness

To examine the robustness of the results presented earlier, I consider three issues: the functional form relating the survival rate to health status, especially the piecewise nature of this relationship; the nature of the experiment underlying Propositions 1 and 2; and the possibility that the fertility rate and unit rearing time are endogenously chosen by individuals.³⁴

First, in the foregoing analysis, a piece-wise function was used to relate the survival rate to health status. This was done mainly to simplify the presentation. A variety of alternative functional forms could be used without altering the main results; what matters is that there exists a range of values of health status along which it has a positive link with the survival rate. The assumption that the function is concave ($f^{\prime \prime }<0$) is important for the existence of a high growth equilibrium; otherwise, the transition curve will diverge for sure when health status enters the intermediate range. A simple functional form that satisfies this condition, together with constancy beyond a certain value of health status [as imposed in (26)] is, as in Mariani et al. (2010, p. 803) for instance:

$$\begin{aligned} p_{t}=f(h_{t}^{A})=\min \left( p_{m}+A\left( h_{t}^{A}\right) ^{\upsilon },p_{M}\right) , \end{aligned}$$

which involves a minimum value $p_{m}\ge 0$ and a maximum value $1\ge p_{M}>p_{m}$, with $A>0$, and $\upsilon \in (0,1)$. Thus, the survival rate remains again constant at $p_{M}$ once $h_{t}^{A}$ reaches the critical value

$$\begin{aligned} h_{H}^{A}=\left( \frac{p_{M}-p_{m}}{A}\right) ^{1/\upsilon }. \end{aligned}$$

The question is whether a more general concave, but smooth function (with no “kink” for health status high enough) generates similar results. Examples of such functions are, as noted by Chakraborty (2004, footnote 4), $f(h_{t}^{A})=\bar{p}h_{t}^{A}/(1+h_{t}^{A})$ ,³⁵ or $f(h_{t}^{A})=1-\bar{p}\exp (h_{t}^{A})$, with $\bar{p} \in (0,1)$ in both cases. Because the slope of these curves falls as $h_{t}^{A}$ increases, it is intuitively clear that for either one of them our results would continue to hold—the condition for $\vert \Phi ^{\prime } \vert >1$ eventually reverses as $h_{t}^{A}$ increases, implying that a high-growth equilibrium will eventually be achieved. However, the precise value of $h_{t}^{A}$ at which $\vert \Phi ^{\prime }\vert <1$ again, a condition involving a (local) linear approximation, must now be evaluated numerically.

Second, to establish Propositions 1 and 2, the survival rate was taken to be exogenous. This is a natural benchmark for comparison with the literature and identify the possible channels through which a change in the survival rate may have a negative effect on output. However, suppose (as discussed earlier) that the survival rate and health status are related through a smooth function, say $p_{t}=\bar{p}h_{t}^{A}/(1+h_{t}^{A})$. An autonomous increase in the survival rate (reflecting, for instance, the discovery of a new vaccine or treatment for a disease previously considered incurable) can be captured by considering a shift in $\bar{p}$.

In line with the previous discussion, the key reason why an exogenous increase in life expectancy may lead to a deterioration in health status is because the drop in the public–private capital ratio (induced by the higher savings rate) may lead to a fall in the supply of health services. However, if life expectancy is endogenous, an initial change in health status will have a feedback effect on the survival rate; if health status deteriorates on impact, this will mitigate the initial increase in life expectancy and therefore dampens the final (general equilibrium) effect on health status. Put differently, the endogeneity of life expectancy makes it less likely that an autonomous improvement in life expectancy will weaken health status and reduce growth. Nevertheless, this does not eliminate entirely the possibility of a perverse effect; much will depend on the strength of the direct and indirect effects on the survival rate and the specific form through with it is related to health status.

Finally, in the foregoing discussion the fertility rate, $n$, and unit time allocated to child rearing, $\varepsilon ^{R}$, were both taken as exogenous, setting in fact $n=1$ and $\varepsilon ^{R}=0$. In the working paper version of this article (available upon request), both variables are endogenized; the analysis shows that an increase in the survival rate reduces the fertility rate, $n$, and total time allocated to child rearing, $n\varepsilon ^{R}$. The effect on unit rearing time, however, is ambiguous. Intuitively, the reduction in the fertility rate allows parents to allocate more time to each of them to improve their health—even though total time devoted to child rearing $n\varepsilon ^{R}$ falls. Thus, the response to a change in the survival rate usually reflects not only a standard intertemporal trade-off, which involves adults substituting leisure today for consumption tomorrow (as indicated in Proposition 1), but also an intratemporal time allocation trade-off, which involves substituting rearing time for time allocated to market work. Because changes in rearing time have persistent effects on health, they also alter in significant ways the dynamics of the economy and the possibility of multiple equilibria. In fact, it can be established that if time allocated to child rearing falls sufficiently with increases in the savings rate, multiple equilibria become less likely—but with the possibility of a stagnation (unique) equilibrium becoming more likely, due to adverse effects on health status in adulthood and labor efficiency.

6 Concluding remarks

The purpose of this paper was to present an OLG model that combines three important issues in the determination of long-run growth in poor countries: interactions between public capital in infrastructure and health outcomes; the dependence of health in adulthood on health in childhood; and a cross-generation effect, in the sense of parental health affecting directly the health of their children, possibly in utero.

The first part of the paper described the model. Infrastructure affects not only the production of goods but also the production of health services. At the end of adulthood, there is a non-zero probability of dying. To introduce serial dependence in health outcomes, health status in adulthood was assumed to depend solely on health status in childhood.

The second part derived the balanced growth path, which is characterized by constant health status and a constant public–private capital ratio. Stability and uniqueness of the equilibrium were also established. In contrast to the existing literature, an autonomous increase in the adult survival rate was shown (despite positive direct effects through savings and labor supply) to have an ambiguous effect on growth, mainly because of the congestion effect associated with the higher private capital stock. This result is important because it provides yet another reason as to why empirical studies have had difficulty establishing a robust impact of life expectancy on growth and standards of living (see Acemoglu and Johnson 2007; Finlay 2007; Ashraf et al. 2008).

The third part of the paper endogenized the adult survival probability by relating it directly to (average) health status. Multiple equilibrium growth rates were shown to be possible, implying that the limiting outcome of the economy depends critically on initial conditions. The role of public policy in that context was also examined; it was shown that an increase in either spending on health or infrastructure may get the economy on a convergent path to a high-growth equilibrium with improved health and labor efficiency outcomes. However, this can only occur only if the quality of public spending is sufficiently high. Consequently, a growth strategy based on increased public expenditure may require the simultaneous implementation of far-reaching governance reforms to allow a country to escape from the type of “health-induced poverty traps”identified in this paper.

Appendix

Before solving the individual’s maximization problem, rewrite Eqs. (10), with $\bar{h}^{C}=\varepsilon ^{R}=0$, and (11) as

$$\begin{aligned} h_{t+1}^{A}=h_{t}^{C}=\left( h_{t}^{A}\right) ^{\kappa }\left( H_{t}^{G}\right) ^{1-\nu _{C}}, \end{aligned}$$

(30)

which implies that both $h_{t}^{C}$ and $a_{t+1}=h_{t+1}^{A}$ are predetermined from the point of view of decisions taken at the beginning of period $t+1$.³⁶

From (1), and with $\varepsilon ^{R}=0$, each individual therefore maximizes

$$\begin{aligned} U=\ln c_{t+1}^{t}+\eta _{L}\ln \left( 1-\varepsilon _{t+1}^{W}\right) +p_{m}\frac{\ln c_{t+2}^{t}}{1+\rho }, \end{aligned}$$

(31)

with respect to $c_{t+1}^{t}$, $c_{t+2}^{t}$, and $\varepsilon _{t+1}^{W}$, subject to (4), which is rewritten here for convenience:

$$\begin{aligned} (1-\tau )\varepsilon _{t+1}^{W}a_{t+1}w_{t+1}-c_{t+1}^{t}-\frac{ p_{m}c_{t+2}^{t}}{1+r_{t+2}}=0. \end{aligned}$$

(32)

First-order conditions yield the familiar Euler equation

$$\begin{aligned} \frac{c_{t+2}^{t}}{c_{t+1}^{t}}=\frac{1+r_{t+2}}{1+\rho }, \end{aligned}$$

(33)

together with

$$\begin{aligned} \frac{\eta _{L}}{1-\varepsilon _{t+1}^{W}}=\frac{(1-\tau )a_{t+1}w_{t+1}}{ c_{t+1}^{t}}, \end{aligned}$$

(34)

Substituting (33) in the intertemporal budget constraint (32) yields

$$\begin{aligned} c_{t+1}^{t}=\left[ \frac{1+\rho }{(1+\rho )+p_{m}}\right] (1-\tau )\varepsilon _{t+1}^{W}a_{t+1}w_{t+1}, \end{aligned}$$

(35)

so that saving is equal to

$$\begin{aligned} s_{t+1}=\sigma (1-\tau )\varepsilon _{t+1}^{W}a_{t+1}w_{t+1},\quad \sigma =\frac{p_{m}}{(1+\rho )+p_{m}}<1. \end{aligned}$$

(36)

Substituting (35) in (34) yields

$$\begin{aligned} \frac{\eta _{L}}{1-\varepsilon _{t+1}^{W}}=\frac{1}{(1-\sigma )\varepsilon _{t+1}^{W}}, \end{aligned}$$

(37)

which can be solved for the optimal value of $\varepsilon _{t+1}^{W}$:

$$\begin{aligned} \varepsilon ^{W}=\frac{1}{1+\eta _{L}(1-\sigma )}<1. \end{aligned}$$

(38)

A higher $p_{m}$ raises the propensity to save [from (36)] and time allocated to work [from (38)]:

$$\begin{aligned} \frac{d\sigma }{dp_{m}}>0, \quad \frac{d\varepsilon ^{W}}{dp_{m}}>0. \end{aligned}$$

To study the dynamics in this economy, substitute first (36) in (19) to give

$$\begin{aligned} K_{t+1}^{P}=N_{t}s_{t}=\sigma (1-\tau )N_{t}\varepsilon _{t}^{W}a_{t}w_{t}, \end{aligned}$$

that is, substituting for $w_{t}$ from (7),

$$\begin{aligned} K_{t+1}^{P}=\beta \sigma (1-\tau )Y_{t}. \end{aligned}$$

(39)

Substituting out for $Y_{t}$ using (9), and given (38), yields

$$\begin{aligned} \frac{K_{t+1}^{P}}{K_{t}^{P}}=\beta \sigma (1-\tau )\big (k_{t}^{I}\big )^{\alpha }\big (\varepsilon ^{W}\big )^{\beta }A_{t}^{\beta }. \end{aligned}$$

(40)

Similarly, from (7), (15), and (17),

$$\begin{aligned} K_{t+1}^{I}=\left( \frac{G_{t}^{I}}{K_{t}^{I}}\right) ^{\varkappa }\, K_{t}^{I}=\left( \frac{\beta \upsilon _{I}\tau Y_{t}}{K_{t}^{I}}\right) ^{\varkappa }\, K_{t}^{I}=(\beta \upsilon _{I}\tau )^{\varkappa }\left( \frac{Y_{t}}{K_{t}^{I}}\right) ^{\varkappa }K_{t}^{I}. \end{aligned}$$

Substituting out for $Y_{t}$ using (9) yields

$$\begin{aligned} \frac{K_{t+1}^{I}}{K_{t}^{I}}=\big [\beta \upsilon _{I}\tau (\varepsilon ^{W})^{\beta }\big ]^{\varkappa }\left[ \frac{(k_{t}^{I})^{\alpha }A_{t}^{\beta }K_{t}^{P}}{K_{t}^{I}}\right] ^{\varkappa }, \end{aligned}$$

that is,

$$\begin{aligned} \frac{K_{t+1}^{I}}{K_{t}^{I}}=\big [\beta \upsilon _{I}\tau (\varepsilon ^{W})^{\beta }\big ]^{\varkappa }\big (k_{t}^{I}\big )^{-\varkappa (1-\alpha )}A_{t}^{\varkappa \beta }. \end{aligned}$$

(41)

Combining (40) and (41) yields

$$\begin{aligned} k_{t+1}^{I}=\frac{K_{t+1}^{I}}{K_{t+1}^{P}}=\frac{\big [\beta \upsilon _{I}\tau \big (\varepsilon ^{W}\big )^{\beta }\big ]^{\varkappa }\big (k_{t}^{I}\big )^{-\varkappa (1-\alpha )}A_{t}^{\varkappa \beta }K_{t}^{I}}{\beta \sigma (1-\tau )\big (k_{t}^{I}\big )^{\alpha }\big (\varepsilon ^{W}\big )^{\beta }A_{t}^{\beta }K_{t}^{P}}, \end{aligned}$$

that is, using (13),

$$\begin{aligned} k_{t+1}^{I}=\frac{\big (\beta \upsilon _{I}\tau \big )^{\varkappa }\big (\varepsilon ^{W}\big )^{-\beta (1-\varkappa )}}{\beta \sigma (1-\tau )}\big (k_{t}^{I}\big )^{(1-\alpha )(1-\varkappa )}\big (h_{t}^{A}\big )^{-\beta (1-\varkappa )}. \end{aligned}$$

(42)

Thus, if $\varkappa =1$, then $k_{t+1}^{I}$ is constant over time. Note that $k_{t+1}^{I}$ depends indirectly on $p_{m}$ through $\sigma$ [see (36)] in two ways: directly (through investment) and indirectly, through $\varepsilon ^{W}$ (time allocation). The net effect is positive, given that both $\sigma$ and $\varepsilon ^{W}$ increase.

The next step is to calculate $H_{t}^{G}$, to determine the dynamics of $h_{t}^{A}$ in (30). From (7) and (15), $G_{t}^{H}=\upsilon _{H}\tau \beta Y_{t}$; substituting this result in (18) yields

$$\begin{aligned} H_{t}^{G}&= \left[ \frac{K_{t}^{P}}{\big (K_{t}^{P}\big )^{\mu }\big (K_{t}^{P}\big )^{1-\mu }} \right] \big (K_{t}^{I}\big )^{\mu }\big (K_{t}^{P}\big )^{-\mu \phi _{H}}\big (\varphi G_{t}^{H}\big )^{1-\mu }\\&= \left( \frac{K_{t}^{I}}{K_{t}^{P}}\right) ^{\mu }\big (K_{t}^{P}\big )^{1-\mu \phi _{H}}\left( \frac{ \varphi G_{t}^{H}}{K_{t}^{P}}\right) ^{1-\mu }, \end{aligned}$$

or, using Assumption 2, $1-\mu \phi _{H}=0$,

$$\begin{aligned} H_{t}^{G}=\left( \frac{K_{t}^{I}}{K_{t}^{P}}\right) ^{\mu }\left( \frac{\varphi G_{t}^{H}}{ K_{t}^{P}}\right) ^{1-\mu }=\big (k_{t}^{I}\big )^{\mu }\big (\varphi \upsilon _{H}\tau \beta \big )^{1-\mu }\left( \frac{Y_{t}}{K_{t}^{P}}\right) ^{1-\mu }. \end{aligned}$$

(43)

This result can be substituted in (30) to give

$$\begin{aligned} h_{t+1}^{A}=(\varphi \upsilon _{H}\tau \beta )^{\nu }\big (h_{t}^{A}\big )^{\kappa }\big (k_{t}^{I}\big )^{\mu (1-\nu _{C})}\left( \frac{Y_{t}}{K_{t}^{P}}\right) ^{\nu }, \end{aligned}$$

(44)

where $\nu =(1-\nu _{C})(1-\mu )$.

Substituting for $Y_{t}/K_{t}^{P}$ from (9) and using (13) yields

$$\begin{aligned} h_{t+1}^{A}=\big [\varphi \upsilon _{H}\tau \beta \big (\varepsilon ^{W}\big )^{\beta }\big ]^{\nu }\big (h_{t}^{A}\big )^{\zeta _{1}}\big (k_{t}^{I}\big )^{\zeta _{2}}, \end{aligned}$$

(45)

where

$$\begin{aligned} \zeta _{1}&= \kappa +\nu \beta ,\\ \zeta _{2}&= \mu (1-\nu _{C})+\nu \alpha . \end{aligned}$$

Equations (42) and (45) form a first-order linear difference equation system in $\hat{h}_{t}^{A}=\ln h_{t}^{A}$ and $\hat{k}_{t}^{I}=\ln k_{t}^{I}$ which can be written as

$$\begin{aligned} \left[ \begin{array}{c} \hat{h}_{t+1}^{A} \\ \hat{k}_{t+1}^{I} \end{array} \right] =\left[ \begin{array}{c} a_{10} \\ a_{20} \end{array} \right] +\left[ \begin{array}{cc} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \end{array} \right] \left[ \begin{array}{c} \hat{h}_{t}^{A} \\ \hat{k}_{t}^{I} \end{array} \right] , \end{aligned}$$

(46)

where

$$\begin{aligned} a_{10}&= \ln \big [(\varphi \upsilon _{H}\tau \beta )^{\nu }\big (\varepsilon ^{W}\big )^{\nu \beta }\big ],\\ a_{20}&= \ln \left\{ \frac{\big [\beta \upsilon _{I}\tau \big (\varepsilon ^{W}\big )^{\beta }\big ]^{\varkappa }}{\beta \sigma (1-\tau )\big (\varepsilon ^{W}\big )^{\beta }}\right\} ,\\ a_{11}&= \zeta _{1}>0, \quad \quad \quad a_{12}=\zeta _{2}>0,\\ a_{21}&= -\beta (1-\varkappa )<0,\quad a_{22}=(1-\alpha )(1-\varkappa )>0. \end{aligned}$$

Setting $\Delta h_{t+1}^{A}=\Delta k_{t+1}^{I}=0$ in (42) and (45) yields the steady-state solutions

$$\begin{aligned} \tilde{k}^{I}&= \left\{ \frac{(\beta \upsilon _{I}\tau )^{\varkappa }\big (\varepsilon ^{W}\big )^{-\beta (1-\varkappa )}}{\beta \sigma (1-\tau )}\right\} ^{1/\Pi }\big (\tilde{h}^{A}\big )^{-\beta (1-\varkappa )/\Pi }, \end{aligned}$$

(47)

$$\begin{aligned} \tilde{k}^{I}&= \big [\varphi \upsilon _{H}\tau \beta \big (\varepsilon ^{W}\big )^{\beta }\big ]^{\nu /\zeta _{2}}\big (\tilde{h}^{A}\big )^{(1-\zeta _{1})/\zeta _{2}}, \end{aligned}$$

(48)

where $\Pi =1-(1-\alpha )(1-\varkappa )\in (0,1)$.

These equations define the steady-state relationships between $h_{t}^{A}$ and $k_{t}^{I}$. Equation (47) defines a concave curve with a negative slope depicted as $KK$ in Fig. 1, whereas Eq. (48) defines a curve called $HH$ in the figure. Under Assumption 3, $(1-\zeta _{1})/\zeta _{2}$ is positive; thus $HH$ is an upward-sloping curve. Given the definitions above, $(1-\zeta _{1})/\zeta _{2}\lessgtr 1$, which implies that $HH$ may be either convex or concave. In the case represented in Fig. 1, it is shown as concave, that is, $1-\zeta _{1}<\zeta _{2}$.³⁷

As can be inferred from Fig. 1, the system (42)–(45) has a unique (nontrivial) equilibrium, regardless of whether $HH$ is concave or convex. To examine its stability in the vicinity of that equilibrium, let $\mathbf {A}$ denote the matrix of coefficients in (46) and let $\det \mathbf {A}$ denote its determinant and tr$\mathbf {A}$ its trace. Let $\lambda _{j},\,j=1,2$ denote the eigenvalues of $\mathbf {A}$; the characteristic polynomial is thus $p(\lambda )=\lambda ^{2}-\lambda \,\mathrm{tr} \mathbf {A+}\det \mathbf {A}$. Thus, $p(1)=1-\mathrm{tr}\mathbf {A}+\det \mathbf {A}$, whereas $p(-1)=1+\mathrm{tr}\mathbf {A}+\det \mathbf {A}$.

From the above definitions,

$$\begin{aligned} \mathrm{tr}\mathbf {A}&= \zeta _{1}+(1-\alpha )(1-\varkappa )>0,\\ \det \mathbf {A}&= \zeta _{1}(1-\alpha )(1-\varkappa )+\zeta _{2}\beta (1-\varkappa )>0. \end{aligned}$$

Given the signs of tr$\mathbf {A}=\lambda _{1}+\lambda _{2}$ and $\det \mathbf {A}=\lambda _{1}\lambda _{2}$, it is clear that $p(-1)>0$. In addition,

$$\begin{aligned} p(1)=1-\zeta _{1}-(1-\alpha )(1-\varkappa )+\zeta _{1}(1-\alpha )(1-\varkappa )+\zeta _{2}\beta (1-\varkappa ), \end{aligned}$$

so that

$$\begin{aligned} p(1)=(1-\zeta _{1})\Pi +\zeta _{2}\beta (1-\varkappa ). \end{aligned}$$

Thus, with $\zeta _{1}<1$, the condition $p(1)>0$ always holds, and the eigenvalues are on the same side of both $1$ and $-1$.³⁸ Moreover, given that $\det \mathbf {A}>0$, the eigenvalues are of the same sign. With $\zeta _{1}<1$ and $a_{22}<1$, tr$\mathbf {A}$ cannot exceed $2$ (that is, tr$\mathbf {A}\in (-2,2)$). Consequently, given that tr$\mathbf {A}>0$, $\det \mathbf {A}>0$, the eigenvalues are not only less than unity in absolute terms but actually positive. The steady state is thus a sink (see Azariadis 1993, p. 65).

From (9) and (13),

$$\begin{aligned} Y_{t+1}=\big (\varepsilon ^{W}\big )^{\beta }\big (k_{t+1}^{I}\big )^{\alpha }\big (h_{t+1}^{A}\big )^{\beta }K_{t+1}^{P}, \end{aligned}$$

that is, using (39),

$$\begin{aligned} Y_{t+1}=\big (\varepsilon ^{W}\big )^{\beta }\big (k_{t+1}^{I}\big )^{\alpha }\big (h_{t+1}^{A}\big )^{\beta }\beta \sigma (1-\tau )Y_{t}. \end{aligned}$$

Thus, the steady-state growth rate of output is

$$\begin{aligned} 1+\gamma =\beta \sigma (1-\tau )\big (\varepsilon ^{W}\big )^{\beta }\big (\tilde{k} ^{I}\big )^{\alpha }\big (\tilde{h}^{A}\big )^{\beta }, \end{aligned}$$

where $\varepsilon ^{W}\$is given in (38), and $\tilde{h}^{A}$ and $\tilde{k}^{I}$ are the solutions of (47) and (48).